Бесплатный фрагмент - Трикутники

Передмова

Трикутник — одна з найпростіших геометричних фігур, а геометрія трикутника — найцікавіший розділ елементарної геометрії. Над її проблемами працювали найвідоміші вчені всіх часів: Піфагор, Евклід, Архімед, Менелай, Чева, Дезарг, Торрічеллі, Паскаль, Лейбніц, Ньютон, Ейлер, Лагранж, Жергон, Понселе та багато інших. Виявлені й доведені ними теореми про властивості трикутників — справжні перлини математики і людського мислення взагалі.

На початку XX ст. Ф. Клейн писав, що «геометрія трикутника набуває характеру прозорої систематичної дисципліни». Відтоді вона ще більш розрослася і збагатилася.

Трикутники вивчають і використовують майже в кожному класі загальноосвітньої школи, тільки — в мінімальному обсязі. А відомості з геометрії трикутника дають добрий матеріал для досліджень математикам-початківцям. Багато з них доступні навіть учням основної школи, тому їх можна використовувати і в навчанні геометрії.

«Геометрія трикутника… перетворилась у струнку й офіційно визнану наукову дисципліну. Тісні взаємини цієї дисципліни зі шкільною математикою, з одного боку, і з широким полем вищої геометрії — з другого, роблять її природним містком між першою і другою, це й пояснює великий інтерес до неї викладачів середньої школи». Так писав харківський методист Ю. М. Гайдук майже півстоліття тому, але й тепер інтерес до геометрії трикутника не слабне.

5 клас

Теорія

Трику́тник в евклідовій геометрії — геометрична фігура, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які їх сполучають.

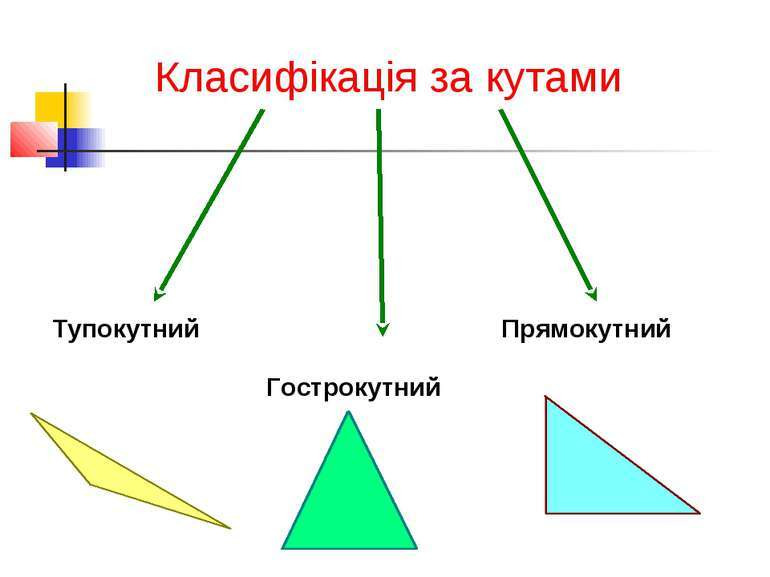
З усіх многокутників трикутники мають найменшу кількість сторін. Трикутники можна розрізняти за видом їхніх кутів.

Якщо всі кути трикутника гострі, то його називають гострокутним трикутником.

Якщо один із кутів трикутника прямий, то його називають прямокутним трикутником.

Якщо один із кутів трикутника тупий, то його називають тупокутним трикутником.

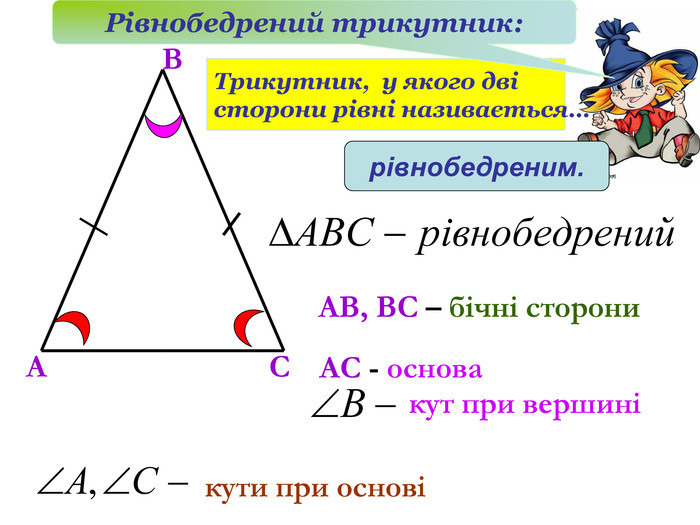
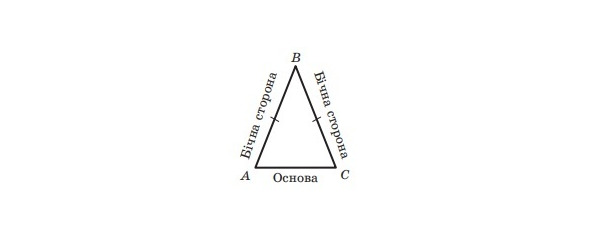
Якщо дві сторони трикутника рівні, то його називають рівнобедреним трикутником. На малюнку зображено рівнобедрений трикутник ABC, у якого AB = BC. На малюнку рівні сторони позначають однаковою кількістю штрихів. Рівні сторони AB і BC називають бічними сторонами, а сторону AC — основою рівнобедреного трикутника ABC.

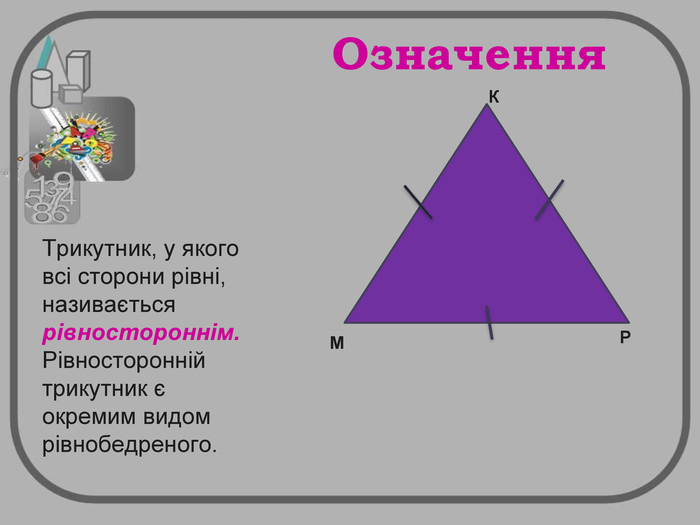
Якщо три сторони трикутника рівні, то його називають рівностороннім трикутником.

Якщо сторона рівностороннього трикутника дорівнює a, то його периметр P обчислюють за формулою P = 3a.

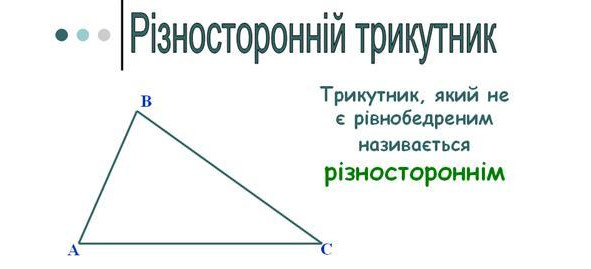
Якщо три сторони трикутника мають різні довжини, то його називають різностороннім трикутником.

Приклади розв’язування задач

1.Умова:

Знайдіть периметр трикутника із сторонами 16 см, 22 см

і 28 см.

Розв’язок:

Периметр-сума всіх сторін.

Отже, P=16+22+28=66 (см.)

Відповідь: 66 см.

2. Умова:

Одна сторона трикутника дорівнює 12 см, друга сторона

у 3 рази більша за першу, а третя на 8 см менша від другої.

Знайдіть периметр трикутника.

Розв’язок:

12 см. — одна сторона трикутника, за умовою задачі.

12*3 = 36 (см.) — друга сторона трикутника, яка у 3 рази більша за першу, за умовою задачі.

36 — 8 = 28 (см.) — третя сторона трикутника, яка більша за першу на 8 см., за умовою задачі.

Тоді: Р=12+36+28=76 (см.) — периметр трикутника.

Відповідь: 76 см.

3. Умова:

Периметр трикутника дорівнює 97 см, одна сторона — a см,

друга сторона — b см. Складіть вираз для знаходження третьої сторони. Обчисліть довжину третьої сторони, якщо a = 32, b = 26.

Розв’язок:

97 — (а + b) = 97 — (32 +26) = 39 (см) — довжина третьої сторони трикутника.

Відповідь: довжина третьої сторони трикутника 39 см.

Відео матеріали

Презентація

Тести

7 клас

Теорія

Розглянемо три точки A, B, C, які не лежать на одній прямій. Сполучимо їх відрізками AB, BC, CA. Утворена фігура обмежує частину площини, виділену на малюнку 1 зеленим кольором. Цю частину площини разом з відрізками AB, BC і CA називають трикутником.

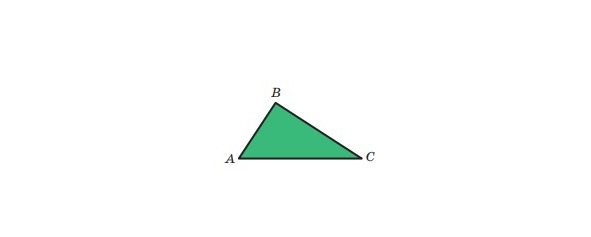
Точки A, B, C називають вершинами трикутника, а відрізки AB, BC, CA — сторонами трикутника.

Трикутник називають і позначають за його вершинами. Трикутник, зображений на малюнку 1, позначають так: ∆ ABC (читають: «трикутник ABC»), або ∆ BCA (читають: «трикутник BCA»), або ∆ ACB і т. д.

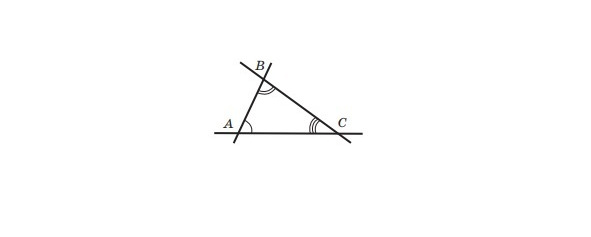
Кути BAC, ABC, BCA (малюнок 2) називають кутами трикутника ABC. У трикутнику ABC (малюнок 2), наприклад, кут B називають кутом, протилежним стороні AC, а кути A і C — кутами, прилеглими до сторони AC, сторону AC — стороною, протилежною куту B, сторони AB і AC — сторонами, прилеглими до кута A.

Означення. Периметром трикутника називають суму довжин усіх його сторін. Периметр позначають буквою P. Наприклад, для периметра трикутника MNK використовують позначення PMNK.

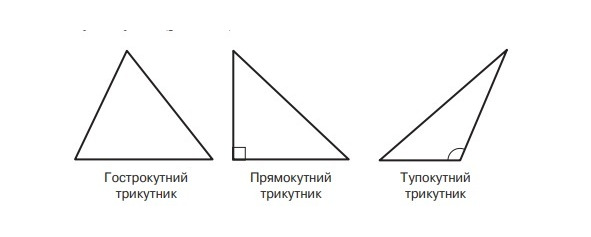
Означення. Трикутник називають гострокутним, якщо всі його кути гострі. Трикутник називають прямокутним, якщо один із його кутів прямий. Трикутник називають тупокутним, якщо один із його кутів тупий (малюнок 3).

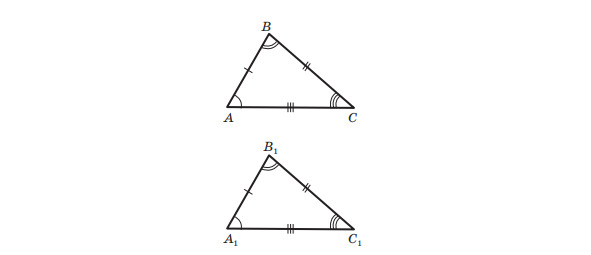
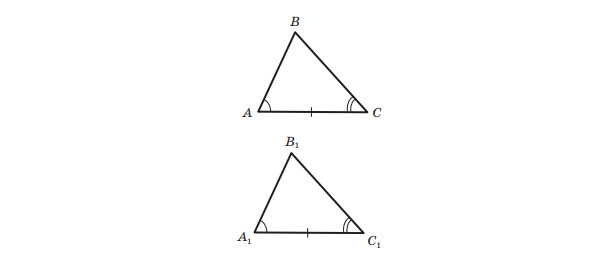
Означення. Два трикутники називають рівними, якщоїх можна сумістити накладанням.

На малюнку 4 зображено рівні трикутники ABC і A1B1C1. Записують: ∆ABC=∆A1B1C1. Ці трикутники можна сумістити так, що вершини A і A1, B і B1, C і C1 збігатимуться. Тоді можна записати: ∠A =∠A1, ∠B =∠B1, ∠C =∠C1, AB = A1B1, BC = B1C1, CA= C1A1.Ті сторони й ті кути, які суміщаються при накладанні рівних трикутників, називають відповідними сторонами й відповідними кутами. Так, малюнку 4 сторони AC і A1C1, кути A та A1 відповідні. Зазвичай на малюнках рівні сторони позначають однаковою кількістю рисочок, а рівні кути — однаковою кількістю дужок. Зауважимо, що в рівних трикутниках проти відповідних кутів лежать відповідні сторони, і навпаки, проти відповідних сторін лежать відповідні кути.

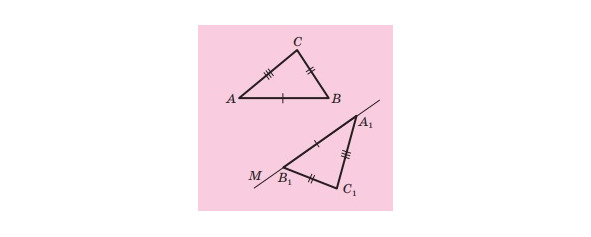
Основна властивість рівності трикутників.

Для даного трикутника ABC і даного променя А1М існує трикутник A1B1C1, який дорівнює трикутнику ABC, такий, що AB=A1B1, BC = B1C1, AC = A1C1 і сторона A1B1 належить променю А1М, а вершина C1 лежить у заданій півплощині відносно прямої А1М (малюнок 5).

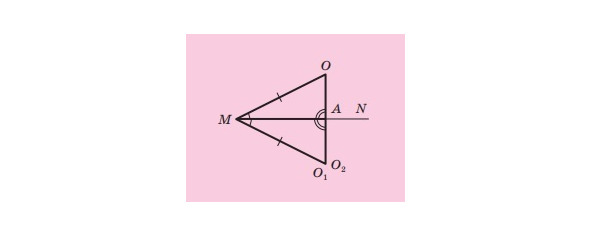
Теорема. Через точку, яка не належить даній прямій, можна провести пряму, перпендикулярну до даної, і до того ж тільки одну.

Доведення:

Розглянемо пряму MN і точку O, яка їй не належить. Спочатку покажемо, що через точку О можна провести пряму, перпендикулярну до прямої MN. Від променя MN відкладемо кут О1MN, що дорівнює куту ОMN. Нехай точка О1 є такою, що МО = МО1 (малюнок 6). Точку перетину прямих ОО1 і МN позначимо буквою А.

Від променя МА відкладемо трикутник О2МА, який дорівнює трикутнику О1МА. Кожний із кутів АМО1 і АМО2 дорівнює куту АМО, тому кути АМО1 і АМО2 рівні. Отже, точка О2 належить куту АМО1. Крім того, кожний із відрізків МО1 і МО2 дорівнює відрізку МО. Отже, точки О1 і О2 збігаються. Таким чином, трикутники АМО1 і АМО2 збігаються. Із рівності трикутників АМО і АМО1 випливає рівність кутів ОАМ і О1АМ. Оскільки ці кути суміжні, то кожний із них є прямим. Отже, пряма ОО1 перпендикулярна до прямої МN.

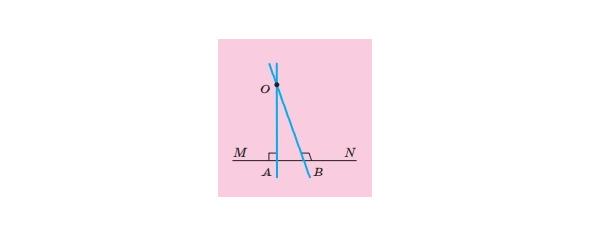
Припустимо, що через точку O проходять дві прямі OA і OB, перпендикулярні до прямої МN (малюнок 7).

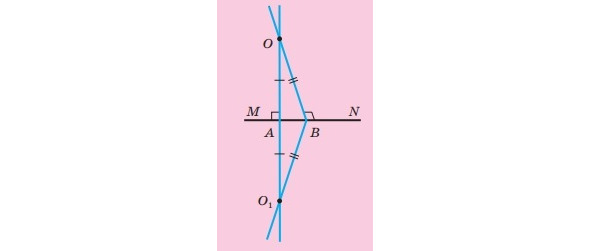
За основною властивістю рівності трикутників існує трикутник O1AB, що дорівнює трикутнику OAB (малюнок 8). Тоді ∠OAB = ∠O1AB = 90°. Звідси ∠OAO1 = 180°, а отже, точки O, A, O1 лежать на одній прямій. Аналогічно доводять, що точки O, B, O1 також лежать на одній прямій. Але тоді прямі OA і OB мають дві точки перетину — точки O і O1, а це суперечить теоремі. Отже, наше припущення є неправильним. Тоді через точку О проходить єдина пряма, перпендикулярна до прямої МN.

Теорему доведено.

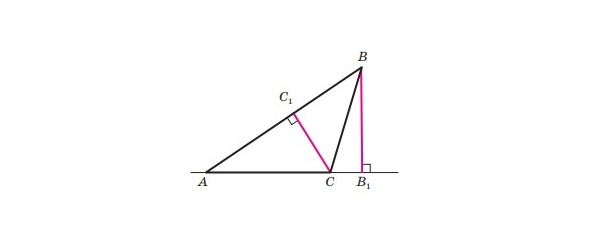
Означення. Перпендикуляр, опущений з вершини трикутника на пряму, яка містить протилежну сторону, називають висотою трикутника.

На малюнку 9 відрізки BB1 і CC1 — висоти трикутника ABC.

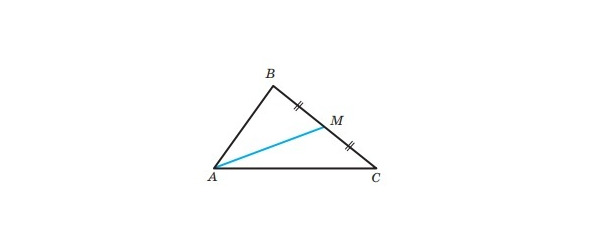
Означення. Відрізок, який сполучає вершину трикутника із серединою протилежної сторони, називають медіаною трикутника.

На малюнку 10 відрізок AM — медіана трикутника ABC.

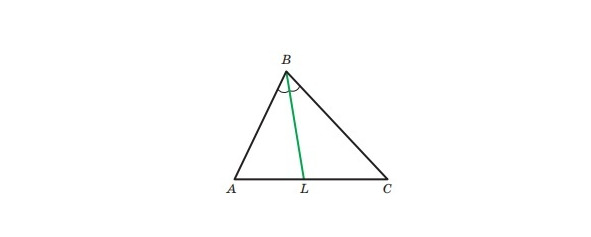
Означення. Відрізок бісектриси кута трикутника, який сполучає вершину трикутника з точкою протилежної сторони, називають бісектрисою трикутника.

На малюнку 11 відрізок BL — бісектриса трикутника ABC. Кожний трикутник має три висоти, три медіани й три бісектриси.

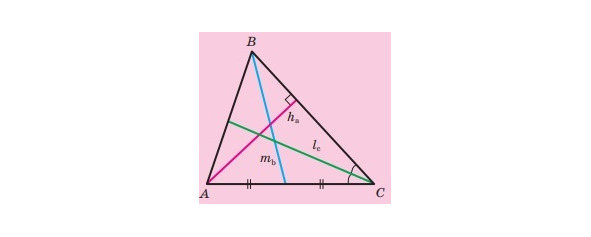
Часто довжини сторін трикутника, протилежних кутам A, B, C, позначають відповідно a, b, c. Довжини висот позначають ha, hb, hc, медіан — ma, mb, mc, бісектрис — la, lb, lc. Індекс показує, до якої сторони проведено відрізок (малюнок 12).

Перша та друга ознаки рівності трикутників.

Якщо для трикутників ABC і A1B1C1 виконуються шість умов: ∠A= ∠A1, ∠ B = ∠ B1, ∠ C= ∠ C1, AB = A1B1, BC = B1C1, CA = C1A1, то очевидно, що ці трикутники сумістяться при накладанні. Отже, вони рівні.

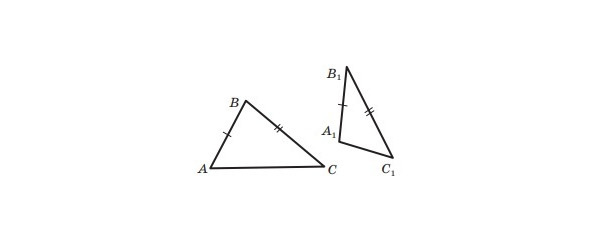
Спробуємо зменшити кількість умов. Наприклад, залишимо лише дві рівності: AB = A1B1 і BC = B1C1. У цьому разітрикутники ABC і A1B1C1 можуть виявитися нерівними (малюнок 13).

Як же скоротити список вимог до мінімуму, зберігаючи при цьому рівність трикутників? На це запитання відповідають теореми, які називають ознаками рівності трикутників.

Теорема 1. (перша ознака рівності трикутників: за двома сторонами та кутом між ними). Якщо дві сторони та кут між ними одного трикутника дорівнюють відповідно двом сторонам та куту між ними другого трикутника, то такі трикутники рівні.

Доведення:

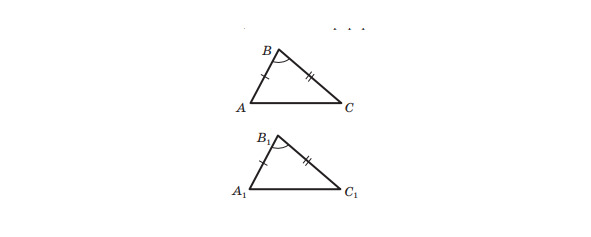
Розглянемо трикутники ABC і А1В1С1,у яких AB = A1B1, BC = B1C1, ∠B = ∠ B1 (малюнок 14). Доведемо, що ∆ ABC = ∆ A1B1C1. Накладемо трикутник ABC на трикутник A1B1C1 так, щоби промінь BA сумістився з променем B1A1, а промінь BC сумістився з променем B1C1. Це можна зробити, тому що за умовою ∠ B = ∠ B1. Оскільки за умовою BA = B1A1 і BC = B1C1, то при такому накладанні сторона BA суміститься зі стороною B1A1, а сторона BC — зі стороною B1С1. Отже, трикутники ABC і A1B1C1 повністю сумістяться, а тому вони рівні.

Теорему доведено.

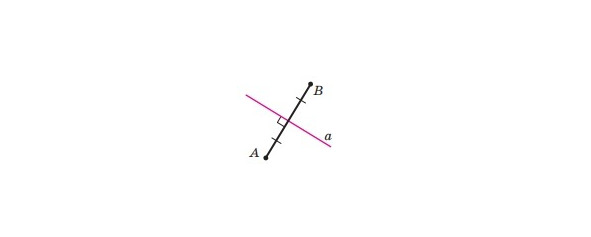
На малюнку 15 пряма a є серединним перпендикуляром відрізка AB. Зауважимо, що точки A і B рівновіддалені від прямої a. Звідси випливає теорема.

Теорема 2. Кожна точка серединного перпендикуляра відрізка рівновіддалена від кінців цього відрізка.

Доведення:

Нехай X — довільна точка серединногоперпендикуляра a відрізка AB. Треба довести, що XA = XB. Нехай точка M — середина відрізка AB. Якщо точка Xзбігається з точкою M (а це можливо, оскільки X — довільна точка прямої a), то XA = XB.

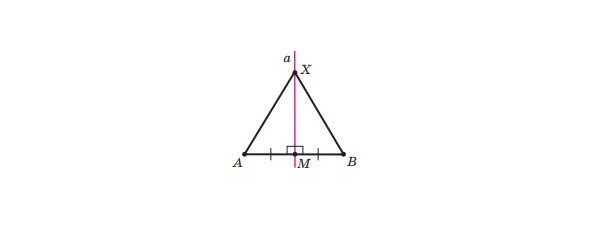
Якщо точки X і M не збігаються, то розглянемо трикутники AXM і BXM (малюнок 16). У цих трикутниках AM = MB, оскільки точка M — середина відрізка AB, сторона XM — спільна, ∠AMX = ∠BMX = 90°. Отже, трикутники AXM і BXM рівні за двома сторонами та кутом між ними, тобто за першою ознакою рівності трикутників. Тоді відрізки XA і XB рівні як відповідні сторони рівних трикутників.

Теорему доведено.

Теорема 3 (друга ознака рівності трикутників: за стороною та двома прилеглими до неї кутами). Якщо сторона та два прилеглих до неї кути одного трикутника дорівнюють відповідно стороні та двом прилеглим до неї кутам другого трикутника, то такі трикутники рівні.

Доведення:

Розглянемо трикутники ABC і A1B1C1, у яких AC = A1C1, ∠A = ∠ A1, ∠ C = ∠ C1 (малюнок 17). Доведемо, що ∆ ABC = ∆ A1B1C1. Накладемо трикутник ABC на трикутник A1B1C1 так, щоб точка A сумістилася з точкою A1, відрізок AC — з відрізком А1С1 (це можливо, тому що AC = A1C1) і точки B і B1 лежали в одній півплощині відносно прямої A1C1. Оскільки «A «A1 і «C «C1, то промінь AB суміститься з променем А1В1, а промінь CB — із променем C1B1. Тоді точка B — спільна точка променів AB і CB — суміститься з точкою В1 — спільною точкою променів A1B1 і C1B1. Отже, трикутники ABC і A1B1C1 повністю сумістяться, а тому вони рівні.

Теорему доведено.

Рівнобедрений трикутник та його властивості.

Означення. Трикутник, у якого дві сторони рівні, називають рівобереним.

На малюнку 18 зображено рівнобедрений трикутник ABC, у якого AB = ВC. Рівні сторони рівнобедреного трикутника називають бічними сторонами, а третю сторону — основою рівнобедреного трикутникика.

Вершиною рівнобедреного трикутника називають спільну точку його бічних сторін (точка B на малюнку 18). При цьому кут B називають кутом при вершині, а кути A і C — кутами при основі рівнобедреного трикутника.

Означення. Трикутник, у якого всі сторони рівні, називають рівностороннім.

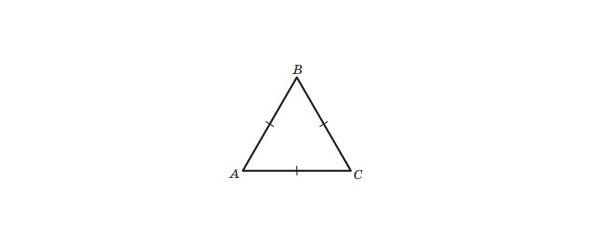
На малюнку 19 зображено рівносторонній трикутник ABC. Рівносторонній трикутник — окремий вид рівнобедреного трикутника.

Теорема4 (властивості рівнобедреного трикутник). У рівнобедреному трикутнику: 1) кути при основі рівні; 2) бісектриса трикутника, проведена до його основи, є медіаною та висотою трикутника.

Доведення:

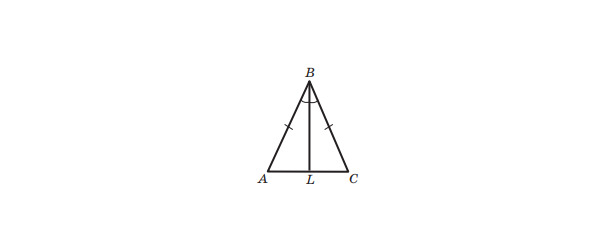
Розглянемо рівнобедрений трикутник ABC, у якому AB = ВC, відрізок BL — його бісектриса (малюнок 20). Треба довести, що ∠A =∠C, AL = LC, BL ⊥ AC. У трикутниках ABL і CBL сторона BL — спільна, ∠ABL = ∠CBL, оскільки за умовою BL — бісектриса кута ABC, сторони AB і BC рівні як бічні сторони рівнобедреного трикутника. Отже, △ ABL= △CBL за першою ознакою рівності трикутників. Звідси можна зробити такі висновки: 1) ∠A = ∠C; 2) AL = LC; 3) ∠ALB = ∠CLB. Оскільки відрізки AL і LC рівні, то відрізок BL — медіана трикутника ABC. Кути ALB і CLB суміжні, отже, ∠ALB+ ∠CLB =180. Ураховуючи, що ∠ALB = ∠CLB, отримуємо: ∠ALB = ∠CLB = 90°.Отже, відрізок BL — висота трикутника ABC.

Теорему доведено.

Із теореми 4 випливає, що:

1) у трикутнику проти рівних сторін лежать рівні кути;

2) у рівнобедреному трикутнику бісектриса, висота й медіана, проведені до його основи, збігаються;

3) у рівносторонньому трикутнику всі кути рівні;

4) у рівносторонньому трикутнику бісектриса, висота й медіана, проведені з однієї вершини, збігаються.

Означення. Якщо в трикутнику довжини всіх сторін різні, то такий трикутник називають різностороннім.

Ознаки рівнобедреного трикутника

У попередньому пункті ми розглянули властивості рівнобедреного трикутника. А як серед трикутників «розпізнавати» рівнобедрені? На це запитання відповідають такі теореми-ознаки.

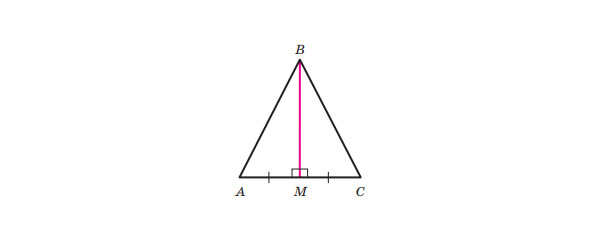
Теорема5. Якщо медіана трикутника є його висотою, то цей трикутник рівнобедрений.

Доведення:

Розглянемо трикутник ABC, у якому відрізок BM — медіана й висота. Треба довести, що AB = BC (малюнок 21).З умови теореми випливає, що пряма BM — серединний перпендикуляр відрізка AC. Тоді за властивістю серединного перпендикуляра AB = BC.

Теорему доведено.

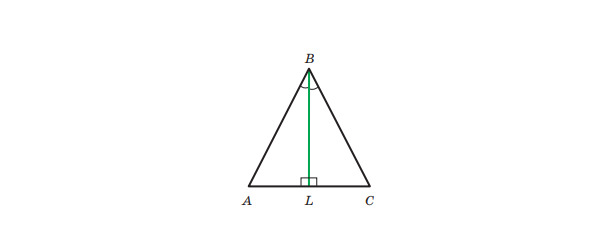
Теорема 6. Якщо бісектриса трикутника є його висотою, то цей трикутник рівнобедрений.

Доведення:

Розглянемо трикутник ABC, у якому відрізок BL — бісектриса й висота. Треба довести, що AB = BC (рис. 167).

У трикутниках ABL і CBL сторона BL — спільна; ∠ABL = ∠CBL (оскільки за умовою BL — бісектриса кута ABC), ∠ ALB= ∠CLB= 90 (оскільки за умовою відрізок BL — висота). Отже, трикутники ABL і CBL рівні за другою ознакою рівності трикутників. Тоді сторони AB і BC рівні як відповідні сторони рівних трикутників.

Теорему доведено

Теорема 7. Якщо в трикутнику два кути рівні, то цей трикутник рівнобедрений.

Доведення:

Розглянемо трикутник ABC, у якому «A «C. Треба довести, що AB = BC.