Бесплатный фрагмент - The use of accelerators and the phenomena of collisions of elementary particles with high-order energy to generate electrical energy. The «Electron» Project

Preface

Our world is immersed in a huge ocean of energy, we are flying in infinite space at an incomprehensible speed. Everything is spinning, moving — all the energy. We have a huge task ahead of us — to find ways to extract this energy. Then, extracting it from this inexhaustible source, humanity will move forward with giant strides!

Nikola Tesla

Energy has been important for all mankind since ancient times. Every day a person consumes more and more energy, and if earlier the main source of energy was fire, today its role is increasingly being performed by electric current. With the help of electricity, lamps are lit, computers work, books are printed, food is heated and cars are already driving. Electricity has entered into all corners of human life and is an essential resource.

For the first time, work on the generation of electric current began with experiments on the study of electromagnetic induction by Michael Faraday, but for a long time these works were not implemented in the face of industrial plants and installations. Initially, only steam engines were used to perform certain work by James Watt, and only after the invention of the armature winding of dynamoelectric machines by the Belgian Zenob Theophil Gram in 1871, it became possible to obtain electric current industrially.

Thus, the first power station was a hydroelectric power station, created in 1878 by an English engineer, Baron William Armstrong at his estate Cragside, in England. The generated electricity was used for lighting, heating, hot water supply and other household work.

But for the people and all mankind, electricity began to serve only 4 years later, in the winter of January 12, 1882, in London, when the world's first public coal-fired electric power station by Thomas Edison, built according to his own project, started working. Since then, mankind has been industrially using electric current, of course, a lot has already changed since then, the technologies of the famous inventor Nikola Tesla have been introduced to use alternators, as in power transmission systems, on the same basis of alternating current.

But also, in order to satisfy their needs, man has invented a number of methods and technologies for obtaining and generating electric current on a large scale. But are all these methods so safe and do they manage to fully perform their function?

To date, to generate electric current and meet the needs of mankind in this resource, technologies for generating electric energy from heat (steam pressure) are used, which is clearly expressed in the technologies of thermal power plants (thermal power plants), where by burning coal, natural gas and other combustible resources having some energy potential in their structure, they receive steam that creates sufficient pressure for the movement of steam generator turbines, which, using the phenomenon of electromagnetic induction, converts kinetic energy (energy of motion, in this case, the energy of rotation, turbines under the action of steam force), that is, the force of steam pressure into an electric current that is already transmitted through power lines (power lines) to consumers for further use.

Also, hydroelectric power plants (hydroelectric power plants), nuclear power plants (nuclear power plants), wind farms (wind farms), SPES (solar panel power plants) are used as sources of electric energy. Other technologies are also known, such as methods of obtaining current from lightning, waves and other natural forces, but they are not used on a large scale, for this reason it is enough to consider only the above types of power plants, with their own methods of generating large electrical energy.

The TPP technology was considered, if we stop at the HPP, then this power plant is based on generating an electric current from kinetic, and in the case of being at a high altitude, potential (energy that an object possesses, being at a certain height due to gravitational force or gravity, while potential energy is involved with a further transition to kinetic) energy water and rotation of the generator turbines at high speed and subsequent generation of electric current, also using the phenomenon of electromagnetic induction, on which the principles of all electric generators are based.

The next type of power plant, namely nuclear power plants, are stations whose principle is based on one of the most progressive and newest methods of generating electric energy, namely, on the basis of generating electric current from atomic energy, which is released after the decay of uranium—235 or uranium-238 nuclei, depending on the type of station after they are bombarded with thermal (having an energy that is numerically equal to the energy at normal temperature) by neutrons. Due to the fact that after each subsequent reaction, a maximum of 3, and more often 2 additional neutrons are released, a chain reaction occurs with the release of 200 MeV, with each reaction, with a rapid increase in the total energy of the body, which leads to an increase in temperature.

And at the same time, there comes a moment when there is enough energy to transfer it to water, which is irradiated and transfers heat to the second water circuit, through which the already circulating water rotates steam generators, while the temperature does not reach critical temperatures, due to the fact that the water is under pressure, which increases the levels of constant temperatures for this liquid.

Describing the wind farm, it is worth noting that the principle of electromagnetic induction is also preserved there and more than one generator is used, which rotate under the force of the wind, although they rotate with a lower frequency, respectively generating less power.

The final one, also becoming more popular and relevant every day, is the SPES. This type of station by the method of generating electric current is radically different from the others. This type of stations is based on the phenomenon of photoelectronic emission, which occurs when specially manufactured panels are irradiated with sunlight, the electric charge generated in this case is output and transferred already to the transmission lines.

But it is also worth noting that each type of power plants has significant disadvantages, of course not in its design, but in the effect exerted on nature and the environment. For example, thermal power plants [8] generate a huge amount of anhydride carbonate, which is released into the atmosphere and causes such an effect, which is referred to as global warming, which is a consequence of the so-called greenhouse effect.

We will describe all these problems for the following power plants:

hydroelectric power plants [9]:

· Disaster risk (difficult construction in case of earthquakes and other natural disasters);

· Danger of fish migration (whole species of various fish may die);

· Danger of nearby cities (in case of a problem with the plate within a radius of many kilometers, cities will be flooded).

NPP [10]:

· Uranium is a non-renewable resource;

· Cannot replace fossil fuels;

· Depends on fossil fuels;

· Uranium mining is harmful to the environment;

· Very persistent waste, decomposed for a long time;

· The danger of nuclear disasters;

· The presence of the effect of changing the planetary radioactive background;

· High explosion hazard;

· Difficulty of recovery, in the event of a disaster.

WES [11]:

· Presence of noise;

· High cost of buildings;

· Long payback period in case of implementation;

· Inconstancy and unregulated wind flow;

· Low energy efficiency.

SPES [12]:

· Lack of energy extraction at night;

· High energy storage costs;

· Relatively high price of solar cells;

· Daily and seasonal variability of solar radiation;

· Local climatic changes unfavorable for the use of solar energy;

· Difficulties with accumulation and concentration of energy;

· The daily energy flux density of solar radiation is low;

· Installation takes up large areas;

· High production and construction costs;

· Low generated power.

Analyzing the above facts, it becomes clear that a development is needed that can generate electric current with greater efficiency, on a larger scale, and also more safely than with the help of technologies used today. And if we consider all possible ways of obtaining electrical energy, then there is an explanation for why this study, which has been going on for more than 12 years, was so called — "Electron".

Initially, the search for a new source of electrical energy began back in 2010. The first stage of the study was to search for such a method in classical mechanisms. More than 500 different mechanisms were analyzed, but all of them were not effective until the first magnetic type of device was presented for the first time in 2016, which, using the force of magnetic repulsion, created vibrations that caused the output of 3—4 water jets, the potential energy of which was converted into electric current. But this version of the device was not strong enough and effective enough, and after an experimental test, a number of shortcomings were found, which caused the rejection of this model.

This was followed by 34 mechanisms, which distinguished themselves by following the first more successful version. But when they did not find their confirmation, it was necessary to abandon them. For 4 years, since 2014, the so-called «electric era» has been going on, when various mechanisms of an electric, magnetic and electromagnetic nature were investigated. And although mechanisms with electric generators, solar panels, transformers, diodes, transistors and many other elements have been developed, but, unfortunately, they have not found their confirmation. Then, starting in 2019, the «quantum era» began.

In March 2019, the first project with elementary particles was developed, and then the project changed its own name and adopted the name "Electron", since the idea was based on splitting an electron and conducting interactions with the creation of a special "structure" already with hypothetical components of the electron particle. Due to this, the components in the face of Umidon and Raanon particles were studied in detail. Then for the first time scientific articles on this topic were published: "Behavior of an electron in an atom", "Electron particle", "Electron features", "Linear Electron Accelerator in Power engineering" and many others. They also took part in the international event InnoWeek 2019.

But after some debate, it was found that this model, as well as the methods of its implementation, cannot be translated into reality. The next model was the technology of collision of two electron beams in the energy output, as it was assumed due to some anomaly that followed from the conclusions of the formulas. But there were problems, the solution of which was not found, as well as a detailed introduction with an explanation of this phenomenon. Therefore, it was necessary to move from this model to technologies for the use of nuclear reactions. At this stage, from the beginning of 2020, the "Nuclear Era" began, when hundreds and even thousands of nuclear reactions were investigated. The total number of studied nuclear reactions, which were analyzed at this stage from the beginning of 2021 to February 2021, is 1,062 reactions.

And thanks to the definition of nuclear reactions with a large energy yield, a whole complex of these interactions was created. And although the technology no longer had a relationship with the electron, but the name of the study has not changed to this day. And although more than 10 scientific articles were published, they were also described in 2 volumes of the work "Constructor of Worlds", as well as presented to several companies, such as Acwa Power in February and a number of energy companies in September 2021. But today this technology has been improved and has a more simplified look, which opens up a number of possibilities.

It is this technology that is described in this research, which is currently considered to have no analogues in the whole world. As can be seen from the history of this study, the path of this technology was not easy, and it is much better than its "brothers" and "predecessors", which demonstrates a lot of experience and a strong desire to achieve this goal for the whole of humanity, which gave strength to overcome a number of very different difficulties, and only a part of which it was described above when retelling the entire history of the study.

As a result, it can be concluded that nuclear reactions deserve more attention as the newest source of electrical energy on a huge scale. Of course, uranium reactions are already actively used today, thermonuclear reactions are also very popular, for which searches are still underway for their use for peaceful purposes.

But it is also possible to use completely new types of nuclear reactions with a larger yield and a larger cross section of the nuclear reaction. But first it is necessary to understand in more detail the concepts of nuclear reactions themselves. This work tells about the technology that will allow generating electric current with the specified parameters and data.

For a better understanding of the material being explained, as well as to create the convenience of describing the device, initially a special introductory course in the very topic of nuclear physics was prepared in the first section. But since this course is not aimed at covering all the material, only the necessary or important points from the entire course of nuclear physics and high-energy physics are indicated.

After the reader is intrigued by unexplained concepts about nuclear reactions and about the purpose of the entire study, the explanation begins with the very explanation of the stages of human cognition of the structure of matter. The first knowledge and thoughts of Aristotle, Herodotus, the great thinkers Avicenna, Biruni, Sir Newton and many others. And also describes the history of classification.

The sudden problem of radioactivity, even more intriguing to the reader, becomes an additional help, after which everything is led to the description of the atom. Then the models of the atom created and described by great scientists with their experimental confirmations are explained, after which the speech smoothly proceeds to the description of the atomic nucleus and many other particles.

And finally, one of the most intriguing moments comes, namely, the description of nuclear reactions, the derivation of formulas, calculations, models, and finally, the description of a variety of experiments that simply fascinate with their scales and designs. And when our dear reader is fully prepared for the research and analysis of the new technology with all its complexities, the second section begins.

There, a complete theoretical description is given, various assumptions and proofs are built that fully support the main idea and intent. And already in the following sections, the experimental representation is analyzed, as well as the whole picture of the implementation of this experiment in reality.

It is in this way that a full-fledged idea, a separate idea, is formed and rises right in front of the reader, which is of enormous importance for all mankind, ensuring the generation of electric energy on a huge scale, buildings will become easier and faster compared to other electric power stations, however, as well as the costs of their construction. At the same time, the possibility of providing electric current to the entire population will increase. The energy and information hunger will disappear, it will be possible not to be afraid of large losses in wires and to increase the transition to the transmission of electrical energy without wires, as Nikola Tesla predicted back in the 1900s.

The number of various experiments conducted in various research institutes, which are now waiting for the latest source of electrical energy, will increase. A person will be able to extend the time of his stay in space several times and may even take a swing at seemingly insane ideas about creating artificial atoms from electrical energy. At the same time, the number of various assumptions and riddles that will be reflected in the works of science fiction writers and writers will increase. The whole human world will sway and begin to move with leaps and bounds and a great future will come.

But in order to realize all this, you need to take the first step, namely, to enter into the depths of the Electron research.

Ibratjon Xatamovich Aliyev

Sharofutdinov Farroh Murodjonovich

Section 1. Theoretical calculations

Chapter 1. The History of Atomism

Everything consists of particles... things differ from each other by the particles they consist of, their order and location…

Democritus

The quantum world of elementary particles and the atomic nucleus is amazing in its beauty, structure and scale. And then this world will also be considered in all its difficulties. But initially it is necessary to understand the very essence of the first steps in the discovery of the atom, the very particle with which everything began. The first chapter is radically different from the rest of the chapters because it was created specifically not only for higher minds who are already operating with rather complex concepts, but also for the young generation just entering the path of this amazing science. Therefore, in this chapter everything is described as simply and elementary as possible. So, without further ado, the history of the greatest atomic science begins…

Since the most ancient times, people have been trying to determine the structure of our world, to understand what it consists of. Initially, all these questions were purely philosophical, for this reason there was such a thing as atomism, according to this theory, all substances, objects, bodies consisted of indivisible particles — atoms. This idea was widely supported in ancient times, first appearing in various parts of our planet from ancient India to ancient Greece and the Eastern world.

For example, in Ancient Greece atomism was also widely supported by Democritus of Abder, Leucippus and others. Opponents of the ideas of atomism could only claim that matter divides indefinitely. Democritus' teaching was also based on the idea that atoms are not only indivisible, but their number is infinite, they are not created, and they are eternal, and the properties of objects depend on atoms. A great contribution to the idea of atomism was also made by the philosopher Epicurus, and later by the poet Lucretius. But if everything was clear with the statement of the very concept of the atom, since the atom is translated from ancient Greek as "indivisible", that is, atoms could not be divided, then there were problems with their forms. For the first time, the idea of the shapes of the atom was put forward by Plato, assuming that atoms have the shapes of Platonic bodies or regular polyhedra like a cube, pyramid, tetrahedron, dodecahedron, octahedron and others, that is, polyhedra whose faces are equal to each other. Atomism deserved a lot of attention after active references to this idea by Aristotle himself, after which this idea began to spread around the world.

In the Eastern world, where outstanding thinkers and geniuses conducted their research and performed excellent research at the Mamun Academy, there were also separate opinions on the topic of atomism. Such outstanding scientists as Abu Rayhan Biruni, ibn Sina, Abu Nasr ibn Iraq, Mahmud Khujandi, Ahmad ibn Muhammad Khorezmi, Ahmad ibn Hamid Naisaburi and many others conducted their experiments at the Mamun Academy itself. Many of them are outstanding scientists, if Abu Ali ibn Husayn ibn Abdallah ibn Sina, also known as ibn Sina or Avicenna in Europe created the "Canon of Medical Science and is considered the father of medicine, then Abu Rayhan Biruni is an encyclopedic scientist who conducted research in physics, mathematics, astronomy, natural sciences, history, chronology, linguistics, indology, earth sciences, geography, philosophy, cartography, anthropology, astrology, chemistry, medicine, psychology, theology, pharmacology, history of religion and mineralogy. He is also considered the creator of the first globe, also the first person to measure the radius of the planet using trigonometric patterns, as well as the first who predicted the presence of the continent of America.

To date, the letters of Abu Rayhan Biruni and ibn Sina have been preserved, along with their works, where scientists also debated on the topic of the structure of matter. According to the assumption of scientists, the world consisted of particles smaller than an atom, it is there that one can see the assumptions that the atom particle, which was then considered indivisible, is divisible, but not to infinity. As for their shape, then it was assumed that the atoms have a spherical shape, since the sphere was considered a kind of ideal model, therefore, the atoms should be like this.

Time passes and a variety of discoveries are made. But about the ideas of Epicurus, however, as well as about atomism, they forget, because the ideas of Epicurus contradicted Christian teachings and the church forbade its use, as well as the assertion that atoms exist. But the French Catholic priest Pierre Gassendi revived the idea of atomism, somewhat changing the notion that atoms were created by God. And after the defense of atomism by the chemist Robert Boyle — an outstanding chemist and author of the work "The Skeptical Chemist", as well as by Sir Isaac Newton, who himself was revered as an outstanding scientist, atomism was adopted by the end of the 17th century.

Let us quote Sir Newton himself on this topic from a translation of his works: "It seems to me that from the very beginning God created matter in the form of solid, weighty, impenetrable, mobile particles and that he gave these particles such dimensions, such shape and such other properties and created them in such relative quantities as he needed it was for the purpose for which he created them. These primary particles are absolutely solid: they are immeasurably harder than the bodies that consist of them — so hard that they never wear out and do not break into pieces, because there is no such force that could divide into parts what God himself created inseparable and whole on the first day of creation. Precisely because the particles themselves remain intact and unchanged, they can form bodies that have the same nature and the same structure forever and ever; for if the particles were worn out or broken into pieces, the nature of things depending on them would change. Water and earth, made up of old, worn-out particles and fragments, would differ in structure and properties from water and earth, built from still whole particles at the beginning of creation. Therefore, in order for nature to be durable, all changes in the bodies of nature can consist only in a change of location, in the formation of new combinations and in the movements of these eternal particles… God could create particles of matter with different sizes and can have different shapes, place them at different distances from each other, endow them, perhaps, with different densities and different acting forces. In all this, at least, I do not see any contradictions… So, apparently, all bodies were built from the above-mentioned solid impenetrable particles, which were placed in space on the first day of creation at the direction of God's mind."

And if at that time Boyle's ideas were established that there are "simple bodies" (chemical elements) and "perfect mixtures" (chemical compounds) and any "perfect mixtures" can be divided into "simple bodies", then in the book "The New System of Chemical Philosophy" of 1808, John Dalton put forward the first idea about which of the substances, to which type is subject. But before that, Lavoisier proved that mass is constant, it does not disappear anywhere and does not appear out of nowhere. Davy also discovered a number of chemical elements: hydrogen, oxygen, nitrogen, carbon, sulfur, phosphorus, sodium and potassium were discovered by him in 1807, and in 1808 he also discovered such elements as calcium, strontium, barium and magnesium. Iron, zinc, copper, lead, silver, platinum, gold and mercury were also discovered.

Their discovery did not take much more work, since many of them were isolated from ores, isolated from chemical compounds. And already water, ammonia, carbon dioxide and many other compounds were already considered perfect mixtures. And now, Dalton, having everything he needed, decided to determine the atomic masses of all chemical elements, and also enter them all into tables, that is, classify them. So, Dalton introduced his own designation for each chemical element, for example, for hydrogen he introduced a circle icon with a dot in the center, for oxygen there was a sign — an ordinary circle, and for carbon there was a sign of a painted black circle, etc. To calculate the masses of atoms, Dalton conducted some experiments.

Initially, he evaporated water, and on the upper part he installed substances with which hydrogen reacted better, calculating changes in both the mass of the substance with which the interaction took place or from the volume of steam, Dalton could determine which part of the water consists of hydrogen and which of oxygen. Thus, having determined that 1/8 of the total mass of water consists of hydrogen, and 7/8 of oxygen, Dalton decided that oxygen is heavier than hydrogen and assigned a mass equal to 1 to hydrogen and 7 to oxygen. The same analysis of ammonia showed 1 for hydrogen and 5 for nitrogen. After analyzing it in this way, Dalton compiled his own table of chemical elements.

Needless to say, although this was the first step on the path of knowledge, all these statements were not true. But it lasted for quite a long time and various assumptions were based on it. One of these hypotheses was published in the journal "Philosophical Annals" by the London physician William Prout and was devoted to the idea that all atoms consist of hydrogen. But of course, this hypothesis was not true like many other assumptions of that time.

And if then, the atomic unit of mass was taken as the mass of a hydrogen atom, then today the exact unit is considered to be 1/12 of the mass of a carbon atom and is named as an A. E. M. or atomic unit of mass. And chemical elements today are usually designated from the first two or one letter of their name in Latin, for example, hydrogen is designated as H due to the name Hydrogenium («Generating water» in Latin), Nitrogen — N or Nitrogenium — «Giving birth to saltpeter», iron — Fe or Ferrum, copper — Cu — Cuprum, carbon — C — Carboneum. This system was adopted on September 3, 1860 after the Italian chemist Stanislao Cannizzaro at the International Congress in Karlsruhe proposed this method in his speech.

After that, it was customary to record chemical compounds using these symbols, and the number of atoms was indicated in the lower right corner, so for example, the compound of carbon and hydrogen (water) is written as H2O, ammonia — NH3, sulfuric acid H2SO4, etc. This method is very convenient because it creates opportunities for using symbolic notation and not there is no need to write down all the symbols several times, for example, for a cane sugar molecule — C6H12O6 (6 carbon atoms, 12 hydrogen atoms and 6 oxygen atoms). Instead of CCCCCCHHHHHHHHHHHOOOOOO, you can easily and simply write C6H12O6.

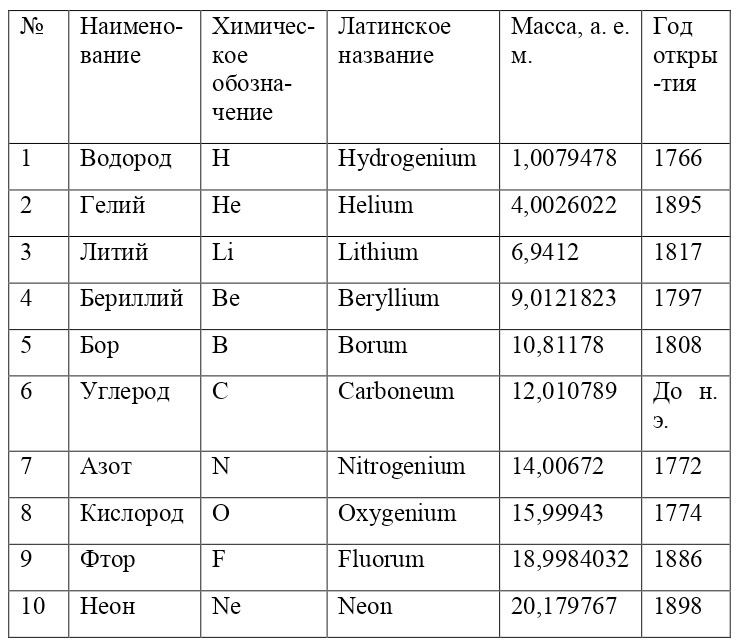
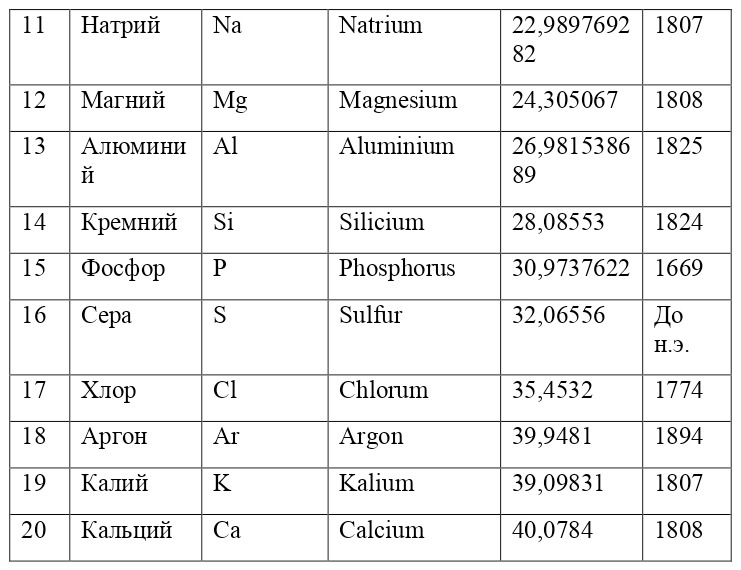
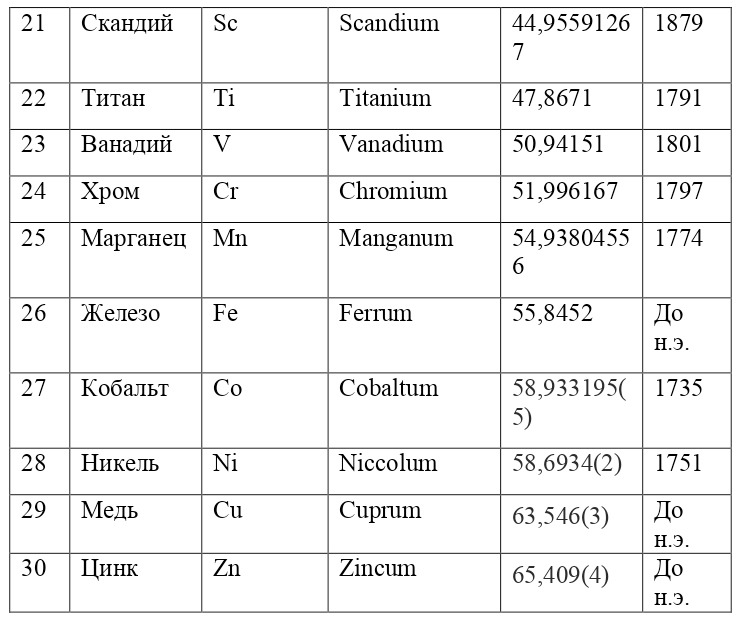
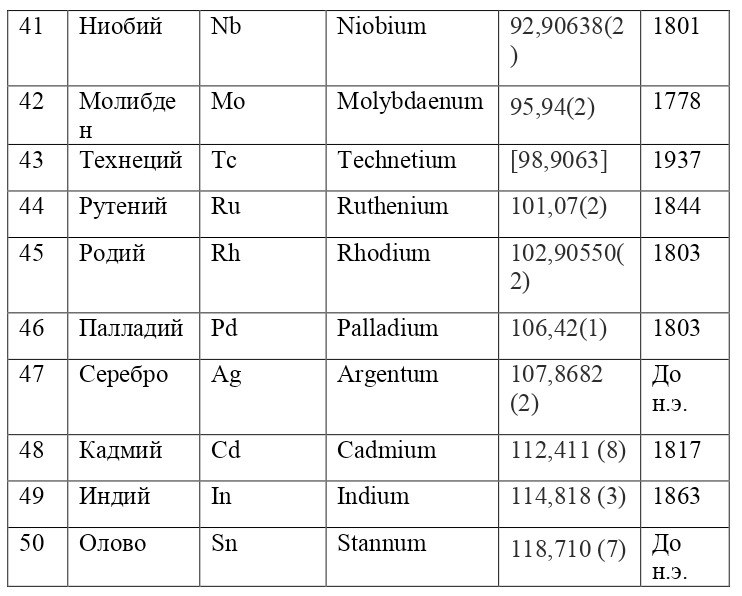
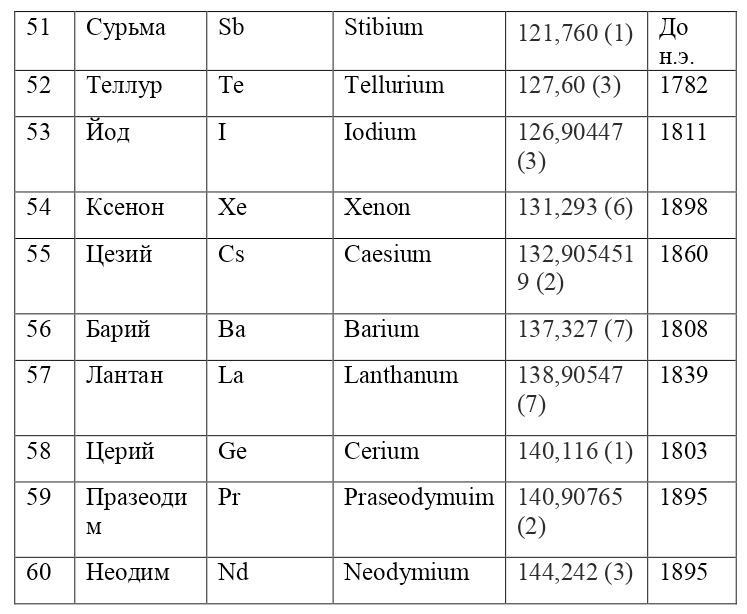
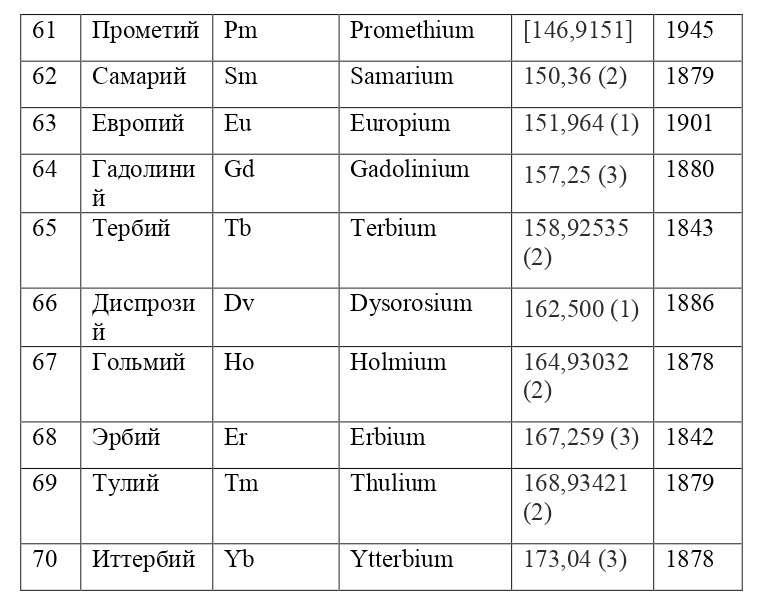
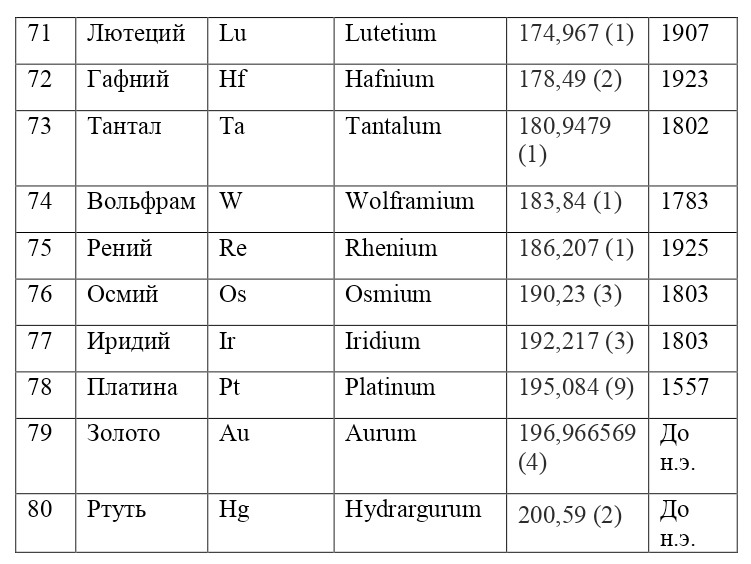
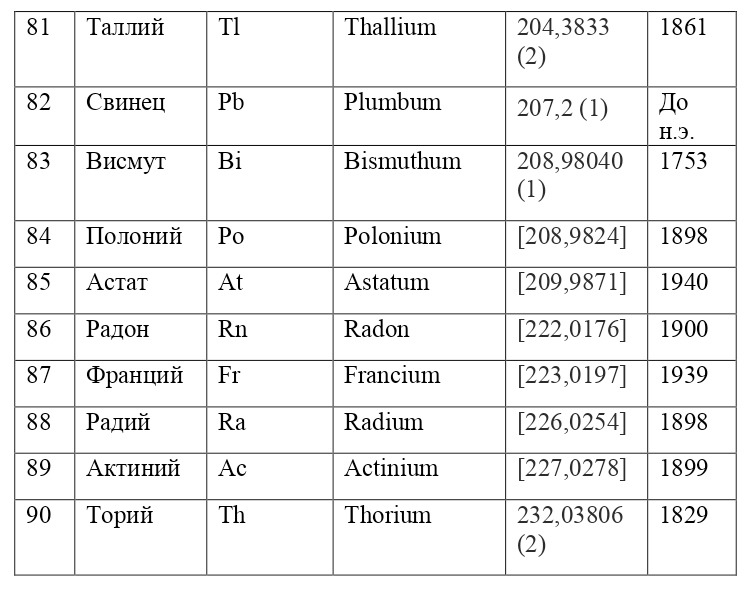
If everything is already clear with the notation, then there remains one very interesting consequence. Taking into account the fact that 1 atomic unit of mass is equal to 1/12 of a carbon atom, this makes it possible to calculate the masses of all chemical elements using compounds with carbon. For a better explanation, let’s give an example. Suppose there is a certain compound of carbon and hydrogen, if you act on it with an electric current or heat it, then it is possible, if it is solid, to melt, if the liquid is evaporated and to obtain a finite volume of carbon and hydrogen. From the ratio of their masses and volumes, it is possible to determine how many hydrogen atoms account for one carbon atom, and already from the ratio of their masses, it is possible to calculate the mass of hydrogen. So if we divide the methane compound into carbon and hydrogen, we get 4 times more hydrogen than carbon in volume, so we can conclude that for 1 carbon atom, there are 4 hydrogen atoms and the CH4 compound is obtained. And as for the masses, in this ratio it turns out that the mass of 1 hydrogen atom is almost 1/12 of the mass of a carbon atom or 1.00811 am. Exactly the same method can be used to determine the masses for all other atoms (Table 1.1).

But what exactly is this value equal to 1 A. E. M.? If you answer this question, you can find the masses of all other types of atoms, at the same time prove their reality. But none of the atoms, even the largest of them, can be seen in any microscope at that time. The situation is saved by the discovery made in 1828 by the English botanist Robert Brown. When a new microscope was brought to Robert Brown, he left it in the garden, and in the morning, dew drops formed on the "table" of the microscope, and Brown himself forgot to wipe them and automatically looked into the microscope. What was his surprise when he saw that the pollen particles in the dew drop were randomly moving. The particles are not alive and cannot move by themselves. It just couldn't be. But then, when this movement was recorded, some assumptions and hypotheses appeared to explain this phenomenon.

Perhaps this movement was explained by the fact that there are flows in the drop itself due to pressure and temperature differences, such as, for example, the movement of dust particles in the air. After all, if microscopic objects have such a movement, then it must also be in particles with a large size, like dust particles. After all, the movement of dust particles is explained precisely by air flows. But this idea was not confirmed, because the particles did not move in the same direction. After all, in the flow or flow of a jet of air, water or other medium, particles should move only in one direction, and the movement of microscopic particles in Brownian motion does not depend on each other.

In that case, perhaps this movement is the result of the environment? From external sounds, table shakes and other objects? This statement has already been refuted by the French physicist Gui. After conducting a series of experiments, he compared the chaotic Brownian motion with the movement in a remote basement in the village with the movement in the middle of a noisy street. The movements, of course, affected, but they affected only the entire drop as a whole, and not the Brownian motion of the particles itself. Moreover, there was the same movement in gases as in liquids, a striking example of such a movement is the movement of coal particles in tobacco smoke. For a visual example, you can compare two pictures. The way tobacco smoke forms and spreads in the air and the picture in the water, after a drop of paint or dye is dropped into it.

The explanation for all this is given by Carbonel, it is he who explains that the particles fall under the tremors from all sides, which causes their chaotic movement. And the smaller the particles, the more active their movement becomes, since the shocks throw them away more and more, and if the bodies are large, then the number of shocks from all sides somehow becomes almost equal, so furniture, buildings and people themselves do not vibrate by themselves and Brownian motion is not observed. It also turns out that as much as the temperature is higher, so is the velocity of these particles.

This picture becomes even clearer when Richard Sigmondi managed to invent his ultramicroscope, on the basis of which even smaller particles could already be seen. And their movement was no longer a simple movement, it was flickering, jumping and splashing, as Sigmondi himself would describe. But in order to better see this picture, the Svedberg method helped, which reduced the time of the passage of light into the microscope, thanks to which it was possible to fix exactly the specified moment, that is, it was possible to photograph this movement. And with a decrease in the time interval, doing less and less, it became possible to reach the moment when the particles in the photo simply froze in place.

And finally, the year 1908 comes, when it was finally established that atoms exist, have mass and are the basic units of matter, and combining with each other form molecules — particles of any complex compound, be it water, acid, the human body, etc.

So, Jean Perrin, a French physicist, decides to study atoms and finds a very amazing way to do it. He takes a drop of gummigut, pieces of rubber resin or yellow paint, if you like. By rubbing this piece in water like a bar of soap, he got yellowish water. But when he took a drop and examined it with a microscope, it turned out that the gummigut was not completely gone, but simply divided into thousands and thousands of small particles of different sizes. Perrin decided that if they are of different sizes and all these are gummigut particles, then they have different masses, therefore, they can be separated using a centrifuge. That is, if you rotate this liquid, then the heavier particles will logically separate to the wall, and the lighter ones will remain.

And with increasing speed, the force increases not twice, but as many times as the speed increased, due to the second degree in the centripetal acceleration formula. Consequently, Mr. Perrin could easily claim that he could separate heavy particles from light particles by strong rotation and he used a centrifuge for this, the same device that rotated with a certain frequency without spilling all the liquid. Perrin used a centrifuge, which thus rotated 2500 times per minute. And even then, only in a small part of the center, places with homogeneous particles were formed, and the rest flew to the edges. Therefore, Mr. Perrin had to use the centrifuge like this several times. Even taking into account the fact that this centrifugal force, even at a radius of 15 cm, already exceeded the force of gravity (the force of gravity of the Earth) by 1,000 times. What can be seen, given that gravity is determined by the product (multiplication) of mass by the acceleration of the fall of any object g, which is the same for all objects and is equal to 9.81 m/ s2 (meters per second squared). And based on the fact that 2500 revolutions per minute are performed, it can be calculated that the angular acceleration according to (1.1).

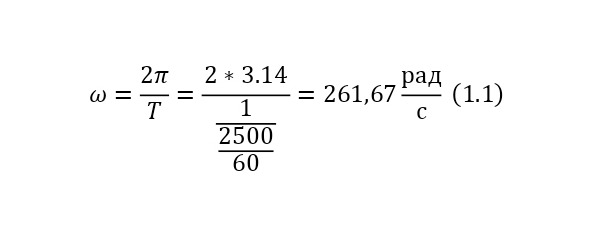
It remains only to calculate the ratio and get the result (1.2).

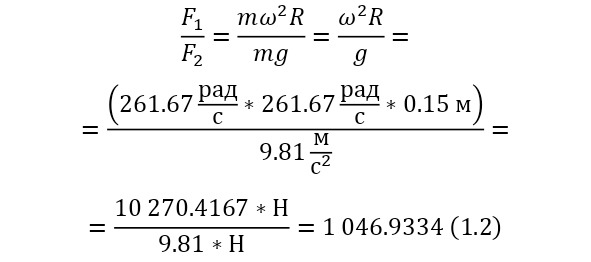
The resulting number is indeed more than 1,000, that is, the force at a distance of only 15 cm is already greater than the force of attraction of the entire planet by 1,046.9 times. Thus, in the end, Perrin managed to obtain water only with the specified particle diameters — 0.5 (5 out of 10 parts), 0.46, 0.37, 0.21 and 0.14 microns (1 thousandth of a millimeter or 10-6 m, which corresponds to a division of 1/1000000). And finally, having obtained such liquids only with a certain type of gummigut particles (such liquids are called emulsions), Perrin decided to experiment and observe them in a microscope. Watching them, turning the entire cuvette on its side, Perrin noticed that these particles decrease with increasing height. If at first they filled the entire liquid evenly or randomly, then they decreased with height, just as the air in the upper layers of the atmosphere decreases. And that was already a thought! If we compare this with the decrease in air at high altitudes, then we can establish a pattern. But in order to check it, Perrin decided to count these grains at each height.

Alas, it was not possible to photograph them, because the photos were not too clear due to the small size of less than 0.5 microns, and Perrin measured the number of gummigut particles several times at different heights, since the particles were moving, it was not possible to accurately count, so Perrin had to count several times even at the same height, and then say the average number. So at one time, he carried out the calculation at a height of 5, 35, 65 and 95 microns. And it turned out that the number of particles at a height of 35 microns was equal to almost half of the number of particles at a height of 5 microns, and at a height of 65 — half of 35, etc. And this already perfectly fell under the law of reducing atmospheric pressure (the force of oxygen pressure on our planet) with an altitude that was determined by Blaise Pascal, the famous French scientist, back in the 17th century. He measured the amount of oxygen using the Torricelli barometer, a pressure measuring device, the principle of which is that at normal air pressure from above, the mercury in the tube is at a certain height, when the pressure becomes less, the mercury can rise, and if the pressure increases, then vice versa — decreases, if there is no pressure, like gravity, it is a kind of weightlessness. Having calculated the difference in the layers of the atmosphere, Pascal even then determined that oxygen decreases with increasing altitude for every 5 km. But why is there a 2-fold decrease in gummigut particles only from 5 to 35, and in the atmosphere from 5 to 10, even if we do not take into account the scale?

And it's all about the particles, because there is oxygen in the atmosphere, and here the gummigut particles are so large that they can be seen in a microscope, their diameter is 0.21 microns. The law also changes for nitrogen, carbon dioxide, etc. due to the difference in the masses of the molecules. And if we consider the e4tu emulsion as a small atmosphere, then it is already possible to calculate the real mass of the atom! It is not so difficult to make this calculation, the height at which the oxygen density becomes 2 times less is 5 km, and for gummigut — 30 microns. And 5 km is 165,000,000 times larger than 30 microns, therefore, 1 such gummigut ball with a diameter of 0.21 microns is 165,000,000 times larger than an air molecule. And it's easier to calculate the mass of this gummigut ball.

The ratio of the mass of 1 cubic meter of gummigut (in the volume of a cube with dimensions of 1 meter wide, 1 meter high and 1 meter long) to its mass is the same as that of this gummigut ball and is equal to 1,000 kg/m3 (kilograms per cubic meter) or 103 kg/m3 (10 in a cube). And the volume of the sphere for the gummigut ball is also simple. After all, in order to calculate the volume of the sphere, it is necessary to circle the circle in space, that is, multiply by its area, the area of the second circle, and then it will turn out and at the same time subtract the part of the circle where such a «revolution» went 2 times. As a result, a formula is derived similar to the formula for the area of the circle (1.3).

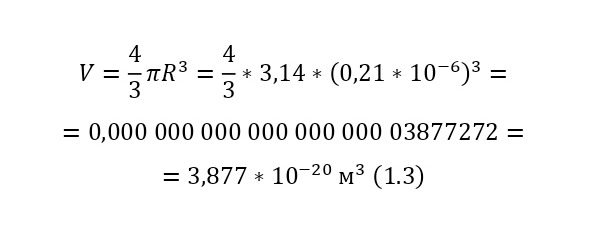
This volume corresponds to the mass, taking into account the force of Archimedes, that is, the force that pushes out of the water, since the gummigut particles are in the water, and not in the air, is about 10-14 grams. And if this grain is 165 million times larger than the oxygen molecule, therefore, the mass of the oxygen atom is 5.33 * 10-23 grams. And this is already, as can be learned from comparisons of the masses of hydrogen and oxygen (taking into account that there are 2 atoms in the oxygen molecule, since it is a gas) 32 times more than the mass of hydrogen, therefore, the mass of the hydrogen atom is 1,674 * 10-27 kg, that is, 1 gram of hydrogen already contains 597,371,565,113,500 597 371 565 114 hydrogen atoms! And so, it was already possible to compare the mass of the atom with A. E. M., having obtained that the mass of the hydrogen atom is 1.007825 A. E. M. It was in this way that Perrin was able to do the seemingly impossible — to weigh atoms and molecules, and now atoms and molecules were not a fairy tale, but a real science with precise calculations, formulas and instructions!

And even Oswald, an ardent opponent of the atomistic theory, wrote in the preface to his chemistry course: "Now I am convinced that recently we have received experimental proof of the discontinuous, or granular, structure of matter — proof that the atomistic hypothesis has been searching in vain for hundreds and thousands of years. The coincidence of Brownian motion with the requirements of this hypothesis gives the right to the most cautious scientist to talk about experimental proof of the atomistic theory of matter. The atomistic hypothesis has thus become a scientific, well-grounded theory."

And finally, one could safely say that everything in this universe, from planets and stars, to you and me, to everything that the eye sees, consists of atoms, but how true was this statement? And perhaps scientists had to find other particles…

Images for Chapter 1

Chapter 2. Inside the atom and the features of the nucleus

The atom was considered indivisible for a long time, its very name means "indivisible", but over time, I still had to agree with the fact that the atom is divisible and has a structure, despite the fact that a lot of time has passed. The description of the further stages of the development of the physics of the atomic nucleus and elementary particles closely borders on various mathematical operations, detailed descriptions of which will no longer be given, as well as many simplifications to general theories, which would greatly increase the amount of information, and some "basics" have already been described in the previous introductory chapter. In the same chapter, the phenomena of radioactivity will be described using analysis using a complete mathematical apparatus.

The world of elementary particles, micro-objects and quanta is amazing in its structure, way of existence and laws. Knowing the structure of matter, one inevitably has to accept the fact that the structure of any matter in the vicinity itself is a separate world, as already mentioned. Today, the theory of atomism is already widely known, which believed that everything in the world consists of the smallest particles — atoms. And if for the first time these ideas began since the time of Leucippus, Plato, Aristotle and many other scientists of antiquity, in whose time these thoughts mostly did not go beyond philosophical conclusions. However, as in the days of such great scientists as Abu Rayhan Biruni, Abu Ali ibn Sina, Al-Khorezmi, Ahmad Al-Khorezmi and other scientists of the East.

So there was even a time when atomism was even banned. And finally, when Sir Isaac Newton himself, along with other scientists, defended this grandiose idea, it began to be recognized and active research in this area began. But for a complete victory and proof of the reality of the existence of atoms, it was necessary to present some experimental evidence. Many scientists like John Dalton, Dmitry Ivanovich Mendeleev, Jean Perrin and many others tried to conduct this experiment, until finally Jean Perrin conducted his experiment with gummigut emulsion. By drawing an analogy of the change in the number of gummigut particles with the change in atmospheric pressure in height, Perrin was able to determine the weight of an atom for the first time.

And after the atom was fully recognized as an existing particle, work began to determine its structure. And now, after a series of studies and experimental confirmations by such brilliant experimental scientists and theorists as John Thompson, Ernest Rutherford, Niels Bohr and many others, the structure of the atom has been determined. And today it is proved not only with the help of indirect experiments, but also with the help of direct experimental evidence, a vivid example of which is the presence of a real photograph of an atom today, that the atom has a clear and clear structure.

But how can we come to this structure? It is worth dwelling on this issue in a little more detail. As you know, all objects are electrified, exchange charges, but where are they located? If all bodies have charges, including dielectrics (albeit small), therefore, charges are present in the structure of matter. Matter, as has already been proven, consists of molecules, and those of atoms, therefore, charges are inside atoms.

And the story of the discovery of the structure of the atom begins in 1897, when Joseph John Thompson discovered electrons while studying electric current in gases. That is, when a current was passed in a tube in which there were two electrodes — the cathode and the anode, the cathode emitted some rays, the so-called «cathode rays», the honor of accurately determining the type of these rays belongs to Mr. Thompson, who, by deflecting them in a magnetic field, as well as accelerating them in an electric field, established that this nothing else but some particles emitted by the cathode, with a negative electric charge, which is why they were called electrons.

And subsequent studies have led to the conclusion that electrons are part of an atom and when they fly out under the influence of an electric field, this leads to the transformation of an atom into an ion. But an ordinary atom is electrically neutral, therefore, in order to balance this charge, there must be a part with a positive charge in the atom. That is, an atom consists of charges that interact in some way. How does this interaction appear and is this interaction an explanation of the behavior of atoms in chemical reactions, in reactions with absorption and emission of light with certain wavelengths. After all, atoms may well be light sources, the same discharged gas emits light with certain spectra, at strict wavelengths, and how is this explained with the help of these interactions?

To explain this, in 1902, Mr. William Thompson, better known as Lord Kelvin, proposed his model of the structure of the atom, and already John Thompson studied it in more detail, so this model is known as the Thompson model. This model was popular until 1904 and is better known as the «raisin pudding model». According to this model, the atom consists entirely of positive matter, and electrons are inside it, moving freely. And with the help of this model, it was quite possible to describe some of the results.

For example, you can describe a hydrogen atom. If we imagine a hydrogen atom in such a model, then the electron will «float» in a positive charge, but it will be pulled to the center of this positive «drop», due to the force of electrostatic equilibrium. If we assume that the electron departs from the center by a certain radius smaller than the radius of the atom itself, then it will be attracted by the mental sphere formed by this radius. But since it is charged uniformly, it can be concentrated in the center and simply written using the Coulomb formula (2.1).

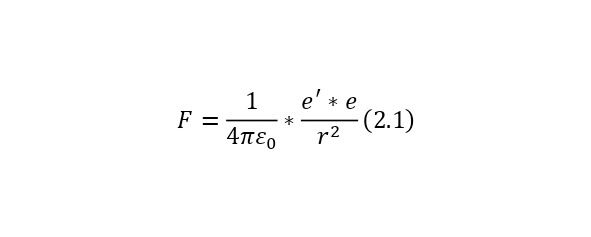
And to determine the charge of an imaginary sphere formed inside a common large charge, you can use the ratio of this imaginary sphere to the entire sphere, and since the charge of the common sphere is already known and equal to the charge of the electron so that the atom is neutral, then the expression (2.2) is obtained, where the charge of the imaginary sphere is derived.

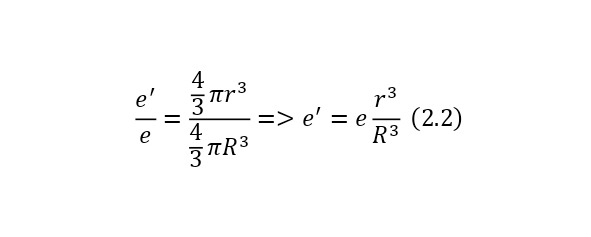
And if we already substitute this value for the Coulomb force, we get (2.3), a rather interesting expression that is directly proportional to the distance by which the electron moves away from the center.

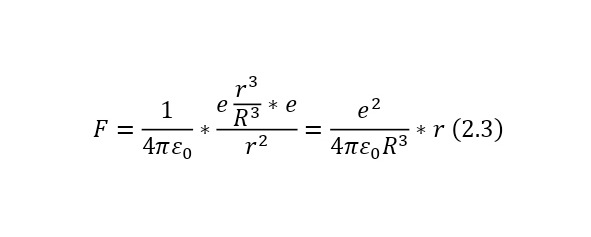
Also, for further convenience, we can introduce here the notion that the coefficient outside the radius of the imaginary sphere is the vibrational stiffness (2.4), and if we write with this stiffness not the Coulomb force formula itself, but its projection onto the radius of the imaginary sphere, then we get the expression (2.5), and negative, due to the fact that the vector the forces and the distance itself (the direction of the electron) are opposite.

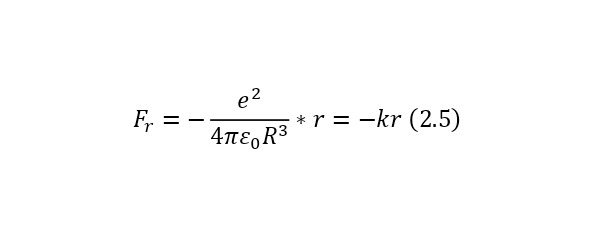
And now, if we assume that the electron oscillates in this way, then it resembles the construction of an oscillator or, more precisely, a mathematical pendulum with its rigidity and frequency determined by (2.6).

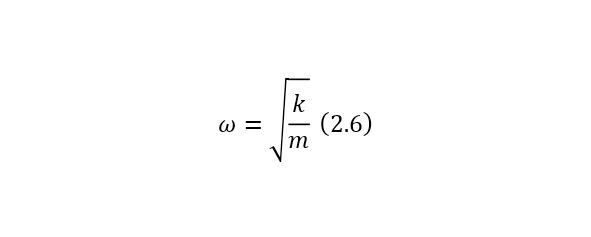
And if we substitute the necessary rigidity for (2.6), and take the mass of the electron as the mass, then the frequency will have the order of optical waves. That is, the atom glows in the visible region and even the glow effect can be explained using the Thompson model, but alas, another problem has arisen here. Even if we assume that the hydrogen atom glows, then according to this model it glows only with 1 frequency, when in reality it emits light with 4 frequencies. So it was proved that the Thompson model was not correct and it was necessary to create new models.

The next model is Ernest Rutherford's 1908-1910 model, which irradiated metal plates of thin gold foil with radioactive radiation, or more precisely with special alpha particles. At the same time, if you remove the plate on a circular screen (a phosphor that glowed), a point appeared, and when the plate was placed, this point scattered to form a spot, but in addition, some of these rays were reflected more than 90 degrees (right angle). And if we assume that the atom consists as the Thompsons were supposed to, then because of such a simply huge "smeared" positive charge on the size of the atom, the deviation should not have exceeded hundredths of a degree, and here there was a deviation of almost 180 degrees.

Then Rutherford suggested that in order to satisfy the results of the experiment, it should be assumed that the positive charge is strongly concentrated in a small area, and all the remaining space is practically empty, so the particles were only slightly scattered under the influence of an electric field or bumped into electrons that simply revolved around the atomic nucleus. This is how Rutherford first created a planetary model of an atom, according to which there is a single nucleus inside, and electrons already rotate around it in their orbits. However, there was still a lot to prove, for example, why did the electrons not fall to the atom, spending their energy on rotation, radiating energy at the same time?

But there was an answer to this question, thanks to Rutherford’s colleague Niels Bohr, who created the model of the hydrogen atom of Bohr, some postulates were accepted according to his model. Namely, the statements that an electron does not emit energy while in stationary orbits and can emit energy in the form of electromagnetic radiation (photons or light particles) only when moving from one orbit to another, and strictly with the energy equal to the energy difference in these two orbits. This has already led to the statement about the quantization of energy, that is, about operating with energy, particles, and their other parameters only in the form of portions. That is, there can be no smooth transition, either the electron is here, or it is not here, or it has released a certain amount of energy, or it has not. This idea was also supported by Max Planck when studying a «completely black body», a topic that would explain the glow when objects are heated.

Thus, when objects are heated, part of the energy from the collision of atoms flows to the nucleus, and after transferring it to an electron and its transition to another energy level, and then back, there is the release of a photon with a certain wavelength, so when bodies are heated, they emit light. And already when an external photon hits an atom, there is also an exit through the electron transition, but with a longer wavelength and, accordingly, a lower frequency, due to which such a phenomenon as absorption and reflection of light is observed. As for the passage of alpha particles during Rutherford's bombardment of gold foil, it was the nucleus with a high potential that caused such results, as well as the fact that almost 99.9% of the atom is empty and the same 99.9% of the atom's mass is concentrated in its nucleus. Thus, the Rutherford model was able to explain not only the results of the Rutherford experiment itself, but also many other phenomena, which confirms the validity of this model.

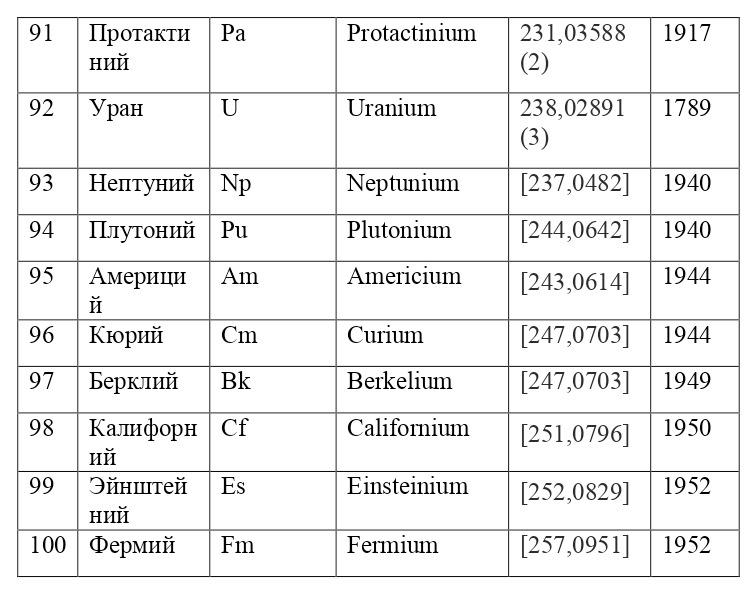
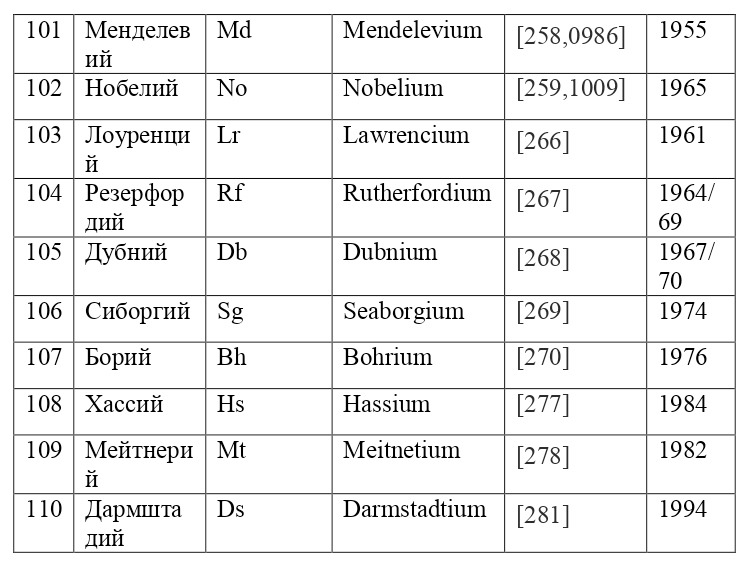
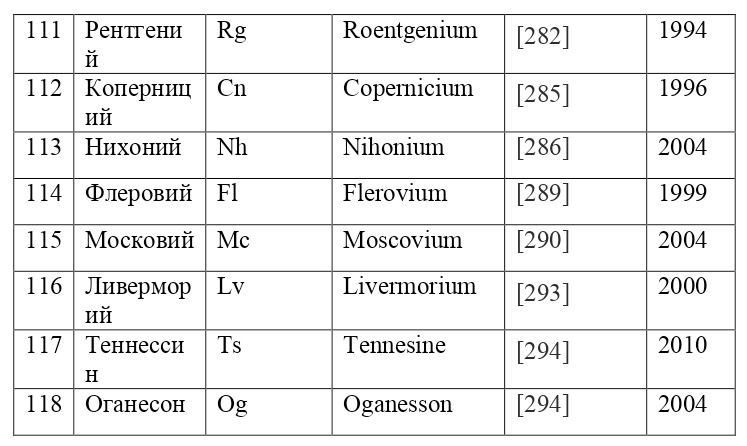
It is also appropriate to point out that the electrons are located not only in circular orbits, but also along their own separately defined paths, the shapes of which resemble "8" on different axes. This allows you to place a much larger number of electrons, for example, for such large atoms as uranium, with the ordinal number 92, neptunium-93, curium-96, californium-98 and many others. These paths are given from a separate theory of orbitals, which also proves the phenomenon of quantization in the world of elementary particles, from which it can be concluded that electrons do not move, however, like all micro-objects, they appear-disappear, appear-disappear, such is their nature of existence.

And all this forms the complete structure of the atom. This structure forms the so-called «quantum ladder», which is clearly manifested when determining the size of all particles. The atom itself has a diameter of about 10—8 cm, of course it differs from each atom, but the average size is equal to this indicator. In the center of the atom there is its own nucleus with a radius of about 10—12 cm. Electrons with a diameter less than 10—17 cm rotate around the nucleus, but this is a point particle for experimenters, since the exact size of the electron is difficult to consider at the moment and even when viewed with such an indicator as 10—17 cm, there will be no loss in accuracy. Unless you take into account experiments with increased accuracy aimed at studying higher resolutions.

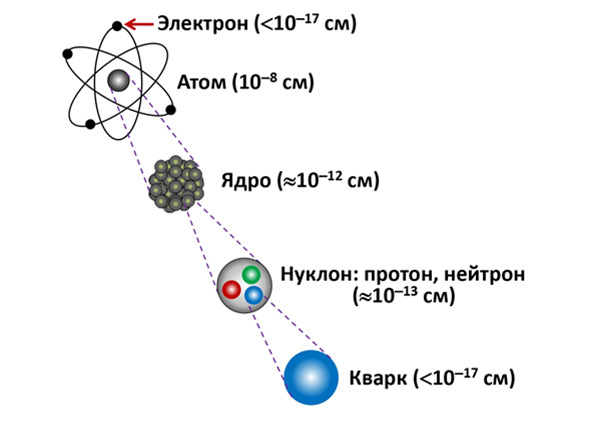
The nucleus itself is composite and consists of particles called nucleons, with further approximation it can be seen that there are 2 types of nucleons inside the nucleus: protons and neutrons. Each of them is approximately 10-13 cm in its own size . And with further approximation, smaller particles — quarks - can be observed. Quarks themselves are already point particles and have a size also smaller than 10-17, as well as electrons.

If we talk about further increase and passage even further into the depths of matter, then what will be there and how it looks is unknown today. But the fact is that it is quite difficult to do this even today.

And today the quantum world appears exactly in this form. Amazing operations are performed with these and many other particles, many other particles are formed. The study of the quantum world itself is very important, because today the study in this area has led to a number of discoveries, a vivid example of which is the creation of nuclear power plant technologies, the creation of particle accelerators, research in the field of thermonuclear reactions, widely known as "the creation of an artificial Sun" and many other studies have their origins in this area. And it was also in this area that the Electron research was born, to which this narrative is being conducted.

The discovery by Conrad X-Ray of special signals emitted by the cathode tube, which later received the name of the X-ray itself, caused a great furor. Many scientists began active research, but before the world could recover from this surprise, amazing materials that emitted these amazing rays were suddenly discovered. Henri Becquerel, who is one of the famous scientists who studied fluorescence, decided to prove the fact of the connection of this phenomenon with a radioactive source — uranium salt. It was then that Becquerel, in 1896, left the material on the photographic plate without illumination by chance and noticed that there were darkenings on the photographic plate, proving that the salt itself emits amazing rays. Many scientists have investigated this phenomenon until it was proved that these emissions are the result of radioactive decay of atomic nuclei.

It is for this reason that 1896 is considered the year of the beginning of research in the field of the atomic nucleus. It was also known that if you direct focused radiation from a radioactive source (uranium salt) by placing it in a lead chamber with a single slit, and then place magnets on the path of this study, then this radiation will be divided into 3 types. At the same time, the radiation flux that was directed to the right has a negative charge, the flux that was turned to the left has a positive charge, which is easily proved from Lorentz's law. And the third radiation that has not been rejected has no charge.

Thus, the positive radiation was called alpha particles, and after measuring the masses of these particles based on the Lorentz force formula, when the magnetic field induction changes (the principle of operation of the mass spectrometer), it was possible to make sure that these are the nuclei of the helium atom. Negative particles, which were called beta particles, with the same analysis turned out to be just fast electrons, and rays that were not rejected were called gamma radiation.

After the initial analysis of the structure of radioactive radiation was carried out, it can be made sure that the radiation itself consists of 2 types of particles and 1 type of waves, namely gamma radiation, thanks to which it is already possible to give a general definition of radioactivity:

Radioactivity is the spontaneous emission of various particles and radiation by atomic nuclei.

Speaking in more detail about the dates of determination and research of radioactivity, it should be pointed out that by 1900 all types of radioactivity had already been investigated, although the atomic nucleus itself was discovered by Ernest Rutherford only in 1911. The first radiation, alpha radiation, which, as already determined, consists of helium nuclei, was discovered in 1898 by the same Ernest Rutherford and became known as alpha decay. Also beta decay or electron flight was discovered by the same Rutherford in the same 1898. But gamma radiation was determined and investigated only in 1900 by Paul Ulrich Willard.

These studies proved that the darkening of the plates observed by Becquerel was caused by radioactive radiation. Consequently, it is now possible to come to the concept of radioactive decay:

Radioactive decay is a spontaneous process characteristic of the phenomena of the microcosm at the quantum level. At the same time, the result of radioactive decay cannot be predicted accurately, only to determine the probability. Such a nature of phenomena is not an imperfection of devices, but is a representation of the processes of the quantum world themselves.

From this statement, we can conclude that there must be some generally accepted law explaining this phenomenon. The conclusion of the law of radioactive decay is as follows:

Let there be N (t) identical radioactive nuclei or unstable particles at a certain time t and the probability of the decay of a single nucleus (particle) per unit of time is equal to λ.

In this case, over a period of time dt, the number of radioactive nuclei (particles) will decrease by dN, which implies the following expression (2.7).

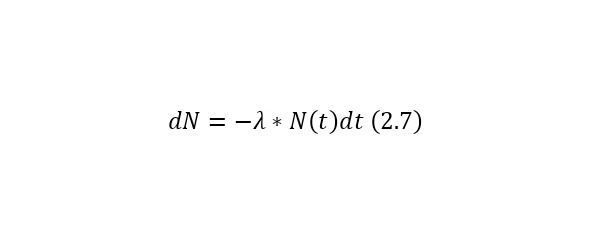
If we deduce a change in time from this ratio, we get (2.8).

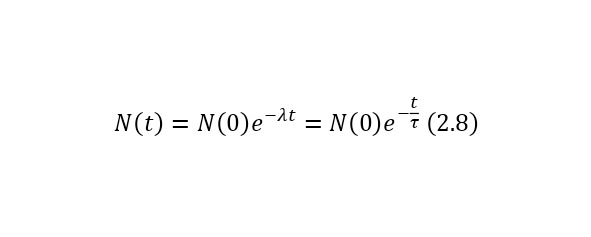
In (2.8), the concept of τ is defined in (2.9) and is the average lifetime of the nucleus (before decay), which is quite convenient to use, and N (0) in this case is the number of nuclei at the initial time.

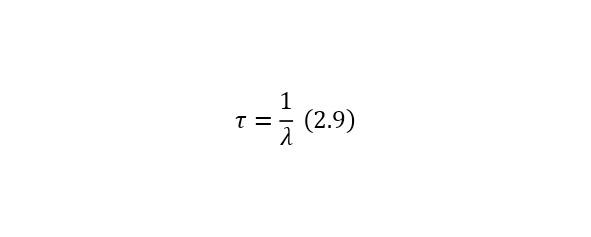
It is also possible to present another more simplified form (2.8) in (2.10).

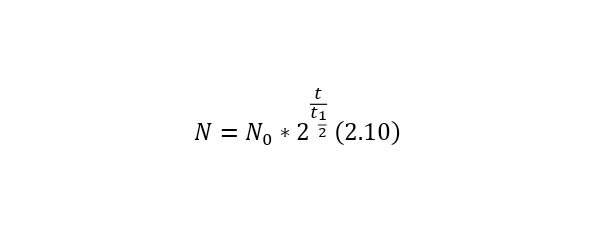
Where the half-index time is the half-life and is calculated by (2.11) and is equal to a separate value for each radioactive nucleus.

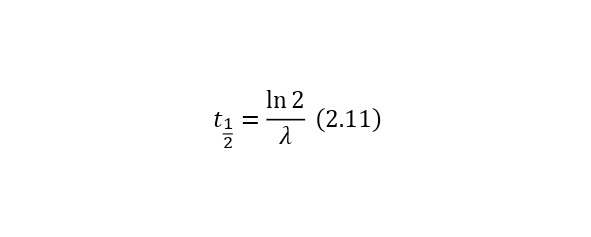
If it is necessary to determine the average number of decays (for low-speed decay), it is calculated by (2.12).

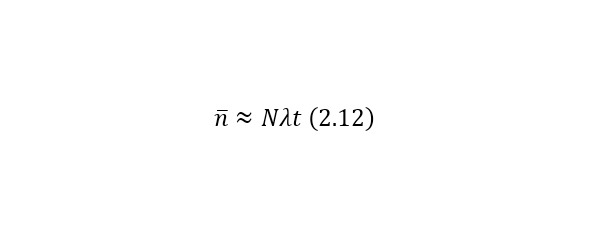
When this pattern is transformed, a radioactive decay curve is formed (Fig. 2.8).

From the graph, you can see that the pattern is exponential and at the same time decreases each time by half of the period, followed by a decrease.

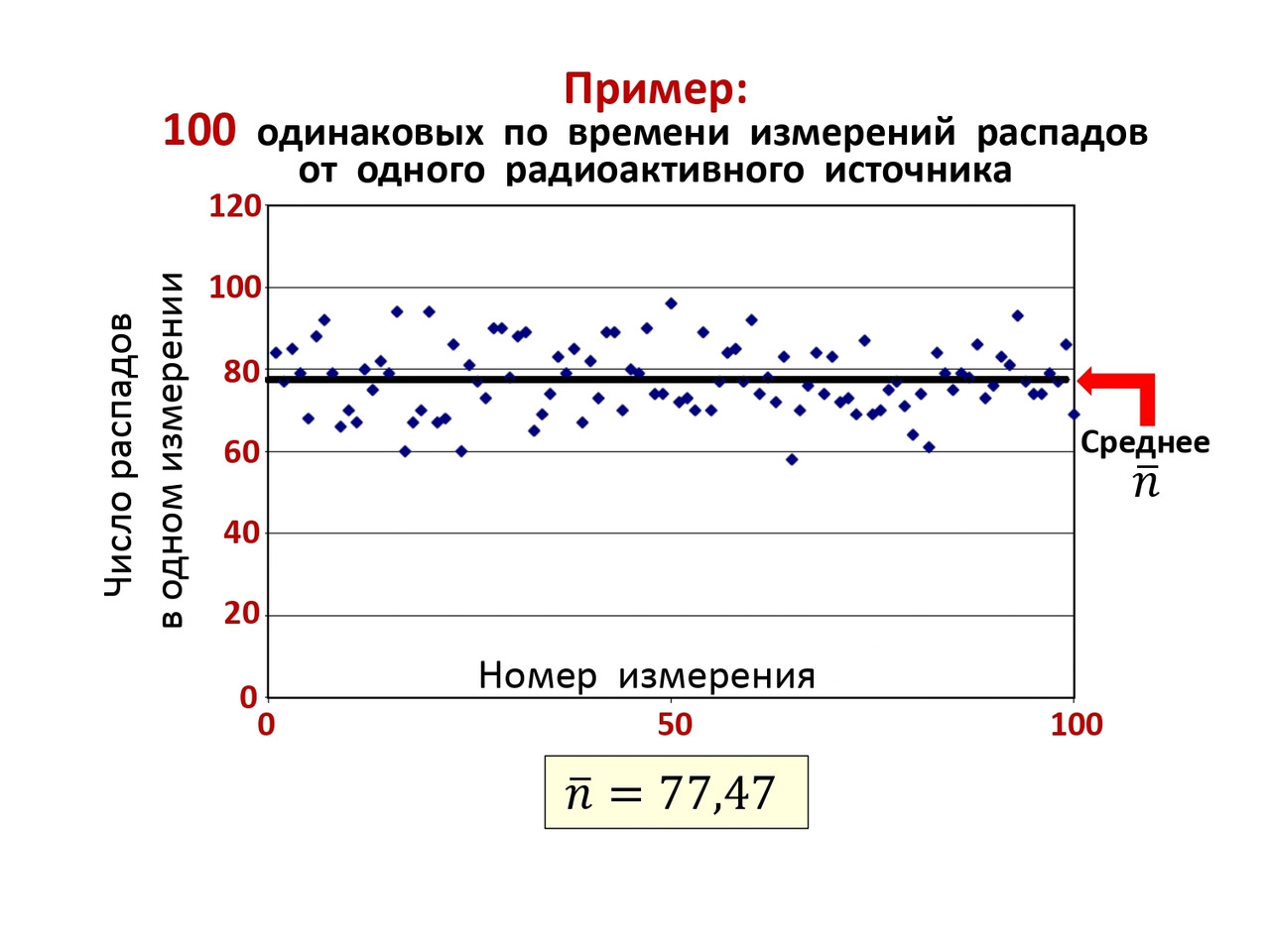
As an experimental analysis of this phenomenon, the following can be shown. 100 measurements were carried out over the same period of time and the number of decays was measured. As a result, a graph was obtained on (Figure 2.9), where the average number of decays equal to 77.47 coincided with the value in (2.12), which is a clear proof of the validity of the general pattern.

The general view of the distribution of these statistics is already presented according to a different law. That is, the probability Pn for the time t for testing the n number of decays is given by the Poisson distribution (2.13).

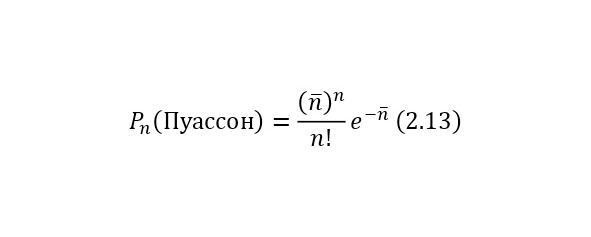
This conclusion is already inherent in probability theory, and if we rely on it, then also for the case when (n>> 1) Gaussian distributions (2.14) are already used.

If we express these two patterns on graphs, we can get almost identical patterns with an increase in the average number of decays. For example, if the average number of decays is 2, then there is some difference in the results of the Poisson and Gauss distribution, but when this number, for example, reaches 7 and higher values, this difference becomes less significant, as shown in (Figure 2.10).

After it has been decided with probability at zero speed, we can pay attention to cases when the effects of the theory of relativity come into play. In the microcosm, where the sizes of the studied objects are practically invisible, for example, for atoms with their sizes of 10-8 cm, for atomic nuclei with their 10-12-10-13 cm and for other particles with 10-13-10-17 cm, the speeds are often comparable, close or even equal to the speed of light. Thanks to this, all the features and effects of the theory of relativity are clearly manifested in the microcosm.

For this reason, it is important to consider in more detail the relations and basic equations from the theory of relativity.

One of the most important elements in the theory of relativity is the Lorentz factor (2.15), which is involved in almost all formulas of the theory of relativity, which can also be derived from the kinetic energy formula (2.16).

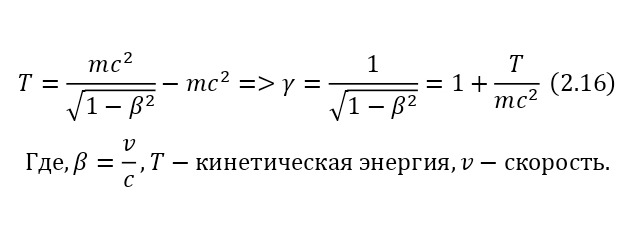
From these relations, it can be concluded that the total energy, which is the sum of the kinetic energy and the rest energy of the particle, is determined by (2.17).

The presence of this equality leads to the fact that the problem of the lack of a formula for calculating the energy of particles without masses (for example, a photon or a gluon) is solved. And already from (2.16) it is also possible to derive a more simplified entry for kinetic energy (2.18). In the case of applying (2.15) for the momentum formula (2.19), a simplified form is also obtained.

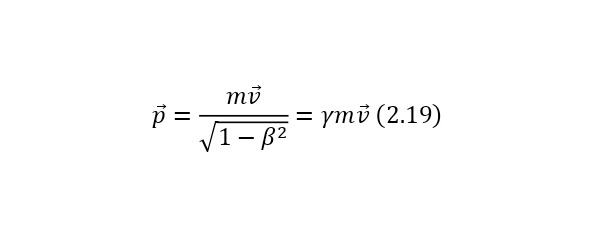
The velocity of the particle derived from the formulas of the total energy (2.17) looks like this (2.20).

An important element also in calculations, this is also the total energy of massless particles, is the formula (2.21), where the conclusions of which are also given from the total energy ratio (2.17).

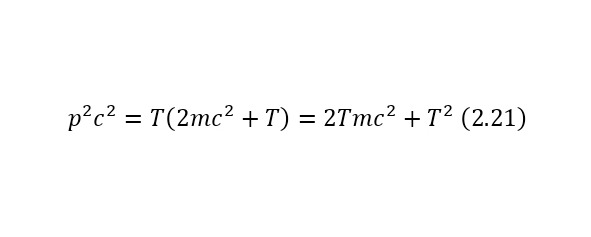
The notion of invariant also plays a role in this definition. An invariant is a constant value, regardless of the system of the report from which the observation is conducted. In this case, the invariant is the square of the mass or (2.22).

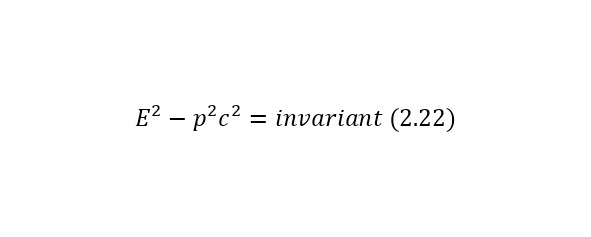
And it does not matter if it is a single particle or a system of particles, so the total energy E also refers to a particle or a system of particles, and the momentum of a particle also refers to a particle or a system of particles.

One of the most important points in the study of the physics of the atomic nucleus and elementary particles is familiarity with the system of units, which is the easiest way to perform calculations — this is the Gaussian system of units together with some non-system quantities.

Speaking of units of energy, due to the small amount of energy, it is convenient to use a unit of electron volts (eV), which is equal to 1.6 *10-19 J or 1.6 * 10-12 erg. This value represents the energy that an electron acquires by passing a potential difference of 1 Volt. Values of 1 keV (kiloelectronvolt) or 103 eV, 1 MeV or 106 eV, 1 GeV or 109 eV and 1 TeV or 1012 eV are also appropriate, which are actively used in the physics of elementary particles and the atomic nucleus.

As a unit of length or distance, it is customary to use the value of 1 Fermi (Fm) in honor of the famous scientist Enrico Fermi, which also coincides with the value of 1 femtometer (fm), where 1 Fm is 10-13 cm. As for the mass, it is expressed in energy units mc2, for example, the mass of an electron, which in the usual SI unit system is 9.11 * 10-28 grams, then in energy units is 0.511 MeV. And the mass of the proton, which is 1.6727 * 10-24 grams, in energy equivalent will be 938.27 MeV.

Special and general relativity have many effects, then 3 of them deserve more attention. The first of them is the time dilation for a relativistic particle, the second is the effect of shortening the distance in the direction of motion of a relativistic particle, and the third effect, which, by the way, comes out of general relativity — the time dilation in a gravitational field, also known as the gravitational redshift of radiation. For a better understanding of these effects, consider 3 cases.

Let some particles undergo decay according to the law of radioactive decay (2.23), where t0 is the lifetime at rest.

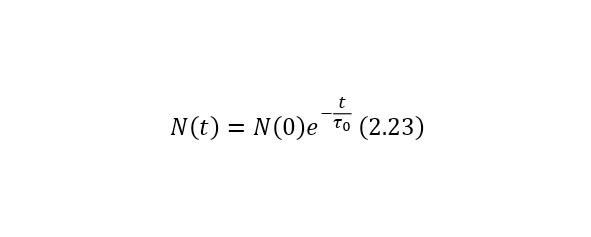
In this case, if the particles move at a certain speed, then their lifetime, due to time dilation, increases and becomes equal to (2.24), where the Lorentz factor is known (2.25) and from here it can already be said that the law of radioactive decay for relativistic particles is represented as (2.26).

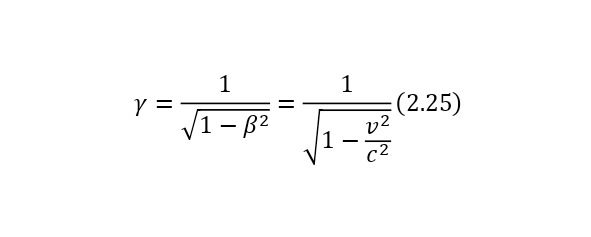
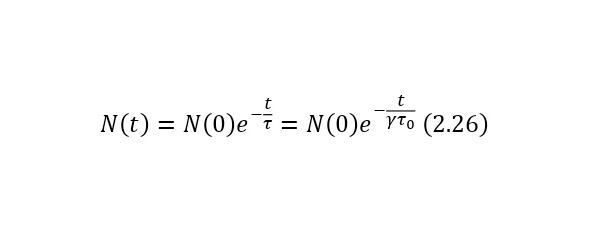
Consider an example. Most of all the particles that fall to Earth together with cosmic radiation are protons with energies of the order of 1020 eV. At the same time, when they enter the Earth’s atmosphere, they collide with nitrogen and oxygen atoms, charged pions are born (some particles that have the designation π+ or π- for a positively and negatively charged pion, respectively), they decay in their free flight into already relativistic muons (other types of particles that are already designated as μ+ or μ- also for a positively and negatively charged muon, respectively), muon neutrinos vμ or their antineutrinos are also isolated from pions.And the lifetime of a peony is 2.6 * 10—8 seconds. Thus, a kind of «shower» of secondary particles is formed, which is born by a proton in the Earth’s atmosphere. And these reactions forming a «shower» can be written as (2.27), (2.28) and (2.29), and also illustrated in (Fig. 2.11).

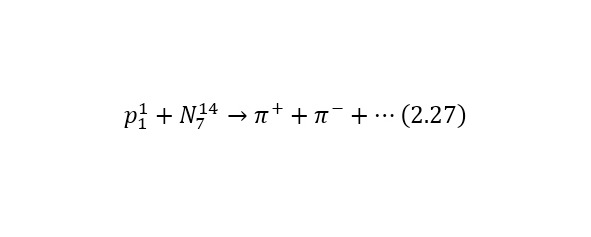
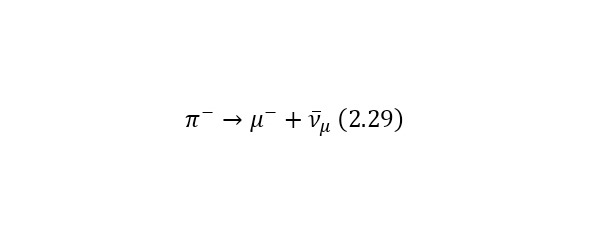
But it is also important to note that (2.28) and (2.29) have their continuation in (2.30) and (2.31), respectively.

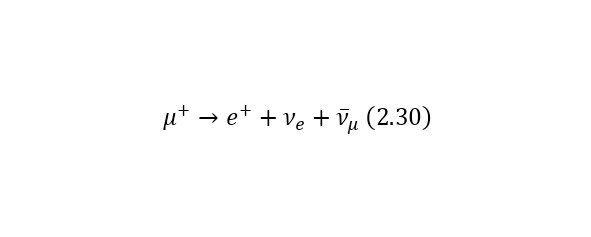
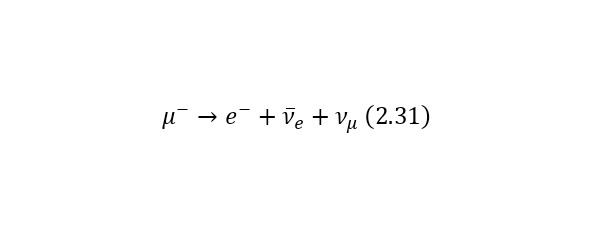
In this case, the muon's own lifetime will be 2.2 * 10-6 seconds. Let muons with kinetic energies of 1 GeV be born at an altitude of 5 km above the Earth's surface, will they be able to reach the surface and if so, what part?

To get an answer to this question, we will use 2 ways, with and without the effect of relativity theory. If we neglect the effects caused by the theory of relativity, even knowing that at an energy of 1 GeV, the velocities will be almost equal to the speed of light, especially for such a light particle as muons, then in a time of 2.2 * 10—6 seconds these particles will overcome only a distance of (2.32), and the proportion of muons that have reached the Earth’s surface according to the law of radioactive decay will be (2.33).

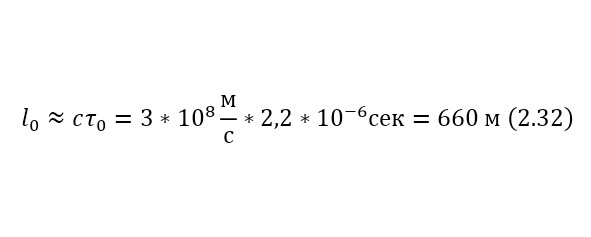
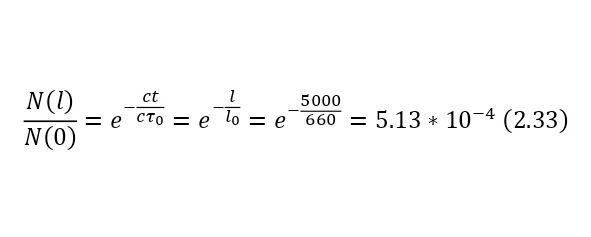
It is clearly seen that part of the flying particles is simply negligible, but if we apply relativism, in this case it is necessary to calculate the Lorentz factor by (2.34), and then substituting it, get the result in (2.35), thereby already in (2.36) showing that the distance has increased decently because of this.

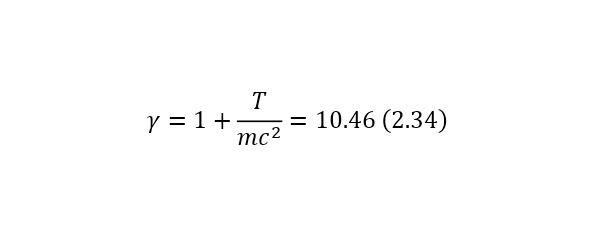
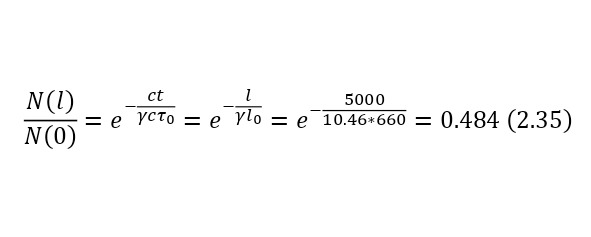
So, relativistic deceleration allows almost half of muons with a kinetic energy of 1 GeV, born at an altitude of 5 km, and moving in the direction of the Earth, to reach its surface.

After the effect of time dilation has been demonstrated, it is worth proving the effect of reducing the longitudinal size of the object at high speeds. A striking example of such an effect can be the same protons accelerating in the Large Hadron Collider (LHC) or in the Large Hadron Collider (LHC) (Figure 1.5), accelerated to energies of 6,500 GeV or approximately 7 TeV. Such protons should decrease their size due to the effect of the theory of relativity, and at the same time this reduction should be determined in terms of (2.37), where L and L0 are the longitudinal dimensions of a moving and resting body, in our case a proton with a kinetic energy of about 7 TeV.

And if we calculate the Lorentz factor (2.38), we get 7463. That is, the radius of the proton will be reduced by 7463 times or almost to 10—4 Fm or 10—17 cm, that is, almost to the size of an electron, demonstrating the picture (Fig. 2.12).

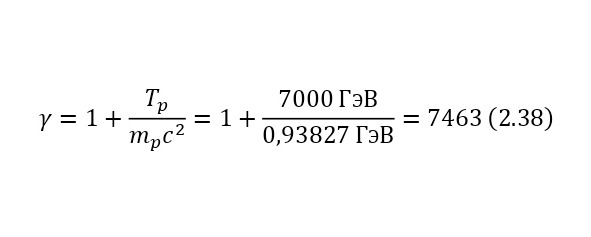
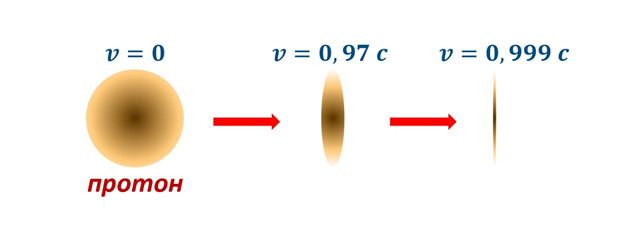
In the Collider, particles are accelerated to incredible speeds that differ from the speed of light by only 10-8 of its part or about 3 m / s, which already gives an idea of how important it is to take into account all kinds of effects of the theory of relativity in this system.

And now that this effect has been explained, we can move on to the effect of gravitational red electromagnetic radiation (time dilation in a gravitational field). Since an object with mass bends space-time, this also leads to the curvature of time itself, so that time goes faster at high altitudes, and with increasing gravity, time also slows down. This acts in such a way that at high altitude the atoms increase their characteristic frequencies. And if a photon (a massless particle of light) also falls under such an effect, that is, it passes through fields with a difference in the gravitational field, then it also reduces its frequency, that is, it "blushes" due to the low frequency of red photons, for this reason this effect is called the gravitational redshift effect, and due to that photons are particles of electromagnetic radiation, so this effect is also applicable to such massless particles.

To prove this effect, it is theoretically possible not to resort to the formalities of the General Theory of Relativity (GR), although it is predicted by GR, but it is enough to accept the formula for the total energy of the photon — hv.

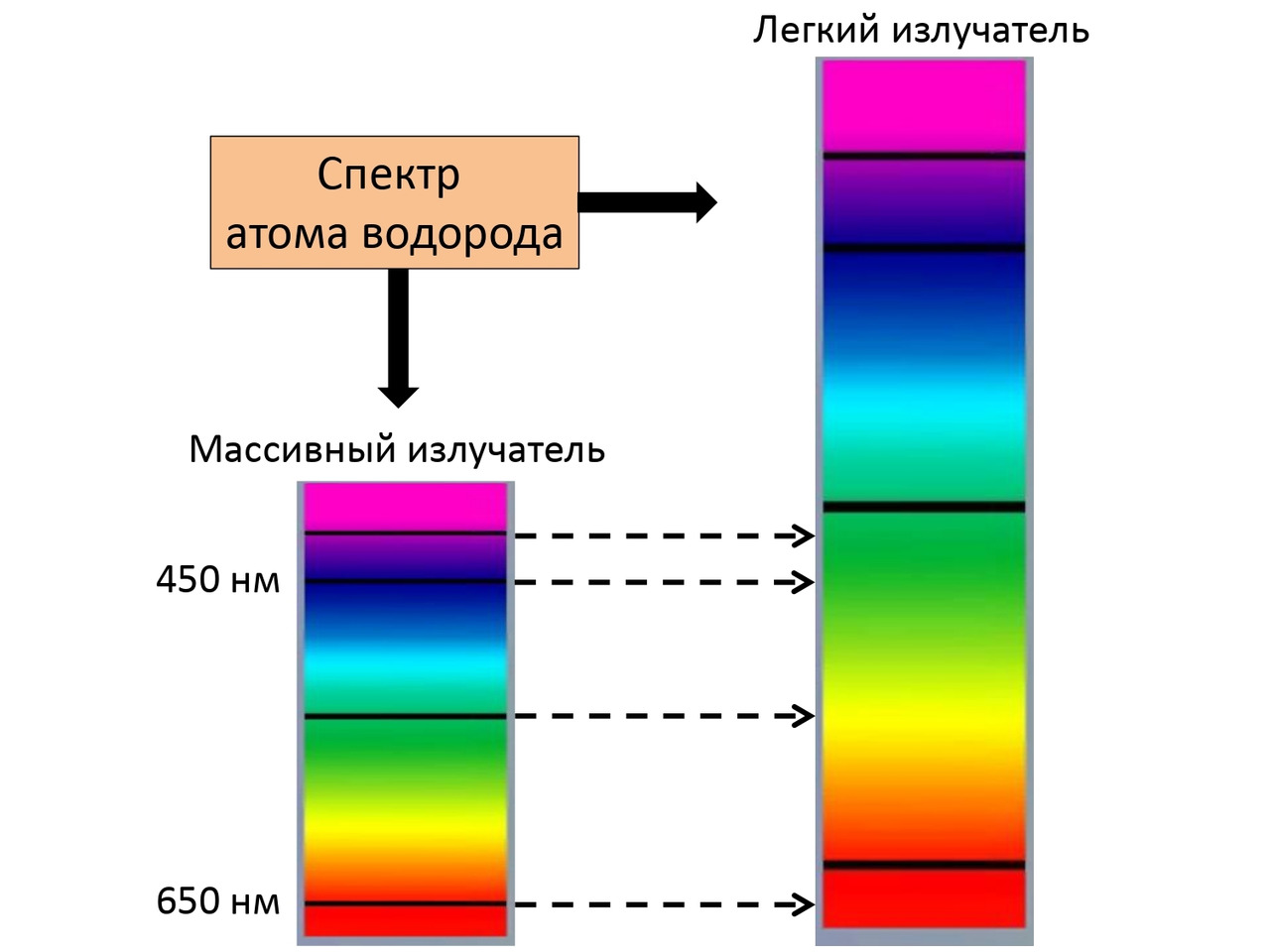
Now it is worth dwelling in more detail on the notion that the atoms themselves, or rather their nuclei, can play the role of clocks and about changing their frequency. The fact is that all atoms and atomic nuclei fully possess the properties of the most accurate ideal clocks. Their speed or pace is determined by their energies, well, or frequencies, if we imagine that wave particles and their energies are defined as photon energies. And this is the energy of the transition of an atom or its nucleus between its any levels. That is, an atom or any other micro-object cannot simply be in some position, and then moving into another state smoothly into it, it will necessarily jump, even though it will be an increase in energy with the acceleration of the proton, even though it will be the excitation of the electron with the transition to another orbit, even though it will be a change in the frequency of the photon. And this statement is also true for atoms, thanks to which it can be argued that the frequency in the formula (2.39) is the course of the atomic clock.

Now, let some atom be fixed at a certain low altitude. And he moved from one energy level to another, higher, under the influence of external forces, then back. At the same time, when it lowers its energy level, it emits a photon with a frequency corresponding to the difference of these atomic or nuclear energy levels, and with an increase in height due to the presence of higher potential or gravitational energy in the upper atoms, the photons already emitted by them will have a lower frequency, due to a decrease in the difference in energy levels, since the initial level of-due to the gravitational energy increases. Consequently, the upper atoms have a faster pace, and the lower ones have a smaller one, which is why we can claim that time slows down with increasing gravity. And the upper observer perceives this decrease in the rate of the lower clock as reddening (an increase in wavelength with a decrease in frequency) of a photon arriving from below, which is clearly seen in (Fig. 2.13).

Or:

The clock goes slower if it is installed near weighty masses. It follows that the spectral lines of light coming to us from the surface of large stars should shift to the red end of the spectrum.

Albert Einstein

It is for this reason that when a massive hydrogen emitter and a light emitter of the same hydrogen are excited, a shift in its spectrum is obtained, which can also be seen in (Fig. 2.14).

And having considered these points, which also led to familiarization with the phenomena of the theory of relativity, the concepts of nuclear reactions themselves were described and considered in detail, and now, finally, the time has come for a detailed study of the most important concept — nuclear reactions.

Chapter 3. Nuclear reactions

After a detailed study of all the effects relative to the atom, now it's time to conduct operations with the atomic nucleus, namely, it's time to explain nuclear reactions. So, speaking about nuclear reactions, the following statement is understood:

Nuclear reactions are transformations of atomic nuclei when interacting with elementary particles and with each other.

That is, another nucleus or particle hits the nucleus, or two nuclei or any particles collide with each other, thereby forming new reaction products. We also remind you that nuclei consist of nucleons — protons and neutrons, and they, in turn, are quarks. At the same time, protons are positively charged and it is they who create a positive charge of the nucleus, and neutrons, as can be seen from the name, are electrically neutral and necessary for the nucleus to be held by itself. At the same time, the nucleus, being outside the nucleus, decays into an electron, proton and antineutrino, and inside the nucleus, the neutron transfers some of the energy to the proton, which allows it to become a proton for a while, and a proton a neutron, then back. And this cycle is constantly continuing, thereby the neutron does not decay, and protons do not fly apart because of their eponymous nature, and the nucleus remains intact. To determine the number of neutrons in the nucleus, it is enough to subtract the mass of all protons from the mass of the entire nucleus, which can be easily calculated by multiplying the charge of the nucleus by the mass of the proton, which is equal to 1.00728 au. M., and after this value is divided by the mass of 1 neutron or 1.00866 A. E. M. By the way, it is worth noting that it is impossible to use the mass of an atom, since there are also electrons, each with a mass of 0.00055 A. E. M. Therefore, previously, if only the atomic mass is known, it is necessary to subtract the mass of all electrons, obtaining the mass of the core.

And now, returning to nuclear reactions, it is worth saying that a striking example of a reaction under the action of alpha particles is the first reaction carried out by Ernest Rutherford (3.1). In this case, the elements are recorded in the left part before the reaction, and in the right, after the reaction.

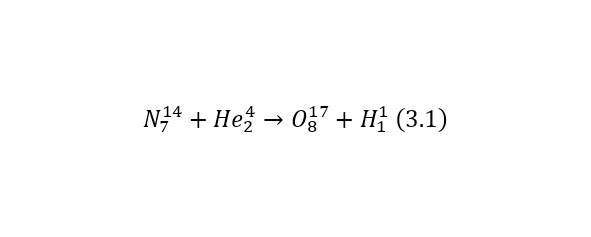
Reaction (3.1) is caused by the action of alpha particles, or more precisely, the nucleus of a helium atom. But nuclear reactions can also be caused by other particles, for example, under the action of a proton or the nucleus of a hydrogen atom (3.2).

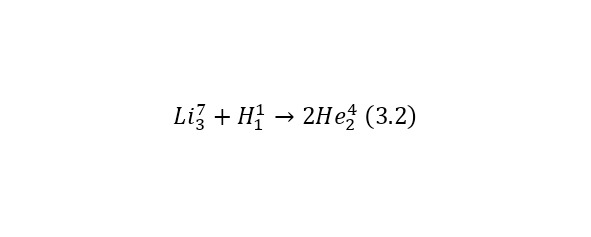
In the second reaction to a lithium-7 atom (the atomic mass is approximately 7 am, and the charge is 3, that is, there are 3 protons and 4 neutrons in the nucleus), a proton with a charge of 1 elementary charge and about 1 am, turns out 2 alpha particles with a charge of 2 elementary

Now, it is important to note such a fact as the Coulomb barrier. That is, the fact that the nuclei, due to their eponymous nature, repel and repel with a decent force. And to calculate this force, it is necessary to use (3.3) or the formula for determining the Coulomb barrier.

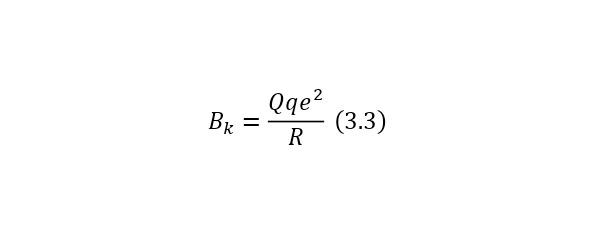
The Coulomb barrier is determined already using some constants. We calculate the Coulomb barrier for the reaction (3.1). To do this, it is necessary to rewrite the formula in the form (3.4).

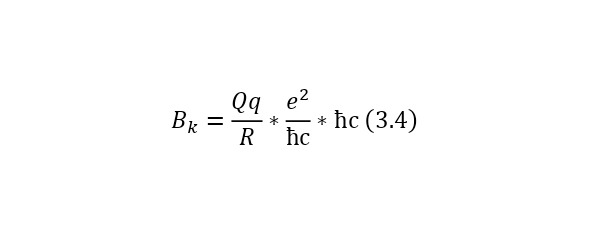
Although in fact nothing has changed, we managed to add 2 permanent ones. The ratio of the square of the elementary charge to the product of the reduced Planck constant and the speed of light, this is a constant called the fine structure constant and is equal to 1/137, this is the second multiplier. And the third multiplier is already a conversion constant and is equal to 197.3 MeV*Fm. That is why the radius is also specified in Fm and the result is a result in MeV. But in this case, the radius of the core is also determined by its formula, which also needs to be given (3.5).

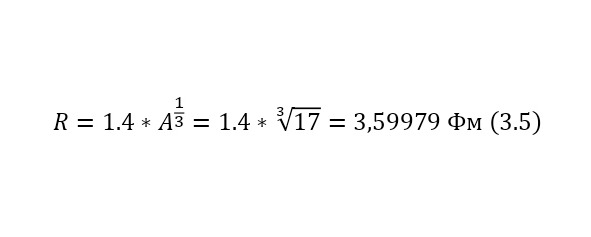
In (3.5), the radius of the nucleus of the nitrogen atom was determined, with which Rutherford carried out the reaction, therefore, it is possible to proceed to (3.6), where the Coulomb barrier itself (3.6) has already to be determined.

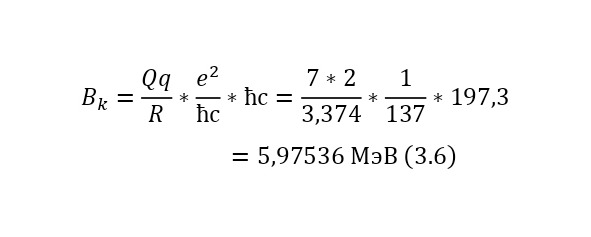
That is, during this nuclear reaction, the alpha particle spends 5,97536 MeV to get close to the nucleus at a sufficient distance to start a nuclear reaction, that is, to the radius where those magical nuclear forces act, which overpower the electric ones and thus the reaction occurs.

It is also important to note the reverse fact, when Coulomb forces act backwards, pushing the reaction products away from each other. For example, in order to determine what energy a proton acquires after undergoing a nuclear reaction, only due to Coulomb forces, it is also possible to use this energy, but already relative to the nucleus of the oxygen-17 atom, as can be seen in (3.7), where the radius of oxygen-17 is determined and (3.8), where the output is calculated the Coulomb barrier.

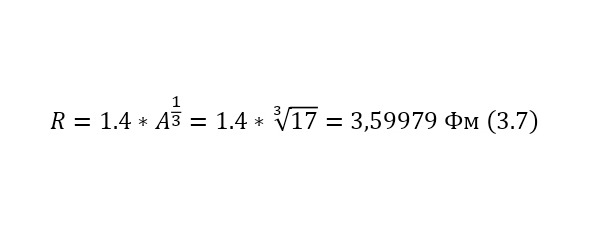
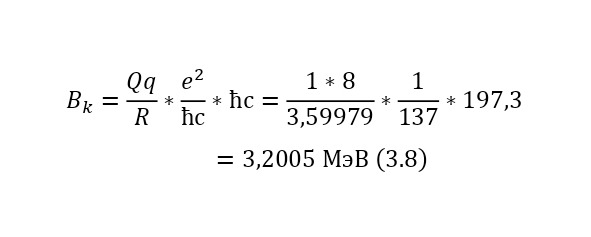
And this, as can be seen from the result, is quite fair, which is fully confirmed experimentally. But this energy is only added at the end, and exactly what kind of energy the particles acquire while inside the nucleus. Just have to find out.

Now it is important to say a few words about the channels of nuclear reactions. The fact is that there are a number of options for the outcome of one interaction. For example, for the same nitrogen bombardment reaction, the following results could pass (3.9).

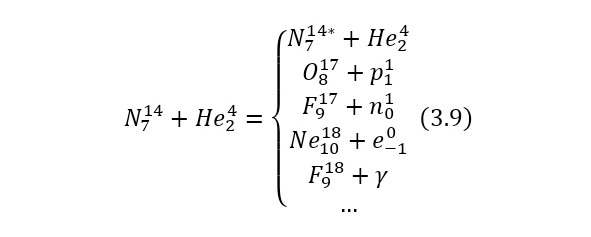
And you can list these options for a very long time, but only some of them have the opportunity to be implemented. For example, the first reaction can occur, but nothing will change, and they will only exchange energies, then the nitrogen nucleus will go into an excited state, as indicated by the "*" icon. And since there are no changes in the structure, this option, they are also called reaction channels, is open and elastic. Exactly like the elastic interaction. And the rest of the channels are inelastic, because the structure of the original nuclei is already changing in them.

To understand which of the inelastic channels is open and which is closed, it is necessary to proceed to the conservation laws. And speaking of them, first of all it is necessary to note the law of conservation of the nucleon number and charge. As you can see, in all reactions, the sum of all nucleons is the same, exactly like the sum of charges. These are the first two conservation laws.

They are followed by the law of conservation of energy and momentum. That is, the energy of the particles before the reaction, meaning the total energy, is equal to the total energy of the particles after the reaction. The same applies to the pulse — the total pulse before the reaction is equal to the total pulse after the reaction. There are other conservation laws, these include the law of conservation of isospin, parity, the amount of momentum and others, but at the moment, we need only the listed conservation laws. So, speaking of conservation laws, we can answer the question of what determines the openness and closeness of the channel. And it determines the implementation of these laws. That is, if the laws for one channel are met, it is open, if not, it is closed. And if there are already several open channels, then which one of them will happen determines the probability, or such an indicator as the cross section of a nuclear reaction, but more on that later.

After the conservation laws have been described, it is important to note the following paradoxes. The first paradox concerns the atomic nucleus. If we determine the mass of the atomic nucleus experimentally, that is, first determine the mass of the atom, then subtract the mass of electrons from it. And the mass of the electrons was determined due to the angle of deflection in the magnetic field when it was outside the atom in the cathode rays, which were mentioned earlier, and thus to obtain the mass of the nucleus, then in fact, it should be equal to the sum of the masses of all protons and neutrons. Let's check the validity of this statement on the example of the nucleus of a helium atom or an already widely known alpha particle.

The mass of the alpha particle is 4.001506179 A. E. M., already without electrons, while it consists of 2 protons with a mass of 1.00728 A. E. M. and 2 neutrons with a mass of 1.00866 A. E. M., the total mass of which will be 4.03188 A. E. M. The difference is 0.030373821 A. E. M., this is and there is a mass defect and is determined by the formula (3.10), and the same value, but already in the form of energy, is determined by the formula (3.11). And due to the fact that 1 A. E. M. in energy equivalent is 931.5 MeV, then the square of the speed of light for such formulas where it is necessary to output the answer in MeV is 931.5 MeV.

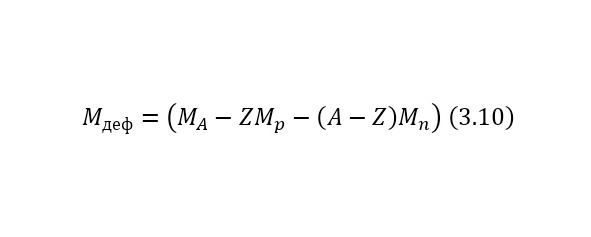
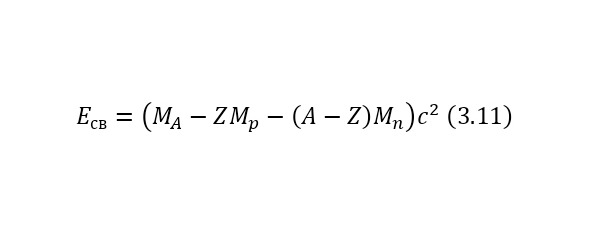
The energy defined in (3.11) is the binding energy of the nucleus and the alpha particle, it is 28.2932 MeV. Each nucleus has its own binding energy, the binding energy parameter per nucleon is also important (3.12), for example, for an alpha particle, the binding energy per nucleon is 7.0733 MeV.

Any nucleus has this parameter, and if we analyze all these values, we get a general diagram, thanks to which we can determine, for example, that it is advantageous for heavy nuclei (uranium, plutonium, etc.) to be divided into lighter ones, with a greater release of energy, or for lighter nuclei (hydrogen, helium, etc.) to combine in heavier ones.

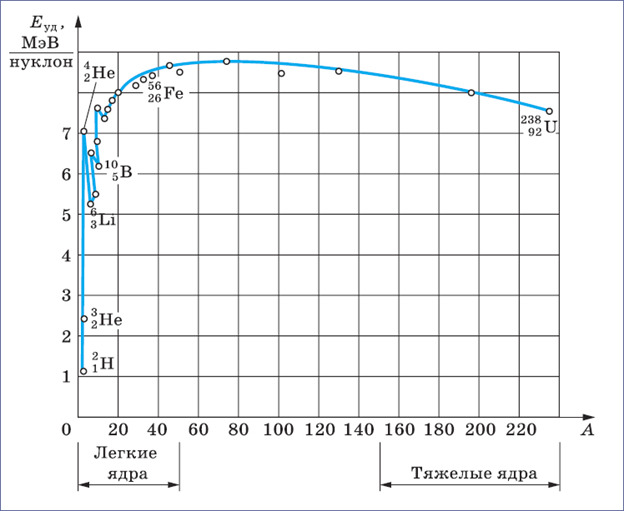
The first paradox is based on this, but there is also a second paradox, already for nuclear reactions. This paradox is based on the nuclear reactions themselves. If you add up the masses of all the elements of a nuclear reaction before and after, you get some difference. For example, if we check for the Rutherford reaction, the mass of nitrogen-14 is 14.0030740048 A. E. M., and alpha particles, as already indicated, are 4.001506179 A. E. M., their sum will be 18.0045801838 A. E. M., and the mass of the proton is 1.00728 A. E. M. and oxygen-17 is 16.9991317012 A. E. M., this amount will already amount to 18.0064117012 A. E. M. The difference in mass is 0.0018315174 A. E. M. Where did this mass come from?

The answer is amazing, this mass appeared from the kinetic energy of the bombarding alpha particle. And the mass difference in the energy equivalent is called the reaction yield (3.13).

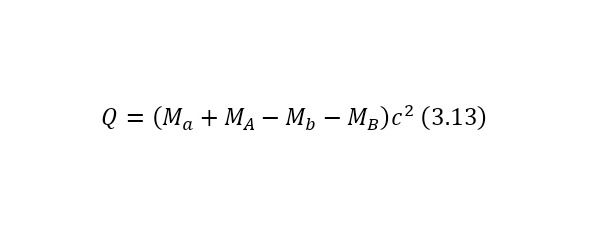
For example, for reaction (3.1) it will be -1.7060584581 MeV, and since this value is less than zero, it means that the alpha particle spent so much energy to undergo this reaction. There are reactions from which energy comes out, for example, the same reaction with uranium, where the output is about 200 MeV. Such reactions are called exoenergetic or exothermic, and absorption reactions where the reaction yield is less than zero are called endo-energetic or endothermic.

The nuclear reaction can be studied in the system of the center of inertia and the laboratory coordinate system. If we consider the reaction in the system of the center of inertia, then this is a situation when two particles collide, and the common center of mass is stationary, both before and after the reaction. And in the laboratory coordinate system, the center of mass moves at a certain speed, for example, the target is stationary, and a particle hits it — this is considered in the laboratory coordinate system. And if viewed from this point of view, then equality (3.14) is indeed true.

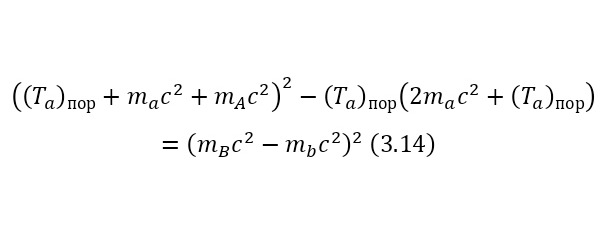
Already from (3.14), it is quite possible to deduce the threshold kinetic energy of the incoming particle (3.15) and, accordingly, simplify it (3.16).

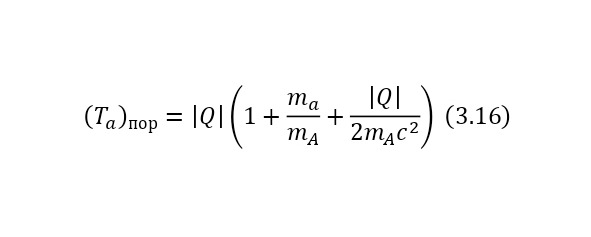
And now a very interesting moment. The energy released during the reaction is directed to all the reaction products at once, but what part of this energy will which product receive?

To understand this, it is necessary to indicate that during the reaction, the so-called «drip model» is used, that is, a particle flying into the core, before flying out as a product, remains inside the common core for a while, and only then flies out. This makes it possible to believe that the momentum is constant to some extent and four-dimensional vectors are considered here, that is, vectors in space and in time. At the same time, the common particle forgets how it is formed, so this gives a chance to believe that its momentum is zero. All the incoming momentum disappears in the nucleus itself between the nucleons and goes to excitation. And two equalities can be written following from the dependence between energy and momentum (3.17), (3.18) taking into account (3.19).

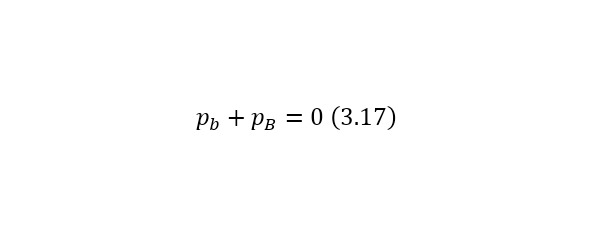
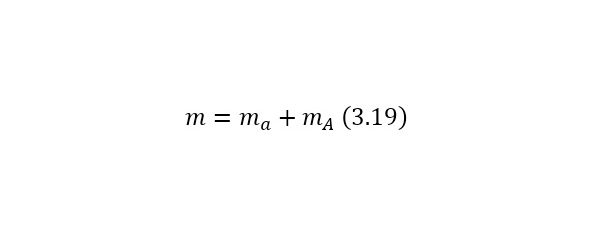
And it is also important to point out that for each of the reaction products there is a ratio between their momentum and mass (3.20) and (3.21), from which the expression (3.22) can be derived.

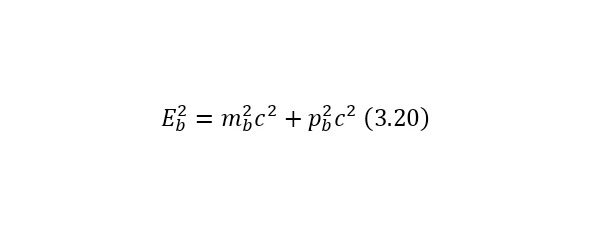
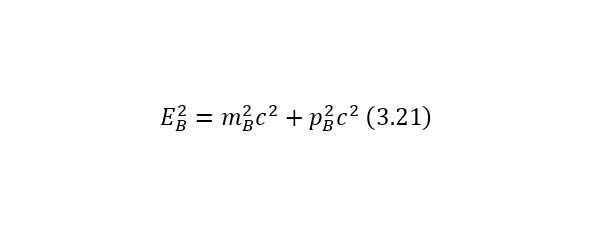
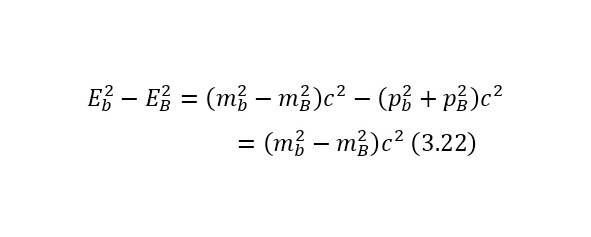
These expressions form a system (3.23) with exactly deducible solutions.

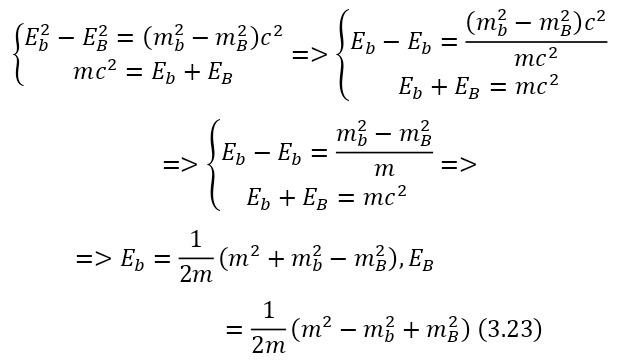
And already (3.23) is easy to convert to (3.24) and (3.25).

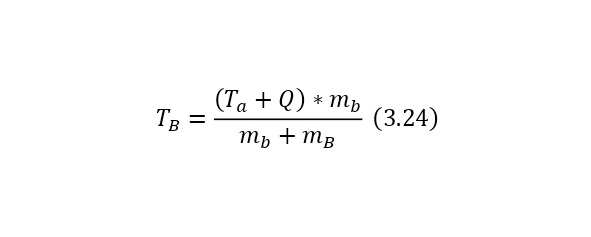
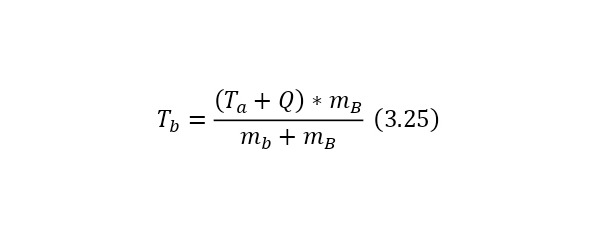
So it is possible to derive formulas for the energies of each of the products of a nuclear reaction. But now the question arises, which part of all the incoming particles will interact? And in order to answer this question, it is quite advisable to use the concept of the cross section of a nuclear reaction. The cross section of a nuclear reaction is considered to be such a region, getting into which the particle enters into interaction. Of course, this is the area of the core itself, but also do not forget that the particle itself is also a wave and has its own wavelength, like radiation, so the wavelength of this radiation is added to the radius of this circle.

Therefore, it is possible to write the formula for the cross section of the nuclear reaction as follows (3.26).

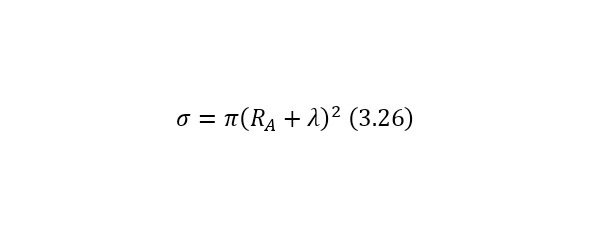
And the wavelength is easy to determine from the de Broglie formula (3.27).

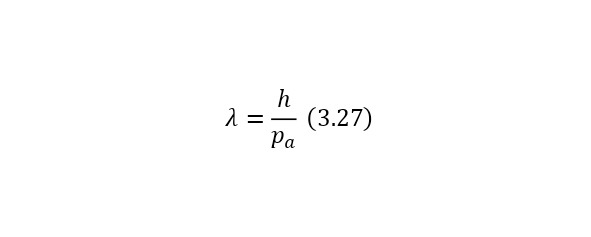
To measure the cross section of the nuclear reaction, a separate unit has been introduced — barn, which is 10—28 m2. At the same time, there is a constant of the nuclear fission reaction of uranium — 584 bn, and for some reactions, it is advisable to introduce some additional constants to enter values in the desired area.

If this is the area where the particle enters into the interaction, then what part does it occupy of the entire bombardment area? In order to derive a formula for the particles involved in the interaction, it is necessary to present the target itself. If the target has a thickness of dx, an area of A, and N0 particles fall on it, then in order to express the area that these particles can touch, it is necessary to calculate the number of atoms per cubic meter in this substance. To do this, it is enough to divide the mass of a cubic meter of matter (density) by the atomic mass in the same units (3.28). Then, having already calculated the volume of the bombarded body, multiplying its area by thickness, multiply it by the number obtained in (3.28), obtaining (3.29).

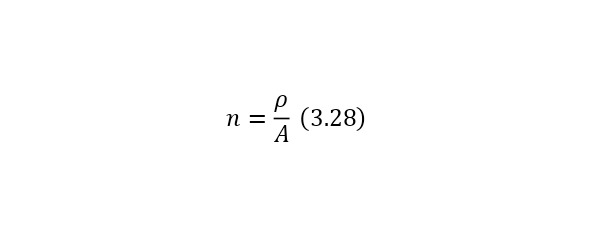
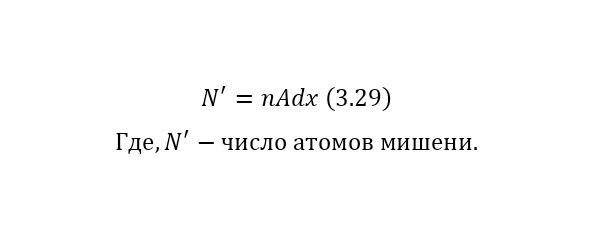
And if we multiply by the cross section, or more precisely, the area for each core on which the interaction will occur, we get the total area of interaction (3.30).

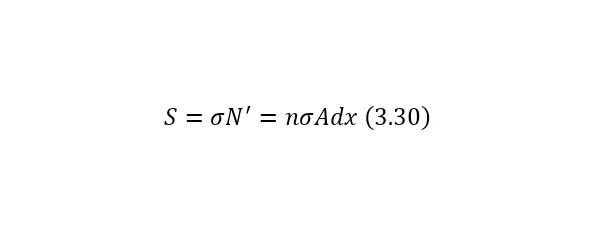
Now, if one number of particles flew in front of the target, and another comes out, then the ratio of this decrease in the number of particles to the total number of those that flew in will be equal to the ratio of this entire bombarded area to the total area (3.31).

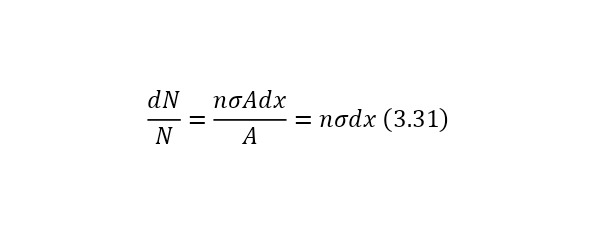
If it is necessary to find the total number of all these interactions, then it is easy to integrate both parts (3.29), thereby obtaining some general equality, from where it is possible to derive a complete formula for the number of interactions (3.32) and (3.33). Integration is carried out for the left part by the number of particles, and in the right by the thickness of the target. At the same time, there is a decrease in the number of particles, not an increase, so a minus is added before the right integral in the expression.

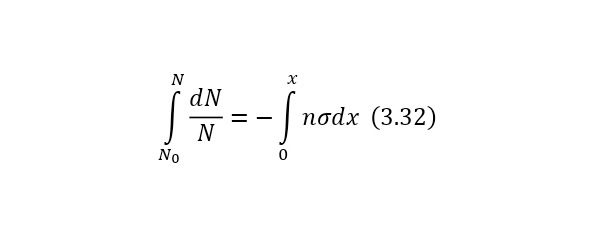
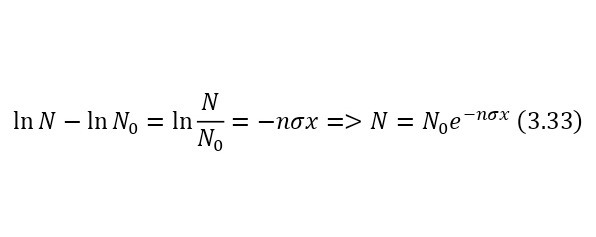
This is how the necessary formula was derived to determine the number of interactions, and for the percentage of interacting particles, it is enough to take the ratios from (3.34).

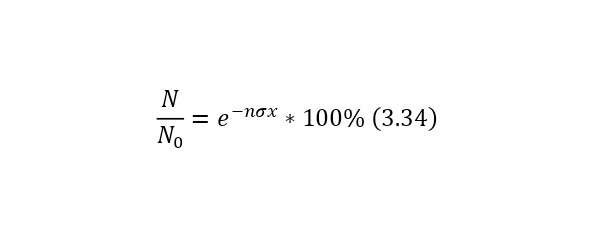
At this point, the complete analysis of nuclear reactions was completed. Thanks to this analysis, it became possible to fully observe not only the energy parameters, theoretical factors, enter the depths of the atom, but also observe the process itself and the practical movement towards calculating the necessary data for any nuclear reaction.

Conclusions to section 1

The first section was entirely devoted only to the analysis of already available data, which may be useful in the subsequent analysis of the issues raised. Of course, until today, quite a lot of work has been carried out in the field of elementary particle and atomic nucleus physics, quantum physics, physics of electromagnetic phenomena, accelerator physics and many other fields, and each of the results is no less important, but in order to analyze the new questions already posed, which will be presented in the next section, it was necessary submit only the most necessary data.

In explaining the course of events, the order, sequence of interpretation and narrative in ascending order is always important, which is why the first chapter was created without any regularities and formulas complicating the process. Thanks to the first chapter, the reader will initially enter the atmosphere of the physics of the atomic nucleus and elementary particles, feel its excitement and all the sensations.

And already in the second chapter, where it was already discussed within the research itself, the concepts of radioactivity and particle decay were introduced for the first time, which will play an important role in the analysis of decays in the second section. Then, the basic concepts of the theory of relativity were introduced, as the primary and most important data needed in the study of elementary particle physics.

And finally, in the third chapter, the very topic of nuclear reactions has already been considered, thanks to which the most basic formulas and the order of analysis of nuclear reactions were indicated. After all, when analyzing a nuclear reaction, it is initially important to determine its yield, that is, its energy potential, if it is positive, then the study of the reaction can be continued by already determining the kinetic energy that each of the reaction products acquire, in the opposite case, the threshold of the nuclear reaction is determined, that is, the minimum kinetic energy that must be given to the nucleus in order for the necessary excitement to occur.

But even if a nuclear reaction with an energy yield is being investigated, it is important to take into account the fact that any nucleus has a repulsive potential or a Coulomb barrier, which is also not unimportant. But it is important to dwell on the processes of the passage of the reactions themselves and their understanding in a little more detail. When a particle hits the nucleus, and if the kinetic energy is sufficient to overcome the Coulomb barrier and the barrier of the reaction itself, if there is a threshold in it, then after that the nucleus and the flying particle combine to form one common nucleus, which will certainly disintegrate in a certain time, and the nucleus itself "forgets" how it was formed. Therefore, after a single channel has been analyzed, it is important to indicate that it can satisfy other decay channels, which are also important to analyze in the study of any nuclear reaction.

An important point, which was also described in the previous chapter, is the presence of each reaction of its cross-section or the impact area of the incoming particle. And as much as this area will be larger, so a large number of interactions occur when passing through the target layer. Thus, this section ends and now we can fully proceed to a detailed analysis of nuclear reactions in the Electron project, which is aimed at using new nuclear reactions with the release of energies.

Section 2. The «Electron» Project

Chapter 1. About the study

And finally, the time has come to move on to a full-fledged description of the idea of this project, which was already the beginning of the whole narrative, which began with the first origins of atomism, went through a number of difficulties on the way to determining the masses of atoms relative to each other, then to determining the mass of the lightest atom. Then this narrative went through the study of radioactivity, the ideas of the theory of relativity, the effects of time dilation, and then moved on to the study of the structure and mechanisms of nuclear reactions.

In fact, the study itself has some purpose, namely: "Generation of a huge amount of electrical energy using the latest safe nuclear reactions at the Electron power plant with its subsequent transfer for consumption." That is, analyzing nuclear reactions, among which there are also thermonuclear ones, some nuclear reactions were selected that were most suitable for using them as new sources of electrical energy, and for greater convenience in organizing this process, a complete model of the general device was developed.

Initially, in the following chapters, the nuclear reactions themselves will be described, and in special chapters, the methods of implementing this device will be briefly described with theoretical calculations.

In total, 6 nuclear reactions were analyzed, each of which forms its own nuclear block with a certain yield and for each block it is necessary to release protons, which will bombard targets with exactly the specified energy.

1. B-block

For the first block, which is also known as the B-block, since the reaction is based on beryllium, it is necessary to generate protons with a kinetic energy of 2,312691131 MeV, this value is determined already during the subsequent study of nuclear reactions. At the same time, the total charge of protons should be 2.845368 ΜL, this charge comes from the consideration that a voltage of 300 V is sufficient for the ionization of hydrogen atoms, after which the nuclei of the hydrogen atom (protons) and electrons are formed separately. Even though the electron energy in the first orbit of the hydrogen atom is on the order of 13.6 eV, which corresponds to 13.6 V, but in order to give sufficient kinetic energy to the formed ions and electrons, it is necessary to create a proper electric field between the cathode and the anode, due to a voltage of 300 V. And already for the presence of a large charge and the number of protons, it is enough to use a current of the order of 15 kA, and the time of charge passage is equal to the time required for a proton to acquire this energy in a charged particle accelerator, which is determined by subsequent calculations and is 189.691 ns.

To obtain such particles, it is necessary to use an ionizer or, more precisely, a gas discharge tube in which there is a cathode and an anode. When hydrogen portions are injected into a gas discharge tube, with the presence of a number of hydrogen atoms not less than the number of protons with the specified charge, this number is determined in (1.1), the atoms undergo ionization and protons with a kinetic energy of 300 eV are released. At the same time, the total work per second will be (1.2), but now the work for 1 act (1.3) is more interesting, which is worth taking note of.

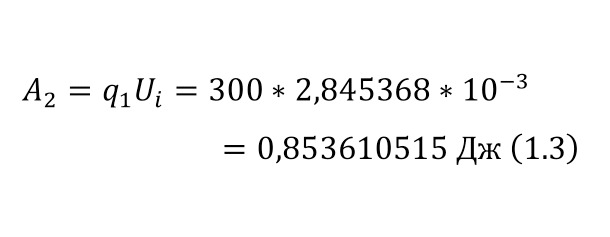
Thus, a total charge of 15 kcal passes through the wires in a second, but in order for the conductors to pass such a current, conductors of large dimensions will be used, which will allow generating high-power energy in the future.

The formed protons fly out of the gas discharge tube under the action of the electric field of the cyclotron duants, which are supplied with high voltage. At the same time, it is important to point out that the number of duants — divisions of one common metal cylinder is not 2, as with conventional cyclotrons, but much more, in this case — 8 parts. Thus, provided that the gas discharge tube is located in the center of the cyclotron, also in a magnetic field that leads only to movement along a helical path, the radius (1.6) is for electrons (1.7), and for protons (1.8), provided that the magnetic field induction is 1 Tl, and the velocity of particles from an energy of 300 eV is determined for electrons in (1.4), protons in (1.5), which was already indicated earlier.

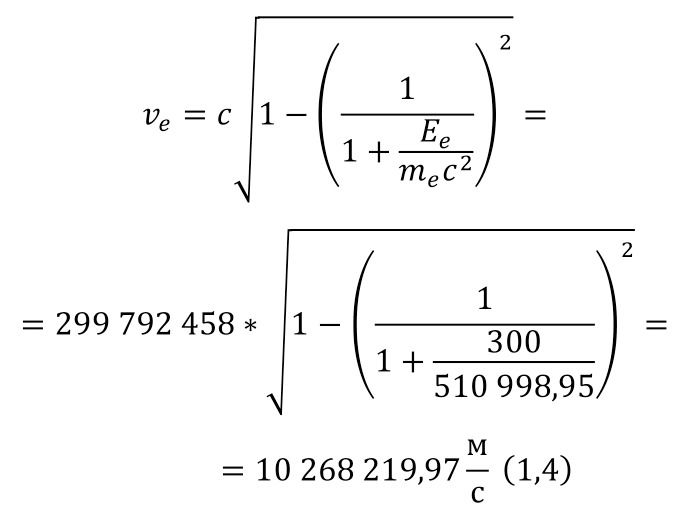
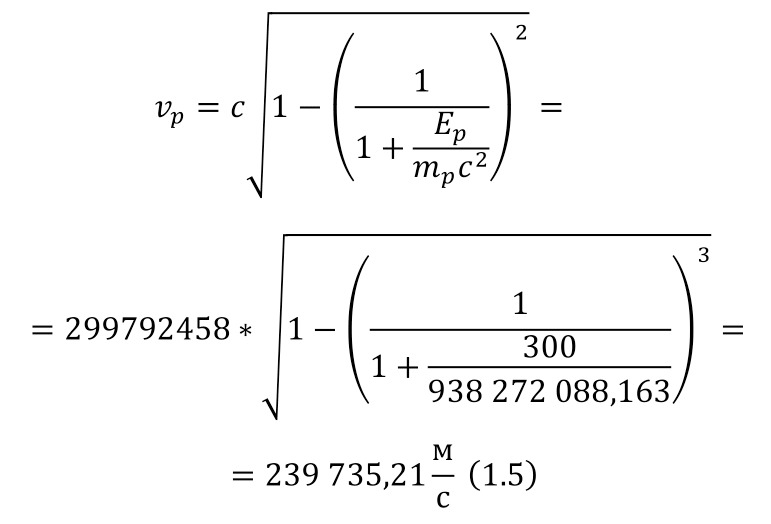
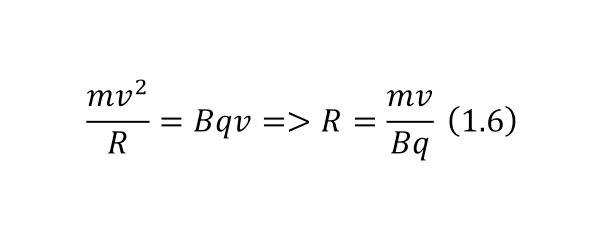
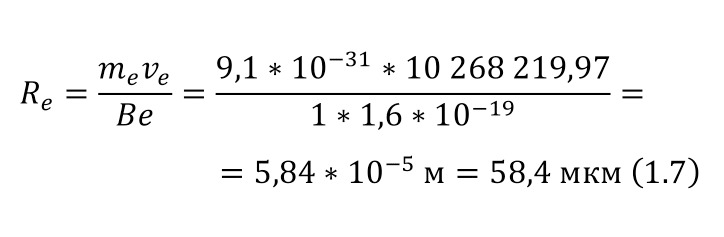
After this small rotation and attraction by one of the duants of protons, they begin to rotate in a flat spiral, due to the potential difference. At the same time, for each revolution, the proton acquires an energy of 800 keV, since the voltage between the duants is 100 kV. The current strength for this supply is also equal to 15 kA, since it is this current that captures the cyclotron during particle acceleration, and not to mention the change in polarity or, more precisely, the frequency of the cyclotron, it is determined by the formula (1.10), and, accordingly, the period (1.9).

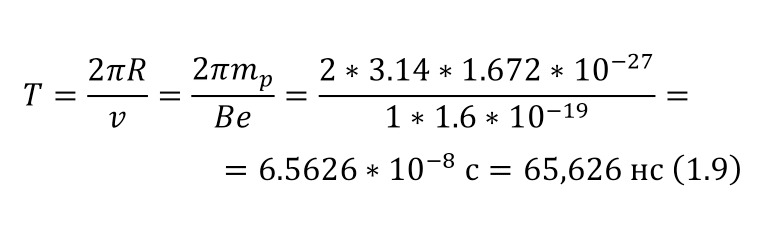
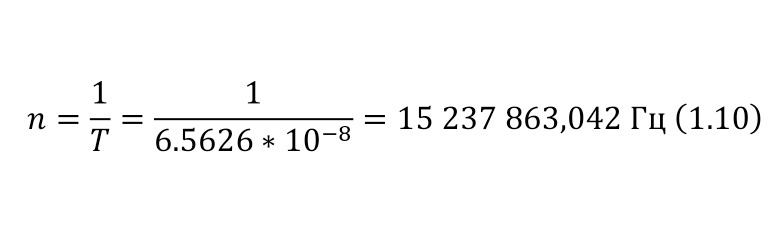
At the entrance to the cyclotron, the proton already has an energy of 300 eV, thus, the energy required to acquire energy of 2,312691131 MeV is 2,312391131 MeV, for which it is necessary to make 2,890488914 revolutions, and taking into account that one revolution takes 65.626 ns, as was calculated in (1.9), the total time of the act is 189,691 ns, which was taken into account earlier, knowing this time it is easy to determine that the frequency of acts will be 5,271,725.13 acts/s. With this account, the work performed by the cyclotron for one acceleration according to (1.11) is easy to determine, with a charge of 2.845368 ΜL and a voltage of 100 kV, and for general acceleration, it is already necessary to use (1.12), which also indicates that this work is equal to the work of the outgoing particles itself.

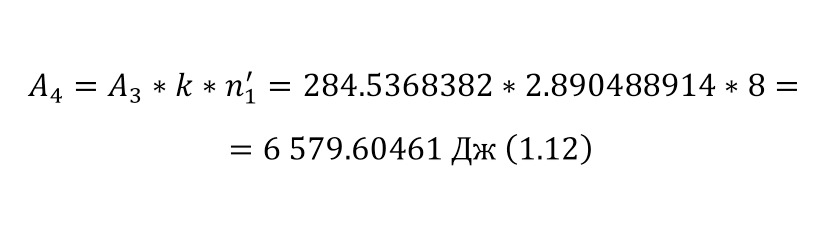
Thus, the total energy consumed per 1 act is 0.853610515 J for the ionizer, and 6 579.60461 J for the cyclotron, and 6 580.458221 J for the entire accelerating unit. At the same time, if we take into account that 5,271,725.13 acts occur per second, then the total work performed is 34,690,366,963.83 J, and if we specify that 1 W * s is 3,600 J, then this value also equals 9,636,213.05 W*h.

All the described data are presented in (Table 1.1).

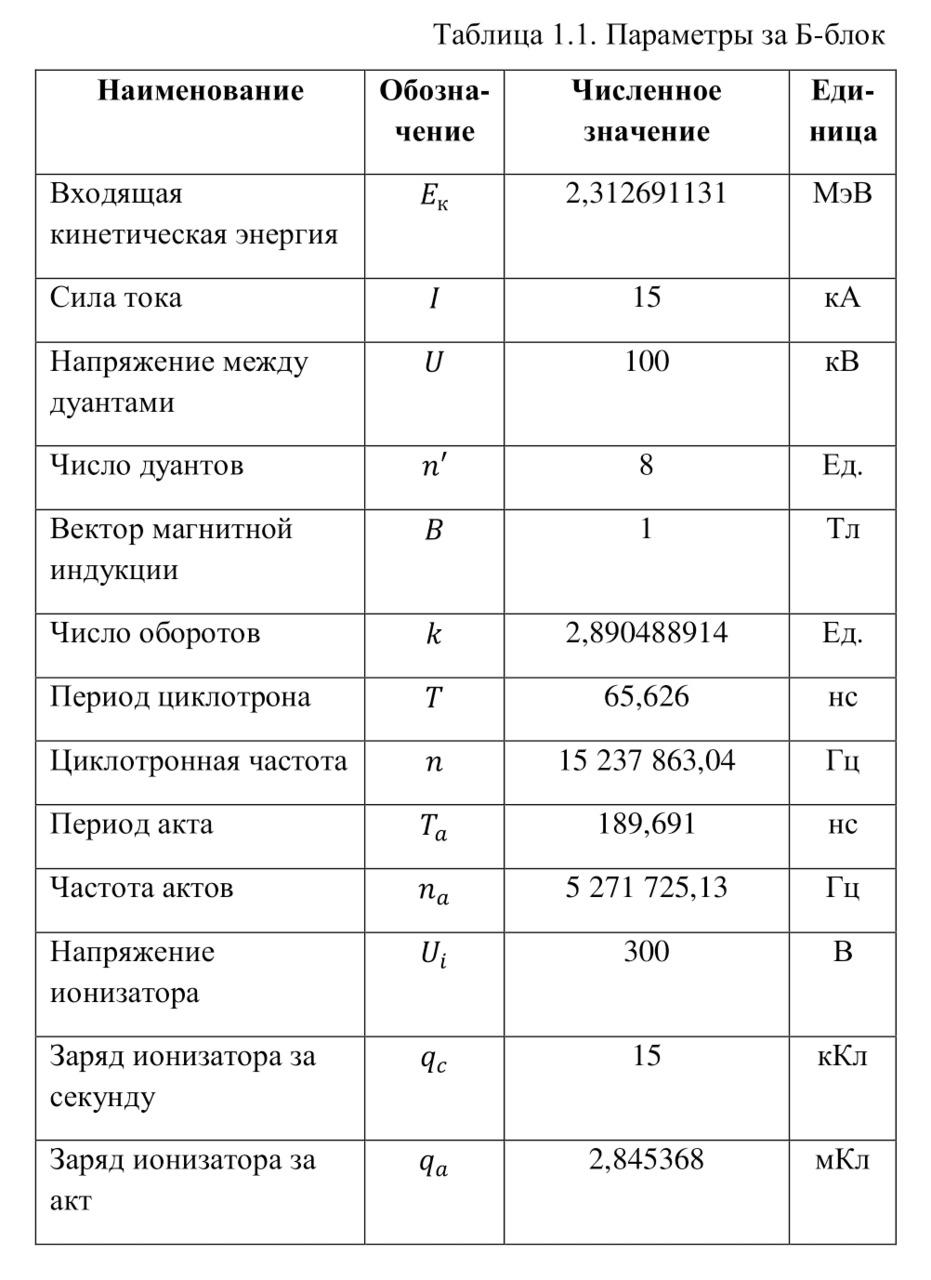
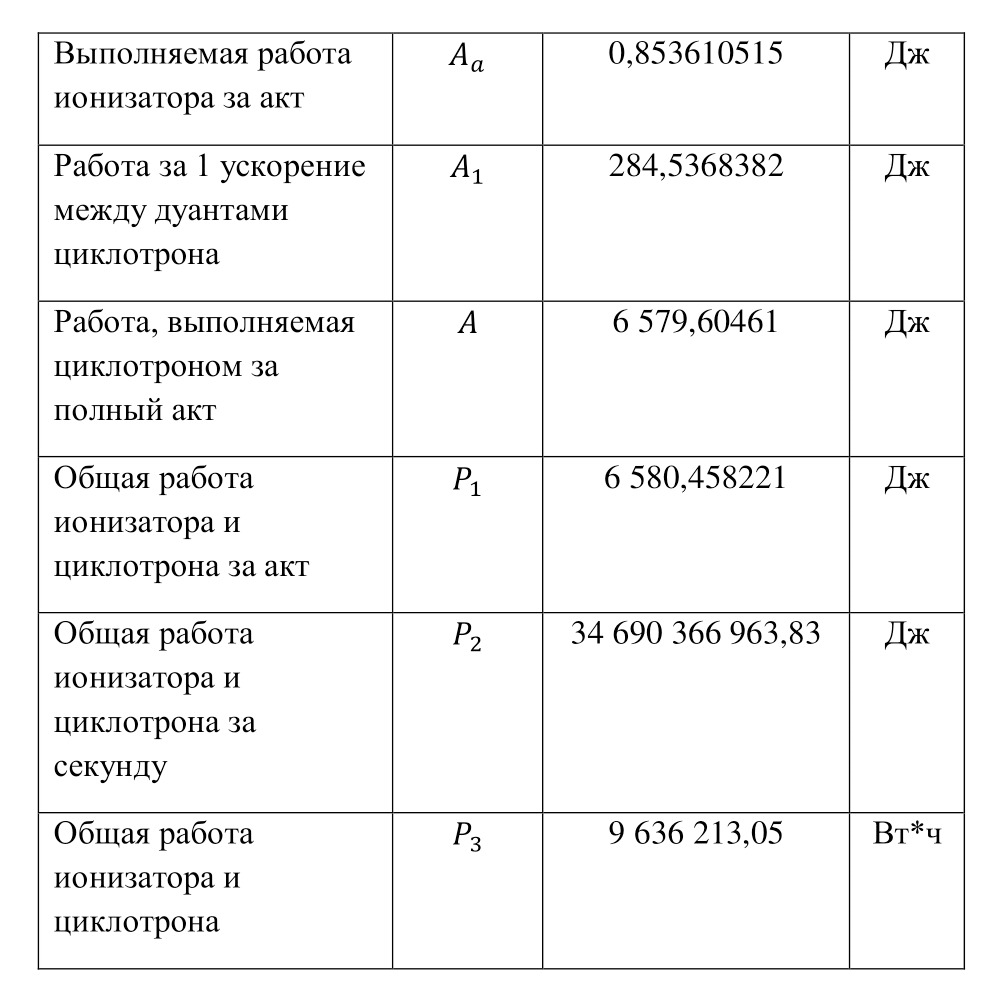
For the second B1-block, it is necessary to have protons with an energy of 1.978143029 MeV with a current of already 5 kA. If you specify that the duants also have a voltage of 100 kV and 8 duants, as well as the induction vector of the magnetic field of the coil is equal to 1 Tl, then to obtain such energy it is necessary to make 2,472303786 revolutions. At the same time, the period of the cyclotron is also equal to 65.626 ns and 15,237,863.04 Hz, and the period of the acts is (1.13) and their total frequency is (1.14).

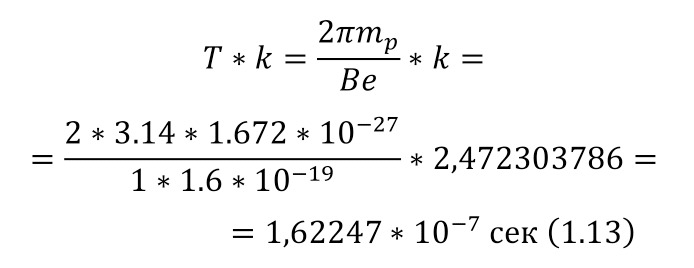
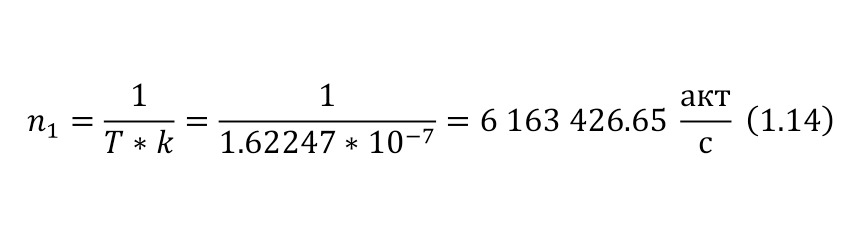
Thus, the total time of the act will be 1,62247 * 10—7 seconds, and the frequency of acts will be 6,163,426.65 acts per second. At a known time of the act, it takes place to specify the parameters of the ionizer, which operates under a voltage of 300 V and a current of 5 kA or 5 kcal per second, respectively, during the act, the passing charge is 811.237 MCL, respectively, the work for 1 act for the ionizer is already 0.243371112 J due to the greater number of revolutions. And already if we take into account that with a known charge and voltage of 100 kV, due to the fact that during the act of 162.247 ns only 2.472303786 turns, then the work for the implementation of 1 acceleration is 81.12370415 J (1.15), and the total work of the cyclotron itself performed for 1 act is 1,604.499527 J (1.16).

Thus, with an ionizer consumption of 0.243371112 J, and a cyclotron of 1,604,499,527 J, the total work is 1,604,742899 J per 1 act, respectively, with a frequency of acts of 6,163,426.65 acts per second, the total work is 9,890,715,145.83 J, which corresponds to 2,747,420.87 W*h.

All the described data are presented in (Table 1.2).

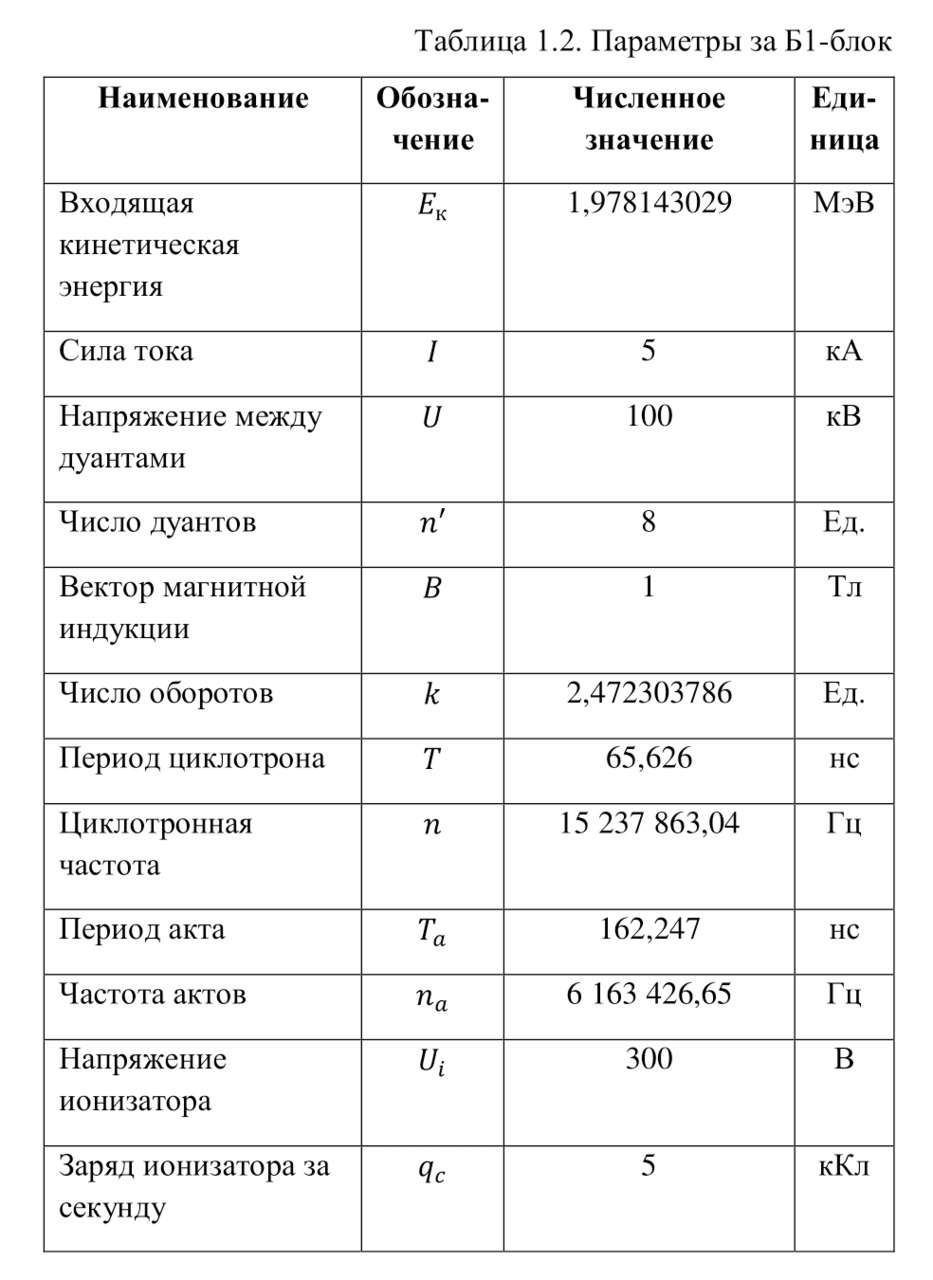
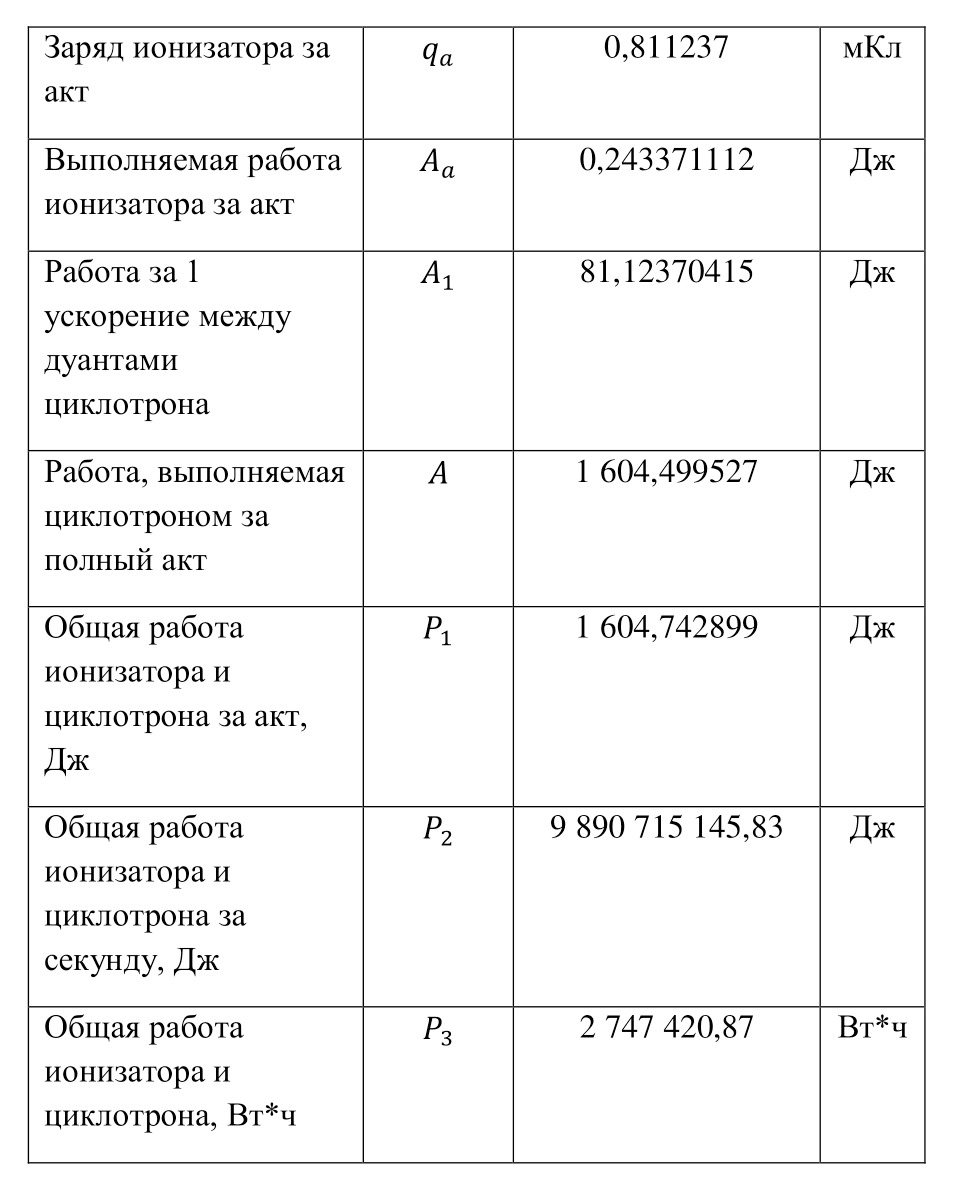
3. L-block

The L-block is launched at the entrance of protons with an energy of 1.613245483 MeV and a current of 15 kA. For this accelerator, the voltage is also 100 kV and there are 8 duants in total and the magnetic induction vector is 1 Tl, and the number of revolutions for this energy is 2.016181854, with a period of 65.626 ns for one revolution and a cyclotron frequency of 15,237,863.04 Hz. And the period of one act, respectively, at known energies, is equal to 132.314 ns and 7,557,782.06 acts per second are performed.

At the same time, if we take into account that there is 300 V on the ionizer, and the current strength is 15 kA, then the charge for 1 act is 1.984709 ΜL, at a known time of the act. And the work performed by the ionizer is 0.595412776 J, and for the cyclotron 3 201.227828 J, therefore, the total consumption is 3 201.823241 J per act, 24 198 682 244.29 J per second or 6,721 856.18 W*h.

In this case, the frequency of acts is calculated by (1.17), and the period by (1.18), from which the formulas for the acceleration operation in the cyclotron (1.19), and for the entire act in (1.20), follow.

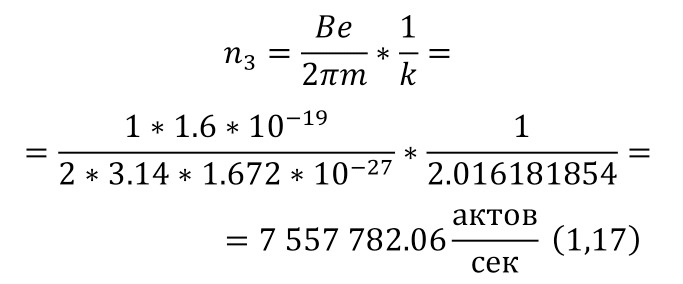
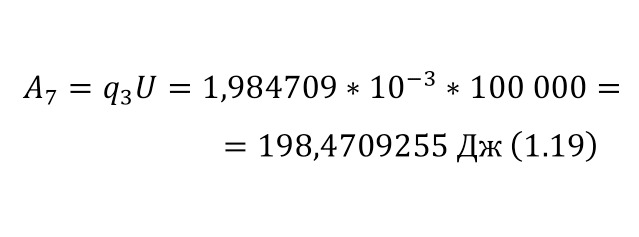
All the described data are presented in (Table 1.3).

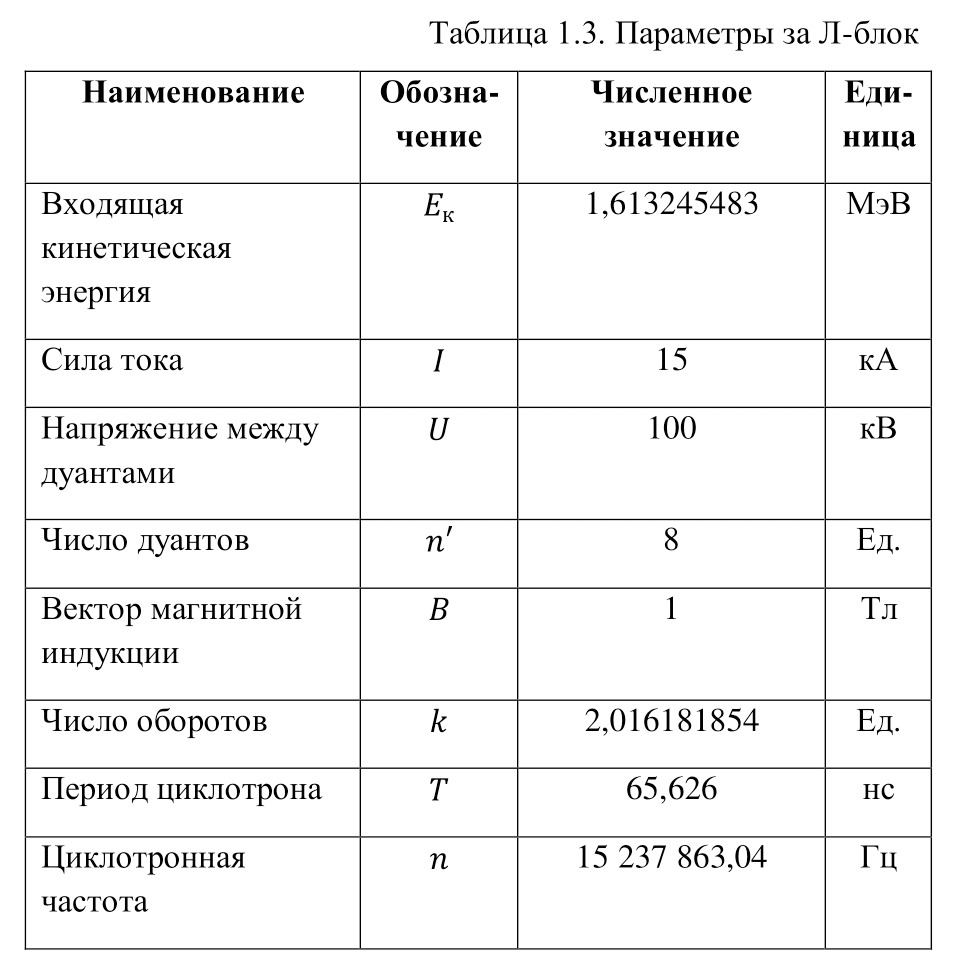
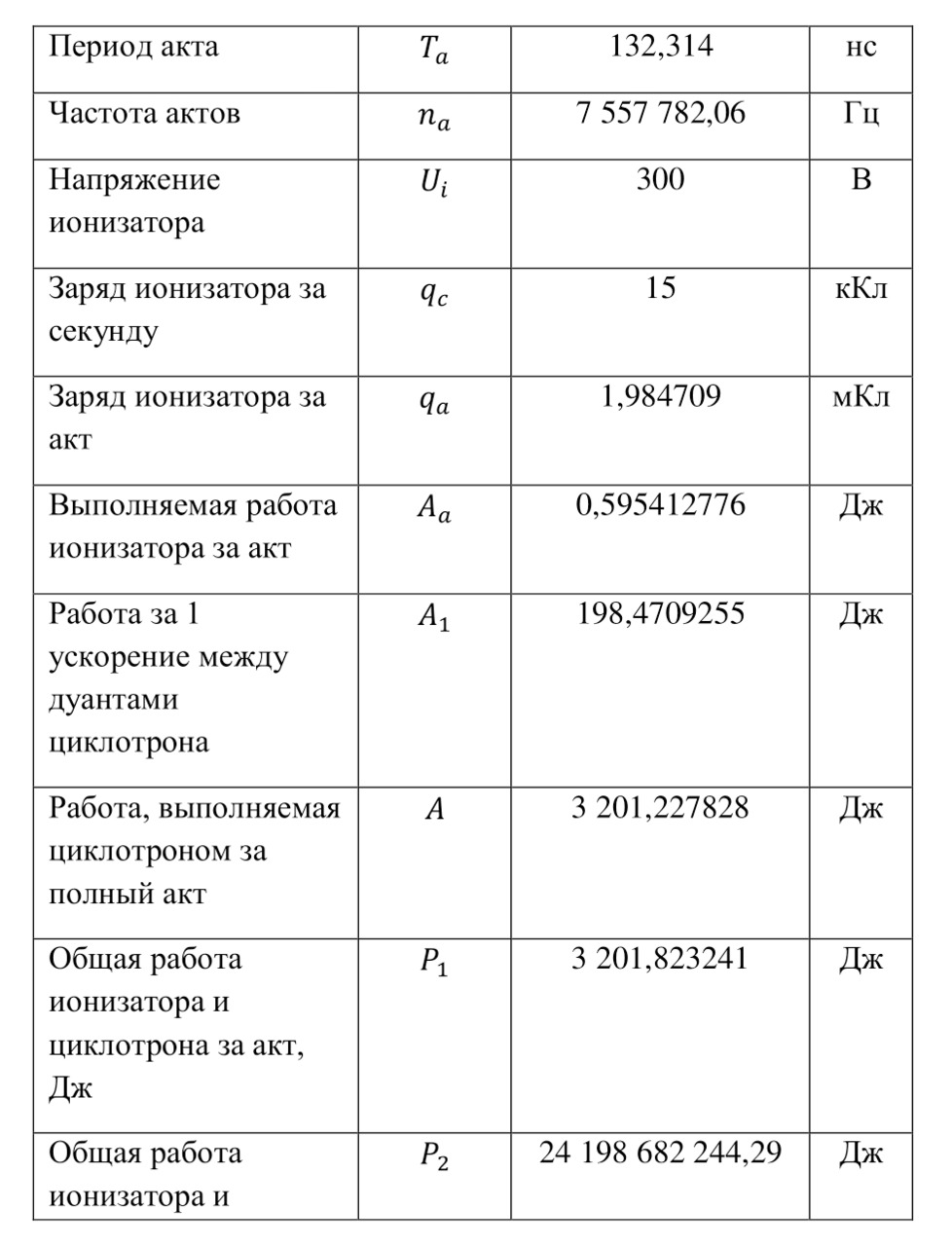
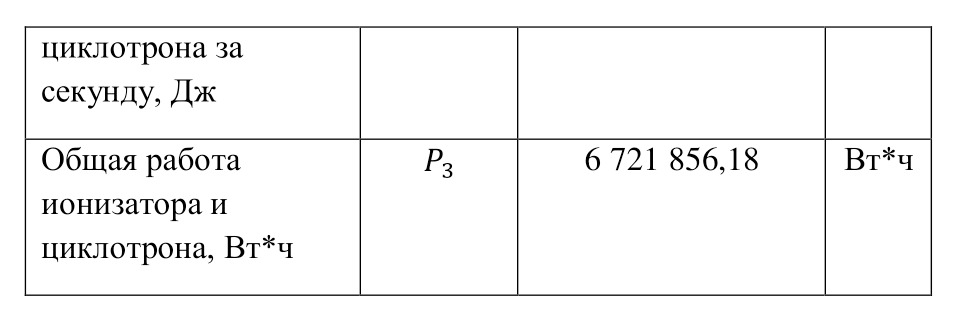
4. A-block

The A-block acts already under the action of protons with energies of 4.457595117 MeV, with a current of 5 kA. At the same time, a voltage of 100 kV, 8 duants and a magnetic induction vector of 1 Tl is also preserved, while the number of revolutions is 5,571618896, with the same period of 65,626 ns and a frequency of 15,237,863.04 Hz, with a period of 365,643 ns (1.21) and a frequency of 2,734,904.63 acts per second (1.22). For the ionizer, the voltage is still the same 300 V, with a current of 5 kA, which corresponds to 5 kl per second or 1.8215 ΜL per act or the work performed per act of 0.548464592 J.

In this scenario, the work for 1 acceleration is 182.8215308 J (1.23) and the total work of the cyclotron is 8 148.895166 J per act (1.24). At the same time, the total expenditure per act is 8,149.44,3631 Joules 22,287,975,583.59 Joules per second or 6,191,104.33 W*h.

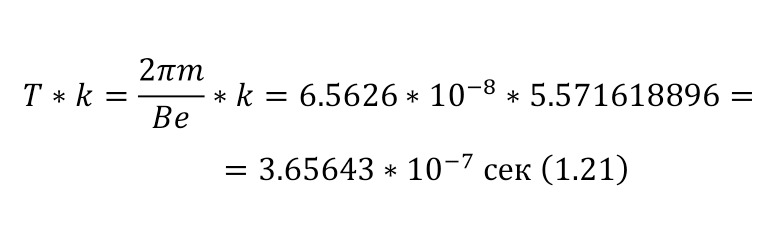
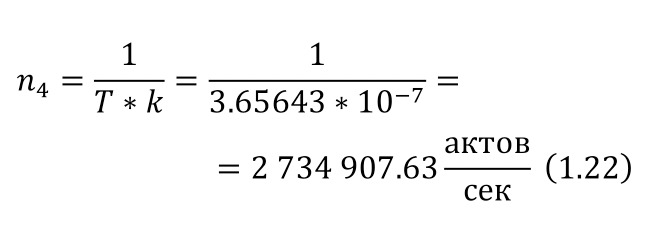
All the described data are presented in (Table 1.4).

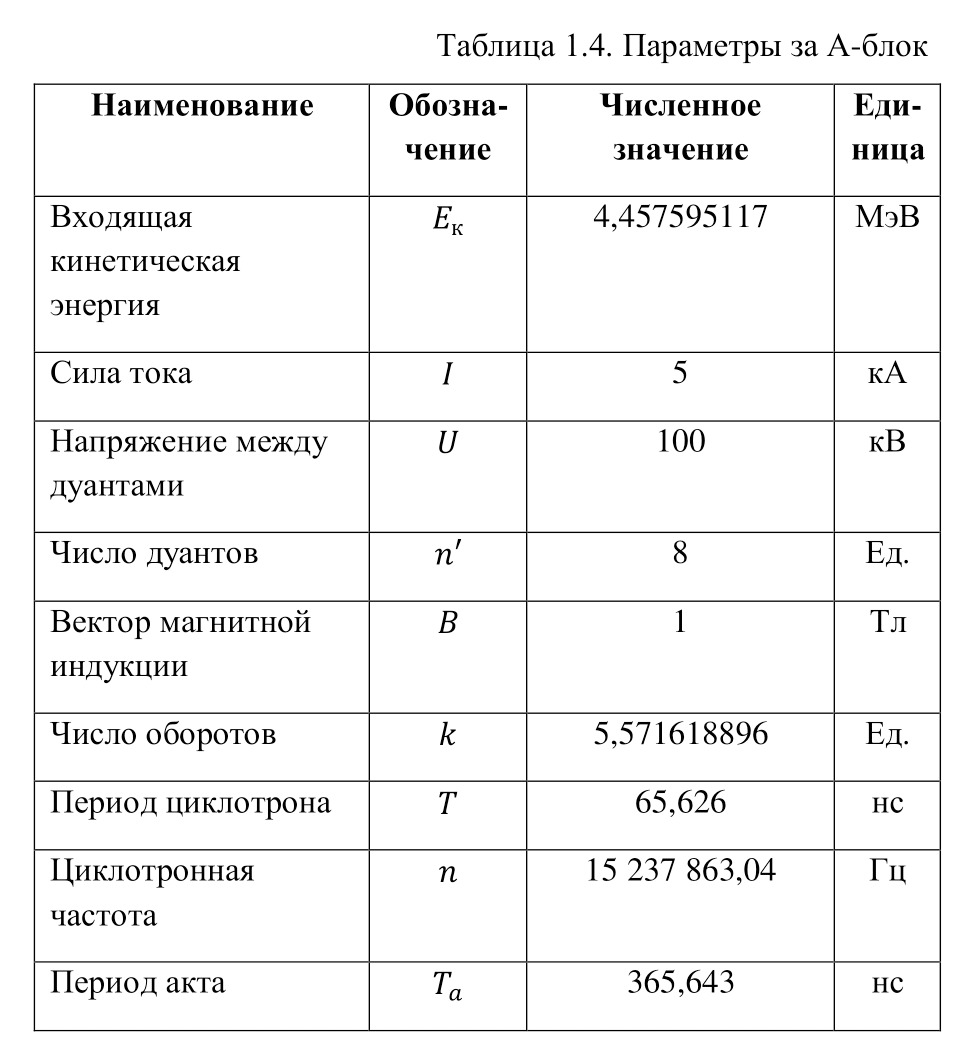
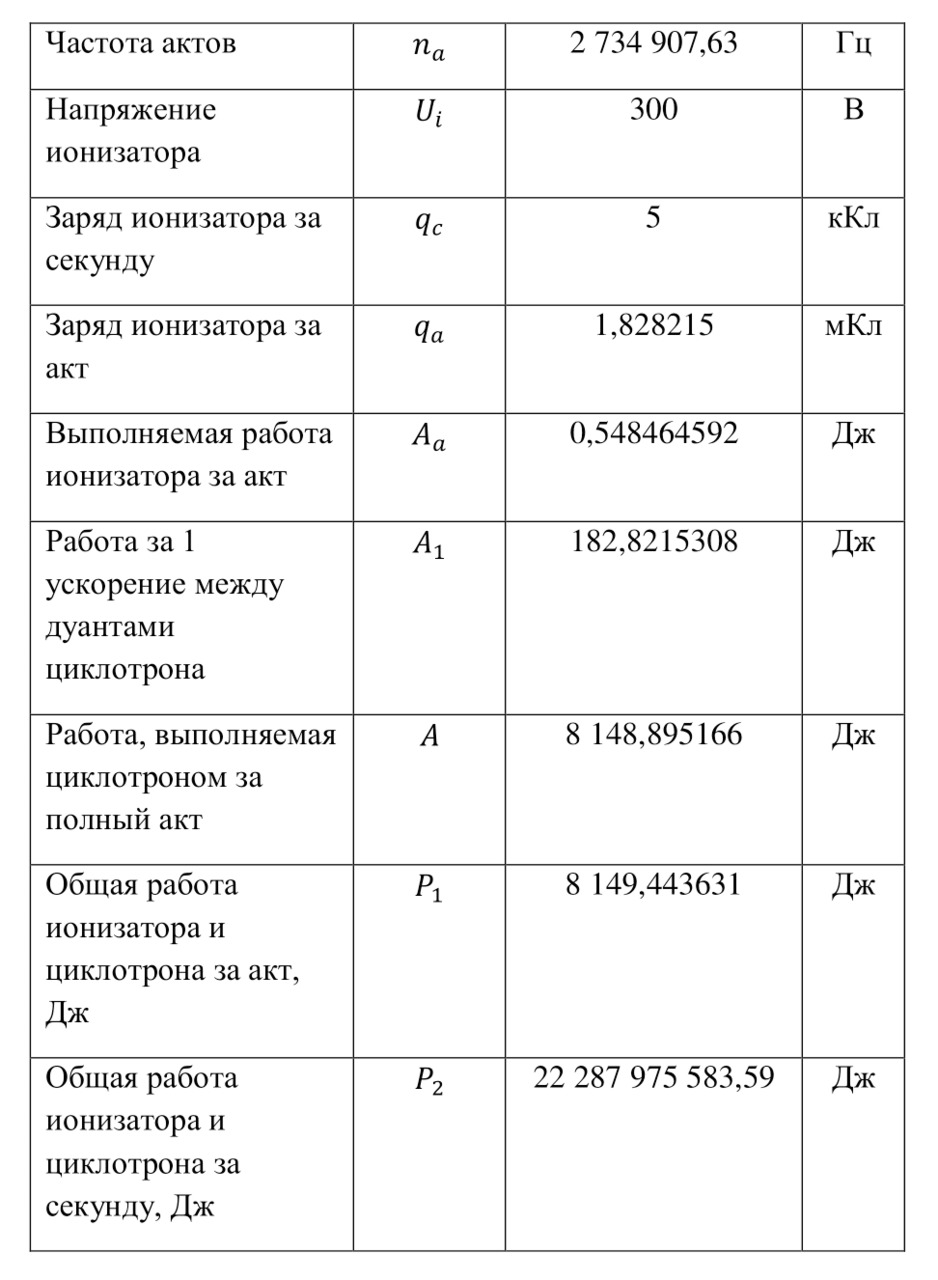
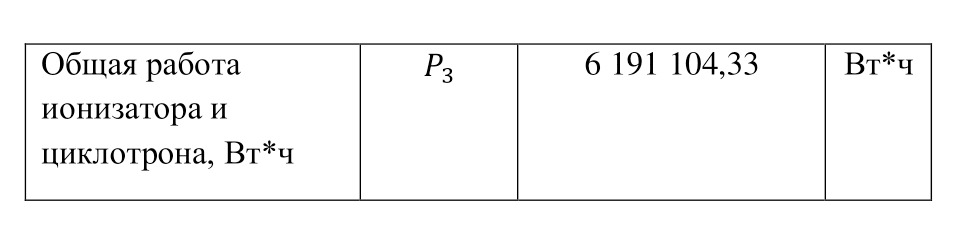
5. D-block

The main difference between this and the next blocks is that they act on deuterium. The same method will be used to generate deuterium, the only difference will be that protons become free only at an energy of 13.6 eV, which acts on 1 electron and only then it acquires an energy of 300 eV between the ionizer plates. In the same case, the picture will not change much for the reason that the deuterium ionization energy is only slightly different and will amount to 14.9 eV. Deuterium itself is stable and is produced together with "heavy water", the production volumes of which are impressive today. Therefore, to obtain deuterium, it is sufficient to carry out the electrolysis of heavy water and obtain deuterium, which is converted into deuterons in an ionizer.

It is also important to note such a fact as the choice of the target thickness for each of the reactions. A particle having a certain energy after passing into the target plate passes only up to a certain distance. Below is a table of proton runs in aluminum with different energies, from which all thicknesses of reaction plates were used (Table 1.5), also indicating in units of cm and mg/cm2, as well as alpha particle runs in air, biological tissue and aluminum (Table 1.6).

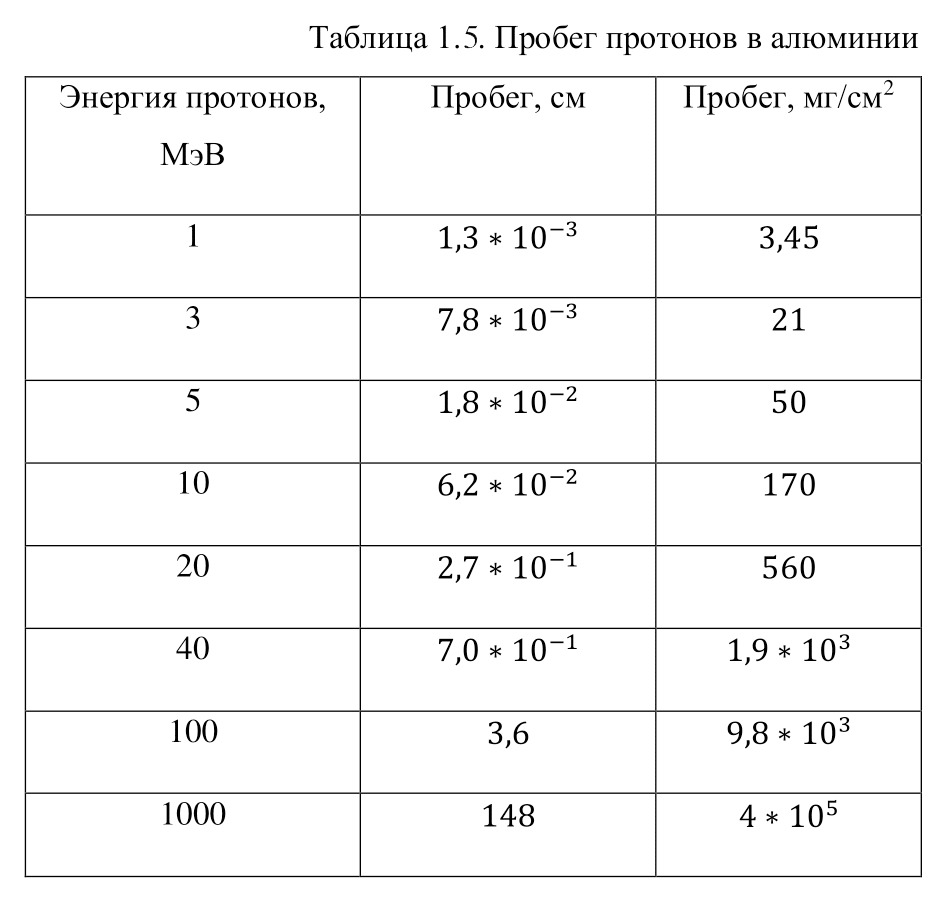
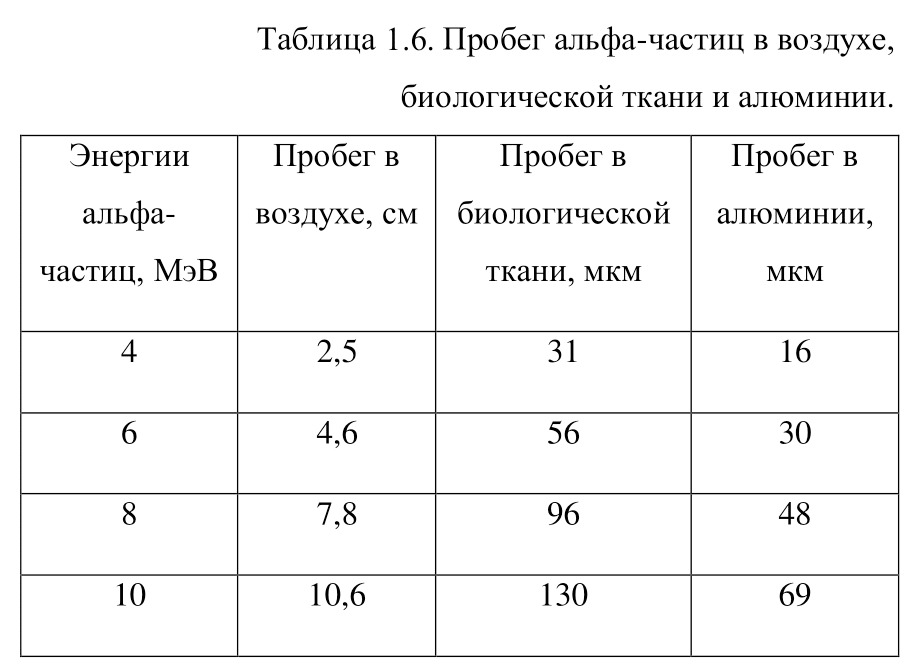
Numerically, the energy loss for some particle is determined through the Bethe-Bloch formula, which takes into account the parameters of both the atom and the incoming particle, but in general, for the reactions under study, there is no need to use the Bethe-Bloch formula for the reason that a thickness corresponding to an energy less than the incoming one is used, this makes it possible to round everything beautifully these values.

The D-block acts already under the action of protons with energies of 1.613245383 MeV, with a current of 15 kA. At the same time, a voltage of 100 kV, 8 duants and a magnetic induction vector of 1 Tl is also preserved, while the number of revolutions is 2.016556729, with the same period of 65.626 ns and a frequency of 15,237,863.04 Hz, with a period of 132.339 ns (1.25) and a frequency of 7,556,377.08 acts per second (1.26). For the ionizer, the voltage is still the same 300 V, with a current of 15 kA, which corresponds to 15 kcal per second or 1.985078 ΜL per act or the work performed per act of 0.595523483 J.

In this scenario, the work for 1 acceleration is 198,5078,278 J (1.27) and the total work of the cyclotron is 3,202,418,367 J per act (1.28). At the same time, the total expenditure per act is 3,203.013891 J or 24,203. 180. 744.29 J per second or 6,723. 105.76 W*h.

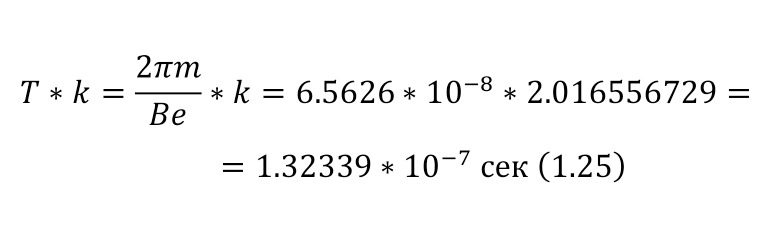
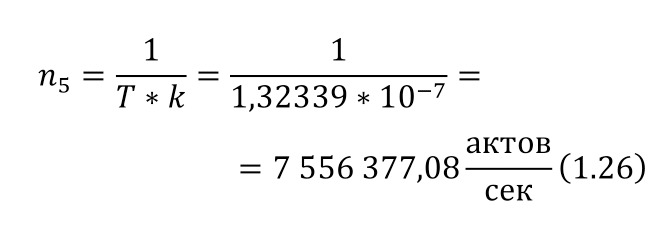
All the described data are presented in (Table 1.8).

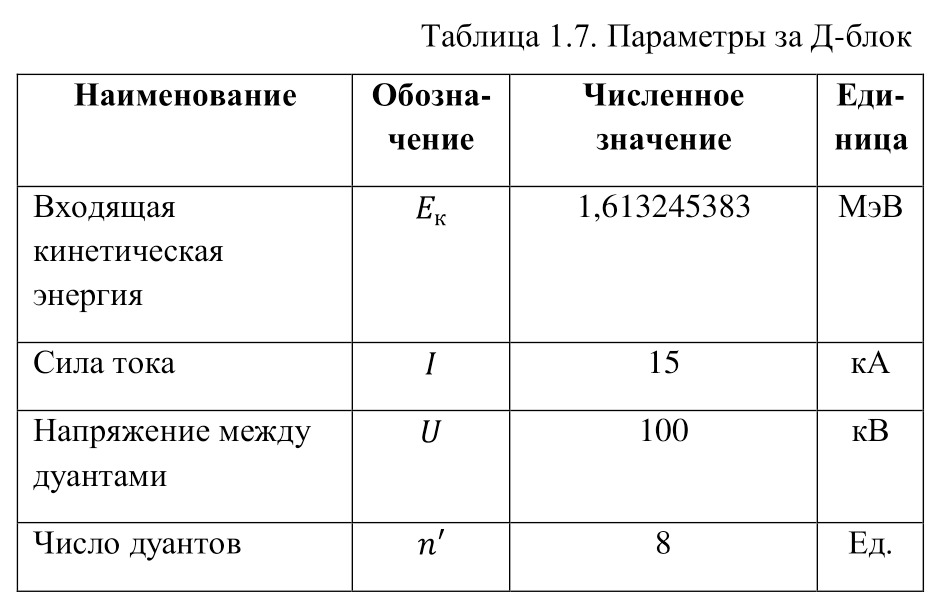
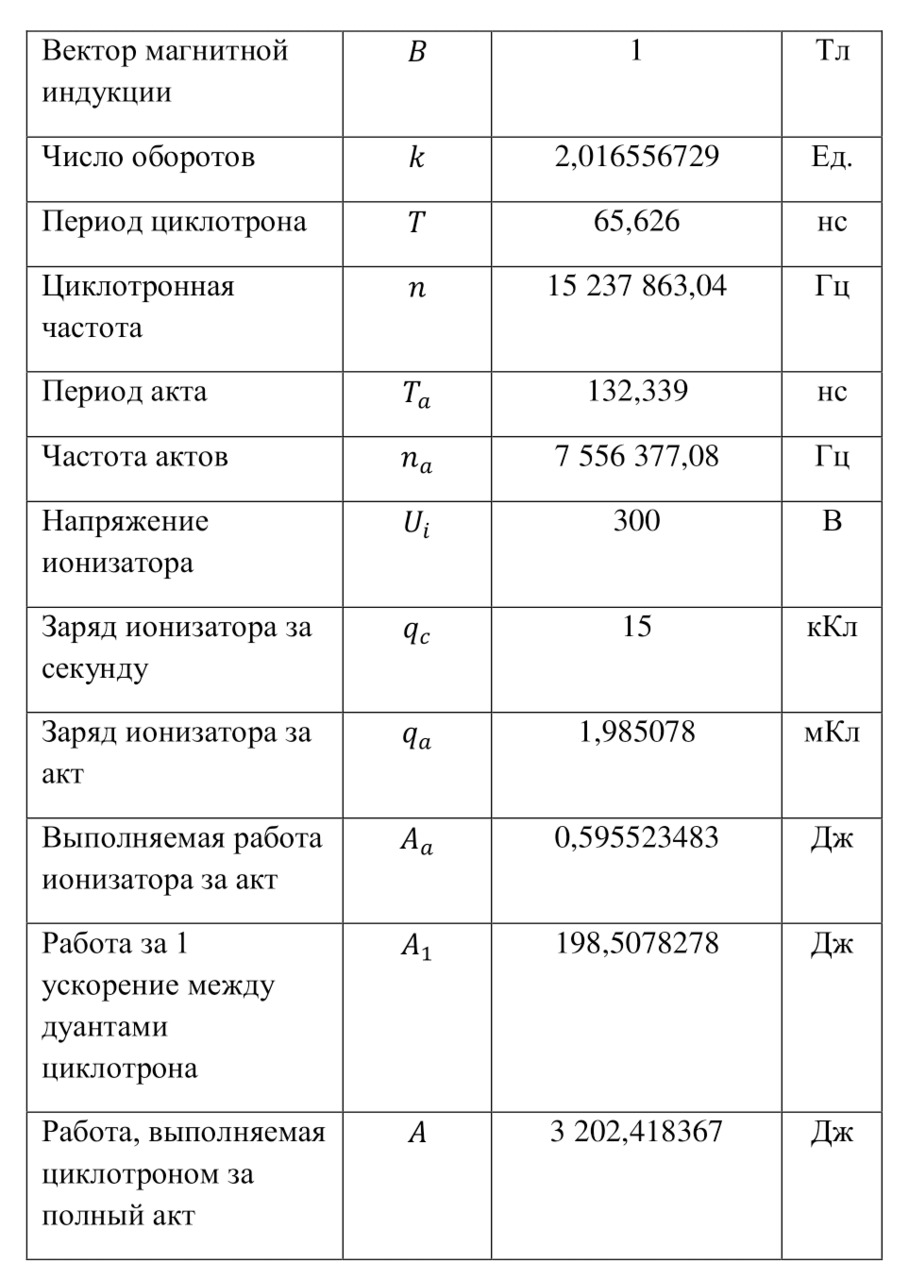
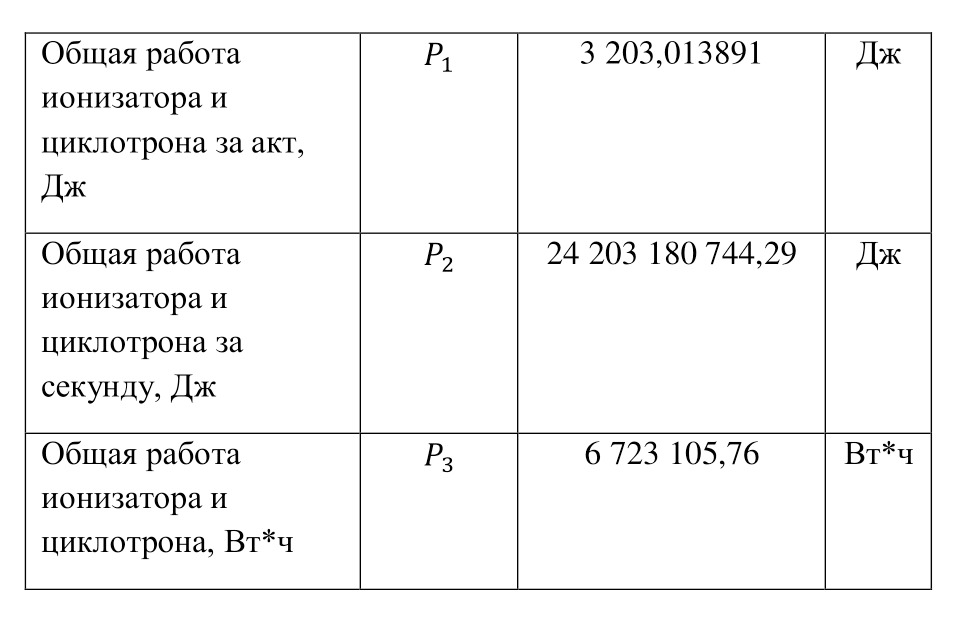
6. D1-block

The D1 block already acts under the action of protons with energies of 1.698306298 MeV, with a current of 15 kA. At the same time, a voltage of 100 kV, 8 duants and a magnetic induction vector of 1 Tl is also preserved, while the number of revolutions is 2,122882873, with the same period of 65.626 ns and a frequency of 15,237,863.04 Hz, with a period of 139,316 ns (1.29) and a frequency of 7,177,910.4 acts per second (1.30). For the ionizer, the voltage is still the same 300 V, with a current of 15 kA, which corresponds to 15 kcal per second or 2.089745 ΜL per act or the work performed per act of 0.626923401 J.

In this scenario, the work for 1 acceleration is 208.9744671 J (1.31) and the total work of the cyclotron is 3,549.026538 J per act (1.32). At the same time, the total expenditure per act is 3,549,653461 J or 25,479,094,476.34 J per second or 7,077,526.24 W*h.

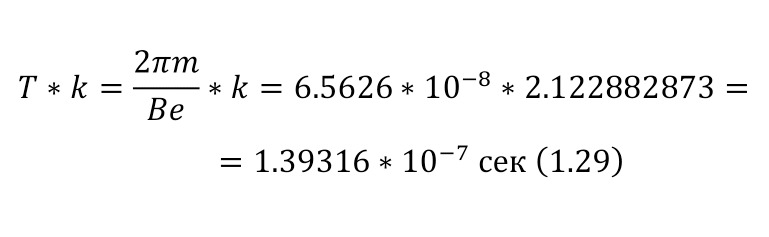
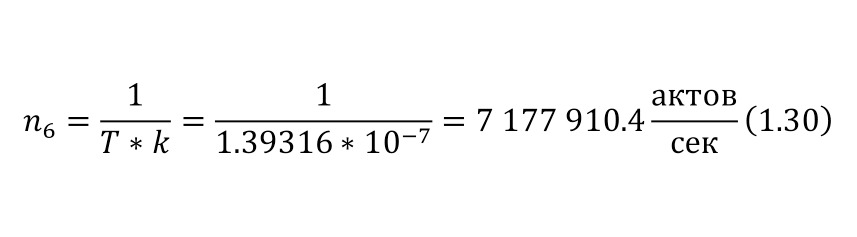
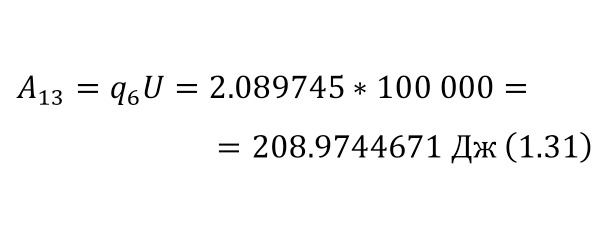
All the described data are presented in (Table 1.9).

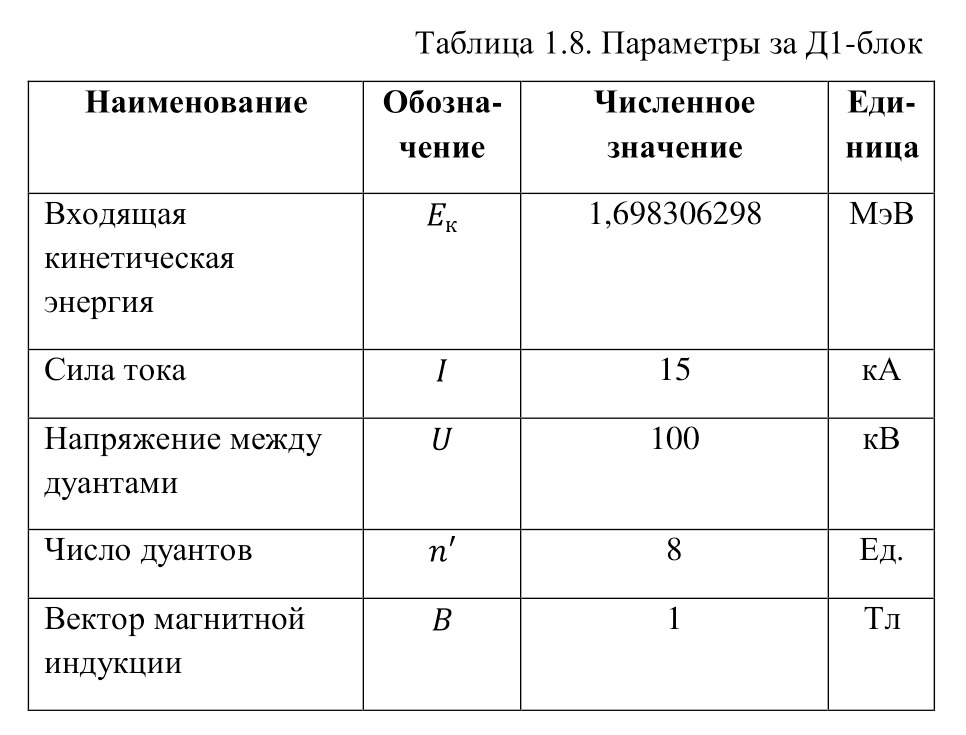
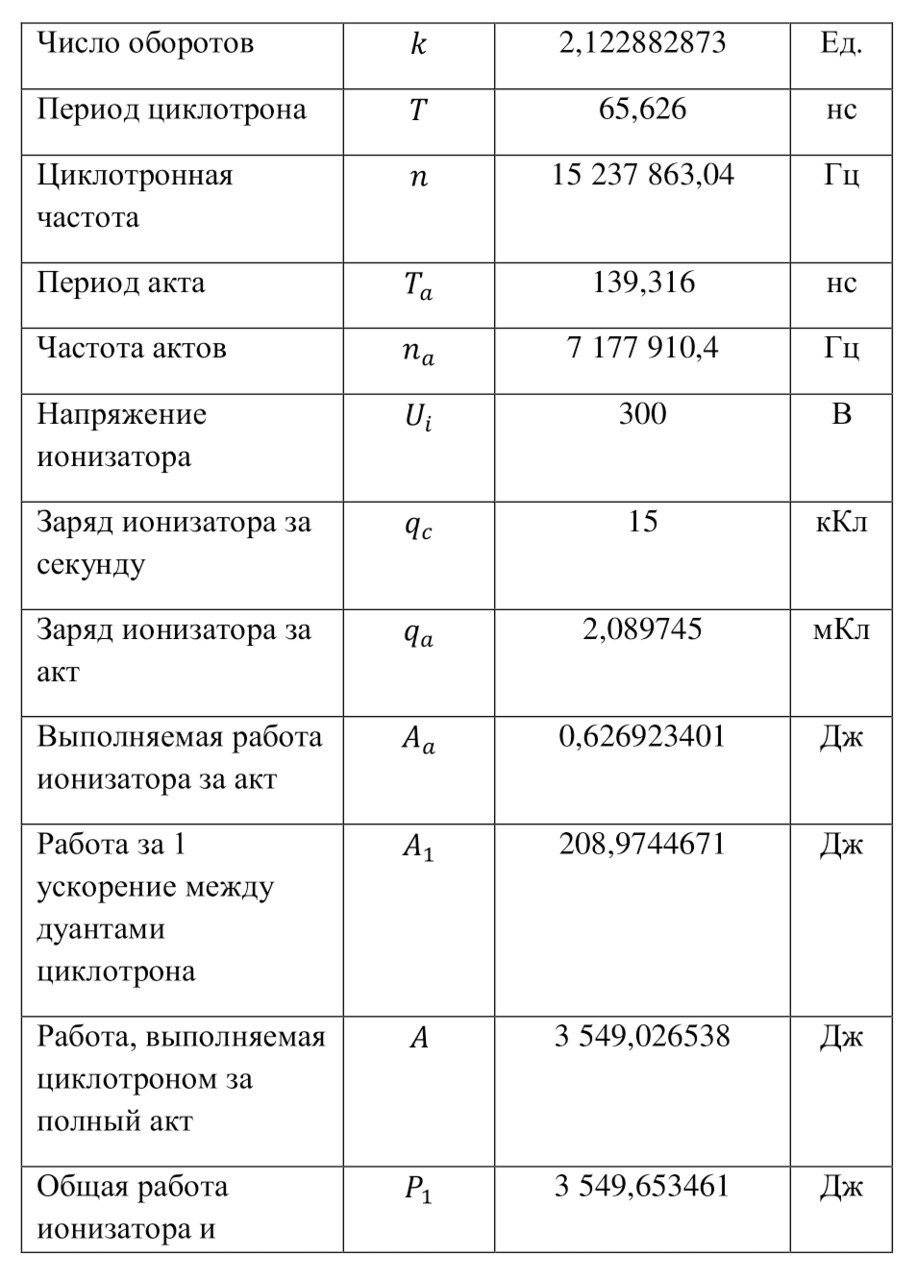
After the consumption system has been specified and discussed, and an additional study will be conducted for a more detailed description of the accelerating system for each of the blocks, there is a transition to a full-fledged analysis of nuclear reactions for the blocks.

Note: In this section, the formulas described in the first section are used, but in the numbering, the section number is not entered when referring to the formulas.

Chapter 2. The first B-power unit

The first nuclear reaction is represented as follows (2.1).

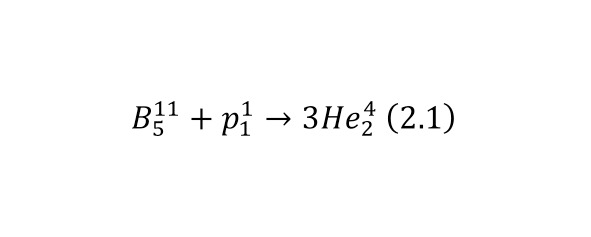
A proton with an energy of 2,312691131 MeV and a mass of 1,00728 a. m., hits boron-11 with an atomic mass of 11,00930517 a. m., with the release of three alpha particles of mass, which amount to 4,001506179 a. m

.Initially, it is necessary to determine how much energy the proton will spend, approaching the boron nucleus-11, namely the height of the Coulomb barrier (2.3), having determined the radius of the boron core -11 in (2.2).