
Бесплатный фрагмент - Review. Benzene on the basis of the three-electron bond
Theory of three-electron bond in the four works with brief comments (review). 2016.
I express my deep gratitude to my son, Bezverkhniy Vitaliy Volodymyrovich, for participation in the development of the theory (some parts as a co-author), and for his invaluable contribution to the English translation.
Abstract: Using the concept of three-electron bond we can represent the actual electron structure of benzene and other molecules, explain specificity of the aromatic bond and calculate the delocalization energy. Gives theoretical justification and experimental confirmation of existence of the three-electron bond.
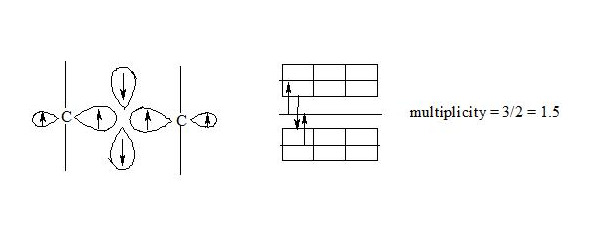
It was shown, that functional relation y = a + b/x + c/x2 fully describes dependence of energy and multiplicity of chemical bond from bond distance.
Keywords: benzene, three-electron bond, semi-virtual particle, fermion, entangled quantum state, Interfering Universe.
1. Introduction
Chemical bond has been always a basis of chemistry. Advancement of chemical science can be considered as evolution, development of concepts about chemical bond. Aromatic bond is fundamental basis of organic chemistry. Concept of three-electron bond in benzene molecule enable to explain specificity of aromatic bond. It also becomes apparent, why planar molecules with 6, 10 etc. electrons (according to Hückel rule 4n +2) must be aromatic, and planar molecules with 4, 8 etc. electrons cannot be aromatic by definition.
Description of chemical bond, that is given by quantum theory, especially in terms of method of molecular orbitals, is just a mathematical model. This model is an approximate representation of molecules and its bonds, whereas quantum-mechanical calculations of organic molecules require considerable simplifications and are extremely complicated.
Concept of three-electron bond and developed mathematical relations in this work are rather simple, illustrative and give exact results of different values (bond multiplicity, chemical bound energy, delocalization energy of benzene). One must clearly imagine, that three-electron bond is joint interaction of three electrons with relative spins, that results in new type of chemical bond (A • • • A (+ — +), A • • • B (+ — +)). This bond type, three-electron bond, makes possible to describe real molecules of organic and inorganic compounds without invoking virtual structures, which do not exist in real terms.
Using of three-electron bond before description of benzene molecule enables to determine delocalization energy of benzene in an elementary way, understand why multiplicity of С-С bond of benzene is more than 1.5 and to understand the main point of aromatic bond in general, which is appeared to be rather illustrative. Besides, for determination of delocalization energy it is not required to select reference structures. Delocalization energy follows from the concept of aromaticity of benzene and its structure on the basis of three-electron bond.
I note that the three-electron bond to describe the benzene molecule used W.O. Kermak, R. Robinson and J. J. Thomson at the beginning of the 20th century [5, 6].
But since it is not taken into account the spin of electrons, have already started cyclooctatetraene problems and therefore the description of the benzene molecule by a three-electron proved unsuccessful. Using the three-electron bond with multiplicity of 1.5 and take account of the spin of each electron leads to very good results in the description of the benzene molecule and explain the aromaticity in general. With the help of three-electron bond with multiplicity of 1.5 can be represented by a real formula of many organic and inorganic molecules without the aid of virtual structures.
2. Structure of the benzene molecule on the basis of the three-electron bond
2.1. Results and discussion
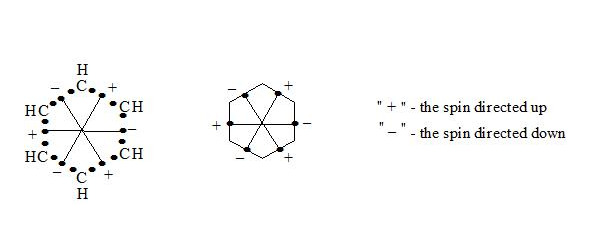
Supposing that the chemical bond between two atoms can be established by means of three electrons with oppositely oriented spins (↑↓↑) the structure of the benzene molecule can be expressed as follows (see figure 1 and figure 2):
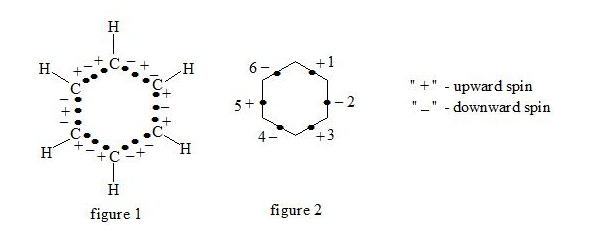
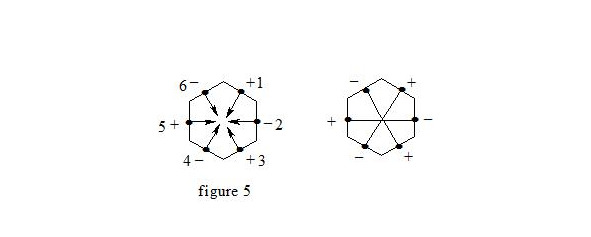
It is interesting to point out that spins of central electrons on opposite sides have an opposite orientation (see figure 2). Now let us consider in detail the interaction of six central electrons between themselves. They will be itemized as shown in figure 2. As the spin of electron 1 and those of electrons 2 and 6 are oppositely oriented (see figure 2) (1 (+), 2 (-), 6 (-)), electron 1 will be attracted to electrons 2 and 6 respectively. Let’s indicate that the distance between electrons 1 and 6 or 1 and 2 is equal to 1.210 Å which can be easily shown taking into account the distance between atoms of carbon in benzene to be 1.397 Å and the angle between carbon atoms amount to 120 degrees. Let us compare the distance between electrons 1 and 6 and 1 and 2 bond lengths in ethane, ethylene and acetylene [7]:
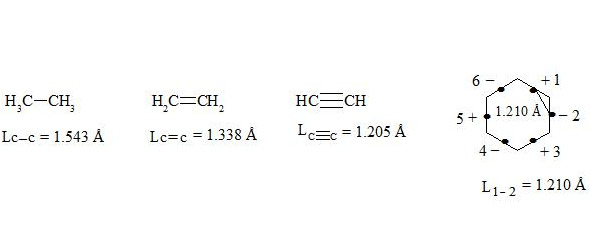
As we observe, the distance between central electrons 1 and 2 and 1 and 6 of the benzene molecule is approximately equal to that between carbon atoms in the acetylene molecule, therefore, the interaction between electrons 1 (+) and 2 (-) and 1 (+) and 6 (-) has to be rather considerable. Let us express the attraction with arrows. According to summing up vectors the resultant vector will be directed to the centre, which means that electron 1 under the influence of electrons 2 and 6 will move to the centre (figure 3):
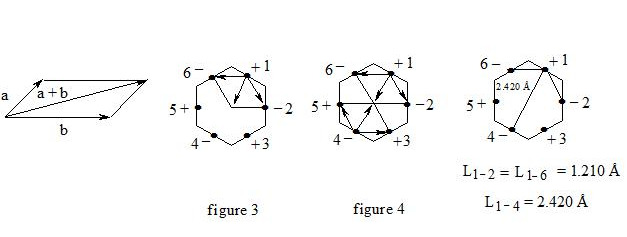
If we take a look at electron 4 we see the similar situation with it (figure 4) and it will also move to the centre and, more importantly, its spin and that of electron 1 will be oppositely oriented, i.e. electron 1 (+) and electron 4 (-) will be attracted through the cycle. Electrons 6 (-) and 3 (+) and electrons 2 (-) and 5 (+) will interact similarly. The distance between electrons 1 and 4 in benzene is equal to 2.420 Å. It is interesting, that this distance is twice as much than distance between electrons 1 and 2, or between electrons 1 and 6 (1.210 Å ∙ 2 = 2.420 Å). This interaction through the cycle constitutes the essence of the delocalization of electrons, of course together with a three-electron bond. Since besides the three-electron bond in the benzene molecule there is an interaction through the cycle, meaning that the benzene nucleus undergoes a kind of compression it is clear that the c-c bond multiplicity in benzene will exceed 1.5.
So, the aromatic system is a cyclic system with three-electron bonds where an interaction of central electrons through the cycle is observed. In the benzene molecule there are three interactions through the cycle-pairwise between electrons 1 (+) and 4 (-), 2 (-) and 5 (+), 3 (+) and 6 (-), as shown in figure 5:
Carbon atoms in benzene are sp²-hybridized. The three-electron bond between carbon atoms in the benzene molecule can be represented as follows:
Carbon atoms in benzene have an octet equal to 8 (3 +3 +2 = 8). It should be pointed out that due to the largest distance from the atoms nuclei the central electrons of the three-electron bond are supposed to be the most mobile compared to other electrons of the three-electron bond. The interaction of central electrons with opposite spins through the cycle can easily explain why cyclobutadiene and cyclooctatetraene are not aromatic compounds:
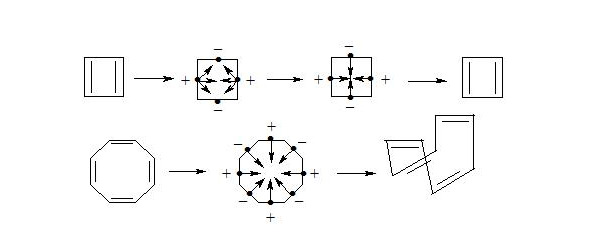
As we see both in cyclobutadiene and cyclooctatetraene, electrons interacting through the cycle have the same spins and, clearly, will be repulsed, therefore there will be no interaction through the cycle and the molecule will not be aromatic. In cyclobutadiene at the expense of small distance it causes the appearance of antiaromatic properties, and in cyclooctatetraene there is a possibility of formation of non-planar molecule, where interaction of central electrons becomes impossible and molecule losing the interaction through the cycle loses also three-electron bonds, that results in a structure, in which single and double bonds alternate.
Explanation, that cyclooctatetraene is non-aromatic, because it is non-planar and does not hold water, insomuch as dianion of cyclooctatetraene is aromatic and has planar structure [8], [9].
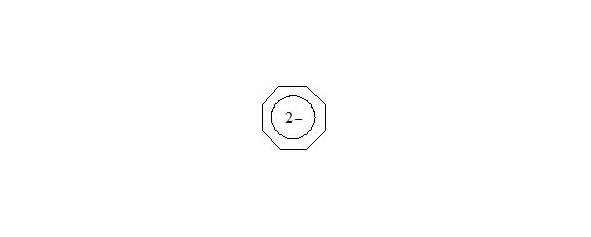
X-ray crystal structure analysis determined crystal structure of potassium salt of dianion 1,3,5,7-tetramethylcyclooctatetraene [10], [11].
Octatomic cycle is planar with lengths of С-С bonds nearly 1.41 Å.
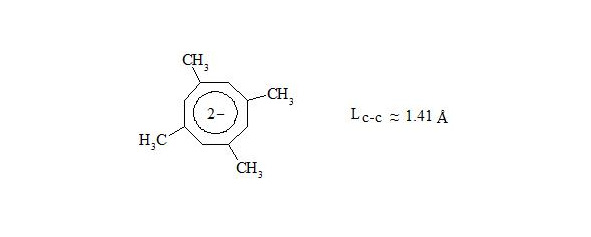
From the mentioned above we can make a conclusion: cyclooctatetraene conforms to the shape of bath tub not because of high angular pressure (15°) at planar structure, but because by interaction through the cycle central electrons of three-electron bonds have equal spin and will push away. Thus for energy reduction cyclooctatetraene conforms to the shape of bath tub and becomes non-planar, that disables interaction of central electrons.
Cyclobutadiene represents rectangular high reactivity diene [8, p. 79].
It is also interesting to observe cyclodecapentaene (cis-isomer [10] -annulene).
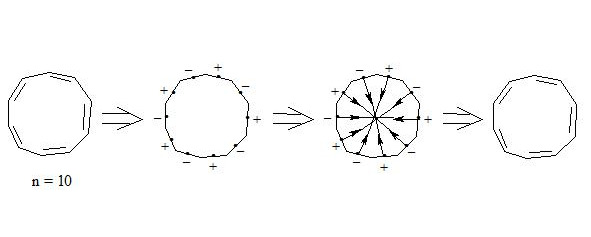
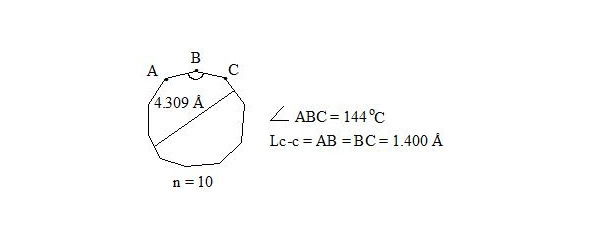
Whereas central electrons of three-electron bonds have opposite spins, then interaction through the cycle is possible. But distances between central electrons on opposite sides, which interact through the cycle, are extremely long (4.309 Å if accept Lс-с = 1.400 Å for regular decagon), angular pressure is high (24°) and that’s why stabilization at the expense of interaction through the cycle at such long distance will be low and cannot cover energy consumption for creation of planar molecule.
Cyclodecapentaene was received in the form of crystalline substance at — 80°С. On spectrums ¹³С-NMR and ¹Н-NMR it was determined, that compound is non-planar and is olefin, that is logical on the basis of long distance between central electrons [8, p. 84], [12].
Lets draw our attention to the fact that in going from benzene to cyclooctatetraene and to cyclodecapentaene distance increases not only between central electrons on the opposite sides (interaction through the cycle), but also between neighboring central electrons.
Lets show it on figure.
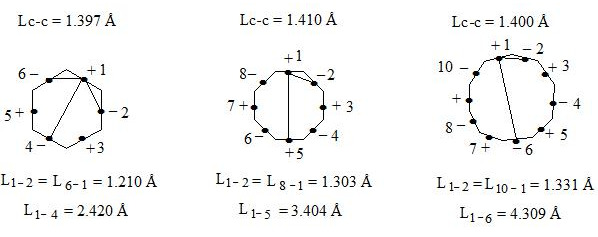
As we can see distance between neighboring central electrons 1 and 2 in benzene makes up 1.210 Å, in regular octagon 1.303 Å, and in regular decagon 1.331 Å (almost as distance between carbon atoms in ethene molecule). That is by going from benzene to regular octagon and decagon not only angular pressure (0°, 15°, 24°) and distance between central electrons increase, which are situated on the opposite sides (2.420 Å; 3.404 Å; 4.309 Å), as well as distance between neighboring central electrons 1 and 2 (1.210 Å; 1.303 Å; 1.331 Å), that causes considerable weakening of interaction through the cycle in regular decagon. That’s why regular hexagon (benzene) is ideal aromatic system. As angular pressure is equal to zero, distances between central electrons both neighboring and situated on the opposite sides are minimal (accordingly 1.210 Å and 2.420 Å). I.e. interaction through the cycle will be maximal. By going to regular decagon these advantages will be lost. That’s why cyclodecapentaene is olefin.
Let us note for comparison that if we take Lc-c = 1.400 Å for the planar cyclooctatetraen, we will have L (1—5) = 3.380 Å, L (1—2) = L (8—1) = 1.293 Å which vary just slightly from the above mentioned distances between the central electrons at Lс-с = 1.410 Å.
By means of the interaction through the cycle together with the three-electron bond, aromaticity of coronen, [18] -annulene, naphthalene and other organics substances can be explained (see conclusion).
Now let’s pass to the definition of delocalization energy of benzene. It is easy to show, that relation multiplicity = f (L) and Е = f (L), where multiplicity is multiplicity of bond, L — length of bond in Å, Е — energy of bond in kj/mole will be described by function y = a + b/x + c/x² for any types of bond (C-C, C-N, C-O, C-S, N-N, N-O, O-O, C-P).
We shall consider ethane, ethylene and acetylene to be initial points for the c-c bond.
For lengths of bonds let us take the date [7]:
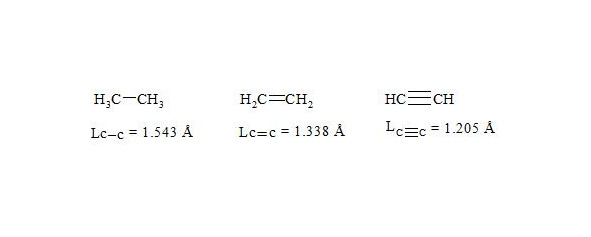
As usual, the С-С bond multiplicity in ethane, ethylene and acetylene is taken for 1, 2, 3.
For energies of bonds let us take the date [7, p. 116]:
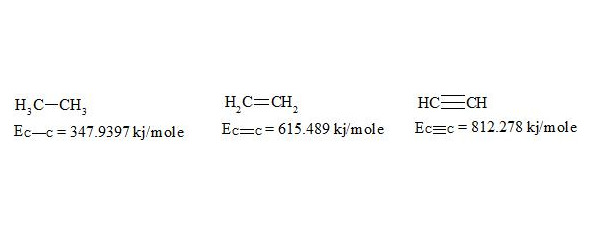
The given bond energies (according to L. Pauling) are bond energy constants expressing the energy that would be spent for an ideal rupture of these bonds without any further rebuilding of the resulting fragments. That is, the above mentioned energies are not bond dissociation energies.
Having performed all necessary calculations we obtain the equation:

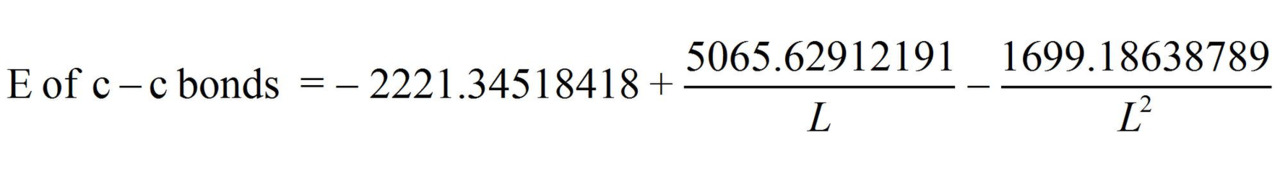
From these equations we find:
c–c benzene multiplicity (L = 1.397 Å) = 1.658
c–c graphite multiplicity (L = 1.42 Å) = 1.538 ≈ 1.54
Ec–c benzene (L = 1.397 Å) = 534.0723 kj/mole
Ec–c graphite (L = 1.42 Å) = 503.3161 kj/mole
Being aware that the benzene has the three-electron bonds and also the interaction through the cycle, we can calculate the interaction through the cycle energy.
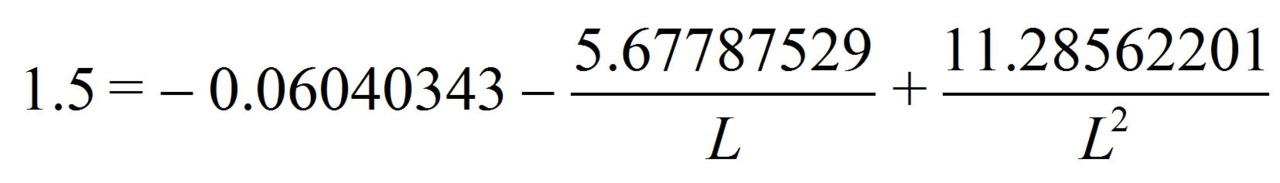
from the equation we find L = 1.42757236 Å.
So, if the benzene molecule had a «clean» three-electron bond with a 1.5 multiplicity the c-c bond length would be L = 1.42757236 Å.
Now let us determine the energy of the «clean» three-electron bond with a 1.5 multiplicity knowing its length L = 1.42757236 Å:
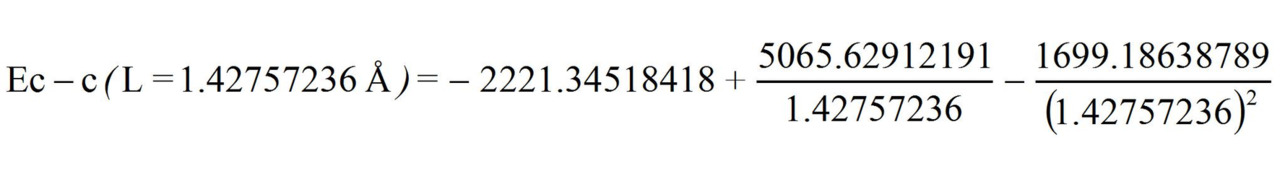
Ec — c (L =1.42757236 Å) = 493.3097 kj/mole
Taking into account that the benzene c-c bond energy with a 1.658 multiplicity is equal to Ec-c benzene = 534.0723 kj/mole, the difference will make:
ΔE = 534.0723 kj/mole — 493.3097 kj/mole = 40.7626 kj/mole.
40.7626 kj/mole is the energy of interaction through the cycle per one c-c bond. Therefore, the energy of interaction through the cycle will be two times higher:
E1 = 40.7626 kj/mole ∙ 2 = 81.5252 kj/mole (19.472 kcal/mole)
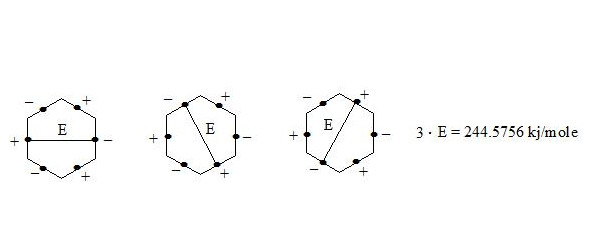
It is clear that the three interactions through the cycle present precisely the working benzene delocalization energy which is:
E = 3E1 = 3 ∙ 81.5252 kj/mole = 244.5756 kj/mole (58.416 kcal/mole)
It is also possible to calculate the benzene molecule energy gain in comparison with the curved cyclohexatriene (let us assume that energy of C-H bonds in these molecules is similar). For this we calculate the sum of energies of single and double c-c bonds in cyclohexatriene:
E2 = 3Ec–c +3Ec═c = 2890.286 kj/mole
The energy of six benzene c-c bonds with a 1.658 multiplicity is equal to:
E3 = 6 · 534.0723 kj/mole = 3204.434 kj/mole
Therefore, the gain energy of benzene compared to cyclohexatriene will amount to:
E = E3 — E2 = 3204.434 kj/mole — 2890.286 kj/mole = 314.148 kj/mole (75.033 kcal/mole).
2.2. Experimental
Let’s show more detailed calculation of ratios for our mathematical relations. Let’s consider relation Multiplicity = f (L) and E = f (L) for С-С bonds, where multiplicity is multiplicity of bond, L — length of bond in Å, Е — energy of bond in kj/mole.
As initial points for the given bonds we will use ethane, ethene and acetylene. For the length of bonds let us take the findings [7]:
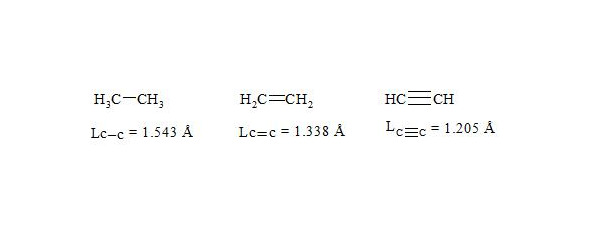
As usual, the С-С bond multiplicity in ethane, ethylene and acetylene is taken for 1, 2, 3. For the energy of bonds let us take the findings [7, p. 116]:
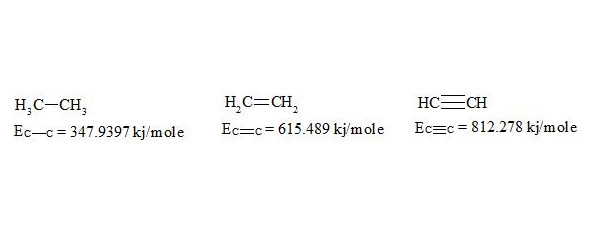
If we have two variants and we received the set of points and we marked them on the plane in the rectangular system of coordinates and if the present points describe the line equation y = ax + b that for choose the coefficients a and b with the least medium-quadratic deflection from the experimental points, it is needed to calculate the coefficients a and b by the formulas:
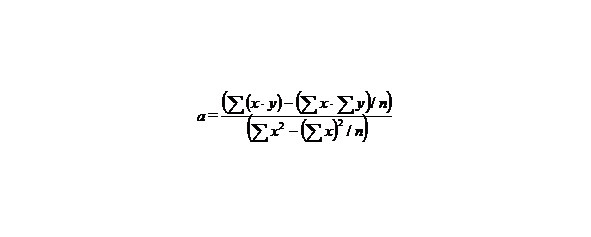
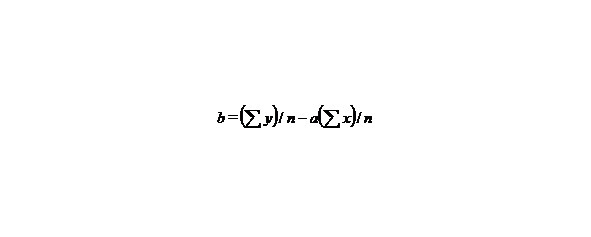
n-the number of given values x or y.
If we want to know how big is the derivative, it is necessary to state the value of agreement between calculated and evaluated values y characterized by the quantity:
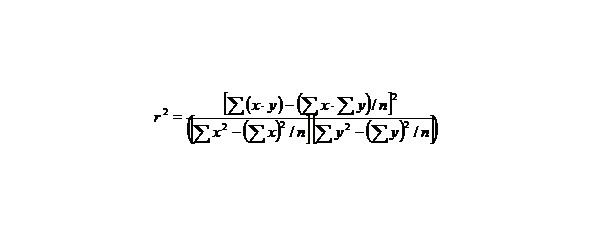
The proximity of r2 to one means that our linear regression coordinates well with experimental points.
Let us find by the method of selection the function y = a + b/x + c/x2 describing the dependence multiplicity = f (L) and E = f (L) in best way, in general this function describes this dependence for any chemical bonds.
Let us make some transformations for the function y = a + b/x + c/x2, we accept
X = 1/x,
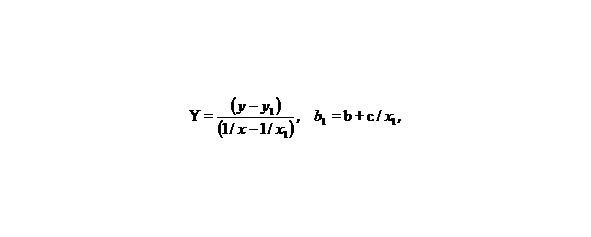
than we’ll receive: Y = b1 + cX, that is the simple line equality, than
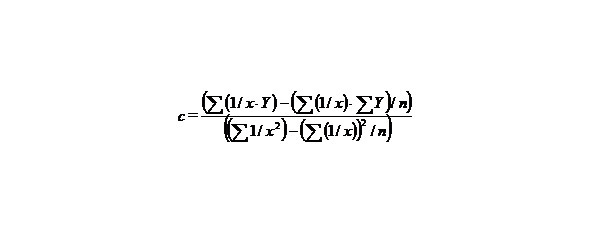
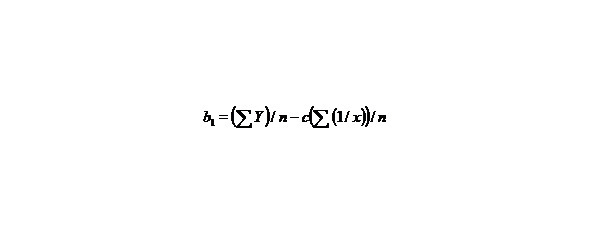
n–the number of given value Y.
Let us find a from the equality:
∑y = na + b∑ (1/x) + c∑ (1/x2), (9)
when n = 3.
Let us find now multiplicity = f (L) for C─C, C═C, C≡C.
Table 1. Calculation of ratios for relation Multiplicity = f (L).
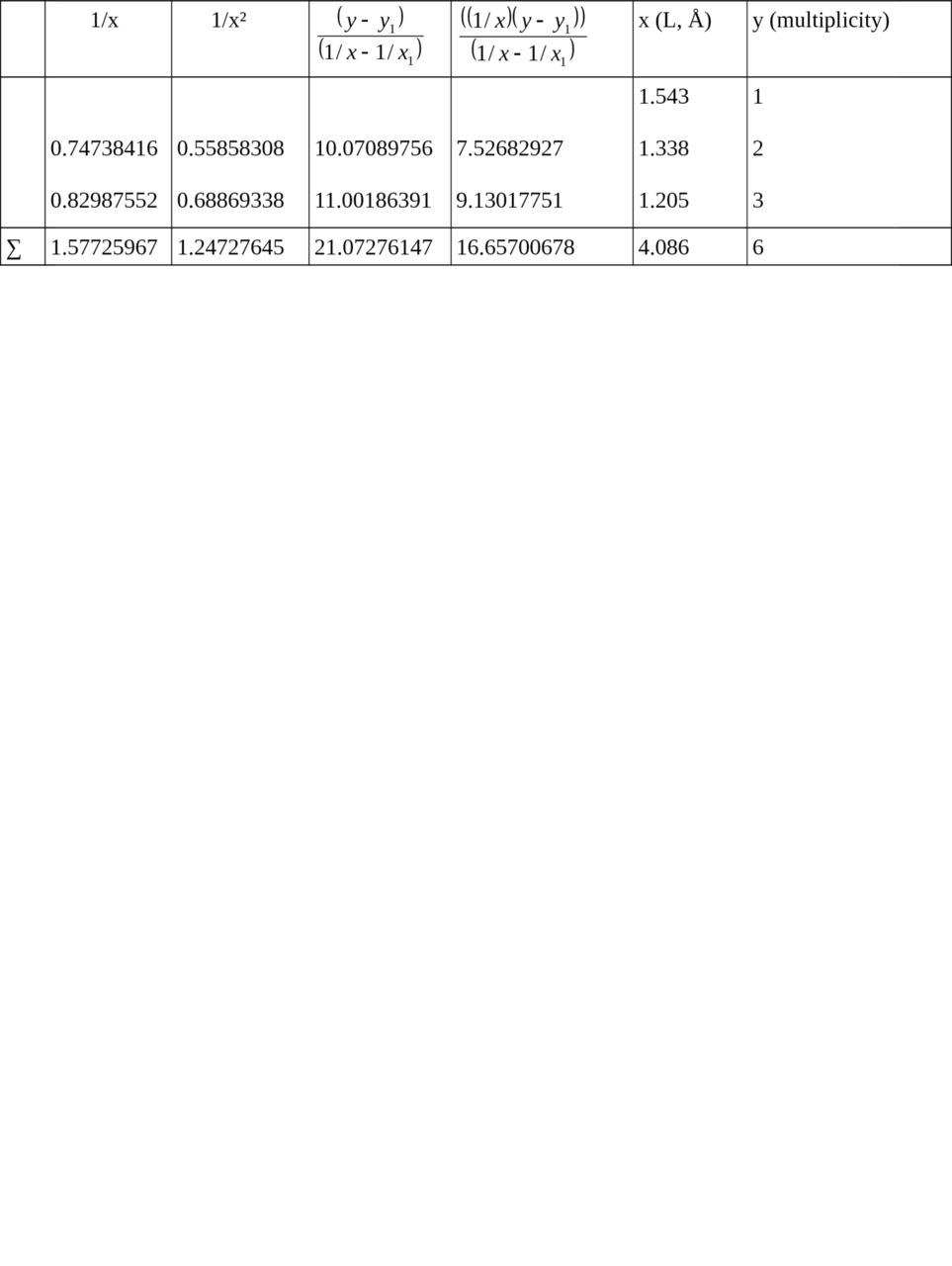
1/x1 = 0.64808814, x1 = 1.543, y1 = 1
Σ (1/x2) = 1.66729469, Σ (1/x) = 2.22534781 when n = 3
c = 11.28562201,
b = — 5.67787529,
a = — 0.06040343
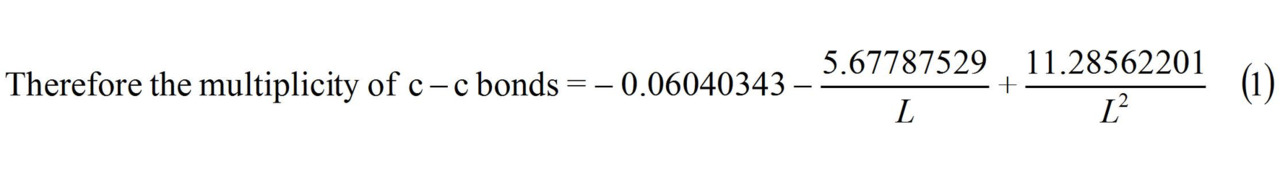
Let us find from the equation:
Multiplicity C−C (ethane) = 1.
Multiplicity C═C (ethylene) = 2.
Multiplicity C≡C (acetylene) = 3.
Multiplicity C−C (graphite) (L = 1.42 Å) = 1.538 ≈ 1.54.
Multiplicity C−C (benzene) (L = 1.397 Å) = 1.658.
As we can see the multiplicity C−C of benzene bond is 1.658 it is near the bond order of 1.667 calculated by the method MO [8, p. 48].
It should be noted that the а, b, с coefficients for this y = a + b/x + c/x² function in case of using three pairs of points (х1, у1), (х2, у2) and (х3, у3) are defined explicitly; actually, they (the coefficients) are assigned to these points. In that way we find these coefficients for working further with the equation. For making certain that this dependence y = a + b/x + c/x² describes well the Multiplicity = f (L) and E = f (L) functions it will take only to perform correlation for four or more points. For example, for the dependence Multiplicity = f (L) for C-C bonds we should add a fourth point (Lc–c = 1.397 Å, Multiplicity = 1.667) and obtain an equation with r² = 0.9923 and the coefficients а = — 0.55031721, b = — 4.31859233, с = 10.35465915.
As it is difficult, due to objective reason, to define four or more points for the Multiplicity = f (L) and E = f (L) equations for a separate bond type, we will find the а, b, с coefficients using three points (as a rule they are the data for single, double and triple bonds). The dependences obtained in such a way give good results as regards the bond multiplicity and energies.
We’ll find the dependence E = f (L) for the C−C bonds
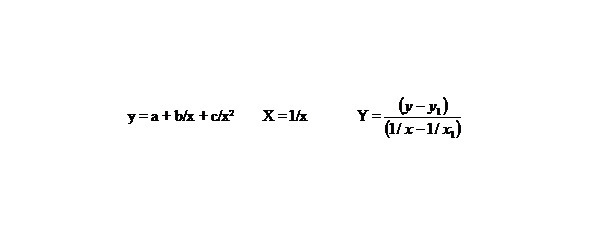
b1 = b + c/x1, Y = b1 + cX
As usual:
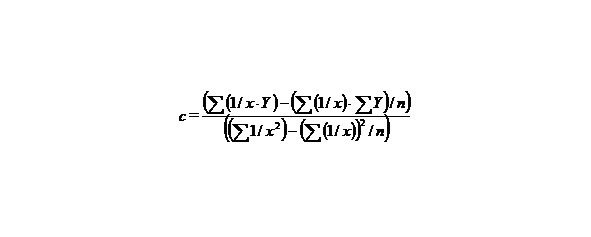
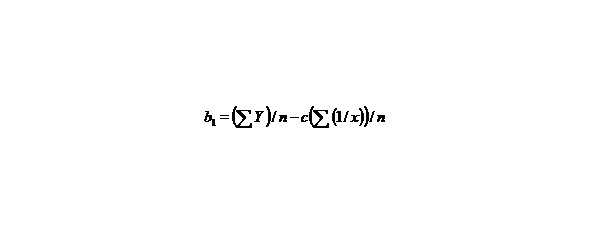
n–the number of given value Y.
Let us calculate a from the equation
∑y = na + b∑ (1/x) + c∑ (1/x2), (9)
when n = 3.
Table 2. Calculation of ratios for relation E = f (L).
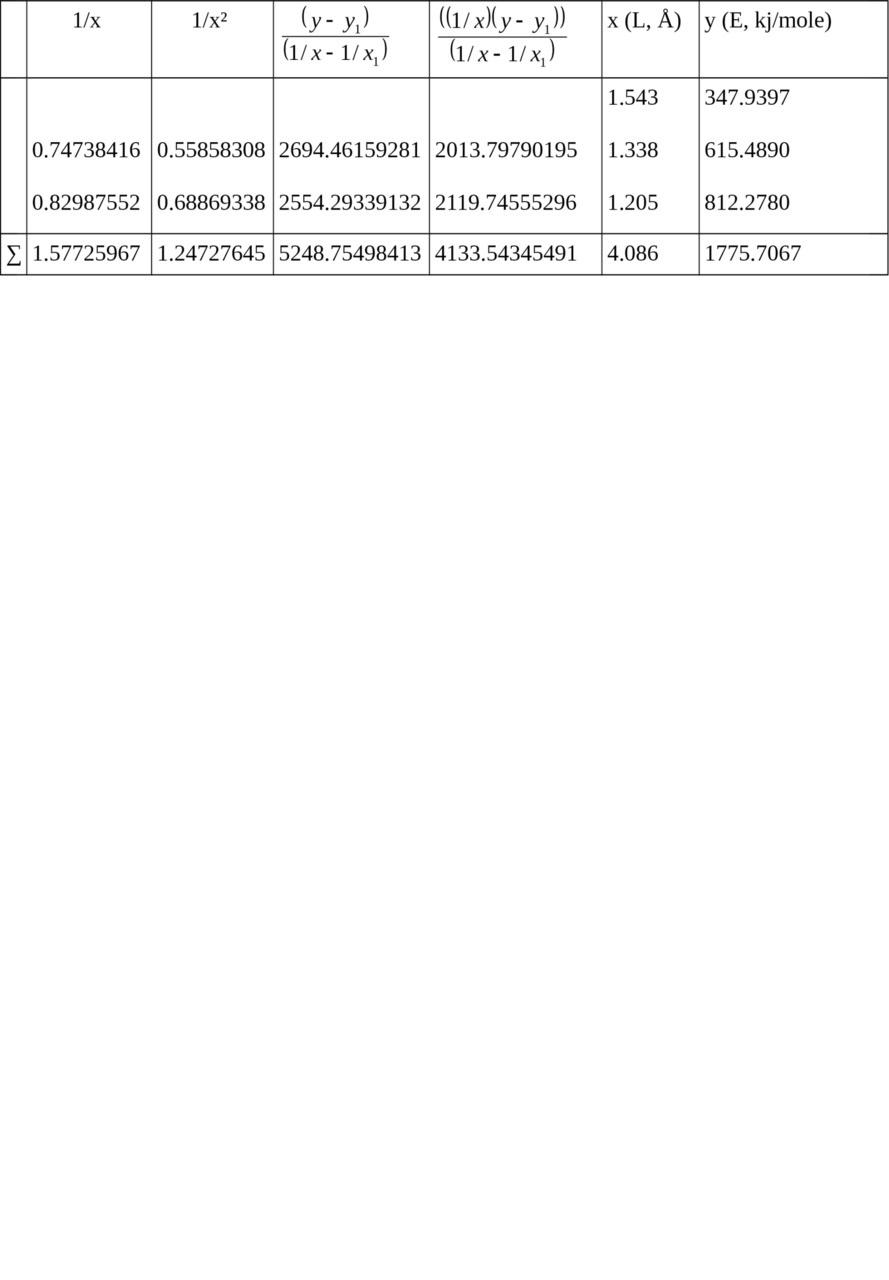
1/x1 = 0.64808814, x1 = 1.543, y1 = 347.9397
Σ (1/x2) = 1.66729469, Σ (1/x) = 2.22534781 when n = 3
c = — 1699.18638789,
b = 5065.62912191,
a = — 2221.34518418

Let us calculate from the equation:
Ec–c (ethane) = 347.9397 kj/mole
Ec═c (ethylene) = 615.4890 kj/mole
Ec≡c (acetylene) = 812.2780 kj/mole.
2.3. Conclusion
As we can see, three-electron bond enables to explain aromaticity, find delocalization energy, understand aromatic bond’s specificity. Aromatic bond in benzene molecule is simultaneous interaction of three pairs of central electrons with opposite spins through the cycle. But whereas central electrons are the part of three-electron bond, then it is practically interaction of six three-electron bonds between themselves, that is expressed in three interactions through cycle plus six three-electron bonds. We shouldn’t forget in this system about important role of six atom nucleuses, around which aromatic system is formed. Properties of nucleuses especially their charge will influence on properties of aromatic system.
Finally, postulates of the three-electron bond theory (TBT) can be presented:
1) A chemical bond between two atoms may be established by means of three electrons with oppositely oriented spins (↑↓↑).
A • • • A (↑↓↑)
A • • • B (↑↓↑)
2) The electron shell of each atom in the stable molecule, ion, radical should have such a number of electrons which corresponds to the octet. A deviation from the octet results in an instability of a particle.
3) The state of the three-electron bond is determined by the octet rule.
4) The number of electrons participating in the chemical bond should be maximal and it’s then that the energy of the system will be minimal. Taking into consideration para 5 and 2.
5) In the course of establishing of the chemical bond electrons (their spins) are located in such a way that enables the interaction (attraction) to be maximal.
6) The aromatic bond is a three-electron bond in flat cyclic systems with a specific interaction of electrons through the cycle.
It is easy to show, that using three-electron bond one can explain paramagnetization and structure of oxygen molecule, structure of carboxylate anion, ozone, naphthalene and other organic and non-organic compounds. Let’s bring for the example structures of some compounds in terms of three-electron bond.
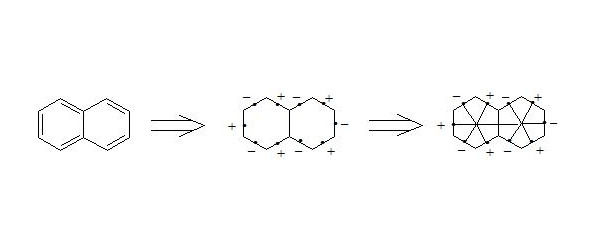
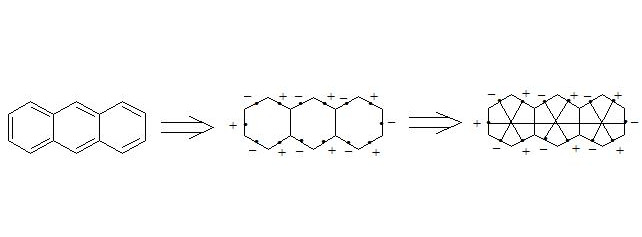
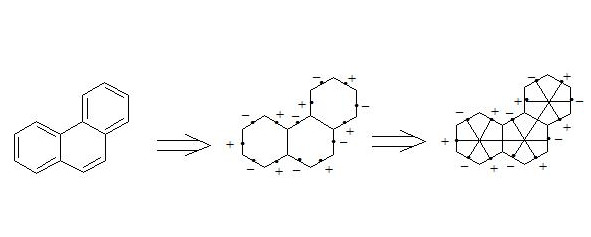
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.
