Бесплатный фрагмент - Ornithopter. Philosophy. Theory. Practic

Preface

“Man will not fly on the strength of his muscles, but on the strength of his mind.”

Н. Tsialkovsky

The book presents materials on the research of characteristics of a manned flying machine with flapping wings — an ornithopter.

The author is a leading aerodynamicist of the Antonov firm, who has a great experience in building aircraft. The author conducted a large complex of aerodynamic research, wind tunnel tests and did a lot of work on the practical creation of manned ornithopter.

For a physical understanding of the principle of creating thrust and lift by a flapping wing, the author has developed a program for calculating the static characteristics of a flapping wing and studied many variants of the wing layout and flapping kinematics.

To study the flight characteristics, stability and controllability characteristics, as well as the flight dynamics, the author developed a principally new mathematical model of an aircraft, which made it possible to calculate the motion of various aircrafts, airships, ornithopters at any flight modes.

This mathematical model allows us, by solving a system of differential equations, to calculate the characteristics of motion in any flight modes, including stall, stall and others, which is not allowed by the currently widely used standard mathematical model.

Numerous numerical studies have made it possible not only to understand the principles of lifting force and thrust of the flapping wing, but also to determine the aerodynamic layout and parameters of the ornithopter.

All materials are presented in an accessible form for non-specialists and may be useful not only for the creators of ornithopter, but also for the people interested in ornithopter flight.

The book consists of the following parts.

General problems of flapping flight

Theory of a flapping flight

Calculation examples for typical types of ornithopters

Flight characteristics of an ornithopter

Practical experience in building an ornithopter

The last part is being prepared for print and will be published as a separate book.

THE MYTH OF DAEDALUS & ICARUS

Daedalus was a highly respected and talented Athenian artisan descendent from the royal family of Ceros, the mythical first king of Athens. He was known for his skill as an architect, sculpture, and inventor and he produced many famous works. Despite his self-confidence, Daedalus once committed a crime of envy against Talus, his nephew and apprentice. Talus, who seemed destined to become as great an artisan as his uncle Daedalus, was inspired one day to invent the saw after having seen the way a snake used its jaws. Daedalus, momentarily stricken with jealousy, threw Talus off of the Acropolis. For this crime, Daedalus was exiled to Crete and placed in the service of King Minos, where he eventually had a son, Icarus, with the beautiful Naucratis, a mistress-slave of the King.

Minos called on Daedalus to build the famous Labyrinth in order to imprison the dreaded Minotaur. The Minotaur was a monster with the head of a bull and the body of a man. He was the son of Pasiphae, the wife of Minos, and a bull that Poseidon had sent to Minos as a gift. Minos was shamed by the birth of this horrible creature and resolved to imprison the Minotaur in the Labyrinth where it fed on humans, which were taken as “tribute” by Minos and sacrificed to the Minotaur in memory of his fallen son Androgens.

Theseus, the heroic King of Athens, volunteered himself to be sent to the Minotaur in the hopes of killing the beast and ending the “human tribute” that his city was forced to pay Minos. When Theseus arrived to Crete, Ariadne, Minos’s daughter, fell in love with him and wished to help him survive the Minotaur. Daedalus revealed the mystery of the Labyrinth to Ariadne who in turn advised Theseus, thus enabling him to slay the Minotaur and escape from the Labyrinth. When Minos found out what Daedalus had done he was so enraged that he imprisoned Daedalus & Icarus in the Labyrinth themselves.

Daedalus conceived to escape from the Labyrinth with Icarus from Crete by constructing wings and then flying to safety. He built the wings from feathers and wax, and before the two set off he warned Icarus not to fly too low lest his wings touch the waves and get wet and not too high lest the sun melt the wax. But the young Icarus, overwhelmed by the thrill of flying, did not heed his father’s warning, and flew too close to the sun whereupon the wax in his wings melted and he fell into the sea. Daedalus escaped to Sicily and Icarus’ body was carried ashore by the current to an island then without a name. Heracles came across the body and recognized it, giving it burial where today there still stands a small rock promontory jutting out into the Aegean Sea, and naming the island and the sea around it after the fallen Icarus.

1. General problems of flapping flight

WHY CAN BIRDS FLY BUT NOT HORSES?

Translated by Frank Burnham

“Only Bellerophont, the young hero, came near the winged horse Pegasus. The horse flapped large wings with the speed of the wind and was carried away to the clouds where he soared like an eagle.”

Legends and Myths of Ancient Greece.

It is known that all classes of flying entities range in weight from 1 ten thousandth of and once for a gnat up to about 26 pounds for an albatross. Nothing heavier flies today because of several aeromechanic problems.

It is known that all classes of flying entities range in weight from 1 ten thousandth of an once for a gnat up to about 26 pounds for an albatross. Nothing heavier flies today because of several aeromechanic problems.

In aviation there is a relationship saying that as the scale of a vehicle increases, its surface area increases proportional to the square of the scale and its weight increases proportional to the cube of the scale. Thus, if the size of the vehicle doubles, its area is increased four times and its weight eight times. We call this law:

1 (L) — 2 (S) -3 (G)

Where: 1-2-3 — are index of exponents;

L — linear size;

S — square of surface, proportional to — L2

G — weight, proportional to — L3

Weight grows very fast, but it is only one factor in considering why horses do not fly.

REQUIREMENT POWER

In aerodynamics, there is a concept of required power (Pr) for maintenance of steady-state horizontal flight, determined by the formula

Pr = (G/k) *V

Where: V — Speed of flight,

k — Lift-to-drag ratio.

Lift-to-drag ratio is a ratio of lift (at steady-state flight it is equal to the weight of the vehicle) to the force of its aerodynamic drag.

The study of birds shows that a large albatross, because of its streamlining, has the highest lift-to-drag ratio of any bird, but even a small swallow has a high lift-to-drag ratio. Therefore, the lift-to-drag ratio of birds does not vary substantially with size.

Consider how the speed of flight varies with the weight of the birds. A bird’s weight varies much faster than its wingspan, corresponding to the 1-2-3 law. If the weight increases faster than the wing area, the weight per unit area increases as the bird’s weight increases.

The study of influence of weight per unit area on the speed of flight of birds shows, that there is a certain regularity between these two parameters: the higher the load per unit area, the more speed of flight. This relation is determined under the formula

V =squareroot (2G/ (S*Cl*р));

Cl — lift coefficient in horizontal flight, defined by formula:

Cl = Lift/ (р*V*V*S/2);

р — density of an air;

Lift — lift force of a wing.

As a first approximation, it is possible to accept that Cl does not depend on the sizes of a bird and therefore the speed of flight is proportional to G/S. We know that the area of the surface varies as the square, the weight varies as the cube, and the speed of flight varies as the square root of the linear size. Therefore, the required power is proportional to an increase of the linear size to the 3.5 power and the law will look like the following:

1 (L) — 2 (S) -3 (G) -3.5 (Pr)

Certainly, there are a lot of exceptions to this rule, but the general tendency is interesting. The required power with increase of weight grows much faster than weight increases and decreases much faster than weight decreases. This is evident in the difference between how small and large birds fly. The large birds only flap their wings to takeoff and gain altitude — in flight, they glide on rising air currents. Small birds like insects vigorously flap their wings at all times.

From the 1-2-3-3.5 law, it follows that with a reduction of weight the required power decreases faster than the weight decreases. And following this law, nature allows small birds with less aerodynamic efficiency to use much less muscle power for flight. They compensate for a shortage of lift-to-drag ratio by some increase of power realized by flapping faster. The large birds compensate for a shortage of power by an increase of lift-to-drag ratio and a change of flight technique.

Insects may be very inefficient flyers. But because of their miniscule weight they can easily supply the required power of flight and overcome any aerodynamic in efficiencies they may have. Now it is clear why the bugs and other insects are able to fly so easily.

A person flew over the English Channel in a manned-power aircraft. What does it mean? Can it be that the law does not work? Let us to consider. The formula of required power (Pr) shows that it varies inversely to the lift-to-drag ratio (k). The inventors of man-powered flight, with the help of modern materials, were able to make such a perfect wing that the lift-to-drag ratio was very large and the required power very small. It was so small that even the power of one man was sufficient for flight.

THE WING CONSTRUCTION

Consider a design of a wing in the context of mechanics. The motional system of a majority of animals consists of a framework of bones supported by muscles. Bones work in compression and muscle in tension with stretching. Such a structure is optimum for movement on the ground. The wing of an insect works as a simple cantilever beam, and the only muscle for flight is inside the body. The wings of birds are more complex where the bones are jointed and supported by muscles within the wing. An increase of weight and size of a bird increases the forces on bones and muscle of the wing.

Pursuant to this relationship, an increase in the size of a bird causes its weight to increase proportional to cube of the size increase and the arm of the center of force for the wing is proportional to the increase of the size. Thus, the load on muscles of a wing is increased proportionally to the 4th power of the increase of the size. The complete law can now be stated as follows:

1 (L) — 2 (S) — 3 (G) — 3.5 (Pr) — 4 (Mx)

MOMENT OF INERTIA

To reverse the direction of the flap twice each cycle requires additional power to be expended in addition to that required for thrust and lift.

It is known that the moment necessary for braking and reversing the direction is proportional to the angular acceleration and moment of inertia of the wing

Mx = Ix* j,

Where: Ix — moment of inertia of a wing about the axes of flapping;

j — angular acceleration of a wing as it brakes and accelerates in the other direction.

The moment of inertia is determined with the formula

Ix = Mi * yi2

Mi — weight of some element of a wing;

yi — distance of an element from an axes of it flapping.

As weight varies proportionally to cube of the linear size, the moment of inertia varies proportionally 5th power of its linear size. This law can then be stated as:

1 (L) — 2 (S) -3 (G) -3.5 (Pr) –4 (Mx) — 5 (Ix)

This is the complete law, which states that:

With a change of the linear size of a flying entity the area of the surface varies as the square, the weight varies as the cube, the required power varies as the 3.5 power, the load on the muscles varies as the fourth power, and moments of inertia varies as the fifth power of the change of the linear size.

Of course, this law is only precise when all the parameters vary proportional to the scale of increasing or decreasing size. Since this never happens in nature, the law has qualitative character and only reflects general tendencies. However, it gives the answer to many problems, such as why large animals are sluggish while small animals are quick. It might even explain the extinction of dinosaurs, which may have been killed by smaller and faster animals, such as the tyrannosaurs.

Still, maybe in the past, nature did manage to make a very large flying animal, such as the pterodactyl. This animal had big wings of about 33 square feet. We can’t know exactly how much it weighed, but we can make an educated guess. The pterodactyl had membrane wings like a bat. The bat has a weight- to- wing surface ratio between one half and one third of an albatross. If we suppose that a pterodactyl had the same weight to wings surface ratio then its weight would be no more than 26 to 33 pounds.

Consider a baby pelican with a weight about 26 pounds the same as the albatross. When it begins to fly, it must reduce its weight to a mere 13 pounds because it has less efficient aerodynamics than the albatross.

Applying the above laws shows the horse must have extremely large wings requiring many horsepower. An aircraft of the same weight, about 1000 pounds, has a wing area of about 160 square feet and an engine of 80 hp. Since a horse only generates about one horsepower, it is unlikely it could ever generate enough power to fly — -even if it had the required monster wings.

Now it is understood, that the laws of nature severely restrict the size and weight of any flying animal.

MUSCLE ORNITHOPTER

A muscle-powered airplane flew over the English Channel some time ago. Now many enthusiasts are trying to make a muscle-powered ornithopter. Let us consider some problems with this idea.

1. The efficiency of a flapping wing is less than the efficiency of a propeller, which is why the muscle ornithopter needs more power compared with a muscle airplane of the same scheme. A man can’t produce the additional power for a flapping wing.

2. If a person wants to decrease the power requirements, he should increase the wingspan. If the wingspan is longer, the inertia forces will increase, the weight of the airframe will increase, and the power requirements will increase also. “Your song is good; start over again.” (Russian proverb).

3. The problem of optimizing the incidence angle for each section requires a special control system, which demands additional equipment with additional weight and so on (look at 1. and 2.).

When Napoleon asked his artillery marshal, “Why are the cannons silenced?”

The marshal said, “There are 100 reasons why: The first, we ran out of shells. The second — “Enough,” said Napoleon. “The first reason is enough.”

The same reasoning can be used for the muscle ornithopter. Every reason is enough to eliminate the possibility of making a muscle ornithopter now or in the near future.

Efficiency of an ORNITHOPTER, AIRPLANE and BIRD

Most enthusiasts of flapping flight are sure that both ornithopter and bird have high aerodynamic efficiency. A comparative analysis of how fuel or food is used in birds, airplanes, and ornithopters will determine the extent that this is true.

The efficiency of an ornithopter varies as the wings move up and down, and also on the characteristics of the engine drive. The efficiency of a bird is more difficult to determine because it involves biological processes. It is possible, however, to consider some common parameters.

In nature many processes of energy transformation constantly take place. Therefore a full statement of the analysis of power efficiency of these flight vehicles is extremely difficult. Consider, then, a narrower problem of the last link of energy transformation in the line-up of energy transformations of a bird, an airplane, and an ornithopter. This is the stage of consumed food for a bird, and a full fuel tank for an airplane or ornithopter.

The general efficiency of transformation of fuel energy to energy of motion of an airplane or an ornithopter can be divided into three stages.

Efficiency of transformation of fuel- to- shaft rotation of the engine,

Efficiency of reduction drive unit.

Efficiency of propeller or flapping wing.

Airplane

The airplanes and ornithopter use the same engines; therefore the efficiency of chemical-to-mechanical motion of the engine is the same.

The two-stroke engine used in an ultra-light airplane is approximately 0.25 efficient, the propeller, 0.75, and of the reduction drive, nearly 0.98 efficient

The general efficiency of fuel to energy of motion of an ultra-light is the product of these separate efficiencies, or about 0.18.

Ornithopter

Very little analysis of ornithopter efficiencies is found in the literature. The author has conducted independent studies of the characteristics of a feasible ornithopter and the following discussion is based on that study:

The engine speed reduction ratio for an ornithopter is greater than that of an airplane — -approximately 100:1, reducing the engine speed to the flapping rate of about 0.8 hertz.

The reduction gearbox transforms rotation of the shaft of the engine n = 75 hertz to slow flap of the wings n = 0.8 hertz. For example ornithopter “Daedalus-1” of firm ANCOM has the calculated efficiency of the reduction gearbox ƞ gb = 0.65.

Let’s consider efficiency of transformation of flapping wing energy in energy of a thrust. During a cycle of flap all parameters vary therefore is difficult to determine efficiency. Let’s make the qualitative analysis, for this purpose we shall consider power losses at flap by wings downwards and up.

At downward flap energy of the engine most effectively is used: the vector of a combined air force of a wing is inclined forwards, and it the projections create lift and thrust. In this phase of flap efficiency is maximum, and it is possible to expect, that it is the same as efficiency of an propeller of an airplane.

At flap up for receiving necessary lift the angle of attack on wings is positive, and the vector of a combined air force is inclined back. Thus the projection of a combined vector to a horizontal axis is directed back, creating drag. For compensation this drag the tip sections of the flapping wings should create a thrust, for what the angle of attack should be negative. The lift of these sections is directed downwards and for compensation of lift’s losses the lift on main sections of a wing should be increased.

It is possible to compensate all losses of a thrust and lift during a cycle of flap at the expense of increase of required power of the engine; therefore in this phase efficiency is less, than at an airplane.

Comparative calculation which made for the DAEDALUS ornithopter shows that requirement power of the ornithopter more than requirement power of the airplane the same aerodynamic scheme about 1.4 times. This efficiency is

Kef = 0.75/1.4=0.55

Besides the part of energy is spent for compensation of moments of inertia at a boost and braking at wings flap that also reduces general efficiency of an ornithopter.

And the general efficiency energy transformation from fuel to energy of ornithopter motion is equal

Kef = Kef gb * Kef fl * Kef eng = 0.65* 0.55 * 0.25 = 0.09.

Thus, the qualitative evaluation shows, the ornithopter efficiency will be almost twice less, than airplane’s efficiency, and hopes of the enthusiasts of a flapping flight on high efficiency of the ornithopter is not justified.

Efficiency of a bird

The bird uses biochemical energy, which was received by eating food. Efficiency of biological energy transformation to energy of motion determines rather difficult. It is possible to state only some qualitative evaluations that are not enough accuracy. I am interested with the approximate sizes.

Let’s begin to consider process of energy transformation since that moment, when the bird pecked at the corn or eaten of a worm. Energy of used food cannot be measured in calories by burning food. The organism of an animal is not firebox of a steam locomotive, in it the complex biochemical processes happens, which allows more completely using energy of food. A part of energy the bird spends for process of digestion of food, on maintenance of the habitability and on regulation of a body temperature.

Let’s consider efficiency of energy transformation of a bird’s flapping wings to energy of motion. Being engaged parametric researches of various scheme of ornithopters I have come to a conclusion, that the wing of a bird is less optimum, than wing of an ornithopter.

Aerodynamic scheme of a wing, and kinematics of a flap of birds are optimised on element base, which is present at a Nature.

The tip parts of a bird’s wing have insufficient torsion flexibility that is why it cannot be installed on optimum angles of attack. They are streamlined by airflow with very large positive and negative angles of attack and have large drag. Besides from a course of aerodynamics of small speeds it is known, that on small speeds (where number Re <105) lift-to-drag ratio decrease, that results reduction efficiency of energy transformation from wings to energy of a bird motion.

It is possible to accept, that the efficiency of transformation of mechanical energy of flap to energy of a bird motion will make no more than 0.5…0.6.

The birds do not have losses on a reduction. We haven’t characteristic of a bird that is why show in a table the transformations of energy an airplane and an ornithopter.

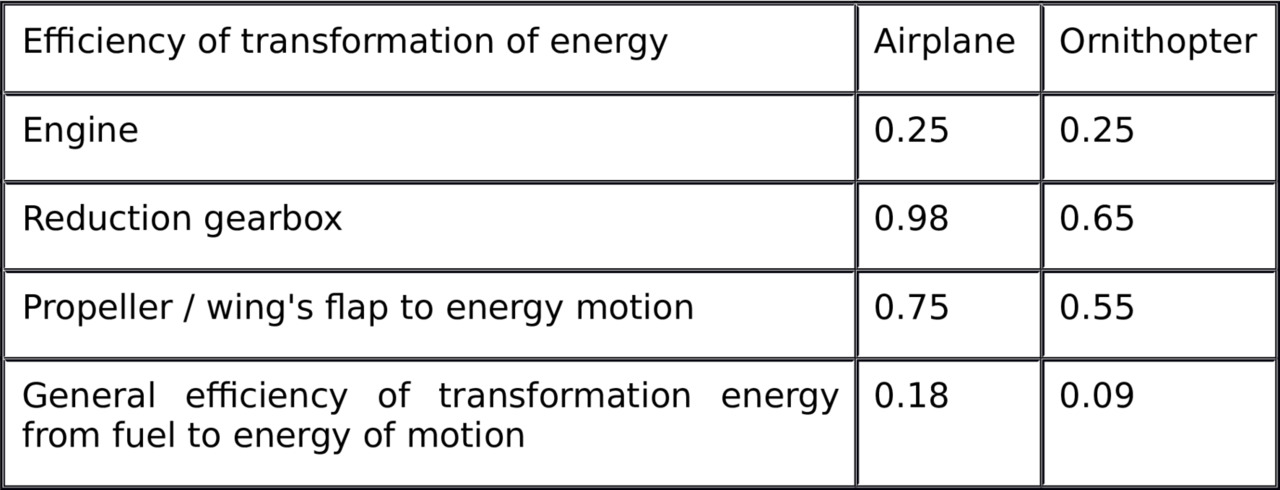
It is necessary to mark, that the adduced figures have qualitative character and will differ for particular flight vehicles nevertheless they demonstrate some general regularities.

By results of the analysis it is possible to make the following conclusions, that an ornithopter will have low efficiency compare the airplane.

Thus, the hopes for creation a more economic flight vehicle are not justified. Nevertheless, ornithopters represent significant sports interest and necessarily will take the place in aviation of the future.

2. Theory of a flapping flight

Edited by Jeremy Bolles

2.1. Thrust and drag of a flapping wing

Let’s consider some section of a fixed wing with the forces of normal pressure and the forces of friction acting on the section’s surface. These separate forces can be replaced by a combined air force R. Let’s consider the components of the combined air force R on a velocity coordinate system, in which the abscissa (x axis) is parallel to speed of airflow, and the ordinate (y axis) is perpendicular to the airflow.

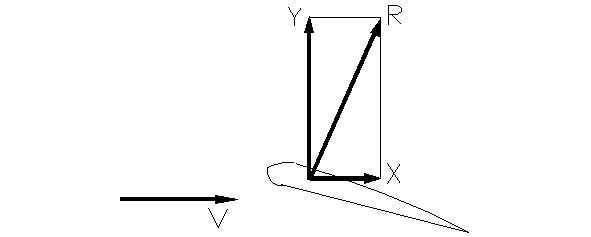
The perpendicular component of vector R is a lift force Z, and the horizontal component opposing the airflow vector is a drag force it is necessary to note that because of the drag component, the vector of the combined air force R of a fixed wing section is always inclined backwards in the direction of airflow. The fixed wing cannot have forward thrust. Note also that the angle between velocity vector of the airflow and vector of the combined air force R depends on the angle of attack.

It has been observed that when a wing section moves perpendicular to the direction of the airflow the sum vector of speed of the combined air force will turn toward the oncoming airflow. In this case a wing section will have a thrust. It appears this principle of thrust generation has been used for a long time in aircraft propellers. Sections of the blade of the propeller move perpendicular to a direction of motion of an airplane. Thus, in order to produce thrust with a wing section, the airfoil must move perpendicular to the oncoming airflow.

2.2. Drag and thrust on various phases of flapping

Let’s consider forces, which act on a wing’s section during the flap downwards and upwards and at the extreme points of deflection where the wing is motionless.

The Push downward

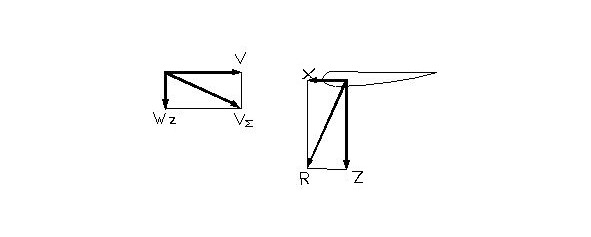
The air speed V is understood to be the vector sum of V, the oncoming airflow vector, and Wy, the vertical vector of the airflow that meets the wing during its perpendicular push downward. The sum vector V Vector R also turns on the same angle forwards resulting in combined air force vector R turning toward the oncoming airflow. When the sum vector is directed forward, i.e. there is a thrust. The greater the perpendicular velocity of the wing Wz, the more vector R is turned toward the flight direction, i.e. the more thrust the wing produces.

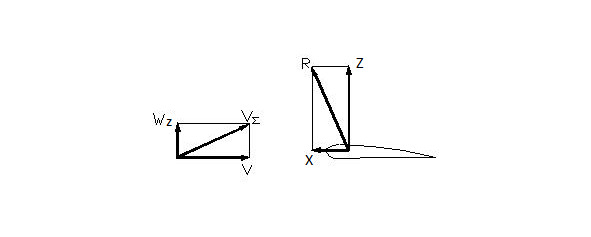
Thus, the downward motion of a wing’s section produces a positive angle of attack, which has positive lift and thrust pulling the wing section into the oncoming airflow. The magnitude of the thrust depends upon the vertical velocity of the wing. The more downward push, the more thrust the wing section produces. The downward push is a favorable phase of flapping — there is a lift and thrust.

The flap up

There are two schemes of upward flapping motion that will be considered here. The first, the positive angle of attack upward flap, is illustrated below.

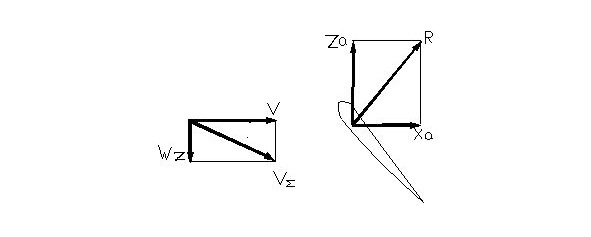
The projection of vector R to a vertical axis gives lift, and projection to a horizontal axis — drag. The more vertical velocity the wing section has the more turn angle of vector R and the more drag.

It is only possible to create thrust and turn the flapping vector R forward with a negative angle of attack, as illustrated below

.

However, in this scenario, with the lift negative, it is still the most unfavorable phase of flapping.

Extreme phases of a flap

Let’s consider the scenario where the wing’s section is motionless in the upper or lower points of a flap. In this case, the vector R force is always directed backward and the horizontal component is always a drag force, as is the usual case for a fixed wing section.

Thus, it is possible to make the following conclusions:

There are lift and thrust at downwards flap with a positive angle of attack;

There are lift and drag at a positive angle of attack when the wing is flapping upwards.

In order to generate thrust during the upward flapping phase, the angle of attack of the wing’s section should be negative. However, the lift also is negative.

At the extreme upper and lower points of a flap, where the wing is motionless, lift depends upon the angle of attack, and there will always be drag.