Бесплатный фрагмент - Геометрия-7

Предисловие

Эта небольшая книжка содержит рассуждения, в которых очень легко разобраться самостоятельно. Она дает возможность ознакомиться со школьной геометрией буквально за несколько часов (не обязательно идущих подряд).

Ее можно использовать как книжку для чтения при семейной форме обучения. Или на стадии обзорных занятий перед экзаменами.

Я старался создать курс, совместимый с большинством действующих учебников, но необходимо пояснить, что могут быть различные системы аксиом, и доказательства теорем также могут варьироваться.

Этот учебник дает способ быстро догнать одноклассников. Он также осознать тот простой факт, что школьный курс геометрии довольно прост. И доступен даже тем, кто совершенно не имеет никаких математических талантов.

Книжка дает возможность очень быстро вспомнить курс геометрии родителям и дает схему простого объяснения материала детям. Я также рассказываю немного об истории геометрии, чтобы сделать курс увлекательнее.

Обычно математика трудно дается детям, которые не привыкли к сложным формулировкам современных учебников, которым плохо даются сложные тексты. Или, возможно, у них другие интересы, и решение тренировочных задач вызывает негативные эмоции. Все эти преграды преодолимы.

Хотелось бы, чтобы школьники почувствовали красоту и гармонию математического мышления, не обремененного чрезмерным наукообразием. Работа в школе и в сфере методики преподавания математики убедили меня, что главным является вовсе не передача информации учащимся, а именно создание интереса, мотивации к обучению. Поэтому-то и была сделана мной попытка подойти к обучению математике отчасти и с эстетических позиций.

Итак. Данный учебник призван компенсировать ряд функций, отсутствующих в большинстве обычных учебников, таких как наглядность, простота, красота, доступность для детей с лексическими трудностями. Он не может претендовать на единственность при обучении. Например, в нем часто отсутствуют стандартные обозначения на чертежах, а также многие мелочи, предусмотренные целостным курсом. Но уверен, он найдет себе место в современном математическом образовании, где велик разброс между уровнями учащихся даже в одном классе. Он позволит выровнять класс и снять проблемы так называемой «математической отсталости», приводящие подчас учеников к полному отсутствию интереса, даже более того — к негативному отношению к предмету.

Так как восприятие математического текста в геометрии для школьников затруднено необходимостью постоянно сопоставлять обозначения на чертеже и в тексте доказательств и определений. Здесь эта сложность снята: вместо буквенных обозначений часто используются стрелки. Это дает возможность быстро интуитивно схватить суть или принцип доказательства. Материал, как обычно в моих книжках разбит на «кванты», единицы изучения. Также присутствуют и некоторые задачи, хотя учебник не заменяет задачника. Книжка состоит из нескольких частей, эта часть соответствует первой четверти 7-го класса.

Автор

Квант 1
Как возникла геометрия

Древние греки утверждали, что геометрию создали египтяне. Не случайно, видимо, в Древнем Египте были созданы такие замечательные дворцы с большими колоннами и такие прекрасные огромные пирамиды. Пирамиды такие огромные, так плотно пригнаны огромные камни, из которых они состоят, что историки до сих пор удивляются: как древние люди, примерно 5 тысяч лет тому назад смогли их создать. Да! Это не ошибка — 5 тысяч лет назад.

Очевидно, к тому времени египтяне уже хорошо знали геометрию, науку о геометрических фигурах. Одна из таких фигур так и называется — пирамида. Изображение египетской пирамиды, как она выглядит в реальности, я приводить не буду — вы найдете его в учебнике истории древнего мира. Зато приведу схематическое изображение, то есть чертеж пирамиды (точнее — три чертежа). Рис.1

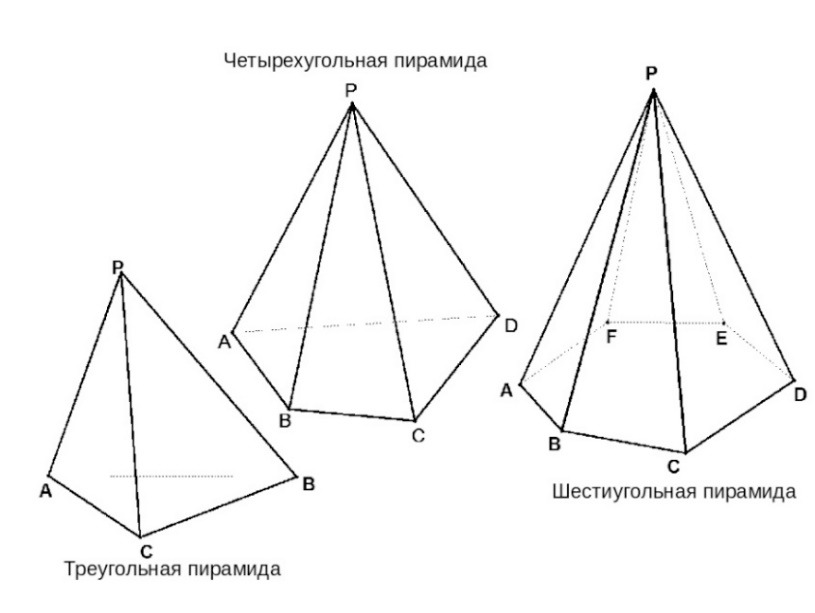
Из них на древнеегипетскую, пожалуй, похожа только средняя, да и та как-то не очень. Потому что у египетской пирамиды снизу мы видим ровный квадрат, а здесь четырехугольник какой-то не правильный. Тем не менее, все три фигуры — пирамиды. Разберемся внимательнее.

Начнем с пирамиды слева. У нее снизу — треугольник. Он называется — основание. Поэтому пирамида называется треугольной. Египетская пирамида не треугольная. Этот треугольник обозначен буквами А, В и С. Поэтому его называют треугольник АВС. С боков к треугольнику АВС примыкают треугольники АРС, ВРС, АВР. Эти три треугольника называются боковыми гранями пирамиды. А вот точка Р, в которой сходятся все боковые грани — это вершина пирамиды.

Средняя пирамида имеет в основании четырехугольник, и поэтому называется четырехугольной. А у правой в основании шестиугольник, поэтому она называется шестиугольной.

У египетской пирамиды есть еще дополнительные свойства. Как мы уже отметили, ее основание — квадрат. А что такое квадрат? Во первых, это четырехугольник, то есть фигура, имеющая четыре угла. Кроме того, эти четыре угла прямые, то есть составляют по 900. Кстати, отмечу, что само название «квадрат» произошло от латинского слова «квадра» — четыре. Также стороны у квадрата — равны.

У египетской пирамиды есть и еще одно свойство: все ее треугольные грани одинаковые, то есть равные. Это все означает, что наша египетская пирамида правильная. Подытоживая, можно сказать так: египетская пирамида — это правильная четырехугольная пирамида. На наших же трех рисунках-чертежах правильных пирамид нет.

Еще я хотел бы добавить, что для того, чтобы построить такие огромные сооружения, сначала, наверно, строили их чертежи. Бумаги тогда не было, но были папирусы, которые делали, склеивая листья растения, которое так и называлось — папирус. Эта бумага была очень прочной, настолько, что некоторые египетские папирусы сохранились до наших дней. На следующей странице вы можете увидеть древнеегипетский папирус с изображением треугольников.

Древнеегипетский папирус, рис.2. Этот папирус называют папирусом Ахмеса. Это 1650 г. до нашей эры. Это учебник по арифметике и геометрии. Наверно — самый древний предшественник наших учебников.

Теперь нам потребуется понятия множество и точка. Что такое точка, вы представляете. Но считается, что математическая точка такая маленькая, что у нее не просто маленькие размеры, но и вообще размеров нет. Осознайте пожалуйста. Нет размеров. Такое представление о точке получается, как говорят, в результате абстракции, то есть отвлечения от каких-то свойств, в данном случае — от размера. Также можно сказать, что точка бесконечно маленькая.

Точка — это будет как бы кирпичик, из которого состоят все геометрические фигуры. Точки маленькие, но из них состоит все. Даже пустое пространство тоже состоит из точек. Вы уже знаете, что точки обозначают большими латинскими буквами. Обычно используют только первые и последние буквы, но я на всякий случай приведу весь латинский алфавит (хотя он такой же, как и английский, но названия букв немного другие).

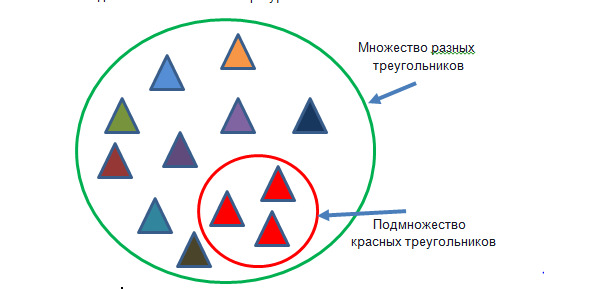
Теперь — понятие «множество». Это совокупность, собрание, коллекция чего-то. Есть множество букв в алфавите, множество черных кошек с белыми хвостами, множество фей на Луне (считается, что это множество пустое, но кто знает…) Итак. Говоря, что геометрические фигуры состоят из точек, мы фактически утверждаем следующее: геометрические фигуры — это множества точек.

Часть множества называют подмножеством. Например, множество кошек с белыми передними лапами — это подмножество множества кошек с правой передней белой лапой. А множество кошек с белой правой передней лапой и черным хвостом — подмножество кошек с белой передней правой лапой. Или. Множество тараканов с одним усом… Нет, плохой пример. Сами придумайте! В общем, часть фигуры состоит из точек, составляющих подмножество точек всей фигуры. Понятно?

Домашнее задание. Склеить пирамиду по развертке. Написать на ней какие-нибудь египетские иероглифы.

Квант 2
Геометрические фигуры

Геометрические фигуры бывают двух типов. Одни, например, треугольники или квадраты, можно нарисовать на чертеже. Все такие фигуры могут быть «помещены» на плоскость. Такие фигуры называются плоскими. А вот, например, пирамиду на чертеже поместить невозможно, она не помещается в плоскости чертежа. Такие фигуры называются объемными. Чтобы нарисовать пирамиду, нужно ее спроектировать на плоскость.

Есть два раздела в геометрии. В одном изучаются плоские фигуры — это планиметрия (легко запомнить от слова «план»), в другом — объемные, это стереометрия. И начинаем мы — с фигур на плоскости, то есть с планиметрии. Египтяне, пишет древний историк Геродот, были большими знатоками планиметрии. Египет располагается по берегам крупнейшей реки — Нила. Периодически Нил разливается и зона разлива покрывается водорослями и орошается водой. Поэтому она очень плодородна. И она разделялась на множество участков, принадлежащих земледельцам. Но при каждом разливе границы между участками смывались, и после отлива приходилось их проводить заново.

Этим занимались так называемые гарпедонапты, специалисты по практической геометрии, в данном случае — по разметке земли (по-нашему — землемеры). Гарпедонапты должны были хорошо знать геометрию, и как минимум уметь строить прямые углы.

Для этого они применяли специальную мерную веревку. На ней через равные расстояния были завязаны 11 узлов. Веревку связывали в большое кольцо, растягивали и получался треугольник со сторонами 3, 4 и 5 единиц (для нас не важно каких). Главное, что получался треугольник с прямым углом.

Такой треугольник называется «египетский».

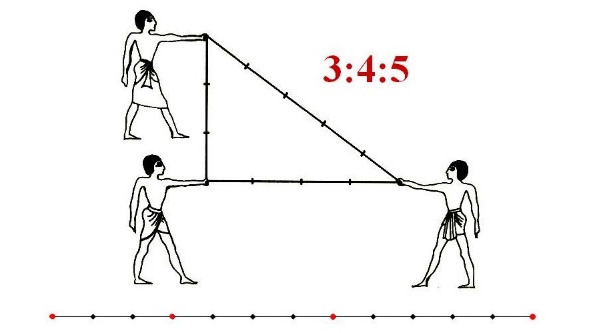
Почему так получается, они об этом не задумывались — жрецы сказали, они верили. Но наука начинается все-таки с вопроса: «Почему?»

Мы определим окружность как множество точек на равном расстоянии от какой-то одной точки, называемой центром окружности. Циркуль (как вы знаете, это прибор для проведения окружностей) стали использовать древние греки в очень давние времена, задолго до Евклида или даже Пифагора (с этими учеными мы еще познакомимся). Изобретателем циркуля греки считали некоего Талоса, ему же приписывали и изобретение гончарного круга.