
Бесплатный фрагмент - Токсичность автомобиля
ВВЕДЕНИЕ
В настоящее время все более актуальной становится проблема уменьшения вредных выбросов автомобилей с отработавшими газами, особенно при движении в городах в сложных циклических скоростных условиях и различных нагрузочных режимах двигателей. Если ранее проблемы загазованности крупных городов, смог и другие сопутствующие вопросы были актуальны лишь для таких стран как США, Англия, Франция, Германия и Япония, то сейчас при колоссально увеличившемся автомобильном парке в нашей стране-эта проблема не только активно дебатируется везде и повсюду, но и так же уже безуспешно пытаются решаться многие годы и здесь (цитата о современности):
Во всех странах ведутся активные научные исследования как непосредственно в этой области, так и просто осуществляются попытки создания радикального, то есть альтернативного экологически чистого транспорта.
1. СОСТОЯНИЕ вопроса И ЗАДАЧИ
ИССЛЕДОВАНИЙ
Далеко не все, но самые основные компоненты в отработавших газах автомобильных выхлопов имеют вредное воздействие на окружающую среду и организм человека. Так, к примеру, углекислый газ не оказывает непосредственно вредного влияния на организм человека: он лишь приводит к появлению «тепличного» эффекта и т. п., поэтому его воздействие находится вне рассмотрения.
Другие же вредные вещества, выбрасываемые с отработавшими газами непосредственно влияют на здоровье людей и окружающую среду, поэтому требуют необходимого анализа.
Это касается всех вредных газов, для основных из которых существуют нормы выбросов, предельно-допустимые концентрации, пороговые дозы и пр. Выброс и канцерогенных ПАУ и НИТРОПАУ вообще являются наиболее вредными и относятся к классу высоких токсичных с очень большим коэффициентом вредности: они приводят к появлению раковых онкологических заболеваний, что уже известно по многочисленным экспериментам на животных и с помощью необходимых статистических данных в этой области.
Все эти факторы могут быть обьеденены между собой и исследованы с помощью самых современных инженерных математических методов, а результаты исследований — могут дать пользу, в частности, при создании микропроцессорных систем управление автомобилем и двигателем, в процессе проведения необходимых научно-исследовательских и опытно-конструкторских работ для создании новых образцов перспективных автомобилей различных классов и т. п.
Таким образом, возникает много вопросов в этом направлении, которые являются весьма актуальными и требуют необходимого решения.
1.1.ОБЩИЙ СЛУЧАЙ ФОРМУЛИРОВКИ
ЗАДАЧИ ДВИЖЕНИЯ
Движение транспортного средства апроксимируется простыми и известными математическими выражениями. Историческая формулировка называется задачей Коши при некоторых граничных условиях. Тогда конкретная формулировка для движения транспортного средства выглядит как дифференциальное уравнение движения, где для разных случаев движения имеются различные факторные условия, часть из которых общая:
— тяговая сила привода, например, на колесах,
— суммарная сила сопротивления движению,
— масса транспортного средства,
— ускорение неравномерного движения.
Другие факторы являются характерными лишь для каждого отдельного транспортного средства. Рассмотрим разные случаи для наземных транспортных средств.
Для автомобилей с колесным или гусеничным приводом (включая так же рельсовый транспорт) это следующие параметры:
— коэффициент учета вращающихся масс, в
суммарную силу
сопротивления движению входят:
— сила сопротивления качению,
— сопротивления воздуха,
— сопротивления подьему.
Для морского транспортного средства: в суммарную силу сопротивления входят:
— равнодействующая сил трения, возникающая в
случае вязкости воды между корпусом движуще
гося судна и ближайшими к нему слоями воды
пограничного слоя,
— сопротивление формы, образующееся при
понижении давления, воды за корпусом судна,
— волновое сопротивление (влияние волны на
распреде ление гидродинамических давленией
вдоль смоченной поверхности корпуса судна,
— сопротивление выступающих частей (рулей,
насадок, кронштейнов).
В данном случае в состав расчетных параметров входят так же плотность воды, безразмерные коэффициенты трения, формы и волнового сопротивления.
Для слуяая амфибийных транспортных средств, т.е. для судов с воздушными подушками полное аэродинамическое сопротивление включает в себя:
— силу воздушного сопротивления,
— силу импульсного сопротивления на преодоление силы инерции воздуха, захваченного вентилятором,
— реактивное сопротивление на преодоление
горизонтальной составляющей реакции струи воздуха из воздушной подушки.
Здесь во всех случаях все силы сопроивления движению пропорциональны постоянным коэффициентам и квадрату линейной скорости, поэтому интегральное уравнение движения в принципе имеет одну форму -и эти случаи могут рассматриваться как один и тот же вид интегрирования.
Для обобщенного варианта судов на подводных крыльях, экранопланов, горизонтального полета самолетов еще появляется дополнительная сила сопротивления, пропорциональная так же и линейной скорости, что и является основным отличием для данных случаев, т.е. интегральное уравнение движения имеет другую форму и здесь не рассматривается.
Таким образом решением дифференциального уравнения такого типа являются различные способы: разложение в ряд Тейлора, численные методы интегрирования, например, Рунге-Кутта, тяговый расчет, неопределенный интеграл и интегральное решение с граничными условиями, т.е. непосредственно новый метод, предложенный автором и названным по аналогии и математической сущности как известные методы из смежных дисциплин естествознания. Но как здесь уже указано данное решение ограничено лишь для первых однотипных условий движения наземных транспортных средств, — а, например, наличие крыльев транспортного средства меняет эти факторные условия координально, не говоря уже о наличии (из теоретических основ):
потенциальной энергии летающего транспорта. В последнем случае появляется хотя бы пропорциональная еще и линейной компоненте скорости движения, что требует совсем других математических моделей и дает другие результаты интегрального исчисления.
Эти факторы сопротивления движению и тяговая сила определяются в каждом случае своими расчетными формулировками, но могут апраксимироваться для всего привода в общем случае (особенно для последнего варианта с дополнительным линейным сопротивлением) как уравнение Лагранжа второго рода.
Поэтому в первых случаях с наиболее простыми факторными силами решение принимается как задача Коши и непосредственно в виде предложенной автором ранее формулировки, то для более общих случаев движения уже необходимо применять уравнение Лагранжа и соответствующие этому математические апраксимации.
1.2.Методы математического моделирования
для решения многосторонних задач.
1.2.1.Проблема использования математических
методов моделирования.
При решении сложных вопросов моделирования различных процессов всегда использует различной сложности математические методы моделирования. Это основной способ нахождения достоверного решения, точность решения которого зависит от выбранной модели и т. п.
Моделирование движения автомобиля или транспортного средства и особенно выбросов вредных веществ с отработавшими газами — очень сложная проблема, имеющая многочисленные аспекты и особенности. Поэтому известно достаточно много подходов в этой области, многие из которых имеют некоторые отличительные особенности, более или менее правильно соответствуют действительности. Различные исследователи и ученые трактуют данные проблемы исходя из своих конкретных представлений по разному, но полностью полагаясь на методы математического моделирования, анализ которых представляет определенный интерес. Таким образом, непосредственно вопросы математического моделирования в данном случае играют ключевую роль и принципиально важны даже в перспективе. Выбор наиболее правильной модели зависит от анализа уже существующих и т.п., поэтому данному вопросу необходимо уделить соответствующее внимание и особый интерес.
1.2.2.Методы расчета в теории движения
автомобиля.
Общий случай движения транспортного средства (из теории)
описывает уравнение Лагранжа второго рода, в котором учитывается переменные в профиле и плане параметры дороги, т.е. временная кривизна, что позволяет определять характеристики с учетом управляемости, однако, что достаточно сложно в виду невозможности точного определения некоторых из них. За обобщенную координату принимается угол поворота коленчатого вала, а за обобщенную силу — момент на валу двигателя, первой производной является угловая скорость вала двигателя.
Учитывая чрезвычайную сложность точного решения для данного уравнения, а также то, что более простая форма
(это математический анализ и теория)
для задач типа Коши без учета переменной кривизны в профиле и плане представляется для движения автомобиля в плане в традиционной классической форме.
Основоположником теории автомобиля в этом плане является академик Чудаков Е.А,который использовал работы Жуковского Н. Е. для анализа движения и позднее создал свою научную школу в виде последователей, но его представления не меняются уже протяжении более 70 лет.
1.2.3.Обзор аналитических методов определения
токсичности вредных выбросов.
Большой вклад в развитие представлений о токсичности двигателей внес д. т. н., профессор Варшавский И. Л. и его последователи. Им была создана основа теории токсичности двигателя и лишь частично-автомобиля, на базе которой проводятся все современные исследования и созданы многочисленные разнообразные методики расчетов..
В зависимости от коэффициента избытка воздуха, например, определяется выброс СО, а также определяется условие не токсичности воздуха в помещении. По другой методике на базе математической апраксимации можно определить выброс токсичного компонента. Необходимое и достаточное условие разбавления отработавших газов воздухом также определяется в его исследованиях, также как и токсичность газовой смеси.
Кроме этого удельную токсичность двигателя и токсичность автомобиля также можно определять в общем случае и для автомобилей с нейтрализаторами. Токсичность компонентов, приведенная к СО по критериям вредности — это также критерии в данном случае.
1.2.4.Инженерные математические методы
для расчетов.
Среди различных оптимизационных методов обычно выделяют метод исследования эксперимента. Однако это не самый лучший из подходов с точки зрения повышения точности результатов расчетов, особенно для задач движения транспортных средств. Кроме того, в расчетах обычно удобнее использовать численные методы на базе известных критериев оптимизации. В непосредственных расчетах этими методами являются такие как метод хорд, метод Симпсона, отрезков, Рунге-Кутта и др. Они также дают приближенное решение задачи с определенной точностью. Как правило, это задачи, по своей сути, на собственные значения, позволяющие определять действительное значение искомого параметра приближенным численным методом.
В задачах оптимизации при многофакторном эксперименте. когда требуется найти экстремум по многим исходным параметрам, обычно используют действительно методы исследования операций. К ним можно отнести методы покоординатного спуска, градиентного спуска, метод Эйлера, Адамса, главного критерия, обобщенного критерия, последовательных уступок, экспертных оценок, наименьших квадратов или Лежандра-Гаусса и т. п.
Некоторые из них являются более общими и могут использоваться не только для многофакторного эксперимента, поэтому четкого различия иногда не проявляется, но проблема точности решения для данных задач остается сложной. К более серьезным и совершенным, но новым методам относится численное моделирование на базе метода конечных элементов. В классе задач теории движения транспортных средств известен лишь ограниченный круг работ. Однако, в целом данный метод известен как самый серьезный и точный инженерный математический метод, обладающий фундаментальными обобщениями для различного класса задач, поэтому он может позволить решить задачи оптимизации на высоком уроне.
Существует несколько вариантов метода конечных элементов с точки зрения его математической формулировки: вариационный МКЭ в виде метода Ритца, метод Галеркина, метод коллокаций, метод наименьших квадратов, метод штрафов. метод невязок. Точность решения с помощью метода конечных элементов, как известно очень высокая и зависит от возможности уменьшения невязки решения. что в отдельных случаях, особенно, для задач на собственные значения, удается достигнуть.
Метод конечных элементов значительно глубже и точнее, чем известные методы исследования операций, поэтому он очень прогрессивен и перспективен. Различные варианты МКЭ имеют свои особенности, которые необходимо учитывать, поэтому далее дается краткая характеристика основных из них.
Метод Ритца отличается заменой величины невязки в вариационной задаче конечно-элементным пространством или последовательностью конечно-элементных подпространств и специально подобранными пробными функциями. На каждом подпространстве минимизация функционала приводит к решению системы линейных уравнений. Апроксимация Ритца–это функция, минимизирующая исходную искомую функцию на области определения. Система линейных уравнений в данном случае решается методом исключений Гаусса. Принцип мини-макса характерен для случая решения задачи на собственные значения, при котором определяются приближенные значения функции.
Метод коллокаций подобен методу Галеркина. При нем такой выбор пробных коэффициентов, что уравнение определяется точно в характерных точках. Эти определенные точки коллокаций берутся в некоторых точках полинома Лежандра, поэтому для данного случая алгебраические уравнения имеет меньшее число членов, чем в методе Галеркина.
При методе наименьших квадратов определяется рекурентная функция на базе уравнения Эйлера-Лагранжа более высокого порядка чем исходное. Экстремумы исходной и данной рекурентной функции совпадают. Вариантом этого является метод штрафов с интегральными функционалами.
Полудискретный метод Галеркина требует интегрирование функции по частям, использование граничных условий типа Дирихле и особой формы записи самой модельной задачи. Этот метод приводит к системе обыкновенных дифференциальных уравнений. Параболические уравнения с частичными производными и соответствующие им системы нового порядка по времени наиболее вероятно решаются методом Кранка-Никольсона-Галеркина.
Обычная вариационная формулировка метода конечных элементов заключается в том, что для эквивалентной вариационной функции условия минимизации адекватны решению исходного уравнения при некоторых определенных условиях: пробные функции непрерывны, имеют кусочно-непрерывные первые производные и удовлетворяют главным граничный условиям. Кроме того. необходимо соблюдать критерий малости в методе невязок. Используя подход Одена можно применять в расчетах и обыкновенные дифференциальные уравнения для некоторых случаев: например, для случая движения последний вариант дает положительное решение, особенно для задачи на собственные значения. Сам вариационный принцип состоит в том, что интеграл от некоторой функции имеет меньшее или больнее значение для реального состояния системы, чем для любого возможного состояния, допускаемого основными условиями системы. Кроме того, должны соблюдаться и граничные условия, определены узловые точки, конечно-элементные формы и т. п. Поэтому данный метод может давать наиболее точные решения для задач данного класса, однако, в некоторых случаях он еще не применялся и малоизвестен.
Метод конечных элементов, т.е. его вариационный принцип, позволяет найти пробную функцию. Минимизирующую заданный функционал потенциальной энергии — это непосредственно апраксимация Ритца, а сам МКЭ — это обобщение метода Рэлея-Ритца-Галеркина. МКЭ использует вариационный принцип, а не апраксимацию отдельных членов дифференциального уравнения. В методе Ритца все бесконечномерное пространство заменяется пробными функциями с гладкими краевыми условиями. Основное уравнение МКЭ определяет ошибку апраксимаций с помощью линейных элементов Ритца можно считать минимальной. В полудискретном МКЭ задача определяется неизвестными значениями функции в узловых точках. Условие экстремума: в таких вариационных задачах функция должна удовлетворять ряду условий — ищется экстремум одного интеграла при условии, что другой интеграл сохраняется постоянным. Для случая движения, например, одномерной массы под действием силы, пропорциональной пройденному пути при условии постоянной пропорциональности равной 1,уравнение МКЭ имеет определенный вид. МКЭ характеризуется следующими особенностями :
1-физическая областъ делится на под-области или конечные элементы,
2-зависимые переменные апраксимируются функцией специального вида на каждом конечном элементе,
3-подстановка апроксимаций в уравнение дает систему уравнений с неизвестными параметрами, которую можно решить,
4-прочие функции являются непрерывными.
Граничные условия для всех типов задач бывают трех видов: условия Дирихле — первого рода. Неймана — второго рода, Коши — третьего рода, случай когда зависимая переменная и ее нормальная производная связаны точками самой функции на границе. Для первого случая иногда используются штрафные функции, во втором случае задачи имеют слой сопротивления, третий случай характерен для задач движения.
Кроме всех уже указанных вариантов МКЭ существуют и другие. Метод Канторовича-полудискретный или прямой метод апраксимаций, где неизвестные коэффициента уже не скалярны, а непосредственно функции. При этом используется дифференциальное уравнение другого рода. Метод Галеркина построен на интегральном разностном подходе и полиномных, в том числе пробных функциях. Метод наименьших квадратов — как самый простой вариант относится к классу обычных численных методов. Его же называют методом Рунге-Кутта: получаем уравнение большего порядка, чем исходное. Метод переменных направлений Галеркина: для одномерной задачи можно получить матрицу исходной системы линейных уравнений алгебраического вида ленточного типа. В методе невязок для пробной функции требуется, чго бы невязка удовлетворяла также некоторому условию малости -это взвешенный интеграл по данной области.
В общем виде решение системы частных диференциальных уравнений с помощью МКЭ является обычной вариационной задачей с приближениями, которые так же являются невязками решения. особенно для уравнений в частных производных для задач типа Коши, т.е. задач движения. Невязка решения — фактическое расхождение между истинным и апраксимированым значением оптимального решения, поэтому это более общее понятие, которое определяет точность решения. На нее существен-но влияют допущения функционален. В частности, ошибка (из математического анализа и исследования операций):
апраксимация, например, по вариационному методу Ритца, с помощью линейных элементов должна быть минимальна. При этом следует учесть. что это лишь один из исходных моментов, влияющих на точность решения задачи, В дальнейшем необходимо записать условия минимизации, т.е. оптимизации всего функционала в матричном виде на базе системы уравнений Гаусса, Однако. можно решать эту задачу иначе в формулировке на собственные значения, тогда подход будет существенно изменен, Эго более простой способ оптимизации без определения экстремумов функции основных параметров транспортного средства, смысл которого излагается несколько иначе.
При расчетах возникает проблема как глобальной так и локальной оптимизации, поэтому можно использовать различные оптимизационные методы. Причем предпочтение дается данному новому подходу на базе МКЭ. При этом можно говорить или об оптимальном решении или об оптимальных значениях. В области теории движения автомобиля в частности и теории движения транспортного средства вообще могут быть использованы любые простые и сложные математические методы, что нашло очень широкое распространение, Однако они часто не дают подходящего точного решения, а, кроме того, не найдены наиболее эффективные способы. Поэтому, например, для поиска глобальной оптимизации в данном случае можно использовать различные методы исследования операций, но МКЭ — более универсальньй и гибкий метод в этом плане, позволяющий с высокой точностью проводить любые расчеты и находить экстремумы любого рода. В связи с этим предпочтение отдается исследованию его всесторонних возможностей.
2.ТЕОРИЯ ДВИЖЕНИЯ АВТОМОБИЛЯ, КАК
ЧАСТНЫЙ СЛУЧАЙ НАЗЕМНОГО
ТРАНСПОРТНОГО СРЕДСТВА.
2.1.Формулировка задачи движения автомобиля
на базе дифференциального уравнения дви-
жения.
Движение автомобиля является частным случаем движения наземного транспортного средства, так как характеризуется наличием тяговой силы и сил сопротивления движению консервативного типа. Поэтому уравнение движения автомобиля аналогично уравнению движения другого вида наземного транcпортного средства и может рассматриваться как частный случай, а действующие в системе силы-как обобщенные факторные
Теория движения автомобиля включает в себя много аспектов, однако, в первую очередь сводится к формализации и определению тягово-скоростных свойств, топливной экономичности и пр. Такие параметры, как устойчивость, управляемость, безопасность и пр. в данной работе не рассматриваются, так как являются отдельными самостоятельными задачами. Кроме того, рассматривается упро-щенный случай курсового движения, т.е. движение с собственной относительной системой координат. Этот фактор упрощает методику и расчеты, но не снижает точности, а, кроме того, позволяет создать базовую имитационную модель, которая может пригодиться и в дальнейших исследованиях в разных задачах.

2.2.Уравнение движения автомобиля и
функционалы интегрирования.
Уравнение движения автомобиля, как и наземного транспортного средства, может быть представлено в виде тягового баланса (2.1) — (2.8),на основании чего получаются данные интегральные зависимости.
В данных выражениях приняты следующие обозначения исходных параметров:
Ga — полная масса автомобиля, н,
fo — статический коэффициент сопротивления качению,
i — продольный уклон дороги, или величина подъема
или спуска,%,
Cx — коэффициент лобового сопротивления,
pв — плотность воздуха, кг/м3,
F — лобовая площадь автомобиля, м2,
bвр — коэффициент учета вращающихся масс при раэгоне,
Jа — ускорение автомобиля, м/с2,
Me — эффективный крутящий момент двигателя, нм,
Uтр — общее передаточное число трансмиссии,
eta — коэффициент полезного действия трансмиссии,
rк — динамический радиус колеса, м,
Для случая выбега при движении за счет сил инерции получаем уравнение движения со свободной силой, которое в дифференциальной форме будет выглядеть как (2.9), где bврв-коэффициент учета вращающихся масс при выбеге, а функционал интегрирования в этом случае будет выглядеть как: (2.10).При равномерной движении исходным уравнением является тяговый или мощностной баланс (2.1).
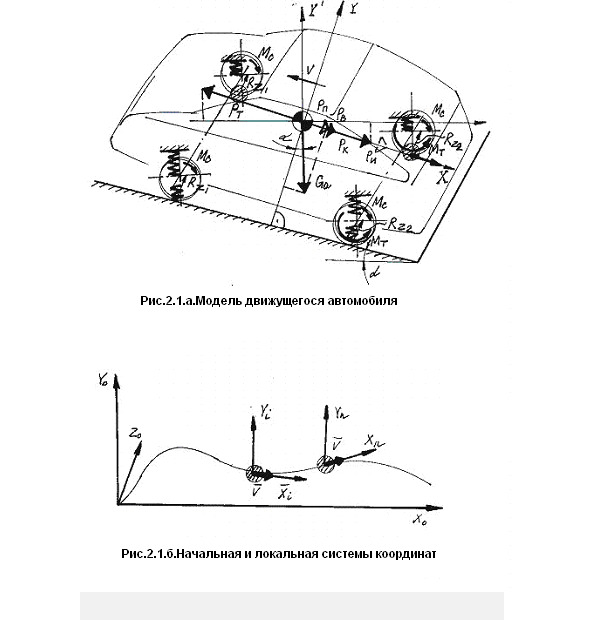
2.3.Математическая модель автомобиля.
Данная математическая модель автомобиля построена на известных классических понятиях этой области и представляет из себя в целом аналогичную схему. Основной проблемой в этом случае является возможность анализа тягово-скорстных свойств и т. п. на базе разработанной модели с учетом принятого подхода. Поэтому можно рассматривать уже известные подходы как базовые в двух координатных сетках: одна базовая-начальная система координат, другая локальная-совмещенная с автомобилем, или точнее с его центром масс. Случай с двумя координатными сетками рассматривается достаточно редко, поэтому является новым элементом и в данном подходе может дать выигрыш в повышении точности расчетов с использованием соответствующих математических методов.
Таким образом, движение автомобиля сводится к криволинейному движению материальной точки с некоторыми степенями свободы и упрощениями, не влияющими на точность результатов. Поэтому рассматривается не общий случай криволинейного движения на базе уравнения Лагранжа второго рода, а данная система с двумя координатным сетками, причем локальная система перемещается с центром масс автомобиля строго по курсу автомобиля, т.е. существует случай курсового движения. Таким образом, движение в локальной системе координат-плоское двумерное. Это упрощение позволяет добиться существенного выигрыша в плане математического эксперимента.
В данной модели существует несколько степеней свободы: движение вперед-назад, возвратно-поступательного типа; вверх-вниз — в пределах определенных углов наклона. Кроме того, существует возможность присоединения элементов расчета, позволяющих в той или иной степени оценить углы подьема и спуска, а также углы продольного крена, и движение «влево-вправо» самой локальной системы координат. Таким образом для данной математической модели существует 8 основных степеней (это из аналитических апроксимаций автора монографии):
свободы, некоторые из которых имеют ограничения и упрощения. Не учитываются, например, такие факторы, как боковые крены, боковые углы рыскания, связанные в частности с уводом шин, но сама модель дает возможность в перспективе подключать соответствующие известные сложные методики для анализа этих случаев. В то же время в модели учитываются многие необходимые факторы с известными в теории автомобиля упрощениями: например, центр приложения силы аэродинамического сопротивления можно учитывать как фактор дорожного сопротивления, упругость шин учитывается аналогичным образом, а угол подъема определяется упрощенно и т. п.
Схема модели приведена на рис.2.1а,б. Здесь показан общий случай для движения автомобиля с произвольным ускорением на полотне дороги с определенным углом подьема. Для случая равномерного движения будет отсутствовать инерционная сила. На рис.2.16 показано расположение начальной и локальных, движущихся и связанных с автомобилем в виде материальной точки систем координат. В этой модели основные движущие, а также силы сопротивления приведены к центру масс автомобиля, представляемого как материальная точка. Кроме того, позволяет учитывать, например, жесткость подвески, а также упругость шин. Последний фактор дает представление об упругости шины как деформируемом элементе, поэтому в перспективе можно применять и более сложные модели качения. Для материальной точки в данной модели автомобиля можно также с помощью известных подходов оценивать динамическое распределение масс в виде ограничений, в некоторых случаях углы рыскания и т.п.Таким образом, связь локальных систем координат с движущейся материальной точкой может производить численный анализ на базе данной модели курсового движения с высокой точностью. При этом некоторые элементы в математической модели автомобиля можно рассматривать как известные, но вместе с тем отчасти трактовать как новые. Упругость шин, например, в данном представлении является коэффициентом сопротивления качению, который является отношением силы сопротивления качению к нормальной реакции на колесе и зависит от многих факторов. При этом можно учитывать коэффициент динамического перераспределения массы автомобиля, так как изменяется величины нормальных реакций в пятне контакта и параметры скольжения силы при передаче крутящего момента, т.е. как дополнительное упругое сопротивление или буксование. Боковые уводы также могут повлиять на точностъ расчетов, однако, в данной модели, как уже указывалось, они не учитываются, что принципиально важно. Их можно будет учитывать в дальнейшем не-посредственно для соответствующих задач математического моделирования Поэтому первоначально рассматриваются два допущения:
— криволинейное движение с большими радиусами, которое близко приближается к прямолинейному и является курсовым движением;
— величина продольного угла наклона изменяется в необхо-димых диапазонах, характерных для случая движения автомобиля, когда тангенс угла наклона принимается непосредственно равным углу наклона, что давно известно в данной области науки (о вопросах исследования):
Существует и ряд некоторых других малоизученных аспектов. Передаточная функция трансмиссии моделируется в данном случае известным образом и характеризует преобразование крутящего момента по его величине не зависимо от типа движителя и непосредственно трансмиссии. Для механической трансмиссии передаточное число общее определяется простым умножением пере-даточных чисел звеньев, а для автоматической или гидромеханической оно определяется по соотношению входного и выходного моментов, на что, в частности, влияет система управления данным механизмом.
2.4.Элементарный тяговый расчет
и его табличный вид.
(классические методы)
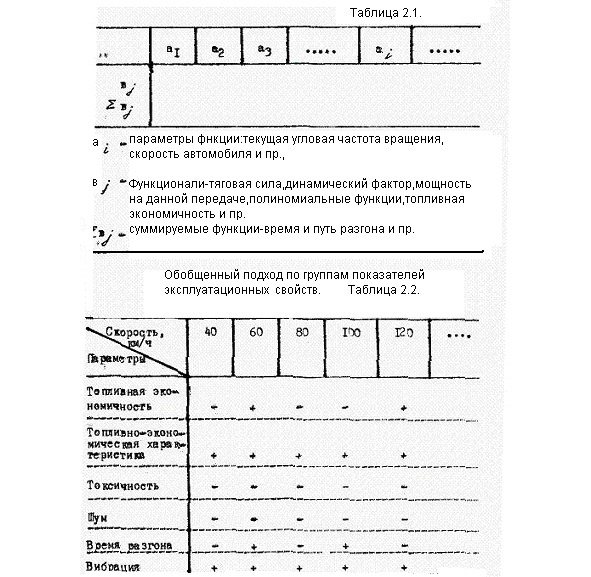
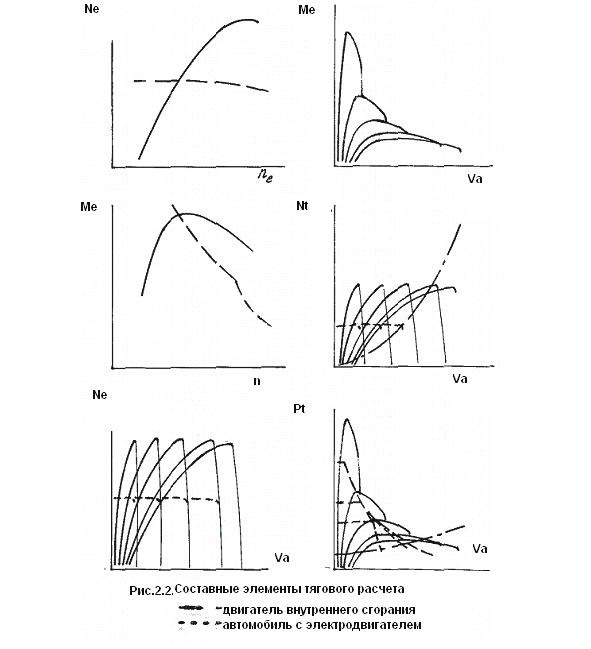
Тяговый расчет является основным известным методом для определения тягово-скоростных и топливно-экономических свойств автомобиля. Однако, он обладает большой погрешностью, так как основан на графоаналитическом методе, из чего следует, что он обладает большой неточностью. Поэтому используя функционалы интегрирования удается не только увеличивать точность расчетов благодаря методу интегрирования, а не графического сложения. но и сделать этот процесс менее трудоемким, простым и быстродейсгвующим. Тяговый расчет в сжатом виде можно представить в виде таблицы 2.1—2.2,а некоторые его составные элементы представлены на рис.2.2.В самом обычном варианте этот метод удобен для расчетов:
в том числе для электропривода
.
Кроме того, можно говорить об обобщении различных групп показателей для оценки эксплуатационных свойств автомобилей на перспективу, так как расширение их номенклатуры и возможность их сопоставимости в функции, например, скорости движения принципиально важно. Этот подход на базе сравнительного анализа продемонстрирован в таблице 2.2. Таким образом, можно даже разнородные показатели свести в единообразную форму и сравнивать их для различных автомобилей.
Поэтому в целом можно расширить возможности и сферу применения для тягового расчета для наземных транспортных средств. При этом можно использовать и новые методы математического моделирования.

2.5.Интегральный вид уравнения движения
и определение параметров движения.
2.5.1.Общий случай интегрирования.
Рассмотрим случай для полиномной интерполяции мощности двигателя и часового расхода топлива.
Путь разгона определяется на основании уравнения (2.7)
как (2.11), а время разгона на основании уравнения (2.8)
как (2.12).Второй интеграл выражения (2.11) представляет собой время разгона, поэтому путь разгона также может быть выражен иначе: (2.13)
В формулах (2.11—2.13) используются следующие расчетные коэффициенты (2.14) — (2.17):
Ме — крутящий момент двигателя при максимальной мощности, нм,
VN — скорость автомобиля, соответствующая макси-
мальной мощности, м/с,
а,в,с — коэффициент полинома (2.18)
We» — удельная угловая скорость,
We — текущая угловая скорость коленвала двигателя, с-1,
WN — угловая скорость при максимальной мощности, с-1,
Vi, Vi+1 — начальная и конечная скорости разгона, м/с,
Выражение (2.12) для определения времени разгона в диапазоне от Vi до Vi+1 может быть записано также в следующем виде (2.19)
где delta — дискриминант.
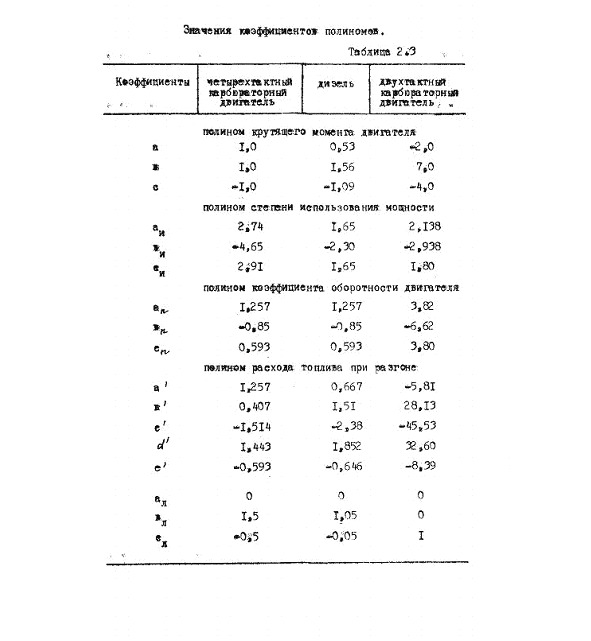
При значениях характерных для случая многих двухтактных двигателей, -интеграл в уравнении (2.8) будет вида: (2.20).Как показывают расчеты выражения (2.12) и (2.20) дают абсолютно идеинтичные результаты. Данный метод интегрирования для основных показателей основан на полиномной интерполяции характеристик двигателей, что сразу дает в аналитическом виде значение решения. Значения коэффициентов полиномов приведены в таблице 2.3,а формы кривых полиномов на рис.2.3.а-в. Значения коэффициентов полиномов можно определить известными методами.

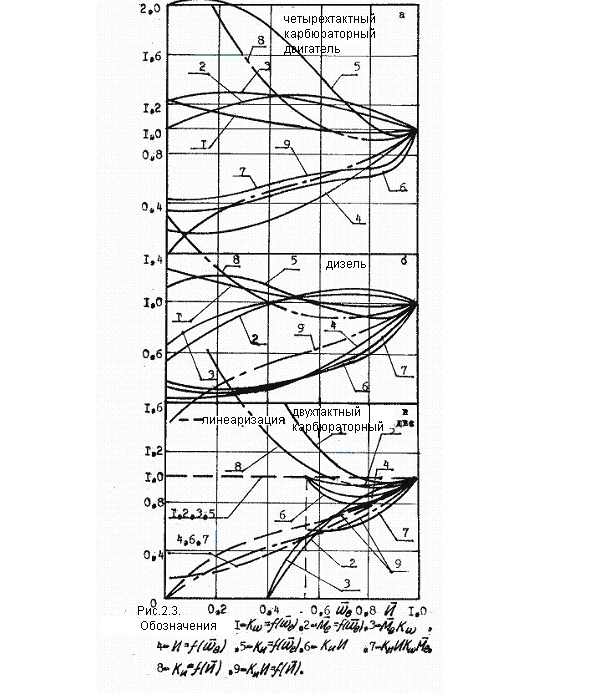
2.5.2.Случай линеаризации.
Кроме того, существует частный случай интегрального вида уравнения движения. Он получается в идеальном случае, если момент двигателя постоянен: случай линеаризации. Иногда линеаризация может оказаться более выигрышной. При этом коэффициенты в уравнении движения (2.3) будут иметь несколько иной вид, а интегральное выражение для определения величины пути можно записать как, м (2.21),а время разгона (2.22). В этом же случае можно записать развернутое уравнение выбега, полученное из уравнения (2.26).Интегрируя его аналогично (2.7) определяем путь выбега (2.27),а время выбега определяется как (2.26),
где bврв — коэффициент учет вращающихся масс при выбеге,
Vв — условная скорость выбега, м/с,
Для вариационных исчисления, т.е. в описанной в дальнейшем задаче метода конечных элементов в теории движения, можно также формулу (2.21) привести к другому виду и использовать его как один из конечных элементов для определения пути разгона: (2.30)
где Vmax — максимальная, в том числе и кинематическая скорость движения автомобиля, м/с,
Для случая определения пути выбега можно получить следующий вид конечного элемента: (2.31)
Данные уравнения могут применяться непосредственно и при вариационной формулировке задачи при правильном подборе коэффициентов полиномов.
2.5.3.Определение расхода топлива при
разгоне автомобиля.
Часовой расход топлива, как известно можно определить через удельный расход топлива:,кг\ч (2.32)
где qe=qnKобКи — удельный расход топлива, г/кВтч,
Коб- коэффициент, учитывающий зависимость удельного расхода топлива от угловой скорости коленчатого вала двигателя,
Ки — коэффициент, учитывающий зависимость удельного расхода топлива от степени использования
мощности двигателя: для разгона при полной подаче топлива можно принимать =1.
Расход топлива при этом можно определить в упрощенном случае путем интегрироваания уравнения часового расхода топлива (2.33)
Определенный интеграл в этом случае будет давать конечное аналитическое выражение в виде:,л (2.34)
где pт — плотность топлива, г/см3.
Последнее выражение может быть также записано в виде:,л (2.35)
где Nmax — максимальная мощность двигателя, кВт.


Данный случай является упрощенной идеальной моделью. Для полиномных моделей коэффициентов Коб и Ки уравнения часового расхода топлива (2.32) пропорционально произведению скорости на коэффициенты полиномов Коб, Ме, Ки, являющиеся полиномами удельной частоты вращения, следовательно зависит от 5-й степени скорости автомобиля: (2.36), (2.37).Коэффициенты полиномов для разных типов двигателей могут быть рассчитаны аналитически, их значения представлены в таблице2.3. Однако, тогда уравнение расхода топлива (2.33) при интегрировании дает значение, пропорциональное 6-й степени скорости, что приводит к усложнению непосредственно интегрирования и уменьшения точности расчетов за счет разложения интеграла в ряд и т. п. Кроме того, необходимо отметить, что реальные характеристики двигателя, например, Ме не всегда могут быть описаны полиномами второй степени точно — для этого требуются полиномы 3-5-й степени.
Аналогичные преобразования необходимы и для полиномов Коб и Ки, поэтому уравнение для определения расхода топлива при разгоне Gр может стать очень сложным и громоздким, пропорциональным 10-й степени скорости и т. п. В этом случае можно получить слишком сложную и неудобную модель на базе рядов Тейлора с остаточными членами, мало влияющими на точность результата. В этом случае приходится либо довольствоваться исходной апраксимацией, либо переходить к численным математическим моделям в виде численного интегрирования и т. п.
Аналитический метод может быть упрощен без существенных погрешностей вычисления: на рис.2.3а-в показаны кривые 3,6,7—9,являющиеся произведениями полиномов для различных типов двигателей. В рабочих диапазонах двигателя они могут быть апраксимированы линейными исходными функциями, коэффициенты для которых приведены в таблице 2.3.В этом случае значительно упрощается уравнение часового расхода топлива: учитывая, Gt=0 при"нулевой"частоте вращения двигателя коэффициент aл=0. Оно будет иметь в этом случае вид, л (2.45).Тогда расход топлива определяется как интегральная функция, л (2.46)
Таким образом, в качестве одной из рабочих исходных моделей для расчетов может использоваться уравнение (2.45) пропорциональное квадрату угловой скорости коленчатого вала двигателя, построенное на упрощенных линейных харакгеристиках для произведения полиномов Коб*Ме, которые получаются простыми осреднениями и понижениями степени полиномов.
Такое упрощение в расчетах обеспечивает удобство для анализа и существенное сокращение вычислений, тем не менее результаты будут реально отражать описанные аналитические процессы.
2.5.4.Уравнение движения с удельной
мощностью.
В данном случае уравнение движения для разгона приобретает следующий дифференциальный вид, путем деления левой и правой частей на Ga, м/с2 (2.47) или развернуто (2.48)
где Nуд — удельная мощность, кВт/т а все остальные параметры представлены в удельном виде.

Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.
