Бесплатный фрагмент - Реконструкция обстоятельств ДТП

Предисловие рецензента

Увеличение производства автомобилей мировыми лидерами автопрома и вступление в рынок новых мощных производителей привело к значительному росту загруженности шоссейных дорог и городских магистралей. В этой связи представляется естественным и увеличение числа дорожно-транспортных происшествий (ДТП). Существующее законодательство требует фиксации каждого из них и проведения при необходимости судебной экспертизы, на основании которой судебными и следственными органами делается вывод о степени виновности того или иного участника ДТП.

Экспертные оценки стали важным звеном в регуляции взаимоотношений не только между водителями транспортных средств, но и между ними и судебными органами, а сами эксперты являются ключевыми фигурами в судебном процессе. Основной задачей судебной экспертизы ДТП является полная и объективная реконструкция обстоятельств этого ДТП, основанное на доказательной базе. В свою очередь, доказательства должны строиться на современной научной основе, с применением апробированных математических моделей, измерительных и вычислительных средств. Логичным было бы появление соответствующих общепризнанных методик и методических пособий, в которых на современном уровне освещались бы вопросы технологии проведения автотехнической экспертизы.

Предлагаемая вниманию читателей монография В. Н. Никонова «Реконструкция обстоятельств ДТП. Введение в современные методы экспертных исследований. Использование краш-тестов» как раз отвечает всем существующим требованиям и законодательным нормам с точки зрения научности и достоверности. В то же время она вполне доступна экспертам-автотехникам, не обладающим специальными знаниями в области прочности элементов конструкций и вычислительной математики. Книга написана корректно с научной точки зрения, а её материал основан на анализе инсценированных в лабораторных условиях столкновений транспортных средств, когда все параметры каждого столкновения зафиксированы специальными приборами.

К достоинствам книги следует отнести способ изложения материала: во вводной части приведено описание движения автомобиля в сопутствующей системе координат, связанной с его центром тяжести, а также даны формулы преобразования координат для описания положения транспортного средства после столкновения. Указываются отличия отечественного стандарта для введения системы координат от его зарубежного аналога, принятого в западных странах.

В краткой и четкой форме даны базовые сведения по механике. В основу этого и следующего разделов положены фундаментальные законы сохранения механики в контексте поставленной задачи анализа столкновения транспортных средств. Все выкладки и формулы сопровождаются детально выполненными схематическими рисунками.

Наконец, самый важный теоретический четвертый раздел книги посвящен анализу результатов столкновения автомобилей с применением данных, полученных при производстве краш-тестов автомобилей. В мировой экспертной практике краш-тесты используются, в том числе, для получения недостающей, но необходимой экспертам-автотехникам информации о жесткости конструкций конкретных транспортных средств в контексте применения расчетных формул в практике экспертизы ДТП. В этом разделе также широко используется иллюстративный материал.

В заключительном разделе книги приведен обзор доступного специального программного обеспечения, необходимого для проведения реконструкции обстоятельств ДТП с использованием баз данных краш-тестов.

В целом книга, по существу, является базовым учебным пособием для эксперта-автотехника, устанавливающим приоритет фундаментальных законов механики и приобретённого автором опыта в практике экспертных заключений.

По этим причинам выход монографии В. Н. Никонова следует всячески приветствовать и поддерживать её распространение в экспертном сообществе.

Саид Федорович Урманчеев,

доктор физико-математических наук, профессор, главный научный сотрудник Института механики им. Р. Р. Мавлютова Уфимского научного центра Российской академии наук, заслуженный деятель науки Республики Башкортостан.

Предисловие адвоката Алексея Куприянова

Много лет занимаясь уголовными делами по дорожно-транспортным происшествиям, я вынужден констатировать снижение инженерного уровня отечественных судебных автотехнических экспертиз. Во-первых, среди экспертов стали встречаться «практики», не имеющие инженерного диплома. Во-вторых, к сожалению, как правило, экспертное исследование ДТП в суде ограничивается применением методик проф. Иларионова В. А., разработанных полвека назад путем эмпирического исследования движения конкретного легкого автомобиля «Москвич-408» с уже забытыми диагональными шинами. И вот сегодня те же методики, годные только для старинного «Москвича», без всяких оговорок повсеместно применяются для анализа столкновения двух джипов «Мерседес», начиненных современными электронными системами контроля движения и распределения сил на колесах, в то время как большинство автоэкспертов мира в таких случаях давно пользуется специальными программными комплексами, базирующимися на современных научных методах исследования столкновений не менее современных моделей автомобиля.

Однако для применения в суде той или иной программы, как например РC-Crash, совершенно недостаточно краткого письма компетентных ведомств, что такой-то программный продукт рекомендован к использованию в судебной автотехнической экспертизе.

Любой опытный адвокат заставит эксперта, решившегося их использовать, «попотеть» в суде, блеснуть своими инженерными знаниями. Замучает вопросами, откуда какая цифра в его выводах взялась и каким образом получилась. Рассуждения эксперта о том, что я вот тут в этой форме ввел в компьютер несколько цифр из уголовного дела, а потом мне с принтера несколько других итоговых цифр было распечатано, не должны приниматься судом.

В этом и причина нежелания экспертов применять новые прогрессивные методики! Эксперты в них не разбираются! Почему не разбираются? А потому, что до сего дня никто еще не написал книги, подобной той, которую вы держите в руках. Аналогичные по глубине, простоте изложения и научной обоснованности методические разработки на русском языке просто отсутствуют. Теперь, думаю, дело переобучения тысяч экспертов-автотехников сдвинется с мертвой точки!

Для полноценного уяснения этого учебного пособия и проведения на его основе судебных экспертиз нужна, понятно, инженерная подготовка, и экспертам-«практикам» с подготовкой на курсах «по безопасности движения» рано или поздно придется сменить специальность. Однако для использования изложенного в книге понятийного аппарата в юридической практике, например, следователями, прокурорами, адвокатами, заинтересованными участниками ДТП, да и самими судьями, вполне достаточно школьных познаний по физике и математике и желания разобраться.

Законное проведение полноценной автотехнической экспертизы, пользуясь непосредственно методами, описанными в этой книге В. Никонова, возможно и вне дорогостоящих программных комплексов, и это делает заключение эксперта проверяемым и прозрачным.

В этой книге просто и понятно показаны результаты научных исследований ученых из разных стран мира в области расчета затрат энергии на деформацию автомобилей при их столкновении — так называемый алгоритм CRASH3, сейчас широко применяемый для судебной экспертизы в большинстве стран мира. В книге приведены доступные для понимания инженеров и юристов примеры использования алгоритма CRASH3. Цель книги — показать читателю методически и на конкретных примерах ДТП, инсценированных в лабораторных условиях, как это делается.

Приведенные на страницах книги примеры — это реальные ДТП, произведенные в специально оборудованных лабораториях. В этих ДТП параметры движения и удара участвовавших в них транспортных средств измерялись десятками датчиков и фиксировались скоростной видеосъемкой. Поэтому хорошее совпадение расчетных, методом CRASH3, скоростей движения этих транспортных средств с данными многочисленных приборов только подтверждает достаточную для судебных экспертиз точность этого метода расчета и эффективность его применения для значительной части реальных ДТП на наших дорогах. При этом автор книги — крупнейший российский ученый в данной области, и ему можно доверять.

Алексей Анатольевич Куприянов,

почетный адвокат России, почетный юрист города Москвы, майор в отставке, инженер-испытатель военной техники.

Предисловие автора

Эта книга — первая из серии книг, которую я намерен написать о современных математических методах реконструкции обстоятельств дорожно-транспортных происшествий (ДТП), существующих в мировой практике судебной экспертизы. Чтобы читателю было легче разобраться в многообразии экспертных методов и приемов, вначале имеет смысл привести их классификацию с точки зрения источников экспертных знаний — наук или областей знаний, из которых эти знания получены.

Любое ДТП, как правило, состоит из движения транспортных средств до их столкновения, собственно, столкновения (удара) этих транспортных средств между собой и движения этих транспортных средств после столкновения в их конечное положение. То же самое можно сказать и про столкновения транспортных средств с подвижными или неподвижными препятствиями, не являющимися транспортными средствами, в том числе и про наезды на пешеходов или животных.

Движение транспортных средств описывается методами теоретической механики — науки, изучающей на основе строгих математических выводов общие законы механического движения и взаимодействия материальных тел. Уравнения теоретической механики или полученные на ее основе описывают и движение транспортных средств. На этих уравнениях, описывающих движение транспортных средств для различных дорожно-транспортных ситуаций, и базируется судебная автотехническая экспертиза в части исследования обстоятельств ДТП.

Важным дополнением и источником данных для судебной автотехнической экспертизы является такая криминалистическая область знаний, как судебная транспортно-трасологическая экспертиза, исследующая следы на месте ДТП и обстоятельства их возникновения. К категории диагностических задач транспортно-трасологической экспертизы относится расшифровка механизма ДТП: установление места столкновения (наезда), определение взаимного расположения транспортных средств в момент столкновения, направления удара при столкновении, перемещения транспортных средств после столкновения, взаимного положения транспортного средства и пешехода в момент наезда (переезда) и т. п. Для математических методов реконструкции обстоятельств ДТП результаты транспортно-трасологической экспертизы важны тем, что позволяют записать дополнительные уравнения к системе уравнений, описывающих удар или движение транспортных средств.

Анализ процесса столкновения (или удара) транспортных средств между собой или с препятствием имеет целью получить данные о величине затрат кинетической энергии на деформацию транспортных средств и препятствий, о величине, направлении и месте приложения сил взаимодействия при ударе, о величине и направлении импульса этих сил взаимодействия.

На сегодняшний день для анализа процесса удара транспортных средств в мировой экспертной практике в основном применяются два независимые друг от друга расчетных метода. Это алгоритм CRASH3 и его модификации, который основан на анализе лабораторных испытаний автомобилей на удар, называемом обычно краш-тестом, и конечно-элементный анализ. В России эти методы имеют легальный характер для их применения в судебной автотехнической экспертизе, так как оба входят, в частности, в состав компьютерной программы моделирования ДТП PC-Crash, рекомендованный научно-методическим советом РФЦСЭ при МЮ РФ решением от 20 марта 2012 г. При этом оба метода разрабатывались отдельно от программы PC-Crash и ей подобных и могут успешно применяться независимо от этих программ.

Современные автомобили испытываются на удары (подвергаются краш-тестам) в специальных сертифицированных и оборудованных лабораториях. Краш-тесты проводятся как на фронтальные удары с полным или частичным перекрытием в неподвижный жесткий или деформируемый барьер, жесткость которого известна, так и на боковые удары в неподвижный жесткий барьер или на удар в неподвижный автомобиль лабораторной тележкой, жесткость ударной части которой также известна. Ряд испытательных лабораторий проводят тесты на столкновения автомобилей между собой, испытания крыш автомобилей или их бамперов и иные испытания.

Из анализа данных краш-теста можно получить значение жесткости передней, боковой, задней или верхней части автомобиля конкретной модели или усредненно для группы моделей автомобилей, близких друг другу по габаритам и массе. В зависимости от условий испытания автомобиля конкретной модели и способа обработки лабораторных данных жесткость той или иной части конструкции автомобиля можно получить как усредненную по всей контактировавшей поверхности, так и дифференцированно для ее отдельных частей в зависимости от локализации.

Алгоритм CRASH3 содержит как правила измерения деформаций автомобиля после ДТП, так и правила расчета затрат механической энергии на образование этих деформаций и величин сил удара. Этот алгоритм достаточно прост в применении. Он при аккуратном и корректном его использовании, как правило, позволяет получать величину затрат механической энергии на деформацию и величину силы удара с небольшой погрешностью, не влияющей на конечные выводы эксперта, для большого спектра повреждений транспортных средств в ДТП.

Краш-тест является феноменологическим исследованием автомобиля как единого целого, когда автомобиль представлен только своей наружной оболочкой, а свойства его внутренней структуры переносятся на свойства его оболочки. Поэтому если условия ДТП существенно отличаются от условий проведения краш-теста, из которого получены данные о жесткости транспортного средства, то результат расчета затраченной на деформацию энергии и силы удара может иметь значительную погрешность.

Таким образом, с точки зрения источников экспертных знаний, классификация современных методов реконструкции обстоятельств ДТП упрощенно выглядит следующей:

· движение до удара — теоретическая механика;

· удар — алгоритм CRASH3 и анализ краш-тестов или конечно-элементный анализ;

· движение после удара — теоретическая механика.

Эта книга посвящена алгоритму CRASH3 как современному и наиболее простому методу реконструкции обстоятельств ДТП. В ней содержатся основные знания, необходимые специалисту для освоения этого метода, и конкретные примеры исследования реальных столкновений автомобилей в лабораторных условиях. Все краш-тесты и примеры ДТП взяты из базы данных NHTSA — Национального управления безопасностью движения на трассах министерства транспорта США.

Приведенные в этой книге примеры исследования лабораторных ДТП показывают, что расчетные скорости транспортных средств, полученные с использованием алгоритма CRASH3, и их фактические скорости, полученные из данных лабораторных акселерометров и скоростной видеосъемки, хорошо совпадают друг с другом.

Поэтому эта книга будет полезна как для судебных экспертов и специалистов в виде учебного и методического пособия, так и для участников ДТП и их адвокатов для знания возможностей современных методов реконструкции обстоятельств ДТП.

Многочисленная судебная практика применения современных методов реконструкции обстоятельств ДТП, в том числе алгоритма CRASH3, мною и другими экспертами систематически публикуется на сайте профессионального сообщества адвокатов и юристов «Праворуб», который я рекомендую и участникам ДТП.

Следующую книгу я планирую посвятить конечно-элементному анализу — второму методу, позволяющему установить затраты механической энергии на деформацию транспортных средств и величины действовавших сил, также широко применяемому при реконструкции обстоятельств ДТП в мировой практике. Этот метод заключается в построении математических моделей наружных и внутренних элементов конструкции, составляющих автомобиль, с их последующей интеграцией в единую модель. И если в первом способе построения математической модели источником фактических данных служат результаты испытаний автомобиля на удар как целого — краш-тесты, то во втором — механические свойства материалов, из которых изготовлены элементы конструкции автомобиля.

Конечно-элементный анализ, по сравнению с алгоритмом CRASH3, является универсальным методом расчета параметров удара, хотя его теория более сложна для освоения. Тем не менее, сейчас уже есть множество бесплатных программ расчета методом конечных элементов, которыми можно воспользоваться для реконструкции обстоятельств ДТП, а как это сделать, я покажу в следующей книге.

В. Н. Никонов

1. Системы координат

Для описания ориентации автомобиля требуется ввести, по меньшей мере, две системы координат. Одна из систем координат — локальная. Она связана с автомобилем и нужна для того, чтобы определить как его ориентацию в пространстве или на плоскости относительно глобальной системы координат, так и для того, чтобы определить, например, движение частей автомобиля и действующие на него силы относительно его центра тяжести. Вторая система координат — глобальная. Эта система координат неподвижна относительно дороги. В совокупности обе системы координат полностью определяют положение автомобиля в пространстве в любой момент времени.

Правая прямоугольная система координат

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Эта наиболее простая и поэтому часто используемая система координат. Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат.

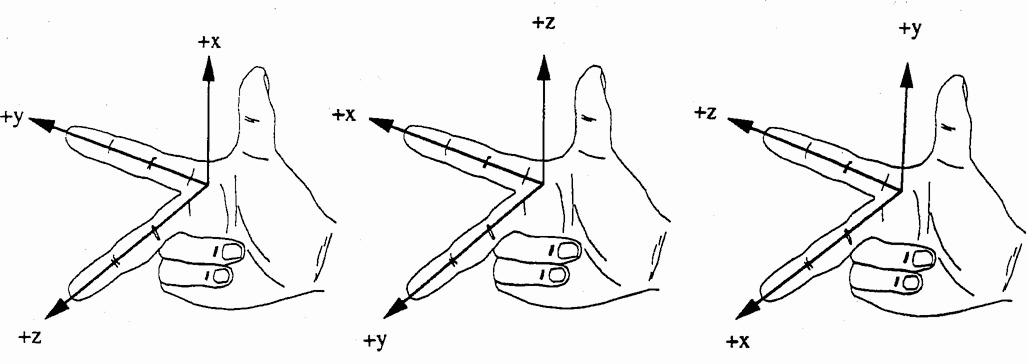
В технике, как правило, используется правая система координат. Правая система координат определяется по правилу правой руки, как показано на рис. 1.1.

В трехмерном пространстве углы между всеми осями прямоугольной системы координат всегда равны 900. Оси системы координат, как правило, обозначаются следующими друг за другом в алфавите латинскими буквами x, y и z. Правило правой руки заключается в том, что если большой палец обозначен как ось x, то ближайший к нему указательный палец — это ось y, а следующий средний палец — ось z. Если большой палец обозначен другой буквой, то далее следует круговая перестановка в алфавитном порядке x — y — z — x — y — …, как показано на рис. 1.1. При этом направления пальцев всегда соответствуют положительному направлению координатных осей.

Ось координат x еще называется осью абсцисс, ось y — осью ординат, а ось z — осью аппликат.

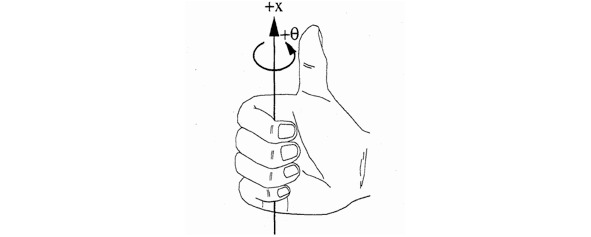
Предположим, что мы начинаем поворачивать ось x вокруг точки начала координат. Так вот — правая система координат имеет такое свойство, что, если смотреть на плоскость xy из какой-либо точки положительной полуоси z, то при повороте оси x на 900 против часовой стрелки ее положительное направление совпадет с положительным направлением оси y.

Это правило так же хорошо иллюстрируется с помощью правой руки. Если приложить ладонь к некоторой оси так, чтобы большой палец был направлен вдоль положительного направления оси, и согнуть остальные четыре пальца, то направление их движения покажет положительное направление вращения вокруг этой оси координат, как показано на рис. 1.2.

В дальнейшем использование только правых систем координат позволяет формализовать уравнения, содержащие координаты или их производные, и избежать путаницы со знаками.

Система координат автомобиля

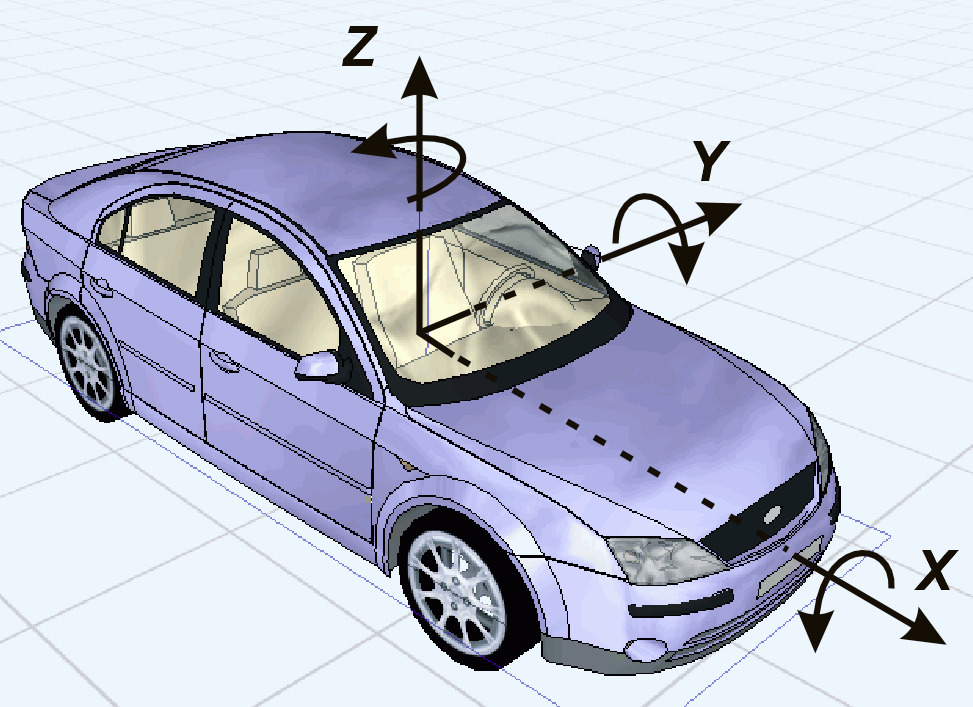
В соответствии со стандартом ISO 8855:2011 «Транспорт дорожный. Динамика транспортных средств и курсовая устойчивость. Словарь», ось X — это продольная ось автомобиля, которая всегда направлена вперед. Ось Y — это поперечная ось автомобиля, которая всегда направлена влево от автомобиля.

Тогда, так как система координат правая, то вертикальная ось Z автомобиля направлена вверх. Начало системы координат располагается в центре тяжести автомобиля, чтобы упростить запись уравнений, описывающих его движение. Система координат автомобиля и положительные направления вращения вокруг осей показаны на рис. 1.3.

Преобразование координат в плоскости

Для определения координат автомобиля в плоскости достаточно трех параметров: координат центра тяжести автомобиля и угла его ориентации, которым может быть, например, угол между продольной осью автомобиля и осью X неподвижной системы координат.

Рассмотрим рис. 1.4, на котором показан автомобиль в некоторой неподвижной системе координат XY, связанной, например, с дорогой. В этой системе координат ось X в плоскости чертежа направлена вправо, ось Y — вверх, а ось Z — перпендикулярна плоскости чертежа и направлена к зрителю. Пусть в этой системе координат положение центра тяжести автомобиля определятся точкой O`, которая, в свою очередь, является точкой начала координат X`Y`, связанной с автомобилем. При этом a — угол между осями OX и O`X`.

Как видно из рис. 1.4, в трехмерном пространстве оси координат Z и Z` обоих систем координат, глобальной и локальной соответственно, параллельны друг другу. Отклонение оси Z` от указанного положения в результате удара в автомобиль в большинстве случаев невелико, и этим можно пренебречь.

Поэтому далее для анализа движения автомобиля в плоскости или положения и направления силы удара нам понадобится только двухмерная система координат. Тогда, кроме параметров XC? YC и a в глобальной системе координат XY, требуется уметь находить координаты любой произвольной точки автомобиля, известные в локальной системе координат X`Y`.

Пусть некоторая точка M задана координатами (p`,q`) в локальной системе координат X`Y`, связанной с автомобилем. Требуется найти ее координаты (p,q) в глобальной системе координат XY.

Координата p точки M по оси абсцисс есть сумма координаты XC центра тяжести автомобиля (начала локальной системы координат) и разности длин проекции отрезка O`p` на ось абсцисс X и отрезка Cp`.

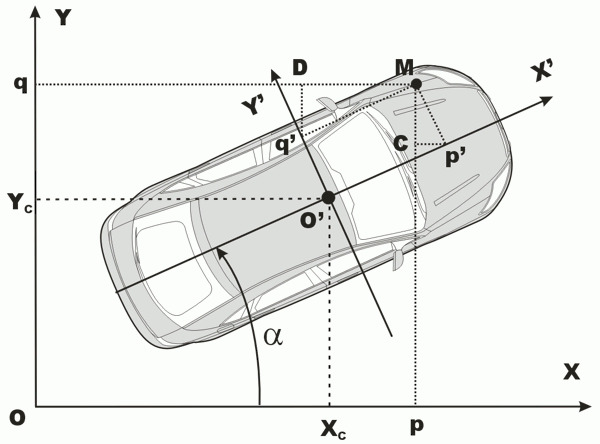
Длина проекции отрезка O`p` на ось абсцисс X есть p`cos (a). Длина отрезка Cp` есть q`sin (a).

Тогда координата точки по оси абсцисс есть

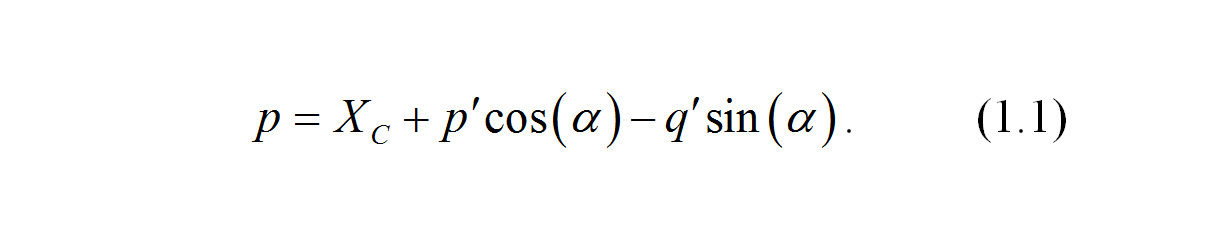
Тогда координата q точки M по оси ординат есть сумма длины проекции отрезка O`q` на ось ординат и длины отрезка q`D, или

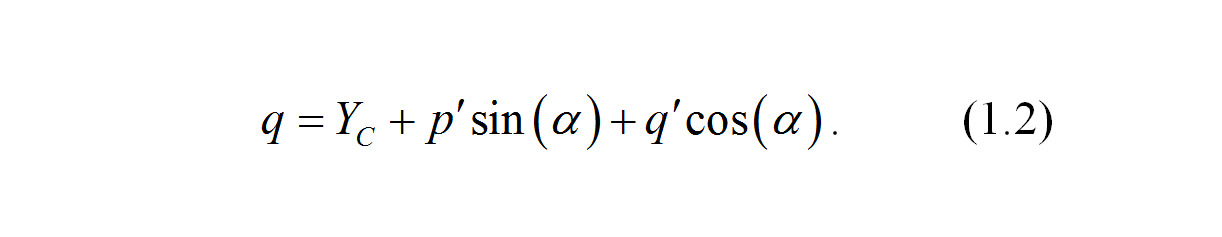
Полученные уравнения важны как для решения задачи движения автомобиля в плоскости, так как позволяют в каждый момент времени определить положение контура автомобиля и его колес в неподвижной системе координат, так и для расчета положения точки приложения силы удара и ее направления.

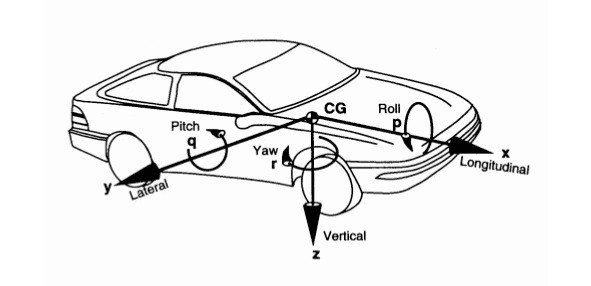
В иностранной литературе по реконструкции обстоятельств ДТП для системы координат автомобиля часто используется стандарт Сообщества автомобильных инженеров (англ. Society of Automotive Engineers, SAE) SAE J670, согласно которому поперечная ось автомобиля Y направлена вправо от автомобиля, а вертикальная ось автомобиля Z направлена вверх, как показано на рис. 1.5.

В этой книге использование системы координат автомобиля SAE оговаривается особо.

Литература

1. Стандарт ISO 8855:2011 «Транспорт дорожный. Динамика транспортных средств и курсовая устойчивость. Словарь».

2. Vehicle Dynamics Terminology, SAE J670 JAN2008.

3. Выгодский М. Я. Справочник по высшей математике. — М.: АСТ: Астрель, 2006. 991с.: ил.

2. Базовые законы механики

Методы реконструкции обстоятельств ДТП базируются в основном на трех законах Ньютона и четырех законах сохранения механики.

Законы Ньютона позволяют записать уравнения движения для любой механической системы, в том числе если известны силовые взаимодействия для составляющих её тел.

Первый закон Ньютона постулирует, что тело находится в покое или движется прямолинейно и равномерно, когда на него не действуют никакие силы (или действуют силы взаимно уравновешенные). Второй закон Ньютона связывает силу, действующую на тело, с его массой и ускорением. Третий закон Ньютона постулирует равенство действия противодействию.

Законы сохранения — фундаментальные физические законы, согласно которым при определённых условиях некоторые измеримые физические величины, характеризующие совокупность тел, не изменяются с течением времени.

Для реконструкции обстоятельств ДТП важны такие законы сохранения механики, как закон сохранения энергии, закон сохранения количества движения (импульса), закон сохранения момента количества движения (момента импульса), и в ряде случаев закон сохранения массы.

Второй закон Ньютона, или основной закон динамики

Второй закон Ньютона — дифференциальный закон механического движения, который описывает зависимость ускорения (если ускорение отрицательно, то его называют замедлением) тела от равнодействующей всех приложенных к телу сил F и массы тела m в виде

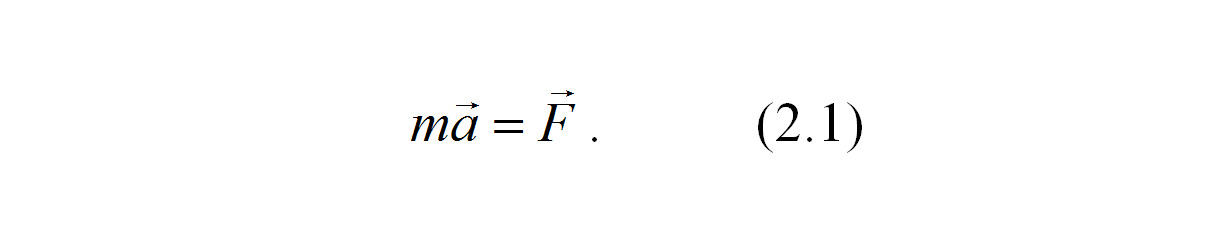
Или ускорение, приобретаемое телом, прямо пропорционально вызывающей его силе F и совпадает с ней по направлению и обратно пропорционально массе m тела. Уравнения, соответствующие данному закону, называются дифференциальными уравнениями движения.

Так, например, если суммарная сила тяги на ведущих колесах переднеприводного автомобиля при его прямолинейном движении, как показано на рис. 2.1, постоянна и равна F, то этот автомобиль в данный момент времени t ускоряется в направлении действия этой силы с ускорением а:

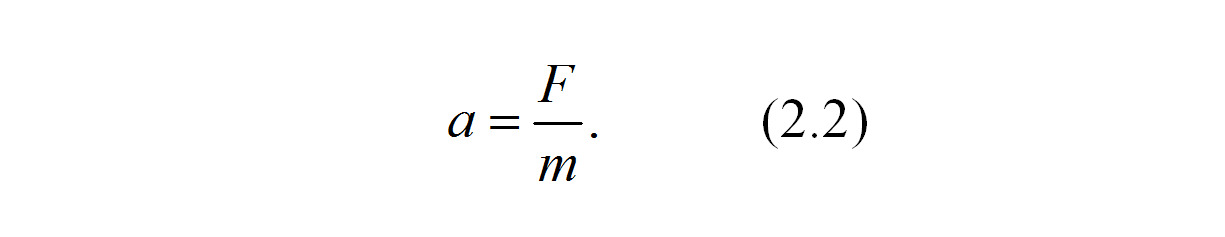
Тогда при неизменном ускорении скорость автомобиля в некоторый момент времени t равна интегралу от выражения для ускорения плюс постоянная интегрирования — начальная скорость автомобиля в момент времени t=0:

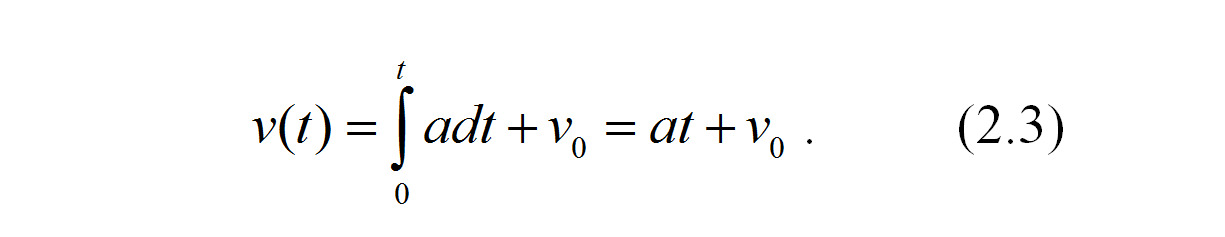
Путь, пройденный автомобилем за время t, равен интегралу от его скорости плюс постоянная интегрирования — начальный путь автомобиля в момент времени t=0:

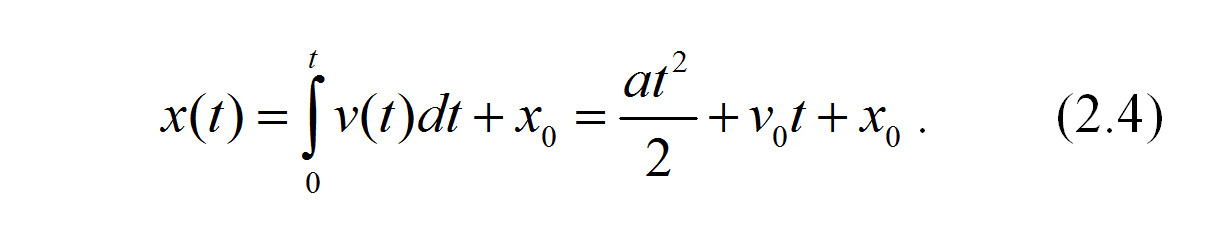
Выражения (2.2) и (2.3) можно записать как производные по времени, где первая производная по времени обозначается символом с точкой наверху, а вторая производная по времени — с двумя точками наверху: скорость есть первая производная от функции пути от времени, ускорение есть первая производная от функции скорости от времени и, соответственно, вторая производная от функции пути от времени:

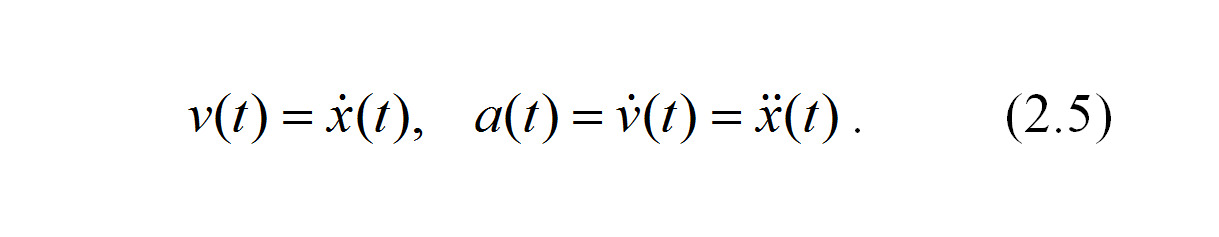
В общем случае сила, ускорение и скорость — векторные величины. Тогда уравнения (2.2) — (2.5) записываются либо в векторном виде, либо в виде проекций на оси неподвижной системы координат.

Чтобы получить связь скорости и пути ускорения (замедления) автомобиля, выражение для ускорения a из (2.5) можно записать в виде

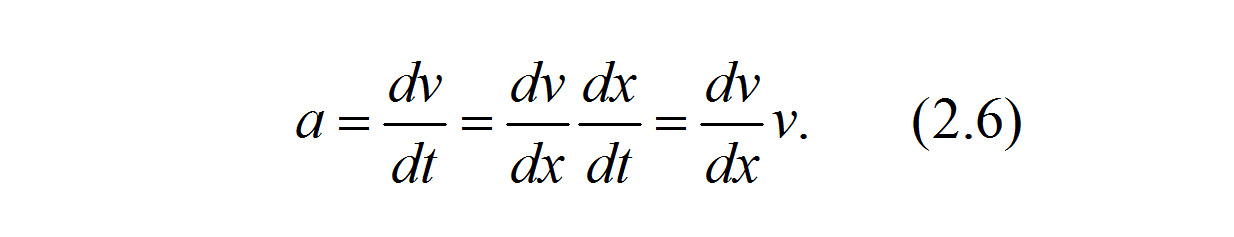
После упрощения выражение (2.6) принимает вид

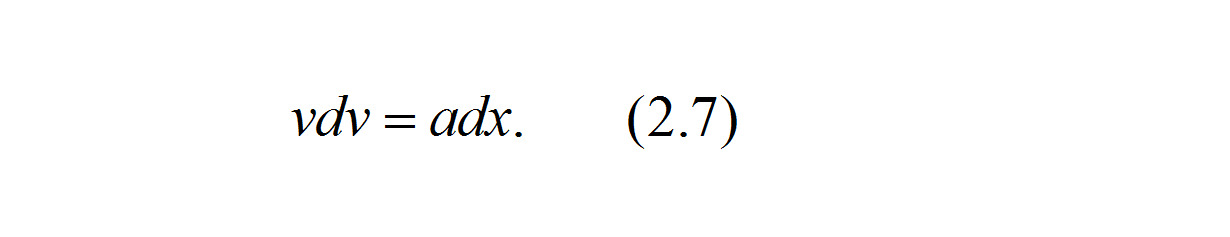
Тогда левую и правую части выражения (2.7) можно проинтегрировать, записав постоянную интегрирования в виде половины квадрата начальной скорости автомобиля:

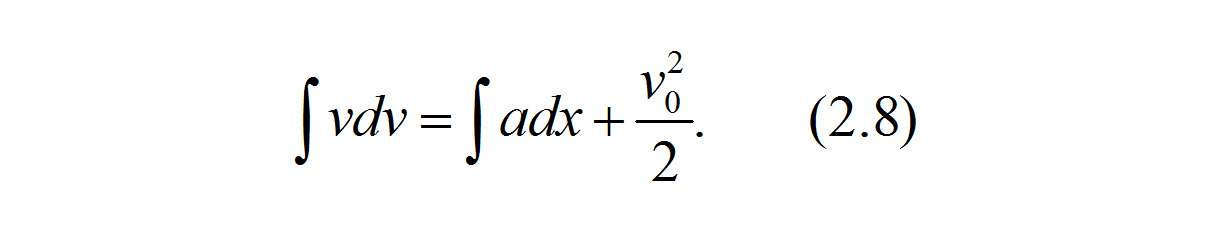
После интегрирования получаем

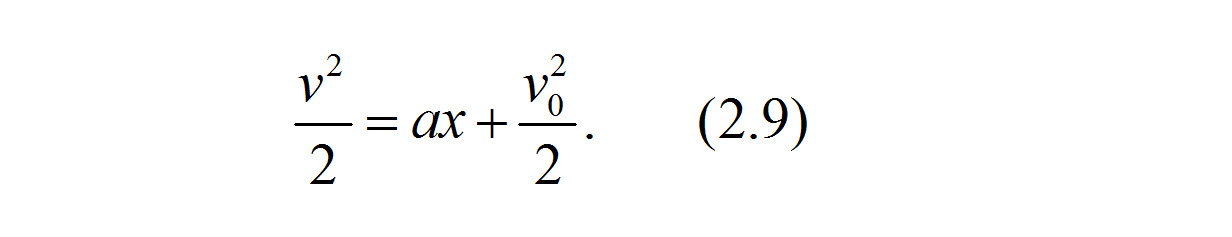
Откуда после преобразования выражение для квадрата скорости принимает вид

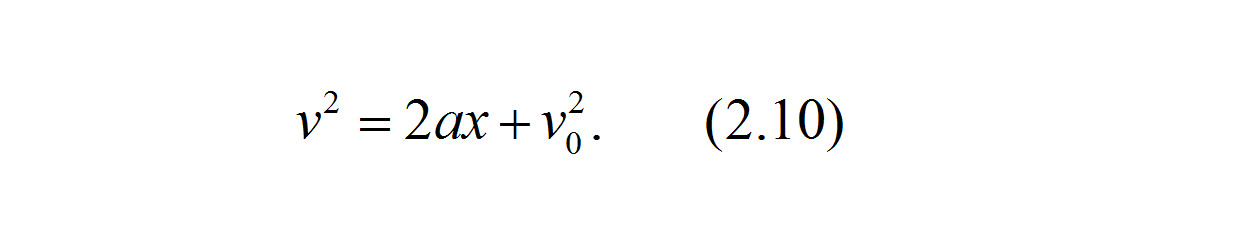
Или, извлекая квадратный корень из левой и правой части равенства (2.10), получаем выражение для скорости автомобиля v в м/с в зависимости от пути x, на котором автомобиль ускорялся или замедлялся:

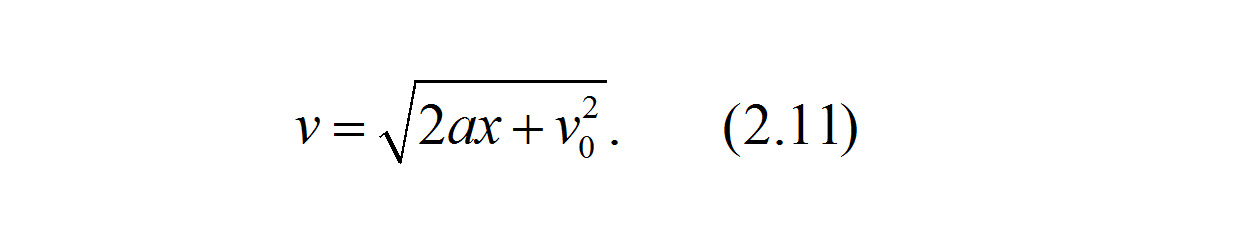
Выражение (2.11) может быть преобразовано для более привычной единицы измерения скорости транспортных средств в км/ч с учетом, что 1 м/с = 3.6 км/ч:

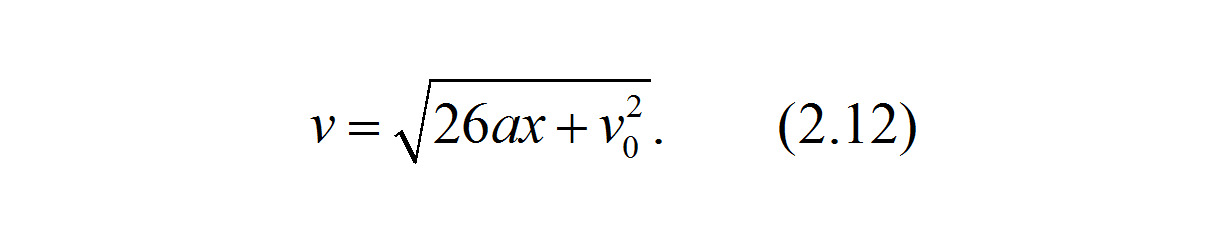
В выражении (2.12) использовано, что 2х3.62=25.92, или с округлением до целого равно 26.

Третий закон Ньютона

Автомобили, как и все тела, в любой момент времени при их столкновении взаимодействуют друг с другом в некоторой точке силами, направленными вдоль одной прямой, равными по модулю и противоположными по направлению, как показано, например, на рис. 2.2.

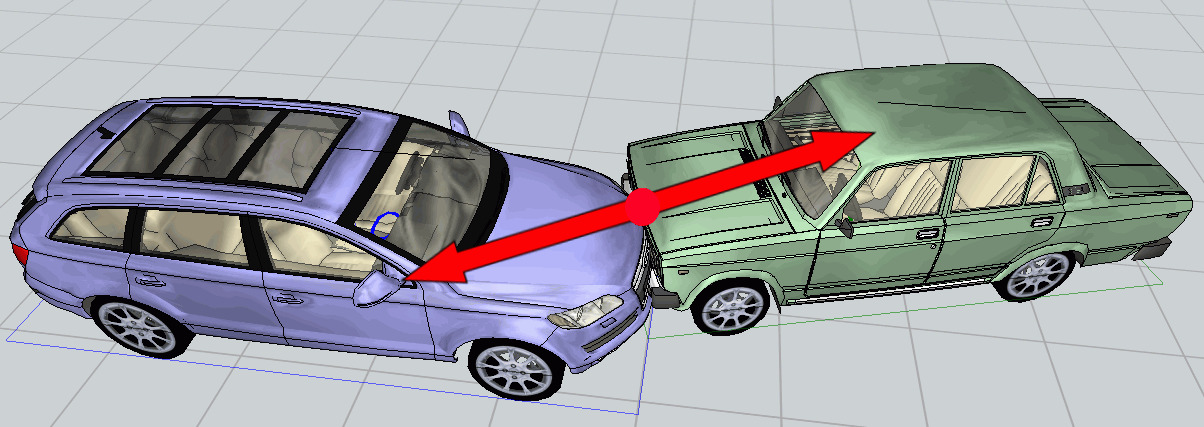
Кажется, что все просто. Однако при рассмотрении реальных ДТП остаются вопросы определения точки приложения силы и направления линии силы взаимодействия во времени и пространстве.

Закон сохранения энергии

В традиционной судебной автотехнической экспертизе закон сохранения энергии применяется лишь частично. Для движения в плоскости эти методики учитывают лишь ту часть кинетической энергии автомобиля, которая затрачивается на его остановку путем торможения или заноса, или, иначе говоря, учитывают работу сил трения автомобиля с опорной поверхностью.

При столкновении автомобиля с другим транспортным средством или препятствием его кинетическая энергия EK расходуется на работу сил трения ET и на деформацию конструкций столкнувшихся объектов ED. Если в результате удара скорость автомобиля не погашена, то он имеет остаточную кинетическую энергию EO. Тогда уравнение баланса энергии можно записать в виде

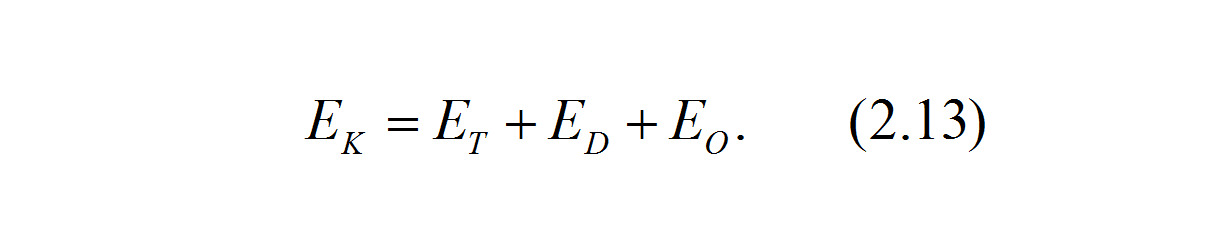
Уравнение (2.13) может быть записано развернуто: с учетом массы автомобиля m, его скорости перед началом торможения или заноса v, коэффициента сцепления шин с опорной поверхностью f, пути во время торможения или заноса S и остаточной скорости vH в виде

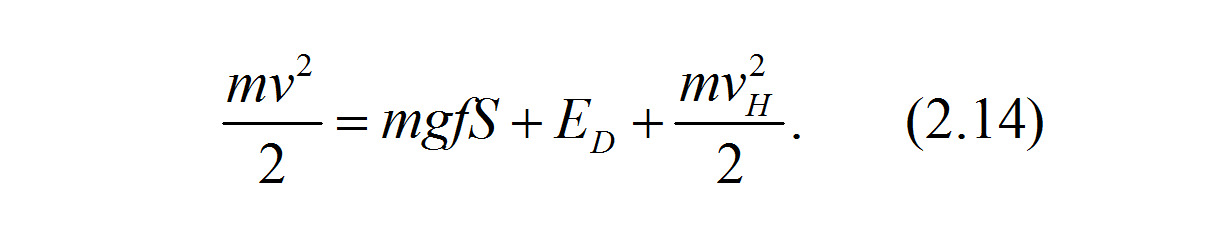
Положим, как это и делает традиционная методика автотехнической экспертизы, равной нулю неизвестную величину затрат энергии на деформацию ED=0, и обозначим как замедление j произведение коэффициента сцепления шин с опорной поверхностью f и ускорения силы тяжести g=9.8 м/с2:

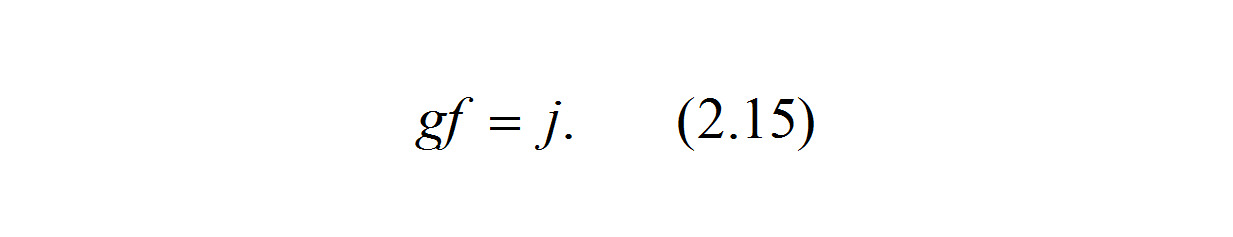
Тогда из выражения (2.14), с учетом (2.15) после преобразования получаем

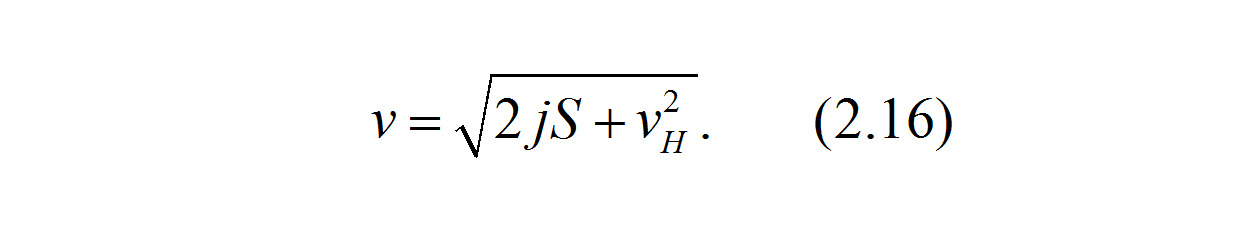
Как видно из выражения (2.16), оно полностью совпадает с выражением (2.11), полученным ранее другим способом.

Далее в этой книге рассматриваются современные методы установления величины затрат энергии на деформацию транспортных средств и препятствий и использование этой величины в автотехнических расчетах.

Закон сохранения количества движения (импульса)

Закон сохранения количества движения (импульса) постулирует, что векторная сумма количества движения всех тел системы есть величина постоянная с точностью до импульса внешних сил.

Для определенности будем называть количеством движения тела произведение его массы на вектор скорости его центра тяжести, или mv. Будем называть импульсом произведение вектора некоторой силы на время ее действия, или Ft. Если сила изменяется за время t, то ее импульс можно найти путем интегрирования вектора силы по времени.

Обозначим массы двух любых деформируемых или твердых тел как m1 и m2, их скорости до столкновения как v1 и v2 и после столкновения как u1 и u2 соответственно. Тогда для них закон сохранения количества движения можно записать в виде

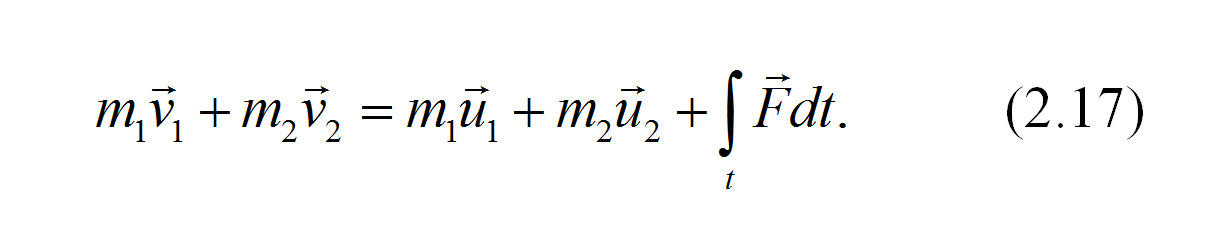
То есть сумма векторов количества движения двух (а в общем случае — любого количества) тел до их удара равен сумме векторов их количества движения после удара и импульса внешних сил F, независимо от того, деформировались ли эти тела при ударе или нет.

При столкновениях автомобилей импульс внешних сил — это, как правило, импульс сил трения колес и иных частей автомобилей об опорную поверхность во время удара. Этот импульс мал по сравнению с количествами движения автомобилей, и им обычно пренебрегают.

В классической механике закон сохранения количества движения (импульса) обычно выводится как следствие второго и третьего законов Ньютона.

Запишем выражение (2.1) для второго закона Ньютона в виде

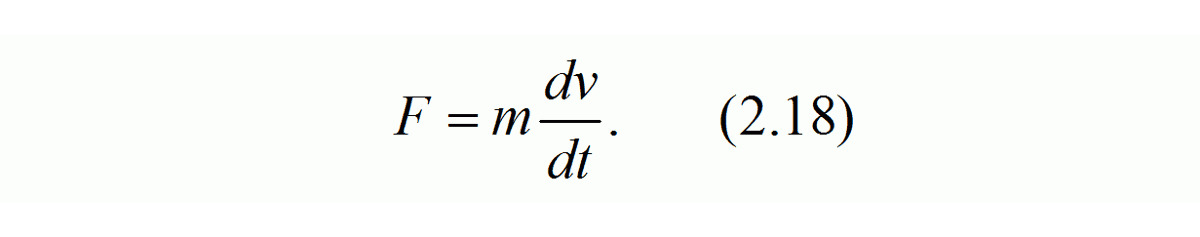
После переноса дифференциала времени dt в левую часть уравнения, получаем

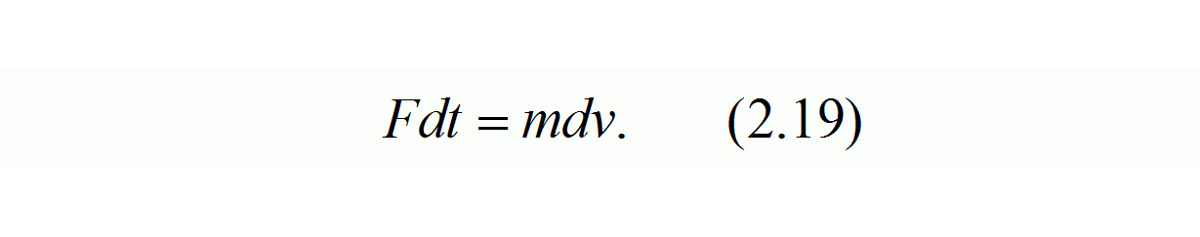
Тогда обе части уравнения (2.19) можно проинтегрировать: левую — для интервала времени от t1 до t2, а правую — для соответствующего этому интервалу времени интервала скорости от v1 до v2

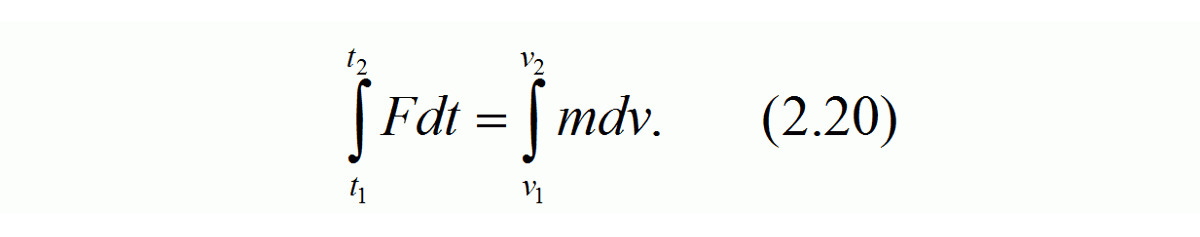
Полагая, что интервал времени от t1 до t2 мал и величина силы F не меняется за это время, получаем следующее выражение для закона сохранения количества движения:

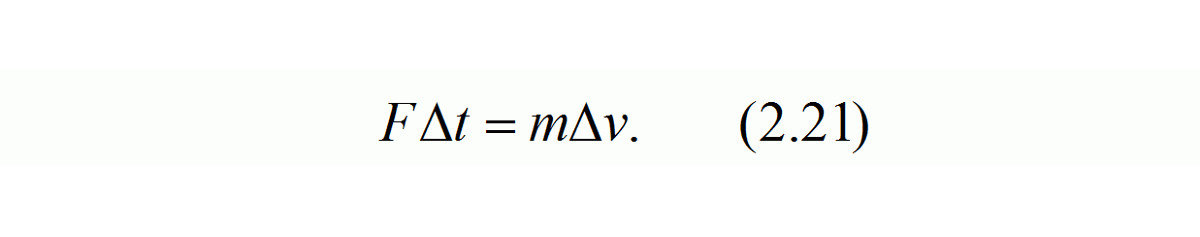
Выражение (2.21) обозначает, что импульс некоторой силы F равен изменению количества движения тела или системы тел массой m.

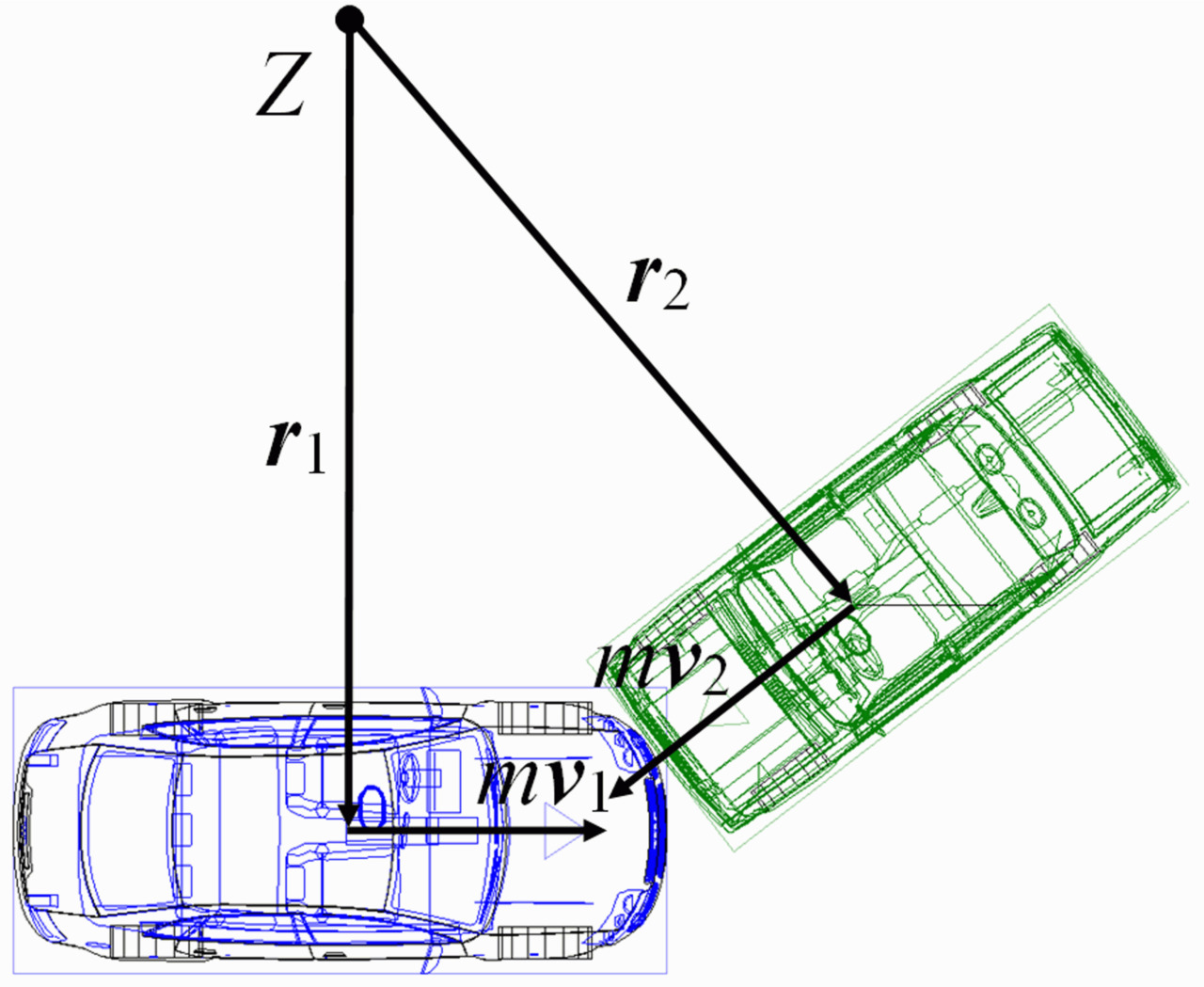
Рассмотрим момент столкновения двух автомобилей, имеющих количество движения mv, как показано на рис.2.3. Координаты центра тяжести каждого автомобиля в неподвижной системе координат относительно некоторой вертикальной оси Z определяются его радиус-вектором r. Для упрощения на рис.2.3 ось Z выбрана в точке пересечения перпендикуляров к векторам количества движения автомобилей.

Тогда для каждого из автомобилей момент количества движения (импульса) определяется векторным произведением радиус-вектора r на вектор количества движения mv

Если количество тел системы несколько (два автомобиля, автомобиль и груз в нем, …), то силы взаимодействия между отдельными объектами системы, в силу третьего закона Ньютона, равны по величине и противоположны по направлению. Поэтому их сумма обратиться в ноль и внутреннее взаимодействие объектов в системе не может изменить количество движения.

По этой самой причине, например, барон Мюнхгаузен не мог вытащить из болота себя и своего коня, так как сила, с которой он дергал себя за косичку, была внутренней для системы барон — его рука — конь, и с какой силой его рука тянула за косичку, с такой же силой и его косичка тянула его же руку в обратную сторону. Поэтому суммарный импульс этой силы был равен нулю, и количество движения системы не могло измениться.

Если же сила F — внешняя для системы объектов, то импульс этой силы изменяет количество движения системы, то есть увеличивает, уменьшает или изменяет направление вектора скорости. Например, парусник разгоняется от силы ветра, автомобиль разгоняется от силы тяги или тормозит и поворачивает от силы трения на его колесах.

Отметим, что выражения (2.21) и (2.17) суть одно и то же, это только разное представление одного и того же закона сохранения количества движения (импульса).

Закон сохранения момента количества движения (момента импульса)

Закон сохранения момента импульса (закон сохранения углового момента) математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел, которая остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем.

Рассмотрим момент столкновения двух автомобилей, имеющих количество движения mv, как показано на рис. 2.3. Координаты центра тяжести каждого автомобиля в неподвижной системе координат относительно некоторой вертикальной оси Z определяются его радиус-вектором r. Для упрощения на рис. 2.3 ось Z выбрана в точке пересечения перпендикуляров к векторам количества движения автомобилей.

Тогда для каждого из автомобилей момент количества движения (импульса) определяется векторным произведением радиус-вектора r на вектор количества движения mv:

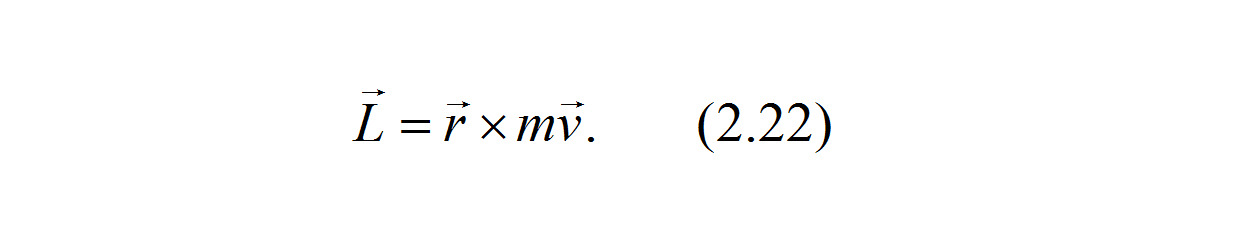
Так как для рассматриваемого случая углы между радиус-векторами и векторами количества движения прямые, то выражение (2.22) далее можно рассматривать как скалярное произведения длины радиус-вектора на величину количества движения, а знак произведения определять по правилу буравчика.

Формула для связи линейной и угловой скоростей через радиус вращения имеет вид

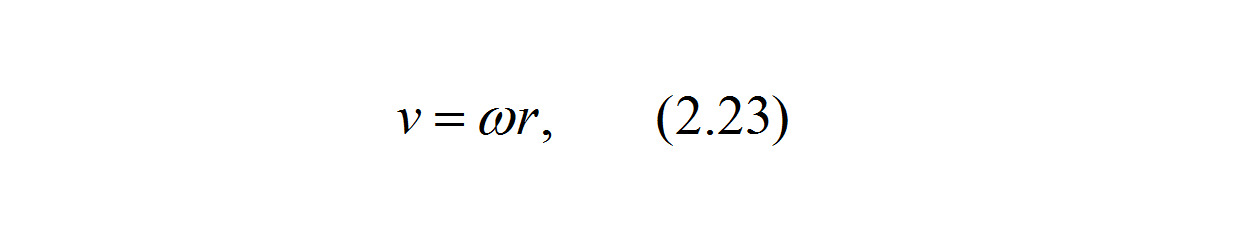
Обозначим момент инерции тела (в данном случае — автомобиля) относительно оси вращения как J. Тогда с учетом выражения (2.23) из (2.22) получаем, что

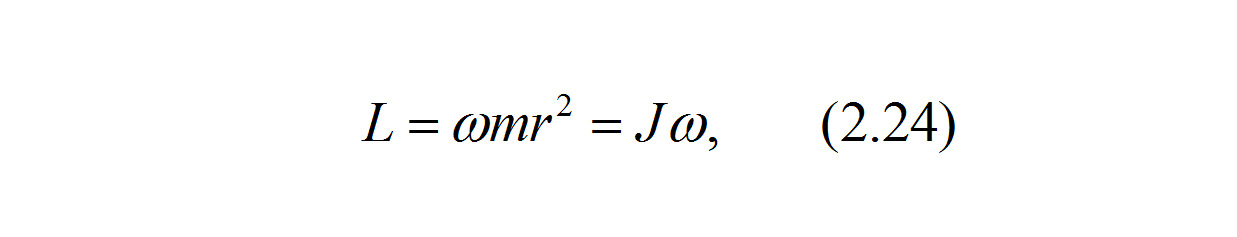
Таким образом, момент импульса автомобиля относительно некоторой оси равен произведению его момента инерции относительно той же оси на его угловую скорость. Так как суммарный вектор количества движения не изменяется в результате столкновения двух автомобилей, то и суммарный момент количества движения (импульса) при столкновении автомобилей остается неизменным.

Литература

1. Яблонский А. А., Никифорова В. М. Курс теоретической механики. Часть I. Статика. Кинематика. М.: Высшая школа. 1966.

2. Яблонский А. А. Курс теоретической механики. Часть II. Динамика. М.: Высшая школа. 1966.

3. Franck H., Franck D. Mathematical Methods for Accident Reconstruction. A Forensic Engineering Perspective. New York: CRC Press. 2010.

3. Удар двух автомобилей

В результате удара между собой два автомобиля получают те или иные деформации своих конструкций, на производство которых затрачивается механическая энергия. Установление величины затраченной на деформацию энергии, в свою очередь, позволяет установить величины изменения скоростей столкнувшихся автомобилей.

В этой главе рассматривается вывод соотношений между массами двух автомобилей, величиной энергии, затраченной на деформацию их конструкций при ударе, и величинами изменения скоростей центров тяжести этих автомобилей.

Центральный удар

Центральным столкновением (или ударом) двух автомобилей называется такое их столкновение с полным или частичным перекрытием, при котором линия силы взаимодействия этих автомобилей проходит через центры масс обоих автомобилей. Центральным с достаточной точностью можно считать и такой удар, при котором момента сил взаимодействия автомобилей не достаточно для их разворота в результате удара.

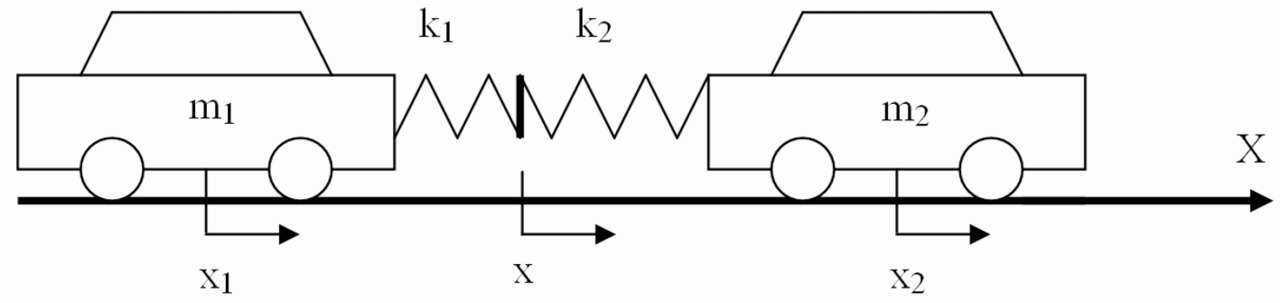
Схематичное представление центрального удара показано на рис. 3.1. Конструкции сталкивающихся автомобилей с массами m1 и m2 имеют периферийные элементы с линейной жесткостью k1 и k2. Текущие перемещения центров масс автомобилей обозначены как x1 и x2, а перемещение соприкасающихся поверхностей конструкций обозначено как x.

Применяя к автомобилям, показанным на рис. 3.1, основной закон динамики (2.1), получаем выражения для действующих на них сил:

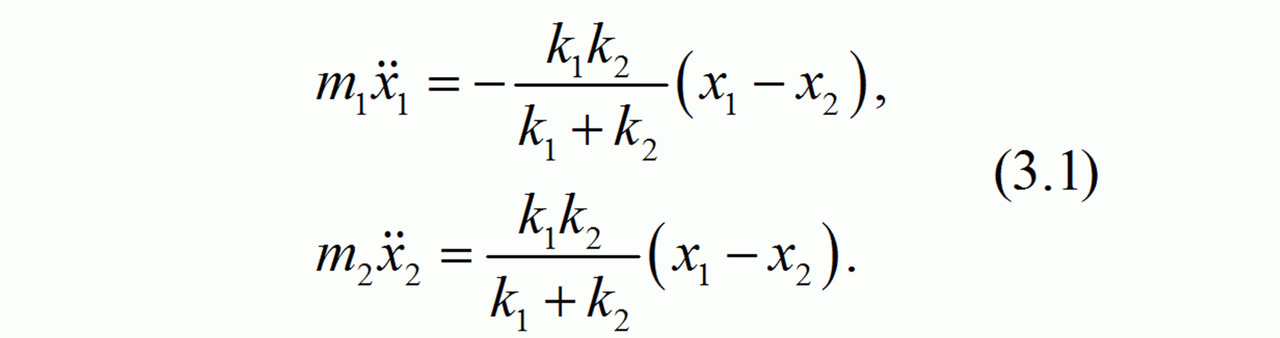
Для упрощения решения уравнений (3.1) обозначим относительное перемещение автомобилей как

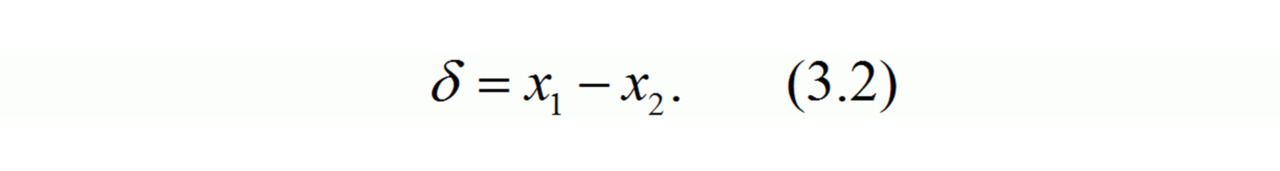
Тогда выражение для относительной скорости автомобилей в момент столкновения запишем в виде

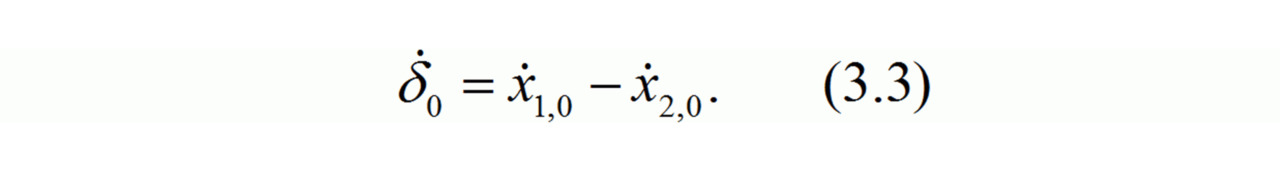
С учетом введенных обозначений (3.2) и (3.3) из уравнений (3.1) легко получить дифференциальное уравнение, описывающее относительное перемещение центров тяжести автомобилей: