
Бесплатный фрагмент - Mathematics of the market
Service random flow
Acronyms
A (Prelative). — relative consumption. The proposed load;
Aloss (t1, t2) — the difference between the incoming supply of goods and serviced supplies of goods;
Ainc. (t1, t2) — incoming supply of goods over a period of time (t1, t2);
Aserved. (t1, t2) — the sum of the quantities of goods handled by consumer group during the period (t1, t2).;
A TGD. — the demand value for time of greatest demand;
Aobs. — the demand value during the observation;
a — the load intensity coming from a single source;
c‘receiv s the number of received requests;
c‘serv — the number of serviced requests;
c‘lost. — the number of lost requests;
c‘— average length of queue or average numbers delays batches of goods;
Pmax- maximum consumption;
P goods. – losses of volume of goods;
P request. — losses in the number of requests for suggestion of goods;
P goods. — losses of volume of goods;
P t- losses of implementation time;
p (γ> 0) the probability that the waiting time is greater than zero — that is, the probability of queue;
p (γ> t) — the probability of waiting for any incoming product over time t;
p (R> r) — the probability that the queue length exceeds the specified value r);
(γ) — the average waiting time in relation all requests received;
γ delay the average waiting time of only a delayed requests;
Λ (t1, t2) -the mathematical expectation of the number of supplies placed on the market in the time interval [t1, t2);
μ (t1.t2). – the instantaneous flow rate;
Chapter 1. What are the REELECTION CONSUMPTION. unit of measure of supply and demand
1.1. So what is the goods?
Let’s start with a quote of Keynes [The General Theory of Employment, Interest, and Money by John Maynard Keynes. Book II: Definitions and Ideas]
“The perplexities which most impeded my progress in writing this book, so that I could not express myself conveniently until I had found some solution for them, are:
firstly, the choice of the units of quantity appropriate to the problems of the economic system as a whole;..
“That the units, in terms of which economists commonly work, are unsatisfactory can be illustrated by the concepts of the national dividend, the stock of real capital and the general price-level:”
“The community’s output of goods and services is a non-homogeneous complex which cannot be measured, strictly speaking, except in certain special cases, as for example when all the items of one output are included in the same proportions in another output.”
In order to take the definition of the unit of goods we use the obvious statement.
We define the goods the market, as something that you want to sell or that you want to buy. Let’s try to express this in numbers
Do you love cakes? I will sell them to you. You will buy and will want again. Finally, you can eat 10 cakes a day. And I offer you still. You say, “Enough!” I suggest to you free of charge 12 cakes a day, and you ungrateful say me “No!”. Moreover, buying cakes, you have some time to consume them, and not buy a new one
What is it? It is the overproduction!
I repeat the question: How much can you eat on the day cakes – 10, 12, 15? It doesn’t matter for math, but in principle there is some maximum quantity which you can consume in a certain period (a day, a month, a year).
Let’s try to find the indicator and we will call its – the relative consumption-
Prelative. If the consumer is not in need of this product (saturation) Prelative.=1,
If the consumer is just starting to purchases a goods
Prelative. =0.
Therefore, the current state of the user can be reflected with help the value of the relative consumption
0 ≤ Prelative.≤1
We will continue the search for the mathematical determination of relative consumption.
More details of this figure can be determined from the following reasoning.
Let’s introduce a unit of measure (denoted it a) “specific relative consumption”. It will the ratio of real consumption ( Prelative) to the maximum possible (Pmax.)
Prelative = Preal/ Pmax=a
Then the maximum consumption in a given period will be equal to Pmax. We assume that no material (money, prices) and external factors (season, fashion) don’t limit you.
Next, let’s see how much you are consuming a really – Preal.. By definition you can’t consume more than Pmax. (Preal. < Pmax.).
If you considered a group of n consumers, applied the name – RELATIVE CONSUMPTION.
It will be
A=an
1.2. Relative consumption
The relative consumption shows the possibility of participation of the consumer in the consumption (similar to a unit load in queuing theory). It indicates how many the goods the consumer is willing to buy. If a=1, the consumer in a given period will not buy a product, the other side it shows how satisfied requests of this user.
For example, from a website on the Internet, you can learn that the Scandinavians consume 8 liters of milk per week, and the Europeans 1 liter per week. One people physically can maximum consume 10 liters per week. Not analyzing for accuracy this information, we take these numbers as truth.
Then the relative consumption is equal for Scandinavians – 8/10, and for Europeans 1/10.
For sale of milk these numbers speak volumes.
1. The propensity for milk consumption in Scandinavia is close to saturation. As we showed research, selling products in a saturated market leads to big losses that are higher the closer the value of the relative consumption to the value 1. This means that the needs of this market are completely satisfied.
2. Judging the relative consumption for the sale of milk are higher Europe prospects because the market is not saturated.
However, it is necessary to make a reservation. Keynes divided the propensity to consume on two categories – objective and subjective factors. He wrote [ THE BOOK THIRD. THE PROPENSITY TO CONSUME. CHAPTER 8 ].
“In order to make our analysis clearer, it is advisable to divide these motives into two big groups: first of them we will include subjective and the second objective factors. Subjective factors, those describe psychological features of human character, and also those public habits and institutes, which though are not invariable, nevertheless hardly whether are subject to significant change over short time periods (excluding any coming out of the ordinary circumstances or revolutionary shocks)”.
In our example, the low level of relative consumption indicates the presence in the European behavior of the subjective factor, but at the same time indicates for the prospect of overcoming it (advertising, development of appropriate European tastes dairy products).
3. Relative consumption can be used to measure the level of poverty and wealth.
Saturation of the population with vital goods is usually calculated by the amount of consumption per person over a certain period (month, year). Relative consumption indicates the degree of saturation (ratio of maximum consumption to real consumption). This example cannot serve as such an indicator because it has a large share of subjective factors.
The low value of the relative consumption indicates poverty if this if this is happens due to the lack of material resources.
The last thing you should specify is the role of relative food consumption. In most cases, this value may wear a medical evaluation.
In this case, the relative consumption indicates that some products, not can provide a normal life, and some goods are consumed excessively,
1.3. Factors affecting relative consumption
1.3. 1.Maximum consumption
Based on statistical data (or on basis common sense) is determined by the maximum possible acquisition of the goods (measured in units that characteristic of this product) for a specified period of time (week, month, year). This quantity we will call the maximum consumption (Pmax)
When choosing the amount of maximum consumption should take into account two types of factors.
The OBJECTIVE restriction and FORMAL restriction.
1. Objective restrictions limit the maximum consumption is that it is limited to physiological causes (for example, a person can’t eat more than 10 cakes in a day) or technical reasons (this car consumes 25 miles/gallon. These parameters can be chosen so that the probability of their change for a short period of time will be small.
Certain goods are restricted to natural causes. For example, the maximum of the index of goods – “park the car in a period of 1 hour” is limited to one hour.
2. A formal limit of maximum consumption – consist that its value is arbitrarily is assigned by the researcher or for harmonization (standardization) with other stakeholders (e.g. maximum consumption of cakes one person 100 cakes per day). Further consideration will show that unrealistically high values of maximum consumption does not affect the main results, does not change the resulting estimates, but complicates the calculations by increasing or decreasing the values of the processed variables.
1.3. 2.Real consumption (demand)
The main ideas are the following:
1. The consumer buys for a certain period (week, month, year) a certain quantity of goods, measured in units characteristic for this product, taking into account needs and price for this item. This is the number we will call real consumption (Preal)
2. After purchase, the buyer consumes it within a certain time of usage.
The reason for the refusal of the purchase may determine subjective reasons.
For example, the impossibility (or unwillingness) every day to eat burgers, or objective reasons, for example, the capacity of the fuel tank is designed for a week.
WHILE WE EXCLUDE THE FACTOR OF SAVINGS “IN RESERVE” (A DELAY SYSTEM).
The time of consumption is different from the time possession of the goods. For example, a car purchased 3 years ago; the owner can use by but if the owner started looking for another car, the time of consumption is 3 years.
1.3. 3. The dependence of demand in units of relative consumption from the price
We determined the relative consumption as
a=Preal/Pmax
We will assume that the unit price the real and maximum consumption is equal; in this case the specific relative consumption does not depend on prices.
If these prices are different, it is possible to introduce coefficients.
Real consumption constitutes the sum of values relative consumption of certain groups of consumers.
Additivity of real consumption will be shown below.
A =Σ niai
Where n is the number of groups of consumers.
The increase in demand can have two sources:
1. The increase in the consumption of individual consumers Preal.
2. The increase in consumption due to the increase in the number of consumer groups.
3. Or the increase of both factors
When prices increase, real consumption is reduced, this leads to lower relative consumption. Conservation measures of the market require an increase in numbers buyers – n. If consumption is reducing then this can only be done by increasing the number of buyers, either through advertising or through the expansion of sales territory.
If prices fall, then real consumption is increases, then same number of buyers buys more goods. The limit this growth is Pmax.
At the stage when the market is not saturated with goods, the factors of maintaining the input flow are valid.
In case of market saturation (overproduction stage) Preal stops growth (every consumer receives the goods close to the maximum consumption). A numbers of groups of consumption at the saturation point, in most cases, cease to grow. During the production of the goods and preference for certain firms, consumer groups and the influence of other factors, such as the geography of sales is stabilized.
Therefore, manufacturers with capacity of production over a certain size (as we will show below) suffering losses, especially when the prices fall.
In this case, the main exit is the agreement to reduce output. This agreement applies to the type of “Nash equilibrium” [3.4]. This agreement brings to all parties to the losses, but the abandonment leads to even greater losses. Such agreements can be reached with great difficulty. This is true in general for the industry.
However, if we consider individual participants of market, the decline in the prices can increase number of groups of consumers which use product this participants reducing the number of consuming products of the other group manufacturers. Competition in the form of lower prices between manufacturers can limit only prime cost. This contest wins by the party that has the least cost, or he can get outside support (from government, banks, etc.).
Non-price factors that affect real consumption [4.4], and which can be influenced a relative consumption:
• The level of income in the society;
• The size of the market;
• Fashion, seasonality;
• Availability of substitute products (substitutes);
• Inflationary expectations.
Resume
So we have established General properties of the concept “the goods”.
It is despite of the large variety of goods, we reduced quantitative characteristics of the goods up to the two indicators.
1. The maximum possible consumption.
2. The real consumption.
However, if we consider the individual participants of market, the decline the prices individually participants of the market (by manufacturers) can increase number of groups of consumers which use his products by reducing the number consuming of products of the other group manufacturers. Competition in the form of lower prices between manufacturers will is limit only prime cost. This contest wins by the party that has the least cost, or he can get outside support (from government, banks, etc.).
In the future we will divide incoming supply of goods and supplies goods which already were serviced. (by analogy with the concepts of the theory of mass service [2.1] – the offered load and. the carried out load).
Incoming supply of goods in the time interval (t1, t2) denoted by Ainc. (t1, t2), it is represents the sum of the quantities of goods handled by this consumer group during the period (t1, t2).
Supplies of goods which already were serviced. over a period of time (t1, t2) is called such the supply of goods if each incoming goods will immediately purchased by the consumer — in moment. (t1, t2). Sometimes this supply will be called — a potential supply.
The difference between the incoming supply of goods and supplies goods which already were serviced will be called a” the losses supplies of goods” :
Alost (t1, t2)=A income (t1,t2)− Aserved.. (t1, t2)
1.4. Numerical characteristics of flows supplies of goods
1.4.1. The intensity of the supplies of goods
By analogy with the concepts of instantaneous and average intensities of random flow may to considered instantaneous and the average intensity of the supply of goods. However, in the theory and practice of calculation of the capacity of the market it is advisable to use the average intensity of the flows offers supply of goods. The intensity the incoming supply of goods means the offer of goods per unit of time. As a unit of measurement of the intensity of the supply of goods adopted the value a=1, i.e. the maximum volume of the supply of goods the (Preal= Pmax).
The following theorem facilitates the determination of intensity of the supply goods
It shows that this value has the property of ergodicity, which is that
Average at the time is equal to the average of the ensemble.
In this case, monitoring the arrival of shipments on time can be replaced by monitoring the number of simultaneously incoming groups of consumers.
The theorem on the quantification of the intensity incoming supply of goods:
The intensity of incoming supply of goods, which is expressed in units o relative consumption, quantitatively equal to the average number of simultaneously busy consumer groups serving this load.
Suppose that during the T hours continuously recorded the number of simultaneously busy groups of consumers market, which receives steady flow of supplies for consumer groups. Let the result of the observations was that during the time t1 was busy υ1 consumer groups, during the time t2. was busy v2 consumer groups, etc. (Fig.1.1). In General can imagine that during the time ti was busy υi consumer groups,
Σni=1 ti= T
and where n is the number, the value of v which is taken, within T hours.
Total time, when busy all consumers of the market at time ti expressed by the product of υit. In the time interval T total time when all users busy of the market will be expressed by amount. This amount, it is supplies of goods all consumers of the market at the time T.
The supplies of goods what, all consumers acquired of the market per unit time are equal to:
Aserv = (1/T) Σni=1vi ⋅ ti
On the other hand, the average number of simultaneously consumer groups occupied during the time T can be defined as a weighted average of ti:
v‘= (v1t1 + v2t2 +•••+ vntn) / (t1 + t2 + ⋯ tn) =
= (1/T) Σ ni=1 (vi ⋅ti)
therefore Aserv= v’
A theorem about the quantitative assessment of the intensity of the incoming floe supplies of goods.
To quantify the intensity of the incoming flow supply of goods you can use the following theorem:
The intensity of the incoming flow supplies of goods, which expressed in terms of relative consumption, creates a simplest flow of goods, which quantitatively equal to the mathematical expectation of the number of goods (c’), received for a time equal to the average duration of one consumption of one batch products (t’cons)
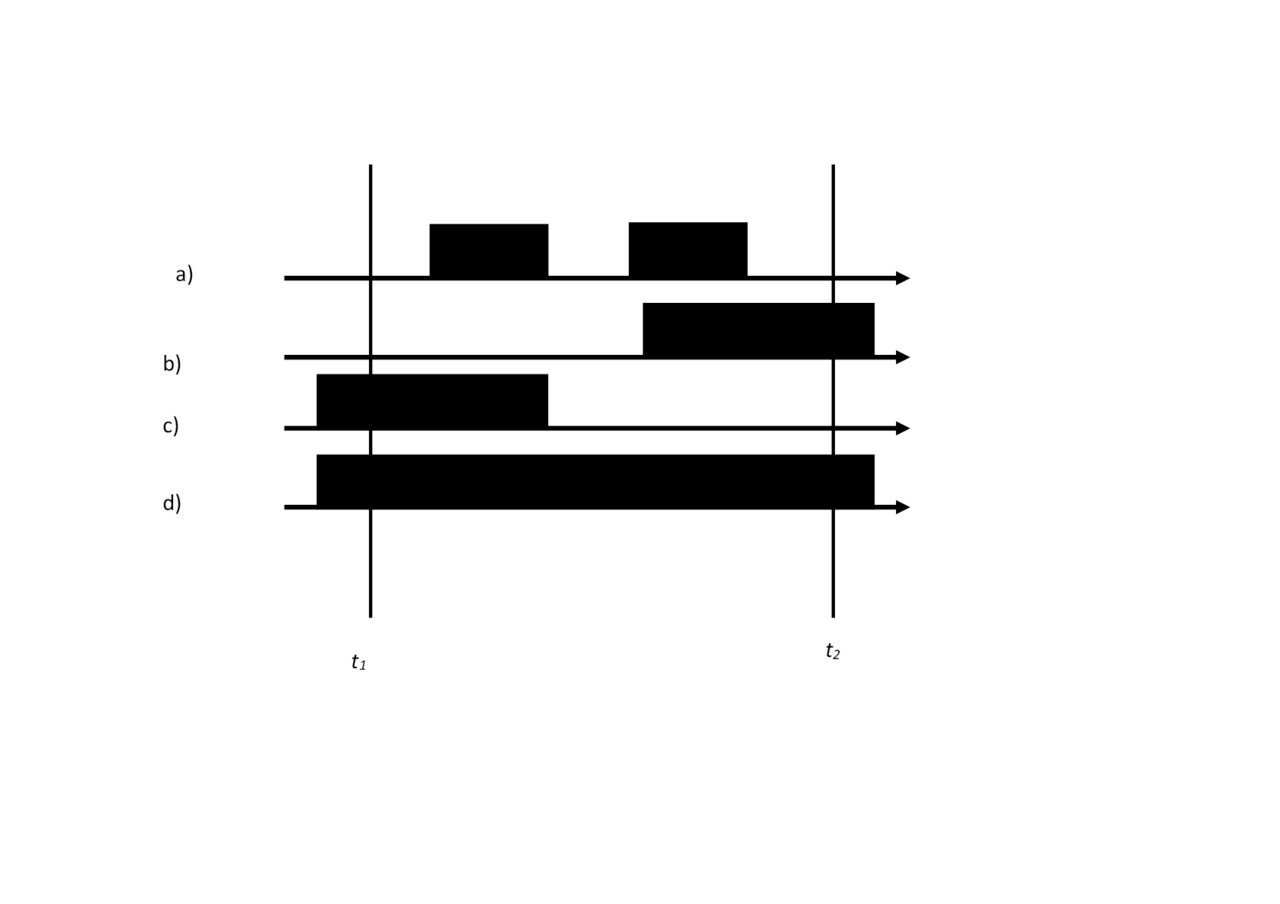
Let the inputs of the market comes a simple flow of goods with the intensity μ. We assume that the duration of consumption — T is a finite random variable
0≤T≤ Tmax is independent of the stream type of the incoming supplies goods with the average value t, Consider the time interval [t1, t2) such that t2 — t1> T max. The mathematical expectation of the number of supplies placed on the market in the time interval [t1, t2) denoted by Λ (t1, t2) =μ (t1.t2).
Part of these supplies is consumed to the moment t2 (Fig. 1.1 a), and the other part does not end in this time (Fig. 1.1 b). Denote the mathematical expectation of the number of goods received in the time interval [t1, t2) and what not purchased to the time t2, denote ρ. In addition to products that arriving to market in the time interval [t1, t2), it is necessary to take into account products that have arrived up to time t1 and the time t2 are not yet purchased. We denote the expected number of goods that began before the time t1 and are ended in the time interval [t1, t2), denote ε (Fig. 1.1), and the expected number of calls that started before t1 and ended after the time t2, denote ζ (Fig. 1.1 g). Since t2 — t1> Tmax, then ζ=0. For the simplest flow ρ=ε.
By definition, the mathematical expectation of entering the market supply of goods during a time interval [t1, t2),
a (t1,t2) = [μ (t2−t1) — ρ +ε] ⋅t ̅=μ⋅ t’consum (t2−t1)
and the intensity of the inbound supplies:
a= [a (t1,t2)] / (t2−t1) = μ⋅ t’cosum
The mathematical product (multiplication) is the mathematical expectation of the number of goods received over the average duration of consumption. The theorem is proved.
For example, suppose that one day (between t1=0 and t2=24 hours) enters N⋅c=100⋅4=400 items of goods.
Let the average duration of a consumption equal per day. Therefore, for time will receive 400⋅ 1/40 =10 items of goods.
At the same time, the number of the mathematical expectation of the number of proposals received per day is equal to:
A= N⋅ c’(T) /T=400⋅ (1/40) =10 items of goods per day
1.5. The demand and its fluctuations
1.5.1. The basic definitions. The time of greatest demand
The intensity of demand called the demand of goods per unit of time. For measuring the size of demand is applied relative consumption. A unit of measurement of the intensity of demand of the goods sometimes may make the value a=1, i.e. equal to the maximum consumption (Preal= Pmax) per unit time.
The intensity of demand in a general case can vary in different hours of the day, days of the week and months of the year. Observations have revealed that, along with random fluctuations of demand, there are exist, relatively regular fluctuations that must be considered when predicting the quantity demanded.
The most significant fluctuations with the seasons.
For some goods the greatest demand falls on a holiday, (e.g. New Year).
Largely they depend on level of life in this area and structural composition of consumers, which serves the market.
Regular fluctuations in demand may depend on the days of the week. On Saturday and Sunday, the demand for goods of mass consumption can be higher than in the other days of the week. Regular fluctuations in demand are observed for the months of the year. The minimum load on the mass consumer goods, excluding resort towns, is observed in the summer months: June, July, and August. The maximum load on the goods of mass demand occurs in February, March and November, December; should be measured demand in these months.
For strategic goods, such as oil, weapons and etc. plays role of the political situation, global and local conflicts.
For the satisfactory quality of customer service at any time, the calculation of the offer you must perform on the basis of the intensity of demand at a time when he is the greatest.
This time will be called the time of greatest demand — TGD (similar to the Busy-Hour of Greatest Traffic — HGT in theory queueing).
The time of greatest demand – TGD it is a continuous time interval during which the average intensity of the demand is the greatest.
The degree of concentration of demand in the TGD estimated coefficient of concentration
kTGD=ATGD/Aobs,
where A TGD. the demand value for TDG;
Aobs. the demand value during the observation.
1.5.2. Main parameters and calculation of the intensity of demand
The main parameters of the demand are:
· the number of consumer groups -n;
· the average number of requests for goods received from one group of consumers per unit time ;
· the average duration of consumption for maintenance of a single application of t.
Consider the possible composition of consumers, which differ in the average intensity and average duration of consumption:
— individual consumers;
— intermediaries (e.g., agencies for the purchase and sale of apartments);
— Firms and government agencies.
By lowering the prices of the goods the number of consumers may increase. The lengthy existence of the product on the market the number of consumers can be stabilized, and they are not changing or changing insignificantly.. A similar reaction may be in case overproduction when the relative consumption is close to 1(unit).Real consumption is stable.
1.5.3. The average number of requests from one consumer per unit of time
In accordance with the categories source of requests average number of request for goods per unit of time respectively
— from one group of individual consumers;
— intermediaries (e.g., agencies for the purchase and sale of apartments);
— firms and government agencies.
We denote in a general way the average number of applications from groups of consumers from sources of the i –th category,
ni – the number of sources i –th category.
Then if on the market have k groups of consumers the average number of applications from one group of consumers will be determined from the expression.
c‘= (Σ Ki=1 ci ni) / Σkini
The average duration of consumption (t’).
The duration of one consumption it is to the period of time from the date of acquisition until the moment you start searching the same product.
Time of consumption is always less time of possession of the goods.
For example, the owner of the car bought it 3 years ago. If he started looking for a new car without selling the old, the time of consumption will be 3 years.
The duration of consumption of food products is determined by the physical needs of the person also by the allowable time storage.
The duration of consumption of clothing is determined by its wear resistance, but now mainly accordance to fashion.
The duration of consumption of control automates, computing machines of cars is limited by their reliability and by their main indicators.
Therefore, the duration of consumption, is a random value and its the mean value can be determined only on the basis of observations of existing markets and statistical studies. The impact of advertising and managing consumer behavior in this book is not considered. Therefore, the duration of consumption, is a random value and its the mean value can be determined only on the basis of observations of existing markets and statistical studies.
Sometimes you must take into account the characteristics of the purchase process that affect time of consumption.
It is possible to allocate
1. Immediate purchase as the initial moment of consumption.
2. Purchases when were refunded or replaced
3. Remote buying (online) with delayed time of consumption.
4. The purchase requisition, which is not satisfied at the lack of product.
5. The purchase requisition, which is not satisfied at the lack of goods acceptable to the buyer.
6. The purchase requisition, which is not satisfied by reason of the expiration of the release of goods etc.
In determining the parameters of the market should be taken into account that the duration of consumption of most goods (except commodities first needs) and the number of users significantly to effects on the demand the stage when the market is not saturated and it very much to depend on the prices.
For example, at higher prices on televisions – the number purchases decreases, the time of consumption increases (less likely to alter the old model).
However, as we will see later, when the market is saturated demand – growth in consumption (purchases) stops regardless of price.
1.5.4. Characteristics of quality of service of goods
Quality of service of suggestion on the market of goods is characterized by the number of unsold within a certain time of the goods or length of expectation of sale.
There are two basic approaches, the two disciplines of servicing coming to market goods: apparent losses and conditional losses.
A discipline services with obvious losses is the discipline in which the marketed product needs to be sold, and if all consumers are busy, then it is removed from sale and no longer has on the market no effect. This discipline is called a discipline with obvious losses. This discipline services implies that if the manufacturer received the refuse due to lack of demand (all groups of consumers are busy), then abandons further attempts to sell the goods (re-attempts of implementation are considered as a special random flow).
To quantify the quality of service with obvious losses are calculated the following quantities:
loss in the number of requests for suggestion of goods —
R request.;
loss of volume of goods – R goods. ;
loss of implementation time — P t
The loss of the number of requests received for supply of goods in the time interval [t 1, t 2) is the ratio of the number of lost (not serviced) during this period (t 1, t 2) to number received in the same time.
Prequest (t1.t2) =clost (t1.,t2) /c (t1.t2)
Losses in volume of goods in the time interval [ t 1, t 2 ) is the ratio of lost quantity (what not sold) in this period of time of the goods – alost (t 1, t 2 ) to the incoming volume goods during the this time, a (t 1, t 2 ).
Losing time over a period of time [t1, t 2) it is the ratio length of all of time periods to time, when all groups of consumption is available for the group of producers are busy.
If in the expression for the loss of the requests number received for supply of goods, the and in expression, the loss of the amount of goods and loss of time insert the mathematical expectation of the corresponding random variables, and then we can talk about the likelihood of losses these goods.
A discipline of service with the expectation (conditional losses) is a discipline in which incoming goods to the time of the lack of free groups of consumers is not losing and becomes on the storage (discipline of service with waiting).
To quantify the quality of service with the expectation calculated in the following characteristics:
— the probability that the waiting time is greater than zero — that is, the probability of queue – p (γ >0);
— the probability of waiting for any incoming product over time t — p (γ> t); the probability of waiting of the delayed goods over time t — p (γ> t);
— the average waiting time in relation all requests received – (γ )
— the average waiting time of only a delayed requests – γ delay ;
— the probability that the queue length exceeds the specified value r is p ( R>r );
— average queue length – C delay.
The main characteristics – p ( γ >0) and p ( γ > t ).
1.5.5. Traffic-carrying capacity market
One of the most important properties of the market is its efficiency.
As indicators of the effectiveness of the market as well as economic (price, cost of goods, etc.) can be used such characteristics as the traffic-carrying capacity market.
Under a traffic-carrying capacity market we will understand the value of the intensity of served supplies of goods (sold goods for a certain period of time) when a certain value of loss (what not sold).
The traffic carrying capacity of market depends on the value of losses that satisfy market participants, the number of consumer groups, distribution of duration of consumption and services discipline ( obvious losses or conditional loss), the type of the input flow.
The quantity of loss which characterizes the condition of the market, different for different categories of goods.
Obviously, the more norm of allowable losses, the more a traffic-carrying capacity market and the worse the quality of producers service, i.e. market can accept from manufacturers a greater of goods and most to lose or will keep on storage more a specified time.
Flow of goods (offer) in mathematical models, often adopted as the simplest flow, flow of Palm or primitive. In these cases it is relatively easy to obtain the solution of the problem using analytical methods.
Real flows of goods have a more complex structure, and the decision of task is usually carried out according results received for the simplest stream in the form of the boundary estimates of indicators (results for simplest stream better or worse).
The most convenient distribution function of service time from the point of view of the analytical description and analysis of the throughput of the market is the exponential distribution, since it has no aftereffect.
Practical widely application founds probability distributions – density distribution, Erlang distribution etc.
Discipline of service has a significant impact on the mathematical model of the market, therefore it is necessary to describe in great detail. For example, in the system with the expectation of the accumulated goods may be return from storage back on market:
— in order of receipt;
— in the reverse order of the order of arrival;
— random order;
— with different kinds of priorities.
Traffic-carrying capacity market of consumer groups may be estimated the ratio of intensity aserv of supplies of goods υ what was serviced.
η =a 0 / υ,
The value η is called the average traffic-carrying capacity market, or average utilization of one group of consumers.
For example, in one people can buy 400 kg of milk per year. By delivery to the dairy market in 1991, was sold to 347 kg of milk per person per year, η = (347/400=0.8675), and in 2014 sold 240 kg of milk per person per year (η =240/400=0.6) [4.5]. Therefore, the capacity of the dairy market fell by 26%/
The capacity market can be analyzed from the point of view of arriving of the supply η =f (y) or in terms of a number of consumer groups η = f ( υ ) ) at fixed values of losses.
The value of η by increasing the intensity of the incoming of supply asymptotically approaches unity. This is due to the decrease in the influence of temporary fluctuations of demand. This property shows the usefulness of combining groups of consumers (larger market), which reduces these oscillations.
1.6. Tests to Chapter 1
1. The intensity of the supply of goods is it_________
a. the number of calls per unit of time
b. the total duration of calls per unit of time
c. the demand of products per unit time
d. amount of goods that passed system
2. Serviced market offer for time period (t1, t2) is it_________
a. the number of products sold over time (t1, t2)
b. the difference between the received and a serviced supply of goods for
the considered period of time.
c. the sum of the quantities of goods handled by this group
consumers for the period (t1, t2)
d. the sum of the requirements for a certain number of goods, served during (t1, t2)
3. The unit of measure of the intensity of demand of the goods is accepted _________
a. the number of purchases per hour
b. the relative value of consumption at the maximum consumption (Preal= Pmax) per unit time.
c. the amount of goods delivered
d. the amount of applications received for the goods
4. The time of greatest demand – THD _________
a. time of the season with the highest demand
b. time from sampling successive periods of time with maximum load
c. time of maximum demand for each month
d. continuous given period of time, with a maximum value of the intensity of demand
5.The main parameters of the demand are: __________
a. the number of consumer groups -n; the average number of bids on the goods unit of time; the average duration of consumption of service the one application t.+
b. the number of consumer groups -n; the average number of bids on the goods, price per time unit; price per unit;
c. the quantity of the goods; the average number of bids on the goods, price per unit of time; the average duration of consumption of service the one application t.
d. the number of consumers is n; the number of served requests for goods; the average duration of consumption of service the one application t.
6. When overproduction of goods and lowering the prices of the goods the number of consumers ______
a. increases
b. reduced
c.do stabilize
7. The average number of requests from one consumer per unit time from the k groups of consumers is determined by ______,
a.. according the group with a large number of requests
b. according the weighted average number of
c. according the most frequently used number
d. randomly
8. The time consumption of the goods can be _________ time of possession
a. equally
b. less
c. more
d. dependent on the storage conditions
9. Under a traffic-carrying capacity market we will understand the value. ________
a. intensity serviced supplies for a certain period of time when a certain amount of losses
b. intensity serviced supplies for a certain period of time
c. the amount of goods sold over a certain period of time
d. the number of applications for a certain product for a certain period of time
10. The more allowable are losses, then_________
a. less a traffic-carrying capacity market and the worse the quality services for producers
b. more a traffic-carrying capacity market and the worse the quality of service manufacturers
c. better quality of service manufacturers
d. stable quality maintenance of producers
11. A traffic-carrying capacity market is estimated –
.a number of consumers
b. value of losses
c. relation the intensity of services supply to the number of groups of consumers
d. number of suppliers
Chapter 2. A mathematical model of the market
2. 1.Definition
For the mathematical estimate of processes in the economy it is necessary to create a model that would reflect them in mathematical form. In conjunction with the definition of units of measure of supply, demand and also definition of relative consumption, this model allows to obtain and to provide a quantitative calculation, analysis and give assessment of possible market behavior. The proposed model is shown in Fig.2.1.
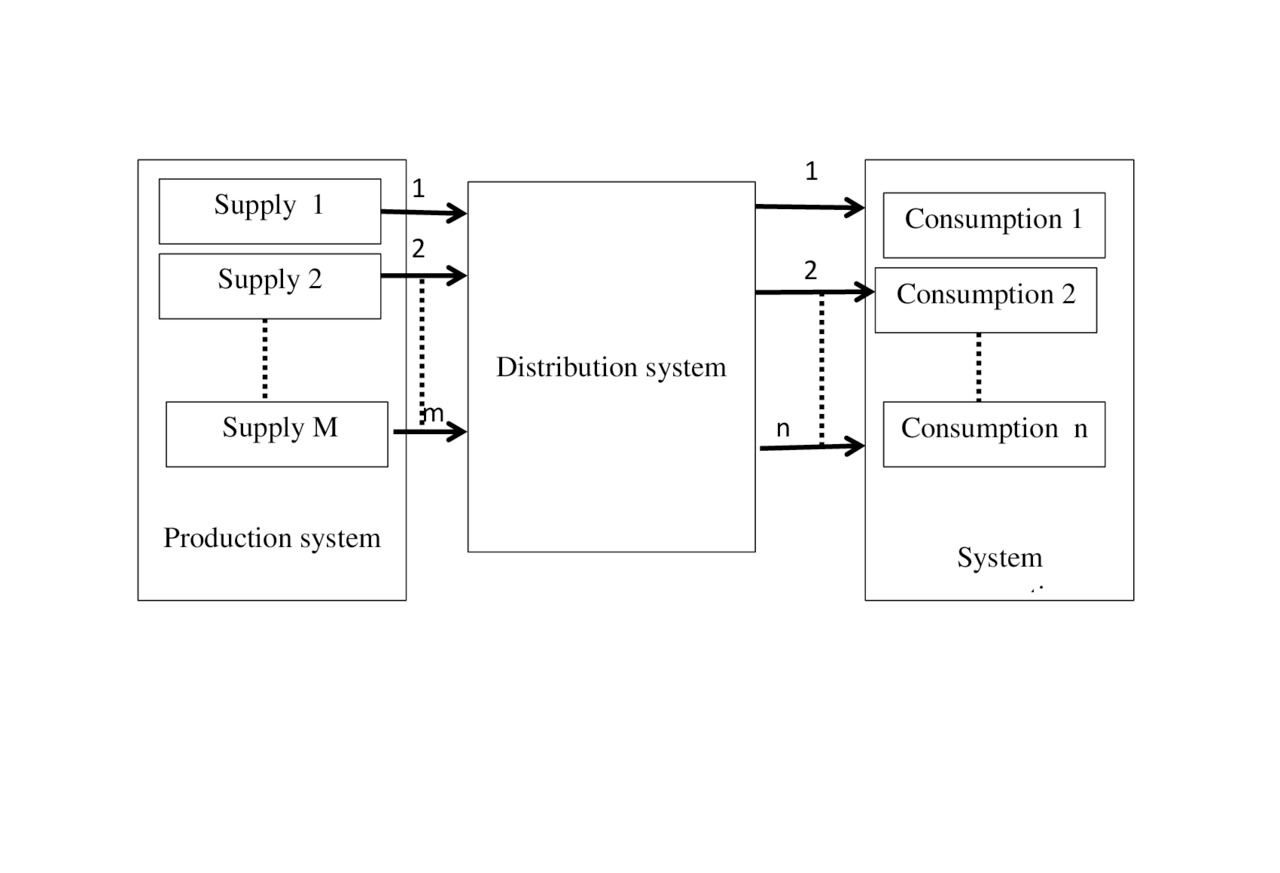
The market contains a subsystems they performs the following tasks.
Production system — generates a random flow of goods (in general case different from each other). Under the product refers to any product or a service offered for sale, in which there is a need (in the following we will show how to define the demand in numerical form). These can be food items such as milk and other food products, cars, homes, cleaning home, stocks, services in construction of houses, etc.
The flow enters the distribution system.
The distribution system can the request handle immediately or with some delay. The refusal can be of two types:
— the refusal to accept the goods because of lack of demand;
— or installation on waiting of implementation (accumulation of goods);
There are two types of distribution systems.
The first of these it is the task as quickly as possible to sell the goods without any additional conditions. In queuing theory, such a system service is called“full accessibility system” because it provides equal access to the system of consumption, and this system can be not take into account for calculation of behavior of the market.
.Systems of the second type – they sell goods given the specified priorities and limitations for individual consumers or consumption. For example, the sale of tobacco, alcohol, weapons … systems of this type is called “not full accessibility system”.
If the order is accepted, the distribution system seeks deliver its in the system consumption.
Consumption system serves the flow of goods. This is reflected in the fact that individual consumer or group of consumers can buy the offered goods or to refuse from the purchase.
If all consumer groups are busy, then the system of consumption is refuses from the purchase of goods, i.e. occur losses.
And not purchased goods more is not offered for example can be removed or in distribution system can be supplied to the queue for waiting the implementation (the accumulation and storage of goods). In this case it is important to know the waiting time t
2.2. Types of SERVICE systems and input flows goods
Flow of events (in our case products) is a sequence of goods coming through any interval or any moment of time.
Deterministic flow of events – the sequence in which events arrive in a certain, strictly fixed non-random moments or in certain, strictly fixed, non-random intervals. For example, sale of products from the conveyor.
The random flow of events is differs from the deterministic, only one property that the moment of the arrive of goods and intervals arriving time between deliveries are not strictly fixed and random variables. Deterministic flow is a special case of random flows and is rare in practice. Strictly speaking, even such flows often contain moment’s fortuity. In this regard, in the theory of mass service flows basic attention is devote the consideration of random call flows.
The flow of events can be determined by one or more of the three equivalent ways:
1. A sequence of moments of occurrence of the event t1, t2,…,tn,,
For example, the probability of admission of a particular product, and at the time t1.
This may be a possibility that mobile phones will be shipped to the store every Friday.
In the lottery is, for example, the probability of occurrence in the draw of lottery with numbers 5, 7, 15 will be the number 6. These events i can be described as moments of time.
2 The sequence of intervals between the events — the moments of z1, z2,…,zn
Example, the probability that mobile phones will be shipped to the store every 7 days.
In the lottery is, for example, the probability of occurrence number 6 every 5 lottery draws.
3. A sequence of numbers k1, k2,…,kn, determining the quantity of events arriving within the time intervals [t0, t1), [t0, t2),…, [t0, tn).
Example, the probability that during 5 months (counted from the initial moment t0 — t15) fresh fish will goes on sale 5,6, … 10 times.
2.2.1. Types of systems service goods
Below show a classify service goods, it is widely used in queuing theory [2.1], but in the economy has not yet is applied.
Types of systems service the goods is shown on Fig.2.2
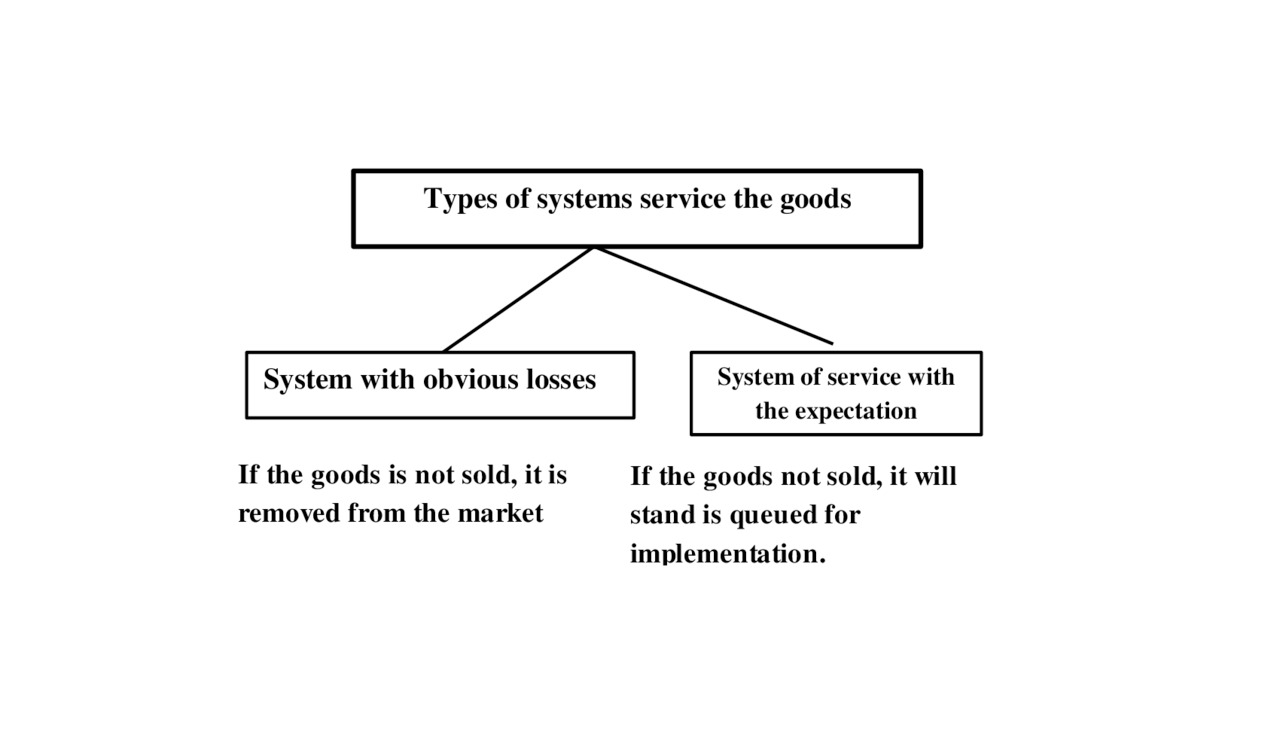
We will explain the figure
System with obvious losses
System, in which if the goods is not sold, then it is removed from the market, is called system with obvious losses
System of service with the expectation
System, in which if the goods is not sold, then it will stand is queued for implementation is called system of service with the expectasion
2.2.2. The types of input flows
The flow of goods is a sequence of goods incoming through any interval or at through any moments of time.
Deterministic flow of events – the order in which events arrive in a certain, strictly fixed non-random moments or in certain, strictly fixed, non-random intervals. For example, sale of products from the conveyor.
The random flow of events differs from the deterministic, those and only, that moments of supply of goods and intervals between deliveries are random variables, but not strictly fixed values. Deterministic flow is a special case of random flows and is rare in practice. Strictly speaking, even in such streams often occurs a random event.
The flow of events can be determined by one or more of the three equivalent ways:
1. A sequence of moments of occurrence of the event t1, t2,…,tn,
For example, the probability of admission of a particular product, and at the time t1.
This may be a possibility that mobile phones will be shipped to the store every Friday.
In the lottery is, for example, the probability of occurrence in the draw of lottery with numbers 5, 7, 15 will be the number 6. This event in the study can be described as moments.
2 The sequence of intervals between the events – the moments of z1, z2,…,zn
Example, the probability that mobile phones will be shipped to the store every 7 days.
In the lottery is, for example, the probability of occurrence number 6 every 5 lottery draws.
3. A sequence of numbers k1, k2,…,kn, determining the quantity of events arriving within the time intervals [t0, t1), [t0, t2),…,[t0, tn).
Example, the probability that during 5 months (counted from the initial moment t0 — t15) fresh fish will goes on sale 5,6, … 10 times.
2.2.3. Principles of classification of event flows
In order to obtain a mathematical description of flows will conduct their classification.
Flows of goods are heterogeneous and homogeneous.
For example, on the sale may be simultaneously delivered cars, spare parts, tools for touch-up chips, tires, etc. This is heterogeneous flow.
In a heterogeneous flow of goods each goods has its own characteristics.
— periods and the volume;
— the relationship of these periods;
— a groups of consumers;
— the duration of consumption of each item and other characteristics
Homogeneous flow of goods is characterized sequence regularly receipt of goods of only one type.
Despite the fact that, in practice, the flows of goods, as a rule, are not homogeneous. In the future the flow of goods we will understand as a homogeneous flow of events.
The flow of heterogeneous goods can be bringing to a uniform flow by combining multiple groups of different products in one product (e.g. spare parts for cars).
In the future, we will restrict ourselves to finite flows of goods, in which on any finite interval of time, at there are a finite number of goods, and the mathematical expectation of incoming goods is a finite value.
Flows of goods are classified (Fig.2.3.) from the point of view of stationarity, the ordinary and the aftereffect.
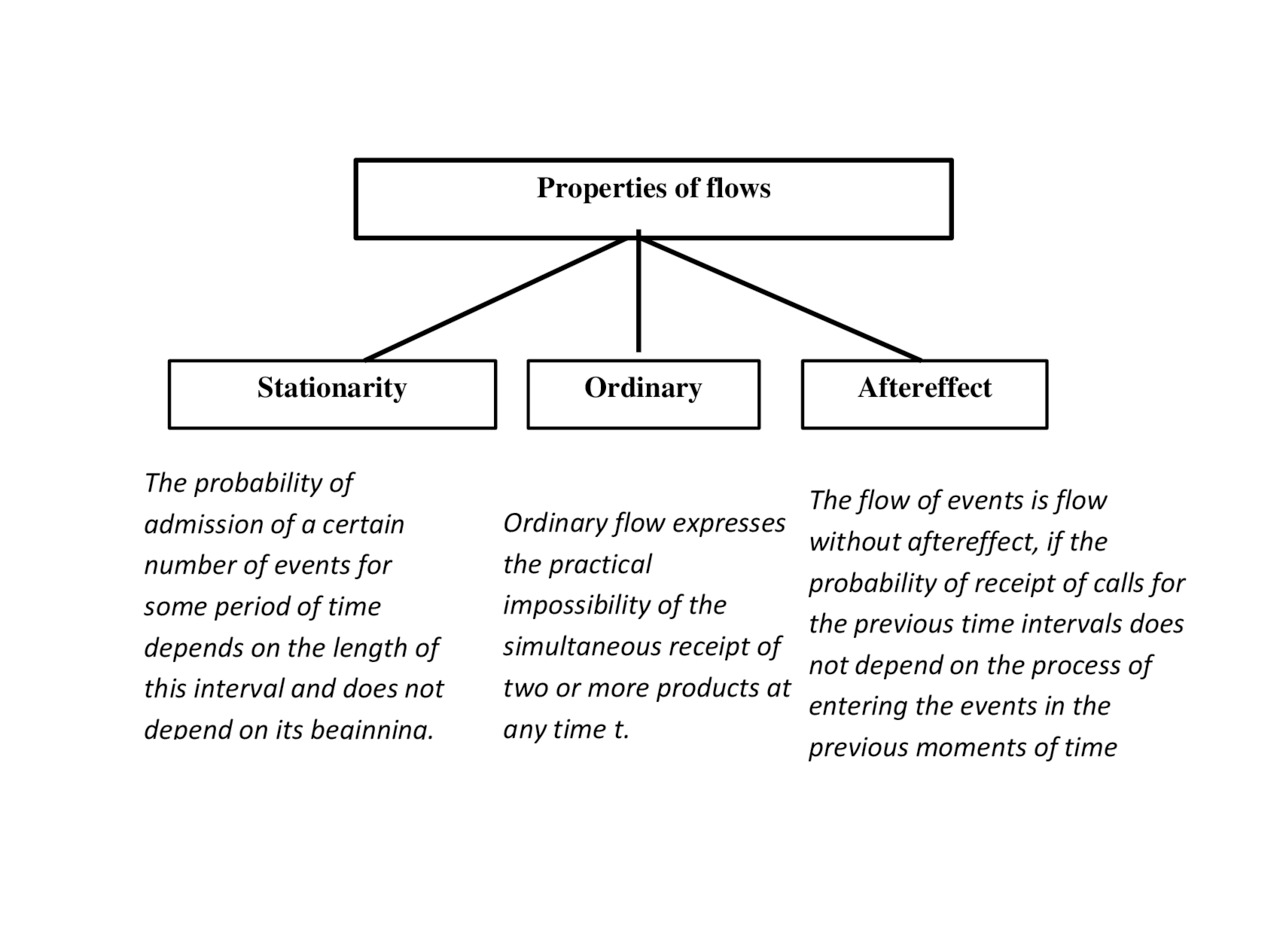
Properties stationarity of the flow, when the probability of delivery of a number of products during the observed portion of time, depends only on the length of this section.
Supply flow of goods in the production system can fluctuate sharply depending on the season, time of day: the quantity of goods supplied to certain daily and evening hours may be the maximum value, and at night may decrease to almost zero. This means that the probability of admission of any number of goods in a certain period of time depends on the location on the time axis of this gap and therefore the flow of goods received during the day from any groups of producers are non-stationary.
During the study of mathematical models of the market in most of the cases in this book discusses the stationary flow of goods
In this type of flow the probability of not depends on where on the time axis is located the time interval [t0, t1), the probability admission K [t0,ti) events of one and the same.
More precisely this means that for a stationary flow the probability of admission of a certain number of events for some period of time depends on the length of this interval and does not depend on its beginning. Otherwise the flow is non-stationary.
Note that inside a limited interval of time, e.g. one hours, no stationarity of the flow of events less perceptible, which allows for many practical problems are considered as a stationary flow, that arrives from a large group of manufacturers (100 or more) for a small period of time.
Ordinariness flow expresses the practical impossibility of the simultaneous receipt of two or more goods (consignments) at any time t.
An example of a transition from consideration of the unordinary flows to the ordinary is the consideration of periodic supply of cars with a random and unordinary period. But if we can consider them in the form of parties, they can be considered as ordinary.
Properties lack of aftereffect of the flow it is, when the probability does not depend on the time and type of committing previous events.
In other words, properties the lack of aftereffect flow means the independence of properties a random flow of goods in any moment from of its behavior up to this point.
An example of a flow without aftereffect may be the flow entering the market of mobile phone shipments. Indeed, the probability of admission of any number of mobile phones on the market with well-established production at any period of time is almost independent from process the admissions items prior this cut of time.
Event flow is a flow with aftereffect, if the probability of admission of events over a certain period of time depends on the process before the beginning of that period. For example, the company monitors the amount of supplied mobile phones, and intentionally reduces the supply, to avoid redundant suggestions.
The flow types (Fig.2.4.) vary in accordance with how they meet to the above properties of the flows of goods and services. [2.1].
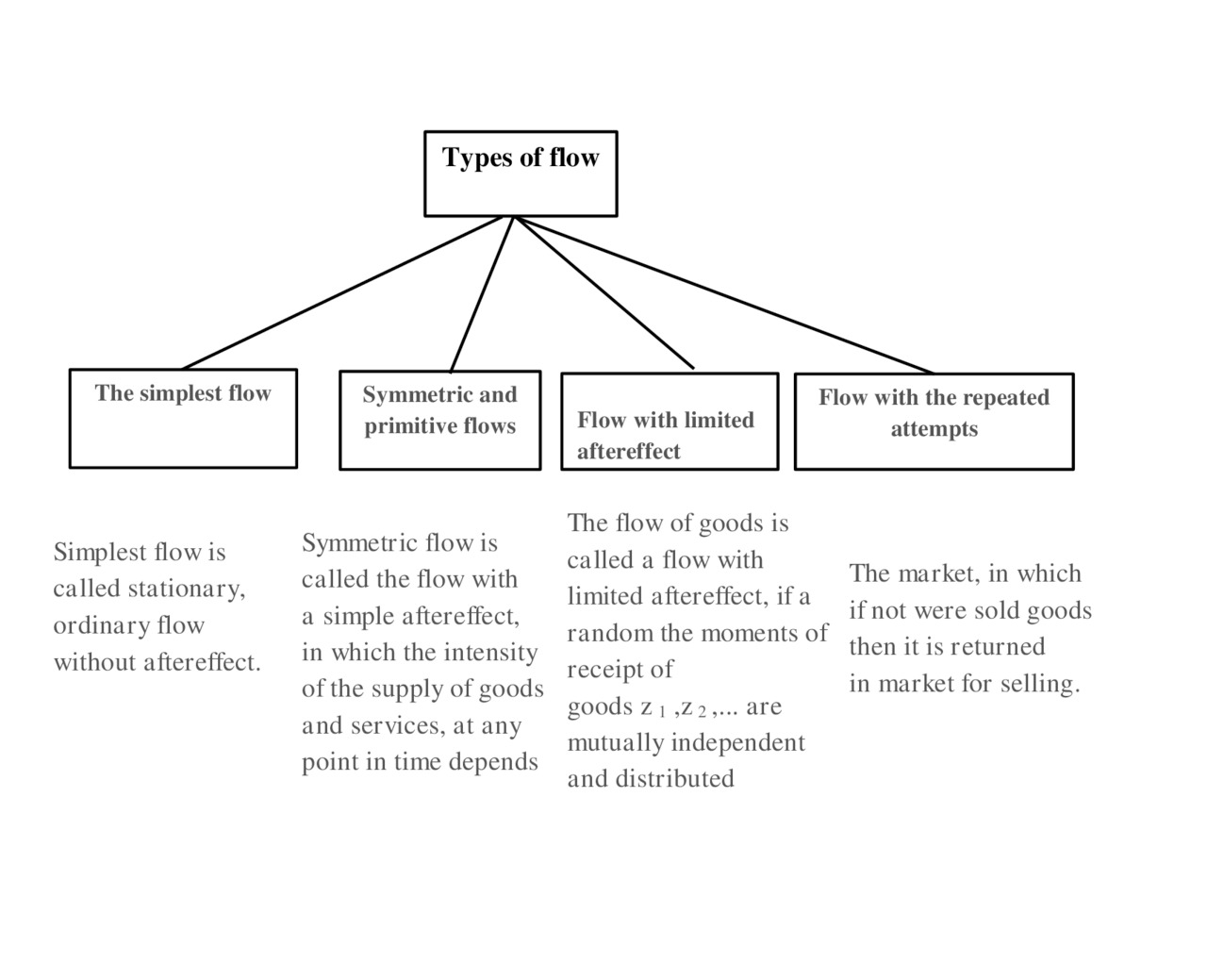
The simplest flow of events. Simplest flow is called stationary, ordinary flow without aftereffect.
The simplest events flow is the most common model of the real flow of goods used in the systems of mass service. Indeed, as noted during the discussion of principles of classification, the flow of products in mass production can be considered without aftereffect. It can be considered ordinary, and when restricting the investigated period and also considered as stationary. The same random flows of events is typical for many sectors of the economy.
Symmetric and primitive flows. Symmetric flow is called the flow with a simple aftereffect, in which the intensity of the supply of goods and services, at any point in time depends only on the number of consumers who have purchased the product, at this point, and no depend on other characteristics that define the state of the system. At this The dependence of the parameter from the number of customers may be to comply with any law
A primitive flow is called ordinary the goods flow with parameter-λ s (t) that is depends on the state market s (t) at a given moment t.
The parameter of this flow:
λ i =α⋅(N−i),
where α is the source parameter in the free state.
For this flow we have a natural assumption that a busy source can’t offer the goods. If a small firm takes the order, she builds a house and this period cannot execute other orders.
The flow is in the literature called Engset flow. This flow is one example of threads with a simple aftereffect.
Flow with limited aftereffect
The flow of goods is called a stream with limited aftereffect, if a random the moments of receipt of goods z 1,z 2,… are mutually independent and distributed according to any law. To specify such a flow, it is sufficient to specify a set of distribution functions of random variables z i :
F i (t) =P (z i <t), i ≥ 1
(for comparison it may be noted that for the simplest flow between the calls distributed by a single exponential
F 1 (t) =F 2 (t) =…=F (t) =1−e – λ⋅t).
Flows with limited aftereffect during the period between arrival of goods. For a simplest flow, there is no aftereffect for one period of time between deliveries, as) with the exponential law of distribution of the remaining part of the interval z i – τ distributed according to the same law as the rest of the interval
zi.
One of the classes of flows with limited aftereffect is recurrent flow — a flow with limited aftereffect, for which all the intervals between calls, except the first, are distributed by the same law:
F 2 (t)=F 3 (t)=…=F(t)
The recurrent flow is determined by the functions:
F 1 (t) =P(z 1 <t)
F (t) =P (z, K <t), K ≥ 2
For example, the flow of goods from a limited number of sources is
flow primitive, since the probability of arrival of new goods depends on the number of already sold goods. This probability directly proportional to the value N – i, where N is the number sources i – the number to the currently established connections
The private class of recurrent flows – a flow of Palma is stationary, ordinary, recurrent flow. Flow Palma is at the same time a generalization of the simplest flow to which the claim of lack of aftereffect is replaced by the broader requirement of limited aftereffect.
Flow with the repeated attempts implementation. The market, in which if not were sold goods then it is returned in market for selling.. For example, some goods are not sold for a number of reasons (all consumers possess already this product, or don’t have the resources to purchase or goods was returned). All or part of goods again are returned to sell.
The repeated flow consists of new and unsold the goods. The parameter of the flow of repeated event depends on the state of the system, and parameters the flow of re-selling
2.2.4 Basic numerical characteristics of the flow of goods
In study the process of functioning of the market need to consider numerical characteristics. We will consider them gradually. We will define at the beginning the characteristics associated with frequency of receipt of the product on the market.
One of the main characteristics of the flow of goods — it is the leading flow function and indicators — it is the parameter and the intensity.
Λ (t) – the leading function of flow of goods may be defined as the mathematical expectation of the arriving of the number of batches of goods in the time interval from 0 to t. goods.
It should be emphasized important for this definition is the quantity of the batches. More simply, it indicates the average batch size of goods can enter during the considered period (week, month, year…). It may be 5 batches, 100 batches, etc. If the flow is extraordinary, they can come in one moment or several moments.
Let be the mathematical expectation quantity of batches of goods arriving in the interval [0, t) Λ (t).. The function Λ (t) called the leading stream function.
Λ (t) =lim n – > ∞ (Σ ni ki (t)) /n
n is the number of observations;
ki (t) — the quantity of batch of goods received during the time interval [0,t) in the i-th observation period (week, month, year…).
By definition, the instantaneous flow rate μ (t) it is limit:
μ (t) = lim Δt→0 (Λ (t + Δt) — Λ (t)) /Δt= lim Δt →0. Λ (Δt) / Δt
For stationary flow the instantaneous intensity is constant at any given time on a given interval. For stationary flow the intensity μ it is the mathematical expectation number of goods arriving per unit of time.
Consider the examples.
Example 1. The probability distribution has the form:
Pk ≥ 1 = a0 + a1t
The flow parameter have constant value λ (t) =a1.
For example, the probability receives of swimsuits batches at the beginning summer of the season increasing linearly 2 times every week.
Example 2. The probability distribution has the form:
PK ⩾ 1=1-e-at
In this example, the probability of batches of swimsuits at the end of the season decreases exponentially every week.
Then the parameter of the flow is determined from the expression
λ(t)=a
Parameter of stationary flow is a constant that does not depend on time λ (t)=λ>0.
For any stationary flow, there is always has taken place
the inequality μ⩾λ. If the stream is still and ordinary, then μ=λ.
Parameter flow of goods λ (t) at time t it is the limit of the ratio of the probability of receipt of at least one batch of goods on the interval [t, t+Δt) to the length of this interval Δt when Δt→0.
λ (t) =lim Δt→0 P K ⩾ 1 (t, t+Δt) / Δt= lim Δt→0 P K ⩾ 1 (Δt) / Δt
λ (t) = d [P K ⩾ 1 (t)] /dt (2.1)
In other words, the thread argument is the derivative of the probability of arrival of goods at the time t — density distribution function It specifies the number of moments of arrival.
In contrast to a leading function Λ(0, t) that determines the expected number of goods arriving in time interval (0, t), the stream parameter λ(t) does not characterize the flow of goods, and the flow of moments of receipt of the goods, and this characteristic applies not to the whole interval (0, t), but only to a fixed moment t.
For any flow of goods μ(t)≥λ(t), for the ordinary stream is μ(t)=λ(t).
For stationary flows, the intensity and parameter are constants: μ (t) =μ, λ (t) =λ (since each time t is supplied to only one batch of goods). For any stationary stream µ≥λ, for stationary and ordinary flows μ=λ.
It is conveniently to carry out classification of flows, taking over the main feature – the aftereffect the flow. From this viewpoint distinguish next classes of threads: without aftereffect, with aftereffect, with simple aftereffect and with limited aftereffect.
We begin consideration these classes of flows with first class -it is the flow of without aftereffect.
2.2.5. The simplest flow of goods and its properties
The simplest flow of goods is a stationary, ordinary flow without aftereffect. The simplest stream of goods is completely determined and is given as the probability of admission exactly K batch of goods during the time [0,t).
Consider the first method task of the stream using sequence of the moments of occurrence of the event t1, t2,…,tn ( section 2.2.1).
We denote this probability Pk (t) for K=0, 1, 2, 3, … and t>0.
And will find the expression for Pk (t):
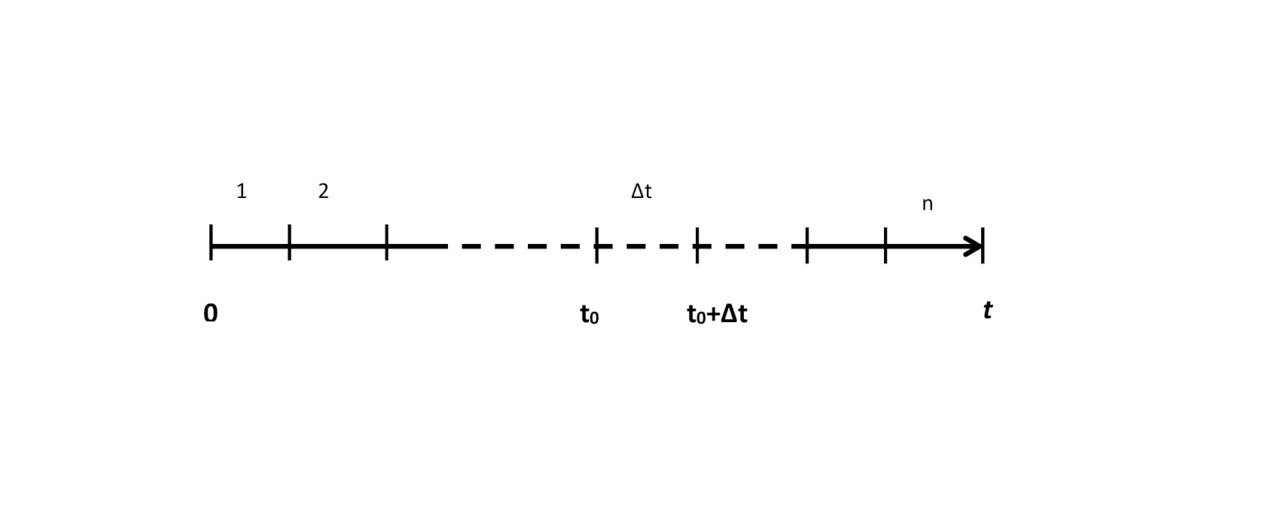
In Fig.2.5 is shown the flow of batches of goods in the time interval [0,t). This period consists of n segments of equal length:
Δt = (t/n)
Consider a small period of time Δt. We will compute the probability that this period of time will received one batch at least. By definition, parameter of flow it is the limit of the ratio (2.1).
Consider a small period of time Δt. We will compute the probability that this period of time will received one batch at least. By definition, parameter of flow it is the limit of the ratio:
P K ⩾ 1 (t0+Δt0) = λ Δt= λ (t/n)
and the probability that be not received of nor one batch of the goods
PK=0 =1− λ Δt =1− λ (t/n)
Because, by definition, the simplest flow is a flow non aftereffect, the probability of receipt of batch of goods in non-overlapping time intervals is independent. Therefore, n periods can be viewed as n independent experiments, each over during a period of time Δt can come batch of goods with probability λ∙t/n.
The probability that among n intervals will have exactly K that will receiving batches goods (the second method of specifying sequence of time intervals between the events of the moments of z1, z2,…,zn) can be determined by the theorem on the repetition of experiments (in the formula, Bernoulli) from the expression.
Pn, k =CnK (λ t /n) K (1- λ t /n) n-K
If number of time intervals n for a sufficiently large, then probability is approximately equal to the probability of admission to exactly K of batches within the interval time [0,t) because the probability of admission of two or more calls in the interval Δt has a negligible probability (Poisson flow it is ordinary).
To find the exact value of PK (t), you need to go to the limit when n→∞
PK=lim𝑛→∞CnK (λ ∙t/n) K (1− λ ∙t/n) n-K= {(λ ∙t) K/K!) e− λ t
The probability distribution PK(t) is called the distribution Poisson. To ensure that the sequence of probabilities PK(t) represents a range of distributions it is necessary to show that the sum of all probabilities PK(t) is equal to one. Indeed, according to the formula of Taylor series.
ΣK=0∞ PK (t) = ΣK=0∞ (x) K /K!=e-x
then we will get:
ΣK=0∞ PK (t) = ΣK=0∞ ( λ ∙t ) K/K!= (Σ 𝐾=0 ∞ ( λ ∙t ) K/K!) ( λ ∙t ) K/K! =
=e− λ t (Σ 𝐾=0 ∞ (𝜆t) K/K! = e− λ t e λ t=1
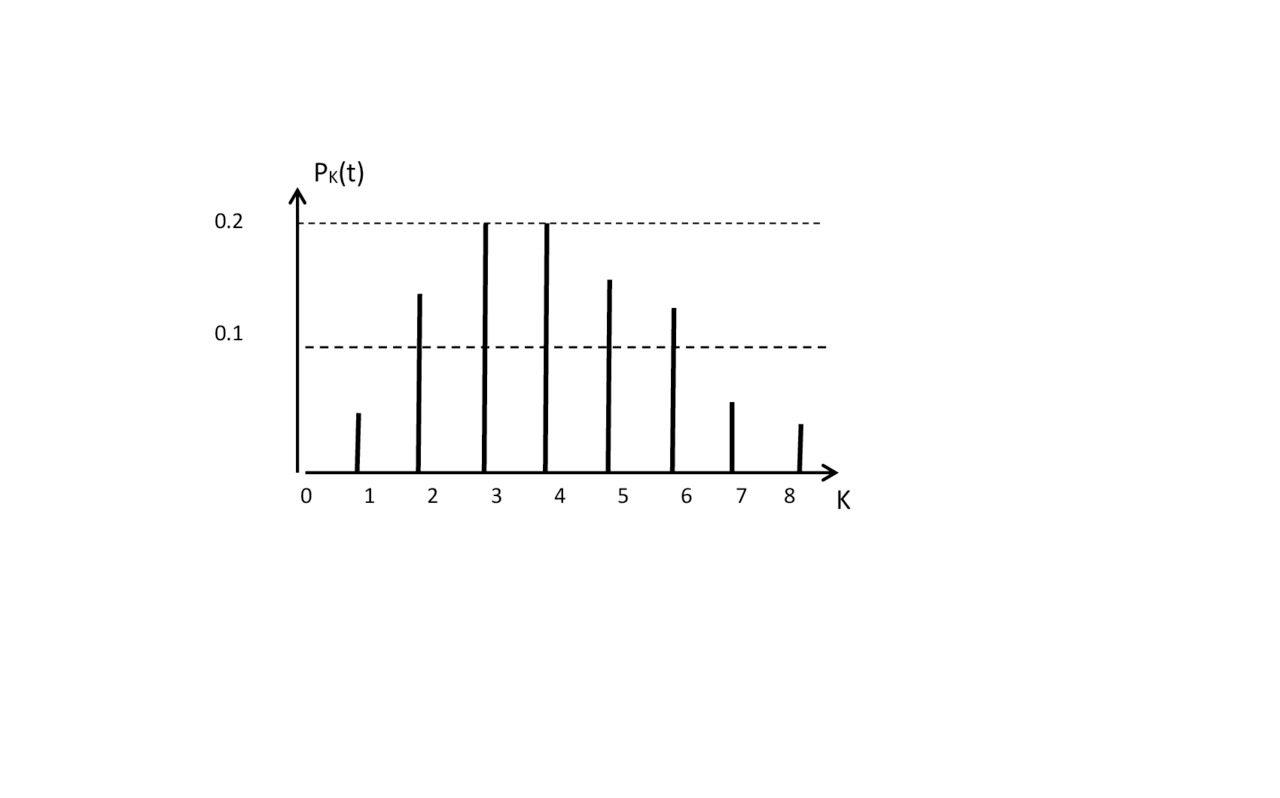
To build the Poisson distribution, is necessary for all K calculate PK (t). This is the distribution of a discrete random variable. for example, when λ⋅t=4 the distribution is as follows (Fig.2.6):
Envelopes Poisson distribution with different λ⋅t have the following form (Fig.2.7):
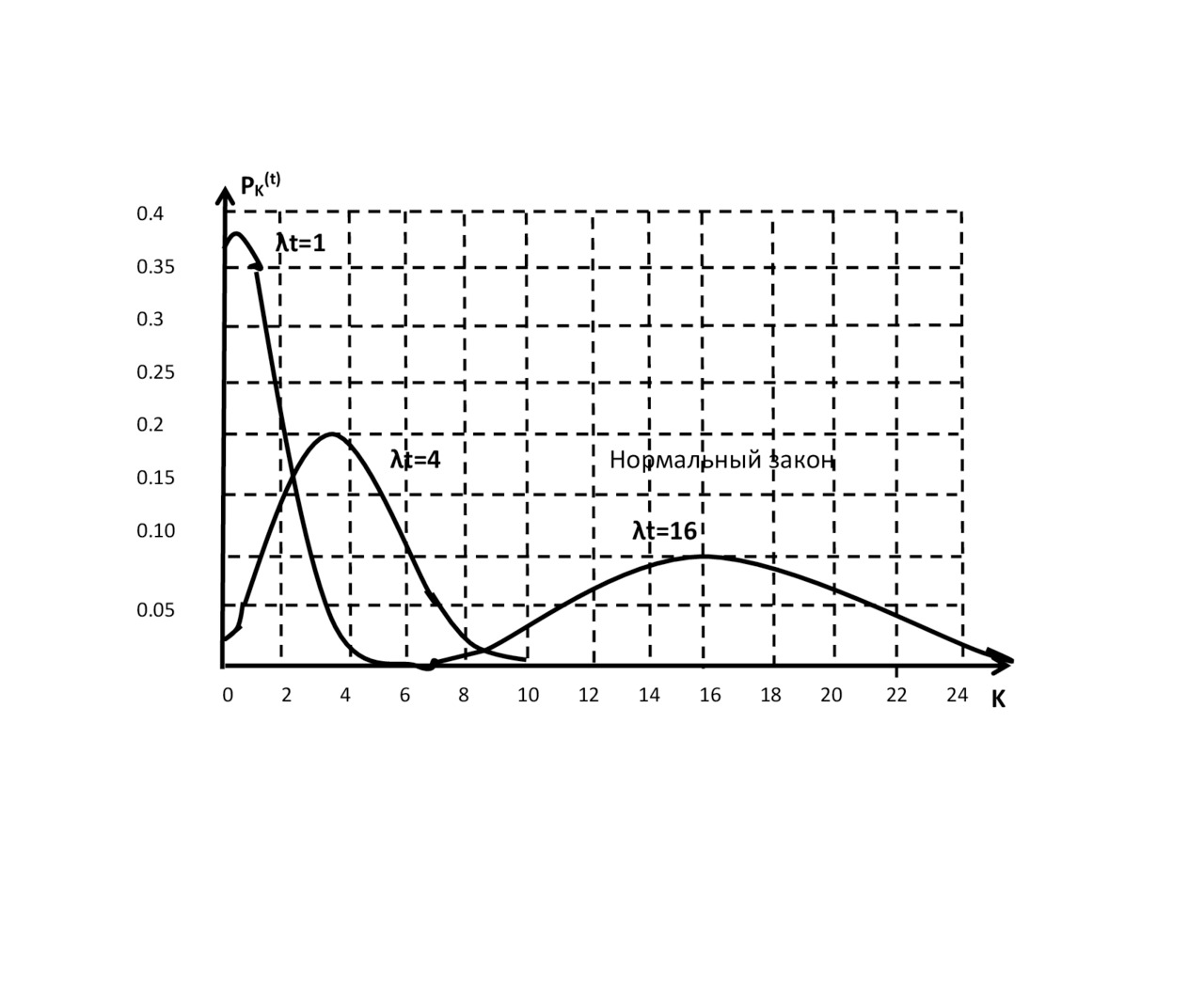
As can be seen from the figure, with increasing envelope is adopt more symmetrical of appearance. When λ⋅t⩾10 there is good accordance between the envelope of the law of Poisson distribution and the normal law distribution (which is the distribution of a continuous random variable), See fig,2.8.
2.2.6. Mathematical expectation and variance of a simplest flow
Let define the mathematical expectation of a batch of goods arriving during interval [0,t) :
MK =Λ (t) = Σ K=0∞ KPK (t) = {Σ K=0 ∞ K ((λ t) k/..K!) e− λ t}
It is an expression of the initial moment of the first order.
The first term of the sum K=0 is zero, therefore
the summation can start from K=1 :
MK =Λ (t) = Σ 𝐾=1∞ {Σ 𝐾=1 ∞ K ((λ t) k/.. K!) e− λ t}} = λ t e− λ t {Σ k=1 ∞ ((λ t) k-1 /. (.K-1)!) e− λ t}.
If denote K−1=r, then using the McLaren series we get:
Λ (t) = λ t e− λ t {Σ 𝑟=0 Λ (t) =∞ ((λ t) r/r!)} =𝜆𝑡
But on the other hand: by definition for a stationary flow Λ (t) =μ⋅t..on the other hand: by definition for a stationary flow Λ (t) =μ⋅t.
Consequently, for the simplest flow, the intensity is numerically equal μ=λ to the parameter.
The variance of a random variable, distributed according to the Poisson law, will be determined from the expression:
DK= (Σ 𝐾=0∞ [K−Mk] 2Pk) = α 2 — M2k
where
M K is the mathematical expectation, M K =Λ(t)=λ⋅t,
α 2 is the initial moment of the second order.
By definition:
α2 =ΣK=0∞ K 2PK
α 2=Σ𝐾=0∞K 2 {(λ⋅t) K/K!} e− λ t=λ⋅t⋅ Σ 𝐾=1∞K⋅ [(λ⋅t) 𝐾−1/ (K−1)!] ⋅
e− λ t =λ⋅t⋅ Σ 𝐾=1 ∞ (K−1+1) ⋅ [(λ⋅t) 𝐾−1 / (K−1)!] =
=λ⋅t⋅ [λ⋅t⋅ Σ 𝐾=1 ∞ (K−1) — [(λ⋅t) K−1/ (K−1)!]
Been proven that:
Σ 𝐾=1 ∞ [(λ⋅t) 𝐾−1 / (K−1)!]] = e -𝜆t {Σ 𝑟=0 Λ (t) =∞ ((λ⋅t) r/r!)} = λ⋅t
As well as
Σ 𝐾=1 ∞ [(λ⋅t) 𝐾−1 / (K−1)!] e -𝜆t= e -𝜆t {Σ 𝑟=0 Λ (t) =∞ ((λ⋅t) r/r!) =
=e− λ⋅t ⋅e λ⋅t =1
therefore:
α2=λ⋅t⋅ [λ⋅t+1]
The dispersion of the simplest flow:
DK=α2−MK2 =λ⋅t⋅ (λ⋅t+1) (λ⋅t) 2=λ⋅t
Thus, for a simplest flow of goods the variance is equal to mathematical expectation:
M K=DK=λ⋅t
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.