
Бесплатный фрагмент - История языком математики
Сборник метапредметных задач
ВВЕДЕНИЕ
Российские школьники участвуют во многих международных исследованиях качества образования и успехов школьников по отдельным дисциплинам. Зачем это нужно? Во-первых, участие в международных исследованиях помогает достаточно объективно оценить уровень образования и сравнить его с другими странами. Во-вторых, если исследование проводится на международном уровне, это значит, что для оценки уровня образования используются самые современные мониторинговые технологии. И Россия может использовать этот опыт в проведении собственных исследований на федеральном и региональном уровнях.
В данном пособии речь пойдет о Международном исследовании PISA.
Международная программа по оценке качества обучения PISA (Programme for International Student Assessment) проводится раз в 3 года, начиная с 2000 г., и проходит под патронажем Организации экономического сотрудничества и развития. Цель этого масштабного тестирования — провести оценку грамотности 15-летних школьников в разных видах учебной деятельности: естественнонаучной, математической, компьютерной и читательской.
PISA и функциональная грамотность
В исследование PISA включены задания разного типа. Почти половину из них составляют вопросы, предполагающие свободные ответы. А есть вопросы с определённым, нерасширяемым списком ответов. Это значит, что ученик должен выдать самостоятельный ответ, который будет ограничен конкретными словами или числами. Почти треть всех заданий в тесте составляют вопросы с готовыми вариантами ответов. Главное отличие программы PISA от ЕГЭ, ОГЭ и других российских тестов заключается в том, что она, в первую очередь, оценивает возможность школьников руководствоваться здравым смыслом и логикой при выполнении нестандартных задач. В этом отношении можно сказать, что PISA следует современным образовательным трендам, ведь способность учеников применять школьные знания в жизни — это важнейший аспект функциональной грамотности и навыков XXI века. Задания PISA проверяют не заученный материал по биологии, географии, физике и обществознанию, а владение учеников компетенциями в различных контекстах этих предметов и межпредметного взаимодействия: здоровье человека, природные ресурсы, окружающая среда, экология, открытия в области науки и технологии. Существуют интерактивные задания, направленные на наблюдение за каким-то объектом, в которых нужно сделать вывод о том, как функционирует этот объект. Есть задания с аналитическим решением, в которых стоит задача предусмотреть дальнейшее развитие событий или действие каких-то предметов.
В 2015 году появились в PISA и задания для коллективного выполнения — коллаборативные. В таких задачах предусмотрено совместное решение проблем. В качестве партнёров выступают виртуальные помощники, с которыми можно обсуждать, анализировать и решать заданную проблему: что-то организовать, создать, придумать, переделать или наладить. Такие задания показывают, как ученик взаимодействует с партнёром, как распределяет обязанности, и умеет ли договариваться.
Результаты в россии
Как в PISA показывают себя школьники из России.
К сожалению, результаты российских школьников в этом исследовании далеки от первых мест — за всё время Россия ни разу не вошла даже в двадцатку стран по трём показателям.
Но надо признать, что в последнее время нашей стране всё-таки удалось немного улучшить свои результаты. Российское Министерство образования решило сделать приоритетными другие направления учебной деятельности и объявило, что коммуникация, совместная работа и умение выстраивать свою деятельность станут ключевыми навыками, развитию которых должно способствовать обучение в школе.
Галина Ковалёва, координатор PISA в России, отмечает: низкие результаты теста в нашей стране связаны с тем, что учителя превосходно обучают предмету, однако не замечают, как знания по этому предмету усваивают отдельные ученики в классе. Кроме того, Ковалёва говорит, что российская система образования заметно отличается, например, от финской (а Финляндия почти всегда лидирует в PISA). У нас существуют целые школы для способных детей, но при этом отстающие ученики оказываются совершенно «заброшенными». В Финляндии же нет «лицейских» классов и школ «с уклоном»: одарённым школьникам разрешено заниматься самостоятельно, а для отстающих разрабатываются специальные индивидуальные программы обучения.
К PISA можно относиться по-разному. Конечно, в этой системе есть свои нюансы, просчёты и даже ошибки. Как и большинство систем оценки знаний, тестирование PISA несовершенно, и слепо гнаться за топовыми позициями в международном рейтинге было бы не самым умным решением для нашей страны. Но игнорировать итоги тестирования и вовсе глупо, ведь изначально исследования PISA направлены не просто на оценку достижений учеников, а на выявление слабых мест в системе школьного образования страны в целом. Результаты PISA — это результаты владения новыми важными компетенциями, ставшими не просто трендами международного образования, а ключевыми навыками современного человека, от которых зависит успех, реализация творческого потенциала и полноценное взаимодействие с обществом.
Исследования в области математической грамотности
Исследование PISA в области математической грамотности.
В данном пособии мы разработали задачи для подготовки к прохождению оценки математической грамотности обучающихся.
Что же такое математическая грамотность?
Математическая грамотность.
Основой высокого уровня математического образования на разных ступенях обучения является математическая грамотность подрастающего поколения. Поэтому обеспечение математической грамотности школьников является первоочередной задачей в деле обеспечения добротности школьного математического образования. А это является основой добротности математического образования в профессиональной школе.
Понятие математической грамотности начало формироваться в конце ХХ столетия в исследованиях Международной ассоциации по оценке учебных достижений учащихся ІЕА. В этих исследованиях под математической грамотностью понимали «готовность выпускников средней школы справляться с жизненными проблемами, для решения которых нужно использовать некоторые математические знания».
Здесь под математической грамотностью понимается «способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину».
Более детально содержание этого понятия экспертами уточнено следующим образом.
Под математической грамотностью понимается способность учащихся:
• распознавать проблемы, которые возникают в окружающей действительности и могут быть решены средствами математики;
• формировать эти проблемы на языке математики;
• решать эти проблемы, используя математические факты и методы;
• анализировать и использовать математические методы решения;
• интерпретировать полученные результаты с учетом поставленной проблемы;
• формулировать и записывать результаты решения.
Из вышесказанного рождается термин функциональная математическая грамотность, которая предполагает способность учащегося использовать математические знания, приобретенные им за время обучения в школе, для решения разнообразных задач межпредметного и практико-ориентированного содержания, для дальнейшего обучения и успешной социализации в обществе.
Главное отличие в конкретизации понятия математической грамотности в указанных исследованиях связано с отличиями между умениями и способностями. Но несмотря на это существенное отличие, толкования понятия математической грамотности имеют одинаковый главный признак — готовность человека применять математику в различных ситуациях, связанных с жизнью.
Именно поэтому, задания, призванные исследовать состояние математической грамотности учеников, в подавляющем большинстве имеют четко выраженную прикладную направленность и их решение предусматривает, прежде всего, владение учащимися приемами деятельности прикладного характера.
Математическая грамотность 15-летних обучающихся является одним из главных направлений международного исследования PISA. Международный тест PISA не замеряет академические знания обучающихся — содержание школьных курсов математики, которые освоил 15-летний школьник. Уникальность инструментария международного экзамена в том, что он определяет те умения обучающихся, которые будут способствовать успешности выпускника школы к полной реализации себя как личности во взрослой жизни.
Оценочная технология теста PISA в направлении математическая грамотность проверяет способности использования данной возрастной категорией математических знаний в ситуациях, требующих логических подходов и математической интуиции.
Таким образом, международные эксперты данного проекта оперируют таким педагогически-практическим понятием как «математическая грамотность». Прежде всего, данное понятие определяется, как способность человека использовать знания из области математики для обоснования личного выбора решения различных реальных жизненных ситуаций.
Тем самым основными тезисами понятия «Математическая функциональная грамотность» является способность обучающихся:
— выявлять проблемы, возникающие в окружающем мире, посредством решения математических задач
В исследованиях PISA понятие математической грамотности уточняется следующим образом. Под математической грамотностью понимается способность учащихся:
— распознавать проблемы, возникающие в окружающей действительности и которые можно решить средствами математики;
• формулировать эти проблемы на языке математики;
• решать эти проблемы, используя математические факты и методы;
• анализировать использованные методы решения;
• интерпретировать полученные результаты с учетом поставленной проблемы;
• формулировать и записывать результаты решения.
Как правильно составить компетентностно-ориентированные задачи? Для составления данных задач учителю необходимо изучить аспекты ключевых компетентностей. Аспекты ключевых компетентностей — это универсальные по отношению к объекту воздействия способы деятельности, входящие в состав компетентностей. А способами деятельности учащихся нужно обязательно обучать.
При решении компетентностно-ориентированных заданий учащиеся должны осуществлять такие виды деятельности как: учение (как основа для дальнейшего образования), взаимообучение, совместное изучение, совместное обсуждение, исследования (в том числе совместные), обмен опытом, проектирование, программирование индивидуальных образовательных программ.
Уровни математической компетентности
Уровни математической компетентности.
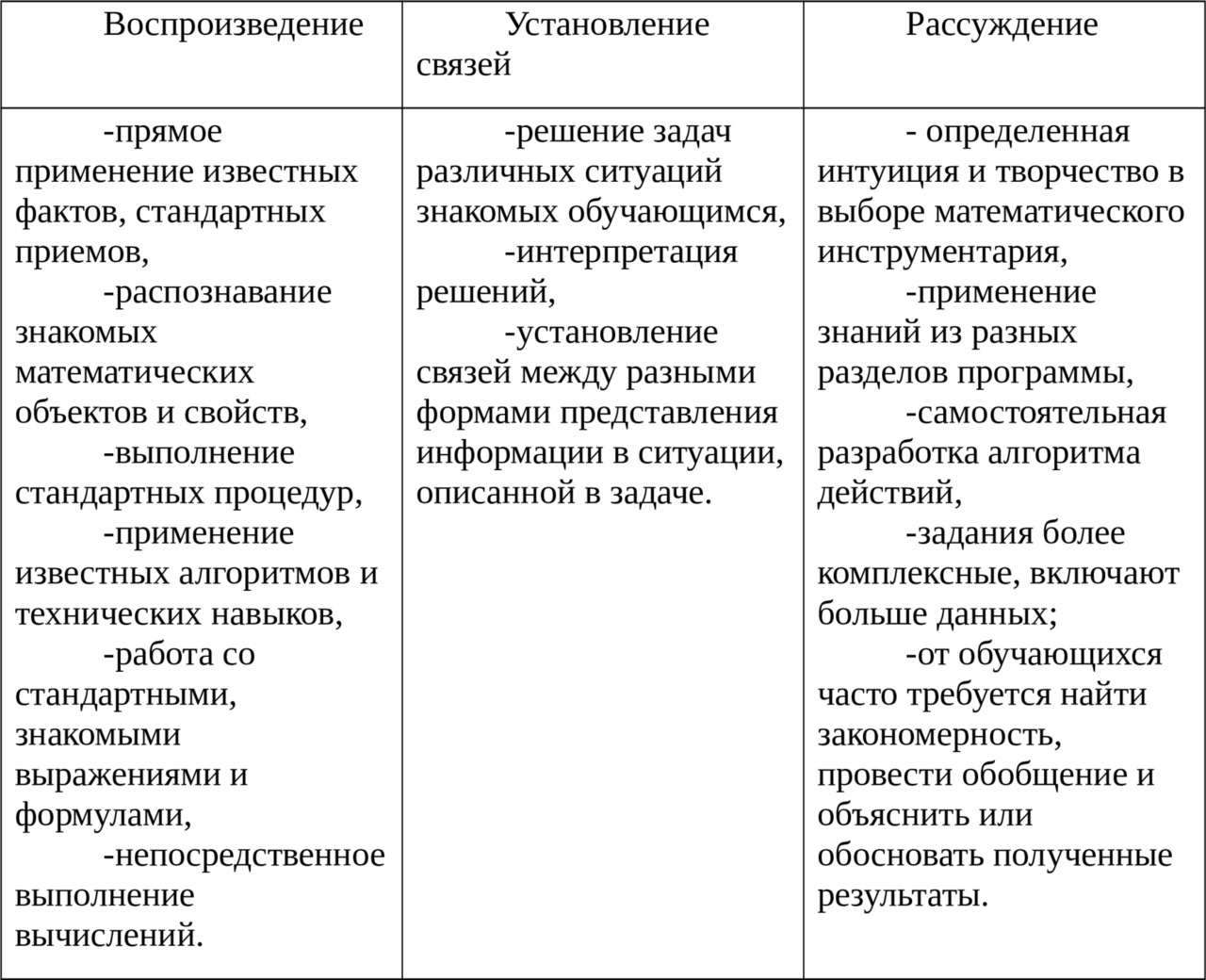
Принято три уровня математической компетентности: уровень воспроизведения, уровень установления связей, уровень рассуждений.
Первый уровень (уровень воспроизведения) — это прямое применение в знакомой ситуации известных фактов, стандартных приемов, распознавание математических объектов и свойств, выполнение стандартных процедур, применение известных алгоритмов и технических навыков, работа со стандартными, знакомыми выражениями и формулами, непосредственное выполнение вычислений.
Второй уровень (уровень установления связей) строится на репродуктивной деятельности по решению задач, которые, хотя и не являются типичными, но все же знакомы учащимся или выходят за рамки известного лишь в очень малой степени. Содержание задачи подсказывает, материал какого раздела математики надо использовать и какие известные методы применить. Обычно в этих задачах присутствует больше требований к интерпретации решения, они предполагают установление связей между разными представлениями ситуации, описанной в задаче, или установление связей между данными в условии задач.
Третий уровень (уровень рассуждений) строится как развитие предыдущего уровня. Для решения задач этого уровня требуются определенная интуиция, размышления и творчество в выборе математического инструментария, интегрирование знаний из разных разделов курса математики, самостоятельная разработка алгоритма действий. Задания, как правило, включают больше данных, от учащихся часто требуется найти закономерность, провести обобщение и объяснить или обосновать полученные результаты.
Характеристика этих уровней дает возможность прийти к таким выводам:
1. компетентность проявляется в решении задач, нуждающихся в применении приобретенных умений в условиях, несколько отличающихся от знакомых учащимся. При этом не предусматривается значительный объем математических умений, нестандартность заданий обеспечивается, прежде всего, их прикладной направленностью;
2. уровни компетентности отличаются составом когнитивных приемов деятельности (распознавание, воспроизведение, установление связей между данными в условии задачи, интерпретация решения, установление закономерностей, проведения обобщения и т. п.).
Итогом тщательного анализа заданий исследования PISA является выделение конкретных приемов деятельности, владение которыми характеризует достижение учащимся определенного уровня компетентности. Первый уровень включает воспроизведение математических фактов, методов, выполнение стандартных процедур, алгоритмов, работу с формулами, вычисления. Для проверки достижения первого уровня применялись несложные задания, с которыми учащиеся имели возможность познакомиться в рамках школьного курса математики. Второй уровень предусматривает установление связей, интеграцию материала, ориентирование в нестандартных ситуациях, интерпретацию. Этот уровень требует, кроме математических рассуждений, обобщения, интуиции, больше творчества и самостоятельности. Для проверки достижения третьего уровня были задействованы более сложные задания, решение которых предусматривает выделение и формулировку проблемы, построение математической модели, обобщения, интерпретацию.
Как видим, для определения уровня математической компетентности исследовалось владение учащимися определенными приемами деятельности, входящими в состав такого обобщенного приема деятельности как математическое моделирование.
Приведенное выше описание математической грамотности в международных исследованиях и уровней ее овладения (уровней компетентности) дает возможность сделать главный вывод о том, что приоритетным направлением усовершенствования математического образования является обеспечение математической грамотности высокого уровня компетентности.
Именно обеспечение практической и прикладной направленности математического образования и составляет сущность компетентностного подхода к обучению математике. Имеется в виду направленность на решение жизненных проблем, к действиям в реальных условиях, в различных плоскостях: когнитивной, операциональной, эмоционально-ценностной.
Обеспечение математической грамотности высокого уровня компетентности заключается в гармоничном формировании трех приемов деятельности:
1. моделировать с помощью математики объекты окружающего мира и отношения между ними;
2. оперировать определенным составом математических знаний и умений;
3. создавать стратегии решения задач.
Целенаправленное формирование умений решать задачи вообще, математические в частности, является, безусловно, одним из важнейших путей усовершенствования образования. А это, в свою очередь, связано с формированием навыков анализа условия задачи, поиска путей её решения, осмысления результатов решения.
Формирование определенной системы математических знаний всегда было в центре внимания в математическом образовании. Объем этой системы является слишком большим с общеобразовательных позиций, а качество владения ими — недостаточно высоким. А главное, формирование этой системы знаний и умений не связана органически с формированием умений применять математику и стратегией решения задач.
Успешное выполнение контекстных заданий может быть обеспечено только при ориентации учебного процесса на решение подобных задач.
Уровни математической компетенции в исследованиях PISA
Сборник задач по подготовке к исследованиям в области математической грамотности
Инструкция по выполнению заданий
Каждая группа заданий PISA рассматривает личностный, социальный или глобальный контекст и предполагает диагностику различных уровней математической грамотности учащихся.
При выполнении заданий предлагается руководствоваться следующей инструцией.
1. Внимательно прочитайте предложенные задания и извлеките основную информацию.
2. Обратите внимание на рисунки, чертежи, графики к задачам и таблицам, облегчающие понимание процесса.
3. Продумайте, какие упрощающие предложения облегчают решение задачи.
4. Попытайтесь сделать схематический чертеж или рисунок, это всегда облегчает ход рассуждений. Помните, что хорошо составленная схема — половина успеха при решении задачи.
5. В большинстве случаев задачу целесообразно решать в общем виде, обозначив все величины соответствующими буквами и производя с ними нужные выкладки.
6. Получив решение в общем виде, попытайтесь убедиться в его разумности, проведя анализ размерностей или сравнив его с уже решенной аналогичной задачей.
В международных исследованиях PISA задания по математике распределены по шести уровням:
1) задания, где дана вся соответствующая информация, и вопрос четко сформулирован. Учащиеся могут отождествлять информацию и осуществить общепринятые методы, в соответствии с определенными ситуациями;
2) задания, для решения которых учащиеся могут применять основные алгоритмы, формулы, способы и методы;
3) задания, которые требуют последовательного выполнения;
4) задания, в которых даны конкретные модели для конкретной ситуации;
5) задания, для решения которых нужно определять, сравнивать, оценивать, создавать определенную стратегию решения проблем;
6) задания, в которых рассматриваются ранее не существовавшие ситуации; развивают новые методы.
В заданиях по математической грамотности рассматриваются задания с одним сюжетом, но ученику предлагается несколько вопросов различного уровня сложности, от простых на вычисление до вопросов 5-го и 6-го уровней сложности, при выполнении которых необходимо использовать знания из нескольких разделов математики или предметов естественнонаучного цикла, а также требуются творчество и логические рассуждения. При выполнении заданий международных исследований PISA рассматриваются и структурированные вопросы, т.е. содержание вопросов подбирается таким образом, чтобы в процессе их последовательного выполнения следующий вопрос связан с ответами на предыдущие вопросы, а также важно умение учащихся анализировать информацию, представленную в виде таблиц, диаграмм, графиков.
Задачи сборника разбиты на 4 области содержания:
— Изменения и зависимости (алгебра);
— Пространство и форма (геометрия);
— Неопределенность и данные (теория вероятности и статистика);
— Количество (арифметика).
Особенностью задач данного сборника является то, что они составлены на основе краеведческого материала. Одной из основных задач воспитания, стоящих на современном этапе перед учителем, является воспитание у школьников любви к Родине, родному краю, чувства гордости за свою Родину. Применение на уроках местного краеведческого материала позволяет успешно решать эту задачу.
Применение краеведческих материалов при изучении математики имеет целый ряд положительных эффектов:
— обеспечивает рост интереса к предмету;
— способствует духовно-нравственному, патриотическому, гражданскому воспитанию учащихся;
— даёт возможность интеграции математических и исторических знаний;
— у учащихся формируются ключевые компетенции — универсальная целостная система знаний, умений, навыков, опыт самостоятельной деятельности и личной ответственности;
— закрепляются вычислительные навыки, формируется логическое мышление.
Удачи вам в решении задач!
Налог на бороду
С 1705 года все мужское население было обязано чисто бриться.

Сумма налога за ношение бороды отличалась в зависимости от сословной принадлежности мужчины. Было установлено четыре разряда налога, которые накладывались как на придворных бояр, так и на простых людей.
Бояре и чиновники платили 600 рублей в год, купцы платили 100рублей в год, посадские люди платили 60 рублей в год, а обычные жители платили по 30 рублей в год.
Вопрос 1
Во сколько раз меньше платили купцы по сравнению с дворянами и чиновниками?
А) 500 Б) 6 В) 3
Ответ:_________.
Вопрос 2
Крестьянин Иван из Москвы решил сбрить бороду. Какую сумму он сэкономит на уплате налога за 5 лет?
Ответ:____________.
Вопрос 3
После 1715 года были внесены некоторые изменения в указ, которые заключались в том, чтобы снимать единую сумму пошлину с каждого бородача, независимо от его сословия, которая составляла 50 рублей.
На сколько процентов уменьшится поступление налога в казну от посадских людей, если их количество в Москве останется приблизительно на том же уровне?
Ответ:____________.
Задача относится к области «Неопределенность и данные»
Место для решения задачи:
Поташ

Историческое ядро России — лесистый район вокруг и севернее Москвы. Вплоть до XVII века русские избегали открытых пространств, да и после заселение степей шло медленно. Поэтому русский человек жил в лесу и лесом, который давал ему материал для постройки жилища, отопления, орудий труда и утвари, транспорта и обуви — лаптей, для которых драли лыко.
Важнейшим предметом торговли был не круглый лес и пиломатериалы, а продукты глубокой переработки древесины. Вывозить ее в Европу было не так выгодно, как товары с добавленной стоимостью — поташ, смолу и деготь. Именно лесохимия стала первой отраслью промышленности России в значимых масштабах.
Из дерева получали уголь, деготь, поташ, скипидар, канифоль, вар (корабельную смолу), уксусную кислоту и многое другое.
Поташ (карбонат калия) вырабатывался из золы. Он шел на изготовление мыла, стекла и селитры для пороха. Россия уже в начале XVII века наладила производство этой соли, ставшей одним из наиболее интересных для иностранных купцов товаров.
Вопрос 1
Для получения 1,2 кг поташа требуется сжечь тонну древесины. Сколько тонн древесины надо сжечь, чтобы получить 125 кг поташа?
А) около 104 т
Б) около 120 т
В) около 500т
Ответ:_______.
Вопрос 2
Голландские, фламандские и английские ремесленники использовали поташ в основном как замену квасцам при окраске тканей.
Бочка русского поташа в 18 веке стоила в Нидерландах от четырех до восьми рейхсталеров.
Какое наименьшее количество бочек поташа может купить в Нидерландах немецкий купец, если у него в наличии 1200 шиллингов (1 рейхсталер = 32 шиллингам)?
Ответ:___________.
Задача из области: «Количество»
Место для решения задачи:
Корабельные рощи
Экспорт собственно леса был сравнительно невелик в XVII–XVIII веках.

Лесная промышленность, понимаемая как лесозаготовки и лесоторговля, постоянно наращивала обороты. Строительство влекло за собой потребность в бревнах и тесе, а также в дровах для отопления.
Лесное хозяйство требовало соответствующего законодательства. До Петра I систематически охранялись только засечные черты, оборонявшие Русь от набегов кочевников. Император же передал леса в ведение Адмиралтейств-коллегии, поскольку главная их ценность рассматривалась им с точки зрения постройки кораблей. За незаконную рубку корабельных рощ по его указу полагалась смертная казнь.
Вопрос 1
Голландский предприниматель Вернер Мюллер в 1670-м году получил монополию на 10 лет на вывоз из Архангельска мачтовых стволов. За каждую мачту он платил в казну по 10 рублей, а в год отправлял два-три корабля с 150–200 мачтами.
Какую максимальную прибыль может получить казна от предпринимательской деятельности Мюллера по вывозу мачтовых стволов за год?
Ответ:________.
Вопрос 2
В 1675 году пуд хлеба в среднем стоил 30 копеек. Оцените, во сколько раз снизилась покупательская способность рубля, если в начале 2019 года 1 кг хлеба в среднем стоит 72 рубля. Справка: 1 пуд равен 16,38 кг.
Ответ:_________.
Вопрос 3.
Используя информацию о снижении покупательской способности рубля в 2019 году по сравнению с 1675 годом, оцените, какую максимальную прибыль могла получить казна от предпринимательской деятельности Мюллера по вывозу мачтовых стволов, если бы объем вывозимого товара остался на прежнем уровне (смотри вопрос 1)?
Ответ:________.
Задача из области: «Количество» и «Изменения и зависимости».
Место для решения задачи:
Башни Московского Кремля
Московский Кремль в настоящее время насчитывает 20 башен.
Познакомьтесь с данными о высоте нескольких из них (в метрах):
— Водовзводная — 61,25;
— Спасская — 71;
— Никольская — 70,4;
— Троицкая — 80;
— Угловая
Арсенальная — 60,2;
Сенатская — 34,3;
Кутафья — 13,5.
Вопрос 1. Какая башня Кремля является самой высокой и какова ее высота в метрах?
Ответ:__________.
Вопрос 2. Какова разница в высоте (в метрах) между самой высокой и самой низкой башней, если данные о них содержатся в представленной диаграмме?
Ответ:________.
Вопрос 3. Известно, что 3 башни, представленные на диаграмме, были построены в 1491 году. Перечислите их названия, если известно, что первая из них имеет вторую по величине высоту, вторая ниже нее на 0,6 м, а третья на 20,8 м выше самой низкой башни.
Варианты:
а) Троицкая, Никольская, Кутафья
б) Водовзводная, Сенатская, Никольская
в) Спасская, Никольская, Сенатская.
Ответ:_______.
Задача из области: «Изменения и зависимости».
Место для решения задачи:
Рака Александра Невского
Мемориальный комплекс раки Александра Невского — выдающееся многосоставное произведение русского декоративно-прикладного искусства XVIII века в стиле барокко, выполненное из серебра весом 1,5 тонны в царствование императрицы Елизаветы Петровны, в комплекс которого входит деревянная, отделанная серебром небольшая рака, выполненная в царствование Петра I и Ивана V.

С 1922 года рака находится в Эрмитаже (в парадном зале Невской анфилады). В 2019 году завершена реставрация.
Как писал искусствовед В. Б. Сапунов: «Рака Александра Невского сразу стала общепризнанным чудом молодой столицы. Можно с уверенностью сказать, что она — единственное в мире столь монументальное сооружение из высокопробного серебра».
Рака была изготовлена в 1746—1753 гг., на работу было выделено серебро с Колыванских заводов.
В книге В. Б. Сапунова можно найти такие сведения: «30 августа 1753 года создание огромного монументального сооружения было завершено. Его вес достиг 89 пудов, 22 фунтов, 1 с третью золотника».
Вопрос 1. Сколько кг железа было потрачено на изготовление раки, если известно, что 1 пуд=40 фунтам=16,38 кг, а 1 золотник равен 4,266 г?
а) около 5200 кг
б) около 250 кг
в) около 1625 кг
Ответ:____________.
Вопрос 2. В какую сумму обошлась рака Александра Невского казне, если пуд серебра в работе стоил 906 рублей 56 копеек?
а) около 70 500 рублей
б) около 81 300 рублей
в) больше 100 000 рублей
Ответ:_____________.
Задача из областей: «Изменения и зависимости» и «Количество»
Место для решения задачи:
Ночной дозор

Воротник Иоанн, житель Воротниковой слободы, служит сторожем крепостных ворот одного из укреплений Земляного города (Земляным городом XVII — XVIII вв. называли часть Москвы между Бульварным и Садовым кольцами, а также Заяузье и Замоскворечье в пределах Садового кольца).
Земляной город достигает в своей окружности 14 верст (1 верста=1066,8 м).
Вопрос 1
Иоанн в ночь своего дежурства должен обойти Земляной город с дозором. Дежурство Иоанна начинается в 2 часа утра, а обойти Земляной город необходимо до 7 часов утра. Воротник прикинул, что обойти это расстояние он может со скоростью 5 км\ч. При движении с этой скоростью остается время на то, чтобы поесть и отдохнуть. Определите самое позднее время, когда Иоанн может начать обход Земляного города.
А. 3 утра
Б. 4 утра
С. 5 утра
D. 2 утра
Ответ:______________.
Вопрос 2
Во время обхода Земляного вала воротник Иоанн сделал 37500 шагов. Оцените среднюю длину шага воротника. Дайте ответ в см.
Ответ:____________.
Вопрос 3
С 1783 года Земляной вал становится одним из любимых мест для прогулки москвичей. Известно, что в период с 1 мая по 1 июля в Земляном валу совершили прогулку около 25000 москвичей.
Сколько примерно в среднем людей прогуливаются в валу ежедневно?
А.600
В.850
С. 410
D. 560
Ответ:______________.
Содержательная область «Количества» и «Изменения и зависимости», контекст задания «общественный».
Место для решения задачи:
Поле Куликово

Куликово поле — урочище на водоразделах Окско-Донского междуречья, представляющее собой протяжённый географический объект со степной растительностью. Обширность Куликова поля всегда вызывала серьёзные затруднения в точной научной локализации конкретного места исторической битвы. Площадь места непосредственного боевого столкновения по новейшим реконструкциям около 3 км². Согласно «Сказу о Куликовской битве» ширина Куликова поля составляет 75% его длины.
Вопрос 1: Найдите размеры места непосредственного сражения на Куликовском поле.
Ответ:________.
Вопрос 2: Согласно тому же «Сказу о Куликовской битве» на поле сошлись 2 таких больших армии, что «невозможно было вместить их всех на том поле Куликовом».
Сколько же воинов принимало участие в битве? Вопрос этот спорен. Но постарайтесь приблизительно определить, какое максимальное количество войнов могло поместиться на Куликовом поле?
При подсчете можно пользоваться классификацией «плотности толпы» Джекобса:
а) «редкая толпа» — 1 чел. на 1 квадратный метр;
б) «плотная толпа» — 2,5 чел. на 1 квадратный метр;
в) «очень плотная толпа» — 4 чел. на квадратный метр.
Ответ:_________
Область задания: «Пространство и формы»
и «Неопределенность и данные»
Место для решения задачи:
Экскурсия в аптекарский огород

В 1706 году по указу Петра I на тогдашней северной окраине Москвы, за Сухаревой башней, был заложен огород для выращивания лекарственных трав. С этого огорода сад и ведет свою историю.
В медицинском саду не только выращивали, заготавливали лекарственные травы и на месте готовили из них лекарства (об этом косвенно говорят находимые в земле старинные аптекарские пузырьки), но и обучали студентов, будущих врачей.
Студент Сергей был приглашен своими друзьями Иваном и Степаном, работниками «Аптекарского огорода» в это интереснейшее место. Во время прогулки по саду Степан рассказал Сергею о лиственнице, которую, по преданию, посадил сам Петр I при открытии «Аптекарского огорода. Исследования лиственницы доказали, что ей действительно около 300 лет и она теоретически могла быть посажена Петром I.
Неподалеку от сибирской красавицы растёт белая ива. Про нее легенд неизвестно, но между Иваном и Степаном разгорелся спор о том, могла ли быть и эта белая ива быть посажена Петром I. Иван считает, что ива слишком молода и не может быть посажена Императором, а Степан считает, что ива-ровесница лиственницы, посаженной Петром. Помоги Сергею разрешить спор друзей.
Вопрос 1.
Изучив способы определения возраста деревьев, Сергей решил использовать бур Пресслера. Возрастной бур — что-то вроде полого сверла — ввинчивают в ствол таким образом, чтобы, по возможности, попасть в сердцевину. Потом на вынутом из ствола «карандаше» из древесины просто считают годичные кольца. Для измерения требуется бур, длина которого не меньше семидесяти пять процентов от диаметра ствола. Таким образом, в дереве образуется лишь небольшое несквозное отверстие, которое в скором времени закрывается смолами или соком, и не вредит дереву.
Сергей в специализированном магазине «Лесное царство» покупает бур Пресслера.

Ассортимент магазина включает в себя буры следующей длины и диаметра:
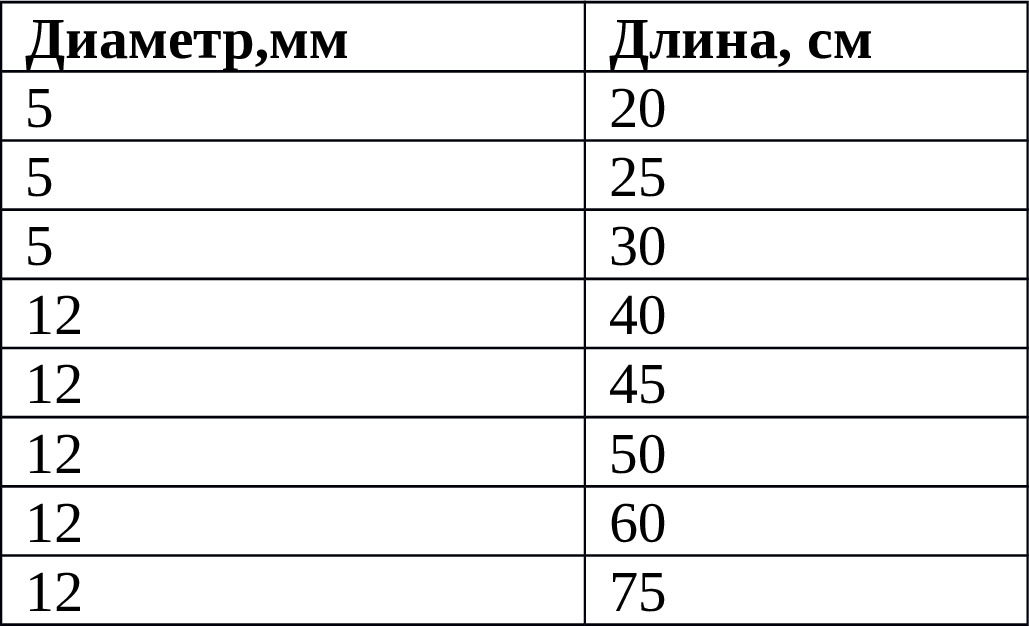
Помоги ему определиться с длиной бура, если обхват ствола ивы составляет 2,30 метра.
Ответ:_____________________.
Вопрос 2
Чтобы извлечь образец для определения возраста дерева, Сергею необходимо просверлить буром ствол на высоте 1,4м от земли до сердцевины ствола. На какую приблизительно глубину необходимо «просверлить» буром дерево?
Ответ:
а) 0,4 м
б) 1 м
в) 0,68 м
Ответ:____________.
Вопрос 3
Сергей подсчитал количество годовых колец на высверленном образце. Их оказалось 126. Кто прав в споре Иван или Степан?
Ответ:________________.
Вопросы 1 и 2 можно отнести к области «пространство и формы», вопрос 3-к области «Неопределенность и данные».
Место для решения задачи:
Красная площадь
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.
