Бесплатный фрагмент - Геометрия homeschooling

Предисловие

Это предисловие предназначено для родителей. Когда моему Никите пришла пора идти в школу (шел 1988 год), он заболел, и надо было срочно менять климат. Мы переехали из Москвы в далекую казацкую станицу Краснодарского края, и там не было хорошей школы. Уже шла перестройка, и я решил учить сына всему сам (благо было у меня образование преподавателя математики, а у нашей мамы — психолога). Потом выросли остальные дети (еще два мальчика и две девочки). Так возникла наша домашняя школа.

Школьные учебники для домашней школы не очень подошли, и я стал сочинять свои. И это мне понравилось. Мы много рисовали, рассуждали, читали вместе, гуляли в полях и лесах, наблюдая природу. И вот прошли годы, дети выросли, закончили институты и колледжи, я тоже набрался опыта преподавания в школе и в методике. И сейчас предлагаю вам уже значительно усовершенствованные те самые мои первые учебники, которые писал в те годы.

Если вы будете их использовать в обучении детей в рамках семейной формы обучения, то помните, что они не заменят школьных учебников, ведь нужно поддерживать связь с жизнью. Хотя, уверен, они облегчат жизнь, поскольку изложение в них максимально простое и понятное. Я специально придумал такие способы объяснения, которые сочетают полную современную строгость, соединяя аксиоматику с элементарностью доказательств. Я математик и воспринимаю учебник математики как математическую задачу по упрощению математического материала без потери строгости.

Много лет я вел в «Учительской газете» математическую тематику. И если кто помнит, там я пропагандировал колмогоровские методы преобразований. Но теперь я все же считаю, что преобразования удобно вводить в курс геометрии только с 8-го класса, и сразу целиком все типы симметрий. В этой же книжке с самого начала довольно красивым, полагаю, способом доказываются три признака равенства треугольников, и на этой основе быстро и просто — все остальные теоремы программы первого года систематического обучения геометрии. Я думаю, и дети, и взрослые будут рады, что теоремы доказываются настолько просто и коротко. Посмотрите, например, доказательство 3-го признака равенства треугольников. Оно умещается буквально на одной строке.

Соотношение с ФГОСами. В настоящий момент (декабрь2019) ФГОСЫ на 2020/21 еще не принты. Однако можно предположить, что они останутся такими же, как и в проекте, и содержание учебника будет соответствовать ФГОСам за исключением замечания о вписанных и описанных окружностях. Но, полагаю, абсурдно говорить о биссектрисах, высотах и т.д. треугольника, не изучив и это.

Учебник содержит только теоретический материал. Собираюсь написать также и задачник (но это в будущем). Пока можно использовать имеющиеся.

Автор.

ЧАСТЬ ПЕРВАЯ. ВВЕДЕНИЕ

Глава 1. Геометрические фигуры

Происхождение геометрии.

Геометрия как наука возникла в Древней Греции. Одним из первых ученых, который стал доказывать геометрические факты (теоремы) был Фалес Милетский (его портрет — на обложке этого учебника), который жил на рубеже 4 и 5 веков до нашей эры. До древних греков много геометрических фактов знали уже в Древнем Египте, но там еще не считали важным делом что-то доказывать: жрецы сказали, значит истина.

В дальнейшем, в 3 веке до н.э. геометрию изложил в своей книге «Начала» математик Евклид из Александрии. Все учебники геометрии с тех пор похожи на его «Начала». Евклид перечислил сначала аксиомы (простые и очевидные утверждения, которые не вызывают сомнений) и потом логически вывел все остальные положения геометрии (теоремы).

Планиметрия.

Геометрические фигуры бывают двух типов. Одни, например, треугольники или квадраты, можно нарисовать на чертеже. Все такие фигуры могут быть «помещены» на плоскость. Такие фигуры называются плоскими.

А вот, например, пирамиду, куб, шар на чертеже поместить невозможно, они не помещается в плоскости чертежа. Такие фигуры называются объемными.

Есть два раздела в геометрии. В одном изучаются плоские фигуры — это планиметрия (легко запомнить от слова «план»), в другом — объемные, это стереометрия. И начинаем мы — с фигур на плоскости, то есть с планиметрии.

Множество и точки.

Нам потребуется понятия множество и точка (элемент множества). Что такое точка, вы, конечно, представляете. Считается, что математическая точка такая маленькая, что у нее не просто маленькие размеры, но и вообще размеров нет. Такое представление о точке получается, как говорят, в результате абстракции, то есть отвлечения от каких-то свойств, в данном случае — от размера. Также можно сказать, что точка бесконечно маленькая.

Точка — это будет как бы кирпичик, из которого состоят все геометрические фигуры. Точки маленькие, но из них состоит все. Даже пустое пространство тоже состоит из точек. Вы уже знаете, что точки обозначают большими латинскими буквами. Обычно используют только первые буквы, но на всякий случай приведем весь латинский алфавит (хотя он такой же, как и английский, но названия букв немного другие). Рис.3. Иногда используют так называемые индексы — маленькие цифры снизу справа. Например, А1, А2 и т. д.

Теперь — понятие «множество». Это совокупность, собрание, коллекция чего-то. Есть множество букв в алфавите, множество черных кошек с белыми хвостами, Итак. Говоря, что геометрические фигуры состоят из точек, мы фактически утверждаем следующее: геометрические фигуры — это множества точек. Часть множества называют подмножеством. Например, множество кошек с белыми передними лапами — это подмножество множества кошек с правой передней белой лапой. А множество кошек с белой правой передней лапой и черным хвостом — подмножество кошек с белой передней правой лапой. Сами придумайте другие примеры множеств и подмножеств.

Окружность.

Мы определим окружность как множество точек на равном расстоянии от какой-то одной точки, называемой центром окружности. Циркуль (как вы знаете, это прибор для проведения окружностей) стали использовать древние греки в очень древние времена, задолго до Евклида или даже Пифагора (с этим ученым мы еще познакомимся). Изобретателем циркуля греки считали некоего Талоса, ему же приписывали и изобретение гончарного круга.

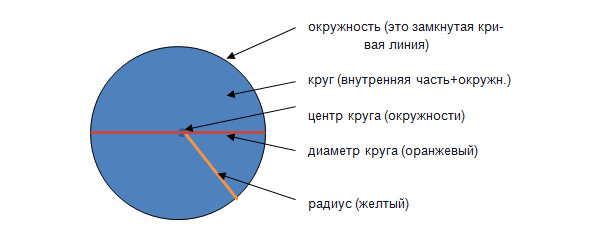
Окружность (рис.5) — это замкнутая кривая (то есть, когда ведешь по ней карандашом, приходишь в точку, с которой начал). Она разделяет плоскость на две части: внутреннюю и внешнюю. Внутреннюю часть с окружностью называют круг. Круг и окружность — это разные фигуры! Окружность — это граница круга. Отрезок, соединяющий центр окружности и любую ее точку, называется радиусом. Понятно, что все радиусы одной окружности равны. Отрезок, проходящий через центр и соединяющий две точки окружности, называется ее диаметром. Радиусом и диаметром также называются длины этих отрезков.

Именно с помощью циркуля греки стали рисовать окружности на сосудах. Вот один из таких сосудов (рис.6), этот стиль декорирования сосудов так и называется «геометрический стиль».

Для сложных архитектурных сооружений требовались разнообразные сочетания окружностей, треугольников, квадратов и т. д. Древние греки написали много книг, в которых изучались свойства этих фигур. Нам предстоит изучить самые главные такие свойства.

Глава 2. Определения

Математика предполагает прежде всего точность. Поэтому каждому новому понятию будем давать определение. Определить или дать определение тому или иному понятию — значит точно описать, что оно означает. Но наиболее простые понятия не определяются. Такие как точка и прямая.

Все фигуры, как мы уже говорили, состоят из точек. Если две фигуры имеют общие точки, то говорят, что они пересекаются в этих точках. Говорят также и о пересечении множеств точек. Например, две прямые могут пересечься в точке. А могут и не иметь общих точек или точек пересечения вообще. В этом случае они называются параллельными.

Также мы не определяем понятие расстояние между точками. Считаем ясным, что каждым двум точкам соответствует число, называемое расстоянием между ними. Расстояние можно измерить по линейке или с помощью какого-либо другого измерительного инструмента (в зависимости от величины расстояний). Это очевидно, поэтому понятие «расстояние» не определяется.

Для математика единица измерения не играет роли, она может быть любой (но все время одной и той же). Расстояние между двумя точками А и В обозначается AB как и отрезок АВ, как его длина и как прямая АВ. Удивительно, но путаницы не происходит.

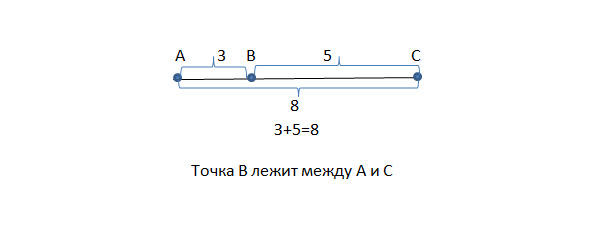
Лежать между.

Теперь — понятие лежать между (рис.7). Пусть есть три какие-нибудь точки: А, В и С. Если выполняется равенство АВ = AC+CB, то говорят, что С лежит между А и В.

Отрезок.

Отрезком АВ с концами А и В будем называть множество точек, лежащих между точками А и В. Длина отрезка — это расстояние между его концами. Отрезки называются равными, если у них равные длины. Как уже говорилось, длина отрезка также обозначается АВ.

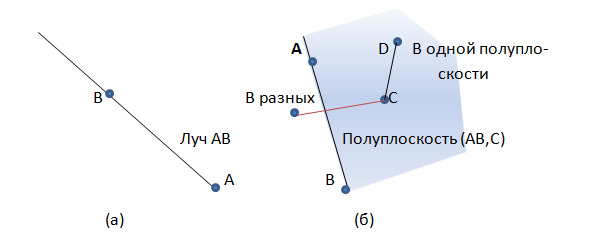
Луч.

Лучом ОА с началом О назовем множество всех точек, лежащих по одну сторону от О с точкой А (рис.8,а).

Что значит «лежать по одну сторону»? Это легко определить, имея понятие «лежать между». Две точки А и В лежат по одну сторону от точки С, если либо А лежит между С и В, либо В лежит между С и А Сама точка А принадлежит лучу ОА.

Полуплоскость.

Нам известно понятие плоскости, а теперь определим полуплоскость. Зададим какую-то прямую АВ. Теперь можно взять еще одну точку С, не лежащую на АВ. Любая точка D, такая, что отрезок CD не пересекает АВ считается лежащей с C в одной полуплоскости. Все точки, лежащие в одной полуплоскости с С, составляют полуплоскость. Обозначение — полуплоскость (АВ, С) Прямая АВ называется границей этой полуплоскости (рис.8б).

Угол.

Два луча с общей вершиной называются углом. Казалось бы, такое простое понятие, но тоже должно иметь определение. Пусть угол образован двумя лучами ОА и ОВ. Он обозначается ∡АОВ. Точка О — вершина угла, ОА и ОВ — его стороны. При обозначении ∡АОВ буква, обозначающая вершину, ставится между букв, обозначающих стороны. Углы на чертежах измеряются с помощью транспортира (рис.9). Если лучи образуют прямую, то такой угол называется развернутым.

Понятие меры угла также не определяется. Считается понятным, что каждому углу ставится в соответствие положительное число от 0 до 180. Причем развернутому углу как раз и старится в соответствие 180. Это градусная мера. Обозначается, как вы знаете, кружочком справа сверху. В принципе возможна другая мера — радиан (он равен приблизительно 57,3о), но по умолчанию предполагается у нас градус. Сейчас используют также так называемые грады (или гоны, что одно и то же), равные 1/100 части прямого угла. Обозначение 1g, 15g и т. д.

Поперечина.

Проведем еще один луч из точки О, например, луч ОС. Считается, что луч ОС проходит между сторонами ∡АОВ, если он пересекает какой-нибудь отрезок с концами на сторонах угла. Этот отрезок называется поперечиной. Рис. 10

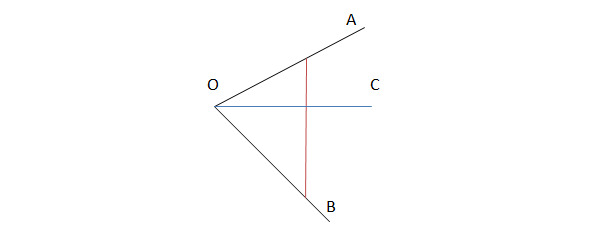
Эквидистантные поперечины.

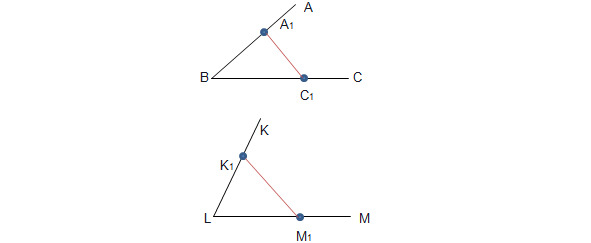
Поперечины двух углов называются эквидистантными, если отрезки, которые они отсекают на сторонах одного угла, равны отрезкам, которые они отсекают на сторонах второго угла. Пусть нам дан ∡ABC и ∡KLM. Откладываем на сторонах ∡ABC отрезки ВА1 и ВС1, а на сторонах ∡KLM отрезки LK1 и LM1. И пусть ВА1=LK1, в то время как ВС1= LM1. В этих случаях и говорят, что поперечины А1С1 и К1L1 эквидистантны.

Эквидистантные поперечины на рис.11 отмечены красным цветом.

Равенство углов.

Эквидистантные поперечины могут быть равными и не равными, как в случае на чертеже (рис.11). Если у двух углов существует хотя бы одна пара равных эквидистантных поперечин, углы называются равными.

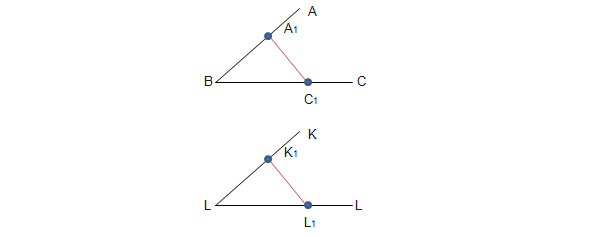
На рис.12 эквидистантные поперечины А1С1 и К1L1 — равные отрезки А1С1 = К1L1. Поэтому ∡ABC и ∡KLM равны. (В дальнейшем среди аксиом мы увидим утверждение, что если углы имеют хотя бы одну пару равных эквидистантных поперечин, то и все другие эквидистантные поперечины у них будут равными).

Угол в 90о называется прямым. Угол в 180о называется развернутым. Стороны развернутого угла образуют прямую.

Ломаная.

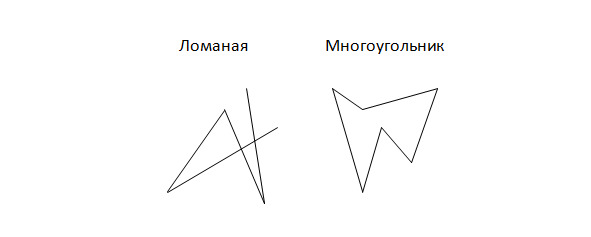
Теперь — ломаная. Пусть даны различающиеся точки А,В,С,D,…,E,F. Ломаной называется совокупность (объединение) отрезков АВ, ВС, CD,..,EF ненулевой длины, где конец каждого отрезка — начало следующего (отрезки называются звенья ломаной АВСD… EF). Если конец последнего отрезка — начало первого (A=F), то ломаная считается замкнутой. Если никакой из отрезков ломаной не пересекает никакого другого отрезка ломаной, то такая замкнутая ломаная называется многоугольником. Внимание! Это очень важное понятие в геометрии. Многоугольник из трех отрезков называется треугольником, из четырех — четырехугольником, из пяти — пятиугольником и т. д. Точки А,В,С… — называются вершинами многоугольника, Отрезки АВ, ВС и т. д. — сторонами треугольника, четырехугольника и т. д.

Теперь такой вопрос: является ли плоскость фигурой? Ответ: да, поскольку плоскость состоит из точек, а любое множество точек есть фигура.

Глава 3. Аксиомы принадлежности

Геометрия (по Фалесу и Евклиду) устроена так, что напоминает дом. Кирпичи кладутся снизу вверх, и те, что расположены сверху, опираются на нижние. Фундамент здания геометрии — это аксиомы, кирпичи — теоремы.

Как мы уже говорили, древние греки впервые поняли, что нужно доказывать даже очень простые утверждения (в целях систематизации геометрии как науки). Но невозможно доказать все утверждения, потому что при доказательстве мы опираемся на что-то, что уже доказано. Поэтому в геометрии некоторые наиболее простые и очевидные утверждения, называемые аксиомами не доказываются, а просто перечисляются с самого начала.

Так сделаем и мы в нашем курсе геометрии. Предлагаемая система аксиом — лишь одна из возможных. В других учебниках могут быть другие системы аксиом. Все 15 аксиом разделены на 5 групп (для удобства). Начнем с первой группы аксиом, потом поговорим о других.

Пусть задано множество (точек), называемое плоскостью, и система его частей или, иначе говоря, подмножеств, называемых прямыми. Выполнены следующие утверждения.

I. Аксиомы принадлежности.

А1. Существует хотя бы одна прямая и каждой прямой принадлежит хотя бы одна точка.

А2. Через две различные точки проходит одна и только одна прямая.

Казалось бы и так ясно, что «хотя бы одна точка существует». Зачем приводить такую «глупую» аксиому? Дело в том, что без этой аксиомы вообще может ничего не существовать. Если не существует ни одной точки, не существует вообще ничего. Полная пустота! Так что это, наверно, самая главная аксиома. Ее смысл: «Да будет мир!»

Вторая аксиома вполне элементарна. Возьмите две нитки за концы правой и левой рукой. Если их растянуть в стороны — нитки сольются в одну. Из второй аксиомы сразу следует и первая теорема. (Ее мы обозначим Т1, дальше будут Т2, Т3, … Так проще запомнить)

Т1. Две различные прямые не могут пересекаться более чем в одной точке. Для доказательства применим метод «от противного», предположим, что две различные прямые пересекаются в двух или более точках.