Бесплатный фрагмент - Физика

Математика — точная наука. Она с одинаковой точностью отражает законы природы и фантазии физиков. Но физики фантазируют не ради фантазии. Они думают, что открывают законы природы. Поэтому задача официальной науки не запрещать физикам фантазировать, а научиться находить в их фантазиях элементы математики природы

А. А. Астахов

Удивительно точную мысль по поводу дальнейшего развития физики сформулировал А. П. Смирнов в статье «Осознание знания откровение XXI века». Человечество накопило огромное количество практических, опытных знаний о природе и эмпирически точно установленных закономерностей. Поэтому не нужно искать физические теории в дебрях формально-математических преобразований, чем сегодня увлекается множество современных исследователей. Многие вопросы можно решить, разобравшись с тем, что мы уже знаем достоверно. Этого вполне достаточно для правильных теорий, построенных на основе математики природы.

А. П. Смирнов, А. А. Астахов

«Может быть, мое мнение меня обманывает; поэтому я хочу быть собеседником, а не судьей, исследователем, а не основоположником; я готов учиться у каждого, кто предлагает что-то более правильное и достоверное… Если же читатель увидит, что оснастка моего сочинения равна той, которая имеется у противоположной стороны, тогда он сам взвесит и рассудит, что имеет большее значение: суждение всех просвещенных людей…, всех университетов…, или же частное мнение того или иного человека… Я знаю, в жизни нередко случается, что большая часть побеждает лучшую. Я знаю, что при исследовании истины никогда не лишне добавить свое прилежание к тому, что было сделано прежде».

Эразм Роттердамский

В мире, как он описывается многими науками, отсутствует смысл. Это, однако, означает не то, что мир лишен смысла, а лишь то, что многие науки слепы к нему. Смысл приносится в жертву многими науками.

Виктор Франкл

ВВЕДЕНИЕ

Настоящая работа посвящена анализу физической сущности современных знаний о природе, связанных с движением и взаимодействием материи. Появляющиеся в последнее время в современной науке мнения о первичности вращательного движения, основанные на строении микромира, а также на вращении эфирных вихрей, образующих элементарные частицы вещества несостоятельны. Строение вещества и движение материи это разные вещи. Любое движение первоначально возникает как прямолинейное движение, т.к. в природе не существует криволинейных сил. Это непосредственно следует из законов динамики Ньютона, которые на сегодняшний день считаются незыблемыми. Все попытки некоторых современных авторов внести свои коррективы в законы Ньютона не меняют их физической сущности.

В первом законе Ньютона говорится исключительно о прямолинейном движении. Второй закон Ньютона определяет силу и ускорение, которые возникают вдоль одной общей прямой линии предшествующего равномерного прямолинейного движения взаимодействующих тел. Если предшествующие движения пересекаются под углом, то результирующее движение в любом случае представляет собой результирующую прямую линию. Об этом же говорит и третий закон Ньютона. Попробуйте представить себе силу взаимодействия, которая действует на взаимодействующие тела в противоположных направлениях, но не вдоль одной прямой, а как-либо иначе. Естественно, что это не возможно, т.к. противоположные направления по определению находятся только на одной прямой, но никак не на кривой линии.

Криволинейное движение возникает только при дополнительном силовом воздействии, имеющим иное направление, чем направление текущего активного или так называемого инерционного прямолинейного движения. Криволинейное движение, образующееся за счет множества разнонаправленных прямолинейных взаимодействий, является более сложным движением, чем прямолинейное движение, а, как известно, сложное не может быть элементом простого.

Таким образом, основным элементом механического движения в природе является прямолинейное перемещение в пространстве. Даже если вещество образовано вихрями амеров эфира, то в свободном пространстве между соударениями они, очевидно, движутся прямолинейно.

Вследствие непрерывных разнонаправленных взаимодействий материальных тел между собой, а также с мировой материальной средой прямолинейное движение в чистом виде в природе встречается довольно редко, что дает ложное основание считать основополагающим движением — вращательное движение. Однако в природе так же редко встречается и вращательное движение в чистом виде. Первичность прямолинейного движения непосредственно следует из физического механизма формирования вращательного движения, которое в свою очередь является простейшим базовым элементом любого произвольного криволинейного движения. Вариант такого механизма приведен в настоящей работе.

По некоторым практическим соображениям мы попытались разобраться в физической сущности вращательного движения на уровне физического механизма преобразования движения по направлению и столкнулись с многочисленными противоречиями не только в существующей математической модели вращательного движения во всех его проявлениях, но и с другими проблемами классической физики, связанными с теорией движения в целом. Как выяснилось, в современной физике практически отсутствует описание явлений природы на уровне их физических механизмов.

В большинстве случаев всё сводится лишь к количественному математическому описанию природных закономерностей, в котором нет места физическому, а иногда и элементарному здравому смыслу. За физический смысл природных явлений зачастую выдается лишь краткое словесное описание математических формул. Причем словесное описание даже правильных формул только подтверждает количественную оценку найденной закономерности, но не отражает ее физическую сущность на уровне причинно-следственных связей. Даже популяризаторы науки в основном преподносят широкой аудитории описание природы на уровне её математического отображения в виде условных символов и знаков.

В природе не существует формальных математических правил. Математика это и есть физика, записанная в условных обозначениях: символах и знаках. Однако современный учебный процесс построен так, что в будущих математиках закрепляют знание математических правил в основном на формальном уровне. Во всяком случае, маститые математики практически забывают физическую основу ставших для них привычными стандартных математических операций.

Например, дополнительные множители не нарушают равенство. Однако если речь идёт о физических величинах, в которых этих множителей нет, то такое равенство не является физическим. Тем не менее, некоторые физики от формальной математики, умножая обе части физических формул на одну ту же величину иногда получают новые физические величины, там, где их нет, нарушая главный закон природы — Закон сохранения истины! На формально математических преобразованиях иногда даже строятся новые физические теории, хотя все должно быть наоборот.

В современной теоретической физике спокойно существуют и обсуждаются на самом высоком научном уровне такие понятия, как: «искривление пространства и времени», «кручение пространства», «пространство-время», «вибраторы-струны», «пятые, шестые и энные измерения». Ни один физик на Земле и даже авторы этих понятий не могут объяснить непосвященному человеку и даже специалистам, что это такое, потому что эти понятия не физические. Они получены из формально математических преобразований не физических величин, а предполагаемых допущений — постулатов и из всевозможной замены переменных. Но это уже не наука, а математическая религия.

Найти убедительные аргументы против откровенных глупостей достаточно сложно. Глупость нельзя опровергнуть в принципе, т.к. логика против нее бессильна. Особенно если эта глупость складывалась веками и формально подтверждена правильными математическими формулами. Это касается преобразования направления скорости без преобразования ее величины; однонаправленных линейных ускорений, которые изменяют скорость якобы только своего вида движения без взаимного влияния друг на друга; утверждения о фиктивности силы инерции без знания ее природы и при реальных энергетических затратах на ее преодоление; невозможности изменения импульса замкнутой системы физических тел в мировой материальной среде, в которой в принципе не может существовать замкнутых систем и многого другого.

Альтернатива откровенной глупости вовсе не означает альтернативы законам природы. А вот некоторые представители классической физики делают её альтернативной законам природы. Однако, как это ни парадоксально умные люди бояться идти против общественного мнения, поддерживающего глупость, чтобы самим не прослыть глупцами или альтернативщиками (альтами), как обидно называют официалы всех, кто выступает против откровенных глупостей современной науки. Мало кто отважится сказать, что король голый, если все вокруг утверждают, что он прекрасно и изысканно одет. В результате все вокруг считаются умными людьми, а физика 21 века топчется на месте только потому, что в свите короля нет честного человека, который не боится прослыть «глупцом».

В известной сказке эту роль выполняет младенец, который, может позволить себе говорить то, что он видит и думает и вовсе не потому, что он глуп, а потому, что он еще не научился лгать. В сказке младенца послушали, но в науке этого недостаточно. В науке люди, выступающие в роли таких младенцев, в лучшем случае просто игнорируются «умными» людьми из свиты короля. А в худшем случае на них спускают придворных псов.

Любые математические модели должны отражать только сложную связь давно устоявшихся и проверенных опытом элементарных понятий в физике. Только тогда они будут достаточно точно отражать природные явления. Наверное, современной наукой открыты еще не все элементарные инварианты. Однако возможности существующих классических инвариантов для определения физической сущности всех известных на сегодняшний день явлений природы еще далеко не исчерпаны.

Нарушений законов природы не может быть в принципе. Все, что происходит в природе, происходит только в соответствии с законами природы или не происходит вообще. Нарушения могут быть только в нашем понимании законов природы. Поэтому все, что на первый взгляд не вписывается в классические теории, объясняется только несовершенством существующей теории, а не нарушением законов природы.

В настоящей работе приведены многочисленные примеры, когда не вписывающиеся на первый взгляд в классическую физику явления природы находят у различных авторов вполне приемлемое объяснение, основанное на привычных элементарных понятиях. Например, полный импульс движения включает в себя не только линейный импульс, но и вращение. С учетом полного импульса разрешаются многие вопросы, связанные с кажущимся нарушением закона сохранения импульса в линейных взаимодействиях и многое другое.

Главной задачей настоящей работы является ни в коем случае не пересмотр давно открытых и проверенных опытом природных закономерностей, а придание им физического, а значит и здравого смысла, которого в современной физике хронически не хватает. Конечно же, исходя из истинного физического смысла, возможны некоторые уточнения существующих взглядов. Однако сделанные нами уточнения не выходят за рамки здравого смысла, т.к. они основаны на классических элементарных понятиях и принципах причинности, а не на постулатах, не подтверждающихся экспериментально и изобретаемых только для реализации далеких от реальной действительности математических моделей.

В работе предпринята попытка выявления физического смысла вращательного движения и его динамики, силы и ускорения Кориолиса, полного ускорения сложного движения, явления инерции, определяющего формирование сил взаимодействия, через которые осуществляется перераспределение энергии взаимодействия, а также физического смысла законов Ньютона. Рассмотрены вопросы так называемого безопорного движения. Дана критика некоторых авторов, а также современных ученых, которые очень уж рьяно, но, к сожалению, неумело или недостаточно аргументировано выступают в защиту своих консервативных взглядов.

Читатель может не согласиться с предложенными физическими механизмами, позволяющими разрешить существующие противоречия аналогичных классических моделей природных явлений. Однако мы не претендуем на истину в последней инстанции. Все существующие научные знания это только грубые математические и физические модели природных явлений. Реальная действительность значительно сложнее любых ее моделей, создаваемых наукой.

Мы можем сколь угодно близко подходить к истине, но никогда ее не достигнем, поскольку логика, построенная на элементарных понятиях не способна объяснить сами эти элементарные понятия. Элементарные понятия являются базой нашей логики, а для объяснения базы необходима другая база ещё более элементарных понятий, которой у нас пока нет. Однако другой логики у нас нет. Поэтому самое важное в любой теории это не абсолютная точность во всех её деталях, а её принципиальное соответствие здравому смыслу и проверенным элементарным понятиям. Окончательную оценку любой теории, как всегда, выставит время. Однако если теория не противоречит здравому смыслу, то со временем она никогда полностью не пересматривается, а только уточняется и дополняется.

Конечно же, на бытовом уровне здравый смысл у всех людей разный, поскольку зачастую он отражает законы человеческой психики, не всегда связанной с объективной реальностью. Как говорится правда у всех своя. Однако в науке здравый смысл может быть только один. Он основан на элементарных понятиях, отражающих основные сведения о природе, подтверждающиеся тысячелетним опытом контакта человека с реальной действительностью на доступном ему уровне.

Мы можем не знать всех закономерностей природы и всех причин, происходящих в ней явлений. Однако новые неоткрытые закономерности не могут противоречить тому, что мы уже знаем о ней достоверно, хотя и на уровне элементарных понятий. Это означало бы, что природа противоречит самой себе, чего не может быть в принципе. Непознаваемость природы может быть связана с её бесконечным многообразием, но никак не с отсутствием в ней причинно-следственных связей, которые и определяют и ее, и наш с вами здравый смысл, который основан на образных представлениях.

Природа оперирует не цифрами и не формулами. Она оперирует реальными явлениями и процессами. Так же, как и человек мыслит не цифрами и не формулами, а образами, которые отражают материю во всех её проявлениях в пространстве в нашем сознании. И если математическую модель, какого-либо явления невозможно представить образно, то это вовсе не значит, что природа непознаваема для человека, как, например, говорят в отношении теории относительности Эйнштейна её защитники.

Это означает, что теория, скорее всего, не верна, т.к. она не совместима с образами, отражающими природу, т.е. с самой природой. Поэтому не поддавайтесь на утверждение консервативной части научного сообщества, что вы якобы не умны, раз не способны понять их несостоятельные теории. Они не более умны, чем вы и только прикрываются своими абстрактными математическими формулами, которые без физического обоснования связи этой абстракции с реальной действительностью ничего не значат.

Если отбросить малопонятные для непосвящённого человека термины, то объяснения природных явлений даже у маститых академиков не выходят за рамки обычной детской логики. Попросите академиков объяснить их формулы и представления, облечённые в мудрёные специальные термины, через образные представления, т.е. на пальцах, как говорят в народе, и вы услышите в ответ такой родной и понятный для всех детский лепет, т.к. логика на всех одна и на детей и на маститых академиков.

Причём это в лучшем случае. А в худшем вам просто намекнут, что вы недостаточно умны, что означает, что академики сами не понимают, о чём говорят.

Как говорил сам автор самой непонятной в науке теории Эйнштейн:

«Если не можете объяснить свою мысль пятилетнему ребёнку, значит, Вы сами её плохо понимаете».

И об этом вы тоже прочитаете в настоящей работе.

Ничего позорного и унизительного в ошибках нет. Без ошибок развитие науки не возможно. Но оно невозможно и без признания этих ошибок. Тем не менее, маститые академики, наделавшие эти ошибки и много лет преподающие их студентам и обществу, не хотят их признавать. И руководствуются они в этом вовсе не интересами науки, а собственными низменными интересами. В этих условиях, только накопив критическую массу критических замечаний в обществе, можно стимулировать развитие науки. Поэтому мы обращаемся к вам. Читайте, думайте, анализируйте! И присылайте ваши критические замечания.

И ещё один момент, на который мы хотим обратить внимание читателя. В предлагаемой работе повествование идёт от множественного числа «мы». Это не значит, что нас много. Автор пока практически один. Но выражение «мы» я употребляю по следующим четырем причинам:

Во-первых, когда автор кому-то что-то пытается объяснить, то он приглашает своих слушателей в собеседники, при этом он справедливо полагает, что он уже не один.

Во-вторых, предлагая своё видение вопроса, каждый автор надеется всё-таки приобрести единомышленников и поэтому ведёт повествование и от имени тех, кто с большой долей вероятности в достаточно большой аудитории может его поддерживать. Если же он говорит «я», то он в некотором смысле противопоставляет себя возможным единомышленникам.

В-третьих, говорить от собственного лица, т.е. «якать» не совсем скромно, потому что каким бы новым не было мнение автора, он всегда в значительной степени опирается на опыт, накопленный другими авторами. Ссылки на них, конечно же, этически необходимы. Однако при этом в любом случае даже самое новое видение автора остаётся не совсем его собственным независимым мнением. Ведь даже свои элементарные знания он получает от общества.

И наконец, в-четвёртых, наверное, именно из приведённых выше соображений обращение «мы» общепринято в практике публичных работ.

1.1. Двойственность сил инерции в современной физике

Один из самых известных видов инерции это центробежная сила. Жуковский Н. Е. «Теоретическая механика» издание второе. ГОСУДАРСТВЕННОЕ ИЗДАНИЕ ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ МОСКВА-ЛЕНИНГРАД 952 г. определяет силу инерции следующим образом:

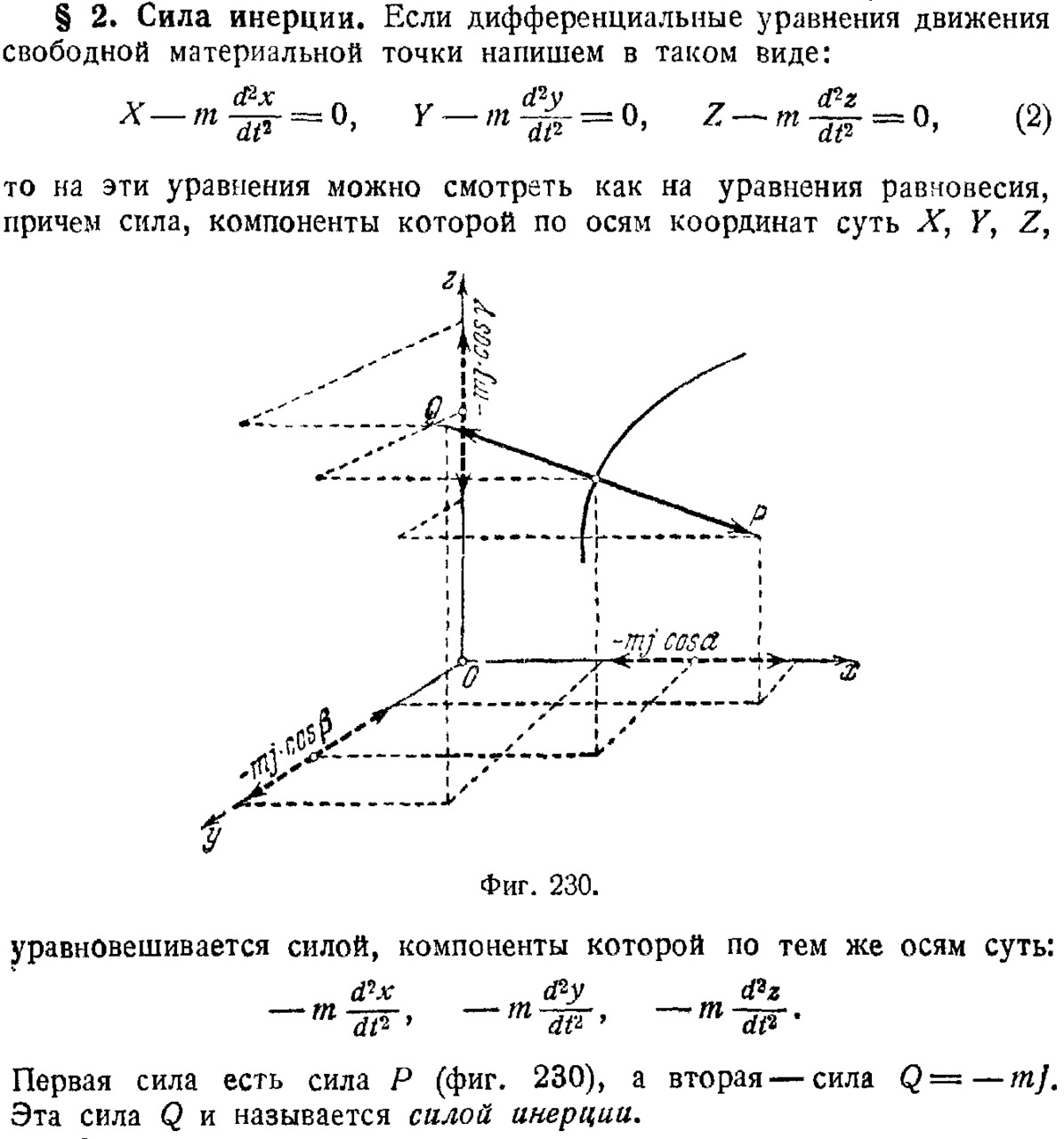
Инерция является неотъемлемым свойством физических тел, которое проявляется в их способности противодействовать любому изменению состояния движения или состояния покоя, являющегося частным случаем движения. По определению Жуковского Н. Е.:

«Силой инерции называется сила, которая по величине равна произведению массы на полное ускорение, а направлена в сторону, противоположную полному ускорению» (см. фотокопию выше, «Теоретическая механика», издание второе, ГОСУДАРСТВЕННОЕ ИЗДАНИЕ ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ МОСКВА-ЛЕНИНГРАД 1952 г., §2 Сила инерции).

Как считается в механике Ньютона, силы инерции из НИСО (неинерциальная СО) не подчиняются третьему закону Ньютона в ИСО, т.к. это не силы взаимодействия, а псевдосилы, «действующие» только на данное тело. Однако по определению силы противодействия, которые возникают при всяком силовом воздействии на материальное тело в соответствии с третьим законом Ньютонав ИСО, в точности соответствуют силам инерции их НИСО.

Сила противодействия из 3-го закона Ньютона в ИСО также равна произведению массы на полное ускорение и также направлена в сторону, противоположную полному ускорению. При этом сила инерции в НИСО приложена к телу фиктивно. Именно потому она и фиктивная. Но точно по этой же причине фиктивной для ускоряемого тела является и сила противодействия из 3-го Ньютона, т.к. она приложена не к ускоряемому телу, а к ответному телу.

Причём силы инерции в НИСО действуют только на одно тело, так же, как собственно и силы противодействия из 3-го закона Ньютона в ИСО, т.к. в классической физике ответное тело для ускоряемого тела нужно, как собаке пятая нога. В классической физике ответное тело заменяется абстрактной силой, синхронно приложенной с ускоряемому телу, что, кстати, создаёт несоответствующую действительности иллюзию движения силы (см. гл. 1.2.1.).

Мы уже не говорим, что сила противодействия из 3-го закона Ньютона в ИСО не перестаёт быть самой собой и в качестве фиктивной силы в НИСО. Так в чём же тогда принципиальная разница между ними и якобы неподчинение сил инерции из НИСО 3-му закону Ньютона из ИСО?! Тем более, что в официальных источниках за силу инерции сплошь и рядом принимают именно силу противодействия из 3-го закона Ньютона, что будет не раз показано ниже в настоящей главе.

Далее Жуковский Н. Е. пишет:

«Введение понятия о такой фиктивной силе облегчает формулировку многих теорем динамики, особенно в вопросе об относительном движении и о движении несвободной материальной точки».

То есть Жуковский относит силы инерции, вводимые в математическую модель ускоренного движения тел к фиктивным силам, которые не оказывают реального влияния на ускоренное движение материальных тел и вводятся в неинерциальных системах отсчета как математический прием только для облегчения формулировок теорем динамики.

В современной физике принято различать «обычные» силы, действующие на тело со стороны других тел в инерциальных системах отсчета и фиктивные силы инерции, возникающие в неинерциальных системах отсчета. А. Н. Матвеев в работе «Механика и теория относительности», 3-е издание, Москва, «ОНИКС 21 век», «Мир и образование», 2003 г. дает следующее определение «обычных» сил:

«В инерциальных системах отсчёта единственной причиной ускоренного движения тела являются силы, действующие на него со стороны других тел. Сила всегда есть результат взаимодействия материальных тел».

Однако в неинерциальных системах отсчета наблюдаются ускорения, которые не являются результатом действия на тела каких-либо сил со стороны других тел. По этому поводу Матвеев пишет:

«В неинерциальных системах можно ускорить тело простым изменением состояния движения системы отсчета. Рассмотрим, например, неинерциальную систему отсчета, связанную с автомобилем. При изменении скорости его относительно поверхности Земли в этой системе отсчета все небесные тела испытывают соответствующие ускорения. Ясно, что эти ускорения не являются результатом действия на небесные тела каких-либо сил со стороны других тел. Таким образом, в неинерциальных системах отсчета существуют ускорения, которые не связаны с силами такого же характера, какие известны в инерциальных системах отсчета. Благодаря этому первый закон Ньютона в них не имеет смысла. Третий закон Ньютона в отношении взаимодействия материальных тел, вообще говоря, выполняется. Однако, поскольку в неинерциальных системах отсчета ускорения тел вызываются не только „обычными“ силами взаимодействия между материальными телами, проявления третьего закона Ньютона настолько искажаются, что он также утрачивает ясное физическое содержание».

Силы, которые проявляются в неинерциальной системе отсчета, в отличие от «обычных» сил Матвеев определяет, как силы «особой природы». При этом Матвеев отмечает, что этот путь был выбран не им, а сложился исторически и предлагает свой альтернативный вариант:

«При построении теории движения в неинерциальных системах в принципе можно было бы идти по пути коренного изменения представлений, выработанных в инерциальных системах, а именно можно было бы принять, что ускорения тел вызываются не только силами, но и некоторыми другими факторами, которые ничего общего с силами не имеют. Однако исторически был выбран иной путь — эти другие факторы были признаны силами, которые находятся с ускорениями в таких же соотношениях, как и обычные силы. При этом предполагается, что в неинерциальных системах, так же как и инерциальных, ускорения вызываются только силами, но наряду с „обычными“ силами взаимодействия существуют еще силы особой природы, называемые силами инерции».

Таким образом, в современной физике в неинерциальных системах отсчёта наряду с «обычными» силами взаимодействия необходимо учитывать силы инерции, которые Матвеев увязывает с ускоренным движением неинерциальной системы отсчета относительно инерциальной.

«Существование сил инерции обусловливается ускорением движения неинерциальной системы отсчета относительно инерциальной. Силы инерции берутся такими, чтобы обеспечить в неинерциальной системе отсчета те ускорения, которые фактически имеются, но обычными силами взаимодействия объясняются лишь частично».

При этом Матвеев, так же как и Жуковский отмечает, что силы инерции, вводимые в неинерциальных системах отсчета в математической модели теории движения, являются фиктивными силами, т.е. реально несуществующими:

«Введение этих сил в уравнения движения, использование их при объяснении физических явлений и т. д. в неинерциальных системах координат является правильным и необходимым. Однако использование понятия сил инерции при анализе движений в инерциальных системах координат является ошибочным, поскольку в них эти силы отсутствуют».

С точки зрения современной физики, связав неинерциальную систему отсчёта с ускоренно движущимся телом можно, прибавив к нему силу инерции, получить условие равновесия для тела в неинерциальной системе отсчёта. В этом случае ускорение движения тела определяется, как ускорение неинерциальной системы отсчёта относительно инерциальной системы без учета сил инерции. Если же тело движется ещё и относительно неинерциальной системы отсчета, то задача значительно усложняется.

В этом случае абсолютное ускорение будет определяться как сумма относительного ускорения, полученного телом в неинерциальной системе в результате «обычных» взаимодействий и ускорения самой неинерциальной системы отсчёта относительно инерциальной системы отсчета. Силы инерции обуславливают разность между относительным и абсолютным ускорением. При этом сила инерции (Fин) определяется выражением:

Fин = m * (а отн — аабсол)

Несмотря на то, что в современной физике существует четкое математическое выражение для сил инерции, их четкое физическое понимание отсутствует. В результате сила инерции определяется в современной физике как минимум двойственно. С одной стороны в математической модели ускоренного движения тел силы инерции считаются фиктивными, т.е. реально не существующими. С другой стороны существование сил инерции признается многими классиками и современными авторами, как объективная реальность. Вот что говорит Н. Е. Жуковский в упомянутой выше работе (стр. 281) о реальности сил инерции:

«Являясь компонентом предполагаемой силы инерции, центробежная сила есть сила фиктивная; она должна быть присоединена к материальной точке, если мы хотим рассматривать вопрос о ее движении, как об относительном равновесии точки. Но в некоторых вопросах центробежная сила является и как некоторая действительная сила, — например, в вопросах об определении давления движущегося тела на препятствия, стесняющие его движение. Но в этом случае центробежная сила приложена не к материальной точке, а к тем телам, которые задерживают материальную точку на ее траектории.»

Как видите, здесь за силу инерции принимается именно ЦБ сила, которая по 3-му закону Ньютона противодействует ЦС силе. Правда сам 3-ий закон Ньютона здесь не упоминается, но в классической физике ЦБ сила является силой противодействия при ЦС силе именно по 3-му закону Ньютона. При ЦС силе — это значит именно в ИСО.

Жуковский признает физическую реальность действия оказываемого силой инерции, однако в этом случае сила инерции превращается в «обычную» силу, которая приложена к телам, задерживающим движущееся тело на его траектории. А. Н. Матвеев также высказывается за то, что с физической точки зрения силы инерции являются вполне реальными силами (стр. 393):

«Являются ли силы инерции реальными силами? Они реальны в том же смысле, в каком являются реальными ускорения в неинерциальных системах координат, для описания которых они введены. Они реальны также и в более глубоком смысле: при рассмотрении физических явлений в неинерциальных системах можно указать конкретные физические последствия действия сил инерции. Например, в вагоне поезда силы инерции могут привести к увечьям пассажиров, т. е. к весьма реальному и осязаемому результату. Поэтому силы инерции столь же реальны, как реален факт равномерного и прямолинейного движения тел в инерциальных системах координат, если отсутствуют „обычные“ силы взаимодействия, как это формулируется в первом законе Ньютона».

Итак, для удобства математического описания ускоренного движения тел в современной физике в неинерциальных системах отсчета вводятся условные фиктивные силы инерции, которые в инерциальных системах отсчета отсутствуют. Однако системы отсчета это только инструменты для математического описания реальной действительности. Фиктивные силы инерции, вводимые в неинерциальных системах отсчета это по сути дела математическая модель реальных сил, порождаемых инерцией в инерциальных системах отсчета.

При переходе в инерциальную систему отсчета фиктивные силы инерции превращаются в «обычные» силы, приложенные к телам, препятствующим движению тел, связанных с неинерциальной системой отсчета. Происходит по сути дела постоянная подмена понятий вполне реальной «обычной» силы, проявляющейся в инерциальной системе отсчета ее математической моделью — фиктивной силой инерции в неинерциальной системе отсчета и наоборот.

В результате, вполне реальные силы по изменению движения или покоя физических тел, которое приводит к реальным физическим последствиям, обеспечивается в современной физике фиктивными, т.е. несуществующими силами инерции! Двойственность понятия инерции в современной физике проявляется уже с первого же определения Ньютона, которое он дал ещё до своего первого закона:

«Инерция или врожденная сила материи, — это сила сопротивления, с помощью которой каждое тело, в какой бы степени оно ни находилось, пытается сохраниться в своем нынешнем состоянии, будь то в состоянии покоя или равномерного движения вперед по прямой линии».

Такая подмена понятий обычных сил и сил инерции, наблюдается у многих авторов. Приведем дословно цитаты некоторых авторов, касающиеся силы инерции.

Н. Е. Жуковский («Теоретическая механика», издание второе, ГОСУДАРСТВЕННОЕ ИЗДАНИЕ ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ МОСКВА-ЛЕНИНГРАД,1952 г., стр. 281):

«Если, например, некоторый шар М (фиг. 232) движется по цилиндрическому своду, описывая круг, то на него действует сила Р давления свода, которая для шара есть центростремительная. Но по третьему закону динамики шар М сам давит на свод с такой же силой N, равной Р. Эта сила N для шара будет центробежной силой инерции, и можно сказать, что свод находится под действием этой силы».

Как видите, здесь Жуковский открытым текстом говорит, что за силу инерции принимается именно ЦБ сила, которая по 3-му закону Ньютона противодействует ЦС силе в ИСО. Фактически это одна и та же сила взаимодействия. Но у Жуковского она меняет свой статус в зависимости от того, с какой стороны на неё смотреть. Одним боком она обычная сила, а другим — фиктивная сила инерции.

Однако, как может шар, являющийся совместно со сводом источником одной и той же силы, воздействовать на свод с силой, которая для него самого якобы не существует? Как можно производить то, что не существует для самого производителя? Это возможно только при искусственном разделении одной общей для всех силы взаимодействия на две разные силы действия и противодействия по фиктивному 3-му закону Ньютона.

А. Зоммерфельд. Механика. Москва. Ижевск. 2001, Задача 3 к главе II:

«II.3. Центробежная сила при увеличенной скорости вращения Земли.

С какой скоростью должна вращаться Земля (тело на уровне её поверхности) для того, чтобы на экваторе сила тяжести и центробежная сила взаимно уничтожались? Какова была бы при этом продолжительность суток?»

Однако, как можно уничтожить фиктивную центробежную силу инерции, которая и так не существует по причине её фиктивности для тела? Очевидно это можно сделать, только уничтожив вполне реальную общую силу взаимодействия, воздействуя на носители поля тяготения. Это свидетельствует о том, что сила взаимодействия одна, общая для всех взаимодействующих тел.

Ещё одни подобный пример приводит Г. С. Ландсберг. «Элементарный учебник физики», Том 1, ФИЗМАТЛИТ. 2004, стр. 267:

«Вследствие вращения Земли на ней также должна наблюдаться центробежная сила инерции (которой мы до сих пор пренебрегали). В §133 мы нашли, что центростремительное ускорение на экваторе равно 0,034 м/с2. Это составляет примерно 1/300 часть ускорения свободного падения g. Значит, на тело массы т, находящееся на экваторе, действует центробежная сила инерции, равная mg/ЗОО и направленная от центра, т. е. по вертикали вверх. Эта сила уменьшает вес тела по сравнению с силой притяжения Земли на 1/300 часть».

Как и в задаче Зоммерфельда, приведенной выше, для того чтобы вес тела по сравнению с силой притяжения Земли уменьшился на 1/300 часть необходимо уменьшить на эту часть их общую вполне реальную обычную силу взаимодействия, воздействуя на носители тяготения. Но в этой задаче интересно то, что Ландсберг открытым текстом говорит, что сила инерции приложена именно к самому телу, а не к «верёке» тяготения: «Значит, на ТЕЛО массы т, находящееся на экваторе, действует центробежная сила инерции…». Это к вопросу о двойственности. А за силу инерции здесь опять же принимается именно ЦБ сила, которая по 3-му закону Ньютона противодействует ЦС силе в ИСО.

Р. Фейнман, Р. Лейтон, М. Сэндс, ФЕЙНМАНОВСКИЕ ЛЕКЦИИ ПО ФИЗИКЕ, 2. ПРОСТРАНСТВО. ВРЕМЯ. ДВИЖЕНИЕ, стр. 78,79:

«Когда мы держим гантели горизонтально, то никакой работы не производим. Выпрямляя руки в стороны и сгибая их, мы тоже не можем произвести никакой работы. Это, однако, верно только, пока нет никакого вращения! При вращении же НА ГАНТЕЛИ действует центробежная сила. Они стремятся вырваться из наших рук, так что, сгибая во время вращения руки, мы преодолеваем противодействие центробежной силы. Работа, которая на это затрачивается, и составляет разницу в кинетических энергиях вращения. Вот откуда берется этот добавок».

Обратите внимание, что и здесь прослеживается, как минимум словесная путаница. Фейнман чётко указал, что центробежные силы действуют именно на гантели, что противоречит точке приложения фиктивных сил инерции. Это опять же свидетельствует об отсутствии ясного определения силы инерции в современной физике.

Можно привести еще множество примеров двойственного подхода к понятию силы инерции и до бесконечности спорить, о какой системе отсчета идет речь и является ли сила инерции фиктивной или реальной в каждом конкретном случае. Однако однозначный ответ о природе сил инерции у классиков теоретической механики найти вряд ли удастся.

Среди современных авторов также нет четкого представления о природе силы инерции, впрочем, как и о природе «обычных» сил. Например, Н. В. Гулиа, являющийся ярым сторонником фиктивности сил инерции независимо от систем отсчета, в которых они рассматриваются в своей книге «Удивительная физика» в главе «Инерция: сила или бессилие?» противореча самому себе, так же дает двойственную оценку силе инерции.

С одной стороны, он категорически отрицает существование силы инерции, причем не только, как математической абстракции, но и как физической реальности. С другой стороны он вынужден, противореча самому себе признавать физическую реальность сил инерции в тех случаях, в которых ее действие невозможно объяснить математической абстракцией. В «Удивительной физике» в главе «Реальны ли центробежные силы?» Гулиа приводит убийственный, по его мнению, пример, подтверждающий именно физическое отсутствие сил инерции в природе:

«Приведем простейший, но, тем не менее, убийственный для этих сил пример. Известно, что Луна вращается вокруг Земли. Спрашивается, действуют ли на нее центробежные силы? Спросите, пожалуйста, об этом своих товарищей, родителей, знакомых. Большинство ответит: «Действуют!» Тогда вы поспорьте с ними, на что хотите и начинайте доказывать, что этого не может быть.

Основных довода — два. Первый: если бы на Луну действовала центробежная сила (то есть сила, направленная от центра вращения наружу), то она могла бы действовать только со стороны Земли, так как других тел поблизости нет. Думаю, что напоминать о том, что силы действуют на тела только со стороны других тел, а не «просто так», уже не надо. А если все так, то, значит, Земля не притягивает, а отталкивает Луну — от себя наружу. Между тем, как мы знаем, существует закон всемирного тяготения, а не отталкивания. Поэтому на Луну может действовать со стороны Земли только одна-единственная сила — притяжения P, направленная точно наоборот — от Луны к Земле. Такая сила называется центростремительной, и она реально есть, она-то и сворачивает Луну с прямолинейного инерционного пути и заставляет вращаться вокруг Земли. А центробежной силы, извините, нет (рис. 54).

Второй довод. Он для тех, кто не знает о существовании закона всемирного тяготения или забыл его. Тогда если бы на Луну действовала центробежная сила (естественно, со стороны Земли, так как других тел, как мы уже знаем, поблизости нет), то Луна не стала бы вращаться вокруг Земли, а улетела бы прочь. Если на Луну не действовало бы вообще никаких сил, то она спокойно пролетела бы мимо Земли по инерции, то есть по прямой (мы же забыли о всемирном тяготении!). А если бы со стороны Земли на Луну действовала центробежная сила, то Луна, подлетая к Земле, свернула бы в сторону и под действием этой силы улетела бы навсегда в космическое пространство. Только бы мы ее и видели! Но раз этого не происходит, стало быть, центробежной силы нет. Вы выиграли спор, причем в любом случае. А появилась эта центробежная сила оттуда же, откуда и силы инерции в прямолинейном движении — из принципа Даламбера. Здесь, во вращательном движении, этот принцип еще более облегчает решение задач, чем в прямолинейном. Еще бы, прикладываем к существующей центростремительной силе несуществующую центробежную — и Луна как бы зависает на месте! Делайте с ней, что хотите, определяйте ускорения, скорости, радиусы орбиты, периоды обращения и все остальное. Хотя все это можно определить и без использования принципа Даламбера».

Наш взгляд, доводы Гулиа не только абсолютно не корректны с точки зрения физики, они просто по-детски наивны. Гулиа совершенно прав напоминая,

«… что силы действуют на тела только со стороны других тел, а не „просто так“…».

Поэтому ему, профессору физики, а вовсе не ребёнку следовало бы знать, что сила притяжения тоже существует «не «просто так»…», ведь прямого контакта между Землей и Луной нет. Следовательно, сила тяготения осуществляется через что-то материальное вокруг Луны и Земли, даже если обтекаемо назвать это что-то просто поле тяготения!

А поскольку небесные тела реально подталкивает друг к другу вполне материальное поле тяготения, но при этом они не падают друг на друга, то надо полагать, что они сопротивляются ему при помощи вполне реальной центробежной силы. И направлена эта реальная центробежная сила вовсе не со стороны Земли на Луну, а со стороны Луны на материальное поле тяготения. Причём в этом участвует каждый элемент Луны. При этом каждый действует на каждого, т.е. эта сила вовсе не формально действует и на элементы самой Луны, поддерживая её движение прочь от Земли.

Далее Гулиа сам вступает в противоречие со своей собственной же позицией:

«Но ради справедливости заметим все-таки, что центробежные или просто направленные от центра силы все-таки бывают, но действуют они вовсе не на то тело, которое вращается, а на связь, удерживающую это тело (рис. 57). То есть не на автомобиль, а на дорогу, не на Луну, а на Землю, не на камень в праще, а на веревку и руку человека и т. д.»

Вот только Гулиа почему-то забыл, что между Землёй и Луной также есть некая «верёвка» тяготения, на которую по его же словам и должны быть направлены центробежные силы Луны. Следовательно, источником НЕ фиктивной, а вполне реальной центробежной силы является сама Луна. Но силы, зарождающиеся внутри Луны, не могут не действовать, прежде всего, на элементы самой Луны.

Ближайшие к Земле элементы Луны, удерживаемые силой тяготения Земли в первую очередь, поддерживают своё движение прочь от Земли за счёт более удаленных элементов Луны. Эти взаимодействия последовательно распространяются на всё тело Луны, т.е. реальные силы инерции Луны действуют не только на «верёвку» тяготения, но на саму Луну изнутри. Это и есть механизм поддержки движения за счет вполне реальных сил инерции поэлементной поддержки (см. ниже).

При математическом моделировании физических взаимодействий современная физика рассматривает физические тела как материальные точки. Это, так же как и принцип Даламбера значительно облегчает математическое описание физических процессов. Однако некоторые профессора вроде Гулиа пытаются делать физику из математики. Конечно же, материальная точка не может действовать «сама на себя». Именно из этого и вытекает классическая фиктивность сил инерции. Однако физическому телу абсолютно все равно за что его принимает современная наука.

Силы инерции зарождаются, прежде всего, внутри каждого физического тела и распространяются по всему его объему, а уже затем передаются другим телам, которые им препятствуют. Причём даже самые упертые профессора вроде Гулиа, хотя бы «ради справедливости» иногда все-таки признают реальность сил инерции. Так что если вы поверили Гулиа, который втянул вас в этот спор и проиграли крупную сумму, то все претензии к нему. Выходит, его физика потому и удивительная, что это и не физика вовсе, а математическая абстракция.

В статье «Алфизики ХХ века» Н. Гулиа пишет:

«Силы инерции — это всего лишь математический прием, но тогда я верил, что они существуют реально и даже могут совершать работу. И предложил „центробежный“ инерцоид».

В этой цитате Гулиа недвусмысленно опять отрицает реальность сил инерции и соответственно возможность совершения ими какой-либо работы. Сначала Н. В. Гулиа был ярым сторонником инерцоидов, т.е. устройств, движущихся без опоры на окружающую материальную среду. После изучения классической механики, Гулиа стал таким же ярым их противником, считая, что силы инерции нереальны и, следовательно, не способны производить реальные действия:

«Сейчас мне стыдно, что, уже окончив институт, я думал, что центробежные силы реальны и могут действовать на грузы, совершая работу. Но, увы, именно так думает множество людей, имеющих дело с техникой, даже инженеры и некоторые ученые, ничуть не задумываясь над тем, что их представления в принципе неверны. Как заметил Т. Эдисон, к сожалению, большинство людей предпочитают безмерно трудиться, вместо того чтобы немного подумать».

Изучив теоретическую механику Гулиа, полагает, что приобрел верные представления о явлении инерции, хотя, как известно природа инерции на сегодняшний день не установлена и поэтому исчерпывающих сведений об инерции в современной теоретической механике Гулиа при всем его желании, тяге и таланте к учению почерпнуть никак не мог. Тем не менее, Гулиа считает («Алфизики ХХ века»), что теперь он свободно ориентируется в лабиринтах теоретической механики, читай в вопросах инерции:

«Теперь, став профессором механики, я довольно свободно ориентируюсь в тех лабиринтах, куда попадают по своей воле создатели инерцоидов. Мне особенно близки и понятны эти ситуации, ибо я не забыл еще, как сам в них оказывался. И я хочу рассказать читателям правду об инерцоидах, почему они движутся по реальным поверхностям и не могут двигаться без опоры и как самому посредством несложного опыта убедиться в этом».

Еще раз адресуем уже «немного подумавшему» Гулиа тот же вопрос, так, в чем же все-таки заключается реальная справедливость, в том, что силы инерции есть, хотя бы ради справедливости или они не существуют? Свободно ориентироваться в лабиринтах существующей теоретической механики вовсе не означает свободно ориентироваться в реальной действительности, это несколько разные вещи. Ниже будет показано, что поскольку процесс взаимодействияэтои есть процесс явления инерции, то абсолютно все силы по своему происхождению являются силами инерции.

В книге «Удивительная физика» в главе «Кто стоял на плечах гигантов?» Гулиа отмечает, что суть понятия инерции отражена в первом законе Ньютона:

«К сожалению, многие из нас часто неправильно толкуют термин „по инерции“. По инерции крутится маховик, по инерции я ударился лбом о стекло, когда автомобиль затормозил… Все это бытовые понятия инерции. Строгое же только то, которое определяется первым законом Ньютона. Который до него, может, не так точно, но сформулировал… нет, не Галилей — Декарт!»

Причем Гулиа считает определение великого Ньютона неточным, т.к. по его мнению, не то движение считается движением по инерции, в котором отсутствуют «обычные» силы взаимодействия, т.е. отсутствуют какие-либо взаимодействия с другими телами, а то в котором все силы, действующие на тело, скомпенсированы.

Гулиа пишет:

«Возьмем первый закон Ньютона (это тот, который иногда несправедливо приписывают Галилею). Сам Ньютон сформулировал его очень уж мудрено, как, кстати, и во многих школьных учебниках. Автор полагает, что более кратко и проще всего говорить так: «Тело пребывает в покое или движется равномерно и прямолинейно, если равнодействующая внешних сил, приложенных к нему, равна нулю». Вроде бы и придраться тут не к чему. А то пишут в некоторых учебниках: «…если на тело не действуют силы или другие тела…». Неточно это,…»

Но в чём здесь собственно разница? С точки зрения физики никаких неточностей в классической формулировке первого закона Ньютона нет. Если тело испытывает реальные «внешние» воздействия внутри себя и при этом продолжает двигаться равномерно и прямолинейно, то это означает, что другие тела, вызывающие эти воздействия движутся синхронно вместе с этим телом, т.е. являются частью одной замкнутой системы. Следовательно, это внутренние взаимодействия замкнутой системы, равнодействующая сила которых естественно равна нулю.

Не соответствует действительности так же и утверждение Гулиа о том, что строгое понятие инерции «определяется первым законом Ньютона». В формулировке первого закона Ньютона, данной классиком, ни слова не говорится об инерции. Не встречается определение инерции и в формулировке первого закона динамики, данной самим Гулиа. Более того, в первом законе Ньютона внешние силы отсутствуют. Следовательно, в нём не могут проявляться и ответные силы инерционного противодействия, т.к. в отсутствие внешних сил противодействовать собственно и нечему! Поэтому называть первый закон Ньютона законом инерции нет никаких оснований не только по тексту его формулировки, но и по смыслу.

Правда, Гулиа считает силы инерции фиктивными, т.е. несуществующими. Однако никто не отменял третий закон Ньютона (мы это сделаем в следующей главе 1.2.), в соответствии с которым даже фиктивные силы инерции появляются только как реакция на обычные внешние силы, которых в первом законе Ньютона нет. В «Удивительной физике» в главе «Инерция: сила или бессилие?» Гулиа приводит слова Ньютона, которые, по его мнению, определяют смысл сил инерции, как несуществующих сил:

«Врожденная сила материи — есть присущая ей способность сопротивления, по которому всякое отдельно взятое тело удерживает свое состояние покоя или равномерного прямолинейного движения».

Гулиа утверждает, что термин «сила» в приведенном высказывании Ньютона употреблен ошибочно, и эту ошибку впоследствии исправил сам Ньютон, а раз так, то сил инерции по Ньютону не существует. Вот, что говорит сам Гулиа по этому поводу:

«Что же это такое — врожденная сила материи, которую сам Ньютон позже назвал „силой инерции“? Да это же просто инерция, не „сила“, а фундаментальное свойство материи. Раньше, во времена Ньютона, все, что угодно, любили называть „силой“: „сила движения“, „сила убеждения“, „сила любви“, наконец. Тем более сам Ньютон потом поясняет, что термин „сила“ может быть растолкован как „свойство“. Итак, „силы инерции“ по Ньютону — совсем не силы».

Однако на наш взгляд, в этом заключении логика начисто отсутствует. Более того это заключение просто противоречит всем законам логики.

Во-первых. Термин «сила» в переводе с латинского означает действие. Он действительно может быть растолкован как свойство, но свойство действовать. Из этого вовсе не следует, что само слово свойство отменяет действие. Наоборот, свойство материи оказывать сопротивление ее выходу из состояния покоя или равномерного и прямолинейного движения вряд ли можно реализовать в отсутствие действия (силы). Сопротивление и сила — это практически синонимы.

К тому же разве чему-нибудь противоречит объяснение понятия силы, как свойства тел сообщать ускорение другим телам при взаимодействии с ними или противиться ускорению других тел при помощи сил?!

Во-вторых, Гулиа или не понимает, или умышленно искажает смысл высказывания Ньютона. Вопрос ведь не в том, что оказывает сопротивление выходу материальных тел из состояния покоя или равномерного и прямолинейного движения «сила» или «свойство», а в том, что такое сопротивление по Ньютону все-таки возникает. А вот для удержания равномерного движения или покоя, которому в отсутствие сил ничто собственно не угрожает, не требуется никакого силового сопротивления!

В переводе с латинского языка инерция обозначает бездействие. Это действительно очень подходит для обозначения физической сущности первого закона Ньютона. Но это прямо противоположно термину сила — действие. Поэтому Гулиа собственно не зря поднял проблему неправильных терминов. Однако и решил он её неправильно. Если есть два чётких определения двух физических явлений, существование которых никто не оспаривает и которые имеют разный физический смысл, то решать проблему следует не по смыслу неверных терминов, приспосабливая под них смысл явления, а по смыслу физических явлений, приспосабливая термины под них.

Из первого закона Ньютона следует, что состояние равномерного прямолинейного движения или покоя может быть изменено только при наличии других тел или под воздействием внешних сил, что в принципе одно и то же. Следовательно, если возникла проблема удержания состояния покоя или равномерного прямолинейного движения, то это свидетельствует о появлении внешней силы. При этом движение перестаёт подчиняться первому закону Ньютона. Внешние силы и вызываемые ими силы инерции определяются вторым законом Ньютона.

Причём поскольку внешнюю силу и силу инерции одной и той же массы, движущейся с одним и тем же ускорением, определяет один и тот же второй и третий закон Ньютона, то сила инерции равна по величине внешней силе. Следовательно, равнодействующая этих сил должна быть равна нулю, что противоречит второму закону Ньютона, в котором внешняя сила является неуравновешенной силой, и одновременно первому закону Ньютона, в котором внешние силы отсутствуют по определению! Это не оставляет никаких сомнений в том, что первый закон Ньютона и закон инерции Ньютона имеют разный физический смысл.

Гулиа не зря упоминал, что движение «по инерции» стало бытовым понятием. Это значит, что всеобщее понимание этого термина вопреки его дословному переводу связано с реальными силами, которые настолько реальны, что могут привести к серьёзным повреждениям, как техники, так и людей. Следовательно, термин инерция фактически давно уже приобрёл смысл не бездействия, а действия. Поэтому название закона инерции, несмотря на несоответствие ему дословного перевода термина инерция, следует сохранить.

Это не нанесёт ущерба так же и первому закону Ньютона, т.к. в его формулировке термин инерция просто отсутствует. Необходимо только Гулиа и другим популяризаторам, и творцам современной науки прекратить вредные для науки попытки перестраивать её сообразно своим лингвистическим познаниям и поучать своих древних предшественников, на которых большинство из них собственно и заработали свои учёные степени и звания. Не следует рубить сук, на котором сидишь! И потом это просто нечестно. Сначала откажитесь от своих степеней и званий, которые вы заработали на своих древних предшественниках, а потом делайте свою физику и зарабатывайте за неё свои звания честно.

В «Удивительной физике» Гулиа жестко критикует Галилея и уличает в неточности Ньютона, однако логика самого профессора, мягко говоря, не всегда понятна, а порою просто отсутствует. В статье «Алфизики ХХ века» Гулиа с пафосом пишет:

«Мне хочется посоветовать молодым изобретателям, рационализаторам, конструкторам не поддаваться авантюрным увлечениям „сумасшедших“ идей, противоречащих науке. Ведь сама наука предлагает нам столько нового, столько интересного… Не пасть жертвой алфизики, не сделать свою жизнь бесплодной и полной разочарований и неудач — одна из задач занимающихся научно-техническим творчеством. Путь к ее решению — через науку, через непрерывное систематическое учение. И я желаю вам удачи в этом!»

Никто не против систематического учения, только не совсем понятно, что подразумевает Н. В. Гулиа под словом «наука». Складывается впечатление, что наука это только то, что соответствует его личным нынешним взглядам на природу вещей. В связи с этим не совсем понятно, кому Гулиа желает удачи в науке? Всем кто хочет установить истинную природу вещей или только тем, чьи взгляды соответствует нынешним взглядам бывшего алфизика и нынешнего профессора механики Гулиа.

Вспомните, ведь когда-то по его же словам он видимо с не меньшим энтузиазмом, чем тот с которым он сегодня отрицает существование силы инерции, ругал тех, кто как раз не признавал инерцию, как реальную силу (см. «Алфизики ХХ века»):

«Как и следовало ожидать, я обругал (про себя) экспертов, назвал их неучами, ограниченными людьми и пожаловался на них, куда следует за то, что они из-за узости мысли не могут разглядеть проблему века».

Конечно же, очень хорошо, когда человек признает свои ошибки, тем более публично. Однако не рановато ли Гулиа переметнулся в лагерь своих тогдашних идеологических противников, ведь относительно физической сущности явления инерции никто еще ничего никому твердо не доказал вопреки мнению самого Гулиа, что он все всем доказал. Так что неплохо напомнить слова самого Гулиа, приведенные в «Удивительной физике» в главе «Аристотель был прав?»:

«Так что не стоит слепо верить мнениям, даже авторитетным. Правильно говорил Козьма Прутков, что если на клетке слона прочтешь „буйвол“, не верь глазам своим!»

А на каком основании можно верить Гулиа? Все примеры Гулиа с тележками никакого отношения к принципам безопорного движения не имеют. Как можно утверждать, что он Гулиа все и всем доказал, если с другой стороны можно со сто процентной уверенностью сказать, что сам Гулиа ничего толком не знает о природе инерции. И это не голословное утверждение. На сегодняшний день природа инерции официальной наукой, приверженцем которой является Гулиа, не установлена. Не известны и революционные работы самого Гулиа о природе инерции. Все его нынешние доводы не выходят за рамки средней школы.

Сейчас Гулиа стыдно за свои прошлые взгляды. Но как бы ему не было стыдно позднее за то, что он отрекся от этих взглядов, не имея на то никаких объективных оснований. Молодой Гулиа и нынешний профессор Гулиа одинаково знают о природе инерции, т.е. ничего толком о ней не знают. Скорее всего, Гулиа просто сумел рассмотреть на клетке современной физики «табличку» «нет» силам инерции» и даже не выясняя, кто и почему эту табличку прибил, слепо поверил этому, да еще и других теперь пытается учить тому, чего сам толком не понимает.

А что касается его ложного стыда, если, конечно же, он не рисуется, то ничего стыдного в том, что человек ошибается, нет. Профессорами не рождаются. Великий Циолковский тоже изобретал инерцоиды. А вот отказаться от своих взглядов, не убедившись на сто процентов в их ошибочности стыдно. Скорее всего, Гулиа просто расписался в своем бессилии решить проблему и переметнулся в лагерь своих бывших идеологических противников.

По крайне мере на сегодняшний день Гулиа не представил никаких объективных доказательств своего личного глубокого понимания явления инерции, кроме своих нынешних взглядов более или мене соответствующих официальной науке. Единственное его доказательство определяется известным выражением «этого не может быть, потому что не может быть никогда»!

В «Удивительной физике» он критикует практически всех классиков, причем не только в научном плане, что само по себе не вызывает никаких возражений, т.к. профессор ХХ века, какой бы он ни был, знает естественно намного больше, чем его предшественники, жившие более 400 лет назад. Негативную реакцию вызывает тот факт, что Гулиа пытается затрагивать нравственные и личностные вопросы в отношении своих предшественников. Особенно достается Галилею. Даже по поводу одинаковой скорости падения на Землю различных по массе тел под действием притяжения Земли Гулиа счел нужным внести свои не совсем уместные в данном случае поправки только для того, чтобы подчеркнуть некомпетентность Галилея:

«Об ошибках Галилея в определении „инерционного“ движения уже говорилось выше. Да и доказательство того, что тяжелые и легкие тела падают одинаково быстро, сформулированное Галилеем, также оказалось неверным. Тяжелые тела падают быстрее, чем легкие, — эта совершенно правильная мысль Аристотеля уже почти 500 лет, со времени Галилея, считается ошибочной. Не верьте на слово даже Галилею, проверьте сами. Что, пушинка и гиря, выброшенные из окна, приземлятся за одно и то же время? Ах, сопротивление воздуха мешает? Тогда проведите этот же опыт хоть на Луне, где почти нет атмосферы, да только время падения измеряйте поточнее. И увидите, что даже в вакууме тяжелые тела падают быстрее легких, а детям в школах уже сотни лет морочат голову, что гиря и пушинка падают за одно и то же время».

Что же такое «время падения тела?» Это время, прошедшее между моментом освобождения тела (отпусканием груза) и его приземлением (прилунением и т. д.). Определим его. По закону всемирного тяготения на груз и на саму планету (Землю, Луну, астероид, и т. д.) действуют одинаковые по величине и направленные друг к другу силы:

F = γ * M * m / r 2,

где γ — гравитационная постоянная; М, m — массы планеты и груза;

r — расстояние между центрами масс этих тел.

Ускорение груза: aгр = F/m, ускорение планеты: aпл = F/M (ускорения m и M для простоты считаем постоянными). Скорости груза и планеты:

Vгр = aгр t; Vпл = aпл t,

где t — время.

Скорость сближения этих тел (скорость падения): Vпад = (агр+апл) t, при этом средняя скорость падения:

Vпад. ср = Vпад. / 2

где Vпад. — скорость приземления тела. Время падения (оба тела приближенно считаем точками):

t = 2r / Vпад.

Подставляя Vпад, получим:

t = корень (2 * r3 / (γ * (M + m))

Запомните эту формулу — вот истинное время падения одного тела на другое. Так как в знаменателе под корнем сумма масс тел, то при постоянной массе планеты М чем больше масса груза m, тем меньше время падения, т. е. тем быстрее тело падает. Уж если мы хотим быть корректными, то надо говорить, что ускорение одновременно падающих в пустоте тел одинаковое, но при падении порознь тяжелое тело даже в пустоте шлепнется с высоты быстрее, чем легкое, согласно Аристотелю. Потому что сама планета, или пусть даже астероид, на который падает тело, будет тем быстрее двигаться навстречу, чем тяжелее (массивнее) падающее тело.

Так что не стоит слепо верить мнениям, даже авторитетным. Правильно говорил Козьма Прутков, что если на клетке слона прочтешь «буйвол», не верь глазам своим!»

Нам же кажется более очевидной версия Галилея, в соответствии с которой ускорение падения легких и тяжелых тел не зависит от их массы, как при синхронном падении, так и при раздельном падении.

Земля в поле тяготения пробных тел действительно движется навстречу им, так же, как и они движутся навстречу Земле в ее поле тяготения. Ускорение Земли в поле тяготения пробных тел зависит от массы пробных тел. Поэтому точка встречи каждого из этих тел с поверхностью Земли при бросании их по отдельности будет изменять свое положение в пространстве в зависимости от массы пробных тел. Соответственно будет изменяться и время встречи пробных тел разной массы с поверхностью Земли при их раздельном падении.

Однако в соответствии с законом всемирного тяготения скорость падения и у гири и у перышка в поле тяготения Земли будет одинаковая при любой последовательности бросания этих тел к Земле с одинаковой высоты. При этом подтверждением этого факта явиляется не одинаковое время встречи пробных тел разной массы с Землей, а одинаковое время прохождения ими одинаковых расстояний в поле тяготения. Поэтому под словами Галилея «совершенно одинаково», раз уж ему отводят такую историческую роль, следует понимать одинаковую скорость падения пробных тел в поле тяготения Земли.

Галилей полагал, что определяет скорость падения на одинаковом по высоте отрезке для каждого из бросаемых тел. Именно поэтому по одинаковому времени падения пробных тел на Землю Галилей вправе был сделать вывод и об их одинаковой скорости падения. Другого способа определения скорости просто не существует. Причем совершенно очевидно, что Галилей имел в виду именно скорость падения пробных тел:

«…Получаемое противоречие снимается одним утверждением — вес предмета не влияет на скорость свободного падения».

При увеличении массы одного из взаимодействующих тел его ускорение в поле тяготения другого неизменного тела не изменяется, т.к. сила тяготения, действующая на первое тело, изменяется, пропорционально его же массе. Поэтому акцентирование внимания на теоретической разнице времени встречи пробных тел разной массы с Землей при рассмотрении специфики закона всемирного тяготения очень напоминает разговор «про Фому» и «про Ерему», уводящий читателей в сторону от главного вывода, сделанного Галилеем из своих пусть несовершенных в метрологическом отношении опытов.

Кроме того, излишне дотошному Гулиа следовало бы учесть, что в момент бросания массы всех пробных тел фактически изымаются из массы Земли. Поэтому, какую бы пробную массу ни взял Галилей время её падения всегда останется одинаковым. Это легко видеть, подставив в выведенную Гулиа формулу для времени, уменьшившуюся массу Земли в результате изъятия из её массы пробного тела и появившуюся в результате этого массу пробного тела:

t = корень (2 *r3 / (γ (M — m + m))

Как видно, суммарная масса тяготеющих тел всегда остаётся неизменной и всегда равна (М). Следовательно, время встречи всегда остаётся постоянным! По общепринятому мнению Галилей правильно истолковал результаты своих опытов. С исторической ролью Галилея не согласен, пожалуй, один только Гулиа, решивший поумничать с высоты современных знаний. Однако совершенно неизвестно какие выводы сделал бы сам Гулиа во времена Галилея, не зная закона всемирного тяготения, и получи он на месте Галилея разное время падения пробных тел разной массы.

Если бы он рассуждал как Аристотель, то возможно это отодвинуло бы появление закона всемирного тяготения на неопределенный срок. Так что софистикой в этой ситуации являются не рассуждения Галилея, а придирки самого Гулиа.

Вывод:

Двойственность сил инерции определяется искусственным разделением общего напряжения взаимодействия на два противоположно направленных вектора сил. При этом вектор направленный на каждое тело принимается за обычную силу, а вектор направленный на ответное тело — фиктивной силой инерции.

1.2. Формирование сил взаимодействия. Механизм явления инерции «Безопорное» движение, как законное и неизбежное следствие всех несимметричных взаимодействий в природе

1.2.1. Мера взаимодействия и инерции

Очевидно, что меру взаимодействия следует искать среди физических величин являющихся свойствами материи-массы, которые изменяются в процессе взаимодействия. Это движение и сила. Предварительно необходимо чётко обозначить физический смысл этих свойств, которые в классической физике выражены очень уж академически абстрактно.

В физике известен принцип Аристотеля — «природа боится пустоты». Однако в реальной действительности всё обстоит ровно наоборот. Направленность всех взаимодействий от большего напряжения к меньшему обусловлена скорее боязнью тесноты и любовью к пустоте. В соответствие с принципом боязни тесноты две единицы чистой материи не могут занимать одно и то же место в пространстве, т.к. это нарушает их свободную локализацию в пространстве, что и является физической основой взаимодействия материи.

Встречное относительное движение тел, претендующих на общее пространство в точке взаимодействия, сначала преобразуется в общее для всех взаимодействующих тел напряжение-тесноту с мерой силой. А затем в соответствии с принципом боязни тесноты природа ликвидирует образовавшуюся тесноту, с помощью обратного преобразования напряжения в новое относительное движение, направленное в сторону пустоты. В этом и заключается принцип боязни тесноты и любви к пустоте.

В классической модели неуравновешенного движения ответное тело не рассматривается. При этом общее напряжение взаимодействия, одинакового принадлежащее всем взаимодействующим телам, академически подменяется одной абстрактной силой, которая непрерывно прикладывается к телу по ходу его движения. В результате, возникает иллюзия, что сила, синхронно движется вместе с ускоряемым телом и является вектором, направленным на тело, который якобы и определяет направление его движения. Причём в современной физике эта иллюзия возведена в ранг официального академического понятия физической величины силы.

В реальной действительности прикладываются друг к другу вовсе не силы, а сами тела. При этом направление нового движения также определяют сами обменивающиеся движением тела. Академичеки это осуществляется через векторы скорости относительного движения ответных тел. А скалярное напряжение является всего лишь промежуточным звеном, которое одновременно передаёт движение всех взаимодействующих тел во всех заданных телами направлениях. Многолучевую звезду напряжения, образующуюся из векторов скорости встречных движений взаимодействующих тел, вряд ли можно назвать вектором. Даже минимальное количество её лучиков, равное двум, это явно не вектор.

Из этого следует, что сила и движение — это взаимоисключающие свойства материи. Преобразуясь в движение, сила исчезает ровно в той мере, в которой появляется новое движение и наоборот, исчезнувшее движение преобразуется в силу. При этом исчезнувшая сила естественно не может двигаться, а исчезнувшее движение не может создавать напряжение. Образно говоря, при взаимодействии тел, состоящих из множества элементарных масс, по всему пространству, занимаемому взаимодействующими телами последовательно перемещается волна точечных взаимодействий, что и создаёт иллюзию движения силы подобно эффекту «бегущие огни».

Однако при этом огонь-сила никуда не движется. Он лишь последовательно во времени «зажигается» в одних и тех же стационарных точках пространства, через которые в текущий момент времени проходит волна взаимодействий. При этом одновременное существование во взаимодействии таких взаимоисключающих понятий, как напряжение и движение, объясняется ещё не подвергшимися взаимному преобразованию и уже преобразованными напряжением и движением.

Конечно же, приведённое объяснение скорее больше философское, чем строго математическое. Однако у физики, кроме математики всегда есть и своя философия, которая важнее любой математики, т.к. вся математика основана на элементарных физических понятиях, которые и есть философия природы. При этом материя и пространство — это базовые философские понятия физики, которое не имеют исчерпывающих объяснений именно потому, что они для нас пока элементарные.

Элементарные понятия не имеют объяснений в принципе, т.к. для этого требуются ещё более элементарные понятия, чем они сами, которых у нас пока нет. Но тогда мы должны принять как объективную реальность, что наряду с бесспорным для нас сегодня элементарным свойством материи — движением существует ещё и такие элементарные свойства материи, как напряжение-теснота и преобразование напряжение-движение, т.е. взаимодействие.

Совершенно очевидно, что мера взаимодействия пропорциональна двум другим её свойствам, которые участвуют в преобразовании напряжение-движение, т.е. силе и импульсу. Очевидно также, что процесс преобразования напряжение-движение не может происходить мгновенно, а растягивается во времени, в соответствии с эффектом инерции. При этом мера взаимодействия естественно пропорциональна ещё и времени. Осталось лишь выяснить механизм явления инерции, в котором все эти физические величины были бы связаны воедино.

По мере расхода напряжения при его превращении в движение во время разгона градиент преобразования напряжение-движение уменьшается, что замедляет процесс разгона. Это создаёт эффект инерционного противодействия движению извне. По этой же причине снижается эффективность и процесса торможения. По мере расхода подпирающего движения тормозящего тела снижается тормозящий перепад напряжение-движение, что замедляет процесс торможения. Это создаёт эффект поддержки движения извне.

Таким образом, формируется отрицательная обратная связь, которая растягивает процесс во времени с коэффициентом регулирования, равным конечному, не нулевому ускорению, что и есть инерция.

Однако никакого реального противодействия движению извне при разгоне и поддержки движения извне при торможении, в реальной действительности не происходит. Это всего лишь без затратное регулирование процесса взаимодействия замкнутой системы во времени без изменения его общей энергии, в отличие от реальных затрат энергии на дополнительные взаимодействия по внешнему противодействию и внешней поддержке движения.

Приведённый физический механизм явления инерции это и есть процесс взаимодействия, в котором за счёт отрицательной обратной связи перепад напряжение-движение никогда не остаётся постоянным, а изменяется обратно пропорционально движению при разгоне и прямо пропорционально движению при торможении. Синхронно же с постоянной силой к ускоряемому телу может прикладываться только опорное тело с бесконечной массой, как это происходит в классической модели неуравновешенного движения. Однако это исключает естественную инерцию. В этом случае она задаётся искусственно через заданную силу ускоряемого тела, что не соответствует физическому смыслу явления инерции.

Из сказанного следует, что мера взаимодействия, т.е. преобразования напряжение-движение или инерции определяется материей-массой, свойствами материи напряжением-силой, движением-скоростью, а также длительностью-временем преобразования. Все эти физические величины совместно сочетаются только в одной физической величине — энергии, которая таким образом, и есть мера взаимодействия:

Е = N * t = F * V * t / 2 = m * V * a * t / 2 = m * V2 / 2 (1.2.0)

Где:

Множитель «1/2» приводит скорость V к средней скорости Vср. процесса преобразования напряжение-движение при изменении скорости от 0 до V.

N — мощность, равная N = Е / t = F * V * / 2 = F * Vср.

Здесь наша точка зрения в корне расходится с мнением Смирнова А. П., который в статье «Осознание знания — откровение XXI века» пишет, что мерой взаимодействия является не сила и не энергия, а мощность:

«В динамике И. Ньютона причиной изменения состояния является не сила, а действие, необходимое для свершения элементарного акта изменения состояния, которое оценивается произведением действующей силы F на скорость ее действия V, то есть мгновенной мощностью F * V. Ибо сила сама по себе ничего не может совершить, не будучи приложенной с определенной скоростью» (выделение наше — ААА).

Однако сила — это результат остановленного движения, которое образует скалярное напряжение взаимодействия. Следовательно, сила не прикладывается с определенной скоростью, как предлагает считать А. П. Смирнов. Прикладываются друг к другу движущиеся физические тела, которые до наступления взаимодействия не несут в себе никакой силы и никакого действия (работы). Поэтому скорость во взаимодействии принадлежит не силе, а движущейся массе.

А теперь уточним сами понятия меры взаимодействия энергии и работы, которые многие путают. Приведём выдержку из учебника физики для 7 класса Пёрышкина А. В.:

«Желая передвинуть шкаф, мы с силой на него надавливаем, но если он при этом в движение не приходит, то механической работы мы не совершаем. Можно представить себе случай, когда тело движется без участия сил (по инерции), в этом случае механическая работа также не совершается.»

Итак, механическая работа совершается, только когда на тело действует сила и оно движется. Если тело или несколько взаимодействующих между собой тел (система тел) МОГУТ совершить работу, то говорят, что они обладают энергией.

Энергия — физическая величина, показывающая, какую работу МОЖЕТ совершить тело (или несколько тел).»

Как видите, ключевые слова в определении энергии МОГУТ, МОЖЕТ. То есть термин «энергия» означает возможную или потенциальную работу, которая может совершиться при определённых обстоятельствах. А обстоятельства, при которых может совершиться работа — это изменение движения или напряжения. Это может быть, как изменение уже существующего движения, так и изменение движения с нуля, т.е. изменения напряжения из состояния покоя. Первое называют кинетической энергией, а второе — потенциальной энергией!

Таким образом, само по себе движение это ещё не работа. Это всего лишь (возможность, потенция) совершить работу, даже если эту потенцию назвать «кинетическая энергия (возможность, потенция)». Точно также и с напряжением, для которого возможность совершить работу названа «потенциальной энергией (возможностью, потенцией)». В результате имеем два противоречивых алогизма и каламбура в виде кинетической энергии, как кинетической возможности (потенции) совершить работу чистого движения и в виде потенциальной энергии, как

— потенциальной потенциальности;

— потенциальной возможности;

— возможной потенциальности

— возможной возможности

совершить работу чистого напряжения.

Несмотря на то, что словосочетание «кинетическая возможность работы» не является каламбуром, в отличие от «возможной возможности работы», как потенции напряжения, и ещё 3-х перечисленных выше подобных каламбуров для потенциальной энергии, оба термина физически некорректны!

Работа одинаково связана, как с движением-кинетикой, так и с напряжением-потенцией! Это единый общий процесс преобразования напряжение-движение, как из стадии чистого, т.е. равномерного и прямолинейного движения, так и из стадии неподвижного напряжения. Поэтому существующие сегодня в классической физике раздельные понятия кинетической и потенциальной энергии — это откровенная глупость. Работа одна и для движения, и для напряжения. При этом работа не гипотетически возможное действие, а самое, что ни на есть настоящее преобразование напряжение-движение и обратно.

У материи есть не только свойство движение, но ещё и свойство напряжение. При этом, преобразуясь друг в друга, движение и напряжение образуют третье свойство материи — взаимодействие (инерция). Соответственно мерой третьего свойства материи — взаимодействия является общая для этого преобразования работа или энергия, но без прилагательного возможная, т.е. в смысле и в качестве реальной работы. Именно этими теперь синонимами мы и будем называть далее процесс преобразования напряжение-движение, т.е. процесс взаимодействия или инерции, исправляя классические алогизмы.

Процесс преобразования напряжение-движение, являющийся следствием свойства материи боязни тесноты, подразумевает сохранение массы и энергии, т.к. чтобы восстановить прежнее состояние необходимо проделать такую же операцию, как и образование тесноты с той же самой массой и с тем же самым действием, но с обратным знаком. Физическая сущность свойства материи преобразование напряжение-движение, т.е. инерции отражена в законе Бернулли для несжимаемой жидкости в отсутствие трения (m * v2 / 2 + Р * V = const, v — скорость, V — объём), который также основан на законе сохранения массы и энергии.

Объём неизменного массового элемента в неразрывном потоке несжимаемой жидкости остаётся неизменным. Поэтому, когда поток жидкости встречает на своём пути сужение трубопровода, что эквивалентно столкновению тел, давление и соответственно сила напряжения перед сужением увеличивается. При этом увеличивается потенциальная энергия (Р * V). Далее потенциальная энергия в полном соответствии с принципом боязни тесноты реализуется в движение массового элемента жидкости внутри сужения, что сопровождается увеличением его кинетической энергии (m * v2 / 2) с одновременным уменьшением силы и соответственно давления на сужении. На выходе из сужения происходит обратный процесс.

Но это и есть не что иное, как физика преобразования напряжение-движение или инерция, которая создаёт эффект прямого противодействия изменению движения в отсутствие такого противодействия в реальной действительности. В природе нет затратной инерции в виде дополнительных взаимодействий сдерживания или поддержки движения. В природе есть без затратное регулирование процесса взаимодействия во времени за счёт отрицательной обратной связи без изменения общей энергии взаимодействия.

Таким образом, Бернулли, сам того не подозревая, фактически открыл закон взаимосвязи двух свойств материи — движения и напряжения, который представляет собой свойство материи: преобразование напряжение-движение или инерции. Причём, как это ни странно, об этом до сих пор не подозревает и вся современная физика, которая ошибочно связывает явление инерции с первым законом Ньютона, в котором какие-либо реальные силы, определяющие взаимодействие и соответственно явление инерции, отсутствуют. Никакой инерции в её традиционном понимании, как силовое удержание массы в своём текущем состоянии движения в первом законе Ньютона нет.

Термин «удержание» связан с понятием «действие». Но поскольку в отсутствие тесноты в свободном движении текущему состоянию движения массы ничто с помощью реальных сил не противится, то не может быть и никакого удержания этого состояния. В этом и состоит сущность бездействия первого закона Ньютона, что в точности соответствует дословному переводу термина «инерция», как «бездействие». Связывать первый закон Ньютона с действием инерции по силовому удержанию текущего состояния движения — это такая же глупость, как действие по удержанию бездействия или бездействие по удержанию действия.

Этот алогизм и каламбур ничем не отличается от алогизма и каламбура вокруг энергии, когда потенциальная энергия — это в дословном переводе возможная возможность совершить работу, а кинетическая — это возможность, связанная с движением, тогда как в работе одинаково проявляется, как превращение движения в напряжение, так и обратно. То есть работа это не только возможности движения, но и напряжения. (см. выше)!

А вот при нарушении безраздельной локализации материи в пространстве в точке пересечения траектории двух движений проявляется естественное свойство материи преобразование напряжение-движение, которое определяется вторым законом Ньютона. Это, конечно же, не соответствует дословному переводу термина инерция, как бездействие. Но это в точности соответствует, хотя и ошибочному, но традиционному пониманию инерции, как силового противодействия изменению состояния движения. В общем алогизм терминов, связанных с законами Ньютона ничуть не меньший, чем с энергией.

Ну, а фиктивные, т.е. бездействующие силы инерции обязаны своим существованием условно-академической классической модели неуравновешенного движения, в которой общее скалярное напряжение взаимодействия искусственно разделяется на два разнонаправленных вектора силы. И хотя каждый из них определяется вторым законом Ньютона, вектор, направленный против ускоряющегося тела приложен к ответному телу. Естественно, что для ускоряющегося тела этот вектор является фиктивной, т.е. бездействующей силой инерции, что в точности соответствует второму закону Ньютона, который в общем напряжении взаимодействия академически имитирует только свой действующий вектор для каждой стороны взаимодействия.

Тем не менее, общее скалярное напряжение взаимодействия одновременно превращается в движение масс сразу всех сторон взаимодействия. Это реально ограничивает энергию преобразования напряжение-движение для каждой ускоряемой массы, что сказывается на ускорении, т.е. на интенсивности процесса преобразования напряжение-движение для каждой массы. Кроме того, как показано выше, ускорение процесса преобразования напряжение-движение определяется его отрицательной обратной связью. Всё это в совокупности и создаёт иллюзию реального вектора силы, направленного против ускоренного движения и вектора силы, поддерживающего останавливаемое движение, что и есть инерция.

Таким образом, классических фиктивных сил инерции в природе действительно нет, но поскольку абсолютно все эффекты явления инерции обусловлены реальными законами взаимодействия, определяющимися третьим свойством материи преобразованием напряжение-движение или другими словами свойством инерции, то все силы Вселенной по своему физическому смыслу являются силами инерции. Но это не соответствует классическому смыслу сил инерции.

Все законы Ньютона тесно взаимосвязаны между собой, главным из которых на наш взгляд является второй закон Ньютона, т.к. именно он определяет все действия в природе, в которых и рождаются все силы во Вселенной. Из него легко получить, в том числе и закон взаимодействия в виде его меры — энергии. Для этого достаточно проинтегрировать силу по пути или умножить второй закон Ньютона на расстояние:

∫F * dS = m * V 2/ 2 = F * S = E

Первый закон Ньютона не является самостоятельным законом. Это всего лишь следствие из второго закона Ньютона в отсутствие силы (F = 0). При этом важность первого закона Ньютона, как определения для инерциальных систем, в которых якобы потом и работает второй закон Ньютона, мягко говоря, сильно преувеличена. Поскольку все ЗН тесно взаимосвязаны, то всё что соответствует одному из них, соответствует и другому. Поэтому определение ИСО через второй закон будет совершенно аналогичным определению этой же ИСО и через первый закон.

Сравните сами. Ниже представлено официальное определение ИСО и наша параллель этого определения на основе второго ЗН:

I закон.

«Существуют системы отсчета, называемые инерциальными, в которых любое тело находится в состоянии покоя или движется равномерно и прямолинейно, если на него не действуют другие тела или действие этих тел скомпенсировано.»

II закон.

Существуют системы отсчета, называемые инерциальными, в которых любое тело приобретает движение исключительно только за счёт приложенной к ней силы, а не за счёт свойств систем отсчета.

Совершенно очевидно, что ускорения, проявляющиеся в СО при (F = 0), вносят искажения и во второй закон Ньютона при (F ≠ 0). То есть, если приобретаемое телом движение соответствует второму закону Ньютона, то это ИСО, а если не соответствует — то не ИСО (НИСО). Если в отсутствие силы (F = 0) тело не приобретёт нового движения, т.е. будет находится в такой системе в покое, либо двигаться равномерно и прямолинейно, то это также ИСО, но уже в соответствии со следствием из второго ЗН в виде первого ЗН.

Таким образом, нет никакой принципиальной разницы через какой ЗН первый или второй определять ИСО. Кроме того, оценка по отсутствию чего-то всегда менее достоверная, чем по несоответствию присутствия чего-то. При этом, как видите, определение ИСО через второй закон более точное и лаконичное.

Третий закон Ньютона — это вообще самое большое недоразумение в современной классической механике. Его вообще следует упразднить и чем скорее, тем лучше для физики и физиков, а также для студентов и школьников, т.к. он вот уже почти три столетия вносит в физику смуту и путаницу, которую, к тому же, усугубил ещё и Даламбер.

Нет никаких разных по направлению и равных по величине, но при этом якобы принципиально разных физически сил действия и противодействия, о которых говорится в 3-ем законе Ньютона. Есть одна единственная общая для всех взаимодействующих тел сила взаимодействия. Образно её можно представить в виде одного единственного резинового мячика-силы между взаимодействующими телами, которая при помощи природных «манипуляторов» в виде молекул воздуха внутри мячика-силы, передают общую силу взаимодействия на все взаимодействующие тела.

С точки зрения здравого смысла, да собственно и классической физики тоже, на два тела есть только одно действие, которое так и называется ВЗАИМ-о-ДЕЙСТВИЕ. Естественно, что одно действие имеет только одно время старта и одно время финиша, а не два разных времени для действия и противодействия. А равенство сил в каждую сторону легко объясняется общим напряжением единого действия, которое, как давление в общем сосуде действует на стенки с одной и той же по величине силой во всех направления от ЦМ взаимодействия, что делает 3-й закон Ньютона бессмысленным.

В общем случае манипуляторы, передающие одну-единственную общую силу взаимодействия, можно обозначить n стрелочками вдоль симметрично расположенных n/2 линий с центром в точке ЦМ взаимодействия, где n — чётное натуральное число. Такую звёздочку вряд ли можно назвать вектором. А разные силы действия и противодействия есть только у математико-физиков, которые в силу своей преобладающей над физической составляющей математической специфики, ошибочно называют две противоположные стрелочки, фактически обозначающие два манипулятора, раздающих одну общую силу, двумя разными векторами силы.

Третий закон Ньютона записывается следующим образом.

F→1 = — F→2

При переносе (- F→2) в левую часть получаем:

F1→ + F2→ = 0

Однако разные вектора, приложенные к разным телам, никак не могут в сумме давать ноль. Вектора равны только по модулю.

|F→1| = |- F→2|

Но и знак модуля не спасёт 3-ий ЗН, т.к. в нём речь идёт не только о модулях, но о разных телах, к которым в разных направлениях приложены разные силы.

Аналогичный абсурд наблюдается и в классическом выводе закона сохранения импульса (ЗСИ), который мошенническим путём получают из 3-го ЗН:

F1→ = — F2→

m1 * a1→ = — m2 * a2→

m1 * V1ʹ→ — m1 * V1→ = — m2 * V2ʹ→ + m2 * V2→

m2 * V2→ + m1 * V1→ = m2 * V2ʹ→ + m1 * V1ʹ→

P1→ + P2→ = P1ʹ→ + P2ʹ→

А мошеннический этот вывод потому что 3-ий ЗН для отдельных тел системы, а ЗСИ уже для всей системы в целом. Правомерным этот вывод будет только если предварительно оговорить, что F1→ и — F2→ это не силы действия и противодействия, а два разнонаправленных воздействия одной внутренней силы на один объект — систему. Или если весь вывод провести в абсолютных величинах |F1→| и |- F2→|

А вот для 3-го ЗН устранение этой проблемы, как показано выше, не возможно в принципе. Можно конечно, как и в случае с ЗСИ, заменить классическое неравенство сил из 3-го ЗН на равенство их абсолютных величин. Но это не решит проблему, т.к. ни складывать, ни вычитать силы, приложенные к разным телам, недопустимо физически ни в каком их виде, в том числе и в виде модулей. Закона сохранения силы в природе нет. Есть одна общая сила взаимодействия в системе и ЗСИ системы. При этом мы просто превращаем 3-ий ЗН в ЗСИ, что опять же свидетельствует о фиктивности 3-го ЗН.

Никто не отрицает, что все силы во Вселенной рождаются только в составе системы тел. Но при этом никто не отменял и 2-ой ЗН, который применяется для отдельных тел вне системы. А значит и 3-ий ЗН, разделённый на две разные силы, подчиняющиеся 2-му ЗН, некорректно искусственно ассоциировать с системой. Сегодня никто уже точно не скажет, что имел в виду Ньютон в разделе «Закон III», в котором он смешал в одну кучу 2-ой и 3-ий законы, а также ЗСИ. Нам остаётся только догадываться, зачем Ньютон пытался совместить несовместимое. Тем не менее, это так (см. И. Ньютон, Математические начала натуральной философии, Закон III, стр. 41, под редакциепй Л.С.Полака, Москва, «Наука», 1989):

«Закон III.

Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны.

Если что-либо давит на что-нибудь другое или тянет его, то оно само этим последним давится или тянется.»

Но если речь идёт о разных силах, действующих на разные тела, как записано в определении 3-го ЗН, то это не система тел, а два неуравновешенных движения, каждое в своём направлении, под действием сил, подчиняющихся 2-му ЗН. В этом случае мы не вправе приравнивать разные силы, по 3-му ЗН. Однако далее в разъяснении формулировки якобы 3-го ЗН в современном его понимании, Ньютон говорит уже фактически не о равенстве сил, а о равенстве импульсов, т.е. о ЗСИ.

Читаем у Ньютона:

«Если какое-нибудь тело, ударившись в другое тело, изменяет своею силою его количество движения на сколько-нибудь, то оно претерпит от силы второго тела в своем собственном количестве движения то же самое изменение, но обратно направленное, ибо давления этих тел друг на друга постоянно равны.

…натянутый канат своею упругостью производит одинаковое усилие на лошадь в сторону камня и на камень в сторону лошади…»

Обратите внимание, хотя две силы здесь всё же упоминаются, но речь идёт вовсе не о самом процессе производства движения тел при помощи сил из 2-го ЗН, а о сохранении уже готового движения системы, что характерно исключительно только для ЗСИ, а не для сил из 3-го ЗН. Как уже отмечалось выше, закона сохранения сил в природе не существует. Есть одна общая сила взаимодействия. «Натянутый канат» у Ньютона производит именно «одинаковое усилие», а не одинаковые усилия. Всё это не соответствует 3-му ЗН. Зато это в точности соответствует ЗСИ, который определяет сохранение количества уже готового движения.

Поскольку импульс определяет количество движения, как такового, то любые его выражения через силу, например, в виде импульса силы (P = F * t = m * V), которые в конечном итоге сводятся к необходимым и достаточным условиям определения количества движения (P = m * V), могут быть верны только количественно. Качественно же импульс, как количество уже готового движения с достигнутой скоростью, не пропорционален ни силе, ни времени.

Ошибочно считать, что импульс изменяется со временем в отсутствие процесса преобразования напряжения в движение, даже если он выражен через силу. Это лишь упоминание о прошлой силе, уже преобразованной в движение. При этом сам процесс преобразования характеризуется энергией, а не импульсом. В выражении же (P = m * V = F * t) нет дополнительного условия в виде второй скорости (квадрата скорости) для дополнительного движения по изменению исходного движения. Следовательно, есть все основания считать, что под 3-м законом Ньютон фактически понимал и открыл ЗСИ.

При этом 3-ий ЗН в его современном понимании абсурден. Он описывает противодействие разных сил, приложенных к разным телам, чего не может быть в принципе. Поскольку прикладываются не силы, а тела, то нет двух сил. Есть два тела и одна общая сила между ними, а точнее одно общее скалярное НАПРЯЖЕНИЕ. А направление замедления старого и ускорения нового движения определяет вектор скорости ответных тел.

Конечно же, никаких резиновых мячиков между взаимодействующими телами в реальной действительности нет. Но есть общий физический котёл взаимодействия, в котором варится одна общая для всех взаимодействующих тел сила. При этом вопрос о равенстве несуществующих в природе сил действия и противодействия снимается естественным образом, без феноменологически необъяснимого фиктивного 3-го закона Ньютона.

Одна и та же сила естественно всегда в точности равна самой себе. А природные манипуляторы в виде физического механизма явления упругости на уровне амеров среды доводят действие этой силы до всех взаимодействующих тел в равной степени (см. ниже — механизм формирования сил взаимодействия на основе явления инерции, как врождённого свойства материи и сил инерции, как сопротивления мировой материальной среды в настоящей главе).

Если же вдруг общая сила (напряжение) взаимодействия не всегда в равной степени доводится до взаимодействующих тел, как показали некоторые последние исследования в электродинамике и т.д., то даже в этом случае никакие законы природы ни в коем случае не нарушаются. В этом случае — следует искать «сбои», а точнее законные механизмы в работе передающих манипуляторов, что вероятно и лежит в основе безопорного движения.

Если силы две, вместо одной силы взаимодействия, то они могут быть только виртуальные или абстрактные, т.е. действующие только в одну сторону, без упора с другой стороны. Именно такой абстрактной стрелочкой и являются силы в классической модели неуравновешенного движения (см. выше в начале главы). Реальным же силам всегда нужен упор. При этом две одинаковые силы, упирающиеся с одной стороны друг в друга, а с другой в тела создавали бы между телами двойное по величине напряжение взаимодействия, чего в реальной действительности не наблюдается.

Вот и получается, что в реальной действительности есть ОДНА общая сила, которая действует во все стороны и по всему объёму, как давление в сосуде, что академически обозначается абстрактной стрелкой, ошибочно называемой в классической физике силой. Прикладываются не силы, а тела. А тела не могут прикладываться в точке ЦМ или в точке поверхности тел. Поэтому нет ничего удивительного и противоречивого в том, что силу мы называем напряжением. А поскольку сил в точке реально не бывает, то можно пользоваться одним термином — сила, но в качестве давления (напряжения).

Сила в точке это всего лишь академический приём для упрощения модели неуравновешенного движения и расчётов по ней. Физически же силы равномерно распределяются по объёмной площади массовых элементов каждого тела так, что на каждое тело взаимодействия в целом приходится одинаковая общая сила взаимодействия (см. ниже — механизм формирования сил взаимодействия… в настоящей главе). Именно поэтому скорость и ускорение каждого тела обратно пропорциональны их массе.

Конечно же, напряжение в процессе взаимодействия может непрерывно изменяться и изменяется. Однако в каждый момент времени общая сила остаётся одинаковой для каждого взаимодействующего тела, подобно давлению внутри сосуда, которое успевает равномерно распределиться по всему его объёму, даже в случае определённых колебаний, как величины самого давления, так и объёма сосуда. В нашем случае речь идёт об упомянутой выше «объёмной площади». Тем не менее, есть все основания полагать, что в динамике силы реальных взаимодействий всё-таки могут распределяться и распределяются не равномерно.

В сторону меньшего тела, которое движется быстрее, напряжение взаимодействия разряжается быстрее, чем в сторону большего тела. Поэтому при выравнивании общего напряжения взаимодействия массовые элементы области деформации воздействуют на меньшее тело с большей скоростью и соответственно с несколько большей силой, чем на бОльшее тело и чем предписывает усредняющий академический закон сохранения импульса и упразднённый нами третий закон Ньютона. При этом может возникать эффект «безопорного» движения всей системы в сторону меньшего тела (см. главу 11.3.).

Но это верно только в том случае, если напряжение взаимодействия разряжается значительно быстрее скорости меньшего тела. В противном случае бОльшая сила буде для бОльшего тела, т.к. меньшее будет убегать от воздействия. Причём этот эффект экспериментально обнаружить очень сложно. Напряжение тут же превращается в движение тел. При этом оставшееся общее внутреннее напряжение взаимодействия тут же выравнивается по всему его объёму.

Именно поэтому мы и вынуждены в расчёте взаимодействий использовать не напряжение на текущей границе каждого тела с зоной деформации, а общее усреднённое напряжение всей текущей зоны деформации, т.е. общую силу взаимодействия.

А теперь опять же в плане «осознания знания» уточним понятие массы.

Материя является основным вещественным инвариантом природы, которая никуда не исчезает и не возникает из ниоткуда. Изменяются только её свойства, что и обеспечивает всё многообразие состояния материи и многообразие явлений природы. Поэтому массу, как меру материи, не совсем корректно называть неким безликим коэффициентом пропорциональности свойств материи, в том числе и силы.

Масса это самый значимый аргумент всех функций, описывающих явления природы, связанные с изменением свойств материи, т.к. именно масса является носителем этих свойств. Поэтому в уравнении силы (F = m * a) коэффициентом пропорциональности является не масса, как принято считать в современной физике, а ускорение, которое является коэффициентом преобразования напряжение-движение. Соответственно коэффициентом самого количества движения материи в уравнении импульса (P = m * V) является скорость, состоящая из двух коэффициентов (V = a * t)).

В классической же физике с массой обращаются даже как-то неприлично. То она — мера инертности, то просто всего лишь коэффициент при ускорении, то мера количества материи. И всё это ошибочно называют тремя свойствами массы. Но это не есть три свойства массы. Это всего лишь три её интерпретации в современной физике, что вовсе не одно и то же со свойствами. Причём все эти интерпретации за исключением интерпретации массы, как количества материи, достаточно спорные. Например инертность может в некоторой степени определять и мировая соеда.

Ну, и раз уж мы поменяли векторную силу на скалярное напряжение, то в плане всё того же «осознания знания» следует уточнить и понятие самого скалярного напряжения-силы. Напряжение-сила это есть мера свойства материи сопротивляться нарушению свободной локализации материи в пространстве, когда две единицы материи (единичные элементы материи) претендуют на одно и то же пространство в следствие своего природного свойства — движения.

Таким образом, сила это мера нарушения локализации материи в пространстве или напряжения-тесноты, которая определяет степень воздействия одного тела на другое. Отсюда следует, что, как мы отмечали выше, природа боится не пустоты, а тесноты.

Кроме врожденных сил инерции в природе существует ещё и механизм инерции поэлементной поддержки в виде реальных сил, которые напрямую обеспечивают реальное противодействие и поддержку движению. Однако физической основой этого механизма в любом случае является механизм врождённой инерции. Механизм инерции поэлементной поддержки легко объяснить, если взаимодействующие тела представить в виде совокупности элементарных масс материи.

На первом этапе взаимодействия в напряжение сначала превращается движение внутренних по отношению к центру взаимодействия элементов материи-массы взаимодействующих тел. При этом, как только появляется первое же напряжение, в то же самое мгновение исчезает и движение, которое в это напряжение превратилось. Однако приостановленная элементарная масса тут же получает новую порцию движения от движущейся за ней ещё не остановленной элементарной массы, что реально поддерживает совместное движение всего тела в целом, препятствуя его торможению.

На втором этапе взаимодействия при разгоне тел всё происходит ровно наоборот. Как только напряжение превращается в движение внутренней по отношению к центру взаимодействия элементарной массы, напряжение тут же и в такой же степени исчезает. Однако эта масса тут же начинает взаимодействовать с ещё не получившей движение внешней массой. При этом вполне реальная сила взаимодействия отнимает часть движения у первой массы, а их общее совместное движение естественно замедляется, что препятствует разгону всего тела.

Тем не менее, внешними эти вполне реальные силы инерции поэлементной поддержки являются только для отдельно взятых элементарных масс, образующих взаимодействующие тела. Для системы взаимодействующих тел в целом эти силы являются внутренними силами. Поэтому для замкнутой системы взаимодействующих тел, состоящих из элементарных масс, эти силы, как и силы врождённой инерции, являются фиктивными.

Если предположить существование мировой материальной среды, то вся Вселенная в целом в принципе является единой замкнутой системой, несмотря на её возможную бесконечность. Однако для взаимодействий внутри отдельных систем макротел сопротивление мировой материальной среды по типу инерции поэлементной поддержки можно считать внешним.

Более того, сопротивление среды, по всей видимости, играет если и не теоретически определяющую, то количественно преобладающую роль в формировании инерционного сопротивления, т.к. весь мир всегда больше любой его части. О количественно преобладающем сопротивлении среды свидетельствует огромная разница сил в разных видах взаимодействия одной и той же материи с одной и той же массой.

Например, гравитационная постоянная определяет огромную разницу сил инертного и гравитационного взаимодействия одних и тех же масс. А поскольку материя и соответственно врождённое свойство материи преобразование напряжение-движение у всех одинаковых масс одни и те же, то остаётся предположить, что эту разницу может обеспечивать только разное сопротивление среды, которая, безусловно, участвует во всех видах взаимодействий.

Силы прямого внешнего сопротивления, оказываемого ускоренному движению материальных тел со стороны мировой материальной среды в отличие от классических фиктивных сил инерции мы условно называем истинными силами инерции, т.к. они реально отбирают энергию у взаимодействия макротел. Силы инерции поэлементной поддержки внутри самих тел назовём Ньютоновскими силами инерции. Эти два вида инерции, наряду с врождёнными силами инерции и обеспечивают явление инерции в целом.

С учётом составляющей силы инерции в виде прямого сопротивления мировой материальной среды, элементы которой покидают зону взаимодействия физических тел, полное противодействие физическим телам, взаимодействующим между собой на макроуровне, завершается во внешнем открытом пространстве на уровне элементов мировой материальной среды далеко за пределами взаимодействующих тел. Поэтому все законы природы, проявляющиеся во взаимодействии физических тел, полностью, т.е. идеально выполняются только с учётом всех элементов материи и мировой материальной среды, участвующих во взаимодействии.

Вполне возможно, что мировая материальная среда не только существует, но играет определяющую роль в природе. Без внешнего связующего давления среды под вопрос ставится само существование совокупности элементарных масс в виде физических тел и вещества. По всей видимости, именно внешнее давление среды и удерживает материю в составе физических тел и вещества. Мы уже не говорим о том, что это строительный материал для вещества физических тел. Мировая материальная среда может ответить на многие неразрешённые вопросы современной физики. А о наличии среды косвенно свидетельствует очень большое количество природных явлений, в том числе и само строение вещества:

Во-первых, что-то всё-таки очень сильно мешает проявлению законов динамики Ньютона и законов сохранения в их чистом академическом виде, да так, что иногда приходится даже сомневаться в их правильности. Для выхода из этого тупика, как раз и не хватает среды, которую физика однажды опрометчиво упразднила в угоду СТО. Восстановление прав среды в физике поможет понять физическую сущность эмпирических и разрозненных сегодня законов физики, которые фактически являются всего лишь разным проявлением единого закона мироздания — явления инерции.

Во-вторых, даже если бы среды изначально не было бы, то она непременно должна была появиться в результате распада вещества в процессе многочисленных контактных взаимодействий и процессов, происходящих в звёздах на уровне взаимодействия элементарных частиц. Да, и строение вещества свидетельствует о том, что оно собрано из чего-то элементарного, находящегося в пространстве помимо готовых тел, иначе ему просто негде находится. И нет никаких оснований считать, что весь строительный материал уже давно закончился.

Кроме того, без среды невозможно объяснить дальнодействие. Даже баллистические теории, которые на первый взгляд обходятся без среды, тем не менее, предполагают её наличие. Ведь так называемые «снаряды» дальнего контактного взаимодействия и неизбежные осколки такого взаимодействия это и есть не что иное, что в последствии становится средой.

В-третьих, как известно все физические тела и вещество, более чем на 99% состоят из пустоты. Следовательно, при контактных взаимодействиях физические тела должны как минимум очень глубоко проникать друг в друга. Однако в реальной действительности этого не наблюдается, следовательно, что-то заставляет тела останавливаться при взаимодействии задолго до сколько-нибудь значительного их проникновения друг в друга. В отсутствие какой-либо жесткой оболочки тел это может означать только одно, во время взаимодействия пустое пространство между структурами вещества тел, заполняется чем-то упругим, принимающим участие во взаимодействии наряду со структурами вещества.

В-четвёртых, если внутренняя среда физических тел и вещества непроницаема для крупных структур вещества, то она не может не взаимодействовать, в том числе и с внешней средой пространства, какой бы разряжённой та ни была. Вот вам и парус взаимодействия. Однако после прекращения взаимодействия инерционное сопротивление исчезает. Следовательно, после прекращения взаимодействия исчезает и внутреннее наполнение тел, т.е. парус взаимодействия. Это хорошо согласуется с беспрепятственным движением практически пустых тел сквозь очень разряжённую среду практически с любыми по величине постоянными скоростями, т.е. по инерции.

В-пятых, в разных типах (видах) взаимодействия одни и те же тела, т.е. одно и то же количество одной и той же материи испытывают разное инерционное противодействие. При наличии единого для всей материи врождённого свойства — инерции это можно объяснить только различным наполнением внутреннего пространства вещества элементарными материальными частицами при взаимодействии, что сказывается на внешнем сопротивлении среды для них. Следовательно, механизм инерции во всех типах взаимодействия определяется тремя факторами: врождённым свойством материи взаимопревращения движения и силы, Ньютоновскими силами инерции поэлементной поддержки и истинными силами инерции, т.е. привнесённым сопротивлением мировой материальной среды.

И, наконец, в-шестых, поскольку разница сил взаимодействия в разных типах взаимодействия, например в инертных и гравитационных взаимодействиях просто огромна, то из этого мы должны сделать единственно возможный вывод. При едином и одинаковым для всей материи врождённом свойстве инерции, силы сопротивления среды, которые в сильных контактных взаимодействиях образуют бОльший парус, чем в слабых гравитационных взаимодействиях, играют в механизме инерции определяющую количественную роль.

Таким образом, инерционность массы, по видимому, определяется не только самой массой физического тела (врождённой инерцией), но и сопротивлением мировой материальной среды, в которой происходит взаимодействие???

***

С учетом среды появляется возможность создать непротиворечивую модель формирования сил взаимодействия на основе явления инерции, как врождённого свойства материи и сил инерции, как сопротивления мировой материальной среды. Назовём силы сопротивления мировой материальной среды «истинными силами инерции». Это позволит дифференцировать сопротивление мировой материальной среды от лежащего в основе любого сопротивления вообще — врождённого свойства материи взаимопревращения напряжения и движения.

Но прежде чем предложить механизм формирования сил взаимодействия и инерционного сопротивления на основе мировой материальной среды следует прояснить вопрос, как среда удерживает элементарные массы в составе физических тел.

Внутренние связи физических тел и вещества, по всей видимости, обеспечиваются внешним давлением со стороны мировой материальной среды. Естественная передача энергии в природе всегда осуществляется только в прямом направлении по ходу движения любых «носителей» энергии. В соответствии с принципом боязни тесноты элементы материи естественным образом могут только выталкивать друг друга из зоны их повышенной концентрации в пространство, в котором материи меньше или она отсутствует, но никак не наоборот.

Пустое пространство не может втягивать материю по той простой причине, что в отсутствие материи в пустом пространстве втягивать в него другую материю просто нечем. Нет таких верёвочек у природы. Даже если материальное тело увлекает за собой другое тело по типу «буксир», происходит прямая передача энергии, как будто буксир, который закреплен с заднего конца буксируемого тела. При буксировке за передний конец между передним массовым элементом и остальным телом образуется разряжение. В результате среда опять же подталкивает всё тело сзади.

Таким образом, любые внутренние связи всегда обеспечиваются внешним давлением, в то время как внутреннее разряжение имеет к этому только формально-опосредованное отношение, как место, в котором образуются физические тела с внутренними связями. За счёт внешнего давления мировой материальной среды осуществляется и упругое взаимодействие между структурными элементами физических тел, которое обеспечивает равномерное «распределение» энергии между ними по всему объёму тел после прекращения действия внешних сил.

Упругое взаимодействие между структурами вещества невозможно в отсутствии инерционного сопротивления (давления) среды со стороны открытого пространства, т.к. в противном случае мы получим безопорное изменение направления движения внутренних элементов тела при отражении их от границ тела и абстрактную ничем не обеспеченную их упругую взаимосвязь между собой. Это относится и к электрическим взаимодействиям, к которым классическая физика, на наш взгляд ошибочно, относит природу сил упругости.

Ну, а теперь перейдем к возможному механизму формирования сил взаимодействия и инерционного сопротивления на основе мировой материальной среды.

По всей видимости, вещество физических тел и мировая материальная среда в конечном итоге состоят из одинаковых элементов, которые представляют собой мельчайшие первокирпичики материи на каком-то базовом для нашего мира уровне деления материи. В веществе базовые элементы присутствуют в более концентрированном виде и приобретают дополнительные связи, образуя укрупнённые структуры вещества и физических тел. Но не исключено, что в структурах вещества материальных тел присутствуют свободные элементы мировой материальной среды, подобно существованию свободных электронов в проводниках.

В невозбужденных физических телах элементы мировой материальной среды и материи компактно концентрируются в непосредственной близости к устойчивым мельчайшим структурам вещества. При этом свободные элементы материи должны удерживаться в веществе не столь сильно в отличие от элементов, непосредственно формирующих структурные образования вещества. Тем не менее, они должны быть связаны с материей физических тел некоторой энергией связи, удерживающей их в составе вещества давлением внутренней среды тела.

Поскольку расстояния между структурами вещества несоизмеримо больше их собственных размеров, т.е. вещество преимущественно состоит из «пустоты», то вероятность непосредственного контакта между структурами вещества и элементами среды открытого пространства при движении тел и частиц относительно мала. Это обстоятельство, очевидно, и обеспечивает инерционное (в традиционном смысле) движение, т.е. практически беспрепятственное равномерное и прямолинейное движение физических тел в мировой материальной среде, что и отражено в первом законе Ньютона.

Сопротивление возникает только при непосредственном контакте элементов среды с веществом. Однако поскольку вещество состоит преимущественно из пустоты, то прямые столкновения маловероятны, а если все же и происходят, то они относительно не многочисленны и не оказывают существенного сопротивления движению. Если элементы среды проходят в непосредственной близости от вещества, то они, прежде всего, взаимодействует с его свободными элементами, находящимися вблизи структур вещества в концентрированном виде.

Поскольку свободные элементы связаны с телом относительно небольшой энергией связи, то при их взаимодействии с элементами среды, последние в соответствии с механизмом абсолютно-упругого удара останавливаются по отношению к телу и захватываются им, а собственные свободные элементы покидают тело. Такое замещение практически эквивалентно беспрепятственному сквозному прохождению элементов среды через физическое тело. И даже в очень редких случаях захвата элементы среды изменяют энергию тела незначительно.

С началом взаимодействия, сопровождающегося деформацией тел, внутренние связи возбуждаются. При этом собственные свободные элементы выделяются в промежуточное между структурами вещества пространство, многократно увеличивая плотность внутренней среды в физическом теле, образуя объёмный парус взаимодействия с внешней средой. Этот парус и тормозит тело при его движении, т.к. теперь мировая материальная среда оказывает ему вполне ощутимое инерционное сопротивление на достаточно большой площади сечения тела по всему его объему.

Поскольку количество высвободившихся свободных элементов и соответственно объёмная (совокупная) площадь контакта паруса взаимодействия с мировой материальной средой пропорциональны его массе, а сила сопротивления пропорциональна ещё и ускорению тела, то инерционное сопротивление прямо пропорционально массе и ускорению тела, что и отражено во втором законе Ньютона.

После прекращения взаимодействия упругая деформация разряжается, и физическое тело вновь приходит в равновесное состояние. При этом свободные элементы вновь захватываются структурами вещества, а площадь взаимодействия тела с мировой материальной средой восстанавливается до состояния невозбужденного тела, т.е. парус сворачивается. Не встречая инерционного сопротивления мировой материальной среды, практически пустое тело без паруса продолжает двигаться равномерно и прямолинейно с достигнутой на текущий момент скоростью.

Предложенная схема образования инерционного сопротивления мировой материальной среды неуравновешенному движению физических тел за счёт свободных первокирпичиков материи в их составе позволяет достаточно непротиворечиво, хотя всего лишь схематично объяснить и физический механизм перераспределения энергии взаимодействия, а также механизм формирования сил взаимодействия. Причём этот механизм не требует никаких постулатов. Нужна только среда, которую хотя напрямую и не открыли, но косвенные признаки её существования не вызывают никаких сомнений.

Рассмотрим для простоты сначала механизм взаимодействия двух одинаковых по массе физических тел.

Под действием внутреннего избыточного давления элементарных масс, выделившихся в зону взаимодействия, которые образуют не только парус, но и дополнительные силы взаимодействия, одинаковые тела получат и одинаковое ускорение и в конечном итоге одинаковую скорость, равную скорости их первоначального движения. Это полностью соответствует законам сохранения энергии, импульса и законам динамики Ньютона, которое легко обосновать, хотя бы полной симметрией такого взаимодействия.

Теперь рассмотрим разные по массе тела. Пусть для простоты взаимодействующие тела представлены параллельными рядами структурных элементов, расположенных друг напротив друга. Причём меньшее по массе тело состоит из одного ряда структурных элементов, а большее тело из двух таких же рядов.

В первое мгновение первые ряды структурных элементов взаимодействующих тел получат одинаковые ускорения. Однако при взаимодействии рядов большего тела между собой выделится дополнительное количество элементарных масс, которые одновременно образуют, как общую силу так и парус взаимодействия. При этом поскольку в двух рядах большего тела вдвое больше структурных элементов, в нём распустится практически вдвое больший по объемной площади парус.

Таким образом, мировая материальная среда открытого пространства со стороны большего тела оказывает ему большее инерционное сопротивление, чем меньшему телу. Следовательно, при одинаковой силе внутреннего давления большее тело получит меньшее ускорение, чем меньшее тело.

Но больший парус одновременно представляет и большее препятствие для движущей силы. Это приведёт к отражению элементов силы взаимодействия от большего тела в сторону меньшего тела. При этом меньшее тело будет испытывать большую силу, чем предписывает третий закон Ньютона, а большее тело соответственно получит силу меньше законной. Получив большую силу, меньшее тело ускорится несколько больше, чем предписывает закон сохранения импульса, а большее тело после оттока движущей силы получит ускорение меньше законного.

Возросшая сила, приложенная к меньшему телу, приведёт к его дополнительной деформации и соответственно к повышению его инерционного сопротивления, что приведёт к его замедлению. Одновременно от него в сторону большего тела отразится и часть движущей силы, что так же способствует замедлению меньшего тела. При этом большее тело, получив отражённую силу, дополнительно ускорится, после чего движущая сила снова отразится в сторону меньшего тела, и весь процесс повторится на меньшем энергетическом уровне, т.к. увеличение расстояния между телами и боковые объемные потери силовых элементов приводят к уменьшению внутреннего давления.

Таким образом, через регулирование сил взаимодействия осуществляется отрицательная обратная связь между импульсами взаимодействующих тел, в результате чего происходит постепенное выравнивание сил и стабилизация импульсов. Это и есть механизм действия закона сохранения импульса и энергии на основе второго закона Ньютона.

При этом поскольку законы природы не должны нарушаться ни при каких обстоятельствах, некоторое отклонение движения взаимодействующих тел от законов сохранения на начальном этапе взаимодействия компенсируется уже за внешней границей тел, где им уже в открытом пространстве оказывается недостающее до полного выполнения законов сохранения и законов динамики Ньютона инерционное сопротивление со своими знаками.

При этом если на уровне физических тел дисбаланс и сил оказался в пользу меньшего тела, то за границами тел в среде открытого пространства дисбаланс отражённых элементов среды складывается в обратную сторону. При этом вся система взаимодействующих тел получает импульс движения в сторону меньшего тела, но с учётом всего взаимодействующего вещества во всём окружающем пространстве общий баланс восстанавливается в полном соответствии с законами сохранения и с законами Ньютона.

Таким образом, все фундаментальные законы природы выполняются только для полной совокупности всех массовых элементов непосредственно участвующих во взаимодействии. Без их полного учёта взаимодействие тел осуществляется с отклонением от законов сохранения импульса, энергии и третьего закона Ньютона.

Образно говоря, мировая материальная среда, расположенная непосредственно вблизи взаимодействия, является рейкой храповика, относительно которого вся система взаимодействующих тел движется только в одном направлении в сторону меньшего тела. При этом «собачкой» храповика являются давление и парус взаимодействия, образующиеся в зоне деформации в соответствии с принципом боязни тесноты.

Это и есть феномен, так называемого «безопорного» движения, который классическая физика категорически отрицает, как нарушение своих священных устоев в виде законов сохранения. Однако устоев природы это нисколько не нарушает, т.к. опора всё-таки есть. Поскольку противодействие самой рейке в дальней среде, безусловно, оказывается, то никакого нарушения законов природы не происходит.

***

Предлагаемый принцип механизма явления инерции и перераспределения сил и соответственно энергии взаимодействия с учётом среды нетрудно смоделировать и проверить на опыте в лабораторных условиях (см. Рис. 1.2.2). Вертикальные линии на концах обоих поршней на рисунке — это паруса, слева большее тело (б), справа соответственно меньшее тело (м). Соотношение масс тел и соответственно их парусов мы сохранили, как и в предыдущем описании (2:1).

За счёт парусов, упирающихся в мировую среду, расстояния (б) и (м) будут несколько меньше их законных значений в соответствии с законом сохранения импульса. Причём это больше отразится на расстоянии (б), чем на (м). Поэтому вряд ли у кого вызовет сомнение, что вся система, изображённая на рисунке (1.2.2) переместится в сторону меньшего тела, т.е. вправо пор рисунку.

Соединив тела после взаимодействия механической связью, мы получим однонаправленное движение всей системы. Правда взаимодействие соединения должно быть по возможности менее интенсивное, т.е. неупругое. Иначе при упругих взаимодействиях мы получим лишь колебания всей системы относительно её неподвижного центра масс.

Этот эффект уже подтверждён опытами современных исследователей С. Д. Иванова и Г. Н. Чернышева, о чем сообщается в их статье «ОБ ЭКСПЕРИМЕНТАЛЬНОМ ПОДТВЕРЖДЕНИИ ВОЗМОЖНОСТИ СОЗДАНИЯ ПРОТОТИПА РЕАКТИВНОГО ДВИГАТЕЛЯ БЕЗ ВЫБРОСА ВЕЩЕСТВА» (см. журнал «Проблемы машиностроения и автоматизации», №3/2004, http://v1100.net/stat/prototype/prototype.shtml). Мы же только попытались найти реалистичное объяснение полученному эффекту на основе предложенного механизма явления инерции с учётом среды.

Выше мы показали, что этот эффект обеспечивается также и за счёт одной только врождённой инерции. В предложенном опыте его проверить невозможно. Однако все знают его опытное подтверждение в боксе. Чем резче удар боксёра, тем большая сила прикладывается к груше. Правда с лёгкой грушей легче и удар. Однако он так же тем тяжелее, чем резче боксёр. А к малому телу взаимодействия, как мы выяснили, взаимодействие прикладывается резче, чем к большому.

Таким образом, «безопорное» движение — это неизбежное следствие всех несимметричных взаимодействий. Оно является одним из самых распространённых явлений природы и одним из самых распространенных видов механического движения.

***

Из приведенного механизма перераспределения энергии взаимодействия следует, что кроме энергии взаимодействия, сила для физических тел в значительной степени определяется количеством активно контактирующих, т.е. работающих элементов материи физических тел и материальной среды. Образно говоря, сила взаимодействия зависит от количества элементов, образующих «ветер» и «парус» взаимодействия.

Естественно, что полная масса взаимодействующих тел всегда больше массы их активно работающих элементов, т.к. не все элементарные массы активно участвуют во взаимодействии. Из этого следует, что тела с одинаковым количеством полного вещества, но с разным количеством работающих элементов при общей силе взаимодействия будут ускоряться по-разному, т.е. инертная масса без соответствующего коэффициента не является мерой полного количества вещества взаимодействующих тел!

Количество работающих элементов только пропорционально полной массе физического тела, из которого они выделяются. Однако эта пропорциональность не является строго фиксированной. Коэффициент пропорциональности может зависеть от физического состояния, от структуры, от химического состава и от величины физических тел, а также от типа взаимодействия. Все эти факторы могут влиять на количество свободных элементов материи физического тела, непосредственно определяющих силовые характеристики взаимодействия и соответственно на приращение движения взаимодействующих тел.

В соответствии с законом сохранения импульса меньшее тело получает большее ускорение и соответственно большую энергию. Это объясняется не только врождённым свойством инерции, которая строго пропорционально количеству вещества в массе, но меньшим сопротивлением мировой материальной среды со стороны меньшего тела, т.к. в нём образуется меньшее количество свободных элементов, оказывающих сопротивление движению тела в условиях мировой материальной среды.

Большее количество свободных элементов в большем теле не только обеспечивает ему большее инерционное сопротивление, но и приводит к преимущественному пере отражению свободных элементов в сторону меньшего тела. В результате меньшее тело в соответствии с приведённым выше механизмом явления инерции должно испытывать большую движущую силу. Но это означает, что большая сила будет действовать не только на меньшее тело, но и на тело с меньшим количеством работающих элементов независимо от общего количества его вещества!

Таким образом, при разном коэффициенте пропорциональности количества свободных элементов и общего количества вещества взаимодействующих тел одинаковое ускорение могут получить и разные полные массы и наоборот. При этом одинаковые по количеству вещества, но имеющие разную внутреннюю структуру, химический состав и соответственно разные внутренние связи материальные тела могут получать разные ускорения при взаимодействии между собой.

Из этого следует, что во всех типах взаимодействий масса взаимодействующих тел, определяемая по ускорению, не соответствует полному количеству их вещества. Следовательно, ни гравитационная масса, ни инертная масса не отражает истинное количество её вещества. Одним из примеров, подтверждающих этот факт, является численное несоответствие инертной и гравитационной массы одного и того же тела, хотя надо полагать, что полное списочное количество вещества в одном и том же теле не может изменяться в зависимости от вида его взаимодействия.

Считается, что гравитационная и инертная массы строго пропорциональны. Как известно, гравитационная масса приводится в соответствие с полной инертной массой только через коэффициент пропорциональности, который входит в состав фундаментальной физической величины — гравитационной постоянной. Присутствие в законе всемирного тяготения коэффициента пропорциональности, который непосредственно входит в состав гравитационной постоянной может быть вызвано двумя причинами:

Во-первых, количество активных работающих элементов тяготеющих тел еще в большей степени не соответствует полному количеству их вещества, чем в контактных взаимодействиях. Возможно, из-за малого паруса сила тяготения осуществляется на уровне близком к врождённым силам инерции.

Во-вторых, при выводе закона всемирного тяготения за эталон массы был принят эталон инертной массы, которая не соответствует инертности гравитационного взаимодействия. Если бы за эталон массы была принята гравитационная масса, понадобился бы коэффициент пропорциональности уже для инертной массы.

Причём этот коэффициент пропорциональности входил бы в состав уже не гравитационной постоянной, а инертной постоянной, которая была бы значительно больше единицы. А если бы за эталон массы было бы принято полное количество вещества эталонного физического тела, то инертная и гравитационная массы имели бы свои индивидуальные коэффициенты пропорциональности, которые входили бы состав их индивидуальных постоянных.

Таким образом, гравитационная постоянная, кроме всего прочего содержит в своём составе, в том числе и коэффициент пропорциональности между гравитационной и инертной работающей массой. Вследствие относительно малого количества свободных массовых элементов, выделяющихся при гравитационных взаимодействиях, гравитационная инертная масса более близка к истинному количеству её вещества, а её инертность близка к врождённой инертности материи.

В связи с малым количеством свободных элементов, образующих парус взаимодействия, коэффициент пропорциональности между свободными элементами тяготеющих тел и полным количеством их вещества должен иметь очень малую величину по сравнению с контактными взаимодействиями, что и подтверждает величина гравитационной постоянной, которая в системе СИ равна (6,673 * 10—11 [м3 / (кг * с2)]).

Следовательно, при одинаковой силе взаимодействия одинаковые массы при гравитационном взаимодействии должны ускоряться значительно быстрее, чем аналогичные массы в контактных взаимодействиях.

Не исключено, что ключ к решению проблемы «черной материи», т.е. дефицита видимой массы во вселенной также следует искать в несоответствии истинного количества вещества материальных объектов их видимой инертности, обеспечиваемой врождённой инертностью совместно с сопротивлением среды.

В зависимости от плотности эфира в разных уголках вселенной коэффициент гравитационного взаимодействия может меняться, что наблюдается в виде несоответствия движения видимой материи законам Кеплера и объясняется тёмной, т.е. невидимой материей. В реальной действительности эффект дополнительной невидимой материи может возникать за счёт большего сопротивления более плотной материальной среды парусам взаимодействия, которые в более плотной среде могут иметь и большие размеры.

Есть и другое вполне прозаическое объяснение тёмной материи. Периферийные объекты галактик движутся быстрее, чем предсказывает теория тяготения Ньютона просто потому, что в расчётах не учитывается вся совокупная масса внутренней области галактик. Учитывается только лишь масса их ядер, в то время как каждый внутренний слой вещества галактики увеличивает массу центрального тяготеющего тела для каждого последующего внешнего слоя.

Не исключено так же, что в предложенном механизме явления инерции и взаимодействия следует искать ключ и к объяснению дефекта массы. Мы не можем пока знать детали механизма выделения свободных работающих элементов при взаимодействии. Но силы связи в ядре атома намного больше сил связи атомов в молекулах. Поэтому ядра атомов могут выделять значительно меньше свободных массовых элементов, чем связки атомов в молекулах и связки самих молекул. А это влияет на обнаруживаемую массу, т.к. массу на уровне амеров мы обнаруживать пока не умеем.

Во всяком случае, абсолютный коэффициент взаимодействия ядер атомов, может значительно отличаться от абсолютного коэффициента взаимодействия вещества и свободных нуклонов. Да, и физическое состояние самих нуклонов после насильственного расщепления атомов тоже исключать нельзя.

Приведённый механизм взаимодействия может разрешить и некоторые нерешенные сегодня фундаментальные проблемы современной электродинамики, связанные со вкладом механической и электрической массы в инертность заряженных частиц. Нет ни механической, ни электромагнитной массы. Есть масса, как количество вещества физических тел и элементарных частиц, в том числе и заряженных. И есть инерция, вызываемая количеством работающих элементарных масс физических тел или элементарных частиц.

Электромагнитные явления — это те же самые взаимодействия материальных объектов на уровне элементарных носителей вещества, подобные гравитационному или инертному взаимодействию. Именно элементарные носители вещества и образуют любые поля любых взаимодействий, в том числе и электрических взаимодействий. Поэтому электромагнитная масса отличается от механической или инертной массы только коэффициентом пропорциональности, определяющим соотношение полного количества вещества заряженных частиц и количеством работающих массовых элементов в электрических взаимодействиях.

1.2.2. Масса — это не энергия, это предмет действия, а энергия — это само действие

Энергия проявляет себя только во взаимодействии. Ни в самой массе-штуках материи (m), ни в её скорости, ни в произведении массы на скорость, ни в произведении массы на скорость в квадрате и даже в одной второй произведения массы на квадрат скорости энергии нет. Энергия это не материальная субстанция, которая может где-то хранится, кем-то переносится или кому-то и чему-то передаваться. Энергия характеризует действие-работу материи-массы или над материей. Вспомните старую шутку бывалых автолюбителей, которые посылают новичков в моторный цех с ведром за компрессией! В результате получается конфуз, над которым потом все смеются, т.к. компрессию, так же, как и энергию нельзя налить в ведро или в тело.

Вообще говоря, у древних греков слово энергия обозначает мощь, силу, действие, деятельность. Но какая может быть деятельность у неодухотворённой материи? У неё могут быть только свойства, которые могут либо проявляться, либо не проявляться при определённых обстоятельствах. Одним из таких свойств является преобразование напряжение-движение, мерой которого и является энергия. При этом говорить о мере действия, которое в отсутствие взаимодействия ещё не проявлено, а каким-то гипотетическим образом спрятано в бездеятельной массе, не имеет смысла, т.к. измерить то, чего нет не возможно. Будущее действие можно только прогнозировать. Однако прогноз действия и его наличие — это разные вещи.

Очевидно, что энергия минимально возможного материального тела — это мера непрерывно осуществляющегося взаимодействия составляющих его частиц, количество которых, как и во всяком взаимодействии, не может быть меньше двух.

Тогда энергия минимального тела равна:

Ет min = Ед + Еод,

где (Ед) и (Еод) энергия действия и энергия ответного действия соответственно.

Очевидно, что единичные и неделимые элементы материи амеры (mа), если предположить, что таковые реально существуют, содержат одинаковое количество материи и соответственно получают одинаковую скорость (Vа) при взаимодействии. Тогда энергия одного амера внутри минимально возможного тела равна:

Ед = Еод = Еа

При этом энергия минимального тела, состоящего из двух амеров (mа) равна:

Ет min = Ед + Еод = 2 * ЕД = 2 * ЕОД = 2 * Еа = 2 * mа * Vа 2 / 2

Или после сокращения на «2»:

Ет min = 2 * mа * Vа 2 / 2

То есть:

Ет min = mа * Vа 2 (1.2.1)

Причём это только энергия взаимодействия внутренних элементарных масс тела — амеров. Однако без внутренних связей амеры не могут составлять единое тело, т.к. при первом же взаимодействии они разлетятся в разные стороны. По Ацюковскому элементарные массы удерживаются в составе тела внешним давлением среды, которое и образует внешнюю оболочку тела. Это и есть то самое «ведро», в которое можно если и не налить энергию, то, как минимум локализовать в нём процесс взаимодействия элементарных масс материи. Очевидно, что при этом амеры должны взаимодействовать не только между собой, но и с оболочкой тела. Причём в соответствии с законом сохранения энергии это должна быть точно такая же энергия, с которой они взаимодействуют и между собой.

Энергия оболочки тела это энергия среды, которая неразрывно сопровождает каждое тело, в какую бы точку пространства оно ни перемещалось. С этой точки зрения, тело локализует энергию оболочки в своём составе, до тех пор, пока оно не разрушится. Но тогда с учётом оболочки минимальное количество объектов взаимодействия обеспечивается одним внутренним амером тела и одним внешним амером оболочки тела, который заменяет ответное тело и соответственно его энергию ответного действия (Еод). При этом энергия минимального тела по-прежнему равна (Ет min = mа * Vа 2).

Понятно, что оболочка, представляет собой замкнутую поверхность и не может состоять из одного амера. Но для однократного взаимодействия каждого внутреннего амера достаточно только одного амера оболочки, на смену которому всегда придёт другой внешний амер из многочисленного внешнего окружения среды. При этом энергия условно меняющихся внешних амеров оболочки остаётся неизменной на уровне энергии ответного действия (Еод). Тогда реальное тело отличается от модели минимального тела только количеством амеров:

Ето = n * mа * Vа 2,

где

Ето — энергия тела с оболочкой,

n — количество амеров тела с оболочкой.

Это справедливо, как для массы макро тела, так и для массы всех составляющих его нуклонов, а также всех элементарных масс материи, составляющих все известные элементарные частицы. При этом короткоживущие частицы, образующиеся в ускорителях, это, по всей видимости, следствие разрушения оболочки устойчивых частиц. Осколки этих частиц, либо приобретают новую оболочку и в дальнейшем существуют в виде других устойчивых элементарных частиц, либо распадаются на элементарные массы, т.е. становятся элементами среды. После этого они естественно исчезают из поля нашего зрения, т.к. ни элементы среды, ни энергию их взаимодействия современная наука зафиксировать пока не в состоянии.

Если произведение (n * mа) обозначить, как массу тела (m), то получим знаменитую формулу энергии массы:

Ет = m * Vа 2 (1.2.2)

У Эйнштейна теоретически нет внешней среды. Однако отсутствие усредняющего коэффициента (½) в его формуле фактически свидетельствует об энергии, как минимум двух объектов взаимодействия. Это как раз и может быть масса и оболочка тела, которые и образуют тело в целом. Иначе формула Эйнштейна с постоянной скоростью (с) противоречит самому понятию работы-энергии, которое связано именно с изменением движения в процессе преобразования напряжение-движение. Постоянная же скорость движения тела без её усреднения в формуле энергии свидетельствует о полном отсутствии работы.

Формулу (1.2.2) можно легко привести к классическому виду, если выразить общую массу тела в виде суммы её внутренних амеров и амеров оболочки:

Е = ½ * (nТ * mа + nО * mа) * Vа 2, (1.2.3)

где (nТ) и (nО) это количество амеров тела и оболочки соответственно.

Все три формулы (1.2.1), (1.2.2) и (1.2.3) физически равнозначны. Однако формула (1.2.3) наиболее наглядно показывает физический смысл энергии массы. В ней присутствует реальное количество составляющих тело элементарных масс самого тела и элементарных масс оболочки тела, а также множитель (½), который учитывает среднюю скорость элементарных масс при её изменении в результате взаимодействия. А вот формула Эйнштейна без множителя (½) показывает только энергию 2-х самостоятельных фотонов без объяснения их роли в структуре тела. Физическая необоснованность формулы Эйнштейна в современной физике со всей очевидностью следует практически из всех её официальных выводов.

Приведём некоторые из них. Предварительно поясним, что реально представляет собой теория всех времён и народов СТО. В основе СТО фактически лежат 3 принципа-постулата. Однако ситуация с эфиром в них не упоминается, хотя она то, как раз и является важнейшим из них, т.к. остальные два не возможны при наличии эфира и эфирного ветра. А чтобы не было путаницы с их оригинальной нумерацией, обозначим постулат об эфире нулевым номером:

0. Отказ от эфира. «…нельзя создать удовлетворительную теорию, не отказавшись от существования некоей среды, заполняющей все пространство». А Эйнштейн [5, т. 1, с.145—146].

1. Принцип относительности Эйнштейна (ПО), который гласит, все законы природы инвариантны относительно перехода от одной инерциальной системы отсчета к другой.

2. Принцип постоянства скорости света. Свет в пустоте всегда распространяется с определенной скоростью, не зависящей от состояния движения излучающего тела.

По нулевому постулату Ацюковский В. А. говорит: «Почему нельзя? Можно предположить, что раз у самого Эйнштейна с эфиром ничего не получилось, то и ни у кого не получится. Значит, нельзя.». Тем более, что в 1920 г. в постулатах к ОТО Эйнштейн сам наделил пространство физическими свойствами, заявив, что «пространство немыслимо без эфира», и окончательно подтвердил это в 1924 г. Однако непонятно по каким причинам первый постулат так и остался официально не опровергнутым. Даже сегодня эфир стыдливо называют физическим вакуумом, неофициально наделяя материей пространство, по определению свободное от материи. Именно так переводится с латинского вакуум.

Не всё гладко и с остальными постулатами. От ПО Галилея эйнштейновский ПО отличается только тем, что кроме законов механики, на которые распространяется ПО Галилея, Эйнштейн распространил своё ПО ещё и на оптические и электродинамические явления. При этом без учёта ветра у Галилея и эфира у Эйнштейна оба ПО не имеют принципиальных отличий. Но в том то всё и дело, что с ветром и с эфиром ни тот, ни другой принцип относительности не работает. Галилей устранил этот недостаток, сделав свои системы замкнутыми, включая среду. А вот на эфирный ветер современная наука до сих пор упорно не обращает внимания, хотя эфир, в конце концов признал и сам Эйнштейн.

Независимость скорости света от движения источника вообще не вызывает никаких сомнений, т.к. этот постулат устанавливает волновую природу света и ничего более. Однако Эйнштейн, как заправский цирковой фокусник, незаметно, не поднимая лишнего шума, фактически втащил в физику совсем другой постулат, по которому скорость света не зависит не только от движения источника, но и от движения приёмника.

Известно, что уравнение распространения электромагнитного поля в неподвижной системе координат согласно Максвеллу имеет вид:

x2 + y2 + z2 = c2 * t2 (1)

Это достоверно установленный факт. При этом Эйнштейн без всяких на то оснований допустил, что в системе координат, движущейся вдоль оси OX первой системы, уравнение распространения электромагнитного поля должно иметь такой же вид (1-й постулат СТО — все законы одинаковы (инвариантны) во всех ИСО):

х12 + y12 + z1 2 = c2 * t12 (2)

Одинаковый вид (1) и (2) возможен только при постоянстве скорости света во всех ИСО не зависимо от скорости движения источника и приёмника, что не соответствует второму постулату СТО, который заявлен Эйнштейном, как независимость скорости света только от скорости источника. При этом в реальной действительности скорость света, измеренная относительно приёмника, зависит от скорости последнего. Таким образом, Эйнштейн фактически совершил научный подлог, на основании которого он и построил свою ложную теорию.

В результате, переход от уравнения (1) из системы покоя в движущуюся систему к уравнению (2) и обратно при помощи преобразований Галилея оказался не возможен. Поэтому в СТО преобразования Галилея были искусственно и искусно подогнаны к ложным постулатам Эйнштейна. Для того, чтобы новые преобразования не противоречили преобразованиям Галилея и одновременно удовлетворяли постулатам Эйнштейна, они должны быть линейными по отношению к преобразованиям Галилея.

Приведём классический вывод этих преобразований:

x1 = А * (x — V * t) (3)

x = А * (x1 + V * t1) (4)

В соответствии со 2-м постулатом:

x = с * t

x1 = c * t1

Тогда:

c * t = А * (c * t — V * t) = А * t * (c — V) (3)

c * t1 = А * (c * t1 + V * t1) = А * t1 * (c — V) (4)

Перемножим (3) и (4):

c2 * t * t1 = A2 * t * t1 * (c2 — v2)

A2 = c2 / c2 — v2 = 1 / (1 — v2 / c2)

A = +/-1 / (1 — v2 / c2) 1/2

Оси направлены в одну сторону, поэтому минус отбрасываем:

A = 1 / (1 — v2 / c2) 1/2 (5)

Подставляем (5) в (3) и (4):

x1 = (x — V * t1) / корень (1 — V2 / C2) (6)

x = (x + V * t) / корень (1 — V2 / C2) (7)

x * корень (1 — V2 / C2) = (x1 — V * t1) (8)

Подставим (6) в (8):

x * корень (1 — V2 / C2) = ((x — V * t1) / корень (1 — V2 / C2) — V * t1)

(x * (1 — V2 / C2) — x — V * t1) / корень (1 — V2 / C2)

t1 = (t — V * x /C2) / корень (1 — V2 / C2) (9)

(5), (7), (9) — это и есть преобразования СТО, которые впоследствии с учётом их первого автора получили название Лоренца-Эйнштейна.

При v <<c преобразования Лоренца-Эйнштейна переходят в преобразования Галилея.

Таким образом, преобразования Лоренца-Эйнштейна и все вытекающие из них следствия — относительность одновременности, сложение скоростей сокращение длины и растягивание времени были получены, непосредственно исходя из соответствия постулатам СТО и преобразованиям Галилея. Это означает — всё, что непосредственно вытекает из СТО было искусственно заложено в неё заранее. По поводу этой чистейшей воды тавтологии Энгельс в «Анти-Дюринг» сказал:

«Если приняты такие предпосылки, которые уже содержат в себе конечный вывод, достаточно той ловкости, какой обладает любой шарлатан, чтобы вытащить из кармана заранее приготовленный результат и кичиться несокрушимостью логики, приведшей к этому заключению.»

С учётом неподвижного эфира в движущейся относительно него системе отсчёта, т.е. фактически с учётом эфирного ветра в любой ИСО, скорость света не инвариантна в разных направлениях, что противоречит постулату инвариантности скорости света. И хотя наличие или отсутствие эфира наукой пока не установлено, тот факт, что вопреки официальной формулировке 1-го постулата, СТО фактически построена на независимости скорости света не только от движения источника, но и приёмника, однозначно свидетельствует против неё. А начав с мошенничества не возможно обойтись без него и в самой теории. Все выводы самой знаменитой во всём мире формулы Эйнштейна (ФЭ) также построены на сплошном мошенничестве.

Приведём примеры, подтверждающие сказанное.

«Физика для углублённого изучения 3. Строение и свойство вещества.», параграф 4, Е. И. Бутикова и А. С. Кондратьева:

«В релятивистской механике сила F вводится таким образом, чтобы соотношение между приращением импульса частицы (ΔP) и импульсом силы (F * Δt) было таким же, как и в классической физике (выделение наше — авт.):

ΔP = F * Δt

Будем считать, что энергия Ек частицы в релятивистской механике, как и в классической (выделение наше — авт.), представляет собой величину, изменение которой на перемещении Δr равно работе действующей силы F:

ΔEк = F * Δr = F * V * Δt = V * ΔP = V * Δ (m * V) (7)

…Из формулы (7) и будем исходить при выводе выражения для релятивистской энергии.

Перепишем релятивистскую формулу для массы m = m0 / √ (1 — v2 / с2) (3) следующим образом:

m2 * (1 — v2/c2) 2 = m0 2

Умножив обе части на с2 и раскрыв скобки, получим:

m2 * c2 — (m * v) 2 = m02 * c2 (8)

При движении частицы под действием силы F ее скорость и импульс меняются. Для нахождения приращения левой части (8) воспользуемся тем, что приращение квадрата любой переменной величины f за малый промежуток времени приближенно равно:

Δf 2 = (f + Δf) 2 — f 2 ≈ 2 * f * Δf

Применяя эту формулу к равенству (8) и учитывая, что правая часть остается при этом неизменной, получаем:

2 * m * c * Δ (m * c) — 2 *m *v * Δ (m * v) = 0,

откуда после сокращения на (2 * m) имеем

Δ (m * c2) = v * Δ (m * v) (9)

Правые части в выражениях (7) и (9) совпадают. Поэтому левая часть (9) представляет собой приращение кинетической энергии частицы:

ΔЕк = Δ (m * c2) (10)

Т.к. кинетическая энергия покоящейся частицы равна нулю, то из дифференциального соотношения (10), определяющего кинетическую энергию с точностью до константы, немедленно следует формула (6):

Eк = E — E0 = m0 * c2 / корень (1 — v2 / c2) — m0 * c2 (6)

Eк = m0 * c2 * (1 / корень (1 — v2 / c2) — 1)».

Однако, если уж и ссылаться на классическую физику при выводе формулы Эйнштейна, как об этом заявлено вначале вывода, то следует учитывать, что в классической физике путь, на котором совершается работа над движущимся равноускоренно телом за время этой работы оценивается средней разностной скоростью движения между конечной и начальной скоростью пути, равной половине этой разности ΔVср. = ((Vк — Vн) / 2). При этом формула (7) в классической физике должна выглядеть следующим образом:

ΔEк = F * Δr = F * ΔVср. * Δt = ΔVср. * ΔP = ΔVср * Δ (m * ΔVср) =

= m * ΔVср.2 / 2 (7*)

В этом случае правые части классического выражениях (7*) и (9) естественно не совпадают, т.к. (9) получена исходя из релятивистских представлений в частности о массе (3), которые не могут совпадать с классической механикой, т.к. это принципиально разные теории. Следовательно, если основываться на классических представлениях о работе-энергии, то вывод ФЭ в корне не верен:

ΔЕк ≠ Δ (m * c2)

А если убрать из классической энергии множитель «1/2», как это безо всяких на то оснований сделали авторы, то нечего собственно и выводить. Достаточно просто подставить в искажённую таким образом формулу скорость с вместо скорости v, что есть прямой подлог вывода!

Кроме того, доказательства, основанные на положениях самой доказываемой теории, т.е. в частности на релятивистской массе (3), которая не имеет никакого отношения к соотношениям (7), являющихся искажением классических соотношений (7*), это чистейшей воды тавтология, которая никому ничего не доказывает. Это нарушение всех мыслимых и немыслимых законов логики.

Таким образом, при «углублённом изучении» оказывается, что вывод формулы Эйнштейна принципиально не может быть основан на классическом понятии работы-энергии и на классической массе, не зависящей от оптических эффектов СТО.

Энергия и работа это мера преобразования напряжение-движение. При этом, как было показано выше в главе (1.2.1.), благодаря отрицательной обратной связи процесса преобразования напряжение-движение, скорость вновь образующегося движения не может установиться мгновенно без ускорения, что и определяет физическую сущность явления инерции с ускорением инерции. Поэтому количество работы или затраты энергии на ускорение массы на участке пути, на котором ускорение изменяется от нуля до его конечного значения, оценивается средней скоростью преобразования напряжение-движение ускоряемой массы.

Тогда с учётом скорости света, выражение для энергии должно иметь вид:

ΔЕк = m * c2 / 2

Но это только половина эйнштейновской формулы энергии. Релятивисты полагают, что дальнейший рост энергии при достижении конечной скорости света, осуществляется исключительно только за счёт роста массы. Однако даже если бы это было и так, то усредняющий множитель должен сохраняться в формуле энергии в любом случае, т.к. ничто в природе не может изменяться мгновенно, тем более масса, которая и есть мера инерции, т.е. противодействия какому-либо изменению чего-либо. Следовательно, рост энергии до величины (ΔЕк = m * c2), если уж (с) является предельной скоростью в природе, к сожалению для релятивистов, принципиально невозможен.

Кроме того, рост массы не является достоверно установленным фактом. В экспериментах по разгону массы в электромагнитном поле, когда скорость массы приближается к скорости распространения ускоряющего воздействия поля, интенсивность разгона за счёт выравнивания градиента скоростей уменьшается даже безо всякой дополнительной массы. Следовательно, аномальный рост энергии поля по отношению к скорости массы вполне может быть обусловлен затратами на генерацию ускоряющего поля. Но тогда выражение для релятивистской массы (3), которое лежит в основе вывода, нельзя считать достоверным.

Релятивистская энергия принципиально противоречит классическому определению работы по преобразованию напряжение-движение, т.к. отсутствие множителя «½» означает и отсутствие изменения скорости движения, т.е. отсутствие собственно самой работы. А если нет работы, то нет и никаких результатов работы ни по массе, ни по размеру, ни по времени, ни по энергии. На нет, как говорится, и суда нет! Это означает, что перефразируя басню Крылова, как бы релятивисты ни садились, в музыканты физики они явно не годятся.

Вот вам и «Физика для углублённого изучения». На протяжении более века великую чушь нам преподносят, как великое достижение — «вершину» человеческой мысли, которое понимают якобы только избранные. Однако на самом деле это есть не что иное, как научное преступление или заговор против человечества, что собственно одно и то же.

Приведём ещё один широко распространённый вывод формулы Эйнштейна. Болотовский Б. Простой вывод формулы E = mc2 //Квант. — 2005. — №6. — С. 2—7.

http://www.physbook.ru/index.php/Kvant._Вывод_формулы_E_%3D_mc2#.D0.92.D1.8B.D0.B2.D0.BE.D0.B4_.D1.84.D0.BE.D1.80.D0.BC.D1.83.D0.BB.D1.8B_E_.3D_mc2

«Рассмотрим покоящееся тело массой m. Предположим, что это тело одновременно излучает два фотона в прямо противоположных направлениях. Оба фотона имеют одинаковые частоты ω и значит, одинаковые энергии E = ℏω, а также равные по величине и противоположные по направлению импульсы. В результате излучения тело теряет энергию

ΔE=2ℏω (9)

Потеря импульса равна нулю, и, следовательно, тело после излучения двух квантов остается в покое.

Рассмотрим теперь ту же картину с точки зрения наблюдателя, который движется по оси x влево (т.е. в отрицательном направлении оси x, направленной вправо) с малой скоростью v. Такой наблюдатель увидит уже не покоящееся тело, а тело, движущееся с малой скоростью вправо. Величина этой скорости равна v, а направлена скорость в положительном направлении оси x. Тогда частота, излучаемая вправо, будет определяться формулой (7) для случая излучения вперед (эффект Доплера):

ω′=ω * (1+ v / c).

Соответственно, частота фотона, излучаемого движущимся телом влево, определяется формулой (8) для случая излучения назад:

ω″=ω * (1− v / c).

Поскольку, из-за эффекта Доплера, частоты излучения вперед и назад различны, энергия и импульс у излученных квантов также будут различаться. Квант, излученный вперед, будет иметь энергию

E′=ℏω′=ℏω * (1+ v /c)

и импульс

p′=ℏω′ / c=ℏω * (1+ v / c) / c.

Квант, излученный назад, будет иметь энергию

E″ =ℏω″ =ℏω * (1− v / c)

и импульс

p″=ℏω″ / c =ℏω * (1− v / c) / c.

При этом импульсы квантов направлены в противоположные стороны.

Важно здесь подчеркнуть, что это один и тот же процесс, но с точки зрения разных наблюдателей. Один наблюдатель покоится относительно излучающего тела, а второй — движется.

Подсчитаем баланс энергии и импульса для второго случая. Потеря энергии в системе координат, где излучатель имеет скорость v, равна

ΔE′ = E′ + E″ = ℏω * (1 + v / c) + ℏω * (1 — v / c) = 2ℏω = ΔE,

т.е. она такая же, как и в системе, где излучатель покоится (см. формулу (9)). Но потеря импульса в системе, где излучатель движется, не равна нулю, в отличие от системы покоя:

Δp′ = p′ — p″ = ℏω * (1 + v / c) / c — ℏω * (1- v / c) / c = ℏωv / c2 + ℏωv / c2 =

= (2ℏω / c) * v / c = ΔE * v / c2 (10)

Движущийся излучатель теряет импульс ΔE * v / c2 и, следовательно, должен, казалось бы, тормозиться, уменьшать свою скорость. Но в системе покоя излучение симметрично, излучатель не меняет скорости. Значит, скорость излучателя не может измениться и в той системе, где он движется. А если скорость тела не меняется, то как оно может потерять импульс?

Чтобы ответить на этот вопрос, вспомним, как записывается импульс тела массой m:

p = mv

— импульс равен произведению массы тела на его скорость. Если скорость тела не меняется, то его импульс может измениться только за счет изменения массы:

Δp = Δmv

Здесь Δp — изменение импульса тела при неизменной скорости, Δm — изменение его массы.

Это выражение для потери импульса надо приравнять к выражению (10), которое связывает потерю импульса с потерей энергии. Мы получим формулу

ΔE * v / c2 = Δmv

ΔE / c2 = Δm

или

ΔE = Δmc2,

которая означает, что изменение энергии тела влечет за собой пропорциональное изменение его массы. Отсюда легко получить соотношение между полной массой тела и полным запасом энергии:

E = mc2»

Но, во-первых, в следствие конечности скорости света наблюдатель получает искажённую информацию о реальной физике наблюдаемых объектов и процессов. Степень искажения определяется скоростью света, скоростью относительного движения объекта и наблюдателя и рассчитывается в соответствии с эффектом Доплера. Объективную информацию можно получить только в неподвижной системе объекта или же в любой другой системе, но при условии бесконечности скорости информационного сигнала, когда не зависимо от расстояния до точки наблюдения любой наблюдатель получает точно такую же информацию, что и в неподвижной системе объекта. В противном случае наука физика превращается в простое описание видений без раскрытия физической сути происходящего.

Во-вторых, совершенно очевидно, что физика процесса в обеих системах объективно не меняется, о чём собственно говорится и в самом выводе: «Важно здесь подчеркнуть, что это один и тот же процесс, но с точки зрения разных наблюдателей.» Поэтому судить о физике процесса можно только по объективной информации, а вовсе не по оптическим иллюзиям наблюдателя.

«Если в системе покоя излучение симметрично, излучатель не меняет скорости. Значит, скорость излучателя не может измениться и в той системе, где он движется.» — пишет автор вывода. Но по той же самой логике не может также измениться частота и скорость фотонов, т.е. их импульс. Если из движущейся системы реально видно, что источник «поехал», а вам предлагается не верить глазам своим, то почему в нарушение этой логики вы должны верить в изменение импульса фотонов в той же самой ситуации?! Если уж говорить об объективности процесса, то она не может быть избирательной, тем более внутри одного и того же вывода. Налицо явное мошенничество автора вывода, перечёркивающее всё доказательство ФЭ.

В-третьих, судить об изменении импульса источника по кажущемуся или отсутствующему изменению импульса или энергии фотонов не корректно. После отрыва от излучателя фотоны уже не имеют к физике самого излучателя никакого отношения. Даже если бы их импульс или энергия после отрыва от источника реально изменились бы в любой системе, на сам источник это уже никак повлиять не может.

В-четвёртых, изменение массы объекта может быть только по причине её изъятия или добавления к объекту любым доступным способом. Судить же об изменении массы источника в добавление к п. 3 по гипотетическому, никем не доказанному превращению материи в нематериальную энергию, в нарушение закона сохранения материи, не корректно. Энергия, т.е. действие изменяет другое действие — движение, но не количество предмета действия — массу. Поэтому переменной величиной в импульсе изолированного после излучения объекта может быть исключительно только скорость, но не масса.

В-пятых, фотоны, об изменении импульса, которых идёт речь в выводе, не имеют массы покоя и не могут двигаться ни с какими другими скоростями, кроме скорости света. При этом в процессе движения масса и скорость фотонов в соответствии со 2-м постулатом СТО не меняется ни в самой ИСО, ни при смене ИСО. Следовательно, ссылка на изменение импульса фотонов, о котором судят по изменению объективно неизменной, кстати, энергии фотонов, несостоятельна.

В-шестых, энергия и работа — это количественная оценка процесса преобразования напряжение-движение, т.е. действия над объектами или их взаимодействия. Как объектов их не существует. Объект и действие над ним — это принципиально разные вещи. Поэтому ни о какой эквивалентности массы, как количества весомой, грубой, зримой материи и энергии, как бестелесной оценки взаимодействия материи не может быть и речи. Реальная потеря материи-массы излучателем связана с потерей им материи-массы фотонов. Но в представленном выводе оценка потери непосредственно массы фотонов отсутствует.

Ну и, наконец, рассмотрим вывод формулы Эйнштейна (ФЭ) в исполнении самого автора (курсив) с нашими комментариями основным текстом.

Эйнштейн А. «Зависит ли инерция тела от содержащейся в нем энергии?», Берн, Швейцария, получено 27 сентября 1905 г.

«Пусть система плоских волн света, отнесенная к координатной системе (х, у, z), обладает энергией L и пусть направление луча (нормаль к фронту волны) образует угол φ с осью х системы. Если ввести новую координатную систему (ξ, η, ζ), движущуюся равномерно и прямолинейно относительно системы (х, у, z), и если начало координат этой системы движется со скоростью v вдоль оси х, то упомянутая энергия света, измеренная в системе (ξ, η, ζ), будет:

L* = L * (1 — v / c * cos φ) / корень (1 — v2 / c2)

где с — скорость света. В дальнейшем мы воспользуемся этим результатом.»

Эта формула следует из эффекта Доплера и из преобразований Лоренца. Но, как показано выше, преобразования Лоренца это всего лишь мошенническая тавтология, не имеющая под собой ни каких объективных физических оснований, что делает весь вывод бессмысленным. Если кого то это не убеждает, то продолжим анализ в поиске дальнейших бессмысленностей.

«Пусть в системе (х, у, z) находится покоящееся тело, энергия которого, отнесенная к системе (х, у, z), равна Eо. Энергия же этого тела, отнесенная к системе (ξ, η, ζ), движущейся, как выше, со скоростью υ, пусть равна Hо.

Пусть это тело посылает в направлении, составляющем угол φ с осью х, плоскую световую волну с энергией L / 2 (измеренной относительно системы (х, у, z)) и одновременно посылает такое же количество света в противоположном направлении. При этом тело остается в покое относительно системы (х, у, z). Для этого процесса должен выполняться закон сохранения энергии и притом (согласно принципу относительности) по отношению к обеим координатным системам. Если мы обозначим через E1 энергию тела после излучения света при измерении ее относительно системы (х, у, z) и, соответственно, через H1 энергию относительно системы (ξ, η, ζ), то, пользуясь полученным выше соотношением, находим:

Eо = Е1 + (L / 2 + L / 2)

Hо = Н1 + (L / 2 * (1 — v / c * cos φ) / корень (1 — v2 / c2) + L / 2 * (1 + v / c * cos φ) / корень (1 — v2 / c2)) = H1 + L / корень (1 — v2 / c2)»

Здесь Эйнштейн впервые ввел энергию покоя массивного тела, обозначив ее до излучения как Ео, а после — как Е1.

«Вычитая второе равенство из первого, получаем:

(Но — Ео) — (Н1 — Е1) = L (1 / корень (1 — v2 / c2) — 1)

В этом соотношении обе разности вида Н — Е имеют простой физический смысл. Величины Н и Е представляют собой значения энергии одного и того же тела, отнесенные к двум координатным системам, движущимся относительно друг друга, причем тело покоится в одной из систем (в системе (х, у, z)).»

На самом деле у Эйнштейна вычитается первое равенство из второго.

«Таким образом, ясно, что разность Н — Е может отличаться от кинетической энергии K тела, взятой относительно другой системы (системы (ξ, η, ζ)), только на некоторую аддитивную постоянную С, которая зависит от выбора произвольных аддитивных постоянных в выражениях для энергий Н и Е. Следовательно, мы можем положить:

Hо — Eо = Ко + С

H1 — E1 = K1 + C,

так как постоянная С при испускании света не изменяется.

Таким образом, получаем:

Ко — К1 = L (1 / корень (1 — v2 / c2) — 1)

Кинетическая энергия тела относительно системы (ξ, η, ζ) уменьшается при испускании света на величину, не зависящую от природы тела. Кроме того, разность Kо — K1 зависит от скорости точно так же, как кинетическая энергия электрона…»

Что касается аддитивной постоянной С, то это характерно только для ньютоновской энергии. В теории относительности энергия и импульс свободной частицы определены абсолютно однозначно соотношением (Е2 — р2 с2 = m2с4).

«Пренебрегая величинами четвертого и более высоких порядков, можно получить:

Ко — К1 = L / c2 * v2 / 2…»

Поясним эту аппроксимацию. Для |х| <<1:

(1 + х) n ≈ 1 + x * n

Тогда:

Ко — К1 = L (1 / корень (1 — v2 / c2) — 1)

Ко — К1 = L * ((1 — (- ½) * v2 / c2) — 1)

Ко — К1 = L * (½ * v2 / c2)

Ко — К1 = L / c2 * v2 / 2

m = L / c2

L = m * c2

«Из этого уравнения непосредственно следует, что если тело отдает энергию L в виде излучения, то его масса уменьшается на L / c2. При этом, очевидно, несущественно, что энергия, взятая у тела, прямо переходит в лучистую энергию излучения, так что мы приходим к более общему выводу. Масса тела есть мера содержащейся в нем энергии.»

Довольно странный вывод.

Это очень даже существенно. Существенней собственно ничего в мире и нет. Основной закон природы — это закон сохранения материи (ЗСМ), который даже выше закона сохранения энергии (действия), т.к. действие определяется материей и её количеством. В выводе же Эйнштейна ЗСМ подвергается вопиющему нарушению в виде прямого перехода массы-материи в нематериальную лучистую энергию.

Причём это голословное заявление Эйнштейна объективно в выводе ни из чего не следует. Объективно масса излучателя уменьшается по причине потери масс двух фотонов. Однако Эйнштейн без всяких на то оснований ассоциирует энергию двух излучённых по условию вывода фотонов L, не просто с их массой, а с массой всего лишь одного из двух излученных фотонов.

Действительно:

L = m * c2 = 2Lф

Тогда:

Lф = mф * c2 / 2

L / c2 = 2 * mф

или

L / c2 = m2ф

Из этого следует, что по факту энергия соответствует старой доброй ньютоновской формуле. Формула Эйнштейна Е = m * c2 несостоятельна. Вообще говоря, формально формулу релятивисткой энергии Эйнштейн получил уже в предшествующей работе «К электродинамике движущихся тел», Берн, Швейцария, от 30 июня 1905 г:

W = m * c2 * (1 / корень (1 — v2 / c2) — 1)

Здесь ключевое выражение — (m * c2), остальное — преобразования Лоренца. В приведённом выводе Эйнштейн утверждает, что «разность Kо — K1 зависит от скорости точно так же, как кинетическая энергия электрона». А поскольку в пространстве Вселенной, кроме материи и её движения в природе собственно ничего и нет, то все виды энергии, т.е. фактически действия с движением материи, это фактически кинетическая энергия. Тогда после подстановки в Эйнштейновский вывод вместо L → m * c2 и с учётом аппроксимации получим:

Ко — К1 = L / c2 * v2 / 2 = Ко — К1 = m * c2 / c2 * v2 / 2 = m * v2 / 2

Выражение m * c2, полученное Эйнштейном из ньютоновской энергии через тавтологию преобразований Лоренца-Эйнштейна вновь приводит релятивистскую кинетическую энергию к ньютоновской формуле, фактически аннулируя тем самым эту тавтологию. Искусственно подогнанный под преобразования Галилея и постулаты Эйнштейна релятивистский корень уже содержит в себе релятивистскую энергию в виде замаскированной степени «1/2». Естественно, что при обратном преобразовании через аппроксимацию бинома Ньютона вновь проявляется заранее заложенное, что и есть тавтология.

Именно в квадратном корне релятивистского коэффициента сначала прячется, а затем при обратном преобразовании вновь появляется коэффициент «½». Причём в англоязычной Википедии в статье Correspondence principle в параграфе Relativistic kinetic energy этот ловкий фокус приведён в качестве подтверждения верности релятивисткой формулы энергии. Есть такой фокус и в наших учебниках:

«Уравнение Лоренца можно записать в форме Mр = Mо (1 — v2 / c2) -1/2.

Используем аппроксимацию для |х| <<1:

(1 + х) n ≈ 1 + x * n

Тогда:

Мр = Мо +1/2 * Mо * v2 / c2

Обозначим энергию через Е, тогда:

Mр = Mо + Е / c2

∆M = Мр — Мо = Е / c2

Обозначим ∆M = m

Тогда Е = m * c2»

Здесь наглядно показано, как из релятивистского корня сначала получается замаскированная при его помощи ньютоновская энергия Е, а затем та же самая Е ловко превращается в релятивистскую энергию уже безо всякой аппроксимации. Вот только вначале в обозначенной через Е энергии была масса покоя Мо, а затем в той же самой Е она вдруг превратилась в приращение массы ∆M = m, что кстати не соответствует даже СТО. Если это полная энергия Еп = Мр * c2, то в ней масса релятивистская Мр.

Е = 1/2 * Mо v2 = m * c2 = ∆M * c2

Как вам такое художество, в котором простым обозначением ньютоновская энергия удваивается и превращается в релятивистскую?! Ничуть не лучше, чем в оригинальном выводе Эйнштейна, в котором удваивается масса, что так же эквивалентно получению формулы Эйнштейна через мошенническое удвоение ньютоновской энергии. Как видите, ни в одном из представленных выводов не обошлось без мошенничества и тавтологии. Врать стали все с лёгкой руки главного шарлатана Эйнштейна.

«Но что ни говори, он добрый малый; в особенности восхищает меня та ловкость, которая стяжала ему репутацию великого умника. Я говорю о его манере отрицать то, что есть, и распространяться о том, чего не существует».

Эдгар По

Один из наших оппонентов утверждает, что формула Эйнштейна не имеет никакого отношения к обычным телам. Это всего лишь выражение скорости ЭМ волны, через плотность энергии (w) и массовую плотность ЭМ поля (р). Он исходил из того, что формула скорости распространения ЭМ волны следует из теории упругости сплошной среды:

v = корень (G / p),

где G: модуль сдвига.

Переходя к скорости света якобы получаем:

с = корень (w / p),

где

W якобы равна G, т.е. (w = G).

Оппонент сослался, что последнее равенство следует из классической физики, он в него особо не вникал, но доверился классике.

В итоге получаем энергию ЭМ волны:

W = m * c2

Мы же решили вникнуть в это дело поглубже и вот что из этого получилось:

Начнём с модуля сдвига.

Итак, модуль сдвига (G) из Википедии:

«G = τ / ɣ = (F / A) / (∆u / ∆r) = (F * ∆r) / (A * ∆u)

Скорость поперечной волны зависит от модуля сдвига:

с = Корень (G / p)

где р: массовая плотность среды».

Теперь выясним правомерность равенства (w = G).

Пусть энергия сдвига возбуждает энергию поля, и соответственно энергию волны. Остаётся определить эту энергию.

Итак, энергия сдвига, поля и волны равна работе силы (F) на усреднённом участке от (0) до (∆u), т.е. на участке (∆u / 2) (см. Рис. из Википедии) равна:

W = ½ * (F * ∆u)

∆u = ɣ * ∆r

F = τ * ∆r2

Тогда:

W = ½ * (τ * ∆r2 * ∆u)

Определим плотность энергии при (V = A * ∆r = ∆r3):

w = W / V = ½ (τ * ∆r2 * ∆u) /r3 = ½ (τ * ∆u / ∆r)

Умножим правую часть на τ / τ:

w = ½ (τ * τ * ∆u / (τ * ∆r))

Заметим, что ∆u / (τ * ∆r) = 1 / G

Тогда:

w = ½ (τ2 / G)

Отсюда:

G = ½ (τ2 / w)

Как видите, (G) это вовсе не то же самое, что плотность энергии (w). Во всяком случае при чистом сдвиге обычного упругого тела.

С учётом (G) получим:

c2 = ½ (τ2 / (w * p))

Очевидно, что из этого формулу Эйнштейна не слепишь ни для фотонов, ни для ЭМ волны, ни для обычных тел. А теперь посмотрим, что можно действительно слепить из последнего выражения.

Умножим правую часть на (V / V = ∆r3 / ∆r3):

c2 = ½ (τ2 * ∆r3/ (w * p * ∆r3)) = ½ (F2 * ∆r3/∆r4) / (w * m) = ½ (F2/∆r) / (w * m)

c2 = ½ (F2 /∆r) / (w * m)

Ещё раз умножим правую часть на (V / V = ∆r3 / ∆r3):

c2 = ½ (F2 * ∆r2) / (W * m) = ½ W2/ (W * m) = ½ W / m

или

c2 = ½ W / m,

Отсюда окончательно получаем нормальную формулу энергии (W) из нормальной классической механики:

W = m * c2 / 2

Модуль сдвига измеряется в единицах силы, отнесённой к единицам площади — паскалях, что при полном раскрытии всех физических величин, входящих в модуль сдвига, формально совпадает с размерностью плотности энергии. Однако энергия — это вовсе не сила, отнесённая к единице площади. Энергия в единичном объёме не перестаёт быть энергией в Джоулях на метр объёма ([дж/моб.). Следовательно, физически модуль сдвига не соответствует плотности энергии. А энергия обычных тел не может отличаться от энергии фотонов или ЭМ-волны, если в основе и того, и другого лежит одна и та же материя.

Приведём ещё одно убедительное свидетельство против вывода формулы Эйнштейна на примере модели фотона профессора, д.т. н. Канарёва Ф. М. Будучи против СТО в принципе, профессор Канарёв, тем не менее поддержал формулу Эйнштейна. Однако его подход принципиально иной, не имеющий ничего общего с фантазиями Эйнштейна.

В «Монографии микромира», 2015 г., http://www.micro-world.su/ Филипп Михайлович Канарёв, человек с исключительно правильной физической и человеческой логикой предложил кольцевую модель фотона, которая, по его мнению, решает проблему с отсутствием множителя (½) в формуле Эйнштейна. Такая идея скорее всего появилась задолго до Канарёва, даже если он и пришёл к ней независимо. Но в любом случае она заслуживает внимания. Канарёв пишет:

«В соответствии с законами классической физики, а точнее, классической механики, энергия Ef = mC2 равна кинетической энергии кольца, которое движется прямолинейно и равномерно…».

Полная кинетическая энергия колеса (бесконечно тонкого кольца) в классической физике действительно равна сумме кинетической энергии его поступательного и вращательного движения.

E = 0, 5 * m * v2 +0, 5 * m * I * ω2

E = 0, 5 * m * v2 +0, 5 * m * r2 * v2 / r2

E = 0, 5 * m * v2 +0, 5 * m * v2 = m * v2

Идея вращающегося фотонного кольца в некотором приближении моделирует все известные свойства света, в том числе и корпускулярно — волновой дуализм. Однако для разделения полной энергии тела на энергию вращательного и поступательного движения строго пополам, а также образование её из таких половинок необходимо обеспечить строго заданное отклонение линии взаимодействия от линии центра масс для каждого типа размера тел, что довольно сложно обеспечить в хаотичных столкновениях материи в реальной действительности. К тому же вращение фотонов не гарантирует равенство угла падения и угла отражения в законе отражения тел. Всё это не добавляет понимания сущности фотона и его энергии.

Таким образом, информационные иллюзии, связанные с запаздыванием информации в виду конечности скорости света, релятивисты ошибочно принимают за реальную действительность. Поэтому-то в современной физике нет ни одного непротиворечивого вывода формулы Эйнштейна. Физика иллюзий несколько отличается от реальной действительности.

Эксперименты по разгону массы до скоростей, близких к скорости света, действительно подтверждают аномальный рост энергии магнитного поля без соответствующего приращения скорости. Однако это вовсе не значит, что по детскому недомыслию релятивистов энергия в нарушение ЗСМ якобы непосредственно превращается в массу. Дополнительная масса может, например, присоединяться к массе покоя тела при его движении сквозь материальный эфир.

Если это так, то при скоростях, близких к скорости света этот фактор может стать весьма заметным и решающим в аномальном росте энергии, опережающем приращение скорости. А поскольку присоединённая масса, как и скорость массы, не может возникнуть мгновенно вне времени, то энергия на разгон присоединённой массы (Еприс.) определяется по классической формуле с учётом усредняющего множителя (1/2) или какого-либо иного, с той лишь разницей, что теперь в ней меняется не скорость, а присоединённая масса:

Еприс. = mприс. v2 / 2

Тогда полная формула энергии принимает вид:

Е = Е0 + Еприс. = m0v2 / 2 + mприс. v2 / 2,

где (Е0 = m0v2 / 2) — энергия разгона исходной массы.

После группировки массы получим:

Е = m0v2 / 2 + mприс. v2 / 2 ≈ (m0 + mприс.) * v2 / 2

Сумма масс в скобках в правой части — это и есть релятивистская масса:

mр = m0 + mприс. = m0 / √ (1 — v2 / с2)

Пусть для примера (v = 0,886 * c)

Тогда релятивистская масса равна (2 * m0). Подставив это значение массы в формулу энергии получим:

Е = 2 * m0 * v2 / 2 = m0 * v2

То есть усредняющий множитель (½) исчезает уже при скорости (v = 0,886 * c). Этот пример, по крайней мере, лишён релятивистского абсурда и опирается на нормальную классическую механику, в которой не хватает только физического механизма образования присоединённой массы. Но, если такой процесс действительно существует, то открытие этого механизма всего лишь вопрос времени. При этом формула релятивистской массы может значительно отличаться от существующей. А вообще приведённый нами пример, это всего лишь абстрактное на данный момент свидетельство того, что адекватные решения этого вопроса может существовать в принципе.

И раз уж мы всё равно отвлеклись от темы настоящей главы, то доведём начатую критику СТО до логического конца. Путенихин П. В. в статье «Три ошибки анти-СТО» пишет: «Многие из желающих опровергнуть СТО не стремятся изучить её. Математика СТО принципиально неопровержима (Выделение наше, авт.). Последняя возможность — это попытаться показать несоответствие математической теории СТО реальному физическому миру. И в этих попытках необходимо опираться на результаты опытов в стиле Маринова».

Но утверждать, что в природе могут якобы отдельно существовать правильная математика и правильная физика — это значит не понимать, ни того, что такое математика, ни того, что такое физика вообще. Математика это не природное явление. Это наше субъективное отражение физики природы. Поэтому математических теорий в природе вообще не существует, есть только физические теории и их записи математическими символами.

И если мы пока чего-то не понимаем в природе, то теоретически мы, конечно же, можем описать это непонятное явление природы правильными математическими формулами, но только случайно. Однако вероятность этой случайности не больше чем вероятность напечатания романа Л. Толстого «Война и мир» обезьяной, которую научили только нажимать на клавиши печатной машинки.

Но люди не обезьяны. Люди умеют не только нажимать на клавиши, они умеют ещё наблюдать и анализировать реальные явления природы, хотя бы по их внешним признакам, даже и не зная пока их истинного физического смысла. Поэтому правильные математические формулы в физике иногда, даже без четкого понимания людьми физики явлений природы появляются с вероятностью намного выше обезьяны.

Так, например, случилось и с преобразованиями Лоренца, которые правильно описывают оптические явления, проявляющиеся на больших расстояниях с учётом конечности скорости света. Однако «практически правильно» это не значит абсолютно правильно. Математика это не самостоятельная наука, это язык физики. Но у каждого языка есть не только прямой смысл дословного перевода, но и скрытый смысл переведённых дословно слов фраз.

Наблюдая за внешними проявлениями оптических явлений, люди правильно перевели их для себя дословно, как математические фразы в виде формул преобразований Лоренца. Но скрытый смысл этих фраз люди так и не поняли в виду отсутствия опыта перевода таких новых для людей фраз и сложности экспериментального приобретения такого опыта.

То есть люди так и не смогли убедиться в ложности принципа инвариантности скорости света на опыте. Поэтому в конечном итоге преобразования Лоренца в СТО оказались неправильным смысловым переводом языка природы. А неправильный перевод языка природы на человеческий язык физики математику — это неправильная математика.

У математики нет собственного смысла. Её дело правильно отражать смысл природы. И это убедительно показано в работе Соколова Г. и Соколова В. «Специальная теория относительности может быть опровергнута экспериментально». http://alaa.ucoz.ru/Skachivanie/sokolovr.pdf Так что напрасно Путенихин говорит о неопровержимости математики СТО.

Сам А. Эйнштейн критично высказался о результатах своих исследований. Отвечая почитателям своего таланта, он писал на склоне лет: «Им кажется, что я в тихом удовлетворении взираю на итоги моей жизни. Но вблизи все выглядит совсем иначе. Там нет ни одного понятия, относительно которого я был бы уверен, что оно останется незыблемым, и я не убежден, нахожусь ли вообще на правильном пути» (Ф. Гернек, «Альберт Эйнштейн Жизнь во имя истины, гуманизма и мира», М: «Прогресс» 1966, с 16).

Французский ученый Л. Бриллюэн отметил, что «…Общая Теория Относительности — блестящий пример великолепной математической теории, построенной на песке и ведущей ко все большему нагромождению математики в космологии (типичный пример научной фантастики)».

Российский ученый В. Рыдник в книге «Увидеть невидимое» отмечает, что представление об элементарных частицах составляют путем синтеза информации упругого и неупругого рассеяний при экспериментах на ускорителях элементарных частиц. Сложность этой задачи, по его мнению, сравнима с ситуацией, описанной в притче о слепцах: «Один потрогал хобот слона и сказал, что слон — это что — то мягкое и гибкое, другой дотронулся до ноги и заявил, что слон похож на колонну, третий ощупал хвост и решил, что слон — это нечто маленькое, и т. д.». Именно такие «научные» результаты сейчас получают учёные на Европейском ускорителе в Церне.

Крупнейший физик XX столетия П. Дирак сказал: «Мне кажется весьма вероятным, что когда-нибудь в будущем появится улучшенная квантовая механика, в которой будет содержаться возврат к причинности и которая оправдает точку зрения Эйнштейна. Но такой возврат может стать возможным лишь ценой отказа от какой-нибудь другой фундаментальной идеи, которую сейчас мы безоговорочно принимаем. Если мы собираемся возродить причинность, то нам придется заплатить за это, и сейчас мы можем лишь гадать, какая идея должна быть принесена в жертву».

Беспричинность базируется на принципе неопределенности, который был введен Гейзенбергом. Согласно этому принципу, невозможно с заданной точностью определить одновременно координату и скорость частицы. Значение этого принципа кратко и ёмко определил американский физик Дж. Б. Мэрион: «Если когда-нибудь будет доказано, что принцип неопределенности неверен, то мы должны будем ожидать полной перестройки физической теории».

«Вне всяких сомнений, — считает итальянский физик Тулио Редже, — квантовая механика будет, в конце концов, преодолена, и, возможно, окажется, что сомнения Эйнштейна были обоснованы. В настоящее же время, похоже, нет ни физиков, которые видели бы дальше собственного носа, ни конкретных предложений, как преодолеть рубежи квантовой механики, ни экспериментальных данных, указывающих на такую возможность».

1.2.3. Физический смысл гравитационной постоянной

В классической физике приводится наглядный смысл гравитационной постоянной. Так, например, С. Э. Хайкин в Общем курсе физики Т1, Механика, издание второе, дополненное и переработанное, государственное издательство технико-теоретической литературы ОГИЗ, Москва, Ленинград 1947 г. на стр. 268 пишет:

На наш взгляд, наглядный «смысл» гравитационной постоянной, приведенный Хайкиным не соответствует ее физическому смыслу. Ничего наглядного, а, значит, и понятного в этом «наглядном смысле», а точнее в наглядной бессмыслице нет.

Принцип эквивалентности масс или сил гравитации и инерции это эвристический принцип, использованный Альбертом Эйнштейном при выводе общей теории относительности. Приведём один из вариантов его современного изложения:

«Силы гравитационного взаимодействия пропорциональны гравитационной массе тела, силы инерции же пропорциональны инертной массе тела. Если инертная и гравитационная массы равны, то невозможно отличить, какая сила действует на данное достаточно малое тело — гравитационная или силаинерции».

Однако сам А. Эйнштейн говорил только о пропорциональности масс: «…пропорциональность между инертной и тяжелой массой соблюдается без исключения для всех тел с достигнутой до настоящего времени точностью, так что впредь до доказательства обратного мы должны предполагать универсальность этой пропорциональности…».

А. Эйнштейн. Собр. науч. тр. в 4 Т.- М.: Наука, 1965. Т.1.

Но, как это ни странно, в современной физике под принципом эквивалентности масс преимущественно понимается не пропорциональность, а именно равенство масс. Это мнение основано на том, что при помощи различных систем физических величин и систем их измерения гравитационная постоянная может быть численно сведена к единице. Однако даже сама по себе необходимость совершения каких-либо действий для того чтобы свести огромную численную разницу между этими массами к единице неопровержимо свидетельствует об отсутствии их численного равенства.

Добиться такого равенства можно только устранив из системы измерения физических величин само понятие массы и соответственно её размерность. Но тогда не будет и принципа эквивалентности массы. Именно по такому ложному пути идут сторонники системы измерения физических величин LT. О правомерности или скорее, о неправомерности упразднения гравитационной постоянной мы подробно поговорим в главе (2.). Однако есть более разумный и естественный путь к пониманию принципа эквивалентности и без упразднения гравитационной постоянной.

Логично предположить, что если одно и то же тело по-разному притягивается или ускоряется инертно, то постоянное и неизменное количество его вещества в этих и вообще любых взаимодействиях просто по-разному участвует в них. Однако Хайкин вместо того, чтобы показать вполне естественное и принципиальное равенство общего количества вещества одного и того же тела и разное участие этого вещества в разных типах взаимодействий, выдаёт за физический смысл гравитационной постоянной вопиющее противоречие?!

Единичное соотношение произведения масс и квадрата расстояния между ними, на которое ссылается Хайкин, справедливо не только для единичных масс и единичного расстояния между ними, но и для любых масс, численно равных расстоянию между ними. Например, «наглядный смысл», приведённый Хайкиным сохранится и для масс 10 кг, 20 кг при расстоянии между ними 10 м, 20 м и т. д.

А вот с учётом размерности силы и гравитационной постоянной равенство, приведённое Хайкиным, вообще не имеет физического смысла. Даже если отношение произведения масс к квадрату расстояния между ними равно единице, то сами массы и расстояние между ними физически никуда не исчезают. Поэтому их нельзя опускать, как это сделал Хайкин.

С физической точки зрения закон тяготения для любых масс можно представить в следующем виде:

F = γ * k,

где

k = m1 * m2 / r2 [кг2/м2]

Коэффициент (k) может принимать любые численные значения, в том числе и единичное значение, причём, как показано выше, не только для единичных масс и единичного расстояния между ними. Однако физический смысл гравитационной постоянной (γ) не становится от этого ни более наглядным, ни более понятным. Наоборот, акцентируя внимание на единичном значении коэффициента (k), Хайкин только уводит физику в сторону от истинного физического смысла гравитационной постоянной.

Физически сила не равна гравитационной постоянной, ни при каких значениях (k) и ни при каких значениях масс и расстояниях между ними, даже если произведение масс численно равно квадрату расстояния между ними, т.к. сила и гравитационная постоянная имеют разную размерность и соответственно разный физический смысл. То есть, даже если численное значение (F) равно численному значению (γ), то физически сила не равна гравитационной постоянной:

F = γ, так как [кг * м/с2] ≠ [м3 / (кг * с2)].

Таким образом, физический смысл гравитационной постоянной никак не связан с наглядной бессмыслицей, представленной Хайкиным. Гравитационная постоянная вообще не может быть исключительно одним только коэффициентом пропорциональности между массами, т.к. она имеет вполне определённую размерность, а это уже физическая величина. Она не перестанет быть физической величиной даже если в её составе есть, в том числе и какой-то безразмерный масштабный коэффициент пропорциональности. А физическая величина, кроме всего прочего имеет ещё и индивидуальный физический смысл.

Численное значение гравитационной постоянной определяется, в том числе и коэффициентом пропорциональности только не между массами одних и тех же тел, т.к. количество вещества одного и того же тела естественно не меняется в зависимости от типа взаимодействия. Как показано выше, меняется только количество работающих массовых элементов. В этом смысле гравитационная постоянная определяется коэффициентом пропорциональности между работающими массовыми элементами, приходящимися на единицу общего количества вещества физических тел в этих двух типах взаимодействия.

Количество работающих массовых элементов, выделяющихся при взаимодействии, определяется потенциально возможным количеством свободных массовых элементов в структурных образованиях физических тел и величиной силы взаимодействия, вызывающей их высвобождение. Поэтому их количество зависит от многих факторов: от физического состояния, от структуры, от химического состава, от величины физических тел, а также от типа взаимодействия и плотности окружающей мировой среды.

Уже сегодня есть опытные данные, свидетельствующие о том, что сила тяготения зависит от химического состава и физического состояния взаимодействующих тел. В соответствии с предложенным механизмом явления инерции количество работающих массовых элементов в контактном взаимодействии в значительной степени должно быть обусловлено так же и размерами взаимодействующих тел.

В периферийных областях крупных взаимодействующих тел свободных массовых элементов выделяется значительно меньше, чем непосредственно в области взаимодействия. Поэтому их сила-парус оказывает несколько меньшее влияние на их инертность и силу взаимодействия, чем в меньших телах, что приближает большие тела к гравитационным взаимодействиям по этому принципу. Из этого следует, что если за эталон массы принять инерционные свойства больших масс, в части, обеспечиваемой мировой средой, то гравитационная постоянная возможно была бы несколько больше, т.е. ближе к единице, чем сегодня для малых масс.

Если согласиться с теорией Ацюковского В. А., то гравитация обусловлена избыточным давлением эфира мировой материальной среды с внешней стороны гравитирующих объектов за счёт охлаждения среды в телах и между ними. Это означает, что в гравитационном взаимодействии тела взаимодействуют не непосредственно между собой, а с мировой материальной средой. Это значительно более слабое взаимодействие по сравнению с контактным взаимодействием непосредственно между физическими телами. Следовательно, в гравитационном взаимодействии выделяется меньшее количество свободных массовых элементов.

Причём поскольку область наименьшего давления свободного эфира находится в центре тел, то наибольшая сила тяготения также должна наблюдаться в центре тел. Это подтверждается опытными данными по измерению гравитации в глубоких шахтах. Вопреки современным теориям, предполагающим уменьшение гравитации с увеличением глубины шахты за счёт гравитации, оставшихся наверху масс, с увеличением глубины шахты гравитация только увеличивается! По этой же причине сила тяготения действует на тела через их центры, т.к. в центре тел сосредотачивается большая часть работающих массовых элементов.

Наверное, есть какое-то предельное разряжение эфира между тяготеющими телами, а также внутри тяготеющих тел, обусловленное предельными параметрами термодиффузионного движения амеров эфира. Поэтому бесконечная концентрация вещества в какой-то ограниченной области пространства и бесконечный рост силы тяготения в этой области исключены, что в свою очередь исключает такие образования, как «черные дыры». По крайней мере сказки о них, видимо, несколько преувеличены. Они точно не стягивают все вещество в одной точке.

По поводу пропорциональности гравитационной и инертной масс С. Э. Хайкин в упомянутой выше работе пишет:

Пропорциональность гравитационной и инертной масс действительно не может быть случайностью, т.к. на наш взгляд, любые взаимодействия между материальными телами, в том числе и явление всемирного тяготения, определяются одними и теми же законами природы. Если учесть, что силы тяготения вызваны обычными контактными взаимодействиями тел с мировой материальной средой, то между законами динамики Ньютона и силами тяготения нет никакой принципиальной разницы.

Хайкин С. Э. говорит, что «в классической физике законы динамики никак не связаны с существованием сил тяготения».

Однако вся небесная механика построена исключительно на законах динамики механического движения. Именно из упраздненного нами третьего закона Ньютона (см. гл. 1.2.1.) непосредственно вытекает, что небесные объекты выступают в гравитационном взаимодействии как равноправные партнеры, которые могут отличаться только массой. Именно из этого и исходил Ньютон, работая над законом всемирного тяготения надо полагать.

Это означает, что закон всемирного тяготения представляет собой только одну из форм записи второго закона Ньютона. Если закон всемирного тяготения выразить через ускорение свободного падения (а = k * Mз / r2), то для гравитационных взаимодействий мы получим тот самый второй закон Ньютона из классической динамики Ньютона (F = m * а), которая по ошибочному мнению Хайкина имеет самостоятельный физический смысл, никак не связанный с законом всемирного тяготения!

Сила из второго закона Ньютона это не просто абстрактная неуравновешенная сила, которая стала таковой в современной физике только по той простой причине, что в классической модели неуравновешенного движения ответное тело взаимодействия искусственно выносится за рамки неинерциальной системы ускоряемого тела и в дальнейшем для него не рассматривается. В реальной действительности ответное тело никуда не делось, т.к. именно его масса и определяет ускорение якобы неуравновешенного движения ускоряемого тела и реально уравновешивает взаимодействие в целом в соответствии с третьим законом Ньютона.

Присутствует в классической динамике, определяемой вторым законом Ньютона и расстояние между взаимодействующими телами. Это размер зоны упругой деформации вдоль линии взаимодействия между взаимодействующими телами. Правда в отличие от силы тяготения, которая обратно пропорциональна квадрату расстояния, сила упругости зависит от удлинения линейно, т.е. сила упругости пропорциональна первой степени удлинения. Эта зависимость была установлена экспериментально и носит имя: закон Гука:

Fупр. = — k * x,

где:

x — удлинение;

k — модуль продольной упругости или модуль Юнга.

Однако это соотношение справедливо для равномерно деформированного тела, в котором установившаяся статическая деформация равномерно распределена по его объёму для постоянной силы, вызывающей деформацию. Если учесть, что в реальном взаимодействии сила в центре зоны деформации не постоянная, а изменяется пропорционально удлинению, то индивидуальная сила, приложенная к каждому массовому элементу в каждом поперечном сечении тела, оказывается пропорциональной квадрату удлинения.

В современной физике считается, что силы упругости имеют электрическую природу. Но силы Кулона имеют квадратичную зависимость от расстояния. А вот почему квадратичная зависимость кулоновских сил от расстояния превращается в линейную зависимость сил упругости от расстояния, классическая физика не поясняет. Учитывая зависимость инертной силы двух взаимодействующих тел от квадрата их упругого удлинения при движении с ускорением, второй закон Ньютона можно привести к форме записи закона всемирного тяготения.

Fкв = k * (m1 * m2 / r2) (1.2.4)

Тогда

а1 = k * (m2 / r2) (1.2.5)

а2 = k * (m1 / r2) (1.2. 6)

где:

r2: удлинение взаимодействующих тел.

k — инертная постоянная.

Теперь видно, что физический смысл гравитационной и инертной постоянной идентичен, разные только их величины. Однако физический смысл гравитационной и инертной постоянной определяется разным количеством работающих массовых элементов только частично.

Из приведённого выше механизма явления инерции или механизма взаимодействия физических тел следует, что работающие массовые элементы образуют объёмное поле распространения энергии взаимодействия. Естественно, что при этом только часть этой энергии сообщает взаимодействующим телам линейное поступательное движение в своих направлениях вдоль линии взаимодействия.

Другая часть рассеивается во всех остальных направлениях, не оказывая прямого влияния на линейное поступательное движение тел в основном направлении взаимодействия. Поэтому величина гравитационной постоянной определяется, в том числе и соотношением объёмно образующейся силы взаимодействия с линейным поступательным движением тел вдоль основного взаимодействия.

Об этом свидетельствует и размерность гравитационной постоянной ([м3 / (кг * с2)]), которая увязывает в ЗВТ величину линейной силы взаимодействия с объёмным распространением энергии взаимодействия. Судя по размерности, которая не определяет, но отражает физический смысл любых физических величин, гравитационная постоянная определяет объёмное распространение энергии взаимодействия ([м3/с2]) приходящееся на один ([кг]) работающего вещества.

При этом количественно величина гравитационной постоянной одновременно учитывает, как разное количество работающих элементов в гравитационном и инертном взаимодействиях, так и разное объёмное распространения энергии взаимодействия в этих взаимодействиях, что влияет на их разные линейные ускорения в основном направлении.

Таким образом, гравитационная постоянная, а также очевидно инертная постоянная и электромагнитная постоянная, т.е. коэффициент видов взаимодействия имеет тройной физический смысл.

Это:

1. Коэффициент взаимодействия, увязывающий объёмный характер распространения сил взаимодействия с линейным ускорением, сообщаемым телам вдоль линии взаимодействия.

2. Коэффициент взаимодействия, отражающий разное количество работающих массовых элементов в одном и том же физическом теле или частице в зависимости от видов взаимодействия.

3. Коэффициент взаимодействия, содержащий в своём составе безразмерный коэффициент пропорциональности между абсолютными коэффициентами взаимодействия разных типов взаимодействий.

Таким образом, гравитационная постоянная, которая в силу названных выше причин не очень-то и постоянная, имеет, тем не менее, естественный природный физический смысл. Точнее физический смысл имеет принципиальная взаимосвязь всех типов взаимодействий. А гравитационная постоянная лишь отражает эту взаимосвязь между инертными и гравитационными взаимодействиями.

***

В контактном взаимодействии коэффициент взаимодействия (k) по отношению к гравитационной массе равен единице, поскольку за эталон массы для этих двух видов взаимодействия была принята именно инертная масса и не учтён истинный механизм полного взаимодействия. Причём, как мы уже отмечали, на этот коэффициент влияют физическое и химическое состояние взаимодействующих тел, а также величина их масс. Следовательно, для контактного взаимодействия масс масштаба крупных космических объектов коэффициент может быть и значительно меньше единицы.

Истинным же эталоном массы, как количества вещества должно являться полное количество вещества материального тела в штуках. При этом в каждом типе взаимодействия был бы свой индивидуальный коэффициент взаимодействия с размерностью гравитационной постоянной и величиной всегда меньшей единицы. Но даже в гипотетическом взаимодействии, в котором работают все массовые элементы тел, коэффициент взаимодействия не может быть равен единице и не сможет быть безразмерным, т.к. он увязывает объёмный характер распространения взаимодействия с линейным ускорением тел вдоль линии взаимодействия.

Поскольку сегодня о количестве вещества можно судить только по результату взаимодействия материальных тел, то практически за эталон массы можно принять инерционные свойства материальных объектов в любом из конкретных видов взаимодействия. Теоретически за эталон массы можно принять хоть инерционные свойства материальных объектов при электрических взаимодействиях. Понадобятся лишь соответствующие коэффициенты перевода электронной массы в гравитационную и контактную массу.

Логично предположить, что контактное взаимодействие также имеет своё поле инертного взаимодействия, природа которого аналогична природе поля гравитационного и электромагнитного взаимодействия. Это распределение давления эфира между взаимодействующими телами. Об этом свидетельствует, как пропорциональность инертной и гравитационной масс, так и безусловная применимость второго и третьего законов Ньютона к гравитационным взаимодействиям.

Основное отличие состоит только в том, что поле инертного взаимодействия возникает лишь при прямом контакте взаимодействующих тел между собой, а гравитационное поле возникает при контакте физических тел непосредственно с носителями гравитационного поля и мировой материальной среды — амерами.

Если при контактном взаимодействии избыточное давление элементарных носителей массы сосредоточено между взаимодействующими физическими телами, то в гравитационном взаимодействии избыточное давление мировой материальной среды действует на тела со стороны открытого пространства с внешней стороны взаимодействующих тел. Однако законы газовой динамики в обоих случаях одинаковые.

Таким образом, механизм контактного взаимодействия не должен принципиально отличаться от механизма гравитационного взаимодействия, кроме противоположной направленности сил, воздействующих на физические тела.

При этом второй закон Ньютона, как в том, так и в другом случае отражает только зависимость мгновенного геометрического приращения движения ускоряемой массы от характера текущего объёмного распределения избыточного давления эфира, действующего на каждую из взаимодействующих масс и от количества связанных с массой элементарных носителей взаимодействия — паруса взаимодействия.

***

Р. Фейнман в Фейнмановских лекциях по физике, Т1, Современная наука о природе. Законы механики. В §5 Всемирное тяготение страстно доказывает, что законы Ньютона абсолютно верны для всей вселенной и на любых расстояниях. Он приводит астрономические наблюдения, которые доказывают, что даже очень удаленные от Земли небесные тела движутся по эллипсу и собираются в скопления. Но:

Во-первых, движение планет по эллиптическим орбитам первоначально следует не из Ньютоновских законов, а из первого закона Кеплера, хотя для сути дела это и непринципиально.

А во-вторых, дело не только в расстояниях, но и в физической сущности гравитационной и инертной масс, про которые Фейнман говорит только то, что они с высокой точностью строго пропорциональны. Их пропорциональность не означает их равенства, Равно только списочное количество их массовых элементов. А законы Ньютона в существующих формулировках не раскрывают физическую сущность гравитационной постоянной, которая не соответствует наглядному смыслу, приведенному Хайкиным (см. выше).

К тому же в разных точках вселенной коэффициенты взаимодействия могут быть разными. Полный коэффициент взаимодействия должен учитывать физическую структуру, химический состав и полную массу взаимодействующих тел. Поэтому говорить об абсолютной верности законов Ньютона в смысле полноты отражения ими реальной действительности в том виде, в котором они существуют на сегодняшний день не совсем правильно.

Как показано выше, законы Ньютона описывают только частные случаи реальной действительности, т.к. не учитывают мировую материальную среду, хотя и имеют статус фундаментальных, т.е. базовых законов природы. Поэтому правильнее было бы сказать, что законы Ньютона верны в своей совокупности и с учётом всех возможных факторов, влияющих на взаимодействие материи, в том числе и плотность мировой материальной среды в области пространства, в которой осуществляется взаимодействие.

Из приведенного анализа следует, что закон всемирного тяготения, так же как и второй закон Ньютона является частным случаем или следствием не существующего пока в современной физике, но, как мы полагаем, безусловно существующего в природе, всеобщего закона взаимодействий. Этот закон одинаково определяет все типы взаимодействий в природе, отличающиеся только коэффициентом взаимодействия. Наиболее общей формой записи всеобщего закона взаимодействий является объёмная форма аналогичная выражению для закона всемирного тяготения.

Представленная схема взаимодействия носит общий неконкретный характер, т.к. современных знаний о природе недостаточно для ее детального обоснования и, конечно же, она имеет свои недостатки. Например, не разрешен вопрос, будет ли испытывать дополнительное внешнее инерционное сопротивление тело, движущееся в отсутствие взаимодействий, т.е., как считает современная физика «по инерции», если его предварительно деформировать?

Например, можно провести эксперимент с болтом и накрученными на него гайками в расслабленном виде и после их затяжки. Ответ, лежащий на поверхности — «не будет», что является серьезным возражением против предложенной схемы взаимодействия. Однако всё не так просто. Возможно в статистке свободные массовые элементы, выделившиеся при деформации, тут же вновь поглощаются или рассеиваются в пространстве. Поэтому нужны динамические эксперименты.

Приведём некоторые из них.

1.2.4. Эксперименты по обнаружению паруса и ветра взаимодействия

В. А. Кучин, М. В. Турышев и В. В. Шелихов ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЗАКОНА СОХРАНЕНИЯ ИМПУЛЬСА

http://alaa.ucoz.ru/Skachivanie/ExpProvImpRuss.doc

Схема этого эксперимента приведена в главе 3.5. на рисунке (3.5.1). Суть его состоит в следующем: Тележка через блок и нить приводится в движение грузом, опускающимся под действием силы тяжести. Если нить привязана непосредственно к тележке, то тележка получает одно ускорение. Если же нить при этом одновременно раскручивает барабан на той же тележке, то она приобретает значительно меньшее ускорение. Формальное объяснение несложное. Во втором случае сила тяжести груза совершает дополнительную работу по раскручиванию барабана, поэтому на разгон тележки затрачивается меньшая работа.

Но работа это не материальный фактор, который может реально препятствовать движению тележки. Это всего лишь количественное описание процесса взаимодействия. А вот то, что физически тормозит тележку, количество работы, затраченное на раскручивание барабана, само по себе не объясняет. С нашей точки зрения это происходит следующим образом.

При раскручивании барабана происходит его деформация, которая приводит к возникновению у него паруса взаимодействия, что препятствует его раскручиванию. Поэтому сила взаимодействия начинает реализовываться в поступательное движение самой тележки. При этом парус установившегося кручения барабана поступательному движению практически мало препятствует, т.к., если одна сторона этого паруса тормозит поступательное движение, то другая фактически «гребёт» в сторону поступательного движения.

С началом поступательного движения появляется парус и у тележки. При этом сила опять переключается на кручение барабана, после чего складывается парус тележки и т. д. Это и создаёт эффект увеличения инертности массы системы, хотя её общее количество вещества не изменяется. Конечно, этот эффект можно объяснить и одним только врождённым свойством инерции. Но есть и другой эксперимент, который приводит Черняев А. Ф. в Русской механике (см. Рис 55).

«Возьмем два ро­тора-гироскопа 1 и электромотор 2, ось которого укреплена неподвижно и пер­пендикулярно гори­зонту. На оси электромотора 3акрепим шарнирно планку 4 (рис. 55, вид сверху), по краям которой уста­новлены гироскопы 1 с осями, параллельными оси элек­тромотора. Вот и вся конструкция.

Раскрутим гироскопы против часовой стрелки до дос­тижения ими постоянной частоты и после этого начнем вращать электромотором планку с гироскопами тоже против часовой стрелки, фиксируя изменение нагрузки электромотора. У меня при проведении этого экспери­мента два гироскопа мощностью по 3 Вт так перегрузи­ли 400-ваттный электромотор, что он сгорел, так и не достигнув нормативного количества оборотов».

Правда, на рисунке гироскопы, вопреки описанию автора вращаются по часовой, а мотор против часовой стрелки. Однако это очень важный момент, который в виду допущенной автором ошибки следует обговорить более подробно. В том виде, как это изображено на рисунке эффекта торможения привода может не быть. С внешней стороны гироскопы «гребут парусом» в сторону вращения, а препятствуют вращения только внутренние паруса гироскопов.

В этом случае эффект может быть обратным, т.е. гироскопы будут в целом содействовать вращению, т.к. подгибающие стороны расположены на большем рычаге, а тормозящие на меньшем. Поэтому для получения эффекта торможения необходимо соблюдать однонаправленность гироскопов и привода, о чём говорит автор. Однако для проверки нашего утверждения эффект облегчения работы привода так же является подтверждающим эффектом.

Похожий эксперимент проводил Пехотин И. Е. (см. его Рис.4). В этом эксперименте стальной шар выбрасывался пусковым устройством и через нить тянул за собой другой такой же шар. Дальность полёта шаров изменялась в зависимости от того была ли нить предварительно навита на буксируемый шар или буксировка осуществлялась без раскручивания буксируемого шара. При наличии навивки длина полёта системы уменьшалась на 30%.

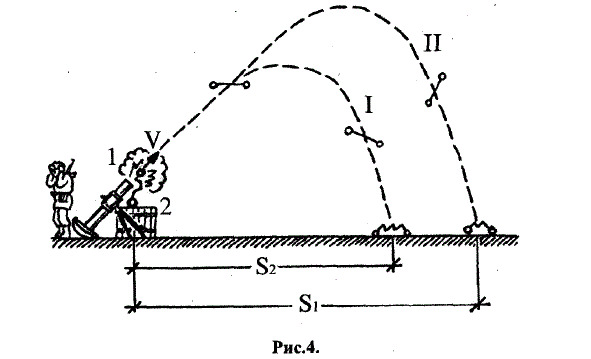
Чтобы исключить какие-либо особенности вращательного движения и связанные с ним кориолисовые силы можно предложить эксперимент без вращающихся частей (см. Рис 1.2.5). На горизонтальном стержне-направляющей могут перемещаться два устройства. Верхний и нижний диск устройств соединены с центральной частью растянутыми и зафиксированными вертикальными пружинами. Между устройствами так же находятся зафиксированные до поры до времени горизонтальные пружины. Напряжённые пружины обозначены красным цветом.

При отпускании замков пружин верхний и нижний диски ударяются о центральное тело устройств, которое может перемещаться вдоль горизонтальной направляющей (Рис 1.2.5 а). Как только деформация от взаимодействия верхнего и нижнего диска с центральным телом достигнет максимума, освобождается пружина в горизонтальном направлении (Рис 1.2.5 б). Разряженные пружины обозначены синим цветом. Предполагается, что в этом случае инертность устройства при его неизменной массе увеличится.

В эксперименте следует предусмотреть возможность включения горизонтальной пружины в разные моменты: до взаимодействия, в момент незавершённого взаимодействия и в момент полного взаимодействия. Это позволит точнее дифференцировать причину возможного эффекта увеличения инертности.

Поскольку вращения и соответственно гироскопических (кориолисовых) сил в этом эксперименте нет, то если предполагаемый эффект подтвердится, объяснить его можно только за счёт дополнительного паруса взаимодействия, распустившегося в результате взаимодействия верхнего и нижнего дисков устройств с его центральным диском. Причём в этом эксперименте сила привода между телами не тратится ни на вращение чего-либо, ни вообще на что-либо другое кроме поступательного движения одних и тех же тел. Следовательно, появление эффекта увеличения инерционности может быть объяснено только за счёт дополнительного паруса взаимодействия.

Кстати, парус распустится, как для сил взаимодействия между устройствам, так и для сил внешнего сопротивления среды. Поэтому эффект будет только в том случае, если воздействие этих сил на парус разное. Мы предполагаем, что большее воздействие будет с внутренней стороны.

Избыточное напряжение среды в зоне взаимодействия, которая определяет силы взаимодействия, формируемые за счёт среды, играет, по всей видимости, если и не теоретически определяющую, то количественно преобладающую роль в формировании сил взаимодействия в разных типах взаимодействий. О этом свидетельствует огромная разница сил в разных видах взаимодействия одной и той же материи с одной и той же массой.

Например, гравитационная постоянная определяет огромную разницу сил инертного и гравитационного взаимодействия одних и тех же масс. А поскольку материя и соответственно врождённое свойство материи преобразование напряжение-движение у всех одинаковых масс одни и те же, то остаётся предположить, что эту разницу может обеспечивать только силы взаимодействия, формируемые за счёт среды.

А вот сопротивление паруса взаимодействия, формируемого из среды, на наш взгляд, оказывает на общий инерционный эффект незначительное влияние, т.к. в момент начала взаимодействия скорости минимальные, а к его завершению парус практически исчезает. Поэтому на существующем сегодня техническом уровне обнаружить влияние паруса взаимодействия будет достаточно сложно, если не невозможно.

1.2.5. Парадокс абсолютно упругого удара

Парадокс абсолютно упругого удара некоторые авторы усматривают в том, что в ИСО, связанной с неподвижным телом-мишенью, ударное тело, движущееся со скоростью V полностью останавливается, передавая своё движение телу-мишени. При этом якобы нарушается третий закон Ньютона, в соответствии с которым тела якобы непременно должны разлетаться в разные стороны.

Один из таких авторов — Спурре А. Ф. в статье «Парадоксы физики» (http://www.sciteclibrary.ru/rus/catalog/pages/7113.html), предлагает разрешить этот парадокс формально математически, совместив логику двух ИСО. Это ИСО, связанная с центром масс взаимодействующих тел (ИСО ЦМ) и неподвижная ИСО, связанная со столом, на котором ещё до взаимодействия покоится тело-мишень. Назовём её условно абсолютной СО (УАСО).

Спурре пишет:

«На столе два одинаковых бильярдных шара массами m. После удара кием шар 1 начинает движение со скоростью V относительно неподвижного шара 2, с которым связана неподвижная система координат ХУ. Центр системы координат ХУ является материальным и обладает массой второго шара m. Шар 1 массой m и центр материальной системы ХУ образуют систему двух материальных тел, которая имеет ЦМ, расположенный в данном конкретном случае точно в середине расстояния между центрами шаров. Движение шара 1 со скоростью V в системе ХУ порождает движение и самого ЦМ в той же системе со скоростью Vцм = V / 2.

Исходя из этого, можно заключить, что шар 1 приближается к ЦМ со скоростью V / 2, но точно с такой же скоростью происходит сближение ЦМ и второго шара, т.е. в системе ЦМ скорость второго шара V / 2.

С учетом того, что ЦМ все время имеет скорость движенияVцм = V / 2 вправо, то в неподвижной системе ХУ, связанной со столом, скорость шара 1 (ударный шар — ААА) будет равна:

Vуд = Vцм — V / 2 = V / 2 — V / 2 = 0,

а скорость шара 2 (тело-мишень — ААА) будет равна сумме скоростей Vцм и V / 2, т.е.

Vм = Vцм + V / 2 = V / 2 + V / 2 = V

Вот таким образом, только с учетом движения самого центра масс системы, можно объяснить, почему шары разлетаются в разные стороны, согласно третьему закону Ньютона, но при этом один остается неподвижным, а другой движется со скоростью V (первого шара)».

В ИСО ЦМ названный парадокс действительно не просматривается. В ней оба тела изначально движутся к ЦМ со скоростью V / 2, а после взаимодействия с такими же скоростями разлетаются от ЦМ в полном соответствии с третьим законом Ньютона. Однако в ИСО ЦМ не видно и самого движения системы, т.к. относительно самой себя система естественно двигаться не может. Поэтому Спурре не забывает и про УАСО стола. Но в решении Спурре появляются новые парадоксы вместо кажущегося парадокса с якобы не выполнением 3-го ЗН, который с учётом физического смысла явления, вовсе парадоксом не является.

У Спурре ИСО ЦМ изначально движется в УАСО. При этом одно из двух тел системы всегда остаётся неподвижным относительно УАСО, не участвуя в общем движении ЦМ системы. Уже одно это логически противоречит поведению единого цельного образования, которое представляет собой замкнутая система. При этом абстрактное движение абстрактно-математической точки равновесия не связанных общим движением тел, Спурре складывает с реальным движением каждого тела, что сводит на нет его решение. Это один из новых парадоксов Спурре.

Замкнутые системы образуются исключительно только в непрерывных взаимодействиях, их составных частей, в пределах ограниченного в среднем пространства. Это означает, что в замкнутой системе непрерывно действуют два противоположных процесса — центробежный и центростремительный, что собственно и позволяет системам быть замкнутыми. При этом однократные взаимодействия образуют временную замкнутую систему только на период взаимодействия. До и после взаимодействия — это отдельные, не связанные между собой тела, сохранение импульса и энергии которых «до» и «после» — не гарантировано.

Другой парадокс решения Спурре заключается в том, что даже абстрактно-математическое движение его псевдо системы необъяснимо прерывается в момент взаимодействия. Спурре пишет, что в момент столкновения, сближение центров шаров относительно их ЦМ прекращается. При этом скорости шаров в ИСО ЦМ становятся равными нулю. А поскольку, как это ни парадоксально звучит, относительное движение абсолютно, а первоначально в УАСО задана именно относительная скорость шаров, один из которых в УАСО всегда неподвижен, то в момент столкновения, скорости шаров в УАСО также становятся равными нулю. Это также гарантированно разваливает решение Спурре.

Известный в физике принцип относительности имеет один, но очень существенный недостаток. Это чисто математический приём, за которым не всегда виден физический смысл явления, не зависящий от того сквозь какие очки в виде различных систем отсчёта его рассматривают. Науке сегодня неизвестна абсолютная система отсчёта, в которой, тем не менее, условно академически в чистом виде по умолчанию рассматриваются все основные законы физики. Поэтому принцип относительности обязательно должен опираться на физический смысл явлений.

Зная физический смысл явления инерции и принцип образования замкнутых систем, которые в однократных взаимодействиях образуются только на время взаимодействия, кажущийся парадокс абсолютно упругого удара можно легко разрешить именно в УАСО. Напомним также, что ньютоновские силы инерции поэлементной поддержки, которые основаны на врождённой инерции (см. главу 1.2.1.), препятствуют не только движению тел с положительным ускорением (тело-мишень), но и поддерживают уже имеющееся движение физических тел (ударное тело) при противодействии их движению. А из этого следует, совершенно очевидные приведённые ниже факты.

До выравнивания скоростей в УАСО поддерживающие ньютоновские силы инерции ударного тела, всегда больше препятствующих движению ньютоновских сил инерции тела-мишени. Они не дают телу-мишени оторваться от ударного тела. Этому способствует так же и истинные силы инерции мировой материальной среды, которые «подпирают» всю вновь образующуюся систему со стороны тела-мишени. В результате вновь образующаяся система постепенно приобретает общий импульс, в реальном физическом взаимодействии.

При (m1 = m2 = m) и скорости каждого тела, равной (V / 2) кинетическая энергия всей системы (m * (V / 2) 2 / 2 + m * (V / 2) 2 / 2 = m * V2 / 4) уменьшается вдвое по сравнению с энергией заданного движения ударного тела (m) со скоростью (V), равной (m * V2 / 2)!

В отсутствие градиента скоростей после их выравнивания кинетическая энергия ударного тела естественно уже не может быть передана телу-мишени. Следовательно, энергия ударного тела, которая не была израсходована при образовании системы, сохраняется в области упругой деформации. При этом объединённая система из двух тел будет двигаться равномерно и прямолинейно со скоростью равной половине первоначальной скорости ударного тела.

Именно этот факт реального движения новой системы и отсутствует в решении Спурре. У Спурре есть абстрактно-математическое движение точки равновесия отдельных тел, в то время когда самой системы ещё собственно и нет. При этом процесс перехода абстрактного в реальное у Спурре никак не объяснён, что вряд ли можно считать заявленным разрешением названного парадокса. Зато новый парадокс Спурре, в котором система якобы может двигаться вся в целом, но без участия в общем движении системы её составных частей — налицо. Если не вся, то — это и не система.

С выравниванием скоростей новая система приобретает уже не абстрактно-математическую, а реальную физическую скорость (V / 2). А вот абстрактная псевдо система Спурре, которая движется только одним своим телом, в момент нулевой относительной скорости между телами, наоборот должна остановиться. Во всяком случае у Спурре о движении объединённой системы с постоянной скоростью ничего не сказано. Очевидно, что двигаться в составе новой системы шары будут недолго. Но без упоминания этого факта невозможно объяснить распад объединённой системы, за что собственно и взялся Спурре.

Равномерно движущаяся система тел не испытывает сопротивления ньютоновских сил инерции ни со стороны ударного тела, ни со стороны тела-мишени. Остаётся только ничем не скомпенсированное внутреннее напряжение. Поэтому после выравнивания скоростей начинается разрядка внутреннего напряжения. На этапе разрядки напряжения каждая из частей системы получит такие же по абсолютной величине приращения движения и соответственно такие же приращения энергии, как и на этапе её формирования.

Ударное тело получит отрицательный импульс движения, равный по величине её оставшемуся положительному импульсу. А тело-мишень получит положительный импульс равный по величине её уже приобретённому вместе с системой положительному импульсу. В результате после полной разрядки напряжения ударное тело на абсолютно законных основаниях полностью остановится в УАСО, а тело-мишень также без каких бы то ни было парадоксов приобретет в УАСО скорость ударного тела (V).

В УАСО можно без каких-либо парадоксов смоделировать и неупругое взаимодействие. Если после выравнивания скоростей блокировать разрядку области упругой деформации каким-либо искусственным механическим способом, то вторая половина кинетической энергии ударного тела, остающаяся после выравнивания скоростей, сохраняется внутри системы до тех пор, пока не будет выведена из нее в виде излучения, теплового рассеивания или каким-либо иным способом. Если же разорвать механическую связь до того как энергия ещё не успеет сколько-нибудь заметно рассеется, то мы вновь получим упругое взаимодействие.

Спурре утверждает, что только в системе ЦМ законы сохранения импульса и энергии имеют реальный физический смысл и точные количественные значения. Однако, как показано выше, физический смыл сохраняется в любой ИСО. С учётом физического смысла явления всегда можно определить и точные количественные значения всех законов в любой системе. Для этого достаточно различать внутренние процессы, которые в чистом виде действительно виднее в ИСО ЦМ, и внешние процессы, которые происходят уже с самой системой ЦМ в целом.

Ну, а если физический смысл явления пока не известен, то никакие СО в этом не помогут. В этом случае необходимо только дальнейшее изучение.

1.2.6. Заключение по явлению инерции

В заключение подраздела о механизме явления инерции разберём два примера, приведённых классической физикой в лице профессора Н. В. Гулиа. Эти примеры призваны, по его мнению, окончательно убедить всех в нереальности сил инерции. Профессор Гулиа в «Удивительной физике» в главе «Инерция: сила или бессилие?», негодуя по поводу довольно часто встречающегося даже в науке мнения о том, что сила инерции является реальной силой, относит это к несуразным казусам, и приводит пример одного из таких, по его мнению казусов:

«Но и при обычном прямолинейном движении таких казусов сколько угодно, и свидетелем одного из них был автор. Дело происходило на защите кандидатской диссертации по теории автомобиля. Молодой диссертант делал доклад по работе, пользуясь формулами, написанными на плакатах. Естественно, диссертант воспользовался принципом Даламбера, по-видимому, даже не подозревая об этом. И уравнение тягового баланса ускоряющегося автомобиля он записал в том виде, как это делается и в большинстве учебников:

Рk (сила тяги) = Рf (сила сопротивления качению) + РV (сила сопротивления воздуха) + Рj (сила инерции).

Шутник — член Ученого Совета — спрашивает диссертанта:

— Вот у вас сила тяги равна сумме всех сопротивлений. Стало быть, автомобиль находится в равновесии, он неподвижен. Почему же вы говорите, что машина разгоняется?

Диссертант долго думал, а потом не нашел ничего лучшего, как сказать:

— Это только теоретически — в равновесии. А на самом деле сила тяги чуть-чуть больше сопротивления, вот он и движется!

Хохот был такой, что проснулись даже обычно спящие члены Совета. А правильный ответ должен быть таким:

— Сила инерции фиктивная, несуществующая. Она добавлена согласно принципу Даламбера для облегчения решения задачи (рис. 44). И вся разница между силой тяги и силами сопротивлений идет на разгон автомобиля, вот он и ускоряется! Но разве виноват диссертант, что он учился по учебникам, где все те же ошибки. Не понимают многие инженеры принцип Даламбера, вот и «оживают» несуществующие силы инерции!»

Хорошо хоть Гулиа сам признал, что силу инерции считают физически реальной не только неграмотные изобретатели инерцоидов и другие неграмотные люди, которые не читали учебников. Оказывается «все те же ошибки» можно почерпнуть и из самих учебников, как говорит сам Гулиа. Надеемся, что после этого автора не будут обвинять в голословности, по поводу его мнения о том, что в современной физике существует–таки двойственное понятие силы инерции и в том, что, заявляя об этом, он якобы просто не правильно истолковывает работы классиков теоретической механики: «Каждый видит в книге свою фигу». В этом автора обвинили на известном физическом форуме МГУ.

Однако оказывается, современный нам и достаточно известный в мире науки профессор классической механики тоже признает, что в учебниках по этому поводу нет исчерпывающей ясности. Правда сам Гулиа двойственность понятия инерции категорически отрицает и никак не хочет признать, что в реальной действительности все–таки «оживают» несуществующие силы инерции», а точнее сказать живут в ней постоянно с самого сотворения нашего мира, если, конечно же, таковое когда–либо было. Гулиа никак не может понять, что абсолютно все силы в природе возникают исключительно только, благодаря явлению инерции. Свойство материи преобразование напряжение–движение это и есть инерция, которая в современной физике ошибочно воспринимается, как противодействие движению при его возникновении и противодействие торможению движения.

В реальной действительности противодействия нет. Есть естественное превращение (преобразование) силы (напряжения) в движение. При этом напряжение расходуется, превращаясь в движение. Поэтому даже без учёта сопротивления мировой материальной среды поддерживать даже неизменное ускорение возможно только за счёт непрерывного пополнения расходуемого напряжения. Формально сила при этом не меняется по абсолютной величине, что связано с классической моделью неуравновешенного движения, в которой источник постоянной силы академически движется синхронно с ускоряемым телом, не неся затрат на собственное ускоренное синхронное с телом движение.

В реальной действительности для получения новой порции даже неизменного ускорения, после превращения в него затраченной на него силы, необходима и новая сила. Об этом свидетельствует непрерывный рост кинетической энергии ускоряющегося тела, несмотря на видимую неизменность силы и ускорения. Неизменна только мгновенная абсолютная величина напряжения-силы. А её количество при этом непрерывно пополняется взамен израсходованного, и эквивалентно это количество — количеству вновь вкладываемого в разгон ускоряемого тела — движения ответного тела. А принцип Даламбера не позволяет увидеть эту реальную картину, такого равновесного внешне, но такого не равновесного по энергии движения!

Постоянство силы для неизменного ускорения ускоряемого тела обеспечивается в процессе регулирования взаимодействия. Но запускает такое регулирование только большая по абсолютной величине неуравновешенная сила опорного тела по сравнению с постоянным в среднем значением силы в процессе регулирования. Мы уже не говорим о прямом сопротивлении мировой материальной среды, на преодоление сопротивления которого также расходуется напряжение взаимодействия. Поэтому раз уж автомобиль движется ускоренно, то «сила тяги…» действительно «…чуть–чуть больше сопротивления, вот он и движется».

Таким образом, ответ диссертанта, пусть неосознанный и интуитивный, гораздо ближе к истине, чем мнение Ученого Совета, основанное на «голой» математике Даламбера. Поэтому, скорее всего, уважаемые члены Совета в конечном итоге смеялись и до сих пор смеются над самими собой. А вот ответ Гулиа, заключающийся в том, что сил инерции в природе физически не существует, является абсолютным казусом. Его «Удивительная физика» воистину удивительна и необъяснима!

***

Есть ещё один пример неправильной интерпретации явления инерции профессором Гулиа Н. В. Будучи ярым противником реальности сил инерции, профессор Гулиа в «Удивительной физике» в главе «Кто стоял на плечах гигантов?» пишет:

«По прекрасному ровному шоссе едет автомобиль с выключенным двигателем (как говорят, «накатом»), медленно сбавляя скорость. И ревя двигателем от натуги, бульдозер тащит перед собой целую гору песка, но движется равномерно и по прямой, хотя и медленно (рис. 26). Которое из этих движений можно назвать движением по инерции? Да конечно, второе, хотя так и хочется указать на первое. Самое главное, что тело движется равномерно и прямолинейно. Все, этого уже достаточно, больше ничего и не нужно. Автомобиль в первом примере хоть и медленно, но замедляется. Следовательно, силы, действующие на него, не скомпенсированы: сопротивление есть, а силы тяги — нет. А на бульдозер действует много тел, каждое со своей силой, но все силы скомпенсированы, их равнодействующая равна нулю. Вот почему он и продолжает двигаться равномерно и прямолинейно, то есть по инерции.

Именно этот пример привел Гулиа, делая свое уточнение к классической формулировке первого закона Ньютона (см. выше). Однако:

Во–первых, не бульдозер движется равномерно и прямолинейно, а система тел «бульдозер — гора песка», поэтому заострять внимание на множестве абстрактных сил, действующих на бульдозер при равномерном движении всей системы «бульдозер — гора песка» физически не корректно. Если внутри системы все силы скомпенсированы, то для движения системы в целом они фиктивные, т.е. на систему «бульдозер — гора песка» не действуют никакие силы. Это намного ближе к определению равномерного движения Ньютона, чем представления Гулиа.

А во–вторых, о непричастности первого закона Ньютона к движению по инерции в отсутствие мировой материальной среды мы уже говорили выше. Движение при полном отсутствии сил не может быть физически отнесено к движению под действием сил инерции, т.к. «ничто» (фиктивные силы инерции) не может являться смыслом или основой «чего–то» (движения). Такое движение, как мы отмечали выше, в лучшем случае происходит под «охраной» сил инерции, возникающих только при нарушении равномерного движения в соответствии со вторым законом Ньютона (см. гл. 1.1).

С точки зрения существующей теории движения система «бульдозер–гора песка» движется под действием абстрактной академической силы тяги, поэтому сам процесс формирования силы тяги бульдозера за счет его взаимодействия с Землей в существующей математической модели движения не рассматривается. Для современной теории движения достаточно того, что абстрактно назначенная сила тяги просто есть. То же самое можно сказать и о силе сопротивления движению системы «бульдозер–гора песка». В существующей математической модели движения она также никак не связана с инерцией Земли. Это просто абстрактная сила сопротивления, образующаяся за счет сил трения с абстрактной дорогой.

Вот и получается, что в классической физике абстрактной силе тяги противодействует такая же абстрактная сила трения. Однако в реальной действительности без истинных сил инерции не может возникнуть, ни сила тяги бульдозера, ни сила трения горы песка. При этом в реальной действительности противоположно направленные сила тяги и сила трения уравновешивают друг друга не в каждый момент времени.

Опорным телом для движения системы бульдозера является Земля, с которой он взаимодействует посредством контакта с дорогой. Через силу тяги, бульдозер фактически периодически подключает к взаимодействию массу всей Земли. Это позволяет ему получить во взаимодействии с Землёй силу тяги и ускорение, необходимые для преодоления сопротивления массы горы песка и её трения с Землёй. Однако при разгоне системы трение горы песка увеличивается, т.е. она со своей стороны так же подключает к взаимодействию дополнительную массу Земли. При этом скорость системы падает, а затем, поскольку это приводит к уменьшению трения, вновь возрастает под действием силы тяги бульдозера.

Таким образом, за счет силы тяги бульдозера, взаимодействующие стороны: подсистема «бульдозер — гора песка» и Земля периодически разгоняются, а за счет дополнительного сцепления горы песка с Землёй, возрастающего при ускорении, и подключения дополнительной инерционной массы Земли в обратном направлении вновь тормозятся. Это и есть отрицательная обратная связь, без которой никакое регулирование, в том числе и равномерного движения в присутствии реальных сил не возможно.

Такое регулируемое движение вряд ли можно считать равномерным движением в отсутствие сил. Оно равномерное в среднем, и силы в нём отсутствуют так же только в среднем. Так что ответ на вопрос о том, какое из движений в приведенном примере является движением по инерции, не так прост, как это предлагает считать профессор Гулиа, который утверждает, что для этого достаточно только факта равномерного и прямолинейного движения:

«…Самое главное, что тело движется равномерно и прямолинейно. Все, этого уже достаточно, больше ничего и не нужно…».

Неравновесное движение автомобиля «с выключенным двигателем» отличается от движения подсистемы «бульдозер — гора песка» с работающим двигателем только не симметричным регулированием реальных сил торможения и сил инерции поэлементной поддержки автомобиля. Из этого следует, что ни одно из движений в приведённом примере, строго говоря, не является движением по инерции в его традиционном понимании, т.е. при полном отсутствии неуравновешенных сил. Только абстрактная сила тяги и сила сопротивления могут полностью абстрактно компенсировать друг друга в каждый момент времени, что равносильно их полному отсутствию. Однако в реальной действительности абстрактных сил нет, а равновесие реальных сил не может быть идеальным, т.к. оно регулируется только в процессе взаимодействия.

А вот если под движением по инерции понимать движение под действием сил инерции, которыми, как показано выше являются все силы во вселенной, то и в том и в другом случае действительно происходит движение по инерции. Благодаря силам инерции возможна сила тяги бульдозера, обеспечивающая в среднем равномерное движение в условиях симметричного регулирования и благодаря силам инерции в условиях не симметричного регулирования замедляется движение автомобиля с выключенным двигателем. В этом смысле в каждом из этих случаев происходит движение по инерции, т.е. под воздействием сил инерционного происхождения. Однако в этом случае законом инерции следует считать не первый, а второй закон Ньютона.

Таким образом, в бытовом понимании движения по инерции, которое подразумевает реальные силы, противодействия изменению состояния движения, скорее всего, заключена народная мудрость, которая предполагает реальное преодоление сил сопротивления движению за счет «обычных» сил инерции поэлементной поддержки. А вот движение по инерции в отсутствие каких–либо сил осуществляется только для того, кто не прислушивается к народной мудрости и судит о явлениях природы только по академическим законам и математическим формулам.

***

Природа сил инерции в современной физике не установлена, поэтому реальность силы инерции не может противоречить современной физике в принципе. Единственным критерием реальности силы инерции может служить только ее соответствие или не соответствие фундаментальным законам природы, которым, как показано выше, явление инерции полностью соответствует. Более того инерция непосредственно обусловлена фундаментальными законами природы, как собственно и законы природы обусловлены инерцией.

Врождённое элементарное свойство материи преобразование напряжение-движение не может быть пока объяснено современной физикой именно потому, что оно элементарное и в физике нет ничего боле элементарного, что можно положить в структуру этого свойства для его объяснения. Однако отрицание мировой материальной среды, сопротивление которой, так же определяет явление инерции, причем, по-видимому, количественно в значительно большей степени, чем врождённое свойство материи преобразование напряжение-движение, приводит к полному абсурду в классической физике.

Современная физика утверждает, что сила инерции всегда приложена только к опорному телу, т.е. источнику активного движения или к ускоряющему телу. Однако это все равно, что сопротивление изменению состояния движения ускоряемого тела со стороны среды оказывается не ему, а непосредственно источнику силы, минуя само ускоряемое тело. Это равносильно тому, что ускоряется одно тело, а сопротивление его ускорению оказывается совсем другому телу — источнику силы! Такое толкование природы взаимодействий противоречит даже общепризнанным на сегодняшний день законам физики и в частности третьему закону Ньютона.

Ни одно физическое тело не может воздействовать на другое тело, не испытывая, как минимум такого же силового противодействия на себе. Поэтому даже если источник противодействия изменению состояния движения физических тел на сегодняшний день наукой не установлен, это противодействие в соответствии с той же самой наукой в первую очередь должно оказываться именно ускоряемому телу, а уже через него противодействие может быть передано ускоряющему, т.е. опорному телу. Это справедливо для взаимодействия тел даже в отсутствие мировой материальной среды. Может быть, именно в этом смысле следует понимать слова Ньютона о том, что инерция это «врожденная сила материи».

По мнению В. А. Ацюковского («Общая эфиродинамика», МОСКВА, ЭНЕРГОАТОМИЗДАТ, 1990) все мировое пространство и промежутки между элементарными частицами любого вещества заполняет мировая материальная среда — эфир, которая представляет собой сильно разреженный реальный газ. Мельчайшие частицы этого газа — амеры и являются первокирпичиками материи, т.е., по–видимому, и элементарными носителями массы.

По Ацюковскому силы гравитации определяются термодиффузионными процессами в эфире, основанными на теплообмене массы вещества с окружающим эфиром. Эфир в составе вещества является более холодным по сравнению со свободным эфиром. Он охлаждает свободный эфир между тяготеющими телами сильнее, чем, с внешней стороны тел. При этом возникает градиент давления, под действием которого материальные тела устремляются в область пониженного давления более охлаждённого эфира между ними. Причем градиент давления мировой материальной среды тем больше, чем больше количество вещества в теле.

Инерция, обеспечиваемая средой также, по-видимому, основана на обмене энергией между веществом и мировой материальной средой. При взаимодействии материальных тел в зоне деформации происходит нагрев окружающего эфира. При этом взаимодействующие тела устремляются в сторону внешнего более холодного эфира. Причём оба взаимодействующих тела в любом случае испытывают сопротивление движению со стороны более холодного эфира открытого пространства (с учётом паруса взаимодействия).

Конечно же, это только предположение. Механизм распределения энергии в материи может быть уточнен по мере накопления соответствующих знаний в науке. Однако совершенно очевидно, что без врождённого свойства преобразования напряжение-движение и без инерционного сопротивления среды никакие силы взаимодействия не смогут распространяться на материальные тела. Сила инерционного сопротивления мировой материальной среды непосредственно воздействует на ускоряемое тело, а уже через него на опорное ускоряющее тело. То есть сила, действующая на опорное тело, в конечном итоге является продолжением силы инерции. Без среды — это инерция поэлементной поддержки, только и всего.

Иллюзию нереальности силам инерции придает только существующая на сегодняшний день математическая модель, которая, кстати, призвана облегчить решение задач динамики, а не усложнять понимание физической сущности реальных взаимодействий, хотя сегодня получается почему-то все наоборот. Некоторые физики от математики склонны принимать существующую математическую модель теории движения «за чистую монету» и распространяют абстрактные математические допущения на реальную действительность.

Причем Даламбер в этом нисколько не виноват. Виноваты, наверное, «неграмотные люди», как говорит Н. В. Гулиа в своей «Удивительной физике», в том числе, видимо, и сам Гулиа. По поводу вводимого в физику для облегчения решения задач движения принципа Даламбера, Гулиа пишет:

«он же (Даламбер — авт.) не подозревал, что в научном мире еще имеются люди не очень образованные…» (см. выше).

Н. В. Гулиа считает, что инерция связана только с принципом Даламбера и не имеет под собой никакой физической основы. Интересно как грамотный вроде бы человек Гулиа вообще представляет себе силу тяги в отсутствие силы инерции?! Тот же самый автомобиль с двигателем любой мощности никуда не уедет на скользком льду вовсе не, потому что отсутствуют силы трения.

Это, конечно важно, но это только второстепенная причина, являющаяся следствием основной причины, т.к. силы трения в данном случае играют лишь роль посредника между взаимодействующими телами. У спортсмена, бегущего на тренажере «Беговая дорожка» с силой трения ног по отношению к полотну дорожки все в полном порядке. Однако все усилия спортсмена не приводят к его сколько-нибудь заметному перемещению относительно Земли, на которой стоит спортивный снаряд.

Силы трения это только промежуточное звено во взаимодействии автомобиля с Землей, отсутствие которой лишает автомобиль возможности взаимодействовать с инерцией Земли. Точно так же как мешает спортсмену взаимодействовать с инерцией Земли спортивный снаряд «Беговая дорожка». Для создания силы тяги необходимо в первую очередь инерционное сопротивление опорного тела, которого из-за отсутствия сцепления со скользкой дорогой лишается автомобиль и из-за свободного перемещения полотна дорожки на барабанах спортивного снаряда лишается спортсмен.

***

Что же является на сегодняшний день «ясным» определением силы инерции в современной физике, о котором говорит Зоммерфельд? Выше в главе 1.1 приведены мнения классиков теоретической механики, в которых ясно прослеживается лишь их двойственное отношение к явлению инерции. Причём причина двойственного отношения к силам инерции в классической физике состоит ещё и в том, что все материальные тела рассматриваются в ней, как материальные точки.

Если разбить физические тела на отдельные элементы, хотя бы в виде его реальных физических структур, то явление инерции частично можно объяснить и обычными внутренними Ньютоновскими силами. Они не только передают движение ускоряемому телу, но и собственно поддерживают это движение при встрече ускоряемого тела с препятствиями. На двоякое проявление силы инерции указывал еще Ньютон. Он говорил, что сила инерции проявляется как сопротивление и как напор:

«Как сопротивление, — поскольку тело противится действующей на него силе, стремясь сохранить свое состояние; как напор, — поскольку то же тело, с трудом уступая силе сопротивляющегося ему препятствия, стремится изменить состояние этого препятствия».

Таким образом, Ньютон по сути дела допускал, что силой инерции может быть «обычная» сила, с которой одно тело передает свое движение другому телу и одновременно поддерживает собственное движение. Ведь «…стремится изменить состояние этого препятствия» невозможно без стремления поддержать собственное состояние движения. Особенно если учесть, что тело это не материальная точка, а сложная материальная структура.

Как показано выше, сила инерции это скалярное напряжение (F = m * a), которое возникает при любом препятствии движению, и которое тут же исчезает при устранении этого препятствия посредством преобразования напряжения-силы (F = m * a) в новое движение. Так образуется инерционное движение. При этом внутренние Ньютоновские силы поэлементной инерции осуществляют этот принцип на уровне структур вещества и физических тел, а истинные врождённые силы инерции реализуют его на уровне элементарных носителей массы вещества и мировой материальной среды.

Понятие инерции в механическом движении является полным аналогом явлению самоиндукции в электродинамике, которое, по всей видимости, как раз и осуществляется на уровне элементарных масс. Правда, самоиндукция объясняется в классической физике через взаимодействие электронов с электромагнитным полем. Но это уже гораздо ближе к взаимодействию элементарных носителей масс, чем взаимодействие физических тел между собой в виде неделимых материальных точек.

Что же касается точек приложения физически реальных сил, как внутренних Ньютоновских, так и внешних сил инерции, то они, как мы уже отмечали, приложены, прежде всего, к структурным элементам вещества или к элементарным носителям массы каждого из взаимодействующих тел. Поэтому в каждом конкретном случае точка приложения сил может меняться в зависимости от решаемой задачи.

Сосредоточение сил в конкретной материальной точке, как в ЦМ физического тела это только частный случай всех возможных вариантов взаимодействий. Если бы классическая физика рассматривала кинематику движения физических тел не только как движение единых и неделимых материальных точек, то в динамике мы сегодня наверняка уже имели бы более реалистичные представления о явлении инерции.

***

В этом отношении интересен пример равномерного вращения массивного цилиндрического стержня на его поперечной оси. Вращающийся стержень представляет собой единое физическое тело, которое растянуто за счет сил инерции, реально поддерживающих прямолинейное движение по касательной всех его элементарных носителей массы. Сила упругости возникает лишь как ответная реакция на реальное внешнее воздействие поддерживающих центробежных сил инерции.

Причём реальная сила упругости не может противодействовать фиктивным несуществующим силам, как впрочем, и сама упругая деформация не может возникнуть под действием фиктивных несуществующих сил. Прежде чем должна появиться сила упругости, стержень должен быть предварительно растянут вовсе не фиктивными силами.

В реальности центробежных сил инерции легко убедиться, представив вращение цилиндра в виде упрощенной академической эквивалентной схемы. На любом расстоянии по обе стороны от центра вращения стержня, кроме максимального радиуса стержня можно условно математически выделить элементарный объем, на который действуют внешние и внутренние силы:

1. С внешней стороны на элементарный объем действует совершенно «обычная» даже с классической точки зрения сила внешней части стержня, которая для самой внешней части стержня, как это ни парадоксально, с классической точки зрения является фиктивной, т.е. несуществующей силой! Однако если иметь в виду силы инерции поэлементной поддержки, то эта сила является реальной и для внешней части стержня.

2. С внутренней стороны на элементарный объем действует динамически уравновешивающая поддерживающую силу инерции «обычная» сила упругости внутренней части стержня, которая фактически является продолжением обычной поддерживающей силы инерции диаметрально противоположной внешней части стержня, соответствующей внешней части стержня по первому пункту.

Совершенно очевидно, что при равномерном вращении диаметрально противоположные части стержня находятся в состоянии равновесия относительно друг друга и относительно центра вращения, т.к. средняя длина стержня остается неизменной. Следовательно, внутреннюю часть стержня можно теоретически условно заменить академическим невесомым упругим связующим телом, а внешние части стержня считать самостоятельными массивными физическими телами. Из полученной эквивалентной схемы следует, что, каждое из этих массивных физических тел (внешние части стержня) через силу упругости воздействует друг на друга с обычной поддерживающей центробежной силой инерции.

Таким образом, во вращательном движении центростремительная сила упругости обеспечивается фактически «обычной» поддерживающей силой инерции, как ни парадоксально с классической точки зрения это определение по отношению к фиктивной силе инерции.

Поскольку «фиктивная» с классической точки зрения поддерживающая сила инерции реально уравновешивается «обычной» силой упругости связующего тела, то обе силы вполне реальны. Классическая же модель вращательного движения отрицает какое-либо равновесие центростремительной силы упругости и центробежной силы инерции, считая последнюю силу несуществующей фиктивной силой инерции.

Однако сила упругости связующего тела противодействует вовсе не только силе инерции массы покоя вращающегося тела, которую в классической физике принято считать фиктивной, но и его прямому «ударному», воздействию на любой рассматриваемый участок связующего тела, которое сложно считать фиктивным. Приложена «обычная» поддерживающая сила инерции к диаметрально противоположному вращающемуся телу или закрепленному центру. Однако не следует забывать, что центробежная сила инерции приложена также и к каждому элементарному носителю массы самого вращающегося тела.

Если связующее тело считать реальным физическим телом, а не академической невесомой упругой связкой, то поддерживающая сила инерции приложена, в том числе и к каждому элементарному носителю массы связующего тела, являющегося частью единого тела стержня, что и утверждает классическая физика. Однако, поскольку в данном случае связующее тело неотделимо от вращающегося тела, то совершенно очевидно, что поддерживающая сила инерции оказывает вполне реальное действие и на вращающееся тело, ответное связующему телу.

Совершенно очевидно, что при, увеличении скорости вращения, а значит и линейной скорости движения тела по окружности растет не «фиктивная» сила инерции неподвижного с классической точки зрения в радиальном направлении тела. Рост центробежной силы обусловлен, прежде всего «обычной» поддерживающей силой инерции, с которой тело, стремясь в первоначальный момент преобразования прямолинейного движения во вращательное движение удалиться от центра вращения, ударно воздействует на связующее тело.

Именно кинетическая энергия прямолинейного движения тела при преобразовании его во вращательное движение энергетически обеспечивает центробежную силу инерции, т.е. «обычную» по сути дела силу, с которой движущееся прямолинейно тело, сопротивляется процессу преобразования движения по направлению. Каждому увеличению линейной скорости прямолинейного движения, которое преобразуется во вращательное движение, неизменно сопутствует увеличение центростремительного ускорения.

Причем сначала должна увеличиться именно скорость прямолинейного движения тела и, только потом в процессе дополнительного удлинения связующего тела и роста силы упругости возникает и новое центростремительное ускорение нового вращательного движения. Без дополнительного удлинения связующего тела, в результате которого в свою очередь и обеспечивается рост силы упругости невозможно физически обосновать рост центростремительного ускорения.

Таким образом, именно кинетическая энергия прямолинейного движения тела, преобразуемого во вращательное движение, питает «фиктивную» с точки зрения классической физики и «обычную» по своей физической сущности центробежную силу инерции, а так же силу упругости связующего тела. А поскольку кинетическая энергия величина вовсе не фиктивная, хотя и абстрактно-академическая, то и центробежная сила, которая передаёт эту величину, не может быть фиктивной. И приложена эта сила, в том числе и к каждому элементу вращающегося тела.

***

Выше мы рассмотрели физический механизм формирования сил с участием сил инерции при взаимодействии тел вдоль одной прямой линии. При таких взаимодействиях силы инерции влияют на формирование абсолютной величины сил, действующих на взаимодействующие тела. Теперь рассмотрим формирование сил взаимодействия, при котором силы инерции, поддерживающие движение направлены под углом к «обычным» силам, действующим на тело. Такие взаимодействия происходят в частности во вращательном движении.

Пусть тело (Т1) (Рис. 1.2.6), движущееся со скоростью V1 захватывается резиновой нитью с одним закрепленным концом, которая действует на него с силой упругости (Fу1). С классической точки зрения тело испытывает только воздействие силы упругости резиновой нити, направленной вдоль ее оси к центру вращения. Однако сила упругости не может возникнуть на пустом месте. По третьему закону Ньютона сила упругости резиновой нити может возникнуть только как реакция на силовое воздействие тела (Т1) на точку закрепления нити (О) через саму нить, т.е. предварительно должно произойти удлинение нити под действием удаляющегося от точки закрепления нити тела (Т1).

Таким образом, сила инерции во вращательном движении первична, что несколько отличается от позиции классической физики, в которой центробежная сила является фиктивной.

Удаляясь от точки (О), тело захватывает свободный конец нити и растягивает ее именно за счет сил инерции своего движения. Ведь не неподвижная же точка (О) растягивает нить! Классическая физика косвенно признает реальность сил инерции. Правда она считает, что силы растягивающие нить приложены не к телу, а к нити (выше мы уже разбирали противоречия такой трактовки действия силы инерции).

Учитывая приведенный выше механизм формирования поддерживающей силы инерции, ее зарождение происходит внутри физического тела и распространяется по всему его объему и только после этого передается на внешние тела. Следовательно, для возникновения полной силы инерции предварительно должны быть задействованы внутренние упругие связи самого тела (Т1), т.е. упругая связь между его элементами должна быть предварительно деформирована, и только после этого можно говорить о выходе силы инерции за пределы тела и ее воздействии на ответные тела.

Пусть тело (Т1) для простоты состоит всего лишь из двух элементарных масс (Э1) и (Э2). В первый момент после захвата тела резиновой нитью ее сила упругости формируется, прежде всего, с учетом инерции движения первого элемента тела (Т1), т.е. инерции элемента (Э1). Поэтому на первом этапе после первичного формирования силы упругости (Fу1) для ее «готового» варианта можно исключить из расчета только ответную реакцию на силу (Fэ1) элемента (Э1), захваченного резиновой нитью.

Однако элементарная масса (Э2) некоторое время продолжает условно в некотором приближении двигаться по инерции, удаляясь от элемента (Э1). При этом по мере нарастания внутренней силы упругости на дальнейшем движении тела начнет сказываться влияние элемента (Э2), который через внутреннюю упругую связь воздействует, в том числе и прежде всего на элемент (Э1) с силой (Fэ2).

Под действием силы (Fэ2) элемента (Э2) и силы упругости (Fу1) формируется результирующая сила (Fрез), которая отклонит тело (Т1) от первоначального прямолинейного движения в сторону центра вращения, однако при этом тело (Т1) еще больше удалится от центра вращения, а скорость его движения естественно замедлится, т.к. часть инерции (кинетической энергии) тела будет израсходована на преодоление силы упругости нити.

Однако, как известно равномерное движение по окружности предполагает движение с постоянной линейной скоростью. Таким образом, для формирования равномерного вращательного движения необходимо, чтобы механизм преобразования движения по направлению обеспечивал не только изменение линейной скорости по направлению, но и ее восстановление по абсолютной величине после каждого изменения направления.

Совершенно очевидно, что восстановить уменьшившуюся на первом этапе скорость может только энергия, запасенная в нити, которая может вновь перейти в кинетическую энергию тела только при ее сокращении. Для этого результирующая сила должна непрерывно изменять свое направление до тех пор, пока ее проекция на радиальное направление не станет положительной по отношению к центру вращения.

Только после этого тело под действием силы упругости нити начнет ускоренно двигаться к центру вращения. Однако после достижения увеличивающейся линейной скорости некоторого значения весь процесс опять должен поменять направление по отношению к центру вращения, иначе линейная скорость может превысить даже свое первоначально установившееся после образования упругой деформации связующего тела значение.

Таким образом, движение по окружности предполагает циклически повторяющийся процесс взаимодействия сил упругости и сил инерции, в котором происходит изменение вектора линейной скорости, как по величине, так и по направлению. Более детально примерный физический механизм преобразования движения по направлению будет рассмотрен ниже в главе 3.4. Задачей же настоящего раздела является обоснование реальности сил инерции, в том числе и во вращательном движении и их роли в формировании любых сил в принципе.

В предложенном механизме образования центробежной силы нет никаких парадоксов и противоречий даже с классической точки зрения. Классическая физика признает, что фиктивная центробежная сила вполне реально проявляется, правда только при воздействии на связующее тело. Однако первоначально вступивший во взаимодействие элемент тела (Э1) принципиально также является связующим звеном элемента (Э2) с центром вращения, т.е. сила инерции, действует, в том числе и на тело. В то же время взаимодействие между элементами тела осуществляется внутри тела, т.е. сила инерции зарождается, прежде всего, внутри тела и только распространившись по всему его объему, выходит за его пределы.

При этом нет никаких противоречий и в отношении точки приложения сил инерции. На рисунке 1.2.6 показана упрощенная, т.е. условная принципиальная схема взаимодействия. Чтобы не загромождать рисунок, центр элементарной массы (Э2) не показан вообще. При этом вполне естественно, что взаимодействие следует рассматривать в совокупности участия в нем всех элементов тела, т.к. сила упругости связующего тела, а также внутренняя сила упругости в конечном итоге последовательно распространяется на все элементарные носители массы тела. Естественно, что положение точки приложения сил, а также величина и направление полной результирующей силы в процессе развития взаимодействия в предлагаемом масштабе будут изменяться.

На рисунке не показана схема разгона тела при ориентации результирующей силы в положительном радиальном направлении по отношению к центру вращения (положение V4). Однако в этом нет особой необходимости, т.к. разгон тела происходит под действием «обычной» силы упругости и не связан с какими-либо противоречиями, кроме самого его существования в равномерном вращательном движении. При обратном движении тела к центру вращения сила инерции будет противодействовать разгону по аналогичной, но реверсивной схеме, в которой сила инерции и сила упругости только поменяются ролями.

Правомерно ли такое представление о реальном влиянии силы инерции на формирование вращательного движения? В реальном физическом теле содержится огромное количество структурных элементов. В предложенной схеме (Рис.1.2.6) все взаимодействия за исключением первого происходят под действием вполне «обычных» сил. Однако если реально смотреть на вещи, первый элемент также осуществляет свое воздействие на связующее тело не «по щучьему велению», а только передает ему силу инерции, формирующуюся из кинетической энергии (из движения) самого тела.

Следует полагать, что силы инерции вполне реальны, хотя субъективно они не всегда обнаруживаются. Во всяком случае, кажущаяся фиктивность силы инерции по отношению к первому элементу это не самое слабое звено в предложенной схеме. Из всего несметного количества элементарных масс в реальном физическом теле это составляет ничтожно малый процент фиктивности, т.к. все остальные элементы воздействуют на связующее тело уже через элементы самого тела через вполне реальную обычную силу. А это означает, что сила инерции приложена, прежде всего, к самому телу.

Масса (Э2) в упрощенной схеме или каждая последующая масса в реальном физическом теле некоторое время условно движется равномерно и прямолинейно по инерции, т.е. в отсутствие внешних сил. Однако эта условность допущена схематично для упрощения понимания предложенного механизма. В реальной действительности силовое взаимодействие между элементарными массами естественно происходит непрерывно, хотя и с разной интенсивностью, что позволяет в некотором приближении условно говорить о движении по инерции на определённых этапах. А вот в классической модели линейная скорость и сила упругости остаются статически неизменными по абсолютной величине, что физически в принципе невозможно при реальных взаимодействиях с непрерывной сменой направления.

С точки зрения классической физики под действием классического центростремительного ускорения должно изменяться только направление линейной скорости. Однако физический механизм изменения линейной скорости без изменения ее величины в классической физике не представлен. Мы полагаем, что такого механизма в природе просто не существует, т.к. он противоречит всем физическим законам и здравому смыслу.

Во всяком случае, существование такого механизма представляется нисколько не менее противоречивым, чем механизм описанный выше. Нам представляется, что сегодня это понимают уже достаточно большое количество здравомыслящих людей. Однако официально многие из них поддерживают классическую точку зрения. Автору довелось в этом доподлинно убедиться на физическом форуме dxdy от МГУ.

Под действием классического центростремительного ускорения тело рано или поздно должно неминуемо столкнуться с центром вращения, причем с нарастающей по абсолютной величине скоростью. Это совершенно очевидное логическое следствие движения с центростремительным ускорением в отсутствие реального противодействия фиктивной силы инерции. Поэтому классическая физика придумала несуразную и очень вредную для науки сказку о том, что под действием центростремительной силы изменяется только направление линейной скорости, а центростремительное ускорение при этом, не приводит ни к какому реальному пространственному перемещению.

1.2.7. Парадокс Эйлера-Даламбера

«Обстоятельства, с которыми мы сталкиваемся, кажутся на первый взгляд совершенно парадоксальными с чисто математической точки зрения, и предусмотреть их можно только из физических соображений».

Ж. Адамар

«Природа с красоты своей

Покрова снять не позволяет,

И ты машинами не вынудишь у ней,

Чего твой дух не угадает».

В. С. Соловьев

В 1742 году петербуржский академик Л. Эйлер рассчитал сопротивление цилиндра, равномерно движущегося в жидкости, лишенной трения, и получил удивительный результат — сила сопротивления оказалась равной нулю! Спустя семь лет выдающийся французский механик Ж. Даламбер с помощью некоторых ухищрений рассчитал обтекание произвольного тела конечного объема и получил все тот же ошеломляющий результат — нулевое сопротивление. Такой вывод резко отличался от «здравого смысла». Даламбер не смог объяснить полученный результат и с горечью заметил, что нулевое сопротивление — «единственный парадокс, разрешение которого я оставляю геометрам будущих времен».

Для нас этот парадокс интересен тем, что он фактически положен в основу Хиггсовского механизма образования массы материи, который в корне противоречит нашему механизму явления инерции. Механизм образования массы по Хиггсу заключается в том, что инертность частицы может проявиться при её неравномерном (ускоренном) движении только сквозь какую-то среду. Такой средой, по мнению Хиггса, может быть физический вакуум, носителями которого являются, так называемые бозоны Хиггса.

Если тело движется с постоянной скоростью сквозь жидкость без вязкости и без турбулентности, то жидкость будет обтекать тело, не оказывая ему в целом никакого сопротивления (в гидродинамике это называется парадоксом Даламбера). Однако при попытке изменить скорость тела у него обнаружится некоторая дополнительная инертность, называемая присоединенной массой. Не задаваясь вопросом приоритета, отметим, что точно такое же объяснение инерции присутствует и в теории Пуанкаре и Лоренца.

Вот как описывает принцип инерции А. Пуанкаре в статье «Динамика электрона», 1908 г.:

«Известно, что тело, погруженное в жидкость, испытывает во время движения значительное сопротивление. Это происходит потому, что мы имеем дело с вязкими жидкостями. В идеальной жидкости, совершенно лишенной вязкости, тело приводило бы в движение жидкость позади себя, создавая нечто вроде струи, образующейся обычно за кормой. Вначале потребуется большое усилие, потому что нужно привести в движение не только само тело, но и жидкость. Но как только движение установится, оно будет продолжаться без всякого сопротивления, поскольку тело в своем движении будет переносить вместе с собой возмущение жидкости, причем полная живая сила жидкости не будет увеличиваться. Все произойдет так, как будто увеличилась инерция тела.»

Таким образом, присоединённая масса по Хиггсу, Пуанкаре и Лоренцу — это масса среды из жидкого гелия у Пуанкаре с Лоренцом и из бозонов Хиггса у Хиггса, которую при изменении скорости движения приходится разгонять или тормозить вместе с самим телом. Но тогда это не инерция самого тела, а инерция присоединённой массы среды. Это не решает проблему инерции в принципе, а только приводит к тавтологии, в которой инерция одной материи объясняется через инерцию другой материи и наоборот.

Если у материи нет своей собственной врождённой инерции в принципе, то её не будет ни в материи тела, ни в материи среды. Кроме того, хиггсовское объяснение инерции пропорционально не количеству материи тела, а скорее его поперечному сечению. Мы уже не говорим об искусственном исключения вязкости из полного процесса взаимодействия тела со средой, которая обеспечивает значительную часть этого взаимодействия.

В нашей модели явления инерции допускается инерция, обусловленная сопротивлением среды. Она связана с парусом взаимодействия, который распускается при деформации тела во время изменения скорости движения и сворачивается при прекращении ускоренного движения. Но, если такое явление существует, то во-первых, оно обеспечивает только некоторую часть инерционного сопротивления. А, во-вторых, оно в свою очередь возможно только за счёт врождённого свойства инерции материи, которое объясняется отрицательной обратной связью механизма преобразования напряжение-движение, т.е. взаимодействия или инерции (см. гл. 1.2.1.).

У Хиггса же главной и единственной причиной образования массы (инерционности) является именно внешнее сдерживание материи средой. При этом никакой связи такой инерционности с изменением физического состояния (деформации) самого тела при ускорении не требуется. Наоборот, через 7 лет после Эйлера, Даламбер доказал, что нулевое сопротивление тела в стационарном потоке жидкости якобы не зависит от его внутренних и внешних геометрических и физических параметров! Однако это противоречит всем известным на сегодняшний день физическим характеристикам взаимодействия тел:

Во-первых, такая «инерционность» не зависит от свойств самого тела, т.е. из процесса образования инерции исключается физическая деформация тела под действием силы при взаимодействии, а, следовательно, сама сила и само взаимодействие.

Во-вторых, модель инерции, основанной только на внешнем сдерживании движения материи средой в отсутствие собственной инерции материи, т.е. в отсутствие свойства материи (среды) преобразование напряжение-движение, не имеет физического смысла, т.к. она не объясняет физическую природу собственно самой инерции. Не имея собственного свойства инерции, материя среды не может передать его телу, т.к. передать можно только то, что есть у самого передающего объекта.

Если массу образуют бозоны Хиггса, то для образования массы самих бозонов Хиггса нужны бозоны Хиггса второго порядка и так до бесконечности. Причём, если в этом бесконечном ряду хотя бы в одном из его бесконечных порядков не будет собственной массы, то её не будет и у всего ряда.

Это означает, что без собственной массы материи, даже вся вселенная не сможет оказать никакого инерционного сопротивления даже самой маленькой из всех известных и даже ещё неизвестных частиц материи.

Из этого следует, что взаимодействие весомого с невесомым принципиально равно нулю. Фактически такого взаимодействия в природе не существует. Но тогда сила, которая приложена к невесомому, напрямую действует на весомое. При этом мы приходим к тому, от чего ушли, т.е. нам опять нужно объяснять инерцию весомого, вместо глупости Пуанкаре и Хиггса.

В–третьих, внешнее сдерживание движения при разгоне и внешняя поддержка движения при торможении требует реальных затрат энергии на дополнительные взаимодействия по внешнему противодействию и внешней поддержке движения соответственно. Это не соответствует природной инерции, которая абсолютно без затратная (см. гл. 1.2.1.).

В-четвёртых, если инерционность проявляется при любом относительном изменении скорости либо потока, либо тела, то нет никакой определённости, что и чью присоединённую массу образует. То ли бозоны Хиггса образуют массу частицы, то ли, наоборот, — частица образует массу бозонов Хиггса!

Причём по отдельности массы нет ни у того, ни у другого, что равносильно появлению чего-либо из ничего! А при прекращении ускорения эта совместная присоединённая масса непонятно чего к чему, вновь обращается ни во что, т.к. при равномерном движении масса не имеет значения, что нарушает все известные законы сохранения.

В нашей версии физическая сущность свойства материи инерции или преобразования напряжение-движение отражена не в парадоксе Даламбера-Эйлера, а в самом законе Бернулли для несжимаемой жидкости. В гидродинамике известен принцип Бернулли, который гласит: «Сумма статической, динамической и геометрической энергии в ламинарном потоке несжимаемой жидкости остается постоянной во всех точках потока, соединенных одной линией тока, т.е. в устойчивом потоке сумма всех форм энергии в жидкости вдоль потока одинакова во всех точках этого потока».

m * v2 / 2 + Р * V + mgh = const,

где

Р — давление

v — скорость

V — объём

mgh — геометрическая энергия, обусловленная высотой столба жидкости

Для давлений уравнение Бернулли имеет вид:

р * v2 / 2 + Р + рgh = const

где

р — плотность

При равенстве сечения (S1) и (S2) имеем:

P1 * S1 — F — P2 * S2 = 0

Тогда:

F = 0.

где:

F — сила давления потока жидкости, которая по всем существующим законам физики должна действовать на тело (А).

Объём неизменного массового элемента в неразрывном потоке несжимаемой жидкости остаётся неизменным. Поэтому, когда поток жидкости встречает на своём пути сужение трубопровода, что эквивалентно столкновению тел, давление и соответственно сила напряжения перед сужением увеличивается. При этом увеличивается потенциальная энергия (Р * V). Далее потенциальная энергия в полном соответствии с принципом боязни тесноты реализуется в движение массового элемента жидкости внутри сужения, что сопровождается увеличением его кинетической энергии (m * v2 / 2) с одновременным уменьшением силы и соответственно давления на сужении. На выходе из сужения происходит обратный процесс.

Это и есть физический механизм преобразования напряжение-движение или инерции. В природе нет прямого противодействия и прямой поддержки движения в виде прямых противодействующих или поддерживающих сил, а также в виде сопротивления присоединенной массы по Хиггсу. В природе есть свойство материи — инерция или преобразование напряжение-движение, в котором кажущийся эффект инерционного противодействия или поддержки движения объясняется не прямыми силами противодействия изменению движения, а отрицательной обратной связью процесса преобразования напряжение движение.

Поэтому сам по себе парадокс Эйлера-Даламбера не может лежать в основе явления инерции, как считает Хиггс. Парадокс Эйлера-Даламбера основан на выравнивании давлений и скоростей жидкости в отдалённых от тела сечениях. При этом голая математика, для которой исходным начальным условием является сам факт выравнивания давлений на расстоянии от тела, не учитывает физические процессы, происходящие непосредственно вблизи тела (массового элемента). Это всё равно, что судить об одном явлении природы совершенно по другому явлению, происходящему совсем в другой точке пространства.

А вот закон Бернулли фактически раскрывает механизм явления инерции, как процесса преобразования напряжение-движение или взаимодействия, который принципиально верен даже несмотря на вязкость реальных жидкостей. Вязкость лишь вносит погрешность в количественные показатели соответствующих опытов, но нисколько не затрагивает качественную, т.е. принципиальную сторону вопроса.

1.3. Ритмодинамика

Ю. Н. Иванов (РИТМОДИНАМИКА, Издание 2-е переработанное, дополненное, издательство «ИАЦ Энергия», г. Москва 2007 г.) объясняет инерцию, как связь физического тела с упругой мировой материальной средой.

Элементы физического тела по Иванову представляют собой когерентные осцилляторы, которые находятся в потенциальных ямах созданной ими стоячей волны.

В момент начала движения вправо (Рис. 1.2.3) активные элементы смещаются относительно потенциальных ям, т.е. потенциальные ямы отстают от элементов. В такой системе возникает деформации стоячей волны: она смещается влево от источников и появляется дополнительное волновое поле справа. Со стороны пучности и возникшего справа волнового поля появляется действие на источники, препятствующее перемещению системы вправо. Сопротивление действию (инерция) будет продолжаться до тех пор, пока не произойдёт подстройка фаз элементов под состояние движения.

На примере элементарной системы осцилляторов процесс формирования инерционности описывается Ивановым следующим образом.

Подействуем на осциллятор с целью перемещения системы. Осциллятор сместится, но при этом изменится длина излучаемой им волны. Второй осциллятор системы продолжает оставаться на своём месте до тех пор, пока не получит сигнала, в виде изменившей параметры волны, от первого осциллятора. Дошедшая до второго осциллятора изменённая волна окажет действие, изменив положение его потенциальной ямы. Второй осциллятор сместится в пространстве в новую потенциальную яму, а излучаемые им, в этот период, волны будут другой длины. Но первый осциллятор продолжает сопротивляться оказанному на него действию.

Когда волна от второго осциллятора к нему вернётся, то произойдёт смещение потенциальной ямы первого осциллятора под его текущее положение и сопротивление прекратится. При этом оба осциллятора разместятся в узлах изменившейся стоячей волны, которая сократится за счет эффекта сжатия стоячих волн в движущейся волновой среде. Поскольку сопротивление первому осциллятору оказывается более длительное, чем второму, то появится сдвиг фаз, который должен соответствовать образовавшемуся движению системы. На этом подстройка фаз завершается.

Для нас в ритмодинамике Иванова, прежде всего, важно то, что в ней силы инерции это реальные силы волнового давления, которые воздействуют на физическое тело со стороны мировой материальной среды, следовательно, сила инерции по Иванову не может быть фиктивной. Причем модель Иванова позволяет объяснить, как тормозящую, так и поддерживающую силу инерции. Механизм действия тормозящей силы описан выше. А поддерживающая сила связана с взаимодействием материального тела с движущейся «живой стоячей волной»:

После подстройки фаз тело движется по инерции синхронно с «живой стоячей волной». При попытке затормозить движение материального тела, сместившиеся в направлении внешней силы осцилляторы, встретят волновое сопротивление со стороны движущейся синхронно с телом «живой» стоячей волны. В результате со стороны движущейся «живой стоячей волны» на сместившееся против ее движения тело будет оказано волновое давление в направлении прежнего движения. Таким образом, движущаяся стоячая волна своим движением поддерживает движение физического тела.

Однако этот механизм не исключает механизма образования поддерживающей силы, предложенного выше в настоящей работе и основанного на последовательной передаче взаимодействий между элементарными массами физических тел. Движутся ли элементарные массы по инерции в отсутствие волнового механизма или их «несёт» живая стоячая волна, это не исключает механизма инерции поэлементной поддержки. В любом случае последующие элементарные массы поддерживают своим движением элементарные массы, вступившие во взаимодействие торможения первыми. А при разгоне первые элементы тормозятся последующими.

У ритмодинамики есть масса достоинств по сравнению с существующими теориями мироустройства, и главное из них заключается в том, что ритмодинамика предлагает ясный физический механизм для наиболее важных физических явлений, таких как движение, инерционность, сила взаимодействия и сила тяготения. Однако это пока только красивая модель, которая нуждается в детальной проработке и уточнении и в которой, на наш взгляд, есть существенные недостатки.

Волновое поле будет действовать на тело только в том случае, если синхронность движения тела и волны каким-либо образом нарушится, т.е. «охранные» функции инерционного движения тела по Иванову выполняет не запас кинетической энергии или точнее движения тела, как в нашей модели, а волна. Это означает, что вся кинетическая энергия тела, как это ни странно заключается не в движении самих физических тел, а в движении живой стоячей волны.

Но тогда волна должна обладать и массой тела. При этом само тело превращается в абстрактный источник излучения, только активно воспринимающий внешние воздействия, т.е. в невесомый придаток волны! В чём же тогда физический смысл такой модели, состоящей из безмассового физического тела и массивной волны и в чём тогда смысл самой массы такого безмассового тела? Кроме того, в волновом взаимодействии проявляется тенденция к выравниванию частот, т.е. синхронизации колебаний. Поэтому для поддержания разности частот, необходимой для осуществления движения по Иванову требуется непрерывное подведение энергии к осцилляторам.

Таким образом, равномерное движение живой стоячей волны может осуществляться только за счёт постоянной подпитки осцилляторов, внешней энергией, что противоречит принципам инерционного движения. Правда, это может быть внутренняя энергия, но и она не бесконечна и тратится-то она фактически на равномерное движение, которое по Ньютону принципиально не требует энергетической подпитки!

Кроме того, для реализации механизма инерционности, предложенного Ю. Н. Ивановым каждый сдвиг активных элементов физического тела из потенциальных ям должен осуществляться в пределах не более четверти длины стоячей волны. Иначе внешнее воздействие может привести к непредсказуемому положению осцилляторов относительно узлов и пучностей волны, вплоть до их непосредственного механического контакта между собой. При этом заработает механизм поэлементной инерционной поддержки, описанный выше. Зачем же тогда нужна волна?

У Иванова отсутствует и сам механизм регуляции необходимого сдвига. Причём неизвестно какая волна образуется при непосредственном контакте осцилляторов и образуется ли она вообще? Возможно, появится общий источник излучения? К тому же современная физика не знает примеров какого-либо заметного влияния эфира на движение физических тел, даже на уровне атомов, иначе он давно был бы обнаружен.

Иванов приводит два примера фазовой интерпретации перемещения:

Пример 1.

«Два человека находятся в лодке и намереваются одновременно с силой бросить два одинаковых по массе камня в противоположные направления (Рис. 1.2.4). Если они бросят их одновременно, то лодка останется на месте. Но что произойдёт, при условии отсутствия трения лодки с водой, если сначала бросить один камень, а по прошествии времени — второй? За промежуток времени между бросками лодка сместится, например, на 100 метров. Вернётся ли после второго броска лодка в исходное положение? Нет, не вернётся, но остановится. Если повторить процедуру, то лодка переместится ещё на 100 метров и это притом, что в обе стороны было отброшено одинаковое количество камней (вещества)! Ну а если этот процесс достаточно длительный и имеет волновую природу, а потому невидим и происходит без потери массы? Не будет ли тогда перемещение лодки казаться нам чудом?

В приведённом примере перемещение лодки связано с конкретными процессами, имеющими фазочастотную составляющую. Именно эти процессы обеспечили перемещение, причём, без какого-либо действия извне».

Пример 2. В эксперименте Иванова-Дидина (Рис. 1.2.5) перемещение системы происходит в среде и обеспечивается сдвигом фаз между колебаниями источников.

В первом примере (Рис. 1.2.4) в промежутке между бросками лодка поочерёдно движется по инерции или покоится, причем уже без взаимодействия с камнями («волной»). Камни нужны только для изменения этих состояний. Поэтому это скорее иллюстрация разгона и торможения с помощью реактивного движения, а не фазочастотного механизма образования движения. Но зачем тогда создавать живую стоячую волну, если после первого импульса лодка будет двигаться по инерции самостоятельно, а для создания живой стоячей волны необходимо затрачивать энергию, которую, возможно, негде взять кроме как из кинетической энергии движения лодки? Причём поэлементный механизм инерционности опять же будет работать и без волны.

Иванов отмечает, что механическое движение в современной физике считается врождённым свойством, у которого нет объяснения. И только якобы с помощью ритмодинамики эту проблему удалось разрешить в 1996 г. на уровне модельного представления. Но какой смысл объяснять механизм перемещения через его периодическое прерывание?! Ведь покой в современной физике это такое же врождённое свойство, как и движение, и сочетанием двух врождённых свойств ни одно из них объяснить не возможно!

В соответствии с классической физикой движение лодки по инерции в отсутствие внешнего сопротивления может обеспечить и один бросок камня, т.е. никакой фазовый сдвиг не нужен. Причем, как у Иванова, так и в классической физике причиной образования движения является сила, образующаяся в результате взаимодействия лодки с камнем (волной). А сила это и есть разность фаз давлений, напряжений и т. д. Но зачем же пытаться объяснять уже образовавшееся естественное инерционное движение в отсутствии сил сопротивления искусственным сопротивлением ему в виде обратного броска, только для того, чтобы вновь показать, как оно затем вновь образуется при прямом броске?!

Бегущие волны, в том числе и движущаяся живая стоячая волна, могут переносить не только энергию, но и вещество. Поэтому никакого чуда в фазочастотном движении материальных тел «на гребне» движущейся волны нет. Мировая материальная среда, если она существует, отличается от вещества только плотностью и размерами составляющих её частиц. Поэтому взаимодействие осцилляторов с волной в конечном итоге подчиняется всем известным законам динамики Ньютона. Но для эффективности взаимодействия плотность волновой среды должна быть сопоставимой с плотностью вещества физического тела.

Пример с лодкой не очень удачен для объяснения предложенного Ивановым механизма фазочастотного движения. Лодка может двигаться по инерции и без фазочастотного бросания камней. Если бы Иванов хотел показать образование ускоренного движения, то для этого он должен был связать его с изменяющейся во времени разностью фаз, т.е. с разностью частот. Этот механизм также можно смоделировать при помощи лодки и камней.

Для наглядности возьмём две лодки, а разность частот смоделируем, как разную скорость бросания камней. Предположим, что с каждой лодки камни бросаются одновременно в двух противоположных направлениях (в обе стороны из каждой лодки), так чтобы после начала такого «излучения» каждая лодка-осциллятор оставалась на своём месте. Причём с каждой лодки камни в двух противоположных направлениях бросаются с разной скоростью. Камни, которые летят во внешние от внутреннего пространства между лодками сторону, покинут систему из двух лодок, а вот внутренние камни могут обеспечить перемещение системы.

Пусть в некоторой точке между лодками внутренние камни встретятся и вступят во взаимодействие. При этом два камня, имеющие разную скорость, а, значит, и энергию, соединятся и, образуя общее тело, полетят в сторону лодки с медленными камнями. Упёршись в лодку с медленными камнями, общие камни приведут её в движение.

По Иванову образуется движущаяся живая стоячая волна, которая подхватит неподвижную лодку с медленными камнями. Естественно, что если лодки связаны между собой жесткой связью, то в это движение включится и неподвижная лодка с быстрыми камнями. Таким образом, вся система, состоящая из двух лодок-осцилляторов и двух камней-волн, будет двигаться на «гребне» волны, состоящей из двух камней-волн в направлении лодки с медленными камнями, т.е. в направлении осциллятора с меньшей частотой.

Причём такое на первый взгляд кажущееся «самодвижение» нисколько не противоречит классической динамике Ньютона, поэтому никакого чуда здесь нет. Действительно, при излучении камней-волн в двух противоположных направлениях лодки-осцилляторы остаются неподвижными до тех пор, пока внутренние камни не встретятся и не вступят во взаимодействие с системой лодок. Внутренние камни образуют тело с неуравновешенным импульсом для системы лодок. Поэтому система лодок придёт в движение.

Но для этого осцилляторы должны быть жестко связаны между собой механическими связями. Живая стоячая волна это общее тело, которое образуют внутренние камни. Но оно оказывает волновое давление только на один осциллятор. При этом второй должен идти за первым прицепом. Однако этот движущий импульс в полном соответствии с законом сохранения импульса уравновешивается внешними камнями, которые в систему больше не возвращаются и поэтому становятся по отношению к ней как бы внешними телами окружающей среды.

Таким образом, система осцилляторов фактически совершает реактивное движение. Но такое объяснение опять же ничем принципиально не отличается от классической интерпретации движения. Точно также можно прокатиться и на гребне живой стоячей волны, если её предварительно создало в среде какое-то внешнее тело.

Модель тела по Иванову связана только волновым образом, без жёстких связей. Причём живая стоячая волна образуется только внутри тела. Поэтому двигаясь в сторону осциллятора с меньшей частотой, она естественно окажет на него волновое давление, которое заставит двигаться только этот осциллятор. Но с внешней стороны осциллятора с большей частотой нет движущегося в нужном направлении гребня волны, волновое давление которой заставило бы его двигаться в нужном направлении. Поэтому модель тела тут же развалится.

Нет сомнений, что явления, подчиняющиеся волновой геометрии Иванова существуют в реальной действительности. По его словам многие химики и особенно кристаллографы уже приходят к выводу, что тела это пакеты стоячих волн, некие волновые решетки, в узлах которых находятся атомы или молекулы. Наверное, есть реальные основания для таких выводов. Однако среда мирового носителя волн и среда внутри материальных тел это вовсе не одно и то же. Есть основания полагать, что внутри материальных образований в промежутках между нуклонами мировая среда значительно плотнее, чем в открытом пространстве, хотя по-прежнему она остаётся значительно более разрежённой по сравнению с плотностью самих нуклонов.

При этом волны, образующие силовой каркас физических тел, при нормальных условиях, т.е. при невозбуждённом состоянии нуклонов могут не выходить за пределы материальных образований. Но тогда более плотная внутренняя среда тел образует с ними одно целое, а движение на гребне внутренней волны невозможно, т.к. это противоречит законам сохранения. При этом все волновые механизмы Иванова, связанные с инерционным движением, разгоном и торможением, а также эффекты сокращения размеров тел теряют смысл. Остаётся только внутренняя самоорганизация физических тел.

Пример с лодкой и эксперимент Иванова-Дидина подтверждают только сам принцип волнового механизма в условиях однородной среды. Однако на наш взгляд переносить этот механизм на общее мироустройство, ничего не зная о свойствах мировой среды в открытом пространстве и в промежутках между нуклонами материальных образований, пока ещё рано.

Устройство Иванова-Дидина движется только потому, что и между осцилляторами и за пределами устройства находится однородная среда — вода. Но если поместить это устройство с водой внутри него в другую среду, т.е. изолировать среду, непосредственно примыкающую к осцилляторам от окружающей среды, то никакого изменения размеров и никакого движения не получится.

Точно также среда внутри физических тел в некотором смысле изолирована от окружающего пространства. Если есть силы, удерживающие в составе системы нуклоны, то они, скорее всего, некоторым образом изолируют и внутреннюю среду. И эту функцию вряд ли выполняет волновой механизм. В нашей версии (см. выше) эту функцию выполняет внешнее давление мировой материальной среды. А впервые об этом сказал Ацюковский В. А.

Поскольку внешняя среда мало влияет на внутренние структуры тела, то фазочастотное движение и релятивистские сокращения размеров материальных образований полностью исключаются. Остаются в силе лишь законы механического движения Ньютона, определяющие взаимодействие отдельных изолированных систем между собой, которые вполне могут иметь волновой, но неизменяемый силовой каркас. По крайней мере, релятивистское сокращение никакими экспериментами пока не подтверждено.

Иванов утверждает, что релятивистское сокращение принципиально невозможно подтвердить экспериментально, т.к. по его теории волновые образования по сути дела ассоциируются с самими физическими телами, которые изменяют свои размеры в соответствии со сжатием волн. Поэтому опыты по определению скорости света всегда дают отрицательные результаты. Однако В. А Ацюковский придерживается другого мнения в отношении результатов опытов по определению скорости света. Он считает, что есть и положительные результаты таких опытов (Критический анализ основ теории относительности» ИЗДАТЕЛЬСТВО «ПЕТИТ», г. Жуковский, 1996 г.).

СТО Эйнштейна оказывает поистине какое-то магическое влияние на современную физику, а самое главное на умы учёных, даже не согласных с ней. Сегодня очень многие критикуют СТО. Однако, выдвигая новые теории все несогласные с теорией относительности, тем не менее, стремятся любыми способами хоть в какой-то степени увязать свои теории с СТО! Не стал исключением и уважаемый нами Юрий Николаевич Иванов, который дополнил эйнштейновское линейное сокращение — объёмным сокращением.

Но если волны и оказывают некоторое влияние на твёрдые тела, что вполне допустимо, т.к. всё в природе взаимосвязано, то вряд ли это влияние является столь глобальным по отношению к геометрическим размерам, как у Эйнштейна и Иванова. На наш взгляд волны в значительной степени больше зависят от состояния среды, чем состояние среды от волн. В отсутствии не только глобально определяющего, но и сколько-нибудь заметного влияния волновых эффектов на физические тела даже в однородной волновой среде, как в плане их движения, так и в плане сокращения их геометрических размеров легко убедиться экспериментально, даже не прибегая к использованию сложных приборов.

Для этого достаточно создать систему управляемых осцилляторов, подвешенных на воздушных шариках без жестких механических связей между ними. В закрытой лаборатории шарики будут самоорганизовываться. Однако стоит только открыть форточку и вся организованная система тут же распадётся на составные части, т.к. никакое волновое давление среды-воздуха не способно противостоять прямому напору этой же среды, если система не изолирована от неё или не связана в единое целое более сильными внутренними связями.

Если механические внутренние связи достаточно прочны, то система, конечно же, будет сохранять свои объёмные и линейные параметры в любых потоках среды. Однако двигаться она сможет только в спокойной среде. При ветре (течениях) она по-прежнему будет двигаться преимущественно по воле ветра (течения). В эксперименте Иванова-Дидина жестко связанные осцилляторы реально движутся по поверхности воды. Но не факт, что решающую роль в этом играют фазочастотные процессы. Есть и другие причины движения системы.

Более мощная волна от осциллятора с большей частотой частично отражается от осциллятора с меньшей частотой и отбрасывается в обратную сторону, т.е. получается обычное реактивное движение. Точно также может двигаться и лодка с парусом, на который дует установленный на ней же вентилятор, а также тележка с вентилятором и экраном. Эти примеры собственно приведены в работе самого Ю. Н. Иванова. В них никакие волновые эффекты существенной роли не играют и только могут сопутствовать основному движущему фактору.

Разность частот в ритмодинамике может быть, как причиной движения физического тела, так и ответной реакцией на его движение. Однако если напор движущегося потока среды превысит некоторое критическое значение, то на наш взгляд, никакие волновые эффекты не смогут ему противостоять. Прямой напор является основной причиной переноса вещества, а волны только подстраиваются под движущуюся среду и не более того. В лучшем случае волновое давление в однородной среде может только сопутствовать движению, обеспечиваемому другими более вескими причинами.