
Бесплатный фрагмент - Discrete Math. Practice
For students of technical specialties
Introduction
This paper presents some of the tasks that can be used in preparation for the Discrete Mathematics course.
The author will be grateful for indicating shortcomings, typos, etc.
1 Examples of completing tasks
Task Problem 1: let A and B be finite sets, | A | = m, | B | = n. How many binary relations exist between A and B?
Solution: the Cartesian product will contain a total of (n*m) pairs, therefore, a total of 2m*n subsets. Each subset is a binary relation on the set of Cartesian products, which means that there are 2m*n relations
Problem No. 2: prove that the comparability relation modulo a positive integer n on the set Z: x = y (modn) is an equivalence relation.
Proof: non the definition of x is comparable with y modulo n if and only if x — y is divisible by n without remainder. It is an equivalence relation, since it holds:
1) Reflexivity — since x — x = 0 is divided by n, then x ≡ x (mod n).
2) Symmetry — if x ≡ y (mod n), then x — y is divided by n, then y — x is divided by n, that is, y ≡ x (mod n).
3) Transitivity — if x — y is divisible by n, then x — y = t1n (t1 is an integer), and if y — z is divisible by n, then y — z = t2n.
Adding these equalities, we have: x — y + y — z = t1n + t2n, whence x — z = (t1 + t2) n, that is, x — z is divided by n. Thus, from x ≡ y (mod n) and y ≡ z (mod n) it follows that x ≡ z (mod n).
Problem No. 3: a partition of a set X is a collection of pairwise disjoint subsets of X such that each element of the set X belongs to one and only one of these subsets.
Proof: such a partition, by definition, defines the relation of belonging to a subset of the partition. Therefore, it remains to prove that this relation is equivalence.
1) reflexivity: if for any element x from X xRx performed.
2) Symmetry: Let x, y belong to the same subset, whereas
if for all x, y from X in xRy yRx follows.
3) Transitivity: If for any x,y,z X from xRy, and yRz follows xRz.
A partition of a set X is a collection of pairwise disjoint subsets of X such that each element of the set X belongs to one and only one of these subsets.
Examples.
— X= {1,2,3,4,5}. Partition: {{1,2}, {3,5}, {4}}.
— The partition of many students of the institute can be a set of groups.
In other words, a partition of a set X is a family: X= ∪i∈IXi ∀i,j Xi ⋂ Xj=0,Xi ⊆X is an element of the partition.
The set of equivalence classes of elements of any set of X by the equivalence relation R sets the quotient of the set X with respect R denoted and X/R. For example, a plurality of student groups of a given university is a factor in a plurality of a plurality of university students in relation to belonging to one group.
Examples.
— (x, ≤) x ≤ y (x,y) ∈ ≤ — are comparable;
— (x,y) ∉ ≤ — are not comparable.
If (x, ≤), ∀ x ∈X ∃ a ∈X| a≤x, then a is the smallest element. If ∃ a ∈X| ∀ x ∈X x≤ a, then a is the largest element.
Statement. The largest or smallest element is unique.
Evidence. Let a and b be the largest elements in (x, ≤), then ∀ x ∈X a ≥ x, in particular a ≥ b. Similar to b ≥ a, therefore a = b.
In a similar way, the statement for the smallest elements is proved.
Task number 4: in the cube with side 1, 9 points are selected. Prove that among them there are at least 2 points, the distance between which is ≤ ((√ 3) \ (2)).
Proof: break a cube into eight identical cubes with side 0.5 — according to the Dirichlet principle, at least one of these cubes will have two points.
The maximum distance between two points in a cube is equal to the size of its diagonal, i.e.0.5* √ 3.
Problem number 5: in a white sphere, 12% of its area is painted red. To prove that a parallelepiped can be entered into the sphere, in which all vertices are white.
Proof: Draw three mutually perpendicular planes through the center of the sphere and for each point of the sphere we consider its images for symmetries about these planes and for compositions of these symmetries. Each point that does not lie on these planes has exactly 8 images. Therefore, red dots and their images occupy no more than 8.12% = 96% of the area of the sphere. Therefore, there is a point for which all 8 images are white. These 8 points are the vertices of a rectangular box.
Problem number 6: prove that among any 10 integers there are several whose sum is divided by 10.
Solution: denote the numbers a1,a2, …,a10. Among the numbers 0,a1,a1+a2, …,a1+ … +a10 there are two that have the same residues when divided by 10. Then their difference will be divided by 10.
Problem number 7: prove Bernoulli’s inequality: if x ≥ 1,then for ∀ n∈N the following holds: (1+x) n ≥ 1+nx.
Solution: we prove the inequality using the method of mathematical induction:
Base of induction: for n = 1 we have: 1+x ≥ 1+x (the inequality holds).
Induction step: let the inequality be true for k = n, we prove the inequality for k = n +1: (1+x) n+1 ≥ 1+ (n+1) x
(1+x) (1+x) n ≥ 1+nx+x (1) We use the property: if a> b and b> c, then a> c, i.e. replace: (1+x) n with (1+nx): (1+x) (1+nx) ≥ 1+nx+x
1+nx+x+nx2 ≥ 1+nx+x
nx2 ≥ 0 (2)
Since x2 ≥ 0 and n ∈ N, then inequality (2) holds. Bernoulli’s inequality is proven.
Problem number 8: prove: 1+3+5+…+ (2n-1) =n2.
Solution: we supplement the left side with even elements up to 2n, we get the arithmetic progression:
1+2+3+4+5+…+2n = ((1+2n) / (2)) *2n= (1+2n) n=n+2n2 (1)
On the other sides we have: 1+2+3+4+5+…+ (2n-1) +2n= 1+3+5+…+ (2n-1) +2 (1+2+3+…+n)
In the second bracket we see again arithmetic progression, we get:
1+3+5+…+ (2n-1) +2 (1+2+3+…+n) = 1+3+5+…+ (2n-1) +2 ((1+n) \ (2)) n= 1+3+5+…+ (2n-1) + (1+n) n= 1+3+5+…+ (2n-1) +n+n2 (2)
Using (1) and (2) we express 1+3+5+…+ (2n-1): 1+3+5+…+ (2n-1) = n+2n2- (n+n2) = n2, as required.
This fact can also be proved using the method of mathematical induction.
Problem number 9: prove that ∀ n ∈ N the inequality holds:2n> n.
Solution: we prove the inequality using the mathematical induction method: Induction
base: for n = 1 we have: 2> 1.
Induction step: let the inequality be valid for k = n, we prove the inequality for k = n +1: 2n+1> n+1
2*2n> n+1 (1) We
use the property: if a> b and b ≥ c, then a> c, i.e. we replace in (1) 2n with n, we have: 2n ≥ n+1
n ≥ 1 (2)
Studying inequality (2), we can conclude that 2n> n only for n ≥ 1, and since. n ∈ N, then this condition is satisfied, the inequality is proved.
Problem number 10: prove the equality: 12+22+32+…+n2= ((1) \ (6)) n (n+1) (2n+1).
Solution: we prove the inequality using the mathematical induction method: Induction
base: for n = 1 we have: 1= ((1) \ (6)) *2*3=1
Induction step: let the inequality be valid for k = n, we prove the inequality for k = n +1: 12+22+32+…+n2+ (n+1) 2= ((1) \ (6)) (n+1) (n+1+1) (2 (n+1) +1)
12+22+32+…+n2+ (n+1) 2= ((1) \ (6)) (n+1) (n+2) (2n+3) (1)
Replace in (1) {12+22+32+…+n2} by {((1) \ (6)) n (n+1) (2n+1)}, we get: ((1) \ (6)) n (n+1) (2n+1) + (n+1) 2= ((1) \ (6)) (n+1) (n+2) (2n+3)
n (2n+1) +6 (n+1) = (n+2) (2n+3)
2n2+n+6n+6 = 2n2+3n+4n+6
2n2+7n+6 = 2n2+7n+6
Equality is proved.
Problem number 11: there is a chessboard, a horse is located in the lower left corner. Cut the bottom right corner from the board. Question: is it possible to get around such a chessboard with a knight?
Solution: it is easy to notice that, making a move with the knight, we alternate the color of the cell on which it is located, i.e. if we started with a black cell our movement, then we must finish on white. It is also clear that the left and right lower cells are not the same color. So at the last step we have 2 cells left (a horse is standing on one of them), which we have not yet walked around, and they are of the same color.
Therefore, it is impossible to get around such a chessboard with a horse.
Problem number 12: to prove the inequality: ((1) \ (√ 1)) + ((1) \ (√ 2)) + ((1) \ (√ 3)) + ((1) \ (√ 4)) +…+ ((1) \ (√ n)) + ≥ √ n for n≥0.
Solution: we prove the inequality using the method of mathematical induction:
Base of induction: for n = 1 we have:1=1.
Induction step: suppose that the inequality is true for k = n, we prove the inequality for k = n +1:
((1) \ (√ 1)) + ((1) \ (√ 2)) + ((1) \ (√ 3)) + ((1) \ (√ 4)) +…+ ((1) \ (√ n)) + ((1) \ (√ n+1)) ≥ √ n+1 (1) We
use the property: if a> b and b ≥ c, then a> c i.e. replace in (1) (((1) \ (√ 1)) + ((1) \ (√ 2)) + ((1) \ (√ 3)) + ((1) \ (√ 4)) +…+ ((1) \ (√ n))) by √ n, we have: √ n + ((1) \ (√ n+1)) ≥ √ n+1
√ n ≥ √ n+1 — ((1) \ (√ n+1))
√ n ≥ ((n+1—1) \ (√ n+1))
n ≥ ((n2) \ (n+1))
n2+n ≥ n2
n ≥ 0 (2)
Studying inequality (2), we can conclude that ((1) \ (√ 1)) + ((1) \ (√ 2)) + ((1) \ (√ 3)) + ((1) \ (√ 4)) +…+ ((1) \ (√ n)) + ≥ √ n, only for n ≥ 0, which coincides with the initial conditions, the inequality is proved.
Task number 13:share the booty n robbers. Each of them has their own opinion on the value of a particular share of production, and each of them wants to get no less than (1 /n) the share of production (from their point of view). How to divide prey between robbers?
Solution: for two robbers, the task is not difficult to solve — one divides the production into two equal shares in his opinion, and the other selects the largest share from them. We will solve the problem by induction on the number of robbers, i.e. Suppose k robbers already have a way to split prey harmlessly. We will divide prey between (k +1) robbers. We divide all the prey between k robbers and then let each of them divide his share into (k +1) equal parts in his opinion. Now let the last robber select one of these parts from each of the k robbers. The last robber took (in his opinion) no less than [1 / (k +1)] the share of each of the k robbers, i.e. In total, he received at least [1 / (k +1)] from all production. Each of the first k robbers also received at least (1 / (k)) * (k / (k+1)) = (1 / (k+1)) from all production.
Problem number 14: prove that an equilateral triangle cannot be covered by two smaller equilateral triangles.
Proof: Each of the smaller triangles cannot cover more than one vertex of a large triangle. According to the Dirichlet principle, there are more cells (in this case, 3 vertices) than rabbits (2 vertices). Therefore, an equilateral triangle cannot be covered by two smaller equilateral triangles.
Problem number 15: prove that (1+x) n ≥ 1+nx.
Proof: (1+x) n+1 ≥ 1+ (n+1) x
(1+x) n (1+x) ≥ (1+nx) +x
(1+x) (1+x) n ≥ (1+x) (1+nx) +x
(1+x) (1+nx) =1+nx+x+nx2
1+nx+x ≤ 1+nx+x+nx2
That is: (1+x) (1+x) n ≥ (1+x) (1+nx) ≥ (1+nx) +x
Problem 16 if (x+ ((1) \ (x))) — an integer, whether integer xn+ ((1) \ (x)) n?
Proof: welimit the answer by induction. For n = 0: 1 +1 = 2. If n = -m, where m is the positive integer: xn+ ((1) \ (xn)) = x-m+ ((1) \ (x-m)) = xm+ ((1) \ (xm))
Let xk+ ((1) \ (xk)) are integers (k=0,…,k). Let us prove that xk+1+ ((1) \ (xk=1)) is also an integer: [(xk+ ((1) \ (xk))) (x+ ((1) \ (x)))] = xk+1+ ((1) \ (xk-1)) + xk-1+ ((1) \ (xk+1)) = [(xk+1+ ((1) \ (xk+1))) + (xk-1+ ((1) \ (xk-1)))] ⇒ xk+1+ ((1) \ (xk+1)) = (xk+ ((1) \ (xk))) (x+ ((1) \ (x))) — (xk-1+ ((1) \ (xk-1)))
The first term on the right-hand side is the product of integers by the assumption of induction, therefore, the integer, the second is similar. So, the sum is an integer, therefore, the left side is an integer.
Problem number 17: qprove that a number made up of 3n identical digits is divisible by 3n.
Proof: Fix one of the numbers — a. Denote the number made up of 3nidentical digits aby An. We use induction on n. Obviously, A1 is divisible by 3. Further, suppose that Akis divisible by 3k. Note that Ak +1 = Ak * 100 … 0100 … 01 (the number of zeros in each ellipse is 3k — 1). Since the sum of the digits of the number 100 … 0100 … 01 is 3, it is divided by 3, and therefore, Ak +1is divided by 3k * 3 = 3k +1. By induction, the statement of the problem is proved.
Problem number 18: how many ways can decompose the number 1024 into a product of three natural numbers, each of which is greater than 1.
Solution: This is the number of solutions to the equation x1+ x2, + x3 = 10, where xi> 0.
Task number 19: a group of 20 students pass tests in mathematics, physics and computer science. Many students who have passed mathematics and physics coincide with many students who have passed mathematics and computer science, and coincide with many students who have passed physics and computer science. Each student has passed at least one test. Find the number of students who have passed all tests, if they have passed mathematics 15, physics — 16, computer science — 17.
Solution: let M be the set of students who have passed mathematics; F — physics and I — computer science.
According to the inclusion and exclusion formula:
|М ∪ И ∪ Ф|= |М|+|И|+|Ф|- |М ⋂ И|- |М ⋂ Ф|- |Ф ⋂ И|+ |М ⋂ И ⋂ Ф|
|М|=15;|И|=16;|Ф|=17;
|М ∪ И ∪ Ф|=20 (Each student passed at least one test on the tap)
|М ⋂ И|= |М ⋂ Ф|= |Ф ⋂ И| ⇒ |М ⋂ И|= |М ⋂ Ф|= |Ф ⋂ И| = |М ⋂ И ⋂ Ф|;
20= 15+16+17—2 |М ⋂ И ⋂ Ф|
2 |М ⋂ И ⋂ Ф| = 15+16+17— 20
|М ⋂ И ⋂ Ф| = ((28) \ (2)) =14
So, 14 students passed all the tests.
Answer: 14 students.
Task number 20: 12 knights are sitting at the round table. From them to choose 5 which would not sit nearby.
Solution: we divide the set of all decisions into two subsets, depending on whether a particular knight is in the select team or not. Then we get: 15 +21 = 36.
Answer: 36
Problem number 21: 9 camels go in jumble. How many combinations of camel rearrangements exist, in which no camel follows the one he followed.
Solution: select the forbidden pairs: (1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7), (7, 8), (8, 9). To solve, we apply the main theorem of combinatorics.
To do this, define what the object is and what the properties are. By objects we mean various arrangements of camels. In total there will be N = 9!. By properties we mean the presence of a certain pair in the permutation. Thus, the number of properties is 8. Then the number of permutations that do not have any of the 8 properties:
N (8) =9! -C81*8!+ C82*7! -C83*6! + C84*5! -C85*4! + C86*3! -C87*2! + C88*1!=142729
Answer:142729.
Task number 22: preference. Cards are laid out in 3 piles and 2 cards are placed in the draw. Play 32 cards, i.e. each player receives 10 cards. Determine the number of layout options.
Solution: using the formula of permutations with repetitions we get: ((32!) \ (10!3*2!))
Answer: ((32!) \ (10!3*2!)).
Task number 23: from a group of 15 people it is necessary to select a team, which should include at least 5 people. How many choices.
Solution: we calculate the number of unfavorable combinations of choice, i.e., we compose options for brigades of 1, 2, 3, 4 people. Their number is: C151+ Cn152+C153+ C154=1940.
And the total number of brigades is 215. The difference gives the number of noble combinations.
Answer: 215 — 1914.
Task number 24: three boys picked 10 apples. How many ways are there to split apples between them.
Solution: We write 10 units and 2 zeros that perform the functions of a separator, and then we begin to rearrange them with all possiblemethods. Each permutation will correspond to some way of dividing 10 apples into 3 heaps. Each section method will correspond to some code containing 10 units and 2 zeros. Therefore, the number of partition methods: P (10.2) = ((10!) \ (2!8!)) =45
Answer: 45.
Problem number 25: a set of 8 elements is necessary to find the number of its partitions.
Solution: The number of partitions of the set is the Bell number => B8=4140.
Answer: 4140.
Problem number 26: find the number of decimal non-negative integers, consisting of numbers, arranged in increasing order.
Solution: 1+ C91+…C99=210.
Answer: 210
Problem number 27: how many word decompositions from the letters ABRAKADABRA
Solution: in the word ABRAKADABRA there are 11 letters, of which five are letters A, two letters B and two letters R. So, we get by the formula of permutations with repetitions, we get: Pn = ((11!) \ (5!*2! *2!)) =83160
Answer: 83160.
Problem number 28: find the sum of all divisors of 300.
Solution: 300 = 1+2+3+4+5+6+10+12+15+20+25+30+50+60+75 +100+150 +300 = 868
Answer: 868. This problem can be solved using the Euler formula.
Problem number 29: How many numbers between 1000 and 10000 consist of:
— odd numbers;
— different numbers.
Solution:
a) Between 1000 and 10000 are four-digit numbers. Because numbers consist only of odd numbers, then the first digit can be selected in 5 ways (digits 1, 3, 5, 7 and 9), the second, third and fourth digit can also be selected in 5 ways (digits 1, 3, 5, 7 and 9). Therefore, there will be a total of such numbers: n=5*5 *5 *5=625
b) numbers consist of various digits, then the first digit can be selected in 9 ways (digits 1, 2, 3, 4, 5, 6, 7, 8 and 9), the second digit in 9 ways (there can be 0 and any of the previous ones, but not repeating), the third digit in 8 ways and the fourth digit in 7 ways. Therefore, there will be a total of such numbers: n=9*9 *8 *7=4536
Answer: a) 625; b) 4536.
The task №30: prove | √ |x||=√x||.
Solution: Let m = | √ |x||
Because the rules ≤ |x|=n <=> nx <n1 should m ≤ √ |x| <m+1
m2 ≤ |x| (<m+1) 2
From the rules: x <n <=> |x| <n
n ≤x <=> n <|x|,where nan integer
must be m2 ≤ x (<m+1) 2
m ≤ √ x <m+1
From (*) => m= | √
Thus | √ |x||= m= | √x|.
Problem No. 31: un +2 = -un +1 +2un, u0 = 0, u1 = 1
Solution: here K (x) =1+x-2x2. We calculate: D (x) =K (x) u (x) = (1+x-2x2) (u0 + u1x+…) 0+x+0=x
We get: u (x) = ((x) \ (1+x-2x2))
The next step is the expansion of the denominator K (x) to the product (a1—1x) (1a2x), then 〈1 and 〈2 — the roots of the quadratic equation: 1+x-2x2=0
and
a1=1
a1= ((-1) \ (2))
arrive to the formula: u (x) = ((x) \ (12+x-x2)) = ((x) \ ((1-x) (1+ ((x) \ (2)))))
We find the decomposition into a sum of simple fractions by the method of indefinite coefficients: ((x) \ ((1-x) (1+ ((x) \ (2))))) = ((A) \ ((1-x))) + ((B) \ (1+ ((x) \ (2))))
We obtain a system of linear equations: ((1) \ (2)) AB=1B+A=0
Its solution: A= ((2) \ (3)),B= ((-2) \ (3)). Hence: u (x) = (((2) \ (3)) \ (1-x)) + (((-2) \ (3)) \ (1- ((x) \ (2)))) = ((2) \ (3)) ∑k=0∞1kxk- ((2) \ (3)) ∑k=0∞ ((-1) \ (3)) kxk
This leads to the answer: un= ((2) \ (3)) — ((2) \ (3)) * ((-1) \ (2)) n
Answer: un= ((2) \ (3)) — ((2) \ (3)) * ((-1) \ (2)) n
Task number 32: 15 students shook hands at a meeting of students, three people made 4 handshakes, and others — 3. How many students were there.
Solution: We will consider a case requiring a smaller number of participants. Since the three made 4 handshakes: we consider. That between them they made maximum handshakes — two, and formed a complete 3x vertex graph and used only 3 handshakes out of the total:

Each «had» two handshakes. The minimum number of vertices that must be added so that the condition «three made 4 handshakes» is met — these are two. Let’s portray them like this:
We get already 9 used handshakes. And the two added vertices have 3 handshakes, which corresponds to the condition. It remains 6. Just the full 4-vertex graph gives us 6 handshakes for each of the 4 students added:

We got the most minimal option. That is, 5 +4 = 9 students made handshake data. The handshake scheme can be depicted, for example, as follows:
Answer: 9 students.
Problem No. 33: prove that the degree of regularity of a graph is an invariant under isomorphism.
Proof: isomorphism means that any 2 vertices adjacent in one graph will be adjacent in the second. In a regular graph, the degrees of all vertices are equal, i.e. each vertex has the same number of neighbors. Isomorphisms preserve degrees of vertices; therefore, a graph that is isomorphic to a regular one is regular and has the same degree (since the degree of a vertex is preserved while maintaining adjacency).
Problem No. 34: a graph is bipartite if and only if it does not contain cycles of odd length.
Proof: a must. Let a bipartite graph contain a cycle of lengthk. Let us prove thatk is an even number. The ends of all its edges belong to different parts, therefore, passing through the cycle, each time we get from one share to another. At the last step, we return to the original vertex, which means we make an even number of such «transitions», sokis an even number.
Adequacy. Suppose that the graph G does not contain cycles of odd length, that is, all the cycles in it of even length. We divide all the vertices of the graph Ginto two parts. The first part includes all the vertices whose distance from the fixed vertexv isan even number, and the vertexitselfv, and the second — all other vertices. It remains to show that no two vertices that fall into the same class are adjacent. Suppose the contrary, that is, some verticesxandybelonging to one of the two sets obtained are adjacent. Consider the cycle obtained by combining the edge (x; y) and the shortest chains connecting the verticesxandywith the vertexv. The length of this cycle is the sum of the lengths of these two chains plus one. But the lengths of these two chains are of the same parity, therefore their sum is an even number, which means the length of the resulting cycle is an odd number. We came to a contradiction, which means that no two vertices that fall from the same class are adjacent.
Problem No. 35: for a discrete graph Γ with n vertices fr (q) =qn.
Proof: discrete graph with isolated vertices.
An isolated vertex is a vertex whose degree is 0 (that is, there are no edges incident to it).
Therefore, each vertex can be painted in q colors. => fr (q) =qn.
Problem No. 36: a Boolean cube Bn of dimension n consists of vertices (ε1, ε2, ⋅ ⋅ ⋅, εn), εi ∈ {0, 1}, where two vertices are adjacent if they differ by the same component εi. Find the chromatic number of the graph Bn.
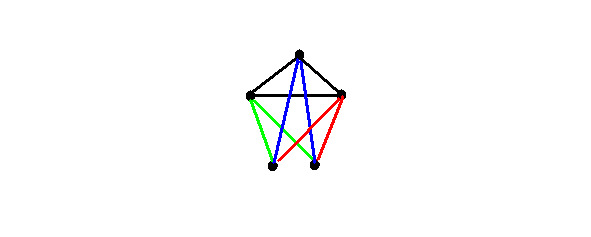
Solution: in a Boolean graph, vertices are adjacent if they differ in the same component, therefore, those vertices that have the same weight of sets will not be adjacent. And for n dimensional Boolean cube, the number of such groups is n. But taking into account the zero and unit sets, which can be added to the group with which the difference in weights of the zero and unit sets is at least 1, then the number of groups is n-1, This is the chromatic number. Let’s check on a 3-dimensional cube:
n = 3 — dimension of sets, total sets 2n= 23= 8 — {0,0,0}, {0,0,1}, {0,1,0}, {0, 1,1}, {1,0,0}, {1,0,1}, {1,1,0}, {1,1,1}. Peaks are not adjacent (by weight by set:
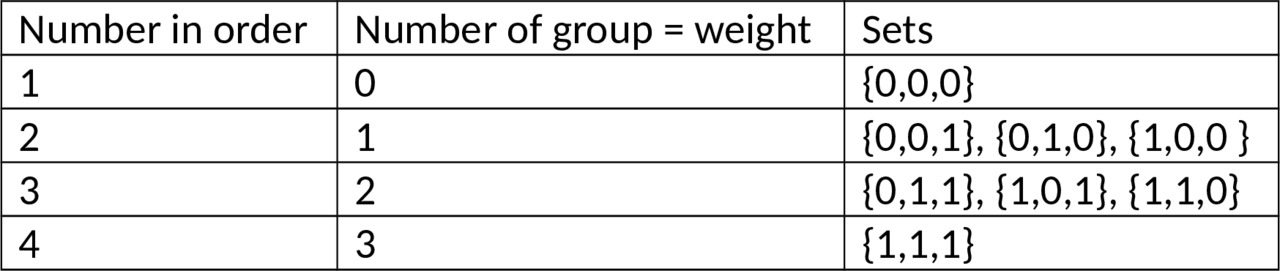
Now we add the zero and unit sets to the group, the difference in weight with which is not less than 1, that is, the set {0,0,0} to group 2, {1,1,1} — to group 1. We get:

Received the number of groups equal to n-1 = 3—1 = 2 is the chromatic number
Answer: n-1
Problem number 37: find the chromatic function of graph An
Solution: for graph An — get F (G,q) =q (q-1) n-1, which is understandable because if we first vertex in can be painted in c, colors the second — in the q — 1 colors, the third — in the q — 1 color, etc.
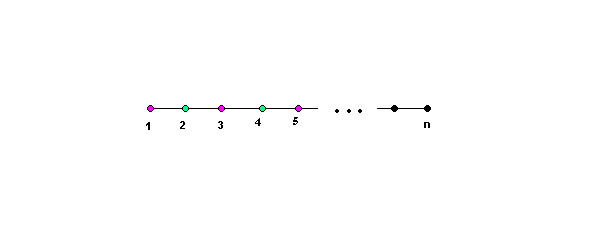
() Answer: F G,q =q (1) n-1 prove.
Task number 38: to that in a simple graph with at least two vertices there are always two vertices of the same degree
Proof: consider a zero graph with n vertices (degrees of vertices are 0) and add an edge to it. Each edge adds 2 degrees to the graph, one to each vertex to which is added. Add the first edge. In any case, it connects two vertices for which the degree becomes equal to 1. We illustrate:

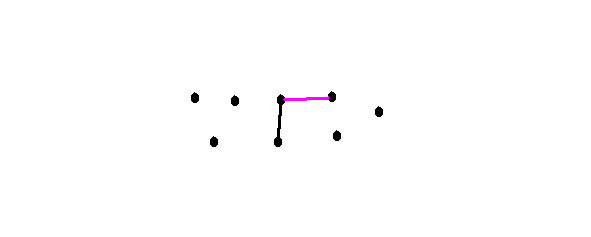
Which corresponds to the proof. Add one more edge. We can add it in two ways:
Then we get 4 vertices with degrees equal to 1. Which corresponds to the proof.
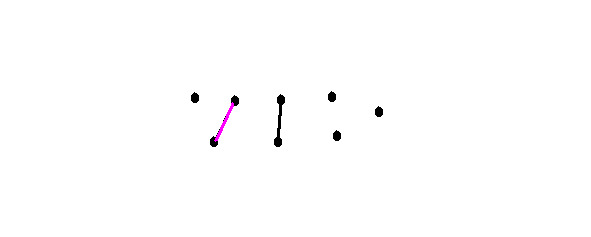
Then we get 2 vertices with the same degree — 1. Which also corresponds to the proof.
Add one more edge. We can add it in five ways:
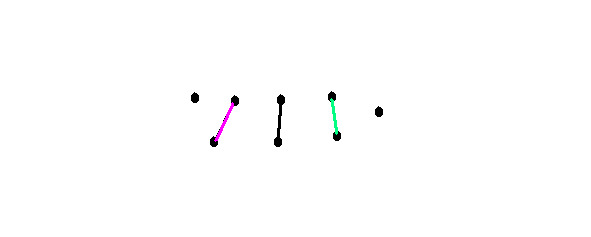
Then we get 6 vertices of degree 1.
There are 2 vertices of degree 1.
There are 4 vertices of degree 1.
3 vertices of degree 1.
3 vertices of degree 2.
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.