Бесплатный фрагмент - Выполнение заданий по Комбинаторике и Теории вероятностей

Основое отличие этой книги от моих предыдущих книг, посвященных Комбинаторике и Теории вероятностей, заключается в том, что в ней основное внимание уделяется рассмотрению задач прикладного характера с широким применением соответствующего теоретического материала справочного характера. Так, например, предлагается решить разными способами следующую задачу:

«Танк делает выстрел по цели. Если цель не уничтожена, то он делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?».

Рассматриваются варианты решения таких задач, как обычными методами, так и с использованием нейросетей.

I. Решение прикладных задач

Задача 1

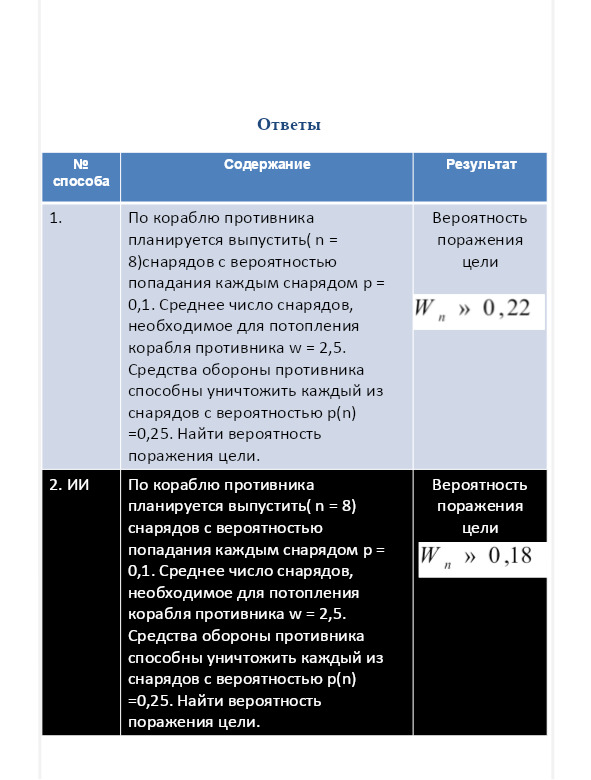
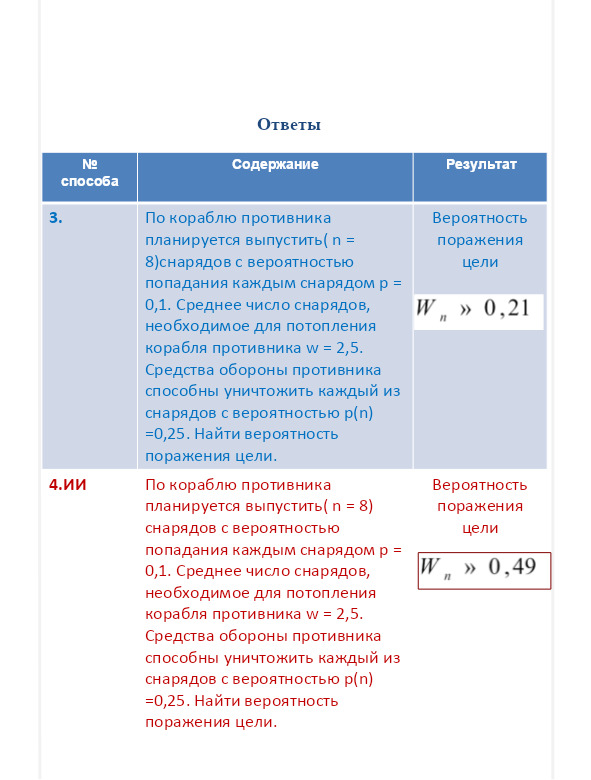
Задача 2

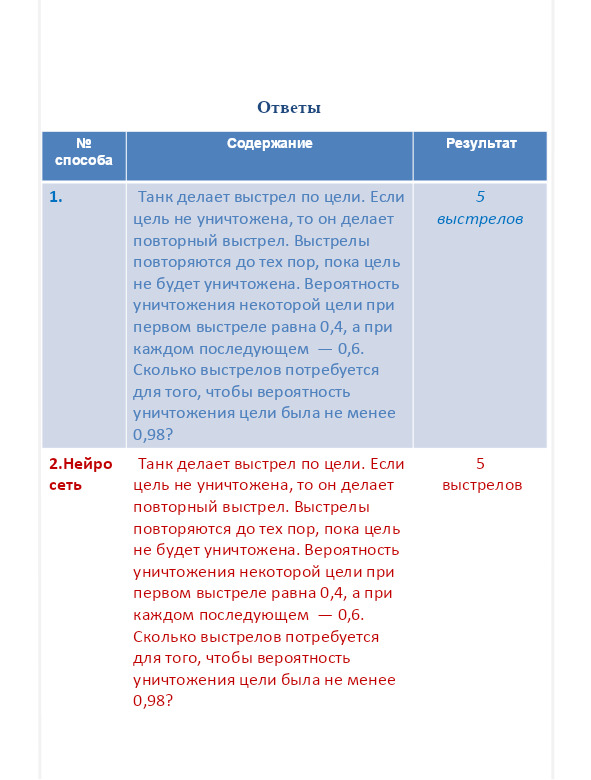
II. Справочный материал

Комбинаторика

1.Основные понятия

Комбинаторика — это раздел математики, изучающий способы формирования и выбора конечных множеств объектов.

Основные понятия включают:

— Множества: Совокупности объектов, которые могут быть определены и изучены. Объекты, являющиеся элементами множества, называются «элементами».

— Перестановки: Различные упорядоченные последовательности элементов множества. Перестановки можно рассматривать как требования к расположению объектов в определенном порядке.

— Сочетания: Подмножества, формируемые из заданного множества без учета порядка. Например, выбор двух элементов из четырех без учета их расположения.

— Разбиения: Способы разделения множества на непересекающиеся подмножества.

Размещениями называются выборки из n элементов по m элементов, комбинации, содержащие m элементов из данных n, отличающиеся составом или порядком элементов. Число всех возможных размещений из n элементов по m элементов обозначается Anm

Перестановками n элементов называются комбинации, состоящие из всех n элементов, отличающиеся порядком элементов. Число всех возможных размещений из n элементов обозначается Pn

Сочетаниями по m элементов из данных n элементов называются комбинации, содержащие m элементов и отличающиеся их составом.

Число всех возможных сочетаний из n элементов по m элементов обозначается Cnm

2. Перестановки

Перестановки могут быть классифицированы по: