Бесплатный фрагмент - Введение в R версия 3.5.2 (2018-12-20)

Предисловие

Данное введение в R получено из исходного набора примечаний, описывающих среду S и SPlus, написанных в 1990—2 Биллом Венэбльзом и Дэвидом М. Смитом в университете Аделаиды. Сделано много небольших изменений для отражения различий между программами R и S, и развернули часть материала.

Выражаем искреннюю благодарность Биллу Венэбльзу (и Дэвиду Смиту), гарантировавших разрешение распространения этой модифицированной версии заметок, поддержав, таким образом, R от пути назад.

Комментарии и исправления всегда приветствуются. Пожалуйста, адресуйте корреспонденцию на электронную почту R-core@R -project.org.

Предложения читателю

Большинство новичков R начнет с вводного сеанса в Приложении A. Он познакомит со стилем сеансов R и, что еще более важно, даст некоторое впечатление о том, что фактически происходит.

Многие пользователи придут в R, главным образом, из-за его средств графики. Смотри Главу 12 [Графика], которую можно прочесть в почти любое время и не следует ожидать усвоения всех предыдущих разделов.

О переводе

Данная книга является переводом документации, доступной на английской языке в составе дистрибуции R. После установки оригинал перевода доступен по адресу \каталог R\doc\manual\R-intro. Если данный файл перевода переименовать в R-intro и заменить оригинальный файл на данный, то из справки по R будет доступен данный перевод.

Перевод выполнен полностью за некоторыми отличиями:

— в частично исключены тексты, относящиеся к иным ОС, кроме Windows;

— исключены справочные приложения, в которых были собраны ссылки на функции и термины в английском тексте;

— расширен раздел по пакетам за счет описания пакетов, применяемым в эконометрике.

Переводчик будет благодарен за выявленные ошибки и неточности.

1. Введение и предварительные замечания

1.1. Среда R

R представляет собой набор программных средств для манипулирования данными, вычисления и графического отображения. Кроме этого возможно:

— эффективная обработка и хранение данных,

— набор операторов для вычислений на массивах, особенно матрицах,

— цельная, непротиворечивая, комплексная коллекция утилит для анализа данных,

— графические средства для анализа данных и отображения или непосредственно на компьютере или при выводе на печать, и

— хорошо разработанный, простой и эффективный язык программирования (называемый «S»), который включает условные выражения, циклы, определяемые пользователем рекурсивные функции и средства ввода и вывода. Действительно, большинство поддерживаемых системой функций сами написаны на языке S.

Термин «окружение/среда» предназначен, чтобы характеризовать ее как полностью запланированную и последовательную систему, а не постепенно возникшего конгломерата весьма специфических и негибких инструментов, как часто имеет место с другим программным обеспечением анализа данных.

R является средством разработки методов интерактивного анализа данных. Она была разработана быстро и была расширена большим количеством пакетов. Однако, большинство программ, написанных в R, принципиально являются программами-однодневками, написанными для конкретного случая анализа данных.

1.2. Связанное программное обеспечение и документация

R можно рассмотреть как реализацию языка S, который разработан в Bell Laboratories Риком Беккером, Джоном Чемберсом и Алланом Уилксом, и который собственно лежит в основе систем S-Plus.

Эволюция основ языка S характеризуется четырьмя книгами Джона Чемберса с соавторами. Для R основой является «Новый Язык S: Среда программирования для анализа данных и графики», написанной Ричардом А. Беккером, Джоном М. Чемберсом и Алланом Р. Уилксом. Новые функции S, опубликованные 1991, даны в «Статистических моделях в S», отредактированном Джоном М. Чемберсом и Тревором Дж. Хэсти. Формальные методы и классы пакета методов основаны на описанных в «Программировании с данными» Джоном М. Чемберсом. См. Приложение F [Ссылки], для точной ссылки.

Сейчас есть много книг, которые описывают использование R для анализа данных и статистики, и документация для S/S-Plus может, как правило, использоваться с R, если помнить различия между реализациями S.

1.3. R и статистика

Наше введение в среду R не упоминает статистику, но много людей используют R в качестве системы статистики. Будем думать о ней как о среде, в пределах которой были реализованы много классических и современных статистических методов. Некоторые из них встроены в основу среды R, но многие предоставлены как пакеты. В составе R существует около 25 пакетов (названных «стандартными» и «рекомендуемыми» пакетами), и еще больше доступно через семейство сайтов CRAN (через http://CRAN.R -project.org) и из других источников. Более подробную информацию о пакетах рассмотрим позже (см. Главу 13 [Пакеты]).

Большинство классических статистик и многое из последних методик доступно для использования в R, но пользователи должны быть готовы к небольшим усилиям для поиска нужного.

Есть важное различие в философии между S (и, следовательно, R) и другими основными статистическими системами. В S статистический анализ обычно делается как ряд шагов с промежуточными результатами, сохраненными в объектах. Таким образом, тогда как SAS и SPSS дадут обильные результаты регрессионного или дискриминантного анализа, R выведет минимум результатов и сохранит их в подогнанном объекте для последующего использования функциями R.

1.4. R и система Window

Самый удобный способ пользоваться R — это использовать графическую рабочую станцию с окнами. Это руководство нацелено на пользователей, у которых есть это средство. В особенности мы будем иногда обращаться к использованию R в Windows, хотя обширный объем того, что сказано, обычно применим к любой реализации среды R.

Большинство пользователей, время от времени, непосредственно сталкивается с операционной системой на своем компьютере. В этом руководстве, главным образом, обсуждается взаимодействие с операционной системой на машинах UNIX. Если R исполняется под Windows или Mac OS, то будет необходимо внести некоторые небольшие корректировки.

Установка рабочей станции, чтобы в полной мере воспользоваться настраиваемыми функциями R, является простой, хотя и несколько утомительной процедурой и здесь рассматриваться не будет. При трудностях пользователям следует найти местного опытного специалиста.

1.5. Использование R в интерактивном режиме

При использовании программы R она выдает запрос ожидания входных команд. Запрос по умолчанию ‘>», который на UNIX совпадает с запросом оболочки, и таким образом, может казаться, что ничего не происходит. Однако, как увидим, при желании легко изменить на другой запрос R. Предположим, что запрос оболочки UNIX — «$».

В использовании R под UNIX предложенная процедура для первого случая следующая:

— Создать отдельный подкаталог, скажем ’work’ для файлов с данными, на которых будет использоваться R. Он будет рабочим каталогом всякий раз при использовании R для этой определенной задачи.

$ mkdir work

$ cd work

— Начать программу R командой

$ R

— Здесь можно давать команды

— Для завершения программы R введите:

q ()

В этом этапе Вас спросят, хотите ли Вы сохранить данные своего сеанса R. На некоторых системах это будет сделано с помощью диалогового окна, а на других Вы получите текстовый запрос, на который Вы можете ответить «да», «нет» или «отмена» (достаточно будет ввести первую букву) для сохранения данных перед выходом, выйти без сохранения, или вернуться в сеанс R. Сохраненные данные будут доступны в будущем сеансе R.

Дальнейшие сеансы R требуют меньше действий.

— Сделайте ’work’ рабочим каталогом и запустите программу как прежде:

$ cd work

$ R

— Используйте программу R, которая завершится командой q () в конце сеанса.

Для использования R под Windows процедура в основном такая же. Создайте папку как рабочий каталог, и установите его в поле «Start In’ ярлыка R. Затем запустите R, дважды щелкая по иконке.

1.6. Первый сеанс

Читателям, желающим испытать R на компьютере, прежде чем приступить настоятельно советуем проработать вводный сеанс, данный в Приложении A [Сеанс выборки].

1.7. Получение справки по функциям и средствам

У R есть встроенное справочное средство. Для получения дополнительной информации о любой определенной именованной функции, например solve, напишите команду:

> help (solve)

Альтернатива:

>? solve

Для средств, указанных специальными символами, параметр должен быть включен в двойные или одинарные кавычки, делая его «символьной строкой»: это также необходимо для нескольких слов с синтаксическим значением, включая if, for и function.

> help (» [[»)

Может использоваться любая форма символа кавычки для исключения других кавычек, как в строке, «It’s important». Наше соглашение состоит в предпочтительности использования символа двойной кавычки.

На большинстве установок R справка доступна в формате HTML, достаточно выполнить:

> help.start ()

что запустит Веб-браузер, предоставляющий возможность использовать гиперссылки в справке. Ссылки «Search Engine and Keywords’ на странице, загруженной help.start (), особенно полезны, так как содержат высокоуровневый список понятий, используемый при поиске доступных функций. Это может оказаться отличным способом быстро решить проблемы и понять широкий спектр возможностей R.

Команда help.search (альтернативно??) позволяет искать справку различными способами.

Например,

>?? solve

Попробуйте ?help.search для деталей и большего количества примеров.

Пример на теме справки обычно можно выполнить:

> example (topic)

У версий R для Windows есть другие дополнительные системы справочной информации. Используйте:

>?help

для получения дальнейшей информации.

1.8. Команды R, учет регистра и т. д.

Технически R является языком выражений с очень простым синтаксисом. Он учитывает регистр, как большинство других программ UNIX, таким образом, A и а являются различными символами и ссылаются на разные переменные. Набор символов, которые могут использоваться для имен R, зависит от операционной системы и страны, в которой R исполняется (технически говоря, от используемой локализации — locale). Обычно разрешены все алфавитно-цифровые символы плюс».» и «_», с ограничением, что имя должно начинаться с».» или буквы, и если начинается с».», то второй символ не может быть цифрой. Имена в фактически неограниченны.

Для портативного кода R (включая использовуемый в пакетах R) должна использоваться только A–Za–z0–9.

Простые команды состоят из выражений (expression), либо присвоений (assignments). Если выражение вводится как команда, то оно вычисляется, выводится (пока специально не сделано невидимым) и значение теряется. Присвоение также вычисляет выражение и передает значение переменной, но результат автоматически не выводится.

Команды разделены либо точкой с запятой (»;»), либо новой строкой. Простые команды могут группироваться в одно составное выражение фигурными скобками (» {» и»}»). Комментарии могут быть помещены практически где угодно, начинаясь со знака «решетки» («#»), при этом все до конца строки является комментарием.

Если команда не полна в конце строки, то R даст особое приглашение, по умолчанию:

+

на второй и последующих строках и продолжит читать ввод, пока команда синтаксически не полна. Этот запрос может быть изменен пользователем. Мы, как правило, будем опускать приглашение продолжения ввода и обозначим продолжение простым отступом.

Командные строки, вводимые на консоли, ограничены в размере доя 4095 байт (не символов).

1.9. Повтор и коррекция предыдущих команд

R реализует механизм для повторного вызова и выполнения предыдущих команд. Вертикальные клавиши со стрелками на клавиатуре могут использоваться для прокрутки вперед и назад по истории команд. Как только команда локализована таким способом, курсор может быть перемещен в пределах команды, используя горизонтальные клавиши со стрелками, и символы могут быть удалены клавишей DEL или добавлены другими клавишами. Более подробная информация предусмотрена далее: см. Приложение C [Редактор командной строки].

Кроме того, редактор текста Emacs предоставляет более полный механизм поддержки (через ESS — Emacs Speaks Statistic) для интерактивной работы с R. Смотри раздел «R and Emacs» в The R statistical system FAQ.

1.10. Выполнение команд из файла или перенаправление вывода в файл

Если команды были сохранены во внешнем файле, скажем «command. R ’ в рабочем каталоге ’work’, то они могут быть выполнены в любое время в сеансе R командой:

> source («commands. r»)

Для Windows Source также доступен в меню File. Функция sink:

> sink("record.lis»)

отклонит весь последующий вывод консоли во внешний файл ‘record.lis’. Команда

> sink ()

восстановит вывод в консоли еще раз.

1.11. Сохранение данных и удаление объектов

Сущности, которые R создает и манипулирует, известны как объекты (object). Они могут быть переменными, массивами чисел, символьными строками, функциями или более общими структурами, построенных из таких компонентов.

Во время сеанса R объекты создаются и хранятся по имени (обсуждается в следующей секции). Команда R:

> objects ()

(также как ls ()) может использоваться для вывода на экран имен (в основном) объектов, которые в настоящий момент хранятся в пределах R. Набор объектов, сохраненных в настоящий момент, называют рабочей областью (workspace).

Для удаления объектов доступна команда rm:

> rm (x, y, z, ink, junk, temp, foo, bar)

Все объекты, создаваемые во время сеанса R, могут храниться постоянно в файле для использования в будущем сеансе R. В конце каждого сеанса R предоставляется возможность сохранить все в имеющиеся в данный момент объекты. Если подтвердить необходимость этого, то объекты записываются в файл, называемый». RData’ в текущем каталоге, а строки команд, использованных в сеансе, сохраняются в файл». Rhistory’.

При последующем запуске R рабочая область загружается из этого файла. Одновременно загружается присоединенная история команд.

Рекомендуется использовать отдельные рабочие каталоги для анализов, проводимых с R. Очень распространено использовать для анализа объекты с именами x и y. Подобные имена часто значимы в контексте отдельного анализа, но может быть довольно трудно решить то, чем они отличаются, если несколько анализов было выполнено в одном и том же каталоге.

2. Простые манипуляции; числа и векторы

2.1. Вектора и присваивания

R оперирует именованными структурами данных (data structures). Простейшая такая структура — это числовой вектор, который является отдельным объектом, состоящим из упорядоченного набора чисел. Чтобы создать вектор с именем x, скажем, состоящий из пяти чисел, а именно, 10.4, 5.6, 3.1, 6.4 и 21.7, используют команду R:

> x <- c (10.4, 5.6, 3.1, 6.4, 21.7)

Это — оператор присваивания, использующий функцию c (), которая в этом контексте может взять произвольное число аргументов вектора и значением которой является вектор, полученный путем объединения аргументов конец с концом.

С другими параметрами кроме типов векторов, таких как параметры режима списка, действие c () довольно отличается. Посмотрите Раздел 6.2.1 [Конкатенация списков].

Отдельное число, входящее в выражении, трактуется как вектор единичной длины.

Учтите, что оператор присваивания (» <-»), который состоит этих двух символов ‘ <’ («меньше чем») и ‘-’ («минус»), выполняется однонаправленно и «указывает» на объект, получающий значение выражения. В большинстве случаев можно использовать оператор ‘=’ в качестве альтернативы.

Также можно сделать присвоение, используя функцию assign (). Эквивалентный выше приведенному способ присвоения выглядит как:

> assign («x», c (10.4, 5.6, 3.1, 6.4, 21.7))

Обычный оператор <- может считаться синтаксическим сокращением для него.

Присвоения могут также быть сделаны в другом направлении, используя очевидное изменение в операторе присваивания. Таким образом, то же самое присвоение могло быть сделано, используя:

> c (10.4, 5.6, 3.1, 6.4, 21.7) -> x

Если выражение используется в качестве полной команды, значение печатается и теряется. Итак, если бы нам пришлось использовать команду:

> 1/x

то обратные величины пяти значений были бы напечатаны в терминале (а значение x, конечно, не изменилось).

В действительности все еще доступно .Last.value до выпполнения любого другого оператора.

Дальнейшее присваивание:

> y <-c (x, 0, x)

создаст вектор y с 11 элементами, состоящими из двух копий x и нулем между ними.

2.2. Векторная арифметика

Векторы могут использоваться в арифметических выражениях, и в этом случае операции выполняются поэлементно. Векторы, используемы в одном выражении, не обязательно должны иметь одинаковую длину. Если длины отличаются, то результат выражения — это вектор с длиной самого длинного вектора, который находится в выражении. Короткие векторы в выражении используются повторно столько раз, сколько это необходимо (возможно не целое число раз), до тех пор, пока они не совпадут с длиной самого длинного вектора. В частности константа просто повторяется. Так, учитывая предыдущие присваивания, команда:

> v <-2*x + y +1

создаст новый вектор v длины 11, составленный путем сложения элемент за элементом 2*x повторенного 2.2 раза, y повторяется только раз, и 1 повторяется 11 раз.

Элементарными арифметическими операторами являются +, -, *, / и ^ для возведения в степень. Дополнительно присутствуют все простые арифметические функции. log, exp, sin, cos, tan, sqrt и так далее, все они имеют свое обычное значение. max и min выбирают самые большие и наименьшие элементы вектора соответственно. range является функцией, значение которой — вектор длины два, а именно, c (min (x), max (x)). length (x) является числом элементов в x, sum (x) дает сумму всех элементов x, и prod (x) их произведение.

Двумя статистическими функциями являются mean (x), которая вычисляет среднее выборки, что соответствует sum (x) /length (x), и var (x), которая дает

sum ((x-mean (x)) ^2) / (length (x) -1)

или дисперсию выборки. Если параметром var () является n-на-p матрица, значение — матрица ковариации выборки p-на-p, полученная путем интерпретации строк как p независимых векторов-выборок.

sort (x) возвращает вектор того же размера как x с элементами, расположенными в возрастающем порядке; однако доступны и другие более гибкие средства сортировки (см. order (), или sort.list (), которые производят перестановку при сортировке).

Заметим, что max и min выбирают самое большое и наименьшее значение в их аргументах, даже если им дают несколько векторов. Параллельные функции максимума и минимума pmax и pmin возвращают вектор (длины, равной их самому длинному аргументу), который содержит в каждом своем элементе наибольшее (наименьшее) значение на этой позиции во всех входных векторах.

В большинстве случаев пользователю не важно, являются ли «числа» в числовых векторах целыми, реальными или даже комплексными. Внутренние расчеты осуществляются в реальных числах двойной точности, или комплексных числах двойной точности, если входные данные являются комплексными.

Для работы с комплексными числами надо явно предоставить мнимую часть. Таким образом:

sqrt (-17)

даст NaN и предупреждение, но

sqrt (-17+0i)

сделает вычисления как комплексных чисел.

2.3. Генерация регулярных последовательностей

У R есть много средств для генерации используемых последовательностей обычных чисел. Например, 1:30 является вектором c (1, 2…, 29, 30). У оператора двоеточия есть высокий приоритет в пределах выражения, таким образом, например 2*1:15 является вектором c (2, 4…, 28, 30). Введите n <-10 и сравните последовательности 1:n-1 и 1: (n-1).

Выражение 30:1 может использоваться для создания обратной последовательности.

Функция seq () является более общим средством для генерации последовательности. У нее имеется пять параметров, только некоторые из которых могут специфицироваться в любом вызове. Первые два параметра, если дано, специфицируют начало и конец последовательности, и если только эти два параметра, то результат аналогичен оператору двоеточия. Например, seq (2,10) дает такой же вектор как 2:10.

Аргументы для seq () и ко многим другим функциям R, могут также быть даны в именованной форме, когда порядок, в котором они появляются, не важен. Первые два аргумента можно назвать from=value и to=value; таким образом, seq (1,30), seq (from=1, to=30) и seq (to=30, from=1) являются одинаковыми с 1:30. Следующие два аргумента для seq () можно назвать by=value и length=value, которые специфицируют размер шага и длину для последовательности соответственно. Если ни один из них не дан, то по умолчанию предполагается by=1.

Например:

> seq (-5, 5, by=.2) -> s3

генерирует вектор c (-5.0, -4.8, -4.6, …, 4.6, 4.8, 5.0). Подобно этому:

> s4 <- seq (length=51, from=-5, by=.2)

генерируется аналогичный вектор.

Пятый аргумент можно назвать along=vector, который используется как единственный аргумент и создает последовательность 1, 2…, length (вектор), или пустую последовательность, если вектор пуст (такое тоже может быть).

Соответствующая функция rep (), которую можно использоваться для тиражирования объекта различными сложными способами. Самая простая форма:

> s5 <- rep (x, times=5)

которая поместит пять копий x от начала до конца в s5. Другая полезная версия

> s6 <- rep (x, each=5)

которая повторит каждый элемент х пять раз перед пересылкой в следующую.

2.4. Логические векторы

Так же как числовые векторы, R позволяет манипулирование логическими величинами. У элементов логического вектора могут быть значение TRUE, FALSE, и NA (для «не доступно», см. ниже). Первые два часто сокращаются как T и F, соответственно. Заметим, однако, что T и F — только переменные, которые установлены в TRUE и FALSE по умолчанию, но не зарезервированные слова и, следовательно, могут быть перезаписаны пользователем. Следовательно, следует всегда использовать TRUE и FALSE.

Логические векторы генерируются условиями. Например:

> temp <- x> 13

устанавливает temp как вектор одинаковой длины как x со значением FALSE, соответствующих тем элементам x, где условие не соблюдается, и TRUE, где имеет место.

Логическими операторами являются <, <=,>,> =, == для точного равенства и!= для неравенства. Кроме того, если c1 и c2 — логические выражения, то c1&c2 — их пересечение («и»), c1|c2 — их объединение («или»), и!c1 — отрицание c1.

Логические векторы могут использоваться в обычной арифметике, в том случае они преобразуются в числовые векторы, FALSE равно 0 и TRUE равно 1. Однако есть ситуации, где логические векторы и их преобразованные числовые дубликаты не эквивалентны, например см. следующий подраздел.

2.5. Пропущенные значения

В некоторых случаях компоненты вектора не могут быть полностью известны. Когда элемент или значение «не доступно» или «отсутствует значение» в статистическом смысле, место в пределах вектора может быть зарезервировано, присваивая ему специальное значение NA. Вообще любое действие с NA дает NA. Обоснование этого правила просто состоит в том, что, если спецификация действия является неполной, то результат не может быть известен и, следовательно, не доступен.

Функция is.na (x) дает логический вектор одинакового размера с x со значением TRUE, если и только если соответствующий элемент в x равен NA.

> z <- c (1:3,NA); ind <- is.na (z)

Заметим, что логическое выражение x == NA очень отличается от is.na (x), так как NA не действительно значение, а маркер для количества, которое не доступно. Таким образом, x == NA — вектор одинаковой длины с x, все значения которого равны NA, поскольку само логическое выражение является неполным и, следовательно, неразрешимым.

Заметим, что существует второй вид «пропущенного» значения, которое произведено числовым вычислением, так называемое значение «Не Число» — NaN. Пример:

> 0/0

или

> Inf — Inf

который оба дают NaN, так как результат не может быть определен заметно.

В итоге, is.na (xx) равно TRUE и для NA и для значения NaN. При дифференцировании их, is.nan (xx) равно TRUE только для NaN.

Отсутствующие значения иногда печатаются как <NA>, когда символьные векторы напечатаны без кавычек.

2.6. Векторы символов

Символьные количества и символьные векторы часто используются в R, например, как метки рисунка. Где необходимо они обозначены последовательностью символов, разграниченных символом двойной кавычки, например, «x-значением», «Новая итерация заканчивается».

Символьные строки вводятся, используя любые двойные (») или одинарные (») кавычки, но напечатаны, используя двойные кавычки (или иногда без кавычек). Они используют escape-последовательности C-стиля, используя \, поскольку символ ESC, таким образом, \\вводится и печатается как \\, и в двойных кавычках, «вводится как \». Другие полезные escape-последовательности: \n — новая строка, \t — табуляция и \b — клавиша Backspace — смотри? Quotes для полного списка.

Символьные векторы могут быть связаны в вектор функцией с (); примеры их использования будут часто появляться.

Функция paste () берет произвольное число параметров и связывает их один за другим в символьные строки. Любые числа, данные среди параметров, принуждены в символьные строки очевидным способом, то есть, таким же образом они были бы таковыми при печати. Параметры по умолчанию разделены в результате одиночным знаком пробела, но это может быть изменено именованным аргументом sep=string, который изменяет их на строку, возможно пустую.

Например:

> labs <- paste (c («X», «Y»), 1:10, sep=«»)

преобразует labs в символьный вектор

c («X1», «Y2», «X3», «Y4», «X5», «Y6», «X7», «Y8», «X9», «Y10»)

Заметим отдельно, что рецикличность коротких списков также имеет здесь место; таким образом, c («X», «Y») повторен 5 раз для соответствия последовательности 1:10.

paste (…, collapse=ss) помещает аргументы в единственную символьную строку, помещая ss между ними, т.е. ss <- "|». Существуют дополнительные инструменты для обработки символов, смотри справку по sub и substring.

2.7. Векторы индексов; выбор и изменение подмножеств наборов данных

Подмножества элементов вектора могут быть выбраны путем добавления к имени вектора индексного вектора в квадратных скобках. Более широко у любого выражения, которое оценивает вектор, может быть подмножества его элементов, так же выбранных путем добавления индексного вектора в квадратных скобках сразу после выражения.

Такой индексный вектор может быть любым из четырех различных типов.

— Логический вектор. В этом случае индексный вектор рециклично приводится к той же самой длине как вектор, из которого должны быть выбраны элементы. Значение, соответствующее TRUE в индексном векторе, выбрано, и те, которые соответствуют FALSE, опущены. Например:

> y <-x [! is.na (x)]

создает (или воссоздает) объект y, который будет содержать не несуществующие (только существующие) значения x в том же самом порядке. Заметим, что, если у x есть отсутствующие значения, то y будет короче, чем x. Также:

> (x+1) [(! is.na (x)) & x> 0] -> z

создает объект z и помещает в него значение вектора x+1, для которого соответствующее значение в x и не пропущено и положительное.

— Вектор положительных целых величин. В этом случае значение в индексном векторе должно лежать в наборе {1, 2…, length (x)}. Соответствующие элементы вектора выбраны и связаны в этом порядке в результате. Индексный вектор может иметь любую длину, и результат имеет одинаковую длину с индексным вектором. Например, x [6] является шестой компонентой x и

> x [1:10]

выбирает первые 10 элементов x (предполагается, что length (x) не меньше, чем 10). Также:

> c («x», «y») [rep (c (1,2,2,1), times=4)]

(по общему признанию вещь маловероятная), производит символьный вектор длины 16, состоящий из «x», «y», «y», «x» повторенных четыре раза.

— Вектор отрицательных целых величин. Такой индексный вектор указывает значение, которое будет исключаться, а не включаться. Таким образом:

> y <- x [- (1:5)]

даст все у, кроме первых пяти значений.

— Вектор символьных строк. Эта возможность применяется там, где у объекта есть атрибут имен для идентификации его компонентов. В этом случае подвектор вектора имен может использоваться таким же образом в качестве положительных целых меток в пункте 2 далее выше:

> fruit <- c (5, 10, 1, 20)

> names (fruit) <- c («orange», «banana», «apple», «peach»)

> lunch <- fruit [c («apple», «orange»)]

Преимущество состоит в том, что алфавитно-цифровые имена часто легче запомнить, чем числовые индексы. Эта опция особенно полезна в соединении с фреймами данных, как увидим позже.

Также индексное выражение может появиться на приемном конце присвоения, когда операция присвоения выполняется только на этих элементах вектора. Выражение должно иметь вектор вида [index_vector], поскольку наличие произвольного выражения вместо векторного имени не имеет здесь большого смысла.

Присвоенный вектор должен соответствовать длине индексного вектора, и в случае логического индексируют вектор, у него должна снова быть та же самая длина как вектор, который он индексирует.

Например:

> x[is.na (x)] <- 0

заменяет пропущенные значения в х на нули и

> y [y <0] <- -y [y <0]

имеет такой же результат как:

> y <- abs (y)

2.8 Другие типы объектов

Векторы — самый важный тип объекта в R, но есть несколько других, которые определим более формально в последующих разделах.

— matrices (матрицы) или более широко arrays (массивы) — многомерные обобщения векторов. Фактически, они — векторы, которые могут быть индексированы двумя или больше индексами и будут напечатаны специальными способами. См. Главу 5 [Массивы и матрицы].

— factors (факторы) реализуют компактные способы обработки категорических данных.

— lists (список) — общая форма вектора, в котором различные элементы могут не иметь одинаковый тип, и являются часто самостоятельно векторами или списками. Списки предоставляют удобный путь к возврату результатов статистического вычисления. См. Раздел 6.1 [Списки].

— data frames (фреймы данных) — подобные матрице структуры, в которых столбцы могут иметь различные типы. Думайте о фреймах данных как о «матрице данных» с одной строкой на отдельное наблюдение, но с (возможно) и числовыми и категориальными переменными. Много экспериментов лучше всего описываются фреймами данных: обработки категоричны, но отклик является числовым. См. Раздел 6.3 [Фреймы данных].

— functions (функции) — самостоятельные объекты в R, которые можно сохранить в рабочей области проекта. Этим реализован простой и удобный способ расширения R. См. Главу 10 [Написание собственных функций].

3. Объекты, их режимы и атрибуты

3.1. Внутренние атрибуты: режим и длина

Рабочие сущности R технически известны как объекты. Примерами могут быть векторы с численными (реальными) или комплексными величинами, векторы с логическими значениями и векторы строк символов. Они известны как «атомарные» структуры, так как их компоненты имеют одинаковый тип или режим (mode), а именно, numeric, complex, logical, character и raw.

numeric режим — на самом деле смесь двух разных режимов, а именно, integer и double precision, как объяснено в руководстве.

У векторов должен быть одинаковый режим для всех значений. Таким образом, любой данный вектор должен быть однозначно или логическим, числовым, комплексным, символьным или строковым (logical, numeric, complex, character или raw). Единственное очевидное исключение к этому правилу — специальное «значение», обозначаемое как NA для отсутствующих значений, хотя реально есть несколько типов NA. Заметим, что вектор может быть пустым и иметь режим. Например, пустой вектор символьной строки обозначается как character (0) и пустой числовой вектор как numeric (0).

R также работает с объектами, называемыми списками (list), которые имеют тип список (list). Существуют упорядоченные последовательности объектов, которые индивидуально могут иметь любой тип. Списки (list) известны как «рекурсивные», а не атомарные структуры, так как их компоненты могут самостоятельно быть списками.

Другие рекурсивные структуры из этого типа — это функции и выражения (function и expression). Функции — это объекты, которые являются частью системы R наряду с аналогичными написанными пользователем функциями, которые в деталях обсуждаются позже. Выражения, как объекты, составляют самую сложную часть R, которая не будет обсуждаться в этом руководстве, кроме как косвенно при обсуждении формул (formulae), используемых при моделировании R.

Типом (mode) объекта обозначили основной тип его фундаментальных свойств. Это — особый случай «свойств» объекта. Другое свойство каждого объекта — своя длина. Можно использовать функции mode (object) и length (object), чтобы узнать тип и длину любой определенной структуры.

Заметим, однако, что length (object) не всегда содержит явную полезную информацию, например, когда object — функция.

Другие свойства объекта обычно получают посредством attributes (object), смотри Раздел 3.3 [Получение и установка атрибутов]. Из-за этого тип и длину также называют «внутренними атрибутами» объекта.

Например, если z — комплексный вектор длины 100, то в выражении mode (z) является символьной строкой «complex», и length (z) равна 100.

R обслуживает изменения типа практически везде, где это имеет смысл сделать, и иногда там, где этого не так. Например, с:

> z <-0:9

можно ввести

> digits <- as.character (z)

после которого digits является символьным вектором c («0», «1», «2»…, «9»). Дальнейшее приведение, или изменение типа, восстанавливает числовой вектор снова:

> d <- as.integer (digits)

Теперь d и z одинаковы. Существует большое количество функций вида as.something () или для приведения от одного типа к другому, или для наделения объекта некоторым другим атрибутом, которым он, возможно, еще не обладает.

В целом приведение от числового к символьному типу и назад не будет точно обратимо из-за ошибок округления в символьном представлении.

Читатель должен консультироваться с различными справочными файлами для ознакомления.

3.2. Изменяющаяся длина объекта

«Пустой» объект может все еще иметь тип. Например:

> e <- numeric ()

делает e пустой векторной структурой типа числовой (numeriс). Так же character () является пустым символьным вектором, и так далее. Как только объект любого размера был создан, новые компоненты могут быть просто добавлены к нему, давая ему значение индексов вне его предыдущего диапазона. Таким образом:

> e [3] <- 17

теперь делает e вектором длины 3, (первые две компоненты, которого равны NA). Это применяется к любой структуре вообще, если тип дополнительного компонента (ов) согласован с типом первого объекта.

Эта автоматическая настройка длин объекта часто используется для ввода, например, в функции scan () (см. Раздел 7.2 [Функция scan ()]).

Наоборот требуется усечение размера объекта для выполнения присвоения. Следовательно, если alpha — объект длины 10, то

> alpha <- alpha [2 * 1:5]

делает его объектом длины 5, состоящим только из прежних компонентов с четным индексом. (Старые индексы не сохранены, конечно). Затем можно сохранить только первые три значения:

> length (alpha) <- 3

и вектор может быть расширен (путем пропущенных значений) аналогичным образом.

3.3. Получение и установка атрибутов

Функция attributes (object) возвращает список всех не внутренних атрибутов, в настоящий момент определенных для этого объекта. Можно использовать функцию attr (object, name) для выбора определенного атрибута. Эта функция редко используются, за исключением довольно особых обстоятельств, когда некоторый новый атрибут создается для некоторой конкретной цели, например, для присоединения даты создания или оператора с объектом R. Понять, однако, очень важно.

Некоторое внимание должно быть уделено, когда присваиваются или удаляются атрибуты как неотъемлемая часть системы объекта, используемой в R.

Когда такое используется на левой стороне присвоения, то оно может использоваться или для присоединения нового атрибута с object или изменения существующего. Например:

> attr (z, «dim») <- c (10,10)

позволяет R обрабатывать z как будто он является матрицей 10-на-10.

3.4. Класс объекта

У всех объектов в R есть класс (class), определяемы при помощи функции class. Для простых векторов это — только тип, например, «numeric», «logical», «character» или «list», но «matrix», «array», «factor» и "data.frame» " являются другими возможными значениями.

Специальный атрибут, известный как class (класс) объекта, используется для учета объектно-ориентированного стиля программирования в R. Например, если у объекта будет класс "data.frame», то он будет напечатан определенным способом, функция plot () выведет на экран его графически определенным способом, и другие, так называемые универсальные функции, такие как summary (), будут реагировать на него как на параметр, способом применимым к его классу.

Чтобы удалить временно эффект класса, используйте функцию unclass (). Например, если у winter есть класс "data.frame» то:

> winter

напечатает его в форме фрейма данных, которая скорее походит на матрицу, тогда как:

> unclass (winter)

напечатает его как обычный список. Только в довольно специальных ситуациях следует использовать это средство, но каждый раз для достижения согласования идеи класса и универсальных функций.

Универсальные функции и классы будут обсуждены далее в Разделе 10.9 [Ориентация объекта], но только кратко.

4. Упорядоченные и неупорядоченные факторы

Фактор — векторный объект, используемый для спецификации дискретной классификации (группировки) компонентов других векторов одинаковой длины. R поддерживает как упорядоченные, так и не упорядоченные факторы. Хотя «реальное» применение факторов имеет место в формулах модели (см. Раздел 11.1.1 [Противоположности]), здесь рассмотрим на специальный пример.

4.1. Специальный пример

Предположим, например, имеется выборка 30 налоговых деклараций из всех штатов и территорий Австралии, и их индивидуальное происхождение указывается символьным вектором аббревиатуры штата как:

> state <- c («tas», «sa», «qld», «nsw», «nsw», «nt», «wa», «wa»,

«qld», «vic», «nsw», «vic», «qld», «qld», «sa», «tas»,

«sa», «nt», «wa», «vic», «qld», «nsw», «nsw», «wa»,

«sa», «act», «nsw», «vic», «vic», «act»)

Заметим, что в случае символьного вектора, «sorted» означает сортировку в алфавитном порядке.

Создаются факторы аналогичным образом с помощью функции factor ():

> statef <- factor (state)

Функция print () обрабатывает факторы несколько иначе, чем другие объекты:

> statef

[1] tas sa qld nsw nsw nt wa wa qld vic nsw vic qld qld sa

[16] tas sa nt wa vic qld nsw nsw wa sa act nsw vic vic act

Levels: act nsw nt qld sa tas vic wa

Чтобы выяснить уровни фактора можно использовать функцию level ():

> levels (statef)

[1] «act» «nsw» «nt» «qld» «sa» «tas» «vic» «wa»

4.2. Функция tapply () и массивы с переменной длиной строк

Чтобы продолжить предыдущий пример, предположим, что у нас есть доходы от каждого налогоплательщика в другом векторе (в подходящих крупных денежных единицах):

> incomes <- c (60, 49, 40, 61, 64, 60, 59, 54, 62, 69, 70, 42, 56,

61, 61, 61, 58, 51, 48, 65, 49, 49, 41, 48, 52, 46,

59, 46, 58, 43)

Чтобы вычислить средний доход в выборке по каждому штату используем теперь специальную функцию tapply ():

> incmeans <- tapply (incomes, statef, mean)

дающей вектор средних с компонентами, маркированными уровнями:

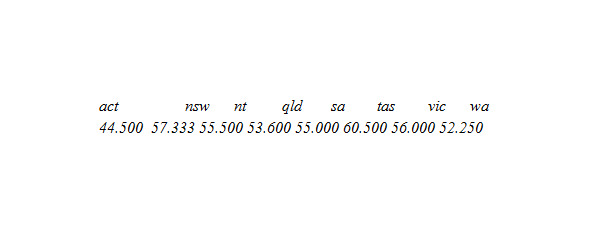
Функция tapply () используется для применения здесь функции mean () к каждой группе компонентов первого параметра, здесь доходов, определенные уровнями второго компонента, здесь statef, как будто они были отдельными векторными структурами. Результат — структура той же самой длины как атрибут уровней фактора, содержащего результаты.

Обратите внимание на то, что tapply () также работает в этом случае, когда его второй параметр не фактор, например, «tapply (incomes, state)», и это верно для довольно многих других функций, так как при необходимости параметры преобразованы в факторы (используется as. factor ()).

Читатель должен консультироваться с документом справки для большего количества деталей.

Предположи далее, что необходимо вычислить стандартные ошибки средних доходов штата. Для этого следует записать функцию R для вычисления стандартной ошибки для любого данного вектора. Так как существует встроенная функция var () для вычисления дисперсии выборки, то такая функция записывается в виде одной строки, задаваемая присвоением:

> stderr <- function (x) sqrt (var (x) /length (x))

Написание функций рассмотрим позже в Главе 10 [Написание собственных функций], и в этом случае было ненужным, поскольку R также имеет встроенную функцию sd (). После этого присвоения стандартные ошибки вычислены:

> incster <- tapply (incomes, statef, stdError)

и затем вычисленные величины:

> incster

В качестве примера можно вычислить обычные 95%-ые доверительные границы для средних доходов штата. Для этого можно использовать tapply () еще раз с функцией length (), чтобы найти размеры выборки, и функцию qt (), чтобы найти процентные точки соответствующих t-распределений. Также можно рассмотреть средства R для t-тестов.

Также можно применить функцию tapply () к более сложной индексация вектора на несколько категорий. Например, можно разделить налоговые счета как по штатам, так и по полу. Однако в этом простом примере (только один фактор) то, что происходит, можно представить следующим образом. Значение в векторе собрано в группы, соответствующие различным позициям в факторе. Затем функция применяется к каждой из этих групп отдельно. Результат — это вектор значений функции, маркированных согласно levels фактора.

Комбинация вектора и фактора меток — пример того, что иногда называют неровными массивами, так как размеры подкласса возможно не одинаковы. Когда размеры подкласса всегда одинаковы, то индексация может быть сделана неявно и намного более эффективно, как увидим в следующем разделе.

4.3. Упорядоченные факторы

Уровни факторов сохраняются в алфавитном порядке, или в том порядке, в котором они указывались к фактору, если они указывались явно.

Иногда у уровней будет естественное упорядочивание, которое записали и хотели использовать в статистическом анализе. Функция ordered () создает такие упорядоченные факторы, но, в противном, она идентична factor. В большинстве целей единственной разницей между упорядоченными и неупорядоченными факторами является то, что прежде напечатанное для упорядоченных уровней отличается от генерируемых для них в подгонке линейных моделей.

5. Массивы и матрицы

5.1. Массивы

Массив (array) можно рассмотреть как множество, приписанное к набору входов данных, например числовых. R позволяет простые средства для создания и обработки массивов, и их особый случай — матриц.

Размерностью вектора является вектор неотрицательных целых чисел. Если его длина равна k, то массив является k-мерным, например, матрица является 2-мерным массивом. Размерности индексированы от единицы до значения, данного в векторе размерности.

Вектор может использоваться в R в качестве массива, только если у него имеется вектор размерности как его атрибут dim. Предположим, например, z — вектор из 1500 элементов.

> dim (z) <- c (3,5,100)

дает ему атрибут dim, который позволяет его обрабатывать как массив 3-на-5-на-100.

Доступны другие функции, такие как matrix () и array (), для более простых и более естественно выглядящих присвоений, как увидим в Разделе 5.4 [Функция array ()].

Значение в векторе данных дает значение в массиве в том же самом порядке, как и в ФОРТРАНЕ, который является «столбцом главного порядка» с первым нижним индексом, изменяющимся быстрее, и последним самым медленным нижним индексом.

Например, если вектор размерности для массива, скажем a, является c (3,4,2) то есть 3 * 4 * 2 = 24 записи в a и векторе данных содержит их в порядке [1,1,1], [2,1,1], …, [2,4,2], [3,4,2].

Массивы могут быть одномерными: такие массивы обычно обрабатываются таким же образом как векторы (включая печать), но исключения могут вызвать беспорядок.

5.2. Индексация массива. Подразделы массива

На отдельные элементы массива можно сослаться, давая имя массива, сопровождаемого нижними индексами в квадратных скобках, разделенных запятыми.

Более широко можно указать подразделы массива, давая последовательность векторов индексов вместо нижних индексов; однако, если какая-либо позиция индекса дана пустым индексным вектором, то берется полный спектр этого нижнего индекса.

Продолжая предыдущий пример, а [2,,] является массивом 4х2 с вектором размерности с (4,2) и вектором данных, содержащим значение:

c ([2,1,1], [2,2,1], [2,3,1], [2,4,1],

[2,1,2], [2,2,2], [2,3,2], [2,4,2])

в том порядке. а [,,] стоит для всего массива, который является таким же с исключенными нижними индексами полностью и использованием а отдельно.

Для любого массива, скажем Z, на вектор размерности можно сослаться явно как dim (Z) (по обе стороны от присвоения).

Кроме того, если имя массива дано только с одним нижним индексом, или индексируется вектором, то только используется соответствующее значение вектора данных; в этом случае вектор размерности игнорируется. Дело обстоит не так, однако, если отдельный индекс не вектор, но он непосредственно массив, как обсуждим позже.

5.3. Индекс матрицы

Включая индексный вектор в любой позиции нижнего индекса, матрица может использоваться с отдельной матрицей индексов в порядке либо присвоения вектора количеству нерегулярной коллекции элементов в массиве, либо в извлечении нерегулярной коллекции как вектора.

Пример матрицы ясно дает понять процесс. В случае вдвойне индексированного массива индексная матрица может состоять из двух столбцов и так много строк как требуется. Входы в индексной матрице — строка и индексы столбца для вдвойне индексированного массива. Предположим, например, что у нас есть массив X 4-на-5, и хотим сделать следующее:

— извлечь элементы X [1,3], X [2,2] и X [3,1] как векторную структуру, и

— заменить эти записи в массиве X нулями.

В этом случае необходим массив нижнего индекса 3-на-2, как в следующем примере.

> x <- array (1:20, dim=c (4,5)) # генерирует массив 4 на 5.

> x

> i <- array (c (1:3,3:1), dim=c (3,2))

> i # i является индексным массивом 3 на 2

> x [i] <- 0 # Заменяет те элементы нулями.

> x

Отрицательные индексы не разрешены при индексировании матрицы. Разрешены NA и нулевое значение: строки в индексной матрице, содержащей нуль, игнорируются, и строки, содержащие NA, производят NA в результате.

Как менее тривиальный пример, предположим, что необходимо генерировать (не приведенную) матрицу проекта для блочной конструкции, определенной блоками факторов (b уровни) и варианты (v уровни). Далее предположим, что в эксперименте есть n рисунков. Можно продолжить следующим образом:

> Xb <- matrix (0, n, b)

> Xv <- matrix (0, n, v)

> ib <- cbind (1:n, blocks)

> iv <- cbind (1:n, varieties)

> Xb [ib] <- 1

> Xv [iv] <- 1

> X <- cbind (Xb, Xv)

Для конструирования индексов матрицы, скажем N, можно использовать:

> N <- crossprod (Xb, Xv)

Однако более простым способом создания этой матрицы является использование table ():

> N <- table (blocks, varieties)

Индексная матрица должна быть числовой: предоставленная любая другая форма матрицы (логическая или символьная) обрабатывается как индексный вектор.

5.4. Функция array ()

Так же, как давая векторной структуре атрибут dim, массивы могут быть созданы из векторов функцией массива array, у которой есть форма:

> Z <- array (data_vector, dim_vector)

Например, если вектор h содержит 24 или менее чисел, тогда команда:

> Z <- array (h, dim=c (3,4,2))

использовал бы h для создания массива Z размером 3-на-4-на-2. Если размер h точно 24, то результат выглядит так:

> Z <- h; dim (Z) <- c (3,4,2)

Однако, если h меньше, чем 24, его значения будут взяты циклически для дополнения до размера 24 (см. Раздел 5.4.1 [Правило рецикличности]), и dim (h) <-c (3,4,2) сигнализировал бы ошибку о несоответствии длине. Как экстремальный, но типичный пример:

> Z <- array (0, c (3,4,2))

делает Z массивом всех нулей.

В этой месте dim (Z) обозначает вектор размерности c (3,4,2), и Z [1:24] содержит вектора данных, как это было в h, и Z [] с пустым нижним индексом или Z без нижнего индекса поддерживает весь массив в качестве массива.

Массивы могут использоваться в арифметических выражениях, и результат является массивом, сформированным поэлементно операциями на векторах данных. Атрибуты dim операндов обычно должны быть одинаковыми, и они становятся вектором размерности результата. Так, если все A, B и C являются подобными массивами, то:

> D <-2*A*B + C +1

делает D подобным массивом с его вектором данных, являющимся результатом данной поэлементно операции. Однако точное правило относительно смешанного массива и векторных вычислений нужно рассмотреть немного более тщательно.

5.4.1. Смешанный вектор и арифметика массива. Правило рецикличности

Точное правило, влияющее поэлементно на смешанные вычисления с векторами и массивами, является более изощренными и точно описаны в ссылках. Из опыта найдено следующее надежное руководство.

— Выражение просматривается слева направо.

— Любые короткие векторные операнды расширяются циклически их значениями, пока они не совпадет с размером любых других операндов.

— Если длинные и короткие вектора с массивами лишь пересчитываются, то все массивы должны иметь одинаковый атрибут dim или будет выдана ошибка.

— Любой векторный операнд более длинный, чем операнд матрицы или массива, генерирует ошибку.

— Если имеются структуры массива, и нет ошибок, или приведение к вектору было выполнено, то результат — структура массива с общим атрибутом dim ее операндов массива.

5.5. Внешнее произведение двух массивов

Важной операуцией на массивах является внешнее произведение. Если a и b — два числовых массива, их внешнее произведение — массив, вектор размерности которого получен, связывая их два вектора размерности (порядок важен), и чей вектор данных получен путем формирования всех возможных произведений элементов вектора а с соответствующим элементами вектора b. Внешнее произведение выполняется специальным оператором %o%:

> ab <-%o % b

Альтернатива

> ab <- outer (a, b, «*»)

Функция умножения может быть заменена произвольной функцией двух переменных. Например, если необходимо оценить функцию f (x; y) = cos (y) / (1 + x2) на регулярной сетке значения с x-и y-координатами, определенными векторами R x и y соответственно, можно продолжить следующим образом:

> f <- function (x, y) cos (y) / (1 + x^2)

> z <- outer (x, y, f)

Особенностью внешнего произведения двух обычных векторов является вдвойне преобразованный в нижний индекс массив (который является матрицей ранга самое большее 1). Заметьте, что оператор внешнего произведения, конечно, некоммутативен. Определение Ваших собственных функций R рассмотрим далее в Главе 10 [написание собственных функций].

Пример: детерминанты с одноразрядными матрицами 2*2

В качестве искусственного, но милого примера, рассмотрим детерминанты матриц [a; b; c; d], где каждый вход — неотрицательное целое число в диапазоне 0; 1;..; 9, которые являются цифрой.

Задача состоит в том, чтобы найти детерминанты ad-bc всех возможных матриц этой формы и представлять частоту, с которой каждое значение имеет место в рисунке высокой плотности. Это количество находится в распределении вероятностей детерминанта, если каждая цифра выбрана независимо и гарантировано случайно.

Аккуратный способ сделать это состоит в двукратном использовании функции outer ():

> d <- outer (0:9, 0:9)

> fr <- table (outer (d, d, "-»))

> plot (fr, xlab=«Determinant», ylab=«Frequency»)

Заметьте, что здесь plot () использует гистограмму как метод рисунка, потому что он «видит», что fr имеет класс «таблица». «Очевидный» способ решить эту задачу с циклом for обсуждается в Главе 9 [Циклы и условное выполнение], что является как неэффективным, так и непрактичным.

Также, возможно, удивительно, что приблизительно 1 из 20 матриц сингулярная.

5.6. Обобщенное транспонирование массива

Можно использовать функцию aperm (a, perm) для перестановки массива a. Параметром perm должна быть перестановка целых чисел {1, …., к}, где k является номером нижних индексов в a. Результат функции — массив того же самого размера как a, но со старой размерностью, вычисленной perm [j], становящейся новой j-й размерностью. Самый простой способ понимания этой операции — это обобщение транспонирования для матриц. Действительно, если A — матрица, (то есть, вдвойне преобразованный в нижний индекс массив) тогда B вычисляется путем:

> B <-aperm (A, c (2,1))

и представляет собой транспонирование. Для этого особого случая доступна более простая функция t (), таким образом, возможно, использовать B <-t (A).

5.7. Матричные инструменты

Как отмечено выше, матрица — это массив с двумя нижними индексами. Однако это такой важный особый случай, что нуждается в отдельном обсуждении. R содержит много операторов и функций, которые доступны только для матриц. Например, t (X) — функция транспонирующая матрицу, как отмечено выше. Функции nrow (A) и ncol (A) дают число строк и столбцов в матрице соответственно.

5.7.1. Умножение матриц

Оператор %*% используется для умножения матриц. Матрицы n-на-1 или 1-на-n могут, конечно, использоваться в качестве n-вектора, если это соответствует контексту. Наоборот, векторы, которые встречаются в выражениях умножения матриц, если возможно автоматически расширяются или на вектор строки или на вектор столбца, который является мультипликативно соответствующим (хотя это не всегда однозначно возможно, как увидим позже).

Если, например, A и B — квадратные матрицы одинакового размера, то

> А * B

матрица поэлементно произведений и

> % * % B

матричное произведение. Если x — вектор, то

> x %*% %*%x

квадратная форма.