Заслуженный деятель науки и техники, профессор Жамол Худойбердиевич Каримов родился 22 февраля 1909 года в городе Фергане. Закончив педагогический техникум, в 1926 году начал свою деятельность в одном из школ города Ферганы в качестве педагога. В 1930 году поступил в Самаркандский государственный педагогический университет на математический факультет. С 1935 года закончив университет с отличием был оставлен в качестве аспиранта под руководством своего наставника П. В. Соловьёва. Окончив в 1939 году аспирантуру, остался преподавателем в Самаркандском государственном университете, вместе с этим совмещая преподавая в народных сельскохозяйственных институтах.

В 1940 году защитил кандидатскую диссертацию на тему «Нелинейные дифференциальные уравнения параболического типа» с отличием в учёном Совете Университета Средней Азии (на сегодняшний день Национальный Университет Узбекистана). В 1940—1943 годах работал в качестве доцента кафедры математики в Ферганском Педагогическом Институте. С 1943 по 1950 года работал в качестве доцента в Ташкентском Государственном Университете, совмещая деятельность заведующего кафедры «Математики и механики» в Научно-исследовательском институте «Математики и техники» при Академии наук Узбекистана. В 1950 году вернулся в Фергану и до своей кончины продолжал свою деятельность в Ферганском Педагогическом Институте (ныне Ферганский Государственный Университет).

Ж. Х. Каримов в течении своей деятельности возглавлял физико-математический факультет в качестве декана на протяжении многих лет. С 1962 года избран заведующим кафедры «Математического анализа». За выдающуюся деятельность в этом же году Высшей Аттестационной Комиссией присвоено учёное звание профессора. Вмести с В. Н. Кондрашовым Ж. Х. Каримов разработали комплекс научно-исследовательских работ «Дифференциальные уравнения нарушаемые на границах». Результаты проведённых работ в данной сфере имели большое значение не только для общей теории нелинейных дифференциальных уравнений, но и для теории фильтрации нефте-газовой продукции, а также имели большое значение в практическом применении при строительстве различных конструкции.

Научная деятельность профессор Ж. Х. Каримова была направлена на малоизученную сферу науки — вопросы нелинейных дифференциальных уравнений параболического типа. Его первая научная работа была посвящена вопросу обоснования решения методом Фурье периодического решения нелинейных дифференциальных уравнений параболического типа. Со стороны Ж. Х. Каримова опубликовано более 100 научных статей. Кроме этого он с большой эффективностью работал над созданием 44 учебных пособий по физике и математике для студентов высших учебных заведений. Также со стороны Ж. Х. Каримова были переведены с русского на узбекские языки важные для студентов ВУЗов учебников «Расчёт курса дифференциалов и интегралов» и «Основы математического анализа», в соавторстве с М. Собировым и С. Сирожиддиновым.

Его вклад в процесс подготовки кадров неизменно велик. Под его руководством его 5 соискателей защитили свои кандидатские диссертации. Во время своей деятельности он отбирал одарённых студентов и отправлял в престижные институты и университеты, предлагая их кандидатуры передовым учёным. По инициативе профессор Ж. Х. Каримова были установлены научные связи с Ташкентский государственным университетом (ныне Национальный Университет Узбекистана), а также государственными университетами Самарканда, Москвы, Санкт-Петербурга, Киева, Баку, Новосибирска с учёными-математиками. Он добился в 1962 году издания приказа Министерства высшего и среднего специального образования Республики Узбекистан о открытии аспирантуры по специальности частных производных дифференциальных уравнений при кафедре математического анализе Ферганского педагогического института и первыми аспирантами, позже получившие звания профессоров стали М. Маматов, К. Бойкузиев, а также ставшие позже доцентами Т. Абдурахмонов и К. Саримсаков.

При этом получившие образование М. Косимова, Б. Калонов, К. Шабадиков и А. Меликулов успешно защитили свои научные работы под руководством профессора Ж. Х. Каримов в Ученом совете при Математическом институте Академии наук Узбекистана и Государственном Университете Баку. Как результат преданных к науке трудов Ж. Х. Каримова была создана научная школа математиков в Фергане. Он обращал большое внимание на воспитание молодых учёных. Ж. Х. Каримов косвенно или прямо был в роли наставника занявших своё почётное место среди мировых математиков современности академика Ш. К. Фармонова, докторов физико-математических наук и профессоров К. Бойкузиева, М. М. Маматова, М. У. Гофурова, А. К. Уринова, А. Меликулова.

За почётные заслуги был достойно награждён. В 1967 году был награждён медалью Кари Ниязи. В 1994 году математическому факультету было дано имя Ж. Х. Каримова.

Б. Х. Каримов

ФИЗИКО-МАТЕМАТИЧЕСКИЕ НАУКИ

АЛГОРИТМ РАЗВИТИЯ УСКОРИТЕЛЬНОЙ ТЕХНИКИ

Алиев Ибратжон Хатамович

Студент 1 курса факультета математики и информатики Ферганского государственного университета
Ферганский государственный Университет, Узбекистан
Каримов Боходир Хошимович
(кандидат физико-математических наук, доцент)
Ферганский государственный университет, Узбекистан

Аннотация. История ускорительной техники берёт своё начало ещё во времена самых первых исследований в области изучения строения вещества, и, хотя вопрос о строении материи был поставлен ещё в глубокой древности, его активное развитие начинается лишь чуть ранее открытия радиоактивности Анри Беккерелем. Самые первые попытки в области увеличения энергии генерируемых частиц были приложены ещё во времена первых трубок Крукса, в которых обеспечивался высокий вакуум, что позволяло обеспечить вылет приличного потока электронов под действием термоэлектронной эмиссии.

Ключевые слова: ускоритель заряженных частиц, МэВ, трубка Крукса, циклотрон, линейный ускоритель.

Abstract: The history of accelerator technology dates back to the time of the very first research in the field of studying the structure of matter, and although the question of the structure of matter was raised in ancient times, its active development begins only a little earlier than the discovery of radioactivity by Henri Becquerel. The very first attempts in the field of increasing the energy of the generated particles were made back in the days of the first Crookes tubes, in which a high vacuum was provided, which made it possible to ensure the departure of a decent flow of electrons under the influence of thermoelectric emission.

Keywords: charged particle accelerator, MeV, Crookes tube, cyclotron, linear accelerator.

Но если исходить из самого начала, то в истории ускорителей можно найти немало выдающихся изобретений, новых и ярких физических идей, в некоторых случаях, имеющих характер научного открытия. Однако развитие методов ускорения заряженных частиц и стремление ко всё большим энергиям никогда не были самоцелью и обязательно подчинялись в основном, логике развития ядерной физики и возникшей из неё физики высоких энергий.

Ранее проводимые исследования и постройки в области ускорительной физики можно изобразить при помощи диаграммы, таким образом в существовании объективных закономерностей развития ускорительной техники просто и наглядно убеждает такая зависимость от времени максимальной энергии, достигнутой в лабораторных условиях. В логарифмическом масштабе эта зависимость отражается прямой линией, на которую с некоторыми оговорками попадают и существующие установки, и проектируемые машины. То есть, энергия искусственно ускоренных элементарных частиц экспоненциально возрастает на порядок каждые семь-восемь лет, что отражает объективную закономерность развития науки и физики высоких энергий. При всей важности новых идей в физике ускорителей нельзя отметить, что заметных изломов на этой прямо их появление не вызвало и не привело к подобному случае, наличия каких-либо явных отклонений.

Вероятно, первые соображения о получении искусственно ускоренных частиц появились вместе с зарождением экспериментальной ядерной физики после исторических опытов Э. Резерфорда в 1919 г., хотя к этому времени уже существовали высоковольтные рентгеновские трубки и установки для получения «канальных лучей», в определённой степени, заслуживающие названия ускорителей. Возможности высоковольтной техники того времени, и энергия альфа-частиц естественных радиоактивных изотопов, с которыми ускорители были призваны конкурировать, определяли и ближайшую цель — получение частиц с энергией порядка нескольких МэВ. Впрочем, были, конечно, ясны и принципиальные преимущества ускорителей — возможность ускорения протонов, иных элементарных частиц, а также направленность и большая интенсивность пучка, эквивалентная десяткам и сотням килограмм естественных радиоактивных препаратов. Интересно, что в 20-е годы было высказано довольно много идей ускорения до большой энергии, опередивших своё время и воплощённых в конкретных установках лишь по прошествии многих лет.

Тем не менее, первая искусственная ядерная реакция — расщепление ядра лития протонами с энергией 700 кэВ — была осуществлена сотрудниками Резерфорда Дж. Кокрофтом и Э. Уотсоном в 1931 году и сразу же повторена в нескольких лабораториях. Эту дату и можно считать началом истории ускорителей.

Установка Кокрофта-Уолтона состояла из двух основных элементов — генератора высокого напряжения и ускорительной трубки. Оба они в техническом отношении претерпели в дальнейшем существенные модификации. Одним из основных этапов в развитии электростатических ускорителей было изобретение в 1929 году Р. Ван-де-Граафом из Пристонского университета в США генератора высокого напряжения с механическим переносом заряда. Повышение энергии в этих машинах сдерживалось в основном электрической прочностью опорных изоляторов и ускорительной трубки, по применение принудительного распределения потенциала позволило вскоре получить энергию 2,5 МэВ. В СССР в 1938 году в Харькове был запущен электростатических ускоритель на 3,6 МэВ. Важно также отметить, что к концу 50-х годов ускорительная трубка серийного электростатического ускорителя выдерживала 16 МВ.

Тем не менее, ограниченные возможности метода электростатического ускорения были очевидны, а развитие физики ядра настоятельно требовало перехода к энергиям порядка десятка МэВ, сравнимой со средней энергией связи нуклона в ядре. Поэтому качественно новым этапов в развитии ускорителей следует считать появление резонансных методов, не требующих высоких напряжений. Первые идеи такого рода были высказаны, как показывают исследования, шведским учёным Изингом в 1924 году, но не привели к созданию работоспособной модели. Линейным вариантом резонансного ускорителя занимался также шведский физик Р. Видерое, внёсший вклад и для разработки бетатрона. В их схемах не было никаких принципиальных недостатков, но увы, лишь отсутствие в конце 20-х годов мощных коротковолновых генераторов не позволило осуществить их на практике. Выше уже упоминалось об обилии появившихся в то время идей, не нашедших технического воплощения. В этой связи следует упомянуть и имя американского инженера Дж. Слепяна, в патентах которого можно найти прообразы некоторых будущих ускорителей, в том числе бетатрона и линейного резонансного ускорителя.

На реальную основу резонансное ускорение было поставлено в работах Э. Лоуренса, проводившихся в лаборатории Калифорнийского университета в Беркли. Практически одновременно в 1930—1932 гг. в этой лаборатории появились работающие модели циклотрона — первого циклического ускорителя, в создании которого важную роль сыграл М. Ливингстон, и линейного резонансного ускорителя с трубками дрейфа (Д. Слоан). Однако линейные системы вскоре отошли на второй план из-за недостаточного развития техники СВЧ по сравнению с циклотроном, который уже начал поистине своё большое триумфальное шествие.

Библиографический список

1. М. П. Бронштейн. Атомы. Электроны. Ядра. Изд-во Онти. 1935

2. В. А. Буравин, В. А. Егоров. Биография электрона. Изд-во Знание. 1985

3. Н. Ш. Турдиев, Д. Турдиева. Физика. Справочник для школьников и абитуриентов. Изд-во NisoPoligraph. 2015.

4. М. П. Бронштейн. Атомы и электроны. Изд-во Наука. 1980.

5. М. И. Каганов. Электроны. Фононы. Магноны. Изд-во Наука. 1979.

6. В. И. Рыдник. Увидеть невидимое. Изд-во Атомиздат. 1981.

АНТИМАТЕРИЯ В ЭНЕРГЕТИКЕ

Каримов Боходир Хошимович

Кандидат физико-математических наук, доцент физико-технического факультета Ферганского государственного университета
Ферганский государственный Университет, Узбекистан
E-mail: b_karimov@mail.ru
Алиев Ибратжон Хатамович
Студент 1 курса факультета математики и информатики Ферганского государственного университета
Ферганский государственный Университет, Узбекистан

E-mail: ibratjon25@mail.ru

Аннотация. Представлена часть исследования в области физики антиматерии, методов столкновения и дальнейшего выделения энергии столкновения. В частности, электронов и позитронов на малых энергиях порядка нескольких сотен кэВ. В расчётах применены и использованы уравнения Дирака, формулы из релятивистской физики. В результате, приведена конструкция ускорителя элементарных частиц, основанная на ускорении пучков электронов и позитронов, при этом ускорения осуществляется на нескольких направлениях. При этом ускоритель оснащен некоторыми дополнительными элементами, с целью получения энергии, в которую преобразовывается масса электронов и позитронов. Целью работы являлось разработка схемы конструкции, которая смогла бы позволить выводить энергию из массы элементарных частиц, без больших затрат, а также с последующим ростом иных показателей.

Ключевые слова: позитрон, антиматерия, электрон, столкновение, море Дирака, уравнение Дирака, волновод, ВЧ технология.

Abstract: Research was present in the field of antimatter physics, collision methods, and further extraction of the energy of the collision. In particular, electrons and positrons at low energies of the order of several hundred Kev. Dirac equations and formulas from relativistic physics used in the calculations. As a result, the design of an elementary particle accelerator based on the acceleration of electron and positron beams, while acceleration carried out in several directions. In this case, the accelerator is equipped with some additional elements, in order to obtain energy, which will turn the mass of electrons and positrons. The aim of the work was to develop a design scheme that could allow energy extracted from the mass of elementary particles, without high costs, as well as with a subsequent increase in the indicator.

Keywords: positron, antimatter, electron, collision, Dirac Sea, Dirac equation, waveguide, RF technology.

Введение

Альберт Эйнштейн был одним из величайших учёных, который задался вопросом превращения материи в энергию и энергии в материю. Данная идея появилась впервые в работе О. Хевисайда 1889 года. Именно тогда появилась формула E=mc2. Сегодня существует несколько практических доказательств данной формулы. В том числе термоядерные реакции, горение метана, реакция деления ядер урана. Но самая эффективная технология на сегодняшний день, доказывающая эту формулу — теория антивещества.

1. Формулы Дирака

Впервые теория антивещества появляется с решением уравнения для беспризорного классического поля электрона. И решение выглядело следующим образом:

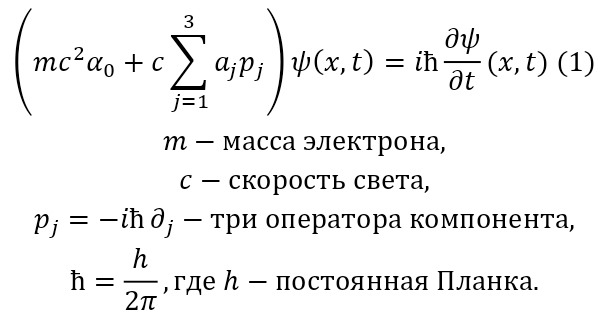
Исследуя выводы из этой формулы, можно прийти к выводу, что она доказывает тот факт, что электрон обладает собственным спином, равным ħ/2. А также магнитным моментом (eħ/2mc). Одним из решений данной формулы было то, что эта формула подходит также и для такой же частицы, как и электрон, но с противоположным зарядом. Так впервые было сделано предположение о существовании частицы, которая в дальнейшем была названа позитроном.

Позитрон был открыт в 1932 году Карлом Андерсоном при наблюдении в камере Вильсона космических излучений. При этом было замечено, что одна из частиц отклоняется при прохождении через электрическое поле в другую сторону, в отличии от электрона.

Позже было открыто такое явление как аннигиляция. Было доказано, что при столкновении обычной частицы с античастицей, они изменяют своё состояние и превращаются в гамма-излучение с КПД в 100%. При этом энергия, выходящая при столкновении электрона и позитрона равна 2mec2, что в численном эквиваленте равняется 1,022 МэВ.

2. Общие теоретические выводы

В результате можно сказать, что теоретически факт того, что возможно получить большое количество энергии при столкновении элементарных частиц подтверждён при помощи точно представленных ныне расчётов. Теперь необходимо рассмотрение ускорительной характеристики.

То есть какая энергия и как именно должна быть приложена для дальнейшего достижения со стороны электронов необходимой скорости и энергий. Кроме того, стоит указать, что в данном случае все явления производятся в вакууме порядка 10-5-10-6 мм. рт. ст.

Именно благодаря этому для электрона обеспечивается полная свобода. Но для поддержание такого давления нет необходимости в постоянном использовании вакуумной установки, вполне достаточен процесс изначального удаления кислорода в максимальном размере и закрытие всевозможных щелей.

Подводя итоги к теоретической части, можно свободно быть уверенными в верности данной технологии.

Заключение

В заключение стоит отметить, что на сегодняшний день активно ведутся исследования, и работа над проектом «Электрон» продолжается. Планируется создание Электронной Электростанции (ЭЭС). Но стоит отметить, что было открыто новое явление, которое смогло найти своё применение, объяснение и принести пользу, не только в экономическом характере, но и расширив знания в данной области.

Также данный проект смог создать огромное количество дочерних проектов. И благодаря ему, стало возможно проведение многочисленных новых исследований в области квантовой физики, физики элементарных частиц, а также других областях науки и техники.

Использованная литература

1. Рыдник В. И. Увидеть невидимое. Москва: Атомиздат, 1985.

2. Бронштейн М. П. Атомы и электроны. Москва: Квант, 1980.

3. Каганов М. И. Электроны. Фононы. Магноны. Москва: Наука, 1979.

4. Буравихин В. А., Егоров В. А. Биография электрона. Москва: Знание, 1985.

5. Матвеев А. Н. Атомная физика. Москва: Знание, 1989.

6. Лебедев А. Н., Шальнов А. В. Основы физики и техники ускорителей. Т. 1. Москва: Атомиздат, 1981.

7. Лебедев А. Н., Шальнов А. В. Основы физики и техники ускорителей. Т. 3. Москва: Атомиздат, 1981.

8. Бурштейн Э. П., Воскресенский Г. В. Линейные ускорители электронов с интенсивными пучками. Москва: Наука, 1970.

9. Вальднер О. А., Власов А. Д., Шальнов А. В. Линейные ускорители. Москва: Наука, 1969.

10. Каганов М. И. Микро и макро. Москва: Знание, 1986.

11. Каганов М. И., Цукерник В. М. Природа магнетизма. Москва: Наука, 1982.

12. Комар Е. Г. Основы ускорительной техники. Москва: Наука, 1975

13. И. В. Баргатин, Б. А. Гришанин, В. Н. Задков. Запутанные квантовые состояния атомных систем. Москва: Наука, 2001.

14. Алиев И. Х. Электрон и его особенности. Точная наука. 2019. №63. С. 37—40

15. А. С. Алимов, Б. С. Ишханов, В. И. Шведунов. Компактный линейный ускоритель электронов для радиационных технологий. Вестник Московского Государственного Университета. С. 3. Физика. Астрономия. 2008. №4. С. 28—30.

16. Алиев И. Х. Электрон и его особенности. Точная наука. 2019. №71. С. 2—5.

17. А. А. Воробьёв. Ускорители. Известия томского ордена трудового красного знамени политехнического института им. С. М. Кирова. Т. 156. 1969. С. 3—16.

18. Алиев И. Х., Каримов Б. Х. Энергия столкновения встречных пучков. Молодой учёный. 2020. №16. С. 7—10

19. Босамыкин В. С. Линейный индукционный ускоритель. Патент 242287 SU. Опубл. 1970.03.17, H05H 9/00 Бюл. №1

20. Бомко В. А. Линейный ускоритель заряжённых частиц. Патент 334931 SU. Опубл. 1972.10.09, H05H 11/00 Бюл. №1/

КВАНТОВО-ЗАПУТАННЫЕ ЧАСТИЦЫ

Кулдашев Аббосхон Хакимович

Доктор технических наук, доцент института полупроводников и микроэлектроники при Национальном Университете Узбекистана

Институт полупроводников и микроэлектроники при Национальном Университете Узбекистана, Узбекистан

Аннотация: Запутанные частицы являются одними из самых удивительных частиц, которые известны науке. С их помощью можно совершать невероятные операции. Именно они завели в заблуждение великого Альберта Эйнштейна. Но сегодня наука смогла разгадать тайну этих частиц и именно сегодня при помощи науки, человечество познало тайну этих невероятных частиц!

Ключевые слова: запутанные частицы, пространство-время, скорость, время.

Abstract: The tangled particles are one of the most amazing particles which known science. With their help possible to make the incredible operations. Exactly they have wound in error great Albert Einstein. However, today science has been able to solve the secret of these particles and exactly today at sciences humankind has to know the secret these incredible particles.

Keywords: tangled particles, the space-time, velocity, time.

Изначально рассмотрим самых обычных представителей запутанных частиц — запутанные фотоны. Эти частицы получаются при прохождении через нелинейный кристалл лазерного луча. В результате получаются два запутанных фотона и один лазерный луч.

Они считаются запутанными, поскольку, когда изменяется спин одного фотона, мгновенно меняется спин второго фотона. Спин — это направление вращения частицы. Все частицы вращаются вокруг самих себя с огромной скоростью, и у каждой частицы направление вращения разное, но его можно определить или изменить.

И если определить спин одного фотона, и он будет направлен, к примеру, направо, то второй будет направлен налево. Это экспериментально подтверждённый факт. Но самое странное то, что информация передаётся мгновенно, то есть со скоростью больше чем скорость света. Как объяснить это явление?

Есть умозаключения, по которым, именно этот факт может отменить всю теорию относительности. Но это не так. Даже не отменяя теорию относительности, возможно, объяснить это явление.

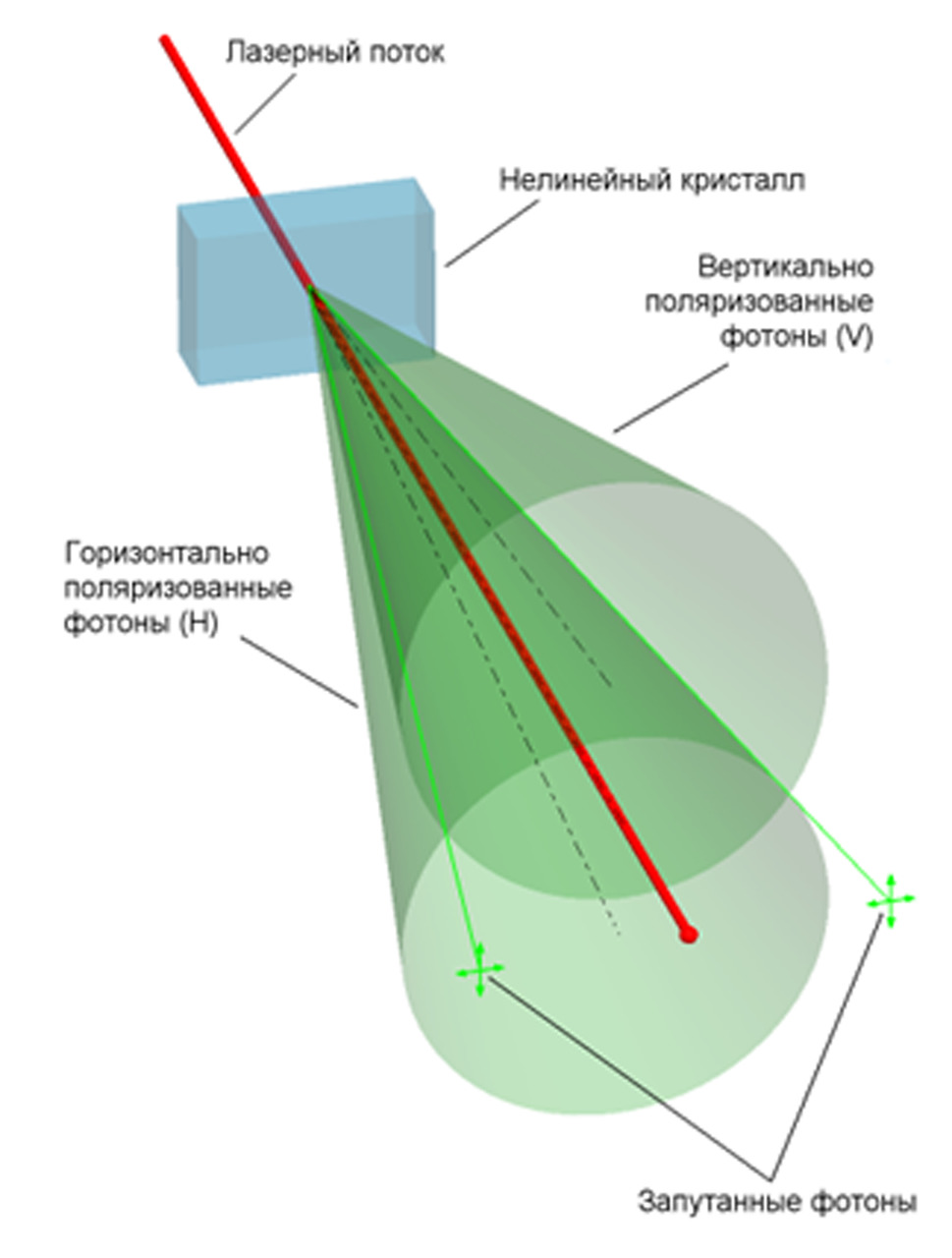
Рис. 1. Схема получения запутанных фотонов

Всё дело в том, что всё координаты частиц в нашем мире предусмотрены заранее. И все эти координаты изображены на полотне времени. Как известно, пространство-время — это некая субстанция или координатное пространство, внутри которой расположен весь космос.

На каждой «У» располагается лист времени и с каждым мгновением он обновляется. И это обновление происходит со скоростью большей, чем скорость света — бесконечной скоростью. И в результате создаётся новый временной мир, где ограничений на скорость просто нет, поэтому скорость времени бесконечно.

А как было отмечено выше, запутанные фотоны появляются в одном и том же месте, то есть отмечаются как одни координаты, а потом расходятся. Это доказывает, что информацию запутанный фотон передаёт второму запутанному фотону через это временное измерение. На листах времени после рождения запутанных фотонов появляются некие порталы. А для изменения или обнаружения спина частицы необходимо применить энергию и эта энергия через портал переходит ко второму порталу и меняет спин второго фотона.

Эта ситуация очень похожа на спектакль, где на виду фокусник говорит в трубу, а из дальнего угла слышится звон, просто проводящая линия расположена за занавесью.

При помощи этой конструкции создаются самые великолепные квантовые компьютеры. Эти компьютеры передают информацию с бесконечной скоростью и в них отсутствуют какие-либо провода. Но используются там не запутанные фотоны, а запутанные электроны, ещё один вид запутанных частиц.

Также с помощью этих частиц можно осуществлять мгновенные перемещения в пространстве, но пока эти перемещения ведутся с помощью частиц и перемещают только их. Поэтому перемещение с человеком пока невозможно, но стоит надеяться, что вскоре станет возможно и перемещение человека…

Библиографический список

1. В. А. Буравихин, В. А. Егоров. Биография электрона. Знание. 1985.

2. Д. тер Хаар. Основы гамильтоновой механики. Наука. 1974.

3. В. А. Балаш. Задачи по физике и методы их решения. Просвещение. 1974.

ПОДРОБНЫЙ АНАЛИЗ ПРОТОН-БОРОВОЙ РЕАКЦИИ С ВЫДЕЛЕНИЕМ ТРЁХ АЛЬФА-ЧАСТИЦ

Руми Ринад Фуадович
Старший научный сотрудник лаборатории ускорительной техники при институте полупроводников и микроэлектроники при Национальном Университете Узбекистана

Лаборатория ускорительной техники при институте полупроводников и микроэлектроники при Национальном Университете Узбекистана, Узбекистан

Аннотация. Рассмотрены теоретические основы ядерная реакция и получения энергии из её осуществления с высокой эффективностью при генерации из выделяемых при этом 3 альфа-частиц. При этом важно указание использование для реализации самой реакции резонансного ускорителя частиц типа ЛЦУ-ЭПД-20.

Ключевые слова: ускоритель, ядерная реакция, энергия, элементарные частицы.

Annotation. The theoretical foundations of a nuclear reaction and obtaining energy from its implementation with high efficiency when generating 3 alpha particles released at the same time are considered. At the same time, it is important to specify the use of a resonant particle accelerator of the LCU-EPD-20 type for the implementation of the reaction itself.

Keywords: accelerator, nuclear reaction, energy, elementary particles.

Первая ядерная реакция представляется следующим образом (2.1).

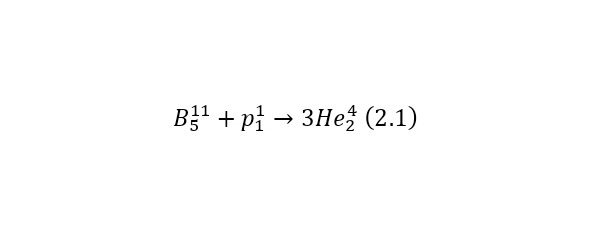
Протон с энергией в 2,312691131 МэВ и массой в 1,00728 а. е. м., налетает на бор-11 с атомной массой в 11,00930517 а. е. м., с выделением трёх альфа-частицы массы, которых составляют 4,001506179 а. е. м.

Изначально, необходимо определить, какое количество энергии затратит протон, приближаясь к ядру бора-11, а именно высоту кулоновского барьера (2.3), определив радиус ядра бора-11 в (2.2).

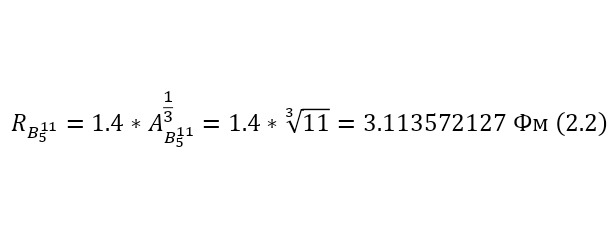
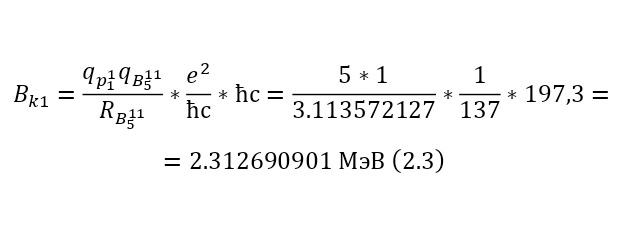
Следовательно, нынешняя энергия протона, после затраты на кулоновский барьер, составляет 0,23 эВ. Важно заметить, что сама кинетическая энергия частицы подобрана так, чтобы после её прохода энергия оставалась минимальной, что привело бы к увеличению вероятности взаимодействия в самой ядерной реакции. Теперь, необходимо вычислить энергетический выход данной ядерной реакции, с указанными массами в (2.4).

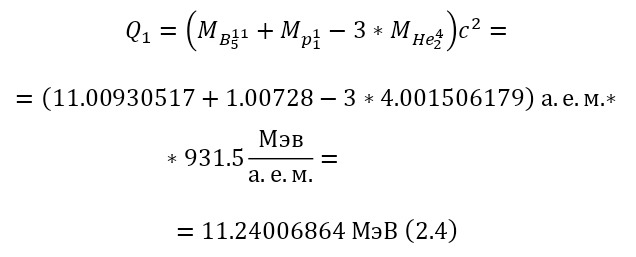
Поскольку эта реакция экзо-энергетическая, то нет смысла вычислять для неё порог реакции, остаётся лишь записать пару энергетических уравнений (2.5—2.6) и затем вычислить энергии, приобретаемые альфа-частицами.

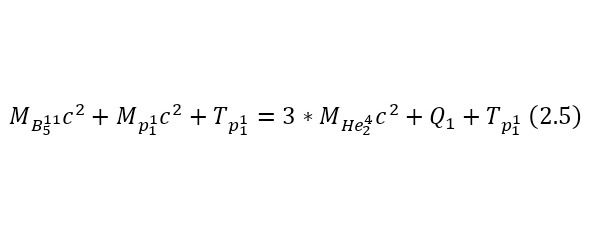
Из этих энергетических уравнений стало ясно, что кроме выхода реакции, добавляется и оставшаяся кинетическая энергия, благодаря чему общая энергия, распределяемая между частицами, составляет 11,24006887 МэВ из равенства (2.7). Теперь, для распределения этих энергий достаточно воспользоваться (2.8), в этом случае, хоть и рассматривается выход уже 3 частиц, они имеют один тип, по этой причине, энергия для них распределяется равномерно, как и импульс.

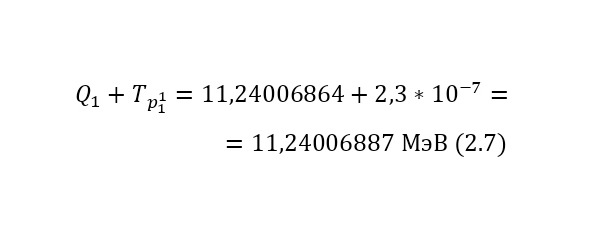
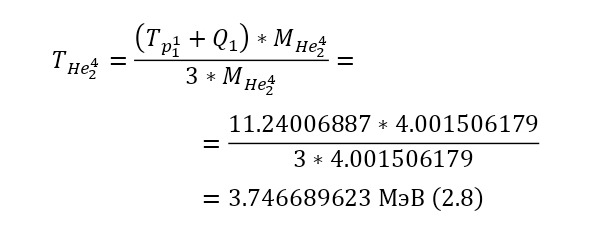
И наконец, остаётся определить сечение ядерной реакции и число взаимодействий. Изначально, необходимо вычислить длину волны налетающих протонов, для этого достаточно определить их импульс через (2.10), перед этим вычислив скорость в (2.9), а затем уже длину волны в (2.11).

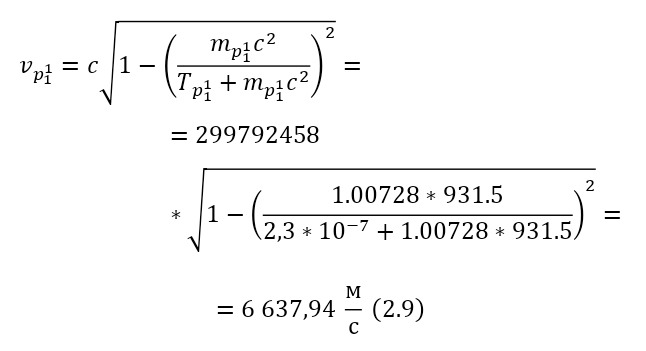
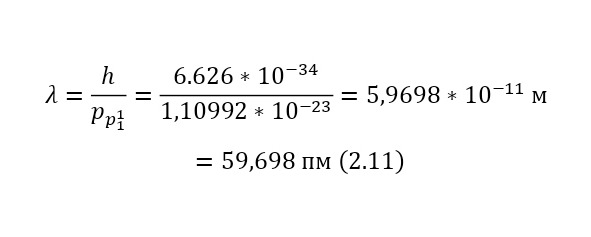
Переходя уже к исчислению сечений, достаточно воспользоваться (2.12), но также необходимо использование коэффициента, о котором говорилось ранее, по этой причине применяется и (2.13), и только после вычисляется истинное сечение (2.14), для некоторых подсчётов, этот коэффициент становится равным единице, поэтому просто не указывается, но в данном случае, если подсчитать таким же образом.

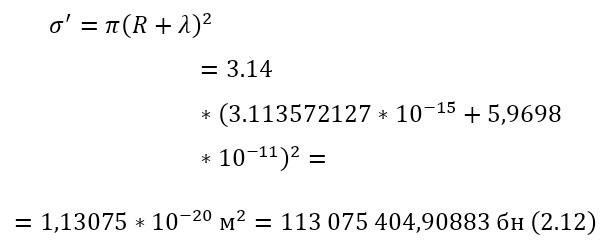
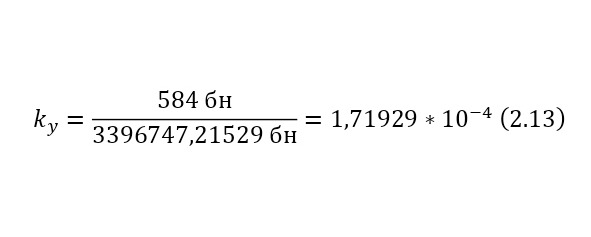
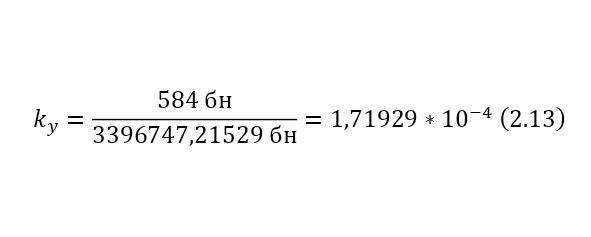
Максимально возможное сечение составляет 20 кбн, в данном же случае меньшее сечение благодаря подобранной энергии в циклотроне. Теперь, когда сечение известно, для этой реакции, остаётся ввести число взаимодействий (2.18), перед этим вычислим число атомов на кубометр (2.15) и указав толщину пластины в 13 мкм, поскольку пробег протона (максимальное расстояние, на котором может пройти при определённой энергии) с энергией 1 МэВ составляет это значение.

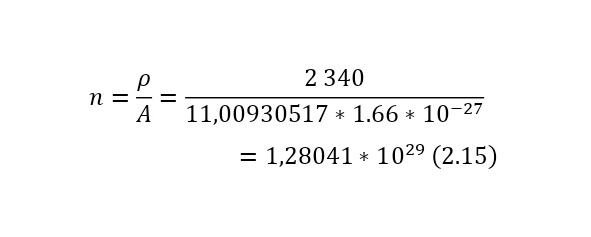
А также необходимо определить в (2.16) начальное число бомбардирующих протонов, указав, что их общая сила тока 100 А, а время одного акта, который вытекает уже из параметров циклотрона, описываемый в предыдущих главах составляет 164,065 нс, что гораздо больше времени даже самой долгой реакции, откуда можно вычислить заряд, а из него уже и число протонов (2.17).

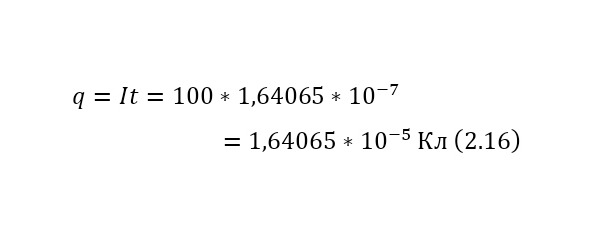
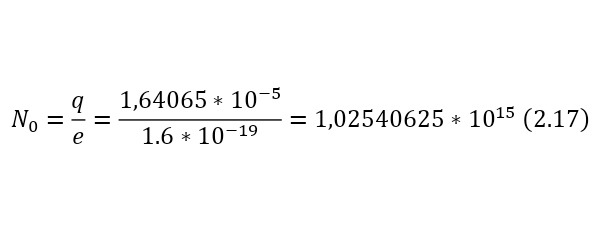
Это число всех частиц, прошедших сквозь пластину и не вошедших в реакцию, а для того, чтобы вычислить те, которые вошли в реакцию, достаточно определить разность в (2.19), а затем уже вычислить из них заряд, с учётом того, что выходит именно 3 альфа-частицы, следовательно, выходящий заряд в 3 раза превышает один выходящий заряд, вместе с этим учитывая, что каждая альфа-частицы несёт в себе по 2 элементарных заряда, то заряд увеличивается ещё в 2 раза (2.20) и силу тока (2.21).

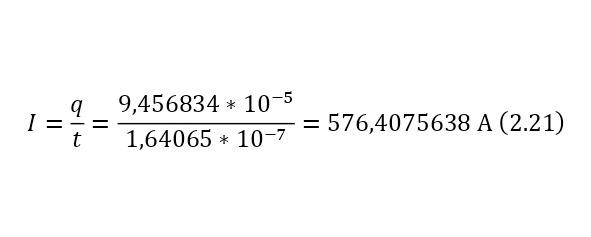
Говоря же о силе тока, выводимой в данном соотношении, важно отметить, что здесь учитывается именно циклотронное время, без участия времени линейного ускорителя или инжектора, из-за чего может наблюдаться изменение или погрешности при реальном детектировании силы тока, но поскольку конечная энергия вычисляется не из силы тока, а из выходящего заряда, то в вычислениях энергий, никаких погрешностей не наблюдается и данное указание действует как для этой, так и для всех в последующем описанных шести ядерных реакциях.

И наконец, для полноты картины остаётся лишь определить выходящее кулоновское отталкивание, определив радиус альфа-частиц, поскольку они будут отталкиваться друг от друга, в (2.22), а уже в (2.23) и сам барьер.

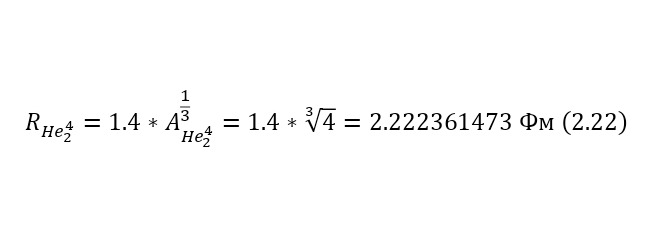
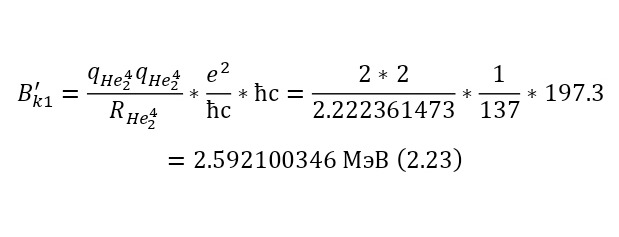
Следовательно, вылетающая альфа-частица также приобретёт дополнительную энергию, и конечная энергия будет составлять 6.338789969 МэВ.

Итак, можно подвести итог, что в данной реакции, с анализом иных каналов будут образовываться протоны с энергией 2,312691131 МэВ и током 100 А, в ионизаторе и циклотроне за 164,065 нс, а затем они будут бомбардировать тонкую пластину бора-11, откуда будут вылетать альфа-частицы с током 576,4075638 А и энергиями 3,746689623 МэВ, а после выходящего кулоновского барьера с энергиями в 6,338789969 МэВ, также будут образовываться атомы углерода-12, благодаря которым температура пластины будет изменяться на 3,214 К.

Вылетевшие альфа-частицы будут направляться в генератор, который устроен либо по принципу МГД-генератора, либо он будет создавать магнитное поле, где альфа-частицы будут двигаться по винтовому пути, образуя некоторую индукцию, благодаря тому, что они имеют заряд.

А изменяя число витков можно изменять поток вектора магнитной индукции, образующуюся в этом движении, в результате этого изменения потока, его можно преобразовать в электричество, получая ЭДС индукции на внешней катушке.

В обоих случаях результат не изменится и выполняемая в данном случае работа за акт составит 599,4486355 Дж, а за секунду уже 3,653726484*109 Дж, а если перевести это значение в Вт*ч, то это получается 1 014 924,023 Вт*ч, что является довольно приличным указанием, момент с потребление для циклотрона определяется как 55,56389 кВт*ч, но более точные показатели рассчитываются в последующих исследованиях.

Библиографический список

1. Р. А. Сюняев. Физика космоса. Маленькая энциклопедия. Советсткая энциклопедия. Изд-во Наука. 1986.

2. Дж. Фейенберг. Из чего сделан мир? Атомы, Лептоны, Кварки и другие загадочные частицы. Изд-во Мир. 1981.

3. В. Голощапов. Физика космоса. Элементарные частицы материи. Супер. 2016.

4. В. А. Фок. Квантовая физика и строение материи. Изд-во URSS. 2009.

5. Дж. Глимм, А. Джаффе. Математические методы квантовой физики. Изд-во Наука. 2017.

6. И. В. Баргатин, Б. а. Гришанин, В. Н. Задков. Запутанные квантовые состояния атомных систем. Редакция им. Ломоносова. 2001.

7. Г. Кейн. Современная физика элементарных частиц. Изд-во Мир. 1990.

ВЛИЯНИЕ РАЗЛИЧНЫХ ЯВЛЕНИЙ ПРИ ПРОХОЖДЕНИИ ЧЕРЕЗ СРЕДУ УЛЬТРАЗВУКОВОЙ ВОЛНЫ

Кучкоров Ахлиддин Мирзохидович

Преподаватель физико-технического факультета Ферганского государственного университета

Ферганский Государственный Университет, Узбекистан

Аннотация. Изучение различного вида волн и колебаний всегда представляло большой интерес в науке и технике, приводя к самым различным изобретениям и открытиям, начиная от слабых звуковых волн, с огромными длинами волн, завершая самыми различными электромагнитными волнами, именуемыми ионизирующим излучением. Важным на сегодняшний день является изучение волн, находящихся в частоте между звуковыми и световыми диапазонами, когда уже частота колебаний заставляет излучать различные кванты энергии.

Ключевые слова: ультразвук, частота колебаний, длина волны, физико-математические характеристики.

Annotation. The study of various types of waves and vibrations has always been of great interest in science and technology, leading to a variety of inventions and discoveries, ranging from weak sound waves with huge wavelengths, ending with a variety of electromagnetic waves, called ionizing radiation. It is important today to study the waves that are in the frequency between the sound and light ranges, when the frequency of vibrations already causes various quanta of energy to emit.

Keywords: ultrasound, oscillation frequency, wavelength, physical and mathematical characteristics.

1. Введение

Сам по себе ультразвук является видом звука, то есть явления распространения механических колебаний в твёрдой, жидкой и газообразной среде. Ультразвук также обладает своей частотой и амплитудой, как и любая иная волна, где амплитуда характеризует громкость звука, а частота его тон или высоту. Если обратить внимание на распределение этого вида колебаний по их частотам, но можно отметить инфразвук — то есть звук, с частотой от 0 до 16 Гц, то есть до частоты слышимости человека. После него идёт слышимый звук, ощущаемых ушами человека, находящегося в диапазоне от 16—20 Гц до 15—20 кГц. Все частоты до 1 ГГц считаются ультразвуком, а от 1 ГГц гиперзвуком.

Указанные частоты являются частотами колебания молекул с постоянными скоростями, зависящими от параметров самой среды и определяемые по формуле (1).

Когда же частота и длина волны звука имеют иную зависимость (2).

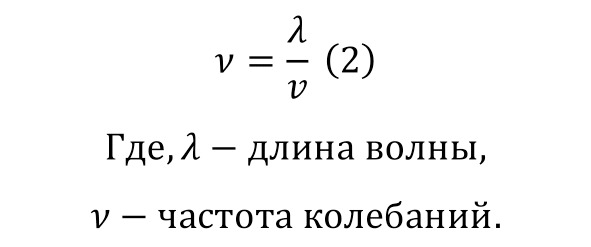
По этой закономерности и можно определить необходимые параметры для определённого вида колебаний, а именно звуковых и анализировать явления с ними.

2. Влажность среды

Перед дальнейшим описанием многих явлений, важно остановится на некоторых изменениях параметров самой среды и анализ эффекта этих изменений на исследуемый объект. И одним из подобных факторов является влажность. Сама по себе — влажность в воздушной среде представляет собой наличие воды (влаги) в воздушном пространстве. То есть при переходе в подобной среде ультразвука, важно указать на частое изменение среды, то есть колеблются в один момент молекулы кислорода, в иной же момент — молекулы самой воды.

Если же вспомнить более точно, то скорость звука в воздухе составляет 331 м/с, когда же в воде 1483 м/с, где видна существенная разница, по этой причине сама концентрация влаги, то есть показатель влажности самой среды и демонстрирует, насколько ускоряется ультразвук в данной среде с определённой влажностью. Если же имеется ввиду концентрация не только влаги, но и иных газов или других объектов в среде, то достаточно рассмотреть переход скоростей самого звука, и средняя скорость колебаний в такой среде определяется по (3) для общего и процентного соотношения (3*).

Бесплатный фрагмент закончился.

Купите книгу, чтобы продолжить чтение.