Бесплатный фрагмент - Властелин механики

Пару слов об этой книге

Так уж сложилось, что почти все книги по физике скучны и совершенно не предназначены для легкого чтения. Даже если человек искренне интересуется вопросом, но не имеет некоторого багажа знаний, то открывает физическую теорию, описываемую в любой обычной книге, и плачет горькими слезами.

Материалы обычно изложены таким образом, что разобраться во всем под силу только прирожденному технарю, ну или тому, кто уже «собаку съел» на этом деле. Почитать подобную книжечку перед сном для общего развития не получится. Нужно будет тратить силы на вникание в материал и его осмысление. Есть и ещё одно обстоятельство — читать такую литературу обычно совсем не интересно. Она не увлекает, а голая формулировка физических законов без примеров из жизни кажется набором бессмыслицы.

Очевидно, что сказывается и сама специфика сложного предмета. Физика пронизывает весь наш мир во всех его проявлениях. Это отражается на формулировках и на стиле изложения теории. Такая наука по определению не может быть простой, так как описывает столь многогранный мир!

Однако, теоретическую информацию вполне можно сформулировать в более простой и приятной для читателя форме. Технические дисциплины на самом деле очень интересны! Нужно только найти эту «скрытую от большинства красоту». После этого вы сможете воспринимать физику как интересную науку об окружающей нас природе, а не набор букв и сложных формул.

Между прочим, в древней Индии некоторые знания специально излагались в очень сложной форме, чтобы понять их могли только избранные читатели, обладающие специальной подготовкой. Использовались различные образы или метафоры, известные только избранным. Всё потому, что знания являлись великим сокровищем, которое можно сделать доступным только для ограниченного числа мудрецов. Другие же могут использовать знания во вред и себе, и обществу. Эта тенденция пронизывает все древние времена.

Сегодня информация стала намного доступнее. Однако, витиеватое изложение не позволяет многим окунуться в этот интересный мир с головой.

Меня зовут Юрий Трифонов. Я ученый, преподаватель и любитель делать различные механизмы своими руками. Руковожу проектом «Инженерные знания», целью которого является популяризация науки.

Предлагаю вам вместе с этой книгой углубиться в изучение семи самых значимых законов окружающего мира и увидеть собственными глазами, что на самом деле всё это очень интересно и просто.

Постараемся изложить всё в легко читаемой и понятной форме. Очень надеюсь, что мои труды не пройдут напрасно, а читатель в итоге полюбит физику и заинтересуется наукой как методом познания окружающего мира.

Начнем с основных законов механики. Их будет семь. Почему семь? Просто мне нравится это число и оно регулярно «преследует» меня повсюду. Кроме того, цифра семь для многих культур являлась особенной. Это число Осириса, которому приписывалась особая сила. Понятно, что странно слышать от технаря такие изречения. Ведь они на границе с эзотерикой. Однако, узость мышления — ещё одна проблема, с которой мне хотелось бы бороться. Отрицать что-то без глубинного понимания проблемы неправильно и этим страдает вся наша наука.

Смею предположить, что правильное понимание изложенного материала сделает из вас настоящих властелинов механики. Законы в книге выбраны не случайно. Они являются базой для понимания множества процессов вокруг нас и всей дальнейшей физической теории. Конечно же, закономерностей в природе намного больше, чем семь. Но начнем с этих, а если вам будет интересно, то продолжим разбирать физику в такой форме.

Сейчас физика видится вам как нечто оторванное от жизни и совершенно бесполезное. Настало время изменить это!

П. с. Написание книги и работа над проектом — это сложный труд. Я постараюсь сделать экземпляры книги максимально доступными для всех. Пожалуйста, не растаскивайте книгу по интернету без её оплаты или хотя бы оставляйте ссылки на мой проект «Инженерные знания»!

Научно-популярный образовательный проект «Инженерные знания» представлен на всех современных платформах и ориентирован на то, чтобы сделать инженерную науку интересной для всех и поднять уровень образованности.

Ссылка на проект «Инженерные знания»

Введение

Мы живем в очень интересном мире, который ещё полностью не изучен. Стоит копнуть чуть глубже, и становится понятно, что ответы на вопросы «Что такое масса» или «Что такое электричество» наука не может дать до сих пор.

На каждый счёт есть множество гипотез и множество споров об их состоятельности. Но однозначных ответов, подкреплённых реальными экспериментами, так и нет. Если есть подтверждение, то часто находится некоторое обстоятельство, которое ставит всю логику под большой вопрос.

Во многих ситуациях возможно только лишь нащупать закономерности, сформулировать их и попытаться объяснить. В некоторых отраслях всё гораздо проще. Закономерности сами лежат на поверхности. Остается зафиксировать это и, как это называется, навести систематику.

К этой сфере относится механика. Там всё просто и линейно, а глубинные ответы на вопросы «почему» не так сложны. Остается, по сути дела, правильно описать окружающий мир.

Механика — это наука об искусстве строить машины. Она линейная и понятная. Применительно к физике это слово используется для обозначения целого раздела, который изучает большую часть взаимодействий между материальными телами.

Интересно отметить, что обнаруженные в этом разделе закономерности работают во всей физике. Скажем, ускорение существует не только относительно велосипедиста, который летит с горы, но и применительно к частицам, из которого состоит тело или электронам.

Мы рассмотрим семь значимых законов механики, которые следует знать и понимать каждому современному образованному человеку. Без них не обходится ни одно взаимодействие в нашей жизни. Будь-то покраска стен в вашем доме или копка колодца. Я очень надеюсь, что в результате прочтения и изучения материала вы и сами сможете всё это увидеть и заинтересоваться вопросом.

Почему это интересно и важно

Физика изучает окружающий мир и, являясь по своей сути, наукой о природе, пытается не просто зафиксировать какое-либо явление, но и выявить однозначные закономерности. Она редко кажется интересной. Увы, но среди всех предметов, она становится иногда чуть ли не самым нелюбимым, хотя на деле и является фундаментальным. Эта участь распространяется и на механику, о которой мы говорим в этой книге.

Виной всему своеобразный подход к преподаванию этой великолепной дисциплины. Никто даже и не подозревает, что речь в физической теории идёт о природе вокруг нас. Просто набор буковок, циферок и неясных изречений.

Ну а когда изучается закон рычага в школе, ребята не представляют, что использование этого нехитрого правила может в дальнейшем помочь открутить прикипевшую гайку на колесе, накинув трубу на ключ. Согласитесь, такой подход сделает жизнь куда более насыщенной, интересной и простой.

Начиная с первых уроков в школе и заканчивая экзаменами в университете, изучение предмета превращается только в повинность.

Вместо того, чтобы показать, как законы механики помогают нам и для чего это полезно изучать, школьников или студентов заставляют штудировать формулы и решать задачки. От такого подхода предмет кажется скучным и неимоверно сложным. Это впечатление закрепляется на долгие годы и «отстрелявшись» человек навсегда забывает физику.

На самом же деле, большая часть взаимодействий вокруг нас становится более приятным, когда оно осознано. Когда-то первобытные люди боялись грозу и не знали, что можно ожидать от такого явления. Каждый удар грома вызывал панику и непонимание. Наша же задача разобраться во всем происходящем вокруг и улучшить себе жизнь пониманием природы. В этом и заключается задача властелина механики! Зная закономерности использовать их себе во благо.

Кстати, винить одних только преподавателей неправильно. Большая часть учеников действительно интересуются только жизнью «звёзд» с экрана. Но правильный подход позволит увеличить количество людей, которым будет приятно разбираться в окружающем мире. Есть ещё и всяческие стандарты на образование, которые на корню ломают интересность. Но рассуждать и жаловаться неправильно.

Давайте всё-таки переходить к изучению нашего предмета с правильным настроем и отличающимся от большинства подходом. Начнем с самого важного.

Про векторные и скалярные величины

В книге мы постоянно будем встречать такое понятие, как векторная величина. Уж так устроена механика, что всё там держится на векторах. Поскольку мы исходим из того, что основные знания об этой штуке у вас уже всё же имеются, то и не расписываем подробно действия над векторами, да и само определение вектора не приводим.

Однако, мы же хотели сделать из сложных теорий увлекательное и интересное чтение, поэтому если вы по какой-то причине не знакомы с понятиями о векторах, то сейчас мы внесем некоторую ясность, достаточную для понимания изложенного ниже материала.

Из школьного курса, или даже уже из институтского, многие запомнили, что «каждому ректору в кое-куда по вектору!». Отсюда легко сделать вывод, что вектор должен хорошо втыкаться. Хорошо втыкается у нас что-то типа стрелы или копья. Вот и вектор представляет собой что-то типа стрелы или копья.

В физике вектор — это направленный отрезок прямой. Он обладает некоторой длиной, как и любой другой отрезок. Длина равна величине вектора.

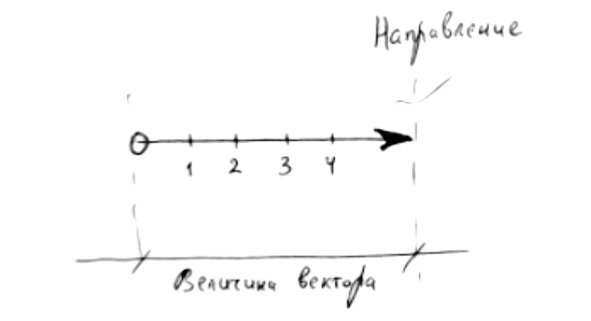
Если возникают проблемы с пониманием этого момента, то просто представьте, что отрезок, длиной 10 см, состоит из 10 отрезков по 1 см. Любую величину можно записать таким образом. Скажем, 15 яблок можно нарисовать в виде прямой, равной 15 см, предположив, что 1 яблоко = 1 см. Это скалярная величина.

Но, по сравнению с обычным отрезком или скалярной величиной, имеющей только длину, вектор имеет ещё и направление.

Представить себе «направление величины» не всегда просто. Для упрощения всегда говорят о движении или воздействии на другое тело. Например, мы можем осознанно толкнуть человека в одном из направлений. Направление, куда мы его толкнули и будет направлением вектора. Сила, с которой толкнули — будет величиной вектора.

Вот и получается, что сила толчка (боже, как звучит!) будет определяться величиной (или модулем) и направлением.

Это направление рисуется стрелочкой, а сила — отмечается в масштабе на длине вектора. Собственно, большего знать про вектора пока и не нужно.

Для окончательного закрепления проведите аналогию в голове между количеством яблок, отмеченным на отрезке (скалярная величина), которое никуда не направлено и вектором, описывающим направление действия удара (векторная величина).

Разве что, нужно помнить — вектора можно складывать, вычитать, умножать и производить с ними самые разные математические действия.

О ценности механики в нашей жизни

Механика — это наука о движении материальных тел и взаимодействиях между ними. Ощущаете ли вы, какой потенциал скрывается за этими относительно простыми словами? Одна эта формулировка описывает, без преувеличения, всю нашу жизнь! Материальные тела всё, что есть, вокруг нас. Движение и взаимодействие таких тел — неотъемлемая часть жизни. Поднять машину домкратом с целью замены колеса тоже механика. И проколовшееся колесо — тоже законы механики. Законы механики — это работа подъемного крана и даже хождение по асфальту без проскальзывания.

Именно механика является наиболее хорошо изученным разделом физики. Его гораздо легче исследовать, потому что всегда можно создать прототип или рабочую модель, а на её примере выявить закономерность. Хотя периодически и появляются пробелы из серии «что такое механическая энергия» или «что является носителем импульса», остальное поддается прямым измерениям.

С законами механических взаимодействий столкнулись ещё при строительстве пирамид. Авантюра безжалостная, бессмысленная и бездумная, однако рабы на своей шкуре испытали все прелести земного притяжения и силы трения. Тогда и стали появляться первые конструкции, способные упростить этот ужасный труд. Первые лифты, рычаги, системы неподвижных и подвижных блоков и другие простые механизмы. Возможно, интересно будет узнать, что первый лифт был придуман одним из египетских рабов, который трудился над строительством пирамиды. Но после того, как он построил это устройство и рассказал об этом фараону, раб был казнён. Цель предположить не сложно. Ведь эти знания не должны были достаться больше никому! Кроме, само собой, фараона.

К большому сожалению, история полна примеров безумного уничтожения и порабощения людей ради неоправданных целей и мы, как люди образованные, должны это понимать. Да и казней из-за излишних знаний предостаточно. Посадить на бочку с порохом за изобретение дельтаплана или сжечь на костре за исследование космоса — в целом-то обычное дело.

Механика является всеобъемлющей. На понимании принципов классической Ньютоновской механики держится и понимание многих других разделов физики. Так, даже элементарные частицы подчиняются законам Ньютона. Именно поэтому важно усвоить все законы механики. Ведь дальнейшее изучение природы будет опираться на эти знания.

Правда тут тоже всё не однозначно. Современные исследования показали, что Ньютоновская механика работает далеко не везде и далеко не всегда. Но это уже совсем другое направление работы. Причем малодоступное Ньютону и физикам того времени из-за отсутствия возможности выполнять столь сложные исследования. От того не стоит так сильно критиковать классическую механику при выявлении некоторых несоответствий в более тонких материях. Кроме того, как мы узнаем чуть позже, труды того же Ньютона часто интерпретировались неправильно, а суть изложения менялась относительно оригинала.

В любом случае, все существующие законы механики позволяют вполне неплохо существовать нам в рамках нашего мира и строить различные машины. Ваш автомобиль или велосипед — это классическая механика и эти устройства работают и подтверждают выведенные законы. По ним были рассчитаны все машины. Всё ещё возникают мысли, что это ошибки? Изучить классическую механику следует обязательно даже если вы собрались её ругать, чтобы было с чем сравнивать.

Выделить самые важные законы механики невозможно. Ведь каждый закон, который был изучен и сформулирован, ценен по-своему. Каждый из них делает вклад в общую картину мира. Но вот отобрать наиболее часто встречающиеся на нашем жизненном пути закономерности вполне можно. Это мы и сделаем. Выберем те, которые встречаются в повседневной жизни чаще других.

Сделать это будет не сложно. Мы вышли из квартиры, и закрывающаяся дверь прищемила палец собственным весом. Только что мы наблюдали закон сохранения механической энергии. Ещё у нас с собой сумка, а она обладает потенциальной энергией. Если выпустить её из рук, то сумка упадет и опять сработает закон сохранения.

При этом первый закон Ньютона подсказал, что дверь продолжит двигаться по инерции и прищемит нам палец, причем палец испытает такое же воздействие, которое передаст и двери уже по третьему закону Ньютона. Исходя из второго закона Ньютона кто-то толкнет нас в метро с некоторой силой, придавая ускорение, а закон тяготения при этом заставит притянуться к полу и упасть.

Закон Паскаля поможет сработать гидравлическому тормозу на транспортном средстве, которое везет нас на работу или по делам.

Закон Гука расскажет о том, насколько сильно прогнется стол, когда мы поставим на него баклажку с водой и выдержит ли вообще такую нагрузку. Но в скором времени появится свободное время и благодаря закону сохранения импульса мы полетим в отпуск на реактивном самолете. Дальше будем купаться и закон Архимеда не даст утонуть в море.

Примерно так и были выбраны семь значимых законов для рассмотрения. Их работу можно увидеть чуть ли не в каждой секунде нашей жизни.

Закон сохранения механической энергии

На базе понимания процессов сохранения строится вся физика. Энергия сохраняется в самых разных процессах. Нас же пока интересует только механика.

Не случайно закон сохранения механической энергии мы разбираем самым первым. Властелин механики просто обязан познать этот принцип для контроля надо окружающим материальным миром.

Начинается всё с простых явлений и заканчивается самыми сложными. Поспорить с существованием данного закона не смогли даже квантовые физики, которые любят регулярно «отменять» классические представления о природе процессов и частенько обращаются к нему.

Базовое представление о факте сохранения энергии заложили ещё античные философы. Более-менее похожее нашему представлению пониманию сформулировал Рене Декарт в 1644 году.

Когда одно тело сталкивается с другим, оно может сообщить ему лишь столько движения, сколько само одновременно потеряет, и отнять у него лишь столько, насколько оно увеличит своё собственное движение.

Правда про количество движения тут стоило бы сказать отдельно, но это совсем другая история. Пока вернемся к сохранению.

Как и во многих других случаях, проще всего разбираться с законом сохранения исходя из механики. Существует тут такой закон сохранения механической энергии. На этом примере и становится понятной основная логика сохранения энергии: если где-то что-то убыло, то где-то столько же этого и прибыло. Кстати, примерно так сформулировал закон сохранения энергии когда-то великий М. В. Ломоносов. Песня немножко из другой оперы, но легко применяется во всей физике.

Анализируя процессы превращения механической энергии очень легко понять и основную суть рассматриваемого вопроса. Ведь исходя из этого очень легко прослеживается постоянный обмен энергией, а не её неожиданное появление и расходование в пустоту.

Где мы видим работу закона сохранения энергии

Закон сохранения энергии встречается нам повсеместно. За прошедший день вы столкнулись с ним как минимум сотню, а то и тысячу раз. Только сделали вы это необдуманно и ничего не заметили.

Но мы же с вами хотим научиться видеть работу подобных законов на практике! Для этого всего лишь следует внимательно наблюдать за окружающим миром. Ведь прежде, чем над чем-то властвовать, нужно научиться это что-то контролировать. Контроль подразумевает длительное наблюдение и выявление закономерностей. Это примерно, как процесс охоты. Рысь охотится на зайца и часами сидит в засаде, выжидая удачный момент для прыжка. Аналогичным образом и мы должны охотиться за знаниями об окружающем мире, хладнокровно фиксируя наблюдения.

Для того, чтобы хорошо ориентироваться в законах физики, нужно научиться видеть их в мире. В случае с механикой это гораздо проще, чем с другими разделами физики. Запомните, чему учит закон, а потом обнаружьте его в природе. Сможете сделать наоборот — встанете в один ряд с Архимедом и Ньютоном.

Но что-то мы отвлеклись от темы. Это было лирическое отступление. Мне кажется так гораздо интереснее что-то изучать, поглощая при этом и другие сопутствующие мысли. В книге и дальше повествование будет строиться таким образом. Так вот…

Закон сохранения энергии можно наблюдать при срабатывании тормозов автомобиля. Колодки нажимают на диск, диск начинает замедляться, а колодки нагреваются. Так энергия движения автомобиля частично передалась колодкам. Механическая энергия превратилась в тепловую. Тепловая энергия в колодках тоже не останется без дела. Она частично превратится во внутреннюю энергию. Кстати, внутренняя энергия тела — это энергия, которой обладают частички тела, входящие в его структуру. Ведь они перемещаются или колеблются, а для этого нужна энергия. Внутренняя энергия тормозных колодок и дисков, в свою очередь, израсходуется на расширение тела.

Подобный пример можно наблюдать при забивании гвоздя. Мы стучим молотком по шляпке гвоздя, а сам гвоздь при этом нагревается. Вновь кинетическая энергия удара молотка превращается во внутреннюю энергию структуры гвоздя, что и приводит к увеличению его температуры.

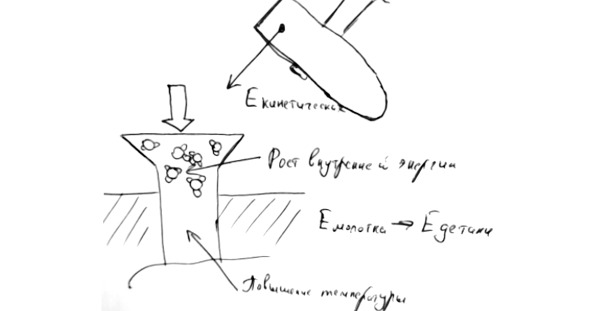
Закон сохранения энергии легко увидеть в различных процессах, связанных «с перемещениями уровней высоты». Например, если велосипедист пытается заехать на высокую горку, то поднявшись на её вершину, он наберет достаточное количество потенциальной энергии, чтобы скатиться вниз без кручения педалей.

Следующий классический пример — лук со стрелами. Там потенциальная энергия, накопленная в результате деформации лука, передается стреле посредством тетивы. Сама же стрела растрачивает эту энергию на передачу тепла воздуху из-за трения о его частички и поражение цели.

При сжатии пружины кинетическая энергия воздействия переходит в потенциальную энергию сжатой пружины. Вот вам очередное превращение.

Подобным образом можно рассмотреть абсолютно любой процесс, происходящий вокруг нас и увидеть работу закона сохранения. Правда помните, что смотреть следует очень внимательно!

Что такое энергия в физике

Сохранение — это конечно хорошо! Но давайте зададим себе вопрос: понимаем ли мы что такое энергия? Что мы в итоге сохраняем? Скорее всего нет. Положительный ответ будет означать неполное знакомство с рассматриваемым вопросом.

Современная физика не способна на него ответить полностью. Слишком много заковырок и противоречий. Самое значимое из них — что именно в пространстве является носителем энергии? Это атом или молекула? А как тогда быть с процессами, где не участвует как таковое вещество? Там энергии нет, потому что её негде сохранить? Как дела с тепловой энергией? Вопросов очень много, а ответов очень мало. Именно поэтому пока стоит отстраниться от поиска правильного ответа и обратиться к существующему определению. Тем более, что для нас сейчас наибольший интерес представляет механическая энергия и воспринимаем мы её только как некоторую величину.

Стандартное определение понятия в физике, всё же, существует. Им и будем пользоваться для дальнейшего объяснения. Более глубокие мысли хоть и интересны, но уже выходят за границы раздела механики и к ним мы вернемся в других работах.

Энергия — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. С древнегреческого языка оно переводится как действие.

Если опустить ряд сложностей, которые не особенно и нужны для понимания применительно к механическим процессам, то всё равно разобраться будет не так-то просто. Перечитав это определение несколько раз, вы вероятно так и не поймете, о чем там написано. Давайте разобьем стандартное определение на фрагменты, а после этого запишем его в более понятной и простой форме.

Скалярная — означает не имеющая направления. Про это поговорили в самом начале книги. Но давайте закрепим на будущее. Это величины, как масса тела или атмосферное давление. Они просто есть и не связаны с движением. Для сравнения — скорость величина векторная, имеет направление. Чувствуете разницу между скоростью и массой? Вот именно такая разница и между векторными и скалярными величинами.

Следующая часть определения говорит, что мы имеем дело с некоторой мерой взаимодействия тел. Причем, применительно к любым видам взаимодействия. Но нас сейчас интересует механика. И тут уместно назвать это именно что «мерой взаимодействия».

Представьте, что вы поддали мячик ногой. Вы передали мячику что-то и это что-то потом начало оказывать воздействие разных типов. Что-то и есть энергия. Или «движение» если обратиться к переводу слова. Его иначе не назовешь. Вот и придумали фразу про меру воздействия, добавив её в определение энергии.

Ещё можно представить камень, который падает кому-то на голову с крыши. Сразу вспоминается великолепный эпизод из фильма «Один дома 2», где Кевин кидается кирпичами в Марва. Вот летящий камень обладает чем-то, что он потом передаст голове нашего отрицательного героя. Это что-то и есть энергия. Или вновь подойдет слово движение. Почему мы так размыто разъясняемся? Наверное потому, что даже механическую энергию, которая наиболее проста для восприятия, пока всё ещё не могут описать в полной мере и дать однозначное определение понятия.

Но для наших целей достаточно указанного выше определения. В целом-то, воспринимать слово механическая энергия, как слово «движение» вполне допустимо. Будут проблемы с представлением потенциальной энергии сжатой пружины, но там мы скажем, что сжатая пружина запасла некоторое количество движения и опять логику передадим.

Закон сохранения энергии в кино и философии

Закон сохранения энергии описывается разными словами и носит разные имена. Интересно отметить, что логика сохранения энергии пронизывает многие философские книги и даже современные фильмы.

Например, в фильме «Звёздные войны» присутствует такая характеристика, как сила. Силой там именуется некоторая субстанция, которую можно использовать как во благо, так и во вред. Но сама по себе сила нейтральна.

Очень легко провести параллели между силой в этом фильме и энергией в нашей жизни. Ведь по философским представлениям, да и по физическим законам, появившимся чуть позже, энергия во вселенной не появляется и не пропадает, а просто превращается из одной формы в другую форму. Аналогично этому представлению, герои Звездных войн как раз-таки и использовали силу, которая не появлялась и не пропадала, а только передавалась от одного объекта другому.

Подобный процесс передачи энергии или силы демонстрировался в некогда популярном фильме «Горец». Когда бессмертному отрубали голову его энергия передавалась победителю в виде разряда молнии.

В философии понятие «энергия» встречается очень часто и только ленивый не попробовал как-то объяснить происходящее. Античные философы описывали энергию как нечто, способное совершать работу и имеющее внутри себя силы. Примерно так описывал это Аристотель.

Фома Аквинский характеризовал энергию как акт чего-либо. Обеспечение процесса живительным действием.

Ну а «божественные теории» относительно термина энергия встречаются в философии регулярно.

Так, сила, которой обладают боги, тоже подходит под определение энергии. Люди могли обратиться к богам и попросить у них эту силу, а сила передавалась и превращалась бы в другие формы деятельности. Например, в случае языческих представлений, она переходила в рост урожая или приводила к появлению дождей.

Сколько убыло столько и прибыло

Физика выделяет разные виды энергии. Они могут неограниченно превращаться из одного вида в другой. Если в одном процессе энергия израсходована, то в другом смежном процессе её гарантированно стало больше. Но об этом чуть позже. Сейчас же запомним, что энергии характерны превращения из одного вида в другой.

Ударьте рукой по столу. А теперь проанализируйте, куда именно была израсходована энергия удара и как она превращалась из одной формы в другую.

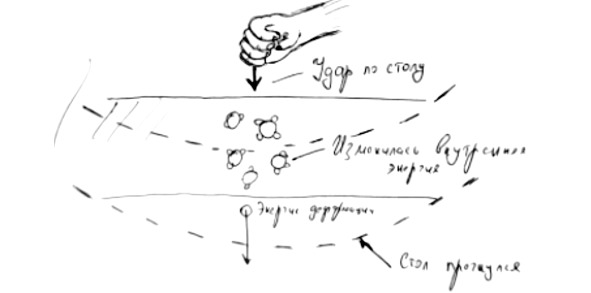
Понятие превращения энергии одно из самых важных в физике. Причем, вне зависимости от раздела. Понятно, что нам сейчас интересна механика, но все принципы работают и в других сферах.

Энергии свойственно переходить из одной формы в другую. Относительно механики выделяют два основных типа энергии. Есть ещё третий, который относится к другому разделу физики из-за своей природы, но на механические процессы также оказывает влияние.

Виды энергии применительно к механике

В механике обычно выделяют два основных вида энергии. Это кинетическая и потенциальная энергии. Есть ещё внутренняя энергия. Это тот самый третий вид, про который мы упомянули. Она тоже частенько трётся где-то рядом, но к механической энергии как такового отношения не имеет.

Правда в задачах, да и в стандартных жизненных ситуациях, связанных с механическим взаимодействиями, внутренняя энергия всегда фигурирует.

Внутренней энергией называется энергия, которой обладает структура тела, его атомы и молекулы. При взаимодействиях этих частиц происходит повышение температуры изучаемого тела. Так, ударив молотком по гвоздю, мы повысили внутреннюю энергию гвоздя посредством механического воздействия. Это воздействие вызвало чехарду в структуре тела и взаимных движениях части внутри него, что привело к нагреванию.

Теперь подробнее про кинетическую и потенциальную энергии.

Кинетическая энергия — та энергия, которой обладают движущиеся тела. Вот, собственно говоря, и всё. Летит в нас мячик и мячик имеет кинетическую энергию, которая будет частично передана нам при ударе.

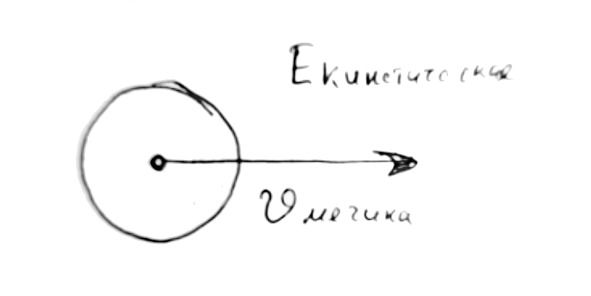
Всегда, когда речь заходит о кинетической энергии, мы имеем дело с движением. Не случайно кинетическая энергия рассчитывается по формуле:

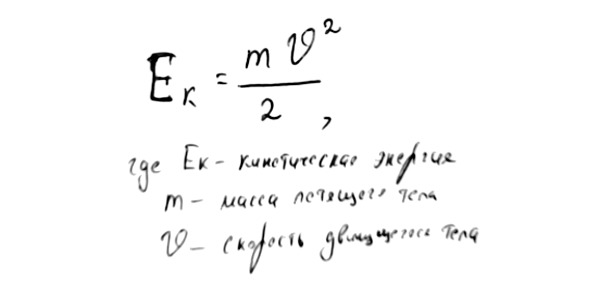
В расчёте участвует скорость, которая обозначена тут буквой V. Само собой, масса (m) тоже будет присутствовать в этом расчёте. Ведь чем массивнее тело, тем сильнее оно может ударить или, говоря научным языком, тем большее количество энергии оно может запасти при движении с некоторой скоростью.

Потенциальная Энергия — это энергия, которая есть у покоящегося тела и которая может высвободиться при изменении некоторых условий.

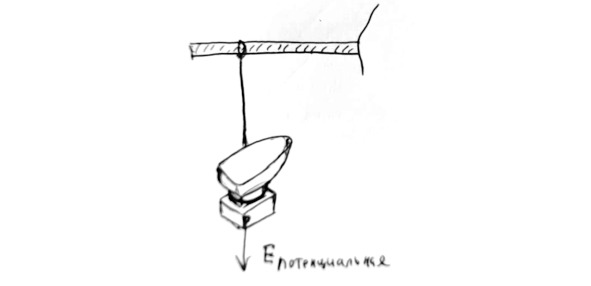
Представим себе, что на ниточке подвешен камень. Пока камень подвешен, он обладает потенциальной энергией. Если камень начнет вдруг падать, то эта потенциальная энергия высвободится. Высвобождение будет сопровождаться превращением потенциальной энергии камня в его кинетическую энергию. Ведь у него появится и скорость, и масса (которая никуда и не пропадала).

Заметьте, что, когда речь заходит о потенциальной энергии, чаще всего мы говорим о падении чего-нибудь куда-нибудь. Даже рассчитывается потенциальная энергия по простой формуле:

Тут тоже есть масса m, ускорение свободного падения g и высота, с которой будет падать тело h.

Если же речь идёт про сжатую пружину, то схема расчёта слегка иная.

Здесь есть деформация пружины x и жесткость пружины k.

Хотя формула и похожа на расчет кинетической энергии, но тут мы имеем абсолютно другой физический смысл. Экспериментальные исследования позволили выяснить, что энергии будет вот столько, но факт того, что величины считаются похожим образом ни о чем не говорит. В одном случае происходит движение со скоростью, а в другом случае есть внутренние взаимодействия в теле, которые вызывают явление упругости.

Кстати говоря, сжатая пружина как нельзя лучше подходит для демонстрации явления потенциальной энергии. Глядя на неё не сложно понять всю суть рассматриваемой проблемы. Мы сжали пружину и пока она находится в таком состоянии, внутренние силы стараются её распрямить. Стоит её отпустить, и пружина отлетит в лоб. Вспомним шутку из Симпсонов, когда Гомер открыл банку от чипсов и оттуда в глаз ему вылетела пружина, с которой он потом бегал по городу. Это и была потенциальная энергия, превратившаяся в кинетическую.

Всегда, когда речь заходит о кинетической энергии, мы имеем дело с движением. Не случайно кинетическая энергия рассчитывается по формуле:

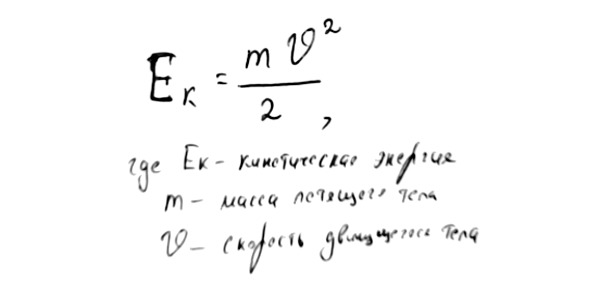
В расчёте участвует скорость, которая обозначена тут буквой V. Само собой, масса (m) тоже будет присутствовать в этом расчёте. Ведь чем массивнее тело, тем сильнее оно может ударить или, говоря научным языком, тем большее количество энергии оно может запасти при движении с некоторой скоростью.

Ну и анализируя теперь пример с рукой и столом, который был в самом начале обсуждения, мы можем провести более глубокий анализ процесса.

Пока рука приближалась к столу, присутствовала кинетическая энергия, которая в итоге была передана столу и вызвала его незначительную деформацию. Несколько миллисекунд, пока стол не вернулся к своей исходной форме, он обладал потенциальной энергией. Сразу произошло несколько интересных процессов — один вид энергии превратился в другой вид энергии, а ещё сработал закон сохранения энергии.

Пример, вероятно, не самый полный и может показаться, что мы попросту забыли о некоторых моментах. Скажем, мы не учли, что деформируется и сама рука. Но в физике принято исключать малозначимые факторы и процессы или пренебрегать ими.

Строится принципиальная схема, а некоторые объекты вполне можно принимать за материальные точки, недеформируемые тела и делать прочие упрощения. Таких допущений огромное количество. Они есть в каждом учебнике при разборе ситуаций. Ведь не внеси мы такое упрощение и самая простая задачка про брусок и наклонную плоскость будет решаться этак на 100 страницах!

В случае с рукой мы исключили множество моментов — стол нагрелся от удара, рука тоже деформировалось, насколько бы это не было сложным для беглого восприятия, но у движущегося тела присутствовала и потенциальная энергия и многие другие. Мы всё это упрощаем для того, чтобы сосредоточиться на основном явлении.

Но! Это не означает, что все остальные факторы пропали вовсе! Они есть. Мы понимаем, что их влияние минимальное и отбрасываем их. Если же считать «по уму», то следует проводить сложнейшие интегральные вычисления и схемку рисовать покруче. Подобные вычисления потребуются, разве что, при проектировке самолета.

Формулируем закон сохранения механической энергии

Из этих нехитрых примеров следует, что при механических воздействия энергия может неограниченное количество раз превращаться из одного вида в другой. Потенциальная энергия переходит в кинетическую, а кинетическая переходит в потенциальную.

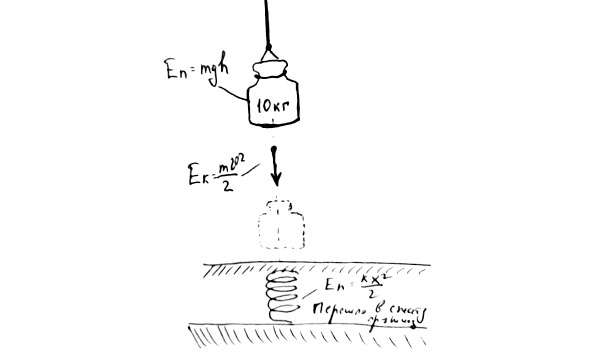
Когда речь идёт о механической энергии всегда рассматривается сумма механической и потенциальной энергий. Это будет так называемая полная энергия системы.

Рассуждения о превращении энергии подталкивают к мысли, что на самом-то деле энергия не появляется и не пропадает. Она просто превращается из одной формы энергии в другую с потерями на другие процессы. И мы пришли к закону сохранения механической энергии.

Закон сохранения энергии гласит, что энергия ниоткуда не возникает и никуда не пропадает. Энергия лишь переходит из одного вида в другой или от одного тела к другому.

Как вы заметили, слово «механической» тут отсутствует. Закон справедлив не только для механики. Как и понятие «энергия» закон сохранения значим для всей физики сразу вне зависимости от раздела. Он работает во всей вселенной.

Но применительно к механике закон сохранения энергии учитывает преимущественно кинетическую энергию тела, потенциальную энергию тела и иногда ещё внутреннюю энергию тела (если происходит передача энергии движения в нагрев и т.п.), о которых мы поговорили чуть выше.

Теперь посмотрим, как сформулирован закон сохранения механической энергии в учебниках:

В замкнутой и консервативной системе тел полная механическая энергия сохраняется: ΔЕ = 0

или Е потенциальная 1 + Е кинетическая 1 = Е потенциальная 2 + Е кинетическая 2

или как вы это привыкли видеть:

Почему замкнутой? Потому что если система не замкнутая, то она будет обмениваться энергией с другими участниками процесса, и энергия в итоге рассеивается. Тот самый пример со столом подходит как нельзя лучше.

Скажем, запустили мы всем известные шарики для демонстрации закона сохранения импульса. Они качаются и передают друг другу энергию в одной замкнутой системе.

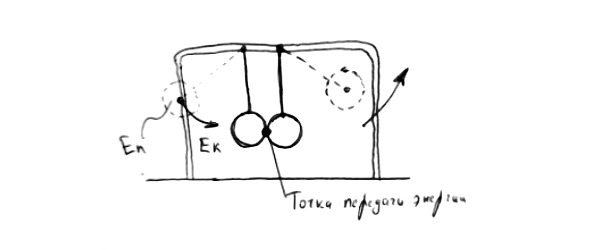
Замкнутая система тут — это рама с нитями и сами шарики. Будь система не замкнутая, шарики должны были бы бить, скажем, ещё и по внешней стенке и отдавать ей часть своей энергии. Практически любую систему условно можно воспринимать, как замкнутую. Этот принцип активно используется при решении задач. Ключевое слово тут условно. Потому что копни поглубже и увидишь, что ни одна замкнутая система не будет замкнутой.

Почему консервативная и что это значит? Потому что если на систему воздействуют внешние силы, то они внесут свой вклад в процесс и уравнение, где общее изменение энергии равно нулю уже будет несправедливым. Консервативная система есть та, где существуют только консервативные силы.

Сила называется консервативной если ее работа не зависит от траектории, а определяется только начальным и конечным положениями тела.

Можно сказать и по-другому. Все действующие на систему внешние и внутренние непотенциальные силы не должны совершать работы, а все потенциальные силы должны быть стационарны. Это и будет консервативная система.

Проще было бы сказать что-то из серии — система варится в своем соку и ни с чем не взаимодействует. Логика бы сохранилась, а формулировка упростилась.

Следовательно, если рассматривать систему, где происходит механическое движение и подул ветер, который заставил тело получить внешнюю энергию, она уже не консервативная. Модель движения автомобиля по дороге далеко не консервативная.

Правда тут возникает один интересный вопрос… Часто обозначенные выше обстоятельства воспринимаются как те, которые мешают работать закону сохранения энергии. Это не совсем так.

Закон сохранения энергии работает всегда. Вне зависимости от того, консервативная ли у нас система и замкнутая ли она. Только вот записать тогда его в форме, привычной нам из школьного курса, уже не получится. Реальная картина будет намного сложнее. Приведенная формулировка закона сохранения механической энергии используется для упрощения ситуации.

Так, простой пример с падением срезанной с веревки гири на пол можно значительно усложнить. Гиря висела на веревке, обладала потенциальной энергией. Веревку отрезали. Потенциальная энергия должна была полностью передаться падающей гири и превратиться в кинетическую, но мы не учли, что была ещё веревка, которая тоже получила часть этой энергии. Пока гиря падала, она воздействовала на воздух и испытывала трение о воздух. Нагрелись воздух и гиря. При падении она частично сломала пол, на который, растратив на разрушение часть энергии ну и частично перешла во внутреннюю энергию.

И пусть всё это значения с приставкой микро-, но реальная картина должна учитывать каждую мелочь. Прыгающий мяч в реальности рано или поздно остановится. Всё из-за постоянных взаимодействий.

Отсюда было логично предложено упрощать подобные взаимодействия и рассматривать гипотетические консервативные и замкнутые системы.

Ну а закон сохранения при таком рассмотрении сводится к простому примеру: висела люстра и обладала потенциальной энергией. Кинетическая энергия этой люстры была равна нулю. Потом веревочку обрезали, и кинетическая энергия появилась из-за превращения потенциальной энергии люстры в кинетическую. Если записать это в виде того самого выражения, что было приведено выше, где Еп1+Ек1=Еп2+Ек2 получим что-то вида 200 Дж +0 Дж = 0 Дж +200 Дж. Кинетическая и потенциальная энергия поменялись местами.

Для решения большей части практических задач достаточно такого понимания процесса и таких знаний.

В чем измеряется энергия

Мы обсудили закон сохранения энергии и даже привели примеры, но так и не упомянули, какая у энергии единица измерения.

Поскольку энергия у нас является мерой совершения телом работы, то и измеряется она в тех же величинах, что и работа. Единицей измерения энергии в системе СИ принят Джоуль.

Но есть и другие системы измерения. Например, в системе СГС энергия измеряется в эргах. Это довольно редкая единица и скорее всего, она вам никогда и не встретится. Но знать про это полезно. Собственно, 1 эрг = 1 дин х 1 см или та же самая сила, умноженная на расстояние, или работа по-нашенски.

Вы наверняка не в курсе, что система СГС — это система единиц измерения, в которой основными единицами являются единица длины сантиметр, единица массы грамм и единица времени секунда.

Ещё в технических расчетах встречается такая единица измерения энергии как килограммометр (кгм) или килограмм силы (кгс) на метр (м): (кгсм). При этом считают, что 1кгсм=1 кгс⋅1 м=9,81 Дж.

Есть и другие варианты единицы измерения энергии, но к механике они отношения не имеют. Например, существуют калории, кВт*ч или электрон-вольты. Единица измерения никак не влияет на факт существования физического понятия или процесса и нужна только для некоторой систематизации.

Почему невозможно создать вечный двигатель

Исходя из закона сохранения механической энергии складывается ложное впечатление, что возможно создать вечный двигатель. Ведь для работы такого агрегата будет достаточным просто играться с превращениями энергии. Это вполне не сложно и может быть реализовано с помощью современных технологий.

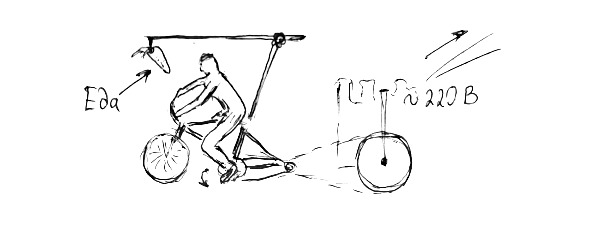
Скажем, скатилось какое-то тело с наклонной плоскости и, обладая инерцией, оно может заехать на другую наклонную плоскость и на ту же самую высоту. Ведь мы выяснили, что энергия передается в полном объеме исходя из закона сохранения энергии.

Делая такие правильные с точки зрения здравого смысла предположения, мы не учитываем все сложности взаимодействий, с которыми приходится столкнуться в реальности. Закон сохранения энергии тут нам вряд ли поможет. Он скорее опишет лишний раз, почему вечный двигатель создать невозможно, а перпетум мобиле останется и дальше уделом фантастов.

Несмотря на то, что энергия неограниченно превращается и передается, нам гарантированы сопутствующие потери. Потери на самые разные вещи. Энергия рассеивается, также как рассеиваются силы у человека в течение рабочего дня. Вот поехали мы на работу и пока ехали уже устали. Виновато метро или любая другая форма транспорта.

Такая же ситуация и с сохранением энергии. Представим даже тот самый пример с наклонной плоскостью. Объект съедет по наклонной плоскости, но на такую же высоту у новой наклонной плоскости уже не заедет. Ведь будут потери на трение. И это как минимум. На самом деле потерь будет гораздо больше и их аналитика займет немалое количество времени.

Вы можете сказать — ну замените тело колесом, вот оно и будет скатываться без потерь. Ведь экстремалы в параболической рампе вполне себе неплохо справляются с обозначенными задачами и кажется, что скатываясь туда-обратно, они делают это только лишь по инерции. Это совсем не так. Опять беглый взгляд на проблему. Там тоже есть потери. Как минимум, на сопротивление воздуху. Кстати, если повторить опыт в вакууме, всё равно вечного двигателя не получится. Энергия будет рассеиваться на тепловую энергию, которая появится во втулках велосипеда или скейтборда, крутящегося в этой рампе.

Выходит, что закон сохранения энергии в правильном его изложении никоим образом не приближает нас разработке вечного двигателя. Он, наоборот, рассказывает, почему такой двигатель мы никогда не сделаем. В данном случае мы расписали самые простенькие примеры, но вне зависимости от конструкции и принципа работы агрегата главный физический принцип обмануть имеющимися методиками не получится.

Самое важное про закон сохранения энергии

Мы не случайно рассмотрели закон сохранения механической энергии самым первым. Для властелина механики он один из главных законов. Ведь без энергии не будет и работы. Чем тогда властвовать и кому нужна механика без движения. Да и обманщиков хватает. Скажем, вечные двигатели многократно пытались представить как реальные установки, используя в качестве движущей силы механизмы с хомяком в колесе или карликом, который едет на велосипеде внутри бочки. Всё это быстро становится понятным, если знать основы физической теории.

В качестве вывода выжимки отметим, что закон сохранения механической энергии учит нас главному принципу нашего материального мира. Энергия не появляется и не пропадает, а только превращается из одного вида в другой.

Записывается аналитически это как ΔЕ = 0 или изменение общей энергии системы равно нулю. Ну а энергией в физике принято называть меру совершения телом работы или «количество движения», которым обладает тело подобно сжатой пружине или летящей пуле.

Три закона Ньютона

Следующее, что нужно для понимания механики — это законы Ньютона. Можно по-разному относиться к Ньютону, его трудам и правильности всех его убеждений, но его законы самые настоящие три кита современной механики.

Без них человеку будет сложно разобраться во всём, что происходит вокруг нас и, само собой, не разобраться и в механике.

Вероятно, вы уже слышали, что к Ньютону и его достижениям существует неоднозначное отношение. Некоторые считают его родоначальником классической механики, а кто-то называет фантазером. Дальнейшая же физическая наука занимается, по их мнению, попыткой прикрывать все Ньютоновские недочеты и неточности, чтобы современная физика не обрушалась из-за отсутствия почвы под ногами.

На мой взгляд Ньютон является человеком гениальным и действительно достоин считаться основателем многих современных подходов. Причем, как к механике, так и к другим областям физики. Хотя критики, или, как их модно сегодня называть, хейтеры, всегда находятся. Многие ненавидят логику Ньютона из-за вопросов в неоднозначности описания того же земного тяготения и других фундаментальных понятий. И это далеко не единственный пример.

Поспорить с обстоятельностью законов Ньютона сложно. Ведь есть результаты лабораторных измерений, и любая критика после этого становится не особенно актуальной. Да и большая часть механических устройств, которые сегодня нас окружают, используют Ньютоновские законы в своем функционировании. Отсюда считаю рациональным не отрицать сами закономерности, которые многократно подтверждены и используются, а называть все разногласия «вопросами терминологии и глубины познания». Да, предположим где-то есть пространства и миры, где законы Ньютона не работают, но в нашей среде они работают всегда. Правда лучше говорить «практически всегда».

Вероятно понятие той же самой инертности действительно истолковывается современной физикой неправильно, однако закон работает. Как уже что называется после этого не столь важно. Это как древние люди когда-то использовали метод трения для получения огня без глубокого вникания в суть процесса. Если невозможно объяснить эффект, это не значит, что он отсутствует.

Мы говорим про механику, а тут «что вижу то и пою». Даже если некоторые вопросы, связанные с описанием гравитационных взаимодействий или неоднозначном понимании инерции существуют, выведенные Ньютоном закономерности всё равно работают. Значит, и законы годятся. Да и многие современные машины и механизмы используют описываемую логику в своей работе. Как же они безошибочно функционируют, если законы Ньютона не работают.

Возвращаясь к самим законам, отметим, что наша основная цель — не зазубрить стандартные определения, а научиться видеть работу этих законов в окружающей жизни и понимать, как их можно применить и о чем таком вообще говорил Ньютон. Пока закон не увидишь, его и не осознаешь. И применять уж точно не научишься.

Благо с механикой всё довольно просто. Если в памяти висит формулировка закона, то рано или поздно его работу можно увидеть и на практике. Было бы желание, да внимательность бы не подвела.

Закона Ньютона всего три. Это база для всего происходящего в современном мире механики.

В простонародье это так называемые:

— закон инерции

— закон силы

— закон взаимодействия

С их помощью и правда можно описать любое механическое взаимодействие, происходящее в нашем мире и в нашей локации (т.е. на Земле).

Многие «продвинутые» читатели отметят, что законы Ньютона как оно говорится — притянуты за уши. В некотором смысле можно согласиться с этими мыслями и фактов, подтверждающих такое обстоятельство, вполне достаточно.

Но, во-первых, мы говорим про модель реального, имеющую набор неопровержимых доказательств в виде проведенных экспериментов. С результатами экспериментов сложно спорить. Во-вторых, законы в мире вокруг нас всё-таки работают и сдаётся мне, что в имеющейся ситуации это куда важнее, чем их ярая критика.

Теперь поговорим про каждый закон более подробно. У всех них есть специфика, но они объединены общей мыслью и общим взглядом на картину мира. Поэтому, невозможно правильно понять один только закон из перечисленных, не зная остальных. Хотя правильнее было бы сказать, что нельзя увидеть мир глазами Ньютона, не принимая во внимания сразу все его наработки.

Первый закон Ньютона

Первый закон Ньютона называют законом инерции. Он является всеобъемлющем (ну или по крайне мере считается таковым в рамках Ньютоновской механики и нашего пространства) и описывает особенности механического взаимодействия всех объектов друг с другом. Частенько можно услышать, что первый закон ещё называют законом инерции.

Именно из-за инерции этот закон сильно критикуется среди продвинутых в данном вопросе людей. Дело в том, что вводится такое понятие, как инертность. Но что такое инертность никто в полной мере объяснить пока не может. Она есть как факт, но не понятна с точки зрения физики! Мы можем отметить, что такое свойство присуще всем материальным телам, как минимум на Земле, а то и в ближайшем космосе. Но когда ученые начали искать причину существования инертности и самой инерции, так и не удалось составить какую-либо внятную картину происходящего. Из-за этих недопониманий и возникает впечатление, что закон Ньютона, как это принято говорить, «ниочем». А если и описывает происходящее, то не может претендовать на глобальность, так как и сущность явления не до конца ясна, что ставит его в один ряд с эзотерикой.

Основы формулировки первого закона заложил ещё Галилей, сформулировав закон инерции. Из него следует, что при отсутствии внешних сил тело либо покоится, либо движется равномерно.

Ньютон же «осовременил» и дополнил эту формулировку, обозначив понятие относительности. Правда увы, оно тоже весьма условно. Ведь сам-то Ньютон не включал его в собственную формулировку первого закона, а замечание про относительность появились позднее. Кстати, наверняка интересно будет узнать, что вовсе не Эйнштейн впервые заговорил про относительность в физике, как это принято считать исходя из СМИ. Эти размышления были присущи ещё ранней физике, и тот же Коперник упоминал вопрос относительности в своих рассуждениях, но в слегка размытой для нашего понимания форме.

Понимание первого закона категорически важно для дальнейшего технического развития вне зависимости от изобилия критики и постоянных сомнениях в его правильности. На данный момент это вполне самодостаточный теоретический постулат, не противоречащий в общем смысле окружающему миру. Без осознания, что закон работает, мы не сможем правильно строить механизмы и планировать их работу. Ведь практически в каждом действии есть первый закон Ньютона. Сомневаетесь?

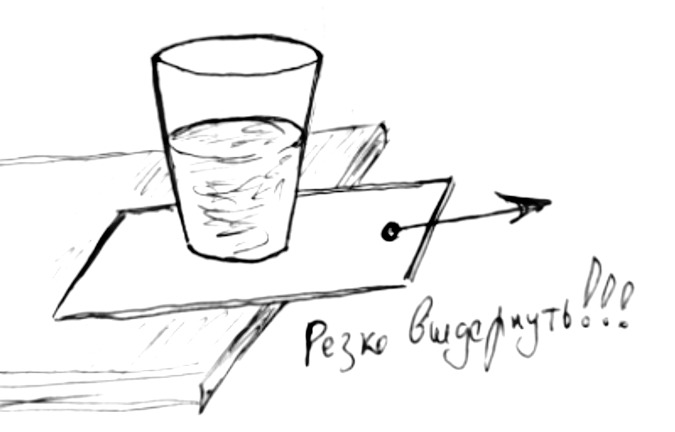
Тогда поставьте стакан воды на лист бумаги и резко выдерните бумагу из-под стакана. Стакан останется на месте, а закон сработает.

Где можно наблюдать работу первого закона Ньютона

Для того, чтобы увидеть работу первого закона Ньютона идти далеко не придётся. Самый простой пример — это лифт. Начинаем спускаться вниз и ощущаем, будто пол уходит у нас из-под ног. Вот вам и здрасти! Закон отработал. Наша инертность не дала упасть сразу со скоростью лифта, и мы почувствовали, что парим в воздухе и у нас пропал вес.

Или другой пример. Едем на велосипеде, нажимаем тормоза и какое-то время ощущаем, что велосипед тянет вперед. Всему виной инерция и на то, чтобы «погасить» этот эффект потребуется некоторое время. Пока энергии не попревращаются несколько раз одна в другую, тело будет тянуть вперед. Применительно к велосипеду есть и ещё один пример. Нажмите передний тормоз резко при большой скорости движения. Гарантированно вас перевернет через переднее колесо. В простонародье этот трюк называется «черезрулька».

Это коварный Ньютон со своим первым законом вставил нам палки в колёса. Инерция перевернула через руль поскольку такова наша система.

Примерно такая же картина наблюдается если мы стоим в вагоне метро, а поезд или резко трогается, или резко останавливается.

Во всех этих случаях появляется ситуация, при которой мы летим или вперед, или назад. Вспоминается шутка из Гриффинов, где Брайн болтался внутри едущего фургона и постоянно бился о стены изнутри. Ведь он же собака. А собаке тяжело устоять в движущейся машине.

Если проанализировать подобную схему, можно будет понять, что подобная особенность движения тоже связана с инерцией и пропорциональна нашей массе. Масса же, как мы узнаем чуть дальше, является мерой инертности тела. Чем оно тяжелее, тем сложнее привести его в движение или остановить.

Получается, что любое движение в нашем механическом мире будет подчиняться первому закону Ньютона. Конкретные примеры можно больше и не приводить. Их очень много и книги на всё это не хватит. Запомните пример про поездку в метро и его резкое торможение. Это и будет демонстрацией работы первого закона, а в голове такое осядет очень хорошо.

Полезно будет отметить, что работа первого закона активно используется в конструкциях машин и механизмов.

Так, маховик в двигателе внутреннего сгорания призван сохранить энергию вращения коленвала и сгладить провалы в работе. Маховик выполнен в виде массивного металлического тела, обладающего приличной массой.

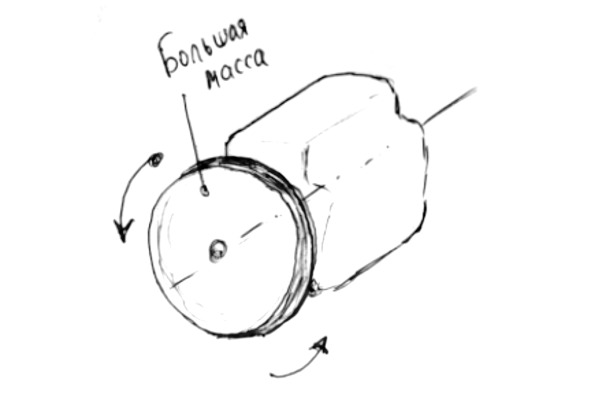
Именно масса заставляет его длительное время вращаться по инерции, что и является следствием работы первого закона.

Интересно отметить, что на попытке сохранить эту энергию строятся целые научные направления. Например, известный ученый Гулиа Н. В., старался сделать механический аккумулятор или энергетическую капсулу, опираясь на эффект инерции. На сей счёт он написал немалое количество научных трудов.

Сформулируем первый закон Ньютона и разберем его на болтики

Давайте сформулируем первый закон Ньютона так, как это обычно сделано в учебниках.

Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.

Вот, вроде бы, мало написано. Но о чём тут вообще? Если вы впервые читаете такую формулировку, то запутаться совсем несложно. Да и уже имея знания по физике и подзабыв что-то, потерять мысль рассуждения вполне вероятно.

Первая мысль, которая появляется при прочтении этих строк — для чего это вообще и что это за бред? Да, именно бред. Набор слов и не более. Такие мысли возникают у большинства читателей.

Когда нам рассказывают про этот закон в школе, аналитическое мышление ещё не до конца сформировано и жизненного опыта маловато. Закон кажется нам набором слов, а память об этом закрепляется на всю жизнь. Поэтому, сейчас будем разбирать вопрос буквально по буквам.

После нашей аналитической работы вы будет воспринимать первый закон Ньютона как один из фундаментальных законов механики, а не что-то там из учебника.

Вся сложность ни в первом законе, а в мудреной формулировке. Оно как на древнерусском языке написано.

Существуют такие системы отсчёта… Стоп-слово системы отсчёта. Что такое система отсчёта? Ничего сверхъестественного!

В данном случае, это обстоятельство указывает на принадлежность рассматриваемых тел к одной системе отсчёта.

Системой отсчета называется совокупность неподвижных относительно друг друга тел (тело отсчёта), по отношению к которым рассматривается движение (в связанной с ними системе координат), и отсчитывающих время часов (системы отсчёта времени), по отношению к которой рассматривается движение каких-либо тел. Если коротко и просто — то это пространство, в котором мы перемещаемся, и часы, а также точка отсчёта, от которой мы отмеряем расстояние. Всё это необходимо для того, чтобы в дальнейшем иметь возможность сопоставить разные виды движения и движения разных тел, а также правильно выполнить расчёты.

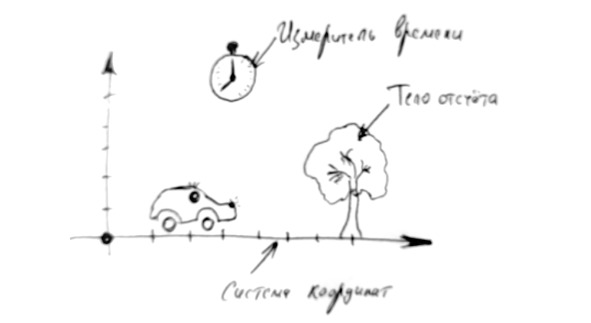
Например, если мы едем на поезде и проезжаем мимо станции, то можно рассматривать и поезд, и станцию в одной системе отсчёта, а можно как разные.

В одной общей системе отсчёта, привязанной к станции, поезд будет ехать, а станция стоять.

В другой, привязанной к поезду, поезд будет стоять, а станция проедет мимо.

Мы можем сидеть на стуле в комнате, а земля в это время крутится. Относительно земли мы сидим, а относительно пространства или, скажем, луны, мы вращаемся.

Именно это обстоятельство и обозначается понятием система отсчёта.

Хорошо, когда речь идёт о таких безобидных ситуациях. Но если говорить про аварии на дорогах, то там уже система отсчёта не кажется такой бесполезной штукой. Ведь в системе автомобиль-водитель, скорости при встречном столкновении с другим автомобилем будут суммироваться, что делает столкновение ещё более опасным. Значит, нужно правильно рассчитать нагрузку, чтобы укрепить автомобиль подходящим образом. Для этого нужно правильно выбрать систему отсчёта и вникнуть в понятие относительности движения.

Следующее новое слово — инерциальная система отсчёта.

Всё тоже очень просто. Это система отсчёта, в которой существует инерция. Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным, а время — однородным. Или, если перевести это на нормальный язык, то это система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно либо покоятся.

Что такое инерция? Это мы, пожалуй, выделим даже в отдельный пункт. Больно важная понятие в физической теории, которое будет преследовать нас постоянно.

Что такое инерция в физике

Инерция есть способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело или компенсации этих действий.

Если поезд разгоняется, мы начинаем падать противонаправлено его движению, когда тормозит — падаем вперед. Вот она инерция. Врезаемся передним колесом велосипеда в бордюр и что-то тянет нас через руль. Опять инерция.

Она появляется в следствие того, что у тела есть некоторая собственная масса. И в случае с поездом, эта масса продолжает своё свободное движение по инерции, тогда как колёса поезда уже тормозятся.

Как мы помним, первый закон Ньютона — это ещё и закон инерции. Количество инерции пропорционально массе. Правда тут стоит отметить некоторый парадокс, обозначенный Эйнштейном. Он установил в своё время, что инерционность одной массы будет зависеть от расстояния до других масс. Чем это расстояние больше, тем меньше будет инерция тела, удаленного от других масс. Значит, инерция зависит не только от массы, но и от взаимного расположения тел, но пока забудем об этом.

Отношение к понятию инерция в физике вообще не однозначное. Большая часть ученых приходят к выводу, что никакой инерции не существует и рассматривать её как силу ни в коем случае нельзя. Допускается воспринимать это понятие только как механизм, упрощающий наше взаимодействие с окружающим миром.

Причиной же инерции (стоит дописать — по последним данным) считается воздействие на тело поля Хиггса, которое ускоряет частицы, придавая им некоторые свойства. Согласно этой гипотезе, существует всепроницающее вакуумное поле Хиггса, и при ускорениях масс поле создает инерцию массы.

Но мы уже слишком далеко отошли от механики. Для нас сейчас принципиально разобраться в самой Ньтоновской закономерности. Поэтому, продолжаем анализировать первый закон.

Следующее, что там было отмечено — это что тела движутся равномерно и прямолинейно.

Здесь, наверное, ничего пояснять и не нужно.

Прямолинейно — это по прямой линии. Равномерно — значит за любые равные промежутки времени проходит одно и то же расстояние, и имеет неизменную скорость.

На них не действуют никакие силы… Для чего это обозначается?

В реальной жизни и в нашем пространстве, мы всегда испытываем действия каких-либо сил.

Если санки катятся с горы, то на них, как минимум, действует сила притяжения Земли и сила трения, возникающая между полозьями и снегом. Представить себе обратную ситуацию в реальной жизни довольно сложно. Тут на этом заостряется внимание специально. Инерция «ломается», если ей мешают другие силы. То есть инерциальное движение пропадет, в случае, когда телу препятствуют внешние воздействия. Опять же, уместен пример с любимым метро. Если поезд резко тормознул, а мы держались за поручень, то инерция не заставит нас упасть, потому что вмешалась вот такая внешняя сила. Она представлена тут рукой, которая держится за поручень и создает противодействие. Мы стабилизируем своё состояние в системе поезд-мы, чтобы исключить своё движение относительно самого поезда.

Действие других сил скомпенсировано…

Понятие более сложное, чем предыдущее. Как представить себе компенсацию сил?

Представьте, что лыжник скатывался с горы и в какой-то момент подул ветер, который остановил лыжника. В момент остановки силы и были скомпенсированы. Или, результирующая всех сил была равна нулю.

Проще всего представить себе эту ситуацию, когда мы говорим про плавание. Плавающее тело в точке равновесия имеет скомпенсированное воздействие внешних сил.

Обратите внимание, что только при таком раскладе будет работать первый закон Ньютона! В случае влияния на тело нескольких сил, только в точке равновесия возможна работа инерции. Чтобы сделать это явление более понятным, представим себе, что мы поставили банку с плавающей в ней телом на тележку. Затем разогнали тележку. И потом увидели, что на тело внутри банки оказала влияние внешняя инерция. Получается, что плавающее тело испытывало на себе скомпенсированное влияние двух сил. Но это не помешало воспринять инерцию!

Простая формулировка первого закона Ньютона

Теперь, изучив всю «матчасть», мы можем сформулировать первый закон в очень простой форме.

Тело, которому передали некоторое движение, будет ехать, пока на него что-то не подействует снаружи. При этом скомпенсированные воздействия и силы не считаются.

Если велосипедист едет по абсолютно ровной дороге, после того, как его кто-то толкнул вперед, дорога без наклона и сила трения колёс, а также сопротивление ветра (как и ВСЕ внешние сопротивления) отсутствуют или уравновешены, то он будет катиться так с одинаковой скоростью бесконечно долго.

Но в реальной системе ВСЕГДА будут действовать силы противодействия (трение, ветер, кочки) и велосипедист начнет останавливаться, если не будет крутить педали. Силы эти всегда не скомпенсированы.

Как бы выглядела бы компенсация сил на примере такого велосипедиста? Довольно хитро.

Пусть в лицо велосипедисту дует ветер и воздействует на него с силой 50 Ньютонов, а за спиной у велосипедиста будет винт, как у Карлсона, который создает силу движения вперед 50 Ньютонов. Вот мы и уравновесили все имеющие силы и получили результирующий ноль. Теперь в этом скомпенсированном бутерброде будет работать инерция и если, как и раньше мы будем исключать трение и т. п. и т.д., то велосипедист будет катиться неограниченно долго по прямой.

Как сам Ньютон сформулировал первый закон и где мы неправы

В начале объяснения мы обозначили, что Ньютон сформулировал первый закон изначально чуть иначе. Звучит он так:

Всякое тело продолжает удерживаться в состоянии покоя или равномерного прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

Согласитесь, все наши объяснения можно было и не делать, будь закон сформулирован именно так в учебниках изначально. Но позвольте, где тут хоть слово про всякие системы отсчета? А где про «существование таких систем отсчёта». Ничего нет.

Всё дело в том, что критика, которая потом посыпалась на Ньютона, как раз-таки и основана на тех самых допущениях. Допущения и приписки сделаны не самим Ньютоном. Ньютон различал только кажущиеся и истинные движения. Кажущиеся читай как относительные. В этом «относительном» всё и завязло. Ведь первый закон про истинные движения.

Вот как сказал сам Ньютон:

Истинное движение не может ни произойти, ни измениться иначе, как от действия сил, приложенных непосредственно к самому движущемуся телу, тогда как кажущееся движение тела может быть и произведено, и изменено без приложения сил к этому телу.

Вроде бы и всё тоже самое, только вопрос относительности не выпячен. Может быть, это слегка упрощает закон, но делает его правильным.

Ещё стоит обратить внимание на системы отсчёта, которые «существуют». Ведь их не существует. Систем, описанных в первом законе в реальности нет! При точных измерениях всегда выявится ускорение из-за той или иной причины (начиная от вращения земли и кончая дуновением ветерка), что уже стирает логику равномерного движения в реальности. Ни одна система отсчета, которую можно представить не является инерциальной в полноценном её понимании. Всё это допущения.

Самое важное про первый закон

Собственно, всё сказанное выше было лишь попыткой расширить кругозор. Нам же сейчас следует запомнить, что существует такая штука, как инерция, которая переворачивает велосипедистов через руль, и что тело будет двигаться по инерции до тех пор, пока ему что-то не помешает.

Количество инерции измеряется массой тела и чем оно массивнее, тем сильнее эта инерция. Такое свойство называют инертностью.

Второй закон Ньютона

Второй закон Ньютона не особенно сложен для понимания. Это основной закон динамики. Динамика — это раздел механики, который рассматривает законы движения тел и те причины, которые его вызывают или изменяют. Для нас тут интересно отметить слово «причины».

По распространенному мнению, второй закон даже проще осознать, чем первый. Всё дело в том, что наше «знание» законов физики, навязанное школьной программой, отталкивается от умения решать задачи. Второй закон Ньютона гораздо легче втиснуть в решение задачи, нежели первый закон. Ведь во втором законе есть формула, которые все так любят!

Однако, самое важное — это понимание изучаемого предмета, а не знание формул наизусть. Ведь не даром говорят «физика процесса» даже не применительно к физическим знаниям.

Собственно, ведем мы к тому, что втюхать формулировку второго закона в решение задачи — это ещё не значит понять его глобальный смысл и познать его в той мере, в которой это предполагалось самим Ньютоном.

При изучении первого закона Ньютона часто возникает мысль, что он, вроде как, и не нужен. В задачки его вставить тяжело и далеко не всегда понятно как, формулировка такая абстрактная, что быстро в неё не вникнешь. То ли дело второй закон! Всё просто и линейно.

Сила равняется произведению массы на ускорение. Вот вам и любимая формула есть. Её можно зазубрить и применять от всего и для всего, где мы видим знакомые ключевые слова типа «масса» и «ускорение».

Второй закон Ньютона довольно интересен и если нырнуть в его изучение, то можно очень многое понять. Он тоже должен быть изучен властелинами механики, ибо его существование являет отражением многих процессов.

Сложно представить себе любое механическое взаимодействие без проявления второго закона. Он был многократно подтвержден и проверен на практике. Правда есть и ряд противоречий, но об этом чуть позже.

Где можно увидеть работу второго закона Ньютона

Лучше было бы сформулировать вопрос иначе: А где нельзя увидеть работу второго закона Ньютона? Тогда мы бы придумали себе не-Ньютоновское пространство, как это любят делать фанаты и любители квантовой физики. Но мы-то с вами работаем сейчас в данной локации и говорим про механику. В механике оно всё «складненько ложится» на реальность.

В своем труде «Математические начала натуральной философии» Ньютон сформулирован закон, который в двадцатом веке был охарактеризован Эйнштейном как главный постулат механики и считается фундаментом теоретической физики. И это не случайно.

Что же, теории предостаточно и даже слишком много. Но где видно, что закон всё же работает? Как бы это проверить?

Можно бросить камень с крыши и внизу попробовать его поймать. Чувствуете, что есть некоторая разница в том, насколько легче было поднять камень перед тем, как его бросить и при попытке поймать камень внизу у дома. Это сработал второй закон. Камень приобрел некоторую силу, пропорциональную его массе и ускорению свободного падения. Вот и Ньютон.