
Бесплатный фрагмент - Тригонометрический зоопарк
Введение
Привет, любители математики и те, кто попал сюда случайно! Представьте себе мир, где древние мудрецы и современные гики объединились ради одной цели — рассказать вам всё о тригонометрии. Да, та самая штука, которая заставляла вас страдать в школе, оказывается, гораздо интереснее, чем кажется!
Здесь мы вспомним всех старых друзей: индийские джья, забытые версинусы и экссекансы, и даже современных ребят типа cas и cis. Каждый из них раскроет вам свои секреты: аналитические описания, графики, и раскраска домена комплексной области (потому что почему бы и нет?).
Но не думайте, что на этом всё закончится. Мы нырнём в глубины гиперболических, параболических и эллиптических тригонометрических функций. Вы слышали о синусах и косинусах лемнискаты и суперэллипса? Нет? А зря!
И, конечно, практическая польза. Навигация, строительство и просто красивые графики — всё это вы найдёте здесь. Мы даже создадим уникальную схему всех древних круговых тригонометрических функций на тригонометрической окружности. Круто, правда?
Так что приготовьтесь к увлекательному путешествию. Эта книга — ваш путеводитель по миру, где математика превращается в магию. Пристегните ремни и поехали!
Очерк истории
Итак, дорогие читатели, приготовьтесь к захватывающему путешествию по волнам синусов и косинусов, и узнайте, как великие умы человечества шаг за шагом раскусывали орех под названием тригонометрия.
Прежде чем нырнуть в тригонометрический зоопарк функций, давайте сначала забросим взгляд на историю возникновения науки об углах. Итак, представьте себе: первым тригонометрическим инструментом был не что иное, как гномон. Да-да, просто столб, воткнутый в землю, который отбрасывал тень. И потом завертелось…
Гномон был как смартфон для древних египтян и вавилонян — простой и эффективный способ отслеживать время и изменения углов. Этот невзрачный столбик показал, что если подойти к углам с умом, можно творить настоящие чудеса. Позже умные ребята начали использовать этот столбик не только для определения времени, но и для того, чтобы предсказывать солнечные и лунные затмения. В общем, столбики стали настоящими предвестниками тригонометрии.
И так началась великая эпопея развития тригонометрии. От древних греков, которые впали в любовную связь с углами, до индийских математиков, которые изобрели свои собственные тригонометрические штучки. Мир не знал покоя. Люди рисовали, вычисляли и доказывали, что тригонометрия — это не просто заумные формулы, а ключ к тайнам Вселенной! И сейчас без этих древних функций, никуда, даже в Квантовой Теории Поля! Но обо всём по порядку. Саму историю становления тригонометрии, как самостоятельной науки, можно разделить на несколько этапов:
Древний Египет и Вавилон: когда тригонометрия была ещё в подгузниках
Начнём с древнего Египта и Вавилона, где задолго до того, как кто-то додумался до интернета, люди уже вовсю играли с углами. Вавилоняне, например, в 2 тысячелетии до н. э. создали первые таблицы синусов. Ну, почти синусов — тогда это были таблицы хорд, но давайте не будем придираться к мелочам.
Эти таблицы можно считать прабабушками современных таблиц синусов. Вавилоняне были настолько крутыми, что их таблицы хорд могли использоваться для решения астрономических задач и предсказания движения небесных тел. Ну, почти как нынешние астрологи, только с реальными математическими вычислениями.

Древняя Греция: когда всё стало серьезно
Перенесёмся в Древнюю Грецию, где тригонометрия нашла своего первого серьёзного гуру — Гиппарха. Этот парень в 2 веке до н. э. не просто забавлялся с углами, он создал первые таблицы хорд для кругов разного радиуса. Да, Гиппарх был настолько зациклен на кругах, что даже по ночам считал углы вместо овец. Но его усилия не пропали даром: его таблицы стали основой для всех последующих тригонометрических исследований.
И тут появляется Птолемей. Нет, не тот фараон, а великий астроном и математик, который в 2 веке н. э. написал «Альмагест» — труд, который можно считать первым тригонометрическим бестселлером. В «Альмагесте» Птолемей объединил знания о хордовых таблицах и сферической тригонометрии, создав своего рода древнегреческий Google Maps для астрономов.
Индия: джья и котиджья — новые тригонометрические магии
Тем временем в Индии всё кипело и бурлило. Ариабхата в 5 веке и Брахмагупта в 7 веке придумали джья и котиджья. Если вы думаете, что это блюда из ресторана, то ошибаетесь — это ранние версии синуса и косинуса. Ариабхата создал таблицы значений джья (синуса) для различных углов, что стало революционным шагом вперёд. Эти ребята не просто изобрели новые функции, но и заложили основу для всех будущих тригонометрических расчётов.
Кроме джья и котиджья, в арсенале индийских математиков был ещё один хитрый инструмент — уктам-джья, аналог ныне уже почти забытого синус-версуса. Эти функции позволяли индийцам решать сложные астрономические задачи с поразительной точностью. В общем, индийская тригонометрия была как айфон своего времени — продвинутая и невероятно полезная.

Исламский мир: эпоха математического ренессанса
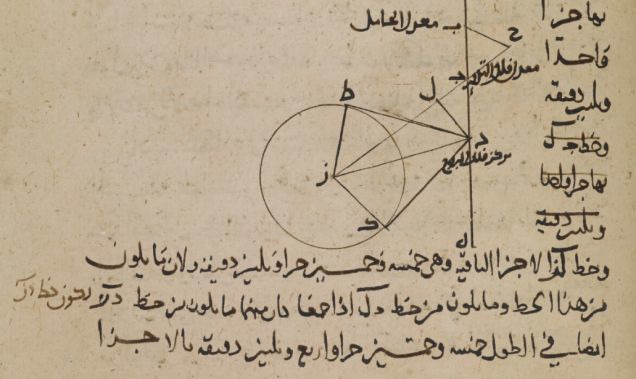
Пока Европа спала в Средние века, в исламском мире тригонометрия процветала. Аль-Баттани в 9 веке и Абу-ль-Вафа в 10 веке развили сферическую тригонометрию и добавили новые функции. Эти ребята играли с углами так, как нынешние подростки играют в видеоигры — только с большей пользой для человечества.
Ещё один важный вклад внёс Абу-л-Вафа, который ввёл тангенс и котангенс в сферическую тригонометрию. Это было как найти священный Грааль — теперь астрономы могли делать точные вычисления для навигации и строительства. Астролябия стала их незаменимым гаджетом, с помощью которого они измеряли углы и строили карты звёздного неба.
Средневековая Европа: возвращение тригонометрии
Наконец, Европа проснулась от средневековой спячки. Герхард Меркатор в 16 веке создал таблицы и карты, которые помогли мореплавателям не теряться в океане. Джон Непер в 1614 году изобрёл логарифмы, что существенно упростило тригонометрические расчёты. Представьте, что у вас появился калькулятор после долгих лет вычислений на пальцах — вот такой эффект произвело его изобретение.
Ренессансные учёные, такие как Виет и Клавий, активно работали над улучшением тригонометрических таблиц и методов вычислений. Это позволило Европе выйти на новый уровень в науке и технике, от артиллерии до архитектуры.
Современная эпоха: тригонометрия выходит на новый уровень
И вот мы добрались до современных титанов математики. Леонард Эйлер в 18 веке ввёл современные обозначения, сделав нашу жизнь проще и понятнее. Карл Фридрих Гаусс в 19 веке работал над неевклидовой геометрией и сферической тригонометрией, доводя всё до блеска. С их помощью тригонометрия стала фундаментом для развития физики, инженерии и даже экономики.
С появлением калькуляторов, тригонометрия потеряла часть своего старого шарма — ведь зачем мучиться, когда можно просто нажать на пару кнопок? Из более чем 30 славных функций в наши дни в ходу осталось всего четыре жалкие штучки. Но не печальтесь, математики-сентименталисты, в этой книге мы устроим настоящее тригонометрическое воскрешение! Поднимем все забытые функции из небытия, потому что иногда красота в математике важнее, чем удобство.
Так что, друзья, когда вы в следующий раз будете ломать голову над тригонометрией, вспомните, что за каждым уравнением стоит многовековая история открытий и приключений. Тригонометрия — это не просто формулы, это эволюция человеческой мысли, путь от древних таблиц хорд до современных методов расчёта.
Немного вспомним о полезном
Прежде чем заниматься тригонометрической некромантией, давайте удостоверимся, что вы знакомы с элементарными геометрическими понятиями. Знаете, что такое треугольник (в современном мире это, увы, не шутка), что такое подобные фигуры, углы; помните теорему Пифагора, известную ещё до него в древнем Египте, и какие существуют угловые меры.
Краткий курс для чайников
Угол: Где без него
Угол — это пространство между двумя пересекающимися прямыми. Если провести две прямые и они встретятся, то угол между ними можно измерить в градусах. Углы бывают острые, тупые и прямые, в зависимости от того, насколько круто пересеклись ваши линии.
Градусы: Легенда о 360 кусочках пиццы
Когда-то давно, в Древнем Вавилоне, сидели мудрецы и думали, как бы им порезать круг так, чтобы никто не обиделся. А круг, надо сказать, не простой, а с самыми что ни на есть магическими свойствами. Решили они, что 360 кусочков будет в самый раз. Почему 360? Да просто! Это число делится на кучу других чисел: 2, 3, 4, 5, 6, 8, 9, 10 и так далее. В общем, под это дело можно было закатить любую вечеринку, и каждый получил бы по своему куску пиццы, то есть круга. Вот и получилось, что полный оборот круга — это 360 градусов. Причём, это не просто красивая цифра, а практически волшебная. Ведь тогда ещё не было калькуляторов и компьютеров, так что мудрецы выбрали самое удобное число для своих расчётов. Это позволило легко делить круг на равные части, проводить измерения и строить свои великие Вавилонские башни. Откуда же такие умные головы знали, что 360 — это магическое число? Ну, есть тут один момент. В Вавилоне ещё и астрономы были что надо. Они заметили, что Солнце за год делает один полный оборот по небу. А год, как известно, это 365 дней (ну почти). Но так как мудрецы любили круглые числа, они округлили до 360. Так и родилась градусная мера угла. И вот так, благодаря древним вавилонским гениям, мы теперь меряем углы в градусах. И это настолько прочно вошло в наш обиход, что даже в космос без градусов не полетишь. Ведь с градусами всё понятно: 90 градусов — это прямой угол, 180 — полукруг, 360 — полный круг. Всё просто и логично. И, конечно же, это дало старт для дальнейших тригонометрических подвигов. У нас теперь есть куча формул и вычислений, основанных на градусах. Так что, несмотря на то, что радианы тоже хороши, градусы — это наша древняя, но всё ещё актуальная мера угла. Всё благодаря мудрецам, которые сидели и ломали голову, как порезать круг на равные части. И сделали это так, что мы до сих пор пользуемся их системой.
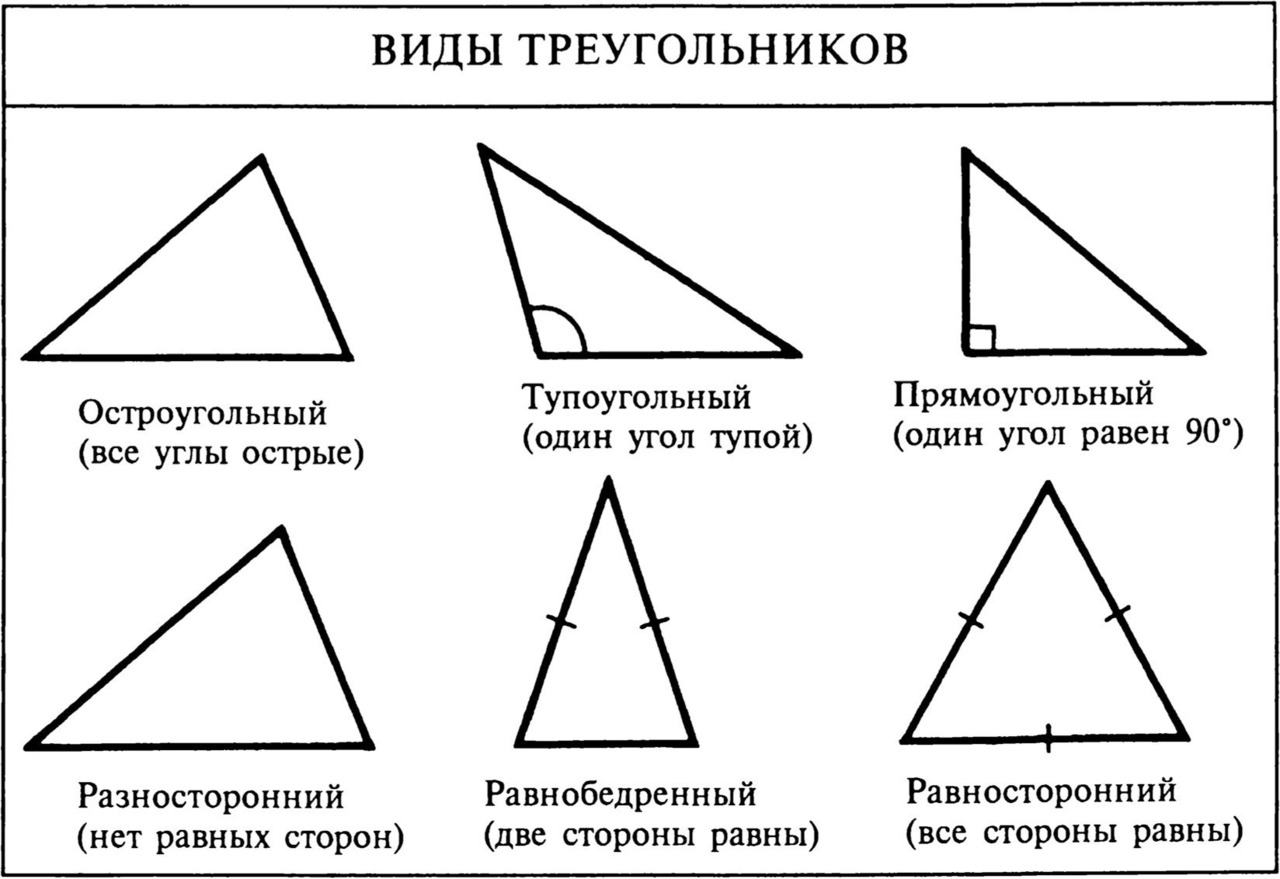
Треугольник — это такая штука с тремя сторонами и тремя углами. Причем, вы не поверите, углы могут быть разной величины, а стороны разной длины. Самая скучная версия треугольника — это равносторонний, все углы и стороны у него одинаковые, но есть и более интересные экземпляры, такие как разносторонний и равнобедренный.
Подобные треугольники: Братья по пропорциям
Подобные треугольники — это такие треугольники, у которых одинаковые углы и стороны пропорциональны. Представьте, что у вас есть большой треугольник и маленький, но они выглядят как увеличенные или уменьшенные копии друг друга. Стороны таких треугольников относятся как A/a=B/b=C/c=k, где k — логично назвать коэффициентом подобия. Он показывает во сколько раз одна фигура является увеличенной копией другой.
И тут начинается магия. Площади подобных треугольников относятся как квадраты длин соответствующих сторон. То есть, если один треугольник больше другого в два раза по стороне, то его площадь будет больше в четыре раза. Простая математика, ничего сложного.
Таким образом, если у вас есть два треугольника и один из них похож на другого, просто в меньшем масштабе, то они подобные. И это открывает перед вами кучу интересных возможностей, как, например, считать их площади, не утруждаясь долгими вычислениями.
В общем, подобные фигуры — это всегда про увеличенные или уменьшенные копии. Будь то треугольник на листе бумаги или гиперкуб в пятом измерении, всё работает по одним и тем же правилам в пространстве любой размерности. Стороны подобных фигур относятся как первая степень k, площади как вторая, объёмы как третья, гиперобъёмы как четвёртая, ну вы поняли…
Окружность
Треугольники — это вообще тема отдельная. Их можно нарисовать сколько угодно, с разными углами и сторонами. А вот с окружностями такой номер не пройдёт. Любая окружность всегда подобна другой. То есть, все окружности, что вы нарисуете, будут одинаково хороши. Это знание в древности привело к понятию числа «Пи».
Если разделить длину окружности изображённой в плоском пространстве (это важно!) на диаметр, то мы аккурат получим 3,1415926… Что бы не писать всю эту бесконечную последовательность цифр, её заменили значком π. Ну а что, удобно и красиво!
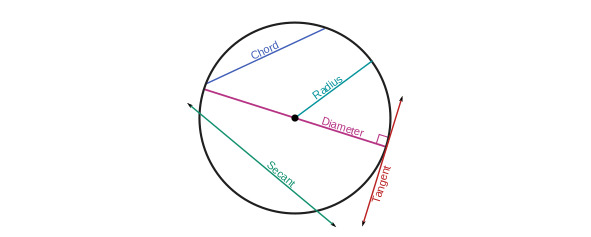
Теперь, зная про π, можем перейти к измерению дуг и углов в радианах. Радиан — это угол, который вырезает дугу длиной, равной радиусу окружности. То есть, если обхватить окружность с радиусом в 1 метр, то угол в 1 радиан вырежет дугу длиной тоже в 1 метр. Логика здесь простая, как дважды два.
Всё это приводит нас к мысли, что π радиан — это 180 градусов. А значит, полный оборот (или 360 градусов) — это 2π радиан. Ну и делаем из этого кучу полезных выводов. Например, что половина оборота (или 90 градусов) — это π/2 радиана. И так далее. Удобно? Ещё как!
Теперь вы можете измерять углы в радианах, как настоящий математический гуру. Плюс, это знание пригодится для расчётов в тригонометрии. И неважно, занимаетесь ли вы древней геометрией или строите новые гиперпространства — всё это работает одинаково хорошо. Так что давайте нырнём глубже в этот удивительный мир тригонометрии и откроем для себя ещё больше магических чисел и функций!
Радианы удобны в математике и физике, потому что они тесно связаны с длиной дуги и радиусом. А как только начали мерять в радианах, оказалось, что это прямо-таки магическая мера. Всё так красиво и просто в формулах получается. Прямо бальзам на душу любого математика. Обозначаются как рад, и международное: rad; от латинского radius — луч, радиус.
Телесные углы, стерадианы: вечеринка продолжается
Но время не стояло на месте, и вскоре люди поняли, что мир-то у нас трёхмерный, и начали думать, как бы им померить углы не только на плоскости, но и в объёме. И тут на арену вышли телесные углы и стерадианы — более продвинутая версия углов для измерения в трёхмерном пространстве.
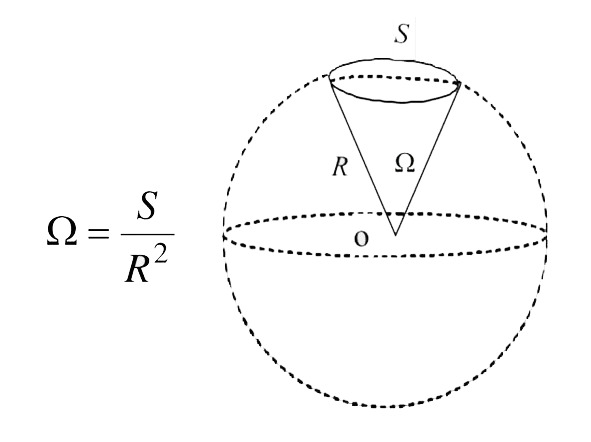
Телесный угол — это такой угол, который вершиной своей упирается в центр сферы, а его «лучи» охватывают часть поверхности этой сферы. Как бы вам это проще объяснить… Представьте, что вы сидите в центре футбольного мяча и светите фонариком. Вот сколько поверхности мяча осветите — это и есть телесный угол.
Теперь к стерадианам. Полный угол вокруг вас в трёхмерном пространстве — это 4π стерадиана (площадь поверхности единичной сферы равна 4π). Если радианами меряют углы на плоскости, то стерадианами — в объёме. Один стерадиан — это такой телесный угол, который отсекает от сферы кусок поверхности, равный квадрату радиуса этой сферы. То есть, если у вас есть шарик радиусом 1 метр, и вы отсекаете кусок поверхности площадью 1 квадратный метр, то это и будет 1 стерадиан. Когда вы смотрите в угол комнаты, то перед вами предстаёт объёмный угол в π/2 стерадиан, что как раз и само просится называться прямым объёмным углом. Плоскость относительно любой своей точки задаёт развёрнутый телесный угол в 2π стерадиан. Круто же?!
Название стерадиан -это смесь древне-греческого στέρεος — твёрдый, объёмный, пространственный, и латыни radius. Обозначается как ср, и в международье как sr. Альтернативой стерадиану является квадратный градус.
Зачем это всё надо? Ну, если вы вдруг решили, что телесные углы и стерадианы — это чисто для гиков-математиков, то глубоко заблуждаетесь. Представьте, что вы астроном, смотрите в телескоп и пытаетесь понять, какой кусок неба охватывает ваше поле зрения. Или вы инженер, занимающийся радиолокацией, и вам нужно точно рассчитать, какой участок пространства покрывает ваш радар. Вот тут-то и приходят на помощь стерадианы. Они делают вашу жизнь проще и точнее.
Так что, хоть на первый взгляд вся эта тригонометрическая магия и кажется сложной, на самом деле это просто разные способы взглянуть на привычные вещи. Градусы, радианы, стерадианы — всё это звенья одной цепи, связывающей плоские и объёмные углы в единую картину. А как только вы это поймёте, мир вокруг станет немного проще и понятнее.
Прямоугольный треугольник: Король тригонометрии
В плоском пространстве у треугольника может быть прямым, только один угол. Если перед вами такой треугольник, то его логично назвать прямоугольным, и это его свойство может значительно упростить вам все расчёты связанные с ним.
Анатомия прямоугольного треугольника проста.
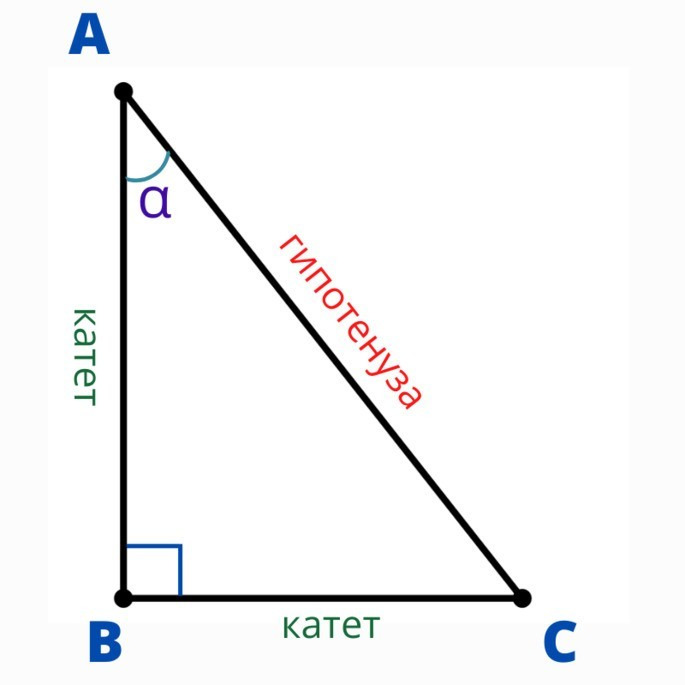
Гипотенуза: Эта самая длинная сторона, напротив прямого угла, является главной звездой шоу. Без неё — никуда.
Катеты: Две стороны, образующие прямой угол. Катеты — это такие скромные труженики, которые всегда в тени гипотенузы, но именно они делают весь тяжёлый подъём.
Прямой угол: Угол в 90 градусов, который делает этот треугольник особенным. Прямой угол — это как VIP-пропуск на любую геометрическую тусовку.
Теорема Пифагора
Пожалуй, самая знаменитая из всех теорем. Ассоциируется прежде всего с древнегреческим математиком Пифагором, но была известна ещё в древнем Египте. Давайте рассмотрим одно из самых простых её доказательств, коих на данный момент насчитывается не менее 400.
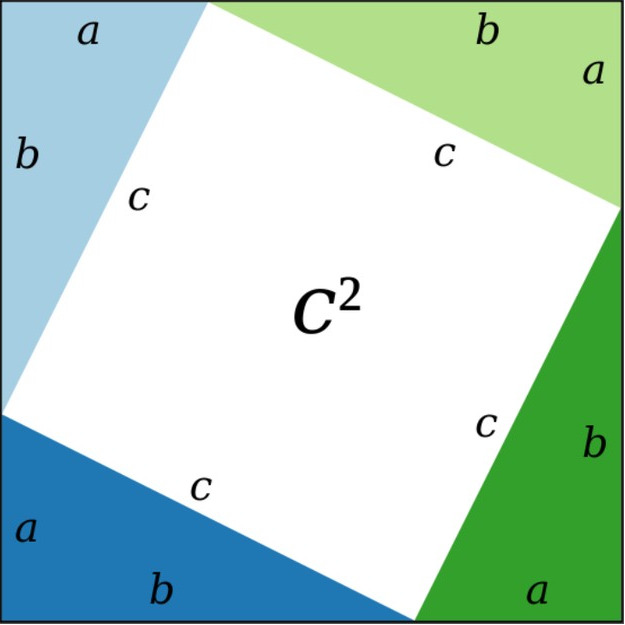
Нужно доказать, что c² = a² + b²:
Это квадрат, в котором есть 4 одинаковых треугольника со сторонами a, b, и c:
Каждая сторона этого квадрата имеет длину a + b, значит его общая площадь: S = (a + b) (a + b); Площадь наименьшего квадрата (который находится внутри, под наклоном): c²; Площадь каждого из треугольников: ab/2. Значит площадь всех четырёх вместе:
4ab/2 = 2ab;
Сумма наименьшего квадрата и треугольников:
S = c² +2ab;
Площадь большого квадрата (S = (a + b) (a + b)) равна сумме наименьшего квадрата со всеми треугольниками. Значит:
(a + b) (a + b) = c² +2ab
a² +2ab + b² = c² +2ab
a² + b² = c²
Что и требовалось доказать.
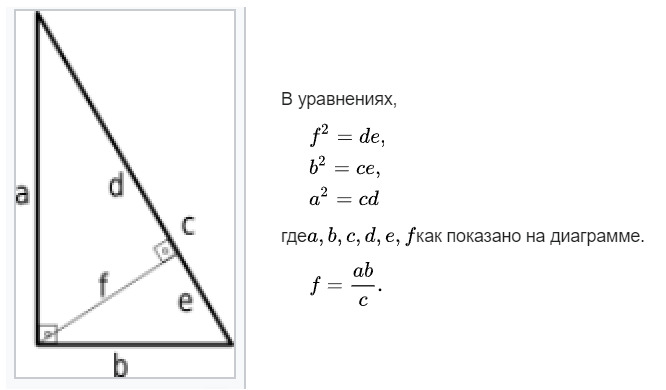
Высота прямоугольного треугольника
Она обладает рядом свойств, которые будут полезны в наших дальнейших изысканиях. Поэтому докажем и их.
Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.
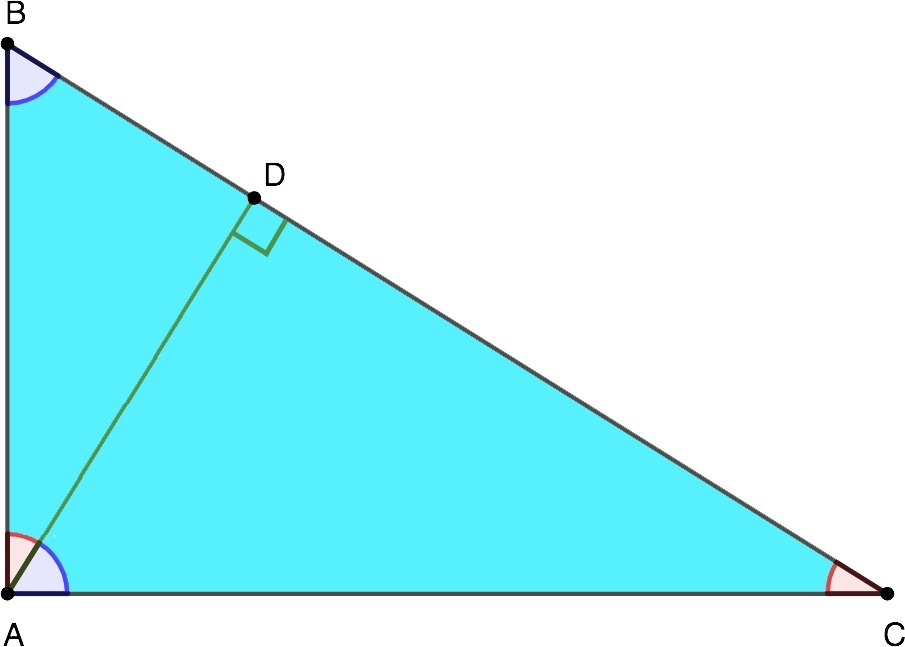
И вот тут начинается самое интересное. Это деление — не хаотичный развод пары катетов, а элегантное создание двух мини-копий оригинала. Каждый из вновь образованных треугольников, как верный сын, наследует черты родителя: прямой угол и острый. А раз два угла равны, то по первому признаку подобия — добро пожаловать в клуб! Они подобны друг другу и большому папе-треугольнику. Это свойство — не просто абстрактная забава для скучающих геометров. Это фундамент, на котором стоит всё здание тригонометрии. Именно из этого подобия вытекают все эти ужасно полезные на практике соотношения, позволяющие, к примеру, вычислить высоту пирамиды по длине её тени, пока ты лениво прислонился к сфинксу.
Этот скромный отрезок вдруг оказывается центральным персонажем драмы, геометрическим Мориарти, который дёргает за ниточки отношений между проекциями катетов. Он устанавливает невидимые, но строгие пропорциональные связи между всеми элементами конструкции, создавая единую, гармоничную систему. И доказывается это элементарно — через подобие тех самых двух маленьких треугольничков, которые она же и породила! Красота и замкнутость логического круга просто поражают.
Таким образом, эта высота — не просто перпендикуляр. Это мост, это преобразователь, это универсальный ключ к решению целого класса задач. Она связывает воедино катеты, гипотенузу и её сегменты, создавая стройную систему уравнений, где, зная два элемента, можно отыскать все остальные. Игнорировать её — всё равно что пытаться собрать пазл, выбросив половину деталей. Она — душа прямоугольного треугольника, спрятанная прямо у всех на виду.

Сама высота имеет ещё приколы. Например, есть теорема о среднем по палате геометрическом для высоты. Нам её поможет доказать уже доказанное.

Из подобия порождаемых высотой треугольника треугольников, следуют весьма полезные свойства катетов. Это можно назвать проецированием катетов.
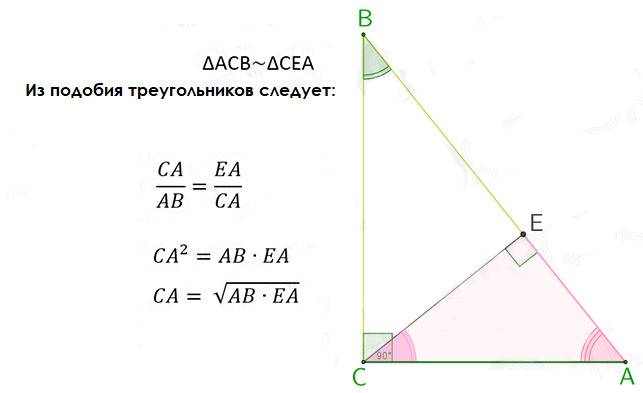
Далее из всего выше доказанного, следует равенство которое в последствии породит ещё одну сущность нашего тригонометрического зоопарка. Но пока обойдёмся без спойлеров.
Сферическая тригонометрия
При первом знакомстве, после освоения плоской категорически выносит мозг. На сфере у треугольников могут быть аж три прямых угла, и при этом их стороны, тоже, ВНЕЗАПНО, измеряются в градусах! Так что если у вас есть несколько шариков разных размеров, и треугольники на них имеют одинаковые углы, но разные (казалось бы) по длине стороны, то на самом деле это одинаковые равные треугольники.
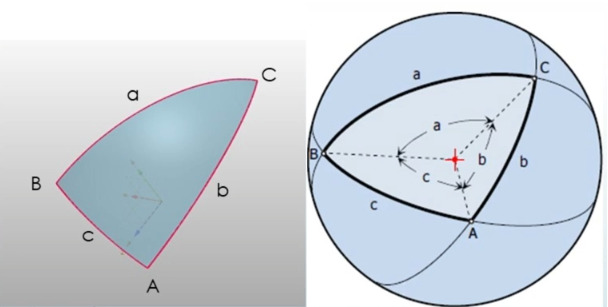
Сферические треугольники образуются окружностями больших кругов — тех сечений сферы, что проходят сквозь её центр.
Но это только начало. В сферической тригонометрии сумма углов треугольника всегда больше 180 градусов, и это может слегка взорвать вам мозг, если вы привыкли к классическим евклидовым правилам. Чем больше треугольник, тем больше его углы. Представьте себе сферическую поверхность, и на ней огромный треугольник, у которого сумма углов может запросто достигать 270 градусов или даже больше.
Сферическая тригонометрия — это как математическая версия «Алисы в Стране чудес». Всё, что вы знали о треугольниках, внезапно становится странным и удивительным. Когда привычные правила плоской геометрии отправляются в отпуск и уступают место новым, экзотическим законам. Представьте себе геометрию на поверхности шара, где прямые линии заменяются дугами больших кругов, и всё сразу становится немного странным.
Ещё одна диковинка сферической тригонометрии — это локсодромы и ортодромы. Локсодрома — это линия, пересекающая все меридианы под одним и тем же углом, что делает её идеальной для навигации, потому что курс корабля или самолёта остаётся постоянным. Ортодрома — это кратчайшее расстояние между двумя точками на сфере, что делает её более экономичным маршрутом.
Сферическая тригонометрия не просто красивая абстракция — она крайне полезна в астрономии, геодезии и навигации. Корабли, самолёты и даже спутники используют эти принципы для точного расчёта маршрутов.
Так что, если вам кажется, что треугольники на плоскости — это скучно и банально, попробуйте сферическую тригонометрию. Она как минимум заставит вас переосмыслить, что такое «прямой угол» и как вообще работают углы и стороны. Мир сферической геометрии — это путешествие в страну чудес, где привычные правила гнутся и ломаются, открывая совершенно новые горизонты!
Зоопарк тригонометрических функций ○
Тригонометрические функции, они же «главные герои» тригонометрии, измеряют отношения сторон в треугольнике, но их влияние простирается гораздо дальше. Эти функции, вроде синуса и косинуса, помогают находить углы и длины сторон. Изначально их можно ввести в треугольнике.
Синус и косинус можно также представить как координаты точки на единичной окружности. Но мы расширяем горизонты.
Как только всё становится более-менее понятно, математики решают добавить ещё больше веселья. Возникают гиперболические функции: гиперболический синус (sh) и гиперболический косинус (ch). Они работают подобно обычным синусу и косинусу, но вместо окружности используются гиперболы. Потом естественно возникает соблазн расширить сиё понятие на остальные конические сечения — параболу, эллипс. Здесь начинается настоящая магия. Вводятся такие чудеса как лемнискатные функции, которые являются «гибридами» тригонометрических и гиперболических функций. Или, например, функция Гудермана, которая связует обычные тригонометрические функции с гиперболическими.
Но каков же тогда критерий тригонометричности?
Настоящие тригонометрические функции обязаны, как минимум, быть связаны с углами и длинами сторон, но не обязательно только в треугольнике. Всё, что вытекает из тригонометрических отношений и может быть выражено через углы, попадает в этот клуб.
И вот так, из простого измерения тени гномона, тригонометрия превратилась в сложнейшую науку с множеством функций и приложений. Так что, готовьтесь к увлекательному путешествию по её лабиринтам! Мы рассмотрим все известные на данный момент тригонометрические функции на треугольнике, окружности и так далее.. Ворота зоопарка открываются!
Синус sin
Синус — это тот самый парень, с которого начинается вся тригонометрия. Представьте, древние математики, тыча пальцем в треугольник, вдруг осознают, что отношения сторон могут быть полезными, и вот вам — синус!
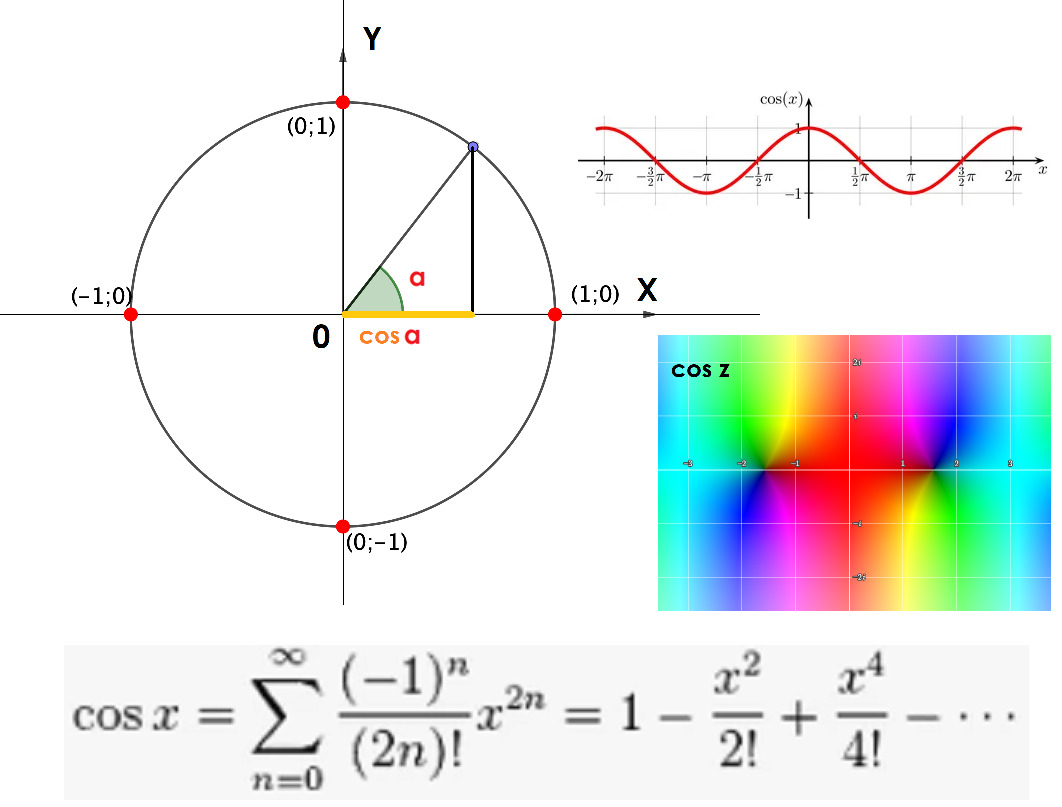
Сначала синус представлялся как отношение противолежащей стороны к гипотенузе в прямоугольном треугольнике. Но потом его нашли на единичной окружности. И там синус — это просто координата 𝑦 y точки на окружности, соответствующей углу α
Происхождение сегодняшнего названия было долгим и полным приключений: Окончательное название «синус» произошло из латинского «sinus», что переводится как «изгиб» или «залива». Однако, всё началось с санскритского термина «джья» (च्), который арабские учёные превратили в «джиба» (جب). Европейцы, видимо, решили, что это слишком скучно, прочитали транскрипцию коряво и назвали его «sinus».
В обычной жизни синус появляется в самых неожиданных местах: от квантовой физики до анализа музыкальных волн.
Итак, синус — это не просто математическая функция, это целый культурный феномен, переживший века и трансформации, чтобы стать фундаментальной частью математики и науки в целом.
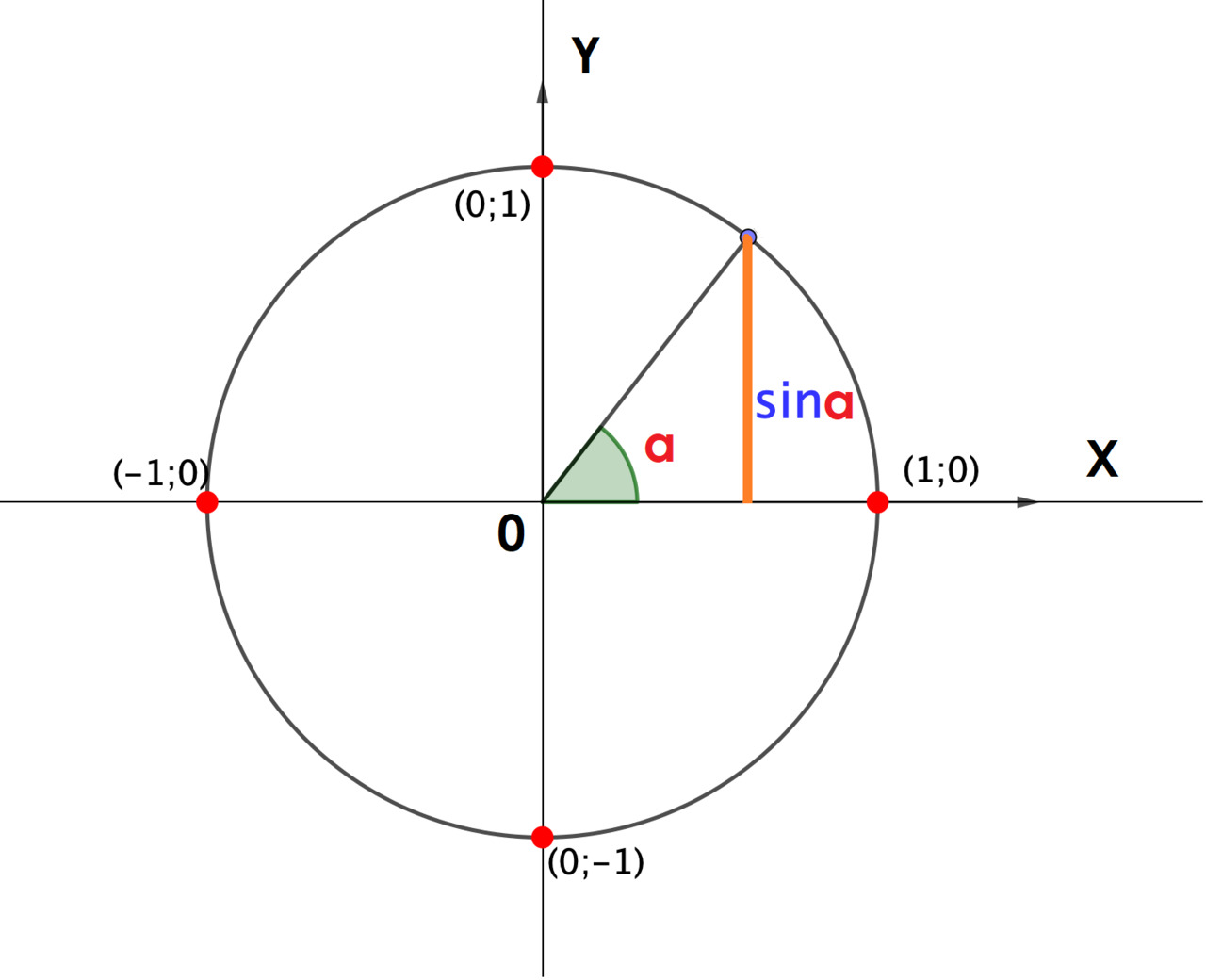
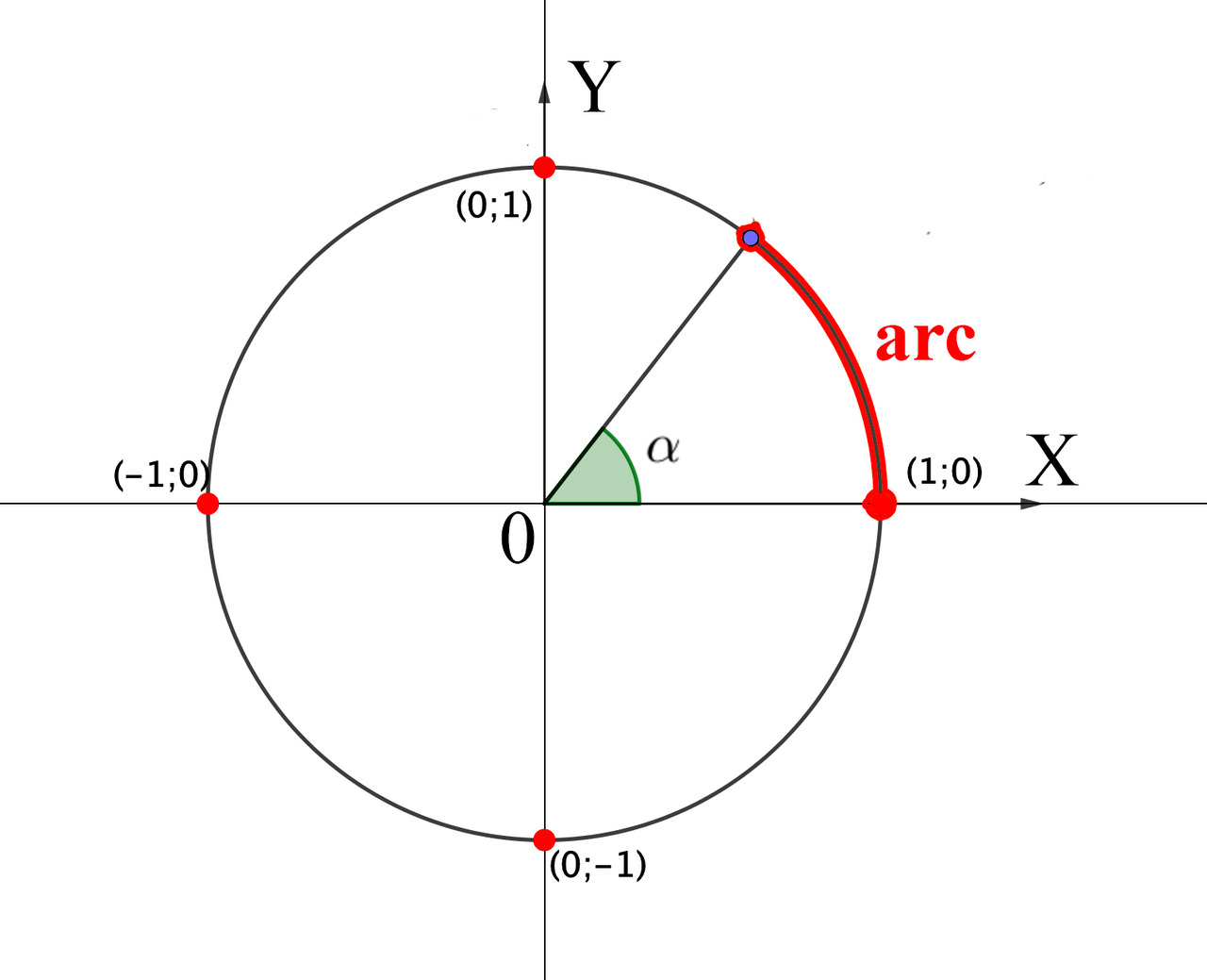
Представьте круг радиусом 1 (да, именно единичный). Берём точку на окружности, соответствующую какому-нибудь углу. Теперь проецируем её на ось y. Ба-бах! Это и есть ваш синус. Да-да, высота от оси x до точки на окружности — это ваш драгоценный синус. Удивительно просто, а как звучит! Любые волны — это модифицированная версия синуса.
Как же из нашей прекрасной единичной окружности рождается синусовая волна? Сначала давайте поймём, что наш угол в радианах (не забываем, единичная окружность) будет гулять по оси x от 0 до 2π. Теперь берём и раскручиваем угол, а точнее его проекцию на ось y. Процесс следующий: Стартуем с угла 0: синус тоже 0. Продвигаемся к π/2: синус растёт до 1. Двигаемся к π: синус обратно падает до 0. Дальше к 3π/2: синус сползает до -1. И наконец, возвращаемся к 2π: синус опять становится 0. Теперь вы разворачиваете эту всю красоту на плоскость, и у вас появляется волна. Да, волна из кружочка! И получается она вот так: перемещая точку по окружности, вы замечаете, как проекция на ось y колеблется вверх-вниз. Эти колебания и образуют синусоидальную волну на графике. Синус — это не просто функция, это целый ритуал превращения углов в волны.
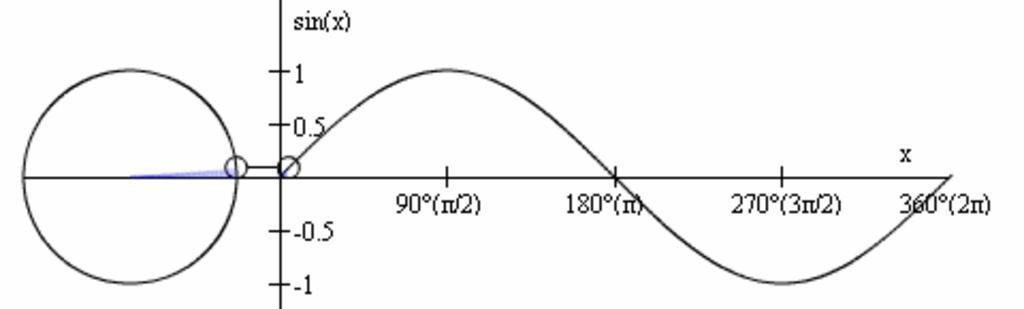
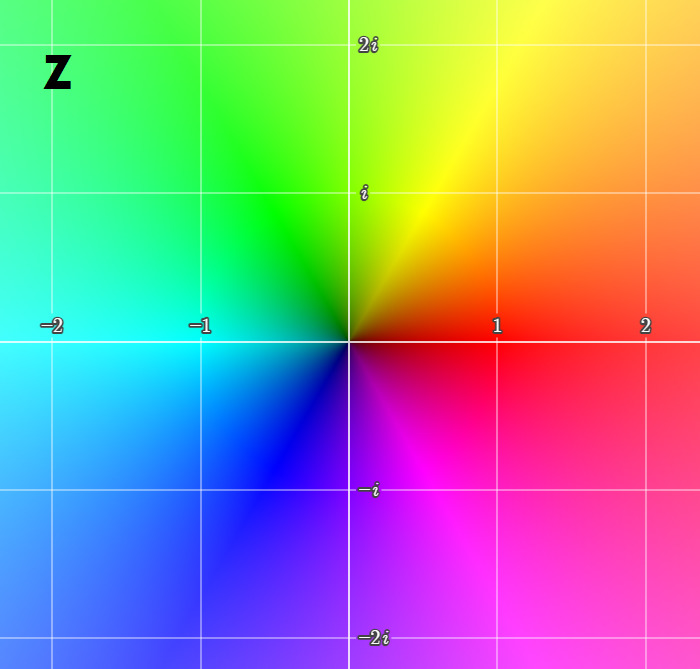
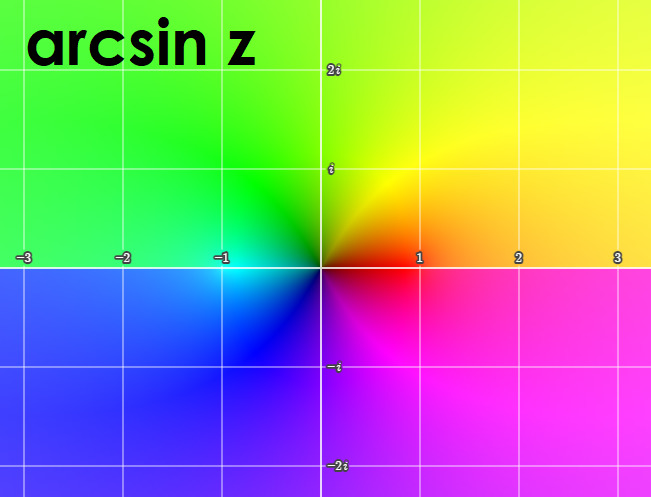
Для построения четырёхмерного графика синуса в комплексной плоскости будем пользоваться такой раскраской аргумента.
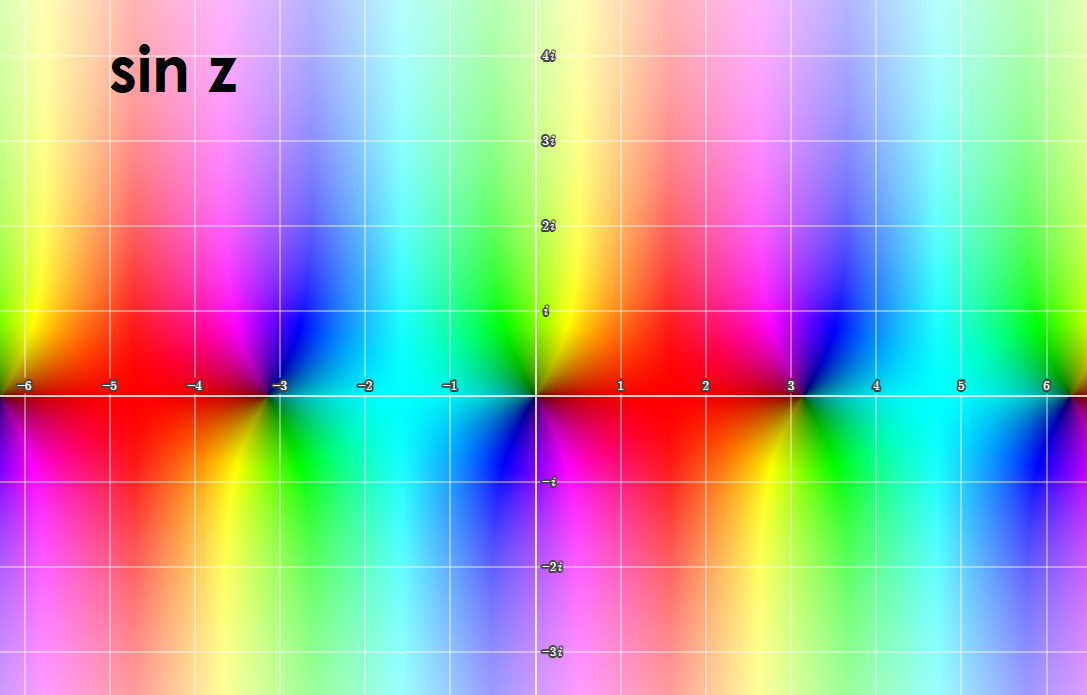
Интеллектуальное большинство рассматривает функции в основном только на прямой вещественных чисел. Но мы то с вами знаем, что это слишком ограниченный взгляд. Поэтому для полноты картины, будем так же приводить графики тригонометрических функций в настоящих, комплексных числах. Кстати, комплексные числа можно считать последним расширением человеческой числовой системы. Это вполне оправданно, ибо дальнейшее (кватернионы, седенеоны, октавы,…) логичнее называть числоподобными объектами, так как они теряют многое, присущее числам (коммутативность, и ассоциативность в ещё более запущенном случае). Более того, оказалось, что комплексные числа реальнее чем те, которыми читатель считает сдачу в магазине.
Мы можем изображать четырёхмерный мир на плоскости, благодаря методу раскраски области определения функции. В этом случае модуль комплексного числа отображается «светлостью»: чёрное — ноль, белое — бесконечность. Аргумент комплексных чисел от 0 до 2π задаём цветами радуги, что на самом деле можно сделать в разном порядке цветов. Поэтому, изображая четырёхмерные миры, не забывайте утруждать себя демонстрацией исходной вашей палитры цветов соответствующей аргументам.
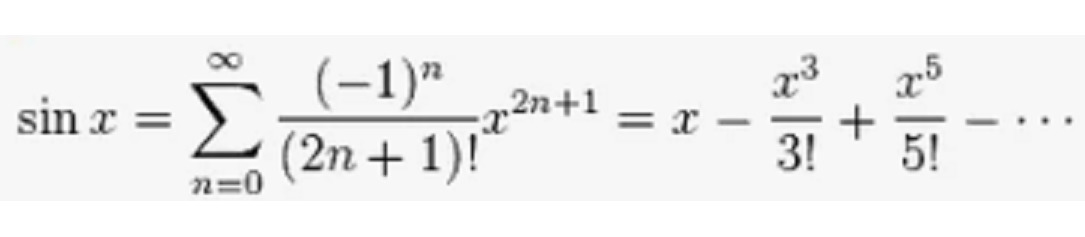
Говоря о тригонометрических функциях, нельзя не сказать и об обратных к ним. Арк-функции, или обратные тригонометрические функции, — это те же самые объекты, только задом наперёд. Как это работает? Очень просто: если тригонометрическая функция переводит угол в значение, то арк-функция берёт это значение и возвращает угол.
Название «арк» пришло не из цирка, а из латинского слова «arcus», что значит «дуга». Потому что арк-функции возвращают угол, который соответствует данной дуге на окружности. Например, арк-синус arcsin говорит: «Эй, синус, давай мне угол, который даёт такое значение на окружности».
Почему это важно? Арк-функции используются в куче математических задач, где нужно найти исходный угол по известному значению тригонометрической функции. Без них геометрия и тригонометрия были бы намного сложнее.
Так что, когда вы видите приставку «арк», знайте: это просто функция, которая берёт значение и возвращает угол. И помните: в мире тригонометрии всё всегда возвращается к кругу.
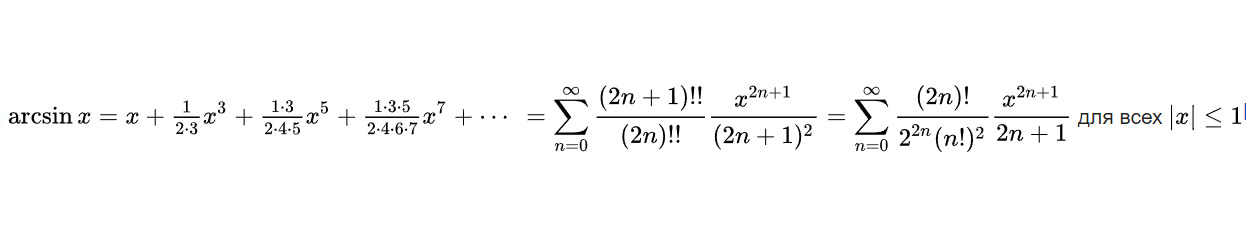
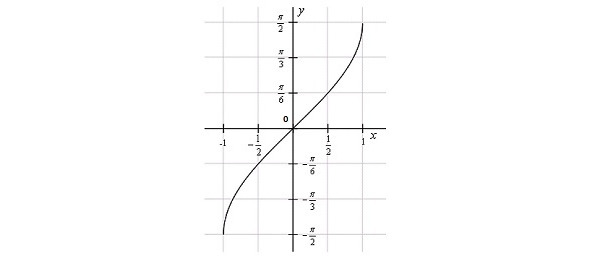
Строим график обратной функции арксинуса мы стандартным образом: Берём наш старый добрый график функции, и отражаем его относительно прямой y=x. Вуаля, график обратной функции готов! Это общий принцип обращения монотонных функций. Но так как синус синусоидален не монотонен, то приходится сталкиваться с необходимостью выбрать один вариант из бесконечного числа возможных воплощений арксинуса. Теоретически его можно было задать разместив вертикальный изгиб, хоть на высоте 500π, но решили не усложнять жизнь и взяли обрубок вокруг ноля. Почему? Да потому что так удобнее и понятнее! Чтобы построить наш график, берём кусок синуса, где он монотонный (то есть, без всяких загибов), и отражаем относительно диагонали y=x. В результате получается график, который растёт ровно там, где нужно, и не делает лишних телодвижений.
Для арксинуса обычно берут кусок синуса от −π/2 до π/2. Потому что на этом промежутке синус ведёт себя прилично, и это покрывает все значения от −1 до 1.
Для исчерпывающего описания тригонометрических функций нашего зоопарка, мы в дальнейшем так же будем приводить их место на тригонометрчиеском круге (если это возможно), происхождение названия, обратную функцию, их вещественный и комплексный 4-х мерный график с рядами Тейлора для удобного вычисления. XXI век всё таки на дворе, и даже реликтовые функции, которые вычислялись ранее с помощью умножения в столбик и таблиц, сейчас, в новой жизни получили удобный способ вычисления в виде бесконечных рядов. Так что готовьтесь, будет весело и познавательно!
Косинус cos
Рассмотрев синус, мы уже познакомились с ещё одним типом функций — арк-функциями. Следующий наш экспонат, одновременно представляет ещё один тип тригонометрических сущностей — ко-функций. Приставка co происходит от латинского complementary, означающего дополнительный. Дело в том, что первично синус рассматривается как отношение противолежащего к углу катета (того что напротив) к гипотенузе. Соответственно в треугольнике, у которого один угол прямой, а другой мы рассматриваем как основной, логично оставшийся третий назвать дополнительным. Тогда можно рассмотреть синус дополнительного угла. Его то и называют ко-синусом. Но если же плясать от основного рассматриваемого угла, то можно определить косинус, как отношение прилежащего катета к гипотенузе. Такие дела. Аналогичным образом будут определяться практически все остальные ко-функции в нашем зоопарке, хотя будут и исключения.
Если синус — это высота точки на единичной окружности, то косинус — это её горизонтальная проекция. Фишка в том, что синус и косинус на самом деле — это просто фазы одной и той же функции. Смещение фазы на 90 градусов (или π/2 радиан) превращает синус в косинус и наоборот. Эта простота и симметрия делают их незаменимыми в математике и физике. Наконец, теперь мы можем начать выражать одни тригонометрические функции через другие:
cos α = sin (π/2 — α)
Есть у косинуса и обратная функция — арккосинус. И для её определения тоже приходится делать выбор из бесконечного числа вариантов.
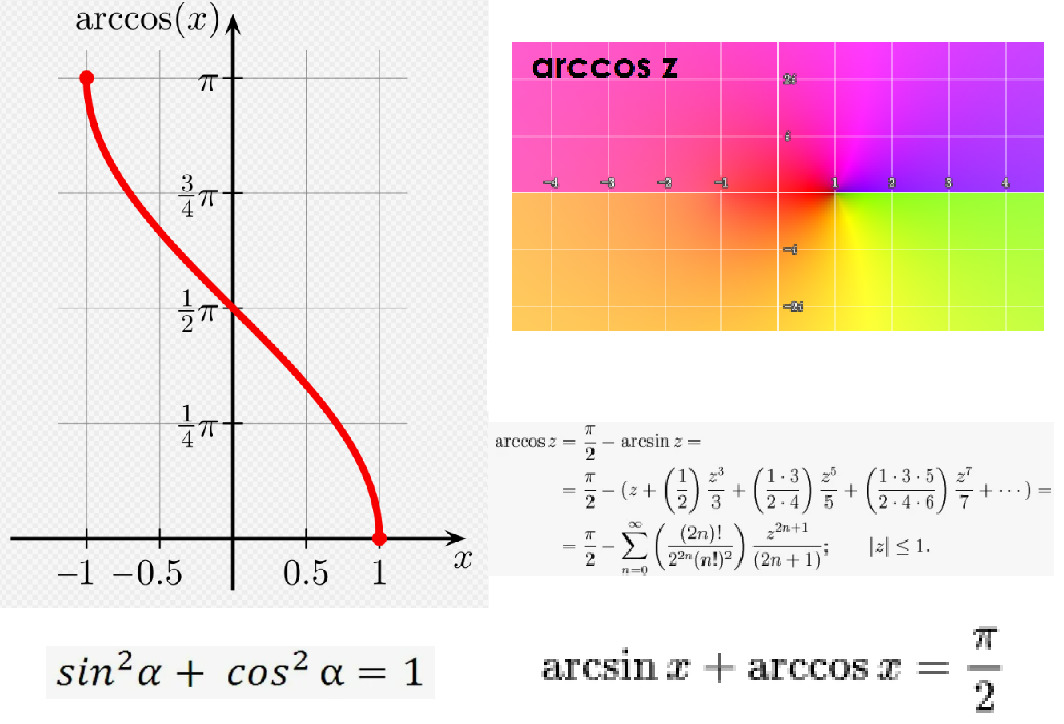
Арккосинус — это та штука, которая любит выглядеть загадочно и сложно, но на самом деле он просто брат арксинуса. Вот представьте, что арккосинус стоит перед зеркалом и видит арксинус. Почему так? Потому что они связаны через π/2. Всё благодаря нашему старому другу, треугольнику. Если у вас есть угол θ, то его косинус — это просто синус угла (π/2 — θ). И наоборот.
Арккосинус выбирается на интервале от 0 до π, чтобы оставаться функцией, т.е. принимать одно значение для каждого аргумента. И в отличие от арксинуса, который прыгает в диапазоне от
-π/2 до π/2, арккосинус решил обитать в более спокойных водах.
Почему они в сумме дают π/2? Потому что арксинус и арккосинус — это два лица одного треугольника. Сумма их углов всегда будет π/2. Если синус измеряет вертикальную часть, то косинус измеряет горизонтальную. Таким образом, если вы знаете арксинус, вы всегда можете найти арккосинус, вычтя его из π/2. Вот такая простая, но гениальная тригонометрическая магия.
Так что, когда в следующий раз вы будете ломать голову над арккосинусом, просто помните: это всего лишь арксинус, смотрящий на себя в зеркало.
Просинус prosin
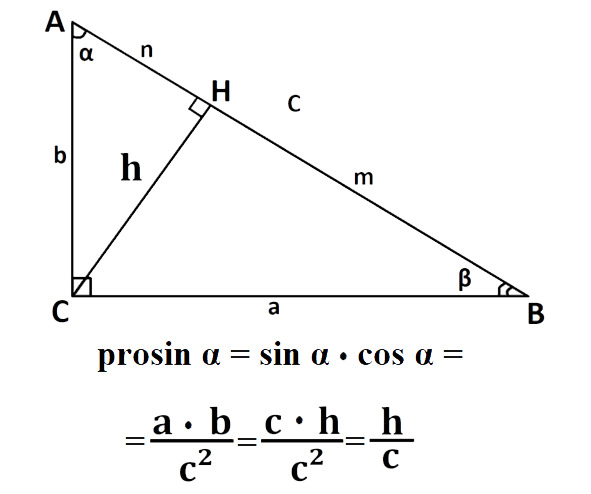
Встречайте первую устаревшую функцию из нашего зоопарка! Просинус prosinus является отношением высоты проведённой из прямого угла к гипотенузе к этой самой гипотенузе. Данную функцию можно так же выразить как просто произведение синуса на косинус. То есть:
prosin α = sin α cos α
Интересно сгинувшее в тьме веков происхождение названия данной древней функции. Действительно, слово «про» в данном случае звучит несколько необычно для обозначения произведения.
Существуют две основные версии происхождения этого термина:
1. От латинского «pro» в значении «вместо», «подобно». То есть просинус функционально похож на синус, но немного отличается, заменяя синус в некоторых вычислениях. Если взглянуть на его график то это действительно фактически копия синуса только слегка масштабированная в сторону уменьшения.
2. От греческого «προ» (про), означающего «перед», «прежде». Просинус могли называть «предсинусом», подразумевая, что это функция, предшествующая синусу в цепочке вычислений.
На кой он был нужен? Просинус, хотя и звучит как зловещий родственник синуса, был весьма полезен в астрономии, особенно при переходе между горизонтальной и экваториальной системами координат. Когда древние звездочёты считали склонение и часовой угол, просинус был их лучшим другом.
Этот странный объект помогал упрощать тригонометрические тождества, касающиеся двойных углов и сумм/разностей углов. В те времена, когда считали на пальцах и пользовались таблицами логарифмов, просинус был гением оптимизации: умножить два числа всегда проще, чем искать синус суммы углов. Да, просинус был вспомогательной функцией, но для навигации и астрономии прошлого он был незаменим. А теперь, когда у нас есть компьютеры, необходимость в нём отпала. Но его вклад в историю математики и астрономии остаётся неоспоримым.
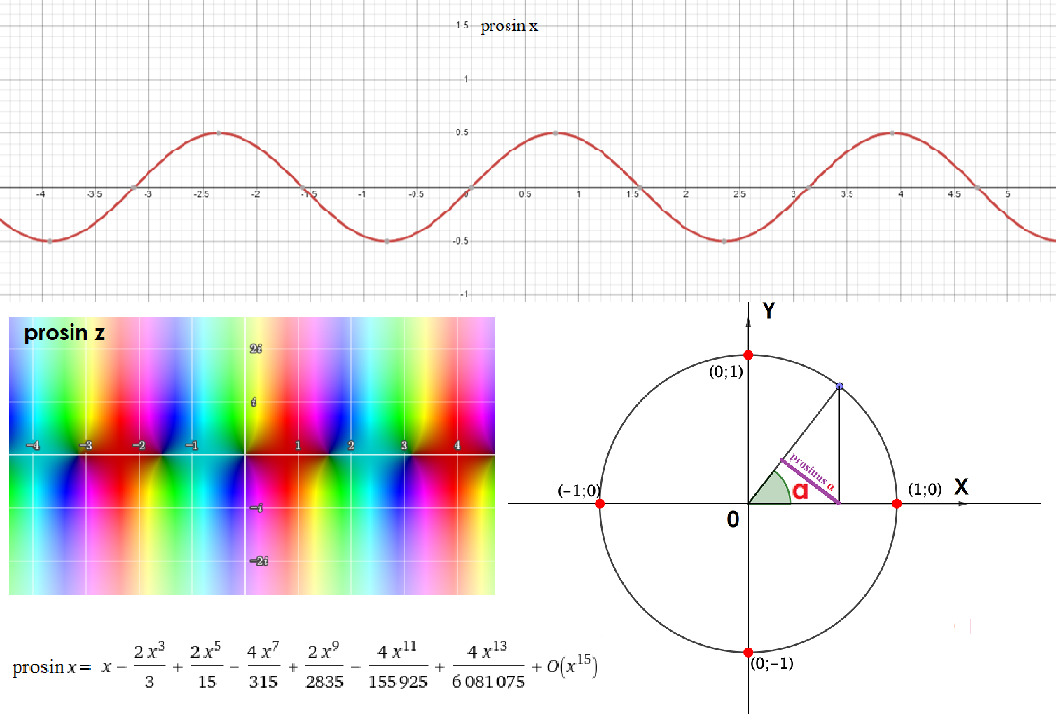
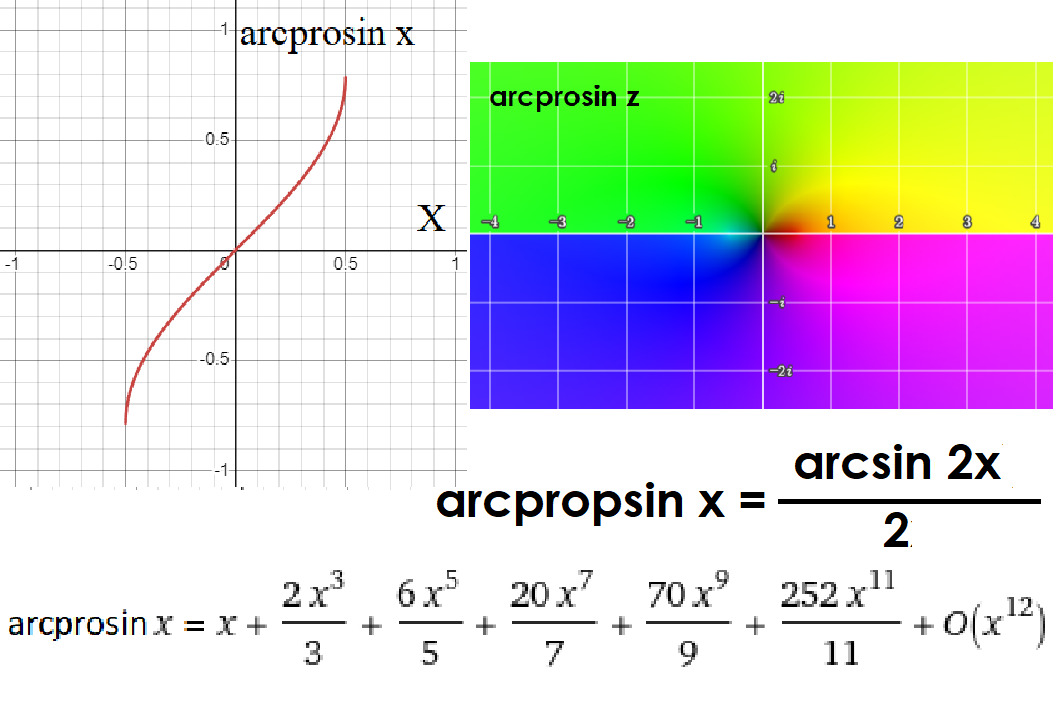
Обратная функция к нему со всей очевидностью называется arcprosin, но вот уже выражается через рассмотренную ранее аркфункцию чуть сложнее. График так же является повёрнутым обрубком исходной функции на участке монотонности. Так как функция эта сама по себе устаревшая, рассмотрим её применение подробнее. Просинус полезен для нахождения высоты прямоугольного треугольника. Зачем это нужно? Ну, представьте себе, что вы моряк, бороздящий просторы океана, или астроном, наблюдающий за звёздами. В обоих случаях вам нужно точно рассчитывать углы и высоты, чтобы не сбиться с курса или правильно направить телескоп. Эта функция также использовалась в навигации для определения расстояний и высот объектов на горизонте. В архитектуре и строительстве она помогала инженерам правильно рассчитывать нагрузки и высоты конструкций, чтобы здания не падали, как карточные домики. Пока не изобрели компьютеры, которые могут всё просчитать за доли секунды, просинус был незаменимым инструментом. Таблицы логарифмов и геометрические отношения, такие как просинус, существенно упрощали жизнь учёных и инженеров прошлого. Сегодня мы можем только восхищаться изобретательностью тех, кто использовал его для великих дел.
Кас cas
Ещё одна комбинация уже известных нам синуса и косинуса имеет таки самостоятельное название. Но это не древняя функция, а новодел. Называется она cas — это сокращение от cosine and sine. Другое её название — ядро Хартли.
cas α = cos α + sin α
В этот раз это просто сумма косинуса и синуса. В математике преобразование Хартли — это интегральное преобразование, предложенное Ральфом В. Л. Хартли в 1942 году. Оно тесно связано с преобразованием Фурье, но преобразует действительные функции в действительные. В отличие от преобразования Фурье, Хартли не требует использования комплексных чисел и является обратным самому себе.
Как и любая уважающая себя тригонометрическая функция, cas α может быть изображена на тригонометрическом круге. Представьте себе комбинацию двух отрезков, отвечающих синусу и косинусу, соединённых вместе одним концом. Красота, да и только!
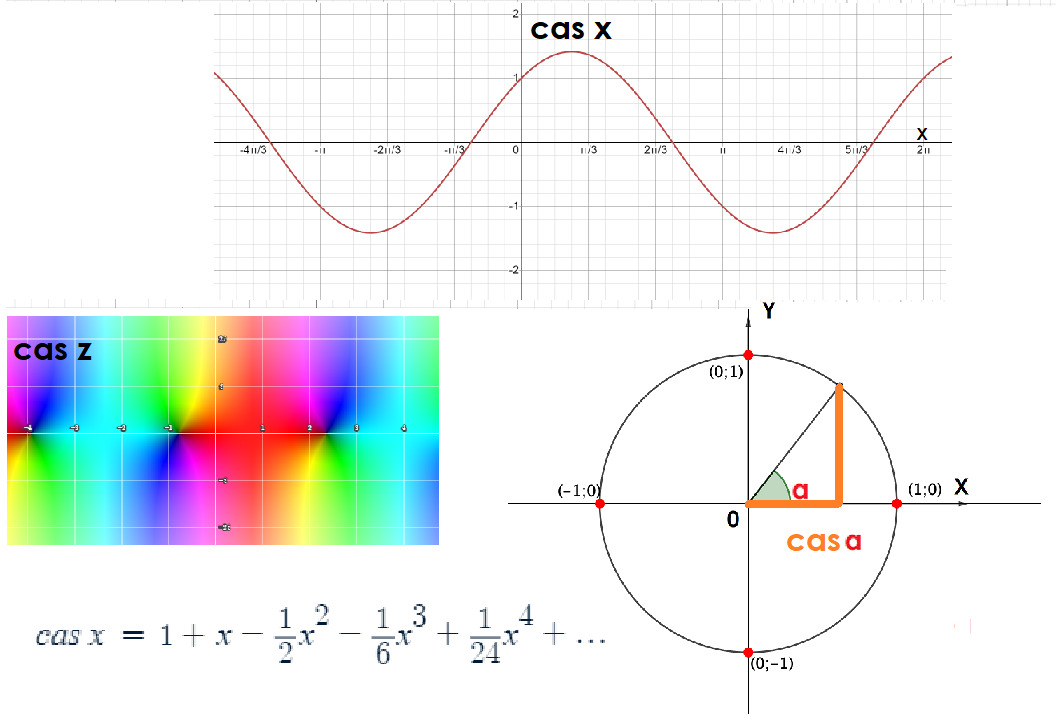
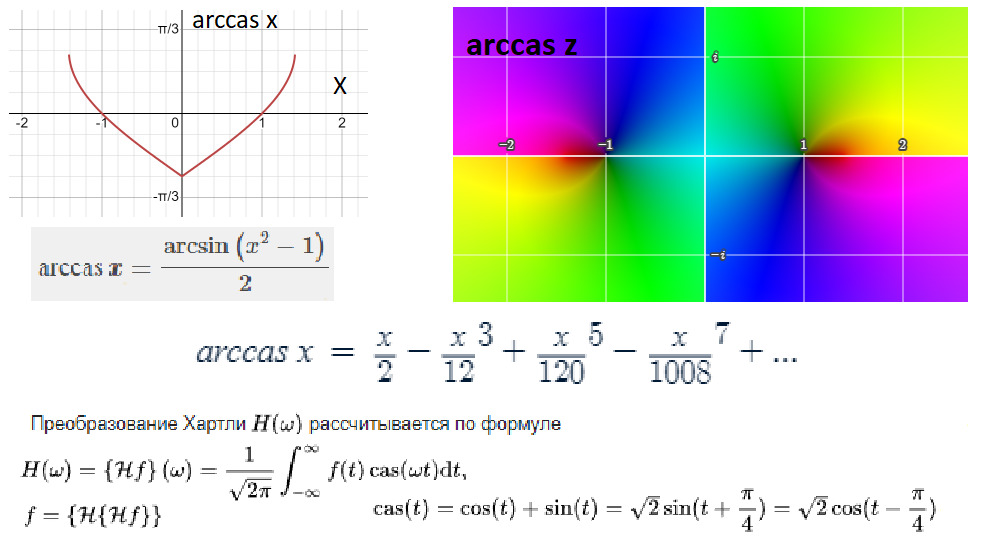
Такое переобозначение через символ cas α упрощает преобразования и расчёты, особенно при работе с действительными функциями. Это отличное дополнение к нашему тригонометрическому зоопарку, превращающее скучные формулы в элегантные математические выражения.
Но есть у cas и обратная функция, которая ведёт себя почти как арксинус, только сломанный в середине и оттого ставший симметричным. Что это значит? Если арксинус изящно поднимается и опускается в пределах [−π/2,π/2], то arccas делает тот же трюк, но с зеркальной симметрией относительно оси ординат. Выглядит странно, но на практике иногда бывает удобным.
Хорда crd
Когда-то давным-давно, в те времена, когда математики были жрецами и гадали на звёздах, появилась функция «Хорда». Хорда — это прабабушка синуса, которая в своё время была чуть ли не звездой античного тригонометрического бала. Она измеряет длину отрезка, соединяющего две точки на окружности, и звучит как «chord» — почти как аккорд, но вместо музыки у нас тут математика. В общем, все древние астрономы и геометры в Египте и Греции обожали её, пока не появился синус и не вытеснил старушку на пенсию.
Когда радианы вошли в моду, стало ясно, что синус — это всего лишь половина хорды. То есть, чтобы получить хорду, достаточно просто удвоить синус половинного угла. Формула звучит примерно так:
crd α = 2 sin (α/2)
Именно из этой формулы видно, что хорда и синус тесно связаны.
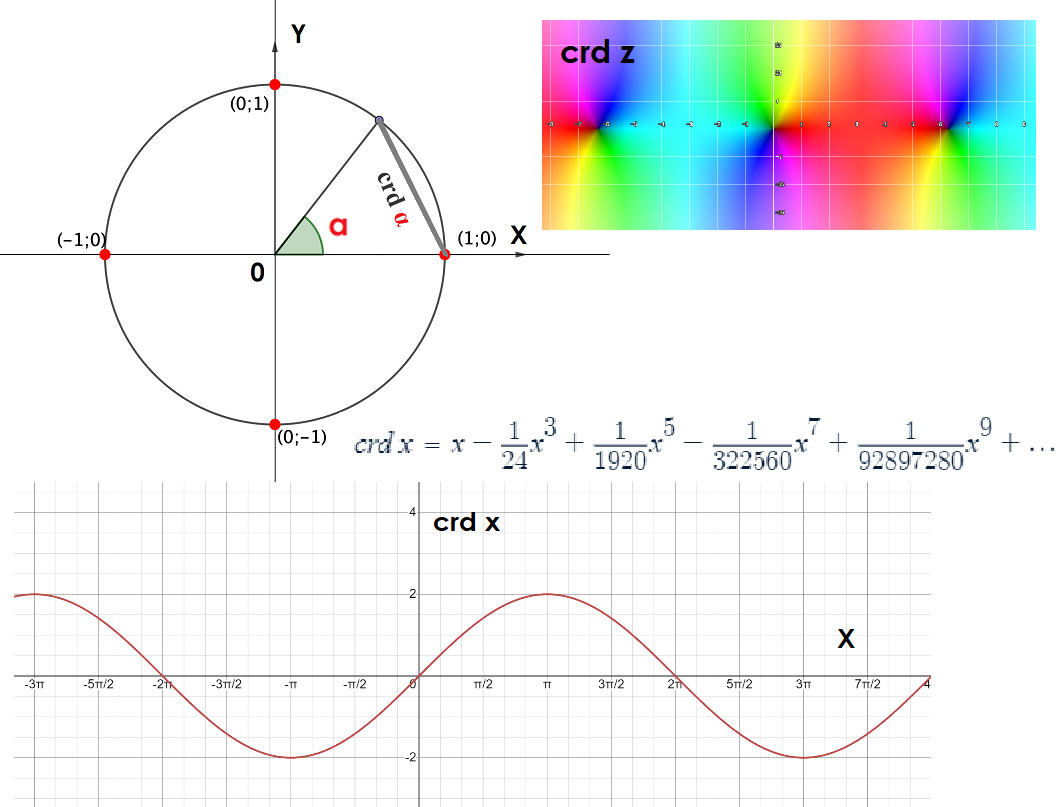
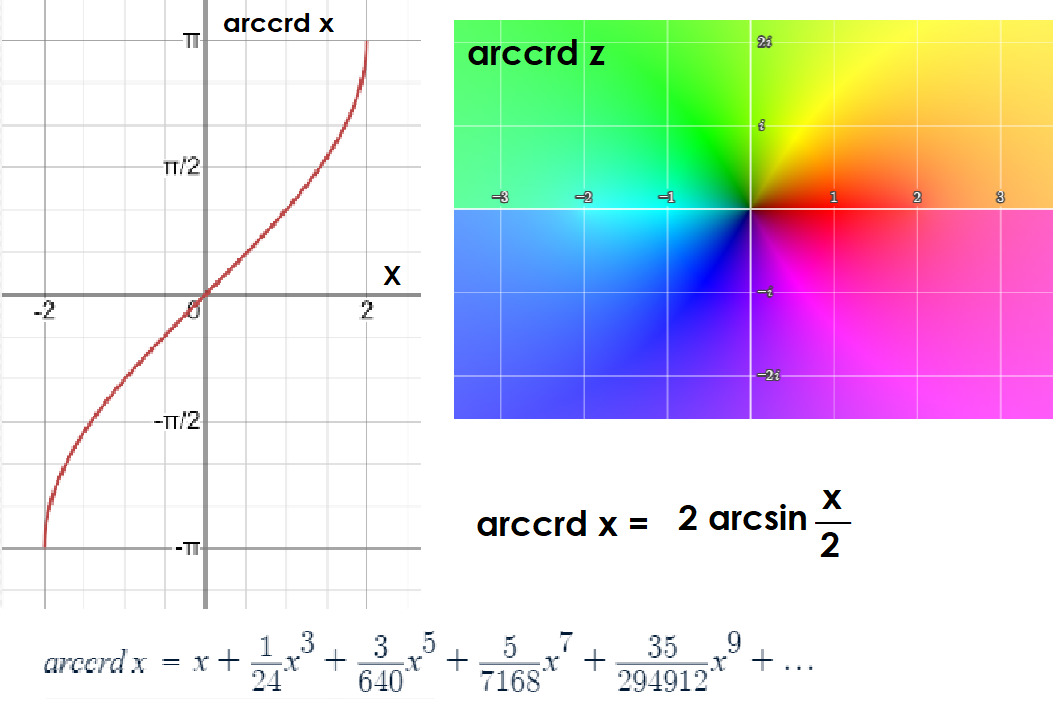
Это выражение также помогает объяснить, почему в более современных системах измерений синус вытеснил хорду: синус оказался более удобен для аналитических вычислений.
У хорды даже был свой аналог основного тригонометрического тождества, где вместо знаменитого ныне
sin α ² + cos α ² = 1 писали менее компактное:
crd α ² + crd (π — α) ² = 4
Древние египтяне и греки обожали хорды. Они были для них чем-то вроде айфона в наше время — мастхэв для любого серьёзного учёного. Гиппарх, например, взял и составил целые таблицы хорд, которые были такими же популярными, как современные таблицы умножения. В Индии астрономы типа Арыабхаты тоже пользовались хордой, пока не поняли, что синус (джья) делает всю работу проще и быстрее.
Ну, и само собой, в те времена так же был популярен квест «найди угол по длине хорды». В современных обозначениях его решает arccrd α аркхорда. Она даёт вам центральный угол, и это было круто полезно для навигации и картографии в те стародавние времена.
Итак, хорда, хоть и вышла на пенсию, остаётся важным персонажем в истории математики. Как ветеран сцены, она уступила место молодым и перспективным, типа синуса и косинуса, но всё равно заслуживает уважения и почёта. Потому что без хорды не было бы той самой «тригонометрической революции», что мы знаем и любим сегодня.
Квадрантид qdr
Квадрантид, или антихорда, как только ни называют эту не столь уж известную тригонометрическую функцию — это настоящая тригонометрическая реликвия, которая, казалось бы, уже давно должна была оказаться на свалке истории, но всё же иногда просыпается, чтобы блеснуть своими специфическими свойствами. Обозначается она как qdr α и определяется как хорда угла, увеличенного на 90 градусов, или, если формально,
qdr α = cdr (α +π/2).
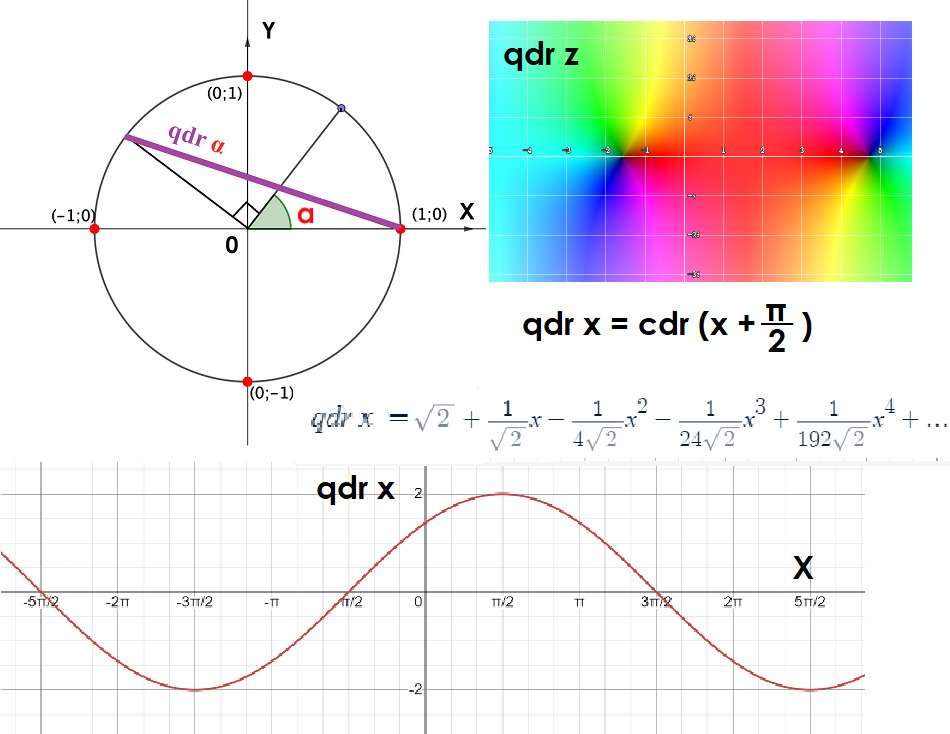
Зачем вообще нужна такая заморочка? Вопрос действительно резонный: зачем, спросите вы, нужны все эти углы, хордированные на 90 градусов? Дело в том, что квадрантид как-то удачно сводит к минимуму ошибки в ряде задач. Например, при переходе из одной системы координат в другую (например, из экваториальной в горизонтальную), или в навигации, где важен учёт углов от горизонта. В этих случаях углы между линиями зрения и вертикалями могут быть выражены через квадрантиды. И хотя всё это выглядит как серьёзная теоретическая физика, на практике квадрантиды помогают не потеряться, скажем, в море или не промахнуться мимо нужного объекта в астрономии.
Возьмём, к примеру, задачу навигации. В стародавние времена, когда GPS и ГЛОНАСС ещё не существовало, мореплаватели и астрономы использовали звёзды для определения местоположения. Звёзды, как известно, двигаться не любят (в пределах человеческой жизни). Но вот Земля крутится, и тут-то и начинается веселуха. Для корректного определения положения звезды или объекта на небе часто используют две системы координат: экваториальную и горизонтальную.
И вот тут выходит на сцену квадрантид. Допустим, у нас есть угол α, который мы измерили в экваториальной системе координат. Чтобы найти нужный объект в горизонтальной системе (или же на морской карте, где координаты также привязаны к горизонту), необходимо учитывать угол, дополненный до 90 градусов. Таким образом, антихорда (или квадрантид) позволяет нам перевести этот угол и, например, легко вычислить высоту небесного тела над горизонтом.
Примеры применения антихорды весьма обширны.
Астрономия и навигация: как уже было сказано, квадрантиды активно использовались в старой доброй астрономии для вычисления позиций звёзд и планет. Особенно полезна эта функция была для расчёта их видимой высоты на горизонте.
Геодезия и картография: в геодезии и картографии, где углы играют ключевую роль, квадрантиды помогали минимизировать погрешности при измерении углов и дистанций, особенно когда нужно было учитывать кривизну земной поверхности.
Морская навигация: старые морские карты нередко содержали специальные пометки, включающие квадрантиды для уточнения маршрутов и расчёта курса корабля.
Таким образом, квадрантид, хоть и является более редкой и специфической функцией, чем его «прямые» родственники, остаётся важным элементом тригонометрического инструментария.
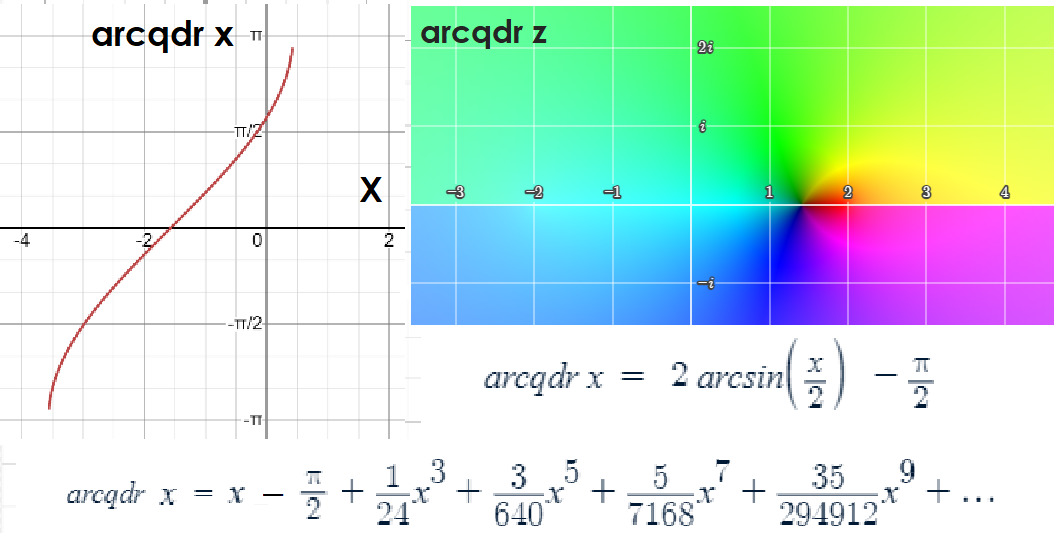
Соответственно его обратная функция arcqdr α отличается от аркхорды вычитанием π/2.
Cинус-верзус versin
Когда-то тригонометрия не была такой гладкой и простой, как в современных учебниках. Таблицы синусов, косинусов и других функций, обложенные кожаными переплётами, лежали на полках каждого уважающего себя математика и навигатора. В этом древнем мире были не только привычные синусы и косинусы, но и такие загадочные сущности, как versin и haversin. Да-да, именно versin, не вертитус или вирус, а настоящая, проверенная временем функция.
Определяется он как стрелка дуги, на тригонометрическом круге, и это сразу позволяет его выразить через уже известные нам тригонометрические функции:
versin α = 1 — cos α
Только и всего. Казалось бы, зачем опять же, вводить целую функцию которая отличается от уже известной на единицу? Но преимущество версинуса в его положительности на вещественной оси! Версинус использовали во времена, когда косинусы и синусы были необходимы для навигации, астрономии и геодезии. Таблицы с значениями versin помогали сократить количество сложных вычислений, особенно когда нужно было избежать отрицательных значений или ноля. Да и вообще, кто бы не захотел получить немного больше точности в технике XVIII века? На борту парусника, где компасы и карты были основными инструментами, versin помогал морякам рассчитать расстояние до горизонта, угол подъёма звезды или определить местоположение. Если синус и косинус занимались общими делами, то versin был тем, кто улаживал детали.
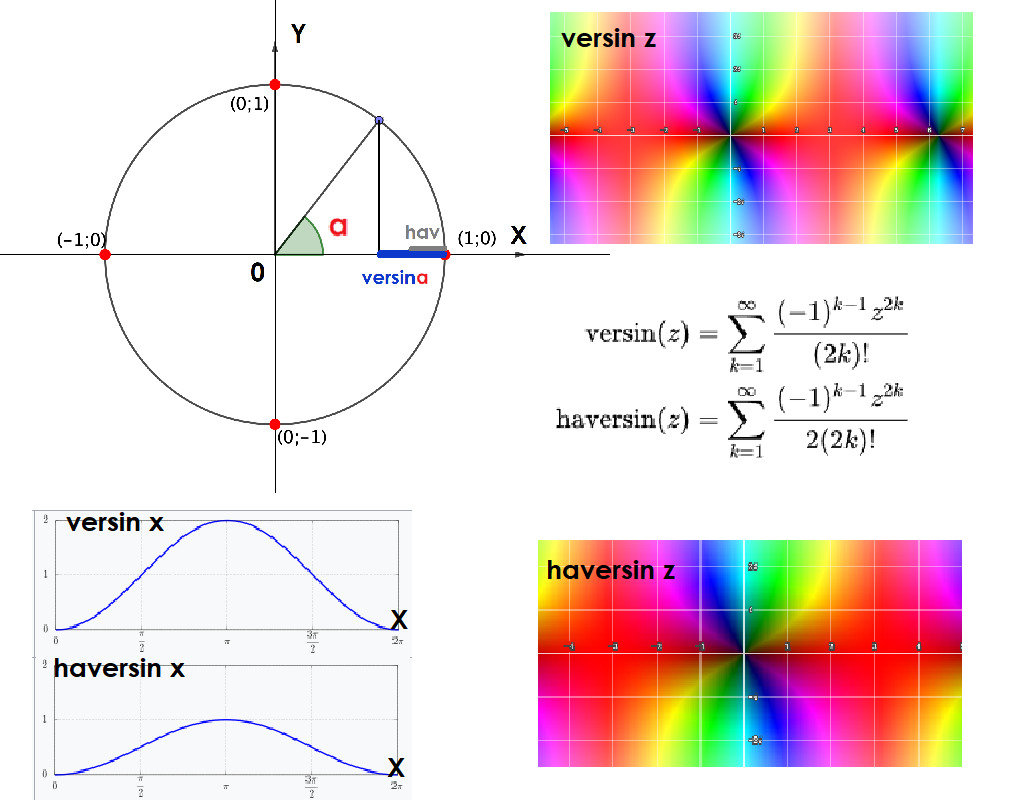
И вот, в одном из закоулков математической истории появилась функция haversin. Почему-то древние решили, что удобно делить versin на два. Возможно, они просто хотели немного упростить жизнь своим коллегам. Так или иначе, haversin — это половинка versin:
haversin α = (1 — cos α) /2
На самом деле, деление версинуса на 2 (hav — половина) связано с тем, что его можно выразить через удвоенный синус половинного угла в квадрате. Двойку перед квадратом синуса лень таскать. Эта лень человеческая и порождает целую новую функцию которая аж собственную теорему имеет!
versin α = 2 sin (α/2) ² при этом
haversin α = sin (α/2) ², что гораздо компактнее.
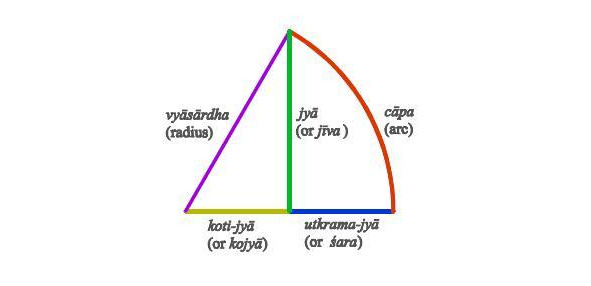
Кстати, в древней индии был первобытный версинус, и назывался он utkrama-jyā (Уктам-Джья). В те тёмные времена, использовать единичную окружность ещё не додумались, и в современном виде эта функция выглядела бы так:
utkrama-jyā α = R versin α
Тут, не единичность окружности учтена домножением версинуса на её радиус R. Ну и раз уж речь пошла о питекантропах в тригонометрии, приведём древний индийский аналог синуса и косинуса — джья, и коти-джья:
jyā α = R sin α, koṭi-jyā α = R cos α
Правда в современном мире математика как-то поуютнее?
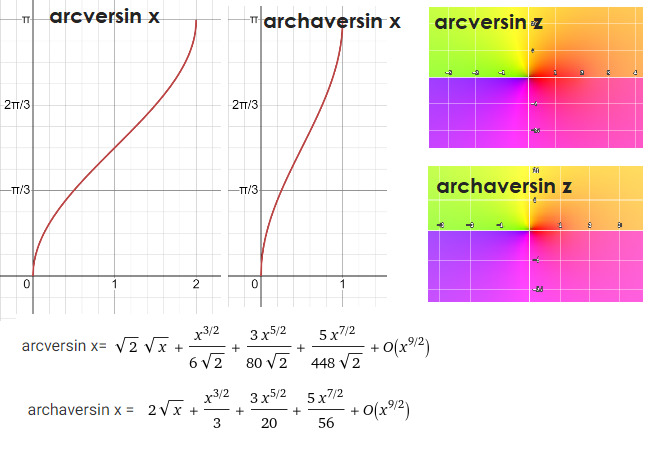
Вообще, название версинус или синус-верзус означает обращённый синус, и в противовес этому привычный нам синус часто называют sinus rectus («прямой синус»). Как и у любых других уважающих себя тригонометрических функций, у версинуса и гаверсинуса есть обратные арк-функции:
arcversin x = arccos (1-x), archaversin x = arccos (1—2x)
Такие дела.
Коверсинус coversin
Если бы синус мог обратиться к психотерапевту, coversin был бы его самым главным разочарованием. Эта функция определяется как
coversin α = 1 — sin α
История coversin так же уходит корнями в те времена, когда математики пытались максимально упростить вычисления. Коверсинус, как и его «брат» версинус, был полезен для работы с углами и расстояниями на окружности. Но тут интересная фишка: приставка «co-" в названии тоже означает «ко-функция», но в немного ином контексте. В то время «co» использовалось для обозначения дополнений, и coversin дополняла функционал versin. Представьте себе астронома древности, стоящего на высокой башне и пытающегося вычислить время затмения или путь звезды на небе. Использование coversin упрощало многие расчёты, позволяя избежать сложных преобразований и использовать более простые таблицы. В эпоху до калькуляторов, каждое упрощение имело огромное значение.
После того, как versin уполовинили, и coversin не избежала той же участи. Так появился хаковерсинус hacoversin, или half-coversin, определяется как:
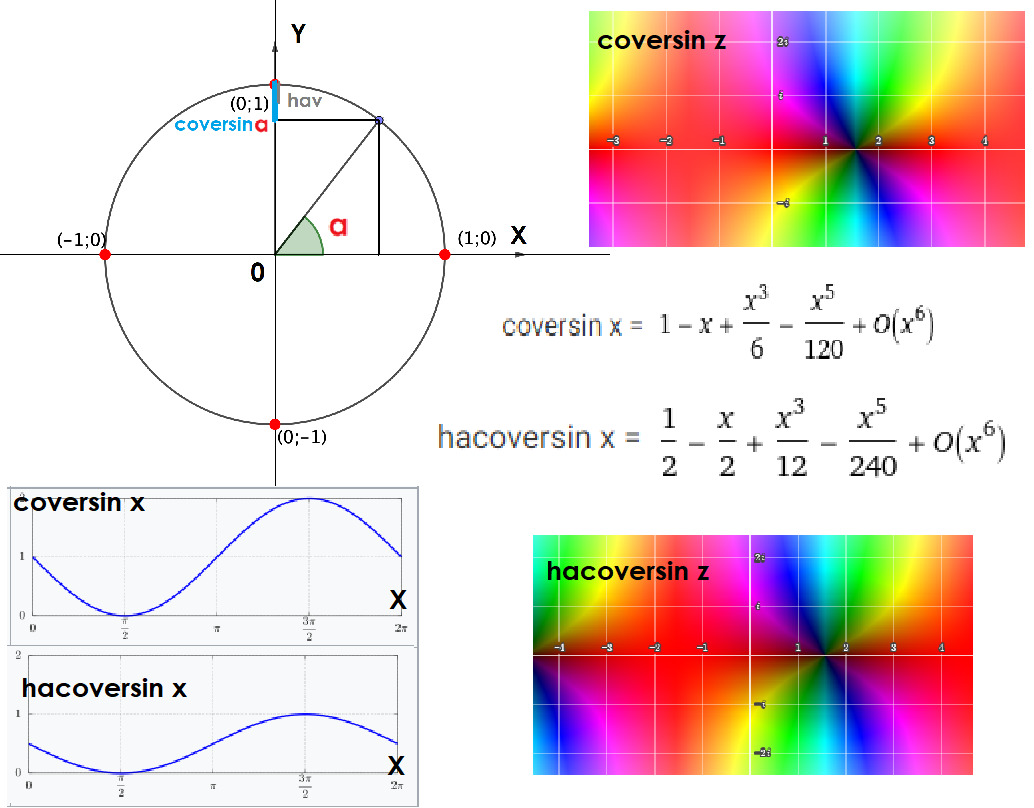
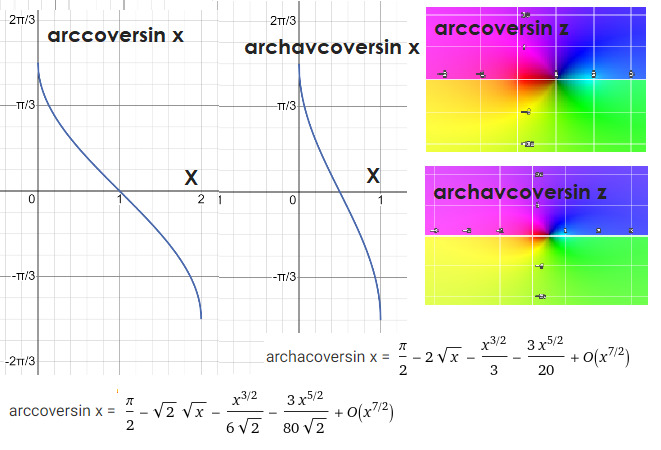
coversin α = (1 — sin α) /2 Зачем это нужно? Хаковерсинус, как и haversin, была полезна в астрономических и навигационных расчётах, когда требовалось максимальное упрощение и сокращение вычислений. Особенно в ситуациях, когда работы велись с очень малыми углами или когда требовалась высокая точность. Моряки и навигаторы прошлого века использовали hacoversin для более точных расчётов при определении местоположения на море, когда углы измерялись очень малыми и требовалась повышенная точность. Эта функция особенно полезна в формуле haversine, которая используется для вычисления расстояний между точками на сфере (например, на Земле).
Названия coversin и hacoversin происходят от латинских слов, где «co» обозначает «сопутствующий» или «дополняющий», а «haver-" указывает на «половину». Эти термины отражают суть функций, которые дополняют основные тригонометрические функции (синус и косинус), но в более узком и специализированном контексте.
Опять же, квест по определению углов из известных расстояний тоже частенько приходилось решать. так что знакомьтесь: arccoversin x = arcsin (1 — x) и archacoversin x = arcsin (1 — 2x).
Функции сoversin и hacoversin — это не просто математические реликты, а важные элементы исторических тригонометрических таблиц и вычислений. Они сыграли свою роль в развитии навигации, астрономии и математики в целом. В наше время они, возможно, кажутся архаичными, но их значение в истории науки трудно переоценить. Это напоминание о том, как далеко шагнула наука с тех пор, как люди начали измерять углы и расстояния на небесах.
Веркосинус vercos
По вычитали? Теперь по прибавляем! Итак, знакомьтесь: vercosinus — это функция, которая любит притворяться чем-то сложным, но на самом деле это просто vercos α = 1 + cos α. Кажется, что-то простое, но её сложность в другом — в историческом контексте и использовании.
Название «vercosin» происходит от латинского versus cosinus, что буквально переводится как «против косинуса» или «перевёрнутый косинус». Тут можно подумать, что математические умники решили пошутить, потому что vercosin на самом деле только добавляет к косинусу единицу. В общем, комедии и трагедии — всё в одном.
Период активного использования этой функции — всё те же древние времена, когда калькуляторов не было и в помине. Всякие такие функции использовались опять же, для упрощения сложных вычислений. Считали всё с помощью таблиц и логарифмов, и тут как раз vercosin был весьма удобен. Надо же как-то справляться без калькуляторов!
Как вы уже заметили, сама идея ver-функций — это игры с косинусом и синусом, но с небольшими модификациями. Например, versin (или versed sine) — это 1−cos x. То есть vercosin — это практически брат versin, но с позитивным подходом к косинусу. Они все вместе образуют такую семью вер-функций, которые были когда-то полезны для решения геометрических задач.
Опять представим себе, что vercosin устал быть таким длинным и решил немного упроститься. Так появилась функция havercos (или half vercosine), которая делит vercosin пополам. То есть
havercos α = (1 + cos α) /2 Это аналогично функции haversine для versin, только тут косинус добавляется, а не вычитается. Вот такие вот математические шуточки и полезности, которые давно потеряли свою актуальность, но всё ещё интересны с исторической точки зрения.
Теперь, как обычно, представим, что вы знаете сумму косинуса и единицы и хотите понять, какой угол их породил. Тут, arcvercosin — ваш путеводитель в этом деле. И выражается он так:
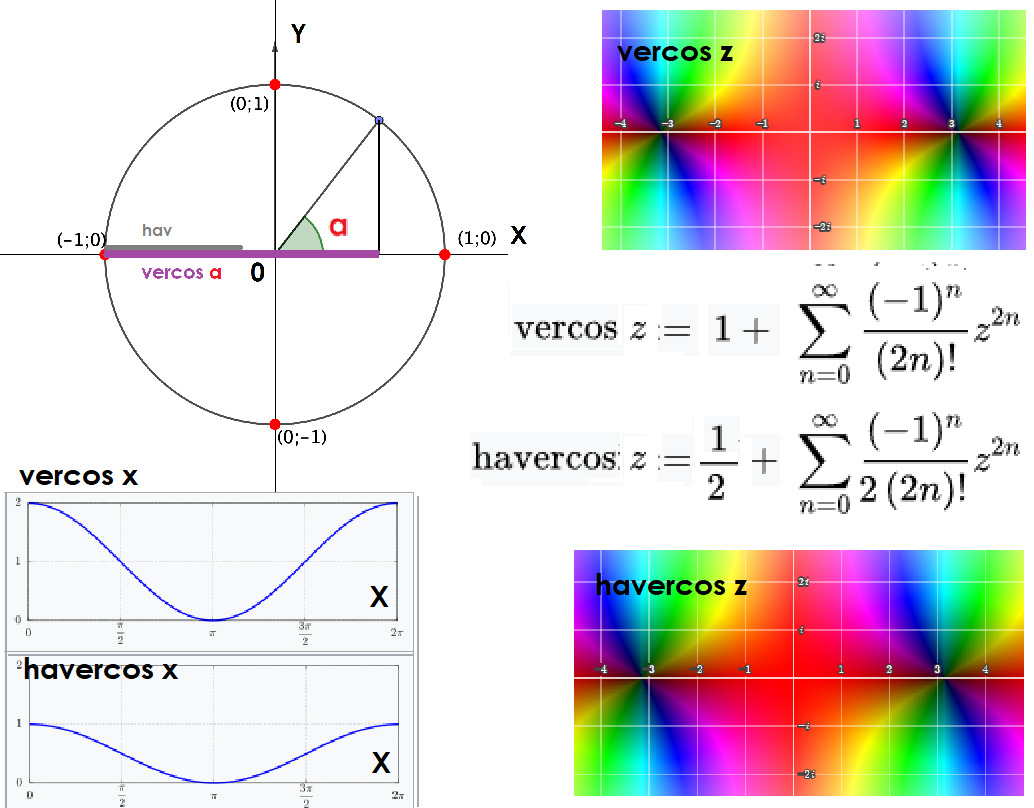
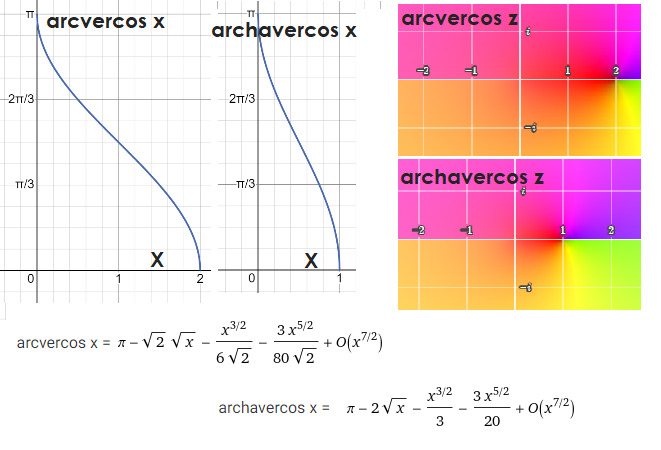
arcvercosin x = arccos (x — 1) и так же
archavercosin x = arccos (2x — 1). Даже несмотря на то, что некоторые из этих функций нынче выглядят, мягко говоря, эксцентрично, они всё ещё имеют своё место в теории и практике.
Старые обозначения, такие как vercos и другие подобные функции, сейчас редко, но всё-таки используются в современной математике и прикладных науках. Они могут встречаться в радиофизике для упрощения математических выражений в расчётах сигналов и волн, в
электротехнике, при анализе колебательных процессов и цепей.
Мелькают эти архаичные символы и в анализе спектральных данных и математическом моделировании.
Эти функции и сегодня помогают упрощать вычисления, особенно в контексте гармонического анализа и моделирования процессов.
Коверкосинус covercos
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.