Бесплатный фрагмент - Triangulation in neural network

Triangulation in neural network

Triangulation in the context of neural networks is the use of a geometric method of dividing a set of points into triangles to solve various problems of data processing, structure analysis, or building connections between network elements.

Main applications of triangulation in neural networks

— Generating connections between neurons: Delaunay triangulation is used to determine the topology of connections between neurons based on the spatial arrangement of the input data. For example, the weights of feedback connections between neurons can be formed based on the distances between them calculated from a triangulation grid [1].

— Data preprocessing: Before training the neural network, data points can be triangulated to identify local structures and neighborhoods, which allows geometric relationships between objects to be taken into account.

— Segmentation and surfacing: In 3D modeling and point cloud processing tasks, neural networks can use triangulation to construct surfaces and meshes, which is important for object reconstruction and shape analysis [2] [3].

Example: Delaunay triangulation in neural networks

In one approach, after constructing a Delaunay triangulation from the input set of points, each neuron’s neighbors in the triangulation are determined. Based on the distances to the neighbors, a scaling constant is calculated, and the weights of the connections between neurons are set taking into account these distances and the constant. This allows the local geometry of the data to be taken into account when forming the network structure [1].

Modern Methods: Learned Triangulation

In modern studies, such as PointTriNet, triangulation is integrated directly into the neural network architecture as a differentiable layer. Here, two networks are used: one classifies whether a candidate triangle should be included in the final triangulation, and the other proposes new candidates. This approach allows for the automatic construction of optimal triangulations for point clouds in 3D space, which is useful for computer vision and 3D reconstruction tasks [2] [3].

Benefits of Using Triangulation

— Taking into account local data geometry

— Optimization of the structure of connections in a neural network

— Improving the quality of segmentation and modeling of complex objects

Conclusion

Triangulation in neural networks is a tool that allows for efficient modeling and analysis of spatial data structures, as well as for constructing more informative and adaptive topologies of connections between neurons, which is especially relevant for tasks related to processing spatial and geometric data [2] [1] [3].

⁂

Delaunay triangulation in neural networks

Delaunay triangulation is a method of partitioning a set of points in a plane (or space) into triangles (or higher-dimensional simplices) such that no point in the original set falls inside the circumscribed circle (or sphere) of any triangle (simplex) [4] [5] [6]. This approach ensures a partition with the largest possible minimum angles, which avoids «thin» and degenerate triangles [7] [5].

Application in neural networks

In neural networks, Delaunay triangulation is used to construct a graph data structure, where points (e.g., point cloud elements or feature vectors) become graph vertices, and edges are determined by the triangulation results. This allows:

— It is optimal to form local connections between data elements, which is critical for tasks related to the processing of geometric information, 3D modeling and surface reconstruction [8] [9].

— Avoid degenerate connections: Due to the Delaunay properties, connections between points do not form «thin» triangles, which improves the stability and quality of information transfer in graph neural networks [7] [5] [9].

— Improve the graph structure: For example, in modern graph neural networks (GNNs), Delaunay triangulation is used to «restructure» the original graph to combat problems such as over-squashing and over-smoothing [9].

Example: DeepDT

DeepDT proposes to use Delaunay triangulation to construct a graph from a point cloud, after which the neural network learns to classify tetrahedrons (in 3D) as belonging or not belonging to the surface of an object. The point features are aggregated according to the structure specified by the Delaunay triangulation, which allows for complex spatial relationships to be taken into account and improves the quality of surface reconstruction [8].

Algorithmic details

— Efficient algorithms such as divide and conquer, incremental edge flip approach, and Boyer–Watson algorithm are used to construct the Delaunay triangulation [4] [6].

— In graph neural networks, edges between vertices are determined based on the results of triangulation, not the original topology, which can significantly change the nature of information dissemination [9].

Briefly about the advantages

— Maximizing the minimum angle: avoiding degenerate triangles [7] [5].

— Optimal local structure: efficient aggregation of information between neighbors [9].

— Flexibility: Can be used in 2D, 3D and higher dimensions [4] [8].

Conclusion:

Delaunay triangulation in neural networks is a tool for constructing efficient and robust graph structures, especially relevant for problems related to geometry, 3D reconstruction and point cloud processing. It allows forming connections between data elements taking into account their spatial arrangement, which improves the quality of training and the final results of models [8] [9].

⁂

How Delaunay Triangulation Helps Avoid «Thin’ Triangles in Neural Networks

Delaunay triangulation helps to avoid «skinny» (narrow, elongated) triangles due to its main geometric property: it maximizes the minimum angle among all angles of all constructed triangles [10] [11] [12]. This means that in any other possible triangulation for the same set of points, the smallest angle will not be larger than in the Delaunay triangulation. This approach prevents the appearance of triangles with very small angles, i.e. «skinny» triangles, which can negatively affect the accuracy and stability of calculations in neural networks, especially when working with geometric or graph structures.

In neural networks, this property is important because «thin» triangles lead to uneven distribution of neighbors and can worsen the aggregation of features between nodes, as well as increase numerical errors. Delaunay triangulation, by avoiding such triangles, provides a more uniform and stable structure of connections between nodes, which has a positive effect on the quality of information transfer and model training [10] [11] [12].

⁂

Implementation of an Oscillatory Chaotic Neural Network Using NVIDIA CUDA Technology to Solve Clustering Problems

Oscillatory chaotic neural networks (OCNNs) are a class of artificial neural networks in which the dynamics of individual neurons are described by oscillatory and chaotic processes. Such networks are particularly effective for clustering tasks, since they are able to detect complex data structures due to synchronization and desynchronization of neurons.

Features of implementation on NVIDIA CUDA

— Parallelization of computations: CUDA allows for efficient parallelization of computations involving the dynamics of a large number of oscillators, which is critical for modeling large-scale chaotic neural networks [13] [14] [15].

— Organization of flows: Various flow schemes (X-flow, Y-flow) are used to calculate the output values of neurons and the synchronization matrix. The optimal number of flows is considered to be no more than half of the maximum number of video card flows, which ensures minimal calculation time [13] [14].

— Buffering and memory: Various options for storing data in memory have been proposed for storing the synchronization matrix, taking into account the network size, which allows for efficient use of video card resources [13] [14].

— Analysis of results: Synchronization between neurons is analyzed using undirected graphs and disjoint set systems, which allows identifying clusters in the data [13] [14].

Stages of solving the clustering problem

— Network initialization: Setting oscillator parameters and initial conditions.

— Parallel simulation of dynamics: At each time step, the states of the oscillators and their interactions are calculated using CUDA cores.

— Calculation of the synchronization matrix: Pairs of neurons that are in a synchronized state are determined.

— Cluster selection: Based on synchronization analysis, clusters are formed — groups of neurons that oscillate in a coordinated manner.

— Post-processing: Clusters are compared with the original data to interpret the results.

Practical significance

Implementation of OHNS on GPU allows:

— Significantly speed up the processing of large volumes of data through massive parallelism [13] [14] [15].

— To effectively solve clustering problems, especially in cases of complex, nonlinear and heterogeneous data, where classical methods may be ineffective [16].

— Apply various algorithmic and structural solutions to optimize network performance and GPU memory usage [13] [14].

Conclusion:

The implementation of oscillatory chaotic neural network using NVIDIA CUDA technology provides high performance and efficiency in solving clustering problems, especially for complex and large datasets. This approach combines the advantages of chaotic dynamics to reveal complex structures and parallel computing to speed up processing [13] [14] [15] [16].

⁂

Analysis of Oscillatory Chaotic Neural Network Method Using CUDA for Solving Projection Problems

The essence of the method

The method is based on the use of an oscillatory chaotic neural network (OCNN) implemented using NVIDIA CUDA technology to accelerate computations. OCNN is a single-layer, recurrent, fully connected network, where the dynamics of neurons is described by a logistic mapping, and the clustering result is revealed by synchronizing the output signals of neurons in time. To improve performance and the possibility of application to big data, the network is implemented on a GPU using CUDA [17] [18] [19] [20].

Algorithm of work taking into account projection tasks

— Data preparation and projection transformations

— The input data is a set of points that can be pre-projected into the desired space (for example, when solving a dimensionality reduction problem or finding clusters in projections).

— Construction of Delaunay triangulation

— Delaunay triangulation is used to determine the topology of connections between neurons. It allows identifying local neighborhoods between points in the projection, which is especially important for correctly accounting for geometric relationships in the projection space. The scaling constant for the connection weights is also calculated based on the triangulation [17].

— Formation of the weight matrix

— The weight coefficients between neurons are calculated using a formula taking into account the Euclidean distances between points (neurons) and a scaling constant obtained from triangulation. This ensures the sensitivity of the network to the spatial relationships between points in the projection.

— Parallel modeling of network dynamics

— Calculations of the dynamics of neurons (their output values at each step) and the analysis of synchronization between them are implemented on the GPU using CUDA. Different flow organization schemes (X- and Y-flows) are used to optimize the work depending on the network size and the capabilities of the video card. This allows for efficient processing of large projection problems [17] [18] [19] [20].

— Synchronization analysis and cluster selection

— After the iterations are completed, the synchronization matrix between neurons is analyzed. Using graph theory methods (search for connectivity components) or a system of disjoint sets, clusters of synchronized neurons are selected, which correspond to groups of points in the projection space.

Advantages of the method for projection tasks

— Accounting for local geometry: Using Delaunay triangulation ensures correct detection of local neighborhoods in projections, which is critical for complex multidimensional data.

— High performance: Implementation on CUDA allows to significantly speed up the processing of large data arrays, which is important for projection tasks with a large number of points.

— Flexibility: The method does not require a priori information about the number of clusters and can be applied to data of any dimension (provided that the projection and triangulation are correct).

— Robustness to noise: Chaotic dynamics and timing analysis make the method robust to outliers and complex structures in the data.

Limitations and Features

— Computational complexity: Despite GPU acceleration, very large networks (tens of thousands of neurons) require significant memory and careful buffering.

— Limitations of triangulation: Triangulation algorithms (e.g. quickhull) may be limited by the dimensionality of the data and require pre-processing on the CPU.

— Threshold parameters: Cluster extraction requires adjusting synchronization thresholds, which may affect the results depending on the structure of the projection data.

Practical efficiency

Experimental results show that the implementation of the CUDA-based OHNN provides a 6–8-fold acceleration of computations compared to optimized CPU implementations, and for large networks, up to 68 times. Thus, the method is an effective tool for solving projection clustering problems, especially when working with large and complex data [17] [18] [19] [20].

Conclusion:

The CUDA-accelerated oscillatory chaotic neural network method using Delaunay triangulation is well suited for solving projection clustering problems. It takes into account spatial relationships between points in projections, efficiently identifies clusters, and scales to large amounts of data due to parallel computing [17] [18] [19] [20].

⁂

Main literature and articles on the topic of oscillatory chaotic neural networks and their implementation on NVIDIA CUDA for clustering

Classic and review articles

— Angelini L. et al. «Clustering Data by Inhomogeneous Chaotic Map Lattices.» Physical Review Letters, 2000, no. 85, pp. 78–102.

— The original work, which first proposed the oscillatory chaotic neural network (OCNN) model for data clustering problems [21] [22].

— Benderskaya E. N., Tolstov A. A. «Implementation of an oscillatory chaotic neural network using NVIDIA CUDA technology for solving clustering problems.» Information and control systems, No. 4, 2014, pp. 94–101.

— A detailed description of the algorithms, architectural solutions and results of hardware implementation of the OHNS on the GPU using CUDA. The article provides the results of testing, recommendations for optimization and analysis of the efficiency of the method [21] [23] [22] [24].

— Benderskaya EN, Zhukova SV «Oscillatory Neural Networks with Chaotic Dynamics for Cluster Analysis Problems.» Neurocomputers: Development, Application, 2011, no. 7, pp. 74–86.

— The theoretical foundations and practical aspects of using chaotic oscillatory neural networks for clustering are considered [21].

— Benderskaya EN, Zhukova SV «Nonlinear Approaches to Automatic Elicitation of Distributed Oscillatory Clusters in Adaptive Self-Organized System.» In: Distributed Computing and Artificial Intelligence (DCAI — 2012), Advances in Intelligent and Soft Computing, vol. 151, Springer, 2012, pp. 733–741.

— Nonlinear methods of self-organization of clusters based on oscillatory networks are described [21].

Hardware and software aspects

— Benderskaya EN, Tolstov AA «Trends of Hardware Implementation of Neural Networks.» Scientific and technical statements of SPbSPU. Computer science. Telecommunications. Management, 2013, No. 3 (174), pp. 9–18.

— Review of trends and problems in hardware implementation of neural networks, including OHNNs [21].

— Benderskaya EN «Perspective and Problems of Parallel Computing Based on Non-Linear Dynamic Elements.» Supercomputers, 2013, No. 1 (13), pp. 40–43.

— Analysis of parallel computing problems using nonlinear dynamic elements [21].

— Liang L. «Parallel Implementation of Hopfield Neural Networks on GPU.» 2011.

— Describes parallel implementations of neural networks on GPUs, which is relevant for OHNNs [21].

— NVidia C Best Practices Guide. Design Guide. DG-05603-001_v5.5. July 2013.

— A Practical Guide to Efficiently Using CUDA for GPU Computing [21].

Latest research and hardware implementations

— SPbPU EL — Chaotic Oscillator for Neural Networks. 2023.

— Dissertation on the development and modeling of hardware implementation of a chaotic oscillatory neural network for clustering problems, including software tools and testing on real data [25].

— Hardware Implementation of Differential Oscillatory Neural Networks (DONNs) with VO₂-based Devices. Frontiers in Neuroscience, 2021.

— Modern hardware solutions based on new materials and memristors for constructing oscillatory neural networks, stability and synchronization analysis [26].

Additional sources

— Ultsch A. «Clustering with SOM: U*C.» Proc. Workshop on Self-Organizing Maps, Paris, France, 2005, pp. 75–82.

— Comparative analysis of clustering methods, including self-organizing maps [21].

— Sørensen HHB «High-Performance Matrix-Vector Multiplication on the GPU.» Proc. of Euro-Par 2011 Workshops. Lecture Notes in Computer Science, vol. 7155, Springer, 2012, pp. 377–386.

— Describes efficient GPU computing methods applicable to the implementation of neural networks [21].

Note:

Detailed descriptions and implementation algorithms of oscillatory chaotic neural networks on CUDA, as well as performance analysis and optimization recommendations can be found in the article by E. N. Benderskaya and A. A. Tolstovaya, available in the public domain [21] [23] [22] [24].

⁂

Literature and articles on projection methods in neural networks

1. Projection neural networks and neural networks with projection learning

— Sujith Ravi. «ProjectionNet: Learning Efficient On-Device Deep Networks Using Neural Projections.»

— arXiv:1708.00630

— A new architectural approach is described in which compact neural networks are trained using projection operations (random projections, locality sensitive hashing). The method allows to significantly reduce the size and computational complexity of models while maintaining high accuracy, which is especially important for mobile and embedded devices [27] [28].

— Sujith Ravi. «Efficient On-Device Models using Neural Projections.»

— Proceedings of the 36th International Conference on Machine Learning, PMLR 97:5370—5379, 2019

— The article discusses in detail the methods for constructing compact neural networks using projections, their training and experimental results on visual and text classification problems [28].

2. Projection methods for dimensionality reduction and representation learning

— Review of representation learning and dimensionality reduction methods

— Yandex Education: Representation learning

— Dimensionality reduction methods such as SVD, autoencoder, PCA and their relationship with neural networks are considered. It is described how modern neural networks automatically construct effective projection representations of data for subsequent solution of target problems [29].

— Overview of Autoencoders for Projections and Dimensionality Reduction

— Habr: Overview of Autoencoders Applications

— The article explains how autoencoders are used to build projections and reduce dimensionality, as well as to pretrain deep networks. Examples of visualizing document projections using an autoencoder and LSA are given [30].

3. Classic sources on neural network architectures and training

— Textbook: «Artificial neural networks and their applications»

— PDF textbook KFU

— The textbook examines in detail multilayer perceptrons, embedding layers, recurrent and LSTM networks, as well as methods of vectorization and projections of feature space for various data analysis tasks [31].

4. Application of projection methods in computer vision and deep learning

— Rajaligappa Shanmugamani. «Deep Learning for Computer Vision.»

— The book presents modern methods for image processing using convolutional networks, including preprocessing, dimensionality reduction, and feature projection techniques to improve the efficiency and accuracy of models [32].

Brief list of key publications:

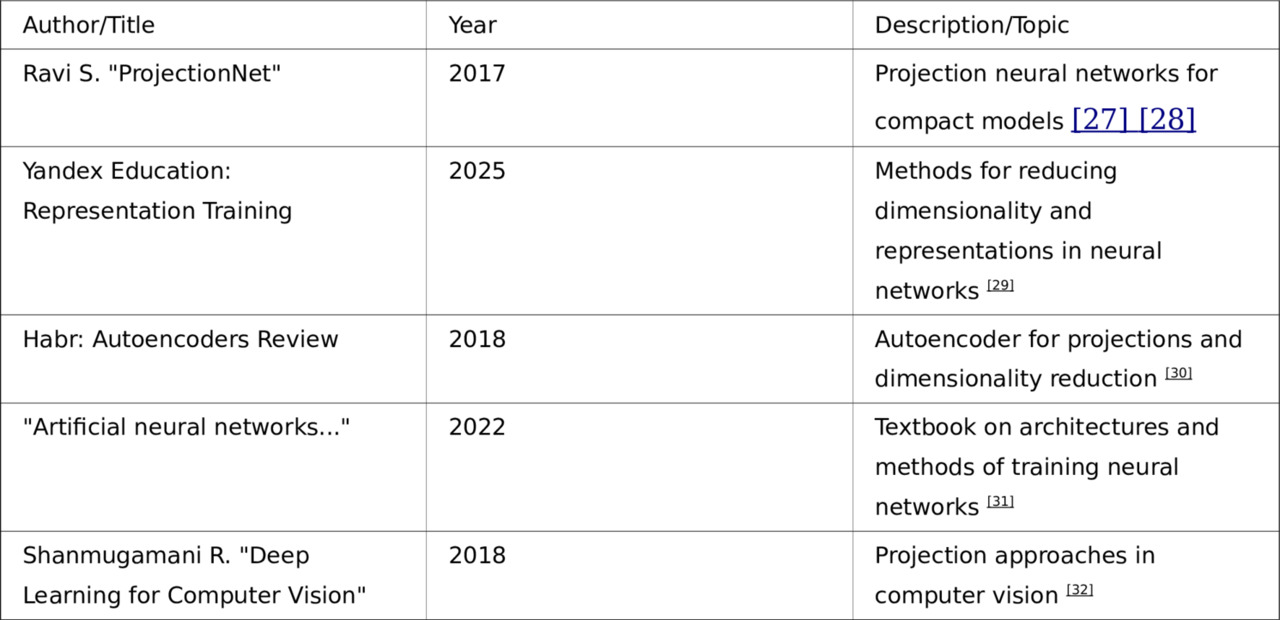
These resources cover the theory and practice of projection methods in neural networks, including modern architectures, dimensionality reduction methods, representation learning, and compact models for resource-constrained devices.

⁂

Which articles describe in detail the use of CUDA for oscillatory neural networks

The most detailed and practically oriented description of the use of NVIDIA CUDA technology for the implementation of oscillatory chaotic neural networks is contained in the following publications:

1. Benderskaya E. N., Tolstova A. A. «Implementation of an oscillatory chaotic neural network using NVIDIA CUDA technology for solving clustering problems»

Information and control systems, No. 4, 2014, pp. 94–101.

— The article discusses in detail:

— architecture of oscillatory chaotic neural network (OCNN),

— Features of parallel implementation on GPU using CUDA,

— algorithms for calculating the output values of neurons with different memory access patterns,

— options for organizing calculations (X-flow, Y-flow, flow per neuron),

— optimization of storage of the synchronization matrix and buffering,

— Performance analysis and recommendations for choosing a parallelism scheme depending on network size and GPU capabilities.

— The results of testing and comparison with CPU are presented, as well as practical recommendations for implementing OHNS on modern NVIDIA video cards [33] [34] [35] [36].

2. Benderskaya EN, Tolstov AA «Hardware Implementation of a Chaotic Oscillatory Neural Network by NVidia CUDA Technology»

Information and Control Systems, 2014, No. 4, pp. 94–101.

— The English version of the above article, available in the public domain, contains a detailed description of the algorithms, architectural decisions and test results, as well as links to the source code of the implementation [34] [35].

Additional articles mentioned in the bibliography:

— Benderskaya EN, Zhukova SV «Oscillatory Neural Networks with Chaotic Dynamics for Cluster Analysis Problems.»

— Neurocomputers: Development, Application, 2011, No. 7, pp. 74–86.

— Describes the theoretical foundations and practical aspects of using chaotic oscillatory networks for clustering.

— Benderskaya EN, Zhukova SV «Nonlinear Approaches to Automatic Elicitation of Distributed Oscillatory Clusters in Adaptive Self-Organized System.»

— Distributed Computing and Artificial Intelligence (DCAI — 2012), Advances in Intelligent and Soft Computing, vol. 151, Springer, 2012, pp. 733–741.

— Considers methods of self-organization of clusters based on oscillatory networks.

Links to publications:

— PDF version of the main article (Russian and English text) [33] [34] [35]

— Article on the magazine website [34] [35]

— Brief description and conclusions on CyberLeninka [36]

Conclusion:

For a deep study of the implementation of oscillatory neural networks on CUDA, it is recommended to read the work of Benderskaya and Tolstovaya (2014), which provides all the necessary algorithms, optimization schemes and testing results on real GPUs [33] [34] [35] [36].

⁂

ProjectionNet: Learning Efficient On-Device Deep Networks Using Neural Projections

ProjectionNet is an architecture for training compact neural networks optimized for execution on devices with limited computing resources (e.g. mobile phones, smartwatches, IoT) while maintaining high accuracy and minimal memory footprint [37] [38] [39] [40].

Key ideas and architecture

— Joint training of two networks :

— ProjectionNet uses joint optimization of two models:

— A full-fledged (trainer) neural network can be any modern architecture (feed-forward, LSTM, CNN, etc.), trained on standard data.

— A projection network is a compact network that uses random projections (e.g., locality-sensitive hashing, LSH) to transform input data or intermediate representations into compact binary vectors.

— Supervised learning :

— Both networks are trained simultaneously using backpropagation, where the projection network learns to reproduce the behavior of a larger network, similar to apprenticeship learning approaches. After training, only the compact projection network is used for inference [37] [38] [39] [40].

— Projections and binarization :

— The projection network uses parameterized random projections to obtain bit representations of the hidden layers. This allows for a significant reduction in the number of parameters and the amount of memory required to store the model, as well as speeding up computations due to simple operations in bit space [38] [39] [40].

Advantages and Features

— Minimal memory footprint :

— ProjectionNet models can be an order of magnitude smaller in size than the original networks, allowing them to run on resource-constrained devices without loss of quality [37] [38] [39].

— Flexibility and scalability :

— The projection network can be trained from scratch or «learn» from an already trained large network. The size and complexity of the projection network can be tuned to the specific task or device [39] [41].

— Generality :

— The approach is applicable to various types of tasks, from visual recognition to text and speech processing. Experiments show that ProjectionNet maintains high accuracy while significantly reducing the model size [38] [39] [40].

— Real-world applications :

— ProjectionNet is used to create fully on-device models, such as Smart Reply on Android devices where privacy and performance are important [42].

Technical details

— Projection functions :

— Modified versions of LSH are used to form hidden layer bit vectors. Can be combined with other operations (e.g. convolutions) for architectural flexibility [39] [43].

— Learning :

— Joint optimization of both networks occurs end-to-end, allowing the projection network to efficiently learn from the larger network [37] [38] [39].

— Experimental results :

— ProjectionNet shows significant model size reduction (up to 100x) while maintaining competitive accuracy on image and text classification tasks [39] [40].

Main publications

— Sujith Ravi. «ProjectionNet: Learning Efficient On-Device Deep Networks Using Neural Projections.» arXiv:1708.00630 (2017) [37] [40].

— Sujith Ravi. «Efficient On-Device Models using Neural Projections.» Proceedings of ICML 2019 [39] [43] [41].

Conclusion:

ProjectionNet is a state-of-the-art approach to building compact and fast neural networks for execution on resource-constrained devices. It is based on jointly training a large and projection network, where the latter uses random projections and bit representations to significantly reduce the model size without significant loss in accuracy [37] [38] [39] [40].

⁂

Find literature on this topic

To learn more about ProjectionNet and how to use neural projections to build efficient, compact models optimized for resource-constrained devices, the following key readings are recommended:

Main article

— Sujith Ravi. «ProjectionNet: Learning Efficient On-Device Deep Networks Using Neural Projections.»

— Full text of the article (arXiv:1708.00630v2, PDF) [44]

— The paper describes the architecture of ProjectionNet — joint training of a large (trainer) and compact (projection) neural network, where the latter uses random projections and bit representations to significantly reduce the model size. The training algorithms, the use of locality-sensitive hashing (LSH) for projections, experimental results on image (MNIST, CIFAR-100) and text classification tasks, and an analysis of the trade-off between model size and accuracy are discussed in detail.

Brief description of the article

— Introduction to the problem: The difficulties of using large neural networks on mobile and IoT devices due to memory, computation, and privacy limitations.

— The proposed solution is joint training of two networks, where a compact projection network learns to reproduce the behavior of a large network using random projections and binarization of hidden layers.

— Technical details: Use of LSH to generate bit vectors, joint optimization using backpropagation, ability to customize model size and complexity.

— Experiments: significant reduction in model size (up to 100 times or more) while maintaining high accuracy on a number of tasks.

— Practical significance: ProjectionNet enables the implementation of efficient, fast and private on-device models for computer vision and text processing tasks.

It is recommended to read the original paper for a complete understanding of the theory, implementation, and practical results of ProjectionNet [44].

⁂

Locality-Sensitive Hashing (LSH): Brief Description and Applications

Locality-sensitive hashing (LSH) is a probabilistic method for reducing dimensionality and accelerating the search for similar objects in high-dimensional spaces, widely used for Approximate Nearest Neighbor (ANN) problems [45] [46] [47].

main idea

Unlike traditional hash functions, which try to distribute objects uniformly across buckets, LSH specifically selects a family of hash functions so that similar objects are likely to end up in the same bucket, while distant objects are likely to end up in different buckets [45] [46]. This allows for quick matching candidates without having to completely enumerate all pairs of objects.

How LSH Works

— Selecting a family of hash functions: For each type of metric (e.g. Euclidean, cosine, Jaccard) there are families of LSH functions. For example, for cosine similarity, random projections are used [48] [49].

— Generating multiple hash tables: To improve accuracy, multiple independent hash tables are used, each built from a random set of hash functions [46].

— Object Hashing: Each object is hashed multiple times to form a bit signature. Similar objects are likely to have matching signatures in at least one table.

— Candidate search: To find nearest neighbors, it is sufficient to compare only objects that fall into the same buckets as the query, which dramatically reduces the number of comparisons [49] [45].

Mathematical formalization

A family of hash functions is called locality-sensitive if the following conditions are met for the chosen metric:

— For similar objects, the probability of ending up in the same basket is high.

— For those who are dissimilar, the probability is low [49] [45].

Application

— Nearest neighbor search in large and high-dimensional data (images, texts, audio, feature vectors) [50] [49] [51] [52].

— Deduplication and duplicate detection (e.g. web pages, documents, audio files) [52].

— Audio and video fingerprinting (e.g. Shazam) [51].

— Recommender systems, bioinformatics, clustering, etc. [47] [53].

Example of use in neural networks

In the ProjectionNet architecture, LSH is used to project input data or latent representations into compact bit vectors. This allows for the construction of ultra-compact models that can be efficiently run on resource-constrained devices [48]. In ProjectionNet, the LSH matrix is fixed before training, and projections are computed as the signs of the dot products between the input vector and random vectors from the LSH family, ensuring that similar objects will have similar bit signatures [48].

Key Benefits of LSH