
Бесплатный фрагмент - Тензоры. Что может быть проще?

Тензоры — это факты вселенной!
Лилиан Р. Либер
Введение
Если вы сейчас читаете эти строки, то, скорее всего, уже слышали слово «тензор» и, возможно, даже пытались его понять в ВУЗе. Но, признайтесь, большинство книг по тензорному исчислению написаны так, что даже самые стойкие студенты начинают подозревать, что их авторы — это инопланетяне, которые решили поиздеваться над человечеством. Все эти громоздкие формулы с индексами выглядят так, будто кто-то просто решил поиграть в «найди 10 отличий» между математикой и искусством абстракции.
Если вы уже успели пострадать от этой тензорной пытки, то эта книга станет для вас настоящим глотком свежего воздуха! Мы вернём наглядность в мир тензоров, и вы почувствуете себя не просто читателем, а настоящим гением, который сам изобрёл все эти сложные штуки. А как иначе? Ведь только тот, кто способен переизобрести нечто, может с гордостью заявить: «Я это понял!» Так что готовьтесь, мы отправляемся в увлекательное путешествие по миру тензоров, где даже самые запутанные формулы станут для вас простыми и понятными!
Большинство математических идей на самом деле просты, как дважды два, и тензоры — не исключение. Вспомните, как в школе даже самые отъявленные двоечники получали неплохие оценки, когда дело доходило до векторов. Всё так просто и наглядно, как счётные палочки, которые, кстати, могли бы стать отличным оружием в битве с математической скукой. Так начиналось ваше первое знакомство с тензорами, ведь вектор — это тензор первого ранга!
Разумно предположить, что читатель, решивший изучить тензоры, уже сведущ в таких вещах, как линейная алгебра и математический анализ. Иначе где бы вы вообще могли услышать данное слово? Поэтому и для чтения данной книги требуется подготовка уровня хотя бы школы. Но не переживайте, даже если вы не гуру математики, вы всё равно сможете извлечь из этого пособия массу полезного благодаря его наглядности.
На страницах этой книги будет использовано ровно столько математики, чтобы помочь, а не мешать непрофессионалу. Её цель — глубокое наглядное понимание основных идей тензорного исчисления. Без математической муштры и заумных терминов. Только суть и наглядность! Большей наглядности не представлено до сих пор нигде! Ни в одном из курсов.
Изложение мы начнём с наглядной интерпретации так называемых ковариантных и контравариантных компонент тензоров. Затем увидим, что одним вектором чаще всего не обойтись и что появление тензоров — естественно и неизбежно. Разберём, как можно начать ориентироваться, оказавшись в неведомых мирах непонятной природы, вводя структуру многообразия. Далее увидим тензоры в самых неожиданных местах, таких, например, как стул, на котором вы сидите. Он ведь имеет верх и низ и некую площадь. А значит, обладает ориентированной площадью. Спойлер: полностью антисимметричным тензором. Потом нас ждёт дуальность Ходжа. И нет, это не новый персонаж Marvel, а магическая операция, которая превращает дифференциальные формы в их альтер-эго. Все эти объекты будут возникать у нас естественно и непринуждённо. Привыкнув к ним, мы познакомимся уже с весьма специальными тензорами, носящими имена сопричастных к ним математиков и физиков. Затем познакомимся с группами Ли и тензорами, обитающими в этих мирах. И напоследок заглянем ещё глубже в Варп-геометрии, обнаружив спиноры. Они крутятся на 720 градусов, чтобы вернуться в исходное положение (да, они странные). Но спиноры помогают ввести спин-тензоры, которые тоже у нас вполне по теме. В итоге мы окончательно развенчаем миф о сложности тензорного исчисления и сделаем все его понятия такими же естественными и наглядными, как ваши любимые счётные палочки. И, прочитав эту книгу, вы воскликнете: «Тензоры — что может быть проще?»
Ковариантность и контравариантность
Для покорения космоса человечеству, как это ни странно, нужно было научиться складывать стрелочки. Ещё Архимед, живший в 287–212 годах до нашей эры, складывал силы, действующие на тело, по правилу параллелограмма, то есть интуитивно вводил особые объекты, которые характеризуются не только величиной, но и направлением. Но вот беда: не всё, что кажется стрелочкой и имеет направление, на самом деле ею является. И в этом разделе нам предстоит сделать важный шаг к пониманию тензоров — понять, что есть два фундаментальных объекта, притворяющихся для неопытного человека векторами. Речь идёт о векторах собственной персоны, знакомых нам ещё со школы, и новой штуковине — ко-векторах.
Вспомним о векторах
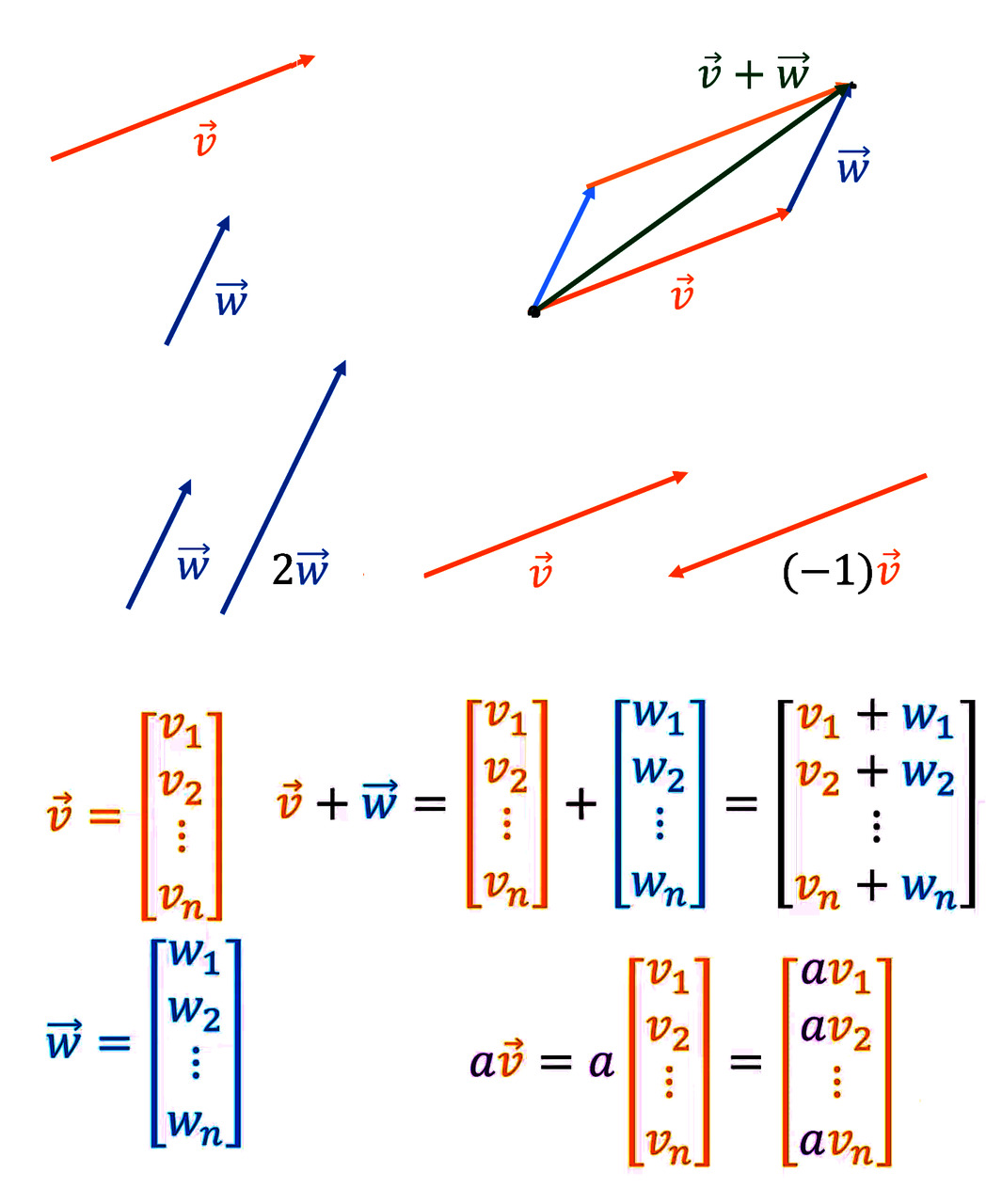
Вектор — это не просто стрелка на плоскости, а настоящий герой в мире математики и физики. Он помогает нам описывать движение, силы и даже сложные явления в природе. Но что же такое вектор в самом простом понимании? Это направленный отрезок, который имеет как величину, так и направление. В повседневной жизни мы сталкиваемся с векторами постоянно: от стрел на картах до GPS-координат, которые помогают нам не заблудиться в большом городе. Векторы — это не просто абстракция, а мощный инструмент, который помогает нам ориентироваться в пространстве и времени.
В науке и технике векторы играют ключевую роль. Они позволяют моделировать физические процессы, анализировать данные и даже создавать новые технологии. Например, векторы используются в механике для описания движения объектов, в электротехнике для анализа электрических полей и в компьютерной графике для создания реалистичных изображений. Но как же мы можем работать с этими векторами? С ними можно иметь дело как с реальными стрелочками, складывая их по правилу «начало к концу» или по правилу параллелограмма. Их можно удлинять или укорачивать, умножая на число, или даже поворачивать вспять, меняя начало и конец посредством умножения на отрицательные числа. Но можно с векторами работать и в более абстрактном виде. Здесь на помощь приходят компоненты вектора. Что же такое компоненты вектора? Это способ представления вектора в виде набора чисел, которые описывают его величину и направление в определённой системе координат.
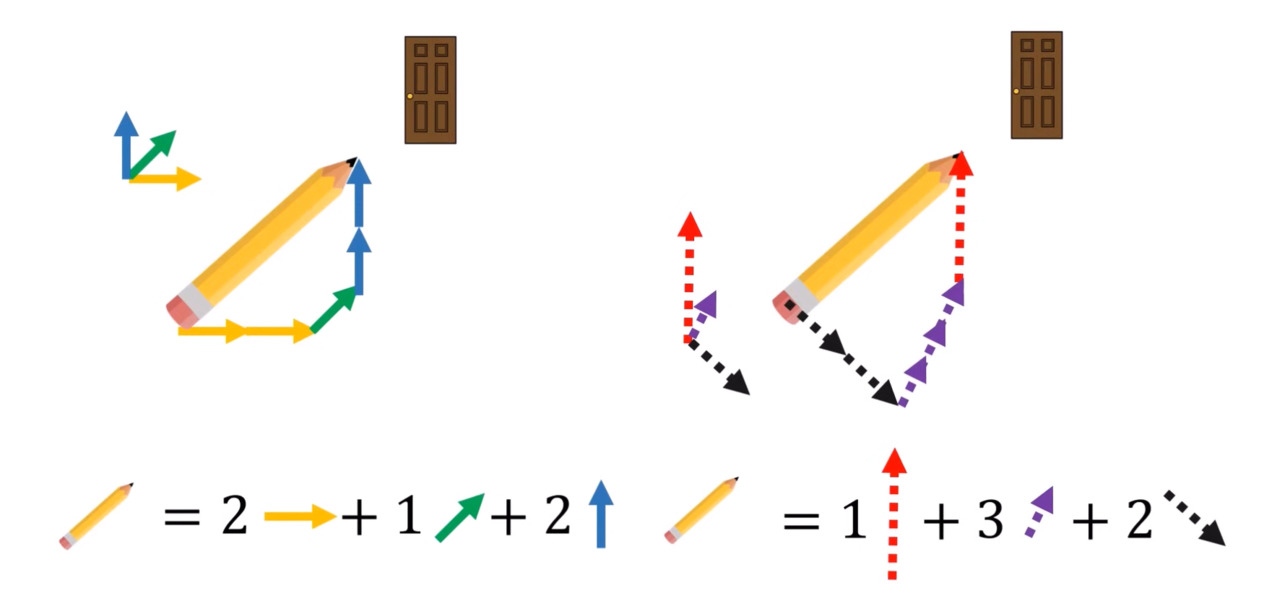
Чтобы представить наглядно компоненты вектора, вы можете направить карандаш на дверь. Где у него начало и конец — очевидно. Если же вы теперь выберете три произвольных направления в пространстве, не лежащих на одной прямой, и зададите для каждого из них единицу измерения, то легко сможете составить из получившихся, так называемых базисных векторов, объект, равный вашему карандашу. Сам карандаш имеет фиксированную длину и указывает на дверь. Какие бы три направления вы ни выбирали, вы всё равно сможете ими описать один и тот же карандаш, указывающий на дверь. Это простейшее представление вектора — в виде стрелки или в виде упорядоченной совокупности чисел.
На самом деле, вектор — это нечто более абстрактное. Это сущность, которая обладает направлением и величиной. Как хороший комиксный герой: у него есть суперспособность (величина) и цель в жизни (направление). Важно понимать: вектор — это не просто координаты. Координаты — это всего лишь способ описать вектор, как паспорт для человека. Без паспорта жить сложно, но паспорт — это не вся личность.
Но, имея все координаты векторов в каком-то конкретном базисе, мы можем складывать их уже не как стрелочки, а как упорядоченные массивы чисел. Компоненты векторов принято обозначать как числа в вертикальном столбце. В такой записи их весьма удобно складывать — этаж с этажом. Также при умножении вектора на число умножаются на него все компоненты на каждом этаже массива.
Для того чтобы оценить положение одного вектора относительно другого, вводят такую штуку, как скалярное произведение. По своей сути это проекция (тень) одного вектора на направление другого, умноженная на длину этого другого. Зачем проецируемый вектор умножать на длину второго, почему нельзя просто спроецировать? Дело в том, что с практической точки зрения хочется сделать эту операцию симметричной, и к тому же простое проецирование на направление, заданное вторым вектором, можно устроить скалярным умножением на единичный вектор. А в практических целях зачастую нужно ещё учитывать влияние второго вектора, на который мы проецируем первый. Также скалярное произведение вектора на самого себя даёт квадрат его длины. Длину вектора часто называют его модулем. Если скалярное произведение векторов равно нулю, то говорят, что они ортогональны (это такой сложный синоним слова «перпендикулярны»). Ортогональность векторов является их особым взаимоположением, крайне полезным и значительно упрощающим многие вычисления.
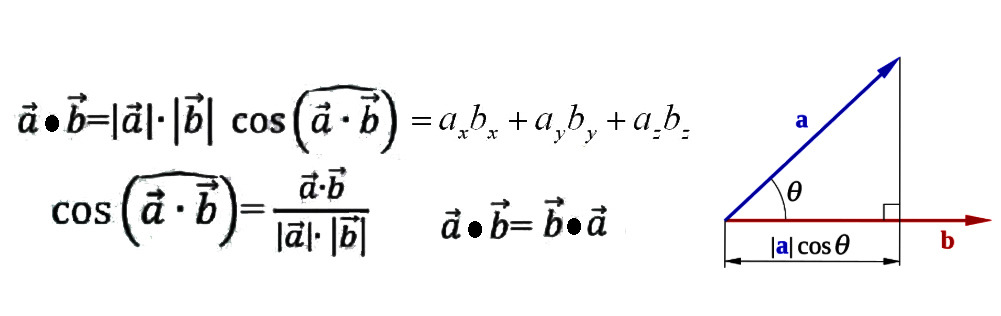
На скалярное произведение можно смотреть и как на свёртку двух векторов. Как на результат их взаимодействия. В последствии мы с вами увидим, как можно вектор прогнать сквозь тензор, также за счёт скалярного произведения уже с ним. Таким образом можно будет узнать, как тензор видоизменяет окружающие явления. Но пока обойдёмся без спойлеров.
Из двух векторов можно породить не только скаляр, но и вектор с помощью уже векторного произведения. Он будет перпендикулярен обоим перемножаемым векторам, а его длина (модуль) будет равна площади параллелограмма, «натянутого» на исходные векторы.
Чтобы узнать направление получаемого вектора, нужно первый множитель будто отвёрткой повернуть ко второму, и куда в этом случае отвёртка будет закручиваться, туда и будет указывать новый вектор.
Само по себе векторное произведение примечательно ещё и тем, что это, пожалуй, первый некоммутативный объект, с которым знакомится человек, начинающий изучать математику. Ведь если переставить в этом произведении множители, то результат будет иметь противоположный знак.

Почему это важно? Потому что это первый раз, когда мозг учащегося осознаёт: порядок имеет значение! До этого он жил в розовых очках коммутативности, где 2+3 = 3+2, а умножение — это сонное чаепитие Алисы в Стране Чудес.
Такой случай некоммутативности весьма прост и называется антикоммутативностью. Бывает, что перестановка множителей у других операций меняет результат до неузнаваемости.
Если честно, то результат векторного произведения — это не совсем и вектор. Его называют аксиальным вектором, или псевдо-вектором. В зазеркалье он ведёт себя как злодей из фильма: выглядит так же, но злорадно меняет знак. И да, это не глюк — так мир устроен!
Не всё то вектор, что им кажется
Вспомнив самые основные свойства векторов, мы теперь можем перейти к более причудливым объектам, которые векторами долго прикидывались. Люди чуть ли не с античных времён пользовались стрелочками в практических задачах. И лишь в 1853 году Джеймс Сильвестр (James Sylvester) заподозрил неладное и ввёл в обиход понятия о ковариантных и контравариантных объектах.
Понятия эти возникают при рассмотрении того, как объекты ведут себя при смене системы отсчёта, а значит, и координат. Величины, которые от смены базиса не зависят, называются скалярными. К таковым, например, относится энергия, температура. Скалярное поле — это число, прикреплённое к каждой точке пространства, словно ценник в супермаркете. Например: температура в комнате: +25° C на диване, +30° C у плиты и -273° C в душе у того, кто включил ледяную воду. Потенциальная энергия: максимум — на диване, минимум — в спортзале. Скалярному полю всё равно, как вы описываете точку. Ваш балкон может быть: с географическими координатами: 55° 75′ с.ш., 37° 61′ в.д.; улицей и домом: «Третий этаж, дом у реки»; в полярных координатах: «500 шагов от памятника, повернуть налево у электрического столба». Но температура там всё равно будет +30° C.
Но помимо скаляров существуют объекты, которые помимо величины обладают ещё и направлением. Это вроде как векторы. Но вот загвоздка в том, что при смене координат их компоненты меняются совершенно по-разному. Причём одним из только двух способов!
Чтобы наглядно увидеть, о чём идёт речь, давайте рассмотрим хрестоматийный пример такого противоположного поведения двух величин, имеющих одно и то же направление.
Давайте рассмотрим простой пример: одномерное пространство. Возьмём числовую прямую, зададим на ней начало отсчёта и единицу длины: 1 метр. Теперь представьте, что у нас есть скалярное поле температуры, которая растёт равномерно. В ноле температура равна нолю, а на каждый метр она поднимается на сто градусов! Таким образом, у нас появляется векторное поле темпа роста температуры, называют его «градиент». В каждой точке он постоянен и равен 100 градусов на метр.
И, наконец, зададим скорость какого-то газа, которая во всех точках одинакова и равна 1 метр в секунду.
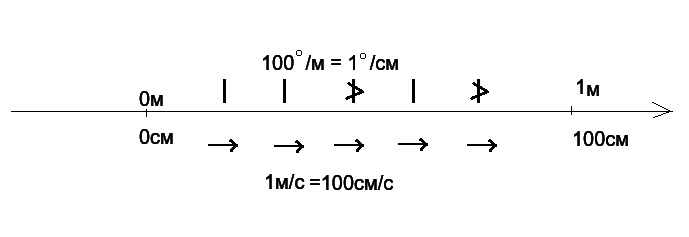
В одномерном пространстве базис можно сменить, лишь сдвинув начало отсчёта или изменив единицу длины. Так что разнообразие координат не велико. Мы же в нашем примере для простоты поменяем единицу измерения! Перейдём от метров к сантиметрам, уменьшив тем самым единицу измерения аж в 100 раз. Температура, как и положено настоящему скалярному полю, никак на эти изменения не отреагирует. В точке «1 метр» или, как мы теперь считаем, «100 см» она как была равна 100 градусам, так таковой там и осталась. При этом градиент температуры, как величина, имеющая направление, изменился. Он был равен 100 градусов на единицу длины, а стал равен 1 градусу на единицу длины. Таким образом, компонента градиента численно уменьшилась в сто раз, как и единица длины, как базисный вектор, если угодно. Запомним это! Скорость газа тоже изменилась, но противоположным образом! Она у нас была 1 единица длины в секунду, а стала теперь равна 100 единицам длины в секунду. То есть её компонента, напротив, выросла численно в 100 раз!
Эти два варианта изменений компонент неких объектов и лежат в основе тензорного исчисления. Давайте более детально всмотримся в причину такого различного поведения координат. Представьте себя на месте учёных прошлых веков и задумайтесь, чтобы вы предприняли на их месте? Как назвали бы новые объекты, которые явно обычными векторами не являются? Как бы их обозначили? Как стали бы изображать геометрически? Для тех, кто уже знаком с математическим анализом и понятием якобиана, приведём математические выкладки, которые прямо-таки намекают на удобный и естественный способ обозначения направленных величин, которые демонстрируют два варианта изменения компонент.
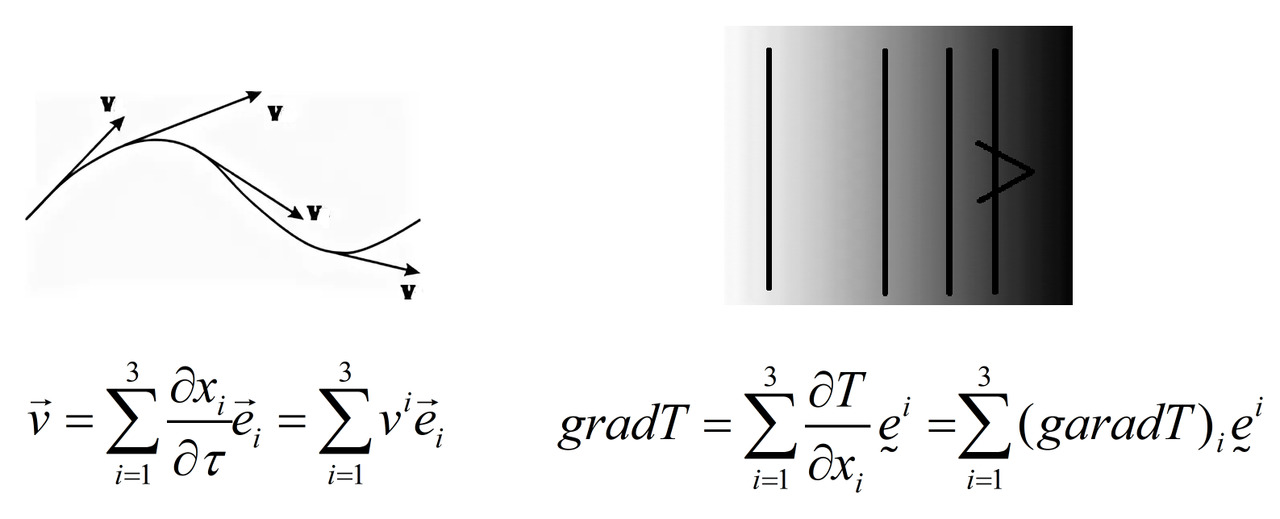
В векторном анализе градиентом называют производную скалярного поля по координатам. Эта величина явно имеет направление. А вектором скорости называют производную координат по параметру (у физиков — это время).
Присмотритесь к формулам этих величин. Где стоят индексы координат в случае градиента и скорости? Правда, идея обозначать разницу в этих объектах через положение индексов просится сама собой?
Вот и учёным мужам прошлого показалось так же. С тех пор объекты типа скорости называют векторами и обозначают буквами с индексами координат сверху, а объекты, подобные градиенту, называют ковекторами, и индексы компонент пишут у них снизу. В англоязычной литературе есть способ запомнить, где какой индекс ставить. Вектора называют контравариантным объектом, так как они преобразуются противоположным способом базису. В слове contravariance латинская буква «n» похожа на стрелочку, указывающую вверх, что напоминает о положении индекса у такого объекта вверху. И наоборот, ковекторы преобразуются так же, как базис, и в символизирующем это слове сovariance буква «v» напоминает стрелочку вниз, также напоминая математику о местоположении ковариантных индексов.
Что касается причин такого различного поведения векторов и ковекторов при смене базиса, то она вполне очевидна. В одном случае координаты стоят в числителе, в другом — в знаменателе дроби или производной. Соответственно, их изменения должны либо увеличивать сами компоненты, или уменьшать. Только и всего!
Вслед за учёными задумаемся над тем, как можно чисто геометрически изобразить векторы и ковекторы. Какая визуализация будет отражать наиболее полно их суть и делать алгебраические действия над ними более наглядными? И здесь ответ напрашивается сам по себе из рассмотренного нами примера. Вектор скорости действительно удобно изображать как стрелку, в более общем случае — это действительно наш классический вектор, касательный к некоей кривой, заданной координатами, зависящими от некоего параметра.
Если же мы внимательно посмотрим на ковектор, в качестве первого примера которого брали градиент, то наглядная аналогия-интерпретация придёт сама. Её подскажет сама суть, сама природа градиента. Что такое градиент? Это направление наискорейшего возрастания некоей величины. Если мы рассматриваем поле температур на плоскости, то можем провести линии через те точки, в которых температура имеет одно и то же значение. Выберем, например, шаг в 10 градусов. И при возрастании температуры на 10 градусов будем отмечать это линией. Допустим, температура возрастает только слева направо. Тогда линии постоянства температуры будут вертикальными. И чем быстрее температура растёт, тем ближе они будут располагаться друг к другу. Вот мы и получаем наглядное представление ковектора! Это стопка линий (в более общем случае — поверхностей), на которой для ещё большего удобства галочкой показывают направление наибольшего роста величины.
Ковекторы — знакомство поближе
В силу того, что с векторами каждый человек знаком со школы, у него уже на уровне инстинктов отработаны все действия над этими объектами. Нам теперь нужно довести до такого же автоматизма и наглядности операции с дуальными к ним объектами — ковекторами. Давайте научимся их складывать как в абстрактном алгебраическом представлении, так и в геометрическом — визуальном.
Мы уже поняли, что удобнее представлять ковекторы как поверхности или линии. Существует немного свободы в обозначениях при начертании этих объектов. Иногда стрелочку ставят в середине стопки линий, иногда на переднем крае. Если у нас величина (энергия или температура, например) меняется сложным образом, то ковекторы мы изображаем изогнутыми линиями, кривизна которых может тоже меняться от точки к точке, или множеством линий в разных областях, имеющих разные направления. Практика показывает, что это очень удобно. Как и векторы, ковекторы являются инвариантными величинами, вещью в себе, которые не зависят от системы координат. Но их описание через компоненты будет выглядеть по-разному в разных базисах.
Для построения алгебры ковекторов полезно будет проводить аналогию с операциями над векторами и смотреть, как отличается их геометрическая интерпретация от собственно знакомых нам векторов. Мы умеем складывать два вектора. Конец одного прилагаем к началу другого и проводим линию от свободного конца первого вектора к свободному концу второго. Ковекторы можно тоже складывать. Но если мы помедитируем над тем, как сделать сложение таковым, чтобы оно сохраняло основные свойства ковекторов, то придём к следующему способу. Чертим первый ковектор в виде линий, затем на нём чертим второй. Линии обоих ковекторов образуют параллелограмм. Суммарным ковектором будут являться линии, проходящие через вершину этого параллелограмма и его диагональ.
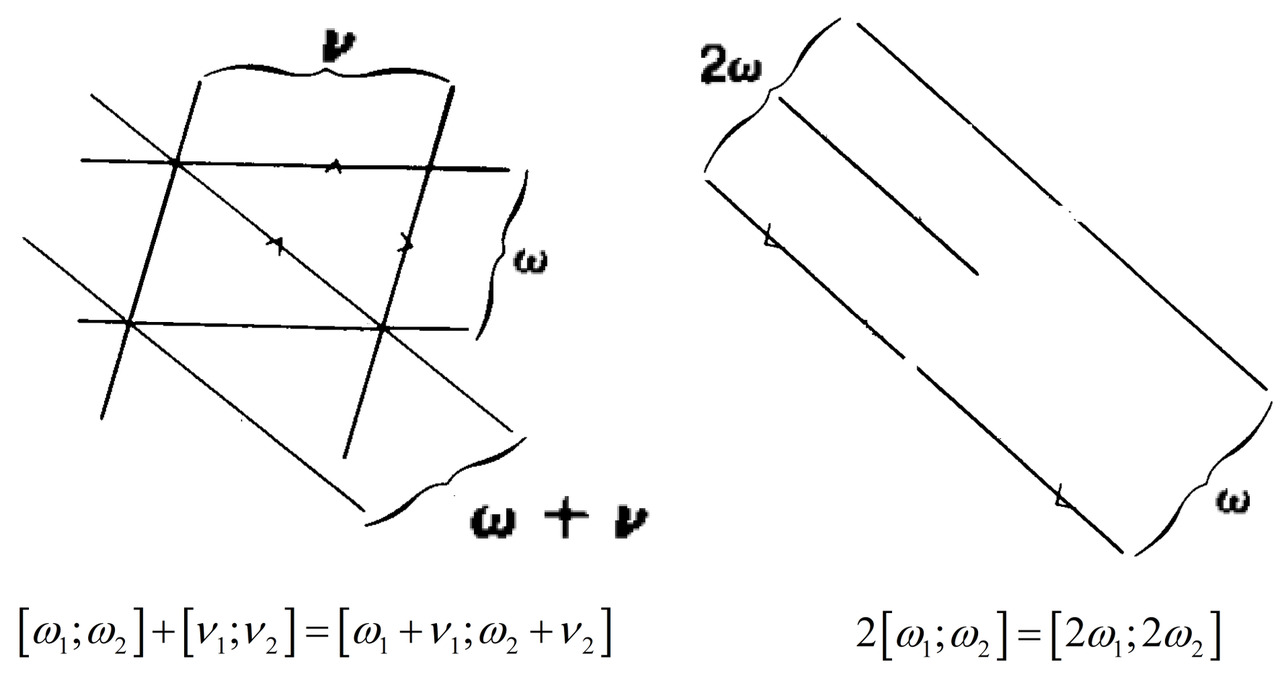
Мы умеем умножать вектор на число. Вектор при этом увеличивается в длине, если число больше единицы, и уменьшается, если оно меньше. Если число отрицательное, то вектор поменяет своё направление стрелочки на противоположное. С ковекторами выполняется в точности как у векторов лишь последний пункт. Если мы ковектор умножим на отрицательное число, он поменяет своё направление. В остальном ситуация иная. Умножение ковектора на число приводит к тому, что у него кратно этому числу возрастает плотность линий. Если число больше единицы, то ковектор становится более плотным, если число меньше единицы, то линии становятся более редкими пропорционально числу.
Чисто алгебраически ковекторы удобно обозначать как матрицы-строки. При этом мы складываем и умножаем на числа эти строки фактически так же как и векторы, записываемые матрицами-столбцами.
Дуальные объекты
Итак, на данный момент что мы имеем? У нас есть два типа объектов, имеющих направление. Над ними можно производить операции сложения и умножения на число (скаляр). Векторы при этом меняют длину, а ковекторы — свою «плотность». Векторы изображаются как столбцы из их компонент, а ковекторы — как строки. Глядя на чисто алгебраическую запись этих объектов в виде строк и столбцов, вы можете подумать, что это всё не так уж и сложно. Что это просто перевёрнутые числовые массивы, превращающиеся друг в друга «транспонированием». Верно? Но это оптическая и смысловая иллюзия! Всё же матрицы-строки и матрицы-столбцы — это принципиально разные типы объектов. И вы могли подумать, что они похожи, потому что вы работали с ними в ортонормированном базисе. То есть в базисе, где все базисные объекты имеют единичную длину и перпендикулярны друг другу. И идея преобразования как простого переворачивания строки в столбец и наоборот в таких системах отсчёта действительно верна. В более общем случае абы какого базиса это уже не работает. Но данное наблюдение всё равно даёт нам возможность задуматься о том, не сопоставить ли нам эти объекты друг другу. Вы наверняка умеете перемножать матрицы. И знаете, что умножение строки, стоящей слева, на столбец справа даёт число. Значит, такое взаимодействие ковектора и вектора можно мыслить как отображение двух объектов в один. Или рассматривать ковектор как функцию, которая «съедает» вектор и даёт число. В математике такую «дружбу» называют дуальностью.
Давайте попробуем развить эту идею и посмотреть, что получится. Мы не рассмотрим ковекторы чисто как матрицы-строки, а как функции, «питающиеся» векторами и выдающие число. И уже исходя из этой идеи построим их геометрическую интерпретацию. Если данный подход приведёт к тому же самому геометрическому облику ковекторов, то можно это считать феерическим успехом, а себя — мега-мыслителем!
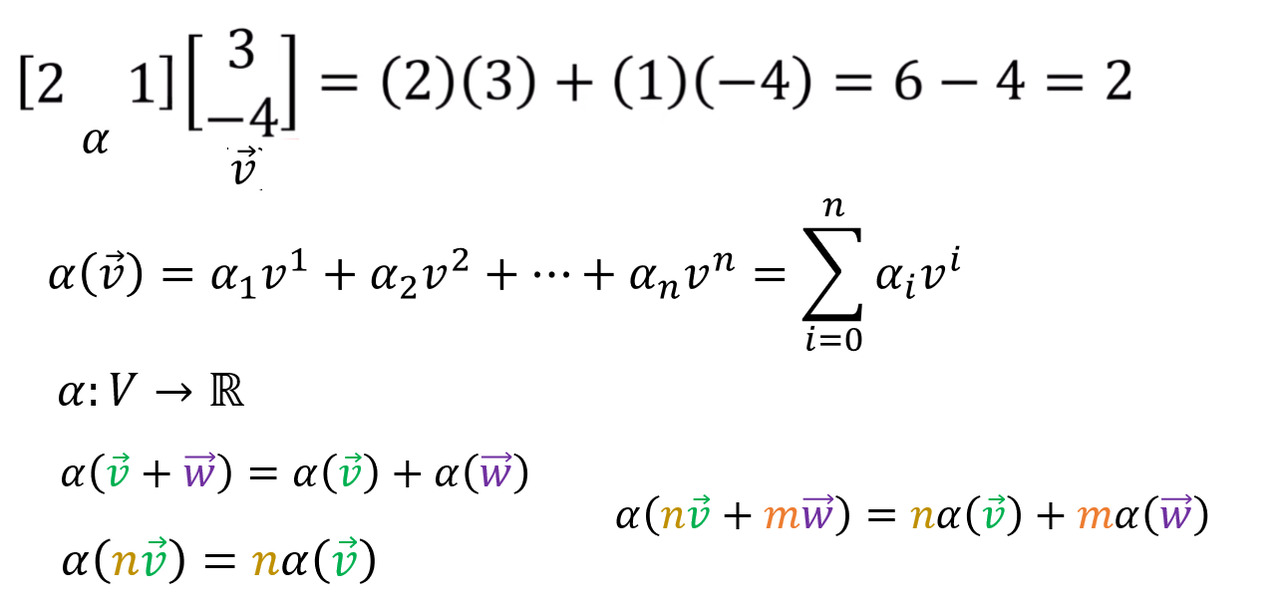
Прежде всего стоит заметить, что ковектор олицетворяет собой линейную функцию. Это весьма удобно. С линейными функциями и операторами крайне просто обращаться. Вынося из-под них множители, не нужно их возводить в какую-то степень или делать ещё более хитрые операции. Проверить это можно непосредственным вычислением в общем виде. Берём сперва складываем вектора, а потом действуем на них ковектором, а потом сперва действуем на оба вектора ковектором и складываем результаты. Значение данного отображения в обоих случаях совпадёт. Так же проверяется и линейность при умножении ковектора на число. Сперва умножаем вектор на число, а затем «съедаем» его ковектором и сравниваем с тем, что получилось при противоположном порядке действий: поглощённый ковектором вектор, после преобразования его в число, умножаем на константу.
Научившись использовать ковектор как функцию и узнав о линейности таковой, давайте попробуем опять понять её геометрический вид, забыв о том, что нам уже известно.
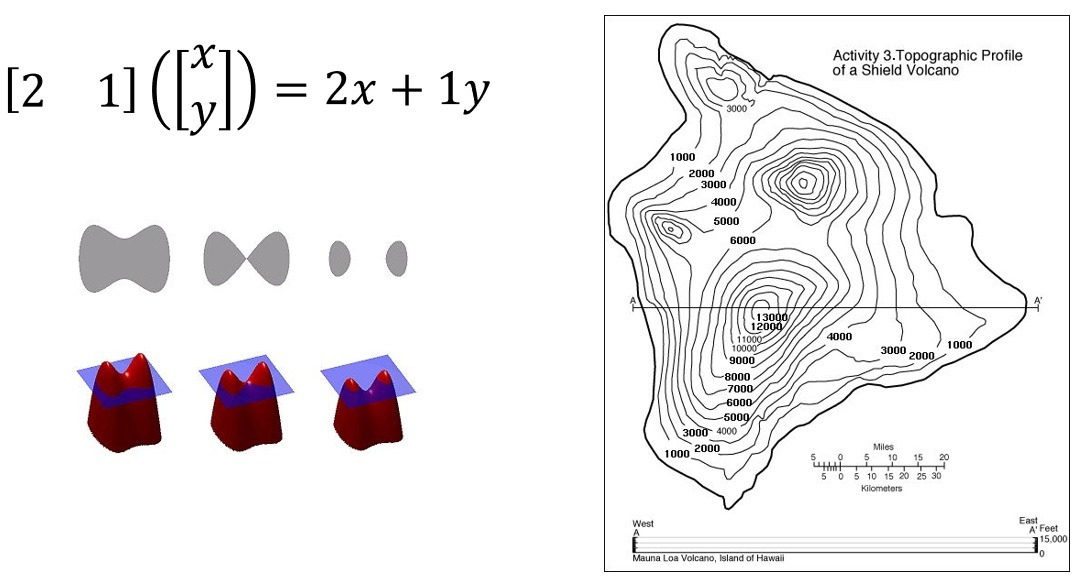
Мы знаем, что обычные векторы мы можем представить в виде стрелок. Но для визуализации функций это не очень удобно. Для геометрической интерпретации конкретного ковектора логично было бы выбрать какой-то один из них и позволить ему воздействовать на любые вектора. Так по деяниям его поймём суть его… Итак, фиксируем ковектор с конкретными компонентами в виде чисел, например [2;1]. А в качестве вектора берём столбец с двумя компонентами x и y, которые могут меняться. Таким образом, мы смотрим на ковектор как на функцию двух этих переменных (x и y). Как мы можем визуализировать функцию от двух переменных, которая выдаёт одно число? Ну что ж. Это очень похоже на проблему, с которой сталкиваются картографы, когда они хотят передать рельеф местности на двухмерном листе бумаги. Когда у вас есть топографическая карта, то вам в основном нужно показать склоны гор и долины, но только с помощью двух измерений. Вот что в этом случае делают топографы: они берут карту и рисуют на ней кривые с постоянной высотой. Так что, просто взглянув на эту карту, мы понимаем, что когда линии идут часто, то склон более крутой. Там же, где линии менее плотные, там местность более пологая, потому что высота меняется не так быстро. Удобно и наглядно! Правда? Так что давайте возьмём и используем эту идею. Возьмём наш ковектор как функцию и спросим себя, где она равна нолю. Спросить в математике означает просто приравнять к нолю нужное выражение, а потом уже угадать недостающие данные. Приравняв наш ковектор, «скушавший» вектор, к нолю, мы получим уравнение на x и y. Оно линейное, и значит, задаёт на плоскости прямую. Теперь спросим себя, где наша функция равна 1, 2, -1, -2 и всем остальным значениям. В итоге мы получим стопку одномерных поверхностей, прямых! Всё в точности как в нашей прежней геометрической интерпретации!
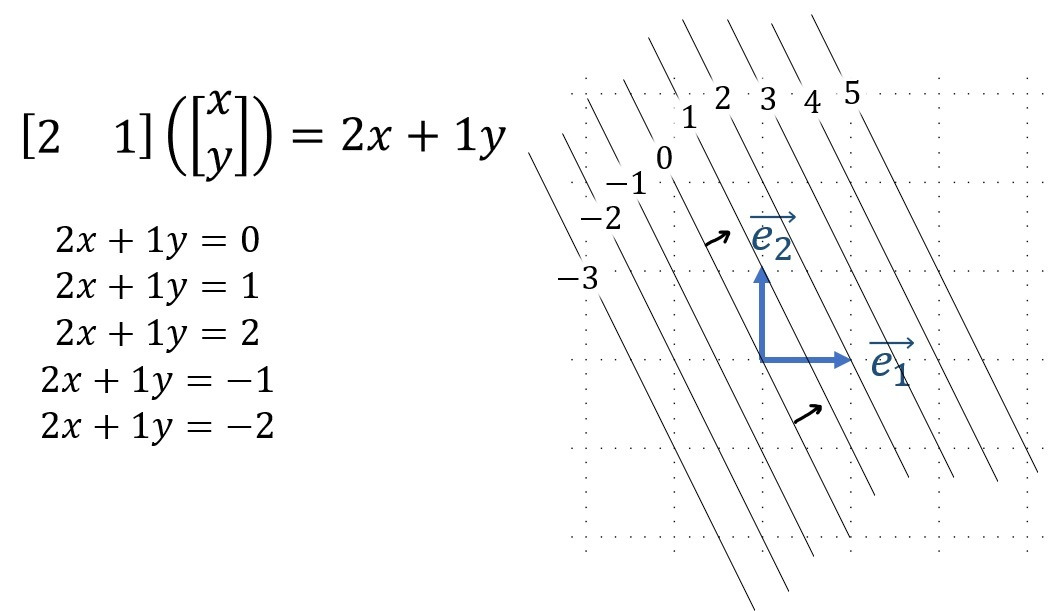
Обратите внимание, поскольку наши стопки увеличиваются вверх и вправо, мы можем добавить сюда маленькие стрелочки, как это делали раньше, указав положительное направления для «линий уровня». Всё вышло так, как мы и предположили в прошлых наших рассуждениях. Но это ещё не все приятности! Мы можем научиться воздействовать ковектором на вектор совершенно без алгебраических вычислений, глядя на их чисто геометрическое взаимодействие.
При этом для такого взаимодействия векторов и ковекторов нам не нужно ничего знать о системах координат и компонентах. Мы чертим их на плоскости и смотрим, какое количество стопок пробивает вектор и в каком направлении он это делает. Это количество пройденных насквозь линий и является значением функции ковектора на данном векторе. Если направление вектора и ковектора противоположны, то значение функции будет отрицательным, если вектор идёт вдоль линии ковектора, то он не пробивает ни одной из них, а значит, значение равно нолю.
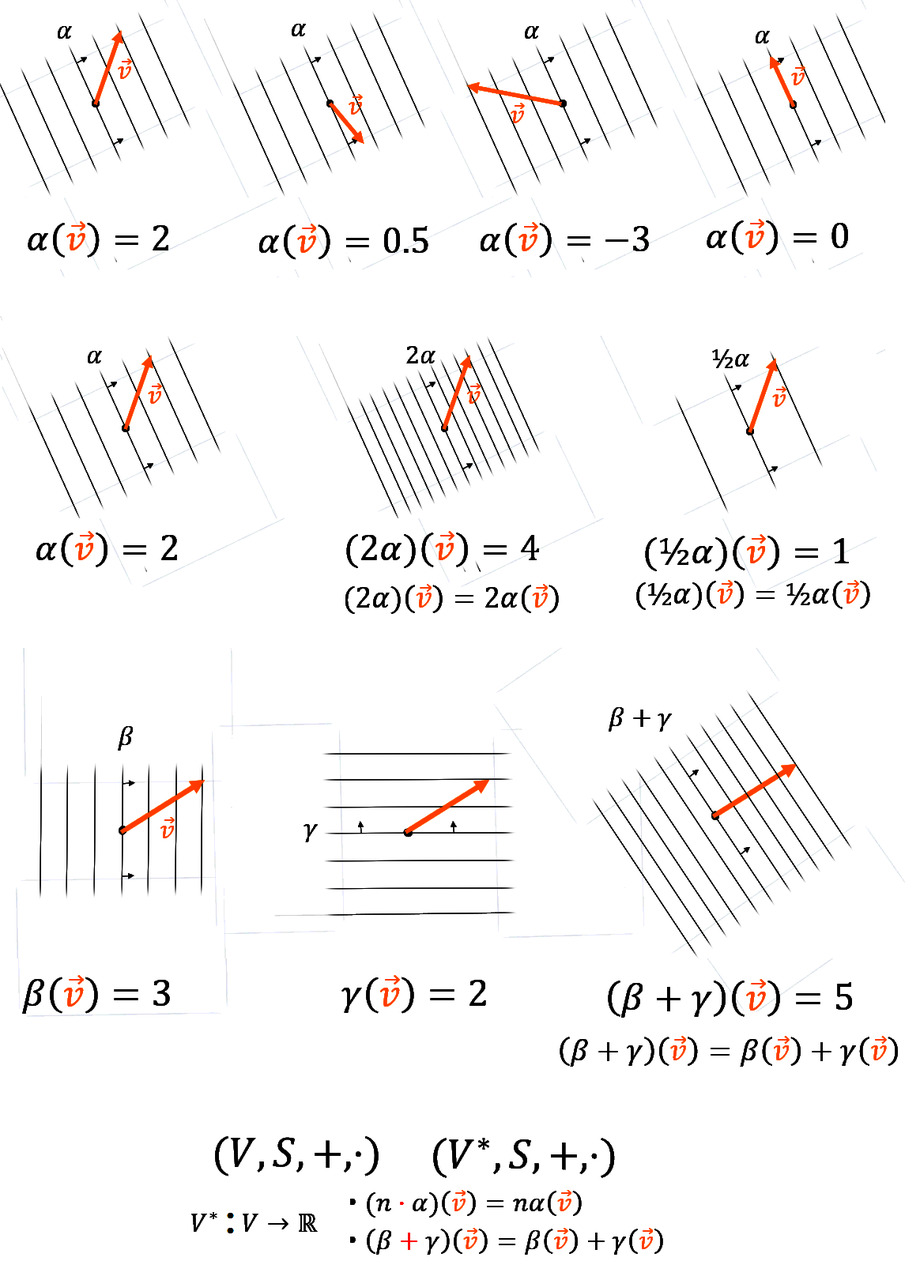
Легко в этой интерпретации узреть и линейность данного рода взаимодействий. Всё в точности как в алгебраических формулах, те же результаты для ковекторов и векторов с заданными компонентами. Умножение ковектора на число приводит к увеличению плотности линий, и, поглощая вектор, он вызывает пробитие стрелкой иного количества линий, что приводит к иному результату. Отлично работает и описанное нами ранее геометрическое сложение ковекторов. Непосредственно и наглядно давая полученные из алгебры строк и столбцов результаты.
В связи со всем этим ковекторы можно называть полноценными дуальными объектами. Обычно это обозначают, ставя звёздочку у соответствующего множества (пространства) V векторов, намекая на то, что это уже пространство дуальных к ним ковекторов V*.
Напомним, что есть такая штука, как линейное векторное пространство. Это когда у вас есть куча объектов, которые можно складывать и умножать на числа. Главное, чтобы эти операции можно было менять местами (коммутативность), чтобы они не зависели от порядка выполнения (ассоциативность) и чтобы в наборе имелись ноль и единица. При этом сами объекты могут быть любыми: не только векторы, но и матрицы, функции или ковекторы.
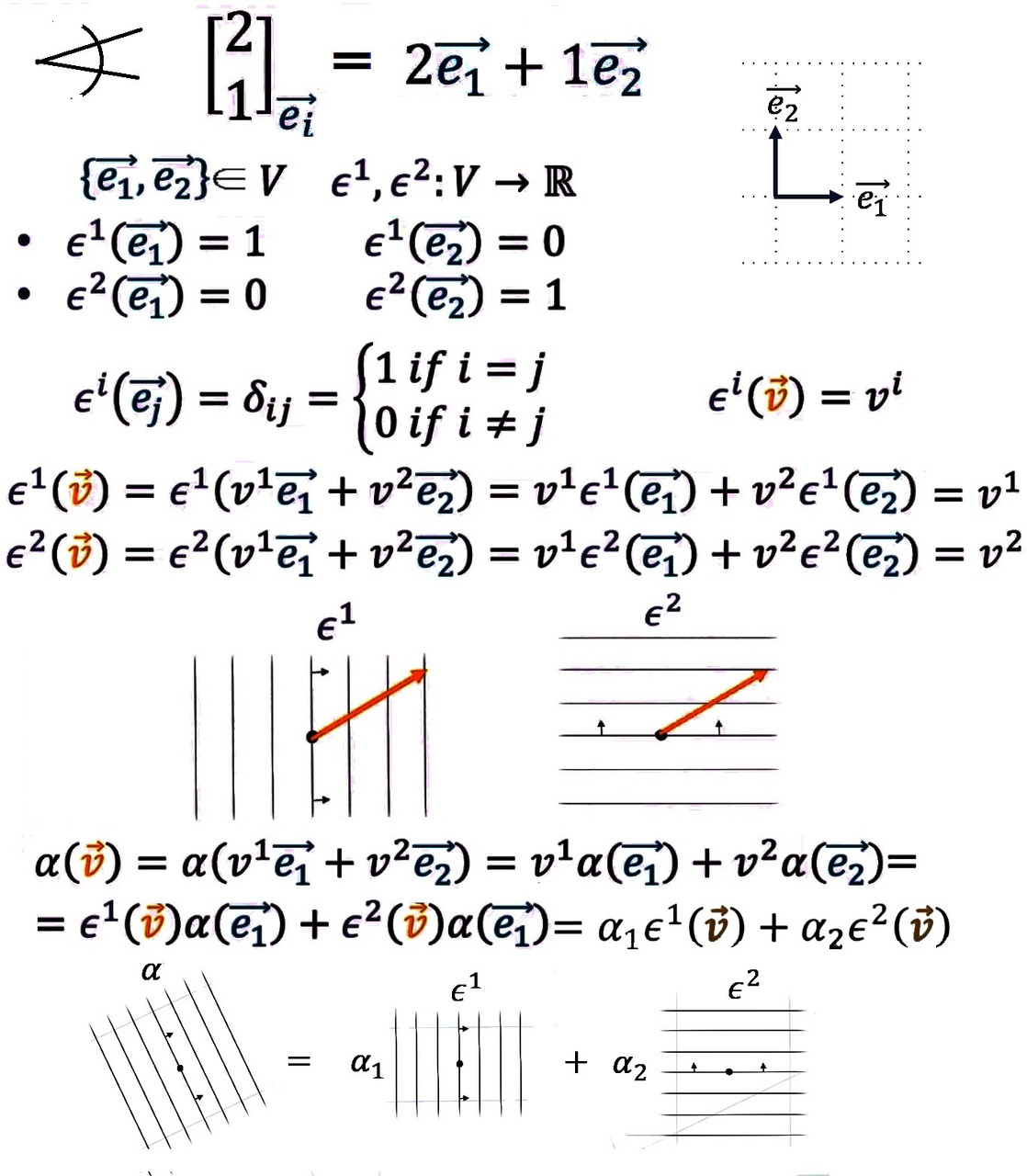
Но раз ковекторы дуальны векторам, а векторы имеют компоненты в некотором базисе, то и для ковекторов можно ввести базис. В качестве такового можно взять любые линейно независимые ковекторы. То есть набор таких ковекторов, каждый из которых нельзя выразить как комбинацию остальных. Линейная независимость является расширением понятия неколлинеарности и некомпланарности на случай большего числа измерений, чем 2 и 3. Но если у нас есть ортонормированный базис векторов, каждый из которых имеет единичную длину и ортогонален остальным, то ему можно сопоставить дуальный, или, как ещё говорят, сопряжённый базис. Он будет уникален для каждого такого набора базисных векторов. Для его получения выбирают такие ковекторы, которые, съедая базисные векторы, выдают в качестве значения либо ноль, либо единицу. Выбрав такие объекты, мы сможем разложить любой ковектор как линейную комбинацию базисных.
Интрига с разными компонентами
Каждый раз, когда имеешь дело с дуальными объектами, невольно задумываешься, чем обусловлена сама эта дуальность. Вспоминаются поговорки про две стороны одной медали и прочие народные премудрости. Не единая ли сущность предстала перед тобой в разных обликах? Что ж, многие знания — многие печали. И на наших новых дуальных знакомых, векторах и ковекторах, нам придётся посмотреть с этой же стороны. А значит, нам придётся опять творить, изощряться и выкручиваться, переводя на корректный и удобный математический язык новые наблюдательные данные.
А поразмыслить действительно есть над чем. Сегодня мы знаем, что по второму закону Ньютона сила является произведением импульса по времени. А значит, по нашей с вами уже установленной классификации сила должна являться вектором. Контравариантным объектом, как и скорость. Если вы решаете задачу о движении тела под действием силы тяжести, то вы можете её найти как производную импульса. Эта операция оставляет контравариантный объект контравариантным. С другой стороны, эту же самую силу можно найти как градиент некоего скалярного поля — гравитационного потенциала. Таким образом, сила предстаёт перед нами классическим ковектором. Но как же так? Не можем же мы приравнять вектор ковектору? Это совершенно разные объекты, хоть и дуальные.
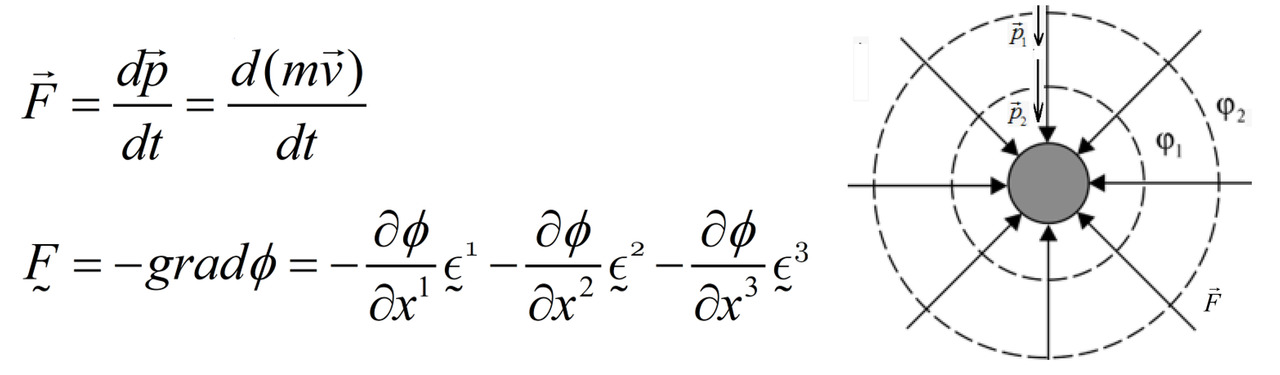
Но такова жизнь, и так устроен мир. Придётся принять сей факт и как-то разбираться и с этим. Вышеописанные наблюдения заставляют нас признать следующее: такой объект, как сила, может быть описан и как вектор, и как ковектор. А значит, это единый объект, проявляющий в определённых обстоятельствах одни свойства, а в других — иные. Нам лишь остаётся смириться с этим и, апеллируя к философии дуальности, придумать, как вектору сопоставить ковариантные компоненты, а ковектору — контравариантные.
Что бы вы предприняли, обнаружив данную проблему, если бы были математиками-первооткрывателями? Иногда полезно самостоятельно попробовать решить проблему и поиграть в первопроходца. Это очень сильно углубляет понимание, и полученные потом знания остаются с вами навсегда, становясь частью вас.
Итак, у нас есть объект, который имеет направление, но иногда при смене координатного базиса удлиняется, а иногда увеличивает плотность, сохраняя свою как бы длину. Как и то, и другое приписать нашему направленному куда-то нечту? В вопросе, как всегда, содержится часть ответа. Описанное свойство говорит о том, что такая штука, как сила, имеет и те, и другие компоненты. И ковариантные, и контравариантные компоненты. А компоненты — это что? Это всего лишь определённые проекции. Поэтому мы можем поступить так. Будем представлять силу в виде более привычной нам стрелки и попробуем спроецировать её на оси координат двумя разными способами, и посмотрим, как эти два типа проекций меняются при смене базиса.
Для большей общности возьмём косоугольную систему координат. Проведём в ней некоторую абстрактную стрелку a. В таких системах координат базисные векторы друг другу не перпендикулярны, а расположены под острым или тупым углом. Но координатную сетку получают, проводя линии параллельно осям координат, задаваемым базисными векторами. Таким образом, просто опустим из начала и конца вектора линии на наши оси параллельно базисным векторам. Координаты нашей стрелки, полученные этим способом, как раз совпадают с тем, что мы изначально считали координатами вектора. Такие координаты мы называли контравариантными. Вспомните наш пример с карандашом, направленным на дверь. Все его разложения, приводимые в том примере, были как раз контравариантными компонентами карандаша в косоугольных базисах.
Чтобы получить ковариантные компоненты, нам нужно получить проекции вектора на базисные направления. Ведь именно проекция будет обладать нужным нам свойством — меняться согласованно с изменением самих базисных направлений и масштабов. Для получения ковариантных компонент нам нужно опустить перпендикуляры к нашим осям координат из начала и конца стрелки. Это и будут наши ковариантные компоненты, по сути проекции стрелки на базисные направления. Сразу становится понятным, почему раньше вы не задумывались о дуальной природе компонент вектора. В картезианской (прямоугольной системе координат, названной в честь Картезия, по-нашему — Де'Карта) контравариантные и ковариантные компоненты будут всегда совпадать!
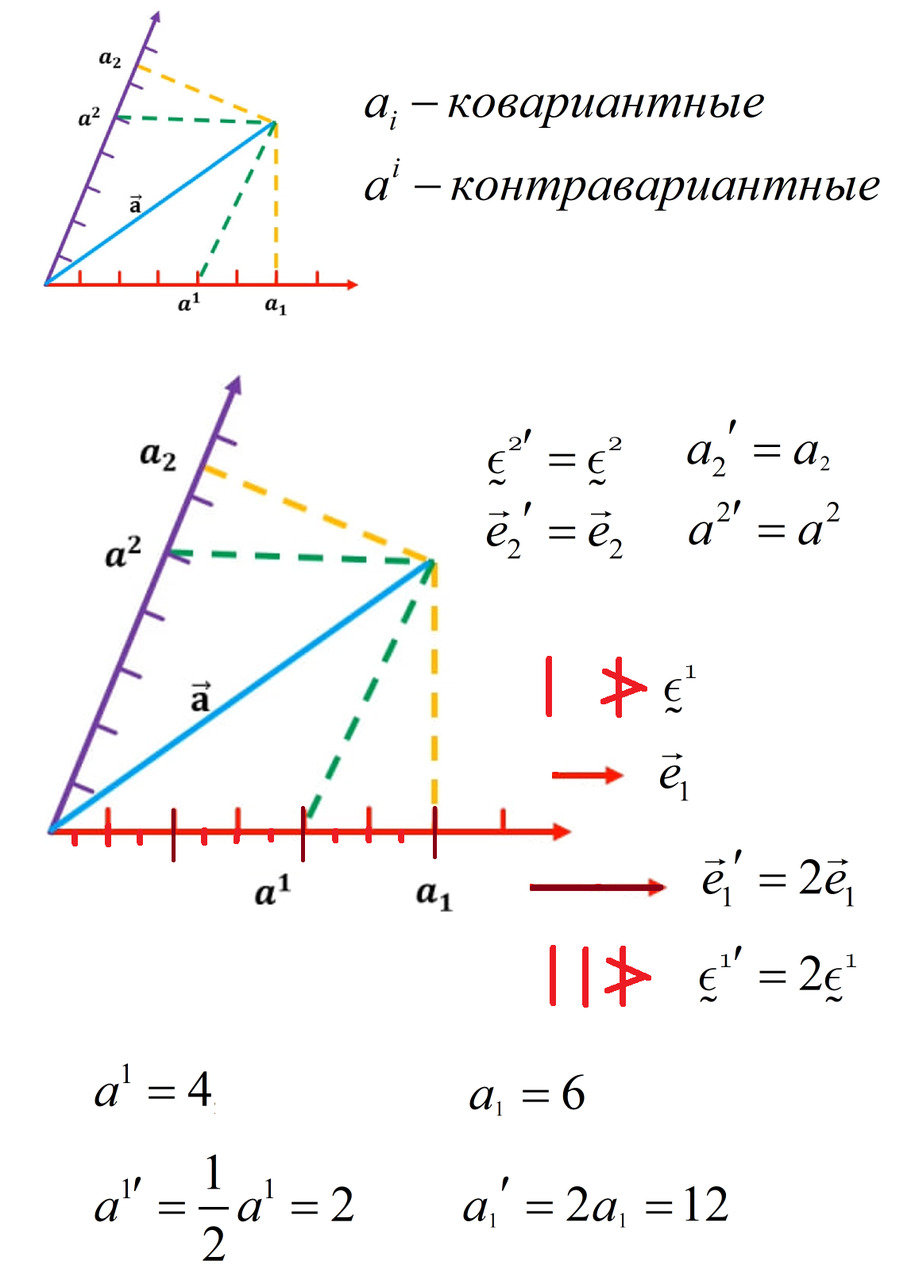
Определившись со способом визуализации ковариантных и контравариантных компонент стрелки, самое время задуматься об обозначениях и утвердить их. Базисные векторы обозначают с индексом внизу. А контравариантные компоненты векторов с индексами вверху. Базисные ковекторы обозначают индексами вверху, а ковариантные компоненты обозначают индексами внизу. Это правило математики ввели, чтобы было удобнее раскладывать объекты на компоненты и дабы индексы были на разных уровнях. Тот факт, что индексы у контравариантных компонент находятся вверху, а у базисных векторов внизу, как бы намекает нам, что они преобразуются противоположным образом. Всё это облегчает восприятие, приятнее суммировать и вероятность запутаться меньше. Сплошные плюсы!
Теперь давайте поиграемся с первой осью нашей системы координат и увеличим базисный вектор в два раза. Видно, что контравариантные компоненты при этом уменьшаются в эти же самые два раза. Контравариантная метка компоненты теперь отсчитывает вдвое меньше базисных масштабов из-за увеличения длины масштаба. Как и должно быть!
А вот ковариантная метка как была воткнута в ось перпендикулярно ей, так и не поменяла своего места. Но зато базисный ковектор увеличил свою плотность в два раза. А значит, численно он увеличивает цену этого же отрезка вдвое! Опять в точку!
Теперь мы можем посмотреть и на другой способ преобразования наших координат — поворот. Две оси поворачивать скучно. Для большей наглядности и информативности давайте чисто визуально в виде стоп-кадров заценим, как по-разному будут вести себя контравариантные и ковариантные компоненты стрелки, если поворачивать, допустим, на этот раз вторую ось.
Пусть изначально оси координат будут ортогональны друг к другу. Затем будем наклонять вертикальную ось вправо-вниз. В этом случае ковариантная компонента неподвижной оси вообще не меняется, а для поворачивающейся следует за изменением её направления, оставаясь всего лишь послушной тенью.
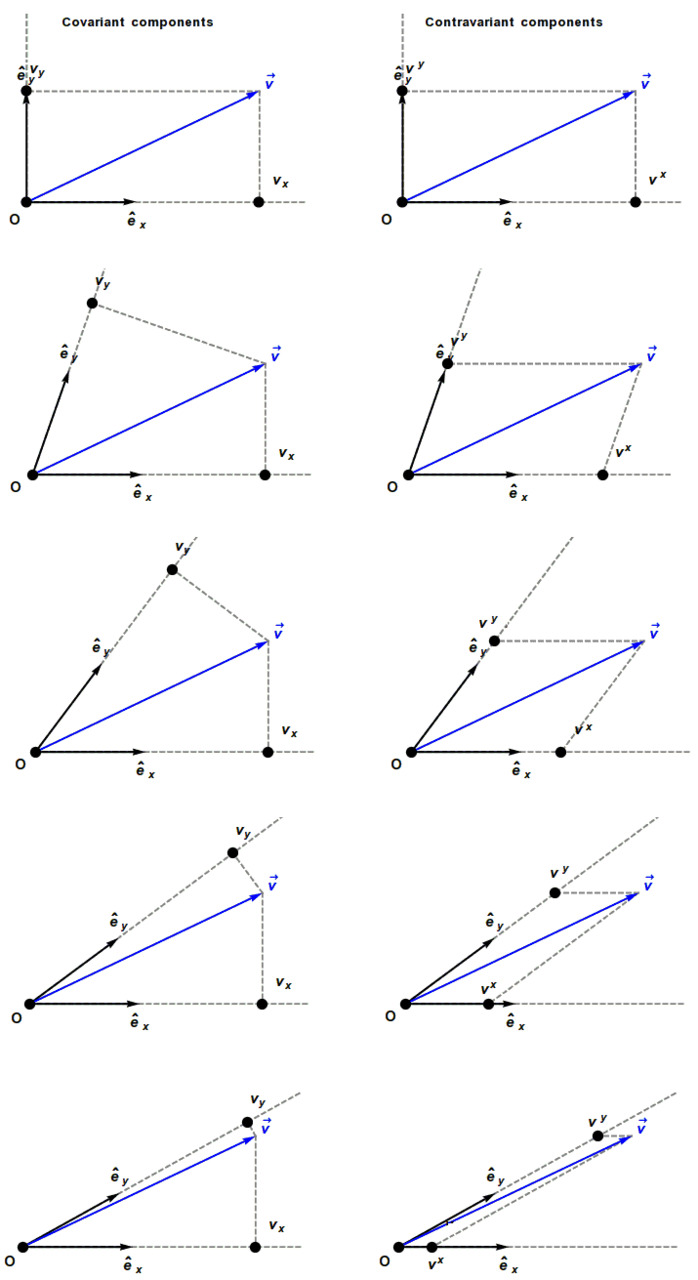
При этом обе контравариантные компоненты вытворяют пируэты. Даже та, что относится к неподвижной оси. Они делают всё, чтобы из видоизменённых контравариантных компонент можно было бы собрать тот самый исходный вектор.
И вот уже это наблюдение наталкивает нас ещё на одну мысль. Мы можем ковариантные компоненты описать в терминах скалярного произведения стрелки на базисные векторы! Это даст ещё одну алгебраическую интерпретацию и методику вычисления ковариантных компонент.
Итак, наши контравариантные компоненты — это просто коэффициенты, стоящие перед базисными векторами в разложении нашего вектора.
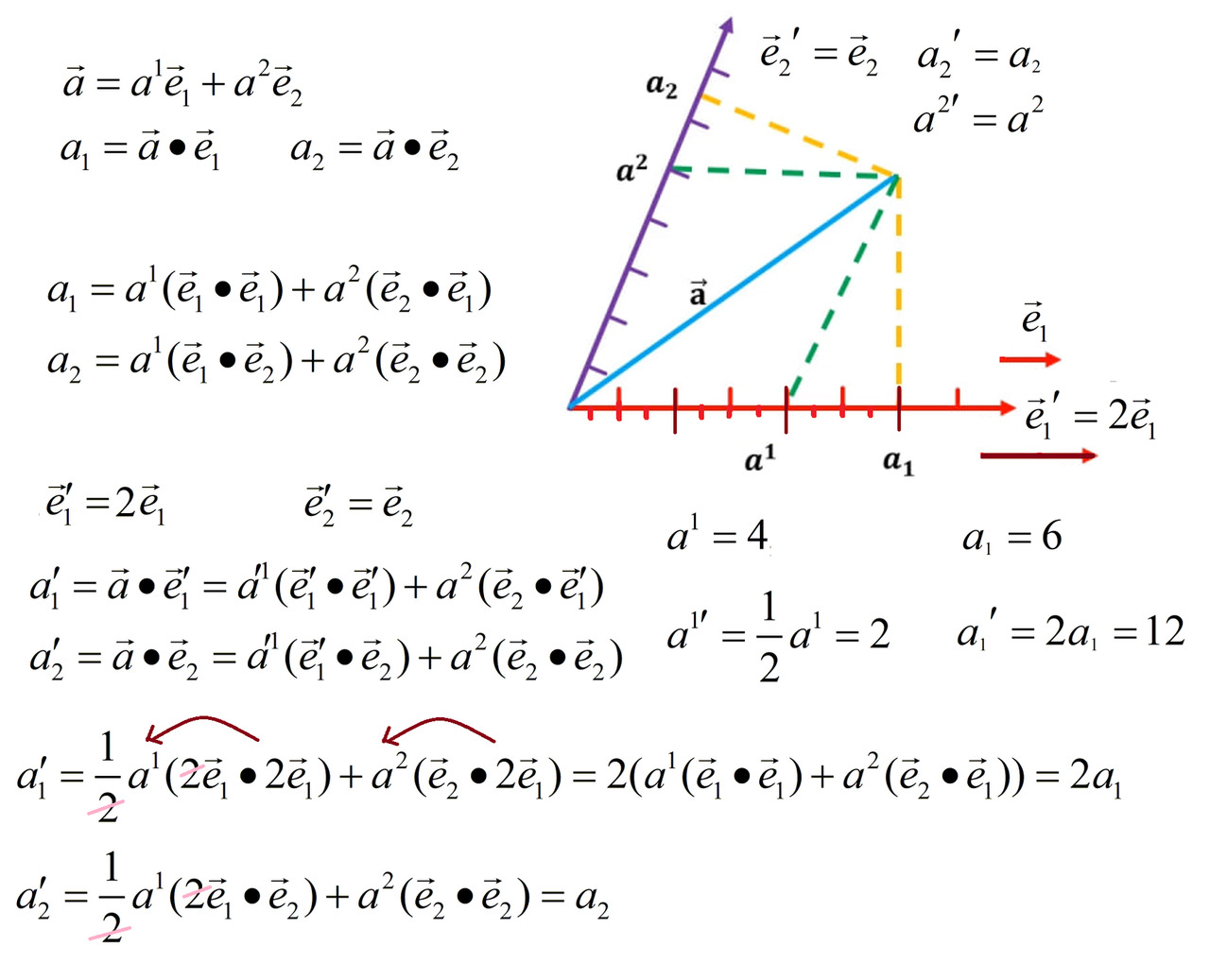
Ковариантные компоненты — это скалярное произведение нашего вектора на базисные вектора. По сути, проекции, тени. Поэтому, когда базис меняется, эти проекции тоже меняются в сторону, следующую за изменением базиса. Только и всего.
Можем для примера вычислить их и увидеть, как масштабные множители, изменившие базис, выносятся, кое-где сокращаются и в итоге дают получить в точности тот результат, который нужен.
Итак, подытожим. Мы с вами увидели, что есть величины, имеющие направление и интенсивность (длину, плотность) как вещи в себе. Их можно мыслить как некие инвариантные объекты, которые, тем не менее, можно представлять разными типами компонент. Компоненты в зависимости от типа преобразуются по-разному. Для каких-то из этих величин ковариантное представление более естественно, для других — контравариантное. Но в силу взаимной однозначности таких представлений нас это волновать уже не должно. Мы научились оперировать с каждым типом компонент как с самостоятельным геометрическим объектом. Получили два вида представления направленных объектов в виде векторов и ковекторов. Что из этого использовать — зависит от задачи. Мы увидели ясно, почему происходит такое разделение. Когда вы движетесь к двери, она движется в противоположную сторону — к вам.
Контравариантность — это дверь, которая «бежит» к вам, когда вы идёте к ней. Ковариантность — это ваши шаги, которые гарантируют: чем больше вы их делаете (в направлении двери), тем ближе она становится. Что может быть проще?
Необходимость введения тензора
Мир вокруг устроен порой весьма сложно. И для исчерпывающего описания явлений, с которыми сталкиваются человеки, одними стрелочками не обойтись. В этом разделе мы с вами естественным образом придём к такому объекту, как тензор. И уже опираясь на этот первый пример, сможем развить это понятие, увидев его элементы и в стрелочках, и в более сложных штуковинах.
Почему вектора не хватило
Представьте, что вы — инженер XIX века, и ваша задача — рассчитать прочность моста. Вы знаете, что сила — это вектор: у неё есть направление и величина. «Отлично! — думаете вы. — Запишу все силы векторами и сложу их!» И тут приходит прозрение: чтобы описать, что происходит внутри материала, вектора недостаточно. Нужен объект, который хранит информацию не только о силе, но и о том, как она распределена по бесконечно малым площадкам, какие в них действуют напряжения. Так начинается история тензоров. Одним из первых примеров тензора ранга больше чем 1 (о рангах позже) был тензор напряжений. Собственно, само слово «тензор» происходит от латинского tensus, означающего «напряжённый».
Напряжение — это мера того, как частицы материала «общаются» друг с другом под нагрузкой. Представьте, что каждая частица — житель многоквартирного дома: Сосед сверху давит на неё (нормальное напряжение); сосед слева пытается выдернуть её с места с доворотом вокруг своей оси (касательное напряжение); и так с каждым из соседей что-то да происходит. Вектор может описать, например, суммарную силу, действующую на весь дом. Но чтобы понять, кто из его элементов кого конкретно толкает, нужна полная сводка по каждому элементу и уровню. Для этого инженеры придумали выделять бесконечно малый кубик материала и смотреть на силы, действующие на каждую из его шести граней.
Отдельно нужно прокомментировать понятие бесконечно малого кубика. Лейбницу и Ньютону часто предъявляли за подобные высказывания. Действительно, что такое бесконечно малый объём? Почему бесконечно малую величину вы иногда считаете не нолём и обращаетесь с ней как с параметром, а иногда отбрасываете как настоящий ноль? В качестве оправдания такого подхода Лейбниц говорил: «Прибавьте к горе песчинку. Вы можете её учитывать, считая частью горы, а можете не учитывать и пренебречь её параметрами в сравнении с величием горы — это и есть бесконечно малая». Исчисление бесконечно малых обогатило человечество колоссальными инженерными достижениями ещё до того, как было переосмыслено и строго непротиворечиво обосновано в трудах Огюстена Коши, Карла Вейерштрасса и других математиков. Это теория пределов и всё то, что вам рассказывают на матанализе. В физике бесконечно малыми считаются реальные (не бесконечно малые!) величины, которые малы в сравнении с другими параметрами системы. Их игнорируют, если их вклад в результат незначителен. Хотя с точки зрения математики с ними работают как в классическом матанализе.
Итак. Представим себе некоторое тело и какой-то маленький элемент внутри него.
Напряжения возникают в теле при его нагружении (деформации, сжатии, скручивании) как реакция частиц на попытку внешних сил изменить их взаимное расположение. Эти внутренние силы сопротивления удерживают частицы от смещения.
В одной и той же точке материала напряжения могут различаться в зависимости от направления. Например, соседние частицы могут «давить» вдоль одной оси и «сдвигать» вдоль другой. В простых случаях, таких как растяжение или сжатие бруса, определить максимальные напряжения относительно легко. Однако при сложных нагрузках задача усложняется: требуется анализировать, как напряжения меняются при повороте условных площадок внутри материала.
Для этого изучают напряжённое состояние — совокупность всех напряжений, действующих на бесконечно малый элемент вокруг точки. Такой подход позволяет найти опасные зоны, где напряжения достигают критических значений, и предотвратить разрушение конструкции. Коротко: напряжения — это внутренний ответ материала на внешние силы, а их анализ требует учёта всех направлений и типов воздействия.
Попытки первооткрывателей справиться с описанием всех этих напряжений, тянущих и сдвигающих точку в разные стороны, были вполне естественны. Кстати, что бы вы сделали на их месте? Как учли бы в едином описании всевозможные силы упругости, действующие на элемент тела?
Наши первооткрыватели первично вводили систему координат XYZ и рассматривали координатные плоскости как основу для бесконечно малых площадочек. Силы, действующие на каждую из площадок, первооткрыватели обозначали максимально просто. Xx, Xy, Xz, Yx, Yy, Yz, Zx, Zy, Zz. Под этими символами подразумевали проекции напряжений, действующих на гранях элементарного кубика или на площадке, соответствующей конкретной оси координат. Вполне естественно выглядит! Согласитесь?
В последствии в XIX веке наступило прозрение, что эти девять чисел — есть единый объект! Его-то и назвали тензором напряжений.
Как видите, всё просто в математике, гениально и просто. Где невозможно обойтись одним вектором, ничто не мешает нам взять их несколько штук!
Сегодня обозначения отличаются от тогдашних. Тензор напряжений принято обозначать чаще всего греческой буквой «сигма» с двумя индексами или латинской буквой P. Первый индекс показывает, о какой грани или площадочке идёт речь, а второй — о каком компоненте вектора напряжения, относящегося к этой площадке.
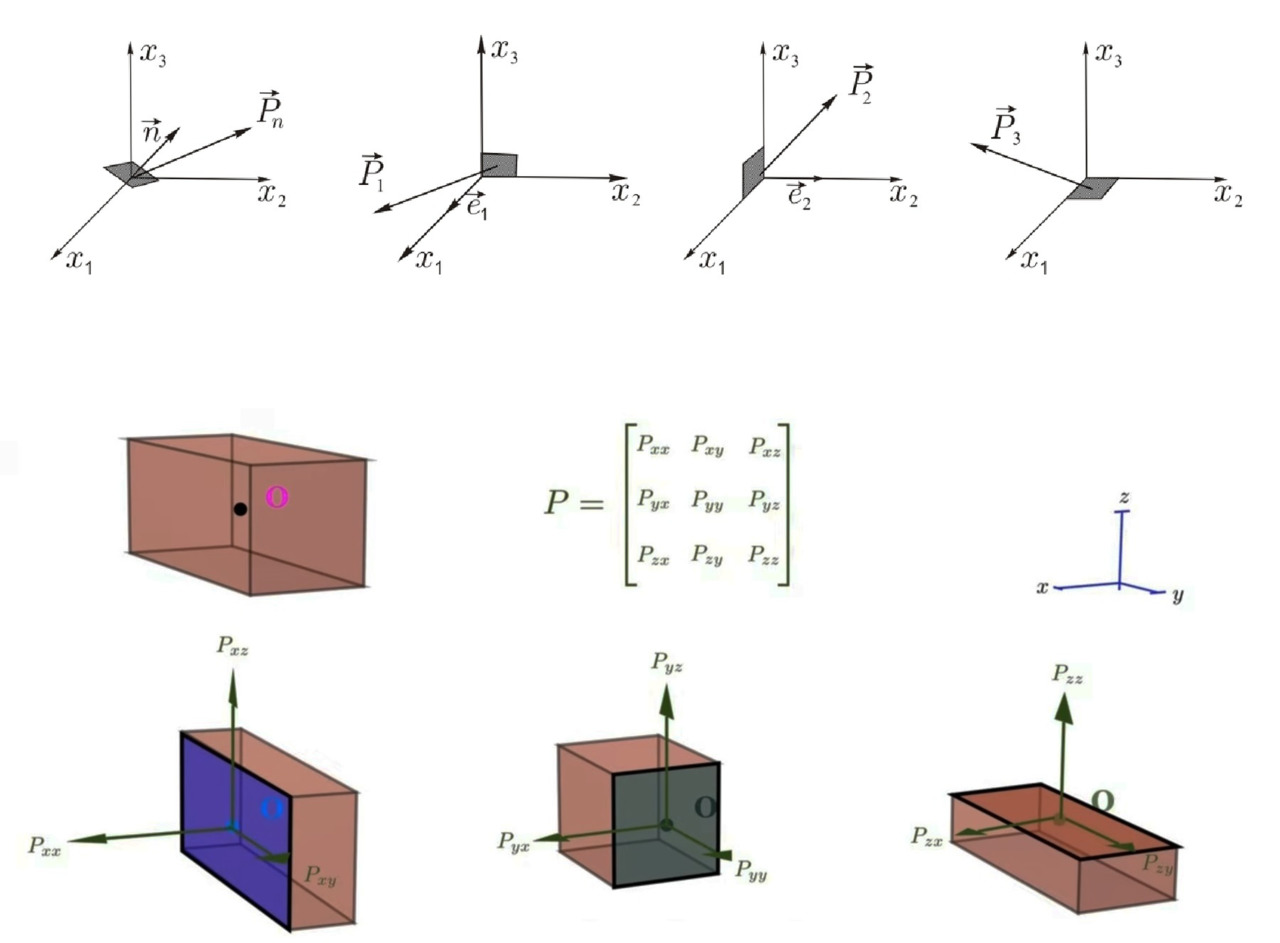
Возможно, вы спросите, почему нельзя просто взять и сложить все эти силы или их компоненты, действующие в одном направлении, приложенных к точке, и получить вектор силы на единицу площади? Почему, например, нельзя сложить Pxx и Pyx? Дело в том, что хотя силы действуют в одном направлении в одной точке, их природа различна. Например, Pxx тянет объект влево и хочет, чтобы соответствующая этой компоненте грань выступала влево. В то же время Pyx действует, чтобы сдвинуть или потянуть выделенную перпендикулярную оси Y грань влево. Эта компонента силы хочет создать трёхмерный параллелограмм вместо выступа. Сдвиг и растяжение приводят к тому, что тело деформируется по-разному в разных направлениях. Поэтому эти компоненты и вектора нельзя складывать. Поэтому же, помимо указания сил, необходимо указывать поверхность, на которую действует сила. Если сложить их «в лоб», получится бессмысленная смесь разнонаправленных векторов. Это как сложить скорость ветра и силу тяжести — формально числа есть, но физического смысла нет.
Представьте кубик, на который действуют: растяжение по оси X, равное 10 МП (Мега Паскалей), и сдвиг по грани XY, равное 5 МП. Если сложить эти силы, мы получим 15 МП, но это не будет иметь смысла: растяжение и сдвиг — разные типы воздействия. Чтобы найти, например, максимальное растягивающее напряжение под углом 30°, нужно использовать тензор, всю совокупность действующих напряжений, а не сумму компонент.
Какой мы теперь делаем вывод из всего этого? Тензор напряжений — это единственный способ корректно описать, как силы распределены по всем направлениям и площадкам в точке материала. Простое сложение компонент:
— смешивает разнородные величины (нормальные и касательные напряжения);
— игнорирует зависимость напряжений от ориентации;
— нарушает законы физики (например, парность касательных напряжений).
Можно привести простую аналогию: Представьте, что тензор — это палитра художника, где каждый цвет (компонент напряжения) отвечает за определённый оттенок. Если смешать все краски в кучу, получится грязно-коричневая масса. Только используя цвета по правилам (тензорный формализм), можно создать точную картину напряжённого состояния.
Исчерпывающее описание
Давайте теперь задумаемся над тем, почему тензора напряжения как совокупности трёх векторов достаточно для описания вообще всех мыслимых и немыслимых напряжений в теле? Всего три вектора, приставленных к трём площадкам, могут решить любой вопрос.
Для этого анализа давайте вспомним доступные нам операции. Мы можем записать три вектора напряжений, приложенных каждый к своей ориентированной площадке, в виде прямоугольной таблицы из девяти компонент, называемой матрицей. Матрицы могут умножаться на другие матрицы, и в частности на матрицы-строки и матрицы-столбцы.
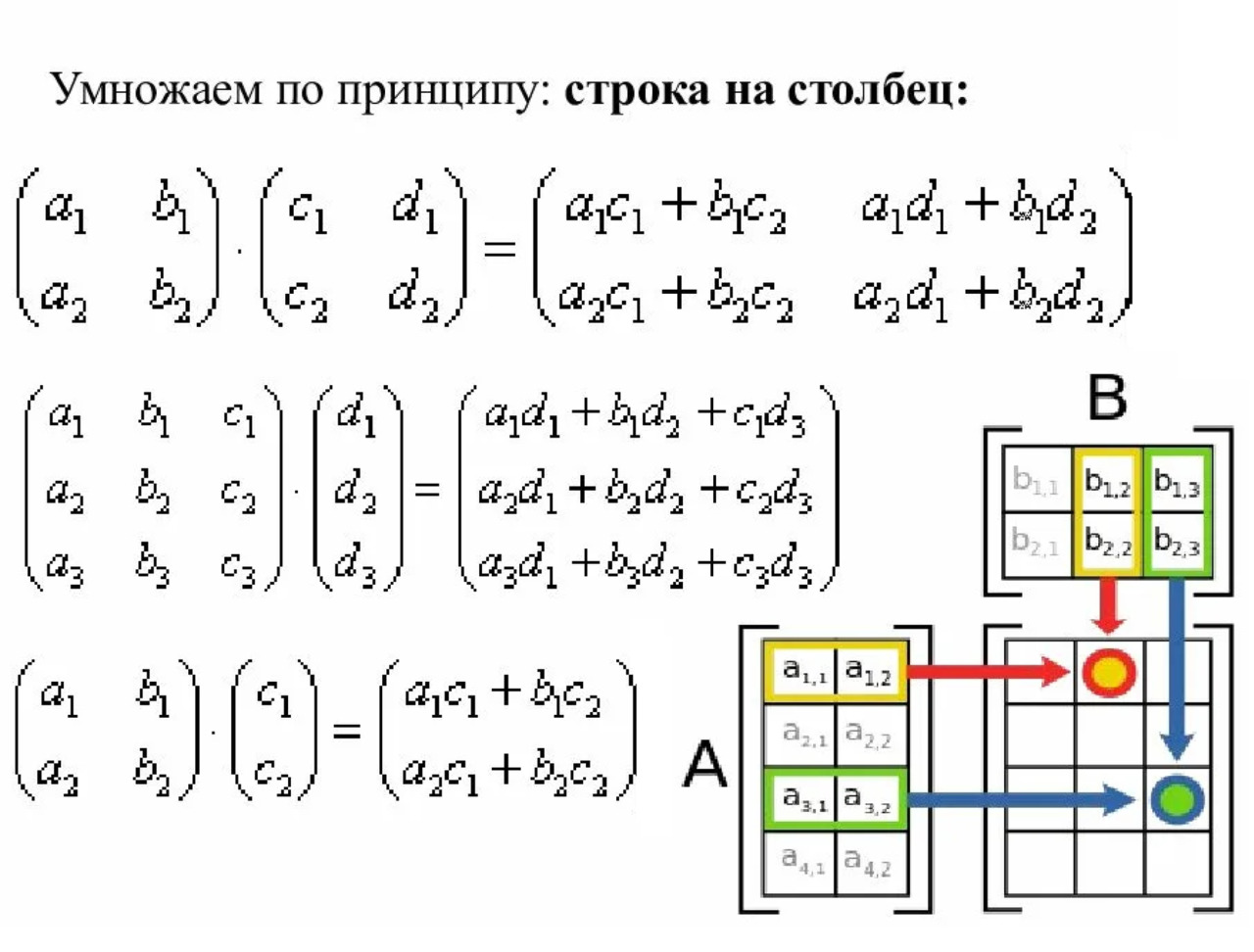
Если из элементов матрицы составить некоторые алгебраические комбинации, то мы можем получить так называемые инварианты — величины, которые будут неизменны при переходе к другой системе координат. На всякий случай напомним, что матрицы умножаются по правилу «строка на столбец». Умножаясь на вектор справа или на ковектор слева, они дают тот же тип объекта (вектор и ковектор соответственно) и в этом смысле являются операторами. То есть объектами, которые преобразуют вектора, превращая их в другие вектора. Матрица — это оператор, то есть превращатель. Если вектора, на которые воздействуем, мы стали рассматривать в новом базисе, то и превращатель разумно тоже рассмотреть с новой точки зрения — из нового же базиса!

I2 — вторая симметрическая сумма,
I3 — детерминант.
У вектора при смене базиса не меняется его «длина» или, как её называют в более абстрактном случае, норма. У матрицы тоже есть несколько типов инвариантов. Это её след — сумма диагональных элементов, определитель (детерминант) и сумма главных миноров второго порядка (или вторая симметрическая сумма). Инварианты — это «душа» матрицы. Они остаются неизменными, даже если вы смотрите на объект под разными углами. Как говорил математик Герман Вейль: «Инварианты — это то, что остаётся, когда всё остальное ушло».
Как эти математические действия помогут нам получать информацию из тензора напряжений? Ну, во-первых, сразу видно, что вместо одной длины вектора у нас есть три каких-то инварианта! Каждый из них наверняка расскажет нам о чём-то своём, специфическом именно ему качестве. Во-вторых, матрица оказалась неким преобразователем, который, беря направление (вектор), видоизменяет его. И по деяниям такого оператора можно смело делать выводы о внутренней структуре, закодированной матрицей, олицетворяющей наш тензор напряжений.
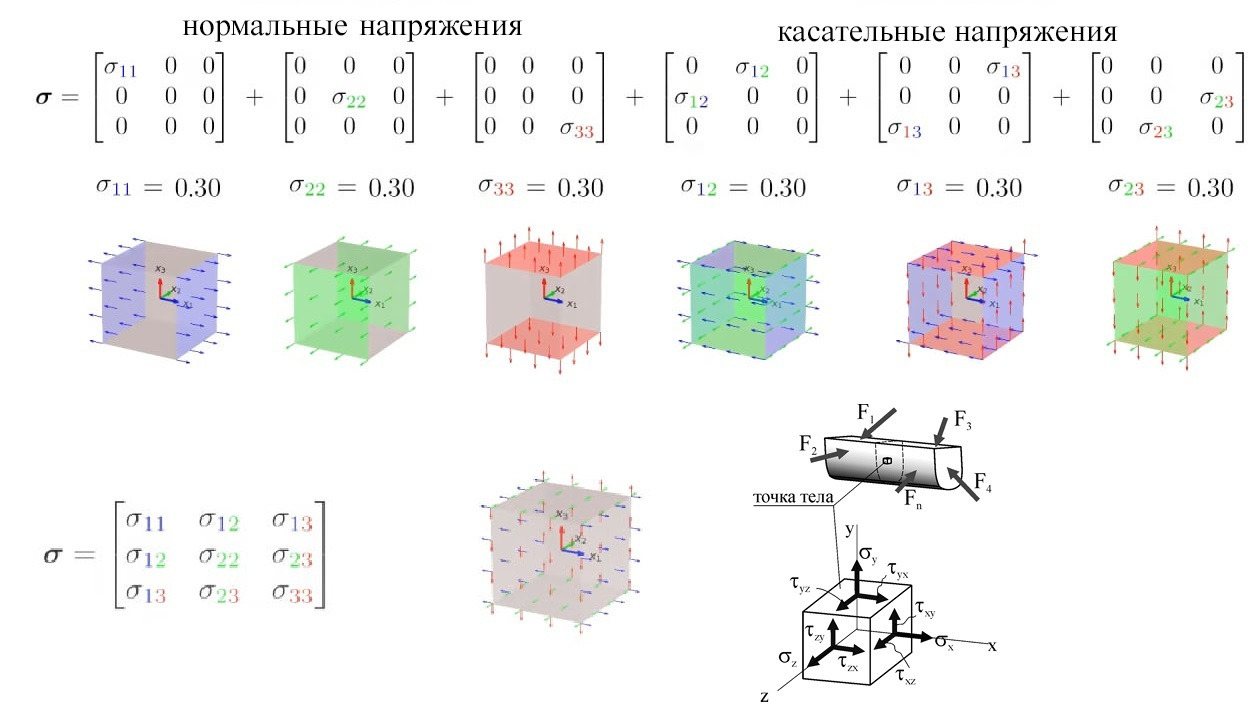
Так почему же трёх векторов тензора хватает для описания напряжений в любом направлении? Всё просто. Тензор напряжений — это не просто три вектора, а математический оператор, который кодирует правила преобразования напряжений при изменении ориентации площадки. Вот как это работает. Три вектора — это базис для всех возможных направлений. Каждый из трёх векторов тензора описывает напряжения на гранях кубика, ориентированных вдоль осей X, Y, Z. Эти направления выбраны не случайно — они образуют ортонормированный базис, то есть охватывают всё трёхмерное пространство. Любое произвольное направление можно представить как комбинацию этих трёх осей. Например, площадка с нормалью под углом 45° к осям X и Y «видит» проекции напряжений с граней X и Y. Тензор позволяет вычислить эти проекции через матричные операции.
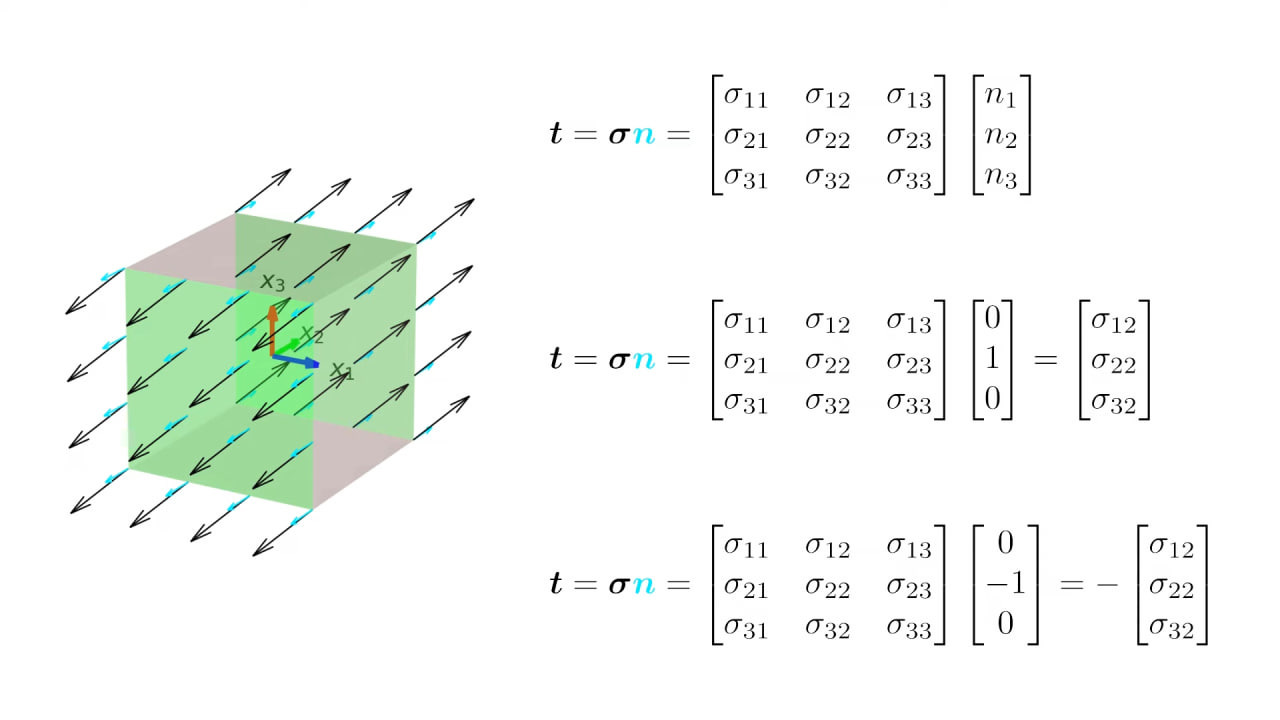
Тензор — это оператор преобразования. Чтобы найти силу напряжения на произвольной площадке с нормалью
n= (nx; ny; nz), нужно умножить тензор напряжений Pij на этот вектор:
F=Pn= напряжение вдоль направления вектора n.
Эта операция «смешивает» вклады от всех трёх базисных векторов тензора, учитывая ориентацию площадки.
Например, пусть нормаль к площадке направлена вдоль оси X:
n= (1; 0; 0). Тогда мы получим просто первый вектор тензора. Если же n повёрнут под углом, в формуле появятся комбинации всех компонент Pij. Таким образом, тензор позволяет «пересчитать» напряжения для любой ориентации, используя всего три базисных вектора.
Представьте, что три базисных вектора тензора — это основные цвета (RGB). Любой оттенок (направление) можно получить их смешением. Тензор — это инструкция, как комбинировать «цвета» -напряжения для получения «оттенка» -напряжения в произвольном направлении. Если бы у нас не было тензора, пришлось бы измерять напряжения для всех возможных углов, что физически невозможно. Тензор даёт компактную формулу вместо бесконечного числа экспериментов.
Почему в тензоре только три вектора, а не больше? Дело в том, что трёхмерное пространство описывается тремя независимыми направлениями (осями X, Y, Z).
Любой вектор или тензор в этом пространстве можно разложить по этим базисным направлениям. Добавление четвёртого вектора избыточно — он будет выражаться через существующие три. К примеру в механике если вы знаете силы, действующие на три взаимно перпендикулярные грани кубика, вы можете найти силу на любой наклонной грани через проекции. Дополнительные измерения не нужны.
Тензор напряжений, несомненно, олицетворяет и чисто физические законы. Симметрия тензора (Pij=Pji) — прямое следствие третьего закона Ньютона (действие равно противодействию) и сохранения момента импульса. Если касательное напряжение на
верхней грани толкает кубик вправо, то напряжение на правой грани должно толкать его вверх с той же силой. Если бы не симметрия соответствующих компонент, возник бы «неуравновешенный» крутящий момент, и кубик начал бы вращаться сам по себе, что противоречит реальности.
Тензор напряжений Pij в трёхмерном случае имеет 9 компонент, но из-за симметрии независимых только 6. Диагональные компоненты P11, P22, P33 представляют из себя нормальные напряжения, действующие перпендикулярно граням кубика.
Если P11=Pxx> 0 положительно, то это говорит о растяжении вдоль оси X. Если же эта компонента отрицательна, то происходит сжатие. Недиагональные компоненты P12, P23, …, представляют собой касательные (сдвиговые) напряжения, действующие вдоль граней. Например, Pxy — напряжение вдоль оси Y на грани, перпендикулярной X.
Существуют так называемые главные напряжения — это максимальные нормальные
напряжения, действующие в направлениях, где касательные напряжения равны нулю. Инварианты тензора напряжений используются в критериях прочности материала, например, в критерии Мизеса. Критерий Мизеса — это «правило», которое определяет, когда материал переходит в состояние пластической деформации (например, начинает течь, как пластилин) под действием сложных напряжений. Он отвечает на
вопрос: «При каком сочетании напряжений материал сдастся?». В основе критерия лежит идея, что пластичность зависит не от конкретных направлений, а от интенсивности касательных напряжений в материале. Для этого и используется тензор напряжений, а точнее — его инварианты.
Инварианты тензора напряжений — это величины, которые остаются неизменными при повороте системы координат. Они отражают фундаментальные аспекты напряжённого состояния материала, не зависящие от того, под каким углом мы на него смотрим. Вот их механическая интерпретация.
Первый инвариант I1 — «шаровая часть». Он олицетворяет среднее нормальное напряжение, действующее на материал, и гидростатическое воздействие. Если I1> 0 — материал сжимается равномерно со всех сторон (как под водой), если I1 <0 — растягивается. Таким образом, I1 отвечает за изменение объёма материала, но не влияет на его пластическую деформацию.
Второй инвариант I2 — «интенсивность искажения». Его физический смысл прост. Он характеризует интенсивность изменения формы материала (девиаторную часть), вызванную разницей между нормальными и касательными напряжениями.
Третий инвариант I3 — «сложность напряжённого состояния». Он отражает степень асимметрии в распределении напряжений.
Если I3 = 0, напряжения симметричны (например, при чистом сдвиге). Если I3 не ноль, то есть комбинация разнотипных напряжений (растяжение + сдвиг + кручение).
Видите, как массу всего полезного может сказать нам тензор напряжений? Если его пронизывать единичными векторами в разных направлениях (умножая его на них), он выдаст напряжение в этом направлении. Его же инварианты расскажут о среднем состоянии материала, причём выдадут три разных полезных характеристики!
Подытожим. Мы столкнулись с ситуацией, в которой одного вектора было мало для описания всех перекосов и растяжений вместе взятых. Но так как трёхмерное пространство — штука тесная, для описания всевозможных напряжений в нём нам хватило введения всего трёх векторов. Эти вектора оказалось возможным упорядочить и объединить в единое целое, записав в виде матрицы. А дальше уже сама математика дала нам возможность извлечь из этой конструкции максимум возможной информации.
Тензор возникает там, где одного вектора мало. Не хватает одного вектора — возьми больше! Что может быть проще?
Тензоры наглядно
В этом разделе мы, опираясь на уже имеющийся опыт работы с тензором, обобщим это понятие и сделаем применимым во всех подобных случаях. Мы научимся изображать тензоры так же наглядно, как вектора, и осмыслим операции над ними столь же естественно, как это делали раньше.
Как понять, что перед вами тензор?
Вектора нам знакомы уже давно и весьма интуитивны. Как только вы видите что-то, что имеет направление, вы можете описать это вектором. Но как понять, что перед вами более сложный объект? С механическим напряжением нам пришлось повозиться. Возникает вопрос: «Есть ли более простые критерии, говорящие о том, что мы имеем дело с тензором? Чтобы так же, как и с векторами, было всё легко и сразу понятно».
Да. Понять, что перед вами тензор, очень легко! Нужно вспомнить, что он является оператором-превращателем. Он берёт один вектор и превращает его в другой, имеющий, возможно, иное направление.
Давайте обратимся к физике и посмотрим, какие в ней есть подобные величины. Если мы вспомним о векторе импульса и о том, что он равен скорости, умноженной на массу (и иногда на релятивистский коэффициент), то поймём, что масса — это просто число. Коэффициент пропорциональности, если угодно., потому как вектор импульса и скорости всегда сонаправлены.
Теперь представим себе спутник, летающий где-то в небесах. Его скорость и импульс так же всегда сонаправлены. Но у вращающегося тела помимо импульса есть ещё и момент импульса. Он равен моменту инерции, умноженному на угловую скорость вращения. Спутник мы можем вращать вокруг разных осей. А значит, момент инерции относительно этих осей будет разным. Поэтому даже если спутник вращается с одинаковой по модулю угловой скоростью в обоих направлениях, из-за разной величины момента инерции его угловой момент будет разным. В одном случае он будет больше, в другом меньше. А значит, если сложить их вместе, получится, что результирующий угловой момент не совпадает по направлению с вектором угловой скорости. Это значит, что момент инерции это не число, а такой же превращатель одних векторов в другие — тензор!

Признаки видны сразу!
Теперь вспомним закон Ома в векторной форме. Вместо тока I у нас там вектор плотности тока J. Вместо напряжения U у нас вектор напряжённости Е. В самых простых случаях эти два вектора пропорциональны друг другу, и коэффициент пропорциональности именуется проводимостью. Но если перед нами необычный кристалл, то пропорциональность этих векторов нарушается. Ведь в специальных анизотропных кристаллах проводимость может зависеть от направления! Тогда вектор тока и напряжённости уже не будут коллинеарны. В этом случае проводимость уже оказывается тензором.
Так что критерий оказался весьма прост. Видя некое линейное уравнение или закон, посмотрите на его правую и левую части и спросите себя, куда направлены вектора, находящиеся по обе стороны, и совпадают ли они в самом общем случае. Если всегда совпадают, значит, перед вами скалярная величина. Если есть ситуации, где коллинеарность нарушается, значит, перед вами тензор во всей красе и информативности. Тензоры в физике и математике возникают повсюду. Даже обычная деформация — и то тензор! Поэтому настало время сделать то, что так любят математики: абстрагироваться от объектов и описать их на абстрактном языке, алгебраическом и геометрическом наглядном.
Абстрагируемся и обобщаем
Окинув мысленным взором всё, что мы уже поняли, давайте поразмыслим, как всё это можно обобщить. Матрицу (оператор) мы составляли из трёх векторов, и она уже позволяла нам изменять входящие векторы, превращая их в другие, имеющие даже другое направление.
Значит, для описания тензора нам нужно три вектора. Но эти векторы должны быть упорядочены. Хорошо это или плохо? На первый взгляд это может смущать. Но если мы вспомним, что вектор можно представить тремя компонентами, которые суть просто упорядоченный же набор чисел, то сомнения отпадут. Три упорядоченных числа для вектора, три упорядоченных вектора для тензора. Что тут такого?
Глядя на эту иерархическую лестницу, возникает интересная мысль. А давайте упорядоченные числа называть тензором первого ранга, а упорядоченные векторы — тензорами второго ранга. Скаляры же тогда само собой просится назвать тензорами нолевого ранга. Ну и логично предположить, что упорядоченные наборы тензоров второго ранга можно называть тензорами уже следующего — третьего ранга.
Ещё один важный момент нужно учесть. Компоненты вектора могут меняться в зависимости от базиса, в котором он рассматривается. Компоненты тензора тоже. Значит, когда мы записываем тензор в виде массива чисел, нужно учитывать, в каком базисе мы рассматриваем этот объект.
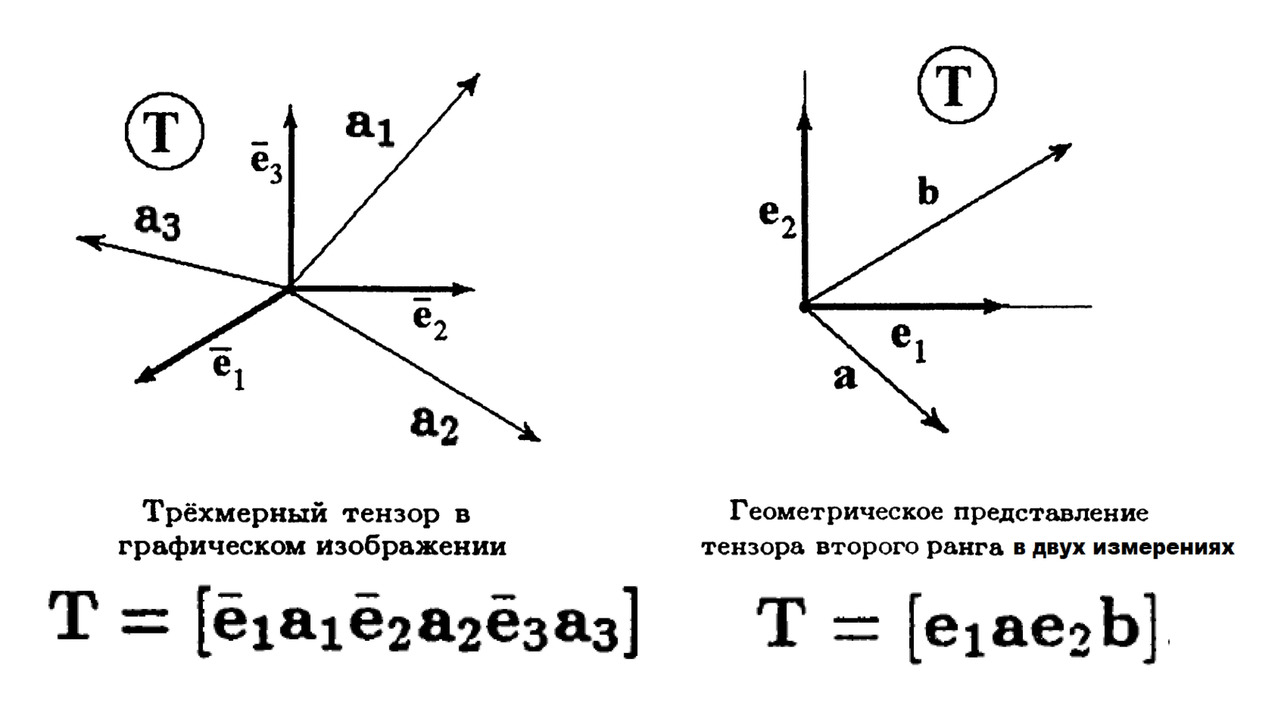
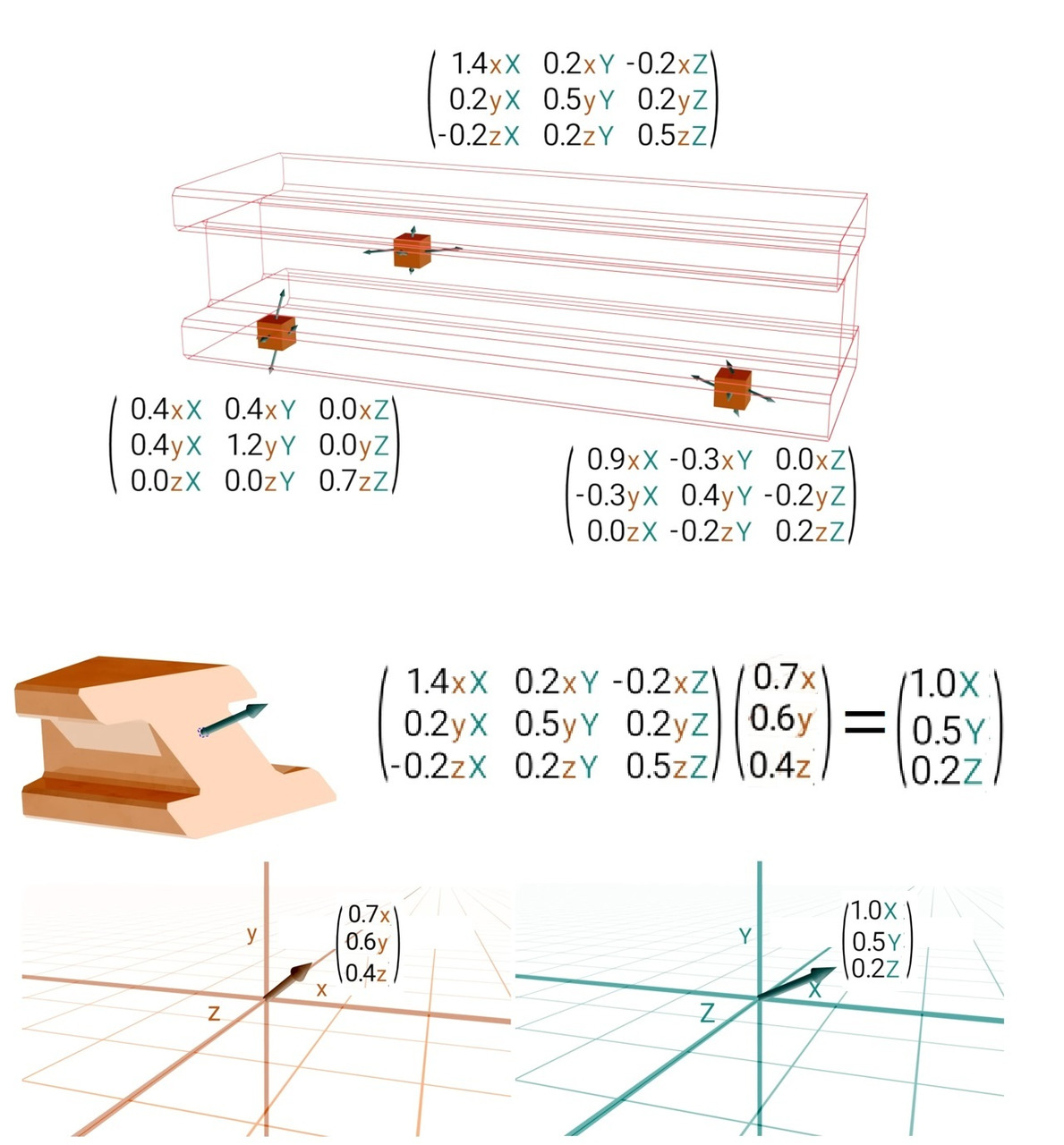
Всё это подводит нас к вполне естественному геометрическому изображению тензоров. Будем называть тензором упорядоченную тройку векторов в некотором базисе. При этом сам рассматриваемый базис тоже упоминать графически и алгебраически. Алгебраически это тоже можно записать в виде набора из упорядоченных базисных и обычных векторов.
Будем называть данные вектора индивидуальными для тензора. Какую они имеют природу? Такую же, как и любой иной объект, имеющий направление и рассмотренный нами ранее. Каждый из индивидуальных векторов тензора может иметь ковариантные и контравариантные проекции на базисные векторы. Будем такие компоненты называть соответственно ковариантными и контравариантными. Но в отличие от вектора, тензор имеет больше свободы, и его можно представить в виде компонент смешанного типа! Один раз ковариантными и один раз контравариантными. Индексов-то два. Значит, один может быть верхним, другой нижним. Могут оба индекса быть внизу или оба наверху. Что в данном случае будет означать, например, двойная ковариантность тензора? Тут всё просто! Если мы базисный вектор увеличим в размере в 2 раза, ковариантные компоненты умножатся на 4. Контравариантные компоненты при аналогичном преобразовании уменьшатся в 4 раза. Если же тензор представлен компонентами один раз ковариантными, один раз контравариантными, то множители в виде 2 и 1/2 скомпенсируют друг друга, и компоненты не изменятся.
Но чтобы более детально говорить о преобразовании компонент, нужно чуть развить наш геометрический формализм. Научиться складывать наши тензоры подобно векторам, умножать на число и разработать иные операции над ними.
Операции над тензорами
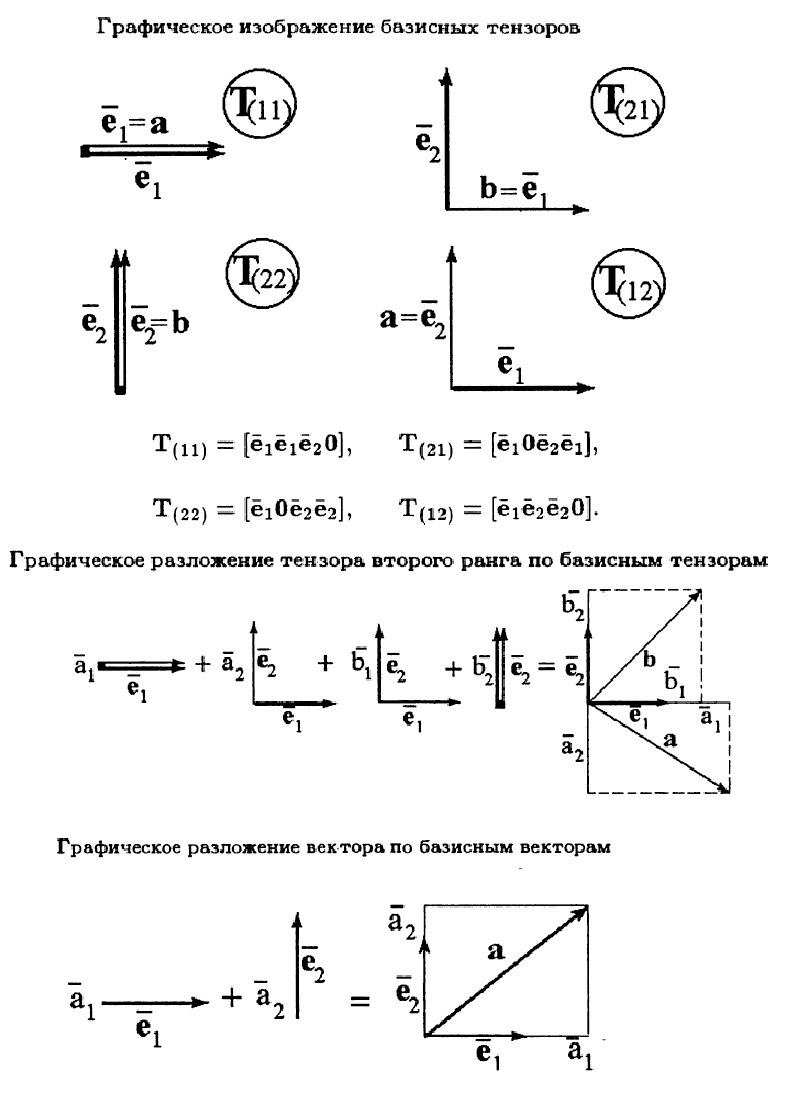
Для простоты будем пока работать с тензорами второго ранга в двухмерном пространстве. Там у них будет всего два индивидуальных вектора, и будет очень наглядно видно, что меняется при применении той или иной операции.
Итак, вспомним, что мы умеем делать с векторами? Мы можем их складывать, умножать на число, скалярно умножать друг на друга, проецировать на базисные вектора. Вполне естественно переосмыслить те же самые операции применительно и к тензорам. Нужно только помнить, что тензор — это не число, это нечто ближе к матрице. И, соответственно, имеет значение, с какой стороны мы к нему подходим, особенно в вопросах умножения. Можно ввести скалярное умножение справа и слева, и они будут отличаться!
Также стоит вспомнить, что скалярное умножение по своей сути — это проекция, или, как её ещё называют, свёртка. Два вектора проецируются друг на друга, и проекция возрастает пропорционально партнёру. Это можно мыслить как взаимодействие вектора и дуального ему ковектора, компоненты которых суммируются (сворачиваются) по верхнему и нижнему индексу и дают число. Но у тензоров второго ранга индексов два! Соответственно, их можно сворачивать (скалярно умножать) с двумя векторами или сворачивать с таким же тензором. Что ж. Учтём и этот факт тоже.
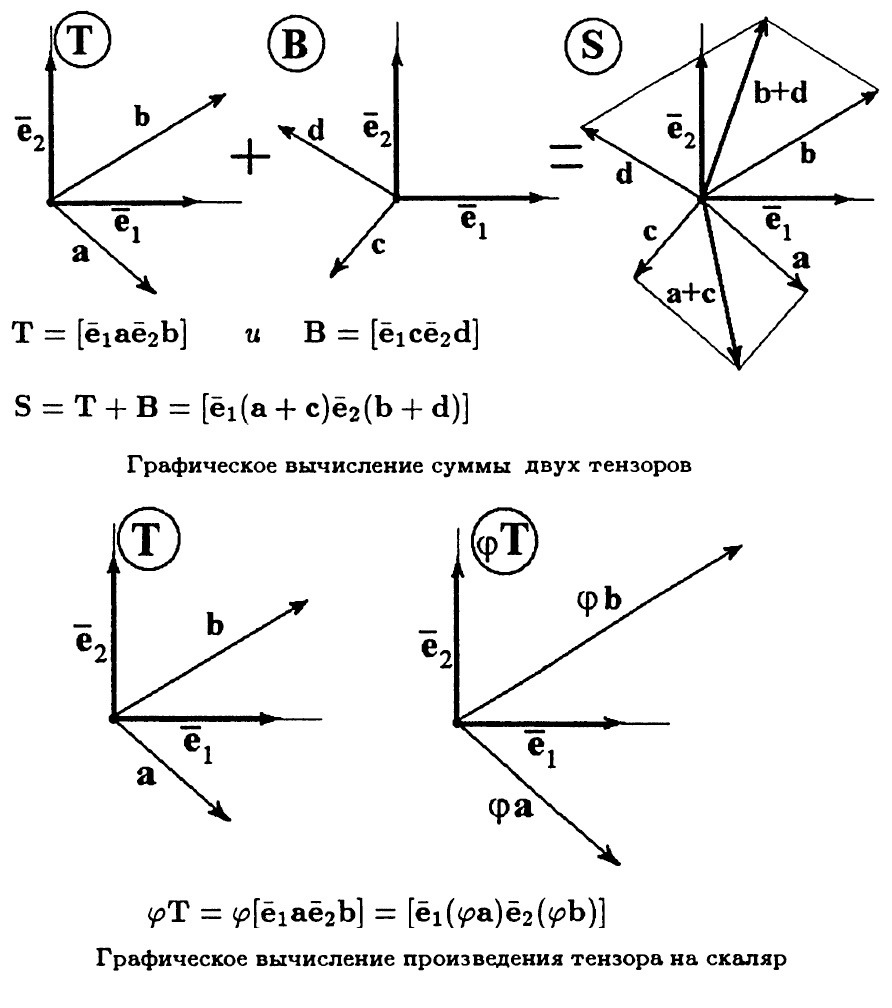
С остальными операциями вопросов быть не должно. Вы наверняка уже сами догадались, как будет выглядеть, например, сложение. Есть, допустим, у нас два тензора T и B. У каждого из них есть свои индивидуальные вектора, имеющие притом свой порядок. Вполне логично под сложением понимать именно сумму векторов, стоящих на соответствующих по порядку местах! Новый тензор S, у которого индивидуальные векторы равны упорядоченной сумме индивидуальных векторов T и B, и будет результатом сложения.
Умножения тензора на число — тоже самоочевидно. Вполне логично удлинить все индивидуальные векторы на этот множитель.
Остальные операции рассмотрим подробнее.
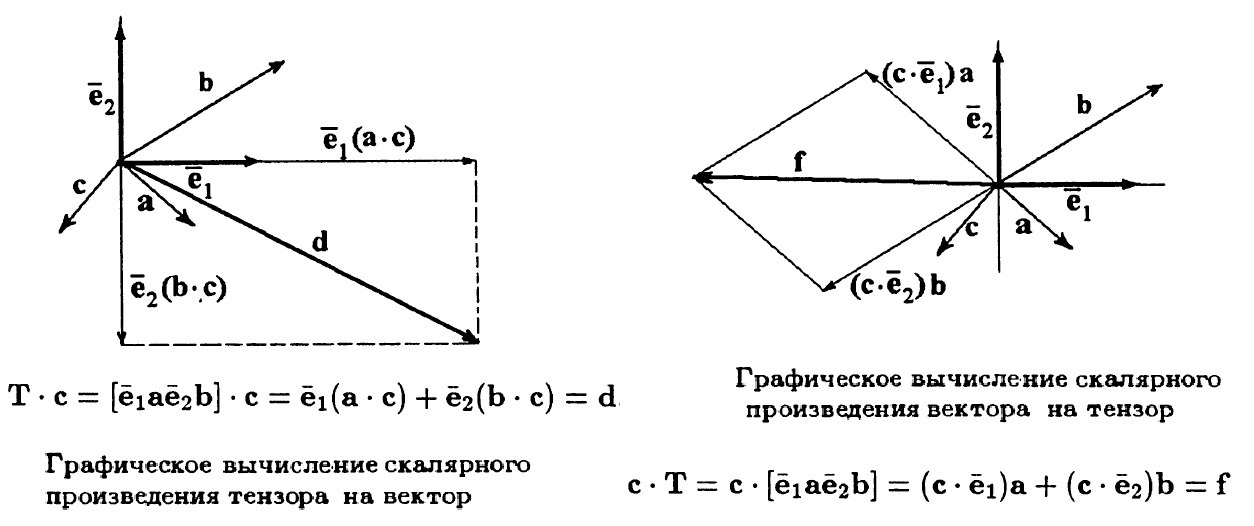
Если мы тензор умножаем на вектор скалярно, то тензор пишем слева, а вектор справа. В результате получим вектор, который является суммой базисных, умноженных предварительно на скалярное произведение индивидуальных векторов с тем, на который умножается тензор.
Если же мы вектор умножаем на тензор скалярно, то пишем уже его справа, а тензор слева. В результате получаем тоже вектор, но он представляет собой сумму индивидуальных векторов, масштабированных скалярным произведением базисных векторов на умножаемый вектор.
Скалярное произведение двух тензоров второго ранга даёт тензор второго ранга. Но его индивидуальные вектора представляют собой комбинацию в виде суммы индивидуальных векторов второго множителя, умноженных предварительно на скалярное произведение индивидуальных векторов первого множителя с базисными векторами.

Двойное скалярное произведение тензоров даёт уже число, являющееся суммой скалярных произведений индивидуальных векторов обоих тензоров.
Скалярное произведение, таким образом, и тут играет роль проекции, по крайней мере части элементов тензора на внешний объект. Соответственно, если мы тензор умножим и слева, и справа на базисные вектора скалярно, то получим его компоненты в этом базисе. Компоненты тензора тогда совпадут с соответствующими компонентами его индивидуальных векторов, что и должно быть! Значит мы всё сделали как надо!
Тензор второго ранга можно разложить по своему специфическому тензорному базису. Всё как и с векторами! Если мы хотим получить базисные тензоры, нам нужно рассмотреть такие объекты, в которых индивидуальные вектора как раз совпадают с базисными векторами. Логично! Ведь именно по базисным векторам разлагаются индивидуальные векторы.
Таким образом, все введённые нами операции вполне естественны и физически оправданы. Например, скалярное умножение тензора на число отражает изменение интенсивности
физической величины без изменения её направления или природы. Например, тензор напряжений в материале, умноженный на скаляр, соответствует увеличению или уменьшению нагрузки в системе. Такое масштабирование сохраняет линейность физических законов (например, закон Гука) и позволяет адаптировать модели к разным условиям (смена единиц измерения, переход к безразмерным величинам).

Умножения тензора на вектор слева и справа часто описывают преобразование векторов в физических системах. Например, как мы видели ранее, умножение тензора напряжений на вектор нормали к поверхности (стоящий справа) даёт вектор силы, действующей на эту поверхность, что используется в механике сплошных сред. В анизотропных диэлектриках умножение вектора электрического поля на тензор диэлектрической проницаемости (вектор слева) позволяет вычислить электрическое смещение. Эти операции физически интерпретируются как проекции тензора на определённые направления или преобразование входных векторов в выходные (например, деформация под нагрузкой).
Двойное скалярное произведение (свёртка) двух тензоров уменьшает их ранг и суммирует взаимодействия компонент. Это ключевая операция для описания энергетических процессов. К примеру, свёртка тензора напряжений и тензора деформации даёт плотность энергии деформации.
как векторы по векторному.
Все эти операции инвариантны относительно преобразований координат, что соответствует требованию ковариантности физических законов. Они позволяют компактно выражать сложные взаимодействия (например, анизотропные свойства материалов) и обеспечивают связь между математическим формализмом и наблюдаемыми величинами (силы, энергии, потоки). Без таких операций моделирование многомерных физических систем (деформируемых тел, полей в пространстве-времени) было бы невозможно.
Разложение тензора по базисным тензорам в физическом контексте соответствует выделению независимых компонент сложной величины, что позволяет анализировать её структуру, взаимодействия и симметрию. Эта операция аналогична разложению вектора на оси координат, но в многомерном и анизотропном случае.

все операции выглядят также.
Тензоры часто описывают сложные многокомпонентные взаимодействия. Разложение на базисные тензоры помогает разделить их на независимые части, каждая из которых соответствует определённому физическому эффекту. Вспомним пример из механики сплошных сред. В ней часто работают с уже знакомым нам тензором напряжений. Его можно разложить на шаровую часть (след тензора) и девиатор (безследовая часть). Шаровая часть соответствует гидростатическому давлению (объёмной деформации). Девиатор описывает сдвиговые деформации, вызывающие изменение формы. Это разделение критично для анализа пластичности материалов или разрушения.
Немного классификации
Когда мы говорим о векторах, у нас уже возникает некоторое их разнообразие. Мы можем говорить как минимум об обычной стрелке, единичном векторе, обратном или противоположно направленном векторе, аксиальном векторе (псевдовекторе), оборачивающемся в зеркале в свою противоположность и часто являющемся продуктом векторного произведения. От тензоров, в силу их более сложной структуры, следует ожидать ещё большего разнообразия их типов и разновидностей.
Начнём знакомиться с тензорным зоопарком с самого простого примера.
Нолевой тензор — это просто тензор в любом базисе, имеющий нолевые компоненты. Его индивидуальные вектора нолевые. Он является нейтральным элементом в случае сложения тензоров. Его прибавление ничего не меняет.
Если в качестве индивидуальных векторов тензора выбрать векторы базиса, то мы получим единичный тензор. Графическое его изображение будет выглядеть как совокупность двух «двойных стрелок». Примечателен он тем, что скалярное умножение единичного тензора на вектор что слева, что справа даёт тот же вектор. А скалярное умножение единичного тензора на другой тензор совершенно не меняет этот самый другой тензор. То есть он ведёт себя как обычная единица, только в мире векторов и тензоров.
Раз у нас появился нейтральный элемент по умножению в виде единичного тензора, то вполне логично будет рассмотреть понятие обратного тензора. У каждого тензора должен быть тот, который отменяет его действие. Он в некотором смысле противоположен исходному. Компоненты обратного тензора легко можно найти из системы уравнений, которая получается при перемножении двух тензоров, заданного и искомого, и приравнивания их произведения к единичному тензору.

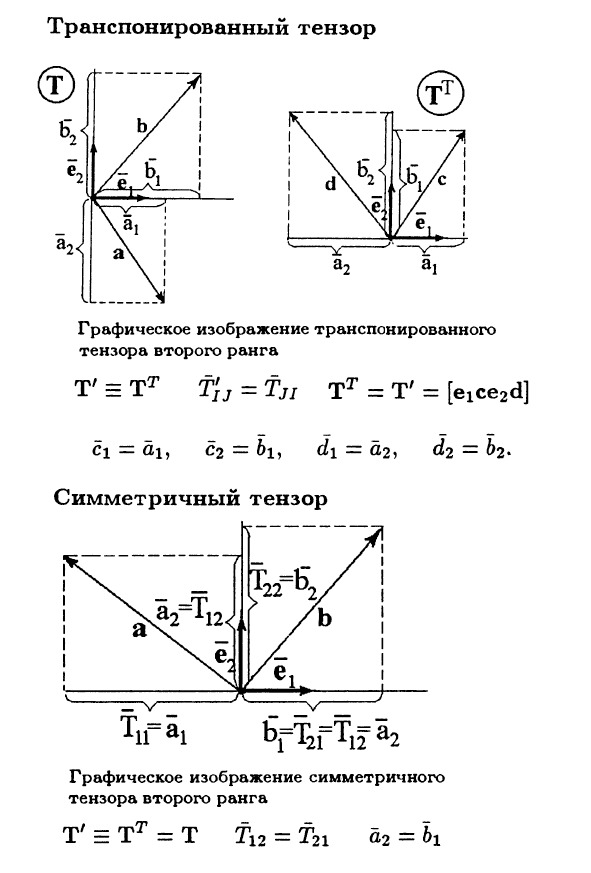
Тензор второго ранга является объектом с двумя индексами. Перестановка этих индексов местами имеет специальное название — транспонирование. Это всё равно что вы матрицу из компонент отражаете вокруг её главной диагонали.
Некоторые тензоры не меняются при транспонировании, и их называют, соответственно, симметричными.
Есть такой особый тип тензоров, у которого обратный тензор совпадает с транспонированным. Такие тензоры называют ортогональными. Их воздействие на вектора сводятся к простому повороту на определённый угол, закодированный структурой тензора. У таких тензоров индивидуальные векторы всегда ортогональны друг другу (откуда и название), по модулю равны единице и отстоят от базисных осей как раз на тот угол, на который поворачивают входящий вектор.
Особым типом тензоров является диада. Её можно сконструировать из компонент двух произвольных векторов. Она так и обозначается: как слитая пара букв исходных векторов. Меняя вектора диады местами, мы получим две разные диады. Индивидуальные векторы диады образует второй вектор, масштабированный на три компоненты первого вектора. Итого — три разных вектора, как и должно быть в трёх измерениях, или два для двух.

Раз есть симметричные тензоры, то могут быть и антисимметричные. Это те, у которых смена местами индексов приводит к смене знака у компоненты. Давайте подумаем, как такое можно изобразить? Ясно, что все диагональные компоненты такого тензора будут равны нолю. Потому что только в этом случае отрицательная величина равна положительной. Таким образом, в трёхмерном пространстве независимых компонент у такого тензора будет всего три, а в двухмерном — две. Значит, этот тензор можно изобразить в виде набора всего трёх компонент — вектора. Или, если мы хотим оставаться в нашей парадигме тензора как набора индивидуальных векторов, можем попытаться понять их вид. Сделать это достаточно просто, если вспомнить про векторное произведение. Действительно! Если взять вектор, в который мы хотели упоковать три независимые компоненты, и векторно умножить его на базисные, то мы как раз получим три разных вектора. И они как раз образуют матрицу, обладающую нужными нам свойствами антисимметрии. Как до этого догадаться? Весьма просто — вспомнить, что векторное произведение само по себе антисимметрично и, следовательно, даст объекты со схожими свойствами.
Где встречаются рассмотренные типы тензоров на практике и что дают? В физике и геометрии различные типы тензоров второго ранга играют ключевые роли, отражая специфические свойства систем и упрощая анализ взаимодействий.
Нолевой тензор, все компоненты равны нолю, в физике моделирует отсутствие воздействия (например, нулевой тензор напряжений в покоящейся жидкости). В геометрии он описывает тривиальные преобразования, не меняющие пространство.

Единичный тензор в физике, в частности в механике сплошных сред, характеризует изотропные материалы, где свойства одинаковы во всех направлениях. В геометрии сохраняет векторы неизменными при преобразованиях (тождественное преобразование).
Транспонированный тензор помогает понять, симметричен ли исходный тензор, а также используется в геометрии при анализе двойственности преобразований (например, в преобразованиях координат).
Симметричные тензоры говорят физикам о законах природы. Например, тензор напряжения нам уже поведал, что уважает третий закон Ньютона, так как является симметричным.
Обратные тензоры позволяют обратить переход от преобразованных векторов к исходным.
Ортогональные тензоры в физике и геометрии описывают повороты и отражения (например, преобразования между инерциальными системами отсчёта). В квантовой механике унитарные операторы (аналог ортогональных) сохраняют вероятности.
Антисимметричный тензор в физике, например, кодирует электрические и магнитные поля (правда, в четырёх измерениях). В геометрии описывает бесследовые деформации (например, чистый сдвиг).
Диадные тензоры — это «кирпичики» для построения сложных тензоров. Их некоммутативность отражает зависимость физических эффектов от порядка взаимодействий (например, сила и плечо в моменте). С геометрической точки зрения они кодируют направленные взаимодействия. Например, в механике деформация материала может быть описана как комбинация растяжений и сдвигов, заданных парами векторов. Любой тензор второго ранга можно разложить в сумму диад.
Таким образом, мы видим, что каждый тип тензора кодирует определённый класс взаимодействий (силовые, вращательные, деформационные), что говорит нам о их вездесущем присутствии в нашей жизни.
Высшие ранги
Давайте сделаем ещё один шаг. Спросим себя, как понять, что перед нами тензор более высокого ранга и как его можно изобразить? Что такое, например, тензор третьего ранга, где с ним можно столкнуться? Наверняка вы в быту уже сталкивались с явлениями, описываемыми этими штуками, если держали в руках пьезовую зажигалку. Когда вы сжимаете некоторые виды кристаллов, их заряды разделяются, создавая электрическое поле. Мы в буквальном смысле выжимаем электричество из кристаллов. Это называется пьезоэлектрическим эффектом. И в значительной степени создаваемое электрическое поле пропорционально силе сжатия или приложенному механическому напряжению. Таким образом, мы получаем уравнение, в котором электрическое поле вроде как с первого взгляда пропорционально электрическому напряжению. И, конечно же, коэффициент пропорциональности называется пьезоэлектрической постоянной. Но присмотритесь внимательно к уравнению и задайтесь вопросом о природе стоящих в нём величин! В левой части у нас вектор, который является тензором первого ранга, а в правой механическое сжимающее напряжение, которое является тензором второго ранга. Так что перед нами уравнение, которое отображает тензор второго ранга на вектор. Так какой же должна быть пьезоэлектрическая постоянная? Подумайте об этом. Она должна брать матрицу и превращать её в вектор. Соответственно, её можно представить как трёхслойный массив чисел. Многомерную матрицу, что ли. То есть она является тензором третьего ранга.
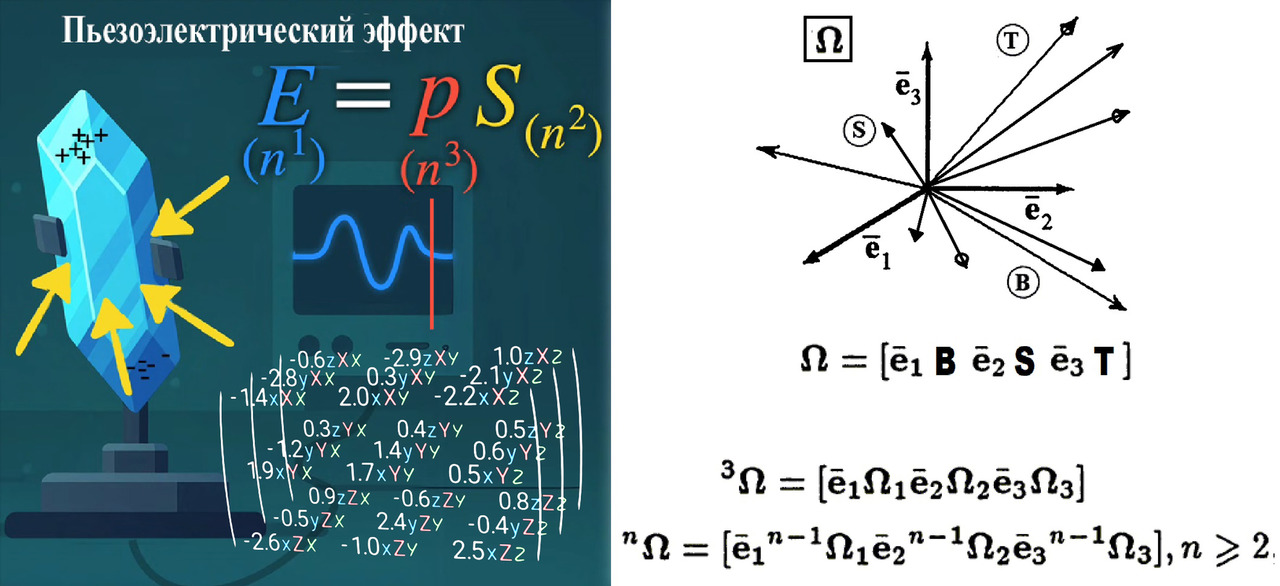
Таким образом, более высшие тензоры описывают связи, где результат зависит от нескольких направлений (например, пьезоэлектричество требует учёта механического напряжения в плоскости и генерации поля в третьем направлении). Они позволяют ещё точнее описать анизотропию в кристаллах и композитах, у которых свойства зависят от направления, что требует тензоров с большим числом компонент. Тензоры высоких рангов возникают в нелинейных теориях (например, в общей теории относительности). Тензоры ранга три и выше — это инструменты для описания сложных физических, механических и геометрических явлений, где простые векторы или матрицы недостаточны. Они позволяют компактно записывать законы природы, сохраняя информацию о многомерных взаимодействиях и анизотропии.
Подытожим. Опираясь на то, что мы знаем о тензоре напряжений, мы смогли обобщить этот формализм, начав работать с тензорами как с совокупностями векторов. А тензоры высшего ранга стали рассматривать как совокупность тензоров предыдущего ранга. В итоге мы получили шикарный способ описывать физические законы наглядно и просто!
Вектор — это упорядоченные числа. Тензор второго ранга — это упорядоченные наборы векторов. Тензоры старше — это упорядоченные наборы тензоров младше. Всюду наборы наборов. Что может быть проще?
Тензорное произведение
Когда-то мы игрались со счётными палочками и вникали с помощью них в суть сложения и умножения. Было всё просто и понятно. Если из общей кучи вытащить по две палочки три раза, мы получим шесть палочек. Можно вытащить три палочки два раза, и результат будет тот же. Умножение после этого казалось таким простым и понятным. Но потом мы узнали, что под ним подразумевается нечто большее — композиция, или иной способ сопоставления двух величин, порождающий третью. Куда-то канула даже коммутативность умножения. А в некоторых особо запущенных случаях (седенеоны) и ассоциативность. Чем нас может порадовать сочетание изучаемых нами объектов — тензорное произведение? Можем ли такая же наглядность, как у счётных палочек, быть совместима с тензорным умножением?
В этом разделе мы рассмотрим тензоры больше с алгебраической точки зрения. Мы увидим, как их можно порождать за счёт специальной операции — тензорного произведения, и также узнаем некоторые его разновидности.
Суть новой операции
На самом деле мы с вами уже производили операцию тензорного произведения. Только её так не называли. Делали её чисто геометрически. Например, когда внутрь вектора вместо чисел воткнули векторы, получив тензор второго ранга. Когда объявили, что тензор следующего ранга — это структура, индивидуальными объектами которой являются тензоры младшего ранга. Всё это было оно — тензорное произведение. Нам остаётся лишь формализовать данную процедуру в алгебраических обозначениях и разобраться с её свойствами.

Обозначают тензорное произведение в виде косого креста, вписанного в круг. Оно порождает новые, более сложные объекты не только в тензорном исчислении. Оно перекочевало и в гомологическую алгебру — в столь специфический раздел математики, в котором даже знак равенства является редким гостем.
Тензорное произведение явно некоммутативно. Это становится ясно уже на примере диад, которые уже фактически своим появлением предвещали подобную операцию. Но оно не настолько сложное, чтобы терять ассоциативность и дистрибутивность. Нарушения этих свойств встречаются в очень запущенных случаях у очень суровых математических объектов. Многие свойства тензорного произведения напоминают свойства матричного. Но это оптическая иллюзия. Перемножая тензор второго ранга тензорно на вектор, мы не получим матрицу. Мы получим тензор третьего ранга, который корректнее изображать в виде трёхмерного массива чисел. Но к этому привыкаешь очень быстро.
Совсем легко вычислять и рассматривать тензорное произведение через компоненты. Нам не важно, сколько у них индексов, и сверху они или снизу. Такие произведения дадут компоненты нового объекта, который будет иметь индексы как первого, так и второго множителя. Можно тензорные произведения раскладывать по базисным векторам и ковекторам, которые тоже, перемножаясь, дают новый объект — базис в пространстве тензоров более высокого ранга.
Часто тензорное произведение определяют как факторизацию. Фактор что? Не слышали о таком? Факторизация — это специальная операция, которая проводится над множествами, пространствами разной природы и различными алгебраическими системами.
Итак, факторизация. Нет, это не новый фитнес-тренд и не рецепт смузи. Это математический способ сказать: «Давайте возьмём всё, что у нас есть, и аккуратно выбросим лишнее». В случае тензоров «всё, что у нас есть», — это свободное векторное пространство, порождённое парами векторов (v, w). Представьте, будто вы набрали в корзину всевозможные комбинации v из первого пространства и w из второго, а потом начали их умножать, складывать и скалярами домножать. Получился гигантский «винегрет» из элементов вида
3 (v1, w1) −2 (v2, w3) + (v5, w4).
Но тензорное произведение — не винегрет. Ему нужно, чтобы всё было билинейно, то есть линейно и по v, и по w. А в нашем винегрете пока царит анархия. Например, (v1+v2,w) и (v1, w) + (v2, w) — это два разных элемента, хотя по смыслу они должны быть равны. Вот тут-то и приходит на помощь факторизация — математический аналог строгой диеты.

Как это работает? Берём наш «винегрет» из формальных выражений — свободное пространство. Делим его на части, склеивая элементы, которые должны быть равными по своей сути. Например, (v1+v2, w) отождествляем с (v1, w) + (v2, w), как бы говоря себе, что это одна и та же конструкция. Это порождает свойство линейности. Далее, a (v, w) склеиваем с выражением (av, w) и (v, aw). Говоря, что это суть одно и тоже, мы даём себе право вносить множитель. Всё, что осталось после этой «уборки», и есть тензорное произведение пространства V на пространство W. Его элементы теперь ведут себя прилично.
Факторизация — это некоторый аналог деления. Когда мы делим число шесть на три, мы как бы тоже делаем нечто похожее на факторизацию. Мы считаем, что шестёрка — это шесть элементов какой-то природы. Грибов, яблок… Деля на три, мы заставляем разделиться всех этих участников шестёрки на группы по три элемента. А потом объявляем, что элементы каждой тройки слились воедино в своей группе. Сколько таких групп получим? Конечно же, две!
В случае факторизации таких объектов, как пространства или наборы буквенных и численных выражений (свободное пространство), мы слепляем в одно целое то, что считаем подобным по нужному нам признаку. Вот и всё.
Зачем так усложнять-то всё? Вводить какие-то формальные свободные пространства, факторизовать? Такова жизнь и математика! После освоения чего-то на понятном уровне возникает потребность шагнуть выше в абстракции и уже там открывать более общие закономерности.
Разновидности и модификации
Тензорное произведение — это как конструктор, который склеивает векторы и тензоры в более сложные объекты высших рангов. Но иногда хочется, чтобы эти объекты обладали уже заведомо дополнительными свойствами: например, не менялись при перестановке индексов (симметрия) или, наоборот, меняли знак (антисимметрия). Для этого математики придумали два специальных «инструмента»: симметричное и антисимметричное тензорные произведения.
Симметричное тензорное произведение превращает два вектора и тензоры старше в симметричный тензор, который не меняется при перестановке аргументов. Обозначается оно кругом с точкой в центре, в точности как символ Солнца в астрономии. Каждый, кто искушён в линейной алгебре, знает, что для определения чего-либо нового достаточно задать его на базисных элементах. Все остальные надстройки подчиняются законам, действующим над базисом. Для симметричного перемножения базисных элементов рассмотрим тензорное произведение первого на второй, затем второго на первый, и сложим их, разделив сумму на два. Аналогичным образом можно строить более сложные симметричные комбинации, только не забывать делить на число всевозможных перестановок из n элементов, то есть на n! факториал.
Антисимметричное тензорное произведение создаёт антисимметричный тензор также гарантированно. Он меняет знак при перестановке индексов. Обозначается оно в виде клина, смотрящего вверх /\, и читается как «клин» или «внешнее произведение». В уравнениях выглядит футуристично, как настоящая математика инопланетян. Основанное на этом символе исчисление было введено Эли Картаном и невероятно упростило некоторые тензорные методы. Это произвело впоследствии настоящую революцию в математике и сейчас ассоциируется с целым отдельным направлением — алгеброй Грассмана.
Опять же, клиновидное произведение строится через базисные вектора, но в этот раз мы после перестановки элементов местами вычитаем один из другого, разность делим на количество слагаемых. Вычитание ведь — это сложение только со знаком минус. Вы ведь помните это?

Вообще, любой тензор можно разложить на симметричную и антисимметричную части. Найти обе из них удаётся, пользуясь тем же принципом, с помощью которого мы строим сами тензорные произведения. Только вместо перемены местами базисных векторов мы меняем индексы у тензоров местами. Такие операции называются симметрированием — когда нужно получить симметричный объект, и альтернированием — когда нужен антисимметричный тензор. Обозначаются они, соответственно, взятием симметризуемых индексов в круглые скобки и обрамлением в квадратные антисимметризуемых индексов. Индексы, не участвующие в данных процедурах, часто отделяются от остальных вертикальной чертой.
Помимо рассмотренных видов умножения, в тензорном исчислении есть ещё произведение Кулкарни-Номидзу. Оно тоже тензорное, ибо порождает объекты высшего ранга. Но данная операция также несёт с собой смыслы, к которым наша психика на данном этапе ещё не готова…
Подытожим. Мы перевели геометрию на язык алгебры. Возникновение тензоров рангом выше из элементов попроще описали чисто алгебраически — тензорным произведением. Эта операция позволяет комбинировать данные из разных источников, сохраняя при этом информацию о взаимодействиях между ними. Например, в физике тензорное произведение используется для описания систем с несколькими взаимодействующими частицами, а в машинном обучении — для обработки многомерных данных. Тензорное произведение является мощным инструментом для работы с тензорами и дублирует геометрические построения на алгебраическом языке.
Тензорное произведение — это как сплести две нити в полотно: каждая остаётся собой, но вместе они держат узор, который не разорвать. Хочешь описать сложное — просто соедини простое. Что может быть проще?
Полилинейные отображения
Математика — это наука об идеях-оборотнях. Задумывались ли вы, как обычная «двойка» меняет свою сущность в зависимости от контекста? Это не просто абстрактный символ. В арифметике она — количество яблок в корзине. В алгебре — результат деления 6 на 3 или логарифм числа 81 по основанию 9. И ординал, и кардинал. В теории колец — элемент, порождающий идеал 2Z в кольце целых чисел Z. Кажется, будто математические объекты наделены магией перевоплощения, оставаясь собой и одновременно превращаясь во что-то иное. «Математика — это искусство называть разные вещи одним и тем же именем», — так выразился Анри Пуанкаре, гений, чьи работы соединили анализ, топологию и философию науки. Его слова отражают суть нашего путешествия: мы будем исследовать, как один объект — тензор — может быть и многомерным массивом чисел, и полилинейным отображением, и элементом тензорного произведения пространств.
Представьте, что вы смотрите на гору с разных сторон: с востока она кажется пиком, с запада — плато, но суть её остаётся неизменной. Так и тензоры. В физике они описывают напряжение в кристалле, в машинном обучении — веса нейронной сети, а в дифференциальной геометрии — кривизну пространства-времени. Их «оборотническая» природа позволяет математике быть универсальным языком, где глубина идеи важнее формы записи. В этой главе мы раскроем, как полилинейность — свойство, сохраняющее структуру при преобразованиях, — делает тензоры ключом к описанию многомерных взаимодействий. Вы увидите, что определение тензора как «многомерной матрицы» — лишь одна из масок, а его истинная суть — в способности связывать векторы и ковекторы, сохраняя гармонию линейности. Пуанкаре напоминал: даже самые абстрактные конструкции рождаются из интуиции. Поэтому, встречая новое определение тензора, спросите себя: «Какая идея скрывается за этим символом?» — и вы услышите эхо его слов: «Красота математики — в единстве многообразия».
Новый взгляд
Мы с вами убедились в необходимости введения тензоров, рассмотрели различные операции с ними, научились получать новые тензоры более высокого ранга с помощью процедуры, которую мы назвали тензорным произведением. Пришло время перейти на новый уровень! Мы перестанем говорить о новых типах тензоров и вместо этого изменим сам подход к уже известным нам тензорам.
Давайте немного порассуждаем. У нас есть векторы и ковекторы. Из этих направленных объектов мы можем порождать тензоры второго ранга, а из них уже тензоры ещё более высокой валентности (валентность — синоним ранга). Какие-то матрицы мы можем породить просто тензорным произведением векторов. Некоторые так не порождаются, но их всё равно можно разложить по базисным матрицам, олицетворяющим базисные тензоры. Поэтому перед нами конструктор, от которого у нас есть все детали! Имея все составляющие, мы можем строить что захотим. И вполне логично на данном этапе ввести альтернативное определение тензоров. Тензор — это совокупность векторов и ковекторов, объединённых с помощью тензорного произведения. И это определение очень хорошее, потому что оно поможет нам упростить жизнь! Многое из того, что мы узнали ранее, мы можем забыть. Потому что это будет автоматически вытекать из нового определения.
Давайте пока отвлечёмся и вспомним, что такое функция. Кто-то скажет, что это график, люди, далёкие от математики, скажут, что это уравнение. На самом деле проще мыслить функцию как некоторое правило, которое гласит, как, зная нечто одно, можно найти что-то другое. Это более адекватное определение понятия функции. Такое правило в математике называют отображением. Действительно, имея график, вы, зная значение одной переменной, легко найдёте значение функции. Имея таблицу чисел, которую используют часто для построения графика, вы тоже можете найти нужные значения как переменной, так и функции. Иногда такое правило можно записать в виде формулы. Функцию можно описать словесно, потому как не всегда понятно, что перед вами написано в уравнении. Например,
y= 3x+1 означает простейшее правило: возьми любое число x, умножь на 3, затем прибавь к результату единицу и получишь значение функции. А если перед вами запись
y = sin x, то человек, не знакомый с функцией синуса, не сможет понять, что от него тут требуется. Ему будет нужен мануал, который описывает следующий квест: построй любой прямоугольный треугольник, один из углов которого равен x, затем противолежащий катет этого треугольника раздели на его гипотенузу и только тогда получишь заветное значение y. А ещё в математике полно функций, которые обозначаются парой символов, а вычисляются так, будто тебе велят: «Продифференцируй несчастный многочлен, найди священный градиент в пятом измерении и принеси его в жертву контурному интегралу — и это ещё не финальный босс». Из всего известного науке зоопарка функций выделяют самые простые — линейные. Ими-то как раз и являются тензоры, если на них правильно посмотреть. Даже больше, они полилинейны!
Итак. Получается, что векторы и ковекторы — это фундаментальные элементы для всех остальных тензоров. Но что делают объекты обоих этих типов? Ковекторы и векторы взаимодействуют друг с другом, выдавая число.
Можно сказать, что ковектор «съедает» вектор, давая число, а можно трактовать это наоборот. Вектор ловит ковектор и выдаёт число. Объекты эти ведь дуальны!

векторами и не только.
А что, если же мы создадим, например, с помощью тензорного произведения ковектора и вектора новый объект? Чем он будет являться? Как говорилось ранее, это будет тензор второго ранга, один раз ковариантный (в честь ковектора) и один раз контравариантный (в честь вектора). Каков его рацион и продукты питания? Эта получившаяся штука будет есть векторы своей ковекторной частью. Но результатом будет объект с одним контравариантным верхним индексом — вектор!
Но этот тензор смешанного типа можно, наоборот, покормить вектором, получив на выходе ковариантный объект — ковектор.
А если взять и перемножить два ковектора и один вектор? Тогда этот объект сможет взаимодействовать с двумя векторами своими двумя ковекторными частями и выдавать вектор. При этом все эти операции будут линейны из-за свойств линейности тензорного произведения. У нас также есть свобода выбора — в какую именно ковекторную пасть поместить вектор. А это сочетание — линейность и возможность делать выбор при взаимодействии с объектом называется — полилинейностью.
Таким образом, тензоры любой природы ведут себя как отображения. Берут один объект, его поглощают, уважая его линейные права, и выдают объект другой природы, даже могут в ранге повысить!
Но давайте вспомним, как происходит само это питание. Ковектор, например, берёт компоненты вектора, умножает их на соответствующие свои и суммирует это всё. С тензорами второго ранга, аки матрицами, также всё сводится к специфическому суммированию перемноженных компонент в определённом порядке. И там и там возникают суммы, порой весьма громоздкие. Но возникают они обязательно.
Данное обстоятельство в 1916 году совсем допекло гениального Эйнштейна. И он вдруг подумал: «А что, если сделать так, чтобы знак суммы выкидывали на помойку, а вместо этого просто договориться, что по повторяющимся индексам мы всегда автоматически суммируем?» Так и родилось правило Эйнштейна: если индекс встречается один раз сверху и один раз снизу — по нему суммируем. И никаких сигм!
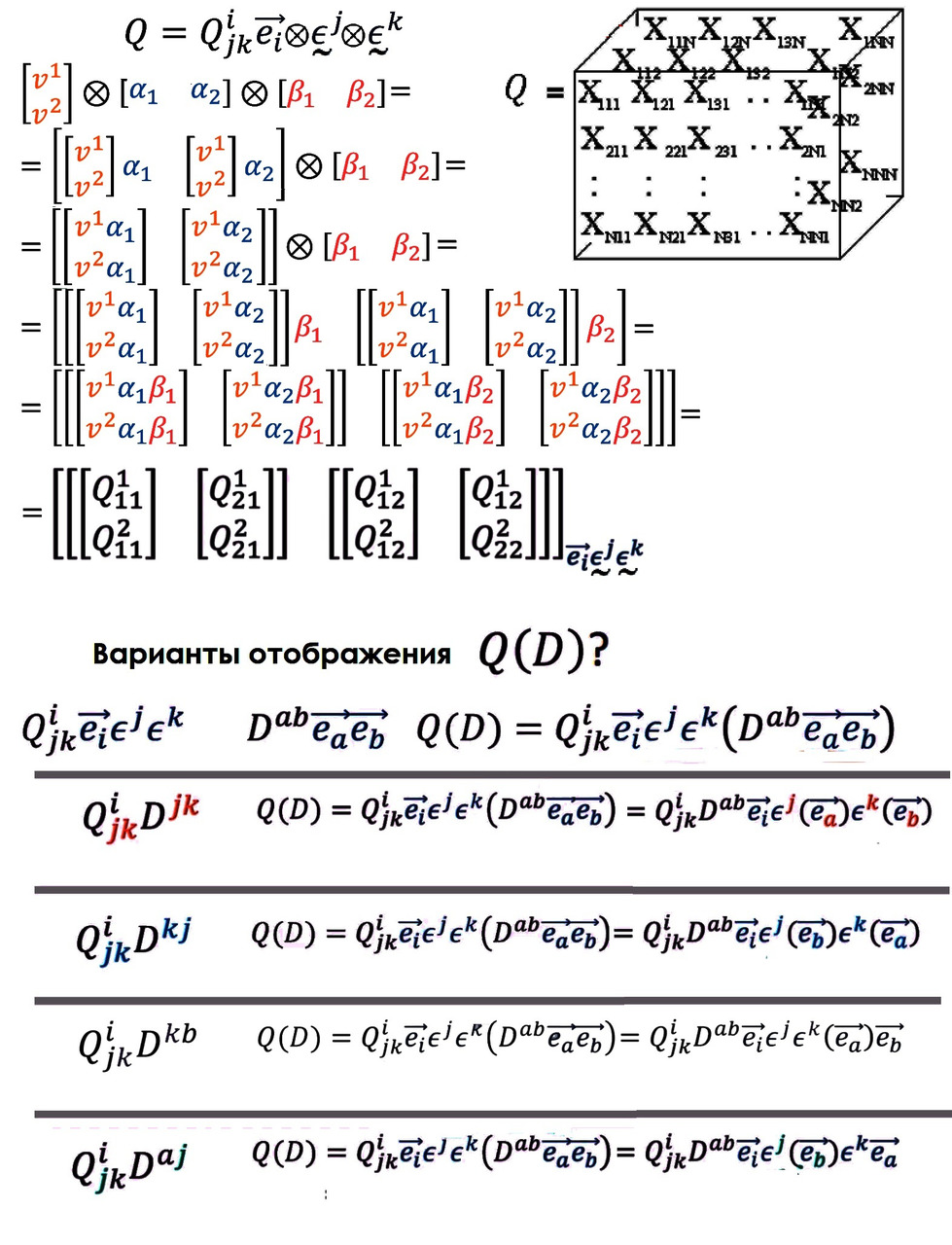
Иногда для краткости записи опускают и сам символ тензорного произведения, когда понятно из контекста, что он там есть. Особенно при матричном перемножении или когда ясно, что вектор на ковектор умножается тензорно и по всему этому новому базису разлагается новый тензор через свои компоненты. Без всех этих упрощений обозначения уравнения Общей Теории Относительности (ОТО) и Квантовой Теории Поля (КТП) занимали бы целую стену, а так помещаются даже на футболке.

Если у нас есть тензоры высоких рангов, то мы их можем заставить взаимодействовать друг с другом огромным количеством способов. Результат будет зависеть от того, по каким индексам мы их сворачиваем (суммируем) с другими монстрами тензорного мира. Главное для нас то, что объект, например, четвёртого ранга может вести себя как вектор, если остальные его три индекса «зацементировать» или заставить их свернуться с другими тензорными объектами. В дальнейшем мы увидим колоссальную пользу и наглядность таких тензоров.

Теперь давайте вспомним ещё один факт. Векторы и ковекторы образуют так называемое линейное векторное пространство. Так называют наборы объектов, которые можно складывать между собой, умножать на числа, ну и нужно, чтобы среди всего этого множества были такие элементы, как единица и ноль в местной интерпретации. Тензорное произведение тоже линейно, и значит сохраняет все свойства линейных векторных пространств. А значит, те объекты, которые получились в результате тензорного произведения, сами являются представителями неких новых линейных векторных пространств. Эти пространства также обозначают через символ тензорного произведения или его симметричных и антисимметричных аналогов.
Математики любят оперировать с абстракциями. И казалось бы, где на практике, а не в математических астралах найдётся место тензорному произведению каких-то пространств?
Однако в современном мире и такие конструкции весьма популярны. Например, архитектура квантовых многочастичных систем строится как тензорное произведение и называется пространством Фока. Пространство Фока — это математическая конструкция, которая позволяет описывать системы с переменным числом частиц (как в КТП). Оно строится как прямая сумма симметризованных (для бозонов) или антисимметризованных (для фермионов) тензорных произведений гильбертовых пространств отдельных частиц. Прямая сумма — это тоже просто. Например, трёхмерное пространство является прямой суммой одномерных пространств, задаваемых координатными осями. Тензорное произведение объединяет гильбертовы пространства частиц в единую систему, сохраняя их независимость до симметризации. Симметризация/антисимметризация «склеивает» частицы в соответствии с их природой (бозоны/фермионы). И без этого сейчас никак не обойтись в передовой физике!
Преобразование тензоров
Основной фишкой векторов и ковекторов являлась их инвариантность. В какой бы системе отсчёта вы их не рассматривали и под каким углом, они всё равно остаются некоей вещью в себе. Тензорное произведение объединяет объекты такой природы в нечто новое. Получившийся тензор наследует все эти качества самостийности от векторов и ковекторов, из которых он собран. А значит, все тензоры должны подчиняться единому универсальному закону преобразования. Давайте его найдём. Собственно говоря, именно им тензоры так знамениты.

Для осмысления этого закона преобразования давайте вспомним о векторах и ковекторах. Это дуальные объекты, которые мы разлагаем по их базисам. Если базисный вектор увеличивается, то базисный ковектор уменьшается. При этом их взаимодействие уже в новом базисе по-прежнему даёт единицу. Это очень хорошо и наглядно видно на рисунке, чисто геометрически.
Как мы преобразуем базис и как находим компоненты векторов и ковекторов в новом? Раньше мы это делали чисто геометрически. Просто могли нарисовать новую систему координат и спроецировать на неё ковариантные и контравариантные компоненты наших объектов. Но алгебраически это проще делать через матрицы. Именно они могут как масштабировать (растягивать и сжимать), так и поворачивать наши векторы и ковекторы, как базисные, так и остальные.
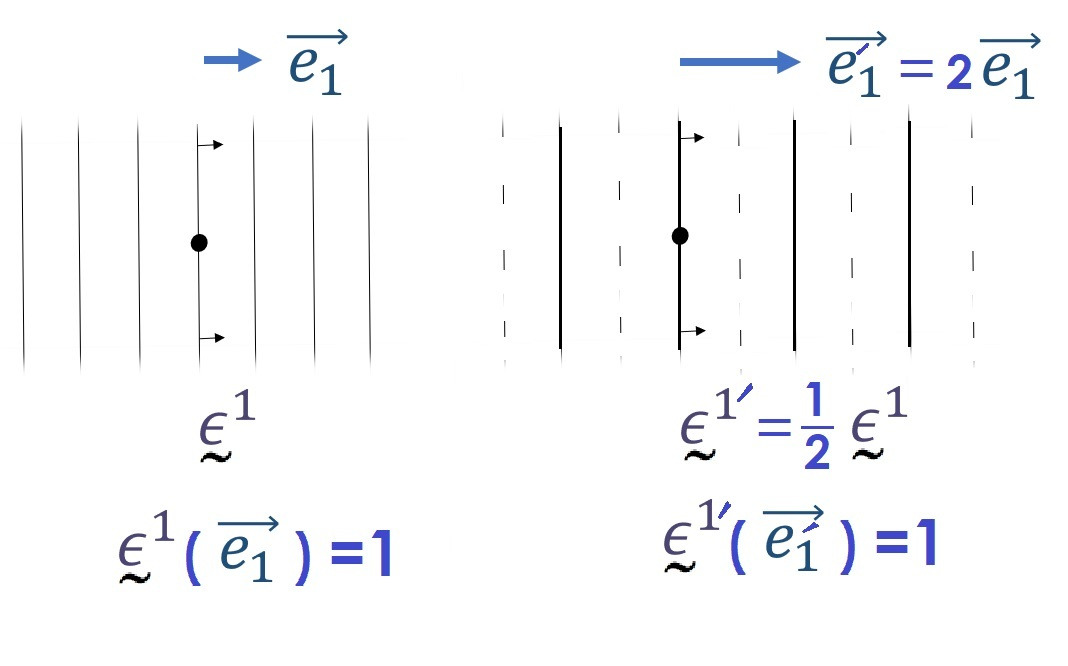
Но мы помним про правило Эйнштейна о суммировании индексов, стоящих на разных уровнях. Помним о том, что это позволяет удобным образом записывать разложение вектора по базисным векторам, у которых индекс пишем внизу. Мы также помним, что векторы и ковекторы преобразуются противоположным образом. Все вместе эти находки позволяют нам описать правила преобразования базиса и обычных объектов в единой системе обозначений.
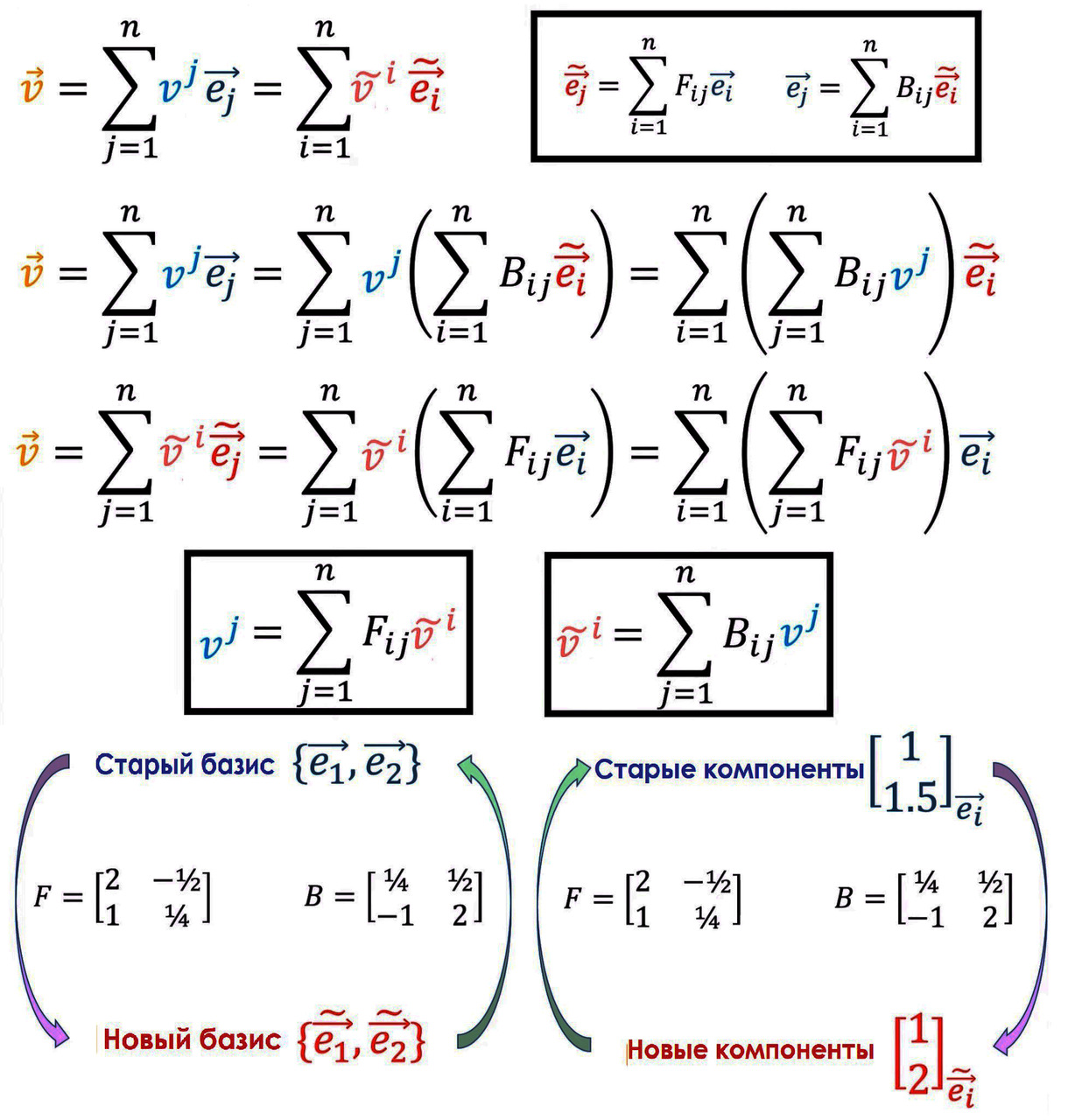
умножаясь на матрицы как столбцы справа.


Допустим, нам нужно перейти к новому базису. Совокупность базисных векторов мы будем записывать в виде строки и умножать на матрицу как ковектор. Такую матрицу перехода к новому базису будем называть F в честь слова Forward (вперёд). Матрицу обратного перехода назовём B в честь Backward (обратно). Это правило возьмём за основу. Из него всё остальное будет следовать автоматически. Разложив вектор по базисным векторам и перейдя к новому базису, мы убедимся, что новые компоненты вектора получены через матрицу обратного преобразования B. В противоположность базисным векторам. Так и должно быть. Если же мы теперь вспомним, что базисным векторам дуальны базисные ковекторы, и найдём их коэффициенты преобразования, то увидим, что их преобразует к новому базису тоже обратное преобразование. А вот уже не базисные ковекторы преобразуются к новому базису по прямому преобразованию. В общем, всё идеально складывается. Красиво и непротиворечиво.

Разобравшись с преобразованием векторов и ковекторов и их базисов, понять, что будет с произвольными тензорами, совсем просто. Для примера давайте рассмотрим смешанный тензор второго ранга. Он один раз ковариантен и один раз контравариантен. Это больше походит на самый общий случай, ибо у него имеются компоненты обоих видов.
Подействуем этим смешанным тензором на вектор и получим на выходе новый вектор. Теперь рассмотрим эту процедуру из нового базиса. Чтобы понять, какие результаты нам принесёт тензор в новом базисе, стоит рассмотреть его воздействие на базисные вектора. Простые алгебраические операции и переименование (больше для красоты) индексов, не нарушающее ничего, ясно показывает закон преобразования такого тензора. Как и ожидалось, он один раз преобразуется как ковектор и один раз как вектор. Эти преобразования осуществляются умножением на прямую и обратную матрицы в должном для этих объектов порядке.
В более общем случае тензоры преобразуются точно таким же образом. На каждый индекс по матрице соответствующего типа.
Особенность закона преобразования тензоров подчёркивает их инвариантность. Сам тензор как геометрический объект не меняется — меняются только его компоненты в разных системах координат. Все индексы преобразуются так, чтобы «компенсировать» друг друга. То, что мы видели геометрически, теперь мы выразили алгебраически.
Смена типа компонент
Теперь нам для полного счастья нужно научиться переключаться между ковариантными и контравариантными компонентами с помощью какого-то отображения, которое это позволит сделать. Вполне логично предположить, что оно связано с базисными векторами и ковекторами. Значит, из них можно составить какой-то тензор и применить для наших нужд — поднятия и опускания индекса.
Базисные векторы заведуют измерением длины вектора и углами между векторами, а следовательно, от этих величин можно попробовать оттолкнуться в наших изысканиях.
Как найти длину вектора на тензорном языке? Геометрически мы это уже делали. В плоском пространстве с ортогональным базисом её можно найти по теореме Пифагора. А что делать, если базис не ортогональный и не единичный? Тогда мы можем выразить компоненты нового базиса через старые и наоборот и путём нехитрых и уже знакомых нам алгебраических преобразований решить вопрос. Если мы внимательно посмотрим на результаты таких действий, то увидим очень знакомую структуру. Преобразования эти напоминают свёртку базисных векторов с некоей матрицей. А матрицы у нас — это как правило что? Разумеется, перед нами тот самый искомый тензор, который организует нахождение длины векторов и углов между ними. Рассмотрев уже его компоненты в старом и новом базисе, мы увидим выполнение установленного закона тензорного преобразования. Такого типа тензоры называют ещё билинейными формами. Ибо они берут два вектора и приготавливают из них число — квадрат длины в данном конкретном случае.
У нас есть успехи: мы научились находить длину вектора через тензоры. Но цель у нас другая. Нам нужно научиться переходить от ковариантных компонент к контравариантным. Мы помним, что эти два типа компонент дуальны друг другу. Но то, что в одном базисе выглядит красиво, в ином может показаться странным. Так как увеличение векторов влечёт уменьшение дуальных к ним ковекторов. Это обстоятельство связано с координатами. Давайте попробуем обойтись без них совсем.
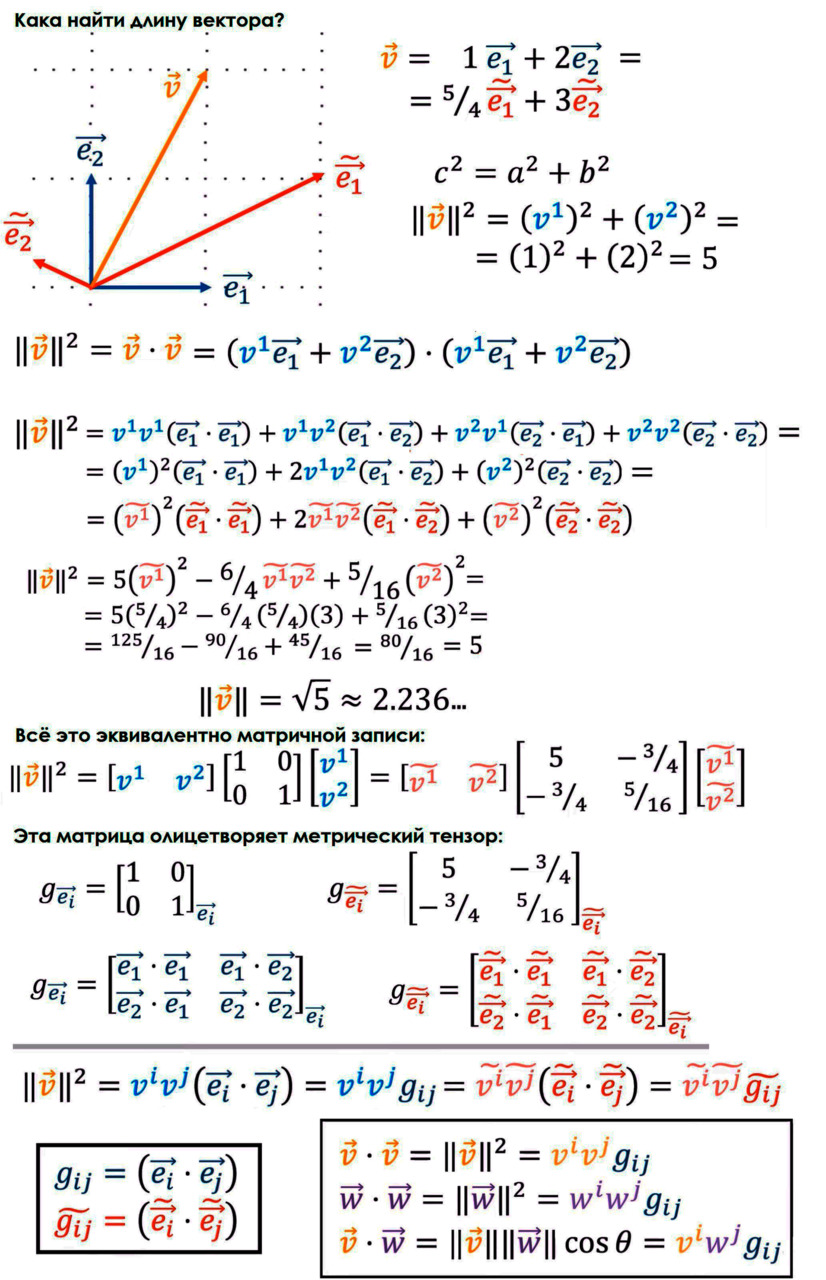
У нас есть для этого всё необходимое. Итак, у нас есть вектор. Чтобы получить его ковектор-партнёр, мы умножаем наш вектор на что-то, где это что-то — просто место для другого вектора. Вы спросите, действительно ли такая конструкция окажется ковектором? Да, это так! Прежде всего, это действительно функция из нашего дуального пространства, потому что она принимает вектор и выдаёт скаляр. Мы можем использовать скалярное произведение, чтобы показать, что эта функция линейна. Кроме того, это новое соответствие, которое мы придумали, вообще не зависит от базиса! Всё и без базиса выглядит достаточно круто. Когда мы умножаем наш основной вектор на 2, мы также на 2 умножаем и его ковектор-партнёр. Таким образом, векторы и ковекторы-партнёры, сопоставленные таким образом, всегда будут увеличиваться и уменьшаться на одну и ту же величину.
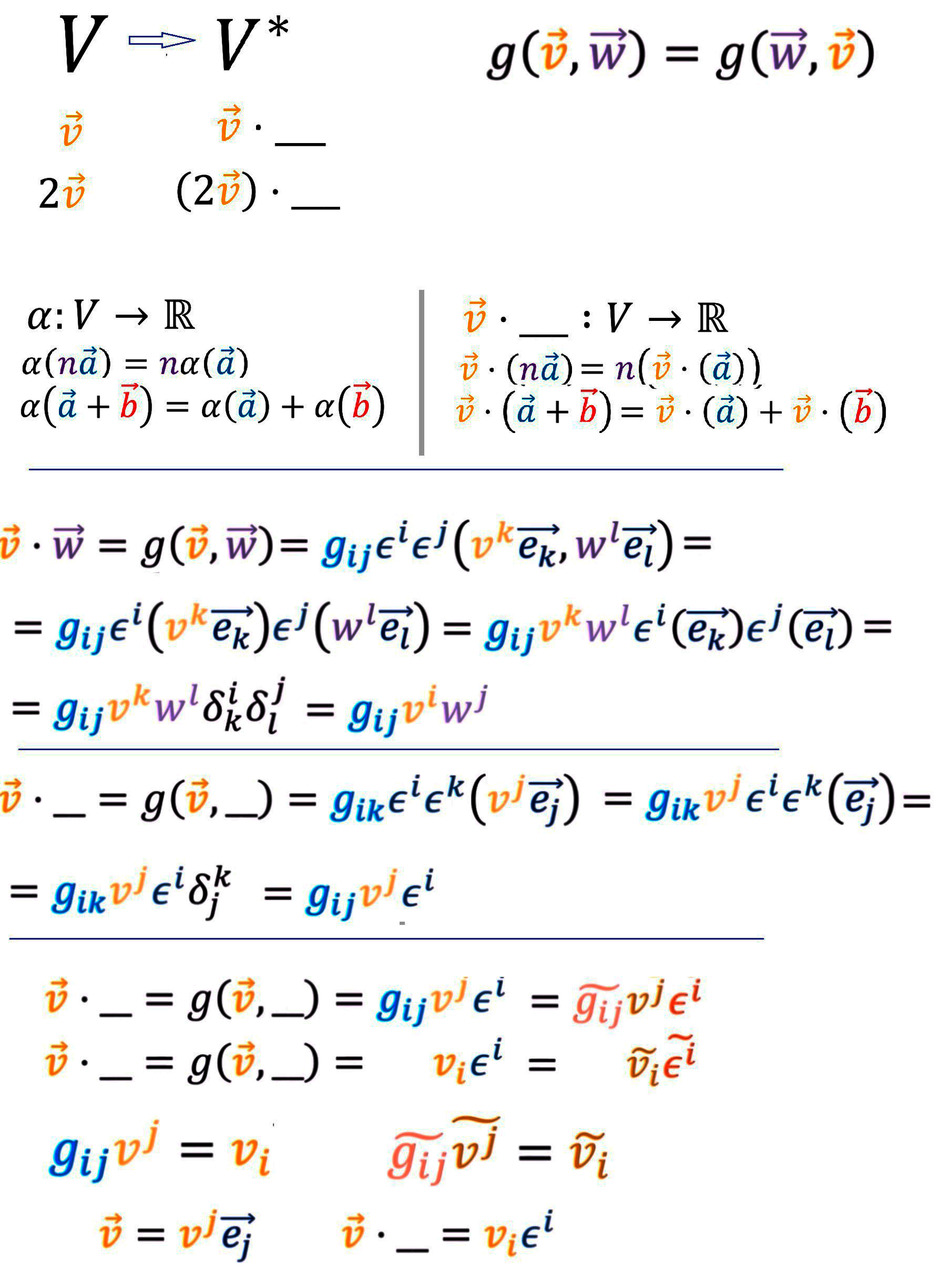
Если наш вектор, умноженный на что-то, действительно находится уже в дуальном пространстве, это значит, что мы можем построить его из базисных ковекторов. Верно? Какие же это будут коэффициенты в ковекторном базисе? Чтобы это выяснить, давайте вспомним, что результат скалярного произведения векторов получается при подстановке этих векторов в метрический тензор. Чтобы вычислить результат, мы просто раскрываем метрический тензор и оба вектора как линейные комбинации. Теперь остаётся только подставить наши векторы в ковекторы в любом порядке. Метрический тензор по своей природе симметричен. Но мы знаем, что у тензоров можно блокировать или оставлять свободным один из входов, один из индексов. Это свойство новой тензорной интерпретации нам как раз сейчас и пригодится!
Метрический тензор берёт два вектора. Для этого у него есть два индекса, две «двери». Но если мы заполним вектором лишь один вход, то в результате всё тех же преобразований увидим на выходе один голодающий базисный ковектор с некоторым численным коэффициентом. Таким образом, мы получили, как и хотели, ковектор, который сопряжён через метрический тензор с нашим исходным вектором. Такой ковектор обозначим той же буквой, что и вектор, только с опущенным вниз индексом. Просто супер! Мы научились у векторов опускать индексы чисто алгебраически, и это полностью согласуется с теми проекциями, которые мы чертили ранее, когда искали ковариантные компоненты вектора чисто геометрически.
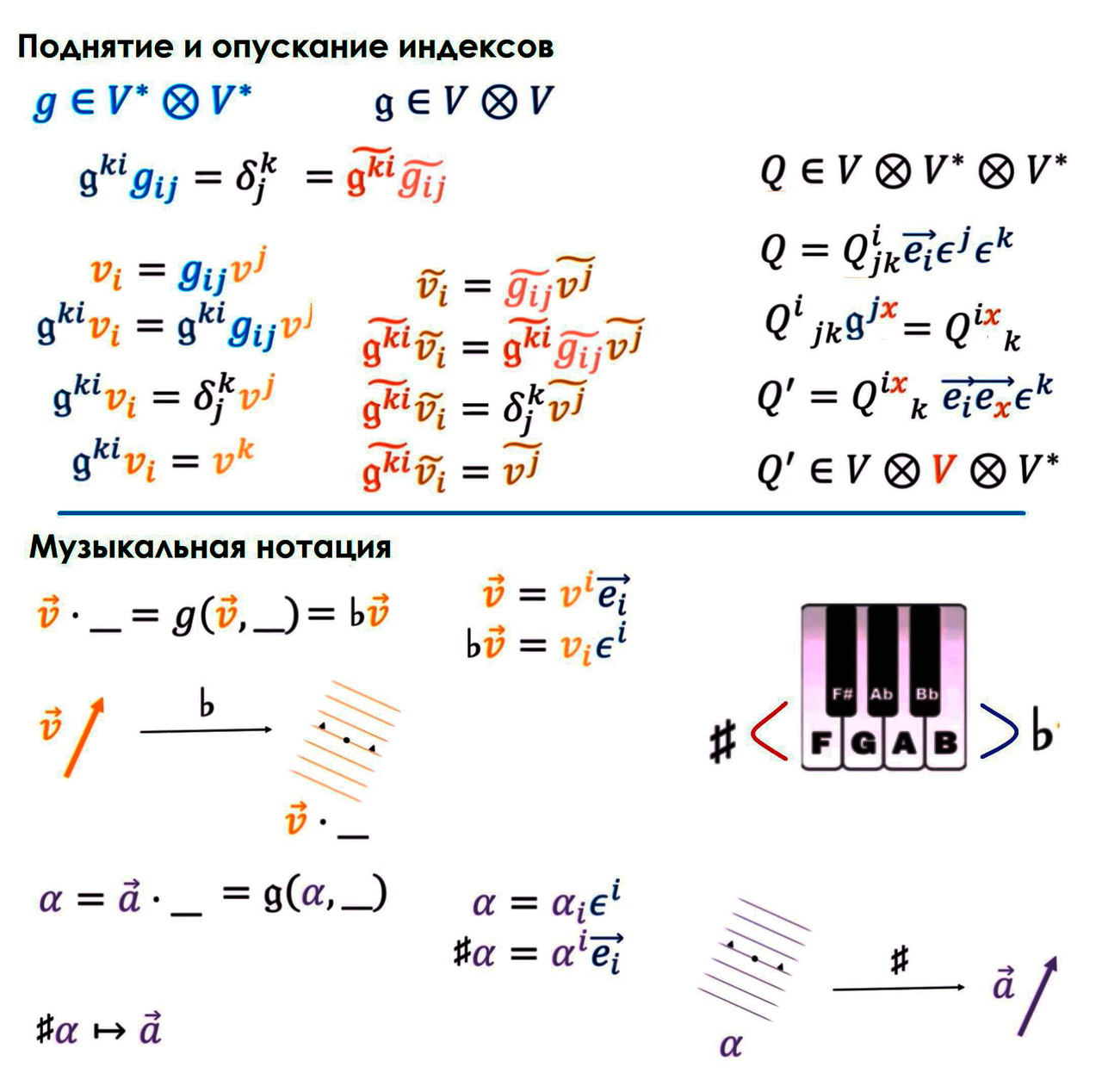
Теперь вы можете спросить: «А что насчёт обратного преобразования? Как, наоборот, поднять индекс у ковектора, превратив его в контравариантный объект?» Разумеется, это делается через тензор, противоположный метрическому. Он стандартно определяется как тензор, свёртка которого с метрическим даёт единичный тензор, компоненты которого проще записать через так называемые символы Кронекера.
С помощью этих объектов мы можем поднимать и опускать индексы вообще любых тензоров. Вы ведь помните, что в силу линейности и того, что любой тензор может быть представлен в виде тензорного произведения векторов и ковекторов, всё присущее им будет работать и со старшими рангами.
Существует и альтернативная запись для векторных и ковекторных партнёров. Речь идёт о так называемой «музыкальной нотации». В рамках этих обозначений используют символы из музыкальной грамоты, а именно бемоль и диез. Знак бемоль перед вектором говорит о том, что мы рассматриваем его ковариантные компоненты с нижним индексом. Оператор бемоль в основном понижает индексы, и это имеет смысл. Потому что символ бемоль в музыке понижает высоту ноты на половину шага. Например, от Си до Си-бемоль. Из-за плоского звучания звук получается более низким. Кроме того, если вдуматься, оператор бемоль преобразует векторную стрелку, которая выглядит как заострённая, в ковекторный стек, который получается красивым и плоским. Так что вы можете представить это как сглаживание заострённой стрелки в плоский стек.
С другой стороны, если у нас есть ковектор, определённый стандартным образом, то в качестве вектора можно использовать его в купе с обратным метрическим тензором, создавая дуальный объект. В этом случае в музыкальной нотации мы можем перейти от ковектора к дуальному ему вектору, используя оператор диез. Действие диеза на ковектор поднимает индекс. И это тоже имеет смысл, потому что в музыке символ диез повышает высоту ноты на полшага. Например, от Фа до Фа-диез. Кроме того, оператор диез превращает плоский ковектор в вектор с заострённой стрелкой. Символы бемоль и диез могут показаться немного глуповатыми, но по смыслу они всё же хорошо подходят для этих операций, добавляя в математику ещё больше эстетики.
Подытожим. Мы с вами рассмотрели чисто геометрические объекты — тензоры любых рангов — с непривычной ранее стороны. Но это лишь открыло ещё больше перспектив для их применения и интерпретации. Мы научились менять ковариантные компоненты на контравариантные и наоборот, опуская и поднимая соответствующие индексы. С этих пор имеет смысл мыслить тензор не как разные компоненты, а как единый геометрический объект, вещь в себе, единую суть. Через какие компоненты его представить — дело десятое. Важны не они, а ТЕНЗОР как некий факт, закон.
Тензор — это смысл, который остаётся, даже если переписать книгу другим шрифтом (ко/контра компоненты).
Что может быть проще?
Многообразия
Начиная с этого раздела всё станет немного жёстче. Но мы с вами справимся. На сей раз мы покинем унылые плоские пространства и погрузимся в весьма причудливые миры, которые единой координатной сеткой порой невозможно окинуть. И в них всё равно могут жить тензоры.
Но чтобы справиться с искривлёнными пространствами, нам нужно сперва покорить идею непрерывности, идя по следам Лейбница и Ньютона. Без этого, увы, никак.
В общем, нас ждёт новая философия познания, новые методы и, конечно же, тензоры, которые тоже изменят свой лик.
Способ ориентироваться
Когда мы говорим о пространстве, у большинства из нас в голове возникает прямоугольник в клеточку — это плоская поверхность, как лист бумаги. Но, мир намного более увлекательнее, чем этот унылый квадрат!. Настало время распрощаться с плоскими пространствами и окунуться в мир многообразий!
Представьте, что вы — древний мореплаватель, который только что узнал, что Земля круглая. «Как так? — воскликнете вы. — Ведь у горизонта она идеально плоская!» Вот она, главная хитрость мироздания: то, что кажется прямым и простым здесь, может оказаться изогнутым и закольцованным там. Мир — это многообразие, так в математике называют пространства, где локально всё подчиняется школьной геометрии, но глобально может быть искривлённым, замкнутым и даже неориентируемым.
Возьмите футбольный мяч. Для муравья, ползущего по нему, поверхность — почти плоскость. Но стоит ему сделать круг почёта, как он вернётся в исходную точку, хотя шёл всё время «прямо». Так и мы: тысячелетия считали Землю плоской, пока не наткнулись на её кривизну. Колумб, открыв Америку, думал, что достиг Индии — вот вам и первая встреча с многообразием! Но именно так рождалась идея: искривлённое пространство можно изучать через его плоские кусочки, как мореплаватели — через карты, которые никогда не показывают весь мир сразу.
Как проще всего описать мяч, тор или пространство-время? Ответ подсказывает география: нарисуйте карту. Карта — это окно, через которое кривизна мира распрямляется в координаты. Широта и долгота для Земли, углы вдоль цилиндра и экватора бублика — всё это попытки «приручить» многообразие.

Но одной картой в причудливых пространствах, как правило, не обойтись. Одна карта — почти всегда обман и искажение. Попробуйте изобразить весь глобус на бумаге: проекция Меркатора растянет полюса, Петерс искривит экватор, а капитан корабля на стыке карт запутается, как в Бермудском треугольнике. Поэтому нужен атлас — набор карт, которые, словно пазл, покрывают многообразие целиком.
приходится иметь дело с многообразием.
Например, для окружности хватит двух карт, хотя можно взять и больше. Там, где они перекрываются, должна работать формула перехода. Без таких формул атлас рассыплется, а многообразие превратится в хаос разрозненных листов из пространств. Но всё-таки почему нельзя сделать единую карту, например, на сферической поверхности Земли без искажений? Ответ прост: сфера — не плоскость. Вы не сможете «разрезать» её на части, которые ровно лягут на стол, как кожура апельсина. Попробуйте очистить апельсин одним куском и распрямить кожуру: она порвётся или соберётся в складки. Точно так же любая попытка «расплющить» глобус в одну карту неминуемо приводит к проблемам. Например, к разрывам — как на карте мира, где Тихий океан разорван на две части. Искажениям — как у Меркатора, где Антарктида превращается в гигантскую белую кайму. Пропаже точек — например, стереографическая проекция «теряет» северный полюс, отправляя его в бесконечность.
«Хотите нанести весь мир на один лист? Придётся пожертвовать либо Аляской, либо здравым смыслом», — вздыхают картографы. Аналогично дело обстоит и с пространством-временем нашей вселенной, на которое даже снаружи неоткуда взглянуть.
Если что, всё вышеописанное — многообразия, карты, атласы — это математические термины! Да, именно так, без изменений эти слова перекочевали в дифференциальную геометрию из географии.
Говоря более строго, многообразием называется пространство, которое локально можно отобразить в евклидово пространство. То есть в микро-масштабе оно кажется плоским. Покрытие локальной картой также является отображением из евклидова пространства на задающее многообразие. Атлас — это просто набор карт. Можно составить несколько атласов, содержащих карты, по-разному покрывающие одно и то же многообразие.

Таким образом, если у нас есть какое-то сложное многообразие, то мы для ориентации в нём можем подстилать себе небольшие и понятные евклидовы коврики в окрестности каждой точки и перепрыгивать на следующие коврики. И вроде как всё в порядке, мы можем двигаться так сколь угодно далеко и ориентироваться, переходя с одной карты на другую с помощью специальных отображений — функций перехода.

Нагляднее это можно увидеть на самом простом примере — окружности. Одной картой её не покрыть. И вот почему. Представьте, что вы пытаетесь развернуть обруч в прямую линию. Если разрезать его в одной точке — получится отрезок. Но тогда место разреза станет «дыркой», которой нет в исходной окружности. Если не разрезать — обруч останется замкнутым, и вы не сможете сопоставить все его точки с интервалом прямой без наложений или разрывов. Говоря совсем просто, окружность нельзя покрыть одной картой, потому что она «замыкается сама на себя», а прямая — нет.
Есть пространства, которые всё-таки покрываются одной картой — это вся плоскость. Декартовых координат достаточно в одном экземпляре. Есть структуры, которые многообразиями ну никак быть не могут (разве что какими-нибудь орбиобразиями). Простейший пример не многообразия — пересекающиеся прямые. Почему? Всё дело в том, что многообразие по определению — это пространство, которое локально выглядит как евклидово пространство (плоское).
А что происходит в точке пересечения двух прямых? Там есть особенность — точка пересечения — это так называемый «разрыв» в структуре. Вокруг этой точки кажется, что пространство «ломается» — оно не выглядит как евклидово в окрестности этой точки, потому что вместо одной гладкой поверхности у нас тут «разрыв» или «узел». Там локально пространство не похоже ни на плоское, а скорее на нечто вроде «разреза», что ломает условие локальной евклидовости.
Покоряем непрерывность
Мы уже осознали проблему: каким бы ни было причудливым пространство, с которым можно столкнуться, изучая окружающий мир, нам придётся рассматривать его в малой окрестности и делать вид, что там оно почти плоское. Если совсем дела плохи, то — в бесконечно малой окрестности каждой точки. А значит, нам нужно вспомнить исчисление бесконечно малых, которое было переосмыслено и сейчас преобразилось в совершенно другую дисциплину — математический анализ. Да-да, те самые производные и интегралы. Возможно, и они на наш взгляд покажутся невероятно простыми и естественными.
Если кратко — то производная это мгновенная скорость изменения чего-либо. Именно её показывает спидометр автомобиля. Если величина меняется непрерывно, то для её исследования приходится довольствоваться именно мгновенным описанием. Ибо в следующее мгновение всё меняется, порой кардинально. К мгновенному описанию можно прийти через пределы, как это делают сегодня, или через отношения бесконечно малых величин, как это делали основатели данного исчисления. Бесконечно малое число — это следующее число после ноля. Вы его никогда не запишите численно, но оно ведь есть!
Сам Готфрид Лейбниц рассматривал кривые линии как ломаные, состоящие из бесконечно малых прямых отрезков. Так было их проще описывать. Эти бесконечно малые величины Лейбниц называл дифференциалами и обозначал как dx и dy, подразумевая под ними бесконечно малые приращения соответствующих переменных. Само понятие функции на тот момент было развито слабо. Речь шла об установлении зависимостей между разными величинами при их почти мгновенных приращениях, которые в конце можно было и отбросить. Идея великолепная и естественная! Но возникала проблема. Можно ли считать дифференциалы переменными? Современники Ньютона и Лейбница ухищрялись решать задачи, выбирая конкретные дифференциалы переменными, а другие меняли. Это превратилось в целое искусство. Кстати, Исаак Ньютон использовал другие обозначения. У него производная называлась флюксией (обозначалась точкой сверху), а аналог дифференциала моментом. Функция была потоком величины — флюентой. Знак интеграла у Ньютона — это просто квадрат, который он пишет перед выражением или просто обводит им интегрируемую величину.
Обозначения Лейбница прижились больше в силу большего удобства. Однако в современной математике потеряли первоначальный смысл. Знак интеграла в виде стилизованной буквы S Лейбниц ввёл позже. Изначально он писал I, а ещё раньше omn от латинского «omnis», что означает «весь» или «всё». Знак дифференциала d происходит от слова от латинского «differentia» — «разность» или «различие» Он мыслил знаки интеграла и дифференциала как операторы, которые взаимно уничтожают друг друга. В связи с чем, его доказательство основной теоремы анализа (формулы Ньютона-Лейбница) выглядит невероятно простым, до наивности.
Что изменилось впоследствии? После работ Огюстена Коши, Карла Вейерштрасса и других учёных исчисление преобразилось до неузнаваемости и перестало быть противоречивым.
Под интегралом сегодня понимается предел суммы. Под производной — угловой коэффициент касательной. Дифференциал же вообще перестал быть бесконечно малой величиной. Теперь это приращение ординаты y касательной при приращении аргумента x, и эта величина может быть любого размера. Если удобно, её всё ещё можно мыслить и как бесконечно малую. Работать уравнения будут всё равно одинаково.
А раз работать будет, то нам всё-таки проще мыслить все эти величины как их основатели. Это привнесёт большую наглядность в наши исследования.
Бросив взгляд на историю становления матанализа, давайте пробежимся по основным его столпам. Чтобы получить производную функции, мы рассматриваем отношение разницы значения функции и значения аргумента в окрестности какой-то точки. Это отношение равно тангенсу наклона секущей, проведённой через данные точки. Если мы уменьшаем приращение аргумента до ноля, то секущая вырождается в касательную. Тангенс касательной — наилучшее приближение для мгновенной скорости! И он-то как раз и будет равен отношению того, что называют дифференциалами — приращение ординаты касательной к её аргументу! Всё сошлось!
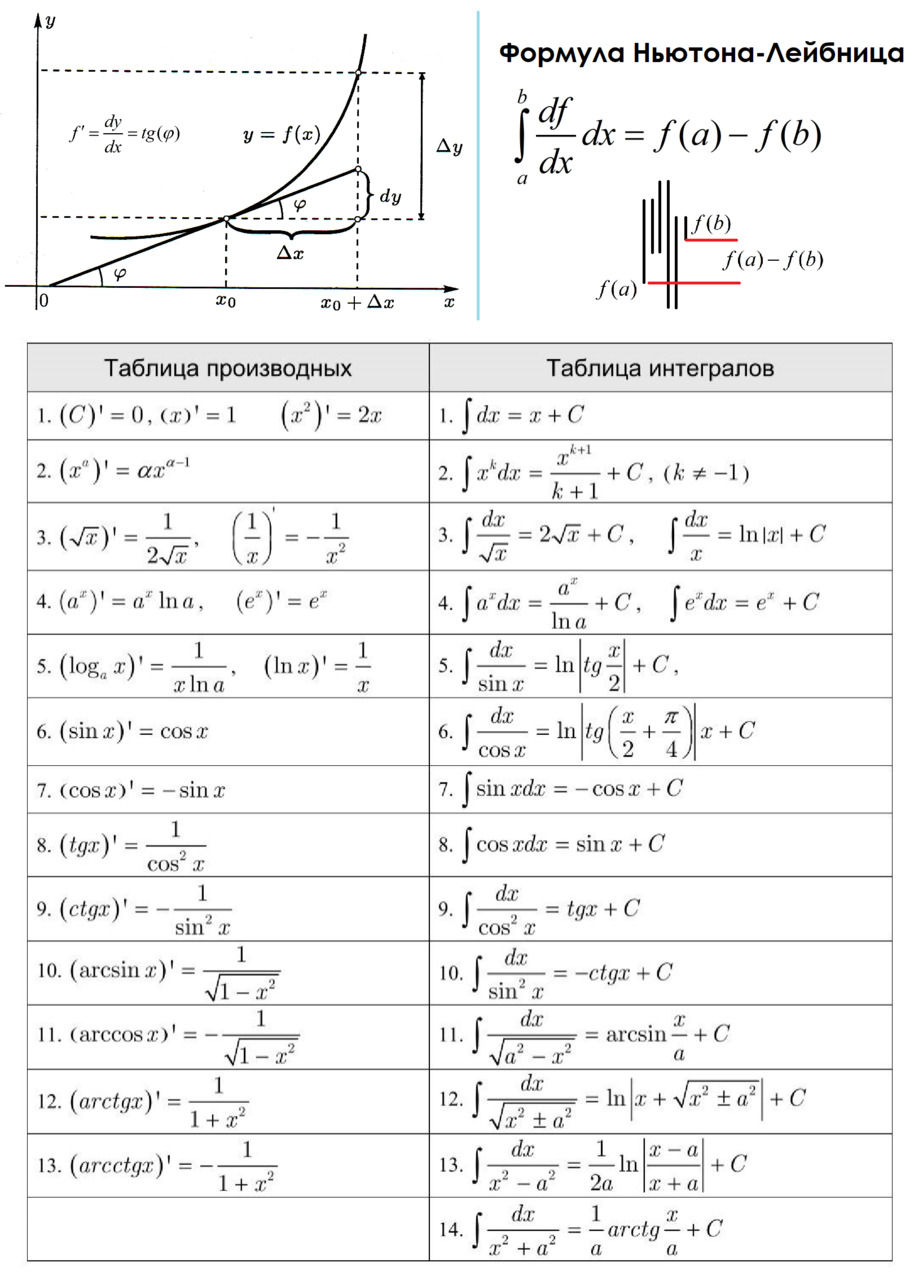
Алгебраически тоже всё просто. Мы прибавляем к аргументу функции бесконечно малую величину, вычитаем из неё неизменённую функцию и делим на бесконечно малую как на число. После алгебраических преобразований получаем удобный ответ, в котором полагаем бесконечно малую равной нолю (устремляем к нолю).
Интегрирование возникает, если мы пытаемся вычислить площадь под кривой функцией. Под прямыми линиями нам хватило бы обычной геометрии. А тут нам приходится разбивать пространство под изогнутой непрерывно фигурой на маленькие участочки, в каждом из этих интервалов рассматривать узкие прямоугольнички и делать их бесконечно малыми. В пределе мы получим интеграл — площадь под кривым графиком.
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.