
Бесплатный фрагмент - Таблица квадратов чисел до 100 за неделю
Как выучить квадраты чисел без зубрежки за неделю
Введение
Хороший способ лучше и быстрее запомнить что-либо — это попытаться объяснить другому человеку то, что нужно запомнить или понять вам самим. Таким образом, вы посылаете в мозг сигнал о том, что изучаемая тема крайне важна.
Автор следует данной рекомендации во многих своих книгах. Они были написаны в период обучения чему-то новому и в период изучения данного вопроса с точки зрения вопросов эффективного обучения.
Автор рекомендует дочитать эту книгу полностью, даже если Вы сочли вполне подходящими методы, представленные в начале книги. В первом разделе автор представит общепринятые методы для вычисления квадратов чисел. Среди этих методов будут известные (их изучают в школьном курсе) и малоизвестные, которые используют различные люди-счётчики (фокусники-математики и т.д.). Эти методы вполне подходят для учеников старших классов (8—11 класс).
Во втором разделе автор напишет собственные исследования и собственную методику вычисления квадратов чисел без использования формул (или с минимальным использованием формул из первого раздела. Этот метод можно уже применять для учеников младших классов (начиная с 3 класса), так формулы будут не очень понятны ученикам младших классов. Можно попробовать метод формул для учеников младших классов показать на многочисленных примерах. Но сам автор ученикам младших классов показывает метод первоначального подсчёта квадратов через поиск по квадрату ближайшего числа.
Для математиков и тех, кто хочет разобраться в формулах, я буду приводить доказательства. Доказательства не обязательны к прочтению и будут оформлены курсивом.
Метод формул
Формула квадратов чисел от 11 до 19
Данная формула применима для вычисления квадратов, как частного случая умножения чисел от 11 до 19, когда оба числа одинаковые.
Детям младших классов (3—5 класс) формулу объясняю как методику.
Обозначим цифры единиц чисел из интервала [11, 19] как Х и У. Тот факт, что число десятков равно 1, учтём в формуле как 1 в нужном разряде. Нижним подчёркиванием (вместо математического верхнего) покажем, что умножаются числа 1Х и 1У. Тогда вся формула будет иметь вид:
1Х*1У= (1Х+У) *10+Х*У= (1У+Х) *10+Х*У
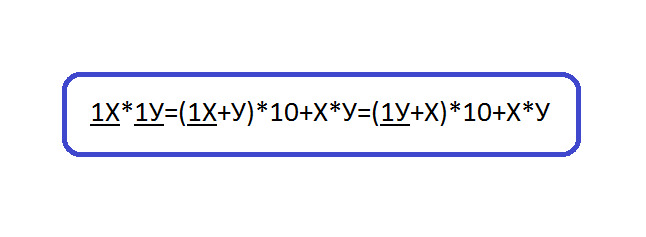
Словами можно объяснить так:
Приумножении чисел из промежутка [11, 19] нужно поступить таким образом. К первому числу надо добавить единицы второго числа (можно наоборот ко второму числу прибавить единицы первого числа). Полученный результат умножить на 10 (приписать справа 0) и прибавить произведение единиц первого и второго числа.
Так как данная книга о квадратах чисел, то применим данную формулу к частным случаям (когда Х=У):
112=11*11= (11+1) *10+1*1=120+1=121;
122=140+22=144;
132=160+32=169;
142=180+42=196;
152=200+52=225;
162=220+62=256;
172=240+72=289;
182=260+64=324;
192=280+81=361;
Необходимо добиться навыка подсчета таких чисел, как в последних двух примерах (18 и 19), когда многие промежуточные выкладки сведены к сумме двух слагаемых. Вполне можно добиться навыка простого запоминания этих квадратов. Подробнее о технике запоминания будет изложено в другом разделе книги, касающегося мнемотехники.
Доказательство.
Доказать справедливость формулы подсчёта таких чисел можно доказать алгебраическими методами.
Перепишем числа 1Х и 1У как 10+Х и 10+У, где Х и У это единицы первого и второго числа.
Тогда (10+Х) * (10+У) =100+10Х+10У+Х*У= (10+Х+У) *10+Х*У.
Выражение в скобках (10+Х+У) это сумма первого числа 10+Х с единицами У второго числа или сумма второго числа 10+У с единицами Х первого числа. Далее полученный результат умножается на 10 и суммируется с произведением единиц первого и второго чисел. Данное правило и было описано словесно в этой главе.
Формула квадратов для чисел, оканчивающихся на 5
Эта формула распространяется и на другие случаи умножения двузначных чисел с одинаковым числом десятков и когда сумма единиц равна 10. Один из частных случаев этой формулы применяется для вычисления квадратных корней для чисел, оканчивающихся на 5.
В этой главе приведу частный случай этой формулы. О самой формуле напишу более подробно в другой моей книге.
Формула вычисления квадратов для чисел, оканчивающихся на 5:
Х52=Х* (Х+1) *100+52=Х* (Х+1) 25
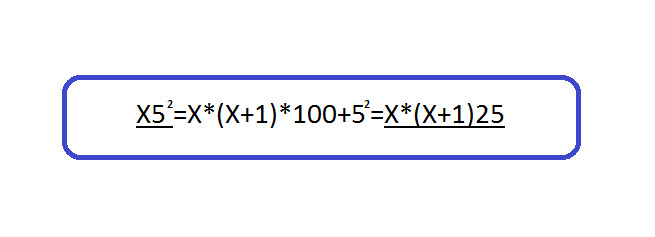
По видим, если число заканчивается на 5, то нужно число десятков увеличить на 1 и перемножить эти числа, в конце полученного результата дописать 25.
Примеры
1) 152=1* (1+1) *100+52=200+25=225;
2) 252=2* (2+1) *100+52=600+25=625;
3) 752=7*8*100+52=5600+25=5625;
4) 952=9000+25=9025;
5) 1152=11*12*100+25=13225
На практике никакого умножения на 100 не производится. На самом деле сначала пишут результат умножения числа десятков на следующее за ним число и к нему приписывается 25:
852=7225.
Доказательство.
Представим число оканчивающееся на 5 как 10*Х+5, где Х-любое число из натурального ряда (5 пример показывает, что число может быть любым, а не только однозначным).
Тогда
Х52= (10Х+5) * (10Х+5) =100Х2+50Х+50Х+5*5=100Х2+100Х+25=100Х* (Х+1) +25=Х* (Х+1) *100+25=Х* (Х+1) 25
Формула квадратов чисел от 25 до 50
Многие вычислители (ментальные счётчики, фокусники-математики) используют следующую формулу для вычисления чисел из отрезка [25;50].
ХУ2= (ХУ-25) *100+ (50-ХУ) 2
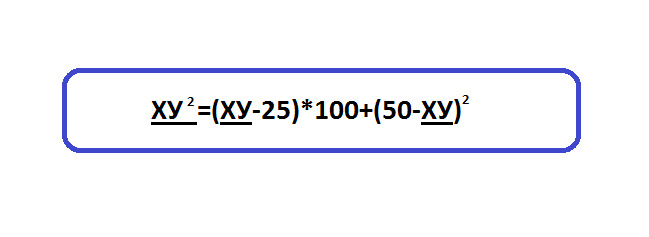
Примеры
1) 392= (39—25) *100 + (50—39) 2=1400+112=1400+121=1521
2) 472= (47—25) *100 + (50—47) 2=2200+9=2209
3) 292= (29—25) *100 + (50—29) 2=400 +212=400 +441=841
Для использования формулы потребуется хорошее знание квадратов чисел до 25.
Формула квадратов чисел от 50 до 100
Вторая формула применяемая вычислителями, используется для чисел от 50 до 100 включительно:
ХУ2= (ХУ-50) *200+ (100-ХУ) 2

Использование формулы потребует знания квадратов чисел до 50.
Например, для подсчёта квадрата 67, необходимо знание квадрата числа 33=100—67.
Пример
1) 672= (67—50) *200 — (100—67) 2=3400 +332= 3400 +1089=4489
2) 722= (72—50) *200 — (100—72) 2=4400 +282=4400 +784=5184
Формулы сокращенного умножения
Для вычисления квадратов чисел используют всего две формулы из всех формул сокращенного умножения:
(a+b) 2=a2+2*a*b+b2;
(a‒b) 2=a2—2*a*b+b2.
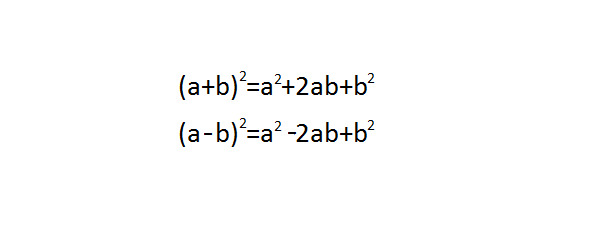
Формулы сокращенного умножения в школьном курсе используются для подсчета квадратов для чисел близких к круглым.
Например, необходимо подсчитать квадрат числа 41. Тогда по формуле сокращенного умножения легко преобразовать:
412= (40+1) 2=402+2*40*1+12=1600+80+1=1681
392= (40—1) 2=402—2*40*1+12=1600—80+1=1521
Квадрат числа, которое на единицу отстаёт (возрастает) от легковычисляемого квадрата приведены выше. Вычислим квадраты чисел, которые отстают (возрастают) на 2 единицы.
422= (40+2) 2=402+2*40*2+12=1600+160+22=1764
382= (40—2) 2=402—2*40*2+22=1600—160+4=1444
Далее, если число отстаёт (возрастает) на 3 единицы сложность вычислений немного увеличивается:
432= (40+3) 2=402+2*40*3+32=1600+240+9=1849
372= (40—3) 2=402—2*40*3+32=1600—240+9=1369
Если рассматривать числа, которые отстают (возрастают) на 4 единицы, то сложность вычислений по сравнению с другими методами или даже другим выбором «круглого» квадрата очень большая:
442= (40+4) 2=402+2*40*4+42=1600+320+16=1936
362= (40—4) 2=402—2*40*4+42=1600—320+16=1296
Сравните с другими методами:
а) формула квадратов для чисел от 25 до 50
442= (44—25) *100+ (50—44) 2=1900+36=1936
362= (36—25) *100+ (50—36) 2=1100+196=1296;
б) формула сокращенного умножения с выбором другого квадрата
442= (45—1) 2=452—2*45*1+12=2025—90+1=1936
362= (35+1) 2=352+2*35*1+12=1225+70+1=1296
Таким образом можно сделать вывод, что формулы сокращенного умножения удобно использовать, если число близко к круглому числу (оканчивающимся на 0 или на 5) на одну единицу. В остальных случаях (числа заканчиваются на цифры 3 и 7) лучше использовать другие формулы для вычислений.
Метод близкого квадрата
Метод близкого квадрата использует формулы сокращенного умножения в другом виде. Для использования метода необходимо знать квадрат числа соседнего с искомым числом. Соседнее число, это число на единицу больше или меньше числа, для которого ищем квадрат. Если непонятно сейчас, то на примерах станет понятно.
Правило:
Чтобы найти квадрат следующего (предыдущего) числа, необходимо к квадрату предыдущего числа прибавить (отнять) число, которое у которого знали квадрат и само число, у которого ищем квадрат.
Метод близкого квадрата неудобно применять для чисел, оканчивающихся на цифры 3 и 7, так обычно немногие помнят или могут быстро подсчитать ближайшие квадраты.
Пример 1.
Необходимо найти 312, зная квадрат числа 30: 302=900
Здесь 31 следующее число после 30. 900 квадрат числа 30, который известен или его легко подсчитать очень быстро.
312=900+30+31=961
Пример 2.
Необходимо найти 292, зная квадрат числа 30: 302=900
Здесь 29 предыдущее число от 30, квадрат, которого известен. Так как нам нужно квадрат предыдущего, то мы отнимаем числа:
292=900-30-29=841
Доказательство.
Доказательство сразу получается, если формулы сокращенного умножения немного переформулировать, учитывая, что b=1
(a+1) 2=a2+2*a*1+12= a2+2*a+1=a2+a+ (a+1)
(a‒1) 2=a2—2*a*1+12= a2—2*a+1=a2‒a‒ (a‒1)
Получим, что a+1 и а-1, это число, которое нужно возвести в квадрат. Число а это число квадрат, которого известен а2.
Формула для квадратов чисел от 91 до 99
На своих уроках я проделываю такой опыт. Выписываем все квадраты от 91 до 99. Квадраты можно посчитать различными способами (смотри соответствующие главы — Метод близкого квадрата, Формулы сокращенного умножения и др.):
912=8281
922=8464
932=8649
942=8836
952=9025
962=9216
972=9409
982=9604
992=9801
Далее даю задание ученикам: Как найти квадрат числа не прибегая к полному вычислению каким-либо способом. По-моему опыту с таким заданием справляются ученики 7—8 класса. Ученики подмечают, что ряд чисел, составленный из разрядов тысяч и сотен увеличивается на 2: 82, 84, 86, 88, 90, 92, 94, 96, 98. В тоже время ряд чисел, составленный из разрядов десятков и единиц это полные квадраты убывающего ряда чисел (9, 8, 7, 6, 5, 4, 3, 2, 1): 81, 64, 49, 36, 25, 16, 09, 04, 01.
Ещё немного подумав и отвечая на направляющие вопросы наконец самостоятельно находят способ как получать квадраты числа зная само число от 91 до 99. Совершив это маленькое открытие, они очень довольны собой и математика немного становится любимым предметом. А для кого-то эта красота мира чисел оказывает решающее значение и определяет выбор жизненного пути.
Для тех, кто не догадался о способах получения квадрата по числу от 91 до 99 приведу две формулы:
9Х2= (100‒ (10‒Х) *2) *100+ (10-Х) 2;
9Х2= (80+Х*2) *100+ (10-Х) 2
На самом деле формулы действительны для чисел от 90 до 99, но вычислять 90 таким способом слишком неоптимально. Поэтому число 90 исключено из этого промежутка. Вторая формула из представленных более предпочтительна из-за меньшего количества операций.
Метод основания
Метод применяется как частный случай умножения двух чисел, которые близки к какому-либо числу. Это близкое число называется основанием. Сам метод возведения таким способом будем называть методом основания. В качестве основания выбираются числа заканчивающиеся на 0. Если число заканчивается на 0, то на такое число легко умножать, так как здесь умножать нужно на однозначное число и потом приписать к результату 0 (умножить на 10).
Число, которое заканчивается на 0, часто называют основанием. А сам метод называется метод по основанию или короче метод основания.
Правило:
Чтобы умножить два числа нужно увеличить и убавить оба числа на одно и тоже число (так чтобы одно из них стало основанием) и прибавить квадрат числа на которое изменяли оба числа.
Примеры:
1) 422
422= (42+2) * (42—2) +22=44*40+4=1764
2) 832= (83+3) * (83—3) +32=86*80+9=6880+9=6889
3) Данное правило можно использовать для умножения не только квадратов
76*77= (80—4) * (80—3) =80*80—4*80—3*80+ (-4) * (-3) =80* (80-3-4) +12=80*73+12=5840+12=5852
Данный способ позволяет возводить очень большие числа (трехзначные, четырехзначные,…) в квадрат. Но нужно довольно быстро уметь умножать и знать квадраты чисел от 01 до 99.
8242=848*800+242=678400+576=678976
Доказательство:
1 способ
(10X+Y) * (10X+Z) =10X*10X+10XY+10XZ+Y*Z=10X * (10X+Y+Z) +Y*Z
Таким образом получили, что основание для данного умножения будет 10х. А другое число (10X+Y+Z) получается, если к первому числу (10X+Y) добавить единицы Z второго числа, или наоборот ко второму числу 10X+Z добавить единицы Y первого числа. К получившемуся произведению добавить произведение единиц Y*Z первого и второго чисел.
Аналогично
(10X-Y) * (10X-Z) =10X*10X-10XY-10XZ+Y*Z=10X * (10X-Y-Z) +Y*Z
(10X-Y) * (10X+Z) =10X*10X-10XY+10XZ-Y*Z=10X * (10X-Y+Z) -Y*Z
Данный метод применен в главе ФОРМУЛА КВАДРАТОВ ЧИСЕЛ ОТ 11 ДО 19 при Х=1.
2 способ
(Х+а) * (Х-а) =Х2‒а2
Перенесем a2 влево и отобразим равенство
Х2= (Х+а) * (Х-а) +а2
А это и есть наш способ возведения квадрат.
Метод кода числа для квадратов
Этот авторский метод я использую для подсчёта и быстрого вспоминания квадрата. Несмотря на то, что теперь просто использую код для припоминания квадрата, метод позволяет со 100% точностью вычислить квадрат любого числа от 01 до 99. При большом навыке использования этот метод сначала позволяет быстро вычислить квадрат, а потом вспоминать его по первым двум цифрам. Я различаю несколько кодов числа для вспоминания квадрата:
1) вспомогательный код;
2) истинный код (в дальнейшем именно его буду называть просто код или код числа). Именно вычислить истинный код и является целью данного метода.
3) двойной код;
4) задний код.
У любого числа всегда есть истинный код. На этом коде и основан метод. Все другие коды не всегда имеются у числа и просто используются для быстро подсчёта либо истинного кода, либо самого квадрата. Например, двойной код есть только у чисел: 51, 68 и 84. Задний код только у чисел 68, 76. Вспомогательный код есть у всех чисел (86—99) лестницы.
Подробнее станет понятно, что автор имеет в виду на примерах в разделе Мнемотехника.
Некоторые особенности возведения в квадрат
Если возвести все числа от 01 до 99 (можно взять и другие числа более 99, но цикл повторится) можно заметить, что квадраты чисел имеют вполне дискретный ряд двузначных окончаний.
Таких окончаний всего 22. Выпишем данный ряд в порядке возрастания:
00, 01, 04, 09, 16, 21, 24, 25, 29, 36, 41, 44, 49, 56, 61, 64, 69, 76, 81, 84, 89, 96
Других окончаний любого квадрата быть не может. В конце главы докажем данное утверждение.
Также можно заметить, что квадраты чисел получающихся путём
Х, 50‒Х, 50+Х, 100‒Х, 100+Х, 150‒Х, 150+Х, 200‒Х, 200+Х, или n*50±Х, где n∈Z (0, ±1, ±2, ±3,…)
всегда заканчиваются на одно и тоже двузначное окончание. Это также можно доказать.
Примеры
1) Квадраты чисел 24, 26, 74, 76, 124, 126 и т. д. заканчиваются на 76
2) 3, 47, 53, 97, 103, 147, 153 и т. д. всегда заканчиваются на 09
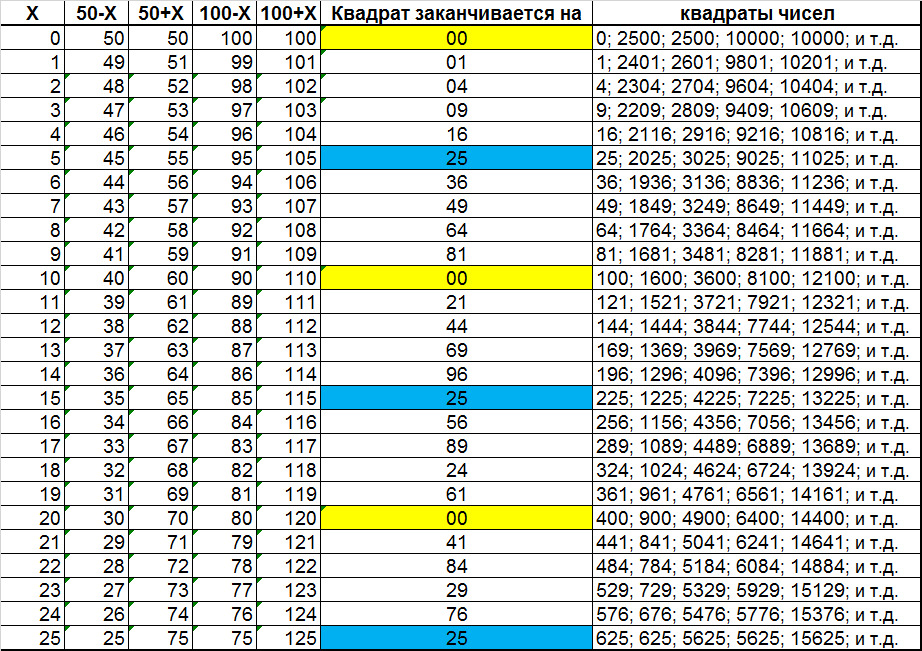
Из вышесказанного можно сделать вывод, что необязательно возводить большие числа любого ряда получающего таким образом, достаточно возвести первое или второе число из этого ряда, чтобы знать окончание квадрата.
Иногда быстрее будет не возвращаться к первому числу, а взять последние две цифры от второго числа. Данное обстоятельство станет понятнее при рассмотрении примеров в других главах книги. Пока не будет на этом останавливаться.
Остальная часть главы написана для любознательных, и читатель вполне может её пропустить.
Окончания квадратов также подчиняются внутренним правилам и для удобства их можно даже упорядочить в таблице и назвать.

Поясним данную таблицу.
Предположим хотим знать на какие две цифры, заканчивается квадрат 62. Смотрим по таблице: видим 6 десятков и 2 единицы. Значит квадрат числа закончится на 44. Действительно 622=3844. Также на 44 закончится и 12, 38=50—12, 62=50+12, 88=100—12:
122=0144
382=1444
622=3844
882=7744
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.
