
Статьи научные
Гравитационная теория удачи
Гравитационная теория удачи была написана после катастрофической потери файлов за весь год работы а аварии компьютера 2012 года. Тем самым было экспериментально доказано, что существует вещественная связь между масштабом и вероятностью в последовательности удач и неудач.
Введение
В этом докладе пойдёт речь об удаче не столько в бытовом смысле слова, сколько в объективном понимании этого явления с точки зрения теории вероятностей и теории математического моделирования. Сугубо для удобства и лучшего понимания в качестве физической модели взята гравитационная модель, которая своим поведением лучше всего повторяет действительное поведение событий и проще всего выглядит для разного рода её представления.
Гравитационная модель удачи
Альберт Эйнштейн сказал, что безумие это проделывать то же самое снова и снова, но каждый раз ожидать иного результата. Некоторые могут понять это высказывание слишком буквально, что если что-то не получилось с первого раза, то не получится никогда. Но Эйнштейн имел в виду гораздо более широкое понятие. Так вероятность какого-либо события в каком-либо опыте не изменяется, хотя само событие может происходить или не происходить от опыта к опыту.
Сегодня мы попробуем подвести научную основу под хорошо известные понятия удачи, везения, успешности, невезения и прочих случайных явлений в нашей жизни. Многим хорошо известно, что есть такие люди, которым всегда везёт: у них никогда ничего не ломается, в магазинах им не продают брак, им всегда попадается хороший преподаватель, они всегда попадают в хороший коллектив, им всегда попадается лёгкий билет и с ними всегда случается только хорошее. И наоборот, есть такие люди, которым не везёт всегда: они всегда выбирают бракованный товар, преподаватели у них всегда худшие, они всегда оказываются не в том месте не в то время, их всегда ловят единственными из всех и так далее.
Разумеется, что для всего есть много закономерных причин: несобранность, лень, невнимательность, рассеянность и прочие, но эти случаи мы рассматривать не будем. Понятно, что у несобранного человека вероятность опоздания на поезд больше, но не каждому не везёт настолько, что именно в тот день, когда ему надо было ехать на поезд, происходит единственный за десять лет снегопад. Именно самолёт неудачника останется без топлива и будет задержан очень надолго, а если он переоформит билеты на другой, то и другой самолёт вернут по причине внезапной технической неисправности.
На первый взгляд может показаться, что все беды и удачи происходят по теории вероятностей и в соответствии с этой теорией всегда найдётся такой неудачник, которому не повезёт ни разу и который соберёт все мыслимые и немыслимые несчастья. Точно так же найдётся такой счастливчик, который получит всю возможные случаи удачи. Это в значительной степени правильно, только не до конца и проявляется это несоответствие в числах.
Если бы все случайности подчинялись хорошо известной схеме Бернулли, то мы бы наблюдали очень мало счастливчиков и неудачников потому, что математическое ожидание числа таких представителей убывало бы практически по экспоненте. То есть на миллиард человек был бы один патологический неудачник и один невероятный счастливчик. А мы наблюдаем таких представителей в тысячи, если не миллионы раз чаще. В чём же причина?
А причина в том, что мы наблюдаем не просто чистую статистику, а статистику с погрешностью на закономерность, которая становится заметной только в краевых областях с очень малым теоретическим заполнением. Одной из причин такой погрешности является то, что теоретическая кривая распределения получается только в случае анализа бесконечного количества данных, чего в реальности не бывает, поэтому возникают закономерные отклонения в соответствии с хорошо известными законами. А вот другим видом погрешности является системная погрешность, которую легко не заметить или принять за первый вид погрешности. То есть погрешность в один миллион слабо заметна в области ста миллионов, зато эта погрешность очевидна в области тысяч и вообще перекрывает всю статистику напрочь. Нас интересует именно это отклонение и выяснение его причин, чтобы иметь возможность повлиять на него в нужную сторону.
Здесь мы заранее определимся, что не будем пытаться выяснить причины происходящего, а будем просто выяснять, как всё происходит. Такой подход широко используется, например, в квантовой механике, где просто принято, что электроны не падают на ядра атомов без объяснения причин, почему этого не происходит. Также в бросании монеты принято, что монета падает на обе стороны приблизительно поровну без объяснения причин такого явления, а просто принято, что так происходит по результатам статистики опытов.
В глубокой теории мы могли бы представить себе причины происходящего и мы сделаем это очень кратко. Мысленно возьмём кирпич, положим на стол и отмерим до угла расстояние линейкой. Второй кирпич на то же место можно положить при добавлении второй координаты. Если мы захотим совместить у кирпичей две координаты, то придётся добавить третью. После добавления третьей координаты положим второй кирпич на место первого, а первый уберём. Понятно, что два кирпича не могут иметь одну координату и каждый кирпич может иметь одну единственную координату в каждый момент времени. Естественный вывод это добавить четвёртую координату и устранить получившийся парадокс. Теперь мы рассмотрим полученную модель.
Каждый предмет имеет всего три координаты положения в пространстве и одну во времени, а также имеет протяжённость в пространстве и во времени, иначе все предметы могли бы находиться в одном и том же месте одновременно. К тому же протяжённость по всем трём координатам у тел нулевой не бывает, следовательно должна быть протяжённость и во времени, которая должна быть очень мала, иначе мы бы видели предметы растянутыми во времени по траектории движения на их протяжённость во времени.
Вопрос протяжённости во времени мы решить пока не можем, как и зависимость плотности материи в прошлом и будущем от расстояния во времени. Вполне возможно, что эта протяжённость бесконечная, а плотность тоже бесконечно убывающая и все события происходят одновременно в прошлом, настоящем и будущем, а из настоящего мы можем только иногда наблюдать их при наличии хорошего восприятия, как у некоторых экстрасенсов. Так свет звёзд приносит мало пользы с точки зрения освещения, но зато имеет огромное значение для навигации. Точно так же многие люди могут бессознательно предвидеть будущее и в зависимости от него выбирать нужные действия с пользой или ущербом для себя.
Вот здесь и появляется объяснение полученной статистической погрешности, но мы не будем пользоваться этой моделью из-за её высокой сложности. Гораздо удобнее схожая с кулоновской гравитационная модель взаимодействия событий. Здесь мы будем говорить об именно модели, а не её физическом смысле. Конечно, события притягивать друг друга в физическом смысле не могут, а теперь изложим основные положения этой теории.
1. Удачные и неудачные события не подчиняются схеме Бернулли. Если в схеме Бернулли вероятность события каждый раз не зависит от предыдущих исходов, то вероятности удачи и неудачи зависят от исхода предыдущих событий.
2. Плотность вероятности удачных и неудачных событий является монотонной функцией и разность её краевых значений имеет знак суммы всех произошедших ранее событий с учётом времени их наступления. Таким образом в вероятности наступлении события с определённым знаком имеется положительная обратная связь.
3. События подчиняются не кулоновскому принципу, а гравитационному но с сохранением знака. То есть положительное событие притягивает к себе положительные события и отталкивает отрицательные, а отрицательное событие притягивает к себе отрицательные события и отталкивает положительные. В случае накопления очень большого количества событий одного знака в коротком интервале времени возможен эффект схожий с эффектом чёрной дыры, которая имеет положительную обратную связь скорости роста.
4. Влияние предыдущего события убывает с расстоянием и временем. Здесь мы можем установить только качественную связь потому, что можем только сказать, что влияние монотонно убывает и не более. Ни о квадратичной зависимости, ни о какой-либо другой мы ничего сказать заранее не можем потому, что более точная физическая модель отсутствует и для каждого конкретного случая зависимость подбирается индивидуально.
Использовать аналоговые модели очень удобно для понимания происходящих событий и дальнейшего их прогнозирования. Хорошо известно, что дифференциальные уравнения малых колебаний маятника, груза на пружине, электрического тока в RLC цепи, жидкости в U-образной трубке и многих других явлений выглядят одинаково. Соответственно и решения этих уравнений тоже выглядят одинаково, поэтому решив одну задачу мы можем считать решёнными и другие с аналогичными условиями, но с иной физической природой.
Здесь мы подходим к ещё одному важному понятию, которое нам понадобится для того, чтобы правильно суметь определить знак события, а именно к понятию удачного или неудачного события. Лучше всего знак и величину события получится определять через разность его величины и её математического ожидания. Так мы сможем гораздо лучше определить степень везения или невезения при рассмотрении нескольких однородных событий через их сумму или среднее значение.
Ещё одним очень важным понятием является то, что удача не является не неудачей. То есть играть в лотерею и не выиграть не является неудачей, а скорее закономерностью, поскольку выиграть в лотерею можно чрезвычайно редко. Точно так же не споткнуться на ровном месте не является удачей, а больше является закономерностью потому, что спотыкаются на ровном месте редко.
Также мы должны разобраться в последовательностях событий. Рассмотрим два простых примера. В одном случае пассажир споткнулся, упал, пока поднимался потерял время и опоздал на свой автобус, а в итоге опоздал на самолёт, который в полёте сломался и разбился вместе со всеми пассажирами. В другом случае пассажир так же опоздал на самолёт, который подорвали террористы, которые собирались подорвать именно этот самолёт.
В обоих случаях наблюдается везение после невезения, но в первом случае события не связанные потому, что самолёт мог и не сломаться, а во втором случае связанные потому, что террористы обязательно подорвали бы именно этот самолёт. Так что в первом случае у нас никакого везения нет, а наоборот есть невезение. Падение самолёта было совершенно случайным и окажись опоздавший пассажир на борту, самолёт мог бы и не упасть. А во втором случае катастрофа была бы неизбежна, но пассажир опоздал и ему повезло.
С точки зрения теории вероятностей в первом случае вероятность неудачи была очень мала, а во втором очень велика, поэтому первый случай как предсказанный мы рассматривать не можем, в вот второй как раз почти полностью предсказан. Так что рассматривать два последовательных события как одну цепочку мы можем только в том случае, когда вероятность наступления второго события высока и не зависит от вероятности первого события.
Для лучшего понимания количественных явлений мы напишем несколько схожую с формулой Байеса формулу влияния собственной удачи B участника опыта на вероятность A его исхода.
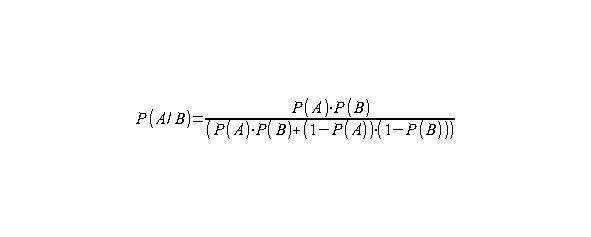
Для примера несколько рассчитанных случаев покажем в виде таблицы.
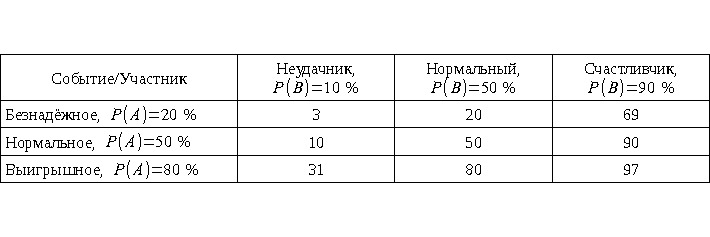
Из таблицы видно, что безнадёжное дело неудачник сильно не испортит, а успешное дело счастливчик сильно не улучшит. Само собой надо понимать, что всё сказанное касается в первую очередь крупных событий, то есть приняв за удачное событие выпадение одной стороны монеты, а за неудачное другой, получить перераспределение частоты выпадений в зависимости от удачливости бросающего не получится. Действительно, ведь в падении монеты экспериментатор никак не участвует, а только пытается предсказать результат. Зато вполне возможен вариант выигрыша или проигрыша крупной суммы денег при той же игре в угадывание стороны монеты.
Определение влияния удачи легко получить через расширение классического определение вероятности. Если событие A из N повторов ожидается n раз из расчёта равновозможных исходов, а под влиянием удачи происходит не n, а m раз, то вероятность события A исходя из влияния удачи можно пересчитать как произведение. При этом предполагается, что N, n и m стремятся к бесконечности, поэтому вероятность определяется как предел.
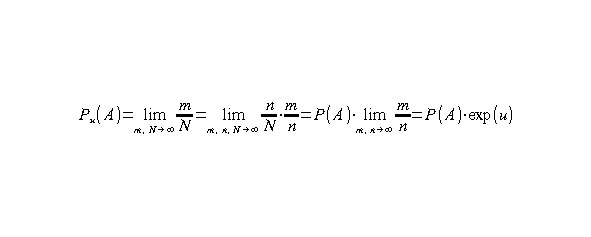
Здесь мы воспользовались условиями, что 0 <m, n и m, n <N и на невозможные или достоверные события удача не влияет. На этом же основании мы смогли перейти к удобному выражению влияния удачи через экспоненту. При нулевой удаче, показатель экспоненты оказывается нулевым и определение вероятности снова становится классическим.
Если вместо множества событий имеется только набор уже известных вероятностей каждого события, то применить классическое определение вероятности напрямую не получится. Вместо него можно по аналогии применить пересчёт каждой вероятности по очень похожей на формулу Байеса формуле, которая получается при переходе к определению вероятности через её классическое определение, но только через математическое ожидание числа каждого из всех возможных событий из их общего числа N и обратно.
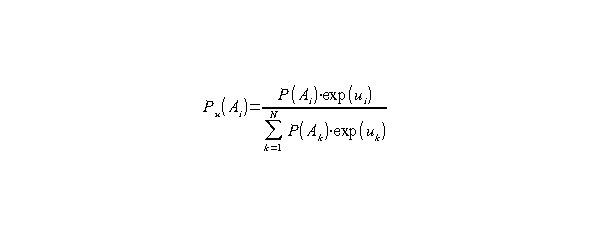
Возникает закономерный вопрос, а что же делать и как бороться за удачу с неудачей? На этот вопрос лучше начинать с ответа, чего делать не надо. В первую очередь не надо повторять одно и то же сразу после каждого провала. Каждая следующая неудача увеличивает массу накопившихся неудач и притягивает очередную новую неудачу. Все опытные игроки в азартные игры знают, что в случае начала невезения надо сразу выходить из игры, не дожидаясь полного проигрыша.
Во вторую очередь надо помнить, что время и место влияют на удачу, а поэтому не надо затевать рискованных мероприятий сразу после крупного провала или в местах многочисленных неудач или несчастий. Недавняя неудача притянет к себе новую и масса неудач будет увеличиваться и увеличиваться, пока для удачи возможности произойти не останется вообще. Точно также все игроки в карты знают, что нельзя садиться играть в паре с неудачником или после недавнего крупного проигрыша, иначе неудача прилипнет и надолго.
Возникает не менее закономерный вопрос об исключении влияния собственного выбора. Действительно, если удача или неудача преследует именно выбор экспериментатора, то было бы неплохо этот выбор исключить вообще. Широко известно использование методов Монте-Карло для решения разнообразных задач. Точно так же мы можем использовать метод Монте-Карло для принятия решений. В качестве простого примера мы рассмотрим применение подбрасывания монеты для упорядочивания списка поставленных задач методом деления группы задач пополам для получения устойчивой к влиянию собственной неудачи нужной последовательности.
Сначала мы расположим все намеченные к выполнению задачи в совершенно произвольном порядке. Так можно поступить потому. что всё равно выбор из списка будет производиться случайным образом. Если у нас есть всего две задачи, то остаётся только назначить каждой задаче соответствующую сторону монеты и подбросив монету получить нужную первую задачу. Гораздо сложнее, когда количество задач окажется нечётное и не кратное степени двойки.
В таком случае мы дополним список задач пустыми задачами до ближайшего числа целой положительной степени двойки. Например одиннадцать задач мы дополним до шестнадцати пятью пустыми задачами, расположив их в совершенно произвольных местах. Полученные шестнадцать задач мы разделим на две группы по восемь задач и сделаем выбор нужной группы подбрасыванием монеты. При этом выбор стороны монеты неважен потому, что для выпадения сторон монеты действует схема Бернулли, но для исключения сомнений мы всё равно зададимся правилом, что одна сторона соответствует, например, группе задач слева и будем следовать этому правилу.
Выбранную группу мы будем так же делить пополам до тех пор, пока не останется выбранной только одна задача. Если в оставшейся группе будут содержатся только пустые задачи, то выбор можно уже прекратить, но мы преднамеренно доведём опыт до конца, чтобы не нарушать его чистоту. Если в итоге мы получим пустую задачу, то мы начнём свой выбор заново с самого начала с шестнадцати задач, пока не выпадет одна из не пустых задач. После этого мы снова дополним список задач одной пустой задачей до шестнадцати и начнём сначала.
Дополнять каждый раз количество задач до их первоначального количества не требуется после того, как оно уменьшится до ближайшего меньшего числа двойки в целой степени. Так в нашем случае после того, как останется только восемь задач, мы будем дальше делать выбор уже из восьми, а потом четырёх и так далее. Но оставшиеся после вычитания одной задачи из восьми семь задач мы всё равно будем дополнять до восьми, а три до четырёх итак далее.
Представленная схема обеспечивает равные вероятности выбора для всех задач и полностью исключает логическое принятие решений, которое уязвимо к неудачам. Через такую схему нельзя получить высокую удачу, но можно снизить отрицательное влияние низкой удачи.
Также хорошим способом борьбы с неудачей являются накопление успехов, которое позволяет притягивать удачные события и понижение рисков при выборе способа действия. Первый способ сам по себе не действует без помощи остальных и без них будет притягивать только неудачи. Понижение риска позволяет резко снизить влияние собственной низкой удачи на исход мероприятия и открывает возможность для её исправления. При нулевом риске успешный исход становится уже неизбежным, но надо помнить, что нулевой риск абсолютно недостижим.
Мы провели только минимальный обзор вопросов и задач управления собственной удачей. На самом деле спектр охватываемых задач гораздо более широк и аппарат методов их решения гораздо более богат. На полном семинаре управления удачей мы рассмотрим весь представленный материал гораздо глубже и научимся решать более сложные задачи. Большую пользу для изучения вопросов управления удачей приносит тот факт, что в области теории вероятностей и математической статистики уже накоплены обширные знания и решено множество задач.
Послесловие
Всё сказанное не следует понимать буквально, как некую расчётную модель для точного вычисления, гораздо лучше будет качественное представление о протекании событий и взаимном их взаимодействии. Само по себе взаимодействие событий носит не физический, а больше условный характер, который и описывает физическая модель.
Корпоративный анализ предприятия
Предисловие
Корпоративный анализ предприятия был написан в ответ на шизофренически бредовое письмо генерального директора НИИ, а также распоряжения его менеджеров.
Корпоративная структура предприятия
По степени корпоративной важности задачи в организации делятся на
1. Некорпоративные.
2. Малокорпоративные.
3. Микрокорпоративные.
4. Миникорпоративные.
5. Корпоративные.
6. Суперкорпоративные.
7. Сверхкорпоративные.
8. Мегакорпоративные.
9. Ультракорпоративные.
10. Гиперкорпоративные.
Особую важность в рамках корпоративного управления организацией представляет определение степени корпоративности задачи в зависимости от числа задействованных исполнителей и их корпоративного уровня. В целях определения корпоративности применяется следующая организационная схема деления на корпоративные уровни задачи. Каждая задача определённого корпоративного уровня содержит в себе не менее одной задачи, нахожящейся на один уровень ниже. Таким образом гиперкорпоративная задача включает не менее девяти взаимовложенных подзадач.
Корпоративный руководитель обладает рангом корпоративности, согласно определению в соответствии с уровнем в корпоративной иерархии. Таким образом, некорпоративные задачи выполняются рядовыми исполнителями без участия руководства.
В случае привлечения для выполнения задачи своего непосредственного руководителя выполняемая задача приобретает корпоративный характер в соответствии с установленным классом корпоративной важности. Таким образом решение гиперкорпоративной задачи возможно только при задействовании не менее десяти работников. При разветвлённой схеме с резервированием не менее одного работника выполнение корпоративной задачи на каждый уровень её повышения требует привлечения не менее, чем удвоенный уровень корпоративной важности с добавлением одного, работников.
Задействование полной разветвлённой схемы с минимальным распределением обязанностей по числу ветвлений не более двух требует удвоения в степени уровня корпоративности задачи за вычетом одного работников. Таким образом для выполнения по минимальной схеме требуется следующее количество работников
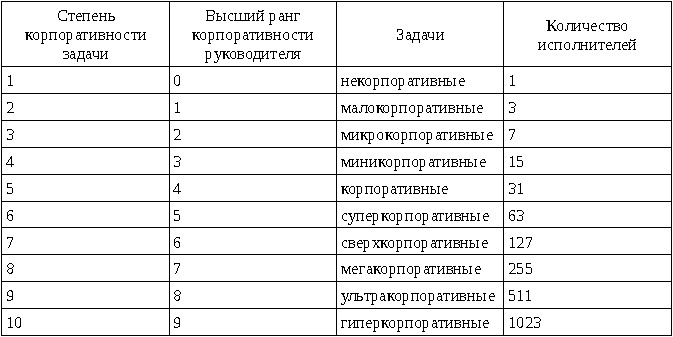
Очевидно, что в таблице приведены минимальные количества работников для выполнения задач с разделением функций на каждом уровне корпоративности. Если для выполнения каждой подзадачи тербуется не менее одного исполнителя, то пирамидальная схема корпоративного выполнения приобретает вид дерева. Случай с разбиением на каждом уровне задачи на не менее, чем две подзадачи, потребует для своего решения выполнения не менее, чем нижеперечисленное количество задач.
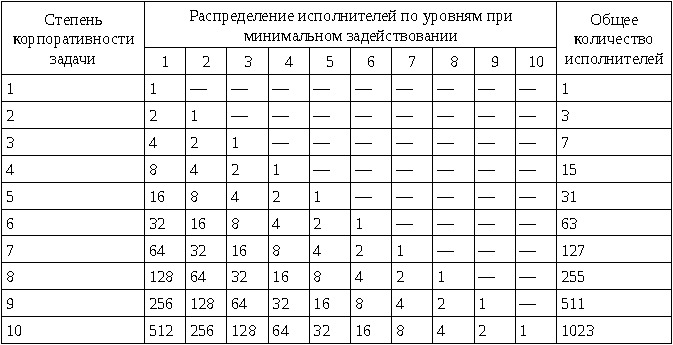
Видно, что и количество задействованных исполнителей, и общее их количество возрастает в геометрической прогрессии с ростом степени корпоративности задачи. В случае предварительного построения корпоративной схемы управления до максимального уровня требуется большее число исполнителей.
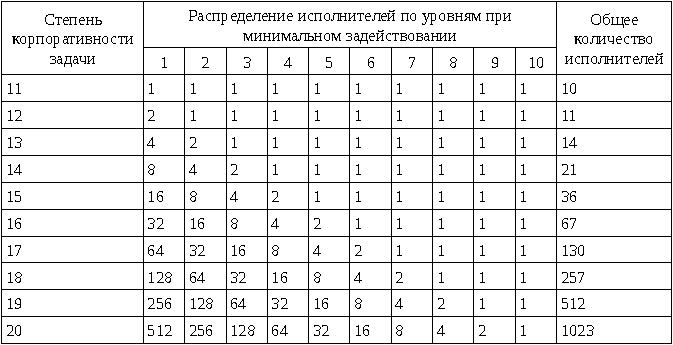
Из сравнения полной и минимальной корпоративных схем может быть определён коэффициент избыточной корпоративности.
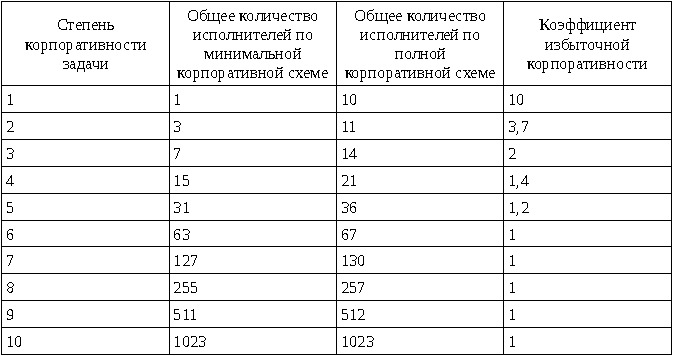
Таким образом организации могут быть неполнокорпоративными с коэффициентом корпоративности меньше единицы, полнокорпоративными с коэффициентом корпоративности равным единице и избыточнокорпоративными с коэффициентом корпоративности больше единицы.
Очевидно, что для организацией выше пятого уровня корпоративности коэффициент корпоративности несущественен, а для организаций четвёртого и пятого уровня корпоративности он невелик. Повышение коэффициента корпоративности усиливает вертикальные взаимодействия при выполнении работ, а понижение расширяет горизонтальные.
Степень упорядоченности организаций с высоким уровнем корпоративности выше, чем у организаций с меньшим уровнем корпоративности, причём зависимость упорядоченности от степени корпоративности носит характер близкий к логарифмическому с показателем 2 и постоянным слагаемым 1.
Схемы корпоративной организации
Корпоративная организация может формироваться только с использованием многоуровневой схемы. Многоуровневые схемы могут быть построены по линейной, пирамидальной, степенной и смешанной схемам.
Наиболее простой схемой является линейная иерархическая схема.
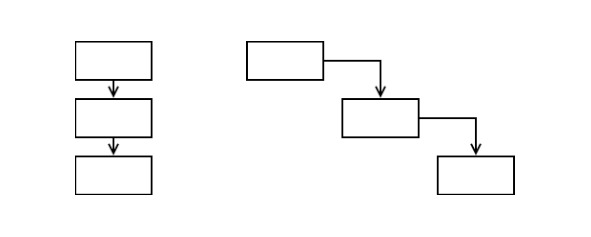
При линейной иерархической схеме легко осуществляется выход в избыточную корпоративность.
Степенная схема подразумевает наличие на каждом уровне не менее двух ветвлений. Она отличается высокой скоростью разрастания вниз при небольшой высоте.
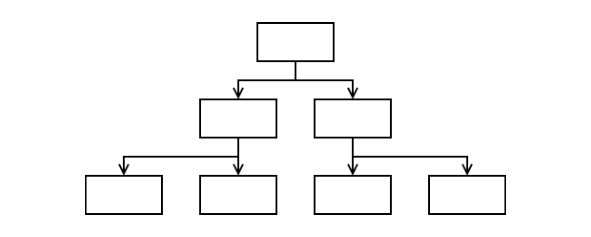
Или в другом представлении
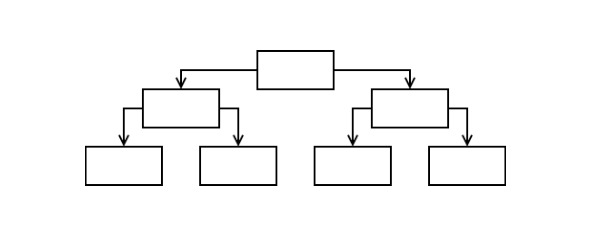
Пирамидальная схема отличается более сложным устройством, эффективно применяется в построении корпоративной схемы по принципу начальник ― заместитель или главный ― помощник.
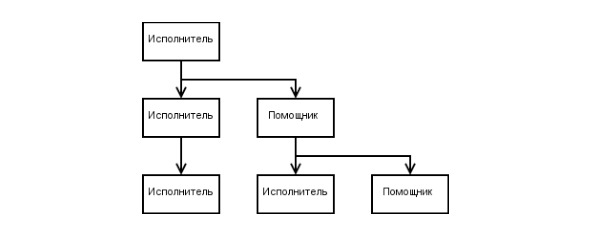
Или в другом представлении
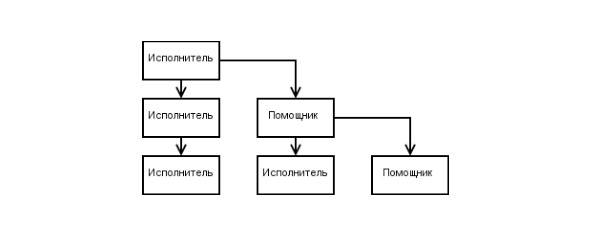
Смешанная схема представляет собой комбинацию из нескольких схем.
Скорость работы схемы управления связана с высотой, то есть с уровнем корпоративности, организации. Достаточно точно скорость работы определяется константой меньше единицы, возведённой в степень уровня схемы. Соответственно постановка вопроса о принятии корпоративной схемы упирается в необходимую скорость работы при определённом числе работников.
Новая соционическая диаграмма
Новая соционическая диаграмма была получена расширением обычной соционической диаграммы потому, что прежняя соционическая диаграмма не удовлетворяла количеству известных мне психотипов и способ её построения был недостаточно точен.
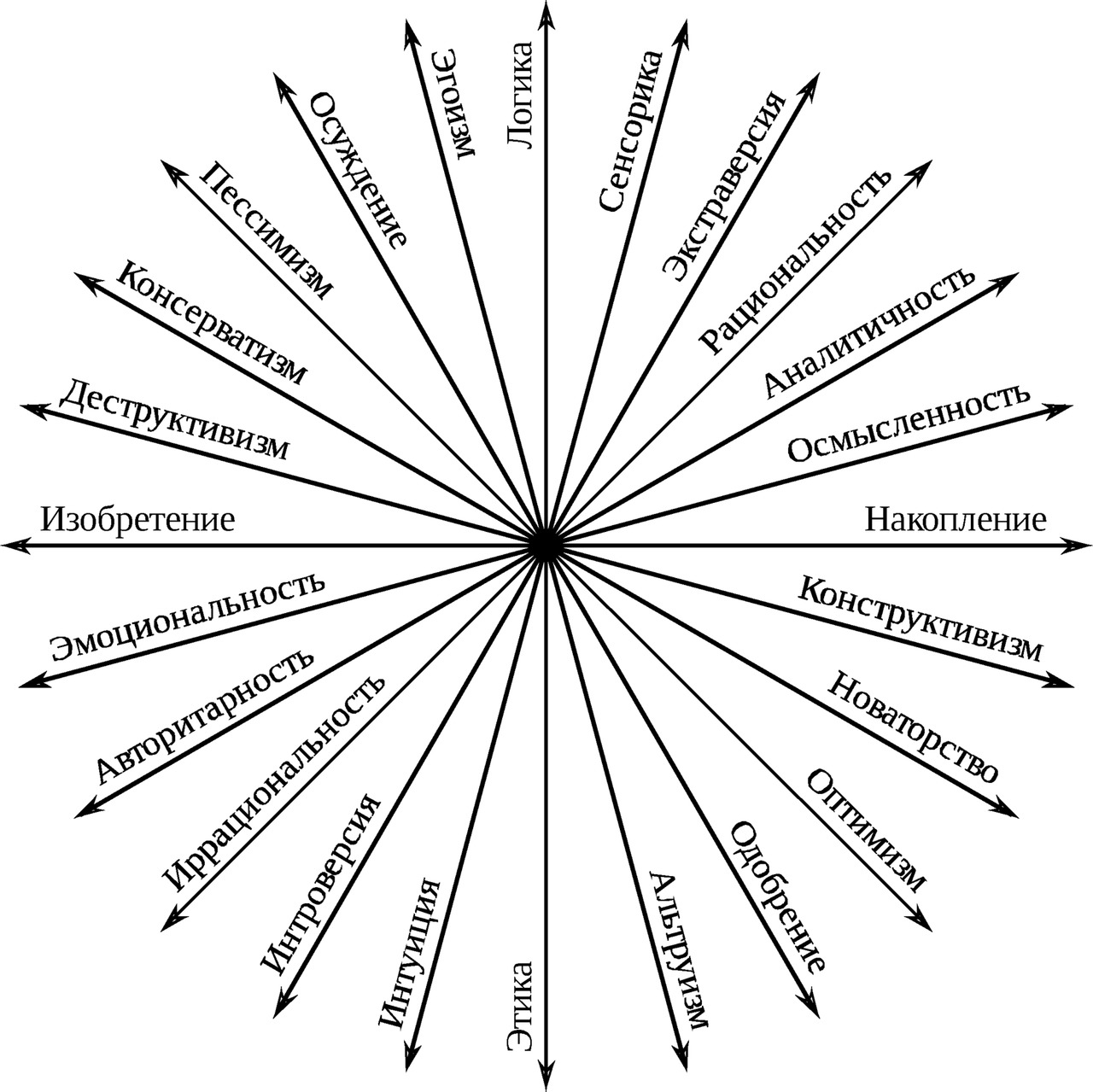
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.
