Бесплатный фрагмент - Сочинения Джорджа Беркли

Аналитик

Впервые опубликовано в 1734 году

Беркли: Фрейзер. III.

Предисловие редактора к «Аналитике»

«Аналитик» был опубликован в 1734 году, в Дублине и в Лондоне, в то время когда его автор покидал Лондон, чтобы вступить во владение удалённой епархией Клойна, после двухлетнего пребывания в Англии, последовавшего за его возвращением из Род-Айленда. Он всё ещё был занят полемикой с «ничтожными философами», когда вернулся в Ирландию; и «Алкифрон» вызвал критику как со стороны теологов и ортодоксальных мыслителей, так и со стороны религиозных скептиков. В апреле 1734 года он сообщает своему другу Сэмюэлю Джонсону в Коннектикуте, что «что касается книги епископа Корка (Брауна) [1] и другой книги, на которую вы ссылаетесь, автором которой является некий Бакстер [2], их здесь очень мало читают и принимают во внимание; по этой причине я не обратил на них публичного внимания. Отвечать на возражения, на которые уже ответили, и повторять те же самые вещи — задача столь же ненужная, сколь и неприятная. И я бы не обратил внимания на то «Письмо о зрении» [3], если бы оно не было напечатано в газете, которая распространила его по всему королевству.

[1] «Божественная аналогия» епископа Брауна, опубликованная в 1733 году. Восьмая глава содержит защиту «аналогического знания» Брауна о Боге от возражений, выдвинутых в «Алкифроне».

[2] Он ссылается на Эндрю Бакстера, шотландца, автора «Исследования о природе человеческой души» (1734), один из разделов которого озаглавлен: «Рассмотрение схемы декана Беркли против существования Материи, или материального мира, и показание её несостоятельности».

[3] См. Предисловие редактора к «Опыту теории зрения» выше.

Кроме того, я обнаружил, что Теория зрения для большинства людей была несколько туманна; по этой причине я был не прочь воспользоваться возможностью объяснить её [1]».

Но «ничтожный философ» Беркли теперь предстаёт как скептически настроенный математик. В начале 1734 года он так отзывается о своём здоровье и занятиях в письме к своему другу Прайору: «Что до меня, то благодаря упорядоченному образу жизни и очень раннему подъёму (что я нахожу лучшим средством в мире) мне стало значительно лучше; настолько, что, хотя я и не могу читать, мои мысли кажутся такими же ясными, как и всегда. Поэтому я, для развлечения, провожу свои утренние часы в размышлениях о некоторых математических вопросах, которые, возможно, приведут к какому-нибудь результату [2]». Им стал «Аналитик».

Его «Записная книжка» показывает, что его мысли уже тогда работали в этом направлении; впоследствии это проявилось более отчётливо в «Трактате о принципах человеческого знания» и в «De Motu». Эндрю Бакстер в своём «Исследовании» выдвигает в качестве возражения против новой концепции материи и пространства Беркли то, что она заставляет тех, кто её принимает, «подозревать, что даже математика, возможно, не слишком основательна в своих глубинах». Сток рассказывает, что Аддисон был связан с крестовым походом Беркли против математиков-вольнодумцев, поскольку он сказал ему, что Гарт на своём смертном одре оставался невосприимчив к христианству на том основании, что Эдмунд Галлей, знаменитый математик и астроном, убедил его, что эта религия является обманом; потому что её предполагаемое откровение о Боге непостижимо. Как бы то ни было, мысли Беркли в течение этой весны в Лондоне и впоследствии в Клойне были сосредоточены на одном из проявлений «ничтожной философии», предположительно распространённом среди математиков, основанном на существовании тайн в религии.

[1] См. мою книгу «Жизнь и письма Беркли» (1871), стр. 222.

[2] Там же, стр. 210.

«Аналитик» обращён к Эдмунду Галлею (1646–1742), знаменитому астроному, в образе «математика-неверующего». В науке Галлей стоял сразу после Ньютона по единодушному признанию его современников, и в его опубликованных трудах нет доказательств религиозного скептицизма. Его «неверие» основывается на общей молве и частных высказываниях, подобно якобы атеистическому «доказательству» Энтони Коллинза; на всё это Беркли, возможно, был опрометчиво склонен опираться. Но его подозреваемый материализм лишил Галлея поддержки Стиллингфлита, когда он был кандидатом на Савилейскую кафедру геометрии в Оксфорде вместе с Дэвидом Грегори. И нам рассказывают [1], что Ньютон остановил его, когда он говорил с пренебрежением о религии, мягким упрёком: «Я изучал эти вещи; вы — нет». Этот вопрос обсуждается в «Защите Галлея от обвинения в религиозном неверии» (1844), написанной преподобным С. Дж. Риго из Ипсвича.

[1] «Жизнь Ньютона» Брюстера

Философская и теологическая цель «Аналитика», отдельно от математических дискуссий, к которым он привёл, может быть смешана с чисто математической полемикой. В уме Беркли это есть аргумент к человеку (argumentum ad hominem) против математиков-вольнодумцев, продолжающий также главный аргумент Седьмого диалога «Алкифрона». Некоторые математики отвергают религию на основании её конечной непостижимости: но их собственная наука в конечном счёте также непостижима; и действительно, некоторые её доктрины покоятся на рассуждениях, которые кажутся несвязными, если не противоречивыми. Математика, как и всё остальное человеческое знание, поддерживается только верой или доверием, которые незаменимы в условиях отсутствия всеведения. Религия неизбежно разделяет эту конечную непостижимость, общую для неё с самой доказуемой частью человеческого знания.

Подобный аргумент появляется в Седьмом диалоге «Алкифрона» и приближается к нему во «Введении» к «Трактату о принципах» (раздел 20), где утверждается, что слова не всегда должны обозначать идеи: без идей они могут выражать практические правила, достаточные для того, чтобы нам действовать. В основе всего человеческого знания лежат рабочие принципы, которые не могут быть сведены к нашим идеям: неразумно настаивать на такой их интерпретации. В этом отношении наука и религия находятся в одинаковом положении. Сила так же непостижима, как благодать. Оба имеют практическое значение; но ни одно из значений не может быть полностью представлено в наших идеях чувств или воображения. Так же и с «математиком-неверующим». Он возражает против религии, потому что Бога нельзя полностью представить в чувственном образе: он должен с тем же основанием отвергнуть математику, потому что она тоже укоренена в подобной тайне.

Метод флюксий Ньютона, тогда столь модный, берётся в качестве примера. Флюксии не представимы в воображении: мы не можем осознать их в идеях чувств; и доказательства, которые их поддерживают, полезные в своих результатах, в конечном счёте человечески непостижимы. Тем не менее, математики-«вольнодумцы» готовы принять в рамках своей собственной науки то, что они отвергают в религии: флюксии, как и религия, при сведении к конечным принципам, включают незавершённые или таинственные концепции, которые превосходят человеческое понимание: и «математики-неверующие» принимают их, доверяя авторитету не до конца понятых принципов, а некоторые неверующие — личному авторитету сэра Исаака Ньютона.

В своей критике обоснования флюксий Беркли, несомненно, затронул спорные моменты в ньютоновской теории. Де Морган в своём очерке «Ранняя история исчисления бесконечно малых в Англии» говорит, что доктрина Ньютона различалась в разные периоды; что до 1704 года он рассматривал бесконечно малые величины; что в том году, в своей «Quadratura Curvarum», он отказался от бесконечно малой величины, и в такой манере, которая могла навести на мысль, что он никогда её не принимал. Де Морган далее полагает, что Беркли в «Аналитике» не мог или не хотел видеть, что Ньютон 1687 года и Ньютон 1704 года придерживались двух разных способов мышления; и что он противопоставляет бесконечно малые моменты «Начал» противоречивым заявлениям в «Quadratura».

В этой близкой ему области Беркли проявляет свою характерную проницательность. Он смело бросает вызов современным аналитикам; доказывает, что математики в своих доказательствах вынуждены принимать то, что не может быть сведено к конечным объектам чувств; и приходит к выводу, что рассуждающие, которые могут принять тайны в своей собственной области, непоследовательны, отвергая религию, потому что она предъявляет подобное требование к не полностью постижимому доверию. Таким образом, всё человеческое знание — физическое, математическое и теологическое — в конечном счёте является скорее практической верой, нежели perfectly постигнутой наукой.

Можно допустить, что природная стремительность Беркли и склонность доводить концепции до крайностей ведут его в «Аналитике» к положениям, которые по меньшей мере легко могут быть misunderstood. Не довольствуясь тем, чтобы подчеркивать непостижимость, если не противоречивость, оснований математики, особенно флюксий, он приписывает фальшь ньютоновскому анализу. Он говорит так, как будто флюксии содержат положительные противоречия, а не merely относительную непостижимость; и математики жалуются, что он был слеп к ньютоновской концепции непрерывности. Но он спорил с лицами, которые, как предполагалось, исходили из того, что слова должны означать нечто, сводимое к данным чувств, и которые отвергали тайны религии потому, что те не поддавались такому анализу иначе как ценой противоречия. Он, по-видимому, рассматривает ньютоновскую концепцию непрерывности как открытую для подобного же возражения, с той же точки зрения; как неспособную быть сведённой к данным чувств и воображения и, следовательно, влекущую за собой противоречия, когда с ней обращаются так, как если бы она была к ним сводима. Если это всё, что он имел в виду, то его язык недостаточно осторожен. Карно и Лагранж, Эйлер и Д'Аламбер впоследствии пытались различными способами разрешить трудности, сходные с некоторыми из тех, которые выявил Беркли.

Беркли много говорит о тайнах, заключённых в количественной бесконечности в математике: можно было бы ожидать, что он сослался бы на тайну бесконечной жизни в религии; которая, более того, включает в себя как качественную, так и количественную непостижимость. Жизнь, продлённая на миллионы лет, умноженные на миллионы, всё ещё конечна и, следовательно, постижима, отличаясь таким образом от жизни, которая абсолютно бесконечна; и «не видел того глаз, не слышало ухо, и не приходило то на сердце человеку» — представить себе жизнь, освобождённую от физических условий смертной жизни на земле. Чувственное воображение не может создать картину бессмертия, и всё же это слово было средством огромного влияния в духовной истории человека. Это яркий пример того, что имеет в виду Беркли, когда говорит, что «сообщение идей не является главной и единственной целью языка, как это обычно предполагается»; ибо у него есть и другие цели, «как-то: возбуждение какой-либо страсти, побуждение к действию или удержание от него, приведение души в некоторое particular расположение»; так что «страхи, любовь, ненависть, восхищение, презрение и тому подобные страсти немедленно возникают в душе при восприятии определённых слов, без всяких идей, являющихся посредниками».

Появление «Аналитика» с его метафизикой послужило сигналом к математической полемике, памятной в истории науки в Англии восемнадцатого века. В течение семи лет, последовавших за его появлением, было выпущено около тридцати pamphlets и сталей в нападение или защиту, в которых приняли участие некоторые из главных математиков того времени.

Впереди всех них был доктор Джеймс Джурин (1684–1750) из Кембриджа, знаменитый врач и физик, близкий друг Ньютона, который напал на «Аналитика» вскоре после его появления, под псевдонимом Philalethes Cantabrigiensis, в pamphlet озаглавленном «Геометрия — не друг неверия; или Защита сэра Исаака Ньютона и британских математиков. В письме к автору Аналитика». «Защита свободомыслия в математике» Беркли, опубликованная в марте 1735 года, является его ответом Джурину. Последовало возражение от Philalethes Cantabrigiensis, в «Ничтожном математике; или Свободомыслящий — не справедливомыслящий, изложенное во втором письме к автору Аналитика; содержащем защиту сэра Исаака Ньютона и британских математиков против недавнего pamphletа, озаглавленного „Защита свободомыслия в математике“». На это второе письмо, датированное 13 июня 1735 года и опубликованное в следующем месяце, Беркли не ответил.

В том же году Уолтон из Дублина предложил «Оправдание флюксий сэра Исаака Ньютона». На это Беркли ответил в «Приложении» ко второму изданию своей «Защиты свободомыслия в математике», Приложении, которое заканчивается серией вопросов. Возражение Уолтона озаглавлено «Катехизис автора „Ничтожного философа“ полностью отвеченный». Этот ответ вызвал со стороны Беркли его «Причины не отвечать на полный ответ мистера Уолтона, в письме к О. Т. П.». На это Уолтон ответил в «Ответе на „Причины не отвечать на полный ответ мистера Уолтона“», приложенном ко второму изданию его «Катехизиса». На этом полемика между Беркли и Уолтоном закончилась.

Обсуждение продолжалось в течение нескольких лет среди математиков, становясь всё более исключительно математическим, в пренебрежении к метафизическому аргументу, который был побудительным мотивом «Аналитика». Ниже приведены наиболее важные из относящихся к делу публикаций:

«Рассуждение о природе и достоверности методов флюксий сэра Исаака Ньютона и о первых и последних отношениях» Бенджамина Робинса. Робинс (1707–51) был выдающимся математиком, который незадолго до этого вступил в полемику с Бернулли о концепции движения Лейбница. Возвращаясь из-за границы, он застал английских математиков горячо занятыми обсуждением, поднятым «Аналитиком». Его «Рассуждение», появившееся в 1735 году, было followed в 1739 году его «Замечаниями на „Трактат о движении“ г-на Кёллера; на сложную систему оптики доктора Смита, магистра Тринити-колледжа в Кембридже; и на „Рассуждение о distinct и indistinct зрении“ доктора Джурина»; таким образом, связанные с теорией зрения. «Рассуждение» 1735 года было рецензировано в «Republic of Letters» в сентябре того же года. В декабрьском номере есть критика Робинсом «возражений против доктрины флюксий и последних пропорций; с замечаниями о методах, принятых для их устранения». Полемика была продолжена в серии статей Робинса и Джурина, которые появились в «Republic of Letters» в январе, апреле, июле и августе 1736 года. Генри Пембертон (1694–1771), врач, друг Ньютона, который поручил ему наблюдение за третьим изданием «Начал» (1726), также участвовал в полемике. Серия из девяти статей и возражений между Пембертоном и Джуриным появилась в «Works of the Learned» в 1737 году, начиная с февраля.

В 1736 году преподобный Томас Байес (?) опубликовал «Введение в учение о флюксиях и защиту математиков от возражений автора „Аналитика“», насколько они предназначены для того, чтобы повлиять на различные методы рассуждения. В следующем году Джеймс Смит выпустил «Новый трактат о флюксиях»; а в 1741 году была опубликована анонимная «Объяснение флюксий». В 1745 году появилось «Утверждение гармонии древней и современной геометрии: в ответ на призыв автора „Аналитика“ к прославленным математикам нынешнего века прояснить то, что он называет их тёмной аналитикой». Этот забытый трактат состоит из документов, представленных Королевскому обществу, в которых флюксии рассматриваются как раздел более общего метода рассуждения, называемого максиминоритет и минимайоритет. В 1739 году Робинс опубликовал «Замечания» на Эйлера, Смита и Джурина, на которые Джурин ответил в том же году. Возражение Робинса в 1740 году повлекло за собой «Ответ» от Джурина в следующем году. В 1742 году Колин Маклорен, знаменитый шотландский математик, опубликовал обстоятельный «Трактат о флюксиях». Все эти работы являются примерами объёмной полемики, родоначальником которой был «Аналитик». «„Аналитик“, — по словам профессора Келланда, — оказал услугу науке, если не другим, то тем, что дал повод для работы Маклорена о флюксиях. Принципы метода были ранее изложены сжато и туманно: он развил их по манере древних геометров».

Беркли ссылается на полемику вокруг «Аналитика» в «Сирис» (раздел 271, примечание), что можно считать его последним словом по этому вопросу. Математическая важность «Аналитика» меньше, чем его метафизическая, или же его биографическая и историческая значимость.

Рассуждение, обращённое к математику-неверующему

1. Хотя я и не знаком с вами лично, сударь, мне хорошо известна та репутация, которую вы снискали в отрасли, составляющей ваше основное занятие. Известен мне и тот авторитет, который вы, вследствие сего, присваиваете себе в вопросах, чуждых вашей профессии; равно как и те злоупотребления, что вы, вкупе с иными особами вашего склада, позволяете себе, опираясь на сей незаконный авторитет. Вы вводите в заблуждение неосторожных людей в вопросах величайшей важности, — в вопросах, где ваши математические познания никоим образом не могут служить мерилом компетенции. Впрочем, справедливость и здравый смысл велят нам пренебрегать суждением людей о вещах, кои они не обдумали и не исследовали. Но некоторые, громче всех заявляющие о своих притязаниях на эти качества, тем не менее, делают как раз то, что, казалось бы, презирают, облекаясь в ливрею мнений других людей и надевая на себя всеобщее почтение к суждению вас, господ, которые почитаются из всех людей величайшими мастерами рассудка, наиболее сведущими в отчётливых идеях и никогда не принимающими things на веру, но всегда ясно видящими свой путь, как люди, постоянным занятием которых является выведение истины путём справедливейшего умозаключения из самых очевидных принципов. С этим предубеждением на уме они подчиняются вашим решениям там, где вы не имеете права решать. И что это — один из кратких путей к созданию неверующих, мне достоверно известно.

2. Поскольку же предполагается, что вы постигаете отчётливее, рассматриваете пристальнее, выводите справедливее и заключаете точнее, нежели прочие люди, и что вы поэтому менее религиозны, ибо более рассудительны, я потребую привилегии свободомыслящего; и возьму на себя liberty исследовать объект, принципы и метод доказательства, принимаемые математиками нынешнего века, с той же свободой, с какой вы, как предполагается, обращаетесь с принципами и тайнами Религии; дабы все люди могли видеть, какое право вы имеете вести за собой, или какое поощрение есть у других следовать за вами. Старое замечание гласит, что Геометрия есть превосходная Логика. И должно признать, что когда определения ясны; когда постулаты не могут быть отвергнуты, ни аксиомы оспорены; когда из отчётливого созерцания и сравнения фигур их свойства выводятся посредством непрерывной, хорошо связанной цепи следствий, причём объекты постоянно сохраняются в виду, и внимание всегда fixed на них; тогда приобретается привычка рассуждать, тесная, точная и методичная — какая привычка укрепляет и оттачивает ум и, будучи перенесена на другие subjects, имеет общее употребление в поиске истины. Но насколько это относится к нашим геометрическим аналитикам, perhaps стоит рассмотреть.

3. Метод Флюксий есть всеобщий ключ, с помощью коего современные математики отпирают секреты Геометрии, и, следовательно, Природы. И, поскольку именно он позволил им столь замечательно превзойти древних в открытии теорем и решении проблем, упражнение и приложение оного стало главным, если не единственным, занятием всех тех, кто в сей век слывёт глубокими геометрами. Но whether сей метод ясен или тёмен, последователен или противоречив, доказателен или сомнителен, я буду исследовать с величайшей беспристрастностью, и так же представлю моё исследование на ваше собственное суждение и суждение каждого беспристрастного читателя. — Предполагается, что линии порождаются [1] движением точек, плоскости — движением линий, а твёрдые тела — движением плоскостей.

[1] [Introd. ad Quadraturam Curvarum.] — АВТОР. В этом и трёх последующих разделах представлено краткое изложение тайн, заключённых в ньютоновских флюксиях, а также в исчислении континентальных математиков, которые, как утверждается, требуют не меньшей конечной веры, чем тайны, которые заключает в себе религия.

И поскольку количества, порождённые в равные времена, бывают больше или меньше в соответствии с большей или меньшей скоростью, с коей они возрастают и порождаются, был найден метод определять количества по скоростям их порождающих движений. И такие скорости называются флюксиями: а порождённые количества называются флюентами (текущими количествами). Говорят, что эти флюксии приблизительно так относятся друг к другу, как приращения флюент, порождённые в наименьшие равные частицы времени; и точно — в первой пропорции нарождающихся, или в последней — исчезающих приращений. Иногда, вместо скоростей, рассматриваются мгновенные приращения или убыли неопределённых флюент под названием моментов.

4. Под моментами мы не должны понимать конечные частицы. Говорят, что это не моменты, но количества, порождённые из моментов, каковые последние суть лишь зарождающиеся принципы конечных количеств. Говорится, что малейшие ошибки не должны быть neglected в математике: что флюксии суть скорости, не пропорциональные конечным приращениям, сколь бы те ни были малы; но лишь моментам или нарождающимся приращениям, где рассматривается одна лишь их пропорция, а не величина. И у упомянутых флюксий есть другие флюксии, которые флюксии от флюксий называются вторыми флюксиями. А флюксии от этих вторых флюксий называются третьими флюксиями: и так далее, четвёртые, пятые, шестые и т. д. до бесконечности. Итак, как наше Чувство напряжено и озадачено восприятием объектов чрезвычайно малых, так же и Воображение, каковая способность происходит от чувства, очень напряжено и озадачено, чтобы формировать ясные идеи наименьших частиц времени или наименьших приращений, порождённых в оных: и ещё более — чтобы постигать моменты, или те приращения флюент в statu nascendi, в самом их первом origin или начале существования, прежде чем они станут конечными частицами. И представляется ещё более трудным постигать отвлечённые скорости таких зарождающихся несовершенных сущностей. Но скорости от скоростей — вторые, третьи, четвёртые и пятые скорости и т. д. — превосходят, если я не ошибаюсь, всякое человеческое understanding. Чем далее ум анализирует и преследует эти ускользающие идеи, тем более он теряется и приходит в замешательство; объекты, вначале мимолётные и minute, скоро исчезая из виду. Несомненно, в любом смысле, вторая или третья флюксия представляется тёмной Тайной. Начинающаяся скорость от начинающейся скорости, нарождающееся приращение от нарождающегося приращения, т. е. от вещи, не имеющей величины — примите это в каком угодно свете, ясное conception оного, если я не ошибаюсь, окажется невозможным; так это или нет, я предоставляю испытанию каждого мыслящего читателя. И если вторая флюксия непостижима, что же нам думать о третьих, четвёртых, пятых флюксиях и так далее без конца?

5. Иностранные математики, по мнению некоторых, даже из наших собственных, действуют manner менее точным, perhaps, и геометрическим, но более вразумительным. Вместо флюент и их флюксий, они рассматривают переменные конечные количества как возрастающие или уменьшающиеся путём continual прибавления или вычитания бесконечно малых количеств. Вместо скоростей, коими порождаются приращения, они рассматривают сами приращения или убыли, которые они называют разностями и которые предполагаются бесконечно малыми. Разность линии есть бесконечно малая линия; разность плоскости — бесконечно малая плоскость. Они предполагают, что конечные quantities состоят из частей бесконечно малых, и что кривые суть многоугольники, стороны которых бесконечно малы, и которые углами, образуемыми ими друг с другом, определяют кривизну линии. Теперь, постичь количество бесконечно малое — то есть, бесконечно меньшее, чем любое ощутимое или вообразимое количество, или любая наименьшая конечная величина — это, признаюсь, выше моей способности. Но постичь часть такого бесконечно малого количества, которая должна быть всё ещё бесконечно меньше его, и, следовательно, будучи умноженной бесконечно, никогда не сравняется с малейшей конечной quantity, это, я подозреваю, есть бесконечная трудность для любого человека whatsoever; и будет признано таковой теми, кто чистосердечно говорит, что они думают; при условии, что они действительно думают и размышляют, а не принимают вещи на веру.

6. И всё же в дифференциальном исчислении, чей метод служит всем тем же целям и намерениям, что и метод флюксий, наши современные аналитики не довольствуются рассмотрением лишь разностей конечных величин: они рассматривают также разности этих разностей, и разности разностей первых разностей: и так до бесконечности. То есть, они рассматривают величины бесконечно меньшие, чем наименьшая различимая величина; и другие, бесконечно меньшие, чем эти бесконечно малые; и всё другие, бесконечно меньшие, чем предшествующие инфинитезимали, и так без конца и предела. Так что мы вынуждены допустить бесконечную последовательность инфинитезималей, каждая из которых бесконечно меньше предыдущей и бесконечно больше последующей. Подобно тому, как существуют первые, вторые, третьи, четвёртые, пятые и т. д. флюксии, так существуют и разности, первые, вторые, третьи, четвёртые и т.д., в бесконечном progression к ничто, к которому ты всё приближаешься и никогда не достигаешь. И (что всего удивительнее) хотя бы ты взял миллион миллионов этих инфинитезималей, каждая из которых предполагается бесконечно большей, чем некоторая другая реальная величина, и прибавил их к наименьшей заданной величине, она от этого ничуть не станет больше. Ибо это есть одно из скромных допущений наших современных математиков и является краеугольным камнем или основанием их умозрений.

7. Все эти положения, говорю я, предполагаются и принимаются на веру некоторыми строгими требователями доказательств в религии, людьми, которые pretendent верить не дальше, чем могут видеть. То, что люди, имевшие дело лишь с ясными положениями, с трудом допускают тёмные, могло бы показаться не совсем необъяснимым. Но тот, кто может переварить вторую или третью флюксию, вторую или третью разность, не должен, мне кажется, брезговать каким бы то ни было положением в богословии. Существует естественное предположение, что способности людей созданы одинаковыми. Именно на этом предположении они пытаются спорить и убеждать друг друга. Следовательно, то, что одному кажется очевидно невозможным и противоречивым, можно предположить таковым же и для другого. Но с каким видом разумности может кто-либо осмелиться утверждать, что тайны не могут быть объектами веры, в то же самое время, когда он сам допускает подобные тёмные тайны быть объектом науки [[1]]?

___________

[[1] «Объекты науки», то есть объекты веры, или разумного доверия, которое лежит в основе математического и естественнонаучного знания, как оно же лежит и в основе религии и богословия.]

— —

8. Действительно, должно признать, современные математики не рассматривают эти вопросы как тайны, но как ясно постигнутые и освоенные их всеобъемлющими умами. Они не стесняются говорить, что с помощью этой новой аналитики они могут проникнуть в саму бесконечность: что они могут даже распространить свои взгляды за пределы бесконечности: что их искусство объемлет не только бесконечное, но и бесконечное из бесконечного (как они это выражаются), или бесконечность бесконечностей. Но, несмотря на все эти утверждения и притязания, можно справедливо усомниться, не обманываются ли и они точно так же, как другие люди в других изысканиях часто бывают обмануты словами или терминами, чудесным образом будучи введены в заблуждение своими собственными особыми знаками, символами или видами. Нет ничего легче, чем придумать выражения или обозначения для флюксий и инфинитезималей первого, второго, третьего, четвёртого и последующих порядков, proceeding в той же правильной форме без конца и предела x. ’x. '’x. «»’x. и т. д. или dx. ddx. dddx. ddddx. и т. д. Эти выражения, действительно, ясны и отчётливы, и ум не находит трудности в том, чтобы представить их продолжающимися beyond любых назначенных границ. Но если мы приподнимем покров и заглянем под него, если, отложив в сторону выражения, мы пристально обратимся к рассмотрению самих вещей, которые, как предполагается, ими выражены или обозначены, мы обнаружим много пустоты, темноты и смятения; более того, если я не ошибаюсь, прямые невозможности и противоречия. Так ли это или нет, каждый мыслящий читатель упрашивается исследовать и судить самостоятельно.

9. Рассмотрев объект, я перехожу к рассмотрению принципов этого нового анализа, основанного на моментах, флюксиях или инфинитезималях; в котором, если окажется, что ваши основные положения, от которых, как предполагается, зависят все остальные, содержат ошибку и ложное умозаключение; тогда последует, что вы, сами не знающие, как вести себя, не можете с какой бы то ни было пристойностью назначать себя проводниками для других людей. Главный пункт в методе флюксий — получить флюксию или момент прямоугольника или произведения двух промежуточных величин. Поскольку отсюда выводятся правила для получения флюксий всех других произведений и степеней; какими бы ни были коэффициенты или показатели, целые или дробные, рациональные или иррациональные. Теперь, можно было бы подумать, этот основополагающий пункт должен быть очень ясно разъяснён, учитывая, сколько на нём построено и что его влияние простирается на весь анализ. Но предоставим судить читателю. Вот что даётся в качестве доказательства [[1]].

___________

[[1] Philosophiae Naturalis Principia Mathematica. Lib. II. lem. 2.] — АВТОР.

—

Предположим, что произведение или прямоугольник AB увеличивается непрерывным движением: и что мгновенные приращения сторон A и B суть a и b. Когда стороны A и B были недостаточны, или меньше на половину своих моментов, прямоугольник был A — 1/2a x B — 1/2b, то есть AB — 1/2aB — 1/2bA +1/4ab. И как только стороны A и B увеличиваются на другие две половины своих моментов, прямоугольник становится A +1/2a x B +1/2b или AB +1/2aB +1/2bA +1/4ab. Из последнего прямоугольника вычтем первый, и остающаяся разность будет aB + bA. Следовательно, приращение прямоугольника, порождённое полными приращениями a и b, есть aB + bA. Что и требовалось доказать. Но очевидно, что прямой и истинный метод получения момента или приращения прямоугольника AB — это взять стороны увеличенными на их целые приращения и перемножить их друг на друга, A + a на B + b, произведение которых AB + aB + bA + ab есть увеличенный прямоугольник; откуда, если мы вычтем AB, остаток aB + bA + ab будет истинным приращением прямоугольника, превосходящим то, что было получено предыдущим неправомерным и окольным методом, на величину ab. И это справедливо universally, будь величины a и b какими угодно, большими или малыми, конечными или бесконечно малыми, приращениями, моментами или скоростями. И не поможет говорить, что ab есть величина чрезвычайно малая: поскольку нам говорят, что in rebus mathematicis errores quam minimi non sunt contemnendi,

10. [[1]] Подобные этому рассуждения в качестве доказательства ничто, кроме темноты предмета, не могло бы поощрить или побудить великого автора флюксионного метода навязать своим последователям, и ничто, кроме слепого доверия к авторитету, не могло бы побудить их принять это.

_________

[[1] [Introd, ad Quadraturam Curvarum.]] — АВТОР.

— — —

Положение действительно трудное. Ничего нельзя сделать, пока вы не избавитесь от величины a b. Чтобы добиться этого, понятие флюксий сдвигается: оно помещается в различный свет: пункты, которые должны быть ясны как первые принципы, запутываются; и термины, которые должны использоваться неуклонно, становятся двусмысленными. Но, несмотря на всю эту изворотливость и искусство, цель избавления от a b не может быть достигнута законным рассуждением. Если человек методами не геометрическими и не доказательными удовлетворил себя в полезности некоторых правил; которые он впоследствии предложит своим ученикам в качестве несомненных истин; которые он предпринимает доказать тонким образом и с помощью изящных и запутанных понятий; нетрудно представить, что такие его ученики, чтобы избавить себя от труда мыслить, могут быть склонны смешивать полезность правила с достоверностью истины и принимать одно за другое; особенно если они люди, привыкшие скорее вычислять, чем мыслить; стремящиеся скорее продвигаться быстро и далеко, чем озабоченные тем, чтобы начинать осторожно и видеть свой путь отчётливо.

9. Рассмотрев сам предмет, я далее приступаю к рассмотрению принципов этого нового анализа при помощи моментов, флюксий или бесконечно малых величин; если в результате окажется, что ваши главные положения, от которых, как полагается, зависит все остальное, содержат ошибки и ложные заключения, то отсюда будет следовать, что вы, не знающий, куда направить самого себя, не можете, хотя бы из чувства простой скромности, быть руководителем для других людей. Главное в методе флюксий заключается в том, чтобы получить флюксию, или скорость движения (momentum), для прямоугольника, т. е. произведение двух неопределенных величин. Ибо именно из этого выводятся правила получения флюксий всех других произведений и степеней, независимо от характера коэффициентов или индексов, будь они целыми числами или дробными, действительными или иррациональными. Можно было бы подумать, что это главное положение должно быть очень четко доказано, принимая во внимание, что на нем основано очень многое и что его влияние распространяется на весь анализ. Но пусть читатель судит сам. Покажем использование упомянутого принципа на примере. Положим, что произведение, или прямоугольник АВ, увеличивается благодаря постоянному движению и что мгновенные приращения сторон А в В соответственно равны а и b. Когда стороны А и В были меньше, положим, на 7» их моментов, прямоугольник равнялся.

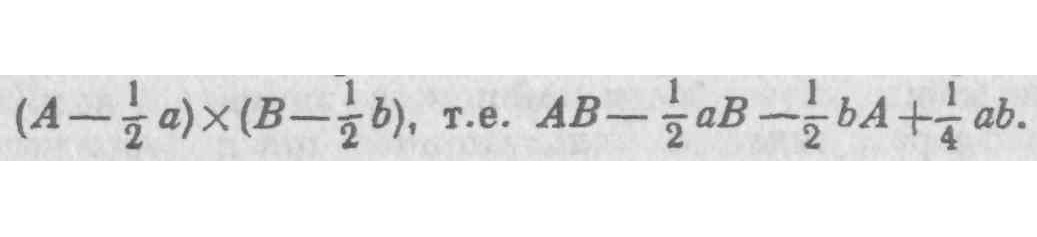
«Naturalis Philosophiae principia mathematica», lib. 2, lem. 2 [5].

Но как только стороны А и В увеличились на оставшиеся две половины их моментов, прямоугольник становится равным

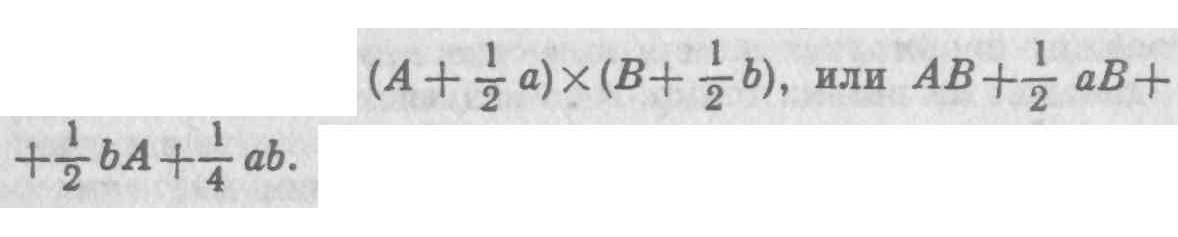
Вычтем из последнего прямоугольника предыдущий, и останется разность аВ + bА. Следовательно, приращение прямоугольника, образованного целыми приращениями а и b, есть аВ + bА, что и требовалось доказать. Однако очевидно, что для получения момента или приращения прямоугольника АВ прямым и истинным методом необходимо взять стороны такими, какими они получились в результате увеличения их на полные приращения, и затем перемножить их (А+а) х (В+b), а полученное произведение (AB+aB+bA-t-ab) и есть увеличенный прямоугольник; отсюда, если мы вычтем АВ, остаток (аВ+bА+аb) и будет истинным приращением прямоугольника, превышающим тот, который был получен предыдущим незаконным и непрямым методом, на величину ab. и это справедливо в любом случае, какими бы ни были величины а и b, — большими или малыми, конечными или бесконечно малыми, приращениями, моментами или скоростями. Не поможет и утверждение о том, что ab — величина чрезвычайно малая, поскольку нам говорят, что in rebus mathematicis errores quam minimi non sunt contemnendi.

10. Ничто, кроме неясности предмета, не могло бы побудить или заставить великого автора теории флюксий навязать своим последователям такой ход рассуждений, который только что был продемонстрирован нами на примере, и ничто, кроме молчаливого уважения к авторитету, не могло бы заставить их принять его. Вопрос действительно трудный. Ничего нельзя сделать до тех пор, пока не избавимся от величины ab. Чтобы добиться этого, понятие о флюксиях смещается; его освещают с разных сторон; положения, которые должны быть ясны как основополагающие принципы, затуманиваются, а термины, употребление которых должно быть неизменным (steadily), делаются двусмысленными. Но, несмотря на всю эту изощренность и искусство, задача избавления от величины ab не может быть решена при помощи законного логического хода рассуждения. Если кто-либо при помощи негеометрических или демонстративных методов убедит себя в полезности определенных правил, которые он впоследствии сообщит своим ученикам в качестве неоспоримых истин и докажет их весьма тонко, с помощью точных и сложных понятий, то нетрудно представить себе, что такие его ученики, чтобы не утруждать себя размышлениями, могут склониться к спутыванию полезности правила с определенностью истины и принять одно за другое, особенно если они привыкли скорее считать, чем думать, и стремятся идти быстрее вперед, а не заботятся о том, чтобы ступать осторожно и ясно видеть свой путь.

11. Точки, или просто пределы зарождающихся линий, несомненно равны между собой, так как величина одной из них не превышает другой, а предел, как таковой, не есть величина. Если под [механическим] моментом (тоmentum) вы подразумеваете больше, чем самый начальный предел, то он должен быть либо конечной величиной, либо бесконечно малой. и действительно, хотя прибегали ко множеству хитростей, чтобы уклониться от признания величин бесконечно малых или как-либо избежать их, все это, кажется, ни к чему не привело. Насколько я понимаю, без признания существования бесконечно малых величин нельзя признать существование величины, занимающей промежуточное положение между конечной величиной и нулем. Приращение, образованное за конечную частицу времени, само по себе является конечной частицей и вследствие этого не может быть [механическим] моментом. Следовательно, для образования [механического] момента вам нужно брать бесконечно малую частицу времени. Говорят, что величина моментов не принимается во внимание, и тем не менее считается, что эти же самые моменты делятся на части. Это не легко понять, не легче, чем представить себе, почему для получения приращения АВ мы должны брать величины меньшие, чем А и В, хотя необходимо признать, что конечная причина или побудительный мотив такого хода рассуждений совершенно очевидны; но не так легко и просто привести справедливую и законную причину в объяснение этого или показать, что она является строго геометрической.

12. Из доказанного таким образом вышеупомянутого принципа выводится общее правило нахождения у флюента флюксии любой степени *. Но так как автор, кажется, испытывал скрытые угрызения совести или сознавал ущербность вышеприведенного доказательства и так как это нахождение флюксии данной степени есть вопрос первостепенной важности, было сочтено уместным вследствие этого доказать то же самое, но иным способом, отличным от приведенного выше доказательства. Однако теперь я перехожу к рассмотрению того, является ли этот другой метод более законным и убедительным, чем прежний; своему рассмотрению я предпосылаю следующую лемму: «Если для доказательства какого-либо предположения выдвигается определенное положение, благодаря которому доказываются некоторые другие положения, и если такое выдвинутое положение впоследствии само будет опровергнуто или отвергнуто противоположным предположением, то в этом случае все другие положения, доказанные при его помощи и вытекающие из него, должны быть также опровергнуты и отвергнуты, с тем чтобы в дальнейшем они не выдвигались и в доказательстве не применялись». Это настолько очевидно, что не нуждается в доказательстве.

13. Второй способ получения правила нахождения флюксии любой степени заключается в следующем. Пусть величина х возрастает равномерно (uniformly) и пусть предлагается найти флюксию хn. За тот же отрезок времени, что х путем возрастания становится (х+0), степень хn становится (х+0) n; т. е. в соответствии с методом бес-

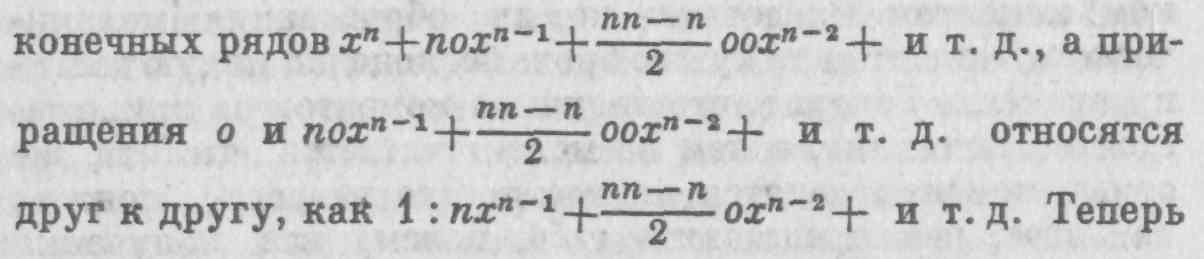
допустим, что приращения исчезают, и их последнее отношение будет составлять 1: nxn-1. Но, представляется нам, такой ход рассуждений не будет справедливым или убедительным. Ибо когда говорят: пусть приращения исчезают, т. е. пусть приращения равны нулю или пусть не будет никаких приращений, тем самым прежнее допущение, что приращения представляют собой какую-то величину или что приращения имели место, отвергается, однако следствие того допущения, т. е. выражение, полученное благодаря ему, сохраняется. А это, в соответствии с вышеуказанной леммой, представляет собой ложный ход рассуждения. Безусловно, если мы предполагаем, что приращения исчезают, то мы должны предположить, что вместе с ними исчезают их соотношения, их выражения и все остальное, выведенное из предположения об их существовании.

14. Чтобы сделать этот вопрос более понятным, я разверну ход рассуждения и изложу его перед вами более полно. Он сводится, следовательно, к следующему, или, другими словами, может быть выражен следующим образом. Я полагаю, что величина х — переменная, что она возрастает в результате изменения, ее приращение я обозначу о, так что в результате возрастания она становится (х+0). Так как х увеличился, из этого следует, что. каждая степень х также увеличивается в соответствующей пропорции. Следовательно, раз х становится (x+0), хn становится (х+0) n, т. е. в соответствии с методом бесконечных рядов

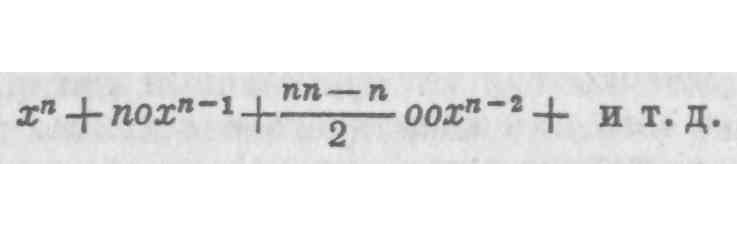
А если из двух возросших величин мы вычтем соответственно основание и степень, то получим в остатке два приращения, а именно 0 и и т.д.,

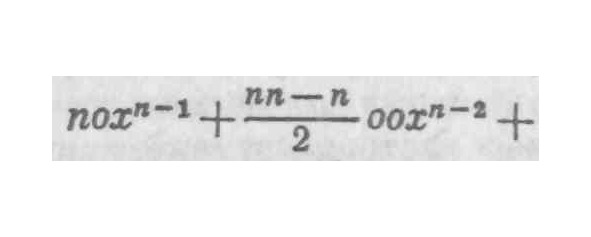
а если оба приращения разделить на общий делитель «о», то получим частные

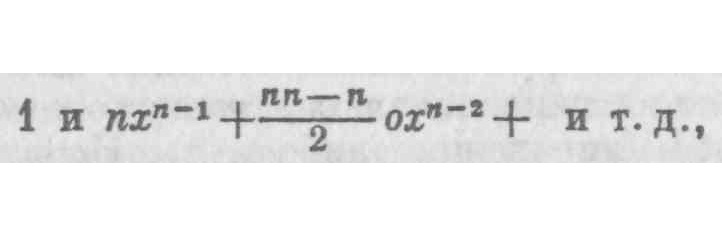
которые, следовательно, являются показателями соотношения приращений. До сих пор я предполагал, что х возрастает, что х обладает действительным приращением, что о есть нечто [определенное]. и я все время исходил из этого предположения, без которого я не смог бы сделать ни одного шага вперед. На основании этого предположения я получаю приращение хn, в состоянии сравнить его с приращением х и нахожу соотношение между двумя приращениями. Теперь я прошу разрешить мне сделать новое предположение, прямо противоположное первому, т. е. я предположу, что нет никакого приращения х или что о есть ничто; это второе предположение опровергает мое первое, несовместимо с ним и, следовательно, со всем тем, что им предполагается. Тем не менее я прошу разрешения сохранить nxn-1 — выражение, полученное благодаря моему первому предположению, необходимо обусловленное таким предположением, причем получение его без первого предположения было бы невозможно. Все это представляется весьма непоследовательным способом аргументации, и притом таким, который не допускался бы в отношении вопросов о божественном.

15. Нет ничего более очевидного, как то, что из двух несовместимых предположений нельзя непосредственно вывести правильное заключение. Правда, можно предположить все что угодно. Но ведь нельзя предполагать то, что может уничтожить первое предположение; или же, если вы так поступаете, то должны начать de novo. Следовательно, если вы предполагаете, что увеличения исчезают, т. е. что увеличений нет, то вы должны начать снова и посмотреть, что следует из такого предположения. Но отсюда не следует ничего, что послужило бы вашей цели.

Таким путем вы вообще не сможете прийти к сделанному вами выводу или, проводя анализ конечных величин, успешно осуществить то, что знаменитый автор называет изучением первого или последнего отношения зарождающихся или исчезающих величин. Я вновь повторяю: вы свободны делать любые возможные предположения; и вы можете опровергнуть одно предположение при помощи другого; но тогда вы не можете сохранить следствия или какую-либо часть следствий вашего первого предположения, опровергнутого таким образом. Я признаю, что можно заставить знаки обозначать что-либо или ничто, и, следовательно, в первоначальной записи (х+0) 0 может означать либо приращение, либо нуль. Но затем, какое бы из этих двух значений вы ему ни придали, вы должны рассуждать последовательно в соответствии с этим значением, а не исходить из двойного значения; делать так было бы явным софизмом. Рассуждаете ли вы при помощи слов или символов, правила здравого смысла остаются теми же. Нельзя также предположить, что вы сможете присвоить себе привилегию — быть свободным от этих правил в математике.

16. Если вы сначала допускаете, что какая-то величина возрастает на нуль и в выражении (х+0) 0 обозначает нуль, то, в соответствии с этим допущением, раз не будет приращения основания, не будет и приращения степени; и, следовательно, из всех членов ряда, составляющего степень бинома, останется только первый член; поэтому при помощи такого способа вы никогда не получите законным образом необходимое вам выражение флюксии. Отсюда вы вынуждены ступить на ложный путь, действуя до определенного момента на основании допущения приращения, а затем сразу же изменяя свое допущение на прямо противоположное (отсутствие приращения). Может показаться, что при осуществлении этого в определенный момент или период требуется большое искусство, поскольку, если бы это второе допущение было сделано до деления на общий делитель о, все бы мгновенно исчезло, и на основании своего допущения вы ничего бы не получали; в то время как благодаря этой уловке — сначала разделить, а потом уже изменить свое допущение, вы сохраняете 1 и nхn-1. Но, несмотря на всю эту ловкость, проявленную для прикрытия ошибки, последняя остается той же самой. Ибо независимо от того, сделаете вы это раньше или позже, как только сделано второе допущение или предположение, в тот же самый миг уничтожается и полностью исчезает прежнее допущение и все то, что вы получили при его помощи. и это справедливо в отношении всего, каков бы ни был объект изучения, во всех сферах человеческого познания; я полагаю, что в любой другой из этих сфер люди едва ли бы допустили подобный ход рассуждений, принятый для доказательства в математике.

17. Быть может, не будет лишним заметить, что метод нахождения флюксии от произведения двух текущих величин, как он изложен в «Трактате о квадратурах», отличается от упомянутого выше, взятого из второй книги «Начал», и по сути совпадает с тем, что используется в дифференциальном исчислении [[1]]. Поскольку предположение о бесконечно уменьшающейся величине и последующее её отбрасывание по сути есть отбрасывание бесконечно малой величины; и, действительно, требуется удивительная острота различения, чтобы суметь отличить исчезающие приращения от бесконечно малых разностей. Возможно, скажут, что величина, будучи бесконечно уменьшенной, становится ничем, и, таким образом, отбрасывается ничто. Но, согласно принятым принципам, очевидно, что никакая геометрическая величина никаким делением или подразделением не может быть исчерпана или сведена к нулю. Принимая во внимание различные уловки и приёмы, используемые великим автором метода флюксий; в скольких смыслах он понимает свои флюксии; и сколькими разными способами он пытается доказать один и тот же пункт; можно было бы склониться к мысли, что он сам сомневался в справедливости своих собственных доказательств и что он не был в достаточной мере доволен ни одним понятием, чтобы неуклонно придерживаться его. По крайней мере, очевидно следующее: он признавал себя удовлетворённым относительно определённых пунктов, которые, тем не менее, не брался доказать другим [[2]]. Проистекало ли это удовлетворение из пробных методов или индукций, которые часто допускались математиками (например, доктором Валлисом в его «Арифметике бесконечностей»), я не берусь определять. Но, какова ни была ситуация с автором, представляется, что его последователи проявили себя более ревностными в применении его метода, нежели точными в исследовании его принципов.

___________

[[1] [Analyse des Infiniment Petits, Part I. prop. 2.]] — АВТОР. Ньютон из «Квадратур» (1704) отличается от Ньютона из «Начал» (1687).]

[[2] [См. Письмо Колинзу, 8 ноября 1676г.]] — АВТОР.

18. Любопытно наблюдать, с какой тонкостью и искусством этот великий гений пытается бороться с непреодолимой трудностью; и сквозь какие лабиринты он старается избежать учения о бесконечно малых; которое, хотя и вторгается в его учение волей-неволей, тем не менее принимается и усваивается другими без малейшего сопротивления; — Лейбниц и его последователи в своём дифференциальном исчислении не делают никакого затруднения, чтобы сначала предположить, а затем отбросить бесконечно малые величины; с какой ясностью в понимании и правильностью в рассуждении, любой мыслящий человек, не предубеждённый в пользу этих вещей, может легко усмотреть. Понятие или идея бесконечно малой величины, как объект, просто постигаемый умом, уже были рассмотрены [[1]]. Теперь я лишь замечу относительно метода избавления от таких величин, что это делается без малейших церемоний. Поскольку во флюксиях пунктом первостепенной важности, который прокладывает путь к остальным, является нахождение флюксии от произведения двух неопределённых величин, так и в дифференциальном исчислении (который метод, как предполагается, был заимствован из первого с некоторыми небольшими изменениями) главным пунктом является получение разности такого произведения. Теперь правило для этого получается путём отбрасывания произведения или прямоугольника разностей. И в целом предполагается, что никакая величина не становится больше или меньше от прибавления или вычитания своей бесконечно малой: и, следовательно, никакая ошибка не может возникнуть от такого отбрасывания бесконечно малых.

___________

[[1] [См. «Сейрис», секции 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35.]]

19. И всё же следует полагать, что какие бы ошибки ни допускались в посылках, пропорциональные ошибки следует ожидать и в заключении, будь они конечными или бесконечно малыми: и что, следовательно, точность геометрии требует, чтобы ничто не было упущено или отброшено. В ответ на это вы, возможно, скажете, что выводы являются точно верными и что, поэтому, принципы и методы, из которых они выведены, также должны быть таковыми. Но этот перевёрнутый способ доказательства ваших принципов через ваши выводы, будучи характерным именно для вас, господа, является также противоречащим правилам логики. Истинность заключения не доказывает ни форму, ни содержание силлогизма истинными; поскольку умозаключение могло быть проведено неверно или посылки могли быть ложными, и тем не менее заключение могло оказаться истинным, хотя и не в силу такого умозаключения или таких посылок. Я утверждаю, что во всех прочих науках люди доказывают свои выводы своими принципами, а не свои принципы — выводами. Но если в вашей науке вы позволите себе этот противоестественный способ действия, следствием будет то, что вам придётся довольствоваться индукцией и сказать прощай демонстрациям. И если вы на это согласитесь, ваш авторитет более не будет указывать путь в вопросах разума и науки.

— 20. У меня нет разногласий с вами относительно ваших выводов; они у меня есть только относительно вашей логики и метода. Как вы проводите доказательство? Какие предметы вам хорошо знакомы и ясно ли вы их себе представляете? На основе каких принципов вы действуете, насколько они правильны и как вы их применяете? Необходимо помнить, что меня интересует не истинность ваших теорем, а лишь способ их доказательства: законный он или незаконный, ясный или туманный, научный или экспериментальный. Чтобы исключить всякую возможность вашего неверного суждения обо мне, я прошу разрешения повторить и вновь настаиваю, что я рассматриваю геометра-аналитика как логика, то есть [изучаю] то, каким образом он рассуждает и доказывает; а его математические выводы рассматриваю не сами по себе, а в их связи с посылками; не в отношении того, являются ли они истинными или ложными, полезными или не имеющими значения, а лишь в отношении того, каким образом они выводятся из таких принципов и при помощи таких приёмов умозаключения. А поскольку может показаться необъяснимым парадоксом, что математики выводят правильные заключения, исходя из ложных принципов, — могут прийти к верному выводу и тем не менее ошибаться в посылках, — я попытаюсь конкретно объяснить, почему это может произойти, и покажу, как ошибка может породить истину, хотя и не может породить науку.

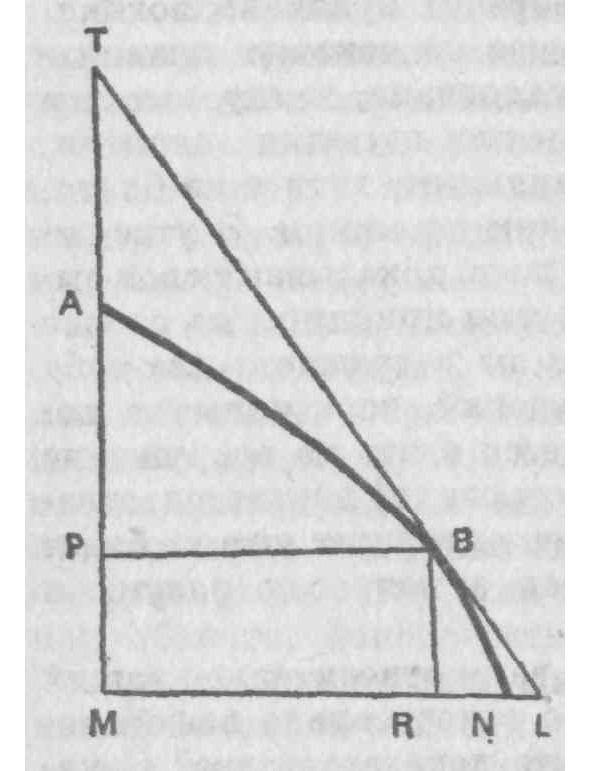
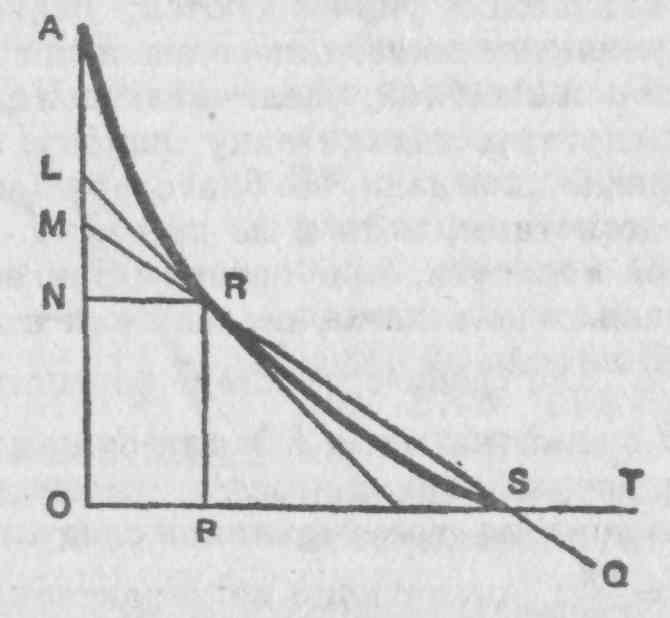
— Следовательно, для того чтобы выяснить это положение, предположим, например, что надо провести касательную к параболе, и рассмотрим решение этой задачи при помощи бесконечно малых дифференциалов. Пусть АВ — кривая, абсцисса АР = х, ордината РВ = у, приращение абсциссы PM = dx, приращение ординаты RN = dy. Теперь допустим, что кривая представляет собой многоугольник и, следовательно, BN, то есть приращение (разность кривой), является отрезком прямой, совпадающим с касательной, а дифференциальный треугольник BRN подобен треугольнику ТРВ. Тогда подкасательная РТ будет определяться из пропорции RN: RB = РВ: РТ, то есть dy: dx = y: РТ. Отсюда подкасательная будет равна y dx/dy.

Но здесь и содержится ошибка, возникшая в результате вышеупомянутого допущения, не соответствующего действительности, вследствие чего величина РТ получается больше, чем она есть на самом деле: ибо в действительности не треугольник RNB подобен РВТ, а треугольник RLB, и поэтому первым членом пропорции должен быть не RN, a RL, то есть RN + NL, то есть dy + z. Отсюда истинным выражением для подкасательной должно было бы быть y dx/ (dy + z). Следовательно, когда dy было сделано делителем, была допущена ошибка, так как была взята меньшая, чем на самом деле, величина, и эта ошибка равнялась z, то есть NL, отрезку, заключенному между кривой и касательной.

Далее, в соответствии с характеристикой кривой, уу=рх, где р — параметр, отсюда в соответствии с правилом дифференцирования 2y dy=p dx и dy= p dx/2y. Но если умножить (y+dy) само на себя и сохранить все произведение, не отбрасывая площадь дифференциала, тогда, если подставить возросшие величины в уравнение кривой, окажется, что действительно. Следовательно, была допущена ошибка, когда сочли, что, приведшая к увеличению истинного значения и вытекающая из ошибочного правила дифференцирования. и величина этой второй ошибки Следовательно, обе ошибки равны друг другу и взаимно уничтожаются; первая ошибка, приведшая к уменьшению истинного значения выражения, исправлена второй ошибкой, увеличивающей его значение.

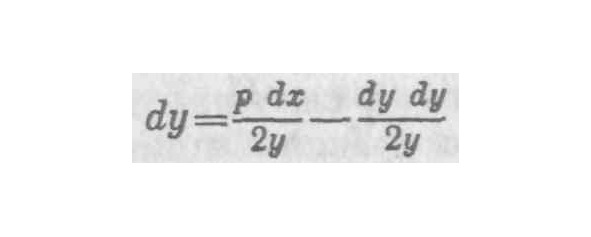
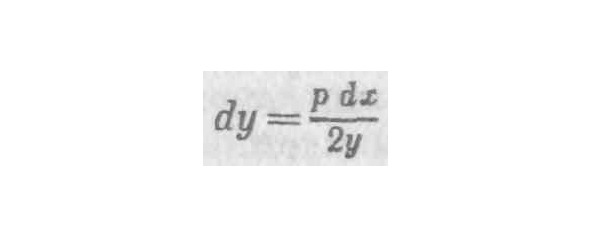
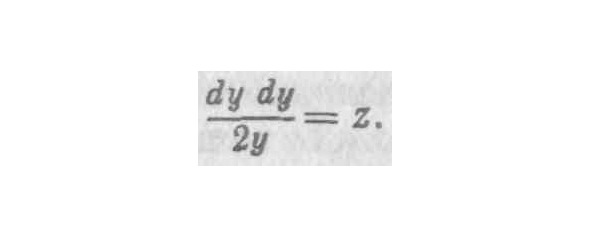
22. Если допустить только одну ошибку, не найдешь правильного решения задачи. Но благодаря двойной ошибке доходишь до истины, хотя и не до науки. Ибо нельзя назвать наукой тот путь, при котором двигаешься вслепую и добираешься до истины, не зная как и при помощи каких средств. Для доказательства равенства обозначим BR или dx как m, a RN или dy как n. На основании 33-й теоремы первой книги «Конусов» [грека] Аполлония [9] и подобия треугольников следует, что 2х: у, как. Аналогично из характеристики параболы следует, что (уу+2уn+nn) =хр+mр, а 2уn+nn=mр; вследствие чего и поскольку будет равно х. Следовательно, подставляя эти значения вместо m и х, мы получим

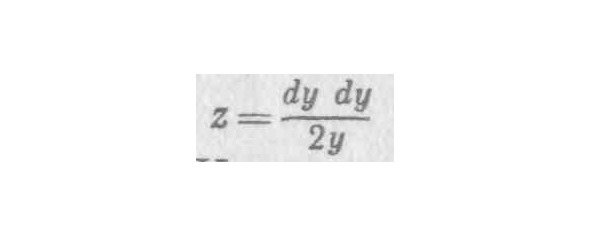
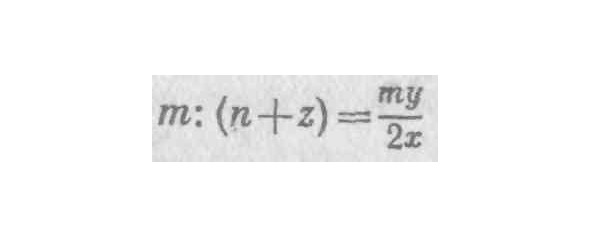
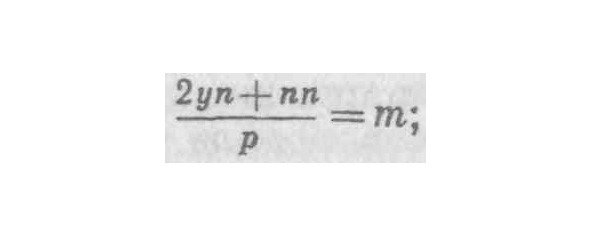
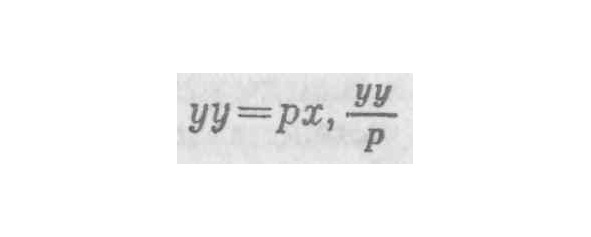
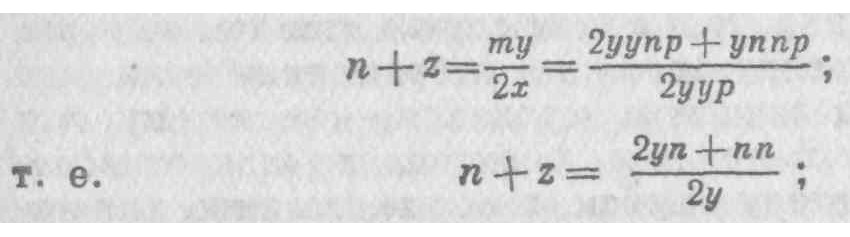
что после сокращения дает что и требовалось доказать.

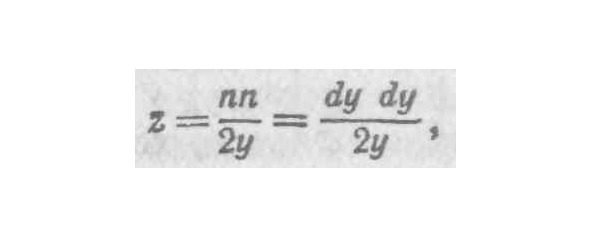
23. Конечно, вот отредактированный текст. Математические рассуждения сохранены в полном объёме, исправлены стилистические погрешности и улучшена структура предложений для лучшей читаемости.

Теперь я, прежде всего, замечу, что итог получается правильным не потому, что отброшенная величина dy была бесконечно мала, а потому, что эта ошибка была компенсирована другой ошибкой, противоположной по своему характеру, но равной ей. Во-вторых, замечу: что бы ни было отброшено, как бы мало оно ни было, если оно было действительным и, следовательно, составляло реальную ошибку в посылках, оно вызвало бы соответственную ошибку в итоге. В силу этого ваши теоремы не могут быть непогрешимо правильными, а ваши задачи — точно решёнными, так как сами посылки неточны; в логике является правилом: conclusio sequitur partem debiliorem. Поэтому замечу, в-третьих: когда заключение очевидно, а посылки неясны, или, когда заключение точно, а посылки неточны, мы можем совершенно свободно заявить, что такое заключение очевидно или точно не в силу упомянутых неясных и неточных посылок или принципов, а в силу некоторых иных принципов, о которых сам автор доказательства, возможно, вообще не знал и не думал.

Наконец, замечу: если предположить, что дифференциалы являются конечными величинами, значение которых может быть и очень велико, то и в этом случае итог тем не менее будет прежним ввиду того, что отброшенные величины игнорируются на законном основании — не потому, что они малы, а по другой причине, а именно из-за противоположных по характеру ошибок, которые, взаимно уничтожаясь, в целом приводят к тому, что в действительности ничего не отбрасывается, хотя по видимости что-то и отвергается. И эта причина в равной степени действительна в отношении величин конечных и бесконечно малых, больших и малых — будь то фут, ярд или наименьшее приращение.

24. Чтобы более полно проиллюстрировать это положение, я рассмотрю его в несколько ином свете и, оперируя вплоть до самого заключения конечными величинами, буду использовать тогда только одну бесконечно малую величину. Положим, что прямая MQ пересекает кривую

AT в точках R и S. Положим, что LR — касательная в точке R, AN — абсцисса, NR и OS — ординаты. Продолжим AN до пересечения с О и проведем RP параллельно NO. Положим, что AN=x, NR=y, NO=v, PS=z, поднормаль (subsecant) MN=s. Пусть уравнение y=xx выражает характеристику кривой; предположив, что у и х возрастают на конечное приращение, мы получаем:

у + z = хх+2xv+vv

отсюда, после вычитания предыдущего уравнения, остается z=2xv+vv. На основании подобия треугольников

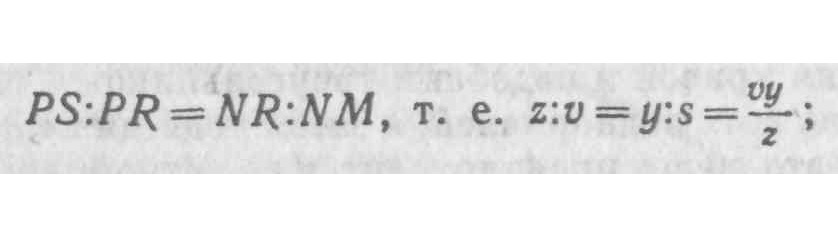
подставив сюда вместо у и z их значения, мы получаем:

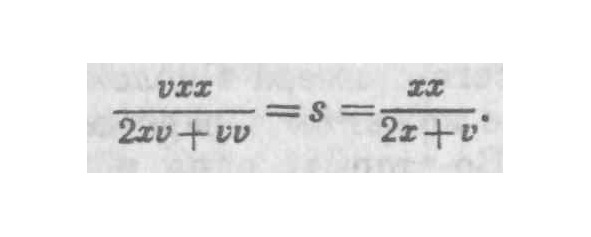
Если предположить, что NO уменьшено до величины бесконечно малой, поднормаль NM будет в этом случае совпадать с подкасательной NL, а v, как величина бесконечно малая, может быть отброшена, отсюда S=NL=, что и является истинным значением подкасательной. и поскольку при его получении была допущена только одна ошибка, т. е. однажды отброшена только одна бесконечно малая величина, то может показаться в противоположность тому, что говорилось ранее, будто можно пренебречь бесконечно малой величиной, или дифференциалом, отбросить его, и тем не менее итог будет истинным и точным, хотя и не была допущена двойная ошибка, т. е. не было исправления одной ошибки при помощи другой, как это имело место в первом случае. Но если тщательно рассмотреть это положение, мы обнаружим, что даже в данном случае допускается двойная ошибка и одна из них компенсирует или исправляет вторую. Ибо, во-первых, мы предполагали, что, когда NO уменьшается до бесконечно малой величины или становится бесконечно малой величиной, тогда поднормаль NM становится равной подкасательной NL. Но это очевидная ошибка, ибо совершенно ясно, что, поскольку секущая не может быть касательной, поднормаль не может быть подкасательной. Пусть разность будет очень мала, все же она будет. А если NO — бесконечно малая величина, даже тогда будет налицо бесконечно малая разность между NM и NL. В силу этого NM или S было слишком мало для вашего допущения (когда вы допускали, что оно равно NL) и эта ошибка была компенсирована второй ошибкой, состоявшей в отбрасывании v, и в результате этой последней ошибки s стала больше, чем ее истинное значение, и вместо него дала значение подкасательной. Таково истинное положение вещей в нашем случае, каким бы замаскированным он ни был. и к этому он сводится в действительности и в основе своей остается тем же самым, даже если мы позволим себе найти подкасательную, сначала определив с помощью уравнения кривой и подобных треугольников общее выражение для всех поднормалей, а затем подведя подкасательную под это общее правило, считая ее поднормалью, когда v приближается к нулю или становится равным ему.

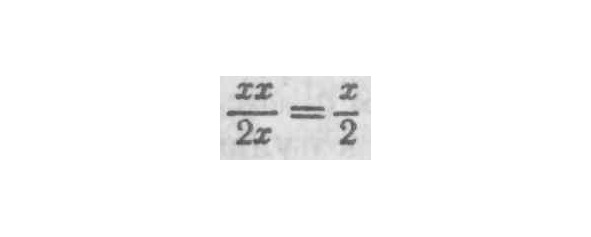
25. По поводу всего примера в целом я замечу, во-первых, что v вообще не может быть равным нулю, поскольку имеется секущая. Во-вторых, одна и та же прямая не может быть и касательной, и секущей. В-третьих, когда v или NO * приближается к нулю, PS и SR также приближаются к нулю, а с ними и пропорциональность подобных треугольников. Следовательно, все выражение, полученное с помощью этой пропорциональности и на ней основанное, приближается к нулю, когда приближается к нулю v. В-четвертых, способ нахождения секущих или их выражения, каким бы общим он ни был, не может с точки зрения здравого смысла распространяться за пределы нахождения именно всех секущих; и поскольку он необходимо предполагает наличие подобных треугольников, то в тех случаях, когда подобных треугольников нет, его применение нельзя даже предполагать. В-пятых, поднормаль всегда будет меньше подкасательной и никогда не может с ней совпадать; допускать подобное совпадение было бы абсурдно, ибо это означало бы допускать, что одна и та же прямая в одно и то же время пересекает и не пересекает другую данную линию; это представляет собой очевидное противоречие, подрывающее гипотезу и служащее доказательством ее ложности. В-шестых, если это доказательство не будет признано, я потребую, чтобы мне назвали причину, почему не это, а какое-либо иное апагогическое доказательство, или доказательство ad absurdum, признано в геометрии, или же между моим доказательством и другими подобными доказательствами должно быть найдено какое-либо реальное различие. В-седьмых, замечу: предположить, что NO или RP, PS я SR являются конечными реальными прямыми, образующими треугольник RPS, чтобы получить пропорции при помощи подобных треугольников, а затем допустить, что таких прямых (а следовательно, и подобных треугольников) не существует, но тем не менее сохранить следствие первого предположения после того, как такое предположение уничтожено прямо противоположным, — это чистая софистика. В-восьмых, хотя в данном случае при помощи несовместимых допущений можно получить истину, тем не менее такая истина не доказана; подобный метод не соответствует правилам логики и правильного мышления; каким бы полезным он ни был, его необходимо считать только предположением, ловким приемом (knack), хитростью, скорее уловкой, но не научным доказательством.

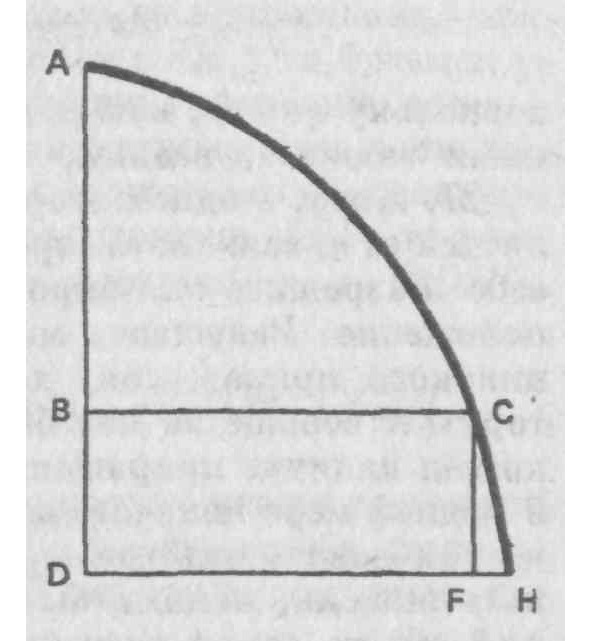
26. Изложенная выше теория может быть далее проиллюстрирована следующим простым и легким примером, в котором я использую приближающиеся к нулю приращения. Положим, АВ=х, ВС=у, BD=o, а хх равен площади ABC; предполагается найти ординату у или ВС. Когда благодаря возрастанию х становится (x+o), тогда хх становится (хх+2хо+оо); а площадь ABC становится ADH, и приращение хх будет равно BDHC, приращению площади, т. е. (BCFD+CFH). и если мы положим, что криволинейное пространство CHF равно qoo, тогда

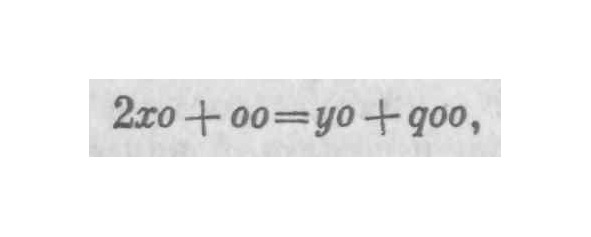
что при делении на о дает 2x+o=y+qo. и если допустить, что о исчезает, тогда 2х=у, и в этом случае АСН будет прямой, а фигуры ABC, CFH — треугольниками. Но в отношении такого хода рассуждений было уже замечено *: допускать, что о приближается к нулю, т. е. равно нулю, неправомерно и нелогично, если только мы одновременно с самим приращением не отбросим все следствия такого приращения, т. е. все то, чего нельзя получить, коль скоро не допускают такого приращения. Необходимо тем не менее признать, что задача решается правильно и вывод, к которому нас привел этот метод, правилен. Поэтому могут спросить: как же получается, что отбрасывание о не сопровождается никакими ошибками в выводе? Я отвечу: подлинная причина этого очевидна: раз q составляет единицу, qo равно о; и в силу этого

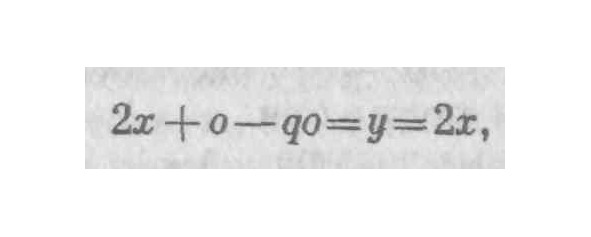
поскольку qo и о, как равные величины с противоположными знаками, взаимно уничтожаются.

27. Хотя, с одной стороны, было бы абсурдным избавляться от о, заявив: «Разрешите мне противоречить самому себе. Разрешите мне опровергнуть свое собственное предположение. Разрешите мне считать доказанным, что нет никакого приращения, хотя я сохраняю величину, которую я вообще не мог бы получить, если бы не предположил наличие приращения», с другой стороны, было бы в равной мере неправильным вообразить, что в геометрическом доказательстве нам может быть позволено допускать ошибки, какими бы незначительными они ни были, или что по самой природе вещей возможно сделать правильный вывод на основе неточных принципов. Поэтому о может быть отброшено не как бесконечно малая величина и не на том основании, что бесконечно малыми величинами можно спокойно пренебрегать, а только потому, что оно уничтожается равной величиной с отрицательным знаком, отсюда (о — qo) равно нулю. и поскольку неправомерно сокращать уравнение путем вычитания из одной его части какой-либо величины, если только она не должна быть уничтожена или если из другой части уравнения не вычитается равная ей величина, то наш способ вести рассуждение необходимо признать в качестве весьма логичного и правильного и в заключение заявить, что, если из равных величин вычесть равные величины или нули, их равенство не нарушится. и это — истинная причина того, что в конечном итоге отбрасывание о не приводит к ошибке, что, следовательно, не должно быть отнесено за счет учения о дифференциалах, бесконечно малых величинах, исчезающих величинах, [механических] моментах или флюксиях.

28. Допустим, имеется самый общий пример и хn равен площади ABC; отсюда при помощи метода флюксий найдем значение ординаты — nхn-1, которое мы примем за истинное, и рассмотрим, как оно было получено. Если мы довольствуемся тем, что придем к выводу самым общим путем, предположив, что найдено * отношение флюксий х и хn, равное 1: nхn-1, и что ордината упомянутой площади считается ее флюксией, мы не увидим ясно свой путь и не поймем, как обнаруживается истина, поскольку, как мы показали ранее, этот метод неясен и нелогичен. Но если мы четко обозначим площадь и ее приращение, разделим последнее на две части BCFD и CFH и будем действовать последовательно при помощи уравнений, составленных из алгебраических и геометрических величин, тогда совершенно четко выявится внутреннее обоснование всего решения. Ибо если хn равен площади ABC, то приращение хn равно приращению площади, т. е. BDHC; другими словами

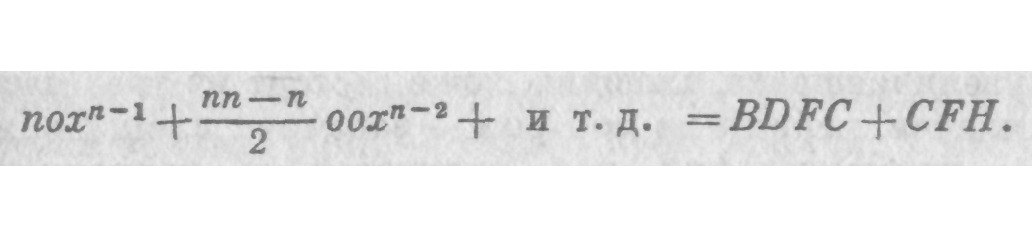
И поскольку сохраняются только первые члены из каждой части уравнения, noxn-1 = BDFC. Разделив обе части на о или BD, получим noxn-1 = ВС. В силу чего допустим, что криволинейное пространство CFH равно величине ooxn-2 и т. д., которую можно отбросить, и, когда одно отброшено из одной части, а другое — из другой, ход рассуждения становится правильным, а вывод верным. и совершенно безразлично, какое значение вы придадите BD — бесконечно малого дифференциала или большого конечного приращения. Отсюда очевидно, что предположение о том, что подлежащая отбрасыванию алгебраическая величина является бесконечно малой или исчезающей и поэтому ею можно пренебречь, должно было бы привести к ошибке, если бы криволинейные не были бы равными ей и не вычитались бы одновременно из другой части уравнения, в соответствии с аксиомой: если от равных величин отнять равные части, остатки тоже будут равны. Ибо те величины, которыми, по утверждению аналитиков, следует пренебречь, или же которые следует считать исчезающими, в действительности вычитаются. Поэтому, чтобы вывод был верен, абсолютно необходимо, чтобы конечное пространство CFH было равно остатку приращения, выраженному через

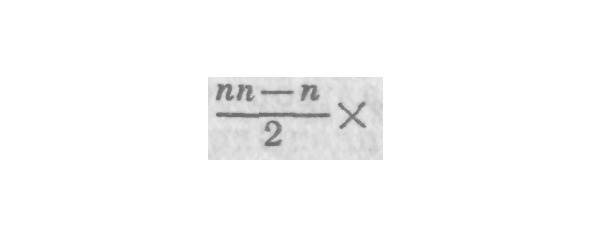
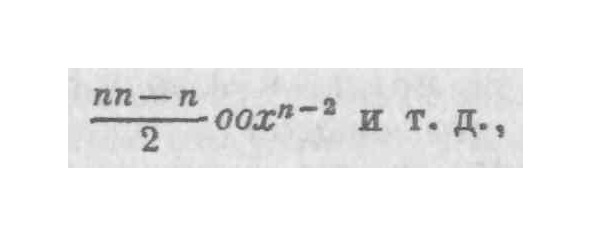
равно, как я сказал бы, конечному остатку конечного приращения.

29. Следовательно, какова бы ни была степень, с какой бы то ни было стороной возникнет алгебраическое выражение, а с другой — геометрическая величина, каждая из которых естественным образом подразделяется на три члена. Алгебраическое, или флюксионное, выражение — на такое, которое не включает ни выражения приращения абсциссы, ни какой-либо её степени; другое, которое включает выражение самого приращения; и третье, включающее выражение степеней приращения. Геометрическая величина, или вся увеличенная площадь, также состоит из трёх частей, или членов, — первый из которых есть данная площадь; второй — прямоугольник под ординатой и приращением абсциссы; и третий — криволинейное пространство. И, сравнивая однородные или соответственные члены с обеих сторон, мы находим, что, как первый член выражения является выражением данной площади, так второй член выражения будет выражать прямоугольник, или второй член геометрической величины, а третий, содержащий степени приращения, будет выражать криволинейное пространство, или третий член геометрической величины. Это указание, быть может, может быть далее распространено и с пользою применено теми, у кого есть досуг и любопытство для подобных предметов. Польза, которую я из него извлекаю, состоит в том, чтобы показать, что анализ справедлив не только для приращений или разностей, но он должен быть справедлив и для конечных величин, сколь бы велики они ни были, как было замечено ранее.

30. Таким образом, по-видимому, в целом можно с уверенностью утверждать, что заключение не может быть верным, если для его достижения какая-либо величина обращается в ничто, или ею пренебрегают, — за исключением того, что либо одна ошибка исправляется другой; либо, во-вторых, на одной и той же стороне уравнения равные величины уничтожаются противоположными знаками, так что величина, которую мы намерены отбросить, сначала аннулируется; или, наконец, что из противоположных сторон вычитаются равные величины. И потому избавляться от величин посредством принятых принципов флюксий или разностей не есть ни хорошая геометрия, ни хорошая логика. Когда приращения исчезают, скорости также исчезают. Говорят, что скорости, или флюксии, являются первоначальными и конечными, как приращения зарождающимися и исчезающими. Возьмите, следовательно, отношение исчезающих величин, оно то же самое, что и отношение флюксий. Оно, следовательно, будет служить всем намерениям столь же хорошо. Для чего же тогда вводятся флюксии? Не для того ли, чтобы избегнуть или, вернее, замаскировать использование бесконечно малых величин? Но у нас нет понятия, посредством которого можно было бы постигать и измерять различные степени скорости, кроме пространства и времени; или, когда времена заданы, кроме одного лишь пространства. У нас даже нет понятия о скорости, отвлечённой от времени и пространства. Когда, следовательно, предполагается, что точка движется в заданные времена, у нас нет понятия о больших или меньших скоростях, или о пропорциях между скоростями, но лишь о более длинных или коротких линиях и о пропорциях между такими линиями, порождёнными в равные части времени.

31. Точка может быть пределом линии: линия может быть пределом поверхности: момент может ограничивать время. Но как мы можем постигать скорость с помощью таких пределов? Она по необходимости подразумевает и время, и пространство и не может быть постигнута без них. И если скорости зарождающихся и исчезающих величин, то есть отвлечённые от времени и пространства, не могут быть постигнуты, как же мы можем постигать и демонстрировать их пропорции; или рассматривать их первоначальные и конечные отношения? Ибо рассматривать пропорцию, или отношение, вещей подразумевает, что такие вещи имеют величину; что эти их величины могут быть измерены и их отношения друг к другу известны. Но, поскольку нет меры скорости, кроме времени и пространства, а пропорция скоростей составляется лишь из прямой пропорции пространств и обратной пропорции времён; не следует ли из этого, что рассуждать об исследовании, получении и рассмотрении пропорций скоростей, исключая время и пространство, — значит рассуждать непонятно?

32. Но вы скажете, что в использовании и применении флюксий люди не перенапрягают свои способности для точного восприятия вышеупомянутых скоростей, приращений, бесконечно малых или каких-либо других подобных идей столь тонкой, утончённой и исчезающей природы. И потому вы, быть может, будете утверждать, что проблемы могут быть решены без этих непостижимых предположений; и что, следовательно, учение о флюксиях, что касается практической части, свободно от всех подобных трудностей. Я отвечаю, что если при использовании или применении этого метода этим трудным и тёмным пунктам не уделяется внимание, они тем не менее предполагаются. Они — основания, на которых современники строят принципы, на которых они продвигаются в решении проблем и открытии теорем. С методом флюксий дело обстоит так же, как и со всеми другими методами, которые предполагают свои соответствующие принципы и на них обоснованы; хотя правила могут применяться на практике людьми, которые ни не уделяют внимания, ни, быть может, не знают принципов. Подобным же образом, следовательно, как моряк может практически применять определённые правила, выведенные из астрономии и геометрии, принципы которых он не понимает; и как любой обычный человек может решать различные численные задачи с помощью общеупотребительных правил и операций арифметики, которые он выполняет и применяет, не зная их оснований: даже так нельзя отрицать, что вы можете применять правила флюксионного метода: вы можете сравнивать и сводить частные случаи к общим формам: вы можете действовать и вычислять и решать проблемы посредством него, не только без фактического внимания к основаниям того метода и принципам, от которых он зависит и из которых выведен, или фактического знания их, но даже без того, чтобы когда-либо рассматривать или постигать их.

33. Но тогда должно помниться, что в таком случае, хотя вы и можете сойти за искусника, вычислителя или аналитика, вы, однако, не можете по справедливости считаться человеком науки и доказательства. И ни один человек, в силу своей осведомлённости в таких тёмных аналитических приёмах, не должен воображать, что его рациональные способности более развиты, чем те способности других людей, которые упражнялись иным образом и на иных предметах; тем более возводить себя в судьи и оракула относительно вопросов, которые не имеют никакой связи с или зависимости от тех видов, символов или знаков, в управлении которыми он столь осведомлён и искусен. Как вы, будучи искусным вычислителем или аналитиком, не можете, поэтому, считаться искусным в анатомии; или, наоборот, как человек, который может искусно препарировать, может, тем не менее, быть несведущим в вашем искусстве вычисления: даже так вы оба, несмотря на ваше особое умение в ваших соответствующих искусствах, можете быть в равной степени неквалифицированны, чтобы выносить решения по вопросам логики, или метафизики, или этики, или религии. И это было бы верно, даже допуская, что вы понимаете ваши собственные принципы и можете их демонстрировать.

34. Если скажут, что флюксии можно объяснить или выразить при помощи отрезков прямых, им пропорциональных; что поскольку эти отрезки можно отчетливо воспринять, познать и на них можно основываться, то их можно подставить вместо флюксий, а их отношения, или пропорции, рассматривать как пропорции флюксий; что благодаря такому приему теория флюксий становится ясной и полезной, — на это я отвечу: для того чтобы получить эти конечные прямые, пропорциональные флюксиям, необходимо предпринять определенные неясные шаги, которые представить себе невозможно; и пусть эти конечные прямые сами по себе воспринимаются очень ясно, тем не менее необходимо признать, что ход ваших рассуждений не ясен, а ваш метод не научен. Например, положим, что АВ — абсцисса, ВС — ордината, a VCH — касательная к кривой АС; Вb или СЕ — приращение абсциссы, Еc — приращение ординаты, которая, будучи продолжена, пересекает VH в точке Т, а Сс — приращение кривой. Если прямую Сс продолжить до К, образуется три небольших треугольника — прямолинейный СЕс, треугольник со смешанными прямо- и криволинейными сторонами СЕс и прямолинейный треугольник СЕТ. Очевидно, что эти три треугольника отличаются друг от друга: прямолинейный треугольпик СЕс меньше треугольника СЕс со смешанными прямо- и криволинейными сторонами, которые представляют собой три вышеупомянутых приращения; в свою очередь последний меньше треугольника СЕТ. Допустим, что ордината bc перемещается на место ВС, так что точка с совпадает с точкой С, а прямая СК и, следовательно, кривая Сс совпадает с касательной СН. В таком случае треугольник СЕс со смешанными криво- и прямолинейными сторонами, приближающийся к исчезновению, в своей последней форме будет подобен треугольнику СЕТ, а его приближающиеся к нулю стороны СЕ, Еc, Сс будут про-

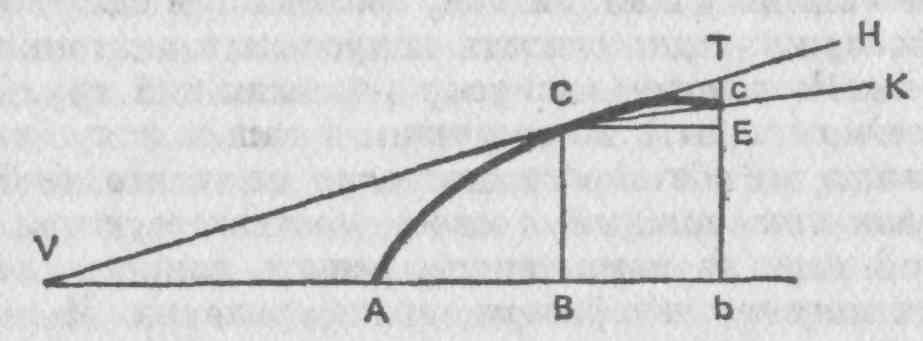
порциональны СЕ, ЕТ, СТ — сторонам треугольника СЕТ. и в силу этого делается вывод, что флюксии отрезков АВ, ВС и АС, входящие в последнее отношение их исчезающих приращений, пропорциональны сторонам треугольника СЕТ, или, что одно и то же, сторонам треугольника VBC, ему подобного *. Великий автор данного анализа специально замечает и особенно настаивает на том, что точки С и с не должны отстоять друг от друга ни на какой самый малейший интервал, но что для нахождения окончательных пропорций отрезков СЕ, Еc и Сс (т. е. отношения флюксий или скоростей), выраженных конечными сторонами треугольника VBC, точки Сиc должны точно совпадать друг с другом, т. е. быть одной и той же точкой. Следовательно, точка рассматривается как треугольник или же допускается, что в точке образуется треугольник. Понять это представляется совершенно невозможным. Однако находятся люди, которые недовольно морщатся, сталкиваясь с какими-либо непостижимыми тайнами у всех других, в то же время не видят ничего трудного в таких же непостижимостях у себя самих, которые подавятся комаром, но проглотят верблюда.

35. Я не знаю, стоит ли особо отметить, что, может быть, некоторые надеются оперировать символами и допущениями, дабы избежать применения флюксий, [механических] моментов и бесконечно малых величин, действуя с помощью следующею метода. Пусть х — абсцисса кривой, а z — еще одна абсцисса той же самой кривой. Положим так/не, что соответствующие площади равны ххх и zzz, что (z — х) — приращение абсциссы, a (zzz — — ххх) — приращение площади, не обращая внимания на то, насколько велики или малы пи приращения. Разделим теперь (zzz — ххх) на (z — х) и получим частое (zz+zx+-хх); если допустим, что z х, тогда это же самое частное будет равно 3 хх, что в каком случае и будет значением ординаты; таким образом, последнее можно найти независимо от флюксий и бесконечно малых величин. Но здесь прямая подтасовка: ибо, во-первых, мы полагаем, что абсциссы x и z не равны между собой, и без такого предположения нельзя было бы сделать ни одного шага; а во-вторых, мы допускаем, что те же абсциссы равны, а это явная непоследовательность, и это равнозначно тому, что уже рассматривалось ранее *. И, действительно, есть основания опасаться, что все попытки поставить эту трудную для понимания и точную геометрию на верный фундамент и избежать теории скоростей, механических моментов и т. п. окажутся бесплодными до тех пор, пока предмет и цель геометрии не будут поняты лучше, чем, как представляется, понимали до сих пор. Великий автор метода флюксий чувствовал эту трудность и поэтому пустился во все эти изящные (nice) абстракции и геометрическую метафизику, без которых, как он понимал, ничего нельзя сделать на основе общепринятых принципов, и читатель сам может судить, что у него из всею этого получилось в смысле доказательства. Правда, надо признать, что он использовал флюксии, подобно лесам при строительстве здания, которые нужно было отбросить в сторону или от которых нужно было избавиться, когда уже было найдено, что конечные линии пропорциональны эгим флюксиям. Но ведь эти конечные показатели определяются с помощью флюксий. Поэтому все, что получается с помощью таких показателей и пропорций, необходимо отнести за счет флюксий, которые, следовательно, предварительно надо понять. А что такое эти флюксии? Скорости исчезающих приращений. А что такое эти самые исчезающие приращения? Они не есть ни конечные величины, ни величины бесконечно малые, но они и не нули. Разве мы не имеем права назвать их призраками (ghosts) исчезнувших величин?

36. Люди слишком часто внушают самим себе и другим, будто они представили себе и поняли явления, выраженные при помощи знаков, тогда как в действительности они не имеют о них ни малейшего представления, а понимают только сами знаки. и есть основания опасаться, что именно так обстоит дело в данном случае. Скорости исчезающих или же зарождающихся величин могут выражаться

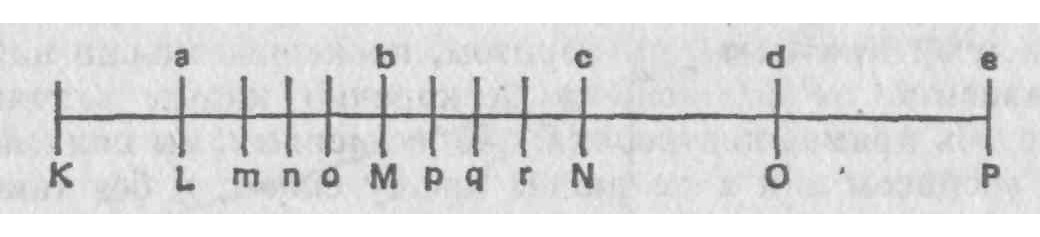
как конечными отрезками определенной величины, так и алгебраическими символами, но я подозреваю, что многие, кто, вероятно, никогда не рассматривал этого положения и считает его само собой разумеющимся, при тщательном его изучении обнаружили бы, что не в состоянии составить какое-либо представление или какое-либо понятие об этих скоростях, вне выражения их такими конечными величинами и знаками.

Положим, прямая КР образуется при движении с постоянным ускорением какой-либо точки и за равные отрезки времени образуются неравные отрезки прямой KL, LM, MN, NO и т. д. [16] Положим также, что а, b, с, d, e и т. д. обозначают скорости точки, образующей прямую, в разные периоды частей или приращений, получаемых таким образом. Легко заметить, что каждое из этих приращений пропорционально сумме скоростей, которыми оно образуется; что, следовательно, полученные несколько сумм скоростей, образованных за равные отрезки времени, могут быть изображены соответственно отрезками KL, LM, MN и т. д., образованными за те же промежутки времени. В равной мере легко сказать, что последняя скорость, образованная за первую частицу времени, может быть выражена символом а, последняя за вторую — b, последняя, образованная за третью, — с и т. д.; что а — скорость LM в statu nascendi, а b, с, d, е и т. д. — скорости приращений MN, NO, OP и т. д. в соответствующих состояниях их зарождения. Можно пойти дальше и считать сами эти скорости текущими (flowing) или возрастающими величинами, взяв скорости скоростей и скорости скоростей скоростей, т. е. первые, вторые, третьи и т. д. скорости ad infinitum; этот последовательный ряд скоростей может быть выражен следующим образом:

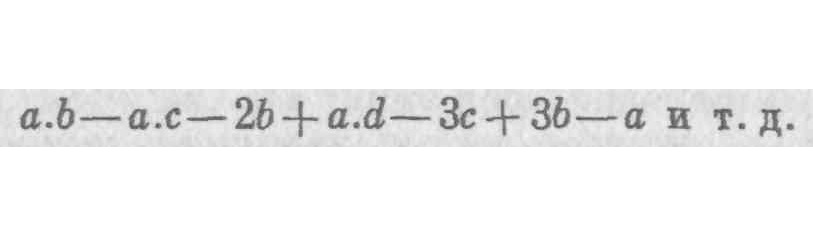
Можно назвать их первыми, вторыми, третьими, четвер­тыми флюксиями. А с целью более удобного выражения можно обозначить переменную текущую прямую KL, KM, KN и т. д. буквой х, а первые флюксиивторые — третьи — и т. д. ad infinitum.

37. Нет ничего легче, как указать названия, символы или выражения для этих флюксий, не трудно также высчитывать и производить действия с помощью таких знаков. Но гораздо более трудным оказывается опустить эти знаки и тем не менее сохранить в наших умах то, что, по нашему предположению, они означают. Рассматривать показатели, будь то геометрические, алгебраические или флюксионные, не трудно. Но, например, составить точное представление о скорости третьего порядка, самой по себе и при помощи ее самой, — Hoc opus, hic labor [17]. Нелегко также составить ясное и четкое представление вообще о любой скорости вне связи со всякой протяженностью во времени и пространстве и в отрыве от нее, а также от всех обозначений, знаков и символов; если же мне позволят судить о других по себе, это просто невозможно. Мне представляется очевидным, что измерения и знаки абсолютно необходимы для того, чтобы понять скорости и рассуждать о них, и что, следовательно, когда мы хотим представить себе скорости просто и сами по себе, нас вводят в заблуждение пустые абстракции.

38. Может быть, некоторые люди вообразят, что было бы легче понимать флюксии, если предположить, что они являются скоростями, с помощью которых образуются бесконечно малые приращения, так что первые флюксии будут скоростями первых приращений, вторые флюксии будут скоростями вторых приращений, третьи флюксии — скоростями третьих приращений и т. д. ad infinitum. Но, не говоря уже о непреодолимой трудности признания или понимания бесконечно малых величин и бесконечно малых взятых от бесконечно малых величин и т. д., ясно, что такое понятие о флюксиях не будет соответствовать точке зрения великого автора, который полагал, что нельзя пренебрегать ни наималейшей величиной, что, в силу этого, теория бесконечно малых приращений не может быть допущена в геометрии, и который совершенно очевидно ввел использование скоростей или флюксий с целью исключить бесконечно малые или же обойтись без них.

39. Позможио, некоторым другим покажется, что у нас будет более правильное представление о флюксиях, если мы допустим конечные неравные изохронные приращения KL, LM, АГХ и т. д. и будем считать и их, и их приращения — в statu nasendli, а также и зарождающиеся приращения тех приращений и т. д., полагая, что первые зарождающиеся приращения пропорциональны первым флюксиям или скоростям, зарождающиеся приращения этих приращений пропорциональны вторым флюксиям, третьи зарождающиеся приращения пропорциональны третьим флюксиям и т. д. А так как первые флюксии являются скоростями первых зарождающихся приращений, то вторые флюксии можно скорее считать скоростями вторых зарождающихся приращений, а не скоростями скоростей. Может показаться, что благодаря такому приему аналогия флюксий может быть лучше сохранена, а само понятие сделано более вразумительным.

40. И, действительно, должно бы казаться, что для получения второй или третьей флюксии уравнения данные флюксии рассматривались скорее не как скорости, а как приращения. Однако представляется, что рассмотрение их иногда в одном смысле, а иногда в другом, то в их собственном виде, то в виде их показателей, в значительной мере вызвало ту путаницу и неясность, которую мы обнаруживаем в теории флюксий. Поэтому может показаться, что это понятие еще можно как-то улучшить и что вместо флюксий флюксий или флюксий флюксий флюксий и вместо вторых, третьих, четвертых и т. д. флюксий данной величины было бы более последовательно и менее вызывало бы возражения, если говорить: флюксия первого зарождающегося приращения, т. е. вторая флюксия; флюксия второго зарождающегося приращения, т. е. третья флюксия; флюксия третьего зарождающегося приращения, т. е. четвертая флюксия, причем имеется в виду, что каждая из этих флюксий соответственно пропорциональна зарождающемуся началу приращения, следующего за тем, флюксией которого она является.

41. Для более четкого понимания всего этого можно принять во внимание, что если конечное приращение LM * разделить на изохронные части Lm, mn, по, оМ, а приращение MN — на части Мр, pq, qr, rN, изохронные предыдущим, то, так как приращения LM, MN пропорциональны суммам их образующих скоростей, соответствующие им части Lm, Мр также пропорциональны соответствующим увеличенным скоростям, которые их образуют. А так как скорость, с которой образуется Мр, превышает ту, с которой была образована Lm, то и часть Мр больше части Lm. и вообще, раз изохронные скорости, образующие отрезки MN, превышают изохронные скорости, образующие отрезки LM, то и отрезки первой больше соответствующих им отрезков второй. и это будет справедливо, какими бы малыми ни были упомянутые отрезки. Следовательно, если LM и MN обе взяты в их зарождающемся состоянии, MN будет больше LM, притом на величину, пропорциональную превышению скорости b над скоростью а. Отсюда мы можем видеть, что в конечном итоге это последнее объяснение флюксий приводит к тому же, что и первое **.

42. Но независимо от всего сказанного надо все же признать, что конечные части Lm или Мр, даже если их взять совсем малыми, пропорциональны не скоростям а и Ь, а каждая — ряду скоростей, меняющихся каждое мгновение, или, что одно и то же, всевозрастающей скорости, с помощью которой эта часть образуется в течение определенной мельчайшей частицы времени; что только зарождающиеся начала или исчезающие окончания конечных величин, которые образуются в мгновение или в течение бесконечно малых отрезков времени, пропорциональны данным скоростям; что, следовательно, для того чтобы представить себе первые флюксии, мы должны представить себе время, разделенное на мгновения, приращения, образованные в течение этих мгновений, и скорости, пропорциональные этим приращениям; для того чтобы представить себе вторые и третьи флюксии, мы должны допустить, что зарождающиеся начала или мгновенные приращения сами имеют также другие мгновенные приращения, пропорциональные соответствующим образующим их скоростям; что скорости этих вторых мгновенных приращений являются вторыми флюксиями, а скорости их зарождающихся мгновенных приращений — третьими флюксиями. и т. д. ad infinitum.

43. Вычтя приращение, образованное за первое мгновение, из приращения, образованного в течение второго мгновения, мы получим приращение приращения. А вычтя скорость, образующую отрезок прямой в первое мгновение, из скорости, образующей отрезок прямой во второе мгновение, получим флюксию флюксии. Подобным же образом, вычтя разность скоростей, образующих отрезок прямой в первые два мгновения, из превышения скорости в третье мгновение над скоростью во второе мгновение, получим третью флюксию. И, действуя аналогичным образом, мы можем перейти к четвертой, пятой, шестой и т. д. флюксиям. А если мы обозначим скорости первого, второго, третьего, четвертого мгновений а, b, с, d, то ряд флюксий будет такой же, какой приводился выше: а.b — а.с — 2b+a.d — 3с+3b — a, ad infinitum, т. е. ad infinitum.

44. Таким образом, флюксии можно рассматривать в разном свете и в различных видах, но, представляется, все они в равной мере трудны для понимания. И, действительно, раз невозможно представить себе скорость без пространства и времени, без конечного значения длины и продолжительности *, то понять даже первые флюксии, должно быть, выше человеческих возможностей. А если первые непостижимы, то что же мы должны сказать в отношении вторых, третьих и т. д. флюксий? Возможно, тот, кто в состоянии представить себе начало начала или конец конца несколько раньше первого или позже второго, будет достаточно проницателен, чтобы понять эти вещи. Но я полагаю, что большинство людей считает невозможным понять их в каком бы то ни было смысле.

45. Можно было бы подумать, что люди должны бы выражаться как можно более точно о таком тонком предмете. и тем пе менее, как было замечено раньше, мы можем часто наблюдать, что показатели флюксий или символы, представляющие флюксии, ошибочно принимаются за сами флюксии. Разве не так обстоит дело в том случае, когда сразу же после того, как флюксии флюент объявлены скоростями их возрастания, а вторые флюксии — изменениями первых флюксий или скоростей, нам говорят, что * представляет собой ряд величин, из которых каждая последующая величина является флюксией предыдущей, а каждая предыдущая является флюентой (fluent), в отношении которой следующая за ней является ее флюксией?

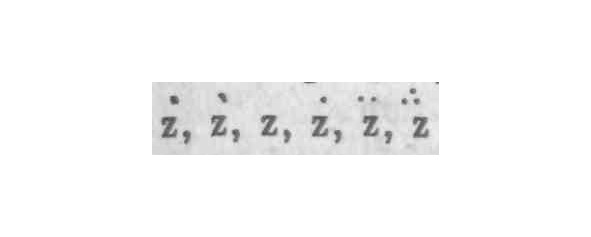
46. Можно легко себе представить различные ряды величин и выражений, геометрических и алгебраических, в виде линий, поверхностей, образов, которые можно продолжать без конца или предела. Но не так-то легко представить себе ряд либо просто скоростей, либо просто зарождающихся приращений, взятых отдельно от них и им соответствующих. Может быть, некоторые могли бы прийти к той мысли, что автор имел в виду ряд ординат, в котором каждая ордината была флюксией предыдущей и флюентой [интегралом] (fluent) последующей, т. е. что флюксия одной ординаты была сама ординатой другой кривой и что флюксия этой последней ординаты была ординатой еще одной кривой и т. д. ad infinitum. Но кто в состоянии представить себе, как флюксия (будь то скорость или зарождающееся приращение) ординаты может быть сама ординатой? Или, более того, — что каждая предыдущая величина или интеграл относится к своей последующей или флюксии как площадь криволинейной фигуры к своей ординате, в соответствии с чем автор замечает, что каждая предыдущая величина в таком ряду является площадью криволинейной фигуры, абсциссой которой является z, а ординатой — следующая за ней величина?

47. В целом представляется, что скорости исключены, и вместо них введены площади и ординаты. Но как бы целесообразны ни были такие аналогии или такие выражения для облегчения современных методов квадратур, мы всё же не обнаружим, что они проливают какой-либо свет на изначальную подлинную природу флюксий; или что они позволяют нам сформировать на их основе верные представления о флюксиях, рассматриваемых самих по себе. Во всём этом общее конечное устремление автора вполне ясно, но его принципы туманны. Однако, возможно, его последователи не слишком глубоко анализируют и обсуждают теории великого автора. Как уже отмечалось, они скорее стремятся использовать его идеи на практике, чем понять их суть. Их больше интересует применение правил и форм, чем проникновение в принципы и идеи автора. Тем не менее, несомненно, что для того, чтобы следовать за ним в его квадратурах, они должны находить флюэнты по флюксиям; а для этого они должны уметь находить флюксии по флюэнтам; а для того, чтобы находить флюксии, они должны сначала знать, что такое флюксии. В противном случае они действуют без ясности и без научного понимания. Таким образом, прямой метод предшествует обратному, и знание принципов предполагается в обоих случаях. Но что касается оперирования согласно правилам и с помощью общих форм, первоначальные принципы и причины которых не поняты, то это следует считать сугубо техническим умением. Поэтому, какими бы глубокими и метафизическими ни были принципы, они должны быть изучены всяким, кто желает постигнуть учение о флюксиях. И ни один геометр не вправе применять правила великого автора, не поразмыслив предварительно над его метафизическими идеями, из которых они были выведены. Эти [идеи], сколь бы ни были они необходимы для обретения научного знания — которое никогда не может быть достигнуто без точного, ясного и строгого понимания принципов — тем не менее, некоторыми беззаботно пропускаются; в то время как внимание задерживается и сосредотачивается лишь на выражениях, с которыми обращаются с великим искусством и ухищрениями, чтобы из них получить другие выражения методами подозрительными и непрямыми (мягко говоря), если рассматривать их сами по себе, как бы они ни были рекомендованы Индукцией и Авторитетом — двумя мотивами, которые признаются достаточными для порождения разумной веры и моральной убеждённости, но не более того.

48. Вы, возможно, надеетесь уклониться от силы всего сказанного и прикрыть ложные принципы и непоследовательные рассуждения общим предлогом, что эти возражения и замечания являются Метафизическими. Но это тщетная уловка. Что касается простого смысла и истинности того, что выдвинуто в предыдущих замечаниях, я апеллирую к пониманию всякого непредвзятого разумного читателя. К нему же я апеллирую, являются ли отмеченные моменты не самой непостижимой метафизикой. И метафизикой не моей, а вашей собственной. Я не хочу, чтобы было понято, будто я делаю вывод, что ваши идеи ложны или тщетны потому, что они метафизичны. Ничто не является истинным или ложным по этой причине. Мало помогает то, называется ли некий пункт метафизическим или нет. Вопрос в том, ясен он или туманен, правилен или ошибочен, хорошо или плохо выведен?

49. Хотя мгновенные приращения, нарождающиеся и исчезающие величины, флюксии и бесконечно малые всех степеней суть на деле столь призрачные сущности, столь трудные для отчётливого представления или постижения, что (мягко говоря) они не могут быть допущены в качестве принципов или объектов ясной и строгой науки; и хотя эта туманность и непостижимость вашей метафизики сама по себе была бы достаточна, чтобы ослабить ваши притязания на очевидность; тем не менее, если я не ошибаюсь, было далее показано, что ваши умозаключения не более справедливы, чем ваши концепции ясны, и что ваша логика так же уязвима для критики, как и ваша метафизика. Таким образом, по всей видимости, в целом ваши выводы не достигаются путём правильного рассуждения от ясных принципов: следовательно, деятельность современных аналитиков, сколь бы полезна она ни была в математических вычислениях и построениях, не приучает и не способствует тому, чтобы ум ясно постигал и справедливо заключал; и, следовательно, вы не имеете права в силу таких привычек поучать вне вашей собственной сферы, за пределами которой ваше суждение должно значить не более, чем суждение других людей [1].

___________

[1] Неэффективность современного математического анализа как упражнения для духовной жизни человека и, соответственно, односторонность культуры, которую он обеспечивает, является общим местом в педагогической и философской критике. Математики-«узкие специалисты» доводят до состояния атрофии способности, которые заняты конечными проблемами конкретной реальности. Беркли осуждает одновременно и метафизическую непоследовательность, и математическую необоснованность некоторых математических вольнодумцев.

— — — — —

50. Уже долгое время я подозревал, что эти современные аналитические методы не являются научными, и дал некоторые намёки на это публике около двадцати пяти лет тому назад. С тех пор я был отвлечён другими занятиями и полагал, что могу употребить себя лучше, чем на выведение и собирание воедино моих мыслей по столь тонкому предмету. И хотя в последнее время от меня потребовали подтвердить мои предположения; тем не менее, поскольку лицо, сделавшее этот вызов, не кажется достаточно зрело мыслящим, чтобы понять ни ту метафизику, которую оно хочет опровергнуть, ни ту математику, которую оно желает отстаивать, я должен был бы избавить себя от труда писать для его вразумления. И я не стал бы теперь утруждать ни вас, ни себя этим обращением после столь долгого перерыва в этих занятиях, если бы не желание предотвратить, насколько это в моих силах, ваше навязывание ложных идей самим себе и другим в вопросах гораздо более высокого значения и важности. И для того, чтобы вы могли яснее постичь силу и замысел предыдущих замечаний и продолжить их далее в ваших собственных размышлениях, я присовокуплю следующие Вопросы: —

Вопрос 1. Не являются ли объектом геометрии пропорции определяемых протяжений? И есть ли какая-либо необходимость рассматривать величины либо бесконечно большие, либо бесконечно малые?

Вопрос 2. Не заключается ли цель геометрии в измерении определяемых конечных протяжений? И не этот ли практический взгляд первоначально побудил людей к изучению геометрии?

Вопрос 3. Не породило ли смешение объекта и цели геометрии излишние трудности и ошибочные направления исследований в этой науке?

Вопрос 4. Можно ли правомерно сказать, что люди действуют научным методом, не отчётливо понимая объект, с которым они имеют дело, поставленную цель и метод, которым она достигается?

Вопрос 5. Не достаточно ли того, что всякое определяемое число частей может содержаться в некоторой определяемой величине? И не является ли излишним, равно как и абсурдным, предположение, что конечное протяжение бесконечно делимо?

__________________

[1 См. «Принципы человеческого знания», разделы 123—134, с которыми, равно как и с рассуждениями в том же трактате и в «De Motu» против абсолютного пространства, времени и движения и об устранении бесконечности, можно сравнить следующие Вопросы; также «Опыт о зрении», разделы 121—126; 149—160. Самые ранние публикации Беркли (в 1707 году) являются математическими.]

— — — — —

Вопрос 6. Не следует ли рассматривать диаграммы в геометрическом доказательстве как знаки всех возможных конечных фигур, всех чувственно воспринимаемых и вообразимых протяжений или величин того же рода?

Вопрос 7. Возможно ли освободить геометрию от непреодолимых трудностей и абсурдностей, до тех пор пока её истинным объектом предполагается либо абстрактная общая идея протяжения, либо абсолютное внешнее протяжение?

Вопрос 8. Не являются ли понятия абсолютного времени, абсолютного места и абсолютного движения наиболее отвлечённо метафизическими? Возможно ли для нас измерять, вычислять или познавать их?

Вопрос 9. Не вступают ли математики в споры и парадоксы относительно того, что они ни постигают, ни могут постичь? И не является ли учение [о силах] достаточным тому доказательством [1]?

Вопрос 10. Не достаточно ли в геометрии рассматривать определяемые конечные величины, не заботясь о бесконечности? И не правильнее ли было бы измерять большие многоугольники с конечными сторонами вместо кривых, чем предполагать, что кривые суть многоугольники с бесконечно малыми сторонами — предположение ни истинное, ни постижимое?

Вопрос 11. Не относятся ли многие положения, на которые не readily дают согласие, к числу тем не менее истинных? И не могут ли таковыми быть положения двух следующих вопросов?

Вопрос 12. Возможно ли, чтобы у нас была идея или понятие о протяжении прежде движения? Или, если бы человек никогда не воспринимал движения, узнал бы или представил бы он ever, что одна вещь удалена от другой [2]?

_________

[1. [См. латинский трактат «De Motu», опубликованный в Лондоне в 1721 году.] — Автор.]

[2 Сравните «Опыт о зрении» с этими двумя содержательными Вопросами, касающимися отношения данного в чувственном восприятии движения к тройному протяжению.]

— — — — — —

Вопрос 13. Имеет ли геометрическая величина сосуществующие части? И не находится ли всякая величина в потоке, так же как время и движение?

Вопрос 14. Может ли протяжение предполагаться атрибутом Существа неизменного и вечного?

Вопрос 15. Не показало бы это известного фанатизма со стороны математиков, если бы они отказались исследовать принципы и распутывать методы, используемые в математике?

Вопрос 16. Не бытуют ли среди аналитиков некоторые максимы, которые шокируют здравый смысл? И не относится ли к их числу обычное допущение, что конечная величина, делённая на ничто, бесконечна?

Вопрос 17. Не является ли главной причиной предположения о бесконечной делимости конечного протяжения, и всех последующих трудностей и абсурдностей, рассмотрение геометрических диаграмм абсолютно или самих по себе, а не как представителей всех определяемых величин или фигур того же рода?

Вопрос 18. Не следует ли из того, что геометрические предложения являются общими, и линии на диаграммах, следовательно, суть общие заместители или представители, что мы не можем ограничивать или рассматривать число частей, на которые делимы такие частные линии?

Вопрос 19. Когда говорится или подразумевается, что некая определённая линия, изображённая на бумаге, содержит более любого определяемого числа частей, не должно ли в действительности понимать под этим более того, что она является знаком, безразлично представляющим все конечные линии, сколь бы велики они ни были. В которой относительной способности она содержит, т.е. обозначает более любого определяемого числа частей? И не является ли в целом абсурдным предположение, что конечная линия, рассматриваемая сама по себе или в своей собственной положительной природе, должна содержать бесконечное число частей?

Вопрос 20. Не предполагают ли и не подразумевают ли все аргументы в пользу бесконечной делимости конечного протяжения, что объектом геометрии являются либо общие абстрактные идеи, либо абсолютное внешнее протяжение? И, следовательно, не прекращаются ли и не исчезают ли такие аргументы вместе с этими предположениями?

Вопрос 21. Не стала ли предполагаемая бесконечная делимость конечного протяжения западнёй для математиков и тернием в боку их? И не являются ли величина, бесконечно уменьшенная, и величина, бесконечно малая, одним и тем же?

Вопрос 22. Необходимо ли рассматривать скорости нарождающихся или исчезающих величин, или моменты, или бесконечно малые? И не является ли введение столь непостижимых вещей упрёком математике?

Вопрос 23. Могут ли противоречия быть истинами? Допустимы ли точки, неприемлемые и абсурдные, в каких-либо предметах или в какой-либо науке? И должно ли позволять использование бесконечностей в качестве достаточного предлога и оправдания для допущения таких точек в геометрии?

Вопрос 24. Не говорится ли правомерно, что величина известна, когда мы знаем её пропорцию к данным величинам? И может ли эта пропорция быть известна иначе, как через выражения или показатели, будь то геометрические, алгебраические или арифметические? И могут ли выражения в линиях или в виде [алгебраических] символов быть полезными далее лишь поскольку они сводимы к числам?

Вопрос 25. Не является ли отыскание правильных выражений или обозначений количества самой общей характеристикой и направленностью математики? А арифметические операции — тем, что ограничивает и определяет их употребление?

Вопрос 26. Достаточно ли математики рассмотрели аналогию и употребление знаков? И насколько специфическая ограниченная природа вещей соответствует им?

Вопрос 27. Не потому ли, что, формулируя общий случай чистой алгебры, мы в полной мере вольны позволить знаку обозначать либо положительную, либо отрицательную величину, либо ничто вообще, мы можем, следовательно, в геометрическом случае, ограниченном гипотезами и рассуждениями о частных свойствах и отношениях фигур, требовать той же вольности?

Вопрос 28. Не является ли подмена гипотезы, или (как мы можем её назвать) fallacia suppositionis, софизмом, который повсеместно заражает современные рассуждения, как в механической философии, так и в запутанной и утончённой геометрии?

Вопрос 29. Можем ли мы сформировать идею или понятие скорости, отличное от и исключающее её меру, подобно тому как мы можем [сформировать идею] тепла, отличную от и исключающую градусы на термометре, которым оно измеряется? И не предполагается ли это в рассуждениях современных аналитиков?

Вопрос 30. Можно ли представить себе движение в точке пространства? И если движение нельзя, то можно ли представить себе скорость? А если нет, то можно ли представить себе первую или последнюю скорость в пределе лишь, будь то начальном или конечном, описанного пространства?

Вопрос 31. Где нет приращений, может ли быть какое-либо отношение приращений? Могут ли ничто рассматриваться как пропорциональные реальным величинам? Или не является ли разговор об их пропорциях бессмыслицей? Также, в каком смысле мы должны понимать пропорцию поверхности к линии, площади к ординате? И могут ли [алгебраические] символы или числа, хотя и правильно выражающие величины, которые не являются однородными, тем не менее, считаться выражающими их пропорцию друг к другу?

Вопрос 32. Если все определяемые круги могут быть квадратированы, не является ли круг, для всех намерений и целей, квадратированным так же, как и парабола? Или может ли параболическая площадь фактически быть измерена более точно, чем круговая?

Вопрос 33. Не было ли бы правильнее честно приближаться [к решению], чем стремиться к точности посредством софизмов?

Вопрос 34. Не было бы более приличествующим действовать путём проб и индукций, чем притворяться, что доказываешь ложными принципами?

Вопрос 35. Нет ли пути к достижению истины, хотя принципы и не научны, и рассуждение не справедливо? И следует ли называть такой путь сноровкой или наукой?

Вопрос 36. Может ли быть наука о заключении, где нет науки о принципах? И может ли человек иметь науку о принципах, не понимая их? И, следовательно, действуют ли математики нынешнего века как люди науки, прилагая столь больше усилий к применению своих принципов, чем к их пониманию?

Вопрос 37. Не может ли величайший гений, борющийся с ложными принципами, потерпеть поражение? И могут ли быть получены точные квадратуры без новых постулатов или допущений? И если нет, не следует ли предпочесть те из них, которые понятны и последовательны, противоположным? См. разделы 28 и 29.

Вопрос 38. Являются ли утомительные вычисления в алгебре и методе флюксий наиболее вероятным методом для совершенствования ума? И не приводит ли привычка людей рассуждать исключительно о математических знаках и фигурах к тому, что они оказываются в затруднении, как рассуждать без них?

Вопрос 39. Означает ли та самая лёгкость, которую аналитики приобретают в постановке задачи или в нахождении подходящих выражений для математических величин, необходимо пропорциональную способность в постижении и выражении других предметов?

Вопрос 40. Не является ли общим случаем или правилом, что один и тот же коэффициент, деля равные произведения, даёт равные частные? И всё же может ли такой коэффициент быть истолкован как 0 или ничто? Или согласится ли кто-либо с тем, что если уравнение 2 x 0 = 5 x 0 разделить на 0, то частные по обе стороны равны? Не может ли поэтому случай быть общим по отношению ко всем величинам и всё же не распространяться на ничто, или не включать случай ничто? И не ввело ли людей в ложные рассуждения подведение ничто под понятие величины?

Вопрос 41. Не могут ли люди в самых общих рассуждениях о равенствах и пропорциях доказывать так же, как и в геометрии? Не обязаны ли они в таких доказательствах к той же строгости рассуждений, что и в геометрии? И не выводятся ли такие их рассуждения из тех же аксиом, что и в геометрии? Не является ли поэтому алгебра столь же подлинной наукой, как и геометрия?

Вопрос 42. Не могут ли люди рассуждать в [алгебраических] символах так же, как и в словах? Не действуют ли в обоих случаях одни и те же правила логики? И не имеем ли мы права ожидать и требовать той же очевидности в обоих случаях?

Вопрос 43. Может ли алгебраист, флюксионист, геометр или демонстратор любого рода рассчитывать на снисхождение за туманные принципы или некорректные рассуждения? И может ли алгебраический знак или символ в конце процесса быть истолкован в смысле, который не мог быть подставлен вместо него в начале? Или может ли какое-либо частное допущение подпадать под общий случай, если оно не согласуется с его рассуждением?

Вопрос 44. Не заключается ли разница между простым вычислителем и человеком науки в том, что один вычисляет на основе ясно понятых принципов и по правилам, очевидно доказанным, тогда как другой — нет?

Вопрос 45. Хотя геометрия и является наукой, и алгебра признаётся наукой, и аналитический метод — превосходнейшим методом в его применении, не могли ли люди, тем не менее, при применении анализа к геометрии допустить ложные принципы и ошибочные методы рассуждения?

Вопрос 46. Хотя алгебраические рассуждения признаются сколь угодно справедливыми, когда они ограничены знаками или символами как общими представителями величин, не можете ли вы, тем не менее, впасть в ошибку, если, ограничивая их обозначать частные вещи, вы не ограничиваете себя рассуждениями, последовательными с природой таких частных вещей? И не должна ли такая ошибка вменяться чистой алгебре?

Вопрос 47. Не кажется ли, что взгляд современных математиков скорее направлен на достижение выражения посредством ухищрений, чем на достижение науки посредством доказательства?

Вопрос 48. Не может ли существовать здравой метафизики так же, как и нездоровой? Здравой логики так же, как и нездоровой? И не может ли современный аналитический метод быть отнесён к одной из этих категорий, и к какой именно?

Вопрос 49. Не существует ли действительно philosophia prima, некая трансцендентальная наука, превосходящая математику и более обширная, чем она, которую нашим современным аналитикам следовало бы скорее изучить, чем презирать [1]?

[1 Так Бэкон: «Поскольку распределения и разделения знания не подобны нескольким линиям, сходящимся в одном угле и, таким образом, соприкасающимся лишь в точке; но подобны ветвям дерева, которые сходятся в стволе, имеющем протяжённость и цельность до того, как он раздробится и разветвится на сучья и ветви; поэтому благо, прежде чем мы приступим к упомянутому распределению, воздвигнуть и учредить Одну Универсальную Науку, под именем Philosophia Prima, Первичной или Сводной Философии, как главный и общий путь, прежде чем мы подойдём к месту, где пути расходятся и разделяются: которую науку, должен ли я считать её недостающей или нет, я остаюсь в сомнении.» («О достоинстве и приумножении наук», Книга II.)]

Вопрос 50. Не было ли с момента возрождения математической учёности постоянных споров и противоречий среди математиков? И не умаляет ли это очевидность их методов?

Вопрос 51. Не может ли что-либо, кроме метафизики и логики, открыть глаза математикам и вывести их из затруднений?

Вопрос 52. Может ли величина на принятых принципах путём какого-либо деления или подразделения, сколь бы далеко оно ни проводилось, быть сведена к ничто?

Вопрос 53. Если целью геометрии является практика, и эта практика есть измерение, и мы измеряем лишь определяемые протяжения, не следует ли из этого, что неограниченные приближения полностью отвечают намерению геометрии?

Вопрос 54. Не могут ли те же самые вещи, которые теперь делаются с помощью бесконечностей, быть сделаны с помощью конечных величин? И не явилось бы это великим облегчением для воображения и понимания математиков?

Вопрос 55. Не могут ли те филоматематические врачи, анатомы и деятели в области животной экономии, которые принимают учение о флюксиях с слепой верой, с хорошей миной оскорблять других людей за веру в то, чего они не постигают [1]?

Вопрос 56. Не поглотила ли корпускулярная, экспериментальная и математическая философия, столь усердно культивировавшаяся в прошлом веке, чрезмерно внимание людей; не могла ли она полезно употребить некоторую его часть?

Вопрос 57. Не были ли умы спекулятивных людей подавлены вследствие этой и других совпадающих причин, что привело к принижению и отупению высших способностей? И не можем ли мы отсюда объяснить ту преобладающую узость и фанатизм среди многих, кто сходит за людей науки, их неспособность к вещам моральным, интеллектуальным или теологическим, их склонность мерить все истины чувством и опытом животной жизни [2]?

Вопрос 58. Не является ли это действительно следствием [недостаточного] мышления, что одни и те же люди восхищаются великим автором [3] за его флюксии и насмехаются над ним за его религию?

[1 Видя, что с точки зрения человеческого понимания всякая наука, включая математическую, должна отступать в область тайны и, таким образом, в конечном счёте покоиться на вере, конечная непостижимость вселенной в её религиозном понимании не в большей степени является аргументом против теизма, чем конечная непостижимость её физической эволюции во времени — причиной для отвержения механической науки.]

[2 Не являются ли привычки, сформированные таким образом, объяснением догматического агностицизма и его узкой веры в настоящее время? Ср. «Сир», разделы 331, 332.]

[3 Сэр Исаак Ньютон.]

Вопрос 59. Если у некоторых философских виртуозов нынешнего века нет религии, можно ли сказать, что это от недостатка веры?

Вопрос 60. Не является ли более справедливым способом рассуждения рекомендовать положения веры по их следствиям, чем доказывать математические принципы по их выводам?

Вопрос 61. Не является ли менее предосудительным допускать положения выше разума, чем противоречащие разуму?

Вопрос 62. Не могут ли таинства с большим правом допускаться в Божественной Вере, чем в человеческой науке [1]?

Вопрос 63. Исследовали ли когда-нибудь такие математики, которые вопиют против таинств, свои собственные принципы?

Вопрос 64. Являются ли математики, столь щепетильные в религиозных вопросах, строго скрупулёзны в своей собственной науке? Не подчиняются ли они авторитету, принимают ли вещи на веру и верят ли в непостижимые положения? Нет ли у них своих таинств, и, что более того, своих непримиримостей и противоречий?

Вопрос 65. Не подобало ли бы людям, озадаченным и смущённых насчёт своих собственных принципов, судить осмотрительно, беспристрастно и скромно относительно других предметов?

Вопрос 66. Не предоставляет ли современный аналитический метод сильный argumentum ad hominem против филоматематических неверующих этих времён?

Вопрос 67. Следует ли из вышеупомянутых замечаний, что точное и справедливое рассуждение есть отличительная черта настоящего века? И можно ли приписать современный рост неверия столь подлинно ценной особенности [2]?

[1 И всё же математики молча исходят из них в математике, в то время как жалуются на них в религии. Ибо, не покоится ли всё человеческое знание в конечном счёте на вере в Бога?]

[2 То, что те, кто претендует на звание «свободомыслящих», на деле являются «мелкими философами», чьё узкое зрение ограничено данными чувств и кто не способен признать сверхъестественное в естественном, является сквозной темой как «Алкифрона», так и «Аналиста». ]

Защита свободомыслия в математике

В ответ на брошюру Филолета Кембриджского, озаглавленную «Геометрия — не друг неверию, или Защита сэра Исаака Ньютона и британских математиков». А также Приложение, касающееся «Оправдания принципов флюксий, изложенных в Аналисте», г-на Уолтона.

(1735)

I. Когда я читал вашу «Защиту британских математиков», я не мог, сударь, не восхищаться вашей смелостью, с которой вы утверждаете с такой безоговорочной уверенностью вещи, так легко опровергаемые. Это казалось мне необъяснимым, пока я не поразмыслил над вашими словами [стр. 32], где, в ответ на мой призыв к каждому мыслящему читателю поразмыслить, возможно ли сформировать какое-либо ясное представление о флюксиях, вы выражаетесь следующим образом: «Прошу вас, сударь, кто те мыслящие читатели, к которым вы взываете? Являются ли они геометрами или же лицами, совершенно не сведущими в геометрии? Если первыми, я предоставляю это им; если же последними, то я спрашиваю, насколько они подготовлены, чтобы судить о методе флюксий?» Надо признать, вы, по-видимому, чувствуете себя в безопасности благодаря благосклонности одной части ваших читателей и невежеству другой. Тем не менее, я убежден, что среди математиков есть беспристрастные и справедливые люди. А для тех, кто не является математиком, я постараюсь так приоткрыть эту завесу тайны и представить спор между нами в таком свете, чтобы каждый читатель, обладающий обычным здравым смыслом и способностью к размышлению, мог стать компетентным его судьей.

II. Вы выражаете крайнее удивление и озабоченность тем, «что я прилагаю так много усилий, чтобы принизить одну из благороднейших наук, опорочить и оклеветать сообщество ученых мужей, чьи труды столь значительно способствуют славе этого Острова [стр. 5], умалить репутацию и авторитет сэра Исаака Ньютона и его последователей, показывая, что они не являются такими повелителями разума, каковыми их обычно считают; и обесценить науку, которую они исповедуют, демонстрируя миру, что она не обладает той ясностью и определенностью, как это принято считать». Все это, настаиваете вы, «кажется вам и остальным членам того знаменитого университета весьма странным, ибо они ясно видят, сколь велика польза математического знания для человечества». Этим вы пользуетесь случаем, чтобы пространно рассуждать о полезности математики в различных ее отраслях, а затем вновь умножаете свое удивление и изумление [стр. 19 и 20]. На все эти рассуждения я отвечаю, что они совершенно не по существу. Ибо я признаю и всегда признавал полную заслугу за всем, что полезно и истинно в математике. Но то, что таковым не является, — чем меньше оно занимает время и мысли людей, тем лучше. И после всего, что вы сказали или можете сказать, я полагаю, что беспристрастный читатель согласится со мной, что вещи неясные оттого еще не становятся священными; и что обсуждать и разоблачать несостоятельные принципы или ложные умозаключения в математике — не большая вина, чем в любой другой области знания.

III. Вам, как видно, весьма трудно понять полезность, направленность или благоразумие моей попытки. Я полагал, что достаточно разъяснил это в «Аналисте». Но для вашего дальнейшего удовлетворения скажу вам здесь: хорошо известно, что некоторые лица, которые отвергают веру и таинства в религии, признают учение о флюксиях истинным и достоверным. Если же будет показано, что флюксии на самом деле суть самые непостижимые таинства, и что те, кто считает их ясными и научно обоснованными, питают безотчетную веру к автору этого метода; не послужит ли это веским аргументом к человеку против тех, кто отвергает в религии как раз то, что допускает в человеческом знании? И не является ли это подходящим способом умерить гордыню и подорвать притязания тех, кто настаивает на ясных идеях в вопросах веры, если показать, что они обходятся без них даже в науке?

IV. Что касается выбора мною времени для этого обвинения; почему сейчас, а не раньше, если я публиковал намеки на это много лет назад? Уверен, я не обязан давать в этом отчет: если того, что сказано в «Аналисте», недостаточно; предположите, что у меня не было досуга, или что я не считал это целесообразным, или что у меня не было такого желания. Когда человек считает нужным опубликовать что-либо, будь то в математике или в любой другой области знания; какой в этом толк, или, в самом деле, какое право имеет кто-либо спрашивать, почему в то или иное время; тем или иным образом; по тому или иному побуждению? Пусть читатель судит, достаточно ли того, что я публикую истину, и что я имею право публиковать такие истины, когда и как мне угодно, в свободной стране.

V. Я не утверждаю, что математики, как таковые, являются неверующими; или что геометрия — друг неверию, что вы лживо внушаете, как и многие другие вещи; откуда вы и черпаете поводы для инвектив. Но я говорю, что есть некоторые математики, которые известны как таковые; и что есть другие, не математики, на которых влияет уважение к их авторитету. Возможно, некоторые, живущие в университете, могут не осознавать этого; но разумный и наблюдательный читатель, живущий в миру и знакомый с духом времени и характерами людей, хорошо знает, что есть слишком многие, кто отвергает таинства, и при этом восхищается флюксиями; кто оказывает ту веру простому смертному, которую отказываются оказать Иисусу Христу, чью религию они делают предметом своего изучения и стараний ее дискредитировать. Признание этого не означает признания того, что люди, которые хорошо рассуждают, являются врагами религии, как вы это представляете. Напротив, я стараюсь показать, что такие люди несовершенны в отношении разума и суждения, и что они делают именно то, что, казалось бы, презирают.

VI. Среди математиков, не сомневаюсь, есть много искренне верующих в Иисуса Христа; я сам знаю нескольких таких; но я обращал моего «Аналиста» к неверующему; и на очень веских основаниях я предполагал, что помимо него, есть и другие отвергающие веру, которые, тем не менее, питают глубокое благоговение перед флюксиями; и я хотел выявить непоследовательность таких людей. Если не существует неверующих, которые претендуют на знание современного анализа, я признаю себя введённым в заблуждение, и буду рад оказаться в заблуждении; но даже в этом случае, мои замечания относительно флюксий не становятся менее верными; также не следует, что я не имею права исследовать их с точки зрения человеческого знания, даже если религия здесь совершенно не замешана, и даже если у меня не было иной цели, кроме служения истине. Но вы очень сердитесь [стр. 13 и 14] на то, что я вступаю в полемику с рассуждающими неверующими и атакую их из-за их притязаний на научность. И этим вы пользуетесь случаем, чтобы выказать свою неприязнь к духовенству. Я не возьму на себя смелость утверждать, что знаю вас как самого «Мелкого философа». Но я знаю, что «Мелкие философы» делают как раз такие же комплименты, как и вы, нашей Церкви, и столь же сердятся, как только можете сердиться вы, на любого, кто берется защищать религию с помощью разума. Если мы все сводим к вере, они смеются над нами и нашей верой. А если мы пытаемся рассуждать, они сердятся на нас. Они притворяются, что мы выходим за пределы нашей компетенции, и они рекомендуют нам слепую, безотчетную веру. Такова непоследовательность наших противников. Но можно надеяться, что никогда не будет недостатка в людях, которые будут сражаться с ними их же собственным оружием; и показывать, что они отнюдь не те повелители разума, за которых они охотно себя выдают.

VII. Я не утверждаю, как вы меня представляете, что у нас нет лучших оснований для нашей религии, чем у вас для флюксий: но я говорю, что неверующий, который верит в учение о флюксиях, действует весьма непоследовательно, притворно отвергая христианскую религию потому, что не может верить в то, чего не постигает; или потому, что не может согласиться без доказательств; или потому, что не может подчинить свою веру авторитету. Существуют ли такие неверующие, я предоставляю суду читателя. Что касается меня лично, я не сомневаюсь в этом, ибо сам видел тому некоторые красноречивые признаки и был весьма достоверно уведомлен о том другими. И это обвинение не кажется менее правдоподобным оттого, что вы так чувствительно затронуты и отрицаете его со столь большой страстью. Вы, действительно, не останавливаетесь перед утверждением, что лица, сообщившие мне это, — сброд подлых, распутных и наглых лжецов [стр. 27]. Насколько читатель сочтет уместным перенять ваши страсти, я сказать не могу; но могу правдиво сказать, что покойный прославленный г-н Аддисон — один из тех, кого вы соблаговолили охарактеризовать столь скромными и учтивыми выражениями. Он заверил меня, что неверие одного известного математика, всё еще живого, было одной из главных причин, названных остроумным человеком того времени, для его собственного неверия. Не то чтобы я предполагал, что геометрия располагает людей к неверию; но что по иным причинам, таким как самомнение, невежество или тщеславие, подобно другим людям, и геометры также становятся неверующими, и что мнимый свет и доказательность их науки придает вес их неверию.

VIII. Вы упрекаете меня в «клевете, поношении и уловках» [стр. 15]. Вы рекомендуете такие средства, которые «невинны и справедливы, а не преступный метод умаления или поношения моих оппонентов» [там же]. Вы обвиняете меня в «Богословской ненависти, неумеренном рвении богословов», в том, что я «стою на старых путях» [стр. 13], и многое другое в том же духе. От всей этой тяжбы я завишу от беспристрастия читателя, что он не поверит вам на слово, но прочтет и рассудит сам. В этом случае он сможет разглядеть (хотя бы он и не был математиком), насколько страстны и несправедливы ваши упреки и как возможно человеку вопить против клеветы и практиковать ее в одном и том же дыхании. Учитывая, сколь нетерпеливо всё человечество, когда в его предрассудках начинают разбираться, я не удивляюсь видеть, как вы бранитесь и негодуете в том духе, как вы это делаете. Но если ваше собственное воображение сильно потрясено и взволновано, вы не можете из этого заключить, что искреннее старание освободить науку, столь полезную и украшающую человеческую жизнь, от тех тонкостей, неясностей и парадоксов, которые делают ее недоступной для большинства людей, будет сочтено преступным предприятием теми, кто в здравом уме. Еще менее вы можете надеяться, что прославленная обитель ученых мужей, породившая столько свободомыслящих искателей истины, разом проникнется вашими страстями и выродится в гнездо фанатиков.

IX. Я указываю на непоследовательность некоторых неверующих аналитиков. Я отмечаю некоторые недостатки в принципах современного анализа. Я позволяю себе прилично расходиться во мнениях с сэром Исааком Ньютоном. Я предлагаю некоторые средства, чтобы сократить трудности математических занятий и сделать их более полезными. Что же во всем этом такого, что заставляет вас пространно рассуждать о полезности прикладной математики? что побуждает вас вопить об Испании, инквизиции, Богословской ненависти? Какою фигурой речи вы распространяете то, что сказано о современном анализе, на математику вообще, или то, что сказано о математиках-неверующих, на всех математиков, или опровержение ошибки в науке — на сожжение или повешение авторов? Но нет ничего нового или странного в том, что люди предпочитают потакать своим страстям, нежели отказаться от своих мнений, сколь бы абсурдны они ни были. Отсюда — страшные видения и трагические вопли людей ослепленных, каков бы ни был предмет их фанатизма. Очень примечательный пример этого вы приводите [стр. 27], где, по поводу моего заявления, что уважение к определенным математикам-неверующим, как мне было достоверно сообщено, было одним из побуждений к неверию, вы с немалым волнением спрашиваете: «Ради Бога, мы в Англии или в Испании? Это язык фамильяра, что нашёптывает инквизитору, и т.д.?» А на предыдущей странице вы восклицаете следующими словами: «Давайте сожжем или перевешаем всех математиков в Великобритании, либо натравим на них чернь, чтобы растерзать их в клочья, всех до единого, будь то троянец или рутулец, мирян или духовных, и т. д. Давайте выкопаем тела доктора Барроу и сэра Исаака Ньютона и сожжем их под виселицей», и т. д.

X. Читателю не нужно быть математиком, чтобы видеть, как тщетна вся эта ваша трагедия. И если он столь же твердо убежден, как и я, что дело флюксий не может быть защищено разумом, он будет столь же мало удивлен, как и я, видя, как вы прибегаете к уловкам всех ослепленных людей, сея ужас и призывая на помощь страсти. Я предоставляю читателю судить, не являются ли те риторические россказни об инквизиции и галерах совершенно смехотворными. Кто также рассудит (хотя бы он и не был искушен в геометрии), дал ли я малейший повод для этого и целого мира подобных рассуждений? и не относился ли я постоянно к тем прославленным писателям со всем должным уважением, хотя и позволяю себе в некоторых пунктах с ними расходиться?

XI. Как я всей душой ненавижу инквизицию в вере, так я полагаю, что у вас нет права возводить ее в науке. Во время написания вашей защиты вы, казалось, были охвачены страстью: но теперь, когда вы, предположительно, остыли, я желаю, чтобы вы поразмыслили, не написана ли она в истинном духе инквизитора. Подобает ли это лицу, столь чрезвычайно щепетильному в этом пункте? И посчитают ли ваши братья-аналитики, что вы оказали им честь или услугу, защитив их учение тем же способом, как любой рассуждающий фанатик стал бы защищать пресуществление? Те же ложные краски, те же неумеренные выпады и то же негодование против здравого смысла!

XII. В вопросе чистой науки, где авторитету нечего делать, вы постоянно стараетесь подавить меня авторитетами и обременить меня завистью. Если я усматриваю софизм в трудах великого автора и, в угоду его пониманию, подозреваю, что он едва ли мог быть вполне доволен своим собственным доказательством: это побуждает вас пространно рассуждать на несколько страниц. Это помпезно излагается как преступный метод умаления великих людей, как согласованный проект подрыва их репутации, как представление их обманщиками. Если я публикую свои свободные мысли, которые я имею такое же право публиковать, как и любой другой человек, это приписывается опрометчивости, тщеславию и любви к противоречию. Хотя, возможно, моя недавняя публикация того, на что намекали двадцать пять лет назад, оправдает меня в этом обвинении в глазах беспристрастного читателя. Но когда я принимаю во внимание затруднения, обступающие человека, берущегося защищать учение о флюксиях, я легко могу простить ваш гнев.

XIII. Есть два рода ученых мужей: одни — те, кто беспристрастно ищет истину рациональными средствами. Эти никогда не против того, чтобы их принципы были изучены и исследованы испытанием разума. Есть другой род, которые заучивают наизусть набор принципов и образ мышления, случайно оказавшиеся в моде. Эти выдают себя своим гневом и удивлением всякий раз, когда их принципы свободно обсуждаются. Но вы не должны ожидать, что ваш читатель станет причастным к вашим страстям или вашим предрассудкам. Я свободно признаю, что сэр Исаак Ньютон показал себя необыкновенным математиком, глубоким натуралистом, лицом величайших способностей и эрудиции. До этого я охотно готов дойти, но не могу идти так далеко, как вы. Я никогда не скажу о нем, как вы: «Преклоняюсь перед следами» [стр. 70]. То же поклонение, что вы воздаете ему, я воздам только Истине.

XIV. Вы, действительно, можете сами быть идолопоклонником, кому вам угодно: но тогда вы не имеете права оскорблять и вопить на других людей за то, что они не поклоняются вашему идолу. Как бы велик ни был сэр Исаак Ньютон, я полагаю, он не раз показывал, что не является непогрешимым. В частности, его доказательство учения о флюксиях я считаю несовершенным, и не могу не думать, что он и сам не был им вполне доволен. И все же это не мешает тому, что метод может быть полезен, рассматриваемый как искусство изобретения. Вы, будучи математиком, должны признать, что в математике допускались различные подобные методы, которые не являются доказательными. Таковы, например, индукции доктора Валлиса в его «Арифметике бесконечностей», и таково то, что Хэрриот и, после него, Декарт писали относительно корней уравнений с произвольными коэффициентами. Тем не менее, из этого не следует, что те методы бесполезны; но лишь то, что их не следует допускать в качестве посылок в строгом доказательстве.

XV. Никакое великое имя на земле никогда не заставит меня принять неясное за ясное или софизмы за доказательства. И вам никогда не удастся удержать меня от свободного высказывания того, что я свободно думаю, теми аргументами к зависти, которые вы на каждом шагу применяете против меня. Вы представляете себя [стр. 52] как человека, «высшее честолюбие которого — в самой малой степени подражать сэру Исааку Ньютону». Быть может, это больше подошло бы вашему прозвищу Филолета, и было бы столь же похвально, если бы вашим высшим честолюбием было открывать истину. В полном соответствии с характером, который вы себе даете, вы говорите о нем как о своего рода преступлении [стр. 70] — думать, что вы когда-либо сможете «увидеть дальше или пойти beyond сэра Исаака Ньютона». И я убежден, что вы выражаете чувства многих других, кроме вас самих. Но есть и другие, которые не боятся просеивать принципы человеческого знания, которые не считают честью подражать величайшему человеку в его недостатках, которые даже не считают преступлением желать знать не только beyond сэра Исаака Ньютона, но и beyond всего человечества. И кто бы ни думал иначе, я взываю к читателю: может ли он быть надлежащим образом назван философом?

XVI. Поскольку я не виновен в вашем низком идолопоклонстве, вы поносите меня как человека, мнящего о своих способностях; не учитывая, что человек с меньшими способностями может знать больше в определенном пункте, чем человек с большими; не учитывая, что близорукий глаз, при близком и узком рассмотрении, может разглядеть в вещи больше, чем much лучший глаз при более обширном обзоре; не учитывая, что это — устанавливать ne plus ultra, положить конец всем будущим изысканиям; Наконец, не учитывая, что это — на деле, насколько это от вас зависит, превращать Республику Литературы в абсолютную монархию, что это даже вводить нечто вроде Философского Папства среди свободного народа.

XVII. Я сказал (и осмеливаюсь сказать и теперь), что флюксия непостижима: что вторые, третьи и четвертые флюксии еще более непостижимы: что невозможно conceiving простую бесконечно малую: что еще менее возможно conceiving бесконечно малую от бесконечно малой, и так далее. [Примечание: Аналист, Разд. 4, 5, 6, и т.д.] Что вы можете сказать в ответ на это? Пытаетесь ли вы прояснить понятие флюксии или разности? Ничего подобного; вы лишь «уверяете меня (на одно лишь ваше слово), по вашему собственному опыту и опыту нескольких других, которых вы могли бы назвать, что учение о флюксиях может быть ясно понято и отчетливо постигнуто; и что если я озадачен им и не понимаю его, то другие понимают». Но можете ли вы думать, сударь, что я приму ваше слово, когда отказываюсь принять слово вашего Учителя?

XVIII. В этом пункте каждый читатель, обладающий здравым смыслом, может судить так же хорошо, как и самый глубокий математик. Простое представление о определяемой вещи не становится более совершенным от какого бы то ни было последующего прогресса в математике. То, что кто-либо явно знает, он знает так же хорошо, как вы или сэр Исаак Ньютон. И каждый может знать, является ли объект этого метода (как вы хотите нас заставить думать) ясно постижимым. Чтобы судить об этом, не требуется глубины науки, но лишь простое внимание к тому, что происходит в его собственном уме. И то же самое следует понимать относительно всех определений во всех науках вообще. Ни в одной из них нельзя предположить, что человек смысла и духа примет какое-либо определение или принцип на веру, без того чтобы не разобрать его до дна и не испытать, насколько он может или не может его постичь. Это — курс, которого я придерживался и буду придерживаться, как бы вы и ваши братья ни рассуждали против него и ни выставляли его в самом невыгодном свете.

XIX. Вам обычно угодно увещевать меня пересмотреть вторично, проконсультироваться, исследовать, взвесить слова сэра Исаака. В ответ на что я осмелюсь сказать, что я приложил столько же стараний, как (я искренне верю) любой живущий человек, чтобы понять того великого автора и найти смысл в его принципах. Уверяю вас, с моей стороны не было недостатка ни в усердии, ни в осторожности, ни во внимании. Так что, если я не понимаю его, это не моя вина, но моя неудача. По другим предметам вы соблаговоляете делать мне комплименты в глубине мысли и необычных способностях, [стр. 5 и 84]. Но я свободно признаю, что не претендую на эти вещи. Единственное преимущество, на которое я претендую, это то, что я всегда думал и судил самостоятельно. И, поскольку у меня никогда не было учителя в математике, я честно следовал указаниям моего собственного ума, исследуя и подвергая критике авторов, которых я читал на эту тему, с той же свободой, которую я применял к любому другому; не принимая ничего на веру и не веря, что какой-либо писатель непогрешим. И человек средних способностей, который следует этому трудному пути в изучении принципов любой науки, может считаться идущим более верно, чем те, кто обладает большими способностями, но начинает с большей скоростью и меньшей заботой.

XX. На чем я настаиваю, так это на том, что представление о флюксии, просто рассматриваемое, никоим образом не улучшается и не исправляется каким-либо прогрессом, сколь бы велик он ни был, в анализе: также и доказательства общих правил того метода никоим образом не проясняются их применением. Причина чего в том, что при операциях или вычислениях люди не возвращаются к созерцанию первоначальных принципов метода, которые они постоянно предполагают, но заняты работой с помощью обозначений и символов, означающих флюксии, предположительно изначально объясненные, и согласно правилам, предположительно изначально доказанным. Это я говорю, чтобы ободрить тех, кто недалеко продвинулся в этих занятиях, смело пользоваться собственным суждением, без слепого или низкого подобострастия к лучшим из математиков, которые не более квалифицированы, чем они, чтобы судить о простом представлении или доказательности того, что излагается в первых элементах метода; люди посредством дальнейшего и частого использования или упражнения становятся лишь более привычными к символам и правилам, что не делает ни предшествующие понятия более ясными, ни предшествующие доказательства более совершенными. Каждый читатель здравого смысла, который только воспользуется своими способностями, знает так же хорошо, как и самый глубокий аналитик, какое представление он формирует или может сформировать о скорости без движения, или о движении без протяженности, о величине, которая ни конечна, ни бесконечна, или о количестве, не имеющем величины, которое тем не менее делимо, о фигуре, где нет пространства, о пропорции между ничто, или о реальном произведении от ничто, умноженного на нечто. Ему не нужно быть далеко продвинутым в геометрии, чтобы знать, что неясные принципы не должны допускаться в доказательстве: что если человек разрушает свою собственную гипотезу, он в то же время разрушает то, что было на ней построено: что ошибка в посылках, не исправленная, должна производить ошибку в заключении.

XXI. По моему мнению, величайшие люди имеют свои предрассудки. Люди изучают элементы науки от других: и каждый ученик питает более или менее почтительность к авторитету, особенно молодые ученики, немногие из такого рода заботятся долго останавливаться на принципах, но склонны скорее принимать их на веру: и вещи, рано принятые, от повторения становятся привычными: и эта привычность со временем проходит за доказательность. Теперь мне кажется, что есть определенные пункты, молчаливо принимаемые математиками, которые ни очевидны, ни истинны. И такие пункты или принципы, всегда смешиваясь с их рассуждениями, ведут их к парадоксам и затруднениям. Если великий автор флюксионного метода был рано пропитан такими понятиями, это лишь показало бы, что он был человеком. И если в силу некоторой скрытой ошибки в его принципах человек втягивается в ошибочные рассуждения, нет ничего странного в том, что он принимает их за истинные: и, тем не менее, если, будучи вынужден затруднениями и нелепыми следствиями и доведен до уловок и ухищрений, он задерживает некоторое сомнение в них, это не более, чем можно естественно предположить, могло приключиться с великим гением, борющимся с непреодолимой трудностью: в каковом свете я и поместил сэра Исаака Ньютона. [Примечание: Аналист, Разд. 18]. Здесь вы, к вашему удовольствию, замечаете, что я представляю великого автора не только как слабого, но и как дурного человека, как обманщика и мошенника. Читатель рассудит, насколько справедливо.

XV. Никакое великое имя на земле никогда не заставит меня принять неясное за ясное или софизмы за доказательства. И вам никогда не удастся удержать меня от свободного высказывания того, что я свободно думаю, теми аргументами к зависти, которые вы на каждом шагу применяете против меня. Вы представляете себя [стр. 52] как человека, «высшее честолюбие которого — в самой малой степени подражать сэру Исааку Ньютону». Быть может, это больше подошло бы вашему прозвищу Филолета, и было бы столь же похвально, если бы вашим высшим честолюбием было открывать истину. В полном соответствии с характером, который вы себе даете, вы говорите о нём как о своего рода преступлении [стр. 70] — думать, что вы когда-либо сможете «увидеть дальше или пойти дальше сэра Исаака Ньютона». И я убежден, что вы выражаете чувства многих других, кроме вас самих. Но есть и другие, которые не боятся просеивать принципы человеческого знания, которые не считают честью подражать величайшему человеку в его недостатках, которые даже не считают преступлением желать знать не только дальше сэра Исаака Ньютона, но и дальше всего человечества. И кто бы ни думал иначе, я взываю к читателю: может ли он быть надлежащим образом назван философом?

XVI. Поскольку я не виновен в вашем низком идолопоклонстве, вы поносите меня как человека, мнящего о своих способностях; не учитывая, что человек с меньшими способностями может знать больше в определенном пункте, чем человек с большими; не учитывая, что близорукий глаз, при близком и узком рассмотрении, может разглядеть в вещи больше, чем гораздо лучший глаз при более обширном обзоре; не учитывая, что это — устанавливать ne plus ultra, положить конец всем будущим изысканиям; Наконец, не учитывая, что это — на деле, насколько это от вас зависит, превращать Республику Литературы в абсолютную монархию, что это даже вводить нечто вроде Философского Папства среди свободного народа.

XVII. Я сказал (и осмеливаюсь сказать и теперь), что флюксия непостижима: что вторые, третьи и четвертые флюксии ещё более непостижимы: что невозможно постичь простую бесконечно малую: что ещё менее возможно постичь бесконечно малую от бесконечно малой, и так далее. [Примечание: Аналист, Разд. 4, 5, 6, и т.д.] Что вы можете сказать в ответ на это? Пытаетесь ли вы прояснить понятие флюксии или разности? Ничего подобного; вы лишь «уверяете меня (на одно лишь ваше слово), по вашему собственному опыту и опыту нескольких других, которых вы могли бы назвать, что учение о флюксиях может быть ясно понято и отчетливо постигнуто; и что если я озадачен им и не понимаю его, то другие понимают». Но можете ли вы думать, сударь, что я приму ваше слово, когда отказываюсь принять слово вашего Учителя?

XVIII. В этом пункте каждый читатель, обладающий здравым смыслом, может судить так же хорошо, как и самый глубокий математик. Простое представление о определяемой вещи не становится более совершенным от какого бы то ни было последующего прогресса в математике. То, что кто-либо явно знает, он знает так же хорошо, как вы или сэр Исаак Ньютон. И каждый может знать, является ли объект этого метода (как вы хотите нас заставить думать) ясно постижимым. Чтобы судить об этом, не требуется глубины науки, но лишь простое внимание к тому, что происходит в его собственном уме. И то же самое следует понимать относительно всех определений во всех науках вообще. Ни в одной из них нельзя предположить, что человек смысла и духа примет какое-либо определение или принцип на веру, без того чтобы не разобрать его до дна и не испытать, насколько он может или не может его постичь. Это — курс, которого я придерживался и буду придерживаться, как бы вы и ваши братья ни рассуждали против него и ни выставляли его в самом невыгодном свете.

XIX. Вам обычно угодно увещевать меня пересмотреть вторично, проконсультироваться, исследовать, взвесить слова сэра Исаака. В ответ на что я осмелюсь сказать, что я приложил столько же стараний, как (я искренне верю) любой живущий человек, чтобы понять того великого автора и найти смысл в его принципах. Уверяю вас, с моей стороны не было недостатка ни в усердии, ни в осторожности, ни во внимании. Так что, если я не понимаю его, это не моя вина, но моя неудача. По другим предметам вы соблаговоляете делать мне комплименты в глубине мысли и необычных способностях, [стр. 5 и 84]. Но я свободно признаю, что не претендую на эти вещи. Единственное преимущество, на которое я претендую, это то, что я всегда думал и судил самостоятельно. И, поскольку у меня никогда не было учителя в математике, я честно следовал указаниям моего собственного ума, исследуя и подвергая критике авторов, которых я читал на эту тему, с той же свободой, которую я применял к любому другому; не принимая ничего на веру и не веря, что какой-либо писатель непогрешим. И человек средних способностей, который следует этому трудному пути в изучении принципов любой науки, может считаться идущим более верно, чем те, кто обладает большими способностями, но начинает с большей скоростью и меньшей заботой.

XX. На чём я настаиваю, так это на том, что представление о флюксии, просто рассматриваемое, никоим образом не улучшается и не исправляется каким-либо прогрессом, сколь бы велик он ни был, в анализе: также и доказательства общих правил того метода никоим образом не проясняются их применением. Причина чего в том, что при операциях или вычислениях люди не возвращаются к созерцанию первоначальных принципов метода, которые они постоянно предполагают, но заняты работой с помощью обозначений и символов, означающих флюксии, предположительно изначально объяснённые, и согласно правилам, предположительно изначально доказанным. Это я говорю, чтобы ободрить тех, кто недалеко продвинулся в этих занятиях, смело пользоваться собственным суждением, без слепого или низкого подобострастия к лучшим из математиков, которые не более квалифицированы, чем они, чтобы судить о простом представлении или доказательности того, что излагается в первых элементах метода; люди посредством дальнейшего и частого использования или упражнения становятся лишь более привычными к символам и правилам, что не делает ни предшествующие понятия более ясными, ни предшествующие доказательства более совершенными. Каждый читатель здравого смысла, который только воспользуется своими способностями, знает так же хорошо, как и самый глубокий аналитик, какое представление он формирует или может сформировать о скорости без движения, или о движении без протяжённости, о величине, которая ни конечна, ни бесконечна, или о количестве, не имеющем величины, которое тем не менее делимо, о фигуре, где нет пространства, о пропорции между ничто, или о реальном произведении от ничто, умноженного на нечто. Ему не нужно быть далеко продвинутым в геометрии, чтобы знать, что неясные принципы не должны допускаться в доказательстве: что если человек разрушает свою собственную гипотезу, он в то же время разрушает то, что было на ней построено: что ошибка в посылках, не исправленная, должна производить ошибку в заключении.

XXI. По моему мнению, величайшие люди имеют свои предрассудки. Люди изучают элементы науки от других: и каждый ученик питает более или менее почтительность к авторитету, особенно молодые ученики, немногие из такого рода заботятся долго останавливаться на принципах, но склонны скорее принимать их на веру: и вещи, рано принятые, от повторения становятся привычными: и эта привычность со временем проходит за доказательность. Теперь мне кажется, что есть определённые пункты, молчаливо принимаемые математиками, которые ни очевидны, ни истинны. И такие пункты или принципы, всегда смешиваясь с их рассуждениями, ведут их к парадоксам и затруднениям. Если великий автор флюксионного метода был рано пропитан такими понятиями, это лишь показало бы, что он был человеком. И если в силу некоторой скрытой ошибки в его принципах человек втягивается в ошибочные рассуждения, нет ничего странного в том, что он принимает их за истинные: и, тем не менее, если, будучи вынужден затруднениями и нелепыми следствиями и доведён до уловок и ухищрений, он задерживает некоторое сомнение в них, это не более, чем можно естественно предположить, могло приключиться с великим гением, борющимся с непреодолимой трудностью: в каковом свете я и поместил сэра Исаака Ньютона. [Примечание: Аналист, Разд. 18]. Здесь вы, к вашему удовольствию, замечаете, что я представляю великого автора не только как слабого, но и как дурного человека, как обманщика и мошенника. Читатель рассудит, насколько справедливо.

XXII. Что касается остальных ваших приукрашиваний и толкований, ваших упрёков и оскорблений и воплей, я пропущу их, лишь желая, чтобы читатель не принимал ваше слово, но прочёл, что я написал, и ему не потребуется другого ответа. Часто замечалось, что худшее дело производит наибольший шум, и действительно, вы столь шумны на протяжении всей вашей защиты, что читатель, хотя бы он и не был математиком, при условии, что он понимает здравый смысл и наблюдал за повадками людей, будет склонен подозревать, что вы неправы. Таким образом, должно казаться, что ваши братья-аналитики мало обязаны вам за этот новый метод рассуждений в математике. Более ли они обязаны вашим Рассуждением, я сейчас исследую.

XXIII. Вы спрашиваете меня [стр. 32], где я нахожу, что сэр Исаак Ньютон использует такие выражения, как Скорости Скоростей, вторые, третьи и четвертые Скорости, и т. д. Вы выставляете это как благочестивый обман и несправедливое представление. Я отвечаю, что если согласно сэру Исааку Ньютону флюксия есть скорость приращения, то согласно ему я могу назвать флюксию от флюксии Скоростью от Скорости. Но для истинности антецедента смотрите его введение к «Квадратуре кривых», где его собственные слова: motuum vel incrementorum velocitates nominando Fluxiones. Смотрите также вторую Лемму второй Книги его «Математических начал натуральной философии», где он выражается следующим образом: velocitates incrementorum ac decrementorum quas etiam, motus, mutationes & fluxiones quantitatum nominare licet. И что он допускает флюксии от флюксий, или вторые, третьи, четвертые флюксии, и т.д., смотрите его «Трактат о квадратуре кривых». Я спрашиваю теперь, не ясно ли, что если флюксия есть скорость, то флюксия от флюксии может согласованно с этим называться скоростью от скорости? Подобным же образом, если под флюксией подразумевается нарождающееся приращение, не следует ли тогда, что флюксия от флюксии или вторая флюксия есть нарождающееся приращение от нарождающегося приращения? Может ли что-либо быть яснее? Пусть теперь читатель рассудит, кто несправедлив.

XXIV. Я заметил, что Великий Автор поступил неправомерно, получая флюксию или момент прямоугольника двух текущих количеств; и что он не честно избавился от прямоугольника моментов. В ответ на это вы утверждаете, что ошибка, возникающая от опущения такого прямоугольника (допуская, что это ошибка), столь мала, что незначительна. На этом вы останавливаетесь и иллюстрируете без иной цели, как только чтобы позабавить вашего читателя и отвлечь его от Вопроса; который в действительности касается не точности вычисления или измерения на практике, но точности рассуждения в науке. Что это действительно так и что малость практической ошибки никоим образом не касается его, должно быть столь ясно для любого, кто читает «Аналиста», что я удивляюсь, как вы могли не знать этого.

XXV. Вы охотно убеждаете вашего читателя, что я затеваю абсурдную ссору из-за ошибок, не имеющих значения на практике, и представляю математиков как действующих вслепую в их приближениях, во всём этом я не могу не думать, что с вашей стороны есть либо великое невежество, либо великая недобросовестность. Если вы намерены защищать разумность и использование приближений или метода неделимых, мне нечего сказать. Но тогда вы должны помнить, что это не Учение о флюксиях: это не тот анализ, с которым я имею дело. То, что я далёк от ссоры с приближениями в геометрии, явствует из тридцать третьего и пятьдесят третьего Вопросов в «Аналисте». И то, что метод флюксий претендует на нечто большее, чем метод неделимых, ясно; потому что сэр Исаак отрекается от этого метода как не геометрического. [Примечание: Смотрите Схолиум в конце первого раздела. Кн. i., Мат. начала натур. филос.]. И то, что метод флюксий предполагается точным в геометрической строгости, явственно для всякого, кто принимает во внимание, что Великий Автор пишет о нём; особенно в его «Введении к квадратуре кривых», где он говорит: In rebus mathematicis errores quam minimi non sunt contemnendi. Каковое выражение вы видели цитированным в «Аналисте», и все же вы, кажется, невежественны в нём, и действительно, в самой цели и Замысле Великого Автора в этом его изобретении флюксий.

XXVI. Сколько бы раз вы ни говорили о конечных количествах, незначительных на практике, сэр Исаак отрекается от вашего оправдания. Cave, говорит он, intellexeris finitas. И, хотя количества, меньшие, чем ощутимые, могут не иметь значения на практике, тем не менее, ни один из ваших учителей, ни даже вы сами не рискнете сказать, что они не имеют значения в Теории и в Рассуждении. Применение в грубой практике — не тот пункт, о котором идет речь, но строгость и справедливость рассуждения. И очевидно, что, как бы ни был мал или незначителен предмет, это не мешает тому, что человек, трактующий о нем, может совершать очень большие ошибки в Логике, каковые Логические ошибки никоим образом не должны измеряться ощутимыми или практическими неудобствами, оттуда проистекающими, которые, возможно, и вовсе отсутствуют. Надо признать, что после того, как вы ввели в заблуждение и позабавили вашего менее подготовленного читателя (как вы его называете), вы возвращаетесь к реальному пункту полемики и принимаетесь оправдывать метод сэра Исаака избавления от упомянутого выше Прямоугольника. И здесь я должен упросить читателя наблюдать, насколько честно вы действуете.

XXVII. Во-первых, вы утверждаете [стр. 44], «что ни в Доказательстве Правила для нахождения флюксии прямоугольника двух текущих количеств, ни в чем-либо предшествующем или последующем ему, не делается ни малейшего упоминания о приращении прямоугольника таких текущих количеств». Теперь я утверждаю прямо противоположное. Ибо в самом отрывке, вами же процитированном на этой же странице, из первого случая второй леммы второй Книги начал сэра Исаака, начинающемся с Rectangulum quodvis motu perpetuo auctum, и заканчивающемся igitur laterum incrementis totis a et b generatur rectanguli incrementum aB + bA. Q.E.D. В этом самом отрывке, говорю я, прямо упоминается приращение такого Прямоугольника. Поскольку это вопрос факта, я отсылаю к собственным глазам читателя. Какого прямоугольника мы здесь имеем Приращение? не ясно ли, что того, чьи стороны имеют a и b своими incrementa tota, то есть, AB. Пусть любой читатель рассудит, не ясно ли из слов, смысла и контекста, что Великий Автор в конце своего доказательства понимает свое incrementum как принадлежащее Rectangulum quodvis в начале. Не явствует ли то же и из самой леммы, предпосланной Доказательству? Смысл которой (как автор там разъясняет) в том, что если моменты текущих количеств A и B называются a и b, то momentum vel mutatio geniti rectanguli AB будет aB + bA. Следовательно, либо заключение доказательства — не то, что должно было быть доказано, либо Rectanguli incrementum aB + bA принадлежит прямоугольнику AB.

XXVIII. Всё это столь ясно, что ничего не может быть яснее; и всё же вы охотно затрудняете этот ясный случай, различая между приращением и моментом. Но всякому, кто имеет какое-либо понятие о доказательстве, очевидно, что incrementum в заключении должно быть momentum в Лемме; и предполагать иное — не делает чести Автору. Это, по сути, значит предполагать его тем, кто не знал, что он доказывает. Но давайте услышим собственные слова сэра Исаака: Earum (quantitatum scilicet fluentium) incrementa vel decrementa momentanea sub nomine momentorum intelligo. И вы сами замечаете, что он использует слово «момент» для обозначения либо приращения, либо убыли. Отсюда, с намерением озадачить меня, вы предлагаете приращение и убыль AB и спрашиваете, которое из них я назову моментом? Дело, говорите вы, трудное. Мой ответ очень прост и легок, а именно: любое из них. Вы, действительно, даёте иной ответ, и из того, что Автор говорит, что под моментом он понимает либо мгновенное приращение, либо убыль текущих количеств, вы хотите, чтобы мы заключили, посредством очень удивительного умозаключения, что его момент не является ни приращением, ни убылью. Не было бы столь же хорошим умозаключением, потому что число либо нечётно, либо чётно, заключить, что оно ни то, ни другое? Может ли кто-либо понять это? Или может ли даже вы сами надеяться, что это пройдёт у читателя, как бы мало он ни был подготовлен? Надо признать, вы стараетесь навязать это умозаключение ему скорее весельем и юмором, чем рассуждением. Вы веселы, говорю я, и [стр. 46] представляете два математических количества как защищающие свои права, как подбрасывающие монету, как дружелюбно спорящие. Вы говорите об их притязаниях на предпочтение, их согласии, их ребячестве и их серьёзности. И после этого остроумного отступления вы обращаетесь ко мне следующими словами — «Верьте мне, нет иного средства, вы должны примириться». Но мой ответ таков, что я не поверю вам и не примирюсь; есть простое средство в здравом смысле; и чтобы предотвратить неожиданность, я желаю, чтобы читатель всегда держал в виду оспариваемый пункт, исследовал ваши причины и был осторожен в том, как он принимает ваше слово, но более всего тогда, когда вы положительны, красноречивы или веселы.

XXIX. Страницей или двумя позже вы весьма чистосердечно представляете ваше дело как дело осла между двумя охапками сена: это ваше собственное выражение. Причина вашего затруднения в том, что вы не знаете, считать ли скорость AB возрастающего или AB убывающего флюксией, или пропорциональной моменту прямоугольника. Моё мнение, согласно тому, что было предпослано, таково, что любая из них может считаться флюксией. Но вы говорите нам [стр. 49], «что вы думаете, почтенный призрак сэра Исаака Ньютона шепчет вам, что Скорость, которую вы ищете, ни та, ни другая из этих, но есть скорость, которую текущий прямоугольник имеет, не тогда, когда он больше или меньше AB, но в тот самый миг времени, когда он есть AB». Что касается меня, в прямоугольнике AB, рассматриваемом просто в себе, без возрастания или убывания, я не могу постичь никакой скорости вовсе. И если читатель моего мнения, он не примет ни ваше слово, ни даже слово Призрака, как бы почтенен он ни был, за скорость без движения. Вы продолжаете и говорите нам, что, подобным же образом, момент прямоугольника не есть его приращение или убыль. Это вы хотите, чтобы мы поверили на авторитет его Призрака, в прямое противоречие с тем, что сэр Исаак сам утверждал, будучи живым. Incrementa (говорит он) vel decrementa momentanea sub nomine momentorum intelligo: ita ut incrementa pro momentis addititiis seu affirmativis, ac decrementa pro subductitiis seu negativis habeantur. [Примечание: Princip. Phil. Nat. Lib. II, Lem. II.] Я не стану в вашем стиле просить читателя верить мне, но «Поверь своим глазам».

XXX. Мне поистине кажется, что вы взялись защищать то, чего не понимаете. Чтобы исправить дело, вы говорите, «вы не рассматриваете AB как лежащий на каком-либо из краёв момента, но как протянутый к его середине; как приобретший одну половину момента и как собирающийся приобрести другую; или, как потерявший одну половину его и как собирающийся потерять другую». Теперь, во имя Истины, я упрашиваю вас сказать, что это за момент, к середине которого протянут прямоугольник? Этот момент, говорю я, который приобретается, который теряется, который разрезается пополам, или различается на половины? Это конечная величина, или бесконечно малая, или простой предел, или ничто вовсе? Примите его в каком угодно смысле, я не могу сделать вашу защиту ни последовательной, ни понятной. Ибо если вы примете его в любом из двух первых смыслов, вы противоречите сэру Исааку Ньютону. А если вы примете его в любом из последних, вы противоречите здравому смыслу; ибо ясно, что то, что не имеет величины или не является количеством, не может быть разделено. И здесь я должен упросить читателя сохранить его полную свободу ума нетронутой, и не позволять слабо подавить его суждение вашим воображением и вашими предрассудками, великими именами и авторитетами, Призраками и Видениями, и превыше всего той крайней удовлетворённостью и самодовольством, с которыми вы изрекаете ваши странные выдумки; если слова без смысла могут так называться. После того как вы дали это невразумительное объяснение, вы спрашиваете с вашей обычной манерой: «Что скажете, сударь? Является ли это справедливой и законной причиной для того, чтобы сэр Исаак поступал так, как он поступил? Я думаю, вы должны признать это таковым». Но увы! Я не признаю ничего подобного. Я не нахожу ни смысла, ни причины в том, что вы говорите. Пусть читатель найдёт это, если может.

XXXI. В следующем месте [стр. 50] вы обвиняете меня в недостатке осторожности. «Поскольку (говорите вы) та величина, которую сэр Исаак Ньютон на протяжении всей своей Леммы и всех различных её случаев постоянно называет Моментом, не ограничивая его быть ни приращением, ни убылью, вами необдуманно и произвольно, и без какой-либо тени приведённой причины, предполагается и определяется быть приращением». На каковое Обвинение я отвечаю, что оно столь же ложно, сколь и категорично. Ибо в вышеприведённой цитате из первого случая Леммы сэра Исаака он прямо определяет его как Приращение. И поскольку этот частный пример или отрывок был тем, на что я возражал, мне было разумно и уместно рассматривать Момент в том же свете. Но примите его приращением или убылью, как хотите, Возражения всё ещё остаются, и Трудности одинаково непреодолимы. Вы затем принимаетесь превозносить великого Автора флюксионного Метода и расточать некоторые резкости тем, кто неосмотрительно осмеливается расходиться с ним. На всё это я не дам никакого ответа.

XXXII. Впоследствии, чтобы устранить (как вы говорите) все Сомнения и Трудности относительно этого дела, вы замечаете, что Момент Прямоугольника, определённый сэром Исааком Ньютоном, и Приращение Прямоугольника, определённое мной, совершенно и точно равны, предполагая, что a и b уменьшены ad infinitum: и в доказательство этого вы отсылаете к первой Лемме первого Раздела первой Книги Начал сэра Исаака. Я отвечаю, что если a и b — реальные количества, тогда ab есть нечто, и, следовательно, создаёт реальную разницу: но если они ничто, тогда Прямоугольники, коэффициентами которых они являются, также становятся ничем: и, следовательно, momentum или incrementum, будь то сэра Исаака или моё, в этом Случае суть ничто вовсе. Что касается упомянутой выше Леммы, на которую вы ссылаетесь и которую вы желали, чтобы я рассмотрел раньше, как для моего собственного блага, так и для вашего; я говорю вам, что я давно уже рассмотрел и обдумал её. Но я очень сомневаюсь, достаточно ли вы обдумали ту Лемму, её Доказательство и её Следствия. Ибо, как бы ни годился этот способ рассуждения в Методе исчерпывания, где количества, меньшие чем назначаемые, рассматриваются как ничто; однако для флюксиониста, пишущего о моментах, утверждать, что количества должны быть равны, потому что у них нет назначаемой разницы, кажется самым неблагоразумным Шагом, какой только можно было предпринять: это прямо разрушает само Учение, которое вы хотите защищать. Ибо из этого последует, что все однородные моменты равны, и, следовательно, скорости, изменения, или флюксии, пропорциональные им, все также равны. Существует, следовательно, только одно отношение равенства повсюду, что сразу опрокидывает всю Систему, которую вы берётесь защищать. Ваши моменты (говорю я), не будучи сами назначаемыми количествами, их различия не могут быть назначаемыми: и если это верно, этим способом рассуждения последует, что они все равны, при каковом Предположении вы не можете сделать ни одного Шага в Методе Флюксий. Отсюда явствует, как несправедливо вы вините меня [стр. 32] за опущение дать какое-либо Объяснение того первого Раздела первой Книги Принципов, в котором (вы говорите) Основа Метода Флюксий геометрически доказана и обширно объяснена, и трудности и возражения против неё ясно решены. Всё это столь далеко от истины, что самая первая и фундаментальная Лемма того Раздела несовместима с учением о Флюксиях и подрывает его. И, действительно, кто не видит, что Доказательство ad absurdum more veterum, proceeding на Предположении, что каждая разница должна быть некоторой данной величиной, не может быть допущено в методе, или совместимо с методом, в котором Quantities, меньшие чем любая данная, предполагаются реально существующими и способными к делению?

XXXIII. Следующий пункт, который вы берётесь защищать, — это тот метод для получения правила нахождения Флюксии любой Степени текущего Количества, который изложен во введении к Квадратурам и рассмотрен в Аналисте [Примечание: Разд. 13, 14, и т.д.]. И здесь вопрос между нами в том, правильно ли я представил смысл тех слов, evanescant jam augmenta illa, переводя их как «пусть приращения исчезают», т.е. пусть приращения будут ничем, или пусть не будет приращений? Это вы отрицаете, но, как в вашем обычае, вместо того чтобы привести причину, вы рассуждаете. Я, напротив, утверждаю, приращения должны пониматься как совершенно исчезнувшие и абсолютно ничто вовсе. Моя причина в том, что без этого предположения вы никогда не сможете привести количество или выражение

вниз к nxn-1, самой вещи, на которую направлено предположение об исчезновении. Скажите, не такова ли правда дела? Не должно ли прежнее выражение быть сведено к последнему? И может ли это быть возможно сделано, пока o предполагается реальным Количеством? Я, действительно, не могу сказать, что вы щепетильны в ваших утверждениях, и всё же я верю, что даже вы не станете утверждать это; ибо самоочевидно, что произведение двух реальных количеств есть нечто реальное; и что ничто реальное не может быть отброшено ни согласно Геометрии, ни согласно собственным Принципам сэра Исаака; в истинности чего я взываю ко всем, кто знает что-либо об этих предметах. Далее, под evanescant должно подразумеваться либо пусть они (приращения) исчезают и становятся ничем, в очевидном смысле, либо пусть они становятся бесконечно малыми. Но что последнее не есть смысл сэра Исаака, явствует из его собственных слов на той же самой странице, то есть в последней части Введения к Квадратурам, где он прямо говорит: volui ostendere quod in methodo fluxionum non opus sit figuras infinite parvas in geometriam introducere. В целом, вы, кажется, рассмотрели это дело столь весьма поверхностно, что сильно утверждаете меня во мнении, на которое вы так сердитесь, а именно, что последователи сэра Исаака гораздо более рьяны в применении его метода, чем точны в исследовании его принципов. Вы поднимаете пыль об исчезающих приращениях, которая, возможно, позабавит и изумит вашего читателя, но я сильно ошибаюсь, если она когда-либо проинструктирует или просветит его. Ибо, чтобы подойти к сути, те исчезающие приращения либо суть реальные количества, либо нет. Если вы говорите, что они есть; я желаю знать, как вы избавляетесь от отбрасываемого количества? Если вы говорите, что их нет; вы, действительно, избавляетесь от тех количеств, в составе которых они являются коэффициентами; но тогда вы того же мнения со мной, каковое мнение вы соблаговоляете называть [стр. 58] «самой осязаемой, необъяснимой, и непростительной ошибкой», хотя это Истина, самоочевидно явственная.

XXXIV. Ничто, говорю я, не может быть яснее для любого беспристрастного читателя, чем то, что под Исчезновением приращений в вышепроцитированном отрывке сэр Исаак подразумевает их фактическое сведение к ничто. Но чтобы вывести это из всех сомнений и убедить даже вас, кто проявляет так мало расположения быть убеждённым, я желаю, чтобы вы заглянули в его «Анализ с помощью уравнений с бесконечным числом членов» (стр. 20), где, в его подготовке к доказательству первого правила для возведения в квадрат простых Кривых, вы найдёте, что по аналогичному случаю, говоря о приращении, которое предполагается исчезающим, он интерпретирует слово evanescere как esse nihil. Ничто не может быть яснее этого, что сразу разрушает вашу защиту. И всё же, как бы ясно это ни было, я отчаиваюсь заставить вас признать это; хотя я уверен, что вы чувствуете это, и читатель, если он использует свои глаза, должен видеть это. Слова Evanescere sive esse nihil (чтобы употребить ваше собственное выражение) смотрят нам в лицо. Вот! Это то, что вы называете [стр. 56] «столь великой, столь необъяснимой, столь ужасной, столь поистине Беотийской ошибкой», что, по вашему мнению, было невозможно, чтобы сэр Исаак Ньютон мог быть виновен в ней. На будущее я советую вам быть более сдержанным в крепких выражениях: ибо, как вы неосторожно разбрасываетесь ими, они могут случайно пасть на ваших друзей так же, как и на ваших противников. Что касается меня, я не стану отвечать тем же. Достаточно сказать, что вы ошибаетесь. Но я могу легко простить ваши ошибки. Хотя, действительно, вы говорите мне по этому самому случаю, что я не должен ожидать никакой пощады от последователей сэра Исаака. И я говорю вам, что я не ожидаю и не желаю никакой. Моя цель — истина. Мои причины я привёл. Опровергните их, если можете. Но не думайте подавить меня ни авторитетами, ни резкими словами. Последние обратятся против вас самих: Первые в деле науки не имеют никакого веса у беспристрастных читателей; а что касается ослеплённых, меня не заботит, что они говорят или думают.

XXXV. На следующем месте вы принимаетесь рассуждать о следующем отрывке, взятом из семнадцатого раздела Аналиста. «Рассматривая различные искусства и уловки, используемые великим автором флюксионного метода: в скольких светах он помещает свои Флюксии: и какими разными способами он пытается доказать тот же пункт: Можно было бы склониться думать, что он сам сомневался в справедливости своих собственных доказательств». На этот отрывок вы жалуетесь как на очень жестокое обращение с сэром Исааком Ньютоном. Вы пространно рассуждаете и стараетесь показать, что помещение того же пункта в различные света имеет большую пользу для его объяснения; что вы иллюстрируете с большой Риторикой. Но вина того отрывка не в жестоком обращении, которое он содержит: Но, напротив, в том, что он слишком скромен и не так полон и выразителен в отношении моего смысла, как, возможно, должен был бы. Понравилось бы вам больше, если бы я сказал, что различные несогласующиеся отчёты, которые этот великий автор даёт о своих моментах и своих флюксиях, могут убедить каждого разумного читателя, что у него не было ясных и устойчивых понятий о них, без которых не может быть доказательства? Я откровенно признаю, что не вижу в них ясности или последовательности. Вы, действительно, говорите мне, в мильтоновских стихах, что вина в моих собственных глазах,

So thick a drop serene has quench’d their orbs

Or dim suffusion veil’d.

в то же время вы признаёте себя обязанным за те различные света, которые позволили вам понять его Учение. Но что касается меня, кто не понимает его, вы оскорбляете меня, говоря: «Ради Бога, на что вы обижаетесь, кто всё ещё не понимает его?» Могу ли я не ответить, что я обижаюсь именно по этой причине; потому что не могу понять его или найти смысл в том, что он говорит? Вы говорите мне, что я весь во тьме. Я признаю это и упрашиваю вас, кто видит так ясно, помочь мне выбраться.