Бесплатный фрагмент - Системы счисления

Введение

С давних времен человечество сталкивалось с проблемой подсчёта и записи количества собранного урожая, накопленных богатств, и т. д. Каждые народы решали эту проблему по-разному — одни использовали узелки на верёвках, другие — зарубки на палочках, камешки или ракушки.

С возникновением письменности одновременно возникали и развивались новые системы счёта и правила выполнения операций над числами.

Известно множество способов представления чисел. В одних случаях для обозначения чисел использовались буквы алфавита, в других — применялись специальные символы. Такие символы называются цифрами.

Система обозначения, записи и правила операций над числами называется системой счисления или системой счёта.

За историю человечества существовало множество различных систем счисления. Некоторые из них до сих пор используются, другие системы не получили широкого распространения.

В зависимости от способа изображения чисел с помощью цифр системы счисления делятся на позиционные и непозиционные.

Наиболее распространёнными непозиционными системами счисления являются римские числа, греческие числа, старославянская система счета, египетские и вавилонские числа. В таких системах значение числа не зависит от положения цифры в записи.

Самой распространенной позиционной системой счисления является десятичная система (арабские или десятичные числа). Этой системой мы пользуемся в повседневной жизни. В этой системе значение числа зависит от положения цифры в записи. Например, в записи числа 152 в десятичной системе цифра 5 — обозначает число десятков. Если переставить цифры местами, то изменится и числовое значение. Так в записи 125 — цифра пять будет обозначать число единиц.

Существовали также и мультипликативные системы счисления, которые несут в себе признаки как непозиционных, так и позиционных систем. Примером таких систем являются китайские числа.

Непозиционные системы счисления

В самой простейшей системе счисления для записи чисел используется только одна цифра. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака (единицы), которую можно изобразить в виде палочки, кружочка или любой другой фигуры.

Числа в этой системе будут записываться примерно так:

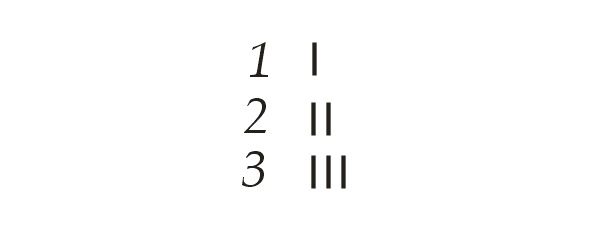
Такая система счисления в основном использовалась народами, не имеющими письменности. Иногда подобной системой счисления пользуются и современные люди, например, отмечая зарубками количество прошедших дней, или карандашом отмечая черточками или точками в тетради количество проданных товаров.

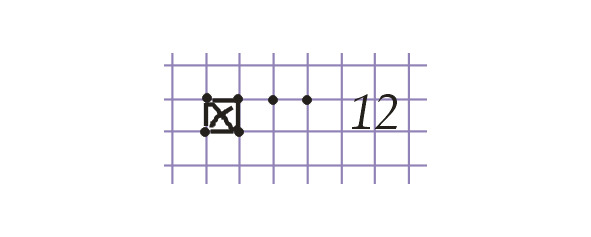
Единичная система — не самый удобный способ записи чисел. Запись больших чисел получается очень длинной и неудобной. С течением времени возникли другие, более удобные, системы счисления.

В непозиционной системе счисления абсолютно неважно, где стоит цифра — на первом или последнем месте. Для определения значения числа нужно сложить (или отнять) все числовые значения. Арифметические действия в непозиционных системах счисления очень неудобны и сложны.

Для обозначения чисел многие народы использовали существующие алфавиты. Такие системы счисления называются алфавитными. Алфавитные системы счисления использовались в Древней Греции, Руси, Риме.

Древние египтяне, Ацтеки и племена Майя для записи чисел использовали специальные символы (цифры). Разные цифры обозначались различными символами. Такие системы называются аддитивными.

Несмотря на то, что непозиционные системы счисления использовались человечеством на протяжении длительного периода, они были далеки от совершенства и имели ряд существенных недостатков: с их помощью нельзя было представлять дробные и отрицательные числа; возникали проблемы при записи очень больших чисел и самый главный недостаток — сложность выполнения арифметических операций.

Римские числа

Достоверных сведений о происхождении римских цифр нет. Скорее всего, эти цифры были заимствованы римлянами у этрусков или других народов.

Числа в римской системе счисления обозначают буквами латинского алфавита I, V, X, L, C, D и M.

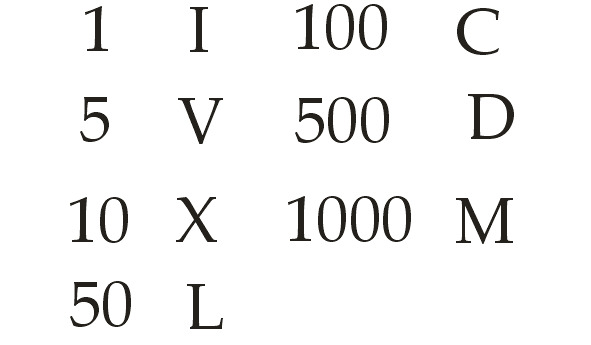
Такие обозначения частично произошли от рисунков, изображавших некогда соответствующие числительные (I — палец, V — пятерня с расставленными пальцами, X — две пятерни), а частично являются сокращениями латинских слов (centum — сто, demimille — пятьсот, mille — тысяча).

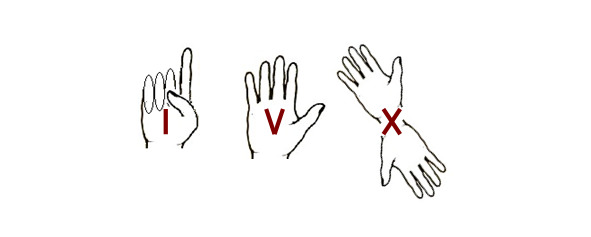
В римской записи буква I всегда означает единицу, буква V -пять, буква X –десять, L — 50, С — 100, D — 500, M — 1000.

В числе XXX, записанном в римской системе счисления, цифра X в любом месте означает десять.

В римской системе существовали и свои правила записи чисел: меньшие по разряду цифры идут после больших. Все числовые значения складываются.

Например, CCXXXVII = 100+100+10+10+10+5+1+1 = 237

Если цифра с меньшим значением записывалась перед цифрой с большим значением, то происходило ее вычитание.

Исключения составляют числа 9 (IX), 90 (XL), 900 (CM) — в этих числах стоящая слева цифра отнимается от следующей за ней цифры.

Например, число 3277 в римской системе записывается так:

МММССLXXVII=1000+1000+1000+100+100+50+10+10+5+2

Также существовало правило, по которому нельзя записывать подряд 4 одинаковых цифры. Такая комбинация заменяется комбинацией цифр с вычитанием от большей меньшей, причем меньшая цифра пишется слева.

Например:

XXXX=XC (50 — 10);

IIII=IV (5 — 1);

CCCC=CD (500 — 100).

Такая система записи чисел существовала в Италии до XIII века, а в некоторых странах Западной Европы — до XVI века.

Римская система счисления в настоящее время используется в основном, для наименования знаменательных дат, времени, разделов и глав в книгах.

Задания для самостоятельной работы

Задание 1. Запишите римской записью десятичные числа…

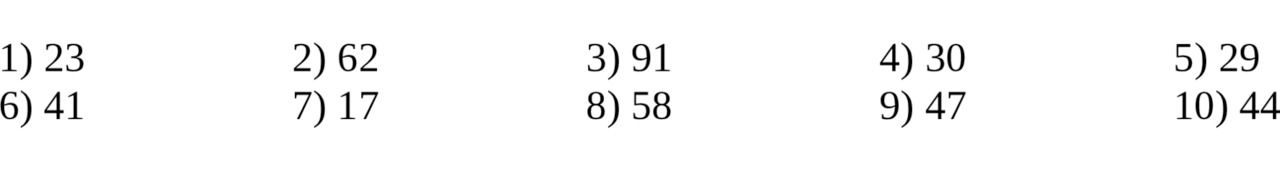
Задание 2. Запишите римской записью десятичные числа…

Задание 3. Переведите римские числа в десятичные…

Задание 4. Переведите римские числа в десятичные…

Задание 5. Выполните сложение чисел…

Греческие числа

В Древней Греции имели хождение две основных системы счисления — аттическая (или геродианова) и ионическая (она же александрийская или алфавитная).

Аттическая система счисления использовалась греками уже к V в. до н. э. По существу это была десятичная система (хотя в ней также было выделено и число пять), а аттические обозначения чисел использовали повторы коллективных символов. В этой нумерации числа 1, 2, 3, 4 изображались соответствующим количеством вертикальных полосок:

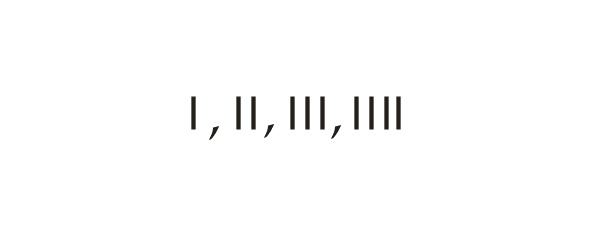
Число 5 записывалось знаком Г (древнее начертание буквы Пи, с которой начиналось слово пять — пенте.

Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков:

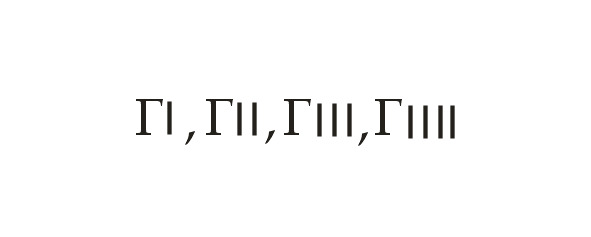
Число 10 обозначалось Δ — заглавной «Дельта» от слова «дека» — «десять».

Так как система была десятичной, грекам потребовались новые символы для каждой новой степени числа 10: символ H означал 100 (гекатон), X — 1000 (хилиои), символ M — 10000 (мириои или мириада).

Ионическая система счисления получила широкое распространение в начале Александрийской эпохи, примерно в III в. до н.э.

Переход к ионической системе счисления произошел в золотой век древнегреческой математики при жизни двух величайших математиков античности — Архимеда и Аполлония. Именно тогда они работали над усовершенствованием системы обозначения больших чисел. Архимед, придумавший схему октад (эквивалентную современному использованию показателей степени числа 10) писал в своем сочинении «Псаммит» («Исчисление песчинок»), что может численно выразить количество песчинок, необходимых для того, чтобы заполнить всю известную тогда Вселенную.

Изобретенная им система обозначения чисел включала число, которое ныне можно было бы записать в виде единицы, за которой следовало бы восемьдесят тысяч миллионов миллионов цифр.

Ионическая система использовала двадцать четыре буквы греческого алфавита и еще три архаических знака.

Первые девять букв соответствует первым девяти числам;

другие девять букв — первым девяти целым кратным числа десять;

последние девять символов — первым девяти целым кратным числа 100.

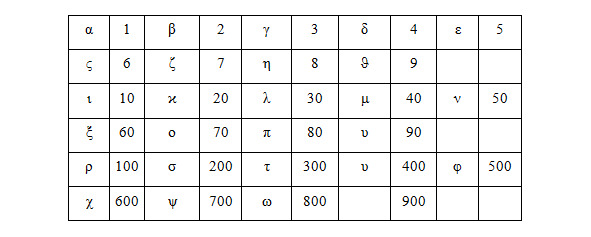
Для обозначения первых девяти целых кратных числа 1000 греки частично воспользовались принципом позиционности, снова использовав девять букв греческого алфавита, снабдив их штрихами слева.

Первоначально числа обозначались прописными буквами, но позднее сменились на строчные. Чтобы отличить числа от слов, греки над соответствующей буквой ставили горизонтальную черту.

Так число 631 в древнегреческой нумерации записывалось так:

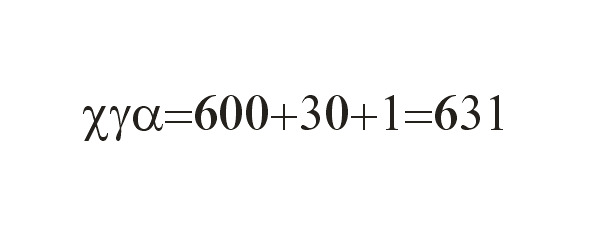
Если бы переставить цифры местами, число все равно обозначало бы 631.

Хотя такой способ записи чисел является простым, вычисления с такими числами были громоздкими и неудобными. Этот способ записи был позже позаимствован другими народами.

Со II века до нашей эры греческие астрономы уже пользовались цифрой ноль — ούδεν (ничто).

Задания для самостоятельной работы

Задание 1. Запишите греческой записью десятичные числа…

Задание 2. Запишите греческой записью десятичные числа…

Задание 3. Переведите греческие числа в десятичные…

Задание 4. Переведите греческие числа в десятичные…

Задание 5. Выполните сложение чисел…

Старославянская система счисления

Как и в других древних письменностях, в славянских азбуках буквы использовались и для обозначения чисел.

В древней Руси имели хождения два алфавита — кириллица и глаголица. Цифры соответственно обозначались либо на кириллице, либо на глаголице. В связи с этим иногда происходила путаница в обозначениях. Так в кириллице буква Б не имела числового значения. До XI — XII веков кириллица и глаголица употреблялись параллельно.

В отличие от кириллицы, на основе которой возникли русская, болгарская, сербская и другие системы письма глаголица просуществовала недолго, причем главным образом у юго-западных славян (в Хорватии и Далмации). Эта нумерация была создана для переписки чисел в священных книгах западных славян. Использовалась она с VIII по XIII в.

Кириллическая нумерация была создана вместе со славянской алфавитной системой для переписки священных книг для славян греческими монахами братьями Кириллом (Константином) и Мефодием в IX веке. Эта форма записи чисел получила большое распространение за сходство с греческой записью чисел. До XVII века эта форма записи была официальной на территории современной России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию.

В древней кириллице — 24 буквы греческого унциального устава и специально созданные буквы, отсутствующие в греческой азбуке и необходимые для передачи соответствующих славянских звуков.

В России славянская нумерация сохранилась до конца XVII века. При Петре I в обиход вошла арабская система, которой мы пользуемся и сейчас.

Для того чтобы при письме отличать числа от слов, над числами ставился специальный знак — титло:

Также был специальный знак для обозначения тысяч:

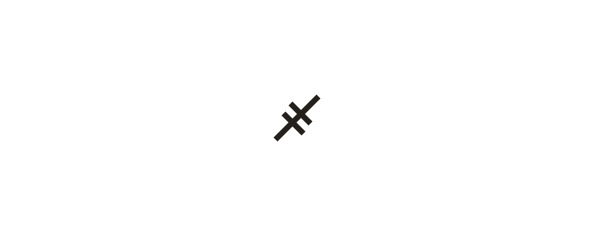
Так 4000 записывалось в виде:

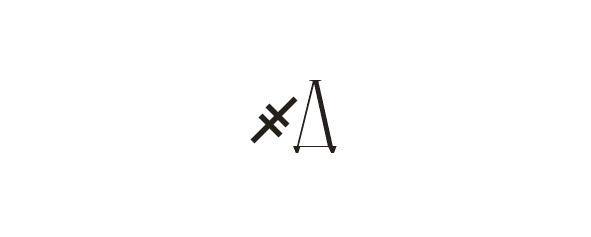
Для больших чисел также были свои обозначения:

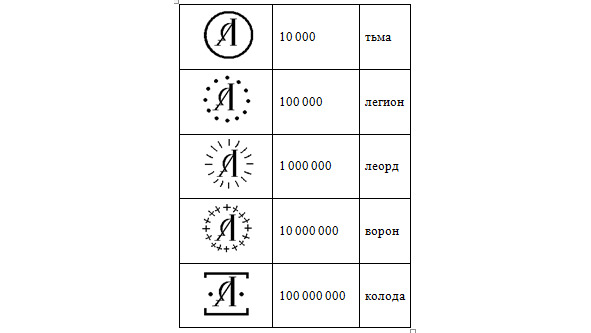
Для единиц, десятков и сотен в обеих азбуках (кириллице и глаголице) служат буквы разных групп. Причем в обозначениях чисел от 11 до 19 на первом месте ставится обозначение единиц, в соответствии с чтением — семнадцать:

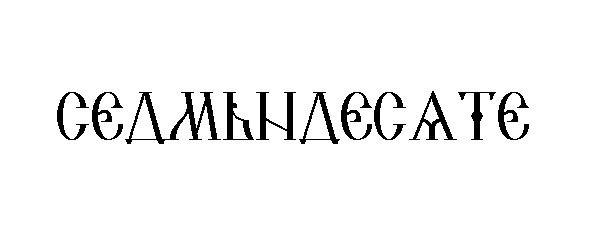
Записывались цифры числа начиная с больших значений и заканчивая меньшими, слева направо. Если десятков, единиц, или какого-то другого разряда не было, то его пропускали.

Интереснее всего записывались числа второго десятка:

Дословно читается «четырнадцать» — «четыре на десять». И так для всех чисел от 11 до 19.

Запись числа, использованная славянами аддитивная, то есть в ней используется только сложение: 800+60+3=863:

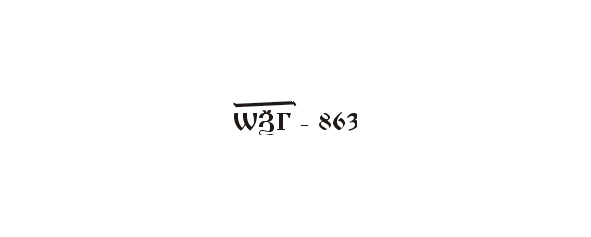
Числовые значения букв алфавита

Кириллица