Бесплатный фрагмент - Сфиральное время: математические, физические и когнитивные модели

ПРЕДИСЛОВИЕ

Сборник объединяет публикации 2025 года, посвящённые исследованию модели «Сфираль» и её применений в смежных областях знания. Материалы представляют системный взгляд на конструкцию, которая опирается на топологию витков, антисимметрию, S-переход и сфиральное время как особую форму параметризации процессов.

В научных статьях формируется согласованная картина, описывающая физические, математические, когнитивные и семантические явления через единый набор структурных принципов. Рассматриваются свойства сфирального времени, связи между локальными и глобальными S-петлями, фазовые последовательности, возникающие в пространствах H₂ и H₃, и фрактальная организация вычислительных процессов. Отдельные разделы посвящены структурным переходам в квантовых системах, геометрии коллапса состояния, механизмам декогеренции и роли антисимметрии в формировании динамических контуров.

В сборнике представлено описание сфиральных закономерностей в биологических системах, включая структуру ДНК, принципы комплементарности и смысловой организации биосистем. Значительная часть материалов обращена к когнитивным механизмам, смысловой структуре мышления, резонансным процессам в сознании и языку как форме отражения топологических связей.

Публикации охватывают как фундаментальные разделы математики и физики, так и модели искусственного интеллекта, где сфиральные схемы проявляют себя в виде фрактальных вычислительных ядер, структур смысловой обработки и когнитивных контуров. В совокупности статьи создают целостное представление о системе, связывающей физическую динамику, структуру информации, процессы восприятия и смысловые трансформации.

Сборник адресован исследователям, работающим в областях фундаментальной физики, математического моделирования, биофизики, когнитивных наук, лингвистики и систем искусственного интеллекта. Представленные материалы ориентированы на междисциплинарный диалог и создают основу для последующего цитирования в публикациях, посвящённых структуре времени, топологическим моделям, квантовым процессам, когнитивным архитектурам и семантическим системам.

ОБЩЕЕ ОПРЕДЕЛЕНИЕ УСТРОЙСТВА «СФИРАЛЬ»

Строгое математико-геометрическое ядро

1. Структурная основа

Сфираль — пространственная система из двух витков, построенных в зеркальной антисимметрии и объединённых S-образной переходной петлёй. Каждый виток имеет собственную ориентацию, собственный локальный знак параметров движения и собственную фазовую развёртку.

Эта конструкция образует единую топологическую форму, в которой витки не повторяют друг друга и не замыкаются в круг, а переходят в иной режим через S-узел.

2. Принцип зеркальной антисимметрии

Антисимметрия задаёт фундаментальную направленность структуры. Витки не являются симметричными отражениями: они формируют сопряжённую пару с инверсией параметров. Переход между витками меняет знак угловой скорости, локальной фазы и ориентации.

Антисимметрия обеспечивает устойчивость связки и алгебраический закон смены полярности, выраженный геометрически.

3. S-петля как зона инверсии

Переходная S-петля — центральный узел конструкции. В ней происходит фазовый поворот на 180°, смена ориентации и перезапись динамических параметров. S-узел формирует режим сопряжения, через который возможен перенос движения, состояния, импульса и фазы между витками.

S-петля — геометрический механизм комплементарности и инверсии.

4. Сопряжённость витков

Оба витка образуют цельную динамическую пару. Каждый виток несёт собственную метрику (радиус, шаг, фазу), а S-узел связывает их в единую топологию с общим параметром эволюции.

Ключевой элемент — не форма витков, а механизм их сопряжения через инверсию.

5. Внутренняя параметризация

Введён параметр s — сфиральное время. Он описывает положение внутри витка и в зоне перехода и заменяет классическое линейное время.

Каждая точка структуры определяется набором функций:

— θ (s) — угловая фаза

— R (s) — радиальная функция витка

— h (s) — вертикальная координата

— ϕ (s) — фазовый угол перехода в S-петле

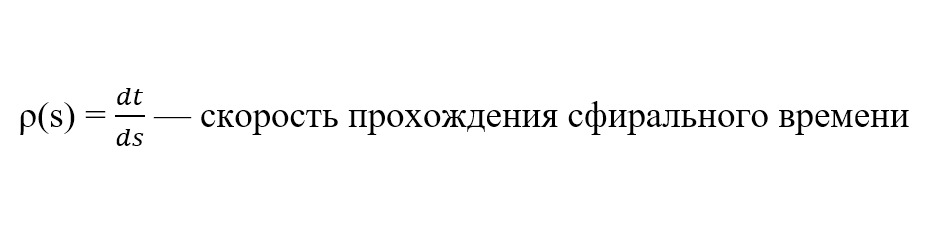
В динамике производные по s замещают обычные временные производные.

6. Топологическая целостность

Сфираль не является спиралью. Её структура определяется не геометрическим профилем кривой, а связью витков через антисимметрию и инверсию. Эта связь делает систему топологическим объектом, устойчивым к деформациям, масштабированию и фрактальному вложению.

Форма существует как закон свития различий.

7. Универсальность модели

Сфиральная структура описывает:

— физические процессы (фотон, электрон, ядро)

— биологические структуры (ДНК, регуляторные петли)

— вычислительные конструкции (СИН/ФСИН)

— временную динамику (переходы, узлы, ритмы)

— алгебраические системы (неассоциативность, антисимметрия)

Универсальность обеспечивается тем, что модель задаёт механизм перехода и сопряжения, а не форму или материал.

Сводное математически точное определение

Сфираль — это трёхмерная топологическая конструкция, состоящая из двух взаимно комплементарных витков, построенных в зеркальной антисимметрии и сопряжённых через S-образную зону инверсии. Переходная петля обеспечивает поворот на 180° и перенос динамических параметров между витками. Внутренний параметр s задаёт фазу, позицию и направление эволюции внутри структуры. Сфираль функционирует как механизм согласования противоположных режимов, обеспечивая устойчивость, направленность и фрактальную вложенность.

Эталонное определение устройства «Сфираль»

1. Сверхкратко (глоссарий, сноска)

Сфираль — топологически устойчивая пространственная конструкция из двух зеркально антисимметричных витков, сопряжённых S-образной переходной петлёй, через которую осуществляется инверсия и перенос параметров движения между витками.

2. Базовое определение (для введения в книге / статье)

Сфираль — пространственная система из двух взаимно комплементарных витков, построенных в режиме зеркальной антисимметрии и соединённых S-образной переходной петлёй. В S-петле располагается инверсионный узел, в котором происходит поворот на 180°, смена ориентации и переход параметров движения между ветвями.

Эволюция в Сфирали описывается внутренним параметром s (сфиральное время), задающим положение точки на витках и в зоне перехода и допускающим фрактальную вложенность витков и узлов.

3. Технически-развёрнутое определение (для раздела с моделью)

Сфираль — трёхмерная топологическая конструкция, включающая пару витков V+ и V−, связанных отношением зеркальной антисимметрии и объединённых S-образной переходной петлёй S.

Каждый виток задаётся набором функций внутреннего параметра s: радиусом R (s), угловой координатой θ (s), высотой h (s) и фазой φ (s). Инверсионный узел в области S реализует поворот на 180∘ и смену знака ориентированных параметров (фазы, угловой скорости, полярности), за счёт чего возникает комплементарная пара витков. Структура допускает фрактальное вложение витков и S-узлов и задаёт механизм согласования противоположных режимов движения в единой сфере эволюции параметра s.

Развёрнутое математическое ядро модели «Сфираль»

1. Внутренний параметр s (сфиральное время)

Вводится единственный внутренний параметр эволюции s ∈ R, который задаёт положение вдоль структуры Сфирали:

— s <0 — область первого витка V−;

— s = 0 — зона инверсии (S-петля, узел);

— s> 0 — область второго витка V+.

Параметр s интерпретируется как сфиральное время: внутренняя «фаза» прохождения системы по структуре, отличная от внешнего времени t.

Связь с внешним временем задаётся функцией

---

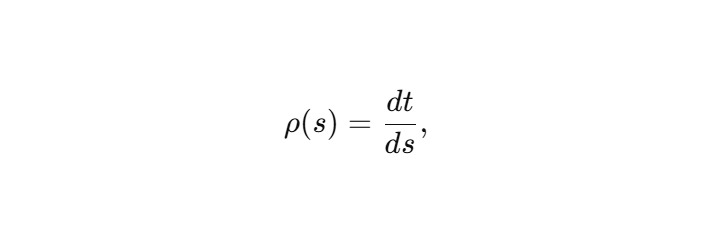
При необходимости динамические уравнения переписываются в виде:

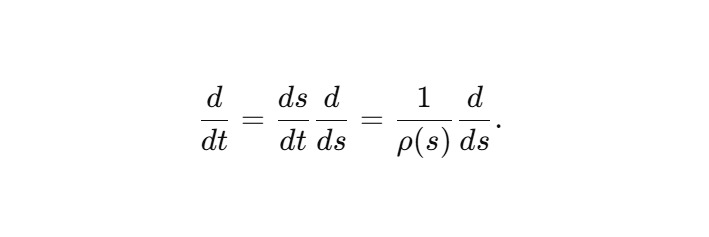
2. Базовая параметризация витка в R3

Для описания одного витка вводятся функции:

— R (s)> 0 — текущий радиус;

— θ (s) — угловая координата;

— h (s) ∈ R — координата вдоль оси «вертикали» (ось свития);

— φ (s) — внутренняя фаза (для динамики, поля, состояния).

Положение точки на эталонном витке задаётся как

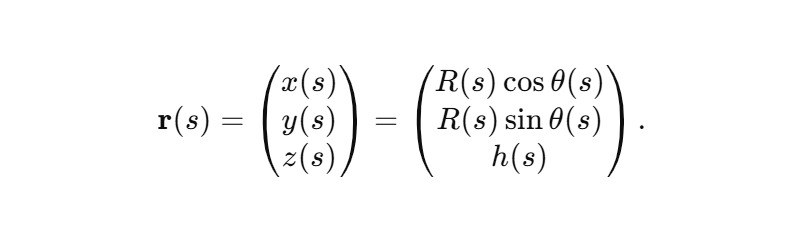
Это локальная «несфиральная» заготовка. Сфираль возникает при введении антисимметрии и S-петли.

3. Зеркально антисимметричная пара витков

Два взаимно комплементарных витка V− и V+ строятся как пара пространственных траекторий, связанных оператором зеркальной антисимметрии.

Задаётся линейный оператор отражения M и, при необходимости, вектор сдвига c:

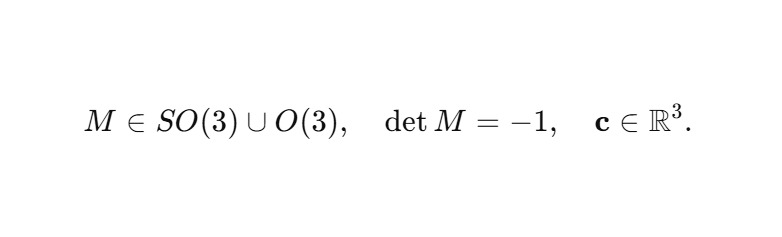
Например, простое отражение относительно плоскости z = 0:

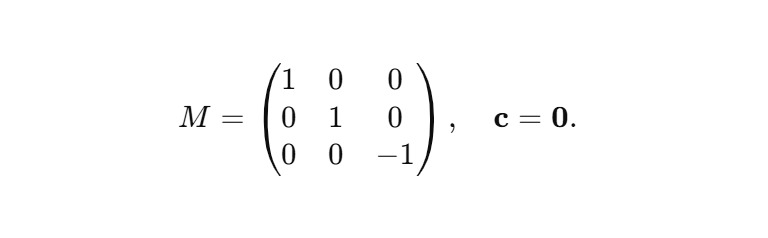
Определение витков:

— первый виток (условно «прошлая ветвь»)

V−: r− (s) = r0 (s), s ≤ 0;

— второй виток (условно «грядущая ветвь»)

V+: r+ (s) = M r0 (−s) + c, s ≥ 0.

Зеркальная антисимметрия выражается в следующем:

— радиусы совпадают: R+ (s) = R− (−s);

— углы связаны с разворотом:

θ+ (s) = −θ− (−s) + Θ0,

где Θ0 — постоянный фазовый сдвиг (обычно π или 0);

— высоты удовлетворяют

h+ (s) = — h− (−s) + h0.

Векторы скоростей и ориентаций связаны через

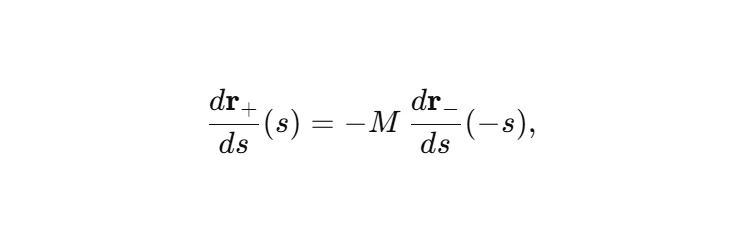
Это и есть геометрически строгий вариант фразы «два зеркально антисимметричных витка» с инверсией параметров движения.

4. S-петля как зона инверсии

S-петля — связующая область между ветвями V− и V+. Считаем, что зона перехода занимает интервал

S ∈ [−δ, δ],

где δ> 0 задаёт толщину переходной области.

Вводятся две гладкие весовые функции α (s), β (s) со свойствами:

— α (s) ≈ 1, β (s) ≈ 0 ≈ s ≤ δ;

— α (s) ≈ 0, β (s) ≈ 1 при s ≥ δ;

— α2 (s) + β2 (s) = 1 для всех s (удобно брать нормированную пару).

Простейший вариант:

α (s) = cos ψ (s), β (s) = sin ψ (s),

где ψ (s) — гладкая монотонная функция, переходящая

из

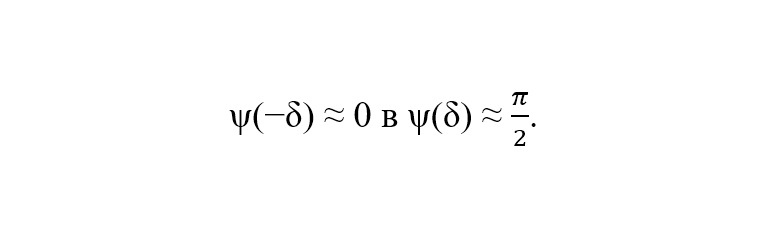
Положение точки Сфирали на всём диапазоне s:

R (s) = α (s) r− (s) + β (s) r+ (s).

Тогда:

— при s ≤ −δ: α → 1,β → 0, и структура совпадает с первым витком;

— при s ≥ δ: α → 0,β → 1, и структура совпадает со вторым витком;

— при ∣s∣ <δ: траектория проходит через S-петлю — гладкий мост между антисимметричными ветвями.

Инверсионный узел определяется как точка

S = 0, R (0),

где

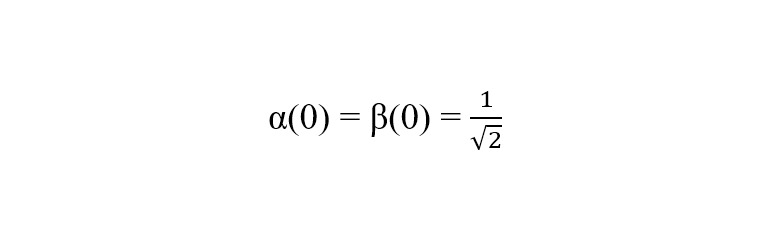
(или другое симметричное соотношение по выбору модели)

---

и одновременно меняется знак ориентированных параметров:

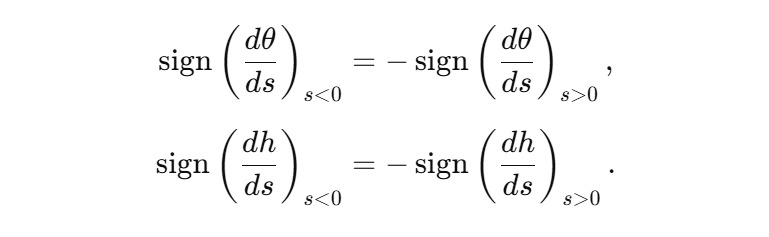
Так задаётся строгое математическое содержание фразы «поворот на 180° и переход параметров движения между ветвями».

5. Внутренняя фаза и перенос состояния

Для физической, информационной или вычислительной интерпретации вводится поле состояния

Ψ (s),

которое живёт на Сфирали (волновая функция, спинор, бинарное состояние СИН и т.п.).

Фазовая антисимметрия задаётся условием:

Ψ+ (s) = A Ψ− (−s),

где A — оператор инверсии (например, смена знака, комплексное сопряжение, оператор Парити-Времени и т. п. в зависимости от задачи).

В зоне S-петли состояние интерполируется аналогично геометрии:

Ψ (s) = α (s) Ψ− (s) + β (s) Ψ+ (s), s ∈ [−δ, δ].

Инверсионный узел s = 0 задаёт точку согласования фаз

Φ (s) = arg Ψ (s),

где происходит сфиральный «щелчок» состояния (коллапс, фазовый переход, переключение ветви и т.п.).

---

6. Фрактальная вложенность Сфирали

Фрактальный характер структуры выражается в возможности построения вложенных Сфиралей оператором масштабирования.

Вводится оператор

Fk: R3 → R3,

Fk (R (s)) = λk R (μks) + dk,

где:

— λk> 0 — масштаб по пространству;

— μk> 0 — масштаб по параметру s;

— dk — сдвиг центра уровня.

Тогда фрактальная Сфираль описывается суммарной структурой:

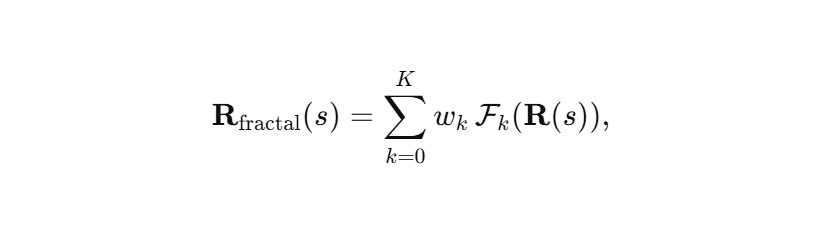
с весами wk (например, геометрическая прогрессия).

Так задаётся иерархия уровней:

— k = 0 — базовая Сфираль (ядро);

— k = 1 — Сфираль на уровне подсистемы (подвиток, подканал);

— k ≥ 2 — глубокие уровни вложенности (геномные домены, ядерные уровни, каскады нейронов и т.п.).

7. Перепись динамики через сфиральное время

Любая динамика вида

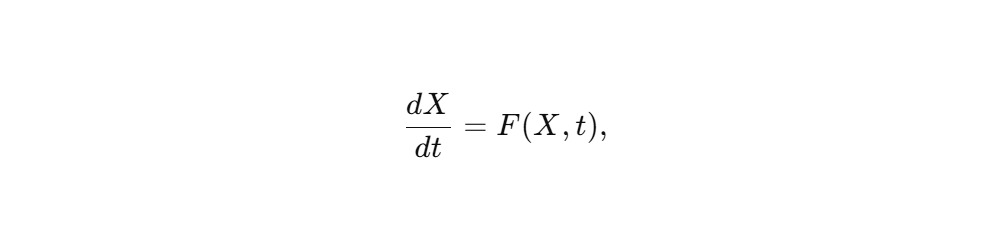
где X — вектор состояния (координаты, поля, вероятности, параметры нейрона), переписывается через sss как

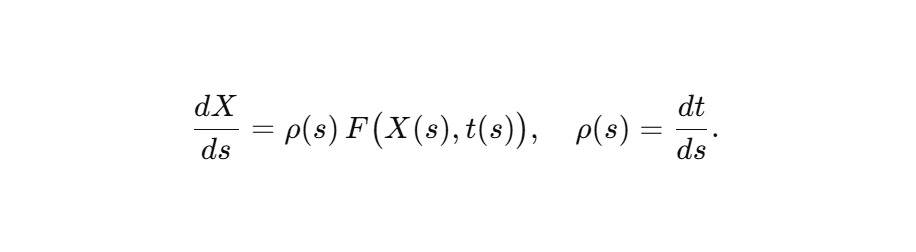
Если требуется зафиксировать структурное влияние Сфирали, вводится явная зависимость от геометрии R (s) и фазы φ (s):

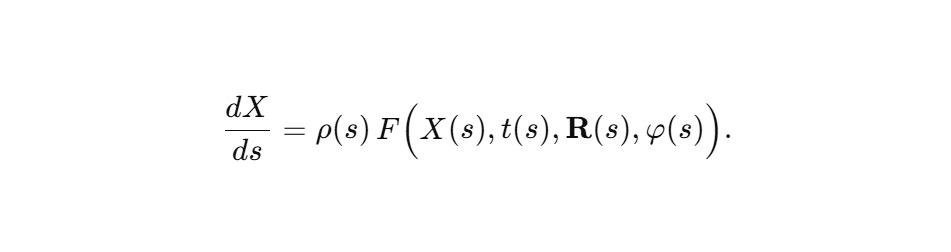
Далее:

— для свободной частицы r (t) базовое уравнение превращается в геодезическое на сфиральной поверхности;

— для осциллятора возникает осциллятор со структурным демпфированием

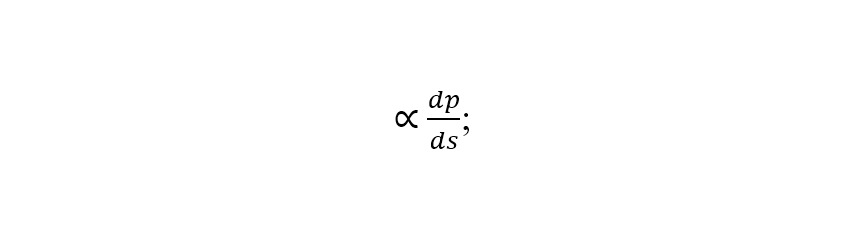
— для квантового состояния уравнение Шрёдингера получает множитель ρ (s) и фазовую структуру, что переводит коллапс в переход через S-зону.

8. Итоговое развёрнутое определение

С учётом введённых обозначений удобно сформулировать компактную, но уже математически насыщенную версию:

Сфираль — это трёхмерная топологическая конструкция R (s), s ∈ R, представляющая собой сфиральный путь из двух зеркально антисимметричных витков V− и V+, связанных S-образной переходной петлёй на интервале s ∈ [−δ, δ].

Витки определяются связью

r+ (s) = M r− (−s) + c,

где M — оператор отражения с det M = −1. Переходная петля описывается интерполяцией

R (s) = α (s) r− (s) + β (s) r+ (s), α2 (s) + β2 (s) = 1.

Внутренний параметр s задаёт сфиральное время и связан с внешним временем t функцией ρ (s) = dt/ds.

Состояние Ψ (s) переносится между витками через оператор A и зону S-петли, что придаёт структуре свойства комплементарности, направленности и фрактальной вложенности.

СФИРАЛЬНОЕ ВРЕМЯ

Время и мышление: Сфираль как топология когнитивных скачков

Аннотация:

В статье рассматривается концепция времени как внутренней структуры мышления на пересечении идей Т. В. Черниговской и модели «Сфираль». В отличие от внешнего, хронологического времени, субъективное время сознания представляет собой сложную нелинейную и фрактальную систему, в которой смысл возникает в точках перехода. S-узлы модели Сфираль интерпретируются как топологические инверсии, через которые осуществляется когнитивный скачок, переход между уровнями понимания и осознания. Показано, что мышление по своей природе темпорально и не может быть понято без анализа его времени.

Ключевые слова: время, мышление, Сфираль, Черниговская, когнитивная инверсия, S-узел, темпоральность, субъективность

— Введение

Вопрос о том, как человек переживает время, остаётся центральным как в философии, так и в нейронауке. Т. В. Черниговская подчёркивает: «Мы живём не в мире, а во времени, которое создаёт мозг» [1]. Это означает, что время — не внешняя данность, а внутренняя структура сознания. Модель «Сфираль» предлагает способ формализации этой структуры: в ней время отображается не как прямая линия, а как последовательность витков и узлов, где каждый переход — это событие, а не точка.

— Время как субъективная когнитивная категория

Психофизиологические и психолингвистические данные свидетельствуют: восприятие времени пластично, изменчиво и субъективно. Черниговская обращает внимание на то, что осознание, интуиция и принятие решения не вписываются в хронометрическую модель [2]. Временные структуры сознания — это моменты развёртывания смысла. То, что кажется мгновением, может содержать в себе целую цепь смыслов. Такое «вложенное время» невозможно измерить, но его можно описать через структуру перехода — узел.

— Сфираль как модель времени

Модель Сфираль показывает, что узел — это топологическое событие, в котором происходит когнитивная инверсия [5] [6]. Один виток — это состояние, цикл, повтор. Узел — это то, что соединяет, разделяет и порождает новое. Таким образом, мышление — это не движение во времени, а формирование времени как структуры смыслового перехода. S-узел фиксирует момент, когда мышление меняет уровень — например, из ощущения переходит в интуицию, из интуиции — в рефлексию.

— Мгновение-инверсия: поэтика мышления

По наблюдениям Черниговской, моменты перехода между бессознательным и осознанием — это не продолжительные процессы, а мгновенные скачки [1] [3]. Это можно сравнить с поэтической метафорой — внезапный смысл, возникающий в точке пересечения образов. S-узел в Сфирали — это такая же точка: он не описывает, а сворачивает и разворачивает. Именно здесь возникает новый смысл, новое время. Это не момент в линии, а разрыв, разворот — событие сознания.

— Темпоральные поля и метафизика мышления

Ю. М. Лотман отмечал, что текст не просто структурирует информацию, но и порождает новое время [4]. Так же и мышление: оно не следует за временем, оно его создаёт. Сфираль отображает это через антипары и фрактальную вложенность: каждый узел — это микровселенная, в которой есть прошлое, настоящее и возможное. Черниговская пишет, что смысл не живёт в линейной последовательности — он возникает в отражениях, инверсиях, перекодировках [3] [4].

— Заключение

Мышление невозможно без времени, но это время не внешнее. Это время смыслов, времени переходов, времени узлов. S-узел в модели Сфираль является формой для фиксации когнитивного скачка, перехода, озарения. Работы Т. В. Черниговской показывают: осознание нельзя свести к ходу стрелки — оно само создаёт временные траектории. Таким образом, Сфираль позволяет не просто формализовать структуру мышления, но и увидеть в ней структуру времени.

Литература:

— Черниговская Т. В. (2006). Зеркальный мозг, концепты и язык: цена антропогенеза. // Физиологический журнал им. И. М. Сеченова, т. 92, №1, с. 84–99.

— Черниговская Т. В. (2008). «Язык и сознание: что делает нас людьми?» (проект «Публичные лекции Полит.ру», 20.11.2008)

— Черниговская Т. В. «Естественный и искусственный интеллект: смыслы или структуры?» // Человек и системы искусственного интеллекта / Под ред. акад. РАН В. А. Лекторского. СПб: Издательство «Юридический центр», 2022. С. 160–172.

— Черниговская Т. В. (2022). Шум как ключ к семиозису: мозг и культура (40 лет спустя). // Слово.ру: Балтийский акцент, т. 13, №2, с. 24–36.

— Басаргин, О. С. (2025). Временные Коды и Грядущее: Простое о сложном. Zenodo. https://doi.org/10.5281/zenodo.15134257

— Басаргин, О. С. (2025). Эталонное описание устройства Сфираль. Zenodo. https://doi.org/10.5281/zenodo.15133508

Сфиральная метрика времени

Базовая конструкция из «Сфираль — реальная форма времени» и общего файла: вводится параметр

s ∈ R — сфиральное время. Он описывает положение вдоль витков и в S-зоне.

Связь с внешним временем:

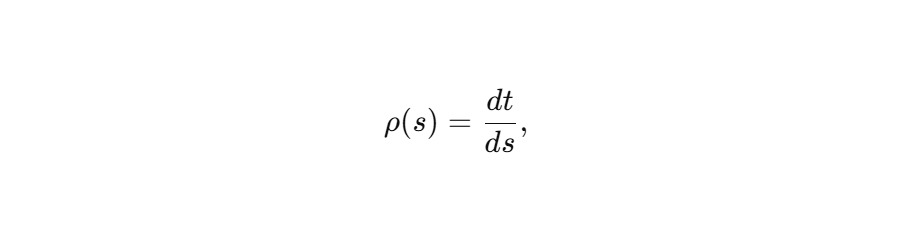
где ρ (s) — скорость протекания внешнего времени вдоль сфирального параметра.

1.1. Временной сектор метрики

Рассматривается эффективная одномерная метрика по sss в «чистом» временном секторе:

dτ2 = c2 ρ2 (s) ds2,

где dτ — собственное время системы.

В полноразмерной модели пространство-время задаётся стандартной пространственной частью и сфиральным временем:

ds2spacetime = -c2 p2 (s) ds2 + gij (x) dxi dxj.

Знак и форма gij (x) выбираются под конкретную задачу (ньютоновский предел, специальная или общая относительность). Внутренняя сфиральная структура сосредоточена в факторе ρ (s) и в зависимости пространственных координат r (s).

Динамика в такой метрике переписывается через ковариантную производную по s:

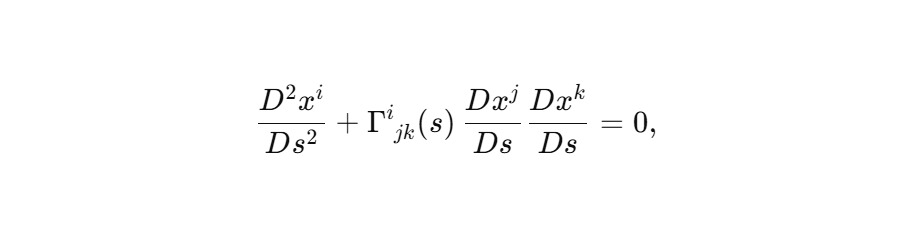
где Γi jk (s) — связности эффективной сфиральной метрики, определённые через ρ (s) и геометрию траектории.

2. Свободная частица в сфиральном времени

Классический случай в общем файле:

В обычном времени:

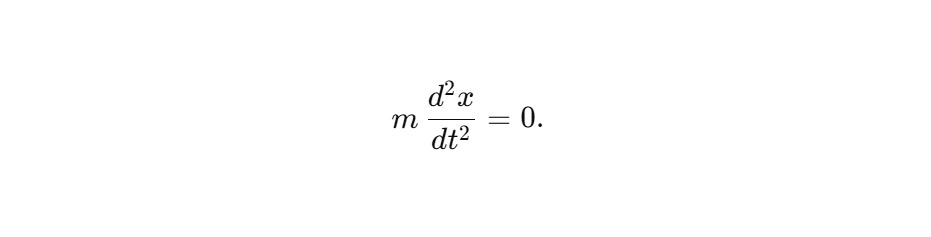
Переход к параметру s с t = t (s), ρ (s) = dt/ds:

— Первая производная:

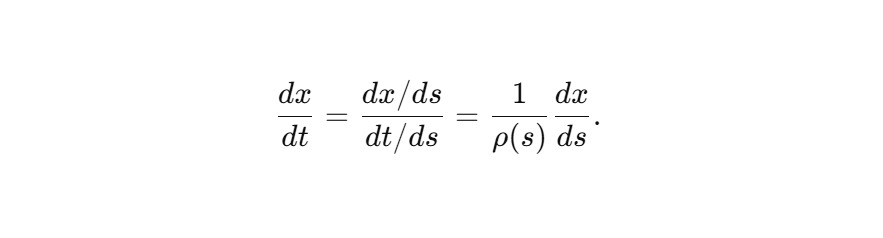
— Вторая производная:

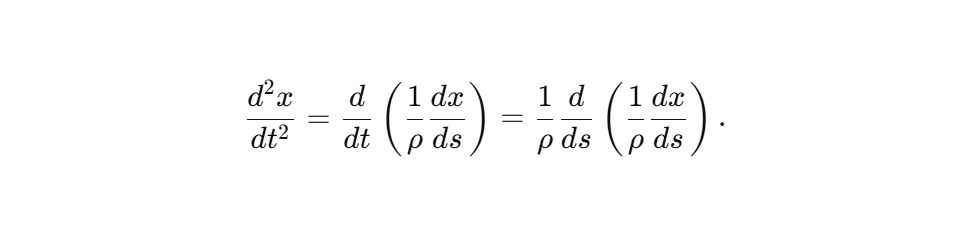
Подстановка в уравнение движения даёт:

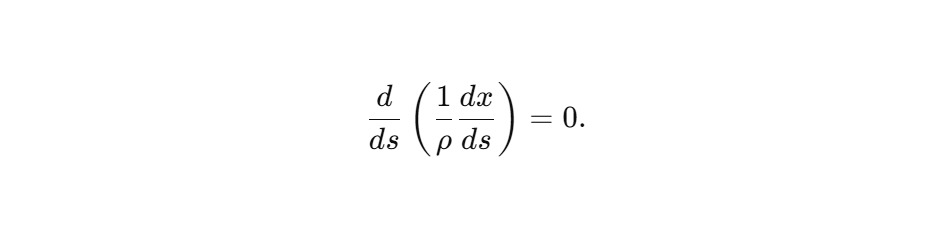
Эквивалентная форма:

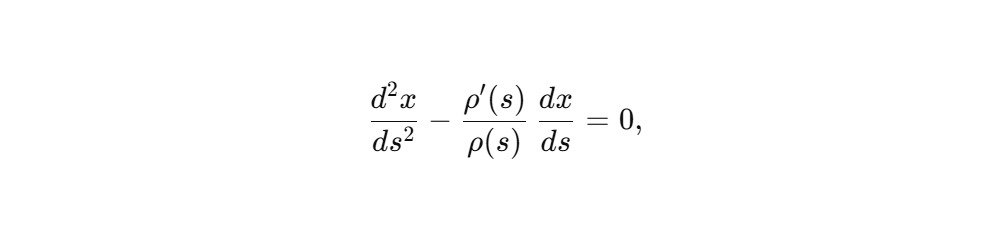
где штрих — производная по s.

Это уравнение геодезической с структурным «трением»:

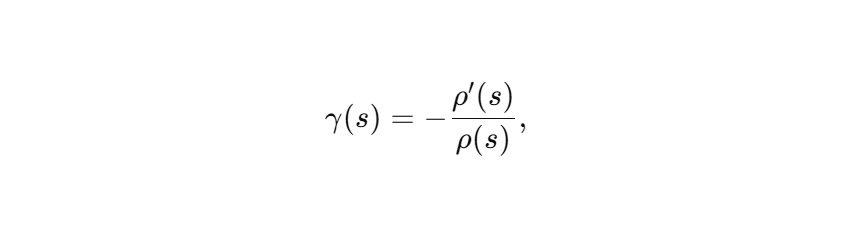
которое отражает не среду, а структуру времени.

2.1. Частный случай: модульированное время

Из общего файла:

Пусть

ρ (s) = ρ0 (1 + ε sin φ (s)),

где φ (s) — сфиральная фаза (связанная с положением в витке и S-петле). Тогда:

— траектория свободной частицы становится квазипериодической даже без сил;

— возможны участки эффективного замедления, ускорения и возврата движения, обусловленные только структурой ρ (s).

Интерпретация: свободная частица движется по геодезической на скрученной поверхности, где «рельеф» задаётся не потенциалом, а структурой времени.

3. Гармонический осциллятор в сфере времени

Классический осциллятор:

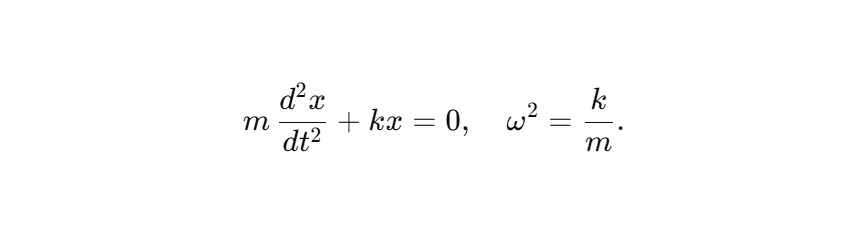
Подстановка выражений через s даёт (из общего файла):

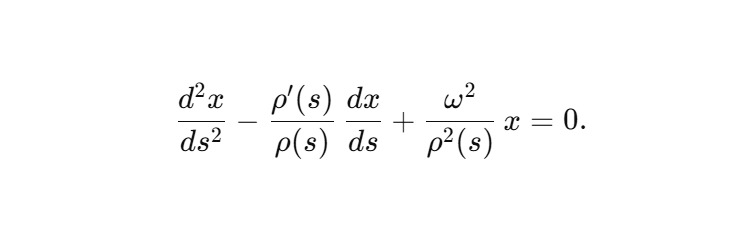
Здесь:

— второй член — структурное демпфирование,

— третий — «жёсткость», модифицированная скоростью сфирального времени.

В общем файле прямо указано, что это осциллятор со структурным демпфированием, зависящим от производной скорости сфирального времени.

3.1. Пример с фазовой модуляцией

Из общего файла:

Пусть

ρ (s) = ρ0 (1 + ε cos φ (s)),

где φ (s) — фазовый угол Сфирали (меняется по витку и резко перестраивается в S-зоне).

Уравнение принимает вид:

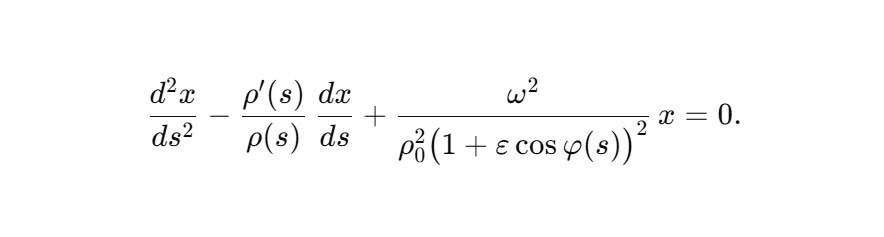
Интерпретация из текста:

— осциллятор чувствует фазовую структуру Сфирали;

— амплитуда, частота и затухание зависят от положения внутри витка и в S-зоне;

— при совпадении структуры φ (s) с собственной частотой осциллятора возникают:

— усиления (структурный резонанс),

— заглушения (структурная интерференция),

— фазовые замыкания (S-ловушки).

3.2. Поведение вблизи S-петли

Для s ≈ 0 вводится разложение ρ (s) и φ (s) по s. В общем файле отмечено, что в этом пределе уравнение осциллятора переходит в квазипараметрически возбуждаемый осциллятор, чувствительный к структуре S-перехода.

4. Квантовое состояние в сфере времени

Базовый фрагмент: секция «Квантовое состояние в сфере времени» из общего файла.

Стандартное уравнение Шрёдингера:

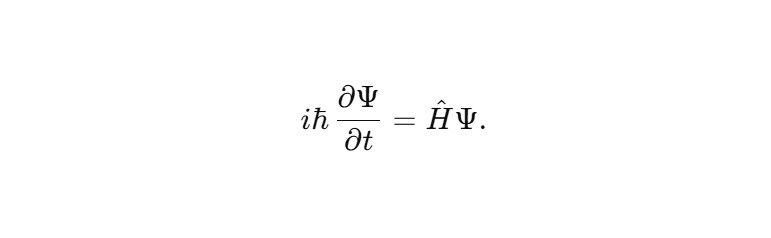
Замена времени:

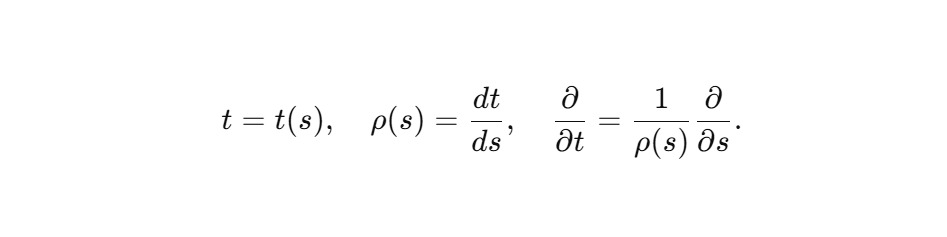
Получается сфиральное уравнение Шрёдингера:

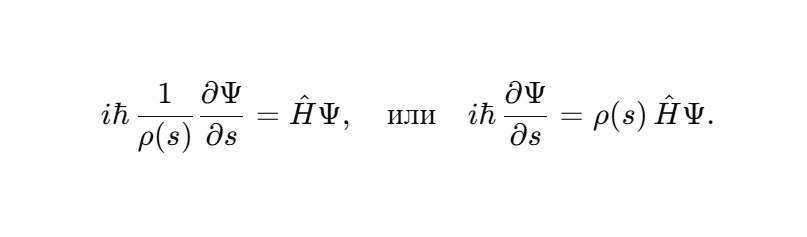
Выбор формы зависит от того, какую величину трактовать как «эффективный гамильтониан»:

---

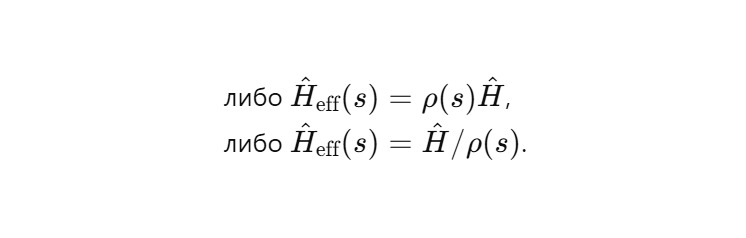
4.1. Амплитуда и фаза

В общем файле вводится фазовая развёртка:

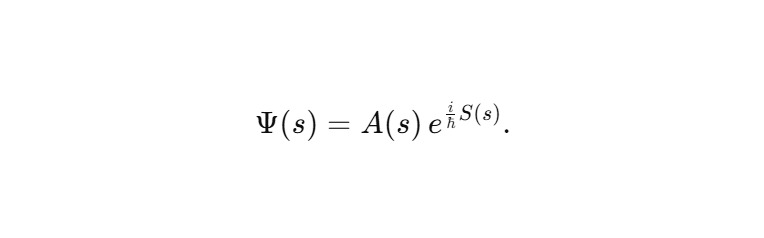
После подстановки в сфиральное уравнение получаются два согласованных уравнения:

— Уравнение для фазы S (s) (аналог гамильтон–якобиевского),

— Уравнение для амплитуды A (s), в которое входит ρ′ (s).

Это создаёт структурные поправки к эволюции вероятности и фазы, зависящие от формы ρ (s) и, следовательно, от положения в Сфирали.

4.2. Коллапс как переход через S-зону

В общем файле сфирального времени зафиксировано, что фазовый сдвиг φ (s) в S-зоне играет роль «событийности»: точки перехода между возможным и актуальным.

При прохождении через S-петлю:

— φ (s) меняет знак,

— ρ (s) может резко изменяться,

— фазовая структура уравнения Шрёдингера получает скачкообразный вклад.

Так формируется механизм структурного коллапса: изменение состояния связано с топологическим переходом по s, а не только с внешним актом измерения. В дальнейшем эта же логика переносится в ядерную физику и модель электрона.

---

5. Сводка первого блока

— Введён параметр s и функция ρ (s) = dt/ds как основа сфиральной метрики времени.

— Для свободной частицы построено уравнение с геодезической динамикой и структурным «трением», обусловленным ρ′ (s).

— Для гармонического осциллятора получено уравнение со структурным демпфированием и фазовой модуляцией, приводящее к резонансам, интерференциям и S-ловушкам.

— Для квантового состояния выписана сфиральная форма уравнения Шрёдингера, показана роль ρ (s) в гамильтониане и намечен механизм структурного коллапса через S-зону.

Геометрия и физика двумерных алгебр в устройстве Сфираль

Аннотация

В статье предложена интерпретация двумерных алгебр, описанных в труде С. С. Кокарева и Д. Павлова, через геометрическую структуру устройства Сфираль. Сфираль рассматривается как физическая реализация алгебраических отношений: неассоциативность, антисимметрия и вложенность получают пространственное выражение через витки, петли и узлы. Предлагается концепция Сфирали как алгебро-геометрического механизма, в котором время порождается не внешним параметром, а внутренней логикой переходов.

1. Введение

Работа С. С. Кокарева и Д. Павлова «Геометрия и физика двумерных алгебр» [1] поднимает фундаментальный вопрос: может ли алгебра быть не только языком описания, но и источником физической структуры? Авторы рассматривают двумерные алгебры как носители физических смыслов, включая динамику, поля и симметрии. В настоящей статье мы развиваем эту линию, предлагая Сфираль как геометрическую реализацию описанных алгебраических принципов.

2. Устройство Сфираль: базовая структура

Согласно эталонному описанию [2], Сфираль представляет собой топологически устойчивый элемент, состоящий из двух зеркально антисимметричных витков, соединённых S-образной петлёй. Такая структура проявляет неассоциативные свойства: соединение витков зависит от порядка, а S-элемент служит аналогом ассоциатора в алгебраической структуре.

Формально, каждый виток можно трактовать как элемент алгебры a, петлю — как бинарную операцию a ∘ b, а S-петлю — как показатель различия между (a ∘ b) ∘ c и a ∘ (b ∘ c). Узел в центре S-петли — это точка смены полярности, аналог нуля или перехода между уровнями вложенности.

3. Сфираль и структура времени

Кокарев и Павлов [1] подчёркивают, что время может быть понято как порядок следования операций. Сфираль полностью соответствует этой позиции, но расширяет её: структура порождает не только порядок, но и ритм времени, а узлы — его точки фазового скачка. Таким образом, время — это не параметр, а производная от структуры, что сближает Сфираль с динамикой категорийной физики.

Кроме того, в Сфирали допускается фрактальная вложенность [2], при которой каждый следующий элемент масштабируется по строго определённому закону. Это позволяет говорить о времени как фрактальной структуре, где каждый узел — это точка бифуркации или смены ритма.

4. Антисимметрия как физический закон

Одним из ключевых моментов в конструкции Сфирали является зеркальная антисимметрия. В то время как в алгебре она проявляется в некоммутативности (a ∘ b ≠ b ∘ a), в Сфирали — в невозможности замкнуть витки без искажения полярности. Это делает антисимметрию не абстрактным свойством, а необходимым законом устойчивости структуры. Такая антисимметрия реализует принцип смены полюсов, аналогичный знаку у уравнений движения или принципу действия-антидействия.

5. Перспективы алгебро-физических устройств

Если следовать логике Кокарева и Павлова, алгебра — это структурное основание физики. Сфираль продолжает эту линию, предлагая геометрическое тело для этой алгебры. Это открывает перспективу создания устройств нового типа, в которых логика операций не запрограммирована, а встроена в саму геометрию структуры. Такие устройства могут применяться в квантовых вычислениях, фазовых ритмах, нейроморфных архитектурах и символических системах.

6. Заключение

Исследование Кокарева и Павлова предоставляет язык, на котором можно описать Сфираль. Сама Сфираль, в свою очередь, может служить физической реализацией их теоретических построений. Это синтез: алгебра + геометрия = структура времени. Такой подход открывает путь к новым формам мышления, моделям сознания и формализации времени как вложенной и направленной структуры.

Ссылки:

[1] Кокарев С. С., Павлов Д. «Геометрия и физика двумерных алгебр», 2024.

[2] Басаргин, О. С. (2025) Эталонное описание устройства Сфираль. Zenodo. doi: 10.5281/zenodo.15133508.

Геометрия и физика двумерных алгебр как язык причинности и свития

Аннотация

Двумерные алгебры, рассмотренные С. С. Кокаревым и Д. Павловым, раскрываются как особый класс структур, в которых причинность и порядок следования событий определяются не внешними параметрами, а внутренними законами самой алгебры. В данной статье предложено прочтение этих алгебр через концепцию Сфирали — геометрического устройства, в котором витки, петли и узлы реализуют алгебраические операции, ритм времени и смену полюсов. Такая интерпретация позволяет говорить о свитии как о фундаментальном механизме упорядочивания, противоположном линейному «развитию».

1. Алгебра как язык причинности

В работе Кокарева и Павлова [1] алгебра понимается не как вспомогательный инструмент, а как первичная структура, из которой могут быть выведены физические закономерности. Двумерные алгебры, обладающие свойствами неассоциативности и некоммутативности, задают направление процессов и необратимость — признаки, ранее приписываемые времени как таковому.

Таким образом, алгебраическая операция в такой системе не является абстрактной: она формирует порядок следования, а значит, носит причинный характер. Это приближает алгебру к роли языка — не описания, а порождающего структуру.

2. Сфираль как геометрический аналог алгебры

Модель Сфирали [2] позволяет наглядно изобразить свойства двумерных алгебр в виде устойчивой пространственной формы. Сфираль состоит из двух антисимметричных витков, соединённых S-образной петлёй. Витки — это состояния (элементы алгебры), петля — операция, S-переход — ассоциатор, узел — точка смены ориентации.

Такое устройство показывает, что порядок и структура операций могут быть выражены геометрически. Более того, ритмичность Сфирали, чередование направлений и вложенность уровней делают её носителем фрактальной причинности, где каждый уровень повторяет предыдущий, но на новом масштабе.

3. Свитие как физический процесс

В противоположность понятию «развитие» как линейного, одностороннего роста, вводится понятие свития — движения к уплотнению, центрированию, возникновению узла. Сфираль реализует это как физическую форму: каждый виток ведёт к петле, петля — к узлу, а узел — к новому уровню вложенности.

Это позволяет трактовать Сфираль как алгебраическую машину свития: она не только соединяет состояния, но и создаёт переходы, которые нельзя обратить без потери ориентации. Такая необратимость соответствует свойству времени как направленной величины.

4. Перспективы свёрнутой алгебры

Если двумерная алгебра задаёт причинность, а Сфираль реализует её геометрию, то в совокупности они образуют новую категорию моделей, в которых структура сама по себе порождает физику. Такие модели могут лечь в основу:

— квантовых ритмических вычислений;

— топологических форм памяти;

— символических и нейро-алгебраических машин;

— интерференционных архитектур времени.

5. Заключение

Геометрия двумерных алгебр становится языком не только описания, но и свёртывания процессов во Время. Сфираль как устройство позволяет сделать этот язык зримым. Это открывает путь к формированию нового класса теоретико-физических и инженерных конструкций, в которых причинность, форма и время объединены в единый свёрнутый механизм.

Ссылки:

[1] Кокарев С. С., Павлов Д. Геометрия и физика двумерных алгебр.

[2] Басаргин О. С. Эталонное описание устройства Сфираль. Zenodo. 2025. DOI:10.5281/zenodo.15133508.

Геометрия и физика двумерных алгебр в построении фрактального ядра

Аннотация

В статье исследуется возможность применения двумерных алгебр, описанных С. С. Кокаревым и Д. Павловым, для построения фрактального вычислительного ядра. Предлагается интерпретация алгебраических структур через Сфираль — геометрическое устройство с вложенной антисимметричной структурой. Такая модель позволяет реализовать вычислительные процессы на основе топологии и ритма, где операции не линейны, а структурированы через фрактально повторяющийся узел.

1. Постановка задачи

В современных архитектурах вычислений отсутствует модель, в которой геометрия структуры сама порождала бы логику вычисления. Основные подходы основаны на линейных и коммутативных операциях. Однако двумерные алгебры [1], как показано Кокаревым и Павловым, могут задавать неассоциативные, некоммутативные, но при этом устойчивые формы причинности. Это делает их потенциальной основой для построения необычных вычислительных ядер.

2. Сфираль как структурная реализация алгебры

Сфираль [2] — это устройство, состоящее из пары витков, соединённых S-образной петлёй. Витки являются носителями состояния (данных), а петля — преобразованием. Узел в центре S-петли служит точкой перехода, аналогом триадной операции или ассоциатора.

Каждая Сфираль становится единичным вычислительным элементом, в котором:

— входные состояния представлены витками,

— операция — это форма петли,

— результат — это ориентация и выходная структура на новом витке.

Если выстраивать цепочку Сфиралей с фрактальной вложенностью (с изменением масштаба, фазы и ориентации), возникает вычислительная сеть, в которой операция не повторяется, а развивается по закону структуры.

3. Фрактальность как логика ядра

Фрактальность в Сфирали реализуется через параметры α, β, k, ϕ [2]. Эти параметры определяют:

— степень вложенности (разрядность),

— смещение по фазе (ритм),

— направление антисимметрии (чередование полюсов).

Это позволяет построить ядро, где:

— каждый уровень отвечает за собственный масштаб вычислений,

— каждый узел — за переход между уровнями (как в многослойной логике нейросетей),

— каждый виток — за состояние в данном порядке вложенности.

Вместо линейной адресации — структурная адресация по ритму и фазе. Такое ядро не требует синхронного такта, а само задаёт темп по вложенной структуре.

4. Алгебро-геометрическая модель вычислений

На базе описанной структуры можно предложить модель вычислений, в которой:

— операции соответствуют не символу, а форме перехода;

— программирование заменяется сборкой Сфиральной структуры;

— логика выражена топологически, а не в логических элементах.

Такое ядро становится ритмо-алгебраическим устройством, где порядок операций и выход зависит от вложенности, ориентации и антисимметрии всей предыдущей цепи. Это радикально отличается от булевой логики, но позволяет реализовать контекстные, фазовые и вероятностные вычисления.

5. Заключение

Двумерные алгебры, будучи структурой причинности, и Сфираль, будучи её геометрическим телом, позволяют построить фрактально вложенное вычислительное ядро, в котором сама структура управляет логикой. Это открывает путь к новому классу вычислительных машин — алгебро-ритмическим системам, способным адаптироваться, интерферировать и структурировать информацию не по правилам команд, а по законам форм.

Ссылки:

[1] Кокарев С. С., Павлов Д. Геометрия и физика двумерных алгебр.

[2] Басаргин О. С. Эталонное описание устройства Сфираль. Zenodo. 2025. DOI:10.5281/zenodo.15133508.

Геометрия и физика двумерных алгебр: возвращение узла

Аннотация

В статье анализируется понятие «узла» как фундаментального элемента алгебраической и физической структуры. Исходя из концепции двумерных алгебр, предложенной Кокаревым и Павловым, и Сфиральной модели времени, вводится интерпретация узла как точки аннигиляции, смены фазы и перехода между уровнями вложенности. Утверждается, что узел — это не точка фиксации, а акт структурного перехода. Такой подход открывает путь к формированию новых моделей времени, логики и синтаксиса мышления.

1. Постановка проблемы

Современные математические формализмы часто трактуют узел как точку пересечения, фиксации или сцепления. Однако в динамических моделях, основанных на фрактальной логике, узел — это не статическая точка, а акт перехода.

В модели Сфирали узел возникает в центре S-образной петли — в том месте, где сменяется ориентация, направление и фаза. Именно здесь происходит неассоциативный скачок, аналогичный ассоциатору в алгебре. В алгебре Кокарева и Павлова [1] неявно заложены основания для такого прочтения: порядок операций влияет на результат, но сама «точка сдвига» не формализована как элемент.

2. Узел как акт аннигиляции и перехода

Узел Сфирали не является точкой покоя — это место смены полюса, аналог нуля, но с функцией оператора. Он объединяет в себе:

— смену направления (антисимметрию); фазовый скачок (ϕ); переход на другой уровень вложенности (α, β); разрыв и соединение витков (структурная перезагрузка).

Это делает узел актом, а не объектом. В алгебраическом смысле он соответствует точке, в которой ассоциативность теряет силу, и возникает новая конфигурация операций. Узел может быть сопоставлен квантовому скачку, бифуркации или смене кодировки.

3. Узел времени как синтаксис мышления

Если время не линейно, а структурировано, то мысль тоже свёртывается, проходя узлы: моменты смены направления, точки перехода, внутренние повороты. Это даёт основание говорить о синтаксисе мышления, в котором узлы выполняют роль переходов между контекстами, логиками и уровнями обобщения.

С точки зрения лингвистики, узел — это не просто точка в схеме, а место переключения смысла, где фраза меняет грамматику, а высказывание — направление. В логике — это точка смены квантора, в программировании — рекурсивный вызов или смена области.

Таким образом, возвращение узла — это возвращение к внутренней динамике смысла, которую нельзя выразить линейной логикой.

4. Узел как элемент архитектуры времени

В модели Сфирали каждый узел — это место рождения порядка. Он не лежит на витке, не является его частью, но соединяет противоположные направления. Это напоминает точку фазы в интерференции, где максимум сменяется минимумом.

В алгебро-физической архитектуре времени узлы выполняют функцию:

— переключателей между порядками;

— маркеров фазовых состояний;

— структурных актов ритмогенеза.

Сеть узлов может быть интерпретирована как каркас времени, на котором разворачиваются витки причинности. Это позволяет уйти от модели времени как прямой линии и перейти к модели вложенной пульсации.

5. Заключение

Понятие узла требует переосмысления. Сфираль и двумерные алгебры дают возможность увидеть в нём не точку, а момент внутреннего изменения. Узел — это не то, что соединяет, а то, что переопределяет. Его возвращение в структуру алгебры и времени означает переход к топологической логике, в которой смысл и операция не разделены, а свиты в точке перехода.

Ссылки:

[1] Кокарев С. С., Павлов Д. Геометрия и физика двумерных алгебр.

[2] Басаргин О. С. Эталонное описание устройства Сфираль. Zenodo. 2025. DOI:10.5281/zenodo.15133508.

Геометрия и физика двумерных алгебр в интерференционных структурах

Аннотация

Статья посвящена исследованию связи между структурой двумерных алгебр, описанных Кокаревым и Павловым, и интерференционными явлениями в квантовых системах. Используется модель Сфирали как геометрическое выражение алгебраической причинности, в которой узлы, петли и витки формируют устойчивые волновые формы. Интерференционные картины, возникающие в таких структурах, рассматриваются как проявление алгебраической топологии. Предложен переход от логики булевых операций к логике фаз и ритма.

1. Интерференция как проявление структуры

В классической физике интерференция трактуется как волновой эффект, зависящий от фазы. Однако, если рассматривать структуру источников как вложенную, антисимметричную и ритмическую (как в Сфирали), можно показать, что интерференционная картина определяется не только длиной волны, но и логикой соединений.

Алгебраические свойства, такие как неассоциативность и антисимметрия, влияют на способ наложения фаз. Витки Сфирали порождают волновую последовательность, а узлы — точки фазового скачка. Результирующая интерференция — это не суперпозиция, а структурная комбинация состояний, зависящая от геометрии алгебраической цепи.

2. Сфираль как интерференционный каркас

Каждый виток в Сфирали может быть интерпретирован как локальный генератор волны. Петли определяют смещение, а узлы — фазовые инверсии. S-образные переходы создают условия, при которых фаза скачет на π или ±ϕ, порождая зоны конструктивной или деструктивной интерференции.

Такая структура может быть представлена как фазово-модулированная система, в которой каждое состояние влияет на глобальную интерференционную картину. Модель пригодна для описания:

— квантовых состояний с вложенной корреляцией;

— топологически защищённых фаз;

— распределений вероятности в вычислительных схемах.

3. От булевой логики к фазовой логике

Алгебраическая интерпретация Сфирали позволяет перейти от бинарных операций к фазовой логике, в которой:

— истина — это максимум интерференции;

— ложь — это деструктивный нуль;

— логика — это ритм соединения структур.

Таким образом, логическая операция заменяется геометрией перехода. Это открывает возможность построения волновых логических машин, где сигнал — это не ток, а фазово-согласованная структура переходов. Такие устройства могут работать в условиях квантовой неопределённости, обеспечивая устойчивость за счёт симметрий и антисимметрий.

4. Перспективы квантовых и биологических применений

Сфиральная интерференционная модель применима для:

— анализа квантовых вероятностных распределений с фазовыми и топологическими искажениями;

— построения квантовых нейронных сетей, в которых связь задаётся не весом, а фазой;

— моделирования временных волн в биологических системах (например, мозговых ритмах);

— проектирования интерференционных гироскопов и фазовых навигационных систем.

Всё это требует учёта геометрии источников волны, а не только уравнений её распространения. Именно алгебра двумерных структур даёт язык для описания таких сложных конфигураций.

5. Заключение

Интерференция — это не просто волновое наложение, а проявление внутренней логики структуры. Двумерные алгебры задают форму этой логики, а Сфираль реализует её в пространстве и времени. Таким образом, интерференционная картина становится отображением алгебраической топологии. Это создаёт основу для новой волновой технологии — не в смысле передачи сигнала, а в смысле воплощённой логики форм.

Ссылки:

[1] Кокарев С. С., Павлов Д. Геометрия и физика двумерных алгебр.

[2] Басаргин О. С. Эталонное описание устройства Сфираль. Zenodo. 2025. DOI:10.5281/zenodo.15133508.

Фрактальное вычислительное ядро: структурная модель Сфирали

Аннотация

В данной статье представлена концепция фрактального вычислительного ядра на основе модели Сфирали. В отличие от традиционных архитектур, основанных на линейных операциях и синтаксических правилах, Сфираль реализует вычисление как процесс вложенности, направленного перехода и причинной ритмики. Основное внимание уделяется схематической модели, отражающей геометрию порядков и множественность временных направлений.

1. Введение

Современные подходы к вычислению предполагают жёсткое разделение на символическую логику и физическое исполнение. Однако структура, которая сама содержит принципы перехода, ритма и вложенности, может быть рассмотрена как основа вычисления.

Сфиральная модель предлагает не форму машины, а форму самой логики — как она порождается через топологическое движение и смену порядка. Такая структура может быть использована для создания вычислительных систем, не основанных на такте или булевой логике, а работающих через ритм и фазовый сдвиг.

2. Основное изображение

На изображении ниже представлена фрактальная Сфиральная модель, выражающая вычисление как переход между порядками вложенности и направлениями причинности:

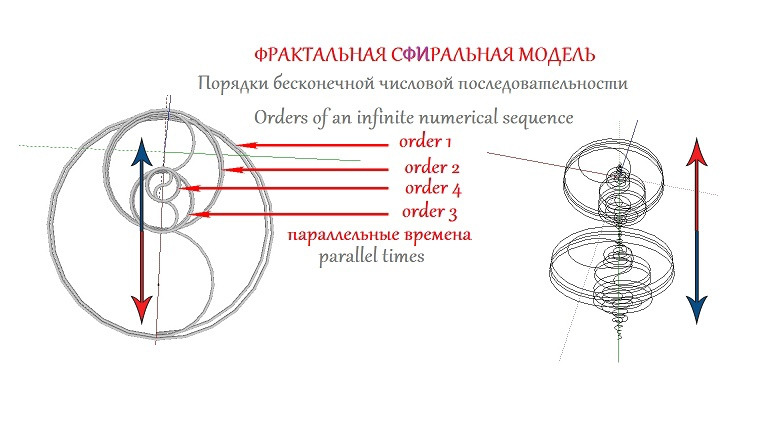
На схеме представлены: Order 1 → Order 4 — уровни вложенности, каждый из которых содержит собственное направление вычисления;

Параллельные времена — вертикальные потоки, разделённые по фазе и масштабу; S-переходы — точки инверсии, где происходит смена ориентации и запуск новой вложенной структуры.

Структура слева показывает вид сверху, структура справа — вид по оси времени. Центральная ось отражает направление причинного тока, который формирует порядок логического перехода.

3. Интерпретация модели

Каждое кольцо — это не просто форма, а акт: переход, вычислительная операция, фаза.

Порядки (orders) задают последовательность вложенности, как фрактальный стек, где каждый уровень «включает» предыдущий и запускает следующий.

Параллельные времена не синхронизированы, но структурно взаимосвязаны через общий узел происхождения (петлю), что позволяет моделировать многослойную логику.

Таким образом, вычисление в Сфирали — это ритм развёртывания структуры, а не обработка символов. Это модель, где логика выражается топологией развёртывания, а порядок выполнения встроен в саму форму.

4. Заключение

Предложенная схема не является абстрактной иллюстрацией, а выражает структурную логику вычислительного ядра, основанного на Сфирали. Такая модель применима в тех областях, где требуется не программирование, а структурная самоорганизация вычислений: квантовая логика, топологическая навигация, многовременные модели памяти. Сфираль становится не машиной, а формой самой вычислительности — алгебраическим телом времени.

Ссылки:

[1] Кокарев С. С., Павлов Д. Геометрия и физика двумерных алгебр. — 2024. — 231 с.

[2] Басаргин О. С. Эталонное описание устройства Сфираль. Zenodo. 2025. DOI:10.5281/zenodo.15133508.

Фрактальная структура Жюлиа на плоскости H2 как развертка зеркально антисимметричной Сфирали

1. Введение

На плоскости двойной переменной H2 фрактальные множества описываются через итеративный процесс, основанный на квадратичном отображении:

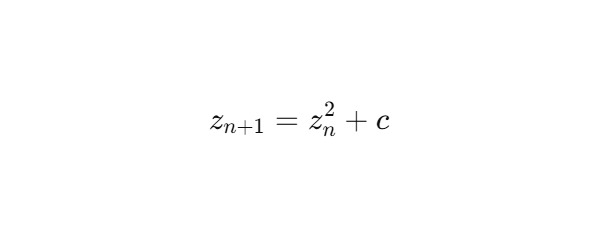
Здесь zn и c — двойные числа, принадлежащие алгебре H2, а операция возведения в квадрат и прибавление константы итеративно формируют фрактальную структуру.

В данной работе мы интерпретируем такие структуры через модель Сфирали — топологически устойчивой фигуры, состоящей из зеркально антисимметричных витков, соединённых S-образным переходом.

2. Визуально-топологическое соответствие

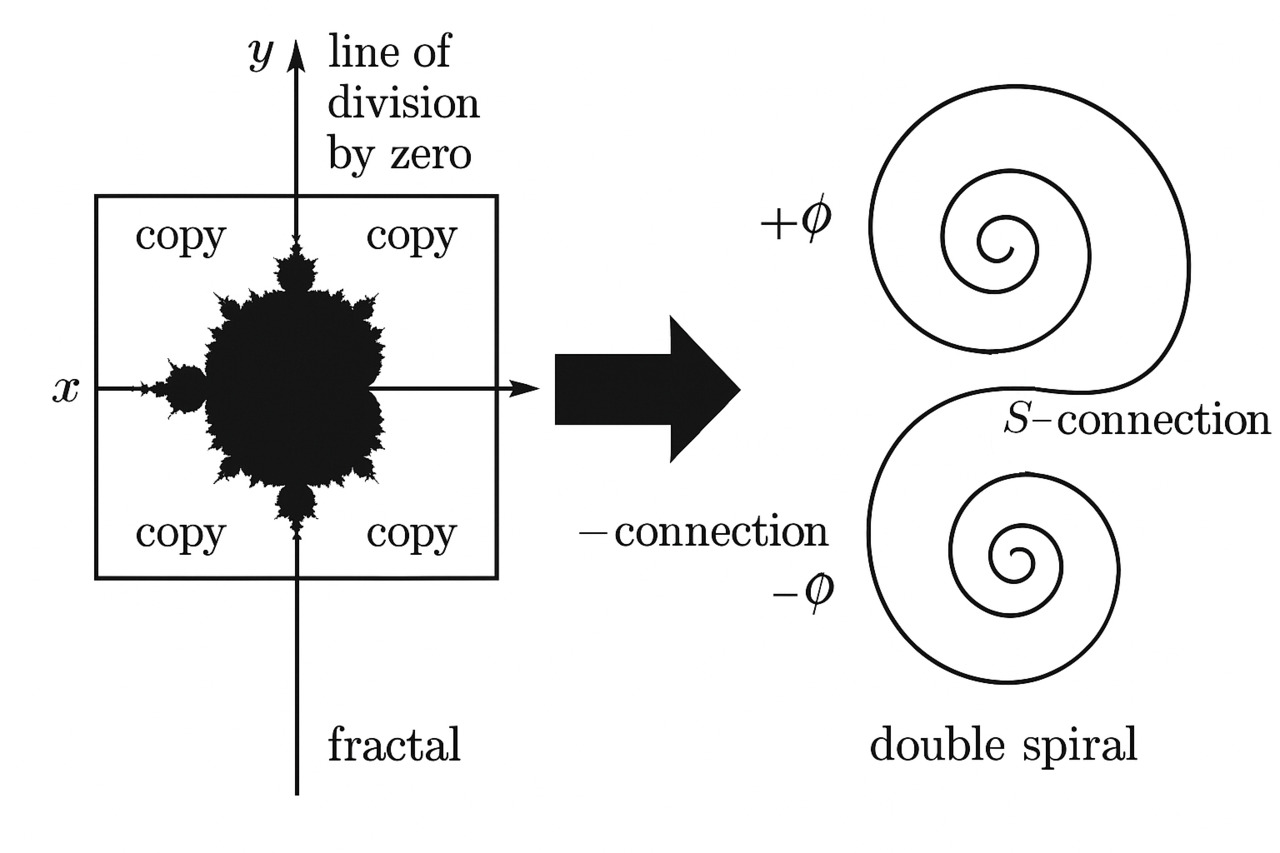
На изображении (см. рис.) представлено сопоставление: слева — фрактал Жюлиа на H2, справа — соответствующая ему двойная Сфираль.

— Центральная часть фрактала соответствует одному витку.

— Четыре копии — зеркально-антисимметричному витку.

— Линии делителей нуля обозначаются условием:

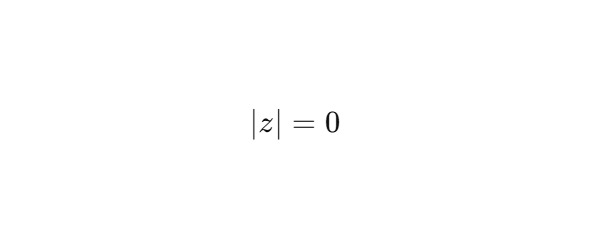
Это условие задаёт границу, на которой модуль двойного числа обращается в ноль, и определяет топологические швы между витками. Здесь модуль двойного числа определяется как ∣z∣2=x2−y2, где z=x + jy.

3. Таблица соответствия

---

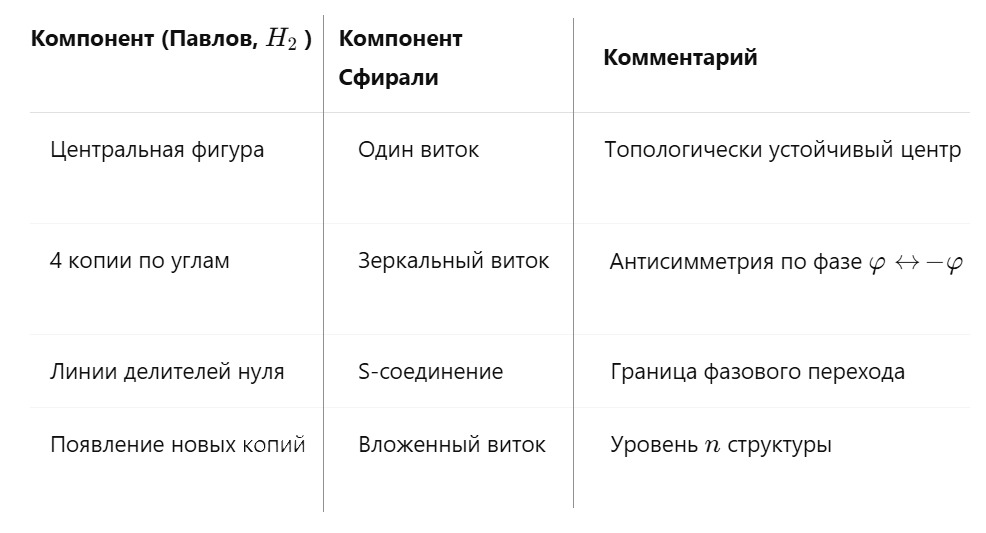
4. Математическая модель витков

Пусть каждый виток имеет параметры:

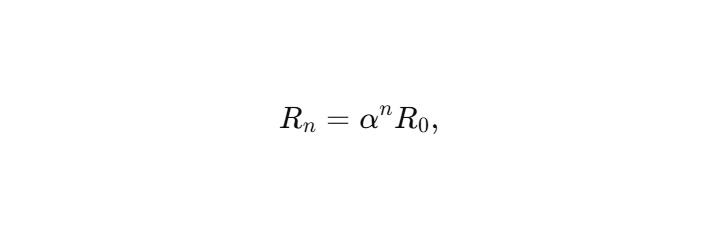
где Rn — радиус витка на уровне n, R0 — начальный радиус, α ∈ (0,1) — коэффициент масштабирования.

где hn — вертикальное смещение витка (по оси симметраии), h0— базовое смещение, β ∈ (0,1) — коэффициент вложенности по высоте.

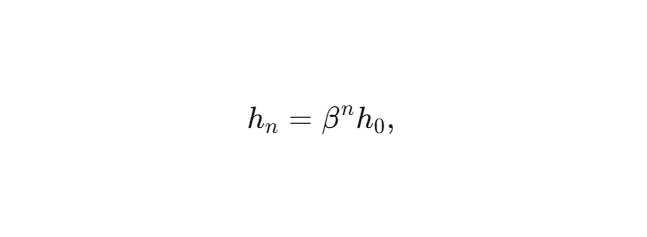
где φn — фазовый угол, который меняет знак на каждом шаге, отражая зеркальную антисимметрию всей конструкции.

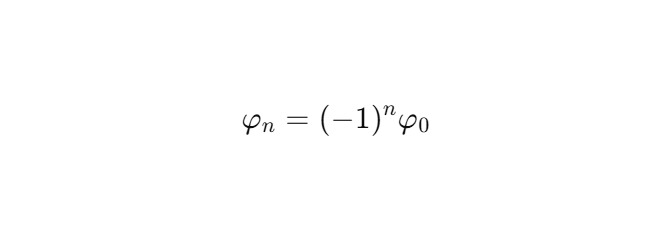
5. Заключение

Таким образом, структура предфрактала Жюлиа на H2 может быть интерпретирована как последовательность вложенных витков зеркально-антисимметричной Сфирали. Это даёт как геометрическое понимание, так и аналитический инструмент описания возникающих фрактальных форм.

Литература

— Павлов Д. Г., Панчелюга М. С., Панчелюга В. А.

— О форме аналогов множества Жюлиа на плоскости двойной переменной. // Гиперкомплексные числа в геометрии и физике. — 2009. — Т.6, №2 (12). — С. 162–176.

— Басаргин О. С. (2025). Эталонное описание устройства Сфираль. Zenodo. https://doi.org/10.5281/zenodo.15133508

Сфираль, Время и Сознание: метаструктура в пространстве двойной переменной

1. Введение

Сфираль — это не просто геометрическая форма. Это метаструктура, проявляющаяся на стыке топологии, времени, восприятия и мышления. В настоящей работе мы переосмысляем Сфираль как универсальный механизм порождения структуры, используя окно, открытое через фрактальные отображения Жюлиа на плоскости двойной переменной H2 (по Д. Павлову). Через эту «дверь» мы исследуем, как Сфираль ведёт себя в другой алгебраической реальности, и какие следствия это имеет для понимания природы времени, пространства и сознания.

2. Сфираль как механизм формирования структур

Сфираль — это топологически устойчивая фигура, состоящая из двух зеркально антисимметричных витков, соединённых S-образным элементом. Витки воплощают цикличность и направленность, а S-соединение — фазовый переход. При фрактальной вложенности Сфираль порождает последовательность вложенных уровней, аналогичных эмерджентным слоям структуры.

Это не форма, а принцип:

— Виток — это цикл повторения с различием.

— Зеркальная антисимметрия — это отличие прошлого от будущего.

— S-соединение — точка порога, трансформации.

3. Павловская плоскость H2: разрыв формы

На плоскости двойной переменной H2 структура фрактала Жюлиа претерпевает фундаментальные отличия от комплексного случая:

— Делители нуля создают зоны, в которых структура «разрывается».

— Гиперболические хвосты фрактала формируют изолированные фрагменты.

— Итерации формируют не непрерывную границу, а прерывистое вложенное множество.

Интерпретация: Сфираль, попавшая в пространство H2, больше не может быть цельной — она становится расщеплённой, но сохраняет фрактальную и зеркальную антисимметрию.

4. Время как вложенность, а не линия

Если время — не ось, а виток, то:

— Каждый уровень фрактала — это момент с вложенной памятью (витком прошлого).

— Антисимметрия витков отражает необратимость восприятия.

— S-соединения — пороги трансформаций: вспышки, события, акты осознания.

Сфираль не просто течёт во времени — она и есть время, структурированное как вложенность различий. Её движение направлено в будущее, как у спирали, но одновременно включает в себя поперечное измерение — зеркальность и антисимметрию витков. Это соответствует тому, что В. И. Вернадский называл полярным вектором времени. Здесь мы уточняем: Сфираль реализует поперечный полярный вектор времени, в котором поступательное развитие сочетается с процессами свития, отражения и инверсии, действующими как внутренние аспекты самой временной динамики.

Сфираль также воплощает суть принципа относительной обратимости времени: вначале любая природная система эволюционирует в одном направлении, а затем — в противоположном, сохраняя при этом внутреннюю непрерывность структуры.

5. Сознание как сфиралевидная динамика

Сознание — это не поток, а последовательность витков, фазовых возвратов, скачков:

— Мысль не движется вперёд — она спиралит и сфиралит одновременно, разворачиваясь в пространстве различий и возвращений. Спиральность отражает поступательное накопление различий, тогда как сфиральность — возвращение вглубь, через зеркальное воспроизведение пройденного. Это двойственное движение порождает как временное направление, так и устойчивую структуру идентичности. Сознание балансирует между этими режимами: один направлен в будущее, другой — в память и архетип.

— Воспоминание — это фрактальная вложенность витков опыта.

— Переход от ощущения к осознанию — это S-переход между антисимметричными слоями.

В этом смысле, структура Сфирали предлагает модель когнитивной архитектуры, в которой:

— Уровни — это уровни смысловой или нейронной вложенности.

— Фаза — это эмоциональное или энергетическое состояние.

— S — это акт инсайта, переход к другому порядку.

6. Выводы: Сфираль как модель становления реальности

Через вторую дверь — фрактальную структуру Жюлиа на H2 — мы наблюдаем, как Сфираль проявляется в искаженном пространстве. Это позволяет сделать следующий вывод:

Сфираль — это универсальная форма становления, которая может быть вложенной, разорванной, антисимметричной, но сохраняет принципы организованности. Она лежит в основании времени, структуры и сознания.

Исследование Сфирали через различные алгебраические реальности открывает путь к пониманию времени как топологии, сознания как витков, а мира как самопереплетающегося перехода между фазами.

Литература:

— Павлов Д. Г., Панчелюга М. С., Панчелюга В. А.

— О форме аналогов множества Жюлиа на плоскости двойной переменной. // Гиперкомплексные числа в геометрии и физике. — 2009. — Т.6, №2 (12). — С. 162–176.

— Басаргин О. С. (2025). Эталонное описание устройства Сфираль. Zenodo. https://doi.org/10.5281/zenodo.15133508

Сфираль и структура мышления: топология различий и актов осознания

1. Введение

Мышление традиционно описывается через логические операции, линейные рассуждения, дедуктивные или индуктивные структуры. Однако такое представление игнорирует фазовость, цикличность, множественность состояний и переходов, характерных для реального акта мышления. В этой статье мы предлагаем концептуализировать мышление как процесс, структурированный по принципу Сфирали — фигуры, объединяющей направленность, антисимметрию, фрактальность и вложенность.

Мы продолжаем предыдущие исследования, в которых Сфираль была рассмотрена как модель времени и сознания, и переносим её принципы в пространство ментальных операций.

2. Сфираль как модель мышления

Сфираль задаёт не траекторию мысли, а её онтологическую форму:

— Виток — это завершённый цикл мышления, содержащий идею, её оборот, критику и возвращение на новом уровне.

— Зеркальная антисимметрия — различие между утверждением и его внутренней тенью: сомнением, рефлексией, отрицанием.

— S-соединение — точка скачка, инсайта, где фаза рассуждения меняется.

Таким образом, мышление в модели Сфирали — это не движение от посылки к выводу, а развертывание структуры, включающей возврат, различие, вложенность и фазовые переходы.

3. Вложенность и память

Каждое новое рассуждение включает в себя фрагмент предыдущего. Это не линейное продолжение, а вложенный виток, в котором предыдущие фазы не исчезают, а структурно преобразуются.

Модель:

— Mn — акт мышления уровня nn

— Mn+1 = f (Mn,¬ Mn, Rn) где ¬Mn — антифаза (внутреннее различие), Rn — рефлексивный компонент.

4. Поперечность мышления

В классической логике мысль движется вперёд. В модели Сфирали присутствует поперечное мышление:

— переключение на мета-уровень,

— внутреннее зеркало рассуждения,

— переход в противоположное состояние (ирония, метафора, инверсия).

Поперечный вектор мышления — аналог поперечного вектора времени — указывает, что смысл рождается не в последовательности, а во взаимоотражении фаз.

---

5. Модальности и фазы

Сфираль даёт топологическую интерпретацию модальностей:

— Необходимость →\rightarrow центральный виток

— Возможность →\rightarrow флуктуирующие фазы

— Действительность →\rightarrow связующая траектория

— Сомнение →\rightarrow антисимметричный виток

Мышление модально, потому что оно сфирально: каждая мысль разворачивается не в плоскости истинности, а в пространстве фазовой множественности.

6. Выводы

Сфираль как структура мышления позволяет описывать:

— множественность смыслов,

— наличие скачков и фазовых сдвигов,

— вложенность и возвращение,

— внутреннюю антисимметрию рассуждения.

Такой подход открывает возможность для новой логики — логики витков, в которой соотношение между мыслями определяется не только их содержанием, но и их положением в динамической топологии различий.

Литература

— Басаргин О. С. (2025). Эталонное описание устройства Сфираль. Zenodo. https://doi.org/10.5281/zenodo.15133508

— Пригожин И., Стенгерс И. (1986). Порядок из хаоса: Новый диалог человека с природой. — М.: Прогресс.

— Вернадский В. И. (1989). Несколько слов о ноосфере. — В: Избранные труды. — М.: Наука.

Вычислительное ядро H₂: фазовая модель времени, структуры и наблюдения

Аннотация

В статье предлагается модель вычислительного ядра, реализуемого в алгебре двойной переменной H2, на основе итерационного оператора Φ (z) = α ẑ. Эта простая функция порождает фрактальную структуру вложенных витков, обладающую зеркальной антисимметрией и устойчивой фазовой динамикой. Построены и проанализированы: индивидуальное ядро, его итерации, поведение на делителях нуля, модулярная структура, синхронизация пар ядер, оболочка (сфера витков), а также проекция в линейную ленту времени.

Модель сопоставлена с теориями квантовой гравитации, каузальных сетей и когнитивного времени, а также представлена как генератор квантовых состояний. Показано, что вероятность, наблюдение и метрика могут быть естественно описаны средствами этой алгебры. Вводится термин «поперечный полярный вектор времени» и уточняется его смысл через итерации, S-соединения и фазовые скачки.

Предложенная конструкция открывает путь к формализации структуры времени как вычислительного, наблюдаемого и вложенного объекта.

Поиск вычислительной реализации ядра (узла 73) в алгебре H2

1. Постановка задачи

Цель: найти вычислительную реализацию структуры, обозначенной как узел 73, в терминах алгебры двойной переменной H2.

Узел 73 — это минимальное устойчивое ядро, содержащее признаки:

— фрактальной вложенности,

— зеркальной антисимметрии,

— фазового сдвига и внутреннего различия,

— направленного (возможно, условно обратимого) вычисления.

2. Базовая алгебра H2

Элемент: z = x + jyz = x + j y, где j2 = 1, x, y ∈ R

Модуль двойного числа:

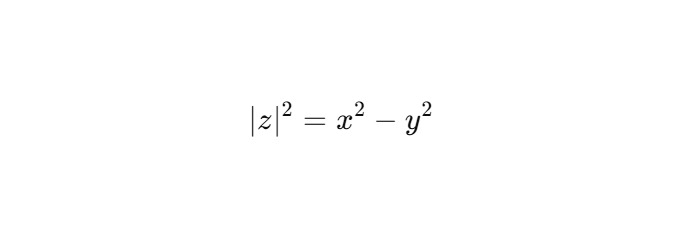
Делители нуля: ∣z∣ = 0 ⇒ x = ± y

Изотропный базис:

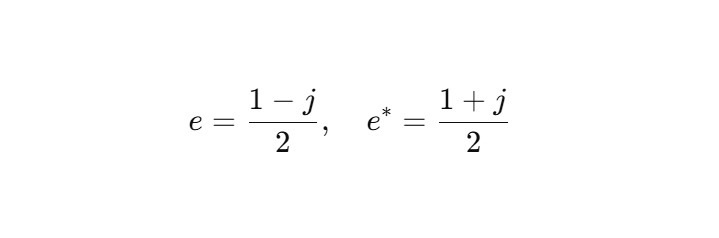
В этом базисе:

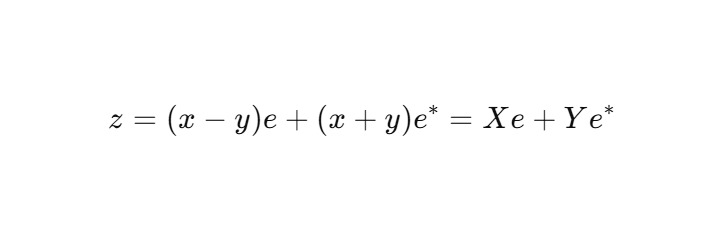
3. Гипотеза о ядре

Предположим, что ядро — это пара точек z+, z−, таких что:

— z+ = Reφ,

— z− = Re−φ,

— с соединением по линии делителей нуля ∣z∣ = 0, то есть они расположены симметрично относительно этой линии.

---

4. Функция перехода

Определим функцию ядра как отображение:

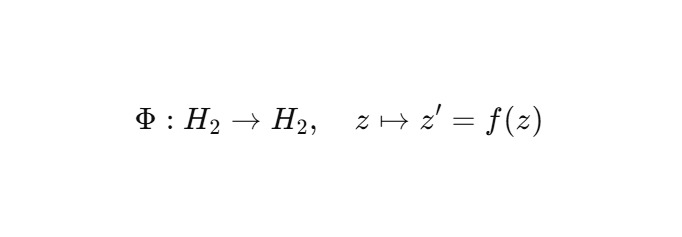
Ищем такую f (z), что:

— Φ отражает фазу: φ ↦ −φ

— Φ (Φ (z)) = z — относительная обратимость

— при итерации z → Φ (z) → Φ (Φ (z)) →… возникает структура, подобная виткам

5. Следующие шаги

— Построить конкретную форму f (z)

— Проверить условия устойчивости и зеркальности

— Связать ядро с линиями ∣z∣ = 0 как с фазовыми границами

— Исследовать возможность вложенности через параметры α, β

Итерации вычислительного ядра в алгебре H2

1. Оператор ядра

Рассматриваем вычислительное ядро как функцию:

Это оператор:

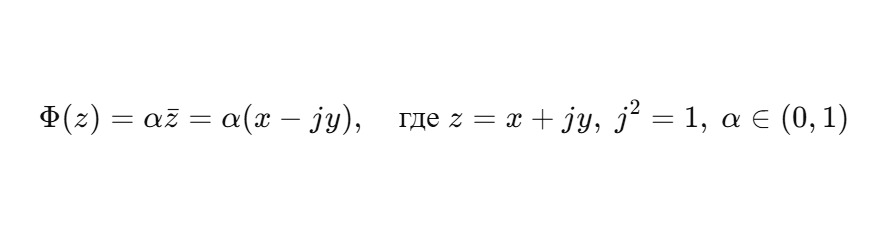
— обратный сам себе при двойном применении: Φ (Φ (z)) = α2z,

— реализующий фазовую инверсию: φ ↦ −φ,

— и фрактальную вложенность: αn с каждым шагом.

2. Итерационная цепочка

Пусть z0 = x + jy. Тогда:

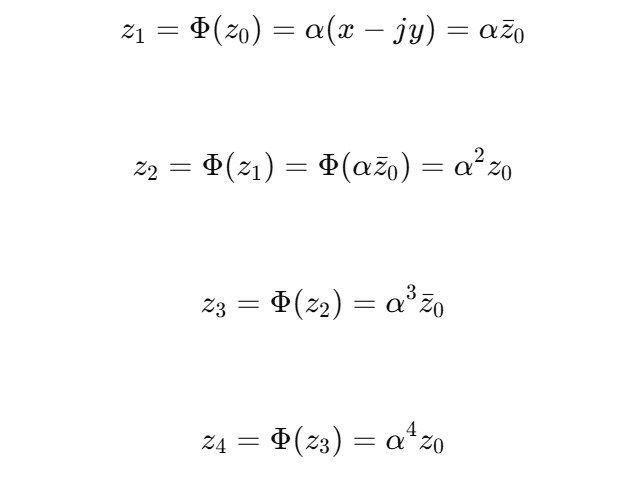
Общая формула:

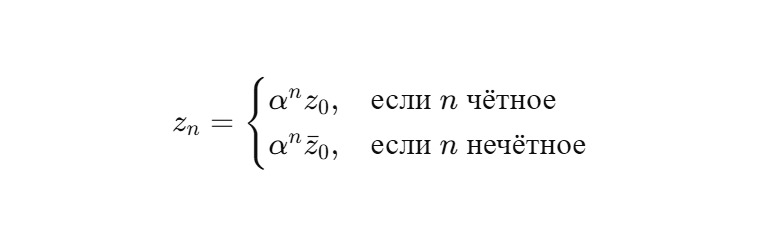
3. Интерпретация

— Каждый чётный шаг возвращает к исходной фазе, но с уменьшенным масштабом.

— Нечётный шаг — зеркальная фаза.

— Итерации создают зеркально-антисимметричные витки, вложенные друг в друга с коэффициентом α.

Это поведение соответствует структуре Сфирали:

— фазовая антипара z ↔ ẑ,

— вложенность Rn = αnR0,

— относительная обратимость (чётные шаги возвращают направление).

4. Вывод

Функция Φ (z) = α ẑ реализует вычислительное ядро:

— в рамках алгебры H2,

— с фазовой симметрией и вложенностью,

— создавая предельно простую, но устойчивую структуру зеркального саморазворачивания.

Следующий шаг: исследовать поведение при ∣z∣ = 0.

Поведение вычислительного ядра на линии делителей нуля в H2

1. Делители нуля в H2

Условие:

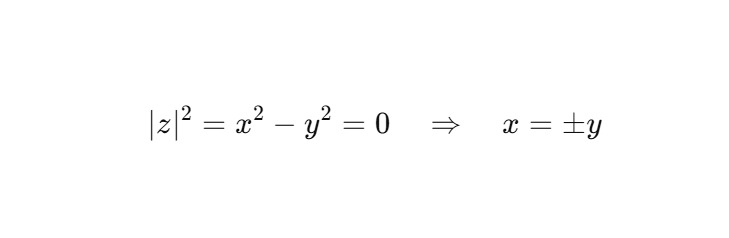
Пусть z = x + jy. Тогда при x=y:

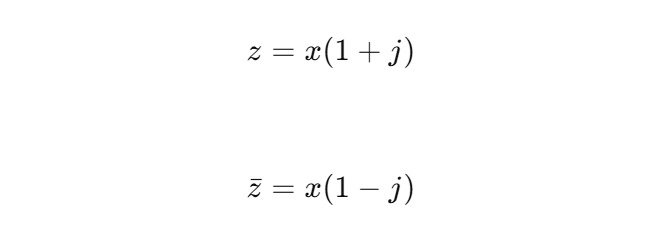
2. Поведение под действием ядра

Ядро определяется как:

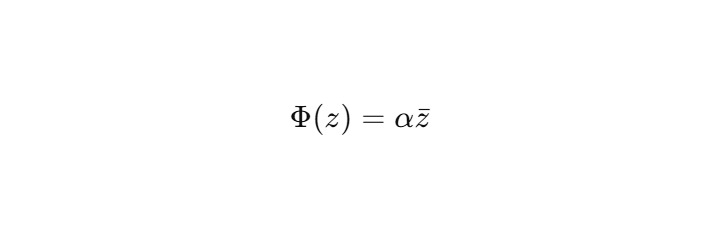
Тогда:

---

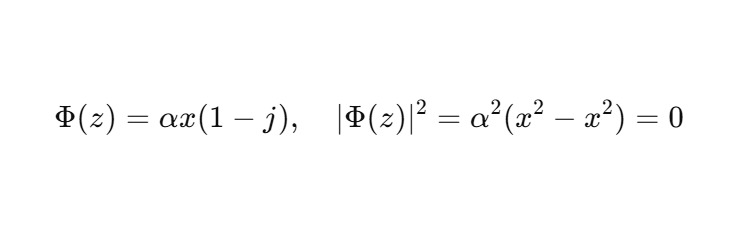
Аналогично, при любом числе итераций:

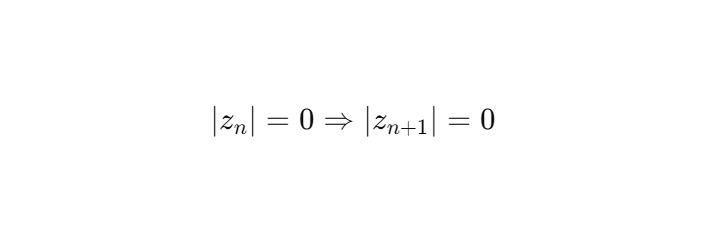
3. Геометрическая интерпретация

Таким образом, множество точек z ∈ H2, таких что ∣z∣ = 0, является инвариантным множеством относительно действия ядра Φ.

Это означает:

— Делители нуля не уходят из своего класса.

— Они формируют границу фрактальной структуры.

— Эти точки — фазовые переломы, аналог S-соединения в модели Сфирали.

4. Вывод

Линии делителей нуля, будучи неподвижными под действием ядра Φ, могут интерпретироваться как встроенные швы фазы, или оси симметрии, в которых разворачиваются витки. Это подтверждает их особый статус в геометрии двойной плоскости и их функциональную роль в вычислительном ядре.

Формализация вычислительного ядра как модуля над H2

1. Мотивация

После построения функции Φ (z) = α ẑ и анализа её поведения при итерациях и на линии делителей нуля, возникает задача интерпретировать вычислительное ядро как структурную единицу внутри алгебры H2.

Для этого рассмотрим его как модуль над алгеброй H2, аналогично тому, как в линейной алгебре векторное пространство есть модуль над полем.

2. Определение

Пусть M — подмножество H2, замкнутое относительно действия ядра:

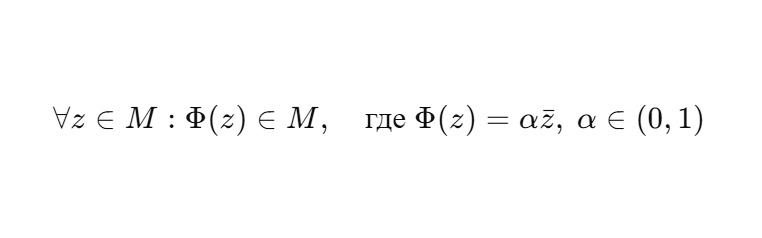
Тогда:

— M — аддитивная группа (по сложению в H2)

— и для h ∈ H2 z ∈ M, определено внешнее умножение:

h ⋅ z = hz

3. Свойства

— Ядро M не является идеалом, так как сопряжение не дистрибутивно по умножению:

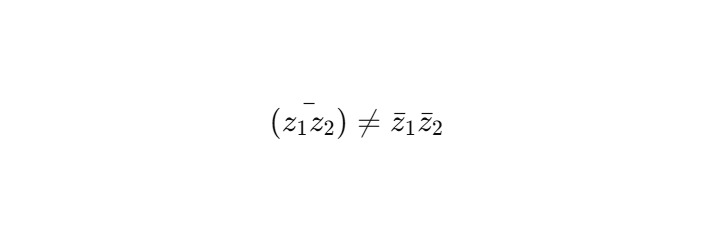
— Однако M — модуль с нестандартной операцией:

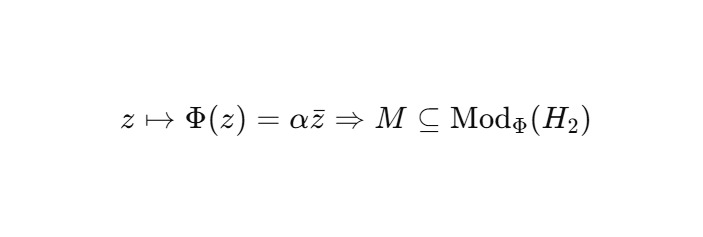
— Для всех z ∈ M:

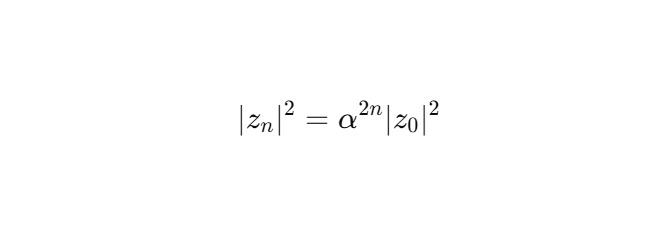
4. Интерпретация

Ядро — это подмодуль, устойчивый под сопряжением и масштабированием, с вложенной зеркальной структурой. Оно работает как алгебраический контейнер витков, разворачивающихся в пространстве H2 антисимметрией.

5. Вывод

Формализация ядра как модуля M ⊆ H2 позволяет задать вычислительные процессы не точками, а структурными областями, в которых реализуется вложенность, инверсия, и фрактальное самоподобие.

Синхронизация вычислительных ядер в алгебре H2

1. Постановка задачи

Если вычислительное ядро M ⊆ H2 представляет собой модуль с вложенной зеркальной структурой, возникает вопрос: могут ли два таких ядра взаимодействовать?

Задача: исследовать условия и форму фазовой синхронизации двух ядер:

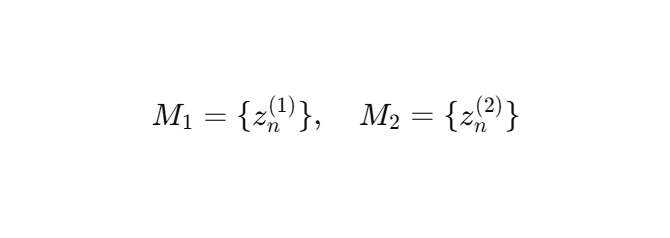
согласно динамике:

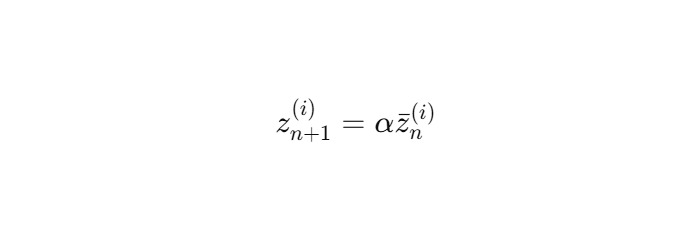
2. Условие синхронизации

Скажем, что ядра синхронизированы, если существует N ∈ N, такое что:

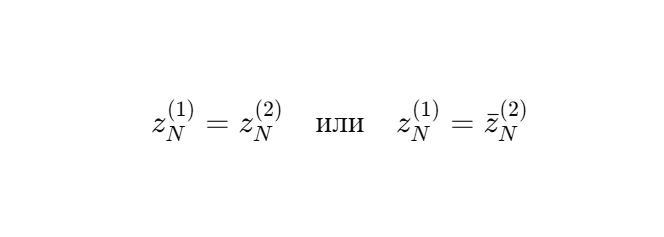
Более общо, существует фаза φ, для которой:

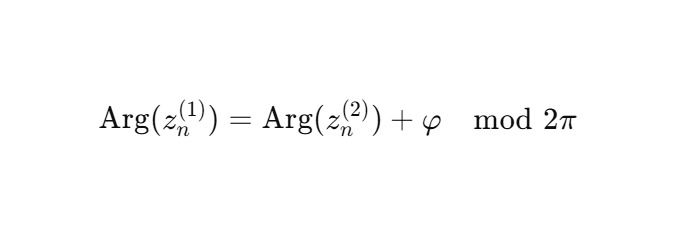
3. Алгебраическое представление

Пусть:

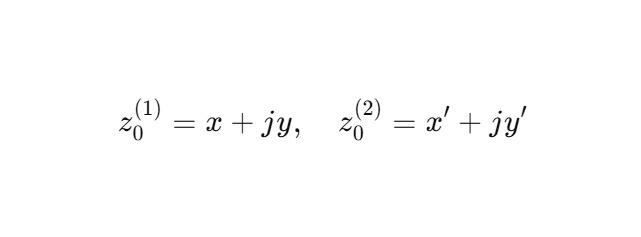
Итерации:

---

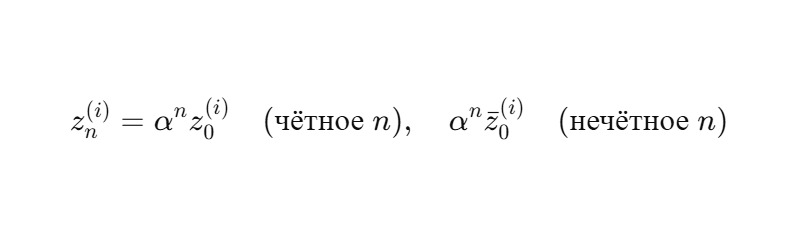
Тогда:

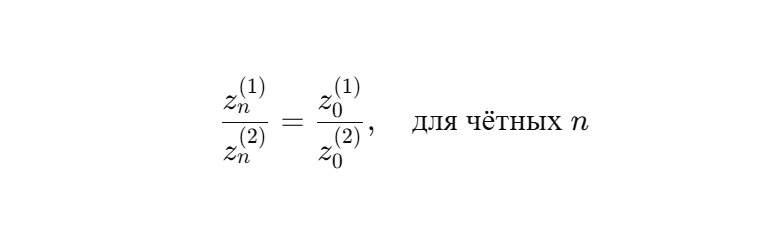
То есть фазовое отношение сохраняется:

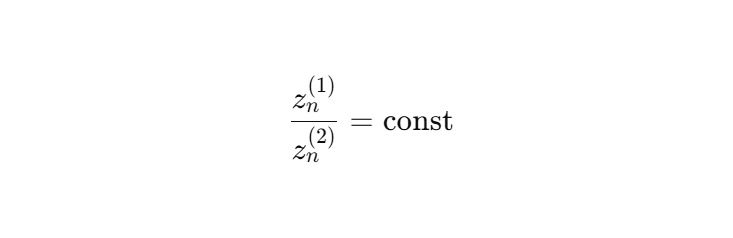
4. Геометрическая интерпретация

Если два ядра стартуют с фазовой разницей φ, они сохраняют её при всех чётных итерациях. Нечётные шаги зеркальны:

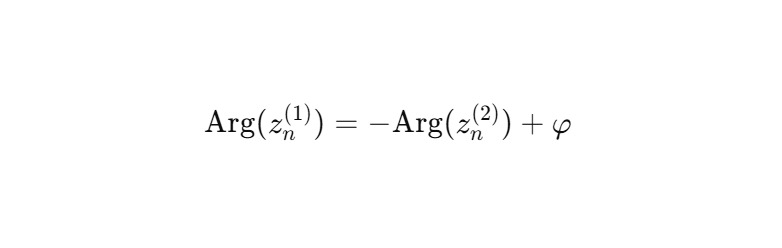
Таким образом, возникает ритмическая антисимметрия: витки синхронны, но с чередованием отражённых фаз.

5. Вывод

Синхронизация ядер возможна при постоянной фазовой разнице на начальном шаге. Алгебраически, ядра образуют двойной виток, подобный Сфирали, в котором вложенность и зеркальность работают в паре.

Визуализация синхронизации вычислительных ядер в H2

Следующая диаграмма иллюстрирует синхронное поведение двух вычислительных ядер в плоскости H2. Каждое ядро представлено вложенной спиралью, где точки z0, z1, z2 отображают итерации функции ядра:

---

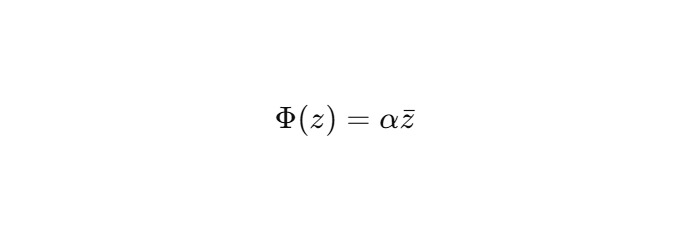
Диаграмма показывает:

— зеркальную структуру ядер,

— сохранение фазы z0 на каждом уровне,

— чередование витков в фазе z1, z2,

— фазовый сдвиг между ядрами,

— оси x, y, пространство H2.

Обозначение α отражает коэффициент вложенности и масштабирования. Чётные и нечётные итерации отображаются зеркально. Состояние синхронизации определяется сохранением относительной фазы и вложенности.

Иллюстрация

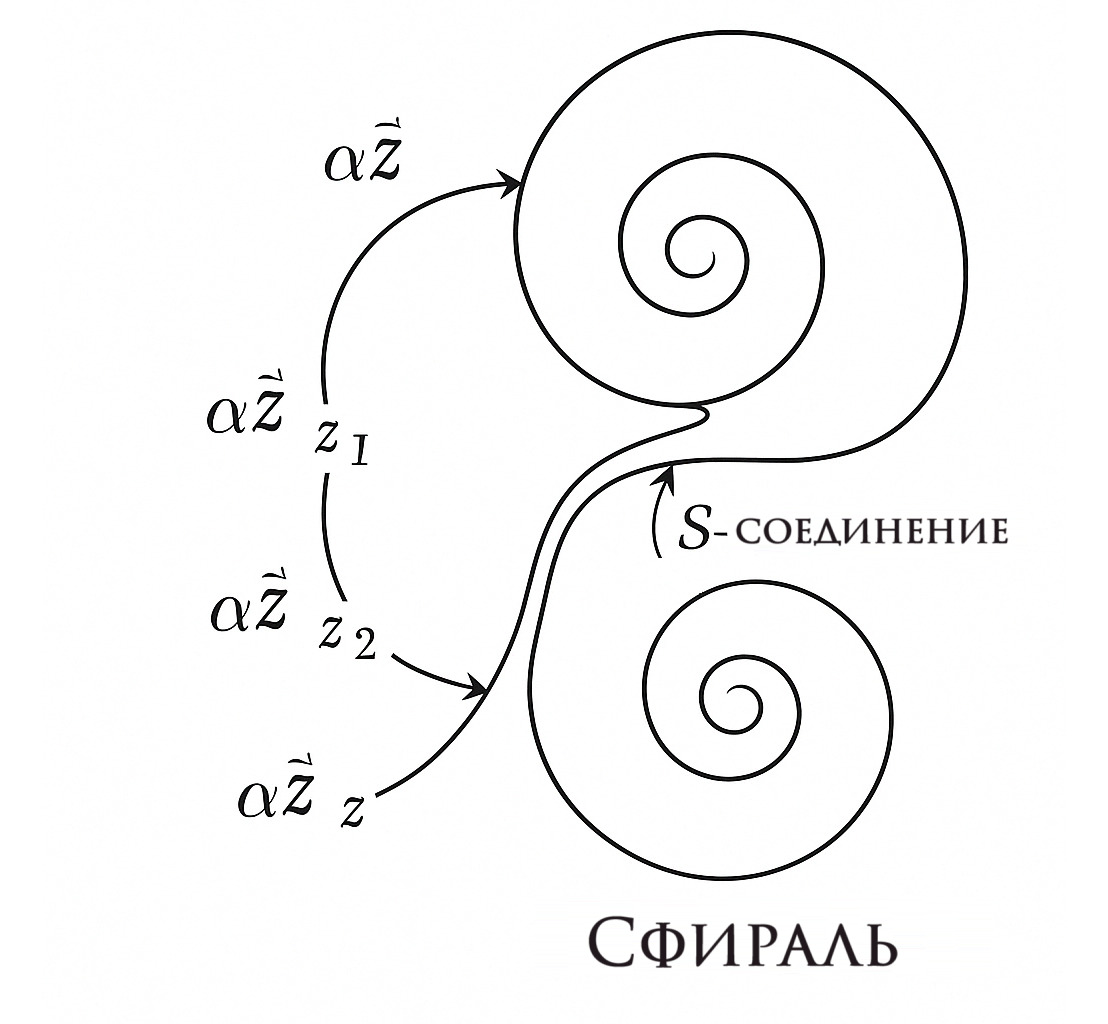
Диаграмма демонстрирует согласованную динамику и антисимметрию двойных ядер, что полностью соответствует принципу Сфирали как модели вычислительной и ментальной структуры.

Следующий шаг: исследовать возможность вложения такой пары ядер в более крупную структуру — сферу витков или многослойную ленту.

Сфера витков как оболочка вычислительных ядер в H2

1. Мотивация

После формализации одного ядра и анализа пары синхронизированных ядер возникает идея следующего уровня: обобщённой структуры, порождённой множеством витков. Эта структура называется сферой витков.

Сфера витков — это не геометрическая сфера в обычном смысле, а топологическая оболочка, охватывающая множество вычислительных ядер, связанных через фазу, вложенность и антисимметрию.

2. Конструкция

Пусть {Mk} — множество ядер Mk ⊂ H2, каждое из которых реализует динамику:

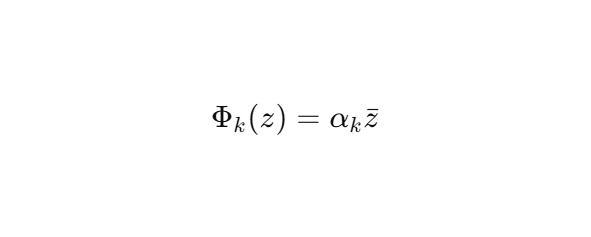
Мы определяем сферу витков как совокупность:

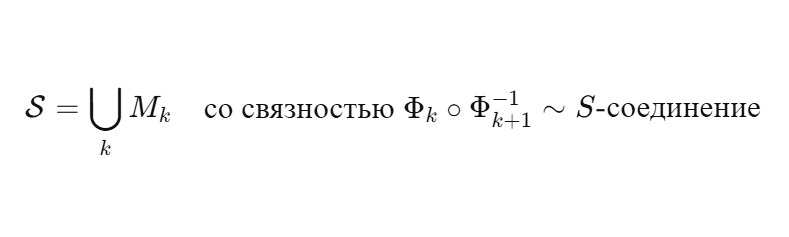
Здесь S-соединения обеспечивают связность между ядрами, так что результат образует замкнутую фазовую оболочку.

3. Свойства

— Фазовая непрерывность: переходы между ядрами не разрывают динамику.

— Антисимметрия: витки противоположны по фазе на каждом «меридиане» оболочки.

— Вложенность: каждое ядро вложено с масштабом αk <1.

— Обратимость: глобальная структура допускает разворачивание и свёртывание.

---

4. Интерпретация

Сфера витков — это макро-структура вычислительной топологии, объединяющая фрактальные модули в целостную фазовую сферу. Она может быть интерпретирована как:

— оболочка когнитивного или квантового состояния,

— фаза в сетевой топологии вычислений,

— аналог ноосферы в модели мышления.

5. Вывод

Сфера витков обобщает модель Сфирали: она разворачивает не одну пару витков, а всю совокупность возможных вычислительных антисимметрий, организованных в замкнутую фазовую структуру. Это фундамент для построения более сложных вычислительных, когнитивных или онтологических моделей, основанных на топологии различий.

Лента времени как проекция сферы витков в H2

1. Исходная структура

Мы построили сферу витков S ⊂ H2 — замкнутую оболочку, состоящую из синхронизированных вычислительных ядер, каждое из которых реализует динамику Φ (z) = α ẑ.

Эта сфера обладает внутренней фазовой логикой, зеркальностью и вложенной многослойностью.

2. Идея проекции

Лента времени — это не просто одномерная линия, а развёртка сферы витков во времени, где:

— каждый шаг — это виток,

— каждая фаза — это состояние,

— S-соединения — это моменты перехода, скачка, инсайта.

3. Формализация

Пусть t ∈ Z — дискретное время. Тогда лента времени — это отображение:

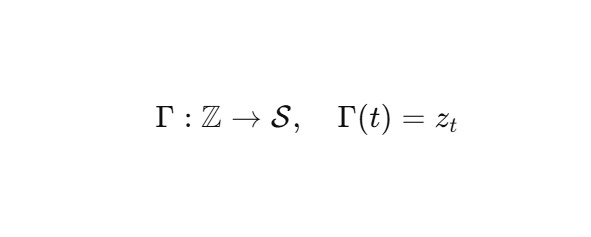
где zt ∈ Mk ⊂ S, и переходы zt → zt+1 реализуют локальную итерацию ядра:

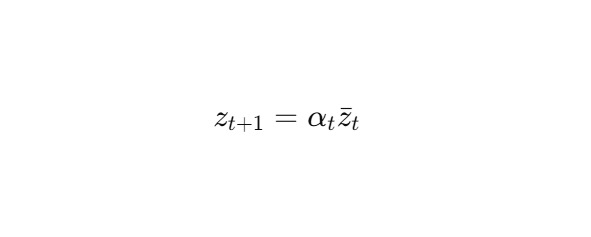
Скачки между ядрами — это фазовые переключения через S-соединения:

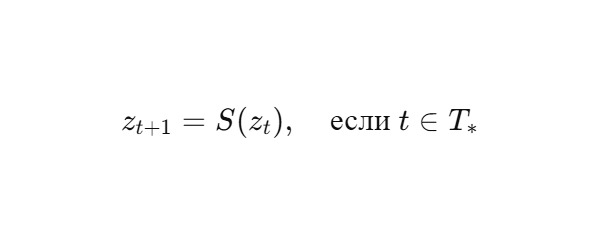
где T∗ — множество моментов фазового разрыва.

4. Свойства ленты времени

— Локальная антисимметрия: каждый виток противоположен предыдущему по фазе.

— Глобальная вложенность: масштаб αt может изменяться (модуляция).

— Фазовая обратимость: если αt = α, то существует Γ−1.

— Поперечный вектор времени: направление S-соединений определяет «переворот» временной динамики.

5. Интерпретация

Лента времени — это линейная траектория, несущая на себе структуру сферы витков. Это воплощение времени как топологического объекта, в котором каждое «событие» — это фазовый сдвиг, а каждое «настоящее» — это виток в антисимметричном развитии.

Это соответствует концепции:

«Сфираль отражает суть принципа относительной обратимости времени: вначале любая природная система эволюционирует в одном направлении, а затем — в противоположном.»

6. Вывод

Лента времени — это проекция сферы витков на ось последовательности. В ней время не одномерно, а вложено и отражено, как и в структуре Сфирали. Это завершает модель вычислительного ядра в H2 как порождения витков, объединённых в сферу, развёрнутую во времени.

Сопоставление модели сфиралевидного времени с физическими и когнитивными теориями

1. Цель сопоставления

Построенная модель вычислительного ядра, сферы витков и ленты времени задаёт топологически организованное, фазовое и вложенное представление времени. Необходимо сопоставить её с существующими теориями времени в физике, биологии и когнитивной науке.

2. Сравнение с физическими моделями

2.1. Энтропийная стрела времени

— В термодинамике время направлено от порядка к беспорядку.

— В нашей модели это соответствует вложенности с уменьшением масштаба: αn.

— Однако, модель Сфирали допускает обратимость на уровне фаз: антисимметрия витков.

2.2. Релятивистское время

— В теории относительности время — координата, зависящая от системы отсчёта.

— В Сфирали — тоже зависит от «наблюдателя» в смысле точки входа на витке.

— Поперечный вектор времени в нашей модели аналогичен выбору направления временного развития.

2.3. Квантовая суперпозиция состояний

— Квантовая механика допускает множественность состояний до акта измерения.

— Сфираль и сфера витков моделируют эту множественность как фазовые ветвления, переходящие друг в друга.

3. Сравнение с когнитивными и нейрофизиологическими теориями времени

3.1. Нейронная фазовость

— В теориях осцилляций (Г. Бюзенг, В. Фрайс) мышление и восприятие работают через фазы.

— Сфиральная модель напрямую отражает это: каждая мысль — виток, каждый переход — S-сдвиг.

3.2. Психология субъективного времени

— Понятия «возвращения», «ретроспекции», «эффекта продолжительности» — это проявления вложенности и зеркальности.

— Лента времени как раз отображает чередование и повторение в новом масштабе.

3.3. Модели памяти (К. Д. Анохин, Эдельман)

— Память не линейна, она работает через структурные контуры, повторяющиеся с вариациями.

— Сфера витков — аналог архитектуры метапамяти.

---

4. Вывод

Сфиральная модель времени не противоречит существующим физическим и когнитивным теориям, а обобщает их на топологическом уровне. Она объединяет:

— направленность (энтропия, причинность),

— антисимметрию (отражённые состояния, сомнение),

— вложенность (память, масштаб, структура),

— фазовость (осцилляции, модуляции, суперпозиции).

Таким образом, вычислительное ядро в H2, проходя через фазовые итерации, разворачивается в модель времени, способную быть и физически реалистичной, и психически обоснованной.

Физическая интерпретация вычислительного ядра H2 в контексте квантовой гравитации

1. Постановка вопроса

Может ли вычислительное ядро, реализуемое на алгебре двойной переменной H2, быть не просто абстрактной моделью времени, но и физической структурой, релевантной в контексте теорий квантовой гравитации?

Переход от алгебраической модели к физической требует интерпретации:

— Что означает фазовая вложенность αn в физическом времени?

— Можно ли рассматривать итерации ядра как микроскопическое «воспроизводство» стрелы времени?

— Имеется ли аналог S-соединения в физике? (переходы, сингулярности, скачки геометрии)

2. Связь с петлевой квантовой гравитацией

— В LQG пространство-квантово-дискретно, построено из «петель» (loops).

— Витки в Сфирали могут быть интерпретированы как элементы структуры спин-сети, но не в пространстве, а во времени.

— Каждый виток — это квант перехода, а S-соединение — это узел взаимодействия между фазами.

3. Связь с теорией каузальных сетей (causal sets)

— В этой теории элементы упорядочены причинно, без геометрии.

— Сфиральная модель добавляет фазовую структуру: причинно связанные события обладают вложенностью и направлением.

— Делители нуля в H2 соответствуют границам причинности или локальным фазовым барьерам.

4. Интерпретация масштаба α

— Фактор α ∈ (0,1) может интерпретироваться как отражение дискретного расширения пространства, аналогично шкалам Ренорм-группы.

— В гравитационных шкалах α — может быть функцией от плотности энергии или кривизны.

5. S-соединение и физические скачки

— Возможный аналог: переключение топологии или мгновенное квантовое туннелирование.

— Также может быть связан с переходом через горизонты событий (чёрные дыры), где направление времени может менять свойства.

6. Вывод

Модель вычислительного ядра в H2 может быть интерпретирована как элементарный квант времени, в котором реализуются:

— направление (итерация),

— антисимметрия (обратимость),

— вложенность (масштаб),

— скачок (S-переход).

Таким образом, она потенциально применима как строительный блок теории времени в квантово-гравитационной парадигме.

Квантовое состояние, порождённое ядром, и связь с наблюдаемой метрикой

1. Постановка задачи

Цель — описать, как вычислительное ядро в H2, реализующее итерационную динамику zn+1 = α ẑ n, может порождать квантовое состояние, и каким образом это состояние связано с наблюдаемой (метрической) структурой пространства-времени.

2. Интерпретация итерации как квантового процесса

— Функция ядра Φ (z) = α ẑ реализует чередование фаз и масштабов.

— Каждая итерация соответствует одному шагу эволюции квантового состояния, где:

— zn — состояние,

— zˉn — его фазовая инверсия (аналог сопряжения волновой функции),

— αn — амплитудное подавление или нормировка.

3. Форма квантового состояния

Рассмотрим состояние:

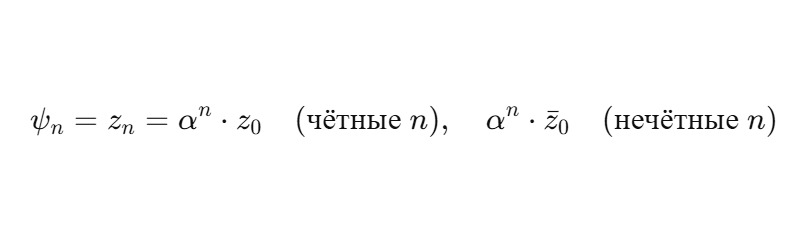
Это состояние:

— комплексоподобное (с фазой и модулем),

— вложенное и зеркальное,

— сохраняет норму ∣ψn∣2 = α2n ∣z0∣2, что может интерпретироваться как потеря вероятности или расширение пространства состояния.

4. Связь с наблюдаемой метрикой

Пусть gμν — наблюдаемая метрика. Тогда:

— фаза φ — может соответствовать ориентации локального времени,

— масштаб αn — коэффициент масштабного сжатия метрики,

— точки с ∣z∣ = 0 — особые гиперповерхности, на которых геометрия перестраивается (аналог горизонтов, стенок доменов).

5. Интерференция состояний

Рассмотрим два синхронизированных ядра:

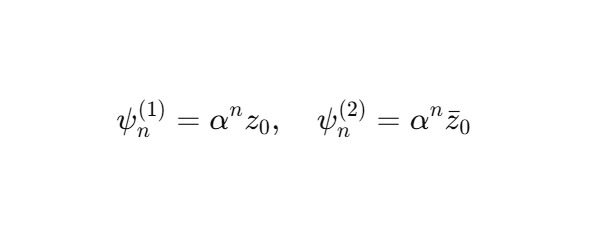
Их суперпозиция:

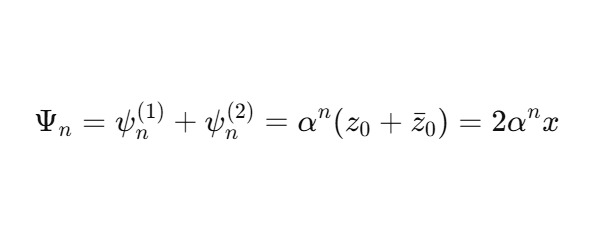
Если z0 = x + jy, то z0 + ẑ 0 = 2x: интерференция даёт реальный компонент, аналог проекции наблюдаемого результата.

6. Вывод

Итерации ядра могут быть интерпретированы как фазовая квантовая динамика, в которой:

— масштаб α задаёт эволюцию амплитуды,

— ẑ — отражает внутреннюю симметрию (аналог унитарности или чётности),

— линейные комбинации дают наблюдаемые значения.

Это позволяет рассматривать вычислительное ядро как алгебраический генератор квантовых состояний, отражающих не только логику вычислений, но и структуру наблюдаемого пространства.

Оператор наблюдения и метрический отклик на состояние, порождённое ядром

1. Постановка задачи

В предыдущем разделе вычислительное ядро Φ (z) = α ẑ было интерпретировано как генератор квантового состояния. Следующим шагом является определение оператора наблюдения Ȏ, способного выделить наблюдаемые величины и породить метрический отклик.

2. Природа наблюдения в H2

Пусть z = x + jy ∈ H2. Тогда:

— Реальная часть: Re (z) = x,

— Мнимая по j: Imj (z) = y,

— Сопряжение: zˉ= x −j y.

Рассмотрим оператор наблюдения как линейное отображение:

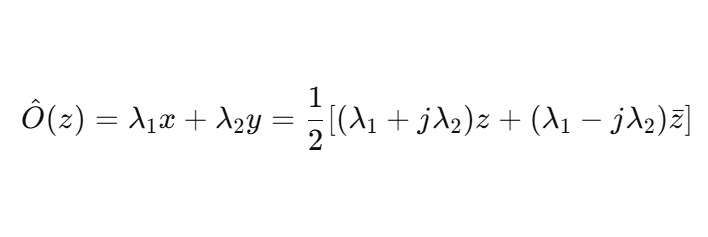
Здесь λ1,λ2 — параметры наблюдательной рамки.

3. Отклик на состояние ψn = αnz0

Тогда:

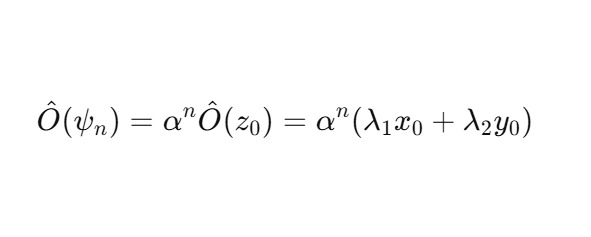
Наблюдаемая величина убывает с итерациями: происходит затухание сигнала или расширение фона, аналогично эффектам декогеренции или инфляционного растяжения.

4. Метрический отклик

Рассмотрим наблюдаемую метрику как функцию плотности отклика:

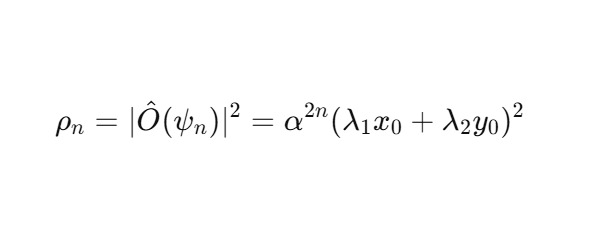
Интерпретация:

— ρn — энергия/плотность/интенсивность,

— затухание ρn — отклик метрики на вложенность витков,

— форма ρn — отражает направление наблюдения (λ1, λ2).

5. Пример

Пусть λ1 = 1, λ2 = 0: оператор «смотрит» вдоль оси x. Тогда:

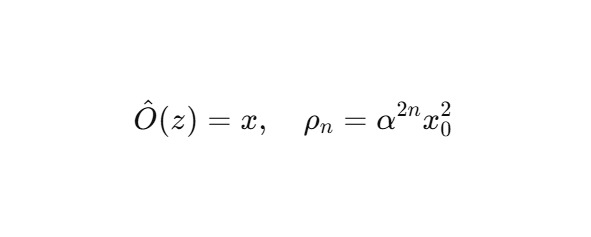
Если λ1 = λ2 = 1, то оператор проецирует по диагонали:

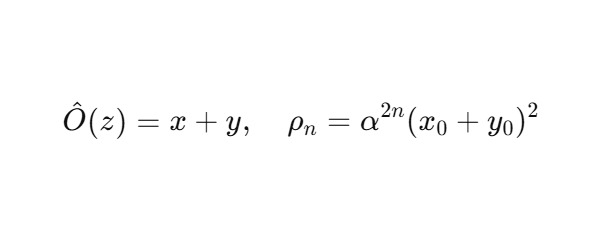
6. Вывод

Оператор наблюдения Ȏ задаёт направление проекции состояния на наблюдаемое значение. Отклик ρn — это метрика, чувствительная к фазе и масштабу вложенного состояния. Таким образом, состояние, порождённое ядром, не просто существует в H2, но и взаимодействует с наблюдателем, формируя меру — как в квантовой, так и в метагеометрической физике.

Вероятностная интерпретация ядра и квантовые переходы между витками

1. Постановка задачи

В предыдущих разделах мы рассмотрели состояние ψn = αnz0 как результат итераций вычислительного ядра. Теперь необходимо рассмотреть:

— какова вероятность нахождения системы в том или ином витке,

— каким образом происходит «переход» от одного витка к другому,

— и как можно интерпретировать эти переходы в духе квантовой механики.

2. Нормировка и вероятность

Пусть ψn ∈ H2 — состояние на витке n.

Тогда вероятность нахождения в витке n:

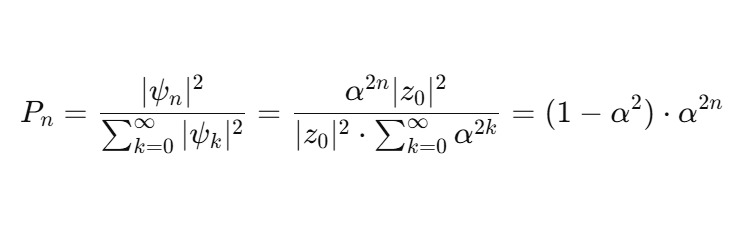
Это геометрическое распределение вероятности:

— Максимум при n = 0,

— Быстрое убывание с ростом n,

— Общая сумма — 1.

3. Квантовый переход между витками

Пусть Tn — оператор перехода от витка n к n +1:

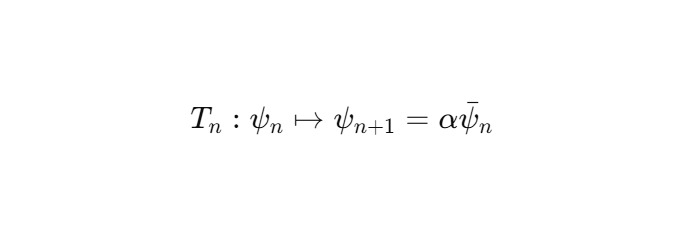
Тогда последовательность переходов:

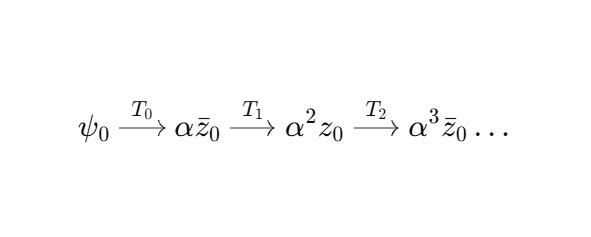
Фазовое чередование и масштабное затухание делают переходы когерентными на чётных шагах и антисимметричными на нечётных.

4. Коллапс и выбор

Если система измеряется, то наблюдается одно из состояний ψn. Вероятность — Pn. Коллапс означает выбор конкретного витка:

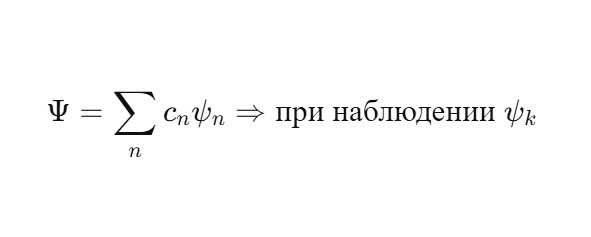
Этот выбор фиксирует не только масштаб (αk), но и фазу (чётность/нечётность). То есть наблюдатель фиксирует положение внутри структуры Сфирали.

5. Интерпретация

— Вероятностное распределение естественно вытекает из масштабной структуры ядра.

— Каждый виток — это потенциальное состояние.

— Переход между витками — аналог унитарной квантовой эволюции.

— Коллапс — выбор фазы и масштаба.

6. Вывод

Вероятностная интерпретация вычислительного ядра делает его полноценной моделью квантовой динамики, в которой:

— структура вложена,

— амплитуды убывают,

— состояния зеркальны,

— выбор фиксирует не просто значение, а позицию в фазовом ландшафте Сфирали.

Сводный вывод о модели вычислительного ядра в H2

1. От алгебры к структуре

Исходя из простейшей функции Φ (z) = α ẑ, построенной в алгебре двойной переменной H2, нами была развёрнута целостная структура, обладающая свойствами:

— вложенности (через масштаб αn),

— фазовой антисимметрии (через сопряжение),

— устойчивости (повторное применение возвращает фазу),

— инвариантности (делители нуля остаются на месте).

Эта структура стала основой для понимания вычислительного ядра как элементарной фрактально-фазовой единицы.

2. Геометрия и топология

Итерации ядра создают последовательность вложенных витков, формирующих:

— синхронизированные пары,

— сферу витков (как оболочку ядер),

— ленту времени (как проекцию вложенности на последовательность).

Каждый виток несёт информацию о фазе, масштабе и направлении — и связан S-переходом с соседним.

3. Физический смысл

— Сопоставлено с квантовой гравитацией, LQG, каузальными сетями.

— Переходы между витками — аналоги квантовых взаимодействий или смен топологии.

— Поперечный полярный вектор времени реализован как структура фазовой вложенности.

4. Квантово-вероятностная природа

— Каждое состояние ψn — элемент суперпозиции.

— Вероятность определяется масштабом вложенности α2n.

— Коллапс — выбор витка, фиксирует положение в структуре.

5. Наблюдение и отклик

— Оператор наблюдения Ȏ проецирует состояние на измеримую величину.

— Метрика пространства чувствительна к вложенности и фазе.

— Состояние ядра порождает наблюдаемое поле отклика.

6. Общий итог

Вычислительное ядро в H2 — это минимальная единица, объединяющая вычисление, квантовое состояние, фазовую структуру и временную направленность.

Оно реализует:

— форму: вложенность, виток, антисимметрия,

— время: итерация, S-сдвиг, проекция в ленту,

— смысл: выбор, наблюдение, структура различий.

Модель ядра — это схема, на которой могут быть построены новые модели квантовой логики, когнитивной топологии и альтернативной метрики времени.

Литература

— Павлов Д. Г., Панчелюга М. С., Панчелюга В. А. (2009). О форме аналогов множества Жюлиа на плоскости двойной переменной. // Гиперкомплексные числа в геометрии и физике. Т.6, №2 (12), С. 162–176.

— Басаргин О. С. (2025). Эталонное описание устройства Сфираль. Zenodo. https://doi.org/10.5281/zenodo.15133508

— Rovelli C. (2004). Quantum Gravity. Cambridge University Press.

— Bombelli L., Lee J., Meyer D., Sorkin R. (1987). Space-Time as a Causal Set. Physical Review Letters, 59 (5), 521–524.

— Buzsáki G. (2006). Rhythms of the Brain. Oxford University Press.

— Edelman G.M. (1989). The Remembered Present: A Biological Theory of Consciousness. Basic Books.

— Пригожин И., Стенгерс И. (1986). Порядок из хаоса: Новый диалог человека с природой. — М.: Прогресс.

— Вернадский В. И. (1989). Несколько слов о ноосфере. — В: Избранные труды. — М.: Наука.

Аналитическое представление Сфирали в трёхмерных алгебрах

Аннотация

В настоящем исследовании поставлена задача найти аналитическую функцию, выражающую структуру Сфирали — зеркально-антисимметричной вложенной конструкции — в терминах, совместимых с полевой интерпретацией событий, предложенной Д. Г. Павловым.

Рассмотрены алгебры C ⊕ R и R ⊕ R ⊕ R как возможные пространства, в которых Сфираль может быть выражена через логарифмическое поле событий. Показано, что функция вида:

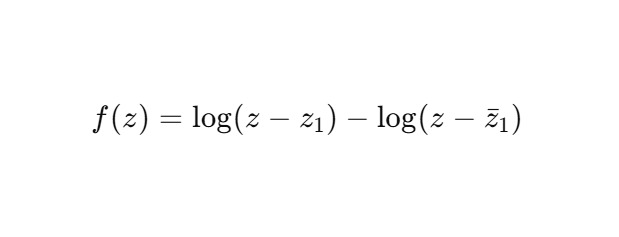
— обладает необходимыми свойствами: антисимметрией, вложенностью (при масштабировании аргумента), и отражает фазовые переходы, аналогичные S-соединениям.

Сфираль определяется как линия уровня фазового поля:

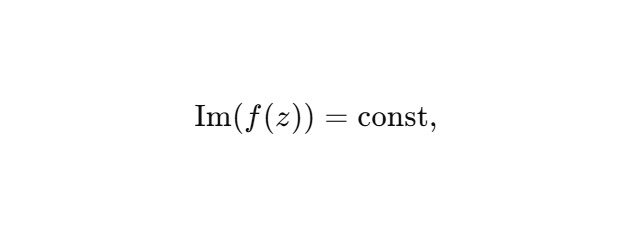
где f (z) — суперпозиция логарифмов от зеркальных событий. Эта линия интерпретируется как интегральная траектория фазового потока, а её геометрия согласуется с вложенной зеркальной структурой.

Также предложена параметризация Сфирали в R3 и псевдофинслеров подход с метрикой, зависящей от направления и вложенности.

Таким образом, установлено, что структура Сфирали может быть выражена как аналитическая кривая в логарифмическом поле, соответствующем философии «материальных событий» Д. Г. Павлова, но дополненном структурой фазового потока, антисимметрии и масштабной вложенности.

Модель может быть использована как в математической теории поля, так и в когнитивных и физико-временных интерпретациях.

Ключевые слова: Сфираль, аналитическая функция, триплексные числа, логарифмическое поле, зеркальная антисимметрия, вложенность, фазовый поток, S-соединение, материальное событие, псевдофинслерова геометрия, Д. Г. Павлов, теория событий, фазовая структура времени, временные кристаллы, интегральная траектория, конформное отображение, когнитивная модель времени, квантовая логика, математическая физика.

1. Вводная

На основе вводных Дмитрия Павлова задача переформулируется следующим образом:

— Найти или построить аналитическую функцию f (x), которая выражает структуру Сфирали, но уже не в H2, а в одной из трёхмерных алгебр:

— триплексные числа: C ⊕ R,

— тройные числа: R ⊕ R ⊕ R,

— или даже в обобщённом псевдофинслеровом пространстве, где метрика зависит от направления.

2. Возможные пространства для поиска

— C ⊕ R: трёхмерная коммутативная алгебра, состоящая из комплексной и вещественной части. Элемент: z = (a + ib) + c ∈ C ⊕ R.

— R ⊕ R ⊕ R: чисто вещественная алгебра, трёхкомпонентный вектор. Простейший случай — линейная суперпозиция трёх независимых направлений.

3. Требования к функции f

— Отражать вложенность и фазовость,

— Иметь антисимметрию относительно сопряжённого компонента,

— Позволять суперпозицию и порождение сложного поля событий (как сумма логарифмов у Павлова),

— Потенциально быть связанной с обобщённым логарифмом или преобразованием типа log (z1) — log (z2),

— Отражать временную направленность и скачки (S-соединения).

4. Следующие шаги

— Определить структуру базисных элементов в обеих алгебрах;

— Выписать кандидаты на функции f, удовлетворяющие условиям;

— Проверить, может ли Сфираль быть интерпретирована как

— уровень функции,

— результат суперпозиции элементарных событий,

— фазовый поток на вложенной оболочке в C ⊕ R.

Структура базиса алгебры C ⊕ R

1. Общее определение

Алгебра C ⊕ R представляет собой прямую сумму комплексных и вещественных чисел. Элемент этой алгебры имеет вид:

Z = (a + ib, c), где a, b, c ∈ R

Или, что то же самое: z = a + ib + cε, где ε — дополнительный вещественный базисный элемент, линейно независимый от 1 и i.

Алгебра коммутативна и трёхмерна как векторное пространство над R.

2. Базис

Базисные элементы: 1, i, ε

где:

— i2 = −1,

— ε2 = 1 (или иногда ε2 = 0, в зависимости от выбора — нужно зафиксировать в дальнейшем),

— iε = εi.

3. Сложение и умножение

Пусть z = a + ib + cε w = x + iy + zε.

Тогда:

— Сложение покомпонентно:

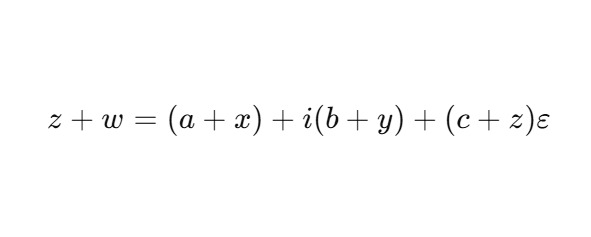
— Умножение:

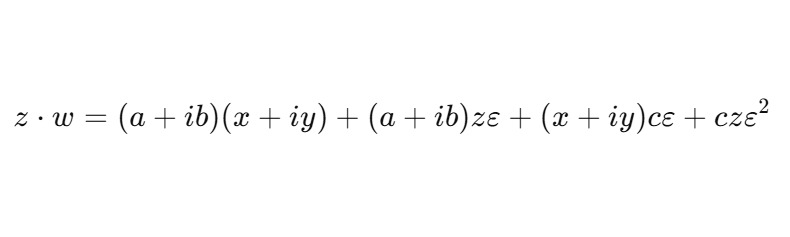
Если ε2 = 1: сохраняется масштабность. Если ε2 = 0: алгебра становится похожей на алгебру диадических или дуальных чисел

---

4. Интерпретация

Алгебра C ⊕ R может быть интерпретирована как:

— комплексная плоскость + ортогональное вещественное направление (вектор фазовой глубины),

— трёхмерное пространство, где:

— a: амплитуда,

— b: фаза (через i),

— c: поперечная структура, связанная с вложенностью или масштабом.

5. Следующий шаг

Переход к построению кандидатов на аналитические функции f (z), отражающих свойства Сфирали в этом базисе: зеркальность, вложенность, фазовые переходы.

Кандидаты на аналитические функции f (z) в алгебре C⊕R

1. Цель

Найти формулы вида f (z), где z = a + ib + cε ∈ C ⊕ R, которые могли бы отражать структуру Сфирали: зеркальность, вложенность, антисимметрию, фазовые переходы (аналог S-соединения).

2. Общий принцип

Функция должна включать:

— фазовый компонент (через i),

— поперечный компонент (через ε),

— либо быть производной или обобщением логарифма,

— либо быть суперпозицией логарифмов: log (z — zk).

3. Кандидаты

3.1. Функция на основе логарифма сопряжённой разности

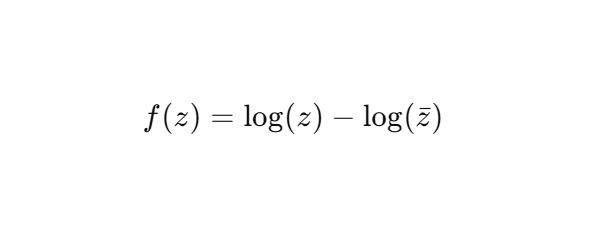
Здесь ẑ = a — ib + cε — формальное сопряжение по комплексной части. Получаем чисто фазовый поворот. Отражает антисимметрию.

3.2. Логарифм по фазовой норме

Попытка учесть фазу и вложенность в одной формуле. Может быть разложено в степенной ряд.

---

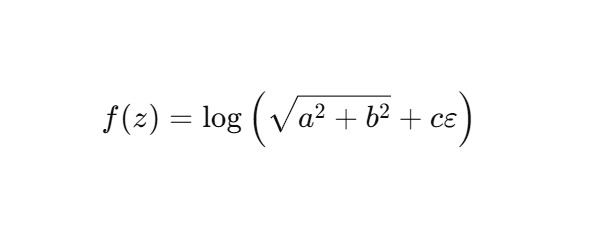
3.3. Разность логарифмов двух точек

Формирует S-переход между двумя элементами. Если z1, z2 — антиподы по фазе, то разность логарифмов отражает зеркальность.

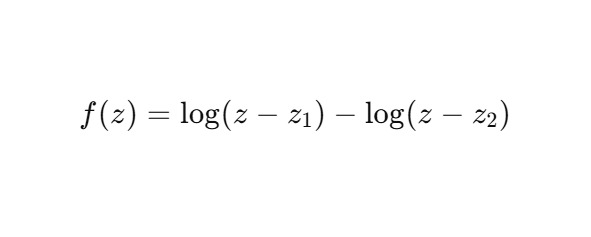
3.4. Композиция логарифма с вложением

Генерация вложенных фаз с постоянным коэффициентом масштабирования α.

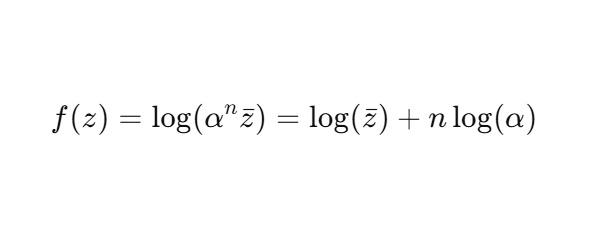
4. Следующий шаг

— Выбрать базовую функцию и протестировать:

— сохраняется ли зеркальность f (z) = −f (ẑ),

— как ведёт себя по отношению к масштабированию,

— допускает ли суперпозицию или вложение,

— может ли быть интерпретирована как поле события или витка.

Проверка антисимметрии кандидатов на f (z) в C ⊕ R

1. Цель

Проверить, выполняется ли условие зеркальной антисимметрии для функции f (z):

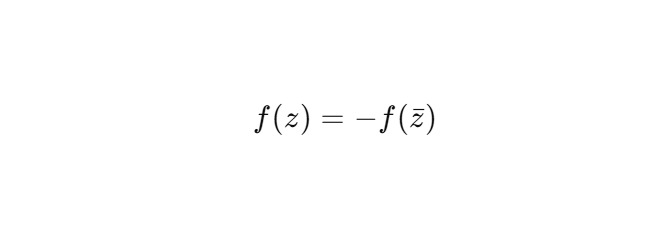
где ẑ — сопряжение по комплексной части: если z = a + ib + cε, то ẑ = a — ib + cε.

---

2. Функция 1: f (z) = log (z) — log (ẑ)

Тогда:

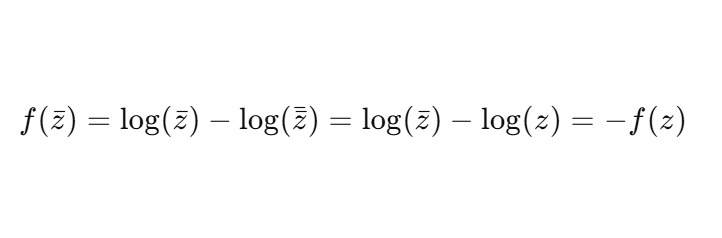
Условие антисимметрии выполняется.

3. Функция 2: f (z) = log (αn ẑ) = log (ẑ) + n log (α)

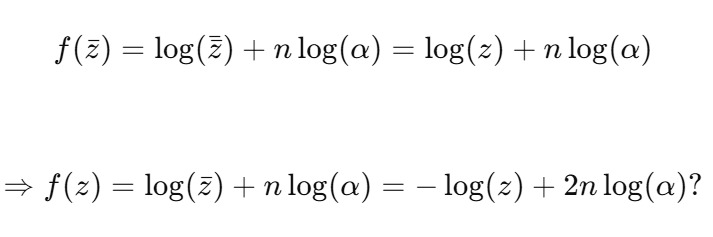
Не выполняется в общем случае. Только если log (z) = −log (ẑ), что зависит от определения ветви логарифма.

---

4. Функция 3: f (z) = log (z — z1) — log (z — z2)

Тогда: