Бесплатный фрагмент - Репетитор по математике. Алгебра

Введение или как работать с этой книгой

«Репетитор по математике. Алгебра» -это вторая книга серии. Первую книгу «Репетитор по математике. Арифметика» вы можете скачать в электронном виде практически из любого книжного магазина в Интернете.

1. Почему репетитор? Название возникло сразу. Не потому, что подобных названий почти нет. Судите сами, это ведь не учебник, где весь учебный материал подаётся от более простого к сложному. В учебнике существует тенденция перескакивания с одной темы на другую, а потом возвращение к уже более сложным заданиям. В репетиторе такого нет. Если вы начали изучать какую-то тему, то изучаете её от начала и до конца. Кроме этого, в репетиторе теоретический материал подан в самом необходимом, минимальном объёме без каких-либо доказательств и выведения формул. Это также и не справочник, где существует множество формул, определений, таблиц, где много теоретического материала, но почти нет практического применения теоретических знаний. Цель же репетитора — обучение практическим навыкам решения разнообразных математических задач. Наиболее похож репетитор на практикум, там тоже большое внимание уделяется практическим занятиям, но в отличие от практикума, где почти нет теоретического материала, в репетиторе он присутствует. Кроме этого, в данном учебном пособии есть тестовые задания, которые, как правило, отсутствуют в учебниках, справочниках, практикумах.

2. Кому прежде всего будет полезна эта книга? Репетитор ориентирован на основные задания, которые могут встретиться на выпускных экзаменах за курс средней школы и на вступительных экзаменах в высшие учебные заведения. Поэтому данное пособие прежде всего станет незаменимым помощником именно для данных категорий учащихся. Он также может быть применим и учителями выпускных классов средней школы, а также тем, кто хочет повысить свою математическую грамотность и научиться решать типовые математические задачи. Автор отдаёт себе отчёт в том, что никакое учебное пособие не заменит реального живого репетитора, который сможет подкорректировать и направить свои усилия на те разделы математики, в которых ученик разбирается не совсем хорошо. Увы, книга лишена такой возможности. Она может служить только дополнением к занятиям с реальным репетитором. Однако репетитор стоит немалых денег и не у всех есть возможность его нанять. Поэтому данное учебное пособие является хоть и неполной, но альтернативой. Ещё будучи учителем в школе, автор обратил внимание, что овладеть основными математическими навыками может практически любой человек. Есть только небольшой процент людей, которые не могут этого сделать по разным объективным причинам. Остальные не знают математику и не умеют решать математические задачи, потому что, или не хотят, или не хватает времени, или просто в жизни это может не пригодится, или лень заниматься каждый день. Таким людям я не рекомендую открывать репетитор. Вы не добьётесь желаемого результата и будете винить во всём автора. А для тех, кто решил серьёзно заняться изучением математики — добро пожаловать на страницы этого пособия. Если хотя бы половине этих людей репетитор поможет, автор будет считать, что его труд не был напрасным.

3. Чем же репетитор отличается от других учебных пособий? Прежде всего простотой подачи материала. Автор общается с обучаемым и указывает на характерные ошибки, которые могут встретиться при решении задач. В репетиторе показано решение типовых задач, а также задач повышенной трудности. Каждая задача или пример решается досконально с пояснениями, что позволяет усвоить базовые навыки даже людям, которые считали, что математика не для них.

4. О структуре данной книги. Вся книга поделена на 23 темы. В каждой теме есть необходимый минимум теоретического материала, примеры решения задач. В конце каждой темы даются один или несколько тестовых заданий (кроме тем 12 и 21) и задачи для самостоятельного решения.

Поговорим отдельно о каждой из этих составляющих.

Теоретический материал. Как было уже сказано ранее, это тот необходимый минимум, без которого невозможно обойтись при решении заданий. Если формула выведена крупным шрифтом — её необходимо запомнить. Тоже самое касается формулировок и прочих элементов теории. Таких обязательных элементов для запоминания в книге немного. Обучение построено по американской системе, где от учащегося не требуется зазубривание теоретического материала, а предпочтение отдаётся только навыкам его применения на практике. Поэтому, при самостоятельном решении задач автор разрешает пользоваться формулами. Запоминание формул произойдёт автоматически при практическом их применении. В конце книги собран и изложен в кратком виде весь теоретический материал. Им вы можете пользоваться при решении задач. Это не значит, что теоретический материал можно совсем не изучать или изучить бегло. Как я уже сказал, в конце каждой темы есть тестовые задания и без базовых знаний теоретического материала, вы вряд ли сможете их пройти.

Примеры решения задач. В репетиторе рассмотрены решения как базовых типовых задач, так и задач повышенной сложности. Многие задания взяты из конкурсных задач по математике, которые были предложены абитуриентам при поступлении в высшие учебные заведения в 70 — 80х годах прошлого столетия. Поверьте, если вы научитесь решать эти задачи, то любой экзамен вам будет по плечу. Часть заданий взята из экзаменационных задач за курс средней школы, часть из других источников. Автор уважает авторские права других, поэтому в конце книги дан список использованной литературы. Как было сказано выше, все примеры решения задач приведены с подробными пояснениями.

Тестовые задания. К каждой теме предложено один или несколько тестовых заданий, в зависимости от объёма теоретического материала. Каждое тестовое задание включает 12 вопросов с четырьмя вариантами ответов, один из которых является правильным. Оценивание тестовых заданий производится по 12-ти бальной системе. Чтобы не путаться, привожу перевод 12-ти бальной системы в 5-ти бальную.

12 баллов — оценка 5+

11 баллов — 5

10 баллов — 5-

9 баллов — 4+

8 баллов — 4

7 баллов — 4-

6 баллов — 3+

5 баллов — 3

4 балла — 3-

3 балла — 2+

2 балла — 2

1 балл — 2 —

Я надеюсь, что последние шесть строчек вам не понадобятся при оценивании тестовых заданий. Только все должно быть по-честному. Помните, если вы будете не объективны, то в первую очередь обманите сами себе.

Теперь, как оценивать тестовые задания. За каждое правильное тестовое задание начисляется 1 балл. По количеству набранных баллов и выставляется итоговая оценка по 12-ти бальной системе. Например, вы ответили правильно на 7 вопросов-это оценка 4-. При 11-ти верных ответах имеете оценку 5, а при 12-ти имеете максимум 5+.

Продолжительность тестирования — 25—30 минут. Выделите для тестирования отдельный день. Берите чистый лист бумаги и вперёд. Тесты — это не только интересно, но и познавательно. Желательно пройти все предложенные тесты (но не более двух за один день), в конце книги имеются ответы на тестовые задания для проверки. Не стоит в них заглядывать раньше времени.

Задачи для самостоятельного решения. Автор сознательно не выделял какими-то знаками задания повышенной сложности и считает, что такое приём способствует более спокойному решению задач без излишнего волнения и стресса. В процессе решения вы сами сможете понять, сложна для вас данная задача или нет. Притом сложность задачи — это субъективная оценка. Некоторые с лёгкостью могут решать подобные задачи, а вот более простые в нашем понимании могут вызвать затруднение. Если вы поняли, что можете приступать к решению задач, то не медлите. Каких-то ограничений по количеству решаемых задач в день нет. Когда поняли, что устали, то занятие можно прекратить, но хотя бы 30 — 40 минут в день вы должны уделять решению задач. Это не обязательно делать изо дня в день. Через какое-то время можно сделать себе 1- 2-х дневный перерыв. Но с отдыхом не затягивайте. Почувствовав, что немного отдохнули и есть свободное время, приступайте снова к решению задач. Автор рекомендует решить все задачи, которые есть в разделе для самостоятельного решения. Решив какую-то задачу, загляните в раздел «ответы» и, убедившись, что вы все решили правильно, продолжайте дальше. Если ваш ответ не совпадает с ответом в конце книги, рекомендуется ещё раз пройтись по своему решению и выявить ошибки. Если вы их не обнаружили, то загляните в раздел «Указания к решению задач». Он находится после раздела ответов. Прочитав указания к решению задач (они есть практически ко всем задачам), снова приступайте к решению сложной для вас задачи. К задачам для самостоятельного решения есть полные и подробные решения, которые находятся в соответствующем разделе. Но это последний раздел, в который вам следует заглянуть. Это в том случае, когда задача не решается без посторонней помощи. Не злоупотребляйте этим разделом, иначе вы так никогда и не научитесь решать математические задачи. Постарайтесь ограничиться только разделом «Указания к решению задач». Этого бывает достаточно, чтобы понять свою проблему и попытаться её искоренить.

В конце книги, как я уже сказал, находится справочный раздел, ответы к тестовым заданиям, ответы к задачам для самостоятельного решения, указания к решению задач, решение задач. Кроме этого, там же находится список использованной литературы. Структура книги максимально удобна для использования. А в начале книги предложены условные математические обозначения, которые будут встречаться в дальнейшем.

Автор будет благодарен за любые замечания и обнаруженные неточности и ошибки при написании этого пособия. А также будет рад любому мнению и практическим советам от учителей и преподавателей математики по улучшению данной книги.

некоторые математические обозначения

Алгебра

Это один из основных разделов математики. В нем мы научимся преобразовывать алгебраические выражения, решать разнообразные уравнения, неравенства, а также их системы (в том числе показательные и логарифмические). Большое внимание уделим текстовым задачам, а также ознакомимся с понятием «функция» и научимся строить графики различных функций. Просьба, по возможности, решить все предложенные задачи в этом разделе и пройти все тестовые задания.

Тема 1

Возведение в степень, свойства степени, корни, действия с корнями

Возвести число в целую степень n, значит повторить его сомножителем n раз т.е.

Вторая степень называется квадратом, третья — кубом.

Запомните!

1) Первой степенью числа называют само это число.

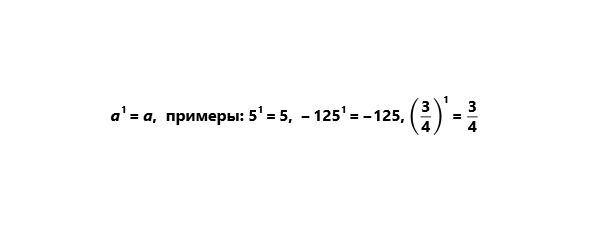
2) Любое число (кроме нуля) в нулевой степени есть единица.

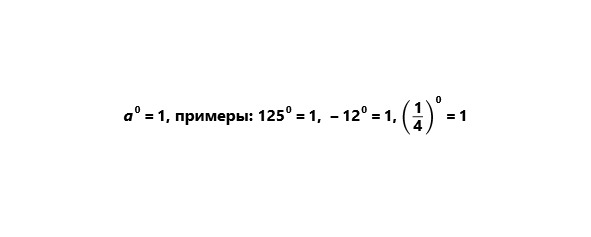
3) Нуль в любой неотрицательной степени есть нуль.

4) Единица в любой степени есть единица.

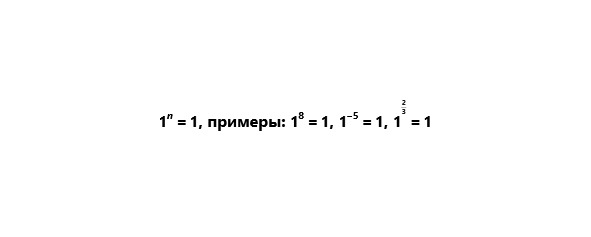
Отрицательный показатель степени.

Дробный показатель степени.

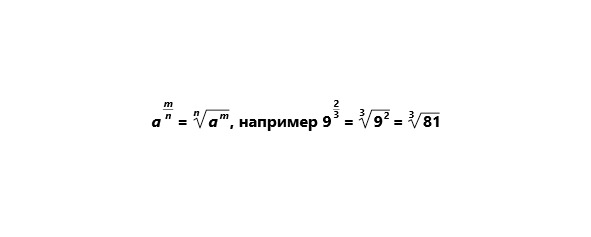
Дробный отрицательный показатель степени

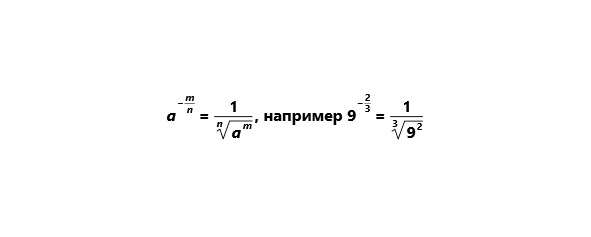
Теперь рассмотрим свойства степени. Для удобства мы составили таблицу, в котором привели примеры не только с натуральными показателями степени, но и с рациональными и действительными.

Необходимые пояснения к свойствам степени.

Первые два свойства указывают на действия со степенями с одинаковыми основаниями. При умножении таких степеней их показатели складываются (свойство 1), при делении — вычитаются (свойство 2). Третье свойство — это свойство возведения степени в степень — показатели степени перемножаются (свойство 3).

Следующие два свойства — это возведение в степень произведения (свойство 4) и частного (свойство 5). Притом, свойство 4 справедливо для любого числа сомножителей. Применение данных правил позволяет существенно облегчить вычисления.

Извлечение корня есть нахождение основания степени по степени и её показателю. Записывается это так

Основные свойства корня.

1) Если за корнем следует степень, равная показателю корня,

то корень можно опустить, например

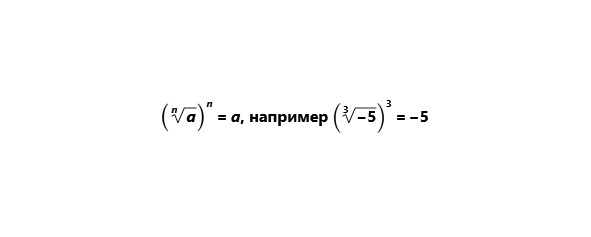
2) Если подкоренное число имеет степень равную

показателю корня, то оно равно модулю подкоренного числа.

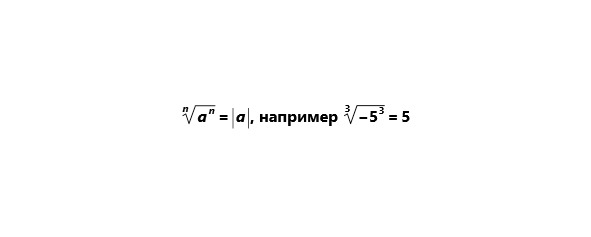
Основные действия с корнями (все эти правила справедливы при

a≥0 и b≥0)

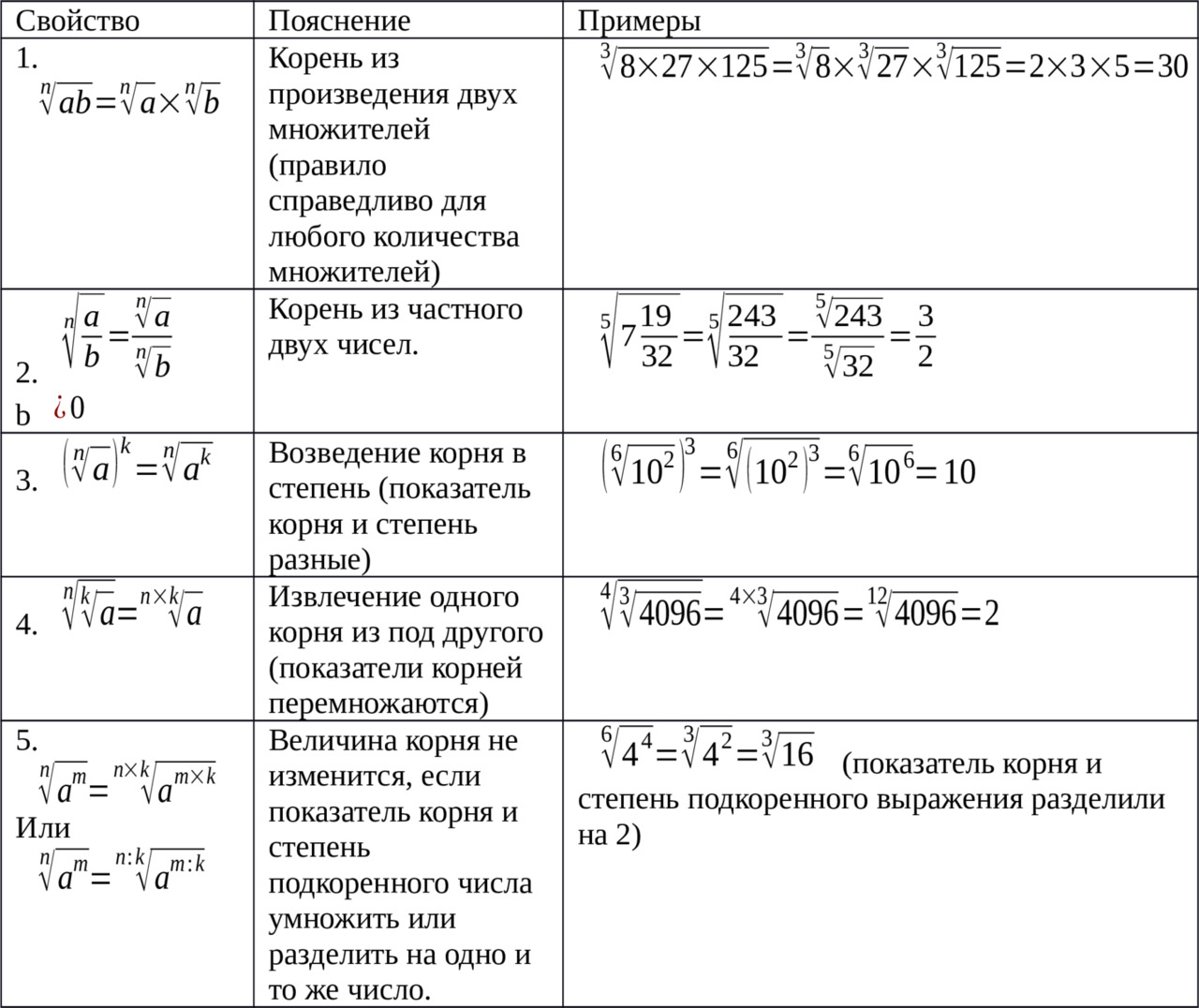
Все вышеизложенные правила позволяют существенно облегчить вычисления.

Рассмотрим две операции: внесение множителя под знак корня и вынесение множителя из-под знака корня при решении задач.

Очень часто при преобразованиях пользуются приёмом уничтожения иррациональности в знаменателе или числителе дроби. Такой метод позволяет упростить приближенные вычисления. Рассмотрим его на примере.

.

Уничтожив иррациональность в знаменателе, мы пришли к такому результату, что нам необходимо разделить приближенное число на целое, что намного точнее и проще, чем делить приближенное число на приближенное и проводить вычисления с большим количеством значащих цифр, чтобы получить два верных знака после запятой.

Тестовые задания к теме 1

Тест 1

Тест 2

Тест 3

Тест 4

Тест 5

Задачи

Тема 2

Одночлен. Многочлен. Преобразование алгебраических выражений. Формулы сокращённого умножения. Разложение многочлена на множители

Мы подошли к одной из самых важных тем алгебры. Ведь без задания на преобразование алгебраических выражений не обходится практически ни один экзамен по математике. Сразу предупреждаю, такие преобразования сложны и требуют не только знаний, но и внимания, смекалки, терпения.

Для начала мы ознакомимся с понятиями «одночлен» и «многочлен».

Одночленом называется произведение двух или нескольких сомножителей каждый из которых есть либо число, либо буква, либо степень буквы.

Например, 6a2x, 2c, 3b3c2, -10y7, -7abc.

Одночлены состоят из коэффициента (числового множителя) и буквенной части.

6a2x = 6 (коэффициент) × a2x (буквенная часть).

Отдельно взятое число, буква или степень буквы тоже рассматриваются как одночлен. Например, -5 (одночлен без буквенной части), с и c5 (одночлены, в которых коэффициент равен 1).

Одночлены называются подобными, если они одинаковы или отличаются только коэффициентами.

Например, 7x2y3, -5x2y3, -x2y3 — подобны.

Сложение двух или нескольких одночленов возможно только тогда, когда среди слагаемых имеются подобные.

Например, 6x2y2 +9x2y2 — 7x2y2 = 8x2y2.

Здесь мы суммировали коэффициенты, оставив буквенную часть без изменений. Такое действие называется приведением подобных членов.

Можно этот пример решить иначе, вынеся общий множитель за скобки:

6x2y2 +9x2y2 — 7x2y2 = (6+9—7) x2y2 = 8x2y2.

Как мы видим, вынесение общего множителя за скобки — операция, идентичная приведению подобных членов.

Произведение двух или нескольких одночленов можно упростить лишь тогда, когда в них входят некоторые степени одних и тех же букв или числовые коэффициенты. При этом показатели степеней у соответствующих букв складываются, числовые коэффициенты перемножаются.

Пример: -10x2y×3x3y2 × (-xy3) = -10×3× (-1) (x2x3x) (yy2y3) = 30x6y6.

Для лучшего понимания, мы расписали это действие более подробно, хотя оно довольно прозрачное и может делаться устно.

Частное двух одночленов можно упростить, если делимое и делитель содержат некоторые степени одних и тех же букв или числовые коэффициенты. При этом показатель степени делителя вычитается из показателя степени делимого, а числовой коэффициент делимого делится на числовой коэффициент делителя.

Пример: 6x3y8z7: 2xy5z3 = 3x2y3z4.

Здесь числовой коэффициент делимого разделили на числовой коэффициент делителя, вычли показатели степени буквы x (3—1=2), буквы y (8—5=3) и буквы z (7—3=4).

При делении двух одночленов могут возникнуть две ситуации, которые требуют дополнительного пояснения.

1.Если показатели степени у некоторой буквы в делимом и делителе одни и те же, то в частное эта буква не войдёт (ведь нулевая степень любого числа равна единице).

Пример: 12x3y4: 4x3y2 =3y2.

2.Если показатель степени какой-нибудь буквы в делимом меньше, чем показатель степени той же буквы в делителе, то вычитание даёт отрицательную степень этой буквы.

Пример: 8x3y5: 2x5y3 = 4x-2y2 = (4y2) / (x2)

При возведении одночлена в степень используется правило возведения степени в степень.

Пример: Возведём одночлен 2a4b2 в четвертую степень.

(2a4b2) 4 = 24 (a4) 4 (b2) 4 = 16a16b8.

Не забывайте, что показатели степеней при данном правиле перемножаются.

Сумма одночленов называется многочленом.

Например, 4x2y +3a -7b2 — многочлен, состоящий из суммы одночленов 4x2, 3a, -7b2.

При сложении и вычитании многочленов снова получается многочлен.

Пример. Сложим многочлены x3 +2x2y2 — 7x2 + y и 3x3 — x2y2 +5x2 — 3y.

Составим сумму многочленов, затем раскроем скобки и приведём в полученном многочлене подобные члены.

(x3+2x2y2—7x2+y) + (3x2- x2y2 +5x2 — 3y) = x3 +3x3 +2x2y2 — x2y2 — 7x2 +5x2+ y — 3y = 4x3 + x2y2 — 2x2 — 2y.

Здесь одновременно с раскрытием скобок мы сгруппировали подобные члены (для удобства вычислений).

Аналогично, производится и вычитание многочленов. Не забывайте, если перед скобкой стоит знак «минус», то все члены, заключаемые в скобки, меняют свой знак на противоположный.

Пример. (4x2y — 7x3 +5y — 3) — (-2x2y +5x3- 3y +2) =4x2y — 7x3 +5y -3 +2x2y -5x3 +3y — 2 = 6x2y — 12x3 +8y — 5.

Произведение многочленов.

Произведение одночлена и многочлена всегда можно представить в виде многочлена.

Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить.

Схема: a× (b+c) =a×b+a×c (открытие скобок)

Например:

— 4x3 (2y3- x +6) = -4x32y3 + (-4x3 (-x)) + (-4x3 ×6) = -8x3y3 +4x4 — 24x3.

Мы выписали здесь промежуточные вычисления, хотя, в принципе, без этой записи можно обойтись.

Умножение многочлена на многочлен.

Произведение многочлена на многочлен равно сумме всех возможных произведений каждого одночлена одного из многочленов на каждый одночлен другого.

Схема: (a+b) × (c+d) =a×c+a×d+b×c+b×d

Пример. (3x2 — 6x +2) × (4x3 — 3x) = 12x5 — 9x3 — 24x4 +18x2 +8x3 — 6x =

= 12x5 — 24x4 — x3 +18x2 — 6x.

Существуют частные случаи умножения многочленов, которые называются формулами сокращённого умножения многочленов. Их желательно запомнить.

1. (a+b) 2 =a2+2ab+b2 (квадрат суммы)

2. (a-b) 2=a2—2ab+b2 (квадрат разности)

3. (a-b) (a+b) =a2-b2 (разность квадратов)

4. (a+b) 3=a3+3a2b+3ab2+b3 (куб суммы)

5. (a-b) 3=a3—3a2b+3ab2-b3 (куб разности)

6. (a+b) (a2-ab+b2) =a3+b3 (сумма кубов)

7. (a-b) (a2+ab+b2) =a3-b3 (разность кубов)

Примеры: (2ma2 +0.1nb2) 2 = 4m2a4 +0.4mna2b2 +0.01n2b4

(5x3 — 2y3) 2 = 25x6 — 20x3y3 +4y6

(0.2a2b + c3) (0.2a2b — c3) = 0.04a4b2 — c6

(5ab2 +2a3) 3 = 125a3b6 +150a5b4 +60a7b2 +8a9

Предлагаю вам самим узнать, какие формулы были использованы в этих примерах.

Деление многочленов.

1. Деление многочлена на одночлен.

Частное от деления многочлена на одночлен равно сумме частных, полученных от деления каждого слагаемого многочлена на одночлен.

Схема:

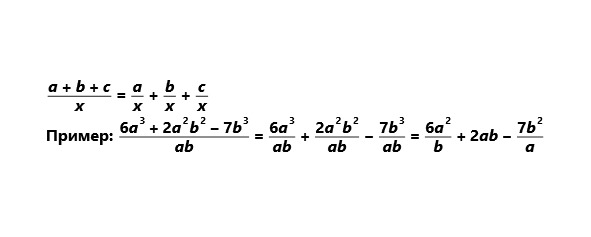
2. Деление многочлена на многочлен в общем случае можно выполнить с остатком, подобно тому, как это делается при делении целых чисел.

Разделить многочлен P на многочлен Q значит найти многочлен M (частное) и N (остаток) удовлетворяющий двум требованиям: 1) должно соблюдаться равенство MQ+N=P и 2) степень многочлена N должна быть ниже степени многочлена Q.

Процесс нахождения частного M и остатка N аналогичен процессу деления с остатком многозначного числа на многозначное. Перед делением члены делимого и делителя располагается в порядке убывания степеней главной буквы.

Например, разделим 6x3 +2x2 — x +12 на 3x2 — 2x +6

Запись деления:

1.Делим первый член делимого 6x3на первый член делителя 3x2. Результат 2x — первый член частного.

2.Умножаем полученный член на делитель 3x2 — 2x +6, результат 6x3 — 4x2 +12x записываем под делимым.

3.Вычитаем члены результата из соответствующих членов делимого, сносим следующий по порядку член делимого, получаем 6x2 — 13x +12

4. Первый член остатка 6x2 делим на первый член делимого, результат 2 есть второй член частного.

5. Множим полученный второй член частного на делитель, результат 6x2 — 4x +12 подписываем под первым остатком.

6. Вычитаем члены этого результата из соответствующих членов первого остатка, получаем второй остаток: -9x. Его степень меньше степени делителя. Деление закончено.

.

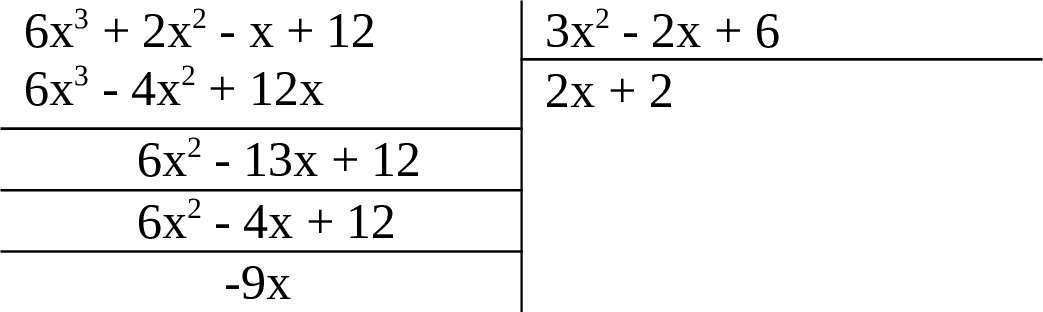
Целая часть: 2x +2

Остаток: — 9x

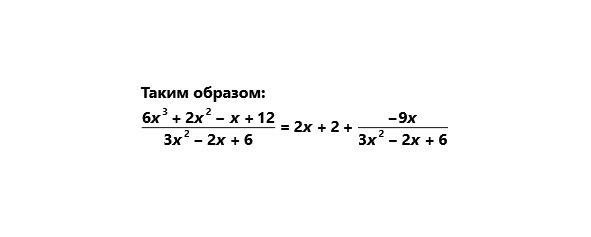
Приведём более сложный пример без дополнительных пояснений.

Целая часть: 3t2 — 7t +5

Остаток: 34t — 37

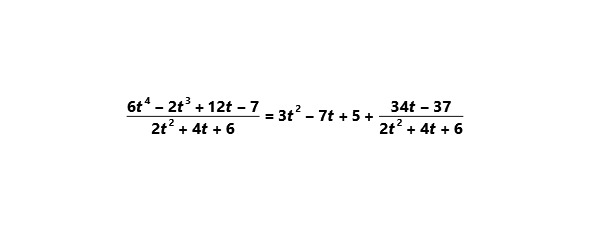
Среди частных случаев деления многочлена на многочлен выделим делимость двучлена xm±am на x±a.

1. Разность одинаковых степеней двух чисел делится без остатка на разность этих чисел, т.е. xm-am делится на x-a

Примеры.

(x2-a2): (x-a) =x+a

(x3-a3): (x-a) =x2+ax+a2

(x4-a4): (x-a) =x3-ax2+a2x+a3

(x5-a5): (x-a) =x4-ax3+a2x2+a3x+a4

2. Разность одинаковых чётных степеней двух чисел делится не только на разность этих чисел, но и на их сумму т.е. xm-am при чётном m делится на x+a

Примеры.

(x2-a2): (x+a) =x-a

(x4-a4): (x+a) =x3-ax2+a2x-a3

(x6-a6): (x+a) =x5-ax4+a2x3-a3x2+a4x-a5

2a. Разность одинаковых нечётных степеней двух чисел не делится на сумму этих чисел.

Например, ни x3-a3, ни x5-a5 не делятся на x+a.

2б. Так как разность чётных степеней делится на x-a и на x+a, то она делится и на x2-a2.

Примеры.

(x4-a4): (x2-a2) =x2+a2

(x6-a6): (x2-a2) =x4+a2x2+a4

(x8-a8): (x2-a2) =x6+a2x4+a4x2+a6

3. Сумма одинаковых степеней двух чисел никогда не делится на разность этих чисел.

Например, ни x2+a2, ни x3+a3 не делятся на x-a.

4. Сумма одинаковых нечётных степеней двух чисел делится на сумму этих чисел.

Примеры.

(x3+a3): (x+a) =x2-ax+a2

(x5+a5): (x+a) =x4-ax3+a2x2-a3x+a4

4а. Сумма одинаковых чётных степеней двух чисел не делятся ни на разность, ни на сумму этих чисел.

Например, x6+a6 не делится ни на x-a, ни на x+a.

Запомнить эти формулы необязательно, но уметь их применять необходимо.

Для удобства и упорядочивания вышеизложенных сведений можно составить такую таблицу.

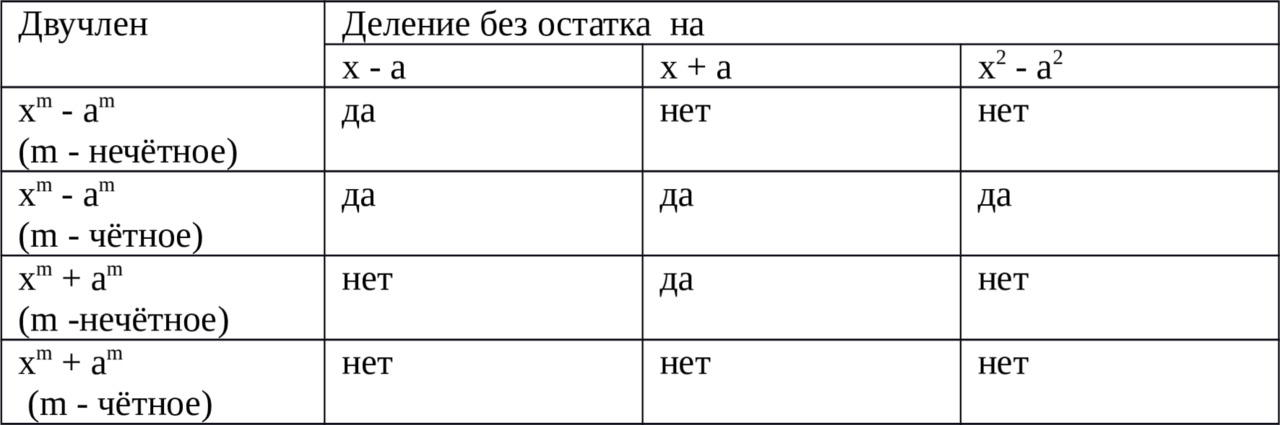
Возведение в степень n двучлена a+b.

(a+b) n=an+k1×an-1×b+k2×an-2×b2+…+bn (эта формула называется биномом Ньютона).

Где коэффициенты k (биноминальные коэффициенты) определяются из треугольника Паскаля.

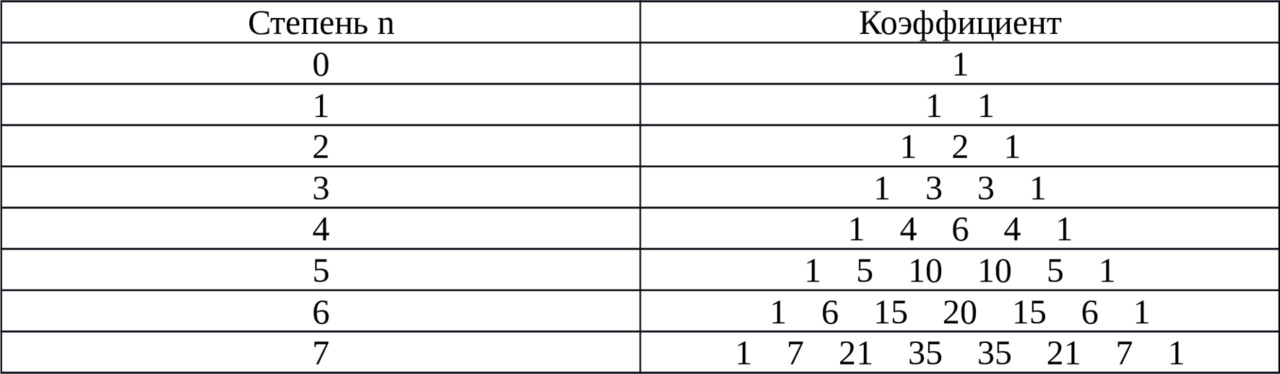
Треугольник Паскаля — таблица бесконечная. Вершина таблицы и боковые стороны каждой строки имеют единицы. Остальные числа (в середине) равны сумме 2-ух чисел, которые находятся в предыдущей строке (над ними).Вы можете легко это проверить, а также потренироваться в составлении коэффициентов для степени 8. Теперь, зная секрет этой таблицы, вы можете без труда вычислить необходимые коэффициенты. Запомните только, что таблица начинается с нулевой степени.

Примеры.

(a+b) 4=a4+4a3b+6a2b2+4ab3+b4

(a+b) 6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6

Разложение многочлена на множители.

1 способ. Вынесение общего множителя за скобки.

Если все члены многочлена содержат в качестве множителя одно и то же выражение, его можно «вынести за скобки».

С этим способом мы косвенно ознакомились раньше. Приведём только пару примеров.

Примеры.

4x2y3+8xy2z=4xy2 (xy+2z)

9a2b2—3ab2c+12abc2=3ab (3ab-bc+4c2)

2 способ. Способ группировки.

Многочлен разбивается на несколько групп, в каждой из групп выносится за скобки общий множитель, после чего в скобках оказывается одинаковое выражение, которое в свою очередь выносится за скобки.

Примеры.

5x3+10x2+3x+6=5x2 (x+2) +3 (x+2) = (x+2) (5x2+3)

20x3—12y3+8xy2—30x2y=20x3—30x2y+8xy2—12y3=10x2 (2x-3y) +

4y2 (2x-3y) = (2x-3y) (10x2+4y2)

При этом способе важно иметь в виду, что выражение a-b можно всегда представить в виде — (b-a). Поэтому, если множители отличаются только знаками, их всегда можно сделать одинаковыми.

Например:

6ab-2cb+9cd-27ad=2b (3a-c) +9d (c-3a) =2b (3a-c) -9d (3a-c) =

(3a-c) (2b-9d)

3 способ. С помощью формул сокращённого умножения.

Примеры.

9x2—1= (3x-1) (3x+1)

4x2+4x+1= (2x+1) 2

4 способ. Разложение квадратного трёхчлена ax2+bx+c=

=a (x-x1) (x-x2)

где x1 и x2-корни квадратного уравнения ax2+bx+c=0

О решении квадратных уравнений мы поговорим позже.

А сейчас просто проиллюстрируем данный способ

одним примером.

Пример.

2x2+13x-24=2 (x-3/2) (x+8) = (2x-3) (x+8)

Сначала решается квадратное уравнение

2x2 +13x -24 = 0 и находятся его корни x1=3/2, x2=-8

Потом по формуле делается разложение.

Как правило, при разложении многочлена приходится комбинировать вышеперечисленными способами, но начинать преобразования, если это возможно, с вынесения общего множителя за скобки.

Пример 1. Разложить на множители многочлен 36x3+24x+4x

Решение: Вынесем общий множитель 4x за скобки.

36x3+24x2+4x=4x (9x2+6x+1)

Трёхчлен 9x2+6x+1 можно представить в виде квадрата двучлена:

9x2+6x+1= (3x+1) 2

Таким образом, 36x3+24x2+4x=4x (3x+1) 2

Пример 2. Разложить на множители многочлен xy3—3y3+xy2z-3y2z

Решение: Вынесем за скобки общий множитель y2:

xy3—3y3+xy2z-3y2z=y2 (xy-3y+xz-3z)

Сгруппировав первый член со вторым и третий с четвёртым, разложим на множители многочлен: xy-3y+xz-3z

xy-3y+xz-3z=y (x-3) +z (x-3) = (x-3) (y+z)

Окончательно получим:

xy3—3y3+xy2z-3y2z=y2 (x-3) (y+z)

Пример 3. Разложить на множители многочлен: a2—4ab-9+4b2

Решение: Сгруппируем первый, второй и четвёртый члены многочлена. Полученный трёхчлен можно представить в виде квадрата разности.

(a2—4ab+4b2) -9= (a-2b) 2—9

Полученное выражение не что иное, как разность квадратов:

(a-2b) 2—9= (a-2b) 2—32= (a-2b-3) (a-2b+3)

Таким образом, a2—4ab-9+4b2= (a-2b-3) (a-2b+3).

Тестовые задания к теме 2

тест 1

тест 2

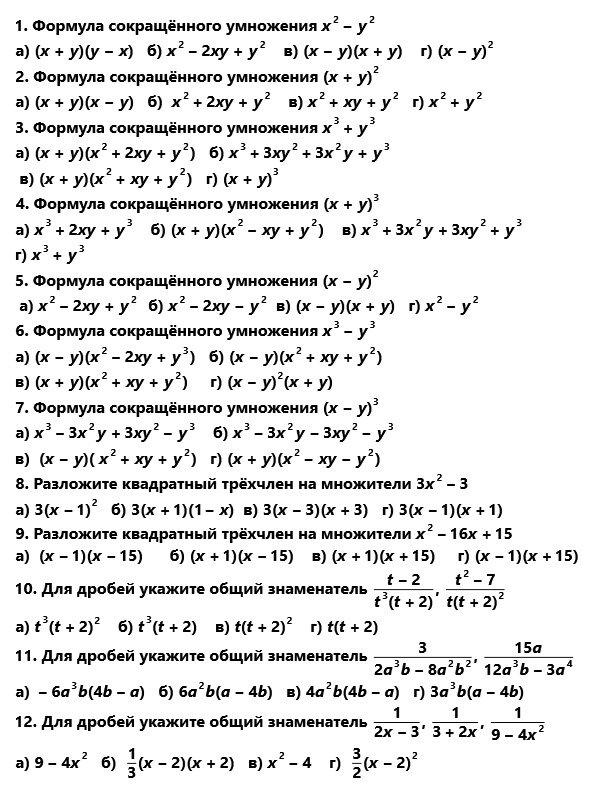
тест 3

тест 4

тест 5

тест 6

ЗАДАЧИ

Тема 3

Уравнение, общие сведения. Равносильные уравнения. Основные приёмы решения уравнений. Классификации уравнений. Решение простейших линейных и квадратных уравнений, а также уравнений приводящихся к квадратным

Понятие уравнения является одним из основных понятий алгебры. От того как вы освоите решение уравнений зависит ваше дальнейшее продвижение по усвоению более сложного материала. Поэтому отнеситесь к этой теме с должной серьёзностью.

Итак, равенство, содержащее переменную, называется уравнением. Корни уравнения — значение переменных, обращающие уравнение в верное равенство.

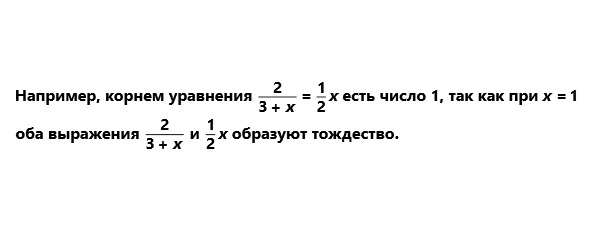
Уравнение может иметь один, два, три и т.д корня, бесчисленное множество корней или не иметь их вовсе.

Упомянутое выше уравнение имеет один корень.

Уравнение (6-x) (12-x) (3+x) = 0 имеет три корня: 6, 12, -3. Действительно, каждое из этих чисел обращает в нуль один из множителей произведения (6-x) (12-x) (3+x) и само произведение соответственно.

Уравнение 8x+4 = 4 (2x+1) при любом значении x превращается в тождество, поэтому говорят, что оно имеет бесчисленное множество корней.

Уравнение 6х+9=3 (2х+4) ни при каком значении х не превращается в тождество, т.е. говорят, что оно не имеет корней.

Уравнения, которые имеют одни и те же корни называются равносильными. Например, уравнения 4x2=1—3x и 4x2—1=-3x равносильны (оба имеют корни x= 1/4 и х= -1.

Процесс решения уравнений заключается в основном замене данного уравнения другим ему равносильным.

Основные приёмы решения уравнений.

1. Замена одного выражения другим, тождественно ему равным.

Например, уравнение (2x-1) 2=3x-8 можно заменить равносильным ему уравнением 4x2—4x+1=3x-8.

2. Перенос слагаемых из одной части уравнения в другую с переменной знака на противоположный.

Например, в уравнении 3x2+5x-3=-12x+4 можно перенести все члены в левую часть. Уравнение 3x2+5x-3+12x-4=0 или 3x2+17x-7=0 равносильно исходному.

3. Умножение или деление обеих частей равенства на одно и тоже число, не равное нулю или на одно и то же выражение (при этом могут потеряться корни, при которых данное выражение равно нулю).

Например, дано уравнение (x-1) (x+2) =4 (x-1).

Разделив обе его части на x-1, получаем x+2=4. Это уравнение имеет единственный корень x=2. Исходное уравнение, кроме этого корня имеет ещё один корень x=1.

4. Можно также возводить обе части уравнения в одну и ту же степень и извлекать из обеих частей корни одной и той же степени. При этом могут появиться новые корни или пропасть старые. Поэтому, после таких преобразований необходимо производить проверку.

Например, уравнение 2x=6 имеет один корень x=3.

Уравнение (2x) 2=62, т.е. 4x2=36 имеет два корня x=3и x=-3.

Особенно важно установить, не пропадают ли старые корни. Появление новых не так опасно, так как в любом случае рекомендуется делать проверку и удостовериться удовлетворяют ли все корни уравнению или нет.

Уравнение называется алгебраическим, если каждая из его частей многочлен и одночлен по отношению к неизвестным величинам. Степенью алгебраического уравнения называется наивысшая степень переменной, входящей в уравнение (после приведения подобных его членов). Если уравнение содержит несколько неизвестных, то для каждого члена уравнения составляем сумму показателей при всех входящих в него неизвестных. Наибольшая из этих сумм называется степенью уравнения.

Например, уравнение 3x3—2x2+12x=3x3+12x-6 есть уравнение 2-ой степени, т.к. после преобразований имеем -2x2+6=0. Уравнение a4x+b6=c10 уравнение 1-ой степени, т.к. высшая степень неизвестного х-первая. Уравнение 5x5+3x3y4—6x2y3=0 есть уравнение 7-ой степени, т.к. наибольшая сумма показателей степеней при неизвестных x и y составляет 7 у второго слагаемого.

Уравнение 1-ой степени называется линейным: ax=b

Уравнение 2-ой степени называется квадратным: ax2+bx+c=0

Уравнение 3-ой степени называется кубическим: ax3+bx2+cx+d=0.

Решение простейшего линейного уравнения.

Любое линейное уравнение можно после преобразований привести к виду ax=b

Его решением будет x=b/a при a≠0,b≠0

Пример: 2x=1 ⇒ x=1/2

Частные случаи линейного уравнения:

1. a=0,b≠0. В данном случае 0×x=b. Уравнение корней не имеет (объясните, почему?)

2.a=0,b=0. В данном случае 0×x=0. Уравнение имеет бесчисленное множество корней (поясните на примерах).

3.a≠0,b=0. В данном случае a×x=0 Уравнение имеет один корень x=0 (докажите это).

Решение квадратного уравнения ax2+bx+c=0.

Обозначения и определения: a — первый коэффициент, b — второй коэффициент, c — свободный член. Если хотя бы один из коэффициентов b или c равен нулю, то такое уравнение называется неполным квадратным.

Примеры.

А) 2x2+4=0 ⇒ 2x2=-4 ⇒ x2=-2

— 2 <0, значит корней нет.

2x2—4=0 ⇒ 2x2=4 ⇒ x2=2

x1=√2, x2=-√2

Б) 3x2+2x=0 ⇒ x (3x+2) =0 ⇒ x=0 и 3x+2=0

x1=0, x2=-2/3

В) 4x2+3=3 ⇒ 4x2=0 ⇒ x=0

Используя теорему Виета можно решить многие нестандартные задачи. Примеры решения таких задач будут показаны ниже.

Решение уравнений высших степеней, разрешаемых с помощью квадратного уравнения.

Есть несколько видов уравнений высших степеней, которые после преобразований сводятся к квадратным.

А) ax4+bx3+cx2=0 и вообще всякое уравнение, в котором левую часть можно легко разложить на множители, из которых каждый — многочлен не выше 2-ой степени.

Решение: Выносим общий множитель x2 за скобки.

x2 (ax2+bx+c) =0

Имеем два множителя, приравнивая каждый из которых к нулю находим корни данного уравнения.

x2+bx+c=0 x2=0

Б) Уравнения вида x3-a3=0 или x3+a3=0 и приводящиеся к ним.

Решение: Такие уравнения раскладываются на множители по формуле разности или суммы кубов (см. формулы сокращённого умножения).

(x-a) (x2+ax+a2) =0 или (x-a) (x2-ax+a2) =0. Отсюда:

x2+ax+a2=0 и x-a=0 или x2-ax+a2=0 и x+a=0

В) Биквадратное уравнение: ax4+bx2+c=0

Решение: Заменой x=t2 приводится к квадратному at2+bt+c=0. Находятся корни t1 и t2. Возвращаемся к первоначальной переменной:

x1=√t1 x2=-√t1 x3=√t2 x4=-√t2

Вообще, любое уравнение, имеющее вид ax2n+bxn+c=0 приводится к квадратному заменой xn=t

Примеры решения задач.

Здесь приводятся решения уравнений «нестандартными» способами, взятыми из замечательной книги «Математика для поступающих в вузы» известного учёного и педагога И. Ф. Шарыгина. А также задачи на применение теоремы Виета, которые часто встречаются на вступительных экзаменах. Все задачи представлены с подробными пояснениями.

тестовые задания

тест 1

тест 2

тест 3

тест 4

тест 5

тест 6

тест 7

задачи

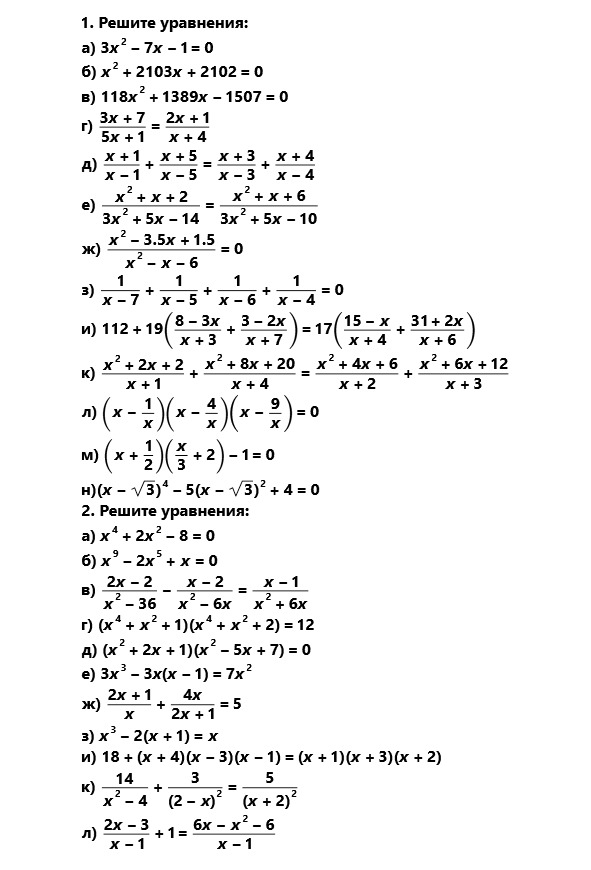
Тема 4

Уравнения высших степеней. Возвратные уравнения. Однородные уравнения. Замена неизвестного. Нахождение рациональных корней многочлена с целыми коэффициентами. Разложение на множители

В прошлой теме мы уже частично рассматривали некоторые элементарные методы решения уравнений со степенью 3 и выше. Сейчас мы рассмотрим более сложные примеры решения некоторых уравнений высших степеней. Одним из главных элементов решения таких уравнений является введение нового неизвестного. Причём этот метод применяется для решения уравнений любых видов и типов.

Наиболее часто встречающиеся замены:

Решение возвратных уравнений 4-ой степени.

Решение однородного уравнения.

Теперь остановимся на характерных ошибках при решении уравнений высших степеней с помощью замены. Таких основных ошибок несколько:

1) неправильное составление уравнения с новой переменной, в результате которого исходное и новое уравнение с учётом замены не являются тождественно равными.

2) нерациональная замена. Замена, которая не приводит к упрощению первоначального уравнения, а делает последующие преобразования более трудоёмкими и вынуждает делать ещё какие-то дополнительные замены неизвестного.

3) невозврат к первоначальной переменной. Многие экзаменующиеся, вычислив значения новой переменной забывают вернутся к первоначальной переменной. т.е. решают уравнение не до конца.

Для решения многих уравнений высших степеней необходимо разложить левую часть уравнения на множители (правая часть равна нулю). Иногда это разложение получается сразу.

Рассмотрим данный метод на примере.

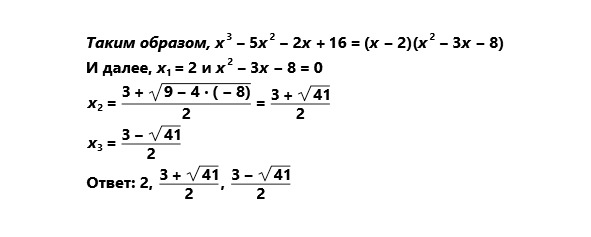
тестовые задания

тест 1

задачи

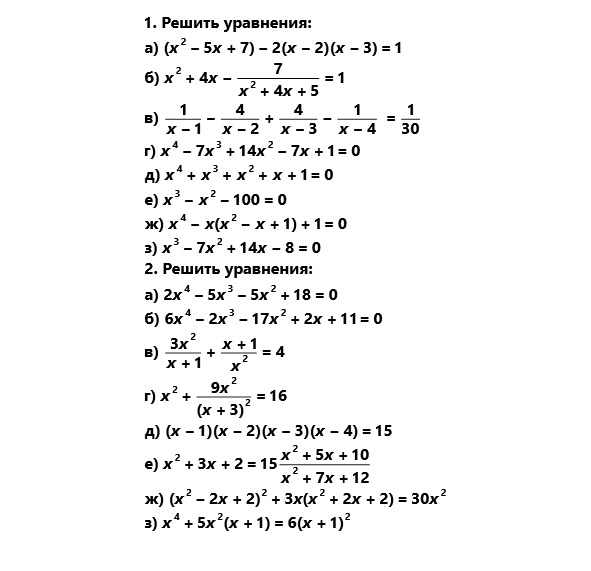
Тема 5

Иррациональные уравнения. Область допустимых значений неизвестного (ОДЗ)

Возведение в квадрат — один из стандартных способов избавления в уравнении от квадратных радикалов. Если таких радикалов несколько, то уравнение приходится возводить в квадрат неоднократно. Необходимо запомнить, что при возведении в квадрат могут появиться лишние корни. Поэтому необходимым элементом решения иррациональных уравнений есть заключительная проверка, чтобы отбросить лишние корни, если они появились. Однако проверку не всегда легко осуществить, поэтому очень часто пользуются таким приёмом. Если при подстановке полученного корня в первоначальное уравнение обе части уравнения имеют один и тот же знак, то данный корень является корнем уравнения. Это правило позволяет избегать длительных вычислений.

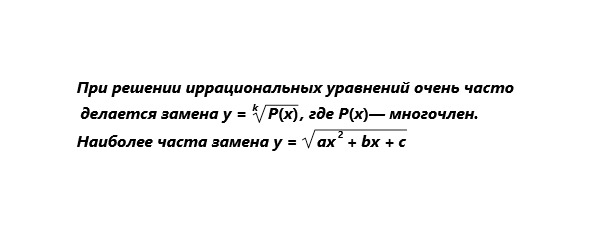
Область допустимых значений (ОДЗ) уравнения называется множество тех значений неизвестного, при которых имеют смысл его левая и правая часть. В частности, в уравнениях, имеющих радикалы чётной степени ОДЗ будет неотрицательность выражения, стоящего под знаком радикала. При решении уравнений ОДЗ можно находить, а чаще всего находить не нужно (в частности, если нахождение ОДЗ представляет собой достаточно трудную задачу).

Примеры решения иррациональных уравнений.

тестовые задания

тест 1

тест 2

задачи

Тема 6

Уравнения с модулем

Геометрический смысл модуля числа: модулем числа x

называется расстояние в единичных отрезках

от начала координат до точки x.

Исходя из этого, модуль числа — это неотрицательное число.

Для отрицательного числа его модуль равен

противоположному числу.

Есть три способа решение уравнений с модулем.

1. Оптимальным и универсальным является метод

раскрытия модуля, который хорошо зарекомендовал себя

при решении разнообразных уравнений. При этом

способе достаточно запомнить алгоритм решения

(он совсем несложный).

1) Раскроем модуль. Для этого приравниваем выражение,

стоящее под знаком модуля к нулю и решаем

полученное уравнение.

2) Корни данного уравнения разбивают числовую прямую

на два или несколько промежутков.

3) Решаем исходное уравнение на каждом из

промежутков, учитывая знак выражения, стоящего под

знаком модуля.

4) Проверяем, входят ли полученные корни в данный

промежуток.

Рассмотрим этот метод на примерах.

2. Решение уравнений с использованием определения модуля. При решении простейших уравнений с модулями этот метод является оптимальным.

3. Третьим способом решения уравнений с модулями является способ, который исходит из того, что равенство |a|=b означает, что b≥0, a=±b.

тестовые задания

тест 1

тест 2

задачи

Тема 7

Системы уравнений. Решение систем линейных уравнений

Уравнения, входящие в систему принято соединять фигурными скобками. Решением системы уравнений с двумя переменными является упорядоченная пара чисел, являющаяся решением каждого из уравнений, входящих в систему. Ясно, что множество решений системы есть не что иное, как пересечение множеств решений уравнений, входящих в эту систему.

Две системы уравнений называются равносильными, если они имеют одно и тоже множество решений.

В ходе решения систему уравнений последовательно заменяют равносильными ей все более простыми системами, пока не получат систему, решения которой находятся без труда.

Системой линейных уравнений называется система, в которую входят только уравнения первой степени.

Рассмотрим решение системы двух линейных уравнений первой степени с двумя неизвестными. В школьной программе рассматривается только два способа решения таких систем: способ подстановки и способ вычитания или сложения. Автор предлагает ещё один способ: решение с помощью определителей. Непонятно, почему этот способ не изучается в школьной программе, а только на первом курсе высшей математики в связи с решением системы трёх линейных уравнений с тремя неизвестными. Способ довольно прост, легко усваивается. Притом он универсальный. Вам самим решать, каким способом удобнее решить систему, хотя я вам дам рекомендации по применению того или иного способа.

Первый способ: способ подстановки.

Алгоритм решения.

1) из одного уравнения мы находим выражение одного из неизвестных, например x через известные величины и другое неизвестное y.

2) найденное выражение подставляем во второе уравнение, в котором после этой подстановки будет содержаться только одно неизвестное y.

3) решаем полученное уравнение и находим значение y.

4) подставляем найденное значение y в выражение неизвестного x, найденное в начале решения, получаем значение x.

Второй способ: способ вычитания или сложения.

Алгоритм решения.

1) обе части одного уравнения умножаются на некоторый множитель, обе части второго уравнения умножаются на другой множитель. Множители подбираются так, чтобы коэффициенты при одном из неизвестных в обоих уравнениях после их умножения на эти множители имели одну и ту же абсолютную величину.

2) складываем два уравнения или вычитаем их друг из друга, смотря по тому, имеют ли уравненные коэффициенты различные или одинаковые знаки, этим одно из неизвестных исключается.

3) решаем полученное уравнение с одним неизвестным.

4) подставим найденное значение первого неизвестного в любое из данных уравнений и решаем получившиеся уравнения с одним неизвестным.

Третий способ: решение с помощью определителей.

Я недаром привёл примеры решения одной и той же системы разными способами. Так легче определить, какой из способов более удобен при решении именно этой системы. Притом это служит и способом проверки. Ответы при решении разными способами должны быть одинаковые. Нетрудно догадаться, что метод подстановки предпочтительнее и удобнее, когда хотя бы один коэффициент при неизвестных x или y равен единице. Способ сложения или вычитания следует предпочесть, когда абсолютные величины коэффициентов при одном из неизвестных равны, когда один из них кратен другому или коэффициенты легко уравниваются при помощи небольших целочисленных множителей. Решение системы с помощью определителей универсально, поэтому и приведено здесь в качестве альтернативы тем способам, которые изучаются в средней школе.

Решение линейной системы трёх уравнений с тремя неизвестными основывается на тех же приёмах, что и решение системы двух уравнений с двумя неизвестными.

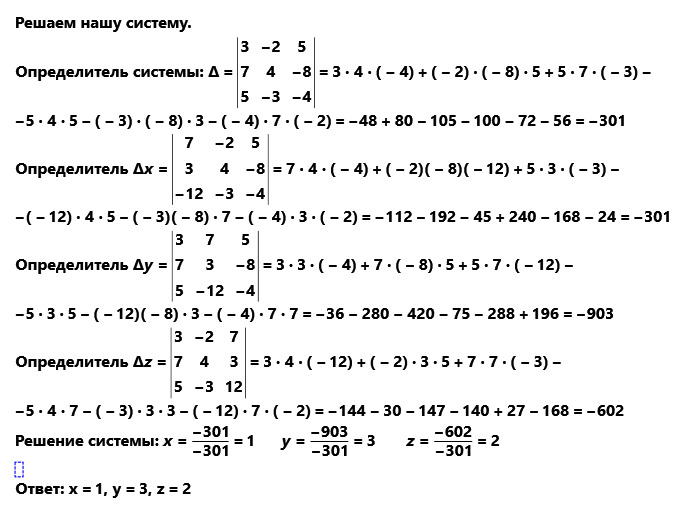
Система трёх уравнений с тремя неизвестными

имеет единственное решение, если определитель,

составленный из коэффициентов при неизвестных,

не равен нулю, т. е. Δ≠0

Если Δ=0 и Δx, Δy, Δz тоже равны нулю, то система

имеет бесчисленное множество решений.

Если, Δ=0, но Δx, Δy, Δz не равны нулю то система

не имеет решений.

Многие задачи решаются составлением системы уравнений,

их мы рассмотрим позже в теме «Текстовые задачи».

тестовые задания

тест 1

тест 2

задачи

Тема 8

Решение систем нелинейных уравнений

Эта тема довольно сложная. Если решение систем линейных уравнений имеет некоторые технические сложности, то решение систем нелинейных уравнений более творческая работа, требующая внимания и логического мышления. Перед тем, как мы рассмотрим решение таких систем уравнений дадим небольшое определение.

Если хотя бы одно уравнение системы не является линейным, то имеем дело с системой нелинейных уравнений. Для решения подобных систем можно применять разнообразные методы: метод подстановки, сложения, введение новых переменных и т. д. Сначала рассмотрим более простые случаи, когда одно из уравнений системы является линейным..

Ⅰ. Решение системы в которой одно из уравнений линейное.

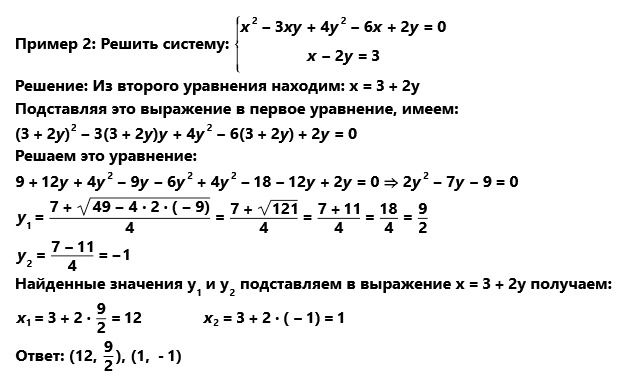
При решении этой системы мы использовали метод последовательного исключения неизвестных. Этот метод является самым распространенным и простым. Любая система линейных уравнений может быть решена этим методом. При решении систем нелинейных уравнений этот метод тоже применим, но не всегда. Нетрудно догадаться, в чем же заключается этот метод. Сначала выражаем одно неизвестное из одного уравнения и подставляем в оставшиеся. Получаем новую систему в которой число уравнений и неизвестных уменьшилось на одно. С новой системой поступаем аналогично до тех пор, пока не получим уравнение с одним неизвестным.

Рассмотрим более сложные системы, в которых все уравнения нелинейные.

Ⅱ. Решение систем в которых все уравнения нелинейные.

Этот метод применим во всех случаях, когда одно из уравнений является однородным относительно двух переменных.

Рассмотрим ещё один сложный пример, который решается методом замены.

тестовые задания

тест 1

задачи

Тема 9

Числовые промежутки. Общие сведения о неравенствах. Основные свойства неравенств. Некоторые важные неравенства. Основные приёмы решения линейных неравенств

Два выражения, соединённых знаками «больше» (>), «меньше» (<), «больше или равно» (≥), «меньше или равно» (≤) образуют неравенство. Решить неравенство — значит указать границы, в которых должны заключаться действительные значения неизвестных величин, чтобы неравенство было верным. Всего имеется 8 промежутков, в которых может быть заключено решение неравенства.

1) Интервал (a,b), a <x <b. Значения a и b не входят в интервал (графически они отмечены пустой точкой).

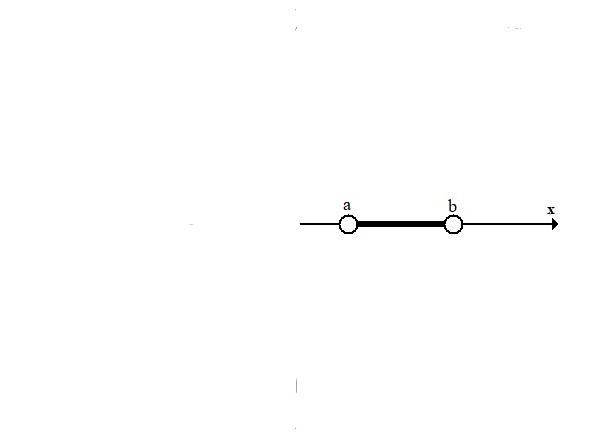
2) Отрезок [a,b], a≤x≤b. Значения a и b входят в интервал (обратите внимание на графический вид этих точек).

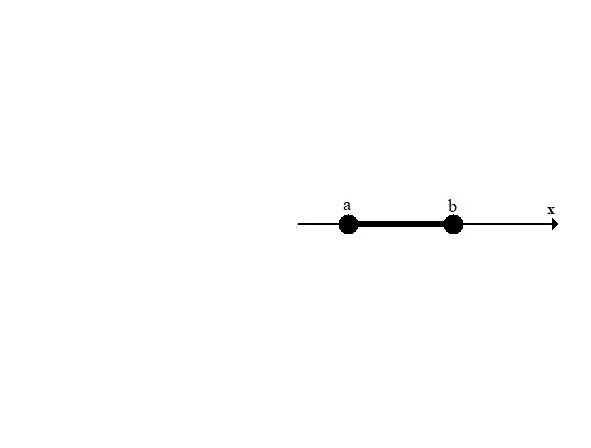
3) Полуинтервал (a,b], a <x ≤ b. Значение b входит, а значение a не входит в полуинтервал.

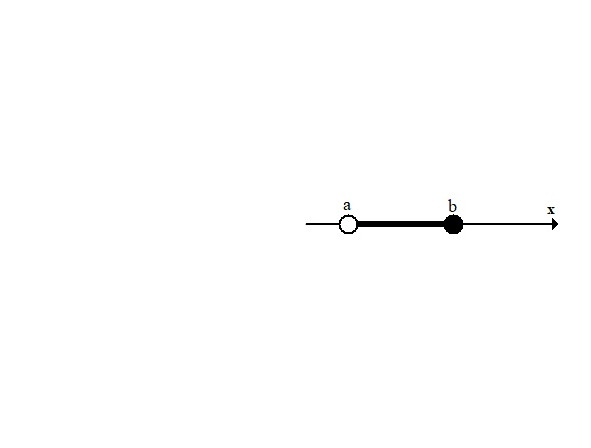
4) Полуинтервал [a,b), a≤ x <b. Значение a входит, а значение b не входит в полуинтервал.

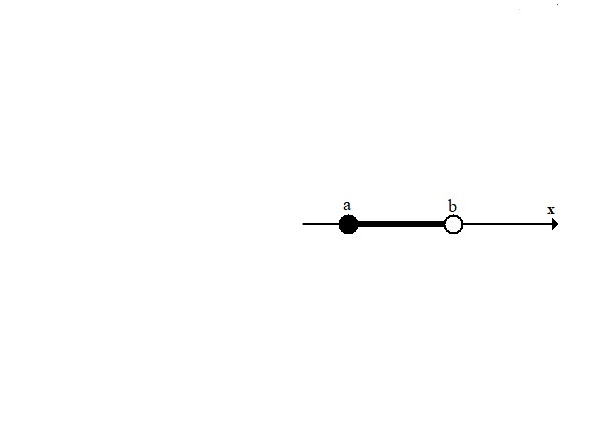
5) Луч [a,∞), x ≥ a

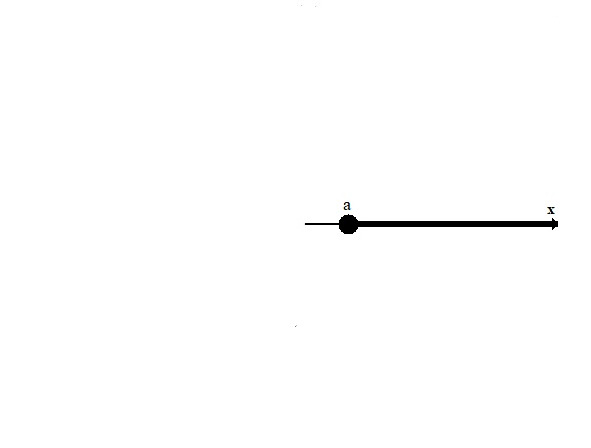
6) Луч (-∞,b], x ≤ b Значения a и b входят в луч.

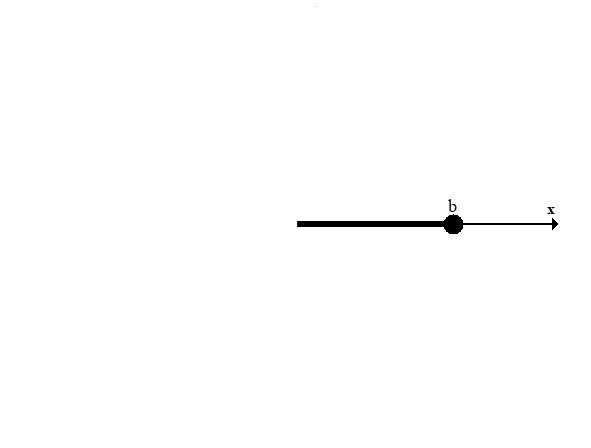
7) Открытый луч (a,∞), x> a

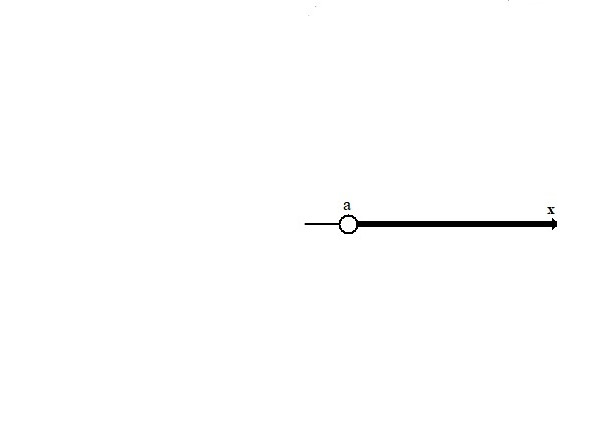
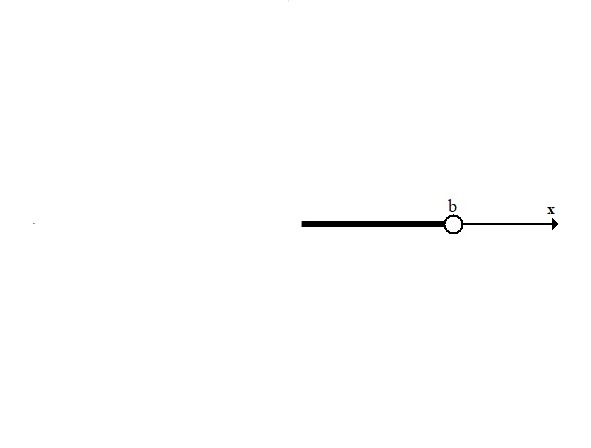
8) Открытый луч (-∞,b), x <b Значения a и b не входят в луч.

Основные свойства неравенств:

1) Если а> b, то b <a и наоборот.

Пример: Если 5х-1> 2х+1, то 2х+1 <5х-1.

Данное свойство настолько явное, что

не нуждается в дополнительных пояснениях.

2) Если a> b и b> c, то a> c.

Пример: Из неравенств х> 5у и 5у> 12, следует, что х> 12.

Здесь тоже все очевидно.

3) Если а> b, то a+c> b+c (и a-c> b-c), т.е. к обеим

частям неравенства можно прибавить

(или из них вычесть) одну и ту же величину.

Пример: Вычитая из обеих частей неравенства х+4> 5

число 4, находим х> 1.

Это свойство имеет явную аналогию со свойствами уравнений.

4) Если a> b и c> d, то a+c> b+d, т.е. два неравенства

одинакового смысла (оба неравенства содержит знак>

или оба содержит знак <) можно почленно

складывать. Два неравенства одинакового смысла

нельзя почленно вычитать. Пример: Неравенства

8> 2 и -3> -5 верны. Складывая их почленно,

находим верное неравенство: 5> -3.

5) Если a> b и c <d, то a-c> b-d.

Если а <b и c> d, то a-c <b-d, т.е. из одного неравенства

можно почленно вычесть другое неравенство

противоположного смысла, оставляя знак того

неравенства, из которого вычиталось другое.

Пример: Неравенства 6 <15 и 10> 2 верны.

Вычитая почленно второе из первого и оставляя

знак первого, получаем верное неравенство: -4 <13.

6) Если a> b и m — положительное число, то ma> mb и

a/m> b/m, т.е обе части неравенства можно

разделить или умножить на одно и тоже

положительное число (знак неравенства остаётся тем же).

Если же а> b и n — отрицательное число, то na <nb и

a/n <b/n, т.е. обе части неравенства можно

умножить или разделить на одно и тоже

отрицательное число, но при этом знак

неравенства нужно переменить на противоположный.

Пример: Из неравенства -8х> 24 следует, что х <-3.

Это одно из самых важных свойств неравенств,

неправильное применение которого даёт

большинство ошибок при решении любых

неравенств. Это свойство надо запомнить.

Мы к нему в дальнейшем ещё не раз вернёмся.

Кроме этих неравенств есть и другие, которые мы не рассматриваем.

Два неравенства, содержащие одни и те же неизвестные, называются равносильными, если они верны при одних и тех же значениях этих неизвестных.

Пример: Неравенства 3х+1> 2х+4 и 3х> 2х+3 равносильны, т.к. оба верны при х> 3 и оба неверны, когда х ≤ 3.

Процесс решения неравенства заключается в основном в замене данного неравенства другими равносильными. При решении неравенства применяются следующие основные приёмы:

1) Перенос слагаемых из одной части неравенства в другую с переменной знака на обратный.

2) Умножение или деление обеих частей неравенства на одну и ту же числовую величину (не равную нулю). При этом, если множитель положителен, то знак неравенства остаётся тем же, если же отрицателен, то знак неравенства меняется на противоположный.

Решение неравенств первой степени с одним неизвестным, как правило, не вызывает особых трудностей. Все эти неравенства можно привести к одному из видов: ax> b, ax <b, ax ≥ b, ax ≤ b. Рассмотрим решения таких неравенств на примерах.

тестовые задания

тест 1

тест 2

тест 3

тест 4

задачи

Тема 10

Квадратные неравенства, дробные и иррациональные неравенства. Неравенства с модулями

1. Решение квадратных неравенств.

Пример 1: Неравенство х2 <9 имеет решение -3 <х <3

Пример 2: Неравенство х2 <-9 не имеет решений.

Пример 3: Неравенство х2> 9 имеет решение х> 3 и х <-3

Пример 4: Неравенство х2> -9 тождественное.

1.3 Решение методом интервалов.

Метод интервалов довольно простой метод решения многих неравенств. В общем случае он заключается в том, что находятся точки, в которых знак функции меняется. Кроме этого находятся точки, в которых функция не существует (не определена). Все эти точки откладываются на координатной прямой и разбивают её на лучи и интервалы. Теперь достаточно определить знак функции на каждом из интервалов.

Рассмотрим этот метод применительно к решению квадратных неравенств.

а) Решаем соответствующее квадратное уравнение и находим корни этого уравнения х1 и х2.

б) Откладываем эти точки на координатной прямой и определяем знак на каждом из этих промежутков.

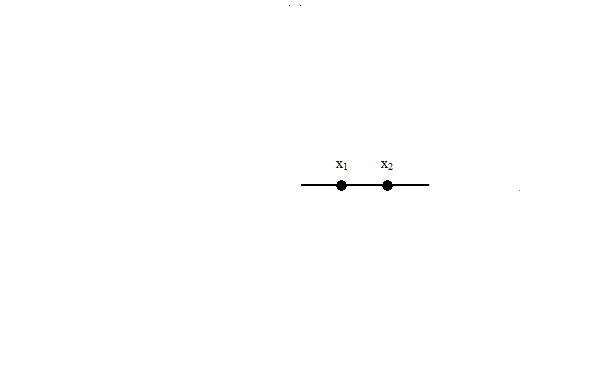
в) Если имеем неравенство вида ax2 + bx + c <0 или ax2 + bx + c ≤ 0, то нас интересуют промежутки, где функция отрицательна.

Если ax2 + bx + c> 0 или ax2 +bx + c ≥ 0, то промежутки где функция положительна.

Пример 1: Решить неравенство: х2 — 7х +10 <0.

Решение: Решим уравнение: х2 — 7х +10 = 0

x=2, x=5

Отметим эти точки на координатной прямой и определим знак на каждом из промежутков (достаточно взять любое число из этого промежутка и установить знак функции). Например, f (0)> 0, значит на первом промежутке функция положительна, f (3) <0, значит на втором промежутке функция отрицательна,

f (10)> 0, значит на третьем промежутке функция положительна.

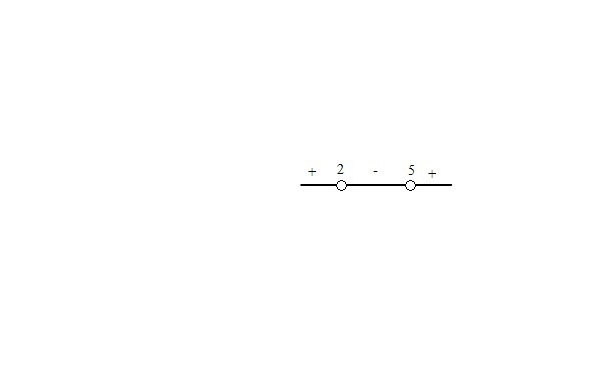
Нас интересуют промежутки, где функция отрицательна. Т.к. у нас неравенство строгое, то точки 2 и 5 не входят в решение.

Ответ: (2,5)

При решении квадратных неравенств возникают случаи, когда дискриминант квадратного уравнения меньше нуля.

Квадратное уравнение в данном случае не имеет решений. Квадратное неравенство может не иметь решений, а может иметь решение (-∞, ∞)

Это зависит от знака члена a при х2. Если а> 0, то неравенства

ax2 + bx + c> 0 и ax2 + bx +c ≥ 0 имеют решение (-∞,∞), а неравенства ax2 + bx + c <0 и ax2 + bx +c ≤ 0 не имеют решений.

Если а <0, то неравенства ax2 + bx + c> 0 и ax2 + bx + c ≥ 0 не имеют решений, а неравенства ax2 + bx + c <0 и ax2 + bx + c ≤ 0 имеют решение (-∞,∞)

Это желательно запомнить.

2.Решение дробных неравенств.

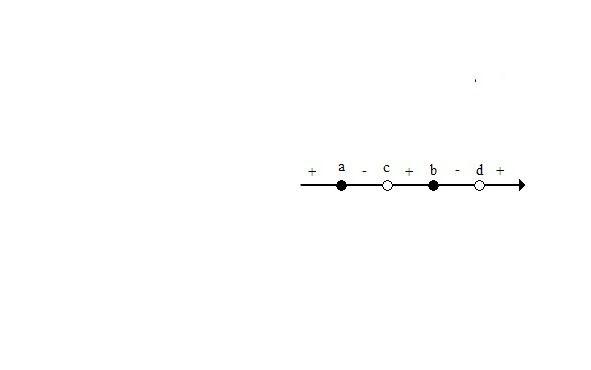
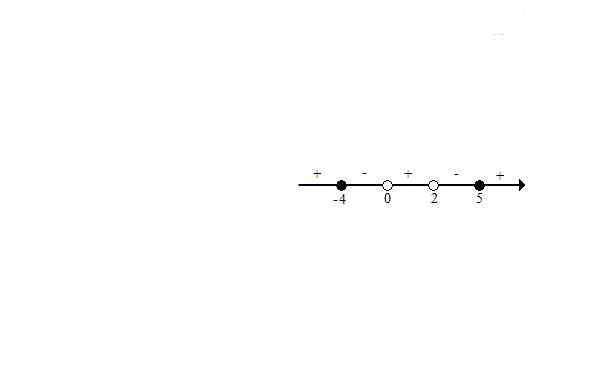
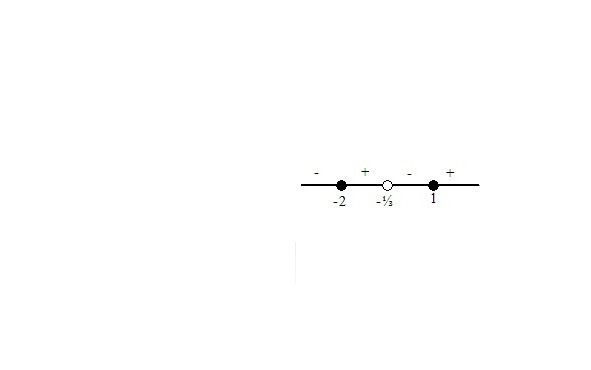
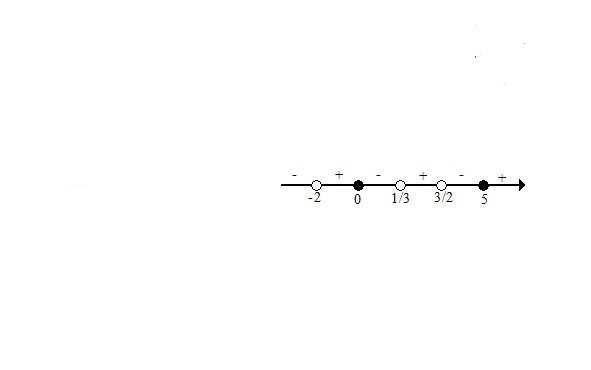
А теперь наберите побольше воздуха в лёгкие и выдохните. Мы приступаем к решению неравенств, которые дают самый большой процент ошибок при решении. Но это отнюдь не значит, что невозможно их научиться решать правильно. При этом вы последовательно будете убеждаться, что « не так страшен чёрт, как его рисуют».

3. Решение иррациональных неравенств.

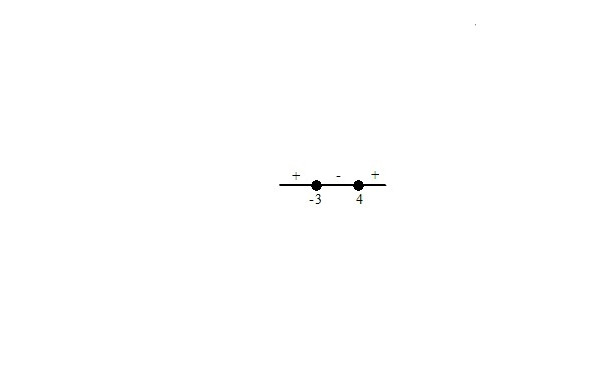
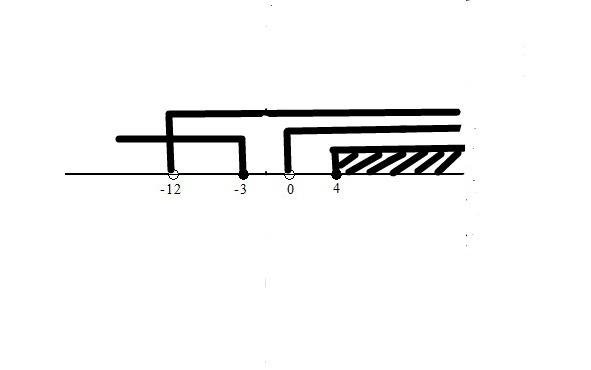
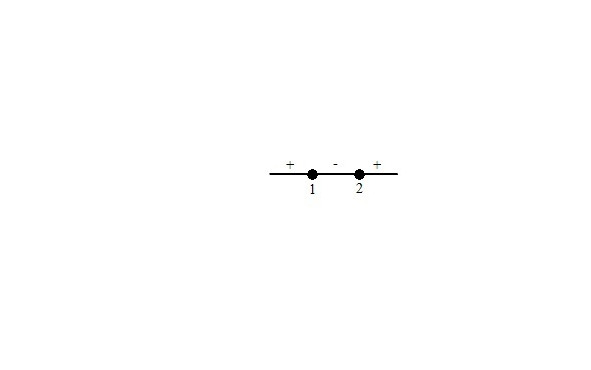
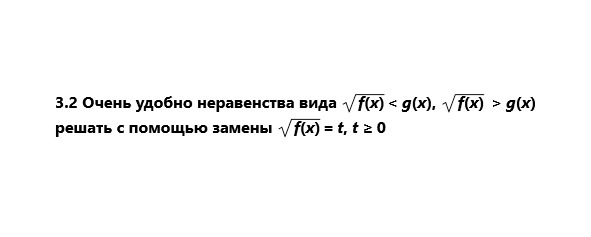
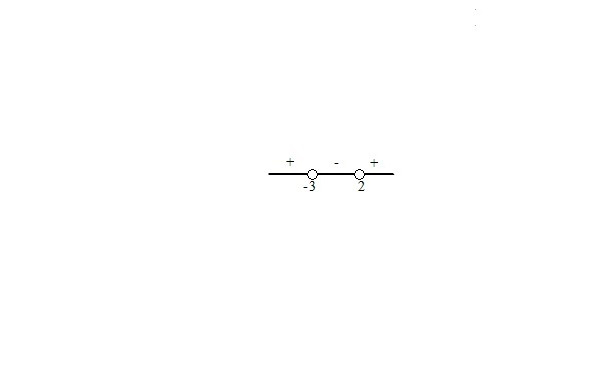
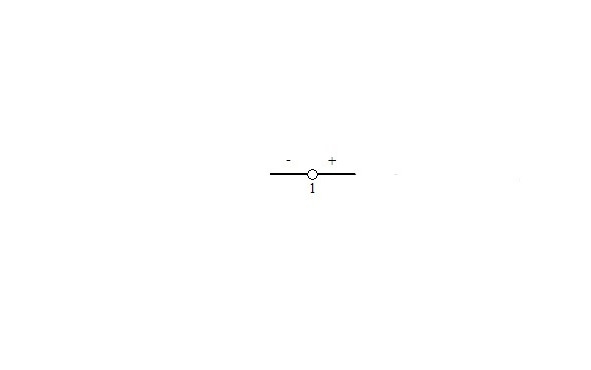
4. Способы решения линейных неравенств с модулями.

Для тех кто не до конца понял решение последнего примера, приведу краткое объяснение. Согласно определению модуля, наше неравенство можно записать, как объединение двух систем неравенств в зависимости от того, является ли выражение под знаком модуля отрицательным или положительным. Далее решаем каждое неравенство системы отдельно и находим общее решение каждой системы. После этого объединяем решение полученных систем. Более

подробно решение систем неравенств мы рассмотрим позже.

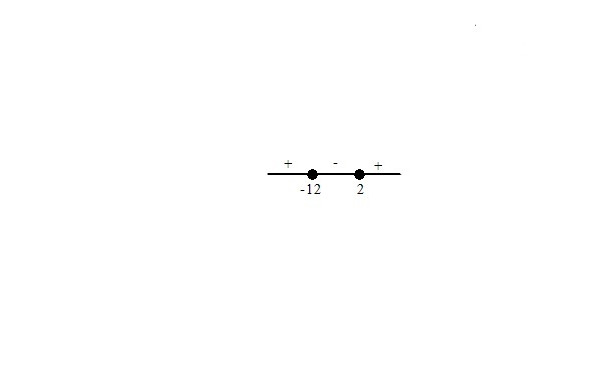
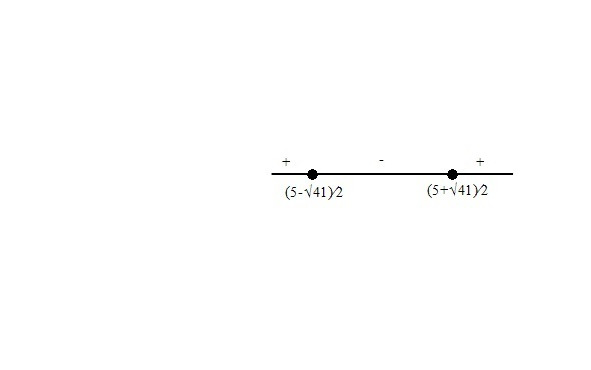
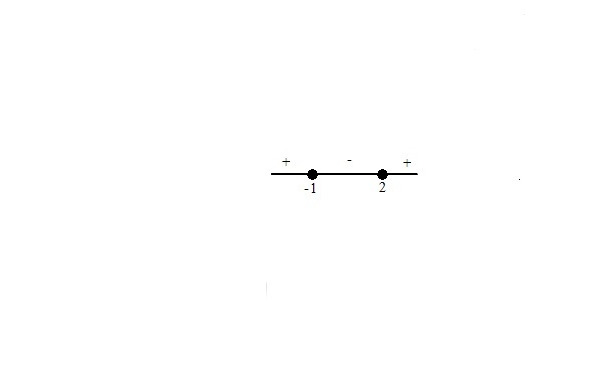
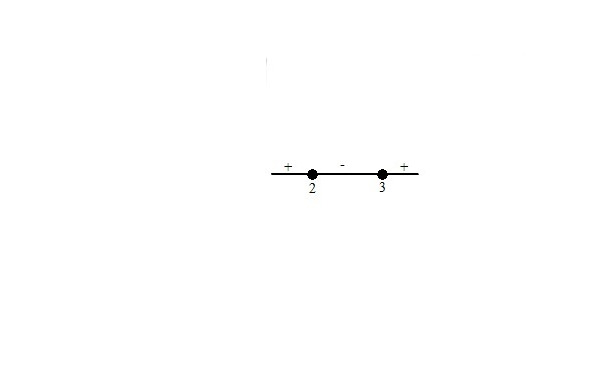
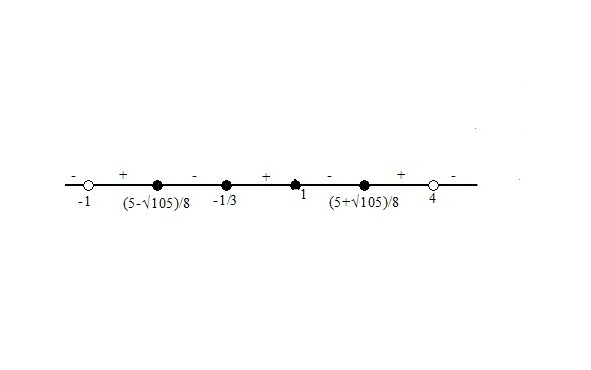
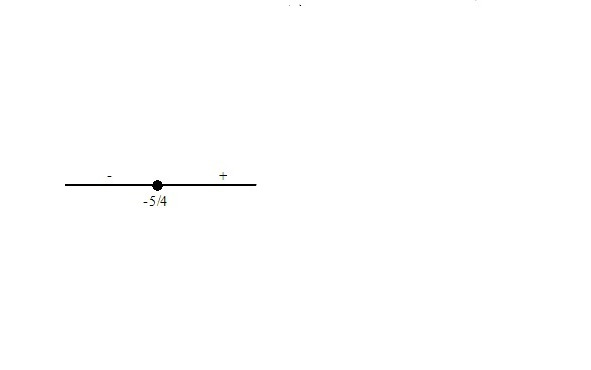
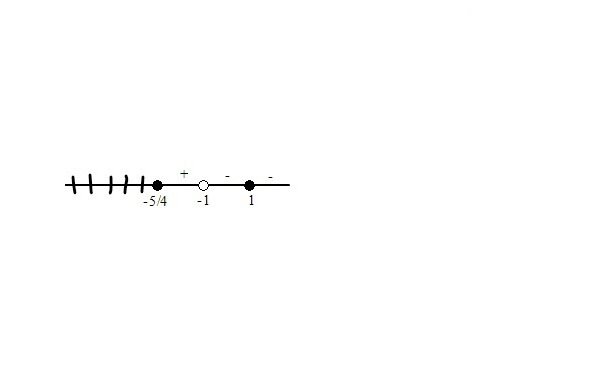
4.4. Более сложные неравенства с модулями практично решаются с помощью метода, подобного методу раскрытия модулей при решении уравнений. Некоторые так и называют этот метод методом раскрытия модулей, другие величают его методом интервалов при решении неравенств с модулем. Оба названия не совсем верны. Метод универсален, хотя и немного громоздкий. Он применим в тех случаях, когда другие методы невозможно применить. Суть метода заключается в следующем. Числовая прямая разбивается на участки, на каждом из которых на основании определения абсолютной величины знак модуля можно снять.

Рассмотрим реализацию этого принципа на примере.

Мы рассмотрели решение типичных неравенств. Этого достаточно, чтобы решить на экзамене большинство предложенных заданий. Однако, может так случиться, что на вступительных экзаменах в высшие учебные заведения будут предложены более сложные неравенства. Чтобы исключить такие случаи, приведём примеры решения таких неравенств.

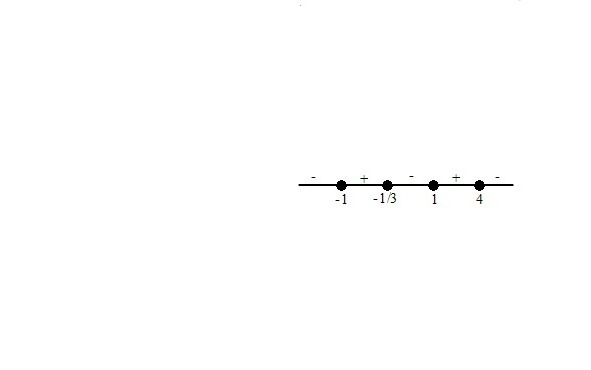
тестовые задания

тест 1

тест 2

тест 3

задачи

Тема 11

Системы неравенств

В этой теме рассмотрим решение систем неравенств с одним неизвестным. Решение систем неравенств с двумя неизвестными, которые решаются графически, будет рассмотрено позже. В предыдущей теме мы уже рассматривали решение таких систем неравенств. Осталось только повторить и закрепить наши знания.

Чтобы решить систему неравенств с одним неизвестным, нужно найти решение каждого неравенства в отдельности и найти пересечение этих решений. Пересечение этих решений либо даёт решение системы, либо обнаруживает, что система не имеет решений. Рассмотрим подробнее решение некоторых систем.

.

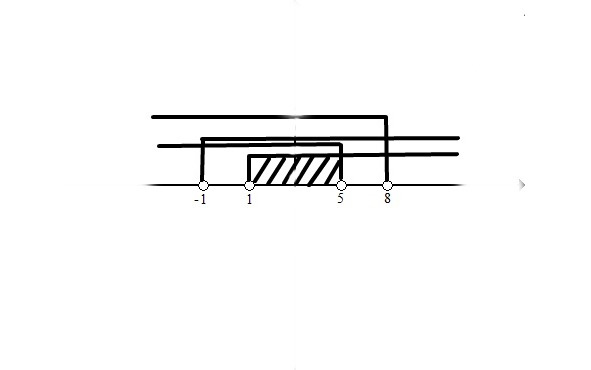
Подобным образом решаются системы неравенств второй степени и выше, системы неравенств с модулями и т. д.

тестовые задания

тест 1

задачи

Тема 12

Текстовые задачи

— О, ужас! — воскликните вы. — Текстовые задачи.

Почему-то текстовые задачи, при решении которых надо составить некое уравнение (или систему) и решить его, вызывают неподдельный страх в рядах учеников. На самом же деле, ничего страшного нет. При составлении уравнения вы просто переводите буквенный язык на язык алгебры. Как это выглядит можно посмотреть на следующем примере.

Чтобы ответить на поставленный в задаче вопрос нужно решить последнее полученное уравнение (5х-330) /2=35. Уравнение довольно простое и с его решением вы справитесь самостоятельно. Если у вас получилось х = 80, то уравнение решено правильно. Но тут возникает другой вопрос, а правильно ли мы составили уравнение? Поэтому при решении текстовых задач обязательным элементом является проверка правильности составления уравнения. Это не касается тех случаев, когда само значение ответа является абсурдным с точки зрения здравого смысла. Действительно, если бы мы получили в ответе отрицательное или любое дробное число, то сразу бы стало понятно, что, или уравнение составлено неправильно, или само уравнение решено некорректно. Об этом мы поговорим конкретнее, рассматривая разные типы задач. Сейчас мы сделаем проверку нашей задачи. Здесь все просто. Проходим по цепочке сверху вниз и вычисляем полученные значения. Итак:

За месяц продали 30 банок: 80—30 = 50.

Завезли половину от оставшихся: 50+50/2 = 75.

Продали 40 банок: 75—40 = 35.

Завезли в 2 раза больше, чем в первый раз: 35+2×25 = 85.

Продали 50 банок: 85—50 = 35.

В магазине осталось 35 банок: 35 = 35.

Ура! Получилось. Задача решена правильно.

Прежде чем я дам общие рекомендации к решению текстовых задач, и мы рассмотрим примеры решения задач разных типов, хочу, чтобы мы ещё потренировались над составлением уравнений. Теперь предлагаю задачу более интересную. Один учитель математики предложил своим ученикам такую задачу:

«Несколько лет назад я скопил некоторый капитал. Половину этой суммы я потратил на покупку квартиры, одну треть вложил в прибыльный бизнес, а 12-ю часть отдал сыну на обучение в Университете. После этого у меня осталось 2000 долларов. Вам предстоит дать ответ на вопрос, сколько стоит моя квартира?»

На самом деле задача совсем несложная. Давайте поэтапно составим уравнение.

Задача сводится к тому, чтобы из последнего уравнения найти х (или х/2, если считаете, что это проще). Решите уравнение самостоятельно. Ответ: стоимость квартиры — 12 000. Не забудьте сделать проверку.

И ещё одна интересная задача.

У брата с сестрой было некоторое количество яблок. Если брат отдаст сестре два своих яблока, то у сестры будет в два раза больше яблок, чем у него. Если же сестра отдаст два яблока брату, то яблок у них будет поровну. Сколько всего яблок у брата с сестрой?

Первые выводы, которые мы делаем из условия этой задачи: у сестры на 4 яблока больше, чем у брата и оба числа чётные. Можно решить задачу арифметически, перебирая разные варианты, но наша цель составить уравнение и решить его. Открою вам секрет, одного уравнения будет мало. Поэтому сразу же введём 2 неизвестных: х — количество яблок у брата и у — количество яблок у сестры.

Понятно, что нам надо найти х и у. Для этого решаем систему уравнений:

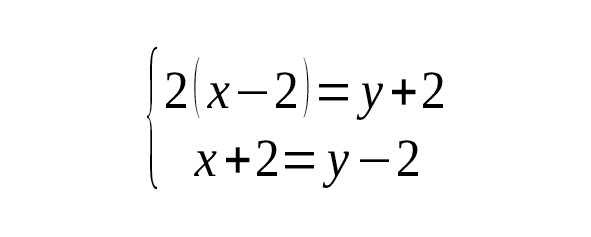
Для вас не составит труда решить эту систему и найти, что х=10, у=14, а общее количество яблок равно 24.

А теперь будет полезно, если вы сами потренируетесь в составлении задач. Попробуйте составить задачи, подобные тем, что приведены выше. Решите эти задачи и проверьте правильность составления уравнений. Чем больше таких задач вы составите, тем вам легче будет решать задачи составленные другими.

При решении, а особенно при составлении тестовых задач может возникнуть интересный случай, описанный И. И. Мельниковым и И. Н. Сергеевым в замечательной книге « Как решать задачи по математике на вступительных экзаменах». Там приводится пример одной задачи.

«Автобус вёз несколько пассажиров. На остановке из автобуса вышли шесть человек и 20 человек зашли в автобус. На следующей остановке вышли четыре человека и зашли 10 человек, после чего число пассажиров в автобусе оказалось равно квадрату исходного числа пассажиров. Сколько пассажиров было в автобусе первоначально?»

Такая довольно несложная задача, которую вы можете решить самостоятельно.

Примем за x — количество пассажиров находящихся в автобусе первоначально и составляем такое уравнение x — 6 +20 — 4 +10 = x2, при условии, что количество пассажиров положительное число, то есть x> 0. Решив это уравнение, получим два ответа x=5 и x=-4. Второй ответ сразу же отбрасываем, единственно правильный ответ: пять пассажиров. Если вы внимательно прочитаете условие задачи или сделаете проверку, то увидите некоторую нестыковку: в автобусе было 5 пассажиров, а вышло из него 6. Не сомневайтесь, задача решена правильно. 5 пассажиров — это единственно правильный ответ. Если вы решаете подобную задачу, то вам нет смысла доказывать, почему возник подобный парадокс. Действительно, может быть водитель сначала впустил на первой остановке пассажиров, а потом какое-то их количество через задние двери выпустил. Условие задачи останется прежним и составленное нами уравнение никаких изменений не претерпит. Поэтому при составлении задачи нужно позаботиться о том, чтобы подобная двусмысленная ситуация никогда не возникла. Ещё один маленький нюанс, эти же авторы считают, что проверка является не обязательным элементом при решении текстовых задач. Следует заметить, что проверка действительно для экзаменатора не нужна. Она в первую очередь нужна самому абитуриенту, чтобы точно быть уверенным в правильности решения текстовой задачи. В некоторых задачах проверка может занять много времени и сил, в таких случаях ею можно пренебречь.

А теперь перейдём к самому главному.

Общие рекомендации: Стандартная схема решения текстовых задач состоит из трёх этапов:

1. Выбор неизвестных.

2. Составление уравнений (систем уравнений, возможно неравенств).

3. Решение составленных уравнений, систем или неравенств, т.е. нахождение неизвестного или нужной комбинации неизвестных.

Успешность решения той или иной задачи зависит прежде всего от удачно выбранного неизвестного (удобнее в качестве неизвестного принять те величины, нахождение которых определено условием задачи).

Искомые величины получают особые наименования. Мы пользуемся для этой цели буквенными знаками, предпочтительно последними буквами латинского алфавита x, y, z, u, v, w. Следует избегать обозначений типа v1, uпар, t2, x0 и т. д. Это может затруднить составление уравнения и в дальнейшем решение. Выбирая неизвестные, мы создаём математическую модель ситуации, описанной в условии задачи.

Выбрав неизвестные, мы расчленяем условие задачи на логические части, каждой из которых соответствует одно ограничение. Таким образом, если неизвестных следует брать столько, сколько потребуется, то ограничений будет столько сколько получится. Таким образом, условие задачи с помощью знаков действий (+, — и т.д.) переводится на математический язык, т.е. связи между данными и искомыми величинами мы выражаем не словами и фразами разговорного языка, а математическими знаками. После этого мы решаем составленное уравнение, систему или неравенство, т.е. находим значение искомых неизвестных величин.

Текстовые задачи, как правило, описывают некоторые процессы (работу, движение), переход из одного состояния в другое, соотношение планируемого и фактического. Исходя из этого, их можно разделить на несколько типов.

1. Задачи на движение.

2. Задачи на работу.

3. Задачи на целочисленные значения.

4. Задачи на концентрацию и процентное содержание (так называемые задачи на растворы и сплавы).

5. Задачи на числа (нахождение чисел).

6. Задачи на проценты.

Каждый тип задач имеет свои особенности, поэтому рассмотрим решение каждого типа задач в отдельности

Задачи на движение самый многочисленный тип задач. Задачи на движение характеризуются тремя величинами: скорость, расстояние и время. Все эти величины находятся между собой в зависимости:

расстояние = скорость × время (1)

Откуда, скорость = расстояние/время (2)

время = расстояние /скорость (3)

Эти формулы знакомы вам из курса физики и здесь можно провести некоторую аналогию с решением задач на движение физическими методами.

А теперь подумаем, какие значения точно не могут быть ответами в задачах на движение. Логично предположить, что и скорость, и расстояние, и время величины положительные (они могут быть дробными). Так, что если у вас из полученных двух ответов, один отрицательный, то можете смело его отбросить. Внимательно также смотрите за размерностью величин. Если в первом примере время задано в сек., а расстояние в м., то найденная скорость будет выражаться в м/с. Во втором примере величины другие, расстояние выражено в км., а время в ч., поэтому скорость будет выражена в км/ч. Учитывайте также реальность полученных величин. Если у вас получилась скорость велосипедиста 100 км/ч, скорость автомобиля 300 км/ч, самое время проверить правильность составления уравнения.

Задачи на работу. Это широкий спектр задач, который охватывает все задачи на совместные действия. Этот тип задач наиболее проблематичный в плане составления уравнений. Хотя они аналогичны задачам на движение и тоже характеризуются тремя величинами: объём работы, время и производительность (скорость работы), которые находятся между собой в зависимости:

объём работы = время × производительность.

Отсюда нетрудно вывести формулы для нахождения времени или производительности (предлагаю вам это сделать самостоятельно).

А теперь поговорим о допустимых значениях в ответах при решении таких типов задач. Как же я люблю творчество Самуила Маршака. Если вы помните, в его произведении о нерадивом ученике есть такие строки:

— Задачу задали у нас.

Её решал я целый час,

И вышло у меня в ответе:

Два землекопа и две трети.

Нетрудно предположить, что ученик решал задачу о совместной работе. Бедные 2/3 землекопа приснилась ему ночью, лежащими в траве, и звери из этого произведения недоумевали, куда делась его треть и решили во что бы то ни стало найти того, кто такое сотворил. Так, что никаких дробных и отрицательных значений в ответе не должно быть (это не касается поиска времени работы и особенно производительности, которое всегда меньше единицы и дробное), иначе ночью вам тоже может приснится какой-нибудь кошмар.

Кстати, среди этих задач попадаются своеобразные задачи наподобие этой:

«Трава на всём лугу растёт одинаково густо и быстро. Известно, что 170 коров поели бы её за 24 дня, а 30 коров — за 60 дней. Сколько коров поели бы всю траву луга за 96 дней?».

Эта задача послужила сюжетом одного юмористического рассказа. Двое взрослых никак не могут её решить, т.к. в ответе у них получаются дробные числа. И только тогда, одному из них пришло в голову принять в расчёт то, что трава все время растёт. Так, что следует внимательно читать условие задачи, ведь первое предложение там написано не просто так. В задачах для самостоятельного решения, я предложил решить вам её. Дам маленькую подсказку, здесь нужно будет ввести вспомогательное неизвестное, которое будет обозначать суточный прирост травы на лугу.

3. Задачи на целочисленные значения. Эти задачи охватывают широкий спектр задач. Как правило, в них нужно найти стоимость чего либо, количество и т. д. Эти задачи не сложные и составление к ним уравнения или системы не представляет особых затруднений.

Само слово «целочисленные значения» подразумевает, что если ищется какое-то количество, то она должно быть натуральным числом. Действительно, трудно предположить, что какой-нибудь магазин продал за месяц три с половиной чайника, а в библиотеке количество книг будет равно 15250.5 экземпляров. Это не касается цены, веса и других величин, которые могут быть дробными (но обязательно положительными). В последней задаче мы увидели, что цена чайника не обязательно должна быть целым числом. И опять-таки смотрите за логичностью полученного ответа. Если у вас получилась масса одного кирпича 40кг., а стоимость одного чайника превосходит общую стоимость всех чайников, то задача решена неверно.

4. Задачи на концентрацию и процентное содержание. Ещё один тип задач, вызывающий определённые сложности. При решении данных задач иногда используется следующее соотношение: масса = плотность × объем.

Единственным ограничением при решение данных задач является тот факт, что ни растворы, ни сплавы не могут иметь более 100% — го содержания какого-либо вещества.

5. Задачи на числа. В программе средней школы таким задачам почти не уделяется времени, поэтому многие выпускники не знают как их решать. Восполним этот пробел.

Если положить х — число десятков искомого двузначного числа, у — число единиц, то само число запишется в виде 10х +у, а число, записанное в обратном порядке, 10у+х. Аналогично, для трёхзначного числа: х — число сотен, у — число десятков, z — число единиц, само число запишется в виде 100х +10у + z, a число, записанное в обратном порядке, 100z +10у +х.

Совершенно очевидно, что в этих задачах мы имеем дело с натуральными числами.

6. Задачи на проценты. Напомним, что процентом называется сотая часть числа, напр., 50% = 0,5, 5% =0.05, 100%=1, 32% = 0.32 и т. п. Простейшие задачи на проценты мы уже рассматривали раньше, теперь решим более сложные задания.

Подобные задачи вводят иногда в заблуждение. И многие думают, что если товар был повышен на какое-то количество процентов, то, чтобы вернуть прежнюю цену товара, её надо понизить на такое же количество процентов. На самом деле это не так и предыдущая задача тому подтверждение. Вся проблема в том, что мы вычисляем процент из разных сумм. Повысив цену на определённое количество процентов, мы уже имеем не первоначальную цену товара, а какую-то новую. И процент с этой новой цены будет уже не такой, как с первоначальной.

Задача кажется настолько простой, что так и хочется сразу дать ответ. Но 30%, как видите, неправильный ответ.

Итак, при проверке ответа помните, что проценты не могут быть отрицательными.

К этой теме нет тестовых заданий, зато есть огромное количество разнообразных задач.

задачи

Тема 13

Понятие функции. Чётные и нечётные функции. Периодичность. Область определения и множество значений функции. Обратные функции

Наша 13-ая (несчастливая) тема в этом разделе посвящена функциям. Самих практических задач на функциональную зависимость на выпускных и вступительных экзаменах может не быть, но эта тема важна при дальнейшем практическом применении: при исследовании функций с помощью производных, а также графическому решению уравнений, неравенств и их систем. Сначала мы рассмотрим общие понятия.

Итак, две переменные величины x и y связаны функциональной зависимостью, если каждому значению, которое может принять одна из них, соответствует одно или несколько определённых значений другой. Примеры функциональных зависимостей: расстояние, пройденное автомобилем, зависит от его скорости, площадь прямоугольника зависит от длины его сторон, температура воздуха зависит от времени суток и т. д. Иными словами, функцией называется соответствие каждого числа x некоторому числу y, зависящему от x. Независимую переменную x называют аргументом, зависимую переменную y — функцией от этого аргумента. Обозначение функции (общее): y=f (x) (игрек равно эф от x). Так скорость автомобиля x, расстояние y. Длина сторон прямоугольника x, его площадь y.

Существует несколько способов задания функции, основные из них:

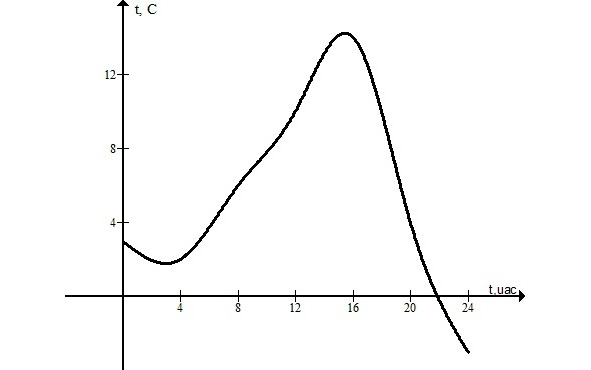
1. Словесный. Например, в 4ч. утра температура воздуха 12℃, в 5ч.-14℃, в 6ч.-15℃, в 8ч.-20℃, в 12ч.-26℃, в 16ч.- 22℃.

2. С помощью формулы. Например, зависимость между площадью круга S и радиусом r представляется формулой: S=πr2

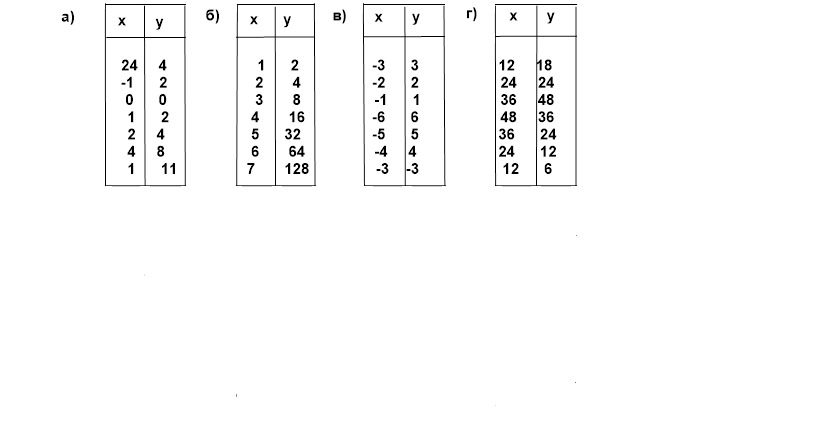
3. C помощью таблицы. Например, функциональная зависимость между давлением P и температурой кипения воды Т представляется такой таблицей.

4. С помощью графов. Например, функциональная зависимость температуры воздуха от времени суток представляется так:

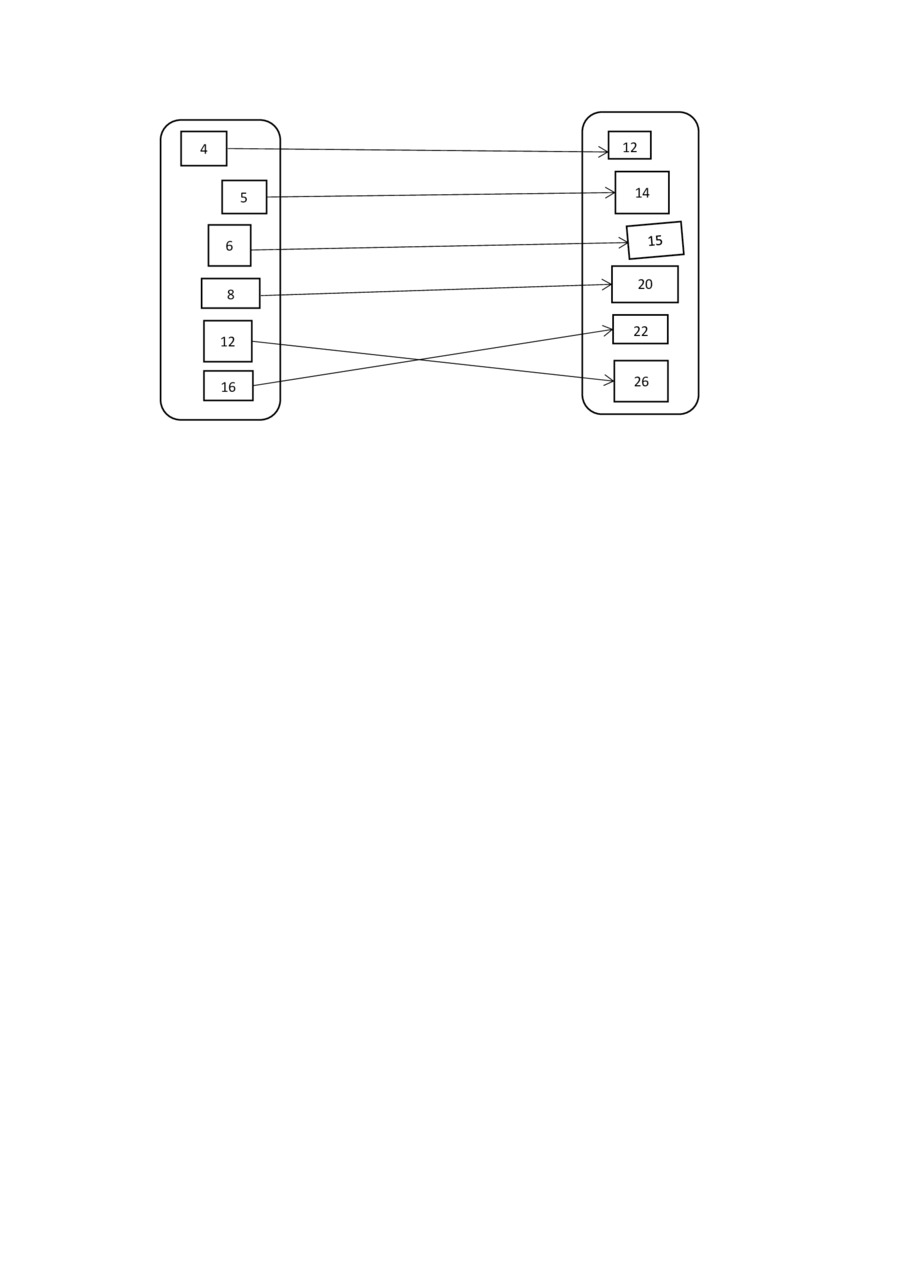
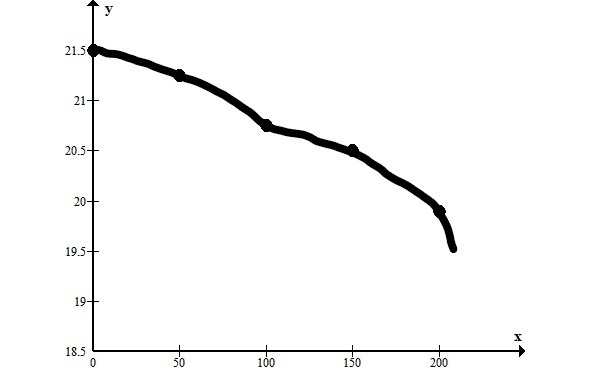
5. Графический. На оси абсцисс отмечаем ряд значений х1,х2,х3 … и строим соответствующие им ординаты у1,у2,у3 …, которые соединяем плавной линией. Например, функциональная зависимость между модулем упругости Е кованого железа и температурой железа Т изображается графиком.

Функция называется чётной, если f (-x) = f (x) для любого x из области определения. Функция называется нечётной, если f (-x) = -f (x) для любого x из области определения. Например, функция у = х2 является чётной. Возьмём произвольное число 3, тогда f (3) = 32 = 9. Возьмём противоположное число -3, тогда f (-3) = (-3) 2 =9, т.е f (-x) = f (x) — функция чётная.

Функция y = x3 — нечётная. Действительно, возьмём произвольное число 2, тогда f (2) = 23 = 8. В случае с противоположным числом имеем f (-2) = (-2) 3 = -8, т.е. f (-x) = -f (x). График чётной функции симметричен относительно оси ординат, график нечётной функции симметричен относительно начала координат. Есть функции, которые не являются ни чётными, ни нечётными.

Функция называется периодической с периодом T≠ 0, если f (x+T) = f (x) = f (x — T). для любого х из области определения. Более подробно о периодических функциях мы поговорим в разделе тригонометрии.

Областью определения функции называется множество чисел, на которых задаётся функция. Проще говоря, это те значения х, которые можно поставить в данное уравнение. Возможные значения у называются областью значений функции. Область определения функции обозначается D (f), множество значений функции E (f). Наиболее часто встречаются задачи, где необходимо найти область определения функции.

Для функций, содержащих радикалы чётных степеней областью определения является значения, при которых подкоренное выражение больше или равно нулю. Для дробно-линейных функции областью определения являются все значения, кроме значений, при которых обращается в нуль знаменатель дроби.

Для тригонометрических, показательных и логарифмических функций нахождение области определения будет показано позже.

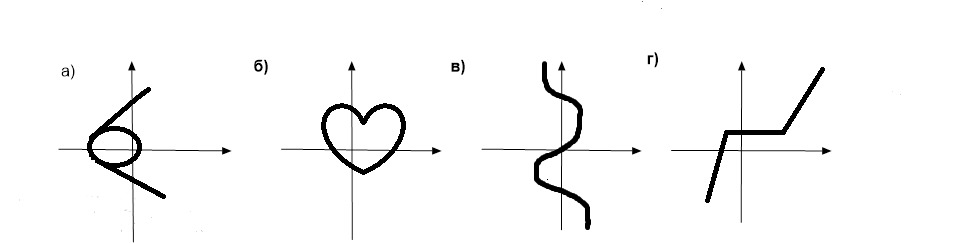
Графики взаимно обратных функций симметричны относительно прямой у = х. Функция f (х) имеет обратную функцию, если на области её определения двум разным значениям аргумента ставится в соответствие разные значения функции.

тестовые задания

тест 1

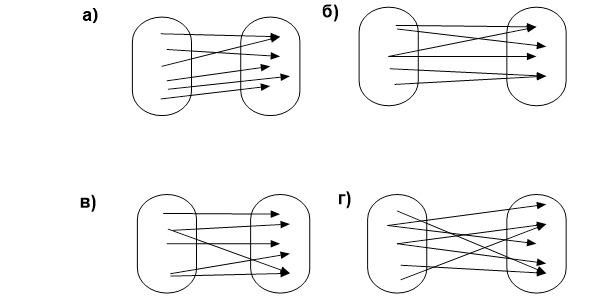
тест 2