
Бесплатный фрагмент - Путешествие в квантовую механику
1. Введение
Осуществляя работу над очередным изданием, я систематизировал и дополнил материал книги «Путешествие в квантовую механику», исправив бесчисленное количество недочётов и опечаток. Как несложно догадаться, настоящая рукопись была оформлена в виде справочника, чтобы каждый человек, заинтересовавшийся указанным научным трудом, смог рано или поздно сделать оптимальный для себя выбор: напрямую обратиться к любому из представленных ниже параграфов и без лишних усилий почерпнуть из нужной главы необходимую информацию или просто-напросто прочитать весь учебник от начала и до конца. Несомненно, речь в данном пособии пойдёт не столько об истории развития квантовой физики, сколько о направленной на решение тех или иных вырожденных дифференциальных уравнений альтернативной методике. Кстати говоря, в основу проведённого в этой монографии исследования был положен новый подход к решению трёхмерного нестационарного линейного уравнения Шрёдингера, выдвинутый Вашим покорным слугой автором. В течение всего повествования, опираясь на заявленное открытие, мне хочется обобщить те знания о микромире, которые сформулировали учёные XX столетия в своих научных изысканиях.
Предложенная мною теория, скорее всего, является непонятной для большинства людей, не посвящённых в точные дисциплины, однако каждый человек, неизменно стремящийся к знаниям, с чего-то всегда должен начинать собственно сам процесс систематизации всей, казалось бы, разрозненной информации об окружающей нас действительности. Примечательно, что на протяжении первых 3-х десятилетий XX века квантовая механика формировалась как отдельное направление в науке. Конечно, многое удалось сделать, но осталось немало важных вопросов, исследование которых постепенно перешло в новое тысячелетие. В этом пособии мне хотелось бы поднять проблему, связанную с универсализацией квантовой физики. В процессе обучения мы рассмотрим исключительно нерелятивистские явления.
Безусловно, ещё одной причиной для проведения настоящего исследования послужила некоторая надежда на дальнейшее развитие квантовой физики. Однажды Р. Ф. Фейнман сказал: «Посмотрите на мир с другой стороны». Так вот, мне хотелось бы, чтобы в качестве эпиграфа к книге «Путешествие в квантовую механику» была использована уже давно обросшая популярностью фраза Фейнмана.
Приятного чтения!
2. О фундаментальных законах физики
Во второй главе этой монографии будут рассмотрены 2 концепции, с помощью которых можно сформулировать те или иные предназначенные для описания окружающей нас действительности физические законы. Очевидно, что первая доктрина направлена на исследование дифференциальных соотношений, позволяющих по меньшей мере обобщить почти все материальные явления и процессы, а вторая связана с определением корреляций в заранее известном наборе функций f1 (x1), f2 (x2),…,fN`` (xN``). Последние могут быть найдены в результате экстраполяции округлённых до рациональных значений, относящихся непосредственно к частным аналитическим решениям тех или иных вырожденных дифференциальных уравнений, или получены опытным путём. К слову сказать, достоверность абсолютно любого численного метода, который опирается на анализ экспериментальных данных, изначально просто нельзя не поставить под сомнение. Впрочем, применяя эмпирический подход на практике, в подавляющем большинстве случаев несложно будет обосновать теоретически как минимум не самую малую долю от всех наблюдаемых в линейных или хотя бы в линеаризованных физических системах фундаментальных взаимодействий. Итак, начнём этот раздел с вывода одномерного стационарного линейного уравнения Шрёдингера. Кстати говоря, методика, ориентированная на поиск зависимостей между математическими величинами Ψ, Up (x), M и ħ, присутствующими в указанном дифференциальном уравнении, базируется на человеческой интуиции. Примечательно, что перечисленные мною тезисы в дальнейшем могут помочь исследователям разобраться в самой сути каждого из представленных на Ваш суд научных открытий.
2.1 Вывод уравнения Шрёдингера
В 1924 году французский физик Луи де Бройль выдвинул смелую гипотезу, согласно которой корпускулярно-волновому дуализму приписывается универсальный характер. Исходя из предположения де Бройля, важно констатировать, что всякая материальная частица обладает волновыми свойствами, причём соотношения (2`), (2``), (2```) и (2````), связывающие между собой волновые и корпускулярные характеристики, например, единичного фермиона, остаются точно такими же, как и в случае электромагнитного излучения веществом. Действительно, полную энергию Ep` и импульс P`` абсолютно любой элементарной частицы возможно выразить через частоту излучения ν и через длину волны де Бройля λ соответственно, тогда:
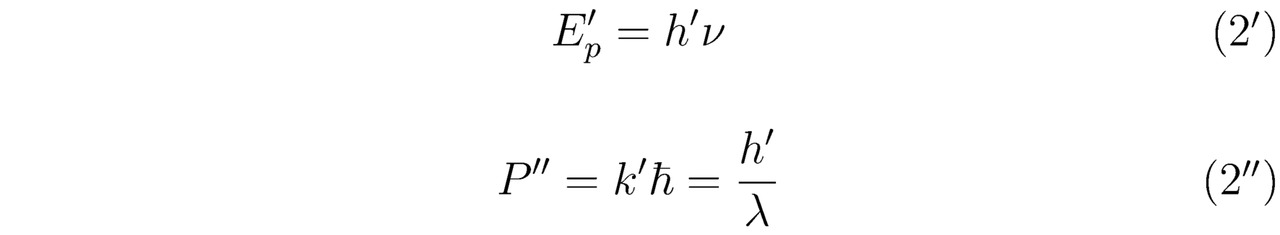
здесь h` — постоянная Планка; k`=2π/λ; ħ=h`/ (2π).
Далее сформулируем закон сохранения энергии для волны де Бройля. Безоговорочно, искомая величина Ep` представляет собой сумму 2-х энергий (кинетической Ek и потенциальной Up (x,y,z)), следовательно:
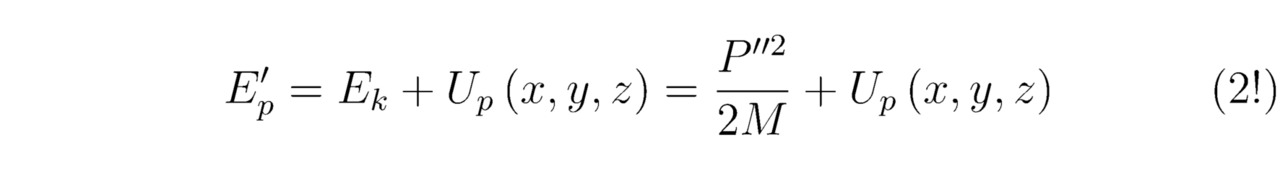
Вместе с тем
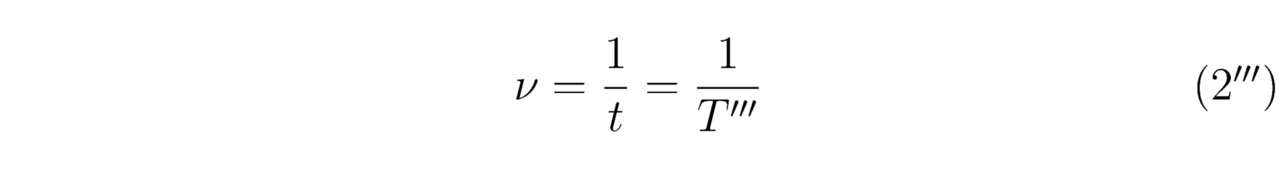
Разумеется, длину волны де Бройля λ удобно выразить через скорость υ (υ=dx/dt), тогда:
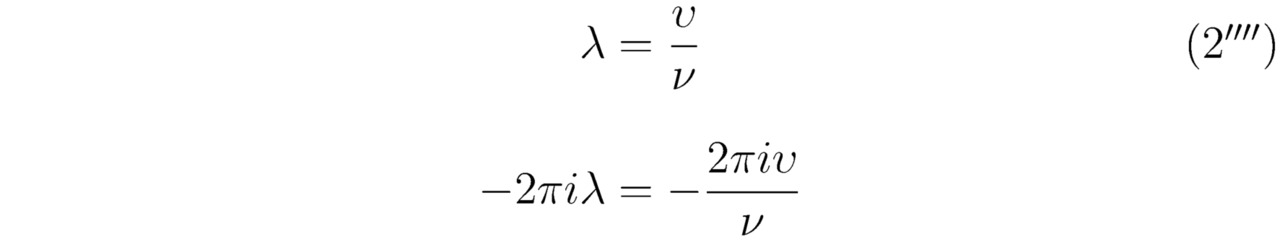
Беспрекословно, вывод того или иного линейного нестационарного уравнения Шрёдингера надо производить в трёхмерном аналитическом пространстве C3, но для упрощения расчётов мы будем использовать полярную систему координат. В довершении всего, переходя от действительных чисел к комплексным λ -> -2πiλ и ν -> -ν/ (2πi) (знаки перед исследуемыми переменными -2πiλ и -ν/ (2πi) выбраны отрицательными, поскольку в противном случае (при λ -> 2πiλ, а также при ν -> ν/ (2πi)) формула (2.1) просто-напросто потеряет смысл, если в неё подставить алгебраическую величину Ψ=∑nt=-∞∞∑nx=-∞∞C (nt, nx) e2iπ (ntt/Rt+nxx/Rx), так как в конечном счёте в любой ситуации должно соблюдаться равенство (2!)), перепишем составленный для волны де Бройля закон сохранения энергии в следующем виде:
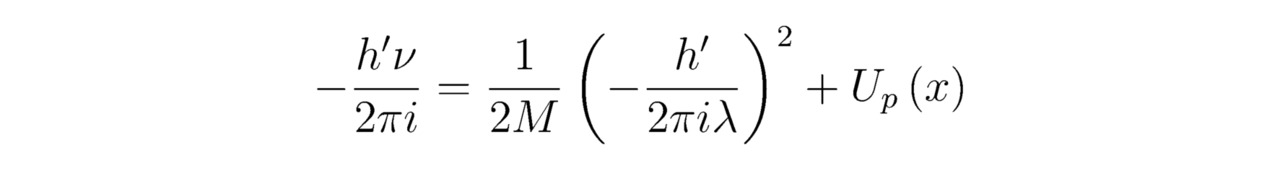
где M — масса электрона (в дальнейшем лептона или фермиона); T``` — период волны де Бройля; t — время; x — координата; Cn — амплитуда колебаний; ω` — угловая частота; Up (x) — потенциальная энергия.
К тому же
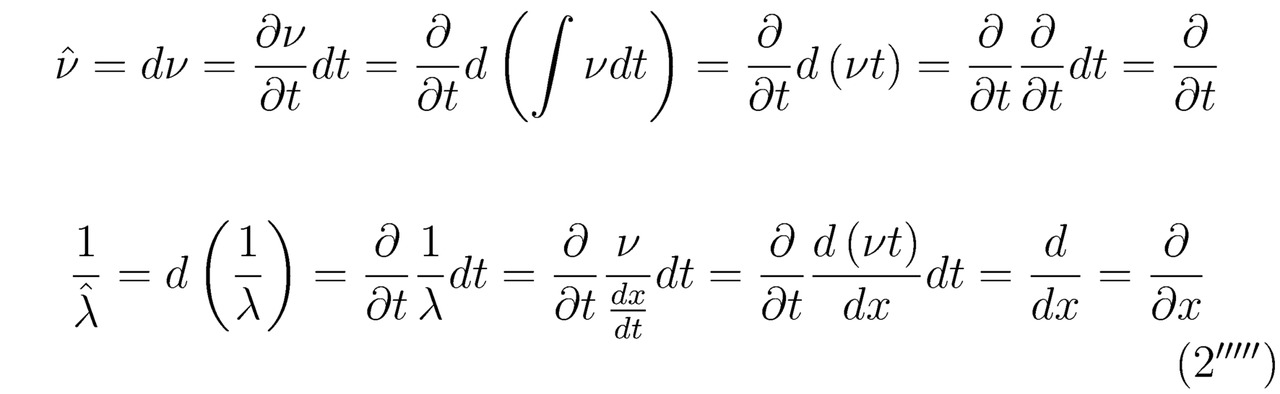
В итоге, ссылаясь на математические преобразования, разобранные выше, найдём тождество:
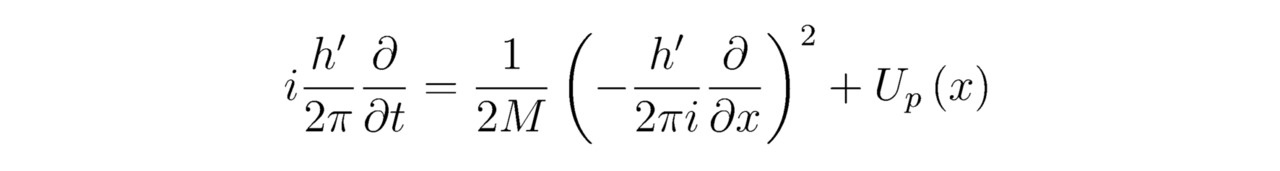
После чего нам потребуется внести новую величину Ψ под каждый из знаков частных производных ∂/∂t и ∂2/∂x2, тогда:
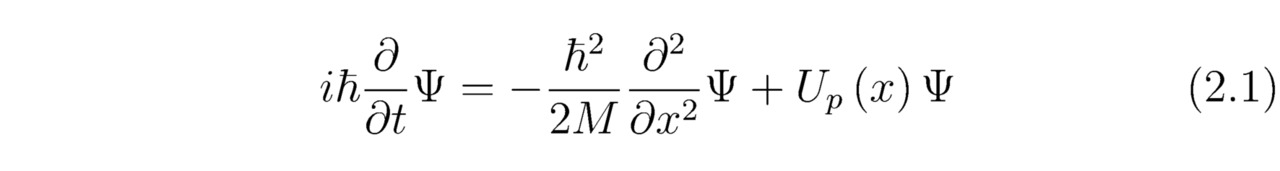
Так вот, полученное выражение (2.1) называется одномерным нестационарным линейным уравнением Шрёдингера. Теперь, опираясь на отыщенные прежде формулы (2``), (2`````) и (2.1), определим оператор импульса P``, следовательно:
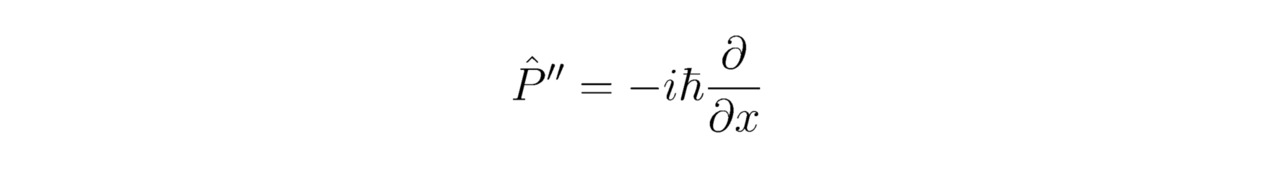
2.2 Эмпирический метод
Обычно с изучением школьной программы почему-то не принято ставить под сомнение справедливость основных положений, позволяющих осуществить вывод фундаментальных законов физики. В этом параграфе мы обобщим сведения о том, как соотносятся между собой некоторая физическая величина F и математически несвязанные выражения f1 (x1),…,fN`` (xN``). Отталкиваясь от постулата о наличии корреляций между искомым параметром F и неравномерно распределёнными вдоль соответствующих осей x1,…,xN`` функциями f1 (x1),…,fN`` (xN``), заданные соотношения f1 (x1),…,fN`` (xN``) надлежит перемножать друг с другом только в том случае, когда последние окажутся независимыми. Иначе говоря, приращение некоторого заранее известного аналитического решения fj (xj), составленного для того или иного вырожденного дифференциального уравнения, по факту будет происходить без взаимного влияния одних действительных значений fj (min (xj)),…,fj (max (xj)) на другие множители f1 (x1),…,fo (xo),…,fN`` (xN``) (o≠j). Итак, запишем тождество (2*) для нахождения алгебраического произведения Пj=1N``fj (xj) γj. Бесспорно, подобранные коэффициенты γ1,…,γN`` будут численно равны вещественным константам (+1 или -1), представляющим из себя степени показательных функций f1 (x1) γ1,…,fN`` (xN``) γN``, тогда:
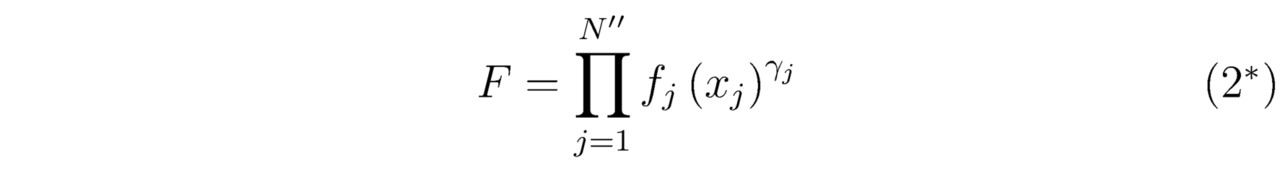
здесь N`` — общее количество независимых величин f1 (x1),…,fN`` (xN``).
Совершенно ясно, что наглядным примером применения эмпирического подхода на практике является закон Кулона, полученный для силы электростатического взаимодействия 2-х заряженных частиц Fe. Таким образом, следующие выражения (f1 (x1), f2 и f3 (x3)) могут быть сгруппированы друг с другом как несвязанные между собой параметры: f1 (x1) — произведение 2-х взятых по модулю электрических зарядов |q1||q2|; f2 — поправочная постоянная K; f3 (x3) — квадрат расстояния (|r1-r2|) 2 между 2-мя имеющимися в нашем распоряжении материальными частицами, где r1 и r2 — соответственно построенные из начала координат (0,0,0) в точки с зарядами q1 и q2 радиус-векторы.
Хорошо известно, что сила Кулона Fe прямо пропорциональна искомым множителям f1 (x1) и f2 (γ1=γ2=1), но обратно пропорциональна математическому соотношению f3 (x3) (γ3=-1). Наконец, запишем сформулированный для 2-х одно- или разноимённых зарядов q1 и q2 закон Кулона, следовательно:
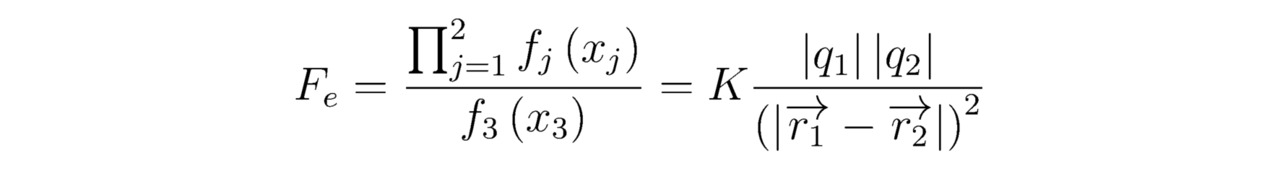
Помимо этого
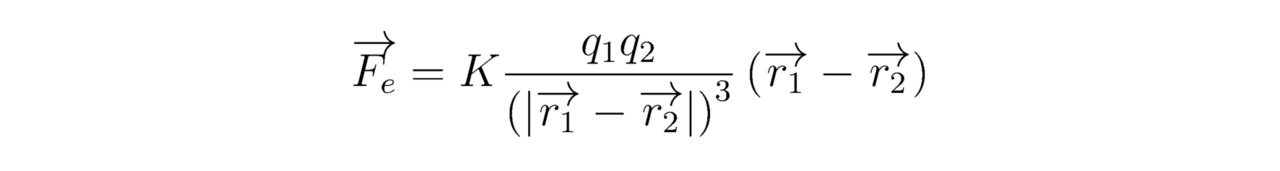
Если найденные величины gj (xj) и gj` (xj) окажутся взаимно зависимыми, то справедливым будет равенство:
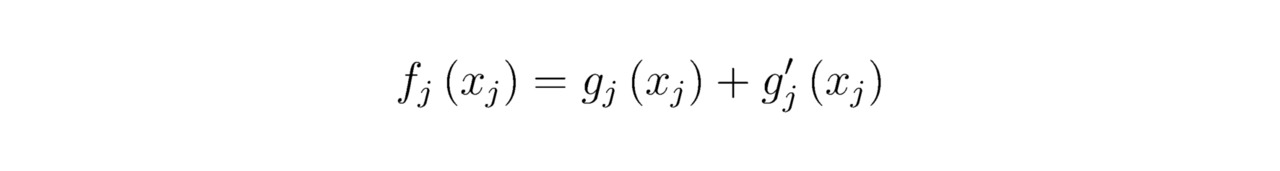
Кстати говоря, подобранные функции gj (xj) и gj` (xj) могут задаваться более сложным образом, нежели упомянутые ранее степенные выражения f1 (x1) γ1, f2γ2, f3 (x3) γ3. Порой с помощью эмпирического метода нельзя описать тот или иной закон природы, тогда для реализации намеченных целей соискатели обычно составляют либо линейные, либо нелинейные дифференциальные уравнения (ДУ). Разрешить нелинейные ДУ в частных производных иногда бывает затруднительно, поскольку абсолютно все современные персональные компьютеры имеют недостаточно высокую производительность. В подобных случаях исследователи используют суперкомпьютеры. В дальнейшем мы сконцентрируемся на проблеме поиска общего аналитического решения того или иного вырожденного ДУ с частными производными.
3. К вопросу о разрешимости дифференциальных уравнений в частных производных
Конечно, опираясь на методику, которая будет рассмотрена в 3-м разделе этого пособия, можно численно решить практически любое приводящееся к обыкновенному дифференциальное уравнение с частными производными и выявить характерные черты эволюции искомой величины Q`` во времени t.
3.1 Интерполяция и ряды Фурье
Представим набор линейных функций F0, F1,…,FRx/Δx -1 так:
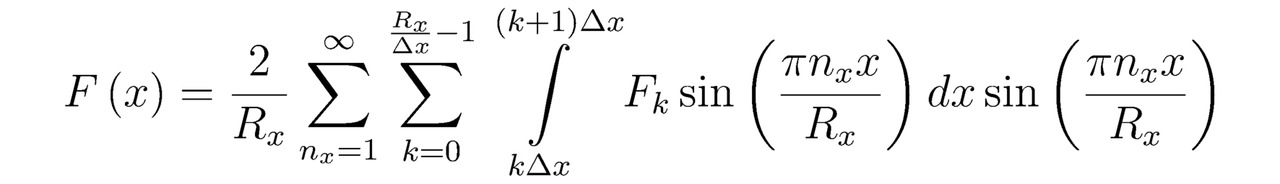
здесь Δx — геометрический размер каждого из интервалов, в которые заключены заранее известные значения переменных F0,…,Fk,…,FRx/Δx -1; k — номер вычислительной операции.
Естественно, что тригонометрический ряд (3*), полученный для совокупности абсолютно всех рациональных и иррациональных значений F (0,0,0),…,F (Rx, Ry, Rz), неравномерно распределённых на отрезках (kΔx, (k+1) Δx), (jΔy, (j+1) Δy) и (χΔz, (χ+1) Δz), примет следующий вид:
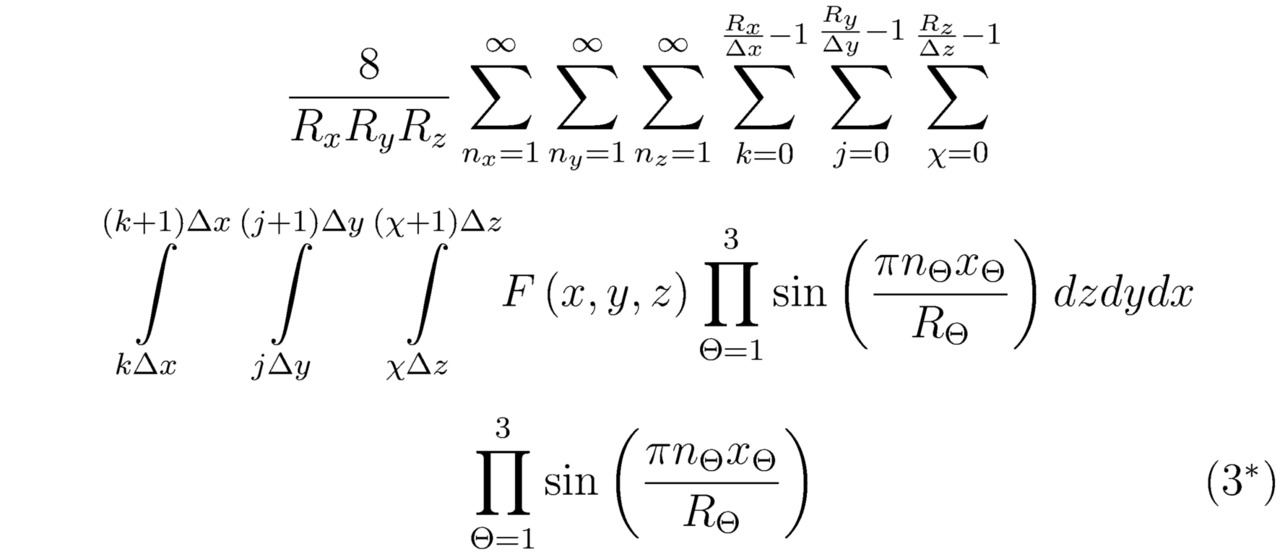
где x∈ [0,Rx]; y∈ [0,Ry]; z∈ [0,Rz]; Θ — индекс, идентифицирующий ту или иную ось координат xΘ; RΘ/ΔxΘ∈N.
Далее построим на расположенном ниже графике один из вариантов кусочно-линейной функции F (x), тогда:
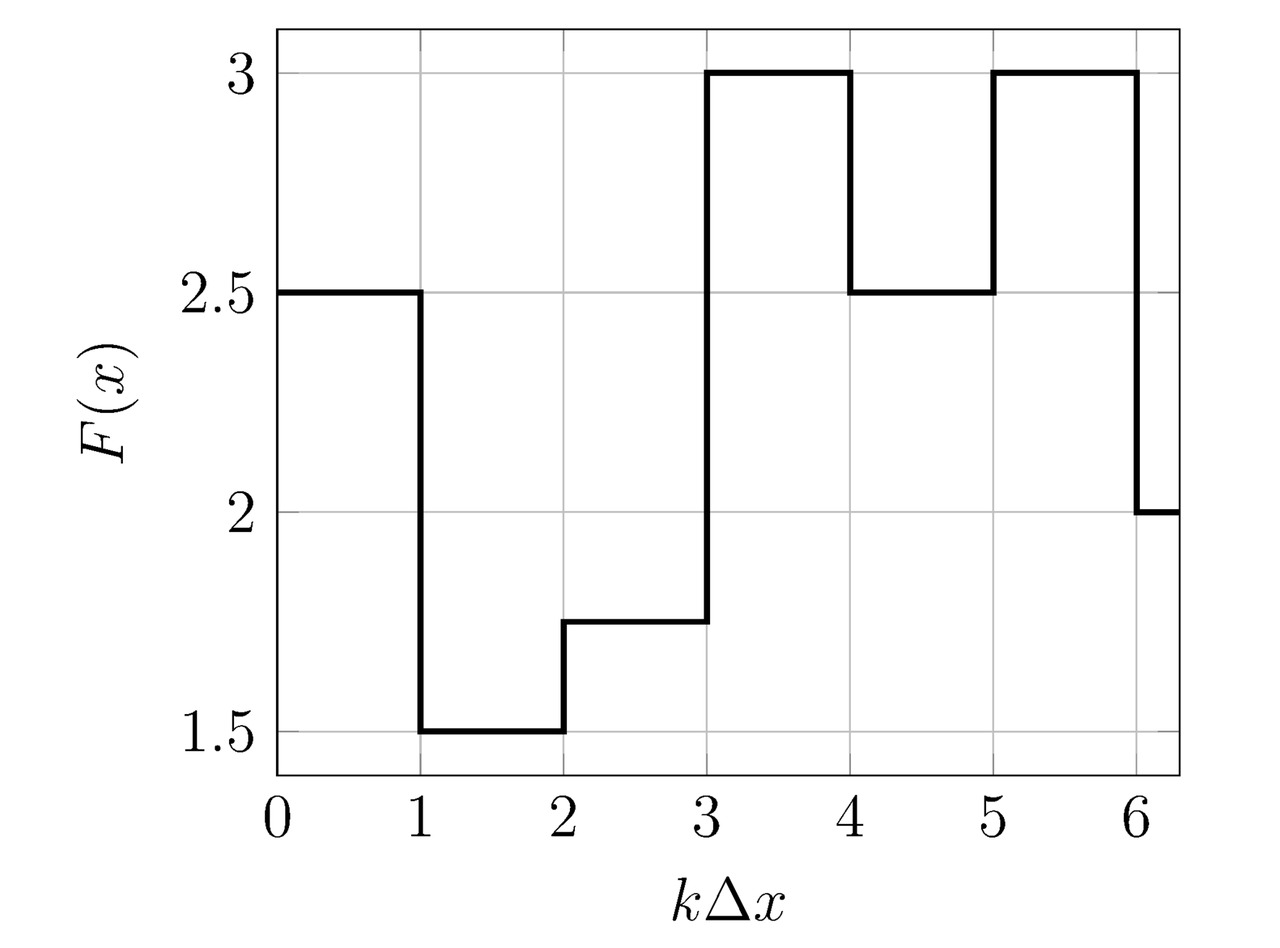
3.2 Общее решение дифференциальных уравнений с частными производными
Обозначим за Q``∈C некоторое аналитическое решение произвольно заданного дифференциального уравнения в частных производных. Отдельно выделим вещественную a*=Re (Q``) и мнимую b*=Im (Q``) части тождества Q``=a*+ib*. Для того чтобы численно решить практически любое вырожденное дифференциальное уравнение с частными производными, необходимо и достаточно найти закон изменения функции Q`` во времени t. Немаловажно отметить, что приведённая ниже теория не является единственной в своём роде. Однако в дальнейшем настоящая концепция позволит нам лучше усвоить материал этой книги. Бесспорно, всякое параболическое дифференциальное уравнение в частных производных возможно преобразовать к общему виду. Итого:
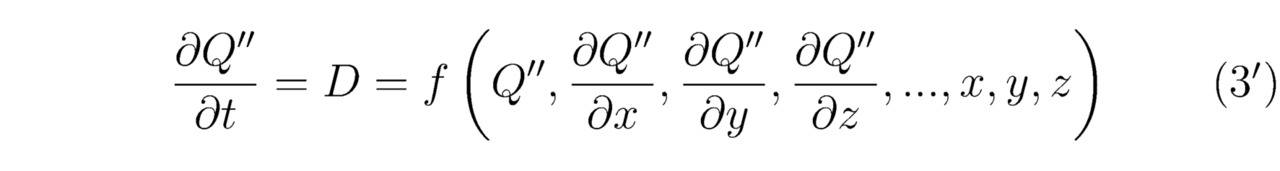
Теперь разложим в ряд Фурье искомое решение Q``, тогда:
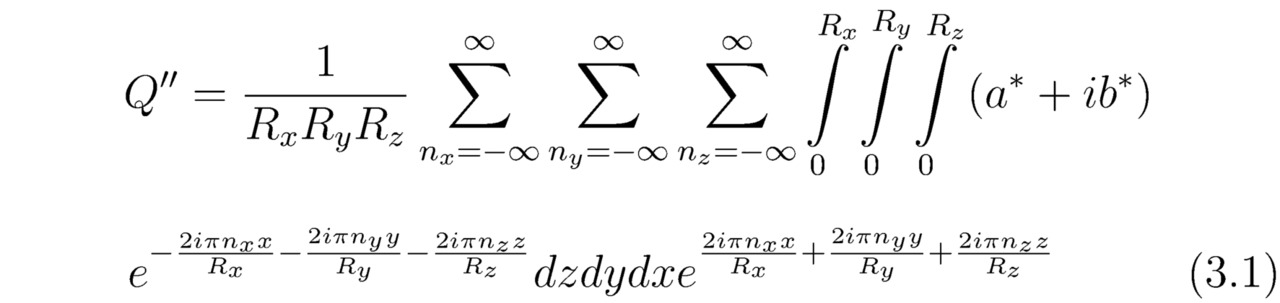
Затем рассчитаем частные производные ∂Q``/∂xΛ, ∂2Q``/∂xΛ2,…, ∂sdQ``/∂xΛsd,…,∂max (sd) Q``/∂xΛmax (sd), имеющиеся в составе равенства (3`), следовательно:
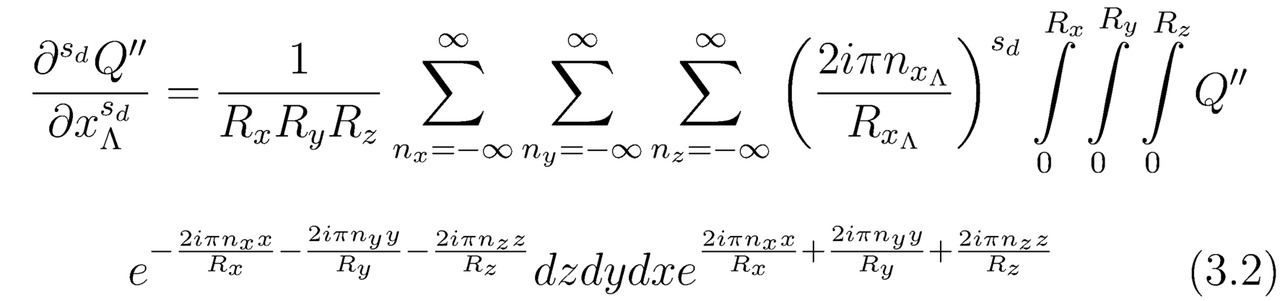
здесь sd — порядок дифференцирования, а xΛ — координата.
После чего осуществим интерполяцию непрерывной функции D. Если рассматривается одномерный случай, то каждой точке (пикселю), расположенной на оси D, понадобится поставить в соответствие находящийся на оси xΘ отрезок (kΔxΘ, (k+1) ΔxΘ). А значит, в трёхмерном комплексном пространстве справедливым будет соотношение:
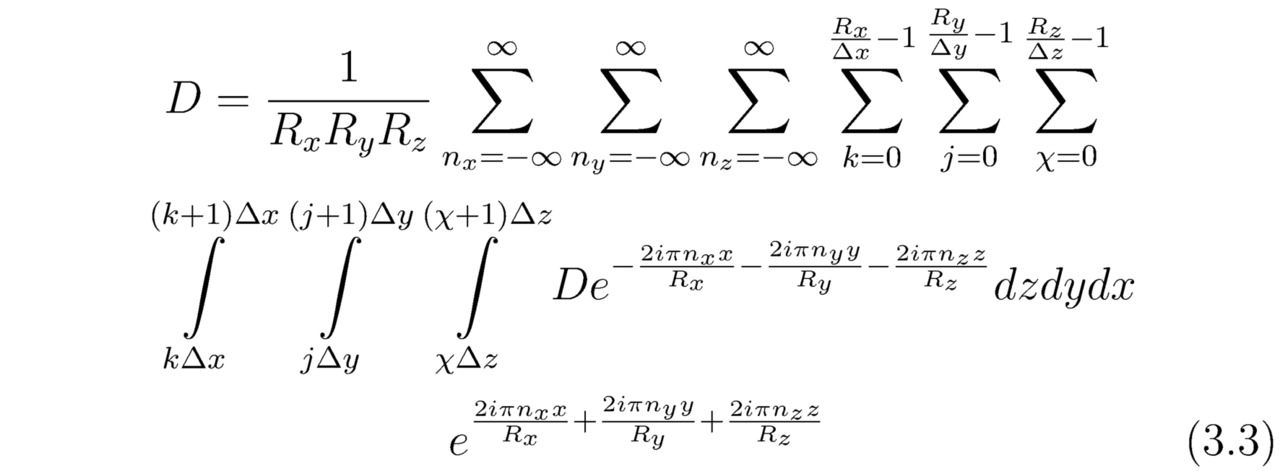
где x∈ [0,Rx]; y∈ [0,Ry]; z∈ [0,Rz].
Далее отыщем частную производную ∂Q``/∂t надлежащего решения Q`` по времени t, тогда:
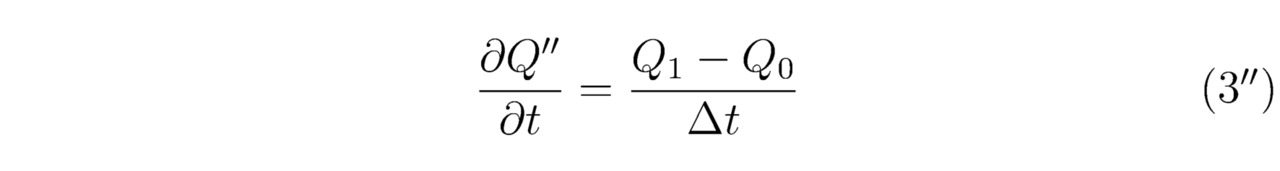
Совершенно ясно, что формулу (3``) удобно записать в следующем виде:
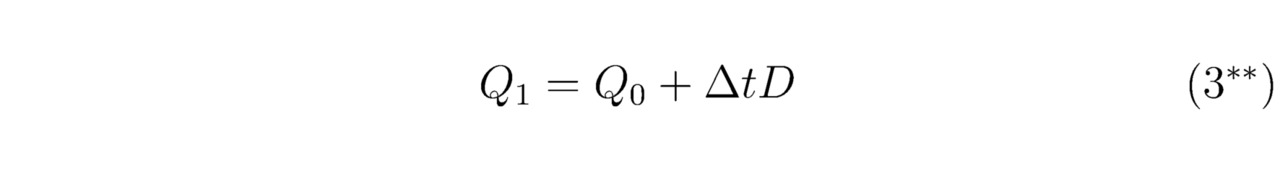
Помимо этого
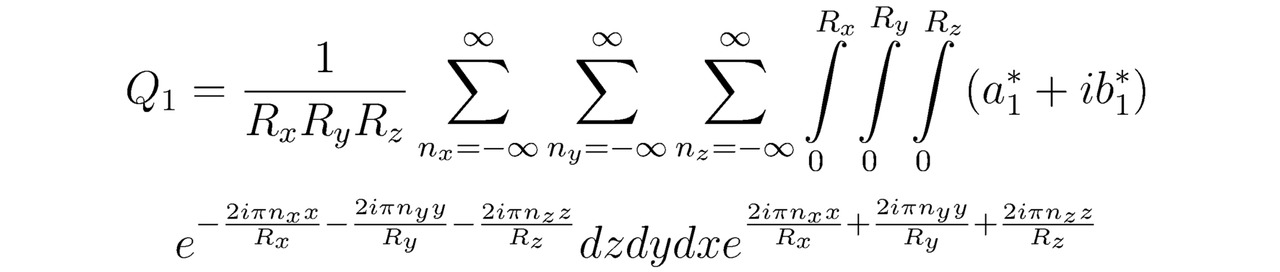
Как нетрудно догадаться, математические функции Q0 и Q`` будут тождественно равны друг другу в рамках одной итерации Q0=Q``. Напоследок подставим полученные величины Q1, D и Q`` в уравнение (3**). В силу чего:
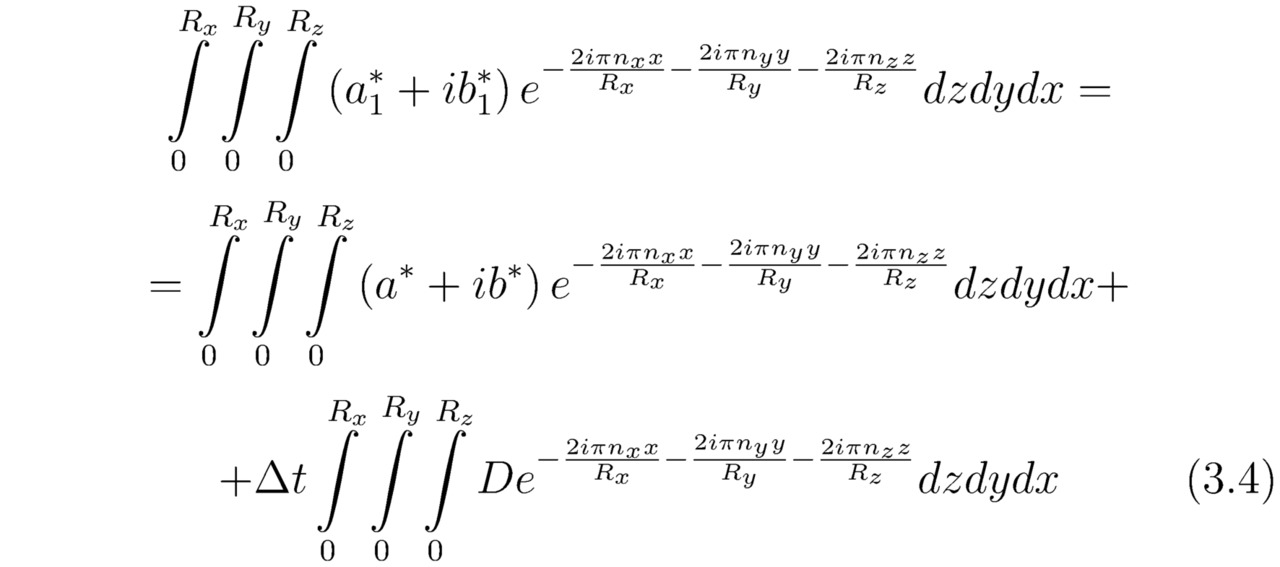
Безоговорочно, с каждой новой итерацией по времени t вместо неизвестного выражения Q`` следует использовать найденную ранее функцию Q1, тогда:
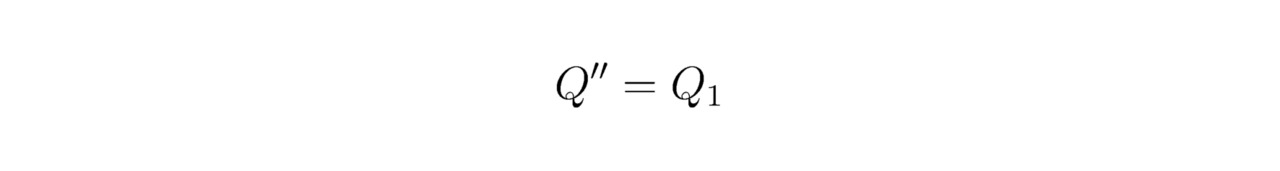
Несомненно, расчёт нужно выполнять до тех пор, пока не будет достигнуто условие V`Δt=T*, здесь T* — определяющий границы эволюции искомого отображения Q`` промежуток времени t; V` — общее количество итераций; Δt — шаг по времени t. Неудивительно, что:
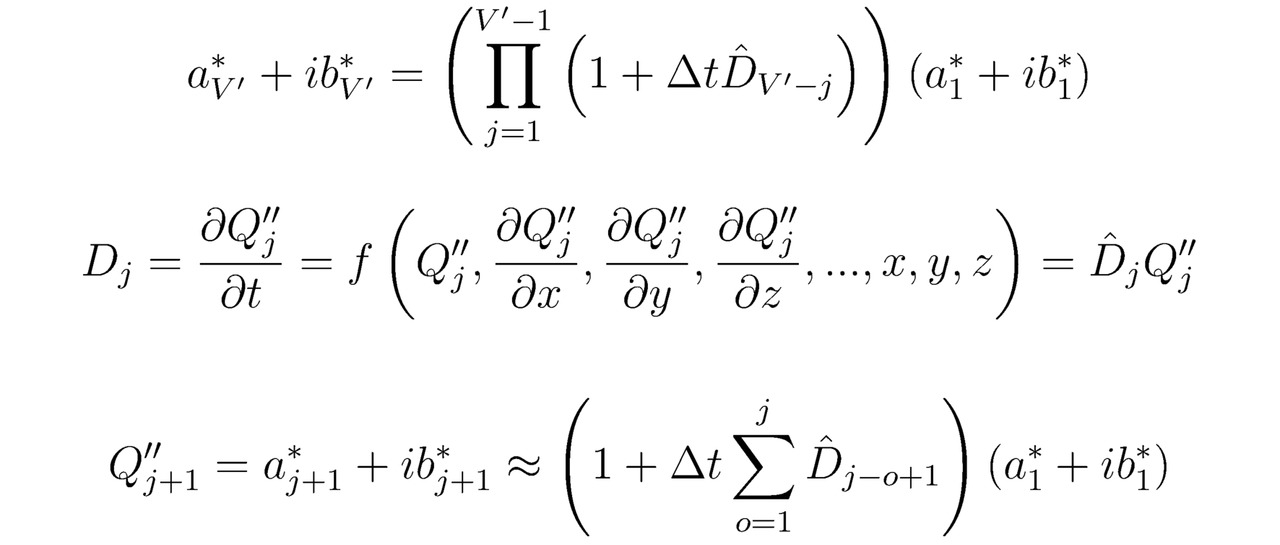
3.3 Решение дифференциальных уравнений в R3
В предыдущем параграфе этой книги мы рассмотрели методику, предназначенную для решения тех или иных приводящихся к обыкновенным дифференциальных уравнений с частными производными, заданных в общем виде. Так вот, акцентируясь на вырожденном случае поставленной прежде задачи, необходимо потребовать, чтобы исследованное в подглаве 3.2 дифференциальное уравнение (3`) было линейным и при этом имело чётные порядки частных производных ∂2Q``/∂xΛ2, ∂sdQ``/∂xΛsd и прочих подобных (когда sd∈A, sd> 0). Если абсолютно все целочисленные коэффициенты nx, ny и nz примут натуральные значения, то в сложившейся ситуации справедливой окажется простая принадлежность Q``∈R. Таким образом, выведенное нами ранее выражение (3*) не составит большого труда свести к тождеству:
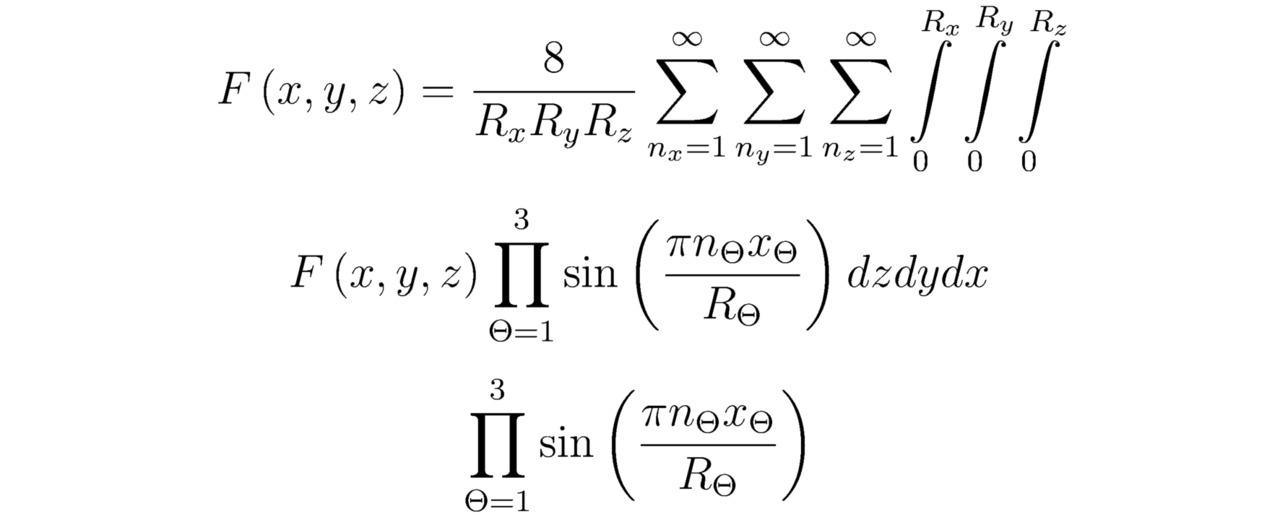
Теперь преобразуем соотношение (3.1) к более приемлемому для нас виду. Итого:
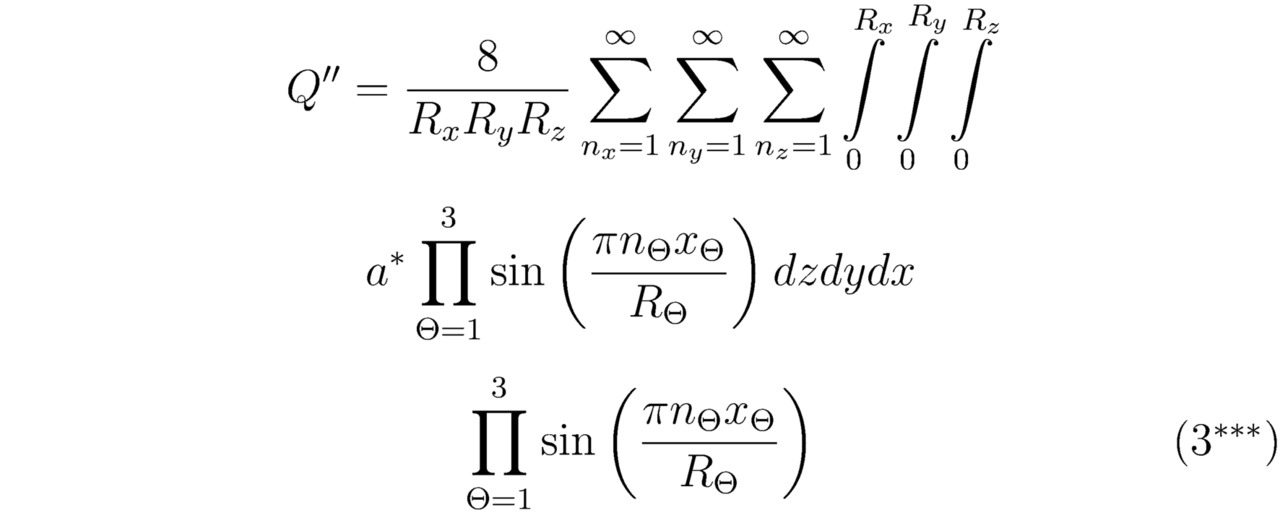
После чего разложим в ряд Фурье дифференцируемую во всех точках функцию D, тогда:
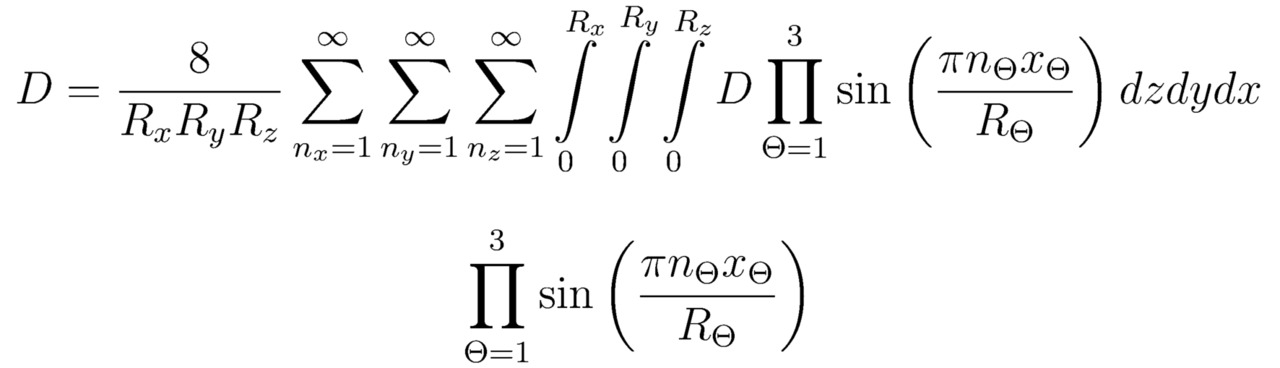
Формулу (3.4) удобно записать как:

Безусловно, абсолютно любой соответствующий следующей по времени t итерации коэффициент Фурье ∫0Rx∫0Ry∫0Rza*1ПΘ=13sin (πnΘxΘ/RΘ) dzdydx легко можно выразить через определённые интегралы ∫0Rx∫0Ry∫0RzDПΘ=13sin (πnΘxΘ/RΘ) dzdydx и ∫0Rx∫0Ry∫0Rza*ПΘ=13sin (πnΘxΘ/RΘ) dzdydx, полученные для предыдущей итерации. К слову сказать, всякое нестационарное линейное уравнение Шрёдингера, составленное для постоянной потенциальной энергии U0p=Up (x,y,z) =const, является параболическим. В связи с этим частное решение рассматриваемого здесь дифференциального уравнения Q``=Q``nxnynz допустимо задать в виде тождества (3.6), поскольку в данном случае, как несложно заметить, подобранные величины nx, ny и nz в конечном счёте примут натуральные значения nx∈N, ny∈N и nz∈N. Если в качестве искомой амплитуды вероятности Ψ подставить в равенство (4!) периодическую функцию Ψp (t, nx, ny, nz) ПΘ=13sin (πnΘxΘ/RΘ), то справедливым окажется следующее выражение:
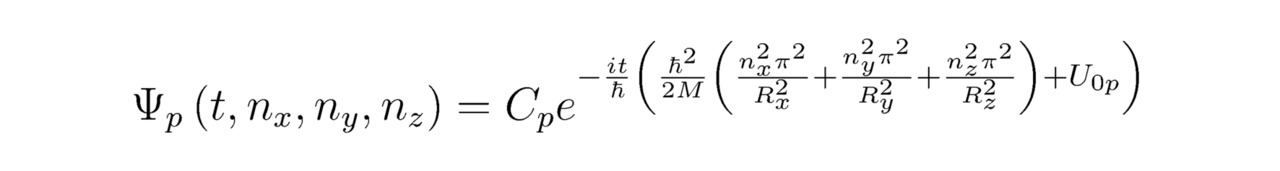
Напоследок найдём частное решение трёхмерного нестационарного линейного уравнения Шрёдингера Ψp=Q``nxnynz (когда U0p∈R), тогда:
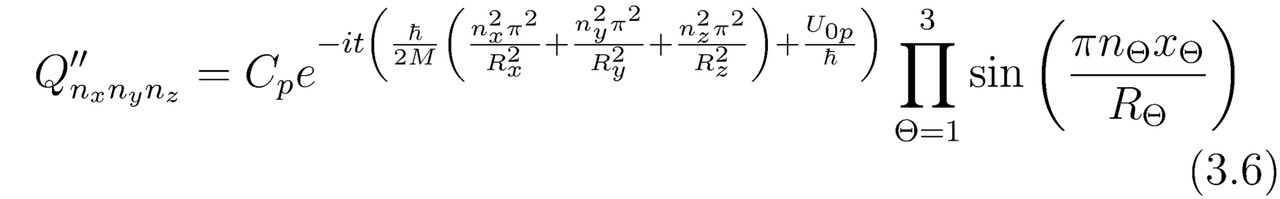
Как известно, общее аналитическое решение Q`` (Q```=Ψ) всякого трёхмерного линейного дифференциального уравнения является суммой всех частных решений Q``111,…,Q``nxnynz,…,Q``∞∞∞ по nx, ny, nz. В силу чего:
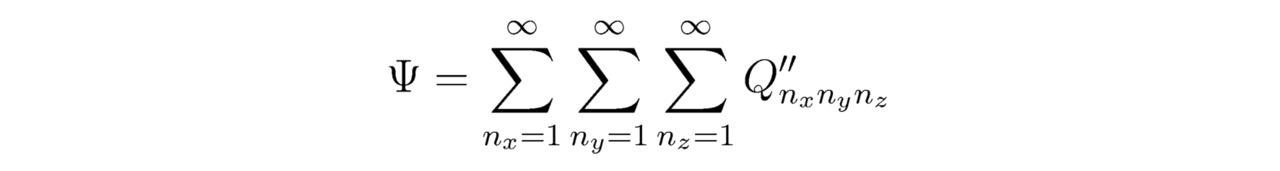
Под обозначением Ψ* понимается комплексно сопряжённая волновая функция. Плотностью вероятности локализации элементарной частицы в точке с координатами x,y,z называют математическое соотношение ΨΨ*. В то же время, исходя из тождества ограниченности вероятности ∫-Rz0Rz0∫-Ry0Ry0∫-Rx0Rx0ΨΨ*dxdydz=1, возможно рассчитать действительный множитель Cp=const для всех p∈N (когда Rx0=RxOx/2, Ox∈N; Ry0=RyOy/2, Oy∈N; Rz0=RzOz/2, Oz∈N; Ox-> ∞; Oy-> ∞; Oz-> ∞), следовательно:
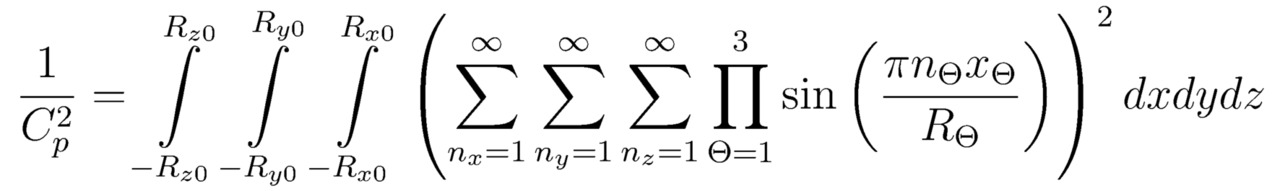
где nx∈N, ny∈N, nz∈N — дискретные квантовые числа.
Для того чтобы построить физическую модель некоторого устойчивого химического соединения, отвечающего требованиям компактности, симметрии и иногда периодичности, надо в первую очередь в качестве потенциальной энергии Up (x,y,z) подставить в формулу (4!) постоянный коэффициент U0p. Например, прибегая к закону Кулона, записанному для надлежащего параметра U0p, можно выяснить условия существования неподвижной в пространстве молекулярной структуры. Конечно, атомы абсолютно любого синтезированного на практике вещества будут сохранять свою стабильность до тех пор, пока сумма всех интересующих нас потенциальных энергий ∑o∑ j,j> oUoj не изменит своего значения ∑o∑j,j> oUoj=const. Модуль |∑o∑j,j> oUoj| окажется минимальным только в том случае, когда в исследуемой физической системе установится электростатическое равновесие между положительными ядрами и отрицательными лептонами ∑Fe=0, если rmax> =roj> =rmin (для всех o∈N, j∈N, j> o), где roj — расстояние между материальными частицами под номерами o и j; rmax, rmin — максимальный и минимальный из возможных делителей r12, roj и так далее соответственно; K — поправочный коэффициент; qj, qo — заряды бозонов и/или фермионов, тогда:
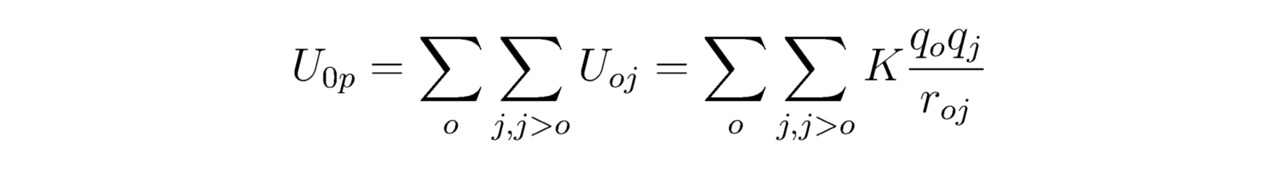
Волновая функция Ψ — это комплекснозначная величина, используемая в квантовой механике для описания чистого состояния системы. Совершенно ясно, что математическое отображение Ψ физического смысла не имеет, но последний приписывается плотности вероятности ΨΨ*. Кстати говоря, упомянутую ранее амплитуду вероятности Ψ удобно представить в виде суммы ∑pΨp. К тому же каждый член Ψp заданной функции Ψ (Ψ=∑pΨp) будет характеризовать то или иное собственное состояние рассматриваемой здесь квантовой системы.
В 4-м разделе этой книги мы ознакомимся с правилами решения абсолютно любого линейного нестационарного уравнения Шрёдингера. Опираясь на методику из параграфа 4.1, можно, с одной стороны, описать большинство явлений нерелятивистской квантовой механики, а с другой — дать теоретическое обоснование коллапсу волновой функции Ψ.
4. Об аналитическом решении уравнения Шрёдингера в C3
В 4-й главе настоящей монографии будет проанализирован новый подход к решению тех или иных приводящихся к обыкновенным дифференциальных уравнений в частных производных. В качестве примера мы разрешим трёхмерное нестационарное линейное уравнение Шрёдингера, полученное для одной заряженной частицы, заключённой внутри декартовой системы координат (x,y,z). Несомненно, исследуемое сейчас дифференциальное уравнение достаточно легко свести к тождеству:
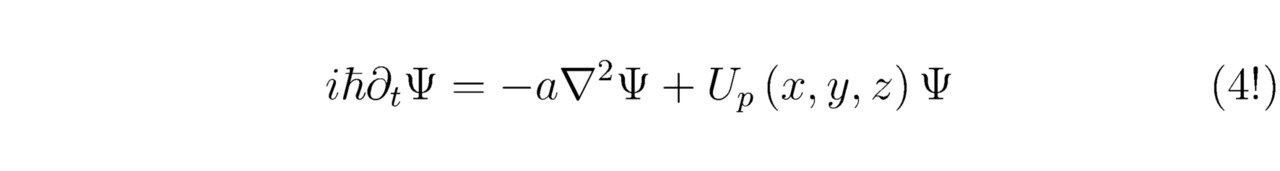
Беспрекословно, в формулу (4!) вместо символа ∇2 возможно подставить сумму дифференциальных операторов ∂2/∂x2+∂2/∂y2+∂2/∂z2; естественно, что знаки ∂t и ∂xx эквивалентны надлежащим обозначениям ∂/∂t и ∂2/∂x2. Наконец, запишем одномерное линейное нестационарное уравнение Шрёдингера, тогда:
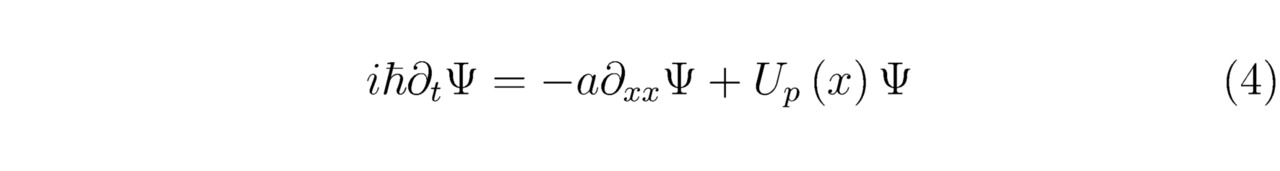
где a=ħ2/ (2M).
4.1 Пример решения уравнения Шрёдингера
Итак, осуществляя поиск общего аналитического решения того или иного нестационарного линейного уравнения Шрёдингера Ψ, разложим в ряд Фурье каждое из следующих выражений:
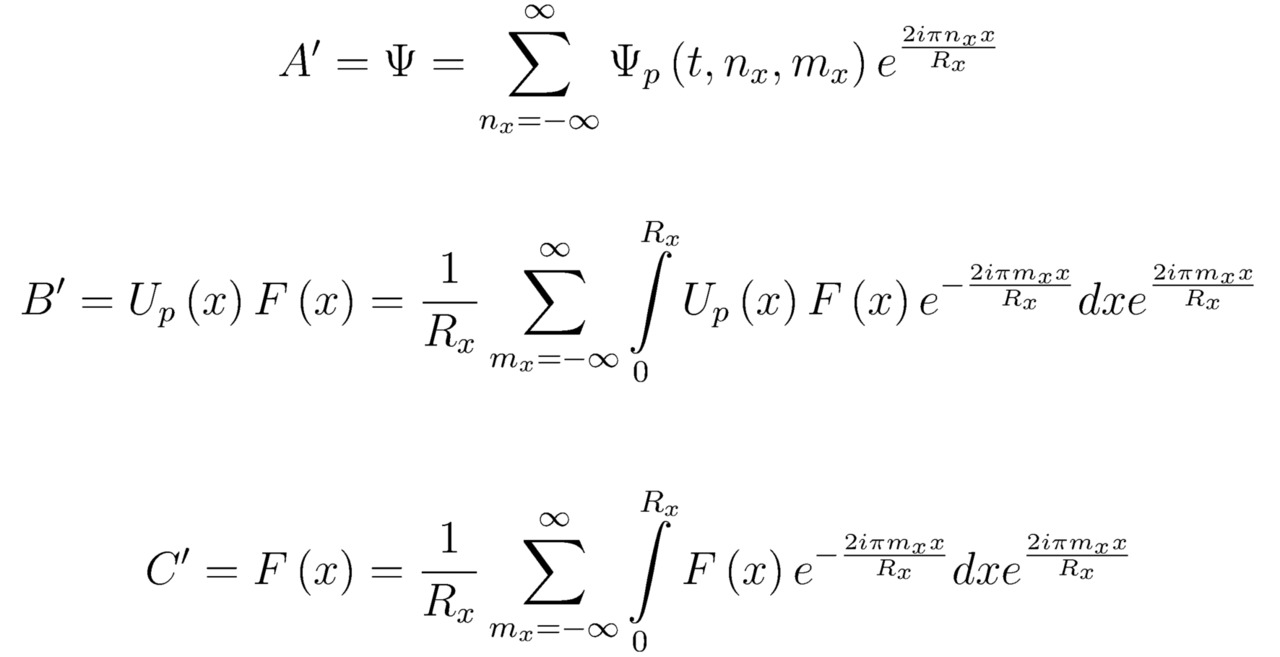
здесь x∈ [0,Rx]; F (x) — произвольно заданная величина (F (x) ∈C); 0 и Rx — координаты граничных условий Дирихле.
Далее поочерёдно домножим обе части тождества (4) на одно и то же случайное отображение F (x), тогда:

Затем заменим неизвестные соотношения Ψ, Up (x) F (x) и F (x), имеющиеся в составе формулы (4`), на соответствующие функции A`, B` и C`, следовательно:
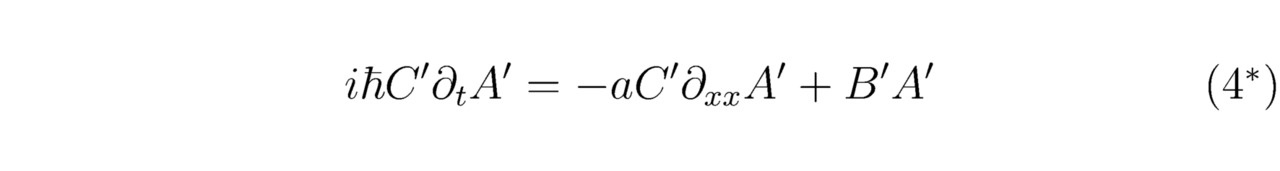
Примечательно, что в равенстве (4*) присутствуют общие экспоненциальные множители e-2iπ∞x/Rxe-2iπ∞x/Rx,…,e2iπmxx/Rxe2iπnxx/Rx,…,e2iπ∞x/Rxe2iπ∞x/Rx, от которых необходимо избавиться, оставив в результате только несокращаемые коэффициенты Фурье H`, H`` и H```. Теперь выполним несколько математических преобразований:

После чего разделим безразмерные переменные в уравнении (4``) относительно комплексного параметра Ψp (t, nx, mx), тогда:
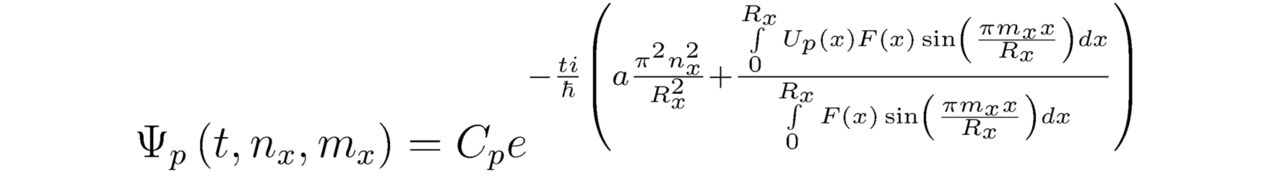
Напоследок, прибегая к тождеству ограниченности вероятности ∫-Rx0Rx0ΨΨ*dx=1, возьмём определённый интеграл ∫-Rx0Rx0ΨΨ*dx. В рассматриваемом примере подобранные коэффициенты Cp и Cp* не будут зависеть от времени t, поскольку сумма ∑p|Cp|2 останется постоянной ∑p|Cp|2=∑pCpCp*=1 в том случае, когда t=0 и/или все Ep∈R. Бесспорно, область определения действительной части волновой функции Re (Ψ) расположится на отрезке [0,Rx]. Вместе с тем для математической константы Rx возможно задать абсолютно любое положительное значение, удовлетворяющее равенству Rx=2Rx0/Ox. Неудивительно, что в рамках настоящей теории непрерывные выражения Ψ и Ψ* являются периодическими, а их графики y=Ψ (x) и y=Ψ* (x) симметричными или асимметричными относительно оси ординат y, следовательно:

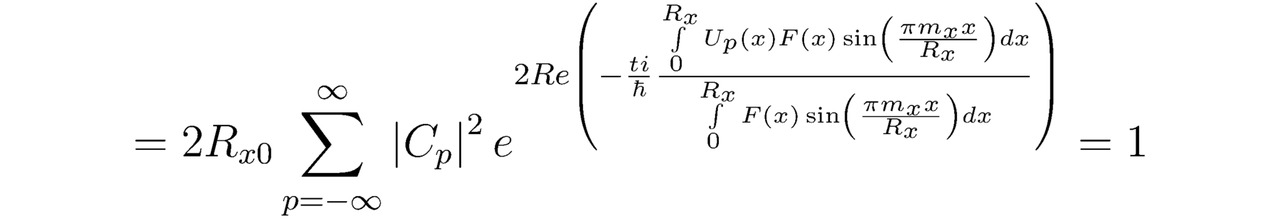
Наконец, отталкиваясь от выведенного ранее одномерного нестационарного линейного уравнения Шрёдингера, рассчитаем полную энергию Ep находящегося в состоянии Ψp электрона, тогда:
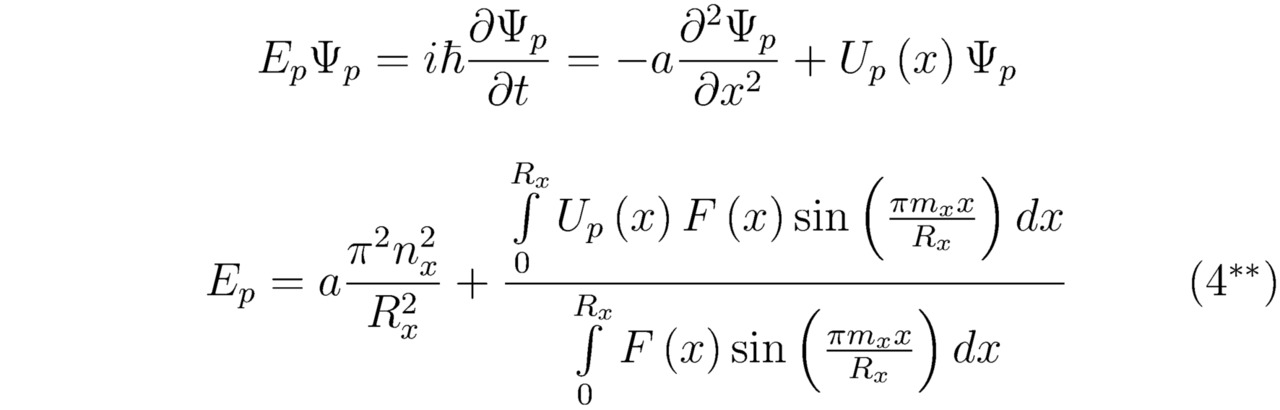
Для трёхмерного базиса (x,y,z) интересующая нас величина Ep составит:

Если в формуле (4**), полученной для полной энергии Ep, произвольная функция F (x) не сократится, то найденный параметр Ep по факту окажется неопределённым (при Up (x) ≠const). Таким образом, опираясь на предложенную в данном параграфе методику, можно констатировать, что абсолютно все выраженные в общем виде соотношения E1, Ep и другие, похожие на эти, будут зависеть в том числе и от степени вариативности случайных процессов, протекающих в исследуемой физической системе. В стационарных условиях, когда Ep=const, левые и правые части тождеств (4**) и (4!!) примут фиксированные во времени t значения.
4.2 Кот Шрёдингера. Коллапс волновой функции
Если функции ψ1 и ψ2 являются волновыми, то их линейная суперпозиция ψ3 = c1ψ1 + c2ψ2 описывает некоторое состояние изолированной от внешнего воздействия квантовой системы. В том случае, когда измерение определённой физической величины f` в состоянии ψ1 приводит к результату f1, а в состоянии ψ2 — к результату f2, тогда измерение состояния ψ3 приведёт к результатам f1 или f2 с вероятностями |c1|2 и |c2|2 соответственно. Конечно, произвольно заданная комбинация частных аналитических решений того или иного нестационарного линейного уравнения Шрёдингера c1ψ1, c2ψ2, cpψp и всех оставшихся всегда может быть представлена как сумма эквивалентных им волновых функций ∑pΨp.
Совершенно ясно, что концепция мысленного эксперимента, связанного с котом Шрёдингера, заключается в следующей идее. Сперва в ящик помещаются банка с ядом, молоточный механизм с детектором и изначально живой кот. Естественно, что в ходе ядерной реакции срабатывает детектор, приводящий в движение разбивающий сосуд с ядом молоточный механизм, после чего кот умирает. Согласно квантовой механике, если над ядром не производится наблюдение, то его состояние описывается суперпозицией 2-х состояний: распавшегося и нераспавшегося. Между тем кот, сидящий в ящике, окажется и живым, и мёртвым одновременно. Если же ящик открыть, то экспериментатор сможет обнаружить только какое-нибудь одно конкретное состояние: «ядро распалось, кот мёртв» или «ядро не распалось, кот жив».
Немаловажно отметить, что в квантовой механике коллапс волновой функции Ψ возникает тогда и только тогда, когда обобщённая комплекснозначная величина Ψ (первоначально выраженная в виде суперпозиции нескольких собственных состояний Ψ=∑pΨp) сводится к одному собственному состоянию Ψp по причине взаимодействия изучаемой здесь физической системы с внешним миром. В дальнейшем это взаимодействие мы будем называть «наблюдением» или «измерением». Под нормированной суперпозицией ∫-Rx0Rx0ΨΨ*dx=1 понимается приравненная к единице сумма проинтегрированных по dx надлежащих плотностей вероятностей ∑p∫-Rx0Rx0ΨpΨp*dx=1, которые допустимо считать взаимно зависимыми. Безусловно, всякая объединённая волновая функция ∑pΨp, несмотря ни на какие обстоятельства, будет продолжать подчиняться тому или иному линейному нестационарному уравнению Шрёдингера, точно так же как и сама величина Ψp.
В 1927 году Вернер Гейзенберг использовал идею редукции волновой функции ψ для объяснения квантового измерения искомой нормированной вероятности |cp|2. Однако в этом параграфе будет показано, что коллапс — это фундаментальное физическое явление, которое возможно обосновать математически, опираясь на общее аналитическое решение того или иного нестационарного линейного уравнения Шрёдингера Ψ. Кстати говоря, сами вычисления нужно производить в трёхмерном комплексном пространстве. Тем не менее для упрощения расчётов мы выберем одномерный случай. Пусть F (x) =d (x) +ib (x), следовательно:
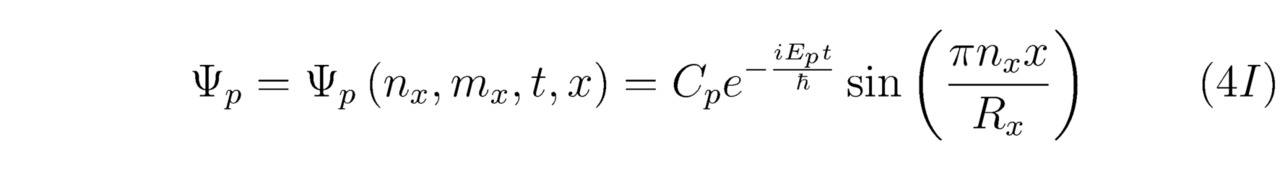
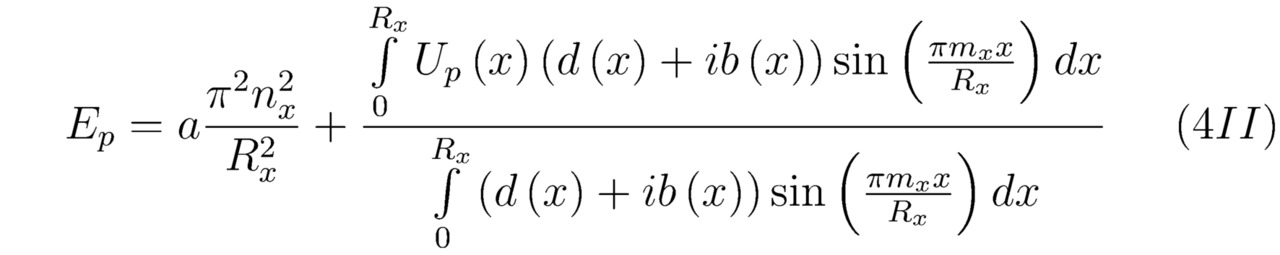
Несомненно, квадрат модуля коэффициента |Cp|2 будет определять начальную нормированную вероятность |cp|2 локализации соответствующей частицы в состоянии ψp. Действительно, постоянный член aπ2nx2/Rx2, входящий в состав формулы (4II), всегда можно опустить, поскольку выше было положено условие зависимости полной энергии Ep от произвольно заданной функции F (x). Для того чтобы осуществить дальнейшие математические преобразования, необходимо в первую очередь выделить вещественную часть Re (iEp) из отыщенного ранее выражения (4II). Допустим, что E*p=Re (-iEp), тогда:
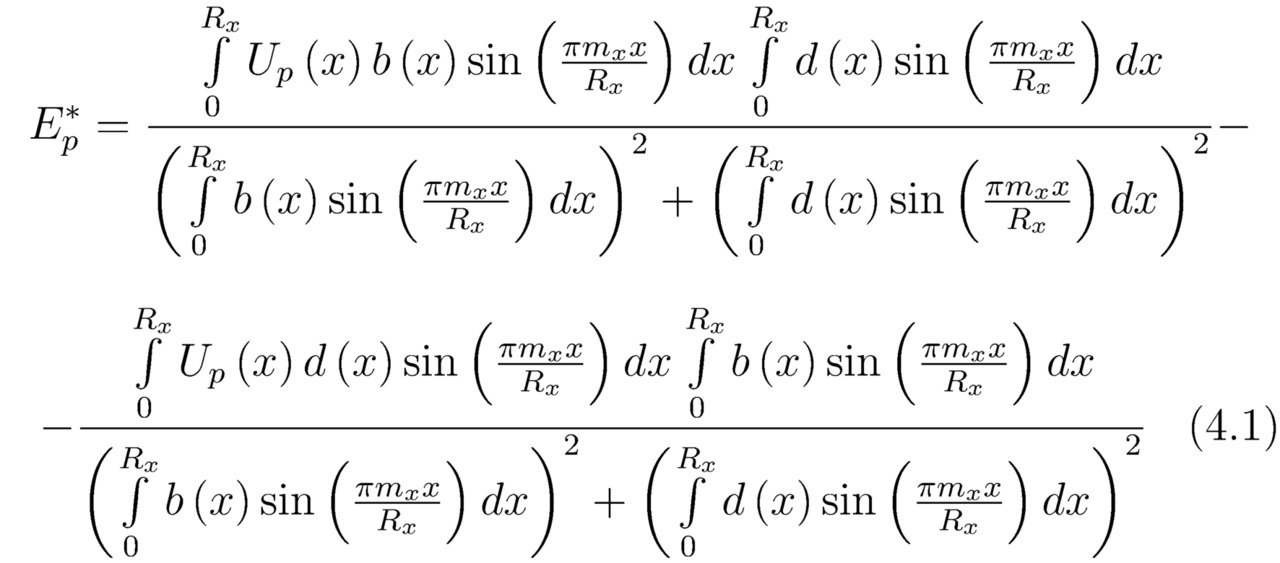
Суперпозицию квантовых состояний Ψ=∑p=1S`Ψp удобно представить так:
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.