Бесплатный фрагмент - Предсказываем тренды

Предисловие

О чем?

При построении торговых систем вообще, и с использованием терминала МТ4/5 в частности, приходится решать целый комплекс взаимосвязанных задач.

Изначально, целью построения торговой системы является предсказание поведения некоторого рыночного инструмента, например, валютной пары. Цели предсказания могут быть разными, мы же ограничимся предсказанием трендов, а точнее предсказанием роста (лонгов) или падения («шортов») значений котировки валютной пары. Кроме этого будем предсказывать боковики — нахождение вне рынка.

Для кого?

Книга доступна для многих читателей и не обязательно только тем, кто силен в информатике или статистике. С помощью Rattle практически любой желающий сможет построить основную часть торговой системы — предсказание котировки, а затем, при отсутствии необходимого опыта и знаний, сделать заказ реальной торговой системы, изложив свои мысли в виде готового кода на R.

Для искушенного в R пользователя Rattle будет также полезен: позволяет быстро апробировать идеи в исходных данных, целевых переменных, используемых моделях, а затем перейти к соответствующим пакетам R, имеющим значительно больший по сравнению с Rattle функционал.

Данная книга является руководством по использованию пакета Rattle (Простое обучение аналитическим инструментам R), который оформлен в виде GUI — графического пользовательского интерфейса, позволяющего значительно упростить использование могучих средств R и необходимых для поставленной задачи пакетов.

Почему Rattle?

В качестве инструмента для предсказания поведения валютных пар выберем систему R, которая идеально подходит для задач предсказания на финансовых рынках и, в частности, предсказания поведения валютных пар. Вместе с тем R остается, прежде всего, языком программирования для высоко квалифицированного статистика и для многих остается вне досягаемости. Сложность самой R усугубляется тем обстоятельством, что инструменты для предсказания являются многочисленными и рассредоточены по многим пакетам, которые и составляют основную функциональность R.

Rattle объединяет множество пакетов R, которые важны для построения торговых систем, но часто не легки для использования новичком. Понимание R не требуется, чтобы начать с Rattle. Но результатом работы с Rattle будет код на R, который может быть использован при построении реальной торговой системы. И на этом этапе потребуется знание R.

В любом случае Rattle является незаменимым инструментом на этапе проектирования торговой системы, позволяет даже новичкам быстро посмотреть результат тех или иных идей и получить их оценку.

Пакет Rattle (Уильямс, 2009) является бесплатным программным обеспечением с открытым исходным кодом, созданным в рамках статистического пакета программного обеспечения R (R Рабочая группа Разработки, 2011). Как бесплатное программное обеспечение исходный код Rattle и R доступен всем без ограничения. Исходный код Rattle написан на С и всем разрешено, и действительно поощряется, рассмотрение исходного кода для обучения, его понимания, проверки и расширения.

Организация материала

Книга состоит из следующих частей.

Часть 1. Введение в предсказательное моделирование изложено в главах 1—11. В этой части книги сжато, но достаточно подробно на описательном уровне рассматриваются основные понятия предсказательного моделирования. Необходимость этой части проистекает из того, что авторы Rattle не объясняют смысл и взаимодействие различных частей своей системы. Изучение первой части позволит осмысленно подобрать в Rattle инструменты для решения конкретно Вашей задачи.

Часть 2. Краткое описание Rattle изложено в главе 12. Эта часть полезна как на этапе первоначального знакомства с Rattle, так и на этапе постоянного использования в качестве краткого справочника.

Часть 3. Полное описание Ratlle 13—29. Эта часть книги представляет собой перевод руководства по Rattle. К авторскому руководству добавлены примеры для рынка Форекс, а также приведены переводы синтаксиса команд R, которые использует Rattle.

Текст книги содержит большое количество программного кода на языке R и MQL4 торгового терминала МТ4 разработки MetaQuotes Software Corp. Это программный код по праву можно считать еще одной частью книги. При желании изложенный в книге код, а также необходимые для него данные, читатель может использовать для повторения, подражания или модификации. Программный код и данные доступны читателю на ЯндексДиск по ссылке https://yadi.sk/d/_pRbllwlHpxnMQ.

Текущее состояние

Новые версии R публикуются два раза в год — в апреле и октябре. R имеет несколько миллионов пользователей, что гарантирует очень малое количество ошибок в коде. Система статистики и графики R очень популярна, быстро расширяется за счет пакетов, имеет обширную информационную поддержку в виде публикаций, учебников и монографий.

Примеры, включенные в эту книгу, используют версию 3.1.1 R и версию 3.0.2 r169 Rattle. Rattle — развивающийся пакет и, хотя понятия остаются, Подробности меняются. Поэтому не следует удивляться, если скриншоты, приведенные в этой книге, будут отличаться от Ваших скриншотов.

Часть 1. Введение в предсказательное моделирование

Первая часть книги является введением в идеологию предсказательного моделирования. В этой части книги сжато, но достаточно подробно на описательном уровне рассматриваются основные понятия предсказательного моделирования.

Первая часть книги дополняет техническую документацию по Rattle, так как авторы Rattle предполагают, что пользователь их продукта знаком с терминологией, проблемами и инструментами, существующими в области предсказательного моделирования.

Первая часть книги будет полезна всем без исключения проектировщиками предсказательных моделей вообще, а не только пользователям Rattle. Излагаемые в первой части материалы охватывают более широкий круг вопросов, чем необходимо для работы с Rattle, готовя читателя к использованию других, аналогичных, но более развитых инструментов для построения предсказательных моделей.

1. Введение

1.1. Анализ, прогноз, предсказание

На финансовых рынках будем различать следующий набор действий: анализ, прогноз и предсказание.

Анализ позволяет ответить нам на вопрос: почему так произошло? Например, можно поставить вопрос: почему произошло падение курса доллара по отношению к евро? Без анализа прошлого, без анализа исторических данных невозможен переход к последующим этапам — прогнозу или предсказанию.

Прогноз. Значение слова «прогноз» буем понимать так, как это понимается в R под словом «forecast» — для прогноза следующего значения используется предыдущее значение, полученное в результате предыдущего шага прогноза. Пакет forecast является примером такого понимания значения слова «прогноз».

Предсказание. Значение слова «предсказание» будем понимать в смысле универсальной функции predict — предсказание будущего на любое число шагов вперед с использованием имеющихся данных.

В данной книге исторические данные используются для обучения моделей, которые в последующем используются для предсказания будущего.

1.2. Процесс предсказательного моделирования

Существует несколько аспектов в процессе построения модели, которые следует обсудить далее, особенно новичкам в предсказательном моделировании.

Технология предсказательного моделирования выглядит следующим образом:

— на основе некоторого набора исходных данных производится обучение модели;

— в последующем обученная модель используется для предсказания целевой переменной на новом наборе данных;

— в зависимости от того, чему мы учили модель: предсказывать целевую переменную на сегодня, на завтра или на n шагов вперед, мы и получим соответствующее предсказание.

1.2.1. Разделение данных

То, как выделяются данные определенным этапам (например, обучение модели, оценка результативности), является важным аспектом моделирования. Наш главный интерес, к примеру, состоит в предсказании тренда на новых данных, которые отсутствуют в момент обучения модели. Это означает, что до некоторой степени необходимо проверить, как хорошо модель экстраполирует на новых котировках. Если бы мы интересовались предсказанием на тех же самых данных (то есть, интерполяцией), то можно было бы взять простую случайную выборку данных. То, как определены набор данных для обучения и наборы данных для тестирования и проверки, должно отразить применение модели.

Сколько данных должно быть выделено обучающему набору и тестовому? Это обычно зависит от ситуации. Если пул данных небольшой, решения разделения данных могут быть критическими. Небольшой (десятки наблюдений) тестовый набор исходных данных ограничил бы суждения о результативности модели. В этом случае, уверенность в результатах могли бы предоставить методы ресемплирования, которые могли бы решить проблему.

На финансовых рынках достаточно часто доступны большие наборы данных. Обычно доступны наборы данных с несколькими тысячами наблюдений, например, цен валютных пар. Казалось бы, что на финансовых рынках отсутствуют проблемы небольших по объему исходных данных. Однако это не так. К примеру, мы обучили модель на растущем рынке, а тестируем на падающем рынке, и выясняется, что модель дает убыток на этом тестовом наборе данных. На этом примере мы видим, что проблема в обязательности разделения котировок для обучения и тестирования остается и для больших наборов данных, так как при разделении необходимо обеспечить примерно равное количество «лонгов» и «шортов».

1.2.2. Целевая переменная

Несмотря на кажущуюся простоту, выбор цели предсказания и данных, которые материализуют эту цель в виде набора цифр, носит краеугольный характер.

Обратимся к идее предсказывать тренд. Эта идея опирается на желание торговать тренды.

Из определения тренда: «тренд растущий, если следующая цена больше предыдущей цены» и, наоборот, для падающего тренда. Из определения следует, что необходимо предсказывать цену валютной пары. Было 1.3500 для eurusd, предсказали 1.3550 — растущий тренд, покупаем.

Но базовыми приказами являются приказы «купить» и «продать», а мы предсказали величину цены. А величина цены используется, к примеру, в торговых системах на пробой уровня. Чтобы реализовать план по торговле трендов, надо будет произвести дополнительное действие по сравнению цен. При этом очевидно, что мы предсказываем не то, что собирались торговать!

Поэтому, если мы собрались делать трендовую торговую систему, то модель должна сразу предсказывать тренд. Учить модель надо трендам, целевая переменная должна принимать только два значения «купить» и «продать» или в закодированном (категориальном) виде «1» и «-1».

Можно уточнить целевую переменную, имеющую два значения за счет того, что неплохо бы предсказывать и боковики, т.е. иметь целевую переменную, принимающую значения «купить», «продать» и «вне рынка». Или закодировав эти значения как: «1», «-1» и «0».

Различие моделей, которые используют совокупность исходных данных для вычисления будущей величины цены финансового актива, и моделей, которые относят совокупность исходных данных к некоторому классу, является принципиальным. Первый тип моделей относится к регрессионным моделям, а второй тип моделей относится к классификационным моделям.

По предсказательным моделям регрессионного типа вычисляется значение некоторой величины в будущем, и когда это будущее наступит, то у нас будет фактическое значение этой предсказанной величины.

По предсказательным моделям классификационного типа вычисляется класс, к которому будет отнесена совокупность поступивших на момент предсказания исходных данных.

Рассмотренные варианты не исчерпывают всего разнообразия целевых переменных, возможных на финансовых рынках. Но вывод из данного раздела: целевая переменная должно точно соответствовать целям торговой системы.

1.2.3. Независимые переменные

Независимые переменные, в дальнейшем предикторы, независимы в том смысле, что поступают в модель извне, являются внешними, измеряемыми переменными, или переменными, вычисленными на основе этих внешних переменных. Например, любые экономические, финансовые данные, включая котировки валютных пар, являются независимыми переменными, так как их значения образуются в результате деятельности субъектов на рынке. К этой же категории переменных относятся и индикаторы из технического анализа, которые вычисляются на основе котировок.

Выбор независимых переменных не менее важен, чем выбор целевой переменной. Более того, именно выбор независимых переменных определяет успешность моделирования. Основное время, затраченное на разработку модели, уходит как раз на анализ и подбор набора независимых переменных.

Этот вопрос рассмотрим в отдельных разделах.

1.2.4. Оценка результативности модели

Тип модели предполагает разные типы оценок.

Для регрессионных моделей — это ошибка предсказания, полученная как разность между предсказанной и фактической величиной (к примеру, RMSE).

Для классификационных моделей — это рассогласование, полученное как совпадение/несовпадение фактических и предсказанных классов.

1.2.5. Выбор модели

Наличие оценки результативности модели позволяет выбрать лучшую модель. Это можно сделать, если «лучшая» модель сильно отличается от своих конкурентов. Если это не так, то, отбросив «худшую» модель при ее наличии, можно сделать предсказание, используя имеющиеся предсказания моделей в качестве предикторов для окончательного предсказания.

1.2.6. Итоги

В первом приближении создание модели кажется ясным: выбираем метод моделирования, учим модель на наборе данных обучения — все готово, можно предсказывать.

Вам очень повезет, если столь просто удастся создать надежную, устойчивую модель, работающую на новых наблюдениях.

Чтобы получить модель, имеющую примерно одинаковые оценки результативности вне набора обучения следует сначала понять данные и цель моделирования. После понимания данных и целей, можно предварительно обработать и разделить данные. После этих шагов можно начинать создание, оценку и выбор моделей. Только после того, как эти шаги сделаны, мы, наконец, начнем создание, оценку и выбор моделей.

Существует целый ряд общих причин неудачности предсказательных моделей:

— не адекватная предварительная обработка данных;

— не адекватная проверка модели;

— неоправданная экстраполяция (применение к данным, которые имеют слабое отношение к обучающему набору);

— наиболее важное: переобучение модели на обучающем наборе данных.

1.3. Терминология

Предсказательное моделирование является одним из многих наименований, которые относятся к процессу выявления отношений внутри данных для предсказания желаемого результата. Машинное обучение, искусственный интеллект, распознавание образов, интеллектуальный анализ данных, предсказательная аналитика — много научных областей сделало вклад, что привело к синонимии разных понятий.

Предсказательное моделирование — это процесс, с помощью которого модель создает, выбирает или пытается сделать лучшее предсказание вероятности результата.

Набор данных — это общий и расплывчатый термин.

Набор данных на внешнем носителе — это файл данных по тексту книги. По расширению файла можно судить о кодировке и, частично, о структуре файла. В пакете Rattle допустимы разные файлы. Наибольший интерес для нас будут представлять файлы со следующими расширениями:

— .txt — обычный текстовый файл;

— .csv — текстовый файл Excel;

— .RData — файл R, в котором хранится рабочая область.

Набор данных в памяти — это некоторая совокупность данных, имеющая структуру. В терминах R — это вектор, матрица, фрейм данных или совокупность этих данных.

Матрица (редко) и фрейм данных в Rattle представлены таблицей, имеющей следующий вид:

Термины выборка (sample), наблюдение (observation), пример, экземпляр (instance) относится к отдельной строке данных. Термин sample также может относить к подмножеству наблюдений, которые объединены, например целью последующего использования — обучающая выборка или обучающий набор данных. Значение термина выборка будет понятно из контекста употребления термина.

Обучающий набор содержит данные, которые использовались для обучения модели, в то время как тестовый и проверочный наборы используются исключительно для оценки результативности модели.

Предикторы, независимые переменные, атрибуты или дескрипторы являются данными, которые используются в качестве входных переменных в уравнении предсказания. На рис.1.1 показаны три предиктора, которые играют роль в модели «входных переменных».

Результат, зависимая переменная, целевая переменная, класс, отклик (response) относится к результирующему событию или количеству, которое предсказывается.

У числовой переменной есть значение, которое является целым числом или вещественным числом, такими как цена валютной пары, объем торгов, процентная ставка. Числовые переменные также известны как количественные переменные. Числовые переменные могут быть дискретными (целыми числами) или непрерывными (действительными). Например, котировка валютной пары. У числовой переменной обычно имеется числовой масштаб. Для валютной пары eurusd числовой масштаб — это диапазон от 0.5 до 2.0, в который укладываются все имевшие место значения цен на эту валютную пару. Совершенно другой масштаб у валютной пары usdjpy — величины цен на эту валютную пару почти на два порядка больше, чем на eurusd.

Категориальные (categorical) данные, известные также как номинальные атрибуты, качественные данные, факторы имеют значения, которые не имеют масштаба. «Лонг/шорт», день недели являются примерами таких данных. «Лонг» не больше и не меньше «шорта». Категориальная переменная, которая имеет два значения, как у нас — (лонг, шорт) называют бинарной (двоичной) переменной. Категориальная переменная «день недели» имеет семь значений.

Категориальные переменные могут быть упорядочены, как в нашем примере Weekdays (дни недели). Понедельник не больше и не меньше вторника, но может быть важным для модели, чтобы ей было известно, что вторник всегда следует после понедельника.

Построение модели, обучение модели, тренировка модели или оценка параметров — все это относится к процессу определению параметров в уравнении модели.

1.4. Используемые наборы данных

Далее по тексту будут использоваться следующие наборы данных:

audit набор данных, поставляемый в составе дистрибутива Rattle.

weather набор данных, поставляемый в составе дистрибутива Rattle.

kot60_110101_131231_UE. txt

На основе регрессионной модели попытаемся сделать «типичный мультивалютник»:

— целевая переменная — EURUSD;

— предикторы — GBPUSD, USDCHF, USDJPY, EURGBP, USDCAD.

zz_1_5.RData

Для классификационной модели создан искусственный разнообразный набор предикторов, которые должны продемонстрировать возможности моделей по предсказанию трендов:

— целевая переменная (три варианта) — тренд;

— предикторы — день недели, час дня, EURUSD, приращение EURUSD, macd, macd (13), macd (26), macd (39), приращение macd (13), macd (26), macd (39)), RSI (14), RSI (21), RSI (28), стеллажирование на 8 уровней (RSI (14), RSI (21), RSI (28)), MA (13), MA (26), MA (52), приращение (MA (13), MA (26), MA (52)).

Описание каждого набора данных приведено в Приложении В. Для zz_1_5.RData приведен скрипт на R, который формирует этот набор из набора kot60_110101_131231_UE. txt

2. Предварительная обработка данных

Методы предварительной обработки данных обычно состоят в добавлении, удалении или преобразовании данных обучения. Хотя мы интересуемся методами моделирования, подготовка данных может оказаться решающей для предсказательной возможности модели. У различных моделей есть разная чувствительность к типу предикторов в модели; как предикторы входят в модель также важно. Преобразования данных для уменьшения воздействия асимметрии данных или выбросов, могут привести к значимым улучшениям результативности. Выделение предикторов является одним из эмпирических методов для создания фиктивных переменных, которые являются комбинациями многих предикторов. Также могут быть эффективными дополнительные, более простые стратегии, такие как удаление предикторов.

Потребность в предварительной обработке данных определяется типом используемой модели. Некоторые алгоритмы, такие как основанные на моделях деревьев, нечувствительны к характеристикам данных предиктора. Другие, как линейная регрессия, не являются таковыми. В этой главе обсужден целый ряд возможных методологий.

Эта глава обрисовывает в общих чертах подходы к обработке данных без учителя: целевая переменная не рассматривается методами предварительной обработки. В других главах обсуждаются методы с учителем, в которых используется целевая переменная для предварительной обработки данных. Например, модели частных наименьших квадратов (PLS) — по существу является версией с учителем анализа главных компонентов (PCA). Мы также описываем стратегии удаления предикторов, не рассматривая, как переменные могли бы быть связаны с целевой переменной.

То, как предикторы закодированы, может оказать значительное влияние на результативность модели. Например, использование комбинаций предикторов может иногда быть более эффективным, чем использование отдельного значения. Отношение двух предикторов может быть более эффективным, чем использование двух независимых предикторов. Часто больше всего эффективное кодирование данных возникает из понимания разработчиком моделируемой проблемы, и таким образом, не получено из какого-либо математического метода.

Обычно есть несколько различных методов для кодирования конкретного предиктора. В качестве примера приведем представление даты, которая может быть представлена многими способами:

— число дней, начиная со ссылочной даты;

— отдельно месяц, год и день недели как отдельные предикторы;

— номер дня в году;

— была ли дата в пределах торговой сессии (в противоположность праздничным дням или новогодним каникулам).

В нашем примере принято следующее решение по дате:

— день недели взят вместо календарной даты, так как интенсивность торгов разная в разные дни недели;

— номер часа взят вместо часа (совпадает со временем), так как интенсивность торгов разная в разное время суток.

«Корректная» разработка предиктора зависит от нескольких факторов. Во-первых, некоторые кодировки могут быть оптимальными для некоторых моделей и плохими для других. Например, основанные на дереве модели разделят данные на два или больше стеллажей. Как будет показано позднее, некоторые модели содержат встроенный выбор предикторов, означающий, что модель будет включать только предикторы, которые помогут максимизировать точность. В этих случаях может привередничать модель, какое представление данных является лучшим.

Отношение между предиктором и целевой переменной — следующий фактор. Существует, к примеру, логистическая модель, которая дает оценку вклада каждого предиктора в вычисление класса (модели классификации). Тем не менее, остаются крайне важным содержательное понимание связи между предикторами и целевой переменной.

Как со многими вопросами статистики, ответ на вопрос «какие методы разработки предикторов являются лучшими?» выглядит как: это зависит. Определенно, это зависит от используемой модели и истинного отношения с целевой переменно.

2.1. Преобразование отдельных предикторов

Преобразования предикторов могут быть необходимы по нескольким причинам. У некоторых методов моделирования могут быть строгие требования, такие как необходимость общего масштаба предикторов. В других случаях создание хорошей модели может быть затруднено определенными характеристиками данных, например, выбросами. В книге обсуждается центрирование, масштабирование и преобразования асимметрии.

2.1.1. Центрирование и масштабирование

Центрирование и масштабирование предикторов является наиболее понятным преобразованием данных. Для центрирования предиктора среднее значение предиктора вычитается из всех значений. В результате центрирования у предиктора средняя равна нулю. Точно так же, для совместимости масштабов данных, каждое значение предиктора делится на его стандартное отклонение. Масштабирование данных приводит к значениям с отклонениями в размере одного стандартного отклонения. Эти манипуляции обычно используются для улучшения числовой устойчивости некоторых вычислений. Некоторые модели, к примеру PLS, извлекают выгоду из предикторов, имеющих общий масштаб. Единственным минусом этих преобразований является потеря интерпретируемости отдельного значения, так как данные больше не находятся в исходных масштабах.

2.1.2. Преобразования для исключения асимметрии

Другая общая причина преобразований состоит в удалении исходной асимметрии — скоса. Распределение без скоса — это то, что примерно симметрично. Это означает, что уменьшение вероятности по обе стороны от среднего распределения примерно равно. У распределений с правым скосом есть большое количество точек на левой стороне распределения (меньшее значение), чем на правой стороне (большее значение).

Общее правило большого пальца в рассмотрении скошенных данных состоит в том, что если максимальное значение превосходит минимальное значение более 20 раз, то имеется значимая асимметрия. Кроме того, статистика асимметрии может использоваться в качестве диагностики. Если распределение предиктора будет примерно симметрично, то значение асимметрии будет близко к нулю. Поскольку распределение становится более отклоненным справа, то статистика асимметрии становится больше. Точно так же, поскольку распределение становится более отклоненным влево, то значение становится отрицательным.

Логарифмирование может помочь удалить скос.

Вне рамок Rattle, но из инструментов R, имеется преобразование Box-Cox (1964), которые предлагают семейство адаптивных преобразований. Эту процедуру можно применить вне Rattle к каждому предиктору, имеющими значения, больше нуля.

2.2. Преобразование групп предикторов

Эти преобразования действуют на группы предикторов, обычно все рассматриваемого множества. Наиболее значимые методы направлены на решение проблем выбросов и уменьшения размерность данных.

2.2.1. Преобразования, решающие проблему выбросов

Мы обычно определим выбросы как наблюдения, которые исключительно далеки от основных данных. При определенных предположениях есть формальные статистические определения выброса. Даже с полным пониманием данных бывает сложно определить выбросы. Однако можно выявить необычное значение, глядя на рисунок. Если одно или более значений предиктора попадает под подозрение, сначала нужно подумать о допустимости этих значений. Необходимо соблюдать особую осторожность и не торопиться удалять или изменять значение, особенно при небольшом объеме выборки.

Есть несколько предсказательных моделей, которые являются устойчивыми к выбросам. Модели классификации на основе дерева создают разделения учебных данных, и уравнение предсказания — ряд логических операторов таких как, «если предиктор A больше чем X, то предсказываем класс Y», таким образом, выброс обычно не имеет исключительного влияния на модель. Машины опорных векторов для классификации обычно игнорируют часть наблюдений набора данных обучения, создавая уравнение предсказания. Исключенные наблюдения могут быть далеко от границы решения и за пределами основных данных.

Если используемая модель чувствительна к выбросам, то существует преобразование данных, которое может минимизировать задачу — это пространственный знак.

2.2.2. Снижение объема данных и выделение предикторов (PCA)

Методы снижения объема данных — другой класс преобразований предикторов. Эти методы сокращают данные, генерируя меньшее множество предикторов, которые стремятся получить большую часть информации из исходных переменных. Таким образом, можно использовать меньше переменных, которые обеспечивают разумную точность для исходных данных. Для большинства методов снижения объема данных новые предикторы — функции исходных предикторов; поэтому, все исходные предикторы все еще необходимы, чтобы создать суррогатные переменные. Этот класс методов часто вызывают экстракцией сигнала или методами выделения предикторов.

Алгоритм PCA — обычно используемый метод снижения объема данных. Этот метод стремится найти линейные комбинации предикторов, называемых главными компонентами (PC), которые содержат наибольшую возможную дисперсию. Первая PC определена как линейная комбинация предикторов, которая получает большую часть изменчивости всех возможных линейных комбинаций. Затем, последующие PC получены так, что эти линейные комбинации получают остающуюся изменчивость, также будучи некоррелированным со всеми предыдущими PC.

Основное преимущество PCA и причина, что он сохранило свою популярность как метод снижения объема данных, состоит в том, что он создает компоненты, которые не коррелированы. Как отмечалось ранее, некоторые предсказывающие модели предпочитают, чтобы предикторы были не коррелированы (или, по крайней мере, с низкой корреляцией) для улучшения устойчивости модели. Используя РСА предварительная обработка создает новые предикторы с требуемыми характеристическими.

Хотя PCA поставляет новые предикторы с требуемыми характеристиками, он должен использоваться с пониманием и вниманием. Особенно практики должны понять, что PCA ищет установленное в предиктор изменение без отношения к дальнейшему пониманию предикторов (то есть, измерительные весы или распределения) или к знанию целей моделирования (то есть, целевой переменной). Следовательно, без надлежащего руководства, PCA может генерировать компоненты, которые суммируют характеристики данных, которые не важны глубинной структуре данных и также к окончательной цели моделирования.

Поскольку PCA ищет линейные комбинации предикторов, которые максимизируют изменчивость, он будет естественно сначала брать предикторы, у которых есть больше изменения. Если исходные предикторы находятся в исходных масштабах, которые отличаются по порядкам величины (например, котировки EURUSD и USDJPY), то японская йена будет довлеть над парой EURUSD. Это означает, что веса PC будут больше для йены. Кроме того, это означает, что PCA будет фокусировать свои усилия на идентификации структуры данных, основанной на исходных масштабах, а не основанной на важных отношениях среди данных для решаемой задачи.

Для большинства наборов данных предикторы имеют разные масштабы. Кроме того, предикторы, возможно, имеют скошенные распределения. Следовательно, для исключения в PCA избегать суммирования исходных различий и информации о масштабе предикторов лучше сначала преобразовывать предикторы, центрировать и масштабировать предикторы до выполнения PCA. Центрирование и масштабирование позволяют PCA найти базовые отношения в данных, игнорируя влияние исходных измеренных величин.

Вторая отрицательная черта PCA состоит в том, что он не рассматривает цель моделирования или переменную отклика при суммировании изменчивости. Поскольку PCA слепой к отклику, это — неконтролируемый метод. Если предсказательное отношение между предикторами и откликом не будет соединено с изменчивостью предикторов, то полученные PC не будут предоставлять подходящему отношению отклик. В этом случае, контролируемый метод такой, как PLS, создаст компоненты, одновременно учитывая соответствующий отклик.

Аналогично PCA, PLS находит линейные комбинации предикторов. Эти линейные комбинации обычно называют компонентами или скрытыми переменными. В то время как линейные комбинации PCA выбираются с целью максимально суммировать изменчивость пространства предикторов, линейные комбинации предикторов в PLS выбираются с целью, чтобы максимально суммировать ковариацию с откликом (целевой переменной). Это означает, что PLS находит компоненты, которые максимально суммируют изменение предикторов, одновременно требуя, чтобы эти компоненты имели максимальную корреляцию с целевой переменной. Поэтому PLS получает компромисс между целью уменьшения размерности пространства предикторов и предсказательного отношения с целевой переменной. Другими словами PLS относится к контролируемой процедуре уменьшения размерности.

Как только выбрано соответствующие преобразования предикторов, то можно применить PCA. Для моделей со многими предикторами следует принять решение о количестве главных компонент, подлежащих использованию. Этот вопрос решается просто при использовании средств R: результат вычислений сопровождается вспомогательной информацией в виде накопленной изменчивости. Обычно берется величина 95% и выбирается такое количество главных компонент, которые совместно накопили такую изменчивость исходных данных.

При разложении исходного набора предикторов на главные компоненты указывается вес каждого предиктора в конкретной главной компоненте. Этот вес называется нагрузкой. Нагрузка близкая к нулю указывает, что этот конкретный предиктор не очень-то важен этому компоненту. Если среди всех отобранных главных компонент окажется предиктор с небольшой нагрузкой, то этот предиктор является кандидатом на его исключение из модели.

2.3. Обработка пропущенных значений

При включении в мультивалютные модели валютных пар с разной ликвидностью, особенно на младших тайм фреймах, может возникнуть ситуация отсутствия значений одной из валютных пар при наличии значений в других валютных парах.

Могут быть и другие причины. Например, ведение торгов в разное время по разным валютным парам. И это не единственные причины возникновения пропущенных значений на финансовых рынках.

Важно понять, причину пропуска значения. Прежде всего, важно знать, как связано пропущенное значение с целевой переменной. В нашем примере трендовой торговой системы можно рассмотреть две ситуации:

— отсутствуют котировки внутри торговой сессии. Можно предположить, что отсутствие значений не влияет на тренды, имеющиеся в данный момент на рынке.

— отсутствуют значения вне торговой сессии, например в выходные дни. Известно, что в выходные дни могут происходить события, которые в случае торгов повлияли бы на котировки.

Заполнение пропущенных значений было интенсивно изучено в статистической литературе, но в контексте проверки гипотез процедурами тестирования при наличии пропущенных данных. Это — отдельная проблема. Для предсказательных моделей мы обеспокоены точностью предсказаний вместо того, чтобы делать допустимые выводы.

Заполнение пропущенных значений — это только другой уровень моделирования, где мы пытаемся оценить значение предикторов, основанных на других значениях предиктора. Соответствующая схема заполнения состоит в использовании набора данных обучения для создания модели заполнения для каждого предиктора в наборе данных. До обучения самой предсказательной модели или предсказания целевой переменной заполняются отсутствующие значения предикторов. Заметим, что этот дополнительный уровень моделей увеличивает неопределенность.

Если число предикторов, на которые влияют отсутствующие значения, небольшое, анализ отношений между предикторами — хорошая идея. Например, могут использоваться такие методы как визуализация или PCA, чтобы определить, есть ли прочные отношения между предикторами. Если переменная с отсутствующими значениями чрезвычайно коррелирована с другим предиктором, у которого есть немного отсутствующих значений, используемая модель может часто быть эффективной для заполнения.

Одним из популярных методов заполнения является модель K-ближайших соседей. Эта модель по значения ближайших соседей может оценить значение отсутствующих значений предиктора.

2.4. Удаление предикторов

Есть потенциальные преимущества для удаления предикторов до моделирования. Во-первых, меньшее количество предикторов означает уменьшение вычислительной сложности и времени вычислений. Во-вторых, если два предиктора чрезвычайно коррелированы, это подразумевает, что они измеряют ту же самую базовую информацию. Удаление одного из них не должно ставить под угрозу результативность модели и могло бы привести к более экономной и поддающейся толкованию модели. В-третьих, некоторым моделям могут нанести вред предикторы с вырожденными распределениями. В этих случаях может быть значимое уточнение в результативности модели и/или устойчивости без проблематичных переменных.

2.4.1. Корреляции между предикторами

Коллинеарность — технический термин для ситуации, где у пары предикторов есть существенная корреляция друг с другом. Также возможно одновременно иметь отношения между многими предикторами (называется мультиколлинеарность).

Если набор данных состоит из слишком большого числа предикторов для визуального исследования, то можно использовать такие методы как PCA для установления характеристик проблемы. Например, если первый основной компонент учитывает большой процент дисперсии, то возникают подозрения в существовании единственной переменной для модели.

Вообще, есть серьезные основания исключить чрезвычайно коррелированные предикторы. Во-первых, избыточные предикторы часто более усложняют модели, чем добавляют информации к ней. Использование чрезвычайно коррелированных предикторов в таких моделях, как линейная регрессия, может привести к очень нестабильным моделям, числовым ошибкам, и ухудшить предсказательную результативность.

У классического регрессионного анализа есть несколько инструментов для диагностики мульти коллинеарности для линейной регрессии. Так как коллинеарные предикторы могут воздействовать на оценку дисперсии параметра в этой модели, то может использоваться статистика, называемая фактором инфляции дисперсии (VIF), для выявления предикторов с коллинеарностью. Вне линейной регрессии этот метод может оказаться не применимым по нескольким причинам: он разрабатывался для линейных моделей и, в то время как он действительно идентифицирует коллинеарные предикторы, он не определяет предиктор, подлежащий удалению для решения проблемы.

Далее будет более подробно рассмотрена значимость предикторов и их выбор.

2.5. Добавление предикторов

Если предиктор категориальный, такой как день недели или время суток, то обычно разделяют предиктор в ряд более определенных переменных. Например, день недели имеет 7 категорий (или 5 категорий, соответствующих рабочим дням).

Обычно вместо одного предиктора вводят 7 «фиктивных» предикторов, каждый из которых соответствует одному дню недели. Обычно этот подход улучшает интерпретируемость модели. Кроме этого некоторые модели лучше работают с бинарными предикторами.

2.6. Группировка предикторов

Будем различать два варианта понятия «группировки предикторов»:

— группировка значений отдельного предиктора;

— группировка нескольких предикторов в один.

В первом случае любой числовой предиктор можно упростить путем разбивки его на несколько категорий или стеллажей. Например, возьмем индикатор RSI, который обычно используется для идентификации разворотов трендов. Разделим значения этого индикатора на 4 части, и вместо числовых значений индикатора будем использовать числа 1,2,3 и 4, где числа 1 и 4 будут соответствовать разворотам тренда. Такой вид укладывания в стеллаж соответствует основной идеи нашей торговой системы — трендовой торговли.

Во втором случае все множество предикторов, которое используется в модели скомпонуем в меньшее число предикторов так, чтобы это меньшее число объясняло большую часть изменчивости всех предикторов. Данный подход известен как «анализ главных компонент» и был рассмотрен выше.

Компоненты, получаемые по алгоритмам PCA (PLS) позволяет использовать существенно меньшее количество новых предикторов. Каждая дополнительная главная компонента объясняет все меньшее количество изменчивости. Если просуммировать изменчивость всех новых предикторов, то сумма будет равна единице, а где-то в середине будет некоторое количество предикторов, которое будет объяснять, например, 95% изменчивости. Обычно для рынка Форекс можно уменьшить количество предикторов примерно в три раза.

2.6. Функции R

Приведем некоторые функции, которые могут быть использованы при работе над данным разделом.

Приведено название функции, а в скобках название пакета, в котором функция расположена. Для использования функция необходима загрузка пакета, а если его еще нет, то и установка.

Если названия пакета не приведено — это означает, что функция имеется в базовом пакете, и не требуется предварительная загрузка пакета.

skewness (e1071)

асимметрия (скос)

boxcox (MASS)

преобразование Box-Cox. Оценивает λ, но преобразование не выполняет.

BoxCoxTrans (caret)

преобразование Box-Cox с преобразованием данных

prcomp

вычисляет главные компоненты (РСА)

preProcess (caret)

предварительная обработка

cor

корреляция

findCorrelation

возвращает список переменных, рекомендованных для удаления из-за сильной корреляции

dummyVars (caret)

создает фиктивные переменные

3. Переобучение и настройка модели

Многие современные классификационные и регрессионные модели высоко адаптируемы; они способны к моделированию комплексных отношений. Однако они могут очень легко отобразить некие случайности в экономическом процессе. Как говорят — отобразить шум. Без методологического подхода к оценке моделей разработчик модели может узнать о проблеме слишком поздно.

Переобучение (сверх подгонка) — широко известная проблема предсказательных моделей вообще и в области финансов в частности. Фактически переобучение отображает базовую проблему моделирования: модель должна отображать некие основные моменты моделируемого процесса, модель должна быть не слишком груба, но и не слишком точна, чтобы она могла находить основные моменты на новых данных, а не давать ложные сигналы, принимая шум за образцы данных.

К сожалению, отсутствуют формальные критерии переобучения. Поэтому приходится руководствоваться некими эмпирическими критериями, которые дадут практическую ценность модели. Эти эмпирические критерии состоят в том, чтобы дать разработчику предсказательной модели уверенность, что поведение модели на обучающем наборе данных и на данных вне этого обучающего набора, будет примерно одинаковым.

Без этого доверия предсказания модели бесполезны.

3.1. Проблема переобучения

Существует много методов, которые могут изучить структуру ряда данных так хорошо, что при применении модели к данным, на которых была создана модель, она правильно предсказывает каждое значение. В дополнение к изучению общих образцов в данных модель также изучила характеристики отдельного шума каждой выборки. Эта модель, как говорят, переобучена, и с плохой точностью предскажет целевую переменную на новой выборке.

Изначально, мы учим модель на наборе данных обучения и по результатам обучения получаем некую величину ошибки для регрессионных моделей, или рассогласование для классификационных моделей.

Уже на этом этапе возможно переобучение модели: оценка слишком оптимистична, например, ошибка подгонки менее 5%. Да и ошибка подгонки в 10% должна насторожить!

В этих ситуациях очень важно иметь инструмент для определения переобученности модели на учебных данных.

3.2. Настройка модели

У многих моделей есть важные параметры, которые не могут быть непосредственно оценены на данных. Например, в модели классификации K-ближайшие соседи предсказание основано на K самых близких точек данных в наборе данных обучения.

Очевиден вопрос: сколько соседей должно использоваться. Выбор слишком большого числа соседей может переобучить модель к отдельным точкам набора данных обучения, в то время как слишком малое число соседей может быть не достаточно чувствительными для получения разумной результативности. Этот тип параметра модели называется настраиваемым параметром, так как отсутствует аналитическая формула, доступная для вычисления соответствующего значения.

Практически у всех предсказательных моделей есть, по крайней мере, один настраиваемый параметр. Так как многие из этих параметров управляют сложностью модели, плохие варианты для значения могут привести к переобучению.

Есть разные подходы к поиску лучших параметров. Общий подход, который можно применить к почти любой модель, должен определить ряд значений кандидата, генерировать надежные оценки модели через значение кандидатов, а затем выбрать оптимальную модель.

Как только множество кандидатов значений параметра было выбрано, то следует получить правдоподобные оценки результативности модели. Результативность вне-выборки суммируется в профиль результативности, который затем используется для определения заключительных настраиваемых параметров. Затем создаем заключительную модель со всеми учебными данными, используя выбранные настраивающие параметры.

При построении моделей доступны подходы, такие как генетические алгоритмы или симплексные методы поиска, которые могут найти оптимальные настраиваемые параметры. Эти процедуры алгоритмически определяют соответствующее значение для настройки параметров и выполняют итерации, пока они не достигают установок параметров с оптимальной результативностью. Эти методы имеют тенденцию оценивать большое количество моделей кандидата и могут превосходить определенное множество настраиваемых параметров, если результативность модели может быть эффективно вычислена.

Как ранее обсуждалось, очевидный коэффициент ошибок может произвести чрезвычайно оптимистические оценки результативности. Лучшим является подход, который проверяет модель на выборках, не использованных для обучения.

Оценивая модель на тестовом наборе, размер набора тестов, возможно, должен быть большим.

Альтернативный подход к оценке модели на единственном тестовом наборе состоит в ресемплирования набора данных обучения. Этот процесс использует несколько измененных версий набора данных обучения, чтобы создать многоуровневые модели и затем использует статистические методы, чтобы обеспечить честные оценки результативности модели (то есть, не чрезмерно оптимистичные).

3.3. Разделение данных

Теперь, когда мы обрисовали в общих чертах процедуру для поиска оптимальных настраиваемых параметров, вернемся к обсуждению основы процесса: разделение данных.

Несколько общих шагов в создании модели:

— предварительная обработка данных предиктора;

— оценка параметров модели;

— выбор предикторов для модели;

— оценка результативности модели;

— правила предсказания класса точной настройки (через кривые ROC, и т.д.).

Одно из первых решений при моделировании, которое следует принять, какие наборы данных или их части будут использоваться для оценки результативности. Идеально, модель должна быть оценена на выборках, которые не использовались при создании или построении модели, так, чтобы они обеспечили несмещенную оценку эффективности модели. «Учебный» набор данных — общий термин для наблюдений, используемых для создания модели, в то время как набор данных «теста» или «проверки» используется для определения результативности.

Из литературы известно, что проверка, использующая единственный набор, может дать плохое решение. Могут использоваться методы ресемплирования, такие как кросс-проверка, для соответствующей оценки результативности модели, используя набор данных обучения. Хотя методы ресемплирования могут быть неправильно употреблены, они часто оценивают результативность точнее единственного набора, потому что они оценивают много вариантов данных. Если тестовый набор считается необходимым, то есть несколько методов для разделения выборки.

В большинстве случаев желательно сделать наборы данных обучения и набор данных тестирования настолько гомогенными насколько возможно. Можно использовать методы случайных выборок для создания подобных наборов данных.

Самый простой способ разделить данные на набор данных обучения и тестовый набор состоит в том, чтобы взять простую случайную выборку. Это можно делать, если известно, что отношения классов примерно равны в обучающей и тестовой выборке. Когда у одного класса есть непропорционально большая частота по сравнению с другим, есть шанс, что распределение результатов может существенно отличаться между наборами данных обучения и тестовым набором.

Чтобы учесть результат при разделении данных, стратифицированная случайная выборка применяет случайную выборку в пределах подгрупп (таких как классы). Таким образом, получим более правдоподобную выборку, которая будет соответствовать распределению результата. Когда результат — число, подобная стратегия может использоваться; числовые значения разделены в подобные группы (например, минимум, среднее и максимум), и рандомизация выполняется в пределах этих групп.

Альтернативно, данные могут быть разделены на основе значения предиктора. Например, на максимальной выборке несходства. Несходство между двумя выборками может быть измерено многими способами. Самый простой метод использует расстояние между значением предиктора для двух наблюдений. Если расстояние небольшое, точки находятся в непосредственной близости. Большие расстояния между точками указывают на несходство. Чтобы использовать несходство в качестве инструмента для разделения данных, предположим, что тестовый набор создан из единственной выборки. Можно вычислить несходство между этой начальной выборкой и освобожденными выборками. Освобожденная выборка, которая является самой несходной, затем была бы добавлена к тестовому набору. Чтобы создать больше наборов тестовых наблюдений, необходим метод для определения несходства между группами точек (то есть, два в наборе тестов и освобожденных точках).

3.4. Методы ресемплирования

Методы ресемплирования для оценки результативности модели работают так: подмножество наблюдений используется для подгонки модели, и остающиеся выборки используются, чтобы оценить эффективность модели. Этот процесс повторен многократно, и результаты суммируются и выводятся итогом. Разности в методах обычно центрируются вокруг метода, по которому сделаны выборки из набора данных. Рассмотрим главные виды ресемплирования в следующих немногих подразделах.

3.4.1. k-кратная кросс-проверка

Выборки в произвольном порядке разделены в k множеств примерно равного размера. Производится подгонка модели на всех выборках кроме первого подмножества (названного первой сверткой). Вне-выборки выполняются предсказания этой моделью и используются для оценки критерии качества результата. Первое подмножество возвращается в набор данных обучения, и процедура повторяется со вторым подмножеством вне-выборки и так далее. В итоге оценивается K-передискретизованная результативность (обычно со средней и стандартной ошибкой), а используются выяснения отношений между настраиваемыми параметрами и формулой модели.

Небольшая разновидность этого метода выбирает k-разделов способом, который делает свертки сбалансированными относительно результата. Стратифицированная случайная выборка, обсужденная ранее, создает баланс относительно результата.

Другая версия, перекрестная проверка «пропуск одного» (LOOCV), является частным случаем, где k является числом наблюдений. В этом случае, так как только одна вне-выборка берется за один раз, заключительная результативность вычислена от k предсказаний от вне-выборок. Дополнительно, повторная k-кратная перекрестная проверки тиражирует процедуру многократно. Например, если бы 10-кратная перекрестная проверка была повторена пять раз, 50 различных вне-выборок использовались бы для оценки эффективности модели.

Выбор k обычно равняется 5 или 10, но нет никакого формального правила. Поскольку k становится больше, разница в размерах между набором данных обучения и подмножествами ресемплирования становится меньшей. Когда эта разность уменьшается, смещение метода становится меньшим (то есть, смещение меньше для k = 10, чем для k = 5). В этом контексте смещение — разность между оцененными и истинными значениями результативности.

Другой важный аспект метода ресемплирования — это неопределенность (то есть, дисперсия или шум). Несмещенный метод может оценивать корректное значение (например, истинная теоретическая результативность), но может привести к высокой неопределенности. Это означает, что повторение процедуры ресемплирования может произвести совсем другое значение (но сделанная достаточно много раз, она оценит истинное значение). k-кратная перекрестная проверка обычно имеет высокую дисперсию по сравнению с другими методами и, по этой причине, не может быть привлекательной. Нужно сказать, что для больших наборов данных обучения, потенциальные проблемы с дисперсией и смещением становятся незначительными.

С практической точки зрения большее значение k в вычислительном отношении обременительно. В экстремуме LOOCV больше всего в вычислительном отношении накладно, потому что требуется много подгонок модели как точки данных, и каждая подгонка модели использует подмножество, которое почти равно размеру набора данных обучения.

3.4.2. Повторные разделения для обучения/тестирования

Повторные разделения набора для обучения/тестирования также известны как «перекрестная проверка, «пропускают группу» или «перекрестная проверка Монте-Карло». Этот метод просто создает много разделений данных в моделировании и много предсказаний. Соотношением данных, входящих в каждое подмножество, управляют числом повторений.

Число повторений важно. Увеличение числа подмножеств имеет эффект уменьшения неопределенности в оценках результативности. Например, для получения грубой оценки результативности модели будет достаточно 25 повторений, если пользователь будет готов принять некоторую нестабильность в получающемся значении. Однако чтобы получить устойчивые оценки результативности необходимо выбрать большее число повторений (скажем 50—200). Это — также функция соотношения наблюдений, в произвольном порядке выделяемых множеству предсказаний; чем больше процент, тем больше повторений необходимо для уменьшения неопределенности в оценках результативности.

3.4.3. Бутстрэпинг

Выборка по бутстрэпингу — случайная выборка данных, взятых с заменой. Это означает, что, после того, как элемент данных выбран для подмножества, он все еще доступен для дальнейшего выбора. Выборка по бутстрэпингу равна исходному набору данных. В результате некоторые элементы будут представлены многократно в выборке бутстрэпинга, в то время как другие не будут выбраны вообще. Не выбранные элементы формируют выборку под названием «вне стеллажа». Для данной итерации ресемплирования в виде бутстрэпинга модель основана на сформированных выборках и используется для предсказания выборки вне стеллажа.

3.5. Функции R

Приведем некоторые функции, которые могут быть использованы при работе над данным разделом.

Приведено название функции, а в скобках название пакета, в котором функция расположена. Для использования функция необходима загрузка пакета, а если его еще нет, то и установка.

Если названия пакета не приведено — это означает, что функция имеется в базовом пакете и не требуется предварительная загрузка пакета.

Разделение

sample

создает простое случайное разделение

createDataPartition (caret)

создает случайную выборку с разделением на классы

maxdissim (caret)

генерирует набор для тестирования, используя максимальную выборку несходства.

createDataPartition (caret)

создает случайную выборку с разделением на классы

Ресемплирование

createDataPartition (caret)

создает случайную выборку с разделением на классы с дополнительным параметром times

createResamples (caret)

для бутстрэпинга

createFolds (caret)

для k-свертки перекрестной проверки

createMultiFolds (caret)

для многократной перекрестной проверки

4. Регрессионные модели

4.1. Результативность регрессионных моделей

Для моделей, предсказывающих числовой результат, используется некоторая мера точности для оценки эффективности модели. Однако есть различные способы измерить точность, каждый с его собственным нюансом. Понять силу и слабость определенной модели, полагаясь исключительно на единственную метрику проблематично. Визуализация подгонки модели, особенно графики остатков, является чрезвычайно важным по отношению к пониманию пригодности модели к цели.

Когда результат — число, наиболее распространенный метод для оценки предсказательных возможностей модели — это среднеквадратичная ошибка (MSE). Эта метрика — функция остатков модели, которые являются наблюдаемыми величинами минус предсказания модели. Среднеквадратичная ошибка (MSE) вычисляется путем возведения остатков в квадрат и их суммирования. RMSE — это квадратный корень из MSE. Значение обычно интерпретируется или как далеко (в среднем) остатки от нуля, или как среднее расстояние между наблюдаемыми величинами и предсказаниями модели.

Другая общая метрика — коэффициент детерминации, обычно обозначаемый как R2. Это значение может быть интерпретировано как величина объясненной моделью информации в данных. Таким образом, значение R2, равное 0.75, подразумевает, что модель может объяснить три четверти изменения в результате. Есть много формул для вычисления этого показателя, хотя самая простая версия считает коэффициент корреляции между наблюдаемыми и ожидаемыми значениями с возведением его в квадрат.

Также важно понять, что R2 зависит от изменения в результате. Используя интерпретацию, что эта статистика измеряет соотношение дисперсии, объясненной моделью, нужно помнить, что знаменатель этого отношения вычисляется с использованием дисперсии выборки результата. Например, предположим, что у результата набора тестов есть дисперсия 4.2. Если бы RMSE предсказательной модели равнялись 1, то R2 составил бы примерно 76%. Если бы у нас был другой набор тестов с точно тем же самым RMSE, но результатами теста было меньше переменной, то результаты выглядели бы хуже. Например, если бы дисперсия набора тестов равнялась 3, то R2 составил бы 67%.

В некоторых случаях цель модели просто состоит в упорядочении новых наблюдений. В этом случае определятся возможность модели, а не ее предсказательная точность. Для этого определяется порядковая корреляция между наблюдаемыми и ожидаемыми значениями, и оценка производится с помощью более соответствующей метрики. Порядковая корреляция берет ранги наблюдаемого значения результата (в противоположность их фактическим значениям) и оценивает, как близко это к рангам предсказаний модели. Для вычисления этого значения получают ранги наблюдаемых и предсказанных результатов, и вычисляют коэффициент корреляции между этими рангами. Эта метрика обычно известна как порядковая корреляция Спирмена.

4.2. Линейные регрессионные модели

Когда мы говорим о линейных моделях, то имеется в виду, что модели являются линейными в параметрах.

При оценке моделей оцениваются их параметры так, чтобы сумма квадратов ошибок или функция суммы квадратов ошибок были минимизированы. Среднеквадратичная ошибка (MSE) может быть разделена на компоненты не уменьшаемого изменения, смещения модели и дисперсии модели.

Явное преимущество линейных моделей состоит в легкости их толкования.

Другое преимущество этих видов моделей состоит в том, что их математический характер позволяет вычислить стандартные ошибки коэффициентов при условии, что делаются определенные предположения о распределениях остатков модели. Затем эти стандартные ошибки могут использоваться для оценки статистической значимости каждого предиктора в модели.

В то время как линейные модели типа регрессии легко поддаются толкованию, их использование может быть ограничено. Во-первых, эти модели состоятельны, если отношение между предикторами и откликом движется вдоль гиперплоскости. Например, при одном предикторе модель будет состоятельной, если отношение между предиктором и откликом двигалось вдоль прямой линии. С большим количеством предикторов отношение должно двигаться близко к плоской гиперплоскости. Если есть криволинейное отношение между предикторами и откликом (например, такое как квадратное, кубическое взаимодействия среди предикторов), то линейные регрессионные модели могут быть расширены с дополнительными предикторами, которые являются функциями исходных предикторов в попытке получить эти отношения. Однако нелинейные отношения между предикторами и откликом не могут быть соответственно получены этими моделями.

4.3. Нелинейные регрессионные модели

Многие из линейных моделей могут быть адаптированы к нелинейным трендам в данных, вручную прибавляя параметры модели (например, квадраты параметров). Однако для этого необходимо знать специфический характер нелинейности в данных.

Есть многочисленные регрессионные модели, которые по своей сути не линейны. При использовании этих моделей точная форма нелинейности не должна быть известна явно или специфицироваться до обучения модели. Рассмотрим несколько таких моделей: нейронные сети, машины опорных векторов (SVM) и K-ближайшие соседи (KNN). Основанные на дереве модели также не линейны. Из-за их популярности рассмотрим отдельно.

4.3.1. Нейронные сети

Нейронные сети — это мощные нелинейные методы регрессии, вдохновленные теориями о работе интеллекта. Как частные наименьшие квадраты (PLS), результат моделируется посредством многих не наблюдаемых переменных (названными скрытыми переменными или скрытыми модулями здесь). Эти скрытые модули — линейные комбинации исходных предикторов.

При обработке этой модели как нелинейной регрессионной модели обычно оптимизируются параметры для минимизации суммы квадратов остатков. Это может вызвать вычислительную проблему, связанную с оптимизацией (вспомним, что нет никаких ограничений на параметры этой комплексной нелинейной модели). Параметры обычно инициируются случайным значением, а затем используются специализированные алгоритмы для решения уравнения.

Кроме того, у нейронных сетей есть тенденция к переобучению отношений между предикторами и целевой переменной из-за большого количества коэффициентов регрессии. Для преодоления этой проблемы предлагается несколько разных подходов.

Один из подходов к решению проблемы переобучения состоит в использовании сходимости весов. В этом случае прибавляется штраф за большие коэффициенты регрессии так, чтобы любое крупное значение имело значимое влияние на ошибки модели. Формально, произведенная оптимизация попыталась бы минимизировать альтернативную версию суммы квадратных ошибок.

Учитывая проблему оценки большого количества параметров, подогнанная модель находит оценки параметра, которые локально оптимальны; то есть, алгоритм сходится, но получающиеся оценки параметра вряд ли будут глобально оптимальными оценками. Очень часто различные локально оптимальные решения могут произвести модели, которые очень отличаются, но имеют почти эквивалентную результативность. Эта нестабильность модели может иногда ограничивать применение этой модели. Как альтернатива, создаются несколько моделей, используя различные начальные значения с последующим использованием средних результатов с целью получения более стабильного предсказания. Такая усредненная модель имеет положительное влияние на нейронные сети.

На модели с нейронными сетями часто оказывает негативное влияние высокая корреляция среди предикторов (так как они используют градиенты для оптимизации параметров модели). Два подхода для смягчения этой проблемы: предварительная фильтрация предикторов для удаления предикторов с высокими корреляциями. Альтернативно, для устранения корреляции до моделирования может использоваться такой метод как анализ главных компонент (РСА). Явный положительный эффект обоих этих подходов состоит в уменьшении количества параметров модели, подлежащих оптимизации, что снижает вычислительную сложность.

4.3.2. Машины опорных векторов (SVM)

SVM — класс мощных, очень гибких методов моделирования. Первоначально теория в основе SVM разрабатывалась в контексте моделей классификации. Существует несколько видов регрессии опорного вектора, и мы остановимся на одном определенном методе, называемом — ε-нечувствительная регрессия.

Вспомним, что линейная регрессия стремится оценить параметры, которые минимизируют SSE. Одним из недостатков уменьшения SSE — это то, что оценки параметра могут находиться под влиянием всего одного наблюдения, которое лежит далеко от основного тренда в данных. Если данные содержат влиятельные наблюдения, то может использоваться альтернативная метрика минимизации такая, как функция Huber, которая менее чувствительна при поиске лучшей оценки параметра. Эта функция использует квадраты остатков, когда они «небольшие», и использует абсолютные остатки, когда остатки большие.

SVM для регрессии используют функцию, подобную функции Huber с важным отличием. Учитывая порог, установленный пользователем (обозначенный как ε), точки данных с остатками внутри порога не способствуют подгонке регрессии, в то время как точки данных с абсолютной разностью, больше чем порог, вносят вклад с линейным масштабом. Есть несколько следствий из этого подхода. Во-первых, так как квадраты остатков не используются, большие выбросы имеют ограниченное влияние на уравнение регрессии. Во-вторых, выборки, к которым хорошо подгоняется модель (то есть, остатки небольшие) не имеют никакого влияния на уравнение регрессии. Фактически, если порог установлен к относительно крупному значению, то выбросы — единственные точки, которые определяют линию регрессии! Это несколько парадоксально: плохо предсказанные точки определяют линию. Однако этот подход, как оказалось, очень эффективен при определении модели.

4.3.3. К-ближайшие соседи

Подход KNN просто предсказывает новую выборку, используя K самых близких точек из набора данных обучения. Построение KNN основано исключительно на отдельных выборках из учебных данных. Чтобы предсказать новую выборку для регрессии, KNN идентифицирует KNN выборки в пространстве предикторов. Предсказанный отклик для новой выборки — это средний из K откликов соседей. Другая итоговая статистика, такая как медиана, также может использоваться вместо средней для предсказания на новой выборке.

Основной метод KNN зависит от того, как пользователь определяет расстояние между выборками. Евклидово расстояние (то есть, расстояние по прямой между двумя выборками) является обычно используемой метрикой.

Поскольку метод KNN существенно зависит от расстояния между выборками, масштаб предикторов может иметь драматическое влияние на расстояния между выборками. Предикторы, которые имеют существенно разные веса, будут генерировать расстояния в виде нагрузок к предикторам, у которых есть самые большие весы. Таким образом, предикторы с самыми большими весами будут способствовать больше всего расстоянию между выборками. Чтобы избежать этого потенциального смещения и обеспечить каждому предиктору одинаковый вклад в вычисленное расстояние, рекомендуется центрировать и масштабировать все предикторы до выполнения KNN.

В дополнение к проблеме масштабирования, может быть проблематичным использование расстояния между наблюдениями, если пропущены некоторые значения предиктора, так как в этом случае невозможно вычислить расстояние между наблюдениями.

Элементарная версия KNN интуитивно ясная и может произвести приличные предсказания, особенно если целевая переменная зависит от локальной структуры предиктора. Однако в действительности у этой версии есть некоторые известные проблемы. Две обычно отмечаемых проблемы — время вычислений и разъединение между локальной структурой и предсказательной возможностью KNN.

Во-первых, для предсказания целевой переменной следует вычислить расстояния между наблюдением и всеми другими наблюдениями. Поэтому время вычисления увеличивается с n, что требует предварительной загрузки всех учебных данных в память для обеспечения возможности вычисления расстояния между новым наблюдением и всеми учебными наблюдениями.

У метода KNN может быть плохая предсказательная результативность, если локальная структура предиктора не относится к целевой переменной. Несоответствующие или шумные предикторы — серьезное препятствие, так как они могут отогнать подобные наблюдения друг от друга в пространстве предикторов. Следовательно, удаление несоответствующих, загруженных шумом предикторов является ключевым шагом предварительной обработки для KNN. Другой подход к улучшению предсказательной способности KNN состоит в загрузке соседей предсказания новым наблюдением, основанным на их расстоянии до нового наблюдения. В этом изменении учебные наблюдения, которые ближе к новому наблюдению, способствуют более предсказанному отклику, в то время как те, которые дальше, способствуют менее предсказанному отклику.

4.4. Регрессионные деревья

Основанные на дереве модели состоят из одного или нескольких вложенных операторов if-then для предикторов для разделения данные. В пределах этих разделений модель используется для предсказания результата.

В терминологии древовидных моделей есть два разделения данных на три терминальных узла или листьев дерева. Чтобы получить предсказание для нового наблюдения, мы следуем операторам if-then, используя значение предикторов в наблюдении, пока не приходим в терминальный узел. Затем используется формула модели в терминальном узле для генерации предсказания.

Основанные на дереве модели — популярные инструменты моделирования по ряду причин. Во-первых, они генерируют ряд условий, которые хорошо поддаются толкованию и являются легкими для реализации. Из-за логики их построения они могут эффективно описывать много типов предикторов (прореженный, отклоненный, непрерывный, категориальный, и т.д.) без потребности предварительной обработки. Кроме того, эти модели не требуют от пользователя указания формы отношения предикторов к отклику как, например, требует линейная регрессионная модель. Кроме того эти модели могут эффективно обработать пропущенные данные и неявно выбрать предиктор, характеристики которого являются требуемыми для многих проблем моделирования действительности.

У моделей, основанных на единственном дереве, имеются определенные слабые места. Два известных слабых места (1) нестабильность модели, то есть, небольшие изменения в данных могут решительно изменить структуру дерева и, следовательно, интерпретацию, и (2) менее оптимальная предсказательная результативность. Последнее является следствием того, что эти модели определяют прямоугольные области, которые содержат гомогенные значения результата. Если отношение между предикторами и целевой переменной не соответствуют прямоугольным подпространствам предикторов, то у основанных на дереве моделей ошибка предсказания будет больше, чем у других видов моделей.

4.5. Бутстрэп агрегированные деревья (bagging)

В 1990-ых начали появляться методы ансамблей (методы, которые комбинируют предсказания многих моделей). Бутстрэп агрегирование — БАГГ, сокращение от bootstrap aggregation, было первоначально предложено Лео Бреименом и было одним из самых ранних разработанных методов ансамблей (Breiman 1996a). БАГГ — общий подход, который использует самонастройку в соединении с любой моделью регрессии (или классификации) для создания ансамбля. Метод справедливо прост по структуре. Используется каждая модель в ансамбле для генерирования предсказания для нового наблюдения, а затем эти m предсказаний усредняются для предсказания с помощью бутстрэп агрегированной модели.

Бутстрэп агрегированные модели имеют несколько преимуществ перед не агрегированными моделями. Во-первых, бутстрэп агрегирование эффективно уменьшает дисперсию предсказания посредством процесса ее агрегации. Для моделей, которые производят нестабильное предсказание, как деревья регрессии, агрегация по многим версиям учебных данных фактически уменьшает дисперсию в предсказании и, следовательно, делает предсказание более стабильным.

Бутстрэп агрегация стабильных моделей с меньшей дисперсией, таких как, линейная регрессия, с другой стороны, предлагает меньшие уточнения в предсказательной результативности.

Другое преимущество бутстрэп агрегированных моделей состоит в том, что они имеют свою собственную внутреннюю оценку предсказательной результативности, которая хорошо коррелирует или с оценками перекрестной проверки, или с оценками тестового набора. Причина следующая: определенные выборки не учитываются при создании выборки бутсрэпа для каждой модели в ансамбле. Эти выборки называются вне стеллажа, и они могут использоваться для оценки предсказательной результативности модели, так как они не использовались для создания модели. Следовательно, каждая модель в ансамбле генерирует меру предсказательной результативности наблюдений вне стеллажа. Затем может использоваться среднее число метрик результативности вне стеллажа для измерения предсказательной результативности всего ансамбля, и это значение обычно коррелирует хорошо с оценкой предсказательной результативности, полученной или с перекрестной проверкой или от набора тестов. Эта оценка ошибки обычно упоминается как оценка вне стеллажа.

В своей канонической форме у пользователя имеется единственный выбор: число бутстрэпов выборки для агрегирования — m. Часто мы видим экспоненциальное уменьшение в предсказательном уточнении при увеличении итераций; большая часть уточнения в результативности предсказания получено с небольшим количеством деревьев (m <10). Это означает, что каждую модель можно создать отдельно, и все модели могут быть объединены в конце для генерации предсказания.

Другой недостаток этого подхода — это то, что бутстрэп агрегированная модель поддается толкованию хуже модели, чем не складированная в стеллаж по бутстрэпу.

4.6. Случайный лес (random forest)

Считается, что укладывание в стеллаж деревьев улучшает предсказательную результативность по отдельному дереву, уменьшая дисперсию предсказания. Генерация выборок бутстрэпом вводит элемент случайности в процесс создания дерева, который стимулирует распределение деревьев, и поэтому также распределение ожидаемых значений для каждой выборки. Уложенные в стеллаж деревья, однако, не полностью независимы друг от друга, так как все исходные предикторы рассматриваются в каждом разделении каждого дерева. Можно предположить, что, если начать с достаточно большого количества исходных наблюдений и отношения между предикторами и откликом, который может быть соответственно смоделирован деревом, то у деревьев для различных наблюдений по бутстрэпу могут быть структуры, подобные друг другу (особенно наверху деревьев) из-за базового отношения. Эта особенность известна как древовидная корреляция и не дает бутстрэп агрегированию оптимально сократить дисперсию ожидаемых значений.

Со статистической точки зрения уменьшить корреляцию среди предикторов можно путем прибавления случайности к процессу построения дерева. Была разработана идея случайного выбора разделения, где создаются деревья, используя случайное подмножество главных k предикторов при каждом разделении в дереве.

Затем используется каждая модель в ансамбле для генерации предсказания для новой выборки, а затем усредняются m предсказаний для предсказания леса. Так как алгоритм в произвольном порядке выбирает предикторы в каждом разделении, корреляция деревьев будет обязательно уменьшена.

Природа ансамбля случайного леса лишает возможности получить понимание отношения между предикторами и откликом. Однако потому что деревья — типичный основной ученик для этого метода, можно количественно определить воздействие предикторов в ансамбле — определить значимость предикторов модели.

Можно показать, что корреляции между предикторами могут оказать значительное влияние на величину значимости. Например, у неинформативных предикторов с высокой корреляцией с информативными предикторами будет неправильно крупное значение значимости. В некоторых случаях их значимость была больше, чем у менее важных предикторов. Также известно, что количество предикторов, которое берут для классификации в каждом узле дерева, имеет серьезное влияние на величину значимости.

4.7. Усиление (boosting)

Модели с усилением первоначально разрабатывались для проблем классификации и были позже расширены на регрессию. История усиления начинается с алгоритма AdaBoost.

Усиление, особенно в форме алгоритма AdaBoost было мощным инструментом предсказания, обычно выигрывая у любой отдельной модели. Ее успех привлек внимание в сообществе моделирования, и ее использование стало широко распространенным.

Алгоритм AdaBoost четко работал благодаря простому, изящному и очень адаптируемому алгоритму для различных видов проблем. Основные принципы усиления следующие: учитывая функцию потерь (например, квадрат ошибки для регрессии) и слабый ученик (например, деревья регрессии), алгоритм стремится найти аддитивную модель, которая минимизирует функцию потерь. Алгоритм обычно инициализируется с лучшим предположением отклика (например, средний из отклика в регрессии). Вычисляется остаток, а затем модель подгоняется к остаткам с целью минимизации функции потерь. Текущая модель добавлена к предыдущей модели, и процедура продолжается для конкретного количества итераций.

Значимость предикторов для алгоритма усиления является функцией квадрата ошибки. Определенно, уточнение по квадрату ошибки из-за каждого предиктора суммировано в пределах каждого дерева в ансамбле (то есть, каждый предиктор получает значение уточнения для каждого дерева). Затем значение уточнения для каждого предиктора усреднено по всему ансамблю для получения полной величины значимости предикторов.

4.8. Функции R

Приведем некоторые функции, которые могут быть использованы при работе над данным разделом.

Приведено название функции, а в скобках название пакета, в котором функция расположена. Для использования функция необходима загрузка пакета, а если его еще нет, то и установка.

Если названия пакета не приведено — это означает, что функция имеется в базовом пакете и не требуется предварительная загрузка пакета.

lm

подгонка линейной регрессии

predict

универсальная функция предсказания. если объект, для которого предсказывают, получен из подгонки линейной регрессии, то предсказание для линейной регрессии.

rlm (MASS)

подгонка устойчивой линейной регрессии

nnet

подгонка нейронной сети

avNNet (caret)

подгонка нейронной сети с усреднением

svm (LIBSVM)

подгонка машины опорных векторов

ksvm (kernlab)

подгонка машины опорных векторов

knnreg (caret)

подгонка k-ближайших соседей

bagging (ipred)

подгонка бутстрэп агрегированных деревьев

bag (caret)

подгонка бутстрэп агрегированных деревьев

randomForest (randomForest)

подгонка случайного леса

cforest (party)

подгонка случайного леса

gbm (gbm)

подгонка усиленных регрессионных деревьев с помощью стохастической градиентной усиливающей машины.

5. Результативность классификационных моделей

В предыдущей части этой книги мы сосредоточились на создании и оценке моделей с непрерывной целевой переменной. Теперь сосредоточимся на создании и оценке моделей с категориальной целевой переменной. Многие методы моделирования регрессии могут использоваться и для классификации. Однако оценка результативность моделей классификации отличается, начиная таких с метрик, как RMSE и R2, которые не соответствуют идеологии классификации.

5.1. Предсказания класса

Модели классификации обычно генерируют два типа предсказаний. Подобно регрессионным моделям модели классификации делают предсказания непрерывных величин, являющихся по смыслу вероятностями, то есть, ожидаемые значения принадлежности к классу для любого отдельного наблюдения между 0 и 1 с суммой, равной 1. В дополнение к предсказанию непрерывных величин модели классификации генерируют предсказанный класс, который представлен в форме дискретной категории. Для большей практичности применения требуется дискретное предсказание категории для принятия решения. Предсказание тренда, например, требует категорического решения для каждого нового тайм фрейма котировок.

Хотя модели классификации производят оба из этих типов предсказаний, часто внимание обращено на дискретное предсказание, а не на предсказание вероятности. Однако оценки вероятности для каждого класса могут быть очень полезными для измерения доверия к предсказанных моделью классов. Возвращаясь к примеру тренда, поступившие котировки могут привести к предсказанию «лонг» с вероятностью 51% или с вероятностью 99%. Если наша модель выдает предсказание только в виде «лонг», то это привело бы к уравниванию доверия к совершенно разным предсказаниям.

В некоторых применениях желаемый результат — предсказанные вероятности класса, которые затем используются в качестве исходных данных для других вычислений. В случае трендовой торговой системы напрашивается использование вероятности как основы для вычисления размера лота, или расстояния до стоп-лосса.

Вне зависимости от использования мы требуем, чтобы оцененные вероятности класса отражали истинную базовую вероятность выборки. Таким образом, предсказанная вероятность класса должна быть хорошо калибрована. Для хорошей калибровки вероятности должны эффективно отразить истинное правдоподобие тренда. Вернемся к примеру тренда. Если модель производит вероятность, равную 20% для правдоподобия наличия «лонгов» на рынке, то это значение вероятности было бы хорошо калибровано, если «лонги» будут встречаться в среднем в 1 из 5 баров.

5.2. Основы предсказаний классов

Диаграмма ROC — метод для визуализации, организации и выбора классификаторов на основе их результативности. Использование диаграмм ROC в машинном обучении было начато в 1989 с демонстрации кривых ROC в сравнении оценки алгоритмов. Последние годы увеличивается использования диаграмм ROC в сообществе машинного обучения. В дополнение к их полезности в составлении графика результативности у диаграмм ROC есть свойства, которые делают их особенно полезными для областей с не равными классами и неравной стоимостью ошибок классификации. Эти характеристики диаграмм ROC стали все более и более важными, поскольку исследование продолжается в области чувствительного к стоимости изучения и изучения в присутствии несбалансированных классов.

У большинства книг по анализу данных и машинному обучению, если они упоминают диаграммы ROC вообще, есть только краткое описание метода. Диаграммы ROC концептуально просты, но есть некоторые неочевидные сложности, которые возникают при построении торговых систем. Есть также распространенные заблуждения и ловушки при их практическом использовании.

Кривая ROC (Receiver Operator Characteristic) — кривая, которая наиболее часто используется для представления результатов бинарной классификации в машинном обучении. Название пришло из систем обработки сигналов. Поскольку классов два, один из них называется классом с положительными исходами, второй — с отрицательными исходами. Кривая ROC показывает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров. В терминологии ROC-анализа первые называются истинно положительным, вторые — ложно отрицательным множеством. При этом предполагается, что у классификатора имеется некоторый параметр, варьируя который, можно получить то или иное разбиение на два класса. Этот параметр часто называют порогом, или точкой отсечения (cut-off value). В зависимости от него будут получаться различные величины ошибок I и II рода.

В логистической регрессии порог отсечения изменяется от 0 до 1 — это и есть расчетное значение уравнения регрессии. Будем называть его рейтингом.

Для понимания сути ошибок I и II рода рассмотрим четырехпольную таблицу сопряженности (confusion matrix), которая строится на основе результатов классификации моделью и фактической (объективной) принадлежностью наблюдений к классам.

— TP (True Positives) — верно классифицированные положительные примеры (так называемые истинно положительные случаи);

— TN (True Negatives) — верно классифицированные отрицательные примеры (истинно отрицательные случаи);

— FN (False Negatives) — положительные примеры, классифицированные как отрицательные (ошибка I рода). Это так называемый «ложный пропуск» — когда интересующее нас событие ошибочно не обнаруживается (ложно отрицательные примеры);

— FP (False Positives) — отрицательные примеры, классифицированные как положительные (ошибка II рода); Это ложное обнаружение, так как при отсутствии события ошибочно выносится решение о его присутствии (ложно положительные случаи).

Что является положительным событием, а что — отрицательным, зависит от конкретной задачи. Укажем три полезных для нас варианта смыслового наполнения предложенной абстракции:

— целевая переменная «лонг/шорт». Для этой целевой переменной можно считать за положительный пример «лонг», а за отрицательный пример «шорт», обозначив в числовом виде как (1, -1). Наполнение «положительных» и «отрицательных» примеров содержательными понятиями «лонг/шорт» приводит к симметричному случаю в том смысле, что если модель ошибочно классифицирует «лонг» как «шорт» и наоборот, то убытки будут одинаковы;

— моделируем две разных целевых переменных. Одна — «лонг/вне рынка», вторая — «шорт/вне рынка», обозначив в числовом виде как (1,0) и (0, -1). Это привело к наполнению «положительных» и «отрицательных» примеров содержательными понятиями «лонг/вне рынка/шорт». Так как мы разбили на две переменные, то пришли к несимметричному случаю в том смысле, что, например, не правильная классификация «вне рынка» как «лонга» приведет к убыткам, а вот обратная ситуация к убыткам не приводит.

При анализе чаще оперируют не абсолютными показателями, а относительными — долями (rates):

— доля истинно положительных примеров (True Positives Rate):

TPR = TP/ (TP+FN)

В случае целевой переменной «лонг/шорт» — это доля правильно классифицированных «лонгов» по отношению ко всему множеству (ко всей выборке).

— доля ложно положительных примеров (False Positives Rate):

FPR = FP/ (TN+FP)

В случае целевой переменной «лонг/шорт» — это доля ложно классифицированных «лонгов» по отношению ко всему множеству (ко всей выборке).

Введем еще два определения: чувствительность и специфичность модели. Ими определяется объективная ценность любого бинарного классификатора.

Чувствительность (Sensitivity) — это и есть доля истинно положительных случаев, т.е.:

Se = TPR = TP/ (TP+FN)

Специфичность (Specificity) — доля истинно отрицательных случаев, которые были правильно идентифицированы моделью:

Sp = TN (TN+FP) = 1 — FPR

Попытаемся разобраться в этих определениях.

Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры).

Если рассуждать в терминах двух наших целевых переменных «лонг/вне рынка» и «вне рынка/шорт», то становится очевидной применение рассматриваемых показателей:

— модель с высокими значениями чувствительности для первой целевой переменной «лонг/вне рынка» проявится в повышенной диагностики «лонгов»;

— модель с высокими значениями специфичности для второй целевой переменной «вне рынка/шорт» проявится в повышенной диагностики «шортов».

Забегая вперед, приведу график кривой ROC, в которой осями является чувствительность Se, она же TPR, и дополнение до единицы специфичности 1 — FPR.

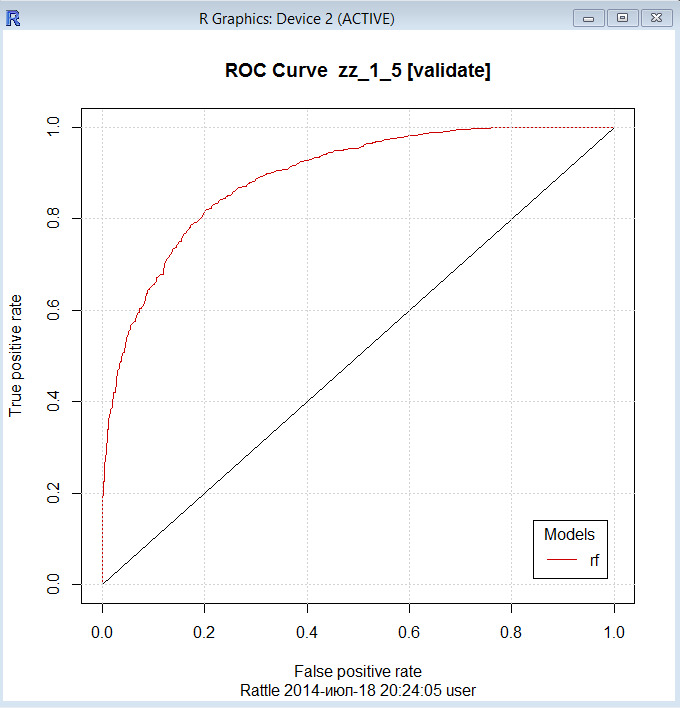
График дополнен прямой х=у.

Для идеального классификатора график ROC-кривой проходит через верхний левый угол, где доля истинно положительных случаев составляет 100% или 1.0 (идеальная чувствительность), а доля ложно положительных примеров равна нулю. Поэтому чем ближе кривая к верхнему левому углу, тем выше предсказательная способность модели. Наоборот, чем меньше изгиб кривой, и чем ближе она расположена к диагональной прямой, тем менее эффективна модель. Диагональная линия соответствует «бесполезному» классификатору, то есть полной неразличимости двух классов.

При визуальной оценке ROC-кривых расположение их относительно друг друга указывает на их сравнительную эффективность. Кривая, расположенная выше и левее, свидетельствует о большей предсказательной способности модели. Так, на рис.5.3 две ROC-кривые совмещены на одном графике. Видно, что модель «rf» лучше модели «ada».

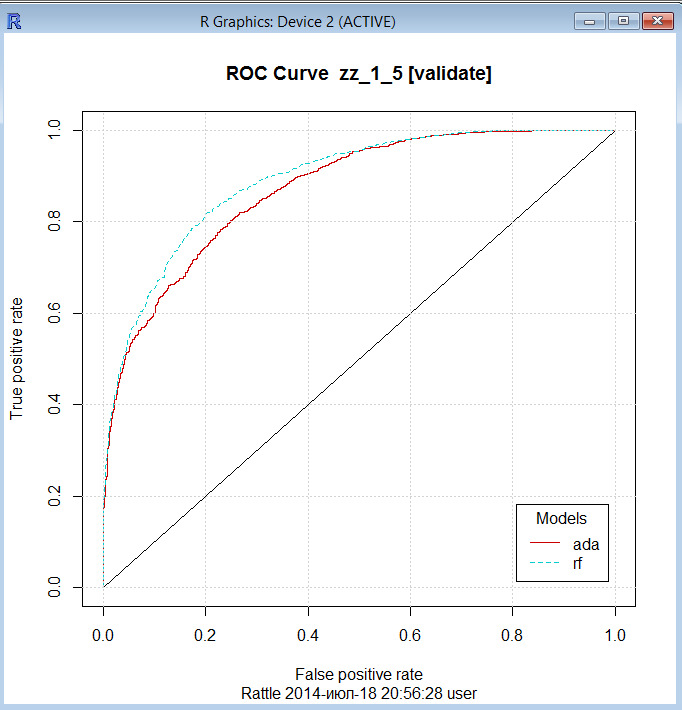
Визуальное сравнение кривых ROC не всегда позволяет выявить наиболее эффективную модель. Своеобразным методом сравнения ROC-кривых является оценка площади под кривыми. Теоретически она изменяется от 0 до 1.0, но, поскольку модель всегда характеризуются кривой, расположенной выше положительной диагонали, то обычно говорят об изменениях от 0.5 («бесполезный» классификатор) до 1.0 («идеальный» классификатор). Эта оценка может быть получена непосредственно вычислением площади под многогранником, ограниченным справа и снизу осями координат и слева вверху — экспериментально полученными точками (рис. 5.3). Численный показатель площади под кривой называется AUC (Area Under Curve). В нашем случае мы получили следующие величины:

Area under the ROC curve for the ada model on zz_1_5 [validate] is 0.8702

Area under the ROC curve for the rf model on zz_1_5 [validate] is 0.8904

Площадь под кривой ROC для модели rf равна 0.8904, а для модели ada равна 0.8702, что подтверждает визуальное наблюдение.

С большими допущениями можно считать, что чем больше показатель AUC, тем лучшей прогностической силой обладает модель. Однако следует знать, что:

— показатель AUC предназначен скорее для сравнительного анализа нескольких моделей;

— AUC не содержит никакой информации о чувствительности и специфичности модели.

В литературе иногда приводится следующая экспертная шкала для значений AUC, по которой можно судить о качестве модели:

Идеальная модель обладает 100% чувствительностью и специфичностью. Однако на практике добиться этого невозможно, более того, невозможно одновременно повысить и чувствительность, и специфичность модели. Компромисс находится с помощью порога отсечения, т.к. пороговое значение влияет на соотношение Se и Sp. Можно говорить о задаче нахождения оптимального порога отсечения (optimal cut-off value).

Порог отсечения нужен для применения модели на практике: относить новые наблюдения к одному из двух классов. Для определения оптимального порога нужно задать критерий его определения, так как в разных задачах присутствует своя оптимальная стратегия. Критериями выбора порога отсечения могут выступать:

— требование минимальной величины чувствительности (специфичности) модели. Например, нужно обеспечить чувствительность теста не менее 80%. В этом случае оптимальным порогом будет максимальная специфичность (чувствительность), которая достигается при 80% (или значение, близкое к нему «справа» из-за дискретности ряда) чувствительности (специфичности);

— требование максимальной суммарной чувствительности и специфичности модели, т.е.

Cut_off = max (Se + Sp)

— Требование баланса между чувствительностью и специфичностью, т.е. когда Se примерно равно Sp:

Cut_off = min (Se — Sp)

Второе значение порога обычно предлагается пользователю по умолчанию. В третьем случае порог есть точка пересечения двух кривых, когда по оси X откладывается порог отсечения, а по оси Y — чувствительность и специфичность модели. Пересечение этих двух кривых и даст порог отсечения.

6. Линейные классификационные модели

Методы классификации стремятся классифицировать наблюдения в группы, основанные на характеристиках предикторов, и способ к достижению этой минимизации отличается для каждого метода. Далее рассмотрим некоторые из них.

6.1. Логистическая регрессия

Линейная регрессионная модель не всегда способна качественно предсказывать значения целевой (зависимой) переменной. Выбирая для построения модели линейное уравнение, мы естественным образом не накладываем никаких ограничений на значения зависимой переменной. А такие ограничения могут быть существенными.

Линейная регрессионная модель может дать результаты, несовместимые с реальностью. С целью решения данных проблем полезно изменить вид уравнения регрессии и подстроить его для решения конкретной задачи.

Вообще, логит регрессионная модель предназначена для решения задач предсказания значения непрерывной зависимой переменной, при условии, что эта зависимая переменная может принимать значения на интервале от 0 до 1.

В силу такой специфики, ее часто используют для предсказания вероятности наступления некоторого события в зависимости от значений некоторого набора предикторов.

Можно использовать логистическую регрессию и для решения задач с бинарным откликом. Такие задачи появляются, когда зависимая переменная может принимать только два значения.

Логистическая регрессия и обычная линейная регрессия попадают в больший класс так называемых обобщенных линейных моделей (GLM), которые охватывают много различных распределений вероятности. Эти модели линейны в том смысле, что функция результата моделируется с использованием линейных предикторов, что приводит к линейным границам классификации.

Эффективная модель логистической регрессии способна учесть нелинейные эффекты. Например, использовать кубические сплайны для создания гибких, адаптивных версий предикторов, которые могут учесть много типов нелинейности.

Модель логистической регрессии очень популярна из-за ее простоты и возможности сделать выводы о параметрах модели. Например, можно оценить наличие у дня календарного года статистически значимого отношения с вероятностью принятия решения о торговой сигнале.

6.2. Линейный дискриминантный анализ (LDA)

Cформулируем проблему классификации следующим образом: найти линейную комбинацию предикторов так, что межгрупповая дисперсия максимальна относительно дисперсии внутри групп. Другими словами необходимо найти комбинацию предикторов, которые дали максимальное разделение между центрами данных, одновременно имея минимальное изменение в пределах каждой группы данных.

Дисперсия внутри групп была бы оценена дисперсией, которая объединяет дисперсии в пул предиктора в пределах каждой группы. Взятие отношения этих двух количеств является, в действительности, отношением сигнала-шум. Получается, что мы определяем такие линейные комбинации предикторов, которые дают максимальное отношение сигнал-шум.

6.3. Регрессия частично наименьших квадратов (PLS)

В случае коррелированности предикторов нельзя непосредственно использовать обычный линейный подход для поиска оптимальной дискриминантной функции. Эта же проблема существует и при попытке удалить чрезвычайно коррелированные предикторы в рамках анализа главных компонент РСА. Если существуют сложные отношения корреляции в данных, то PCA может использоваться для уменьшения размерности пространства предикторов. Однако PCA может не идентифицировать комбинации предикторов, которые оптимально разделяют выборки на группы с учетом целевой переменной. Цель РСA состоит в поиске подпространства, которое с максимальной меж-внутри групповой изменчивостью. Однако далеко не факт, что выделенные факторы оптимальным образом будут связаны и целевой переменной, поскольку задача метода РСА состоит в объяснении связей предикторов. В этих случаях рекомендуется использовать регрессию частично наименьших квадратов PLS.

Регрессия PLS решает задачу формирования небольшого количества новых предикторов, в пространстве которых связь между зависимой переменной и предикторами достигает максимального значения.

6.4. Функции R

Приведем некоторые функции, которые могут быть использованы при работе над данным разделом.

Приведено название функции, а в скобках название пакета, в котором функция расположена. Для использования функция необходима загрузка пакета, а если его еще нет, то и установка.

glm (glm)

логистическая регрессия (модель логит).

pcr (pls)

регрессия частично наименьших квадратов.

7. Нелинейные классификационные модели

Предыдущая глава описала модели, которые были собственно линейны — структура модели произведет линейные границы класса, если вручную не указать нелинейные функции предикторов. Эта глава имеет дело с некоторыми собственно нелинейными моделями. Как в разделах регрессии, есть другие нелинейные модели, которые используют деревья для моделирования данных.

За небольшим исключением (модели FDA) на методы, описанные в этой главе, может оказать негативное влияние большое количество неинформативных предикторов. Комбинируя эти модели с инструментами выбора предиктора, можно значительно увеличить результативность.

7.1. Нейронные сети

Как мы видели выше при обсуждении нейронных сетей в регрессионных моделях С классов могут кодироваться в двоичные С столбцов фиктивных переменных, а затем использоваться в модели. Хотя предыдущее обсуждение нейронных сетей для регрессии использовало единственный отклик, модель может легко описать много результатов и для регрессии, и для классификации. Ниже обсудим классификацию нейронной сетью.

Для получения многозначного результата вместо единственного результата у нижнего слоя есть много узлов для каждого класса. Заметим, что, в отличие от нейронных сетей для регрессии, дополнительное нелинейное преобразование используется на комбинации скрытых модулей. Каждый класс предсказан линейной комбинацией скрытых модулей, которые были преобразованы в значения между нулем и единицей (обычно сигмоидальной функцией). Однако даже при том, что получаемые предсказания находятся между нулем и единицей, они не «подобны вероятности», так как они не составляют в целом единицу.

Как их аналоги для регрессии, у нейронных сетей для классификации есть значимый потенциал для переобучения. Оптимизируя ошибку сумм квадратов или энтропию, сходимость веса ослабляет размер оценок параметра. Это может привести к сверх гладким границам классификации.

Много других аспектов нейронных сетей в моделях классификации зеркально отражают свои аналоги для регрессии. Коллинеарность и неинформативные предикторы окажут сопоставимое влияние на результативность модели.

7.2. Машины опорных векторов (SVM)

Машины опорных векторов (SVM) развились в один из самых гибких, эффективных и доступных инструментов машинного обучения.

В SVM определяется метрика под названием промежуток. Проще говоря, промежуток — это расстояние между границей классификации и самой близкой точкой набора данных обучения. Промежуток, определенный точками данных, может определяться количественно и использоваться для оценки возможностей модели. В терминологии SVM, наклон и смещение границы, которые максимизируют расстояние между границей и данными, известны как максимальный классификатор промежутка.

Что происходит, когда классы не вполне отделимы? Стоимость помещается в сумму точек набора данных обучения, которые находятся на границе или на неправильной стороне границы.

Для машин опорных векторов стоимость используется, чтобы оштрафовать число ошибок; как следствие большая стоимость стимулирует более высокую сложность модели, но не ограничивают ее.

7.3. K-ближайшие соседи (KNN)

В то время как многие идеи KNN для регрессии непосредственно применимы для классификации, выделим специфические аспекты по применению метода для классификации.

Методы классификации, обсужденные выше, ищут линейные или нелинейные границы, которые оптимально разделяют данные. Затем эти границы используются для предсказания классификации новых наблюдений. KNN использует другой подход при использовании географического окружения наблюдения для предсказания классификации наблюдений.

Подобно регрессии, KNN для классификации предсказывает новое наблюдение, используя K самых близких наблюдений из набора данных обучения. «Близость» определена метрикой расстояния, например Евклидовой, и выбор метрики зависит от характеристик предиктора. Важно помнить, что для любой метрики расстояния исходные измерительные веса предикторов влияют на получающиеся величины расстояний. Это подразумевает, что при наличии существенно разных масштабов предикторов, значение расстояния между выборками будет склоняться к предикторам с более широкими масштабами. Для гарантии равных возможностей каждому предиктору одинаково влиять на расстояния рекомендуется центрировать и масштабировать все предикторы до выполнения KNN.

Как в контексте регрессии, чтобы определить классификацию новой выборки, K самых близких наблюдений набора данных обучения определяются через метрику расстояния. Оценки вероятности класса для нового наблюдения вычисляются как соотношение соседей набора данных обучения в каждом классе. Предсказанный класс нового наблюдения — это класс с самой высокой оценкой вероятности. Если два или более классов связаны самой высокой оценкой, то связь разрушается наугад.

Любой метод с настраивающимися параметрами может быть склонным к переобучению, и KNN особенно восприимчив к этой проблеме. Слишком мало соседей приводят к чрезвычайно локализованной подгонке (то есть, к переобучению), в то время как слишком много соседей приводят к границам, которые могут не определить местоположение необходимой структуры разделения данных. Поэтому, следует взять обычную перекрестную проверку или подход с передискредитизацией для определения оптимального значения K.

7.4. Функции R

Приведем некоторые функции, которые могут быть использованы при работе над данным разделом.

Приведено название функции, а в скобках название пакета, в котором функция расположена. Для использования функция необходима загрузка пакета, а если его еще нет, то и установка.

Если названия пакета не приведено — это означает, что функция имеется в базовом пакете и не требуется предварительная загрузка пакета.

В R существует много пакетов для нейронных сетей: nnet, RSNNS, qrnn и neuralnet.

nnet (nnet)

подгонка нейронной сети

В R существует много пакетов для машин опорных векторов (SVM): e1071, kernlab, klaR и svmPath.

ksvm

Подгоняет модель машины опорных векторов.

knn (caret)

Подгонка K-ближайших соседей.

8. Классификационные деревья

Классификационные деревья относятся к семейству моделей, основанных на деревьях, подобных регрессионным деревьям, и состоят из вложенных операторов if-then.

Ясно, что структура деревьев и правил подобна структуре, которую мы видели в регрессии. И преимущества и слабые места деревьев в классификации аналогичны: они могут хорошо поддаваться толкованию, могут описывать много типов предикторов так же как пропущенных данных, но страдают от нестабильности модели, и могут не дать оптимальную предсказательную результативность. Процесс поиска оптимального разделения и правил, однако немного отличается из-за изменения в критериях оптимизации, которые будут описаны ниже.

8.1. Основные классификационные деревья

Как с деревьями регрессии, цель деревьев классификации состоит в разделении данных на меньшие, но более однородные группы. Однородность в этом контексте означает, что узлы разделения более чисты (то есть, содержит большее соотношение одного класса в каждом узле). Простой способ определить чистоту в классификации — это максимизировать точность или эквивалентно минимизировать ошибку неправильной классификации. Точность как мера чистоты, однако, немного вводит в заблуждение, так как мера ориентирована на способ разделения данных, который минимизирует неправильную классификацию, а не на способ разделения данных, который помещает наблюдения, прежде всего, в один класс.

Две альтернативных меры, индекс Gini и кросс энтропия, которая также упоминается как отклонение или информация, и смещаются от точности к чистоте.

Деревья, которые созданы с максимальной глубиной, имеют тенденцию к переобучению на данных обучения. Более обобщенные деревья — это те, которые являются сокращенной версией начального дерева, и могут быть настроены по стоимостной сложности с критерием чистоты, оштрафованным фактором общего количества терминальных узлов в дереве. Коэффициентом стоимостной сложности называют параметр сложности, который может быть включен в процесс настройки так, чтобы можно было оценить оптимальное значение.

После того, как дерево было оборвано, оно может использоваться для предсказания. В классификации каждый терминальный узел производит вектор вероятностей класса, основанных на наборе данных обучения, который затем используется в качестве предсказания для нового значения целевой переменной.

Подобно деревьям регрессии, деревья классификации могут обработать пропущенные значения. В построении дерева только наблюдения с непропущенной информацией рассматривают для создания разделения. В предсказании суррогатные разделения могут использоваться вместо разделения, в которых пропущены значения. Аналогично, может быть вычислена значимость переменной для деревьев классификации.

Если предиктор непрерывен, то процесс разделения прямолинеен для решения об оптимальной точке разделения. Если предиктор категориальный, то процесс может взять несколько одинаково допустимых путей, один из которых отличается от традиционного подхода статистического моделирования.

Для древовидных моделей процедура разделения может делать более динамичное разделение данных, такие как группы двух или больше категорий по обе стороны от разделения. Однако для этого алгоритм должен обработать категориальные предикторы как упорядоченное множество битов. Поэтому при подгонке деревьев следует сделать выбор относительно обработки предикторов с категориальными значениями:

— каждый категориальный предиктор может быть введен в модель как отдельная сущность так, чтобы модель принимала решение о группировке или разделении значения. В тексте это будет упоминаться как использование сгруппированных категорий.

— категориальные предикторы сначала преобразовываются в двоичные фиктивные переменные. Таким образом, полученные фиктивные переменные рассматривают независимо при принудительном двоичном разделении на категории. В действительности разделение на двоичную фиктивную переменную до моделирования налагает «one-all» разделение категорий. Этот подход будет маркирован как использование независимых категорий.

То, какой подход более соответствует проблеме, зависит от данных и модели. Например, если подмножество категорий очень предсказательное для результата, первый подход является, вероятно, лучшим. Однако этот выбор может иметь значительное влияние на сложность модели и, как следствие, результативность.

8.2. Бутстрэп агрегированные деревья

Бутстрэп агрегирование для классификации является простой модификацией бутстрэп агрегирования для регрессии.

Подобно настройке регрессии, могут быть вычислены меры значимости переменных путем суммирования значений значимости переменных для отдельных деревьев в ансамбле.

8.3. Случайные леса

Алгоритм случайных лесов для классификации является двойником соответствующего алгоритма для регрессии. Как и в случае с бутстрэп агрегированием каждое дерево в лесе голосует для классификации нового наблюдения, и часть голосов в каждом классе во всем ансамбле является вектором вероятности предсказания.

По большей части, у случайного леса для классификации есть аналогичные регрессии свойства, включая:

— модель относительно нечувствительна к значению mtry — числа предикторов, которое рассматривается в узле;

— как с большинством деревьев, требования предварительной обработки данных минимальны;

— могут быть вычислены меры результативности из стеллажа, включая точность, чувствительность, специфику и матрицы рассогласования.

8.4. Усиление

Хотя мы уже обсуждалось усиление при настройке регрессии, этот метод первоначально разрабатывался для проблем классификации, в котором много слабых классификаторов, например, классификатор, который предсказывает незначительно лучше, чем случайный, были объединены в сильный классификатор. Есть много разновидностей усиливающих алгоритмов, и здесь обсудим основные.

В начале 1990-ых появились несколько алгоритмов усиления для реализации оригинальной теории. В 1996, наконец, появилась первая практическая реализация теории усиления в виде известного алгоритма AdaBoost, которая использовалась в ранних версиях Rattle.

Кратко, алгоритм AdaBoost генерирует последовательность слабых классификаторов, где на каждой итерации алгоритм считает лучшим классификатором тот, который основан на текущих весах наблюдения. Наблюдения, которые неправильно классифицированы на k-й итерации, получают больше веса в (k +1) итерации, в то время как наблюдения, которые правильно классифицированы, получают меньше веса на последующей итерации. Это означает, что наблюдение, которое трудно классифицировать, получают все более и более большие веса, пока алгоритм не идентифицирует модель, которая правильно классифицирует эти наблюдения. Поэтому, каждая итерация алгоритма обязана изучать другой аспект данных, сосредотачиваясь на областях, которые содержат наблюдения, трудные для классификации. На каждой итерации вычисляется вес этапа, основанный на коэффициенте ошибок на этой итерации. Природа веса этапа подразумевает, что у более точных моделей есть более высокое положительное значение, а у менее точных моделей есть более низкое отрицательное значение, затем полная последовательность взвешенных классификаторов объединяется в ансамбле и имеет большой потенциал для лучшей классификации, чем любой из отдельных классификаторов.

Усиление может быть применено к любому методу классификации, но деревья классификации — популярный метод для усиления, так как они могут быть превращены в слабых учеников, ограничивая глубину деревьев для создания деревьев с немногими разделениями (также известные как пни). Известно объяснение того, почему деревья классификации работают особенно хорошо при усилении. Так как деревья классификации являются методом (малое смещение) / (большая дисперсии), ансамбль деревьев помогает понижать дисперсию, приводя к результату, у которого есть малое смещение и малая дисперсия. Глядя на алгоритм AdaBoost можно показать, что методы с низкой дисперсией не могут быть значительно улучшены посредством усиления.

8.5. Функции R

Приведем некоторые функции, которые могут быть использованы при работе над данным разделом.

Приведено название функции, а в скобках название пакета, в котором функция расположена. Для использования функция необходима загрузка пакета, а если его еще нет, то и установка.

Если названия пакета не приведено — это означает, что функция имеется в базовом пакете и не требуется предварительная загрузка пакета.

Для практической реализации положений данного раздела могут быть полезны следующие пакеты: C50, caret, gbm, ipred, partykit, pROC, randomForest и RWeka.

Категориальные предикторы кодируются в R как факторы с помощью функций: SponsorCode, ContractValueBand, CategoryCode и Weekday.

rpart (rpart)

подгонка отдельно классификационного дерева.

bagging (rpart)

подгонка бутстрэп агрегированного дерева.

randomForest (randomForest)

подгонка случайного леса.

gbm (gbm)

подгонка усиленного дерева. Возможно два вида распределений: «bernoulli» и «adaboost».

blackboost (mboost)

подгонка усиленного дерева.

adaboost (ada)

авторский алгоритм подгонки усиленного дерева.

9. Несбалансированность классов

9.1. Влияние несбалансированности классов

Моделируя дискретные классы, относительные частоты классов могут оказать значительное влияние на эффективность модели. Неустойчивость происходит, когда у одного или более классов есть очень низкие соотношения в учебных данных по сравнению с другими классами. Неустойчивость может присутствовать в любом наборе данных или применении, и, следовательно, практик должен знать о тонкостях моделирования этого типа данных.

Рассмотрим наши целевые переменные (классы) с этих позиций.

Первая целевая переменная имеет два класса: «лонг» и «шорт» («1» и «-1»). Их количество в наборе данных примерно одинаково.

Вторая целевая переменная имеет три класса: «лонг», «шорт» и «вне рынка» («1», «-1» и «0»). Позиций «вне рынка» примерно в три раза меньше, чем «лонгов» или «шортов».

Если мерять эффективность моделей такими показателями как общая точность, Каппа, область под кривой ROC, то выявить влияние несбалансированности классов не удастся.

Несбалансированность классов имеет серьезно влияние на предсказание вероятности класса. Здесь можно получить распределение с чрезвычайно большим скосом.

9.2. Настройка модели

Самый простой подход к противодействию отрицательному влиянию неустойчивости класса — это настройка модели с целью максимизации точности класса меньшинства. К сожалению, этот подход зависит от используемого набора данных и не может быть рекомендован как универсальный.

9.3. Случай неравных весов

У многих предсказательных классификационных моделей есть возможность установки весов наблюдениям (строкам матрицы), где каждой строке можно дать больше акцента в фазе обучения модели. Например, это возможно в моделях усиления, деревьев классификации.

Этот подход позволяет вновь балансировать набор данных обучения, увеличив веса наблюдений в классах меньшинства. Для многих моделей это может быть интерпретировано как наличие идентичных двойных точек данных с тем же самым значением предиктора.

9.4. Методы сэмплирования

Если есть априорное знание о неустойчивости класса, то можно уменьшить его воздействие при обучении модели путем формирования выборки для набора обучения таким образом, чтобы получить примерное равенство. Появление этого подхода устраняет фундаментальную проблему неустойчивости при обучении моделей. Однако если набор данных обучения составлен сбалансированным, то тестовый набор должен иметь естественное состоянием и должен отразить неустойчивость для вычисления честных оценок будущей эффективности.

Если априорный подход к выборке не возможен, то реализуют апостериорный подход к выборке, который может помочь ослабить влияние неустойчивости во время обучения модели. Два общих апостериорных подхода — это понижающая дискретизация и повышающая дискретизация данных. Повышающая дискретизация — любой метод, который имитирует или приписывает дополнительные наблюдения для улучшения балансов классов, в то время как понижающая дискретизация обращается к любому методу, который сокращает количество наблюдений для улучшения баланса классов.

Возможен подход к повышающей дискретизации, в которой наблюдения из классов меньшинства выбираются с заменой, пока классы не становятся примерно равными. Предположим, набор данных обучения содержит 6466 «лонгов» и 1411 «вне рынка». Если сохранить исходные данные класса меньшинства, а затем добавить ресемплированием 5055 случайных наблюдений (с заменой), то получим дополнение меньшей части до размера большей части. При выполнении некоторые наблюдения класса меньшинства могут обнаружиться в наборе данных обучения со справедливо высокой частотой, в то время как у каждого наблюдения в классе большой части есть единственное наблюдение в наборе данных.

Понижающая дискретизация выбирает наблюдения из большего класса так, чтобы он сравнялся размером с меньшим классом.

9.5. Обучение, чувствительное к стоимости

Вместо того чтобы оптимизировать типичный критерий качества работы, такой как точность или примесь, некоторые модели могут альтернативно оптимизировать функцию стоимости или потерь, которая дифференцировано взвешивает определенные типы ошибок. Например, может быть уместно полагать, что неправильная классификация истинных событий (ложные отрицания) в X разы более дорогостоящая, чем неправильно предсказание непримечательных событий (ложные положительные стороны). Объединение определенных затрат во время обучения модели может склонять модель к менее частым классам. В отличие от использования альтернативных сокращений, неравные затраты могут влиять на параметры модели и таким образом имеют возможности сделать истинные уточнения классификации.

Для моделей, использующих машины опорных векторов (SVM), затраты могут быть присоединены к определенным классам (в противоположность определенным типам ошибок). Вспомним, что эти модели управляются сложностью, используя функцию стоимости, которая увеличивает штраф, если выборки находятся на неправильной стороне текущей границы класса. Для неустойчивости класса неравные затраты для каждого класса могут скорректировать параметры для увеличения или уменьшения чувствительности модели к определенным классам. Заметим, что этот подход отличается от того, где у определенных типов ошибок могут быть дифференцированные стоимости. Для машин опорных векторов (SVM) всему классу можно дать увеличенную значимость. Для двух классов эти два подхода аналогичны.

Одно следствие этого подхода состоит в том, что вероятности класса не могут генерироваться для модели, по крайней мере, в доступной реализации. Поэтому нельзя вычислить кривую ROC и следует использовать иную метрику результативности. Поэтому используем статистику Каппы, чувствительность и специфику для оценки воздействия взвешенных классов.

Дополнительно, много моделей классификационных деревьев могут включить дифференцированные стоимости. К ним относятся CART и C5.0. Потенциальная стоимость предсказания принимает во внимание несколько факторов:

— стоимость определенной ошибки;

— вероятность получения ошибки;

— априорная вероятность классов.

Для деревьев предсказанные вероятности класса (или доверительное значение) не могли бы быть непротиворечивыми с дискретными предсказаниями класса при использовании неравных затрат. Заключительное предсказание класса для выборки является функцией вероятности класса и структуры издержек. Вероятности класса в терминальном узле могут заметно одобрять определенный класс, но также и иметь крупную ожидаемую стоимость. Поэтому есть разрыв между доверительным значением и предсказанным классом. Отсюда, простые вероятности класса (или доверительные значения) не должны использоваться при этих обстоятельствах.

9.6. Функции R

Приведем некоторые функции, которые могут быть использованы при работе над данным разделом.

Приведено название функции, а в скобках название пакета, в котором функция расположена. Для использования функция необходима загрузка пакета, а если его еще нет, то и установка.

Если названия пакета не приведено — это означает, что функция имеется в базовом пакете и не требуется предварительная загрузка пакета.

Для реализации идей данного раздела могут быть использованы следующие пакеты: caret, C50, DMwR, kernlab, pROC и rpart.

createDataPartition (caret)

стратифицированная случайная выборка;

coords (pROC)

оптимизирует чувствительность и специфичность на кривой ROC;

downSample (caret)

upSample (caret)

выравнивает классы;

ksvm (kernlab)

с параметром class. weights подгоняет модель SVM в режиме взвешивания.

10. Значимость предикторов для целевой переменной

Под значимостью предикторов понимается степень влияния предиктора на целевую переменную как самостоятельно, так в совокупности с другими предикторами.

Функции оценки значимости предикторов могут быть разделены на две группы: те, которые используют информацию о модели и те, которые не используют информацию о модели. Преимущество подхода, основанного на модели, состоит в том, что в этом случае подход связан с результативностью модели и что он, скорее всего, включает структуру корреляции между предикторами при вычислении значимости. Независимо от того, как вычислена значимость для большинства моделей классификации у каждого предиктора будет отдельная значимость предиктора для каждого класса (исключения — деревья классификации, бутстрэп агрегированные деревья и усиленные деревья).

10.1. Метрики значимости, полученной из моделей

Величина значимости предикторов, полученная из сведений, входящих в результат подгонки моделей, ценна тем, что значимость предикторов тесно связана с другими параметрами модели. При оценке модели в целом мы всегда получаем оценку значимости предикторов, а произведя манипуляции с предикторами (объединение, удаление) всегда можно сравнить полученный результат по результативности модели в целом.

В рамках R доступны следующие методы для оценки вклада каждого предиктора в модель:

— линейные модели: используется абсолютное значение t-статистики для каждого параметра модели;

— случайный лес: при подгонке модели вычисляется четыре меры значимости для каждого предиктора модели. В Rattle печатаются вычисленные значения значимостей, а также может быть построен график для визуального обзора;

— частные наименьшие квадраты (PLS): более полезный для нас аналог главных компонент (РСА). В PLS мера значимости предикторов основана на взвешенных суммах абсолютных коэффициентов регрессии. Веса являются функцией приведения сумм квадратов по числу компонентов PLS и вычисляются отдельно для каждого результата. Поэтому, вклад коэффициентов взвешивается пропорционально;

— рекурсивное разделение (пакет rpart): приведение функции потерь (например, среднеквадратической ошибки), приписанной к каждому предиктору в каждом разделении, сводится в таблицу. Кроме того, предикторы-кандидаты, которые также были важны, но не использовались в разделении, также сводятся в таблицу в каждом разделении. Эти сведения можно получить в функции rpart.control. Этот метод в настоящий момент не предоставляет достоверный результат при категориальной целевой переменной;

— бутстрэп агрегированные деревья (Bagged trees): для улучшенных деревьев применена методология, аналогичная отдельному дереву. Возвращается итоговая значимость предикторов;

— усиленные деревья (Boosted trees): этот метод использует подход, аналогичный отдельному дереву, но суммирует значимость предикторов при каждой усиливающей итерации. Подробности в пакете gbm;

— многомерные регрессии адаптивных сплайнов: модели пакета MARS включают программу выбора предиктора для удаления, которая смотрит на уменьшение оценки ошибки в результате обобщенной перекрестной проверки (GCV). Функция varImp следит за изменениями в статистике модели, такой как GCV, для каждого предиктора и накапливает уменьшение статистики, при добавлении каждого предиктора к модели. Это полное уменьшение используется в качестве меры по значимости предиктора. Если предиктор не использовался в функциях MARS, то его величина значимости равна нулю. Есть три статистики, которые могут использоваться для оценки значимости предикторов в моделях MARS. При использовании varImp отслеживается уменьшение обобщенной статистики перекрестной проверки при добавлении предикторов. В другом случае varImp наблюдает изменение сумм квадратов остатков (RSS) при добавлении предикторов. В третьем случае функция varImp возвращает количество включений предикторов (в заключительной, сокращенной модели). Ранее функция varImp являлась внутренней функцией для оценки значимости предикторов для моделей MARS. В настоящий момент — это обертка функции evimp в пакете earth.

10.2. Независимые от модели метрики

Если отсутствует определенный для модели способ оценки значимости, то значимость каждого предиктора оценивается индивидуально, используя подход «фильтра».

Для классификации анализ кривой ROC проводится для каждого предиктора. Для задач двух классов уменьшается набор предикторов для предсказания класса. Вычисляются чувствительность и специфика при каждом уменьшении количества предикторов, и вычисляется кривая ROC с вычислением площади под кривой AUC. Эта область используется в качестве меры значимости предиктора.

10.3. Другие подходы

Алгоритм Relief является универсальным методом для определения величины значимости предиктора. Первоначально разрабатывался для проблем классификации с двумя классами, но был расширен для решения широкого диапазона проблем. Алгоритм Relief может упорядочить непрерывные предикторы, фиктивные переменные, а также может опознать нелинейные отношения между предикторами и целевой переменной. Алгоритм Relief использует случайно выбранные наблюдения и их ближайших соседей для оценки каждого предиктора в отдельности.

Для определенного предиктора алгоритм пытается определить расстояние между классами в изолированных пространствах данных. Для выбранных в произвольном порядке наблюдений из набора данных обучения алгоритм находит самые близкие наблюдения из обоих классов (названный «хитом» и «пробелом»). Для каждого предиктора вычисляется разность мер значимости между случайным наблюдением и удачами и неудачами.

10.4. Функции R

Приведем некоторые функции, которые могут быть использованы при работе над данным разделом.

Приведено название функции, а в скобках название пакета, в котором функция расположена. Для использования функция необходима загрузка пакета, а если его еще нет, то и установка.

Если названия пакета не приведено — это означает, что функция имеется в базовом пакете и не требуется предварительная загрузка пакета.

Много моделей имеют встроенные средства по оценке значимости предикторов. Пакет caret содержит общий класс для вычисления и возврата этих значений. Существуют следующие методы для этих классов: C5.0, JRip, PART, RRF, RandomForest, bagEarth, classbagg, cubist, dsa, earth, fda, gam, gbm, glm, glmnet, lm, multinom, mvr, nnet, pamrtrained, plsda, randomForest, regbagg, rfe, rpart, sbf,

Для реализации идей данного раздела могут быть использованы следующие пакеты: caret, CORElearn, minerva, pROC и randomForest. Перечень полезных функций:

cor

оценивает корреляцию между предикторами и целевой переменной;

corr

оценивает ранговую корреляцию по Спирмену между предикторами и целевой переменной;

filterVarImp (caret)

количественно оценивает отношения между предикторами и целевой переменной;

mine (minerva)

вычисляет статистику MIC между предикторами и целевой переменной;

t. test

для категориальных предикторов оценивает по одному связь между предиктором и целевой переменной. Применение ко всем предикторам выполняется по apply;

attrEval (CORElearn)

для категориальных целевой переменной вычисляется статистика Relief нескольких версий. Также функция может быть использована для индекса Gini;

spls (spls)

для категориальной целевой переменной отбирает наиболее значимые для нее предикторы. Имеет высокую вычислительную эффективность;

plsda (caret)

для категориальной целевой переменной отбирает наиболее значимые для нее предикторы.

11. Выбор предикторов

С практической точки зрения модель с меньшим количеством предикторов легче поддается толкованию, а для платных источников котировок может привести к уменьшению затрат. Статистически более привлекательно оценивать меньше параметров. Кроме того, что более важно, на некоторые модели могут негативно влиять не информативные предикторы.

Некоторые модели естественно стойкие к неинформативным предикторам. Модели, основанные на дереве, например, интуитивно проводят отбор предикторов. Например, если предиктор не используется ни в одном расщеплении во время построения дерева, уравнение предсказания функционально независимо от предиктора.

Важное различие, которое будет сделано в выборе предиктора, является различием контролируемых и безнадзорных методах (методы с учителем и без учителя). Если значение целевой переменной игнорируется во время устранения предикторов, то метод безнадзорный (без учителя). В каждом случае целевая переменная не зависит от фильтрования. Для контролируемых методов (с учителем) предикторы определенно выбраны с целью увеличения точности или поиска такого подмножества предикторов, которое уменьшает сложность модели. Здесь значения целевой переменной обычно используется для определения величины значимости предикторов.

Проблемы, связанные с каждым типом выбора предиктора, очень отличаются, и имеются большие объемы литературы по этой теме.

11.1. Следствия использования неинформативных предикторов

Прежде всего, выбор предиктора направлен на удаление не информативных или избыточных предикторов из модели. Как со многими проблемами, обсужденными в этом тексте, выбор значимости предиктора зависит от используемой модели. Во многих моделях оцениваются параметры каждой составляющей в модели. Из-за этого присутствие не информативных предикторов может прибавить неопределенность к предсказаниям и уменьшить полную эффективность модели.

Учитывая потенциальное негативное воздействие, есть потребность поиска минимального подмножества предикторов. Основная цель состоит в уменьшении их количества, но таким способом, который максимизирует результативность. Как мы можем уменьшить сложность, негативно не влияя на эффективность модели?

11.2. Подходы для сокращения количества предикторов

Кроме моделей со встроенным выбором предиктора, большинство подходов для сокращения количества предикторов может быть разделено на две главных категории:

— методы обертки оценивают многоуровневые модели, используя процедуры, которые прибавляют и/или удаляют предикторы для поиска оптимальной комбинации, которая максимизирует результативность модели. В основном методы обертки являются алгоритмами поиска, которые принимают предикторы на входе и используют результативность модели как результат, подлежащий оптимизации.

— методы фильтра оценивают уместность предикторов за пределами предсказательных моделей и впоследствии моделируются только предикторы, которые удовлетворяют некоторому критерию. Например, для задач классификации индивидуально оценивается каждый предиктор для проверки существования вероятного отношения между ним и наблюдаемыми классами. Только предикторы со значимыми отношениями включаются в модель классификации.

У обоих подходов есть преимущества и недостатки.

Методы фильтра более эффективны в вычислительном отношении, чем методы обертки, но критерий выбора непосредственно не связан с эффективностью модели. Кроме того, большинство методов фильтра оценивает каждый предиктор отдельно, и, следовательно, могут быть выбраны избыточные, то есть чрезвычайно коррелированные предикторы, и важные взаимодействия между предикторами не будут определены количественно.

Преимущество метода обертки состоит в оценке многих моделей (что может потребовать настройки параметров), и таким образом приведет к увеличению времени вычислений. Также методы обертки увеличивают риск переобучения модели.

11.3. Методы обертки

Методы обертки ищут предикторы, которые при включении в модель улучшают результат. Простой пример — классический прямой выбор для линейной регрессии. Здесь, предикторы оцениваются по одному в текущей модели линейной регрессии. По статистическому тесту проверяется значимость каждого из недавно добавленных предикторов. Если, по крайней мере, у одного предиктора есть р-значение ниже порога, предиктор добавляется к модели, и процесс запускается снова. Алгоритм останавливается, когда ни одно из р-значений для остающихся предикторов статистически не значимо. В этой схеме линейная регрессия — основной ученик, и прямой выбор — процедура поиска. Целевой функцией является оптимизируемая статистическая величина — р-значение.

Есть несколько проблем с этим подходом:

— прямая процедура поиска не переоценивает прошлые решения.

— использование повторных тестов гипотезы этим способом лишает законной силы многие их статистические свойства, так как одни и те же данные оцениваются много раз.

— максимизация статистического значения может не приводить к максимизации результативности предсказания.

Обычно рассматривают следующие оценки результативности предсказания: ошибка RMSE, точность классификации, размер области под кривой ROC.

Другой подход основан на корреляции предикторов, при котором ищут сильную корреляцию между целевой функцией и предикторами и слабую корреляцию между предикторами.

Для предсказательных моделей, а не объясняющих, есть два важных положения:

— большая часть критики методов обертки основана на использовании гипотез статистических тестов;

— методологии, основанные на сомнительных статистических принципах, все же могут привести к очень точным моделям в случае полного, методического процесса проверки с независимыми данными.

Следующие подразделы описывают различные методы поиска для использования с методами обертки.

11.3.1. Выбор вперед, обратный и пошаговый

Пошаговый выбор — популярная модификация, в которой после добавления предиктора к модели, переоценивается каждый параметр для удаления из модели. В некоторых случаях порог р-значения для добавления и удаления предикторов может сильно отличаться. В обратном выборе начальная модель содержит все предикторы P, которые затем многократно удаляются для определения тех, которые не значительно способствуют модели. Эти процедуры могут быть улучшены путем использования, например, статистики AIC для добавления или удаления предикторов из модели.

Имеется разновидность обратного алгоритма выбора, названная рекурсивным устранением предиктора. При создании полной модели вычисляется мера значимости предиктора, по которой упорядочиваются предикторы от самого важного предиктора до наименее важного. Вычисления значимости могут быть основаны на модели (например, критерий значимости случайного леса) или на использовании более общего подхода, который независим от полной модели. На каждом этапе поиска наименее важные предикторы многократно устраняются до восстановления модели. Как прежде, при создании новой модели оценивается целевая функция для модели. Процесс продолжается для некоторой предопределенной последовательности, и отобранное подмножество, соответствующий оптимальному значению целевой функции, используется в качестве заключительной модели.

11.3.2. Генетические алгоритмы

Генетические алгоритмы (ГА) оптимизации основаны на эволюционных принципах биологических совокупностей и, как признается, были эффективны при обнаружении оптимальных решений сложных, многомерных функций. Определенно, ГА создавались для подражания эволюционному процессу, при котором воспроизводится текущая совокупность решений, генерирующая дочерние элементы, которые конкурируют за выживаемость. Самым живучим разрешают воспроизводство, создавая следующее поколение дочерних элементов. По истечении времени поколения сходятся к пригодному варианту, и может быть выбрано оптимальное решение.

Как мы видели к настоящему времени, проблема выбора предиктора является, по сути, комплексной проблемой оптимизации, в которой ищут комбинацию предикторов, обеспечивающую оптимальное предсказание отклика.

11.4. Методы фильтра

Методы фильтра оценивают предикторы до обучения модели, и, основываясь на этой оценке, подмножество предикторов включается в модель. Так как оценка предикторов отделена от модели, многие из метрик значимости предикторов пригодны для фильтрования. Большинство этих методов одномерное, что означает оценку каждого предиктора по отдельности. В этом случае существование коррелированных предикторов позволяет выбрать значимые, но избыточные, предикторы. Очевидным следствием этой проблемы является выбор слишком большого числа предикторов, и в результате возникают проблемы коллинеарности.

Кроме того, если используются гипотезы, основанные на тестах для определения статистически значимых отношений с другими предикторами (такие как t-тест), то может возникнуть проблема кратности. Например, если уровень значимости α = 0.05 используется в качестве порога р-значения для значения у каждого отдельного теста, то есть теоретический ложно-положительный уровень 5%. Однако при проведении большого количества одновременных статистических тестов полная ложно-положительная вероятность увеличивается по экспоненте.

В то время как методы фильтра достаточно простые и быстрые, есть субъективизм в процедуре. У большинства методов нет очевидной точки разделения для отбора предикторов в модель. Даже в случае гипотез, основанных на статистических тестах, пользователь все равно должен выбрать уровни значимости, которые будут применены в итоге.

11.5. Выбор смещения

В то время как некоторые методы фильтра или процедуры поиска более эффективны, чем другие, более важный вопрос связан с тем, как вычисляется результативность модели (особенно при небольшом объеме выборки). Может произойти переобучение предикторов к учебным данным, что без надлежащей проверки может остаться незамеченным.

Коэффициенты ошибок «пропускают один», были основаны на модели SVM после выбора предикторов. Было предположено, что при повторении выбора предиктора с немного отличающимся набором данных, результаты могут измениться. Оказывается, что в некоторых случаях неопределенность, стимулированная выбором предиктора, может быть гораздо больше, чем неопределенность в модели (как только предикторы были выбраны). Более того было показано, что стратегия перекрестной проверки «пропускает один» может достигать нулевых ошибок даже при полностью не информативных предикторах.

Логическая ошибка в исходном подходе четкая. Модель создавалась из набора данных обучения и, используя эти данные, предикторы были оценены и упорядочены. Если модель подогнана снова, используя только важные предикторы, результативность почти наверняка изменится к лучшему для этого же набора данных.

Методологическая ошибка произошла, потому что выбор предиктора не рассмотрели как часть процесса построения модели. Также, этот процесс следует включить в пределах процедуры ресемплирования так, чтобы изменение выбора предиктора было получено в результатах.

Чтобы должным образом повторно дискретизировать процесс выбора предиктора, необходим «внешний» цикл ресемплирования, который охватывает весь процесс.

Было показано, что при бутстрэпинге, 10-кратной перекрестной проверке или повторения набора тестов должным образом использовать методы ресемплирования, то результаты модели определяются правильно.

У дополнительного уровня ресемплирования может быть значимое негативное воздействие на вычислительную эффективность процесса выбора предиктора. Однако особенно с небольшими наборами данных обучения, этот процесс решительно уменьшит возможности переобучения к предикторам.

Риск переобучения этим способом не ограничен рекурсивным выбором предиктора или обертками вообще. При использовании других процедур поиска или фильтрации для сокращения количества предикторов риск все еще остается.

Следующие ситуации увеличивают вероятность смещения выбора:

— набор данных небольшой;

— число предикторов большое (так как возрастает вероятность объявления значимым неинформативного предиктора);

— предсказательные возможности модели не оправданно велики (например, модели черного ящика), которая, более вероятно, переобучена на данных;

— независимый набор тестов не доступен.

Когда набор данных большой, рекомендуются отдельные наборы данных для выбора предикторов, настройки модели и проверки заключительной модели (и набор предикторов). Для небольших наборов данных обучения надлежащее ресемплирование критично. Если объем данных не слишком маленький, то также рекомендуется отделить небольшой набор для тестирования, чтобы проверить дважды на отсутствие грубых ошибок.

11.6. Инструменты R для выбора предикторов

11.6.1. Пакет Boruta

Представим реализацию алгоритма для вычисления всех релевантных предикторов пакетом Boruta. Алгоритм использует подход обертки, созданный вокруг классификатора случайного леса. Алгоритм — расширение идеи для определения релевантности методом сравнения релевантности реальных предикторов к их случайным пробам.

Устанавливаются пороги, ниже которых предикторы отбрасываются. В результате по каждому предиктору получаем фактор со значениями Confirmed, Rejected или Tentative. Отвергнутые предикторы помечаются.

Устанавливаются параметры типа классификации. По умолчанию — случайный лес из пакета randomForest. В результате выдается индекс Gini.

11.6.2. Пакет varSelRF

Пакет для выбора предикторов в случайном лесе для объекта randomforest.

Выбор предикторов случайных лесов, используя как обратное удаление предикторов (для выбора небольших множеств безызбыточных переменных) и выбора, основанного на спектре значимости (что-то похожее на рисунки каменистой осыпи для выбора больших, потенциально чрезвычайно коррелированных предикторов). Основное применение для данных большой размерности (например, применение для данных геномики и протеомики).

11.6.3. Пакет FSelector

Методы для выбора предиктора могут быть разделены на два подхода: ранжирование предикторов и выбор подмножества. В первом подходе предикторы упорядочены по некоторым критериями, а затем выбираются предикторы выше определенного порога. Во втором подходе ищется промежуток между подмножествами предикторов для оптимального подмножества. Кроме того второй подход может быть разделен на три части:

— подход фильтра: сначала выбираются предикторы, а затем используется их подмножество для выполнения алгоритма классификации.

— встроенные подходы к выбору предикторов выполняются при выполнении алгоритма классификации.

— подход с оберткой алгоритма для классификации применяется к набору данных для идентификации лучших предикторов.

Пакет FSelector предлагает алгоритмы для фильтрации предикторов, алгоритмы с оберткой классификаторов, и алгоритм поиска разделения предикторов на подмножества (например, поиск по первому наилучшему совпадению, обратный поиск, поиск вперед, поиск восхождения на вершину). Пакет также позволяет выбрать подмножества предикторов с учетом их весов, выполняя различные способы отсечения.

11.6.4. Пакет «CORElearn»

Пакет «CORElearn» имеет большое число критериев упорядочения предикторов по их важности. Особое место занимают критерии, которые основаны на Relief, что позволяет оценивать предикторы, имеющие корреляцию между собой. Учет этой корреляции позволяет строить модели случайного леса, дающие устойчивые характеристики вне выборки.

11.7. Функции R

Приведем некоторые функции, которые могут быть использованы при работе над данным разделом.

Приведено название функции, а в скобках название пакета, в котором функция расположена. Для использования функция необходима загрузка пакета, а если его еще нет, то и установка.

Если названия пакета не приведено — это означает, что функция имеется в базовом пакете и не требуется предварительная загрузка пакета.

Для реализации идей данного раздела могут быть использованы следующие пакеты: caret, klaR, leaps, MASS, pROC, rms и stats.

11.7.1. Выбор вперед, назад и пошаговый

Есть несколько функций R для этого класса:

— может использоваться step в пакете stats для поиска соответствующих подмножеств для линейной регрессии и обобщенных линейных моделей (функции lm и glm, соответственно). Аргумент direction управляет методом поиска признака (например, «both,» «backward» или «forward»). Более общая функция — функция stepAIC в пакете MASS, который может обработать дополнительные типы моделей. В любом случае, статистика AIC (или в ее разновидности) используется в качестве целевой функции;

— функция fastbw в пакете rms проводит подобные поиски;

— у функции regsubsets в пакете leaps есть подобная функциональность;

— пакет klaR содержит функцию stepclass, которая ищет пространство предикторов для моделей, максимизирующая точность кросс-проверки.

Функция train пакета caret позволяет уменьшить риск смещения при выборе предикторов.

11.7.2. Рекурсивное удаление предикторов

Пакеты caret и varSelRF содержат функции ля рекурсивного удаления предикторов.

varSelRF (varSelRF)

рекурсивное удаление предикторов только в моделях случайного леса

rfe (caret)

универсальная обертка для любых предсказательных моделей

11.7.3. Методы фильтрации

В пакете caret имеется функция sbf, которая выбирает предикторы для модели с оценкой результативности ресемплированием.

Часть 2. Краткое описание Rattle

Вторая часть книги является краткой инструкцией для работы с Rattle. Организация материала продиктована порядком построения моделей, предусмотренным Rattle в виде последовательности вкладок программы.

Вторая часть книги является переводом краткого руководства по Rattle.

Эта часть полезна как на этапе первоначального знакомства с Rattle, так и на этапе постоянного использования в качестве краткого справочника.

Текст не содержит подробностей и будет полезен тем, кто либо только начинает работать с предсказательными моделями, либо хочет апробировать некоторую идею.

12. Работа новичка с Rattle

12.1. Интерфейс Rattle

Рассмотрим интерфейс Rattle. Интерфейс основан на ряде последовательных вкладок, через которые выполняется предсказательное моделирование трендов. Для любой вкладки, как только мы предоставили запрошенную информацию, нажмем кнопку Выполнить для выполнения действия. Отметим в меню кнопку Help (Справка).

Интерфейс Rattle спроектирован как простой интерфейс к мощному комплекту базовых инструментов для моделирования финансовых данных. Общий процесс состоит в последовательном движении по вкладкам, слева направо, выполняя соответствующие действия. Для любой вкладки мы конфигурируем опции и затем нажимаем кнопку Выполнить (или F2) для выполнения соответствующей задачи. Важно отметить, что задачи не выполняются, пока кнопка Выполнить (или F2, или пункт меню Выполнить в закладке Tools (Инструменты)) не нажата.

Строка состояния внизу окна укажет на завершение действия. Сообщения от R (например, сообщения об ошибках) могут появиться на консоли R, на которой был запущен Rattle. Так как Rattle — простой графический интерфейс, находящийся поверх R, важно помнить, что некоторые ошибки, с которыми встречается R при загрузке данных (и фактически во время любой работы, выполняемой Rattle), могут быть выведены на консоли R.

Код R, который Rattle передает R для выполнения, записан в журнале, доступном на вкладке Log. Это позволяет рассматривать команды R, которые выполняют соответствующие задачи анализа данных. Фрагменты кода R можно копировать как текст с вкладки Log и вставлять в консоль R, в которой исполняется Rattle. Это позволяет развернуть Rattle для основных задач, и дает нам полную мощность R, которую, при необходимости, можно развернуть, возможно, с использованием большего количества опций команды, чем представлено через интерфейс Rattle. Этим предоставляется возможность экспортировать целый сеанс как файл скрипта R.

Журнал служит записью предпринятых действий и позволяет повторить выполненные действия непосредственно и автоматически в R в более позднее время. Просто выберите (чтобы вывести на экран) вкладку Log и щелкните по кнопке Export. Будет экспортирован журнал в файл, у которого будет расширение R. Можно будет включить или исключить обширные комментарии, имеющиеся в журнале и переименовать внутренние переменные Rattle (с символов «crs$» в символы по выбору).

Теперь рассмотрим главные элементы пользовательского интерфейса Rattle, особенно панель инструментов и меню. Начнем с основной концепции — проекта.

12.1.1. Проекты

Проект — упаковка набора данных, выбранные переменные, исследования и модели, созданные из данных. Rattle позволяет сохранять проекты для последующего продолжения работы.

Проект обычно сохраняется в файле с расширением. Rattle. Фактически, файл — это стандартный двоичный файл RData, используемый R для хранения объектов в более компактной двоичной форме. Любая система R может загрузить такой файл и, следовательно, иметь доступ к этим объектам, даже не исполняя Rattle.

Загрузка файла. Rattle в Rattle (используя кнопку Открыть) загрузит проект в Rattle, восстанавливая данные, модели и другую выведенную на монитор информацию, связанную с проектом, включая информацию об итогах и журнале. Затем можно возобновить анализ данных от прошлой точки.

С точки зрения файловой системы можно переименовать файлы (так же как расширение, хотя это не рекомендуется), не воздействуя на сам файл проекта, у имени файла нет формальной опоры на содержание, так что используйте его с содержательным значением. Лучше избегать пробелов и необычных символов в именах файла.

Проекты открываются и сохраняются с использованием соответствующих кнопок на панели инструментов или из меню Project.

12.1.2. Панель инструментов

Самая важная кнопка на панели инструментов — это кнопка Выполнить. Все действия инициируется Выполнить. Заменой клавиши Выполнить является функциональная клавиша F2. Также доступен пункт меню Выполнить. Стоит повторить, что парадигма пользовательского интерфейса, используемая в пределах Rattle, состоит в том, чтобы задать параметры на вкладке, а затем Выполнить соответствующее действие.

Следующие некоторые кнопки на панели инструментов касаются понятия проекта в пределах Rattle. Проекты были обсуждены выше.

Щелчок по кнопке Создать восстановит Rattle в свое изначальное состояние запуска без загруженного набора данных. Это может быть полезно, когда исходный набор данных был внешне изменен (внешний к Rattle и R). Мы, возможно, например, управляли данными в электронной таблице или программе базы данных и реэкспортировали данные в файл CSV. Чтобы перезагрузить этот файл в Rattle, если мы ранее загрузили его в текущий сеанс Rattle, следует очистить Rattle щелчком кнопки Создать. Затем указать имя файла и перезагрузить его.

Кнопка Report предоставит отформатированный отчет, основанный на текущей вкладке. Rattle имеет много шаблонов отчетов и генерирует документ в открытом стандартном формате ODT для открытого исходного кода и поддерживается стандартом LibreOffice. Пока поддержка генерируемых пользователями отчетов ограничена, журнал предоставляет необходимые команды, используемые для генерирования файла ODT. Таким образом, можно создать собственные шаблоны ODT и применить их в пределах контекста текущего сеанса Rattle.

Кнопка Export экспортирует различные объекты и сущности из Rattle. Подробности доступны в соответствующих разделах в следующих главах. Природа экспорта зависит от активной вкладки и в пределах вкладки от активной опции. Кнопка Export не доступна для всех вкладок и опций.

12.1.3. Меню

Вкладка в меню Tools обеспечивают альтернативный доступ ко многим функциям интерфейса. Ключевой пункт в использования меню состоит в том, что по нему можно перемещаться из клавиатуры.

Вкладка меню Project предоставляет доступ к опциям Открыть и Сохранить для загрузки и сохранения проектов «в» или «из» файлов. Меню Tools предоставляет доступ к некоторым другим функциям панели инструментов, а так же доступ к определенным вкладкам. Пункт меню Settings позволяет нам управлять многими дополнительными настройками Rattle. Они включают подсказки и использование более современного устройства графики.

Обширная справка доступна через пункт меню Help. Структура меню следует за структурой вкладок главного интерфейса. При выборе темы справки краткий выпадающий текст выведет на экран некоторую основную информацию на английском языке. Для многих из открытых опций отображается дополнительная информация, которая будет выведена на экран в пределах Веб-браузера на английском языке. Эта дополнительная документация предоставляется непосредственно из документации R или соответствующим пакетом R.

12.1.4. Перемещение с помощью клавиатуры

Перемещение с помощью клавиатуры обычно инициировано функциональной клавишей F10. Клавиши со стрелками клавиатуры могут использоваться для перемещения. Нажатие клавиши Enter клавиатуры выберет выделенный пункт меню.

Разумное использование клавиатуры (в частности клавиши со стрелками, ключи Tab и Shift-Tab и клавиша Enter, вместе с F2 и F10) позволяет нам полностью управлять Rattle с клавиатуры.

12.2. Введение в моделирование с Rattle

Предсказательное моделирование комбинирует понятия, инструменты и алгоритмы из машинного обучения, искусственного интеллекта и статистики для обучения моделей на исторических данных и последующего предсказания целевой переменной на тестовых и проверочных данных.

Rattle (Простое обучение аналитическим инструментам R) является инструментом в виде графического интерфейса пользователя (GUI) (Уильямс, 2009b). Он определенно разрабатывался для упрощения перехода от первых прикидочных шагов к созданию предсказательных моделей, что предполагает наличие GUI, к сложным вариантам предсказательных моделей с использованием мощного статистического языка R.

Rattle объединяет множество пакетов R, которые важны для построения предсказательных моделей, но часто не легки для использования новичком. На первоначальном этапе применения Rattle понимание R не требуется. Пользовательский интерфейс Rattle открывает дверь в R как инструмента статистического моделирования данных.

12.3. Построение модели

Rattle определенно использует простую концепцию, основанную на вкладках, для пользовательского интерфейса, выполняя операции над данными в соответствии с назначением вкладки. Типичный поток операций следует с левой вкладки (вкладка Data — Данные) направо (вкладка Log — Журнал). Для любой вкладки пользователь должен указать доступные параметры, а затем нажать кнопку Выполнить (или F2), чтобы выполнить соответствующую задачу. Строка состояния внизу окна укажет завершение действия.

Можно показать, что очень просто, если нереалистично, Rattle создает предсказательную модель всего четырьмя щелчками мышью. Запускаем R, загружаем пакет Rattle и даем команду Rattle (). Затем:

— щелкаем по кнопке Выполнить;

— щелкаем по Yes в раскрывшемся окне;

— щелкаем по вкладке Model;

— щелкните по кнопке Выполнить.

На основе демонстрационных данных мы получили предсказательную модель классификационного типа в виде дерева решений.

Одним или еще двумя щелчками могут быть созданы альтернативные модели. Еще несколькими щелчками получим на мониторе диаграмму оценки для сравнения результативность созданных моделей. Затем еще пара щелчков — и применили обученные на первом этапе модели на новых наборах данных.

Конечно, применимость древовидной модели на финансовых рынках крайне ограниченна. Но простой пример наглядно демонстрирует простоту применения Rattle.

Общие шаги при проектировании предсказательной модели в итоге выглядит как:

— загрузите исходные данные (Source) в одном из возможных форматов и выберите переменные и назначьте их роли.

— исследуйте (Explore) данные, чтобы понять распределения.

— протестируйте (Test) распределения;

— преобразуйте (Transform) данные, чтобы удовлетворить моделированию.

— создайте Модели (Model);

— оцените (Evaluate) модели на разных наборах данных.

— рассмотрите Log (Журнал) процесса предсказания целевой переменной.

Код R, созданный и выполняемый Rattle, записан в журнале, доступном на вкладке Log, вместе с поучительными комментариями. Это позволяет пользователю рассматривать фактические команды R. Фрагменты кода R также могут быть скопированы как текст на консоль R для исполнения, или экспортированы в файл — вкладка Export (Экспорт) при нахождении во вкладке Log. Эти возможности Rattle позволяют решать задачи моделирования, а при необходимости использовать всю мощь R с использованием всех возможностей R и его пакетов, недоступных из Rattle.

12.4. Данные (вкладка Data)

Если нет желания использовать свой набор данных в Rattle, то нажимаем кнопку Выполнить (например, стартуем Rattle, и сразу щелкаем по Выполнить), и предоставляется опция для загрузки одного из наборов данных, например, из файла CSV.

Rattle может загрузить данные из различных источников. Он непосредственно поддерживает CSV (запятая как разделитель данных), TXT (табуляция как разделитель данных), ARFF (общий формат наборов данных анализа данных, который добавляет тип информации к файлам CSV), и соединения ODBC (позволяет соединение со многими источниками данных, включая MySQL, SQLite, Postgress, MS/Excel, MS/Доступ, SQL-сервер, Oracle, IBM DB2, Netezza и Teradata). Фреймы данных R, присоединенные к текущему сеансу R и наборам данных, доступным из пакетов, установленных в библиотеках R, также доступны через интерфейс Rattle.

Для исследования Rattle как инструмента по созданию предсказательных моделей, считаем набор данных со сведениями об аудите, предоставленный в составе пакета Rattle. Данные искусственные, но отражают набор данных реального мира, используемый для рассмотрения результатов исторических финансовых аудитов. Сведения, например, полученные налоговиком налога на доходы, основаны на информации, предоставленной налогоплательщиком. Можно выполнить тысячи случайных аудитов, а результаты покажут, требуется ли корректировка предоставленной информации, приводящая к изменению ответственности налогоплательщика.

Контрольный набор данных предоставлен и как набор данных R и как файл CSV. Путь к файлу следующий: \R\library\Rattle\csv\audit\.

Набор данных состоит из 2,000 вымышленных налогоплательщиков, которые контролировались для выполнения налоговых требований. Для каждого случая результат после аудита записан (должны ли финансовые требования были быть скорректированы или нет). Фактическая сумма в долларах корректировки, которая закончилась, также записана (заметим, что корректировки могут пойти в любом направлении).

Контрольный набор данных содержит 13 переменных (или столбцов), первым из которых является уникальным клиентским идентификатором.

При загрузке данных в Rattle могут использоваться определенные специальные префиксы к именам переменных для указания роли переменной по умолчанию. Например, если имя переменной начинается с «ID_», то переменная отмечена как имеющая роль идентификатора. Другие префиксы включают: «IGNORE_», «RISK_», «IMP_» (для оценки) и «TARGET_». В нашем примере имеются IGNORE_Accounts и TARGET_Adjusted.

Если префиксы в именах переменных отсутствуют, то Rattle пытается самостоятельно назначить роли переменных, но в этом случае обычно приходится вручную корректировать роли переменных после загрузки.

Опция CSV вкладки Data предоставляет самый простой подход к загрузке данных в Rattle. Если на вкладке Data нажать кнопку Выполнить без имени файла CSV, то Rattle предлагает опцию для загрузки набора данных примера. Щелчок по полю Filename перечислит другие доступные наборы данных выборки, включая «audit. csv».

Как только Rattle загрузит набор данных, текстовое окно будет содержать список доступных переменных и их ролей по умолчанию (рис.12.2).

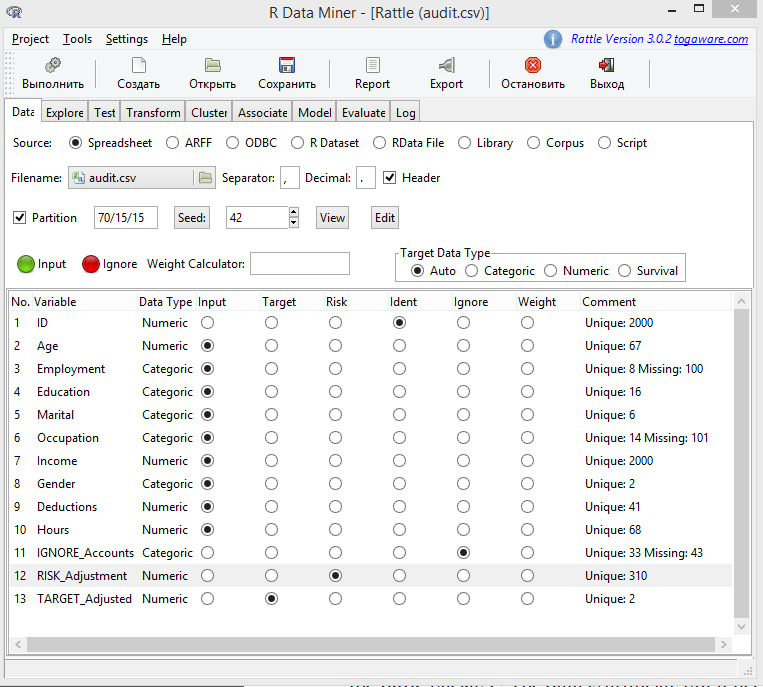
По умолчанию у большинства переменных есть роль Input (Вход), что указывает на то, что эта переменная содержит исходные данные для моделирования. Одну переменную можно указать как Целевую (Target) переменную, и дополнительно указать другую переменную как переменную Риска (risk) (которая является мерой «целей»). Другие роли Ident (идентификатор) и Ignore (Игнорировать).

Rattle по умолчанию разделит исходный набор данных на обучающий (Training), проверочный (Validation) и тестовый (Testing) в пропорциях (70/15/15). Это разделение полезно в исследовательских целях, когда данные достаточно большие. Его основная цель, тем не менее, состоит в выборе 70%-ой выборки для обучения моделей, оставляя 30% от исходного набора данных для проверки.

12.5. Исследование (вкладка Explore)

Исследовательский анализ данных важен в понимании данных. Вкладка Explore предоставляет многочисленные числовые и графические инструменты для исследования данных.

12.5.1. Опция сводки (Summary)

Опция Summary использует команду R summary () для предоставления основной одномерной сводки. К ней добавлены contents и describe из пакета Hmisc. Расширенные сводки включают дополнительную статистику, предоставленную пакетом fBasics, эксцесс и асимметрия, так же как сводка пропущенных значений, использует возможности по пропущенным значениям из пакета mice.

12.5.2. Опция распределения (Distributions)

Опция Distributions (Распределений) предоставляет доступ к многочисленным типам рисунка. Всегда полезно рассмотреть распределения значений каждой из переменных до анализа данных. Хотя вышеупомянутые сводки помогают, визуальные исследования часто могут быть исключительно полезными.

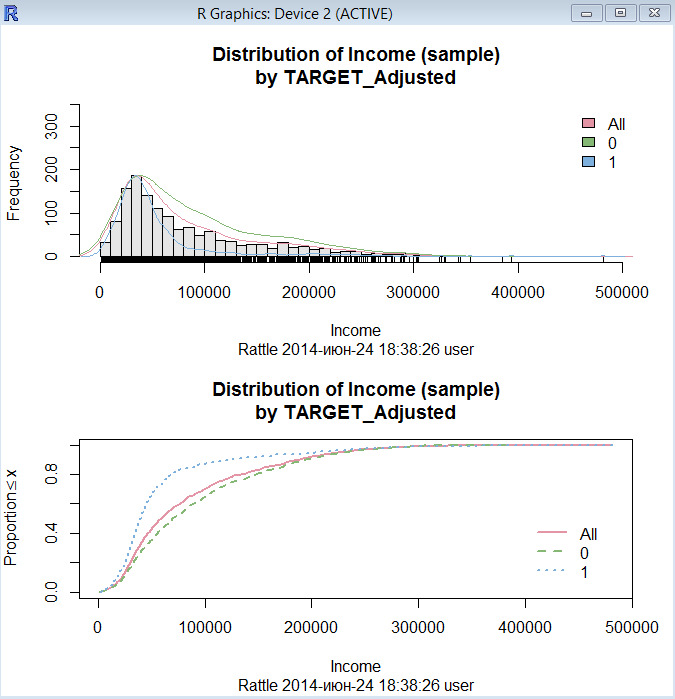
12.5.3. Опция преобразования (Transform)

Очистка данных и создание новых инструментов (получение новых переменных) занимают намного больше времени для разработчика моделей. Есть много подходов к очистке данных, и язык программирования, подобный R, поддерживает их. Вкладка Transform Rattle предоставляет ряд возможностей для преобразования, включая масштабирование, уменьшение асимметрии, заполнение пропущенных значений, превращение числовых переменных в категориальные переменные, и наоборот, работа с выбросами, а также удаление переменных и наблюдений с пропущенными значениями. Здесь рассмотрим некоторые из преобразований.

12.5.4. Опция масштабирования (Rescale)

Опция Rescale (Масштабирование) предлагает ряд операций масштабирования, используя команду масштаба scale базового пакета и команду масштабирования rescale из пакета reshape. Масштабирование включает центрирование вокруг нуля (Перецентр-Recenter), масштабирование в промежутке 0—1 (Scale [0,1]), преобразование в ранговое упорядочение (Ранг-Rank), устойчивое масштабирование около нуля, используя медиану (-Медиана/MAD), и повторное масштабирование, основанное на группах в данных.

Для любого преобразования исходная переменная не меняется, но помечается как игнорируемая. Новая переменная создается с префиксом, добавленным к имени переменной, чтобы указать на преобразование. Префиксы бывают: «RRC_», «R01_», «RRK_», «RMD_» и «RBG_», соответственно.

Эффект масштабирования может быть исследован, используя вкладку Explore (рисунок 12.3). Заметьте, что Rattle накладывает столбиковые диаграммы с рисунком плотности по умолчанию.

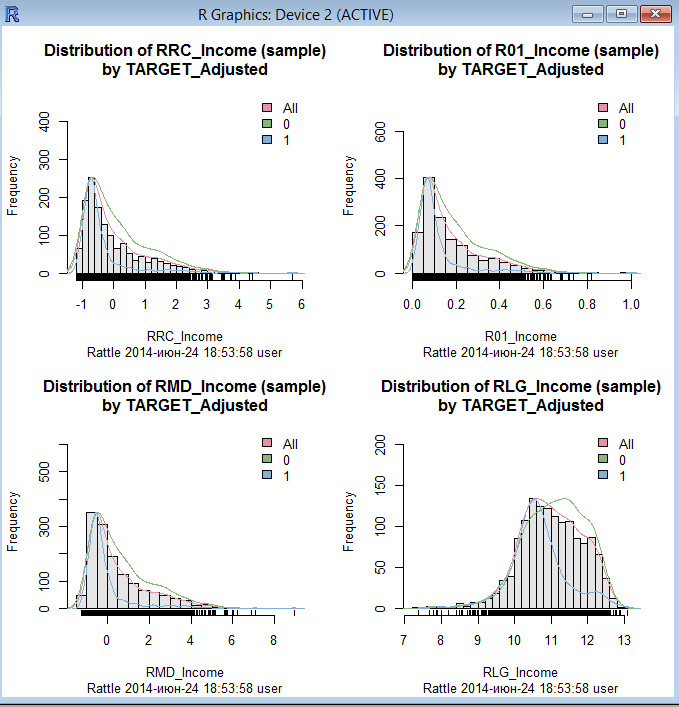
12.5.5. Опция заполнения (Impute)

Заполнение пропущенных значений — хитрая тема и должно делаться только с хорошим пониманием данных. Часто, наблюдаемые данные (в отличие от экспериментальных данных) будут содержать пропущенные значения, и это может вызвать проблему для алгоритмов анализа данных. Например, опция Forest (использующая randomForest) без уведомления удаляет любое наблюдение с пропущенным значением! Для наборов данных с очень большим количеством переменных и неразумным числом пропущенных значений это вполне может привести к небольшому, нетипичному набору данных, или даже отсутствию данных вообще!

Есть много типов возможных заполнений, но только некоторые из них непосредственно доступны в Rattle. Далее, Rattle еще не поддерживает множественное заполнение.

Самое простое, и наименее рекомендуемое, заполнение заменяет все пропущенные значения переменной единственным значением. Это имеет смысл, когда мы знаем, что отсутствующие значения фактически имеют значение «0», а не неизвестную величину. Например, в контексте налогообложения, если налогоплательщик не предоставил значение для определенного типа удержаний, то можно предположить, что они равны нулю. Точно так же, если число потомков в семействе не записано, то разумно предположить, что это нуль.

В общем, для пропущенных значений, которые, как известно, не равны нулю, следует использовать некоторое «центральное» значение переменной. Это часто среднее, медиана, или мода. Можно использовать среднее, например, если переменная нормально распределена (и в особенности имеет небольшую асимметрию). Если данные действительно имеют некоторую асимметрию, например, есть некоторое количество очень больших значений, то предпочтительней медиана.

Опасайтесь любого выполняемого заполнения. Оно, в конце концов, изобретает новые данные!

12.5.6. Опция перекодирования (Recode)

Опция Recode (Перекодирование) предоставляет многочисленные операции повторного отображения, включая укладывание в стеллаж, логарифмирование, отношения и отбор категориальных переменных в переменные индикатора для ситуации, где построитель модели требует числовых данных. Rattle предоставляет возможности использовать укладывание в стеллаж по Квантилям, KMeans и с равной шириной. Для каждой опции число стеллажей по умолчанию равняется 4, но можно изменить под свои потребности. Генерируемые переменные снабжены префиксом «BQn_», «BKn_» и «BEn_» соответственно, с «n», указывающем число стеллажей. Таким образом, можно создать много стеллажей для любой переменной.

Есть также опции Join Categorics (Соединение категориальных) — удобный способ расслоить набор данных, основанный на многих категориальных переменных. Преобразование Логарифма также доступно.

12.6. Модель (вкладка Model)

Алгоритмы предсказания часто описываются как описательные, так и предсказательные. Rattle, в настоящий момент, поддерживает два общих описательных или безнадзорных подхода к построению модели: кластерный анализ и анализ зависимости. Поддерживается ряд предсказательных моделей: деревья решений, усиление, случайные леса, машины опорных векторов, обобщенные линейные модели и нейронные сети.

Идеи классификации являются сутью предсказательных моделей. Rattle поддерживает как двоичную классификацию (два класса), наиболее распространенную, так и классификацию на много классов. Попутно поддерживает предсказание на основе регрессии.

Rattle предоставляет прямой интерфейс для набора описательных и предсказательных моделей, доступных в R. Для каждой модели простой набор настраиваемых параметров представлен через графический интерфейс. Где только возможно Rattle пытается представить хорошие значения по умолчанию (часто те же самые по умолчанию как выбрано автором соответствующего пакета), что позволяет пользователю просто создавать модель без настройки или с минимальной настройкой. Это, быть может, не всегда правильно, но является, конечно, разумным в начале работ по моделированию.

В данном разделе в пределах Rattle рассмотрим моделирование на основе деревьев решений и случайных лесов.

12.6.1. Деревья решений (Tree)

Один из классических методов машинного обучения, используемых в предсказательных моделях, является дерево решений. Используя простой алгоритм и простую древовидную структуру для представления модели, подход, оказалось, был очень эффективен. Используются пакеты rpart и party для классификации. На рисунке 12.6 показана вкладка Model с результатами создания дерева решений, выведенного на экран дословно (обычный результат команды сводки для объекта «rpart»).

Rattle увеличивает ценность основных функций rpart за счет показа дерева решений со списком правил (используются кнопки Draw и Rules, соответственно).

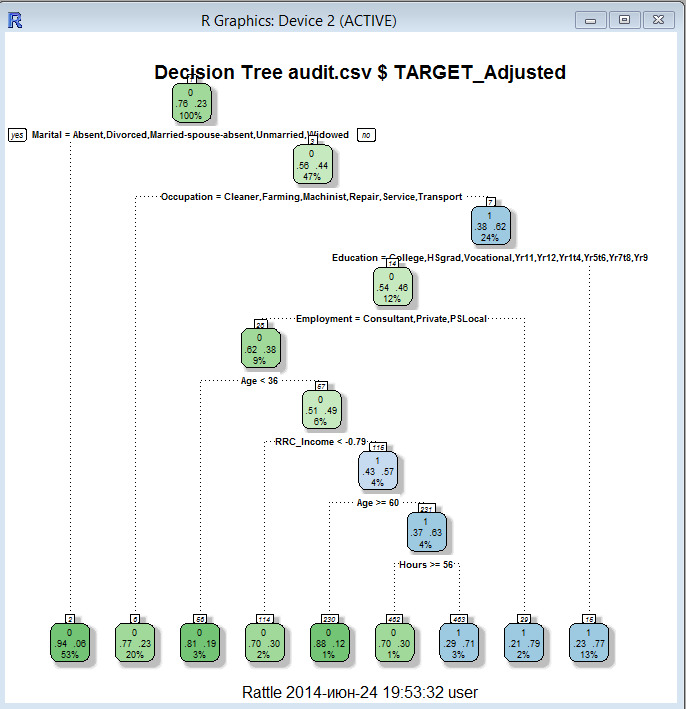
Замечание. Ошибка классификации в корне дерева составила 15%.

12.6.2. Случайный лес (Forest)

Случайный лес создает много деревьев решений. Случайные леса часто используются, когда имеется очень большие обучающие наборы данных и очень большое количество входных переменных (сотни или даже тысячи входных переменных). Обычно модель случайного леса состоит из десятков или сотен деревьев решений, каждое создается использованием случайной выборки из набора данных, и при создании любого дерева рассматривают случайную выборку переменных в каждом узле.

Случайная выборка и данных, и переменных гарантирует, что даже создание 500 деревьев решений может быть эффективным. Модель также достойно противостоит шуму, выбросам и переобучению по сравнению с единственным древовидным классификатором.

Rattle использует пакет randomForest для создания леса деревьев. При необходимости Rattle может перечислить все правила, генерируемые для случайного леса. Для сложных задач таких правил может оказаться несколько тысяч.

Опция Forest (Случайный лес) также может вывести на монитор относительную значимость переменных, чем предоставляется понимание, какие переменные играют больше всего важную роль в предсказании результатов класса. Кнопка Importance выведет на монитор две меры относительной значимости переменных в нашем наборе данных относительно предсказания класса.

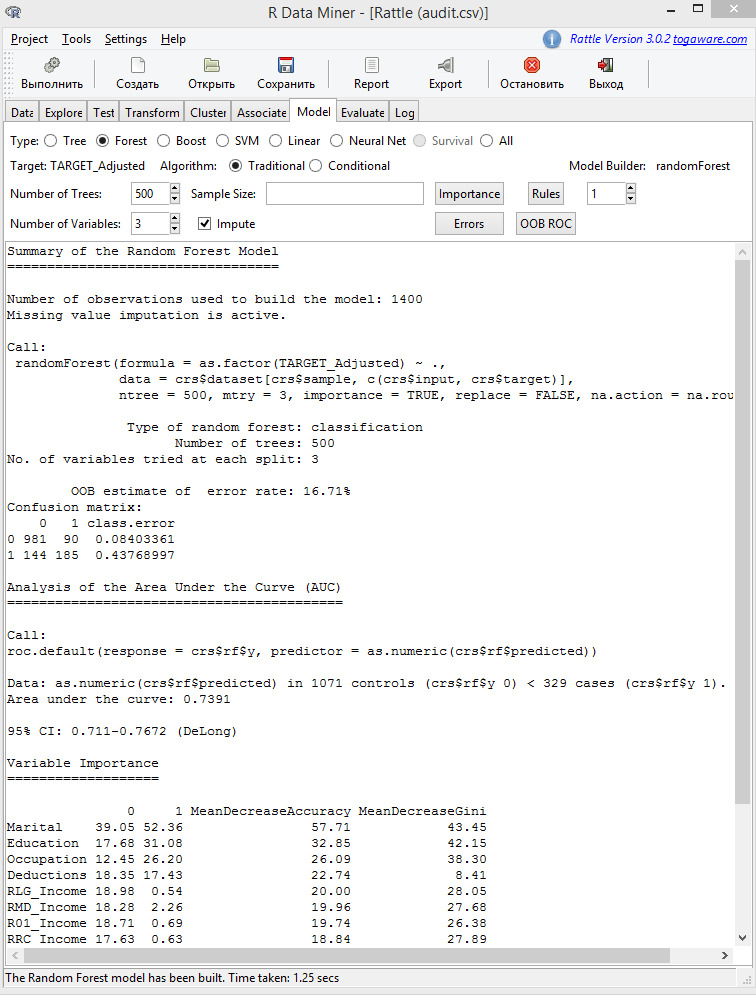
Замечание. Ошибка классификации составили 16.7%

12.7. Построение всех моделей и их настройки

Вполне поучительно использовать все типы моделей для одного и того же набора данных. Для этого имеется опция All.

Мы можем рассмотреть результативность каждой из созданных моделей и выбрать ту, которая лучшие удовлетворяет наши потребности. В выборе единственной модели можно не обязательно выбрать самую точную модель. Могут играть роль и другие соображения. Например, если простое дерево решений почти так же точно как 500 деревьев в случайном лесе, то можно отказаться от сложности случайного леса.

Эффективная альтернатива, где объяснения не требуются, а требуется точность, состоит в создании модели каждого типа, а затем составления ансамбля, который является линейной комбинацией этих моделей.

12.7.1. Оценка (вкладка Evaluate)

Rattle предоставляет стандартный набор инструментов для оценки и сравнения результативности моделей. Он включает матрицу ошибок (или таблицу рассогласования), диаграммы подъема, кривые ROC и кривые стоимости, использующих, например, пакет ROCR.

Совокупное изменение кривой ROC реализовано в Rattle как диаграммы риска. Диаграммы риска особенно подходят для задач двоичной классификации, которые распространены в анализе данных. Цель состоит в эффективном отображении на экране легко понятую меру результативности модели относительно доступных ресурсов.

Диаграмма риска особенно полезна в контексте контрольного набора данных и для задач анализа рисков вообще. У контрольного набора данных есть две целевых переменных класса так же как так называемая переменная риска, которая является мерой размера риска, присоединенного с каждым наблюдением.

Rattle использует идею диаграммы риска для оценки результативности модели в контексте анализа рисков.

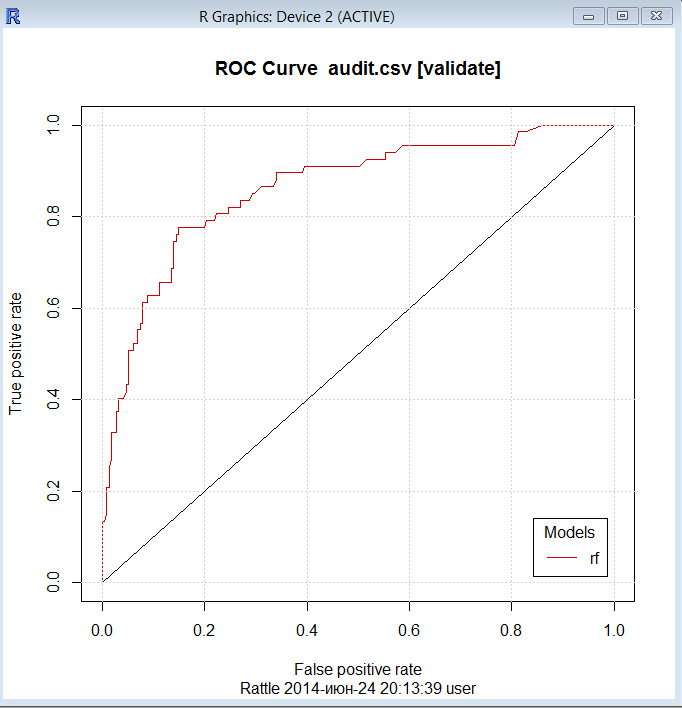
Прочтение этой диаграммы очень простое. Площадь под красной кривой — это процент правильно классифицированных случаев. У нас это 86%.

12.7.2. Развертывание модели

Как только мы выбрали модель, которая представляет приемлемое уточнение нашим бизнес-процессам, мы сталкиваемся с развертыванием. Развертывание может колебаться от непосредственного исполнения модели до полностью автоматической и тщательно управляемой средой развертывания.

Далее обсудим некоторые проблемы и исследуем, как Rattle поддерживает развертывание.

12.7.3. Скрипты R

Самый простой подход к развертыванию — это применение модели к новому набору данных. Это часто упоминается как оценка выигрыша. В контексте R это — не что иное, как использование функции predict.

Вкладка оценки Rattle поддерживает оценку выигрыша опцией Score. Есть дальнейшие опции, чтобы отметить обучающий набор данных, набор данных теста или данные, загруженные из файла CSV (который должен содержать те же самые переменные).

Любое число моделей может быть выбрано, и результаты записаны в файл CSV.

Выигрыш часто наступает через некоторое время после создания модели. В этом случае модель должна быть сохранена для более позднего использования. Понятие проекта Rattle полезно в таких обстоятельствах. Текущее состояние Rattle (включая фактические данные и модели, созданные во время сеанса), может быть сохранено в проекте, и позже загружено в Rattle. Можно будет использовать новый набор данных для сохраненной модели.

Команды сохранения модели randomForest имеет вид:

> myrf <- crs$rf

> save (myrf, file = «model01_090501.RData»)

Затем позже можем загрузить модель и применить модель (используя скрипт, основанный на командах, показанных на вкладке Rattle Log) на новом наборе данных:

> library (randomForest)

> (load («model01_090501.RData»))

[1] «myrf»

> dataset <- read. csv («cases_090601.csv»)

> pr <- predict (myrf, dataset,

type = «prob») [, 2]

> write. csv (cbind (dataset,

pr), file = «scores_090601.csv»,

row.names = FALSE)

> head (cbind (Actual = dataset$TARGET_Adjusted,

Predicted = pr))

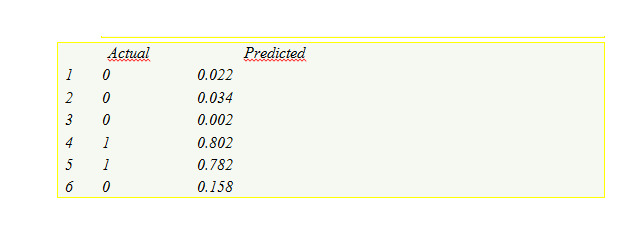
Как видим, что модель случайного леса имеет неплохой результат на немногих наблюдениях.

12.8. Журнал (вкладка Log)

GUI не так полон и гибок, как полный язык программирования R с расширяющими его пакетами. Rattle достаточен на начальных этапах проектирования предсказательных моделей, очень полезен новичкам. Но у профессионального разработчика моделей очень скоро возникнет потребность выйти за возможности Rattle. Rattle поддерживает такое желание через вкладку Log (Журнал).

Как упомянуто выше, журнал команд R, которые сконструировал Rattle, доступен через вкладку Log. Смысл состоит в том, чтобы команды R были доступны для копирования в консоль R, в которой можно было бы изменить или дополнить код R.

Вкладка Log протоколирует все действия Rattle, которые можно выполнить позднее, а также для образования. Включены информативные комментарии использованных шагов. Протокол действий Rattle предоставляет учебное введение в использование R из командной строки, где мы получим гораздо больше возможностей.

Весь журнал может быть экспортирован в файл скрипта (с расширением». r»), а затем загружен в R или редактор скриптов R. В дальнейшем, исполняя скрип, мы полностью воспроизводим действия Rattle. Вообще, можно рассмотреть код и поправить его в соответствии с вашим целям. После экспорта вкладки Log в файл с именем файла «myrf01.R» получаем файл, который можно выполнить как скрипт в R:

> source («myrf01.R»)

12.9. Справка

Меню Help (Справка) предоставляет доступ к кратким описаниям возможностей Rattle, структурирована в соответствии с пользовательским интерфейсом. Также многие сообщения справки предоставляют прямой доступ к базовой документации по используемых в Rattle пакетах R.

Часть 3. Подробно работаем с Rattle, включая R и МТ4

Третья часть книги является подробной инструкцией по работе с Rattle. Организация материала продиктована порядком построения моделей, предусмотренным Rattle в виде последовательности вкладок программы.

Излагаемый текст является переводом технической документации Rattle, который дополнен следующими компонентами:

— демонстрационным пример, с которым поставляется Rattle, заменен примером с котировками валютных пар рынка Форекс;

— кодом на языке R, который генерируется Rattle при его работе;

— переводом технической документации по компонентам R, используемым Rattle;

— возможности Rattle по переносу созданного им кода на R в сторонние программные системы заменены материалом по использованию кода, полученного из Rattle в терминале MT4, принадлежащий MetaQuotes®.;

— авторским комментарием по существу выполняемых действий.

Третья часть книги предназначена для читателя, имеющего целью создания предсказания моделей для последующего использования. Читатель, который владеет R на минимальном уровне, а также владеет программированием на языке MQL4 (принадлежащий MetaQuotes®) сумеет создать работоспособный советник высокого качества.

13. Начало работы

13.1. Стартуем R

При запуске R на экране в окне (рисунок 13.1) выводится запрос R (>), указывая, что R ожидает команд. Обычно это окно именуется Консолью (Console) R. Консоль R в Microsoft Windows предоставляет дополнительные меню для работы с R. Оно включает опции для работы, которые мы, в данной книге подробно рассматривать не будем.

Сосредоточимся на Rattle. Предварительно следует установить Rattle. Для этого произведем следующие действия.

Откроем вкладку R Пакеты/установить пакеты. Откроется окно, показанное на рисунке 13.2.

Нажимаем Ok. Чуть ниже находится зеркало, имеющее отношение к России — я пользуюсь облаком.

Открывается еще одна вкладка с перечнем пакетов, имеющихся в R. В этом списке необходимо найти Rattle и щелкнуть по нему.

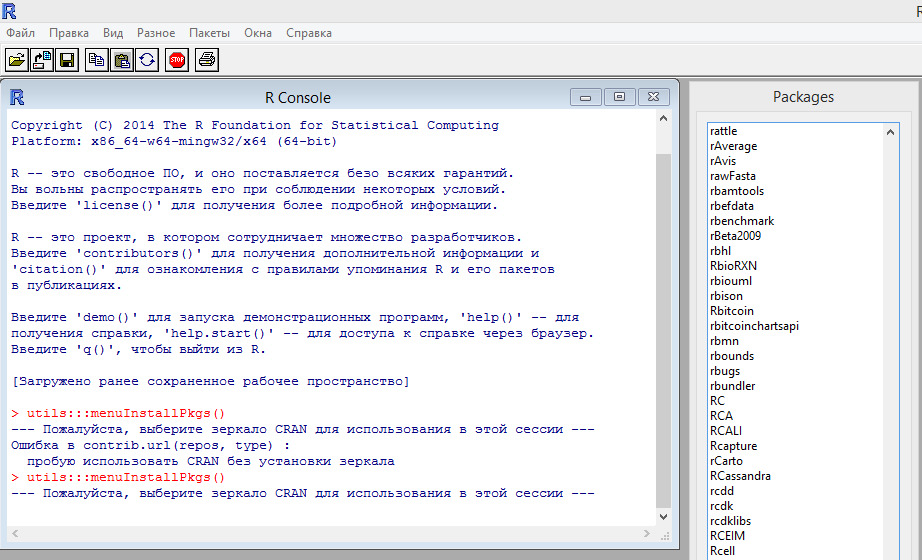
В результате Rattle будет установлен в R. Не будем путать этот процесс с установкой в Windows. Установка любого пакета в R — это копирование кода соответствующего пакета в раздел /R/library. В этом разделе находится большое число пакетов, и все они считаются «установленными» в R.

Теперь необходимо загрузить библиотеку Rattle в рабочую область. Этот последний шаг необходимо выполнять каждый раз при запуске самой R.

> library (Rattle)

При установке пакета Rattle может возникнуть ситуация, что потребуется вручную установить пакеты, которые используются Rattle при его работе. Список будет выдан, а затем следует установить пакет за пакетом из этого списка. Продемонстрировать этого я не могу, так как все пакеты, необходимые для работы Rattle, у меня уже имелись в R.

Продолжим.

Вводим команду Rattle () с пустым списком параметров, как показано ниже. В результате увидим следующее, как на рис.13.5.

> Rattle ()

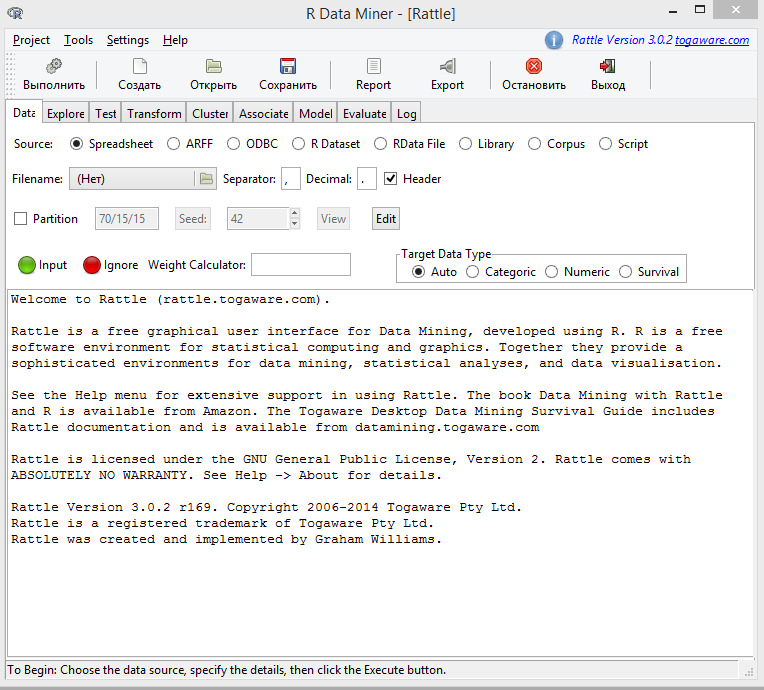
Пользовательский интерфейс Rattle — простой, основанный на вкладках интерфейс, с идеей работы от крайней левой вкладки до правой вкладки, подражая типичному процессу анализа данных и моделирования.

Подсказка: использование Rattle, как показано в строке состояния при запуске Rattle, состоит в предоставлении соответствующей информации для определенной вкладки, а затем нажатии кнопки Execute для выполнения действия. Не забывайте нажимать кнопку Выполнить до перехода к следующему шагу.

13.2. Выход из Rattle и R

До перехода к деталям довольно важная информация по выходу из применений. Для выхода из Rattle просто нажимаем кнопку Выход. Вообще, Консоль R не будет завершена. Для R сообщение запуска требует ввода q () для выхода. Вводим эту команду в Консоль R, включая круглые скобки. Нажатие Enter приводит к запросу выхода из R:

q ()

Save workspace image? [y/n/c]:

Отвечаем n — сохранять рабочую область не будем.

13.3. Пробуем «естественные» котировки

Для трейдера самыми «естественными» исходными данными будут данные, которые он может получить из терминала. Таковыми данными является набор валютных пар, например, следующий:

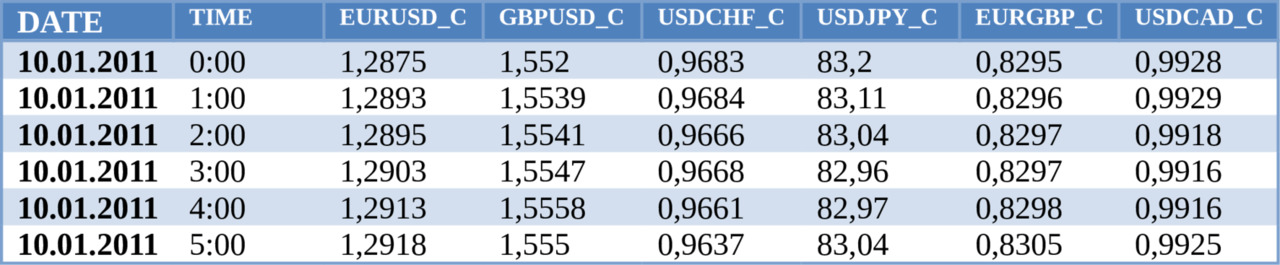
Этот набор данных имеет имя kot60_110101_131231_UE. txt, является текстовым с разделителем табуляция и поставляется вместе с книгой.

Попробуем создать модель на этих данных.

Сначала прочтем этот файл в Rattle. Для этого укажем настройки, показанные на рисунке 13.6, выберем файл и откроем.

Затем, как всегда, Выполнить. Получаем следующее:

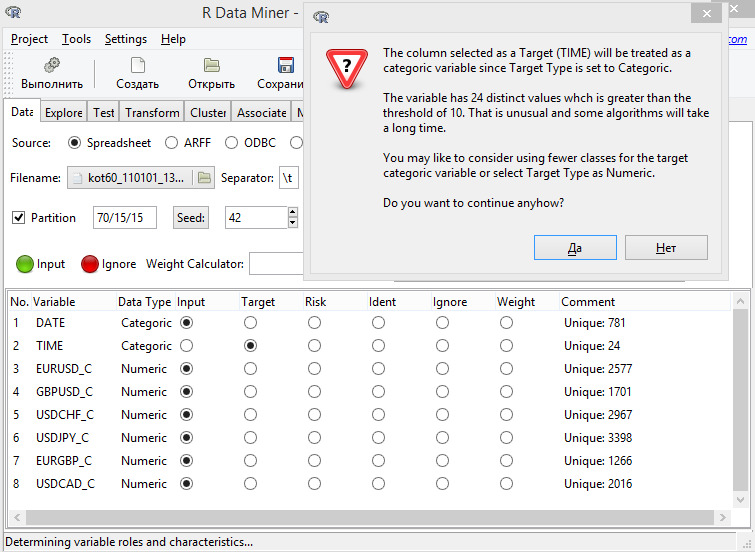
Rattle предупреждает нас о сомнительности автоматически назначенной целевой переменной TIME. Это понятно — такая целевая переменная нам не нужна. Назначим в качестве целевой переменной EURUSD_C и попытаемся построить обычную мультивалютную модель, которая предскажет нам значение EURUSD по значениям других валютных пар, а заодно будет использовать временные метки.

Окончательно в качестве исходных данных:

Нажимаем Model, отмечаем Tree и Выполнить для построения модели дерева. Затем для оценки нажимаем Evalute и снова Выполнить. Получаем:

Область под кривой (Area under the Recall (green) curve: 154% (1.541)) 154%! Количество правильно классифицированных цен валютной пары EURUSD более 100% — модель вообще не работает.

Попробуем еще нейронную сеть. Результат точно такой же.

Наши надежды получить хоть какой-либо результат, хотя бы пригодный для обсуждения, не увенчались успехом. Исходные данные являются краеугольным камнем моделирования.

Вернемся к набору данных, поставляемому вместе с Rattle, и попробуем научиться подбирать исходные данные. Это параграф можно пропустить и сразу перейти к исходным данным с котировками, но уже менее «естественными», но имеющими большую практическую ценность.

13.4. Создание модели на демонстрационных данных погоды

Используем файл данных, поставляемый в составе дистрибуции пакета.

Убедимся, что сможем создать модель с Rattle лишь несколькими щелчками мышью. Для этого:

1. Щелкните по кнопке Выполнить.

Rattle заметит, что не указан какой-либо набор данных, как показано ниже:

2. Щелкните по Yes в пределах выпадающего меню.

Набор данных weather предоставляется в составе Rattle. Автоматически открылась вкладка Data.

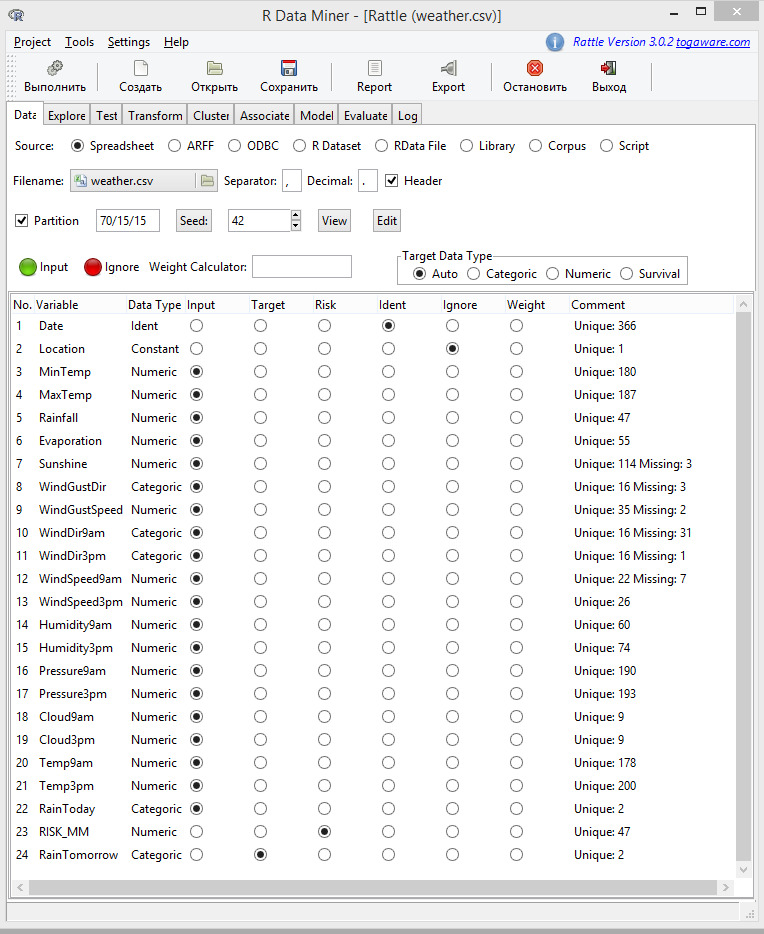
На этом рисунке отметим пункт Partition с разбивкой = 70/15/15, что означает, что исходный набор данный разделен на три части: обучающий/проверочный Validation) / тестовый (Тesting).

Из демонстрационного примера вынесем еще одну важную мысль — это роль переменных в модели, которая указывается в колонках.

Сводка набора данных (рис.13.11) предоставляет список переменных, их типы, роли по умолчанию и другую полезную информацию. Типы обычно будут Numeric (числовыми) (если данные будут числовыми, как температура, ливень и скорость ветра), или Categorical — категориальные (если данные состоят цифр из алфавита, как направление ветра, которое могло бы быть N или S, и т.д.), хотя мы можем также видеть Ident (идентификатор). Часто Ident — это одна из переменных (столбцы) в данных, которая однозначно определяет каждое наблюдение (строку) данных. Столбец Комментариев включает общую информацию как количество отдельных (или различных) значений переменных и у скольких наблюдений есть отсутствующее значение для переменной.

На данном этапе для нас представляет принципиальный интерес деление переменных на входные (Input) переменные и целевую (Target) переменную.

Все входные переменные — это измеренные величины, не зависимые в модели, аргументы, в статистике называемые «предикторы».

Целевая переменная одна — Дождь завтра (Rain Timorrow). Это предсказание. Его нельзя измерить. Но на исторических данных мы можем посмотреть соответствие значений сегодняшних данных и сопоставить их с данными на завтра. Отметим, что предсказание находится в одной строке с сегодняшними данными.

Отсюда основная идея предсказательных моделей: обучим модель на исторических данных, используя «заглядывание вперед», а затем, получив данные на текущий день, сделаем предсказание на следующий день.

Двинемся дальше.

3. Щелкните по вкладке Model. Получим следующее окно:

В строке Type мы видим список моделей, с отмеченной моделью Tree (Дерево).

4. Щелкните по кнопке Выполнить.

Через короткий промежуток времени получим результат. Получающаяся модель дерева принятия решения, выведенная на экран дословно в текстовом виде Rattle, основана на наборе данных выборки исторических ежедневных погодных наблюдений. Этап Model еще называют этапом обучения модели. Для этого этапа используется 70% исходного набора, как было указано на вкладке Data.

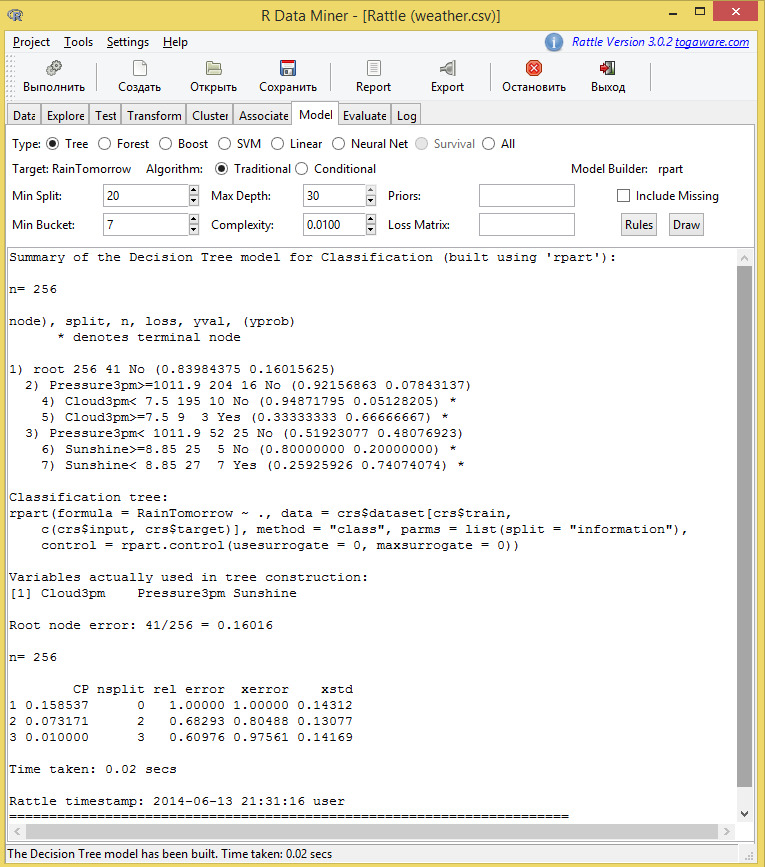
Можно было бы вникнуть в результат, но предсказание погоды не интересно для нас. Только отметим, что ошибка в корне дерева составляет 16% — очень не плохой результат по меркам трейдинга. Еще раз отметим, что этот результат получен на обучающем наборе данных.

Столь же просто можно получить другие модели, указанные в строчке Type, но в отдельности каждой из моделей мы не будем заниматься.

13.5. Оценка модели на данных о погоде

Произведем оценку модели. Для этого откроем вкладку Evaluate и нажмем Выполнить. Получаем:

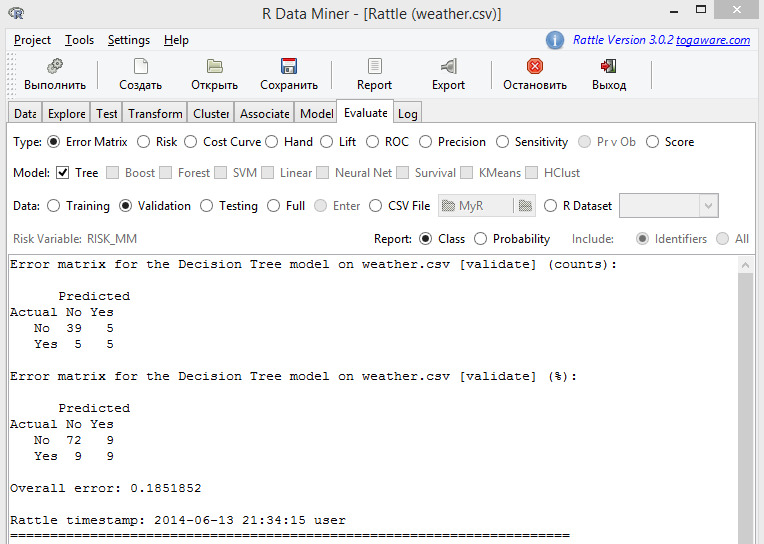
Здесь отметим предпоследнюю строчку, в которой указано, что общая ошибка классификации составляет 18%. Этот результат получен на проверочной части исходного набора, что составляет 15% исходного набора данных и хорошо коррелируется с ошибкой, полученной при обучении модели.

Теперь продемонстрируем общий алгоритм работы с Rattle.

Вернемся на вкладку Model и отметим в строке Type кнопку All — все модели. Нажимаем Выполнить.

Переходим на вкладку Evaluate. И снова нажимает Выполнить. Видим:

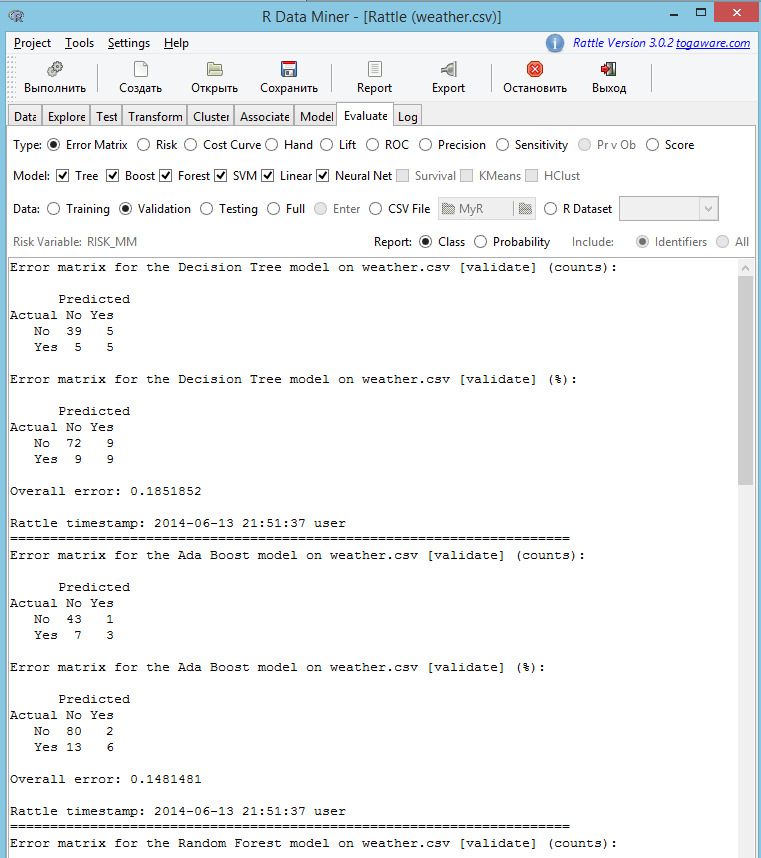
Все оценки не поместились в окно, но каждый может проверить и убедиться, что получена оценка разных моделей, лучшей из которых является Forest (Случайный лес — лес случайных деревьев.) с ошибкой 10% на проверочном наборе данных.

Итак, на этом примере было показано, что, не владея R, не разбираясь в очень сложных моделях, мы смогли построить очень сложные модели и выбрать лучшую из них для нашего набора данных, а именно: случайный лес.

13.6. Загрузка набора данных с котировками

Показанный выше набор данных, поставляемый в составе Rattle, не представляет для нас интереса, поэтому перейдем к более привычным данным — котировкам валютных пар и величинам, вычисленным на основе этих котировок.

Вернемся на вкладу Data.

Используя умолчания, заложенные в Rattle, мы загрузили набор данных weather. В строке Source помечена кнопка Spreadsheet, что указывает формат набора weather — файл Excel.

К сожалению, просто выгрузить данные из терминала и поместить их в файл Excel, оказалось недостаточным для целей демонстрации. Поэтому мною на R был создан необходимый набор данных, который в терминах Rattle имеет тип R Dataset. Этот файл имеется в поставке с данной книгой. У меня он находится в H:/MyR/Book с именем zz_1_5, в котором находится фрейм данных (терминологии R) следующего состава:

> str (zz_1_5)

«data.frame»: 18251 obs. of 43 variables:

$ WeekDays: Factor w/ 7 levels «воскресенье»,..: 6 6 6 6 6 6 6 6 6 6…

$ TimeDays: Factor w/ 24 levels «0:00», «1:00»,..: 20 21 22 23 24 3 45

$ eurusd: num 1.33 1.33 1.33 1.33 1.33…

$ gbpusd: num 1.59 1.59 1.59 1.59 1.6…

$ usdchf: num 0.964 0.964 0.961 0.961 0.961…

$ usdjpy: num 82.6 82.6 82.5 82.5 82.5…

$ usdcad: num 0.987 0.986 0.986 0.985 0.985…

$ fit1: num 1.33 1.33 1.33 1.33 1.33…

$ fit2: num 1.32 1.32 1.32 1.33 1.33…

$ fit1.dif: num 0.000198 0.000852 0.000719 0.001288 0.001265…

$ fit2.dif: num 0.000215 0.000685 0.000609 0.001012 0.001042…

$ eurusd. dif1: num 0.0014 0.0031 -0.0003 0.003 0.0005…

$ gbpusd. dif1: num 0.0013 0.0015 0.0002 0.0016 -0.0001…

$ usdchf. dif1: num -0.0002 -0.003 0.0006 -0.0008 -0.002…

$ usdjpy. dif1: num -0.04 -0.08 0 -0.04 0.06…

$ usdcad. dif1: num -0.0004 -0.0006 -0.0006 -0.0004 -0.0002…

$ eurusd. dif2: num 0.0045 0.0028 0.0027 0.0035 0.0042…

$ gbpusd. dif2: num 0.0028 0.0017 0.0018 0.0015 0.0012…

$ usdchf. dif2: num -0.0032 -0.0024 -0.0002 -0.0028 -0.0036…

$ usdjpy. dif2: num -0.12 -0.08 -0.04 0.02 0…

$ usdcad. dif2: num -0.001 -0.0012 -0.001 -0.0006 0.0013…

$ eurusd. dif3: num 0.0042 0.0058 0.0032 0.0072 0.006…

$ gbpusd. dif3: num 0.003 0.0033 0.0017 0.0028 0.009…

$ usdchf. dif3: num -0.0026 -0.0032 -0.0022 -0.0044 -0.0029…

$ usdjpy. dif3: num -0.12 -0.12 0.02 -0.04 0.03…

$ usdcad. dif3: num -0.0016 -0.0016 -0.0012 0.0009 -0.0002…

$ fit1.Lag1: num 1.33 1.33 1.33 1.33 1.33…

$ fit1.Lag2: num 1.33 1.33 1.33 1.33 1.33…

$ fit1.Lag3: num 1.33 1.33 1.33 1.33 1.33…

$ fit2.Lag1: num 1.32 1.32 1.32 1.32 1.33…

$ fit2.Lag2: num 1.32 1.32 1.32 1.32 1.32…