Бесплатный фрагмент - Практическое использование нейронных сетей в Среде Matlab

ВВЕДЕНИЕ

В учебном пособии предложены примеры практического применения активно используемого инструмента по направлению искусственного интеллекта: искусственным нейронным сетям.

Необычайно высокий интерес к нейронным сетям, проявляемый специалистами из разных областей деятельности, объясняется, прежде всего, очень широким диапазоном решаемых с их помощью задач, а также рядом преимуществ перед другими методами.

Анализ работ, связанных с использованием нейронных сетей для решения физико-математических задач, показывает, что нейросетевой и нечеткий подходы имеют преимущества перед традиционными математическими методами в трех случаях.

Во-первых, когда рассматриваемая задача в силу конкретных особенностей не поддается адекватной формализации, поскольку содержит элементы неопределенности, не формализуемые традиционными математическими методами.

Во-вторых, когда рассматриваемая задача формализуема, но на настоящее время отсутствует аппарат для ее решения.

В-третьих, когда для рассматриваемой, хорошо формализуемой задачи существует соответствующий математический аппарат, но реализация вычислений с его помощью на базе имеющихся вычислительных систем не удовлетворяет требованиям получения решений по времени, энергопотреблению и др. В такой ситуации приходится либо производить упрощение алгоритмов, что снижает качество решений, либо применять соответствующие нейросетевой подход при условии, что он обеспечит нужное качество выполнения задачи.

В пособии приведены примеры в системе MATLAB с использованием пакета нейронных сетей Neural Networks Toolbox. Предложены решения с помощью нейронных сетей практических задач регрессии, классификации, кластеризации, распознавания образов.

Практическая работа 1. Использование нейронных сетей для решения задач регрессии

Цель работы: научиться использовать нейронные сети для решения задач аппроксимации и прогнозирования.

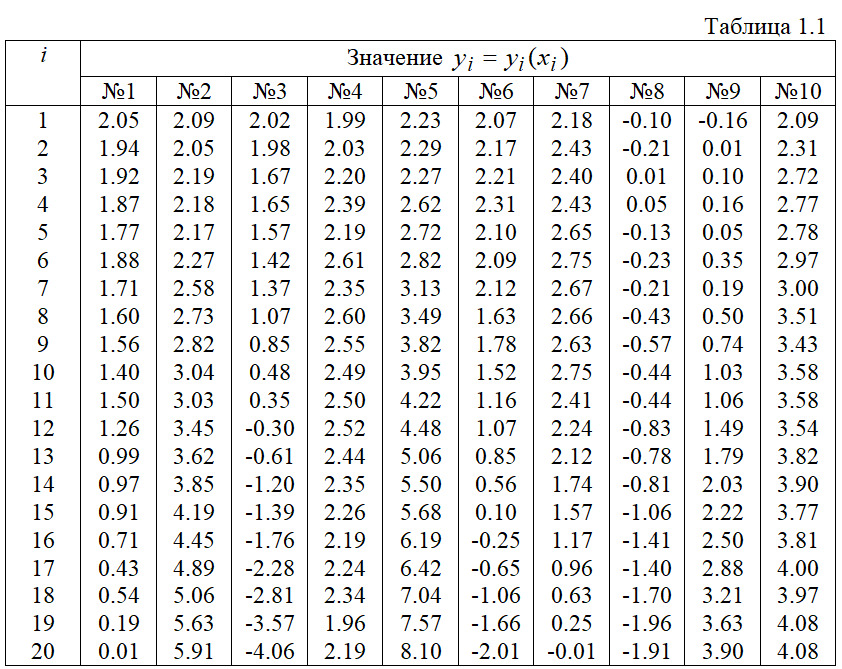
Задание 1: В среде MATLAB необходимо построить и обучить многослойную нейронную сеть для аппроксимации таблично заданной функции yi=f (xi), i=1,2,…,20. Разработать программу, которая реализует нейросетевой алгоритм аппроксимации и выводит результаты аппроксимации в виде графиков. Варианты задания представлены в табл. 1.1.

Задание 2: Используя инструмент NNTool решить задачу прогнозирования на основе следующих данных: имеется 100 входных значений х от 0.1 до 10 с шагом 0.1 и соответствующие им значения выходной переменной y. Зависимость y от x следующая:,y (x) =x2—2x+1 но исследователю данная зависимость неизвестна, а известны лишь числовые значения yi, i=1,2,…,100. Требуется найти значение y от x> 10.

Задание 3: В среде MATLAB необходимо построить и обучить нейронную сеть радиально-базисных функций для аппроксимации заданной функции yi=f (xi) =sin (xi) -cos (xi), x=0, 0.5,…,10, i=1,2,…,21.

Варианты заданий

Значения xi=i*0.1, i=1,2,…,20 одинаковые для всех вариантов

1.1. Основные теоретические сведения

При изложении теоретических сведений использовались работы [1–4].

Под искусственными нейронными сетями (далее — нейронными сетями) подразумеваются вычислительные структуры, которые моделируют простые биологические процессы, обычно ассоциируемые с процессами человеческого мозга. Они представляют собой распределенные и параллельные системы, способные к адаптивному обучению путем анализа положительных и отрицательных воздействий. Элементарным преобразователем в данных сетях является искусственный нейрон или просто нейрон, названный так по аналогии с биологическим прототипом. К настоящему времени предложено и изучено большое количество моделей нейроподобных элементов и нейронных сетей.

Нейрон является составной частью нейронной сети. На рис. 1.1 показана его общая структура.

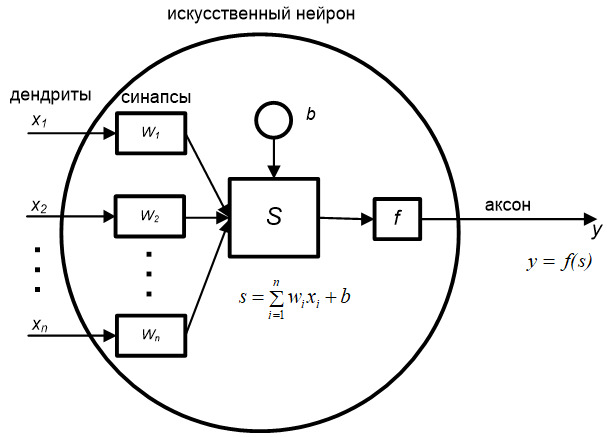
Он состоит из элементов трех типов; умножителей (синапсов), сумматора и нелинейного преобразователя. Синапсы осуществляют связь между нейронами, умножают входной сигнал на число, характеризующее силу связи, (вес синапса). Сумматор выполняет сложение сигналов, поступающих по синаптическим связям от других нейронов, и внешних входных сигналов. Нелинейный преобразователь реализует нелинейную функцию одного аргумента — выхода сумматора. Эта функция называется функцией активации или передаточной функцией нейрона. Нейрон в целом реализует скалярную функцию векторного аргумента.

На рис. 1.1 S — результат суммирования (sum); wi — вес (weight) синапса, i=1,2,…,n; х — компонент входного вектора (входной сигнал),i=1,2,…,n; b — значение смещения (bias); n — число входов нейрона; у — выходной сигнал нейрона; f — нелинейное преобразование (функция активации).

В общем случае входной сигнал, весовые коэффициенты и смещение могут принимать действительные значения, а во многих практических задачах — лишь некоторые фиксированные значения. Выход y определяется видом функции активации и может быть как действительным, так и целым.

Синаптические связи с положительными весами называют возбуждающими, с отрицательными весами — тормозящими. Описанный вычислительный элемент можно считать упрощенной математической моделью биологических нейронов. Чтобы подчеркнуть различие нейронов биологических и искусственных, вторые иногда называют нейроноподобными элементами или формальными нейронами.

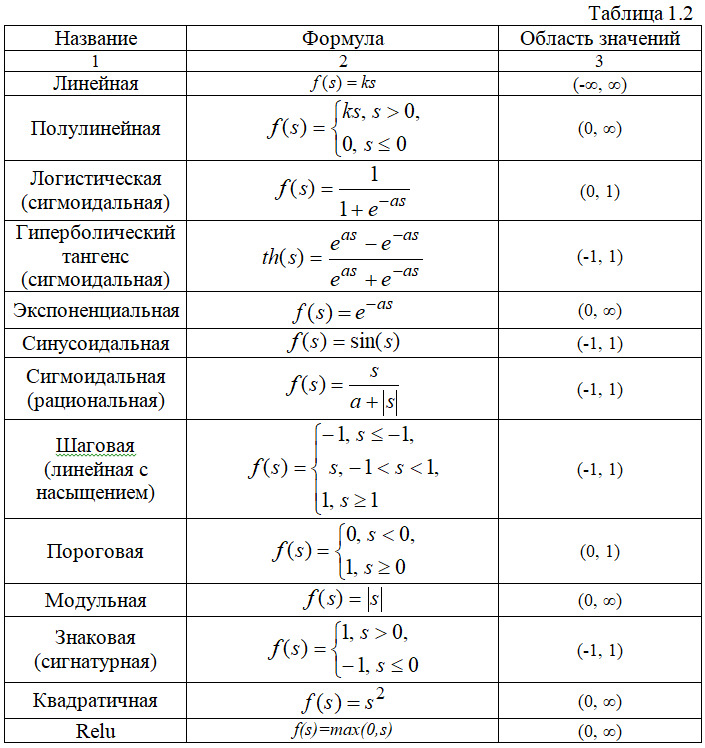
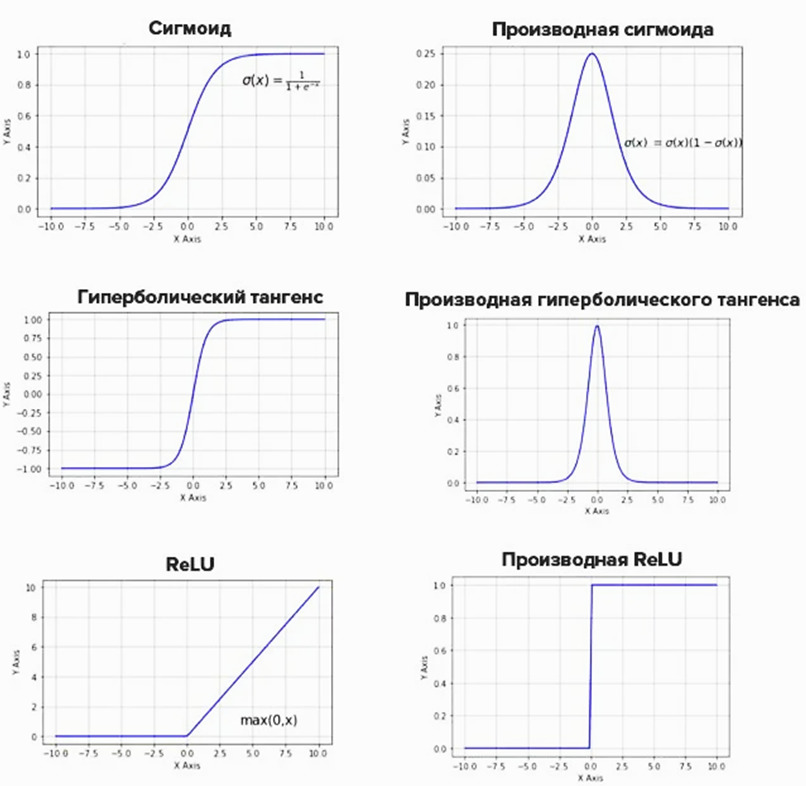
На входной сигнал S нелинейный преобразователь отвечает выходным сигналом f (S), который представляет собой выход y нейрона. Примеры активационных функций представлены в табл. 1.2.

Основные парадигмы обучения нейронных сетей

Существует три основные парадигмы (формы) обучения нейронных сетей:

— обучение с учителем (supervised learning);

— обучение с подкреплением (reinforcement learning)

— обучение без учителя (unsupervised learning, self-organized).

В первом случае обучение осуществляется под наблюдением внешнего «учителя». Нейронной сети предъявляются значения как входных, так и желательных выходных сигналов, и она по некоторому внутреннему алгоритму подстраивает веса своих синаптических связей.

Во втором случае обучение включает использование «критика», с помощью которого производится обучение на основе метода проб и ошибок.

В третьем случае выходы нейронной сети формируются самостоятельно, а веса и смещения изменяются по алгоритму, учитывающему только входные и производные от них сигналы. Здесь за основу взяты принципы самоорганизации нервных клеток. Для обучения без учителя не нужно знания требуемых ответов на каждый пример обучающей выборки. В этом случае происходит распределение образцов по категориям (кластерам) в соответствии с внутренней структурой данных или степенью корреляции между образцами.

Рассматривают также и смешанное обучение, при котором весовые коэффициенты одной группы нейронов настраиваются посредством обучения с учителем, а другой группы — на основе самообучения.

Основные правила обучения нейронных сетей

Известны четыре основных правила обучения, обусловленные связанными с ними архитектурами сетей: коррекция ошибки, правило Больцмана, правило Хебба и метод соревнования.

Коррекция ошибки

Для каждого входного примера задан требуемый выход, который может не совпадать с реальным. Правило обучения при коррекции по ошибке состоит в использовании разницы для изменения весов, с целью уменьшения ошибки рассогласования. Обучение производится только в случае ошибочного результата. Известны многочисленные модификации этого правила обучения.

Правило Больцмана

Правило Больцмана является стохастическим правилом обучения, обусловленным аналогией с термодинамическими принципами. В результате его выполнения осуществляется настройка весовых коэффициентов нейронов в соответствии с требуемым распределением вероятностей. Обучение правилу Больцмана может рассматриваться как отдельный случай коррекции по ошибке, в котором под ошибкой понимается расхождение корреляций состояний в двух режимах.

Правило Хебба

Правило Хебба является самым известным алгоритмом обучения нейронных сетей, суть которого заключается в следующем: если нейроны с обеих сторон синапса возбуждаются одновременно и регулярно, то сила синаптической связи возрастает. Важной особенностью является то, что изменение синаптического веса зависит только от активности связанных этим синапсом нейронов. Предложено большое количество разновидностей этого правила, различающихся особенностями модификации синаптических весов.

Метод соревнования

В отличие от правила Хебба, в котором множество выходных нейронов могут возбуждаться одновременно, здесь выходные нейроны соревнуются между собой. И выходной нейрон с максимальным значением взвешенной суммы является «победителем» («победитель забирает все»). Выходы же остальных выходных нейронов устанавливаются в неактивное состояние. При обучении модифицируются только веса нейрона-«победителя» в сторону увеличения близости к данному входному примеру.

Алгоритмы обучения с учителем

Алгоритмы обучения нейронной сети с учителем подразумевают наличие некоего внешнего звена, предоставляющего сети кроме входных так же и целевые выходные образы. Алгоритмы, пользующиеся подобной концепцией, называются алгоритмами обучения с учителем. Для их успешного функционирования необходимо наличие экспертов, создающих на предварительном этапе для каждого входного образа эталонный выходной.

Если имеется множество обучающих примеров и задана функция ошибки (функционал качества), то обучение нейронной сети превращается в задачу многомерной оптимизации, для решения которой могут быть использованы следующие четыре группы методов:

— итерационные методы локальной оптимизации с вычислением частных производных первого и второго порядков;

— методы стохастической оптимизации;

— методы глобальной оптимизации.

К методам локальной оптимизации с вычислением частных производных первого порядка относятся: градиентный метод (наискорейшего спуска); методы с одномерной и двумерной оптимизацией целевой функции в направлении антиградиента; метод сопряженных градиентов; методы, учитывающие направление антиградиента на нескольких шагах алгоритма.

К методам локальной оптимизации с вычислением частных производных первого и второго порядка относятся: метод Ньютона, методы оптимизации с разреженными матрицами Гессе, квазиньютоновские методы, метод Гаусса-Ньютона, метод Левенберга-Маркардта, байесовский метод обучения, при котором осуществляется регуляризация процесса обучения.

Стохастическими методами являются: поиск в случайном направлении, имитация отжига или метод модельной закалки, метод Монте-Карло (численный метод статистических испытаний).

Задачи глобальной оптимизации решаются с помощью перебора значений переменных, от которых зависит целевая функция. Здесь находят применение также и генетические алгоритмы обучения нейронных сетей.

Достоинством методов первой группы является их высокое быстродействие. Их очевидный недостаток, связанный с возможностью находить только локальные экстремумы, преодолевается путем применения специальных мер и они используются на практике для обучения НС с многоэкстремальными целевыми функциями. Одним из самых широко распространенных в силу своей простоты методов этой группы является итерационный метод обратного распространения ошибки, который явился обобщением на случай многослойных сетей алгоритма Видроу-Хоффа (дельта-правила) обучения однослойных сетей.

К достоинствам методов двух следующих групп можно отнести их более высокое качество обучения, а к их недостаткам — очень большое число шагов обучения, что затрудняет их применение для обучения НС больших размерностей.

Эффективное обучение рекуррентных нейронных сетей остается темой требующей внимания и активного исследования. Несмотря на огромный потенциал и возможности рекуррентных нейронных сетей, главной проблемой является трудность обучения их, сложность и низкая сходимость существующих алгоритмов обучения.

Нейронные сети радиально-базисных функций

При изложении теоретических сведений использовались работы [1, 12—13].

Сети радиально-базисных функций (РБФ) имеют ряд преимуществ перед рассмотренными многослойными сетями прямого распространения. Во-первых, они моделируют произвольную нелинейную функцию с помощью всего одного промежуточного слоя, тем самым избавляя разработчика от необходимости решать вопрос о числе слоев. Во-вторых, параметры линейной комбинации в выходном слое можно полностью оптимизировать с помощью хорошо известных методов линейной оптимизации, которые работают быстро и не испытывают трудностей с локальными минимумами, так мешающими при обучении с использованием алгоритма обратного распространения ошибки. Поэтому сеть РБФ обучается очень быстро — на порядок быстрее, чем с использованием алгоритма обратного распространения ошибки.

На рис. 1.3 представлена структурная схема нейронной сети радильно-базисных функций с n входами и m выходами, осуществляющая нелинейное преобразование.

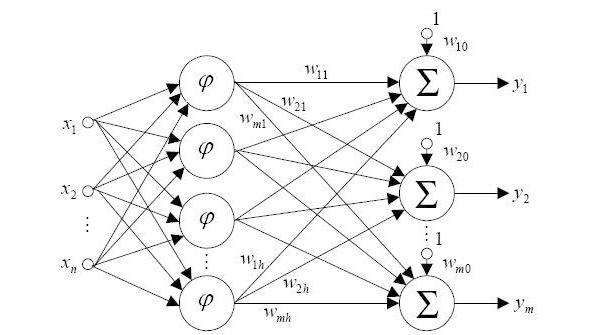
Нейронная сеть радиальных базисных функций содержит в наиболее простой форме три слоя: обычный входной слой, выполняющий распределение данных образца для первого слоя весов; слой скрытых нейронов с радиально симметричной активационной функцией, каждый i-й из которых предназначен для хранения отдельного эталонного вектора в виде вектора весов; выходной слой. Для построения сети РБФ необходимо выполнение следующих условий.

Во-первых, наличие эталонов, представленных в виде весовых векторов нейронов скрытого слоя. Во-вторых, наличие способа измерения расстояния входного вектора от эталона. Обычно это стандартное евклидово расстояние. В-третьих, специальная функция активации нейронов скрытого слоя, задающая выбранный способ измерения расстояния. Обычно используется функция Гаусса, существенно усиливающая малую разницу между входным и эталонным векторами. Выходной сигнал эталонного нейрона скрытого слоя — это функция (гауссиан) от расстояния между входным вектором x и сохраненным центром wi.

Обучение слоя образцов-нейронов сети подразумевает предварительное проведение кластеризации для нахождения эталонных векторов и определенных эвристик для определения значений.

Для нахождения значения весов от нейронов скрытого к выходному слою используется линейная регрессия.

К недостаткам сетей РБФ можно отнести то, что заранее должно быть известно число эталонов, а также эвристики для построения активационных функций нейронов скрытого слоя. Данные сети обладают плохими экстраполирующими свойствами и получаются весьма громоздкими при большой размерности вектора входов.

В моделях РБФ могут быть использованы различные способы измерения расстояния между векторами, а также функции активации нейронов скрытого слоя.

В среде MATLAB в качестве радиально-базисной функции по умолчанию используется функция radbas, пример которой приведен на рис. 1.4:

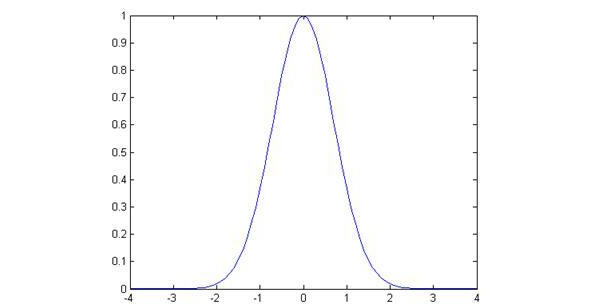
Пакет для работы с нейронными сетями математической среды MATLAB содержит множество функций для нейросетевого моделирования. Ниже приведен список основных функций Neural Network Toolbox.

Список функций Neural Network Toolbox

Функции создания новой сети

network — создание нейронной сети пользователя

Запись:

net=network

net=network (numInputs, numLayers, biasConnect, inputConnect, layerConnect, outputConnect, targetConnect)

Описание. Функция возвращает созданную нейронную сеть с именем net и со следующими характеристиками (в скобках даны значения по умолчанию):

numInputs — количество входов (0),

numLayers — количество слоев (0),

biasConnect — булевский вектор с числом элементов, равным количеству слоев (нули),

inputConnect — булевская матрица с числом строк, равным количеству слоев и числом столбцов, равным количеству входов (нули),

layerConnect — булевская матрица с числом строк и столбцов, равным количеству слоев (нули),

outputConnect — булевский вектор-строка с числом элементов, равным количеству слоев (нули),

targetConnect — вектор-строка, такая же, как предыдущая (нули).

newc — создание конкурентного слоя

net=newc (PR, S, KLR, CLR) — функция создания слоя Кохонена.

Аргументы функции:

PR — R 2 матрица минимальных и максимальных значений для R входных элементов,

S — число нейронов,

KLR — коэффициент обучения Кохонена (по умолчанию 0.01),

CLR — коэффициент «справедливости» (по умолчанию 0.001).

newcf — создание каскадной направленной сети

net=newcf (PR, [S1 S2…SNI], {TF1 TF2…TFNI}, BTF, BLF, PF) —

функция создания разновидности многослойной нейронной сети с обратным распространением ошибки — так называемой каскадной нейронной сети. Такая сеть содержит скрытых N1 слоев, использует входные функции типа dotprod и netsum, инициализация сети осуществляется функцией initnw.

Аргументы функции:

PR — R 2 матрица минимальных и максимальных значений для R входных элементов,

Si — размер i-го скрытого слоя, для N1 слоев,

TFi — функция активации нейронов i-го слоя, по умолчанию ’tansig’,

BTF — функция обучения сети, по умолчанию ’traingd’,

BLF — функция настройки весов и смещений, по умолчанию ’learngdm’,

PF — функция ошибки, по умолчанию ’mse’.

newelm — создание сети обратного распространения Элмана (Elman)

net=newelm (PR, [S1 S2…SNI], {TF1 TF2…TFNI}, BTF, BLF, PF) —

функция создания сети Элмана. Аргументы такие же, как и у предыдущей функции.

newff — создание однонаправленной сети

net=newff (PR, [S1 S2…SNI], {TF1 TF2…TFNI}, BTF, BLF, PF) —

функция создания «классической» многослойной нейронной сети с обучением по методу обратного распространения ошибки.

newfftd — создание однонаправленной сети с входными задержками

net=newfftd (PR, ID, [S1 S2…SNI], {TF1 TF2…TFNI}, BTF, BLF, PF) —

то же, что и предыдущая функция, но с наличием задержек по входам. Дополнительный аргумент ID — вектор входных задержек.

newgrnn — создание обобщенной регрессионной нейронной сети

net=newgrnn (P, T, spread) — функция создания обобщенно-регрессионной сети.

Аргументы:

P — R Q матрица Q входных векторов,

T — S Q матрица Q целевых векторов,

spread — отклонение (по умолчанию 1.0).

newhop — создание рекуррентной сети Хопфилда

net=newhop (T) — функция создания сети Хопфилда. Использует только

один аргумент

T — RQ матрица Q целевых векторов (значения элементов должны быть +1 или -1).

newlin — создание линейного слоя

net=newlin (PR, S, ID, LR) — функция создания слоя линейных нейронов.

Аргументы:

PR — R 2 матрица минимальных и максимальных значений для R входных элементов,

S — число элементов в выходном векторе,

ID — вектор входной задержки (по умолчанию [0]),

LR — коэффициент обучения (по умолчанию 0.01).

Возвращается новый линейный слой.

При записи в форме net=newlin (PR, S, 0, P) используется аргумент

P — матрица входных векторов,

возвращается линейный слой с максимально возможным коэффициентом обучения при заданной P.

newlind — конструирование линейного слоя

net=newlind (P, T) — функция проектирования нового линейного слоя.

Данная функция по матрицам входных и выходных векторов методом наименьших квадратов определяет веса и смещения линейной нейронной сети.

newlvq — создание квантованной сети

net=newlvq (PR, S1, PC, LR, LF) — функция создания сети встречного распространения.

Аргументы:

PR — R 2 матрица минимальных и максимальных значений для R входных элементов,

S1 — число скрытых нейронов,

PC — S2 элементов вектора, задающих доли принадлежности к различным классам,

LR — коэффициент обучения, по умолчанию 0.01,

LF — функция обучения, по умолчанию ’learnlv2».

newp — создание перцептрона

net=newp (PR, S, TF, LF) — функция создания перцептрона.

Аргументы:

PR — R 2 матрица минимальных и максимальных значений для R входных элементов,

S — число нейронов,

TF — функция активации, по умолчанию ’hardlim’,

LF — функция обучения, по умолчанию ’learnp’.

newpnn — конструирование вероятностной нейронной сети

net=newpnn (P, T, spread) — функция создания вероятностной нейронной

сети. Аргументы — как у функции newgrnn.

newrb — конструирование сети с радиальным базисом

net=newrb (P, T, goal, spread) — функция создания сети с радиальными

базисными элементами. Аргументы P, T, spread — такие же, как у функции newgrnn; аргумент goal — заданная среднеквадратическая ошибка.

newrbe — конструирование точной сети с радиальными базисными функциями

net=newrbe (P, T, spread) — функция создания сети с радиальными

базисными элементами с нулевой ошибкой на обучающей выборке.

newsom — создание самоорганизующейся карты

net=newsom (PR, [D1, D2,…], TFCN, DFCN, OLR, OSTEPS, TLR, TND) —

функция создания самоорганизующейся карты с аргументами:

PR — R 2 матрица минимальных и максимальных значений для R входных элементов,

I — размеры i-го слоя, по умолчанию [5 8],

TFCN — топологическая функция, по умолчанию ’hextop’,

DFCN — функция расстояния, по умолчанию ’linkdist’,

OLR — коэффициент обучения фазы упорядочивания, по умолчанию 0.9,

OSTEPS — число шагов фазы упорядочивания, по умолчанию 1000,

TLR — коэффициент обучения фазы настройки, по умолчанию 0.02,

TND — расстояние для фазы настройки, по умолчанию 1.

Функции обучения

[net, tr] =trainbfg (net, Pd, Tl, Ai, Q, TS, VV, TV) — функция обучения,

реализующая разновидность квазиньютоновского алгоритма обратного распространения ошибки (BFGS). Аргументы функции:

net — имя обучаемой нейронной сети,

Pd — наименование массива задержанных входов обучающей выборки,

Tl — массив целевых значений выходов,

Ai — матрица начальных условий входных задержек,

Q — количество обучающих пар в одном цикле обучения (размер «пачки»),

TS — вектор временных интервалов,

VV — пустой ([]) массив или массив проверочных данных,

TV — пустой ([]) массив или массив тестовых данных.

Функция возвращает обученную нейронную net сеть и набор записей tr для каждого цикла обучения (tr. epoch — номер цикла, tr.perf — текущая ошибка обучения, tr. vperf — текущая ошибка для проверочной выборки, tr.tperf — текущая ошибка для тестовой выборки).

Процесс обучения происходит в соответствии со значениями следующих параметров (в скобках приведены значения по умолчанию):

net.trainParam. epochs (100) — заданное количество циклов обучения,

net.trainParam.show (25) — количество циклов для показа промежуточных результатов,

net.trainParam. goal (0) — целевая ошибка обучения,

net.trainParam. time (∞) — максимальное время обучения в секундах,

net.trainParam. min_grad () — целевое значение градиента,

net.trainParam.max_fail (5) — максимально допустимая кратность превышения ошибки проверочной выборки по сравнению с достигнутым минимальным значением,

net.trainParam.searchFcn (’srchcha’) — имя используемого одномерного алгоритма оптимизации.

Структуры и размеры массивов:

Pd — No NiTs — клеточный массив, каждый элемент которого P {i, j, ts} есть матрица DijQ,

Tl — N1TS — клеточный массив, каждый элемент которого P {i, ts} есть матрица ViQ,

Ai — N1LD — клеточный массив, каждый элемент которого Ai {i, k} есть матрица SiQ,

где

Ni=net.numInputs (количество входов сети),

N1=net.numLayers (количество ее слоев),

LD=net.numLayerDelays (количество слоев задержки),

Ri=net.inputs{i}.size (размер i–го входа),

Si=net.layers{i}.size (размер i–го слоя),

Vi=net.targets{i}.size (размер целевого вектора),

Dij=Ri*length(net.inputWeights {i, j}.delays).

Если массив VV — непустой, то он должен иметь структуру, определяемую следующими компонентами:

VV. PD — задержанные значения входов проверочной выборки,

VV.Tl — целевые значения,

VV.Ai — начальные входные условия,

VV. Q — количество проверочных пар в одном цикле обучения,