
Бесплатный фрагмент - Операции над матрицами средствами MS Excel
Этой книгой я продолжаю курс практических занятий по Линейной алгебре, которые я проводил со студентами университета культуры и искусств в городе Санкт — Петербурге. но уже с широким применением приложения MS Ofice Excel.
1.Определители матрицы
1.1.Определители 2-го порядка
Пусть дана квадратная таблица из следующих чисел:
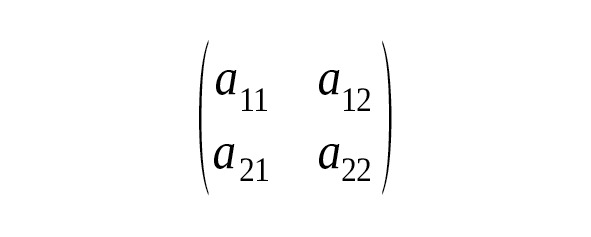
Число A = а11∙а22 — а12∙а21 называется определителем 2-го порядка и соответствует приведенной выше матрице Этот определитель обозначается символом det A и вычисляется по следующему правилу:
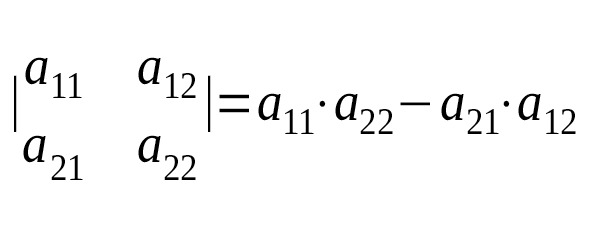
Числа а11,а22, а12,а21 являются элементами определителя. Говорят, что элементы а11,а22 лежат на главной диагонали определителя, а а12,а21 — на побочной.
Таким образом определитель 2-го порядка равен разности между произведениями элементов, лежащих на главной и побочной диагоналях.
1.2.Определители 3-го порядка
Рассмотрим таблицу из 9-ти элементов:
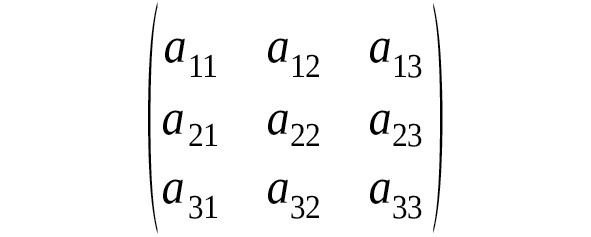
Определителем 3-го порядка, соответствующим зтой таблице, называется число, равное:
а11∙а22∙а33 + а21∙а23∙а31 + а21∙а32∙а13 — а13∙а22∙а31 — а11∙а32∙а23 — а21∙а12∙а33
Этот определитель обозначается символом det:
При вычислении определителя 3-го порядка удобно пользоваться правилом треугольника (правилом Саррюса):
1.3.Свойства определителей
1) Равноправность строк и столбцов: определитель не изменится, если его строки заменить столбцами или наоборот.
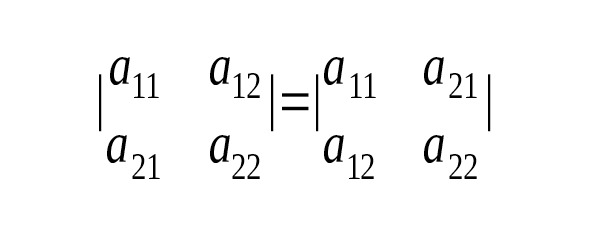
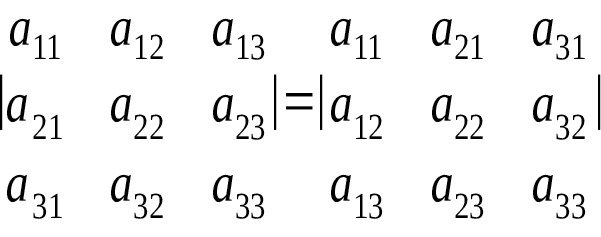
2) При перестановке двух параллельных рядов, определитель меняет знак.
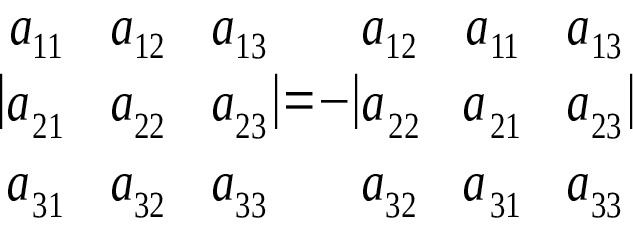
3) Определитель, имеющий два одинаковых ряда, равен 0
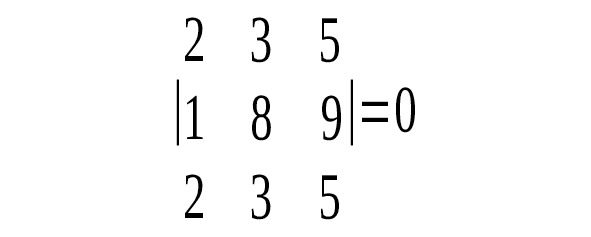
4) Общий множитель элементов какого-либо ряда определителя можно выносить за знак определителя.
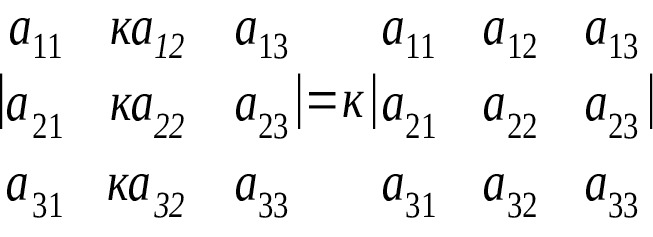
Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен 0
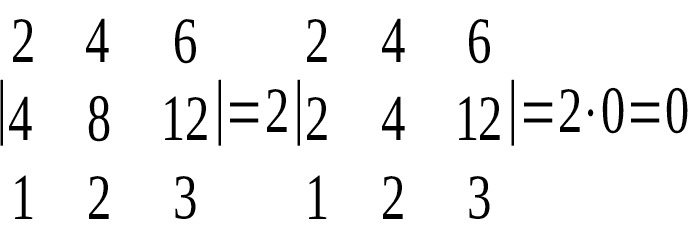
5) Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
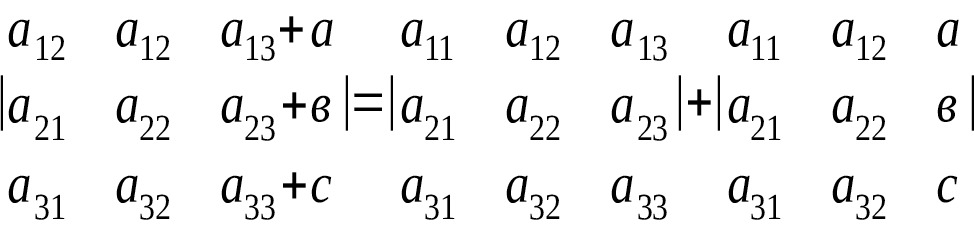
6) Элементарные преобразования определителя.
Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число:
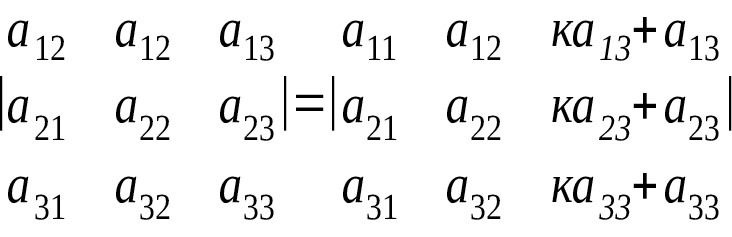
Минором некоторого элемента аij определителя n-ого порядка называется определитель n-1 –ого порядка, полученный из исходного, путем вычеркивания i — строки, j — столбца
Обозначается Мij
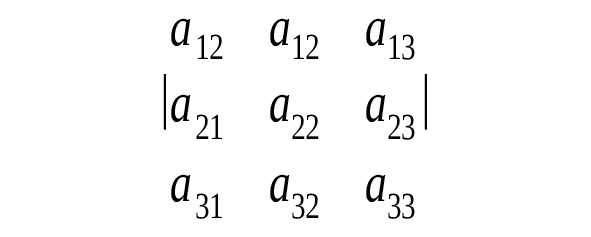
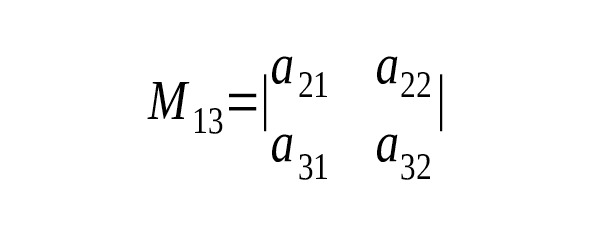
Алгебраическим дополнением элемента Аij определителя называется его минор (Мij), взятый со знаком «+», если сумма i+j — четное число, «-» если i+j — нечетное число.
А = (-1) i+j∙Mij
7) Разложение определителя по элементам некоторого ряда.
Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения:
= а11А11+а12А12+а13А13
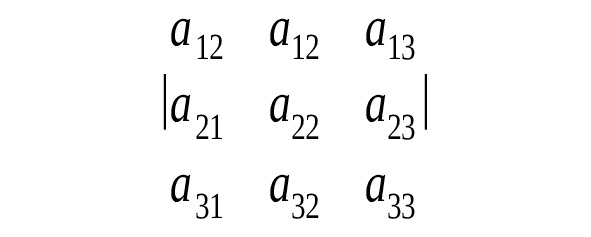
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.
