Бесплатный фрагмент - Очерки теории музыкального моделирования

Очерки теории музыкального моделирования

Книга третья

Преамбула

Первая книга серии «Очерки теории музыкального моделирования» была выпущена в 2020 году издательством Ridero. Предполагалось этим и ограничиться. Однако постепенно накопились новые материалы, и в 2021 году появилась вторая книга, выпущенная этим же издательством. И вот теперь, спустя еще четыре года предлагаю вниманию читателей третью книгу. В ней главный акцент смещается на анализ структурных и функциональных особенностей музыкальной моделирующей системы. Система эта мыслится не в отрыве от человека, не в качестве изолированного от него объекта, а в контексте человеческой деятельности, как продукт и инструмент этой деятельности. Одним из важнейших культурных результатов этой деятельности является формирование музыкальной художественной реальности. Поиску подходов к изучению этой реальности также посвящено немало страниц данной книги.

Рефлексия запоздалая

Мой сравнительно небогатый опыт объяснения кому бы то ни было своей «теории музыкального моделирования» (ТММ) позволяет сделать вывод: отвлеченные теоретические идеи, пусть и отвечающие на некие важные вопросы, не найдут отклика до тех пор, пока соответствующие вопросы не появятся в голове у того, кому вы пытаетесь свои идеи излагать. Именно на это я достаточно часто натыкался (хотя были и приятные исключения), предпринимая очередные попытки поделиться к кем-то своими мыслями. Ответом мне часто бывало или вежливое равнодушие, или удивленное «А зачем это всё?».

Сейчас, понимая, что в моих текстах по ТММ есть существенная брешь, что в них отсутствует часть, предъявляющая те самые вопросы, на которые я пытался искать ответы во времена своей студенческой юности, я попытаюсь мысленно вернуться назад (лет эдак на пятьдесят с лишним) и восстановить то, что происходило в моем тогда ещё только формирующемся теоретическом сознании.

Аристотелю принадлежит тезис «наука начинается с удивления». Плохо, когда она этим и заканчивается, но без удивления, по-видимому, никак не возможно. Поэтому первое, с чего я хочу начать, это со своих удивлений, возникавших у меня с первых шагов в музыкальной науке. Оставим в стороне те (весьма многочисленные), которые связаны со всякими «странностями» традиционного музыковедческого языка. Их много, но это отдельный разговор. Начнем с существенного, с того, что действительно связано с серьезными и не до конца разработанными проблемами. Именно, пережив подобные удивления, я начинал думать и искать способ понять непонятное. Так и возникли первые предположения, которые затем обретали теоретическую форму.

Первое подобное удивление было связано с интервалом октава. Более, чем через пятьдесят лет я прочел в книге Ю. Н. Холопова «Гармония. Теоретический курс» главу, которая так и называлась: «Проблема октавы». Всячески рекомендую для прочтения. Но тогда я, естественно, ничего об этом не знал, и с Холоповым познакомился позднее. (Впрочем, самой этой книги тогда еще не было).

Что же удивительного было в этом, таком знакомом каждому музыканту с самого детства, интервале? А вот что. Каждый знает — да и как можно этого не знать, — что, идя по ступенькам вверх от ноты «до» по белым клавишам, мы через семь шагов снова приходим к ноте «до». А если идти не по белым клавишам, а по всем подряд, не зависимо от цвета, то шагов будет не семь, а двенадцать. Но результат будет тот же самый — мы снова придем к ноте «до». Есть даже песенка про это из фильма-мюзикла «Звуки музыки», где поется «и мы приходим снова к до».

Так мы узнаём о множественности до. Существует не одно до, а множество до. Они находятся на разной высоте, но все они суть до. Затем мы узнаем, что такая множественность свойственна и ре, и ми, и вообще всем звукам музыкальной системы. Каждый из них предстает, так сказать, во множестве своих «воплощений». Особых возражений и вопросов это обстоятельство, как правило, не вызывает. Во-первых, узнаем мы об этом в детском возрасте, когда критическое мышление еще не развито (впрочем, у многих оно так и остается неразвитым и в более зрелом возрасте). Кроме того (это всего лишь предположение), игровое по преимуществу сознание ребенка воспринимает музыкальный звук не как колебание струны или столба воздуха, имеющее определенную частоту, а, скорее, как игровой элемент, как «сказочного персонажа», который предстает во множестве просто потому, что таковы условия игры. А условия игры обычно не обсуждают. Их просто принимают.

Но если об этом все же подумать, и подумать по-взрослому? Тогда и возникает удивление. Так это все же один и тот же звук, или несколько разных звуков, хотя и похожих? В каком отношении похожих? Звуки разной высоты, исполненные на одном и том же инструменте, обнаруживают похожесть. А звуки одной и той же высоты, исполненные на разных инструментах, могут разительно отличаться друг от друга. Утверждение похожести всегда предполагает уточнение — «в каком отношении они похожи?». А в каком отношении не похожи? Если брать чисто акустические основания, то есть делать акцент исключительно на «объективной» стороне вопроса, то, как это показал Ю. Н. Холопов в упомянутой выше статье, найти убедительный ответ на этот вопрос не получается. Попробуем подойти с несколько иной стороны.

Как проявляет себя октава в контексте «живой» музыкальной практики и, следовательно, в непосредственном человеческой восприятии? Что мы знаем об этом? Оказывается знаем. Во-первых, звуки, отстоящие друг от друга на некоторое целое число октав (включая ноль, то есть образующие приму), ведут себя одинаково в контексте любой ладовой системы. Прежде всего, в отношении устойчивости-неустойчивости. Например, в До мажоре звук до является наиболее устойчивым, он никуда не тяготеет. Это в одинаковой степени относится ко всем до, независимо от их высоты. Если же в какой-то тональности этот самый звук до является неустойчивым, то неустойчивыми опять-таки являются все звуки, принадлежащие этому октавному множеству. Получается, что звуки одного и того же октавного множества эквивалентны относительно фактора устойчивости-неустойчивости.

Во-вторых, из практики хорошо известно, что если сыграть некую мелодия с гармоническим сопровождением, а затем, оставив без изменения гармоническое сопровождение, переместить эту мелодию на октаву (или большее число октав) вверх или вниз, то мелодия и сопровождение будут все так же подходить друг к другу. И это со стопроцентной гарантией. Перемещение мелодии на любой другой интервал, столь же гарантированно резко изменит общий характер музыкального построения. Этот эффект в определенном смысле является продолжением, а именно обобщением, первого. В первом случае речь шла о функции тоники (абсолютная устойчивость), а во втором вообще обо всех функциях, которые при транспонировании мелодии на некоторое целое число октав вверх или вниз, остаются неизменными.

Кажется, всё разъяснилось? Скорее, наоборот. Возникают новые вопросы. Например, в каком смысле здесь употребляется слово «функция»? Функция звука или аккорда — это что? В чем состоит эта функция? По отношению к чему она осуществляется? Если все эти и тому подобные смыслы не прояснить, то мы попадаем в ситуацию объяснения неизвестного через неизвестное. А ведь понятие «функция» относится к таким, которые при их применении требуют уточнений. Многое зависит от контекста. В математике функция — это особое отношение между множествами. В биологии — это роль, которую выполняет тот или иной орган, или иная биологическая система. Если речь идет об искусственной механической системе, то можно говорить о функциях рычагов управления. У педали газа одна функция, у педали тормоза — другая, руль осуществляет третью. Во всех случаях они в том или ином направлении меняют состояние системы, или характер её движения. И всё это можно достаточно точно определить и описать.

Но что можно в этом смысле сказать о функции аккорда — тонического трезвучия или доминант септ аккорда? Где та система, на которую эти объекты оказывают влияние? Быть может это какие-то другие аккорды? То есть, мы должны допустить, что одни аккорды каким-то таинственным образом влияют на другие? Звучит фантастично и вряд ли может быть сколько-нибудь рационально описано. А может быть они влияют на человека, на слушателя, например, на его эмоциональное состояние и т. п.? Это уже более убедительно, более обнадеживающе и даже весьма интригующе. Но мы так мало еще знаем о воздействии подобных музыкальных феноменов на человеческую психику. И, следовательно, надеяться на простое объяснение известных музыкальных феноменов с помощью данных этих наук мы не можем. Кроме того, здесь мы явно выходим за пределы теории музыки и вторгаемся в область психологии и психофизиологии. А теории музыки необходимо наводить порядок в собственном хозяйстве.

А что если допустить такую, в общем-то естественную мысль, что речь здесь должна идти о какой-то художественной функции. Ведь музыка, как-никак — вид искусства. Правда на этот счет существуют всякие «соображения» и авторитетные мнения, ставшие привычными и приобретшие характер аксиом. Речь идет о тезисе, согласно которому музыка не относится к числу «подражательных» искусств, то есть она ничего не изображает, а сама по себе является игрой прекрасных форм. То есть, функцией «мимесиса» она как бы и не обладает. Нельзя сказать, что этот тезис открыто и в явной форме поддерживается большинством теоретиков музыки и практических музыкантов. Но он как бы исподволь, косвенно действует на общее умонастроение, заставляя воздерживаться от высказываний на эту тему. И эта фигура умолчания мешает не только высказываться на данную тему, но и даже думать в соответствующем направлении.

Но почему бы не нарушить это «табу», хотя бы только в порядке мысленного эксперимента? Для того, чтобы сознательно нарушить запрет, нужно его сначала сформулировать. Хотя бы так: «запрещается, анализируя какие-либо элементы музыкальной системы и, пытаясь найти им объяснение, ставить вопрос об их отношении тем или иным объектам, явлениям, процессам, выходящим за пределы мира музыкальных феноменов». По отношению к феномену октавы этот запрет означает отказ от попыток искать каких-либо внешних по отношению к музыке аналогий. В крайнем случае можно эти аналогии использовать на правах метафоры, просто как языковое средство для более яркого и запоминающегося описания. Это, как раз, нередко происходит.

Мы, как и собирались, этот запрет нарушим и поставим вопрос именно таким образом. Что я, собственно, и сделал, будучи учащимся музыкального училища. Я поставил вопрос примерно так: чем, собственно, отличается устойчивый звук от неустойчивого? На что это могло бы быть похоже? Ответ, во-первых, лежал на поверхности, а во-вторых, на слуху были сравнения, используемые не столько в научных, сколько в педагогических целях. Основным понятием (не столько объясняющим, сколько нуждающимся в объяснении) было понятие «тяготение». Под этим понималось примерно следующее. Неустойчивый звук «стремится» переместиться в определенном направлении и занять положение, при котором он станет устойчивым. А устойчивый звук никуда не стремится. А если он и «хочет» чего-то, так это оставаться на своем месте.

Разумеется, никто не считал, что звук сам по себе может чего-то хотеть. Это было бы слишком странным. Поскольку такая возможность исключалась, тяготение следовало считать чем-то присущим звукам «объективно». Но что значит объективно? Независимо от человека, его восприятия, его сознания? Тогда возникает вопрос, присутствуют ли тяготения в музыке, которую никто не слышит? Ну, например, включили проигрыватель и ушли все из дома. Музыка звучит, но её никто не слышит. Есть ли в этом случае тяготения?

Обе эти возможности выглядят несколько экстравагантно, мягко говоря.

О том, как можно выйти их этого положения, скажем несколько позже. А пока вернемся к вопросу «на что это похоже?». Для начала просто заменим слово «стремится», вызывающее ненужные ассоциации, на какое-нибудь более нейтральное выражение. Собственно, даже слово «тяготение» выглядит гораздо более свободным от этих ассоциаций. Тяготеет значит обладает потенциалом к движению. А можно сказать и точнее, используя общенаучный термин — обладает потенциальной энергией.

Здесь мы, вообще-то говоря, ничего нового не открыли. Об энергии в связи с музыкой писали многие. Скажу лишь о двух авторах. Первый — Аристотель. Второй — Эрнест Курт. Их концептуальные подходы к этому предмету существенным образом отличались. Аристотель рассуждал об этом в русле идей теории подражания, мимесиса, каковой он считал существенным признаком искусства. Искусства любого, в том числе и музыки. Он говорил о том, что в музыке присутствуют энергии. Энергии по своей природе деятельны. А уже отсюда в музыке появляются этические качества. Что касается Курта, то он больший акцент делал на психических энергиях. А заодно и музыку как таковую он как бы переносил в сферу человеческой души. «Музыка есть борьба сил, становление внутри нас» — писал он.

Так что, об энергии в связи с музыкой уже немало было сказано. Если и была в моих тогдашних рассуждениях небольшая толика новизны, то связана она лишь с тем, что феномен октавы, о котором мы ведем речь, был как-то связан с идеей музыкальной энергии. А связь эта в общем лежала на поверхности. Звуки, принадлежащие одному октавному множеству либо все устойчивы, либо все неустойчивы. В рамках энергетических представлений (энергетической терминологии) мы могли бы сказать, что они (эти звуки) обладают одинаковым энергетическим потенциалом. Например, если до1 — тоника, то есть никуда не тяготеет, то есть обладает нулевым уровнем потенциальной энергии, то и до2 является тоникой, никуда не тяготеет, обладает нулевым уровнем потенциальной энергии. А если до1 является неустойчивым звуком, то уровень потенциальной энергии (энергетический уровень) этого звука не равен нулю, а равен, скажем, некоторому x. В таком случае энергетический уровень любого до тоже будет равен x. Так мы всего лишь по другому сформулировали, то, что подтверждается опытом восприятия, и о чем все говорили, но только другими словами. Суммируя только что сказанное, мы можем сформулировать некое обобщение, а именно: разность энергетических потенциалов двух звуков, находящихся на расстоянии октавы всегда равна нулю. Из этого напрямую следует, что разность энергетических потенциалов двух звуков, находящихся на расстоянии любого числа октав также всегда равна нулю. Просто потому, что сумма нескольких нулей всегда равна нулю. Сказанное относится и к приме, ибо прима есть октава минус октава, то есть ноль минус ноль.

Все это на уровне простой арифметики выглядит крайне просто и очевидно. Сложность в другом — в интерпретации этих положений, в правильном их понимании. Что же это за энергия такая, и что значит «звук обладает некоторым энергетическим уровнем»? Как он может им обладать, и в чем это может выражаться?

На острие этих вопросов находится необходимость как-то определиться с соотношением объективного и субъективного моментов. Что собой представляет эта музыкальная энергия? Где она находится? В сознании субъекта? Тогда как она связана с реально звучащей музыкой? И за счет чего достигается достаточно очевидная общезначимость связанных с ней моментов? Ведь огромный культурный опыт доказывает, что многое здесь разными людьми воспринимается одинаково. В частности, то, что говорилось выше по поводу октавы. Да, и многое другое.

Может быть эта энергия присуще музыке объективно? То есть, это физическая энергия акустических колебаний? Другой энергии в музыке «объективно» нет. Эта (физическая) действительно есть. И ее роль в музыке действительно велика. Но это — другая энергия. И она определяется иными причинами, зависит от других факторов. Здесь речь должна идти об амплитуде звуковых колебаний, воспринимаемых нами как громкость. Как же обойти эти крайности? Как избежать ведущего в тупик «или — или»? Иными словами, речь шла о необходимости найти такой способ понимания музыкальной энергии, который позволил бы удержать обе стороны — и объективную и субъективную — и объяснить характер их взаимодействия.

И здесь тоже не пришлось изобретать чего-то особенно нового. Сформулированному выше требованию соответствует, в частности, теория подражания, сформулированная ещё Аристотелем, о чём уже шла речь. В известном трактате «Поэтика» Аристотель формулирует основные её принципы применительно литературе и драматургии, но в иных источниках применяет её ко всем искусствам, включая музыку. «Как кажется, поэзию создали вообще две причины, притом естественные. Во-первых, подражать присуще людям с детства; они отличаются от других живых существ тем, что в высшей степени склонны к подражанию, и первые познания человек приобретает посредством подражания. Во-вторых, подражание всем доставляет удовольствие». Мы видим, что оба аспекта — объективный и субъективный — здесь даны в единстве. Объективный — то, чему происходит подражание, или предмет подражания, который сам является стороной (комплексом сторон) некоторого объекта. А также система средств, с помощью которых осуществляется подражание. Субъективная составляющая — человек — в этом определении упоминается дважды. Во-первых, он склонен к подражанию с детства. Во-вторых, он испытывает от подражания удовольствие.

Фактически Аристотель рассматривает подражание как особого рода деятельность. А деятельность всегда включает в свой состав и объективную и субъективную стороны.

Не давая строгого определения понятия «подражание», Аристотель подробно рассматривает структуру этого действия применительно к искусству поэзии и драмы. Отсутствие четкого определения не вызывало серьезных затруднений в использовании этого понятия. Оно представлялось интуитивно понятным. Тем не менее, это создавало предпосылки для неявного проникновения в смысловой состав этого понятия неких теневых, неявных презумпций. Одной из таких теневых презумпций является представление о том, что между образцом и образом всегда должно иметь место очевидное и непосредственно воспринимаемое сходство. А что, если такого прямого сходства нет? Или оно недостаточно очевидно? А если оно лишь иногда бывает достаточно очевидным, но, к сожалению, далеко не всегда? В таком случае и напрашивается вывод о том, что не все искусства относятся к «подражательным». Есть и неподражательные. Например, архитектура и музыка.

Как уточнить (эксплицировать) понятие «подражание» не вступая в обреченное фиаско единоборство с прочно устоявшейся многовековой традицией его применения? Такое уточняющее понятие найти было нетрудно. В 60-70-е годы выходило немало литературы, где оно активно обсуждалось. Это понятие «моделирование». Ему давались различные определения. Но при всем разнообразии смысловых оттенков это понятие сохраняло нечто общее и исключительно важное именно для нашей ситуации — наличие очевидного и непосредственно воспринимаемого сходства не является существенным признаком модели. Если такое сходство есть, то модель становится наглядной. Для моделирования существенным является целесообразное использование подобия (между вещами и процессами) в человеческой деятельности. Наглядность — далеко не обязательное условие создания моделей, используемых в человеческой практике.

Обязательна ли наглядность в искусстве? Во всяком случае, это ни откуда не следует. В искусстве вообще далеко не все очевидно и наглядно. Это относится и к форме, и к содержанию. Очень многое и весьма существенное скрыто в глубине бессознательного. Все это хорошо известно. Нет никаких оснований считать, что отношение подобия, возникающее между произведением искусства и какими-нибудь иными объектами (вещами и процессами) является исключением из этого общего правила.

Во всяком случае, у нас есть все основания попытаться вести исследования (в том числе и строить теории) исходя из соответствующих допущений. А точнее сказать, исходя из отрицания предвзятого убеждения в том, что музыка «ничему не подражает и ничего не моделирует», что она, так сказать, беспредметна. Это, прежде всего, разрешает нам задавать самим себе вопросы на соответствующую тему.

И вот мы задаём такой вопрос по поводу феномена октавы, обнаружившим для нас со всей отчетливостью то, что можно назвать феноменом музыкальной энергии. Есть ли в окружающем нас мире, да и в нас самих, нечто такое, чему соответствовала бы музыкальная энергия? Наблюдается ли, в частности, такое явление, когда некий объект, изменяя свое положение в пространстве, меняет и свой энергетический уровень? Сколько угодно и на каждом шагу! Поднимающийся и опускающийся груз, качающийся маятник и т.д., и т.п..

Может быть это — отвлечённая наука, физика? А есть ли в живом человеческом опыте непосредственное переживание энергетических феноменов? И опять мы должны дать положительный ответ. Тот же самый маятник, но только с непосредственным участием человека — качели. Когда я качаюсь на качелях, я непосредственно ощущаю, всем своим существом переживаю превращение кинетической энергии в потенциальную и обратно. И какое же это захватывающее ощущение! А езда со скоростью и прежде всего моменты ускорения и торможения?! А «американские горки» с их внезапными поворотами?! А горные лыжи?! А фигурное катание?!

Но ведь и любая мышечная деятельность представляет собой энергетическое взаимодействие с внешним миром. При этом мое самочувствие, отражающее степень моей готовности к такому взаимодействию, разве не является энергетическим переживанием? Энергия в общем смысле нередко определяется как способность совершить работу. Но ведь и в моем самочувствии всегда присутствует оценка моей способности совершить работу, сделать нечто. Есть, в частности, такая вещь, как ощущение тонуса, есть чувство бодрости и чувство усталости. Если же говорить об эмоциях как таковых, то энергетические смыслы обнаруживаются и тут. Ведь существует деление эмоций на стенические и астенические… Таким образом, энергия и вокруг нас, и внутри нас. Она универсально присутствует в нашей жизни. Жизнь как таковая есть в том числе и энергетический процесс. И борьба за существование включает в себя борьбу за энергию.

Таким образом, энергия — вещь для нас не абстрактная и не отвлеченная. Она в нашем дыхании, в биении сердца, в каждом глотке воды и в нашей пище, в любом движении и даже в состоянии неподвижности.

А музыкальная энергия есть форма художественного освоения этого жизненно значимого параметра. Что же касается октавы, то энергетическое равенство образующих её звуков и есть модельная функция данного музыкального интервала.

На этом месте разумно задать вопрос и о других интервалах. Обладают ли и они подобной модельной функцией? В частности, найдутся ли интервалы с энергетическим потенциалом, не равным нулю?

Как минимум, один такой интервал безусловно имеется. Он достаточно давно привлекал моё исследовательское любопытство. Раньше, чем октава. Но именно октава помогла мне задать соответствующий вопрос. Этот интервал — квинта. Чем он интересен? Чем выделяется среди прочих? Уже с младших классов музыкальной школы внимание учащихся обращают на этот интервал. Его особенность подчеркивается с разных сторон.

— Он присутствует и в мажорном, и в минорном трезвучии, образуя в них своего рода костяк, опорный элемент. И в мажорном, и в минорном трезвучии он остается одним и тем же. А вот терцовый тон аккорда демонстрирует изменчивость. В миноре он находится на расстоянии малой терции от основного тона, а в мажоре — на расстоянии большой терции. В зависимости это этого меняется и общее настроение (окраска) трезвучия. Мажорное трезвучие звучит весело, минорное — грустно. Таким образом, имеет место сочетание стабильности и изменчивости. Квинта среди прочих интервалов (за исключением октавы, роль которой в системе особая) обладает максимально выраженным качеством стабильности.

— Если квинту сыграть снизу вверх, то она звучит, как вопрос. Если сверху вниз — звучит, как ответ, получается утвердительная интонация. Такой поляризации и такой однонаправленной иерархии не наблюдается у других интервалов.

— Все 7 звуков натуральной мажорной или минорной гаммы можно расположить в ряд по квинтам. Это же самое можно сделать и по отношению к 12-ти звукам хроматической гаммы. Просто квинтовый ряд будет длиннее. Никакой другой интервал такой возможности нам не дает. Обязательно будут пропущенные элементы.

— Интервал квинта составляет основное (системообразующее) отношение между основными тонами главных трезвучий. Именно на квинтах строится основная связь и основная иерархия аккордов в тональности, а затем и самих тональностей. Таким образом — квинта является основой всей звуковысотной системы.

Основными характеристиками квинты, привлекшей тогда моё внимание были а) универсальность, охват квинтовым рядом всей без исключения системы звуков, б) максимальная определенность, однонаправленность иерархии элементов.

Таким образом, можно сказать, что квинта также, как и октава моделирует некий тип отношений.

— Октава — равенство, эквивалентность (взаимозаменяемость), «равноправие».

— Квинта — четкая и однонаправленная иерархия, неравенство. А это уже некая смысловая бинарная оппозиция.

Если взять два звука квинты и вслушаться в их отношения с точки зрения устойчивости-неустойчивости, то мы, при прочих равных условиях определим нижний звук квинты (основание) в качестве устойчивого, а верхний (вершина) в качестве относительно неустойчивого. Положение нижнего звука есть положение покоя, отсутствия стремления куда-либо. Положение верхнего звука несет в себе потенцию к движению, к перемещению, причем именно на позицию нижнего звука. Ни один другой интервал не дает нам такой отчетливой и такой однозначной динамической картины.

Теперь применим к этому интервалу тот же подход, который мы опробовали в связи с октавой. Примем энергетический уровень нижнего звук квинты за ноль. В принципе, мы вправе сделать это без каких-либо особых обоснований. Ведь принятие за ноль (за систему отсчета) — действие условного характера. Чему тогда будет равна энергия верхнего звука? Исходя из всего вышесказанного, она будет отличаться от нуля. В какую сторону — в положительную и отрицательную? В силу того, что верхний звук квинты обнаруживает в себе определенное стремление переместиться в нисходящем направлении, его энергетическое значение естественнее определить в качестве положительной величины.

Мы видим еще одно отличие октавы от квинты. Октава внутри самой себя не содержит потенции к движению. Она — сфера покоя. Квинта содержит. Другое отличие в том, что октава не содержит в себе иерархии, неравенства, направленности в том или ином определенном направлении. Квинта в себе всё это содержит.

Итак, примем энергию основания квинты за ноль. Чему будет равна энергия вершины квинты? Некоторой положительной величине. Условно примем её за единицу.

Пусть до1 — основание квинты. Её энергия равна 0. Соль1 — вершина квинты. Её энергия, согласно нашим рассуждениям, равна +1. А если энергию Соль1 принять за 0, то какова будет энергия до1? Очевидно, то -1. Элементарная арифметика. Столь же элементарная арифметика позволит нам определить энергию соль2 относительно до1. Ведь расстояние от соль1 до соль2 равно октаве. Энергия октавы равна нулю. Следовательно, энергия соль2 также, как и энергия соль1 будет равна +1.

Возможность производить эти нехитрые расчеты очень радовала. А как обстоит дело с другими звуками? Можно ли определить и их энергию? Оказалось, что можно. Ведь мы знаем, что музыкальная система построена таким образом, что от любого звука до любого другого можно добраться перемещаясь исключительно по квинтам и октавам. А энергию (разность энергетических потенциалов) и квинты, и октавы мы уже знаем. Значит, последовательно суммируя энергии всех посредствующих интервалов, мы получим искомое значение. Например, от до1 до ре1 можно дойти следующим образом: до1 — соль1 — ре2 — ре1. Тогда до1 — 0, соль1 — 1, ре2 — 2, ре1 — 2. Итак от любого к любому звуку. Такова структура музыкальной системы.

Далее было нетрудно построить таблицу энергетических значений для всех интервалов, а затем и аккордов. Столь же простым делом было построить энергетические графики для основных семиступенных ладов.

Следующим шагом была постановка вопроса о модельных функциях иных музыкальных параметров — высоты звуков, громкости и прочих. Возникали и другие вопросы. Например, почему в мажоре, миноре и других диатонических ладах именно семь ступеней, а не больше, и не меньше. Чем чистая семиступенная диатоника отличаются от хроматики. Чем пентатоника отличается от семиступенной диатоники?…

По мере ответов на эти и другие вопросы, вырастала более-менее цельная логическая конструкция, которую я условно назвал «теорией музыкального моделирования». В процессе этого движения, я все больше убеждался в том, что утверждение о «неподражательном» характере музыкального искусства ничего не доказывает, ничего не объясняет, а лишь закрывает от взгляда исследователя целый ряд интересных и важных вещей. Подход с позиций моделирования, конечно же, не может объяснить всего. Но он позволяет двигаться. И в этом движении я еще не пришёл к ощущению, что уперся в непроходимую стену. Наоборот, чем дальше идешь, тем больше вопросов и тем больше ответов.

О музыкальной моделирующей системе

Для начала введём несколько вспомогательных понятий и дадим предварительные разъяснения. Их функция состоит в создании необходимых предпосылок для того, чтобы сформулировать основные определения (и чтобы эти определения были по возможности однозначно поняты).

ЭЛЕМЕНТЫ МУЗЫКИ. Так мы будем называть звуковые феномены, их комплексы, их параметры и отношения, включенные в музыкальную практику (деятельность).

Этот последний признак (включенность в музыкальную практику) является существенным. Это означает, что звуковые феномены, не включенные в музыкальную практику, нами не будут рассматриваться в качестве элементов музыки. Собственно, это так потому, что музыка — это и есть определенная практика (деятельность). Включенность в эту практику и есть включенность в музыку.

Включенность в практику означает реализацию (выполнение) определенных, связанных с этой практикой функций. Без этого нет включенности. Функций существует множество. Они связаны с тем, что в этой музыкальной практике человек реализует свои отношения к реальности (к объективному миру), к социуму, т. е. к другим людям (в частности, коммуникативная функция), к культуре, к самому себе.

Говоря именно о звуковых феноменах, мы хотим тем самым подчеркнуть, что имеются в виду лишь то, что воспринимаемо, слышимо, осознаваемо. Так, звуки не слышимые (по причинам слишком низкой амплитуды колебания или частоты, лежащей за порогом восприятия) не входят в объем этого понятия. Точно также, к этому не имеют отношения чисто физические параметры и их значения (частота, амплитуда колебания, обертоновый состав и пр.). Этим «чисто объективным» параметрам соответствуют такие качества звуковых феноменов, как высота, громкость и тембр. Эти параметры описывают именно то, как мы слышим и осознаем звуковые явления. Акустические явления, чтобы стать элементами музыки, должны быть, как минимум, восприняты и осознаны.

Введенное только что ограничение, делает понятным, что исследовательский подход, предполагающий изучение музыки как чего-то совершенно «объективного», независимого от человека, наподобие того, как изучаются явления и процессы в природе, вступает в противоречие с вышеизложенным пониманием элементов музыки. Происходит это потому, что эти «чисто объективные», отделенные от человека и его практической деятельности вещи элементами музыки не являются по определению.

Возникает вопрос, относятся ли к элементам музыки такие «не акустические» характеристики, как ритм, метр и темп? Ведь ни то, ни другое, ни третье не относится к разряду собственно звуковых феноменов. Все это не про звук, а про время. Давайте вернемся к определению. В нем, помимо прочего, говорится об отношениях. Но среди отношений между звуковыми феноменами, входящими в состав музыкального целого, важнейшую роль играют именно временны́е отношения, которые в контексте музыки обретают значение ритма, метра и темпа, а также аспектов музыкальной формы. Да и сам звук как таковой сущностно связан с категорией времени. И объективно (как циклический процесс, имеющий частоту), и субъективно (длительность, метрическая структура). Аналогичным образом и по аналогичным причинам к числу элементов музыки принадлежит и пауза («нулевой звук»).

По своей значимости для музыкальной практики, звуковые комплексы стоят выше, нежели отдельные звуки, звуковые параметры выше, чем звуки как таковые, а отношения между параметрами выше, чем сами параметры.

МУЗЫКАЛЬНАЯ МОДЕЛИРУЮЩАЯ СИСТЕМА (ММС) понимается нами как организация элементов музыки, обладающих определенными модельными функциями.

Таковыми по определению должны обладать звуковые феномены, их комплексы, параметры и отношения. Без этого условия они не входят в состав музыкальной моделирующей системы. В дальнейшем нашим непосредственным предметом становится именно музыкальная моделирующая система. Все остальное может иметь лишь косвенное значение.

Поскольку отношение к реальности является атрибутивным качеством искусства, а моделирование является необходимым аспектом отношения искусства к реальности, постольку моделирование является необходимым элементом (атрибутом) художественной практики (музыкальной, в том числе). Это значит, что музыкальная практика как таковая, с необходимостью включает в свой состав моделирование реальности. Следовательно, музыкальная система не может не быть моделирующей. Другое дело, что далеко не всегда предметом изучения оказывается именно эта ее сторона. Поэтому, говоря о музыкальной моделирующей системе, мы тем самым подчеркиваем, что основным предметом нашего исследовательского интереса является именно функция моделирования реальности.

ММС в таком ее понимании является абстрактным объектом. К сожалению, в традиционном музыкознании нередка путаница, когда привычные музыковедческие понятия, а также многие выражения, описывающие реальную музыкальную практику (например, лады, тональности, интервалы, аккорды и прочее) без каких либо оговорок интерпретируются, как эмпирические понятия. При этом упускается существенная разница между языком, служащим организации практического действия («играем в до мажоре», «сделай модуляцию в тональность доминанты» и т.п) и языком теории, оперирующей отвлеченными понятиями, облеченными в слова, которые произносятся и пишутся так же, но имеют иной смысл. Реальная музыкальная практика, подчиняющаяся определенным культурным нормам, содержит в себе множество инвариантов музыкальной деятельности (сочинения, исполнения, восприятия), каковые находят свое отражение в обслуживающем музыкальную деятельность языке.

Возьмем в качестве примера понятие «До мажор». Игра в До мажоре, звучание До мажора, восприятие До мажора суть реальные эмпирические факты. Они всегда привязаны к определенным условиям места, времени и пр. Но «До мажор вообще» таковым не является. Его существование не нуждается ни в исполнении, ни в чьем-то восприятии. Это — отвлеченный теоретический конструкт. Здесь возникает определенная теоретическая трудность. Дело в том, что музыкальная практика людей, даже не имеющих какого-либо музыкального образования и никогда не слышавших подобных слов, все же каким-то образом управляется этими «инвариантами» (правилами). Люди так слышат, так поют и т. д. Это рождает множество сложных вопросов, которые условно можно свести к одному — «каким образом это происходит?».

Но мы в данном конкретном случае ограничимся лишь тем, что укажем на наличие этих вопросов, их сложность, их важность и их весьма малую исследованность. Сами же сосредоточим свое внимание непосредственно на особенностях строения ММС.

ЗВУК. Понятие «звук» является многозначным, что порождает неизбежную путаницу. Поскольку понятия «звук» и «музыкальная система» в музыковедческих работах, как правило, так или иначе связываются, нам необходимо уточнить собственные позиции относительно их использования.

Прежде всего, будем отличать друг от друга понятия «ФИЗИЧЕСКИЙ ЗВУК» и «ЗВУКОВОЙ ФЕНОМЕН». Физический звук мы понимаем как материальный процесс — колебание физического тела, обладающий такими существенными для него характеристиками, как частота, амплитуда, длительность, обертоновый состав, скорость распространения в той или иной среде и др. Изучается таким разделом физики, как акустика. Для физического звука в общем-то не существенно, слышит его кто-либо или нет, какое он производит впечатление и пр. Звуковой феномен, напротив, есть то, что воспринимается и осознается тем или иным образом. Многие свойства и параметры физического звука находят свое соответствие на уровне звукового феномена. Так частоте соответствует высота, амплитуде — громкость, обертоновому ряду — тембр. Но соответствие не есть тождество.

ЗВУК И МУЗЫКАЛЬНАЯ МОДЕЛИРУЮЩАЯ СИСТЕМА. Правильно ли будет сказать, что музыкальная моделирующая система состоит из звуков? Нет, в нашей логике это будет, как минимум, не точно. Дело в том, что мы определяем музыкальную систему не как множество реальных физических звуков (нам, честно говоря, даже не понятно, где и как такое множество может существовать), а как принцип организации, где элементы системы становятся узлами отношений, образующих структуру системы. Тогда реально звучащие звуки оказываются средством проявления-опредмечивания этой системы. Без такого проявления на материальном плане система перестает быть предметом или средством человеческой коммуникации, а также регулятором деятельности, обеспечивающим связь композиторской, исполнительской и слушательской активности. Но, при всей важности такой функции реальных физических звуков, они не являются непосредственно элементами системы. Система — абстрактный объект, и все ее элементы суть абстрактные объекты.

В этой логике «звук» как элемент музыкальной моделирующей системы не является звуком в обычном смысле слова. От многих его качеств мы просто абстрагируемся. В том числе, он даже «не обязан» звучать. Он, как было сказано выше, есть узел внутрисистемных отношений. И в этом смысле, он вторичен по отношению к самой системе. Тут нет ничего недопустимого или странного. Он — абстрактный объект. Такой же, как материальная точка, идеальный газ и т. п. Здесь нет чего-то нового. Вторичность элементов по отношению к системе есть необходимый аспект взаимодействия части и целого. Объединяясь в систему, элементы как бы теряют некоторые свои прежние свойства, которые присущи им вне системы. При этом они, как правило, приобретают какие-то новые свойства.

В этом системном контексте связи и отношения элементов приобретают более важное значение, нежели сами элементы. Например, интервалы (мелодические ходы) в мелодии оказываются важнее, чем собственно звуки, последовательностью которых может показаться мелодия на первый взгляд. Примером, убедительно подтверждающим это, является транспонирование мелодии. Заостряя эту мысль, можно сказать, что музыка состоит не из звуков, а из их отношений. Причем, именно из внутрисистемных отношений.

МУЗЫКАЛЬНАЯ МОДЕЛИРУЮЩАЯ СИСТЕМА КАК ПРЕДМЕТ МУЗЫКАЛЬНО-ТЕОРЕТИЧЕСКОГО ИССЛЕДОВАНИЯ. Мы исходим из предположения (а точнее, из убеждения), что музыкальная моделирующая система обладает своими особенностями, свойствами, организационными принципами, обуславливающими необходимость (целесообразность) ее специального рассмотрения. Иными словами, она вполне достойна того, чтобы быть специальным предметом исследования. В настоящее же время она а) изучена далеко не в должной мере, б) по большей части «растворена» в иных музыкально-теоретических предметах, что приводит к размыванию ее специфики. Перечислим некоторые такие музыковедческие предметы, где ММС так или иначе находит хотя бы частичное отражение.

ЭЛЕМЕНТАРНАЯ ТЕОРИЯ МУЗЫКИ. Прежде всего отметим прикладную (практическую) направленность этой не столько научной, сколько учебной дисциплины. В ней говорится не о музыкальной моделирующей системе, а просто о музыкальной системе. Система эта, как правило, мыслится как состоящая из звуков. Ее структура чаще всего выводится из структуры обертонового ряда, что делает обертоновый ряд «объективной причиной», объясняющей строение музыкальной системы. Своего рода зерном, из которого она вырастает «естественным образом». В результате на первый план выдвигается физическая составляющая процесса, а человек, его деятельность и культура «выносятся за скобки».

Лишенная, фактически, непосредственной связи с практикой, музыкальная система и ее свойства мыслятся так, что не возникает даже вопросов о функциях ее самой и ее элементов. Соответственно, нет речи и о модельной функции (шире — об отражательно-познавательной функции).

Такие важные структурные составляющие ММС, как лады, интервалы, аккорды и пр. описываются, как правило, вне связи с системой, как независимые от нее самостоятельные сущности, имеющие те или иные свои характеристики потому, что «так исторически сложилось».

ГАРМОНИЯ. Между предметами элементарной теории музыки и гармонии есть определенная связь в силу того, что первая, помимо прочего, выполняет функцию подготовки ко второй. Поэтому понятия звукоряда, лада, тональности, ладовых функций, аккорда и пр. вводятся уже в курсе элементарной теории музыки, но в курсе гармонии рассматриваются значительно более полно и обстоятельно.

Следует заметить, что между собственно научным направлением развития музыковедческого знания и учебно-преподавательским направлением грань весьма условная, граница прозрачная. И мы с трудом можем отделить одно от другого.

ПОЛИФОНИЯ. Этот предмет отличает ещё более определённо выраженная технологическая направленность. Это обстоятельство в значительной мере предохраняет от всяческой теоретической путаницы. Предмет здесь вполне чёток и ясен — приёмы (алгоритмы) композиторских действий. Можно сказать, правила игры. В рамках строго стиля господствуют одни правила. В рамках свободного — другие. Сама по себе данная дисциплина не ставит перед собой задачу причинного объяснения этих правил. Это обстоятельство по началу может вызвать некоторое недоумение. Но потом к этому привыкаешь.

АНАЛИЗ МУЗЫКАЛЬНЫХ ПРОИЗВЕДЕНИЙ. Здесь мы имеем дело с дисциплиной, сила которой является одновременно причиной её слабости. Речь идёт о её синтезирующей (интегрирующей) направленности. Внутренний пафос развития этой области музыкальной науки состоит в значительной мере в том, чтобы выработать теоретический аппарат, позволяющий любое конкретное музыкальное произведение проанализировать и объяснить не с какой-то отдельной точки зрения, а целостно и всесторонне. В определенном смысле такой анализ становится уже не научной деятельностью, а своеобразным искусством. При этом, упомянутое стремление к всесторонности, как правило, упускает из виду такую сторону музыки, как её связь с человеком. Произведение берется по возможности целостно, но как бы «объективно», как существующая сама по себе «вещь». Другая сторона бытия музыки, которая также «выносится за скобки» — это отношение музыки к отражаемой ею реальности. Соответственно, вопрос о моделировании и модельных функциях в данном контексте вообще не ставится.

* * * * *

МУЗЫКАЛЬНАЯ МОДЕЛИРУЮЩАЯ СИСТЕМА состоит из некоторого множества относительно самостоятельных блоков. К ним, в частности, относятся

— Звуковысотная система.

— Темпоральная система. Сюда входит то что относится к музыкальному времени — ритм, метр, темп, форма.

— Субстанциальная система, которая имеет две стороны — количественную (громкость) и качественную (тембр)

Вышеперечисленные системы чаще всего называют средствами музыкальной выразительности. Нисколько не возражая против такой трактовки, мы, тем не менее, всего лишь сосредотачиваем внимание на других сторонах функционирования этих вещей, на иных связях и взаимодействиях. Они интересуют нас с точки зрения моделирования музыкой явлений действительности (формирования картины мира).

Эти блоки находятся во взаимодействии и служат для создания единого художественного целого, для реализации единого художественного замысла. Тем не менее, изучать и описывать их можно и по отдельности. Условно отделить друг от друга, чтобы затем поставить вопрос об их взаимодействии.

В рамках настоящего текста (статьи, главы) мы сконцентрируем свое внимание на звуковысотной системе.

Что касается употребления термина «звуковысотная система», то мы с самого начала должны договориться о следующем. Под этим термином мы не будем подразумевать только лишь материальную сторону музыкального звука и его отношений с другими музыкальными звуками. Поскольку нас интересует прежде всего модельная функция любого музыкального параметра, постольку подобная трактовка в принципе исключена для нас.

Модельная функция представляет собой отношение параметров моделирующей системы к параметрам моделируемой системы. Это отношение не возникает и не реализуется без активного участия субъекта — человека, создающего и использующего модели в процессе своей деятельности. Таким образом, любой из блоков музыкальной моделирующей системы изначально представляет собой единство субъективного и объективного, материального и идеального. Это их единство должно не просто голословно утверждаться (чтобы затем о нём забыть), но и быть предметом специального анализа.

Если мы отвлекаемся от роли человека, его деятельности, от роли общественной музыкальной практики, то есть, от всей гуманитарной составляющей становления и функционирования музыкальной системы, то в нашем распоряжении остается вовсе не нечто конкретное, материальное, физическое, как это может показаться на первый взгляд. В нашем распоряжении оказывается абстракция, которая лишь выглядит описанием чего-то простого. Простота эта возникает от того, что реальная сложность явления «выносится за скобки». Если мы понимаем это, помним об этом, то использование такой абстракции может оказываться полезным. Но если забыть об этом, то неосознанная абстракция легко превращается в заблуждение.

От чего же мы отвлекаемся? Прежде всего, от физической и физиологической сложности процесса. От всего, что предшествует превращению энергии материального воздействия в феномен восприятия, в «факт сознания». Во-вторых, мы отвлекаемся от сложности, связанной с «психологией». В частности, говоря о том, что музыкальный звук есть частный случай «слышимых звуков», мы, как правило, не уточняем, на каком уровне — сознательном или бессознательном — этот звук воспринимается. А ведь это далеко не одно и то же. Причем, и то, и другое (и их взаимодействие) имеет существенное значение в процессе художественного восприятия. В-третьих, мы отвлекаемся от того, что музыкальная система, а следовательно и звук как элемент этой системы, есть факт культуры со всей ее сложностью. Музыкальная система как культурологический феномен не может быть представлена лишь в виде множества звуков и их отношений.

От всего этого мы отвлекаемся и образуем абстрактное понятие, формально простое и весьма полезное своей простотой. Нужно лишь воздержаться от искушения гипостазировать эту абстракцию, то есть, приписать ей «объективное», независимое от нашей деятельности существование. В этом случае понятие «музыкальная система» становится удобным теоретическим инструментом. Как и многие другие абстрактные научные понятия («идеальный газ», «абсолютно твердое тело» и т. п.).

Теперь, когда мы отвлеклись от всего вышеперечисленного, оказалось ли в нашем распоряжении нечто совсем уж простое? Оставим размышления над этим вопросом на потом, а сами перейдем к рассмотрению (построению) звуковысотной системы.

ЗВУКОВЫСОТНАЯ СИСТЕМА. В статье Ю. Н. Холопова в музыкальной энциклопедии (1974 года) она называется «звуковая система». Там, в частности, написано: «Звуковая система — высотная (интервальная) организация муз. звуков на основе к.-л. единого принципа. В основе з.с. всегда лежит ряд тонов, находящихся в определенных, поддающихся измерению отношениях». Из дальнейшего изложения следует, что автор рассматривает звуковую систему прежде всего в историческом аспекте, как нечто развивающееся, меняющееся со временем. Поэтому, звуковая система в разные эпохи выглядит по-разному. И эти различия существенны.

Большинство авторов так или иначе солидаризируются с таким подходом. Другим общим моментом является то, что звуковая система («звуковысотная система», «музыкальная система») рассматривается ими как состоящая из звуков (тонов), то есть как вполне физический объект. По этому поводу мы уже высказали свою позицию. Поэтому, не вдаваясь в полемику с этими взглядами, попробуем несколько изменить (или дополнить) подход и взглянуть на предмет под иным углом зрения.

Во-первых, об «историзме». Кто бы спорил, что музыкальное искусство исторически развивается, а следовательно изменяемся во многих своих существенных проявлениях. И хорошо бы иметь средства, позволяющие эти изменения фиксировать и описывать. Однако этого мы не сможем делать, если в нашем распоряжении нет ничего относительно устойчивого, относительно стабильного, относительно чего эти изменения мы наблюдаем. Простой пример. Во многих домах, где есть маленькие дети, на стене висит некий красиво оформленный аналог сантиметровой линейки, позволяющий наблюдать рост ребенка. А теперь подумаем, что произошло бы, если бы эта линейка росла вместе с ребенком и одновременно увеличивались бы все отмеченные на ней сантиметры и дециметры? Ребенок бы рос, а показания линейки оставались бы прежними.

Так и с развитием музыкальной системы. Для наблюдения за ходом этого процесса было бы полезным иметь некие устойчивые структуры, относительно которых мы могли бы более точно фиксировать направления и динамику изменений. С одной стороны, такие структуры могут быть продуктом теоретических построений и базироваться на тех или иных абстракциях (по типу абсолютно твердого тела). С другой стороны, и в самом «живом» процессе исторического развития музыки имеют место, как «быстрые» процессы, так и «медленные», которые можно и известной долей условности принять за «неподвижные» структуры.

Теперь об акценте на «материальности» изучаемого объекта. Исключить роль субъективного момента при изучении искусства (музыки в том числе) невозможно. Даже если речь идет просто о музыкальном звуке. Не говоря уже о таких более сложных явлениях, как лад, устойчивость — неустойчивость, тяготения, диссонансы — консонансы и пр. не является исключением и музыкальная (звуковысотная) система. Он тоже являет собой единство субъективного и объективного, материального и идеального. И это каким- то образом нужно уметь теоретически описывать и анализировать.

«Каверзные вопросы» подстерегают нас самого начала. «Ряд тонов» (у других авторов — «звуков»). Что здесь означает «ряд»? Упорядоченное множество? А где и когда этот ряд (множество) реально существует? Должны ли звучать эти звуки? Предположим, что мы имеем дело с музыкальной системой, сложившейся в Европе за последние несколько столетий. Где и когда мы можем услышать этот «супер-кластер»?

Мы вынуждены признать не только материальный, но и идеальный характер нашей системы. И не только в том смысле, что теоретик, изучающий музыку, использует различного рода абстрактные понятия. В самой культурной практике музыка во всех ее проявлениях, на всех уровнях ее организации являет собой особое взаимодействие идеального и материального. Примерно так же обстоит дело и с языком. Где и как он существует помимо языковой практики? И чем окажется любое слово, если лишить его смысла? А есть ли смысл в слове, оторванном от людей, их мышления, их общения? В слове «самом по себе»?…

* * * * *

Попробуем построить звуковысотную систему, с которой будем иметь дело в дальнейших рассуждениях. Теоретически таких систем может быть не одна а неопределенное число. Но мы будем иметь дело с одной, с той, которая сложилась в Европе за многие столетия и остается господствующей до настоящего времени.

Здесь мы с самого начала сталкиваемся с одной интересной особенностью. У этой системы существует больше чем один способ ее порождения (построения). Мы рассмотрим три наиболее влиятельных (общепринятых) способа.

Способ первый. Выбирается некий исходный звук (точка на звуковысотной шкале). От этого звука строится ряд восходящих и нисходящих квинт. Какие-либо дополнительные ограничения при этом не вводятся. От каждого из получившегося таким образом звука (элемента) строится (потенциально бесконечный) ряд восходящих и нисходящих октав. Назовем такой способ порождения квинто-октавным. Наиболее непосредственно ему соответствует так называемый «пифагоров строй», хотя этим объем данного понятия не ограничивается. Что касается содержания понятия, то оно не совпадает с понятием «пифагоров строй» по той простой причине, что строй есть характеристика музыкального инструмента. Здесь же это не имеется в виду. Поэтому воздержимся от того, чтобы отождествить квинто-октавную систему с пифагоровым строем.

Способ второй. Выбирается некий исходный звук (точка на звуковысотной шкале). От этого звука строится другой, на одну октаву выше или ниже. Получившийся интервал (октава) делится на 12 равных интервалов — полутонов. О каждого из получившегося таким образом звука (элементов) строится (потенциально бесконечный) ряд восходящих и нисходящих октав. Назовем такой способ порождения октавно-полутоновым. Наиболее близко ей соответствует темперированный строй. Хотя, опять же, строй и музыкальная (звуковысотная система) — это не одно и то же.

Способ третий. Выбирается некий исходный звук. От него строится так называемый «натуральный звукоряд» — ряд гармонических обертонов. Как далеко простирается этот ряд? Теоретически, до бесконечности. А на практике все ограничивается четырьмя октавами. Далее, от получившихся таким образом звуков строятся октавы вниз так, чтобы «спроецировать» все порожденные элементы на диапазон (в пределы) одной октавы. Далее, получившиеся таким образом элементы переносятся на иные октавные диапазоны. На практике, однако, этой операции подвергаются не все порожденные на предыдущем шаге элементы, а лишь некоторые (о чем подробнее скажем позже). Назовем такой способ порождения обертоново-октавным. Наиболее близко порожденной таким образом конструкции будет натуральный строй. По своему звучанию он считается наиболее совершенным. Однако ценой за это совершенство будет то досадное обстоятельство, что в тональностях, далеких от той, где тоникой является исходный звук нашей конструкции, это совершенство звучания оборачивается появлением весьма неприятных для слуха созвучий (например, так называемые «волки»).

Мы воздержимся от того, чтобы принимать участие в споре на тему, какая из этих систем является более «правильной» или более совершенной. Нас интересует сам тот факт, что их несколько, что они очень близки, но все же отличаются друг от друга, и что в самой живой музыкальной практике каждая из них в тех или иных случаях, так или иначе обретает «свой голос».

Интересно и то, что в этом странном «музыкальном космосе» действует нечто похожее на соотношение неопределенностей. Чем точнее звук соответствует одной системе, тем меньше точность его соответствия другой. При таком взгляде на вещи, мы должны признать, что имеем дело не с тремя разными системами, а с одной, но обладающей тремя логиками построения, результаты которых совпадают лишь с известной долей приблизительности. Эти три логики построения, хотя и относятся к одной (единой) системе, позволяют, тем не менее, говорить о трех подсистемах — квинто-октавной, октавно-полутоновой и обертоново-октавной. Способ порождения элементов этих подсистем различен. Если придерживаться такого подхода, что элемент определяется способом порождения, то следует признать, что элементы у этих систем разные, но сами системы конгруэнтны друг другу, хотя и не вполне точно, с известной долей приближения.

И это — одно из фундаментальных свойств нашей звуковысотной системы. Она органически соединяет в себе точность и приблизительность. Составляющие ее конструкции оказываются как бы дополнительными друг по отношению к другу.

Рассмотрим теперь более подробно логику порождения этих трех вариантов музыкальной системы, и их взаимоотношений. Начнем с октавно-полутоновой.

Строго говоря, выбор исходного звука — это не начало. Сама возможность такого выбора базируется на неких основаниях, которые не заявлялись в явном виде, а лишь молчаливо подразумевались. Такой предпосылкой прежде всего является изначально (условно) бесконечная в обе стороны звуковысотная шкала без каких-либо делений. Ей соответствует потенциально бесконечный звуковысотный континуум. Естественное ограничение (на практике) задается тем, что диапазон слышимых звуков ограничен. Приблизительно, от 16 до 20000 герц. На этой континуальной шкале выбирается исходная точка, строится октава, которая делится затем на 12 равных частей (полутонов). Почему именно 12? Об этом чуть позже. Отложим этот вопрос на потом, и просто примем это как факт. Следующий шаг — распространим это деление на весь диапазон.

Что получилось в результате? С одной стороны, мы можем считать, что превратили таким образом континуальную шкалу в дискретную. С другой стороны, не менее правильным будет сказать, что мы построили дискретную шкалу поверх континуальной, которая таким образом не исчезла, но продолжает существовать «в тени» дискретной шкалы и наряду с ней. И эта интерпретация является вполне правомерной, ибо континуальная шкала постоянно напоминает о себе с помощью таких явлений, как глиссандо и вибрация. В работе «Очерки теории музыкального моделирования» обосновывается положение, согласно которому полутоновая шкала (а, по сути, композиция двух шкал — дискретной и континуальной) обладает модельной функцией пространства (моделирование пространственных отношений и движения в пространстве).

Теперь о квинто-октавном порождении. Прежде всего отметим, что в логике квинто-октавного порождения исходный интервал (квинта) является квантом. Он не делится на меньшие единицы и не складывается из них. Тот факт, что квинта равна семи полутонам всецело относится к той «картине» которую мы видим на полутоновой шкале. И если встает вопрос, откуда мы взяли эту исходную квинту (равно, как и октаву), то мы можем указать в качестве источника на обертоновый ряд, как на объективно данное физическое основание. Однако, строго говоря, нам нет особой нужды отвечать на этот вопрос, ибо мы исследуем структуру музыкальной системы, анализируя те комбинаторные возможности, которые она содержит в себе для формирования разных способов (алгоритмов) ее порождения.

Итак, квинта — это квант. Из этого вытекает одно интересное отличие квинтовой шкалы квинто-октавной системы от полутоновой. Полутоновая шкала возникает в результате «дискретизации» исходного звуко-высотного континуума. За ней постоянно прячется континуальность, но столь же постоянно обнаруживается, чтобы спрятаться вновь. Между элементами полутоновой шкалы что-то есть. Между элементами квинтовой шкалы изначально ничего нет. Там находится ничто. Эта шкала сущностно дискретна. Ее кванты неделимы ни при каких обстоятельствах и ни в каком отношении.

В теории музыкального моделирования ее модельная функция определяется как энергия. И величина эта дискретна. В этом отношении музыкальная энергия ведет себя примерно так, как это происходит в квантовой физике. Хотя, было бы слишком смелым полагать, что музыка таким образом моделирует этот уровень реальности. Ведь он недоступен человеческому восприятию и вряд ли человек мог бы воспроизводить его в своей художественной деятельности. Впрочем, если встать на точку зрения Артура Шопенгауэра, считавшего музыку непосредственным выражением Воли, то, почему бы и нет?

Возникает интересный вопрос: а не связана ли каким-то образом модельная функция квинтового ряда (энергия) с тем обстоятельством, что между его элементами находится пустота, ничто? Не рождает ли сама по себе эта пустота некоего стремления ее заполнить? Ведь «природа не терпит пустоты». Квинта же (в контексте квинтового ряда) дает нам возможность ощутить пустоту со всей ясностью и отчетливостью. Мы воспринимаем абсолютную пустоту как нечто невозможное, но существующее, то есть, противоречивое в своей основе, как существование несуществования (бытие небытия, против чего так яростно возражали элеаты). Данное противоречие содержит в себе потенцию к движению, к преодолению этого противоречия, к его разрешению.

Это энергетическое качество квинты становится качеством всей квинто-октавной шкалы по той причине, что квинта выступает здесь в качестве порождающего элемента для всей системы и потому определяет собой её базовые смыслы.

Сказанным отличие квинто-октавной координаты от октавно-полутоновой не ограничивается. Стоит обратить внимание на различное отношение этих двух систем к интервалу октава. На октавно-полутоновой шкале мы находим для любого элемента его октавные соответствия. То есть, здесь мы найдем звуки, соответствующие и до1, и до2, и все остальные. Для этого не нужно делать каких-либо дополнительных шагов. Все эти элементы (звуки) уже непосредственно даны на полутоновой шкале.

На квинтовой шкале мы видим существенно иную картину. Здесь есть и до, и ре, и любой другой элемент. Но только мы ничего не знаем, об их конкретном звуко-высотном положении. Здесь есть только одно до и оно является представителем всего множества до во всех октавах. Точно также обстоит дело и с любым другим элементом. Чтобы получить множество разных по высоте до, необходимо осуществить следующий шаг квинто-октавного порождения — найти эти звуки, построив соответствующие октавы.

Получается интересная картина. На полутоновой шкале мы изначально видим множество эквивалентных элементов. Октава же является здесь средством сведения этого множества в единый элемент высшего порядка (множество как элемент). На квинтовой шкале нет таких исходных множеств. И до, и ре, и пр. существуют здесь в единственном числе. Как некое абстрактное до, абстрактное, ре, абстрактное ми и т. д. Октава в этих условиях служит превращению их абстрактного единства в конкретную множественность. Лишь после этого квинтовая шкала превращается в квинто-октавную систему.

Заметим, что на квинтовой шкале мы не найдем октавы. Октаву мы привносим «извне», что является необходимым шагом квинто-октавного порождения. Например, мы найдем здесь только одно до, а для того, чтобы построить октаву, нам нужно, как минимум, два. Мы можем найти до и си диез. Но эти два звука не составляют октаву. Из них может получиться, к примеру, увеличенная септима. Что касается октавно-полутоновой шкалы, то здесь октава дана уже на первом шаге.

Формирование обертонового ряда существенным образом отличает его и от полутонового, и от квинтового. Здесь я обратил бы внимание на следующие моменты его генезиса и его логоса.

Он не складывается из элементов, но рождается на физическом уровне в результате многократного деления целого. Колебания целой струны (или иного тела) дают основной тон. Колебания половины струны дают первый обертон. Колебания трети струны дают второй обертон. И так далее. Эта математическая закономерность физического явления давно известна. Я бы хотел обратить особое внимание именно на логику порождения. На движение не от элемента к целому, а наоборот — от целого к элементам. Движение, уходящее вглубь.

Каждый из «шагов» обертонового ряда на соответствующем ему месте шкалы является неделимым. Внутри соответствующего ему интервала, если не отрывать этот интервал от его исходной позиции, ничего нет (как и в случае квинты на квинтовой шкале). Получаются своего рода «кванты», но «кванты» эти разные. Они отличаются друг от друга по своей величине.

С точки зрения восприятия, этот ряд является изначально скрытым, спрятанным, латентным. Мы непосредственно не слышим обертонов. Но воспринимаем некое интегральное качество, тайным от нас образом складывающееся в неделимый на элементы феномен тембра. Так невидимые для нас закономерности строения атомов и молекул проявляются на уровне качеств вещества.

Этот «невидимый микромир» музыкального звука обладает, тем не менее, тенденцией проявляться и облекаться в непосредственно воспринимаемую форму. Так, при определенных условиях мы начинаем слышать отдельные обертоны. Примеры — флажолет, горловое пение. Современная электронная музыка также иногда использует аналогичные эффекты. Гораздо интереснее другая требующая дальнейшего исследования закономерность, заключающаяся в том, что те или иные структуры, порождаемые этим рядом, проявляют себя на тех или иных уровнях организации музыкального целого. К таковым случаям относятся октава, кварто-квинтовое отношение (прообраз функциональных связей), терцовая структура (прообраз аккорда), целотоновый ряд, полутоновый ряд. Эта закономерность рождает искушение трактовать подобные отношения как результат непосредственного генезиса устойчивых структур музыки (музыкальной деятельности) из элементов обертонового ряда, элиминируя из этого процесса человека, человеческую деятельность и культуру.

Суммируя сказанное выше, можно увидеть, что этот ряд несет в себе некое «встречное движение» — а) движение от целого к частям, бесконечное деление, б) движение от невидимого к видимому, в) от внутреннего к внешнему. При этом, физическая (объективная) основа характеризуется математически точными количественными характеристиками, а соответствующий феноменальный план превращает эти количественные характеристики в непосредственно воспринимаемые качества. Определенные стороны этой качественности подлежат сравнению (являются количественно сравнимыми). Таковы, в частности, те, которые получили название диссонантность-консонантность. Чем дальше от основного тона, тем выше уровень напряженной диссонантности. В этом смысле мы можем назвать данную шкалу шкалой упорядоченного фонизма.

Ограниченное совершенство. Выше мы уже писали о том, что попытки выстроить на основе обертоновой шкалы соответствующий музыкальный строй — натуральный строй — постоянно приводили к весьма неприятному эффекту. Одни тональности звучали безупречно, а в других появлялись «фальшивые» созвучия, в частности, так называемые «волки». Т.е. при расширении границ порождения, неизбежно возникают искажения исходных отношений. Это же самое относится и к так называемому «пифагорову строю». Об этом написано много и мы не будем более останавливаться на подробностях этой темы. Для того, чтобы преодолеть этот эффект пришлось ограничить совершенство самой квинты, то есть распределить указанное несовершенство равномерно между всеми интервалами строя. Так и возник равномерно темперированный строй.

А теперь, едва ли не самое принципиальное отличие обертоново-октавного порождения от двух остальных. Результатом этого порождения оказывается не звукоряд типа гаммы, который бы равномерно заполнял диапазон октавы, а некий набор интервалов (как бы интервальных эталонов), на основе которых уже нечто строится. В частности, с помощью дополнительных приемов можно выстроить и различного рода гаммы (вплоть до хроматической). Но непосредственным образом здесь возникает далеко не все. Известный пример — невозможность получить таким образом минорное трезвучие, что заставило придумывать некий не существующий в природе «унтертоновый ряд». Если же мы посмотрим, какой звукоряд можно получить непосредственно с помощью такого порождения, скажем, от ноты до, то получим: до, ре, ми, фа#, соль, ляb, ля, сиb, си…. Как видим, некоторых звуков здесь нет.

Зато интервалы, используемые не практике, все в наличии: октава, квинта, кварта, большая терция, малая терция, большая секунда, малая секунда, тритон. Мы тут несколько погрешили от строгости в использовании терминологии. Дело в том, что интервалы, перечисленные нами только что, обладают двумя величинами — ступеневой и тоновой. Здесь же у нас пока нет возможности (оснований) для различения этих моментов. Поэтому следует понимать написанное и известной долей условности. Например, «интервал, соответствующий по величине большой терции».

И еще один момент, на который стоит обратить внимание. В набор интервалов, практически используемых, входят не все элементы обертонового ряда. Некоторые выпадают. Вот как это выглядит:

Мы видим здесь явные пропуски. Объяснить это можно лишь тем, что люди в своей практике выбирали именно те сочетания, которые им каким-то образом «лучше подходили». Какие и почему — вопрос отдельный.

А пока вернемся в октавно-полутоновому порождению. На втором шаге этого порождения, если мы помним, исходная октава делилась на 12 полутонов. Почему именно на 12, а не на 13, 14 и т. д.?

Не берусь отвечать на вопрос «почему?». Все-таки это получилось не само собой, а в результате чем-то мотивированного выбора людей. А здесь строить догадки несколько затруднительно. Зато можно посмотреть, что получилось в результате такого выбора, и что было бы в том случае, если бы выбор оказался иным.

На первый вопрос ответить нетрудно. Он, можно сказать, лежит на поверхности. В результате именно такого выбора все три подсистемы — квинто-октавная, октавно-полутоновая и обертоново-октавная — оказались конгруэнтными. В геометрии конгруэнтными называют фигуры, которые полностью совпадают при наложении. В нашем случае это совпадение, как известно, является относительным. Какие-то элементы и их отношения совпадают полностью, а какие-то нет. Но на практике это несовпадение оказывается несущественным и им попросту пренебрегают (от него абстрагируются).

Теперь обратим внимание на квинто-октавное порождение. Возьмем, к примеру, ноту до и будем двигаться по квинтам вверх до тех пор, пока не придем к звуку, который на некоторое целое число октав отстоит от исходного звука. Этим звуком (являющимся своеобразной точной пересечения двух линий — квинтовой и октавной) будет звук си диез. От исходного звука он отстоит на 7 октав. А если считать по квинтам, то таких (квинтовых) шагов у нас окажется 13. Уберем совпадающий с исходным звук и получим разных звуков именно 12. Теперь соберем эти элементы в границах одной октавы и получим ряд, соответствующий 12-ти ступенной хроматической гамме.

Посмотрим теперь, как соотносится получившаяся таким образом квинто-октавная подсистема с обертоново-октавной. Как было сказано, результатом порождения последней является набор интервалов (октава, квинта, кварта, большая и малая терции, большая и малая секунды, тритон, а также все их обращения). Таким образом, мы видим полное совпадение большинства и почти полное (очень близкое) совпадение остальных интервалов этой системы с теми интервалами, которые образуются в условиях квинто-октавной системы — системы, где октава делится на 12 частей.

И если теперь предположить, то октаву разделили бы не на 12 частей, а на какое-то другое их число, то получившаяся таким образом система не совпала бы с другими двумя. Собственно, так называемый равномерно темперированный строй и явился оптимальным компромиссом между натуральным (соответствующим обертоново-октавному порождению) и пифагоровым (соответствующим квинто-обертоновому порождению). Это не только компромисс, но и способ приведения в соответствие всех трех подсистем, позволяющий минимизировать их потенциальные несоответствия.

Аналогичным образом мы можем теперь объяснить и то обстоятельство, что обертоново-октавное порождение не выходит за границы четырех октав (16 обертонов). Просто, если идти дальше, то интервалы, получаемые таким образом, окажутся меньше полутона, а это придет в противоречие с квинто-октавной и октавно-полутоновой подсистемами.

Далее останется лишь размышлять, почему эта конгруэнтность трех подсистем музыкальной системы оказалась столь ценной, какие возможности такая система открывает и какие смыслы несет. Теперь же заметим, что указание на конгруэнтность (не вполне, впрочем, безупречную) трех подсистем является не вполне достаточным, для характеристики отношения между ними.

Существенно общим моментом для всех трех подсистем является то, что в их основании лежат два исходных отношения. Одно из них — равенство. Во всех трех случаях эту функцию выполняет интервал октава. Заметим, что октава — один из тех интервалов, который у всех трех подсистемах совпадает абсолютно. Второе отношение — неравенство, на основе которого формируется некоторое отношение порядка. В случае квинто-октавного порождения это квинта. В случае октавно-полутонового порождения это полутон. В случае обертоново-октавного порождения это второе отношение оказывается более сложным. Это отношение порядка в ряду интервалов, где исходным является октава — 2/1, а последующий ряд составляют квинта, кварта и т. д., то есть интервалы с отношением частот 3/2, 4/3, 5/4 и т. д. Если квинто-октавное и октавно-полутоновое порождение при сохранении исходного интервала приводят к появлению все новых звуков (элементов), то в случае обертоново-октавного порождения мы наблюдаем появление все новых интервалов, которые таким образом и выступают в качестве порождаемых элементов. Эти элементы представляют собой нечто вроде набора лекал для построения разных звуковых конструкций.

В целом получается весьма интересная картина. Три подсистемы ММС, если рассматривать их отношение чисто формально, можно считать (с небольшими натяжками) конгруэнтными. Причем, некоторые интервалы совпадают точно, а некоторые приблизительно. Но если проанализировать с точки зрения содержания (с точки зрения смысла) сами алгоритмы их порождения, то мы увидим, что эти подсистемы являются качественно разными. Это различие порождается тем, что по своему смыслу ряд квинт, ряд полутонов и упорядоченное множество интервалов сильно отличаются друг от друга. И если с формальной точки зрения мы имеем дело лишь с досадным несовпадением в деталях, которое можно тем или иным способом купировать, то с содержательно-генетической точки зрения мы видим три разных мира. И это различие — не досадное обстоятельство, а источник богатства смыслов. Два разных взгляда на музыкальную систему раскрывают нам ее и с точки зрения единства, почти тождества трех подсистем, и с точки зрения их качественного разнообразия. И нельзя сказать, что какая-то одна точка зрения является правильной, а другая нет. Они обе правильные.

Мы видим, что изучение музыкальной системы ведет нас далеко за пределы темы музыкальных строев. Другая предмет во весь рост встает перед нами. Это — присущий музыкальной системе ЛОГОС, диалектика которого в значительной мере связана в взаимодействием разных алгоритмов его порождения. А взаимодействие это, как мы видим, не очень простое.

Базовая модель традиционного музыкознания

Выражение «базовая модель» в данном контексте строгим не является. Речь идет об одной из самых важных и самых широко используемых моделей «музыкальной реальности», которая, как правило, не только не объявляется таковой, но и даже не осознается в этом качестве.

Любое исследование, так или иначе опирается на некоторые модели, которые опосредуют взаимодействие с изучаемым объектом. И даже тогда, когда мы как бы впрямую, непосредственно манипулируем с интересующим нас объектом, мы чаще всего используем модели а) для организации наших действий, б) для интерпретации их результатов.

Практическая работа с объектом также чаще всего не обходится без использования тех или иных моделей. Так, путешествуя по некоторой местности, мы часто используем карту этой местности. Собирая радиоприемник, радиолюбитель опирается на схему, в соответствии с которой он паяет детали (пример из не очень далекого прошлого). В музыке такими моделями выступают нотный текст или ряд буквенных обозначений аккордов.

В данном тексте мы обсудим одну очень важную модель, используемую и в музыкальной практике, и в музыкальной теории. В явном или неявном виде она присутствует постоянно. Причем, модель эта сопровождает каждого музыканта (или любителя музыки) буквально с первых шагов обучения музыке. Вот она:

Это фортепианная клавиатура. Все ее видели и многократно с ней взаимодействовали. В основном, практически. Но редко кто воспринимал ее именно как модель.

Если это действительно модель, то модель чего? Пока скажем в самом общем виде — модель устройства музыки. Оговоримся сразу, далеко не все стороны организации музыкального целого отображает эта модель. В частности, она «не видит» музыкального времени и всех его аспектов — ритма, метра, темпа, музыкальной формы и пр. «Не видит» и многого другого. Собственно, модель и не должна охватывать все стороны моделируемого объекта. Какие-то она она выделяет, от каких-то абстрагируется. На то она и модель, а не буквальная копия. И если уточнить, то данная модель отражает некие фундаментальные закономерности звуковысотной организации музыки.

Опираясь на нее, дети получают первые сведения из области музыкальной грамоты. Получают представление о звукоряде, гаммах, о направлениях (восходящем и нисходящем) мелодического движения. Узнают о тональности и ее ступенях. О диатонике и хроматике… Эта модель давно уже доказала свое удобство и практическую полезность. Впрочем, как и у любой модели, есть здесь и некоторые «ловушки», в которые мы попадаем, если теряем необходимую бдительность и критичность.

Попробуем разобраться по порядку.

Начнем с того, что сама по себе фортепианная клавиатура — это всё же не вполне модель. Точнее, не вполне полноценная модель. Для того, чтобы стать таковой, ей нужны еще и некоторые правила обращения с ней, в том числе и правила интерпретации её элементов, а также определенный рабочий язык. Все это в культуре давно присутствует и исправно работает. При всей важности «культурной оболочки», даже и без нее эта модель несет для нас значительное содержание.

Итак, что мы видим?

— Перед нами упорядоченное множество элементов, выстроенных в единый ряд, в чем-то напоминающее шкалу, или линейку с нанесенными на нее делениями на равном расстоянии. Если последняя ассоциация верна, то этот ряд имеет направленность, то есть, направление слева направо отличается от направления справа налево. Это предположение нетрудно проверить экспериментально. Нажимаем на разные клавиши и убеждаемся — чем левее клавиша, тем ниже звук и наоборот.

— Мы видим, что клавиши двух цветов — белые и черные. Что бы это могло значить? Во-первых, это могло быть сделано для удобства, чтобы играющий мог легко различать их между собой. Во-вторых, за этим может стоять нечто большее, некие содержательные отличия, связанные с особенностями внутренней организации мира звуков, соответствующих этим разноцветным «кнопкам». Впрочем, может иметь место и то, и другое. В дальнейшем мы узнаём, что именно так и есть на самом деле.

— Приглядевшись чуть внимательнее, мы обнаруживаем постоянно повторяющийся «орнамент», особую последовательность белых и черных. Сосчитав число клавиш этой повторяющейся последовательности, мы узнаём, что их число всегда ровно 12. Данную последовательность легко записать в виде своеобразного двоичного кода: бчбчббчбчбчб, где б — белая клавиша, а ч — черная. Внутри этой последовательности (этого «орнамента») каждая клавиша имеет свой единственный и неповторимый вариант отношений к другим клавишам, свое неповторимое среди них расположение («адрес»). Это приводит к тому, что мы с первого взгляда видим ее и отличаем от всех остальных.

— Эта неповторимость внутри 12-клавишного диапазона уравновешивается регулярной и точной повторяемостью через каждые 12 клавиш. Повторяется вся последовательность. Структурно здесь имеет место полный изоморфизм. Последний нарушается лишь тем обстоятельством, что повторение реализуется на другом звуко-высотном уровне (в другом диапазоне). Последнее, правда, обнаруживается лишь тогда, когда мы начинаем играть на инструменте, а мы до сих пор обсуждали лишь то, что видно. А видим мы лишь буквальную повторяемость узора (орнамента) и, соответственно, одинаковое расположение в этом узоре всех до, всех ре и т. д. Таким образом, сам вид клавиатуры сообщает нам об октавной эквивалентности (эквивалентности звуков, отстоящих друг от друга на некоторое целое число октав) еще до того, как мы попытались сыграть и услышать хотя бы одну ноту.

Это всё, пожалуй, и есть то главное, что клавиатура может сообщить нам сама по себе, как находящийся перед нами, непосредственно наблюдаемый материальный объект. Дальнейшее мы усваиваем по мере обучения музыки. То есть, из общения с другими носителями музыкальной культуры (учителями, прежде всего), из учебников и собственной практики. Перечислим наиболее важные для нас моменты.

— Прежде всего, мы узнаем о вопиющем неравенстве, в соответствии с которым, собственными именами обладают только белые клавиши, тогда как черные получают производные названия в зависимости от их положения по отношению к белым. Возьмем, к примеру, ноту ре. Ближайшая от нее клавиша слева получит от нее название «ре бемоль», а ближайшая справа — «ре диез». Почему именно так, обычно никто не объясняет. Чаще всего об этом никто и не спрашивает. Ведь эти сведения попадают в нашу голову в очень раннем возрасте, когда мы многое просто принимаем на веру. Потом мы к этому просто привыкаем и подобных вопросов не задаем. Хотя вопросы могли бы и возникнуть.

Во-первых, чисто теоретически можно представить себе такой вариант, когда были бы поименованы вообще все клавиши. Но ведь этого не произошло. И на это были какие-то причины. Об этих причинах модель нам ничего не сообщает. Во-вторых, можно было бы дать свои имена всем черным клавишам, а белые получали бы названия так, как сейчас это происходит с черными. Наконец, можно вообразить и какое-то иное сочетание «главных» (имеющих имя) и «подчиненных» (безымянных), а также и вообще иное взаимное расположение черных и белых.

Но все сложилось так, как сложилась, и у этого есть своя определенная логика. Наша модель (клавиатура) эту логику обнаруживает «в снятом виде», по результату, не обнажая причин. По этому поводу обычно говорят, что «так сложилось исторически». Возразить тут нечего. И нельзя сказать, что модель эта указывает на какие-то ошибочные вещи. Дело в том, что она изначально не призвана объяснять. Она просто фиксирует то, что сложилось в культуре. И предлагает нам это как постулат. Сложный, наглядный постулат.

— Вслед за названием нот, мы обычно узнаем о том, что белые клавиши (те, что имеют свои имена) составляют гамму До мажор. Поскольку эта гамма складывается из «привилегированных» звуков (клавиш, нот — эти понятия мы пока не различаем), мы неосознанно делаем вывод, что До мажор — это «привилегированная» (главная) гамма («тональность», как мы потом научаемся говорить).

— Это убеждение подкрепляется тем, что по ходу дальнейшего обучения мы узнаем, что звуки, имеющие собственное название, составляют основные ступени звукоряда (термин из элементарной теории музыки). Мы обычно не задумываемся над тем, что ряд терминов этой теории связан не столько с логикой теоретического исследования предмета, сколько с удобством в практической деятельности. И мы еще больше укрепляемся в убеждении, что звуки музыкальной системы изначально неравноправны, что тут есть какая-то априорная иерархия, и эта иерархия именно такова.

— Главная гамма — До мажор — все-таки не одинока. Есть у нее параллельная — ля минор, из тех же звуков состоящая. И эту общность составляющих обе гаммы звуков мы видим наглядно. Заметим, что слово «параллельная» может указывать на ее производность, несамостоятельность, а следовательно зависимость. Чаще всего именно так и происходит потому, что ля минор попадает в сферу нашего внимания несколько позже, чем До мажор. Кроме того, слова «мажор» и «минор» означают «больший» и «меньший», соответственно. К тому же названия мажорных гамм принято писать с большой буквы, а минорных с маленькой. Все опять косвенно указывает на иерархию. Мы это «впитываем». Но, как правило, мы об этом не задумываемся.

— Вместе с понятием гаммы мы усваиваем понятие ступени. Здесь используется метафора лестницы. Гамма (последовательность звуков) — это лестница, а звуки, ее образующие) — ступени. Этот «простенький» ход мысли скрывает в себе непростые содержательные моменты.

Момент первый связан с тем, что расстояние между ступенями не всегда одинаково. Большинство лестниц, которыми мы пользуемся, такой странной особенностью не обладает (это порождало бы риск несчастного случая). Но не в этом суть. Главное состоит в том, что происходит приравнивание неравного. Рождается новое понятие и даже новая мера — «ступеневая величина». И с этой новой точки зрения расстояние между ре и ми и расстояние между ми и фа равны друг другу. Здесь нет ни какой ошибки. Просто само понятие «ступеневая величина» возникает в результате абстрагирования от точного звуковысотного соотношения, измеряемого в полутонах. Так появляется два разных, но взаимосвязанных и взаимодополняющих способа измерения интервалов — тоновая величина и ступеневая величина. Те интервалы, о которых только что шла речь, с точки зрения их тоновой величины различны, а с точки зрения величины ступеневой одинаковы.

То обстоятельство, что тоновая и ступеневая величина выражают разные смыслы подчеркивается тем, что интервалы, имеющие одинаковую тоновую величину могут иметь разную ступеневую (до — ре диез и до — ми бемоль), а интервалы, имеющие одинаковую ступеневую величину, могут иметь разную тоновую (ре — фа и ре — фа диез). И тут вмешивается практика языкового обозначения этих величин, перекочевавшая в теорию. Так, «секунда» или «терция» — это ступеневая величина, а «большая секунда» или «малая терция» — ступеневая и тоновая одновременно. Это провоцирует путаницу.

Второй момент чуть более сложный. Дело в том, что гамма — это не просто упорядоченное множество (до, ре, ми, фа, соль, ля, си), но и определенная структура, то есть совокупность отношений между элементами. В самом простом виде — это последовательность интервалов (расстояний) между звуками. Эта последовательность известна всем, кто хоть немного учился музыке: тон, тон, полутон, тон, тон, тон, полутон. Так строится любая мажорная гамма. Любая. В этом суть. Значит последовательность белых клавиш — это не только последовательность конкретных звуков. Это еще и структура мажорной гаммы, которую, в принципе, можно сыграть по этому общему алгоритму от любого звука. Абстрактный образец, «лекало». Картинка как бы раздваивается. С одной стороны — конкретное множество элементов. С другой стороны — абстрактная структура. И эта структура действительно «начинает жить своей самостоятельной жизнью».

Чтобы сделать это «раздвоение» более наглядным, воспользуемся следующим приемом. Построим схему из двух клавиатур. Одна будет представлять материальную, «настоящую», из определенных материалов сделанную. Другая — абстрактную, идеальную. Будучи мысленно отделенной от настоящей, она может свободно относительно нее перемещаться.

Это настоящая.

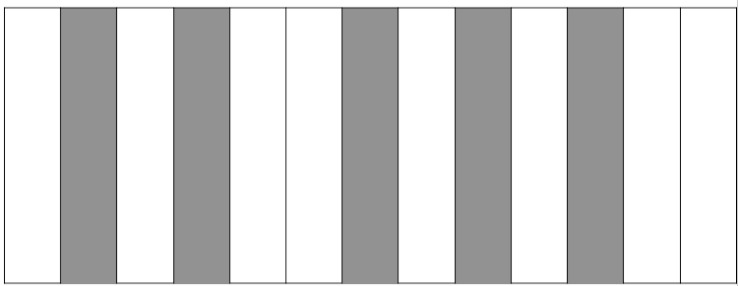
А это абстрактная. «Клавиатура-призрак».

Договоримся, что клавиши абстрактной клавиатуры «забыли» как их зовут. «Помнят» только номера соответствующих ступеней. А теперь сдвинем абстрактную клавиатуру так, чтобы первая ступень мажорной гаммы оказалась бы напротив клавиши «ре» настоящей клавиатуры:

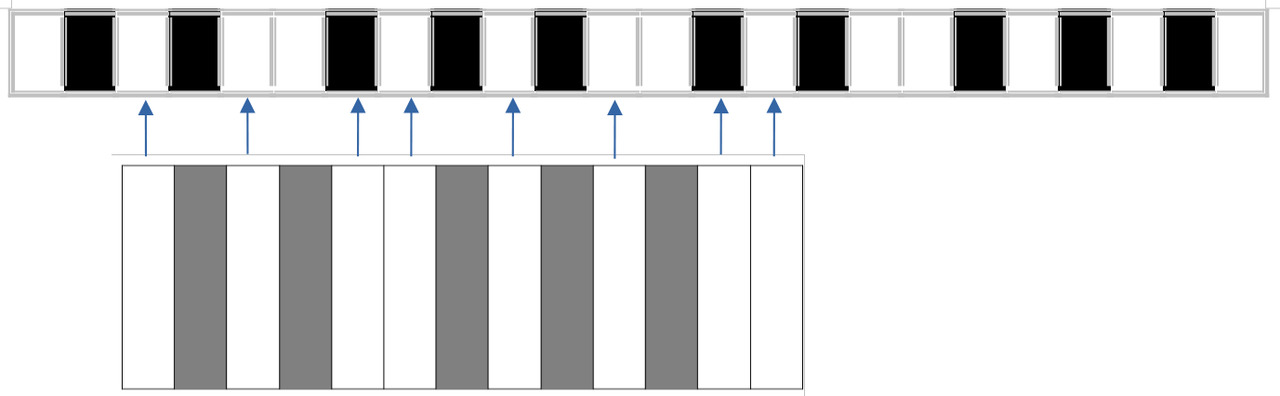
Мы получили гамму Ре мажор (ре, ми, фа диез, соль, ля, си, до диез, ре). Результат конечно же тривиальный. Но нас интересует не он. Гораздо интересней и важней то, что наша базовая модель музыкальной системы существует и действует на двух планах — материальном и идеальном. На материальном плане воплощены структуры и алгоритмы построения, которые могут быть отвлечены и затем работать как идеальные объекты. И эти идеальные объекты могут затем вступать во взаимодействие с исходной материальной моделью. Таким образом, у нас есть все основания считать нашу модель материально-идеальной. Таков фактический деятельностный статус разбираемой нами базовой модели музыкальной системы, так она в действительности работает и существует в культуре.

Неважно, насколько типичным является сознательное использование такого именно способа построения гаммы (данной конкретной, или какой-либо другой). Важно то, что помимо материального плана, так или иначе в культуре существует и действует план идеальный, делающий исходную модель гораздо более сложной и гибкой.

Приглядимся теперь к тому, как взаимодействуют между собой части нашей схемы.

— На основе материальной модели формируется ее идеальный образ и как бы отделяется, отслаивается от исходного образца.

— Этот идеальный образ меняет свой смысл. Он превращается из копии, из описания того, что есть в руководящий принцип, в проект того, что нужно сделать, что должно стать. Дескрипция обретает статус прескрипции.

— Эта поменявшая свой статус идеальная модель «возвращается» к исходному образцу, накладывается на него. Но не на прежнее место, а со сдвигом (в нашем случае на большую секунду вверх).

— Возникают некоторые несовпадения — не совпадают ноты фа и до. Но исходная модель «покоряется» воле идеальной. Фа заменяется на фа диез, а до — на до диез.

Стоит ли специально указывать на то, что только что разобранный пример является частным случаем работы материально-идеальной модели музыкальной системы? Во-первых, новая гамма может быть построенной от любого из 12-ти звуков. Во-вторых, число различных идеальных моделей достаточно велико. Не только структура мажорной гаммы (ионийского) лада, но и вообще любого лада и любой из разновидностей (гармонический и мелодический мажор и минор и пр.). Сюда же отнесем все варианты пентатоники. Прибавим к этому образцы различных аккордов и иных созвучий. Все, что можем построить на материальной модели, а затем отвлечь и обобщить, перенеся на идеальный план. Таким образом, идеальный план модели образует целый «пакет» всевозможных идеальных схем, которые затем могут различным образом «возвращены» на план материальный.