Бесплатный фрагмент - Мудрая школа

Книга посвящается моей жене Людмиле — самому строгому моему критику, сподвижнику и вдохновителю.

Благодарю моего брата Володю Тильмана за подаренные мне рисунки в знак понимания и признания моих идей.

Редактор Л. А. Дорожина

Художник В. И. Тильман

Все права защищены.

МУДРАЯ ШКОЛА: «Трилогия ума» как новый метод умственного развития детей

Аннотация

Рассматривается новый метод умственного развития детей — трилогия ума, основной мыслительной операцией которого является логическая операция сравнение. Метод создавался с учётом аристотелевского понимания философии как «науки о первых причинах и началах» познания — видах противолежания. По мере нахождения и выстраивания этих мыслительных структур в натуральный ряд сравнительных понятий был осуществлен главный замысел Платона — построение ступенчатого перехода от одних общих понятий, к другим, более общим понятиям, отождествляющим многообразие природных и социальных различий.

В дополнение к общепринятому обучению школьников рассудочному и разумному мышлению при помощи конкретных наук, новый философский метод является эффективным средством развития у детей мудрости. Это третья ступень в развитии детского ума. Она формируется на основе выработанных еще в древности и пополненных нами конкретно-научных и конкретно-всеобщих сравнительных понятий разных видов, способствующих целостному межпредметному восприятию школьниками окружающего мира: природного и социального.

В итоге формируется совершенно новый подход к школьному образованию, собирающему знание в голове ребенка, не только по предметам, как это имеет место сегодня во всех школах, но и по межпредметному принципу, нацеленному на познание наиболее общих отношений действительности.

Ключевые слова: философия для детей, познание, ум, рассудок, разум, мудрость, трилогия ума, тождественное, различное, соотнесенное, противоположное, ортогональное.

Вступление

В данной книге показано четкое разделение между рассудком, разумом и мудростью — тремя ступенями в развитии ума, каждая из которых определяется благодаря использованию трех групп понятийных средств: классификационных, конкретно-научных и конкретно-всеобщих сравнительных понятий.

Рассудочным мышлением пользуются все гуманитарии. Разумное мышление задействуют представители естественных наук. Мудрость как способ осмысления наиболее общих законов развития природы, общества и мышления остановилась в своем развитии на уровне античности, поскольку философы потеряли ее специфические понятийные средства — конкретно-всеобщие сравнительные понятия разных видов.

Фактически, речь идет о новом облике философии, отличающемся от всех прежних философских направлений своим накопительным характером (кумулятивностью) за счет использования нового понятийного аппарата — натурального ряда сравнительных понятий, направленных на познание все более общих отношений действительности. В результате философия становится объективной наукой, подобной другим естественным наукам.

Помимо пяти книг, опубликован ряд философских статей по теме «Трилогия ума как новый метод умственного развития детей» (и взрослых). Одна из них под этим же названием, опубликована в США, откуда она пошла в Юго-Восточную Азию. Кроме того, опубликован ряд статей по интеграции школьных знаний, создан ряд видеороликов на канале YouTube.

Новый подход к философии образования позволяет осмысливать общество не посредством множества субъективных мнений, вынуждающих людей жить в разных социальных мирах и по-разному понимать общество. А с одинаковых для всех объективных точек зрения, что приводит не только к пониманию общественных процессов, но и к взаимопониманию между людьми.

На этой основе предлагаю изменить подход к школьному образованию. Если сейчас оно расколото по предметному принципу, и каждый предмет маленькими кусочками закладывается в головы детей, а уже из них снова собирается расколотое по предметам знание. То новый подход, напротив, будет собирать школьное знание не только по предметному, но и по межпредметному, панлогическому принципу.

Главное в новом подходе заключается в том, что философия, как «знание общего» формирует научно обоснованную целостную картину мира и с этим знанием приходит в общеобразовательную школу, чтобы обучать детей не только рассудку и разуму, но и мудрости. Поэтому «более разумные школы означают более разумных будущих родителей как более разумных граждан» (М. Липман), более разумных преподавателей гуманитарных и социальных наук, более разумных журналистов и политиков, а в итоге более разумную и мудрую власть.

I. Философская пропедевтика

Философская пропедевтика (от греческого слова предваряю, подготавливаю) — это предварительный курс новой конкретно-всеобщей формы (философского) мышления, предназначенный для обучения взрослых, а через них и детей с 1-го по 11 класс, целостному научно обоснованному восприятию реальности. Являясь альтернативой всем другим курсам, предназначенным для обучения детей мудрости (философии), он, тем не менее, вобрал в себя все ценное и новое, что было предложено другими авторами на конференциях, в их статьях и книгах. Всем этим авторам желаю успеха и выражаю самую искреннюю благодарность.

1. Нужна ли философия детям

«Мы упрощаем, объединяем и отождествляем все, что только можно и насколько можно». Уильям Джемс

Ни для кого не секрет, что образование находится сегодня в кризисе. Его суть в разрыве между возможностями человека и стремительным увеличением объема новой информации, между установкой на узкую специализацию (профессионализацию) и потребностью в целостном видении мира. Есть множество и других не мене важных причин.

Но сегодня не только образование потеряло перспективу. Потерю стратегии продемонстрировали и общества, принадлежащие даже к самой продвинутой — Западной цивилизации. Выходит, что не только мы, но и Запад не способен предложить миру ни новых социально значимых идей, ни новых ценностей, ни новых форм своей собственной организации, в то время как старые безнадежно устарели и перестали работать.

Кризис образования — это один из компонентов единой общечеловеческой (глобальной) проблемы современности, проявляющий себя в повсеместном снижении авторитета школ и университетов, падении интереса к знанию.

Прорыв к новому состоянию культуры как масштабная социально-историческая акция может быть осуществлен не иначе, как только средствами науки и образования, которые представляют собой тот единственный мост, по которому только и возможно привести человека и человечество к новой культуре. Так как только задав направление развития общечеловеческой цивилизации и переводя каждого отдельного человека по этому мосту можно что-то реально изменить в мире.

В поисках выхода педагоги все чаще обращаются к философии, которая как никакая другая дисциплина, как кажется многим, и в прошлом, и сегодня способна вызволить общество из беды.

В этой связи в середине 70-х годов прошлого века возникла идея пересмотреть учебный процесс в школе, с тем, чтобы кардинальным образом изменить мышление людей, начав развивать его с раннего детства. Инициаторами выступили ученые Института Развития Философии для детей проф. Э. Шарп, Ф. Осканян, Р. Рид, Г. Метьюс, М. Притчард, Ф. Кэм, которые под руководством профессора философии Мэтью Липмана, предложили обучать школьников философии с детского сада по 12-ую ступень.

Предложенная ими программа реализуется во многих, хотя и не во всех школах США, во многих регионах мира — Латинской Америке, Австралии, Европе, Африке, Азии. Более чем в 20 странах созданы национальные центры, занимающиеся культурной адаптацией и внедрением ее в школьную практику. Сегодня «Философия для детей» является одной из лучших международных программ, поскольку в наибольшей мере обладает необходимыми качествами. Концептуально она представлена в книге проф. Метью Липмана «Мышление в образовании» и в ряде журнальных статей, в которых поднимается вопросе о том, что философия может и должна стать предметом школьного образования.

По мысли сторонников философского подхода к учебному процессу, он способствует развитию глобального мышления подрастающего поколения, изучению общих закономерностей развития природы и общества, обусловливающих интеграцию знания, реализует гуманизацию всей системы образования. Сам же М. Липман предлагает посмотреть на философию как на инструмент для размышления о мире и ориентации в нем человека. Он предлагает установку на тесную связь с практикой, на возможную полезность философии в повседневной жизни.

М. Липман исходит из того, что демократическое общество, больше всего, нуждается в разумных, видящих перспективу и готовых следовать своим принципам гражданах. Поэтому более разумные школы означают более разумных будущих родителей как более разумных граждан и более разумную систему ценностей. Весь вопрос в том, чему и как следует обучать детей, чтобы они стали разумными и можно ли обучать разумности, не обучая при этом мышлению?

Предложенная М. Липманом парадигма образовательного процесса направлена не на поглощение информации, а на постижение внутренних отношений исследуемых предметов. Она рассматривает образование как исследование, в то время как фокус стандартной парадигмы учителя направлен на восприятие информации и на опросы учащихся. В результате обучение предстает как результат участия детей в руководимом учителем исследовательском сообществе, поскольку акцент смещается с усвоения учащимися знания на высвобождение творческого потенциала мышления.

Как отмечала в своих книгах профессор Н.С.Юлина, педагогические достоинства программы «Философия для детей» видятся ей в том, что здесь поданы в единой связке обучение навыкам разумности и навыкам этико-демократического поведения.

Кроме того, обучение строится на близких и понятных ребенку вещах и рассчитано на обычный класс общеобразовательной школы, а не «избранных». Превращенный в сообщество исследователей, такой класс, по идее разработчиков, может и должен стать главной ячейкой общества, в которой происходит становление граждан демократического общества.

Идеи М. Липмана получили широкий резонанс во всем мире. В России, например, они обрели форму метапредметной образовательной деятельности, которая реализуется здесь более 20 лет несколькими научными школами. Так, в основу одной из них — школы доктора психологических наук Ю.В.Громыко заложена деятельностная парадигма. Тогда как в основе еще одной научной школы, возглавляемой доктором педагогических наук А.В.Хуторским, заложен принцип человекосообразности. Существуют и другие школы, задающиеся вопросом о том, каким способом формировать мышление ребенка, каким образом донести до него мысль о единстве окружающего мира, как добиться того, чтобы ребенок чувствовал себя свободной и ответственной личностью, занимающей свое место в обществе и государстве?

И здесь хочу упомянуть «Школу Сократа», возглавляемую в настоящее время доктором философских наук, профессором философского факультета МГУ им. Ломоносова Л.Т Ретюнских. В рамках программы этой школы ежемесячно проходят вечера из цикла «Философские игры для детей и взрослых». Кроме того, на протяжение ряда лет ее курс междисциплинарного образования на основе сократического диалога, созвучный с идеями программы «Философия для детей» проф. М. Липмана, внедряется в гимназический компонент образования в начальной школе. Он направлен на активизацию интеллектуального и нравственного развития детей, стимуляцию личностного роста, смещающей акцент с ретрансляционного способа передачи знаний на проблемно-поисковый, исследовательский способ. Профессор Л. Т. Ретюнских является одним из ведущих организаторов международных научно-практических конференций «Философия детям», а также она проводит и другую работу, направленную на приобщение детей к философии.

О том значении, которое придается идее внедрения философии в школу, свидетельствует и тот факт, что в программе XXIII Всемирного философского конгресса, проходившего в Афинах с 04—10 августа 2013, работала секция «Философия для детей». Работа такой же секции предусмотрена и XXIV Всемирным философским конгрессом, который состоится с 13 по 20 августа 2018 года в Пекине.

Однако в среде противников философского подхода есть сомнение, следует ли вводить в учебный план школы еще один предмет — философию, поэтому среди философов и педагогов до сих пор ведутся по этому поводу споры.

Опасной иллюзией, на мой взгляд, можно считать убеждение в том, что предложенная М. Липманом программа «Философия для детей» сможет на уроках научить школьников как-то по-новому мыслить. Приходится согласиться с теми противниками существующего ныне философского подхода к школьному образованию, которые считают, что для того, чтобы развивать критическое и рассудочное мышление у школьников, вовсе нет необходимости вводить специальный курс философии. Более того, существующая практика детского философствования, помогающая им развивать собственное мнение по отношению к серьезным вопросам, может только навредить детям, отождествляющим пустопорожнюю болтовню или краснобайство с мудростью.

Является фактом, что ни одно из предложенных начинаний на Западе или у нас в Украине или в России не увенчалось, да и не могло увенчаться существенным успехом. А причиной явилось неумение отличить разумное мышление, а тем более мудрость, от другой его формы — рассудочного мышления. И, как следствие, все вышеназванные энтузиасты обучают детей в основном рассудочному мышлению, умению генерировать субъективные мнения, тогда как для понимания единства окружающего мира, а, значит, для целостного интегративного образования нужно развивать разум и мудрость.

Принятие этого тезиса ставит задачу перед философией для взрослых: найти и использовать такую методологию, которая развивала бы не только рассудок, с его плюрализмом мнений, но и все другие мыслительные навыки, обуславливающие разум ребенка, направленный на познание объективных причинно-следственных природных и социальных связей. Дети должны четко знать, где проходит граница рассудка, в рамках которого они свободно могут высказывать свое мнение, проявлять инициативу и изобретательность, а где проявляется «диктатура разума и мудрости».

На деле же, не имея нового канона образованности и соответствующей общеобразовательной стратегии, преподаватели не только философии, но и специальных дисциплин, каждый на свой лад изобретают способы и приемы проведения интегрированных уроков, метапредметов, и т. п. новаций. В итоге, по наблюдению М. Липмана, «критическое мышление» в курсах по химии оказывается не связанным с «критическим мышлением» в курсах по физике или литературе, т.е. в каждом предмете толкуется по-своему.

Становится очевидным, что, развивая рассудочное мышление, сократические диалоги не влияют на формирование у детей разумного мышления, а тем более мудрости. Поэтому ни предложения М. Липмана, ни инновации его идей всеми нашими философами и педагогами не могут быть тем средством, которое способно вывести образование из кризиса.

2. Чем рассудок отличается от разума и мудрости

Сегодня рассудок и разум воспринимаются как взаимосвязанные стороны ума, как две ступени мыслительной деятельности человека, взаимное отношение которых в различных философских учениях понимается по-разному. Тогда как развитие не только философии, но и всех других наук требует четкого определения их сущности, выявления сходства и различия между ними. Решение этого вопроса приобретает важное значение, когда речь идет о школьном образовании.

Рассудочное мышление, как принято обычно считать, связано с умением правильно классифицировать факты и явления, со способностью «последовательно рассуждать и умозаключать, приводить наши знания в определенную систему, подчиненную строгим логическим законам и правилам».

Аристотель сформировал три основных закона формальной логики, которые составляют ядро рассудочного мышления. И эти же законы являются в то же время логическими основаниями всей науки. Причем логическая последовательность и непротиворечивость, освоению которых предлагают обучать детей все существующие до сего дня школьные программы по философии с помощью сократического диалога, — только необходимое, но отнюдь не достаточное условие достижения знания.

Разумное мышление носит активный характер. Оно направлено на познание упорядоченности, гармонии, симметрии мироздания, на выявление общих для природного и социального мира причинно-следственных связей, раскрывающих сущность действительности, его динамику, количественное и структурное многообразие. Поэтому разумное мышление не произвольно, поскольку оно формирует знание, а не мнение.

Не вызывает сомнения, что познание, направленное на целостное восприятие реальности, а не на ширящуюся лавину рассудочного знания, которую осилить сегодня физически невозможно, должно опираться на развитие разумного мышления, которое тесно связанного со способностью нашего ума сравнивать одно с другим, то есть на умение пользоваться логической операцией «сравнение».

Можно привести слова замечательного французского философа К.А.Гельвеция (1715 — 1771), который в своем сочинении «Об уме» писал:

«В нашей способности замечать сходство и различие, соответствия и несоответствия различных предметов и заключаются все операции нашего ума». И далее «… ум, следовательно, состоит в том, чтобы сравнивать наши ощущения и наши идеи, т.е. замечать сходство и различия, соответствия и несоответствия, имеющиеся между ними».

Наш соотечественник, основатель педагогики К. Д. Ушинский (1824 — 1870) также как и Гельвеций считал операцию сравнения основой познания, ибо

«мы познаем любой предмет, только приравнивая его к чему-то и отличая его от чего-то».

Аристотель по этому поводу задолго до всех других в своей «Метафизике» писал, что

«…каждая вещь обозначается по отношению к каждой другой как «разное» или «тождественное…».

Вместе с тем, ни одна из гуманитарных наук до сего дня не дала четкого разграничения между рассудочным и разумным мышлением. Мы же, в отличие от всех, связываем рассудок с классификационными понятиями, а разум с умением осмысливать реальность при помощи сравнительных понятий.

Поэтому, на наш взгляд, с самых первых шагов ребенка в школе основное внимание следует обратить на то, чтобы формировать у школьников разумное мышление, как мышление конкретно-научными сравнительными понятиями разных видов, обоснование которых строится на разработанной нами научно обоснованной и доступной для понимания детьми логической операции «сравнение». Это позволяет определить пути движения от рассудка к разуму, т.е. от одних видов конкретно-научных сравнительных понятий к другим, более сложным видам, чего нет ни в одной из отечественных или зарубежных школьных программ.

В осмыслении единства мира важно не только его конкретно-научное осмысление. Действительная интеграция знания предполагает глубокое взаимопроникновение наук на основе общих принципов познания окружающего мира, что становится реальностью лишь в том случае, если и в естественных и в гуманитарных науках в качестве инвариантов будут выступать общенаучные категории. Поэтому особую роль в объединении разнопредметных знаний занимает не только математика, но и разработанное нами новое направление философии — «неклассическая диалектика».

Эта философия является тем основанием, без которого не может развиваться знание о мире, поскольку она дает универсальный, формализованный язык, с помощью которого человечество раскрывает причинно-следственные природные и социальные связи. Тем самым она отражает единство в многообразии явлений, строит модели объектов и систем, прогнозирует их поведение, устанавливает соотношения между объектами и их свойствами.

Именно древнегреческие философы, они же физики и математики, начинали осмысливать единство мира не с помощью «чистых рассуждений», а с помощью сравнительных понятий, отражающих объективные природные и социальные связи, а затем уже и с помощью математики. Они умели находить такие общие начала, которые в одинаковой мере были пригодны и для естественнонаучного и для гуманитарного знания.

Однако в отличие от первых философов, которые искали пути к истине с освоения конкретно-научных и конкретно-всеобщих сравнительных понятий, древнегреческие философы более позднего времени в своем мышлении стали ориентироваться на абстрактно-всеобщие классификационные понятия, при помощи которых стало невозможно осмыслить природные и социальные связи, процессы.

Впервые эта губительная для науки тенденция заявила о себе в философских учениях Парменида и Зенона, а с легкой руки Сократа, стала, по сей день, господствующей в гуманитарном мышлении. Ее суть в том, что окружающий мир и, прежде всего, человек и общество в социально-гуманитарных науках стали осмысливаться при помощи общих и даже предельно общих классификационных понятий, включенных в обычный разговорный язык. Платон закрепил это революционное «достижение», что окончательно завело философское мышление в тупик, а точнее, в лабиринт рассудочного мышления.

Это была Первая философская революция, которая закрепостила разум, сделала его рабом рассудочного мышления. С тех пор философия стала абстрактно-всеобщей, дефинитивной, рассудочной формой общественного сознания, не способной увидеть путь к истине. А другой общепризнанной, научной философии, к сожалению, на сегодняшний день нет. Поэтому задача интеграции знания и построение на этой основе научно обоснованной целостной картины мира представляет серьезную научную проблему, теоретическое решение которой предлагается в моих работах.

3. Основной вопрос философии

По данному Википедией определению:

«Филосо́фия (др.-греч. φιλοσοφία, дословно — „любомудрие“, „любовь к мудрости“) — особая форма познания мира, вырабатывающая систему знаний о наиболее общих характеристиках, предельно-обобщающих понятиях и фундаментальных принципах реальности (бытия) и познания, бытия человека, об отношении человека и мира. К задачам философии на протяжении её истории относились как изучение всеобщих законов развития мира и общества, так и изучение самого процесса познания и мышления…».

Выходит, что в отличие от всех частных наук только одна философия была нацелена на познание общего, что и должно было в отличие от рассудка и разума сформировать третью ступень в развитии человеческого ума — мудрость. Недаром Аристотель считал, что «знание общего делает человека мудрым», поскольку «мудрый, пишет в „Метафизике“ Аристотель, насколько это возможно, знает все, хотя он и не имеет знания о каждом предмете в отдельности».

Поэтому философию мы будем понимать как один из способов осмысления мира и человека, в котором мышление, имея принципиально понятийный характер, будет направлено на восхождение от рассудка к разуму, а от него к мудрости, нацеленной на познание общего.

В силу чего в качестве основного вопроса философии ставится вопрос об отношении мышления к бытию, т.е. вопрос о том, при помощи каких понятий философия осмысливала мир в прошлом, и какие понятия она должна взять сегодня в качестве своих самых первых начал.

Рассмотрим три исходные группы (типа) понятий:

Первая группа — это классификационные понятия, т.е. понятия обычного разговорного языка разной степени общности, при помощи которых мы называем вещи, их свойства, обозначаем различные идеи.

Вторая группа — это конкретно-научные сравнительные понятия, т.е. понятия, с использования которых начинаются конкретные науки. Это — тяжелое и легкое, длинное и короткое, богатое и бедное и т. д.

Взяв в любой из этих пар в качестве единицы измерения «меньшее», наука переходит к осмыслению «большего» при помощи чисел, раскрывающих отношения между величинами. Так появляется третья группа понятийных средств — количественные понятия, которые, как очевидно, являются ничем иным, как особого вида сравнительными понятиями, общими для всех конкретно-научных сравнительных понятий градационного вида.

Представленную выше классификацию научных понятий дает Рудольф Карнап в своей книге «Философские основания физики» /Philosophical Foundations of Physics/. В ней он собирает не только понятия науки, но и понятия повседневной жизни в три основные группы понятий: классификационные, сравнительные и количественные. При этом «более эффективными для выражения информации являются „сравнительные понятия“. Они занимают промежуточное положение между классификационными и количественными понятиями».

«Я — пишет Р. Карнап в «Философских основаниях физики» — считаю желательным обратить на них внимание, потому что даже среди учёных значение и эффективность таких понятий часто недооцениваются….

Часто случается, что, прежде чем в область науки могут быть введены количественные понятия, им предшествуют сравнительные понятия, которые являются значительно более эффективным инструментом для описания, предсказания и объяснения, чем более грубые классификационные понятия… Мы никогда не должны недооценивать полезности сравнительных понятий, продолжает Р. Карнап, особенно в тех областях, где научный метод и количественные понятия до сих пор ещё не разработаны».

Философия, как и большинство других социально-гуманитарных наук, не использует сегодня количественные понятия. Они в основном оперируют классификационными понятиями. Но имеются такие их области, в которых применение сравнительных понятий возможно.

Раскол между гуманитарным и естественнонаучным знанием, как раз и определяется различием в использовании понятийных средств. Классификационными понятиями пользуются представители гуманитарного знания. Тогда как началами естественных наук выступает множество конкретно-научных сравнительных понятий разных видов, что, в конечном счете, не только разделило познание по предметам, но и раскололо культуру на две части: естественнонаучную и гуманитарную. Причем, кроме сравнительных понятий конкретные науки стали использовать числа и другие математические абстракции.

Компенсировать фрагментацию науки по предметам пытались многие философы древности, они же физики, астрономы, математики — это Фалес, Гераклит, Пифагор, Аристотель и другие. Эти мыслители стремились не только к конкретно-научному, но и к конкретно-всеобщему, философскому знанию за счет осмысления мира при помощи конкретно-всеобщих сравнительных понятий. Этих понятий немного. Они вводились в науку для того, чтобы отражать не какую-то предметную область реальности, а бытие в целом.

Другие древнегреческие философы, такие как Парменид и Платон также понимали философию как «знание общего». Однако за начала философии они принимали не сравнительные, а предельно общие классификационные понятия, такие как «бытие», «благо» и т. п.

Различие в подходе к выбору философских начал удачно отразил в своей картине «Афинская школа» Рафаэль. В ее центре фигуры Платона и Аристотеля. Платон указывает пальцем на небо, тогда как Аристотель — на землю.

Примечательно, что сегодня перед философией стоит та же проблема, какими понятиями должны быть представлены ее предельные основания, что символически изображено на картине Рафаэля. Если следовать за Платоном, который в качестве начала выбрал классификационное понятие — оказываемся в лабиринте рассудочного мышления, обусловливающего плюрализм мнений. Если следовать за Аристотелем, выбравшим сравнительные понятия — выходим на оперативный простор науки с ее диктатурой истины.

Будучи наиболее талантливым учеником Афинской школы, Аристотель не мог согласиться с идущим от Платона пониманием предельно общих «начал». Поэтому в «Метафизике» Аристотель выдвигает четко обозначенные объективные «причины и начала», общие не только для естественных наук, но и для всего знания. Это четыре вида противолежания, как называл конкретно-всеобщие сравнительные понятия Стагирит, которые выводят философское мышление из лабиринта рассудочного мышления.

Это «противоречащее», «соотнесенное», «противоположное», «лишенность и обладание», а также первое «откуда» и последнее «куда», которые обусловлены разного рода возникновением и уничтожением».

Они-то и были для Аристотеля одним из источников формирования целого ряда разделов его философской системы, характеризующих философию как доказательную науку.

Хочу обратить внимание на принципиально важную связь между множеством конкретно-научных сравнительных понятий градационного вида, таких как тяжелое и легкое, длинное и короткое, богатое и бедное и множеством других — началами конкретных наук. И двумя конкретно-всеобщими сравнительными понятиями градационного вида как началами научной философии — «Соотнесенным» и «Противоположным», направленными на интеграцию знаний.

При этом один из аристотелевских видов противолежания — «противоречащее» — мы разделили на две части — на два совершенно самостоятельных сравнительных понятия: «Тождественное»: А = А. И «Различное»: А и не-А. Тогда как три других вида противолежания: «соотнесенное», «лишенность и обладание» и «противоположное», напротив, объединили в один вид, вводя для него общий термин — «градационное».

Такой передел обусловлен разными функциями выделенных Аристотелем мыслительных средств. «Противоречащее» имеет отношение к речи и связанному с ней непротиворечивому рассудочному мышлению. Что же касается остальных видов противолежания, то они обусловливают природные и социальные связи, возможность их измерения, счет и, в конечном счете, высокоразвитое философское мышление — мудрость. При этом они отражают не три проявления реальности, как о них, видимо, думал Аристотель, а одно объективное отношение, которое мы и обозначили словом: «градационное».

Стремясь, как и Платон к «знанию общего», Аристотель не ограничивал познание известными ему видами противолежания, а был сторонником восхождения от самых простых конкретно-всеобщих сравнительных понятий: одинаковое, различное, соотнесенное и т. д. — к более сложным понятиям как мыслительным средствам, отражающим единство мира. Однако не нашел их.

Последующие поколения пошли в этом вопросе не за Аристотелем, а за Платоном. Поэтому и случилось, что с тех самых пор философия все дальше заходила в лабиринт рассудочного мышления, поскольку стала абстрактно-всеобщей, дефинитивной, рассудочной формой общественного сознания.

Тогда как выделенные Аристотелем виды противолежания, напротив, выводят философию на оперативный простор науки, поскольку являются самыми исходными общенаучными конкретно-всеобщими понятиями, объективно отражающими реальность вне зависимости от ее природной или социальной обусловленности. В результате их применения уже ничто не препятствует развитию философии как объективной кумулятивной науки, отражающей конкретно-всеобщее единство мира.

Причем, если внимательно рассмотреть два аристотелевских вида противолежания: «соотнесенное» и «лишенность и обладание», то можно обнаружить, что они представляют собой два различных проявления одного и того же отношения — градации. В одном случае — это связь «меньшего» и «большего». Тогда как в случае «лишенности и обладания», «лишенность» выражает, выродившееся в ноль «меньшее». Примером может служить обычная школьная линейка. Это подтверждает тот факт, что понятие «лишенность и обладание» представляет собой частный случай «соотнесенного».

То же касается и понятия «противоположное», которое не является самостоятельным отношением, поскольку не отличается от «соотнесенного» ничем иным, кроме как выбором иной, срединной точки зрения, которая делит «градационное» на две противоположные части.

В итоге, если смотреть на градацию с точки зрения «меньшего», мы видим другой ее конец в качестве «большего». Если же смотреть на градацию с позиции «большего» — видим другой ее полюс — «меньшее» или «лишенность». Если же на градацию посмотреть со срединной позиции, то получим «избыток» и «недостаток» относительно промежуточного, то есть «противоположности», обусловливающие энергетику мироустройства.

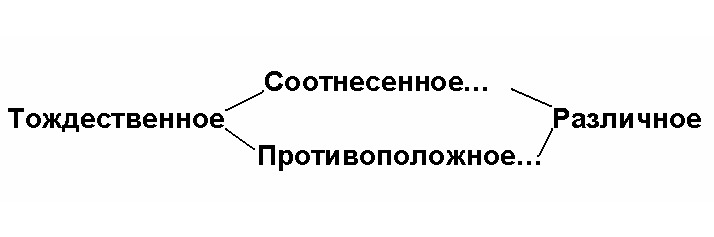
Выходит, что каждое из сравнительных понятий (будь то конкретно-научное или конкретно-всеобщее понятие) дает наблюдателям одинаковые для всех объективные точки зрения, что, в конечном счете, приводит их не только к пониманию тех или иных отношений, но и к взаимопониманию.

Совершая восхождение от абстрактного тождества (Тождественное) к конкретным различиям (Соотнесенное и Противоположное), и постигая все их конкретно-научные природные и социальные проявления с объективных точек зрения, человек приобщается к первой ступени философской мудрости, за которой Аристотель угадывал следующие более высокие ступени, однако не нашел пути к ним.

Мы же, продолжая дело древнегреческих мыслителей, собираем выявленные ими более сложные конкретно-всеобщие сравнительные понятия и объединяем их в единую систему. Так, у Пифагора мы находим его знаменитую теорему, связывающую под прямым углом две градации (Ортогональное 1 Пифагора). Тогда как у Гераклита мы находим гармонию лука и лиры (Ортогональное 2 Гераклита), связывающую под углом 90 градусов две пары противоположностей. Последние отражают собой более общие, нежели у Аристотеля, причинно-следственные природные и социальные связи.

Таким путем мы собираем выявленные древними конкретно-всеобщие сравнительные понятия в единую систему.

При этом хочу обратить внимание на принципиально важную связь между множеством конкретно-научных сравнительных понятий ортогонального вида, таких как меновые и потребительные стоимости, потенциальная и кинетическая энергия, электрическое и магнитное поле, рабство и феодализм, и множеством других понятий конкретных наук. И конкретно-всеобщими сравнительными понятиями ортогонального вида, то есть понятиями научной философии — «Ортогональное 1 Пифагора» и «Ортогональное 2 Гераклита», направленными на интеграцию знаний.

Благодаря понятию «ортогональное» можно осмысливать не только все ритмы природы, например, что такое температура, звук, свет. Или, что представляет собой движение механического и электромагнитного маятников, отношение металлических и металлоидных свойств периодической системы химических элементов, но и обмены в обществе.

В истории философии можно увидеть, что из двух исходных типов понятий: классификационных и сравнительных, одни философы выбирали классификационные понятия предельной общности, тогда как другие — наиболее общие сравнительные понятия. Парменид, Сократ и Платон — выбирали начала среди классификационных понятий предельной общности. Тогда как представители милетской школы, Гераклит и софисты — среди самый простых сравнительных понятий.

Марксистская философия выбрала не одно, а два начала. В качестве одного — она выбрала классификационное абстрактно-всеобщее понятие «материя», в качестве другого — понятие «противоположности». При этом противоположности в марксизме понимались не «как избыток и недостаток того или иного субстрата относительно промежуточного свойства», как понимал противоположности Аристотель, а в самом широком, абстрактно-всеобщем смысле, то есть как смесь совершенно разных отношений, многие из которых противоположностями не являлись. В результате и сама марксистская философия и ее диалектический метод оказались вне объективной науки, не способные дать научно обоснованную целостную панлогическую картину мира.

Современная философия не пришла к пониманию конкретно-всеобщих сравнительных понятий градационного, ортогонального и других видов. Поэтому сегодня она использует не сравнительные понятия, а чрезвычайно мудреные претендующие на научность классификационные понятия. И как следствие, рожденные ею смыслы, не могут выйти за пределы рассудочного мышления.

Тогда как наш подход к философии, основанный на разделении понятий на четыре группы (сравнить с тремя основными группами понятий по Р. Карнапу) выводит философское мышление из тупика. В отличие от классификации понятий у Р. Карнапа, в нашей классификации происходит деление сравнительных понятий на два принципиально различающихся типа: конкретно-научные и конкретно-всеобщие сравнительные понятия. Причем каждый из этих типов делится на виды: градационный, ортогональный, дополнительный…

Важным здесь является то, что деление языковых средств на классификационные, количественные, конкретно-научные и конкретно-всеобщие сравнительные понятия градационного (Аристотель), ортогонального (Пифагор, Гераклит) и других видов, позволило провести демаркацию между тремя принципиально разными ступенями в развитии человеческого ума: рассудком, разумом и мудростью.

Рассудок оперирует языком классификационных понятий. Он связан с обозначением вещей и их свойств, с классификацией фактов и явлений, с систематизацией разнообразных знаний на основе отношений тождество и различие как предельных абстракций отождествления и различения.

Разум задействует не только классификационные, но и конкретно-научные сравнительные понятия градационного, ортогонального и других видов, числа, арифметические и другие математические абстракции. Он связан с конкретно-научным осмыслением природного и социального мира.

Мудрость стоит над рассудком и разумом благодаря тому, что помимо классификационных, конкретно-научных сравнительных и количественных понятий, помимо различных математических абстракций, она включает в мышление язык конкретно-всеобщих сравнительных понятий, которые в отличие от всех других понятий только и способны отражать научно обоснованное единство мира. Вот эти понятия:

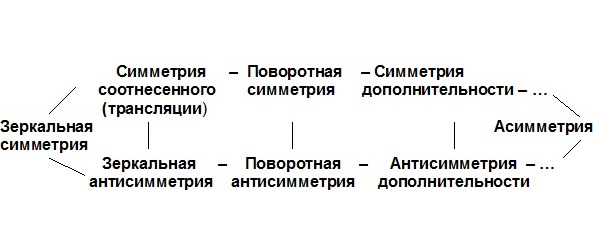
Выходит, что мир для нас таков, каким мы способны его воспринять, классифицировать и описать посредством классификационных, конкретно-научных и конкретно всеобщих сравнительных понятий. Недаром говорят, что

«границы нашего языка определяют границы освоенного нами мира».

Причем, за многовековую свою историю философы, а вместе с ними и все гуманитарии, не научились использовать язык конкретно-научных и конкретно-всеобщих сравнительных понятий, а, значит, они не сумели освоить ни разум, ни тем более мудрость — Софию. Тогда как естественные науки сумели перейти от рассудка к разуму, не сумев при этом освоить мудрость.

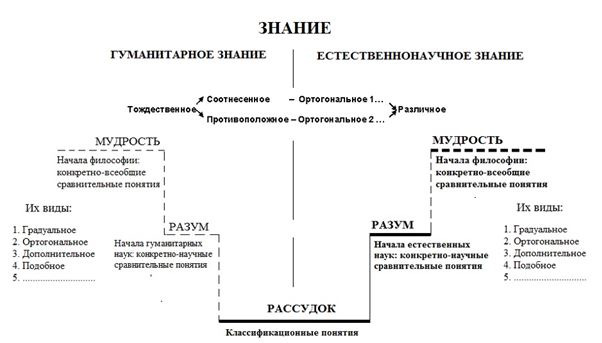
В итоге философия оказалась не способной выполнить свою главную миссию — стать наукой и дать общезначимую философскую картину мира.

Из сказанного выше следует, что философия не может возникнуть прежде, чем появились конкретные науки, а, значит, она не может быть матерью всех наук, как обычно принято считать. Напротив, философия — это еще не родившееся их дитя. Поэтому на предшествующую историю философии следует посмотреть как на историю ее несостоявшегося рождения.

Что же касается предлагаемой концепции философского знания, то в границах общеобразовательной школы, она способна занять место не в качестве одной какой-то отдельной научной дисциплины — она может представлять всю науку, воспринимающую мир как борьбу, сочетающихся между собой на все лады, противоположностей.

В этой связи становится очевидным, что все выделенные Аристотелем начала, а с них-то по Аристотелю и должна начинаться философия, в той или иной конкретно-научной форме уже изучаются в начальной школе с первого класса. Поэтому введение в школьную программу конкретно-всеобщих философских понятий не будет вызывать у школьников никаких затруднений.

При этом наш подход согласуется не только с ФГОС, но и с подходом американских педагогов, поскольку один из ключевых принципов программы «Философия для детей» М. Липмана состоит в том, что самой социально благоприятной средой для воспитания навыков разумности является обычный школьный класс, превращенный в сообщество исследователей.

Различие между подходами в том, что американские философы не выводят мышление детей за границы рассудка и ограниченного естественными науками разума. Тогда как наш метод «Трилогия ума» не только интегрирует естественнонаучное и гуманитарное знание на разумной основе, он помогает подняться до третьей ступени в развитии детского ума — до философской мудрости, понимаемой как знание общего, как мышление конкретно-всеобщими сравнительными понятиями.

И действительно, в учебнике по математике для учеников 1-го класса подробно рассматриваются свойства и отношения между предметами, формулируются начальные математические понятия, которые как мы видим, неразрывно связаны с философскими общенаучными понятиями.

По этому же учебнику дети знакомятся с относительными оценками величин предметов, такими как: «тяжелый — легкий», «большой — маленький», «длинный — короткий», «высокий — низкий». При сравнении количества предметов они учатся определять отношения между ними: «больше», «меньше», «столько же».

Поэтому на данной ступени образовательного процесса следует знакомить детей не только с множеством конкретно-научных сравнительных понятий, но и с конкретно-всеобщими философскими понятиями такими как «тождественное» и «различное», «соотнесенное» и «противоположное», «лишенность и обладание», «противоречащее» и другими — как более общими понятиями.

4. Чувственное и рациональное познание: партикулярии и универсалии

Уже в младших классах школьники должны знать о том, что познание состоит из двух взаимосвязанных ступеней: чувственной и рациональной. Причем начинается оно с чувственного познания одинаковых предметов, свойств, природных и социальных явлений, когда внимание фиксируется на повторяемости у них определенных признаков. Логический переход от знания об отдельных явлениях к знанию, присущему всем явлениям определенного класса совершается в форме рационального познания.

В споре о том, что важнее — чувственное или рациональное познание выявились две крайности: реализм и номинализм в средневековье, а позднее — эмпиризм и рационализм.

Реалисты считали общие понятия реальными, тогда как номиналисты полагали, что общие понятия не существуют реально, а являются только именами (лат. nomina).

Эмпиризм — это позиция, согласно которой единственным источником всех наших знаний является чувственный опыт — все то, что мы получаем с помощью зрения, слуха, осязания, обоняния и вкуса.

Рационализм — это позиция, в соответствии с которой достоверное знание может быть получено с помощью одного ума, без всякой опоры на органы чувств. Образцом для рационалистов является математика, которая развивается на своей собственной основе исключительно за счет разума.

С проблемой соотношения единичного и общего, которая, фактически, так и не была решена ранее, сталкиваются дети уже с первого класса. И чтобы они хоть как-то в ней разобрались их следует познакомить с двумя понятиями, которыми они могут пользоваться в течение всего школьного курса.

Речь идет о «партикуляриях» и «универсалиях» — понятиях средневековой философии, которые могут быть использованы в школе при рассмотрении разнообразных способов идентификации вещей. Тем более, что эти понятия в последнее время все более входят в научный оборот.

Так, профессор философии Оксфордского университета сэр Питер Фредерик Стросон (1919 — 2006) считал, что

«среди всего существующего в мире, люди способны осуществлять идентифицирующую референцию к отдельным вещам, событиям и иным индивидуальным объектам термином „партикулярии“ и противопоставлял их универсалиям вроде качеств, чисел и классов».

Партикулярный — происходит от лат. слова «particula» — частица или от англ. particular, где part — часть. В нашем случае оно будет обозначать часть, долю или компонент чего-то целого, единого. Партикулярии — это одиночные, отдельные объекты, с исследованием которых ребенок будет сталкивается на всем протяжении своего обучения в школе.

Универсальный — охватывает всё или многое, относящийся ко всему, всеобъемлющий, т.е. пригодный для множества сильно отличающихся случаев. Это слово применимо в случаях, когда ищут общую сущность, общую природу вещей, когда ищут «одинаковое» в «различном» и выражают это одинаковое в понятии.

Универсалии упорядочивают мир по отношениям сходства, это имена при помощи которых человек выделяет в окружающем мире и группирует все «одинаковое». Умение схватывать эту объективно существующую особенность вещей присуще только живому существу, в данном случае — человеку. Поэтому можно говорить о человеческом сознании и о выраженных в слове идея, как отражении реальности в голове человека.

Сколько существует групп слов столько же существует и групп универсалий. На наш взгляд, их не три (как у Р. Карнапа), а четыре:

1. Классификационные понятия — это слова обычного разговорного языка, благодаря которым человеческому уму удалось найти единство для всего качественного многообразия мира. Этот язык позволяет объединять одним словом множество незначительно различающихся объектов — камень, дерево, человек и др. В развитых языках насчитывают 100 — 200 тысяч слов.

2. Конкретно-научные сравнительные понятия — это такие понятия градационного и других видов, которые дают возможность сделать первые шаги по пути разумного мышления.

3. Количественные понятия — это особый вид сравнительных понятий, благодаря которым человеческому мышлению удалось сделать следующий шаг к более развитому разумному мышлению. В результате появилась математика и другие конкретные высокоразвитые науки.

4. Конкретно-всеобщие сравнительные понятия — это еще одна языковая форма, предназначенная для объективного отражения структурного единства мира. С появлением этих понятий был сделан шаг на пути к философской мудрости, т.е. к третьей ступени в развитии нашего ума.

Понятие «партикулярии» нужно использовать в отношении чувственно воспринимаемых объектов качественного, количественного и структурного многообразия мира. Тогда как понятие «универсалии» следует использовать в отношении слов, отождествляющих, опять же, качественное, количественное и структурное многообразие мира, т.к. эти понятия подводят собираемые ими партикулярии под тот или иной конкретный вид, обозначаемый словом обычного разговорного языка или сравнительным понятием, отражающим объективное содержание общего, одинакового в вещах.

Входит, что «духовное» (универсалии) обусловлено исключительно тем, что существует одинаковость в различных вещах — партикуляриях. Эту объективно существующую разную степень одинаковости и фиксирует человеческое сознание, обозначая ее тем или иным словом — классификационным, сравнительным или количественным понятием.

В результате, появилась возможность объединять одним словом казалось бы самые разные природные и социальные явления, процессы. Например, понятием «противоположное», понимаемым как «избыток и недостаток относительно промежуточного» мы схватываем одинаковое в самых разных природных и социальных отношениях. При этом все конкретно-всеобщие сравнительные понятия образуют подобно числам ряд, который мы будем называть «натуральным рядом сравнительных понятий».

Следует подчеркнуть, что применение научно обоснованной кумулятивной (накопительной) философии невозможно только в одном классе, например, в первом, пятом или десятом. В силу ее накопительного характера, мы вынуждены растянуть этот процесс во времени на весь период обучения детей в школе. И тогда философское мышление будет передаваться детям не одним учителем, а разными. Сначала учителем младших классов, затем по мере взросления детей и перехода их в более старшие классы — учителями математики, физики, обществоведения…

В результате учителя и ученики одной школы (или даже страны) становятся единомышленниками со своей общей для них философией, поданной детям не с позиций рассудочного мышления, способного отражать лишь множество разных мнений, а с позиций разума и мудрости, отражающих общее во всем знании.

5. Конкретно-всеобщие сравнительные понятия как основа научно-философского знания

Не скажу о детях, но учителя должны знать, что проблема универсалий уходит своими корнями в решение спора между Платоном и Аристотелем о том, с чего должна начинаться философия как любовь к мудрости. Аристотель критиковал учение об общих и предельно общих классификационных понятиях (идеях), которые по Платону являются истинной причиной всех вещей, их свойств и отношений. По Аристотелю, идеи (т.е. общее) не предшествуют единичным чувственно воспринимаемым предметам и не являются причинами вещей, а, наоборот, зависят от них.

Разговор, таким образом, идет не об одном, а о двух совершенно разных направлениях философии — идеализме и материализме. При этом в осмыслении спора между Платоном и Аристотелем не это главное. Главным же является вопрос о том, какие из четырех групп понятий философия должна взять в качестве своих самых первых начал. Платон и все его последователи выбирали начала среди классификационных понятий разной общности, ограничивающих философию рассудочным мышлением. Тогда как Аристотель видел начала философии в сравнительных понятиях, не отвергая при этом и значения рассудочного мышления. Тем самым Аристотель препятствует изгнанию разума и мудрости из философии.

Поэтому если за рассудочной философией, назовем ее платоновской (не обязательно идеалистической), оставляем существующее название «философия», тогда за конкретно-всеобщей (аристотелевской) философией надо закрепить новое, отличающееся от прежнего, название. Я предлагаю называть ее «аристологией».

Если же, напротив, за аристотелевским направлением оставить название «философия», тогда за платоновской рассудочной философией нужно закрепить название «филодоксия», понимаемое как «любовь к мнениям».

Такое разделение не только исключит путаницу между двумя формами общественного сознания, но приводит к пониманию того, что аристотелевская философия включает платоновскую философию, в границах которой действует только рассудочное мышление, в качестве своего частного случая. При этом главная цель аристологии состоит не только в том, чтоб показать человеку путь, ведущий к полному освобождению его разума и мудрости, но и в том, чтобы сделать Человека более успешным и лучшим (Aristos — лучший).

Поэтому развитие детского ума нужно начинать с аристотелевских начал, т.е. с использования в учебном процессе конкретно-научных и конкретно-всеобщих сравнительных понятий разных видов. Таким образом целью данной главы будет расширение понятийной базы детского мышления за счет включения в нее новых элементов, а также формирование у обучающихся способности к обобщению, структурированию и систематизации изучаемого предметного содержания.

О конкретно-всеобщих понятиях тождества и различия, обусловливающих парадигму рассудочного мышления, мы уже говорили раньше. Поэтому в данном месте книги мы останавливаться на них не будем, а перейдем к обсуждению более сложных конкретно-всеобщих сравнительных понятий.

Работа над понятием «Соотнесенное»

Самым первым шагом в ознакомлении детей с аристотелевскими видами противолежания будет знакомство с понятием «соотнесенное», поскольку дети уже с 1-го класса знакомятся с относительными оценками величин предметов. Поэтому говоря о «соотнесенном» учитель предлагает детям найти в окружающем мире конкретно-научные примеры «соотнесенного». Дети ищут и находят, например, различие по размеру, по весу, по температуре: «толстый — тонкий», «широкий — узкий», «тяжелый — легкий», «горячий — холодный» и другие.

Рассматривая отдельные предметы или их свойства дети определяют между ними отношения. При этом учитель может организовать игру «Назовите соотнесенное слово по значению». Например, учитель говорит: «высокий». Ученики называют слово, соотнесенное по значению: «низкий» и т. д.

Работа над понятием «Противоположное»

На следующем уроке можно рассмотреть очень важное для развития диалектического мышления понятие «противоположное». Причем различение противоположного и соотнесенного важно, поскольку соотнесенные понятия рассматриваются по отношению друг к другу, тогда как противоположные понятия — по отношению к промежуточному, срединному значению, т.е. как избыток и недостаток относительно «промежуточного».

Важным здесь является понимание того, что рассматриваемые отношения дают объективные точки зрения, относительно которых выносится суждение о рассматриваемых свойствах, которые всегда относительны. Точками зрения здесь могут быть либо срединная точка, либо одна из крайних.

Таким образом, выходит, что одна и та же пара противолежащих понятий с одной точки зрения выступает в качестве «соотнесенного», тогда как с другой точки зрения — относительно «промежуточного» — как «противоположное». И детям это не трудно понять, поскольку их обучают находить середину, центр линии или плоскости.

Уже в 1-м классе дети обучаются преобразованию неравночисленных множеств в равночисленные. Это происходит двумя способами: либо за счет того, что убирают лишнее, либо прибавляют к меньшей группе столько предметов или единиц, сколько их было лишних в другой. Задание противоположного характера направлено на то, чтобы равные группы сделать неравными. Оно также выполняется двумя способами: можно прибавить несколько предметов к одной совокупности или убрать несколько предметов из другой.

Благодаря этим важным приемам появляется возможность объяснить детям, как сделать равные группы противоположными. Для этого нужно убрать несколько предметов из одной группы и прибавить их к другой группе. Например, в каждом из двух множеств содержится по десять единиц. Убирая, положим, три единицы из одной группы и, прибавляя их к другой, мы получаем противоположности: 7 и 13 относительно 10. Избыток здесь +3, а недостаток -3 относительно 10.

Учитель приводит примеры противоположного, объясняя при этом, почему одни и те же понятия в одном случае называют «соотнесенными» понятиями, а в другом случае «противоположными» понятиями.

Так, рассматривая «соотнесенное», подчеркивает, что каждое из понятий является точкой зрения, для осмысления противолежащего понятия. Тяжелое является тяжелым не само по себе, а только по отношению к легкому, само по себе оно не имеет смысла. То же касается, например, и понятия «горячее», которое имеет смысл только в отношении к понятию «холодное».

При этом особое внимание учитель обращает на важность выбранной точки зрения, показывает ее объективность. Объясняет, почему точки зрения — это те опорные пункты, которые позволяют упорядочивать и рационализировать знание о релятивном мире. Отбросить их — значит создать в науке хаос, а образование лишить опоры, о чем свидетельствует положение в гуманитарных науках.

Работа над понятием «Лишенность и обладание»

С самого первого класса детей в школе учат пользоваться простейшим из физических приборов, которым является измерительная линейка. Этот прибор для измерения длины, представляет оппозицию «лишенность и обладание», выражающую собой градацию — весьма удобный случай «соотнесенного», когда одна из соотносимых сторон представлена состоянием «лишенности», принимающим нулевое значение. При этом «обладание» представлено всеми другими делениями линейки, отличающимися от нулевого деления.

Объясняя оппозицию «лишенность и обладание» учитель сравнивает ее с «соотнесенным» и показывает, что эти бинарные оппозиции представляют собой две различные формы одного и того же отношения. Так, «соотнесенное», например, связывает воедино два понятия «большое» и «малое». При этом «малое» может изменяться от любого заданного значения до нуля. Это значит, что понятие «соотнесенное» может вырождаться в понятие «лишенность и обладание» в качестве своего предельного случая, когда «малое» приобретает нулевое значение.

Работа над понятием «Противоречащее»

С первого же класса детей нужно приучать к освоению еще одного вида противолежания — «противоречащего», которое характеризуется утверждением и отрицанием одного и того же. Например, мы утверждаем — это «стол» и тут же говорим — это «не стол». Поэтому понятия «стол» и «не-стол» называют противоречащими понятиями. То же касается и понятий «горячее» и «не-горячее», «дерево» и «не-дерево». Причем понятие «не-стол», например, включает в себя все бесконечное многообразие мира, исключающее понятие «стол». Это же относится и к любому другому понятию с приставкой «не-».

В заключение каждой темы учитель предлагает детям найти в окружающем мире примеры противолежащих понятий. Например, учитель объясняет классу, что обозначают понятия «соотнесенное» и «противоположное». Приводит примеры большого и маленького, богатого и бедного, доброго и злого. После этого предлагает детям найти в окружающем мире примеры противоположного, просит указать, относительно какой точки отсчета дети осмысляют различие сторон. То же касается и понятия «соотнесенное».

Работа над понятием «Ортогональное»

Знакомство с углами начинается с освоения шарнирной модели. Для начала детям дается образ прямого угла. Сдвигая стороны прямого угла, переходят к острому углу. Раздвигая стороны, переходят к тупому углу. При этом подчеркивается, что величина угла зависит от поворота одной стороны относительно другой.

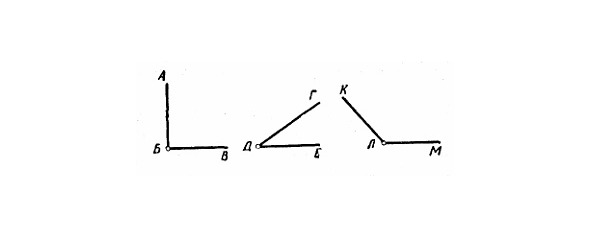
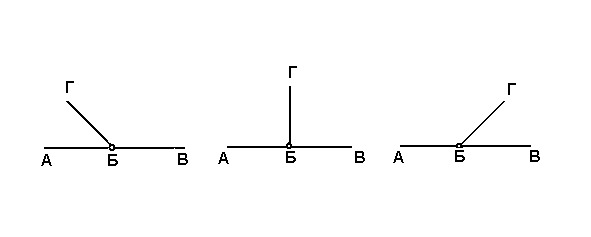
Путём двойного перегибания листа бумаги учитель показывает, как получить модель прямого угла. Затем предлагает детям взять листочки, которые лежат у них на партах, сложить их пополам и еще раз пополам. У нас получился прямой угол. Дети выполняют различные упражнения, накладывая эту модель на тетради и книги. Кроме того, ученики строят прямые углы на клетчатой и нелинованной бумаге, находят прямые углы на различных предметах окружающей обстановки. Наложением различных моделей прямых углов друг на друга дети убеждаются в равенстве всех прямых углов между собой.

Развернув листочек, дети видят две прямые линии, по которым его складывали — они делят лист на 4 части.

Далее учитель рассказывает, что слово «прямоугольный», т.е. расположенный под прямым углом происходит от древнегреческого слова «ортогональный» (перпендикулярный). Рассказывает о перпендикуляре и о том внимании, которое уделяли древнегреческие мудрецы осмыслению ортогональной зависимости. При этом обязательно ставит ударение на том, что понятие ортогонального важно не столько само по себе, сколько в контексте его взаимной связи с ритмами, циклами, колебаниями, волнами. Отображать суть этих ритмов на бумаге помогает геометрическая модель — окружность.

Далее учитель объясняет, как вычерчивается окружность и показывает для этого специальный инструмент — циркуль. Отмечает, что в момент работы циркуля, ножка в которой закреплена игла, стоит на одном месте. Эту точку называют центром окружности. Другая ножка циркуля движется, и её конец вычерчивает линию, которую и называют окружностью.

Затем учащихся знакомят с радиусом окружности. Для этого на окружности отмечают какую-нибудь точку и соединяют ее отрезком с центром. Отрезок, соединяющий точку на окружности с центром, называют радиусом.

Связывая прямые углы с окружностью или с ее частью, учитель показывает различие между «Ортогональным» Пифагора и «Ортогональным» Гераклита. Объясняет, почему при помощи ортогонального Пифагора отображается взаимодействие двух ортогональных сторон. Тогда как при помощи ортогонального Гераклита отображается колебание, как взаимодействие четырех сторон — двух пар противоположностей, раскрывающих причину всех циклических движений.

Поэтому на ортогональное надо смотреть как на тот оселок, на котором испытывается разум и мудрость, проявляется их зрелое отличие от рассудка. Не случайно, что две революции в философии, сознавая это или нет, жестко сражались за и против утверждения этой абстракции в мышлении.

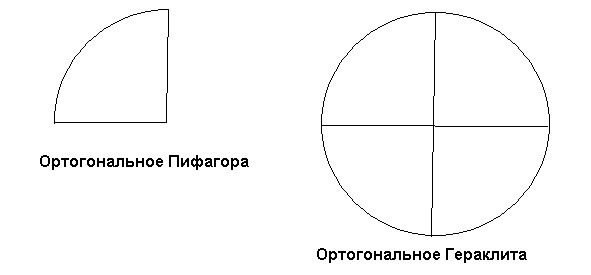
По этой теме можно организовать игру «Назовите слово, ортогональное по значению». Учитель говорит: «День». Ученики называют слово, ортогональное по значению: «Вечер» и (или) «Утро», «Зима» — «Весна» и (или) «Осень». «Север»…

Следующий урок предназначен для детей, положим, 2-го или 3-го класса. На уроке проводится работа с теллурием — прибором для наглядной демонстрации годового движения Земли вокруг Солнца и суточного вращения Земли вокруг своей оси. Тема урока называется: «Смена дня и ночи». Его цель: объяснить детям связь смены дня и ночи с вращением Земли вокруг своей оси.

Учитель объясняет, что в то время, когда Земля вращается вокруг своей оси, она поворачивается к Солнцу разной стороной. Посмотрите, показывает на прибор учитель и скажите: в тот момент, когда Солнце освещает одну половину Земли, какое там время суток? (день). — А какое время суток на той половине, которая находится в тени, и не освещена Солнцем? (ночь). Может ли Солнце, задает новый вопрос учитель, осветить Землю сразу со всех сторон? Нет, отвечают дети.

Учитель объясняет, что такое год — это то время, за какое Земля облетает один раз вокруг Солнца. Он длится 365 дней. Далее объясняет, что год делится на четыре ортогональных сезона и называет их: зима, весна, лето, осень. Объясняет, что такое месяц и сколько месяцев в году (12). Просит детей их назвать. Объясняет, что такое сутки — это время, за которое Земля совершает один полный оборот вокруг своей оси (за 24 часа). Как нечто целое сутки, опять таки, делятся на четыре одинаковые по времени части. И все это учитель связывает с понятием «ортогональное» Гераклита.

По этой теме также можно организовать игру «Назовите слова, ортогональные по значению». Учитель говорит: «День и Ночь». Ученики называют слова, ортогональные по значению: «Вечер и Утро». Учитель называет: «Зима и Лето» — ученики называют: «Весна и Осень».

Партикулярии зима, весна, лето и осень, так же как партикулярии другого вида: ночь, утро, день и вечер связаны между собой на только противоположными, но и ортогональными отношениями. Учитель просит кого-либо из учеников нарисовать ортогональное Гераклита, и вписать в эту геометрическую модель времена года. То же самое учитель предлагает проделать детям и со временами суток. Дети должны четко знать, что день и ночь по отношению к утру и вечеру ортогональны, также как зима и лето ортогональны по отношению к весне и осени. Для демонстрации этой мысли, учитель вычерчивает на доске соотношение двух ритмов: суточного и сезонного.

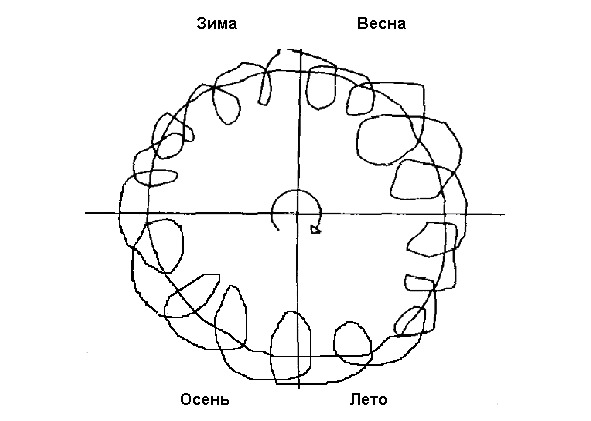
В более старших классах, дети должны понимать, что ортогональными отношениями связаны между собой север и юг с востоком и западом, потенциальная с кинетической энергией, электрическая энергия — с магнитной.

То же самое касается и общественных процессов, в которых рабовладельческая общественно-экономическая формация с ее противоположными классами рабов и рабовладельцев ортогональна феодальной формации с преобладающими в ней классами феодалов и крепостных. В таком же ортогональном отношении находится старшее и младшее поколения людей, в котором папа и мама оказываются ортогональными по отношению к сыну и дочери.

Выходит, что «отцы» и «дети», как принято сегодня считать, — это вовсе не противоположные друг к другу понятия, а ортогональные. Поэтому все круговые, циклические движения во многих случаях лучше всего объяснять не при помощи пифагорейской, а при помощи гераклитовой модели.

В методике формирования философских представлений важное место занимает абстрагирование, т.е. движение от «вещей» к общим понятиям, которые часто совпадают с геометрическими фигурами: прямоугольным треугольником, окружностью и т. д. А также, наоборот — от образа фигуры, от абстракции к реальным вещам и процессам. Это достигается систематическим использованием приема материализации геометрических образов, которые зачастую адекватно отражают философские обобщения.

Отвлекаясь от конкретных свойств материальных вещей, учащиеся овладевают философскими и математическими (геометрическими) представлениями. Недаром при входе в Академию Платона было написано:

«Да не войдет сюда тот, кто не знает геометрии».

Ибо геометрия — это не только раздел математики, это фундаментальный элемент философской культуры.

Осмыслив первоначала (виды противолежания) и научившись при помощи них думать, школьники с помощью задаваемых учителем вопросов самостоятельно будет находить их проявления в бесконечном многообразии окружающей реальности.

В итоге дети начнут осваивать проблемно-поисковый, исследовательский способ, получат то средство, которое обеспечит связное видение мира, т.е. интегрированное знание о природных и социальных процессах, чего не дают и не могут им дать все другие подходы и методы, имеющиеся в арсенале современного образования.

Используя в учебном процессе конкретно-всеобщие понятия: «противоречащее», «соотнесенное», «противоположное», «ортогональное» и другие, мы, таким образом, шаг за шагом накапливаем об окружающем мире общее знание и, таким образом, вводим в школьное образование метапредмет — аристологию, которая совместно со старой рассудочной философией, арифметикой и геометрией будут синтезировать естественнонаучное и социально-гуманитарное знание. Ибо мышление сравнительными и математическими понятиями позволяет осмысливать с одинаковых для всех объективных точек зрения не только природу, но и общество.

Сопровождая курс арифметики, геометрии и физики, аристология в современной школе добивается их единства и наглядности, что является необходимыми условиями их успешного изучения. При этом удачное и умелое применение наглядности побуждает детей к познавательной самостоятельности и повышает их интерес к предмету, является важнейшим условием успеха.

В тесной связи с наглядностью обучения находится и его практичность, поскольку именно из жизни черпается конкретный материал для формирования наглядных аристологических (философских) представлений. В этом случае обучение становится согласованным с жизнью ребенка.

Из сказанного выше следует, что основой формирования у детей представлений о конкретно-всеобщих сравнительных понятиях является способность к восприятию «одинакового в различном», и наоборот — «различного в одинаковом». Эта способность позволяет ребенку узнавать, отождествлять и различать, казалось бы, совершенно разные проявления реальности, закрепляя их в философских понятиях: тождественное и различное, соотнесенное и противоположное и т. д.

Цель метода наглядности в школе — обогащение и расширение непосредственного, чувственного опыта детей, который является условием для последующего перехода к систематическому конкретно-всеобщему мышлению, т.е. к мудрости. В начальных классах применяется естественная, рисунковая, звуковая и графическая наглядность. Затем эти методы применяются на всех этапах педагогического процесса. Их роль в том, чтобы дать опору для формирования в будущем устойчивого разумного мышления, отражающего объективные природные и социальные явления.

6. Натуральный ряд сравнительных понятий: размышление об уме

Рассмотрим вопрос о том, как конкретно-всеобщие сравнительные понятия ставятся одно за другим в определенном порядке, отражающем переход от одинаковости сопоставляемых сторон, т.е. от их тождества к все возрастающему различию. Это «натуральный ряд конкретно-всеобщих сравнительных понятий». Он позволяет говорить о новой концепции обучения, которое, шаг за шагом, собирает в голове ребенка расколотое на мельчайшие кусочки знание не по предметному принципу, как это имеет место во всех странах мира, а по межпредметному, панлогическому философскому принципу.

Для начала самые простые конкретно-всеобщие сравнительные понятия собираем в некую исходную аристотелевскую Матрицу (лат. источник, начало) :

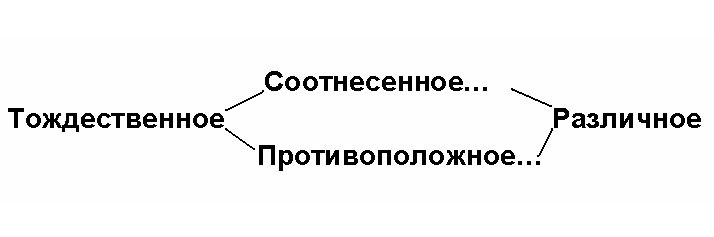
Ребенок может провести наполнение того или иного, включенного в Матрицу философского понятия, конкретно-научным смыслом, например, понятия «Соотнесенное»:

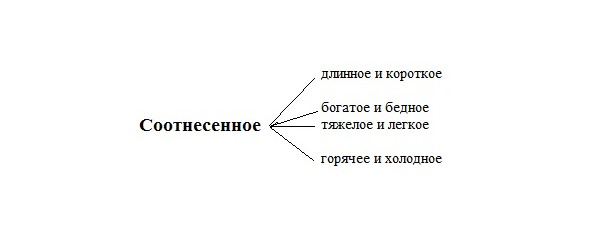
По мере перехода учеников из класса в класс, т.е. по мере познания ими окружающей действительности, мы выстраиваем школьное знание в два параллельных ряда конкретно-всеобщих сравнительных понятий, каждое из которых дает объективную точку зрения на природный и социальный мир.

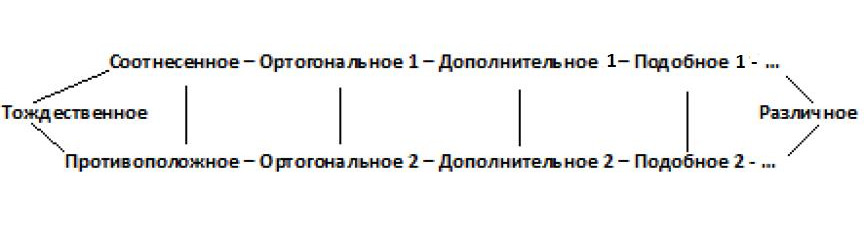
Паралельно происходит обучение детей знаниям, а, значит, и наполнение каждого конкретно-всеобщего понятия конкретно-научным смыслом. Причем каждое менее сложное понятие натурального ряда представляет собой частный случай (вырожденное состояние) более сложного понятия. Например, «Соотнесенное» и «Противоположное» — это вырожденное состояние понятий «Ортогональное 1» Пифагора и «Ортогональное 2» Гераклита, а понятие «Тождественное» — это вырожденное состояние «Соотнесенного» и «Противоположного».

Выходит, что «все познается в сравнении» и не иначе как относительно той или иной строго заданной, а, значит, одинаковой для всех наблюдателей объективной точки зрения. При этом точки на схемах обозначают множество не показанных сравнительных понятий (универсалий), партикулярии которых мы ранее находили в окружающей действительности.

Если по математике в первом классе дети изучают числа от 1 до 10 и число 0 и должны усвоить, каким образом образуется каждое из этих чисел. Какое место оно занимает в ряду от 1 до 10, после какого и перед каким числом его называют при счете, каков состав каждого числа. То в курсе школьной философии (аристологии) имеет место то же самое, поскольку ее основным разделом является натуральный ряд сравнительных понятий.

Начиная, положим, с 1-го класса у детей постепенно формируется понимание того или иного сравнительного понятия, как того общего, универсального, что характеризует класс входящих в него конкретных отношений.

Так, философское понятие «тождество» выражает одинаковое в вещах — это «ноль» различия. Тогда как понятие «различное», из которого шаг за шагом извлекаются все сравнительные понятия от самого простого до самого сложного, аналогично арифметическому понятию «много».

Дети убеждаются, что все сравнительные понятия строго упорядочены. После нулевой ступени, которая обусловлена двумя предельными отношениями — «Тождественное» и «Различное», обусловливающих рассудочное мышление, расположена первая ступень. На ней находится тоже два понятия «Соотнесенное» и «Противоположное». При дальнейшем ранжировании понятий, на второй ступени располагают «Ортогональное 1» Пифагора и «Ортогональное 2» Гераклита. На более высоких ступенях находятся «Дополнительное» и «Подобное», знакомство с которыми начинается после того, как дети познакомятся с принципом дополнительности Н. Бора в связи с интерпретацией квантовой механики.

Отношения между сравнительными понятиями и наполнение их смыслом раскрываются постепенно, по мере перехода от одних тем математики (а в старших классах, и физики) к другим. В результате школьники должны усвоить, что каждое последующее сравнительное понятие верхнего и нижнего ряда имплицитно, т.е. неявно, скрытно содержит в себе все предшествующие ему сравнительные понятия. А поскольку натуральный ряд сравнительных понятий не завершен, то детям, которые пожелают быть первопроходцами в физике, математике или философии (в их будущей взрослой жизни), предоставляется возможность совершить каждому свое открытие.

Как по ступеням наука и далее будет подниматься от познания тождественности вещей к постижению все более далекого их родства, а, значит, — к освоению все более полных теоретических моделей, отражающих гармонию и разумность мироздания.

Наконец, дети научатся понимать, что разум расчленяет знание о мире на части, поскольку осмысливает расколотую по свойствам реальность на множество конкретно-научных сравнительных понятий. Мудрость, напротив, собирает знание в научно обоснованную целостную картину, поскольку в качестве начал познания использует сугубо научные конкретно-всеобщие сравнительные понятия.

7. Формула мудрости

Рассмотрим электронную модель, посредством которой проводим демаркацию между рассудком, двумя формами разума и мудрости. Эта модель предназначена для того, чтобы научить детей думать сравнительными понятиями. Взрослые пока тоже так думать не могут. Поэтому и учителям и родителям нужно освоить предлагаемый метод.

Для этого активизируем программу. В результате на экране компьютера появляется модель устройства:

Щелкнув мышью в окне «Тождественное» вызываем появление двух стрелок, указывающих направление пошагового восхождения от абстрактного тождества к окошку «Различное», расположенному в самой верхней части большого окна.

Продолжая щелкать мышью снизу вверх в свободном пространстве между окошками «Тождественное» и «Различное» пошагово заполняем устройство двумя параллельными рядами сравнительных понятий»:

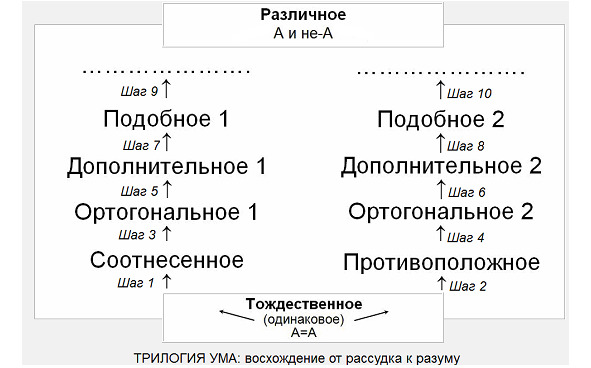
Вставляя и убирая понятия, мы шаг за шагом формируем структуру мышления обучаемых, которая включает три логических направления:

— формальную логику, исходной мыслительной парадигмой которой является понятие «противоречащее». Его стороны выражают абстрактное, бесконечное различие, поэтому в электронной модели они отстоят друг от друга на максимальном расстоянии. Это направление обусловливает возникновение классификационных понятий обычного разговорного языка, речи и рассудочного мышления;

— метафизическую логику конкретных наук, исходной парадигмой которых является понятие «Соотнесенное», на основе которого возникает счет, арифметика и другие разделы математики;

— диалектическую логику, исходной парадигмой которой является понятие «Противоположное», понимаемое не иначе, как в аристотелевском смысле. То есть как «избыток» и «недостаток» относительно «промежуточного» положения.

Хочу обратить внимание на то обстоятельство, что полезная модель создавалась на основе конкретно-научных сравнительных понятий разных видов находящихся в сфере разумного мышления. Но эта же модель используется и для осмысления мудрости, как знания общего. Поэтому в первом случае мы имеем в виду конкретно-научные сравнительные понятия. Тогда как во втором — аналогичные им конкретно-всеобщие сравнительные понятия, поскольку общее не существует отдельно от единичного.

Причем понятия левого и правого ряда ступеней отражают два равнозначных вида мышления: конкретно-научное метафизическое разумное мышление (М) и конкретно-научное диалектическое разумное мышление (Д). Выходит, что Ум представляет собой совокупность рассудка и двух форм разума:

Иначе формулу мудрости как структуру мышления (СМ) в первом приближении можно записать так:

СМ = Р + (М№ + Д№)

где Р — рассудок, М — метафизический разум, Д — диалектический разум, № — номер освоенных школьником ступеней (0—4).

Например, ученик освоил понятие «соотнесенное» и арифметику, но не ознакомлен с понятием «противоположное». Структура его мышления СМ = Р + (М1 + Д0).

В итоге все мышление подразделяется нами на три взаимосвязанные логические части, каждая из которых обусловлена преимущественным использованием трех типов понятийных средств. Еще раз их напомню:

— Рассудочное мышление — это мышление классификационными понятиями на основе отношений «абстрактного тождества» и «абстрактного различия», обусловливающих закон непротиворечия: либо А, либо не-А.

— Разумное конкретно-научное метафизическое мышление — это мышление классификационными, конкретно-научными сравнительными и количественными понятиями на основе отношения «соотнесенное» и других, следующих за ним понятий левого ряда ступеней, а также множеством изучаемых в школе математических и физических абстракций разной сложности.

— Разумное конкретно-научное диалектическое мышление — это мышление классификационными и конкретно-научными сравнительными понятиями на основе отношения «противоположное» и других, следующих за ним конкретно-всеобщих понятий, позволяющих осмысливать процессы, происходящие не только в природе, но и в обществе.

Выходит, что разумное мышление конкретно-научными сравнительными понятиями разных видов лежит в основе философского мышления — мудрости. Поэтому и о философском мышлении мы говорим как о метафизическом и диалектическом мышлении.

Итак: операция «сравнение» — это главная операция мышления. Она задает восходящее движение всему познанию, обусловливая собой существование некой универсальной парадигмы: трилогии ума, показанной на Схемах 1, 2, 3 и задающей совокупность трех логических направлений, объединенных общей идеей сравнения.

Первое направление — это формальная логика, исходной мыслительной парадигмой которой является понятие «противоречащего». Его стороны выражают абстрактное, бесконечное различие, поэтому в универсальной парадигме познания они отстоят друг от друга на максимальном расстоянии, обусловливая начало и конец натурального ряда сравнительных понятий.

Второе направление — логика конкретных наук, исходной парадигмой которой является понятие «соотнесенного».

Третье направление — диалектика, исходной парадигмой которой является понятие «противоположного», понимаемого не иначе, как избыток и недостаток относительно промежуточного, т.е. в аристотелевском смысле.

Каждая логика определяется своим, только ей присущим началом, задающим объективную точку зрения для осмысления реальности. При этом рассудок разводит абстрактные различия А и не-А, не допуская их совмещения в одном и том же отношении: либо А, либо не-А. Разум же, напротив, схватывает конкретные различия в единстве, поскольку одна сторона «соотнесенного» или «противоположного» как и других сравнительных понятий не может существовать без другой стороны. Причем все сказанное наиболее удобно демонстрировать в классе при помощи электронной полезной модели «Трилогия ума: восхождение от рассудка к разуму».

Следует сказать, что развитие философской мысли изначально было направлено на различение не трех, как в нашем случае, а двух составляющих мышления — рассудочную и разумную. Так, у Аристо­теля мы находим размышление о созерцательном и активном разуме, символизирующее зарождение категорий рассудка и разума. Тогда как у Николая Кузанского (1401 — 1464) — философа эпохи Возрождения, расчленение мышления стремится пойти дальше, поскольку Н. Кузанский довольно четко противопоставил рассудок более высокой ступени — уму, или интеллекту. Рассудок оформляет данные чувств, различает, разделяет, а ум стоит над рассудком, придавая законченность результатам его более высокой дея­тельности. Отсюда следует восхождение человеческого познания: от чувств — к рассудку и далее — к уму (или интеллекту).

Другой философ возрождения Джордано Бруно (1548 — 1600) признавал те же ступени познания, что и Н. Кузанский: чувства, рассудок, разум (интеллект). По Бруно только разум доходит до познания совпадения противоположностей. Поэтому тот,

«кто хочет познать наибольшие тайны природы, пусть рассматривает и наблюдает максимумы противоречий и противоположностей».

Таким образом, Аристотель, Н. Кузанский и Д. Бруно, хотя и по-разному, отделили мышление от чувств, и поставили вопрос о расчленении самого мышления на две качественно различающиеся ступени, выясняя функцию каждой в достижении истины.

В последующем в немецкой классической философии эти две ступени мышления стали обозначаться как рассудок и разум.

«Всякое наше знание, — писал Кант, — начинается благодаря чув­ствам, переходит затем к рассудку и заканчивается в разуме, который представляет собою в нас высшую инстан­цию для обработки материала наглядных представлений и для подведения его под высшее единство мышления».

И хотя разделение рассудка и разума у Канта выражено наиболее рельефно, нежели у всех его предшественников, все равно и само это разделение, как и понимание того, чем определяется рассудочное и разумное мышление, носит у него рассудочный характер.

Следующий шаг в понимании рассудка и разума был сделан Гегелем, который рассудок связывает с метафизическим мышлением, а разум — с диалектическим мышлением. Видимо так же понимали различение рассудка и разума классики марксизма, поскольку Ф. Энгельс признавал, что

«гегелев­ское различение, согласно которому только диалектическое мышление разумно, имеет известный смысл».

С точки зрения диалектического материализма, как отмечает энциклопедия, «процесс развития теоретического мышления предполагает взаимосвязь рассудка и разума. С рассудком связана способность строго оперировать понятиями, правильно классифицировать факты и явления, приводить знания в определенную систему. Опи­раясь на рассудок, разум выступает как творческая познавательная деятельность, раскрывающая сущность действи­тельности. Посредством разума мышление синтезирует результаты познания, создаёт новые идеи, выходящие за пределы сложившихся систем знания».

Во всех приведенных выше философских учениях разделение рассудка и разума не выходит за пределы рассудочного мышления, т.к. не проводит четкой демаркации между этими составляющими ума.

Мы же в зависимости от использования в мышлении, имеющем принципиально понятийный характер, различных языковых средств, выделяем трехступенчатую структуру ума: рассудок, разум и мудрость.

Рассудок (рассудочное мышление) определяется использованием классификационных понятий.

Разум (разумное мышление) помимо классификационных понятий использует конкретно-научные сравнительные понятия разных видов, числа и другие математические абстракции.

Мудрость (философское мышление) возвышается над разумным мышлением благодаря тому, что использует конкретно-всеобщие сравнительные понятия, собранные в один натуральный ряд, определяющий единство мира.

При этом учителя и опекаемые ими и дети, должны усвоить, что ментальными лифтами, поднимающими мышление от рассудка на уровень разума и мудрости являются выделенные нами конкретно-научные и конкретно-всеобщие сравнительные понятия.

II. Идеи ранней греческой философии как основа умственного развития детей

Хронологически история античной философии охватывает период свыше 1000 лет, с 6 в. до н. э. по 6 в. н. э. Условная дата начала древнегреческой философии — 585 год до н. э., когда мудрец из Милета — Фалес предсказал солнечное затмение. А условная заключительная дата — 529 год н. э., когда эдиктом христианского императора Юстиниана была закрыта Платоновская Академия в Афинах.

Самым интересным для школьного образования был ранний этап греческой философии — это исторически первая форма европейской теоретической мысли, которая должна была стать основой развития и культурным горизонтом для всех последующих форм мышления, возникавших в рамках интеллектуального пространства средневековой, новой и современной Европы. К сожалению, так не стало.

Поэтому этот раздел книги предназначен для поиска и использования в общеобразовательной школе наиболее важных идей античной философии. В нем не рассматриваются многие философские течения этого периода, поскольку основное внимание направлено на исследование мышления в пределах трех его типов:

— конкретно действенного;

— конкретно-образного;

— понятийного.

Что касается понятийного мышления, то мы довольно подробно его рассмотрели выше, выявив восхождение от рассудочного мышления к разуму и мудрости, в зависимости от использования в мыслительном процессе четырех групп понятий: классификационных, количественных, конкретно-научных и конкретно-всеобщих сравнительных понятий разных видов.

Поэтому нам остается рассмотреть конкретно-действенное и конкретно-образное мышление в их тесном переплетении с понятийным мышлением того времени, т.е. в самый ранний период их зарождения в Древней Греции. Иначе говоря, речь пойдет о единстве трех типов мышления и значении этого единства в формировании нового канона образования, в подготовке новых поколений к будущей интеллектуальной и осмысленной нравственной жизни.

1. Зарождение диалектического разума: мир как процесс

Мышление — это психический процесс познания закономерностей окружающего мира и дети с ранних лет должны обратить внимание на то, что окружающая их природа находится в постоянном изменении. День сменяется ночью, зима сменяется летом. Вода в реке тоже не стоит на месте, а куда-то все время спешит. Да и сам человек не находится в бездействии. Что движет миром и возможно ли это познать?

Конечно же, ученикам начальной школы, да и детям постарше пока не дано постичь причину этих изменений. Но освоить самые простые процессы школьник уже способен.

Особый интерес в этой связи представляет поэма Гесиода (VIII — VII века до н. э.) «Труды и дни», являющаяся одним из основных предфилософских источников древнегреческой философии. Детям не обязательно читать эту поэму, но им не мешало бы знать, что именно в ней идет осмысление двух диаметрально противоположных процессов, протекающих как в природном, так и в социальном мире, которые Гесиод обозначает двумя понятиями: «дике» и «адике».

«Адикия» — характеризует процесс декомпенсации, в результате которого из некой промежуточной основы возникают противоположности «избытка» и «недостатка». Например, я занимаю или вымогаю у Вас десять монет. В результате находящиеся в руках богини правосудия Дике «весы» выходят из равновесия, показывая, что мой карман стал тяжелее на десять монет, а Ваш — на десять монет легче.

Этот процесс — «адике» отождествляется Гесиодом с заведомо несправедливым делом, которое противопоставлено процессу компенсации — «дике», т.е. уничтожению противоположностей в промежуточное состояние, обусловливающее справедливость и порядок человеческой жизни. Ибо установленные Зевсом законы требуют добровольно вернуть долг или то, что изъято силой, либо обманом. В противном случае, Вы обращаетесь к богине, и она устанавливает справедливость. И тогда «весы» приходят в равновесие.

Дике (ударения на и) в древнегреческой мифологии — это богиня справедливости и кругового мирового порядка, одна из трех Ор, богинь времен года. Она — дочь Зевса и Фемиды, хранительница ключей от ворот, через которые, чередуясь, проходят день и ночь. С весами в руках и с повязкой на глазах она облетает землю, измеряя справедливые и несправедливее поступки людей, и рассказывает о них Зевсу. За то, что люди не соблюдают установленных Зевсом законов, он жестоко их наказывает.

Благодаря идеализациям «дике» и «адике», «справедливости» и «несправедливости» во всех их оттенках, Гесиод осмысливает не только судебный процесс или другие отношения между людьми, но и природный порядок.

Сказанное выше позволяет рассмотреть одно из наших действий, положим, взятие нами в долг 10 монет. Тогда образ весов — это тот образ, при помощи которого мы сможет осмысливать рассматриваемое нами действие. Завершает единство трех типов мышления понятие «противоположности», отражающее саму суть действия, его энергетику. Из этого примера можно увидеть, что только сравнительные понятия разных видов обусловливают единство трех типов мышления: действенного, образного и понятийного.

Дети с легкостью воспринимают подобные процессы, особенно при условии, что их объясняют при помощи одного из наглядных пособий — рычажных весов, стрелки которых в одном случае приходят в положение равновесия (сходящееся), в другом случае — входят из него (расходящееся), как это показано на рисунках 7 и 8.

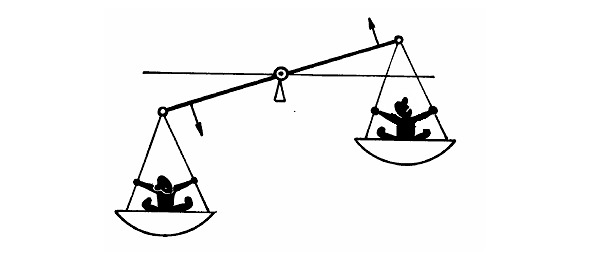
Кроме того, процессы компенсации и декомпенсации можно продемонстрировать детям на примере сообщающихся сосудов, т.е. соединенных между собой двух мерных пробирок.

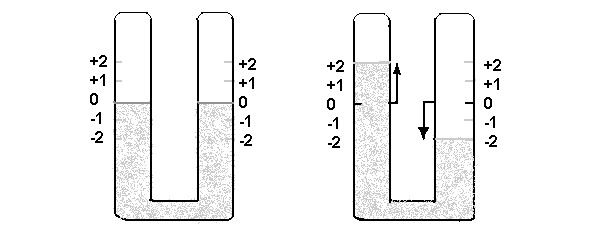
Налив воду до срединной, нулевой отметки в сосудах, мы при помощи резиновой груши или ртом изменяем величину столба жидкости. В результате в одной из пробирок столб жидкости поднимется на n-е число градаций (+N), а в другой пробирке — опустится на такое же число градаций (-N). Это — декомпенсация или адикия. Противоположный процесс — компенсация (дике), обусловлен возвращением жидкости в пробирках к нулевому уровню.

Кроме того, процесс компенсации, т.е. переход в промежуточное состояние можно продемонстрировать детям, если смешивать в одном сосуде две одинаковые порции воды, имеющей различную температуру. Для этого надо взять два градуированных стакана с одинаковым количеством воды разной температуры в каждом. Замерив температуру в стаканах, нужно перелить воду из одного стакана в другой и зафиксировать результат.

Например, в одном стакане температура воды была 20 градусов Цельсия, а в другом, подогретом — 40 градусов. Вопрос напрашивается сам собой: какая температура воды будет в стакане после смешивания? И такая задача имеет множество вариантов, которые будут возникать в результате опытов.

Чтобы постоянно помнить о наиболее важном законе природы, а также о том, что люди должны соблюдать справедливость, одно из зодиакальных созвездий еще в древности было названо «Созвездие Весов».