
Бесплатный фрагмент - Математика: история возникновения, становления и современные пути развития
Том 1
Математика: история возникновения, становления и современные пути развития
Аннотация: в данной книге предлагается уникальное путешествие сквозь многовековую историю математики, которое охватывает её зарождение в древних цивилизациях и проходит через ключевые этапы становления, ведущие к современным научным парадигмам. Автор исследует богатое наследие математических идей, прослеживая их эволюцию от Древнего Египта и Вавилона до выдающихся открытий учёных XVI — XVII веков, таких как Рене Декарт, Исаак Ньютон и Лейбниц, а также влияние математических теорий на развитие естественных и социальных наук.
Книга включает детализированные очерки о жизненном пути и открытиях великих математиков разных эпох, связывая их личные достижения с более широкими историческими контекстами и культурными изменениями. Отдельные разделы сосредоточены на возникновении и усовершенствовании основополагающих понятий и разделов математики, таких как алгебра, геометрия, анализ и теория вероятностей.
Особое внимание уделяется современным направлениям и вызовам, с которыми сталкивается математика в XXI веке, включая новые технологии, компьютерные модели и многомерное мышление. Книга содержит множество задач и упражнений, ориентированных на различные исторические эпохи и системы, что позволит читателю не только освоить теоретические аспекты, но и применить полученные знания на практике.
«Математика: история возникновения, становления и современные пути развития» предназначена для студентов, преподавателей, а также всех, кто интересуется удивительным и порой мистическим миром чисел и форм. Эта книга станет надежным путеводителем для тех, кто хочет постичь не только алгоритмы и формулы, но и глубинный смысл и красоту математической науки на протяжении всей её истории. Но исторический материал по математики настолько обширный, поэтому вряд ли можно его уместить в одном томе, а связи с чем первый том книги у нас будет посвящён исключительно и в основном Древнему периоду истории математики с отсылкой на результаты его развития в современной математической теории и практике.
Предисловие
Дорогие читатели!
Перед вами книга, которая станет ваших проводником в страну, где соединяются математика и история, прошлое и будущее, идеи и их воплощение. «Математика: история возникновения, становления и современные пути развития» — это не просто сочинение, это своеобразный магический свод о числах, формах и закономерностях, которые в течение веков пробуждали воображение и изменяли судьбы целых обществ.
Вдохновленная трудами выдающихся ученых прошлого и современности, данная книга погружает вас в безбрежный океан математических идей, от древних цивилизаций до самых современных научных открытий. Мы вместе пройдем путь от первых навыков счета пещерного человека до виртуозных аккордов высшей математики, которые формируют цифровую эпоху. Вы сможете увидеть, как математика не просто может быть точной наукой, но и искусством, пронизанным философией, экономикой, геополитикой, и как она обретала свою форму под влиянием человечества и его культурных контекстов.
В последние десятилетия преподавание математики (РМ) активно развивается и приобретает статус самостоятельной научной области в рамках гуманитарных наук. В настоящем исследовании мы вслед за греческим учёным-математиком стремимся предложить целостный подход к этой области, обращаясь к эпистемологическим вопросам, которые формируют ее фундамент.
Эти вопросы включают:
1. Какова природа знаний, которые мы стремимся и можем получить о процессах изучения и преподавания математики?
2. Как эти знания усваиваются и становятся достоверными?
3. Какие правила и критерии оценки исследований приняты в научном сообществе?
4. Какие эпистемологические предпосылки лежат в основе этих правил и критериев?
Эти вопросы были рассмотрены на примере трех научных исследований, представленных в РМ: позитивистского, интерпретативного и критического подходов. На текущем этапе развития РМ, по-видимому, преобладает критический взгляд на поиск истины.
В этом исследовании мы стремимся к поиску трансцендентальных истин о явлениях и стремимся к непредвзятости и объективности. Мы применяем разнообразные интерпретационные подходы, принимаем множество теорий, руководствуемся установленными правилами и критериями. Мы считаем, что такое исследование может служить убедительным аргументом. Создание первых международных журналов, таких как ESM (Educational Studies in Mathematics), ZDM (Central Journal for Didactics of Mathematics), JRME (Journal of Research in Mathematical Education), ICME (International Congress on Mathematical Education) и PME (International Group for Psychology of Mathematical Education), посвящённых проблемам математического образования, можно считать началом развития преподавания математики (RM) как структурированной области исследований. Эта область существует уже четыре десятилетия, с конца 60-х годов (хотя её корни уходят гораздо глубже).
В качестве исследовательской дисциплины, RM черпает идеи, перспективы и методологии из различных научных сфер, таких как математика, философия, эпистемология, психология, когнитивные науки, информатика, история, социология и других. Эти знания помогают в изучении процессов изучения и преподавания математики.
Объединение различных точек зрения и их интеграция считаются необходимыми в силу сложности изучаемых явлений и уникальных характеристик математики как предмета изучения.
До 1970-х годов в рамках дисциплины RM основное внимание уделялось разработке методологий, основанных на позитивном опыте эмпирических наук, где доминируют количественные методы исследования. В условиях поведенческого контекста на ранних этапах развития фирмы наиболее подходящими методами считались измерения с помощью тестов, экспериментальные методы для проверки гипотез и статистическая обработка данных.
Однако с 1980-х годов и особенно быстро в 1990-е годы исследования в области РМ начали приобретать иной характер. Особое влияние оказали конструктивизм и перспективы когнитивной психологии, что привело к соответствующему изменению методов исследования. Акцент был смещен на мысленные процессы, осуществляемые студентами, что потребовало проведения клинических собеседований, наблюдений и длительного изучения.
Тематические исследования и другие качественные методы сбора и анализа информации.
Передача данных. Этот процесс ускорился и приобрёл новые формы с появлением. В центре внимания оказались социальные и культурные условия обучения студентов, а также взаимодействие между учащимися на уроках математики. Теория обучения, основанная на идеях социокультурного подхода (с опорой на труды Выготского), а затем и на концепции обучения на месте (Саконидис, 2007), стала основополагающей.
Для изучения важности математики и особенностей ее изучения в различных культурных, профессиональных и других контекстах начали применять этнографические методы и совместное наблюдение. Кроме того, переход к изучению математики в классе, а также улучшение преподавания и профессионального развития учителей создали основу для развития исследовательской деятельности и формирования исследовательских сообществ практиков, в которых преподаватели и исследователи работают вместе.
Однако не все проходило гладко. Килпатрик (1992) отмечает, что в конце 70-х годов в образовательных исследованиях наблюдался кризис, и появились разговоры о «фундаментальном сдвиге парадигмы». «Смена парадигмы» подразумевает…
В 80-е и 90-е годы активно обсуждались количественно-качественные методы, что привело к появлению качественных методов исследования наряду с количественными и к возникновению интерпретативной парадигмы.
Можно сказать, что акцент смещался с предмета (математика) на человека (психология), а затем на контекст (социология), что отразилось на используемых методах в RM.
В конце XX века наблюдался стремительный рост оптики, теорий и технологических методов. С одной стороны, это, несомненно, было положительным моментом: область, освободившаяся от парадигматических и теоретических ограничений начала века, наполнилась энергией и энтузиазмом. Необходимо начать задавать сложные вопросы о теории и методах, которые помогут нам двигаться вперед. (Шенфельд, 2002)
Эпистемологические вопросы являются важными в контексте целостного подхода к ИТ как к зрелой научной дисциплине, наравне с другими науками.
Во-вторых, многие исследователи иногда склонны отходить от этих вопросов или игнорировать их под давлением практических результатов исследований.
Мы считаем, что поиск ответов на эпистемологические вопросы должен быть основан, с одной стороны, на исследовательской практике в этой области — на том, что делают ученые, — а с другой стороны, на более широких эпистемологических теориях и подходах.
Наше исследование представляет собой обзор литературы, в котором рассматриваются ответы исследователей космоса на эпистемологические вопросы, и мы стремимся объединить эти взгляды в рамках более общего эпистемологического подхода. Для первобытного человека понятие числа как меры размера или количества окружающих предметов, безусловно, было одним из самых важных математических достижений. На протяжении веков, особенно после 3-го тысячелетия до нашей эры, математика, сначала как эмпирическое знание, а затем как наука, играла важную роль в истории человеческого интеллекта.
Отправной точкой и первыми шагами математики как науки принято считать период с 600 до 300 лет до нашей эры. Этот период стал неотъемлемой частью древнегреческой культуры.
Примерно в 600 году до нашей эры произошли исторические события: зарождение философской мысли и первые математические доказательства в школе Милет. А около 300 года до нашей эры Евклид представил научному сообществу одну из самых важных книг, когда-либо созданных в мире — «Элементы». Пожалуй, ни одна другая книга, кроме Библии, не выдержала такого количества переизданий.
Этот увлекательный исторический период был изучен многими исследователями.
Отличным отправным пунктом для понимания этой истории может стать начало второго тысячелетия до нашей эры. Именно тогда были обнаружены важные письменные памятники в ходе археологических раскопок в Месопотамии.
Тысячи глиняных табличек с клинописными рельефами были извлечены из земли, и примерно пятьсот из них оказались математическими. На них содержались различные числовые расчёты.
Одной из самых известных и часто фотографируемых табличек является знаменитая Плимптонская табличка 322, которая хранится в Колумбийском университете в США. Её содержание — пифагорейские триады чисел. Многие писатели и учёные в античной Греции описывали рождение философии, основой которой является математика, на побережье Ионии как «чудо».
Действительно, если посмотреть на стремительный прогресс математических исследований в последующие годы, по крайней мере, 600 лет назад, термин «чудо», вероятно, отражал реальность. Однако, как отмечают исследователи истории философии, трактовка этого явления как «чуда», то есть как чего-то необъяснимого и сверхъестественного, умаляет вклад греков в развитие человеческого интеллекта.
Вклад древних греков в развитие «мышления» заключается в поиске естественной логики и причин, которые не зависят от воли богов, в явлениях природы. Хотя это выходит за рамки моей научной компетенции, я считаю, что это заслуживает внимания.
Переход от царской власти к микенскому типу демократических городов и появление решающей роли гражданина стали ключевыми факторами. Устаревающие королевские заповеди и догматические, общепринятые мистические фразы религиозной церемонии были заменены противостоянием аргументов на рынке, в муниципалитете и перед толпой.
Таким образом, причина и убеждение, что божество, как всегда, занимает особое место в греческом пантеоне, обретают новый смысл и независимость в новых политических структурах.
Накопленные эмпирические знания стали как семена, которые упали на благодатную почву городов. С помощью мощного инструмента — языка — мы можем наблюдать, как эти знания приносят обильные плоды. Это настоящее чудо!
Особое внимание уделено тому, как социокультурные и экономические факторы сплетаются воедино, чтобы дать толчок для величайших открытий — как необходимость ведения торговли и исследовательская жажда побуждали человечество прояснять сложные математические концепции. Истории гениев, от Архимеда до Гаусса, и от Гёте до Эдисона, станут живыми и яркими перед вашими глазами, а их идеи смогут вдохновить нас на новые свершения.
Но не только великие умы займут ваше внимание; мы заглянем и в будни математиков, чьи незаметные идеи обогатили наше понимание чисел и форм. Их жизнь, как сплетение нитей, переплетает математику с живым опытом человечества, подчеркивая, что за каждой формулой стоит целая история страстной борьбы за знание.
Этот труд призван поднять занавес над загадочным и чарующим миром математики, где каждый параграф полон света открытий и тени недоумений. Мы часто забываем о том, что математика — это не только числа и уравнения; это любовь, разочарование, усилия и надежды на лучшее будущее, собранные в единое целое.
Пусть эта книга станет вашим спутником в исследовании увлекательной истории математики, наглядно открывающей перед вами необъятный космос идей, позволяя задуматься о том, как дальше развивать эту великую науку, проникая в самые глубокие ее тайны. Откройте ее страницы, и путь, который вы предпримете туда, превратится в захватывающее приключение, полное магии и колдовства знаний!
С уважением,
Ершов Денис Иванович, автор книги «Математика: история возникновения, становления и современные пути развития».
Введение
Введение к книге «Математика: история возникновения, становления и современные пути развития»
Математика — это не просто набор абстрактных правил и формул, а живой процесс, история которого переплетается с развитием цивилизации. В книге «Математика: история возникновения, становления и современные пути развития» мы предлагаем читателю увлекательное путешествие через века, где математические идеи и открытия освещают путь к современным достижениям науки и технологии.
История математики — это своего рода окно в культуру и мышление людей разных эпох и народов. В этой книге мы стремимся рассмотреть не только хронологию математических теорий, но и контекст их возникновения, что позволит лучше понять глубокую взаимосвязь между математикой и другими научными дисциплинами, философией и искусством. Мы уверены, что глубокое понимание истории математики способствует гуманизации образования, делает процесс обучения более увлекательным и значимым для каждого студента.
Перед нами стоит задача внедрить историко-генетический метод, который позволяет показывать, как математика развивалась, каких результатов достигли учёные, и как эти результаты формируют наш сегодняшний взгляд на математические дисциплины. Мы проанализируем эволюцию таких понятий, как число, геометрическая фигура, функция и вероятность, соединяя их с ключевыми событиями и фигурами, открывавшими новые горизонты знаний.
Книга содержит множество справочных материалов и задач, которые помогают сделать исторический контекст доступным и увлекательным. Мы рассмотрим работы выдающихся математиков, от древнегреческих и древневосточных философов и математиков до современных исследователей, и покажем их вклад в развитие теории и практики математики. Также мы уделим внимание вместе с тем воспитанию интереса у студентов к математике как к искусству решения задач и поиска логических связей. История математики — это увлекательная область исследований, которая охватывает изучение происхождения математики и, в меньшей степени, математических методов, существовавших в прошлом.
До начала современной эры, когда знания распространялись по всему миру, новые математические достижения появлялись в письменной форме очень быстро. Среди самых древних доступных нам математических текстов можно выделить «Плимптон 322» (Вавилонская математика, 1900 год до н. э.), Математический папирус Рида (математика египтян, 2000—1800 годы до н. э.) и Московский математический папирус (математика египтян, 1890 год до н. э.). Московский математический папирус, также известный как «математический папирус Голенищева», представляет собой древнеегипетский документ, который был создан в период правления 13-й династии, примерно в 1850 году до нашей эры. Он был обнаружен в Фивах в 1892 или 1893 году Владимиром Голенищевым, известным египтологом, который впоследствии приобрел этот ценный артефакт для своего собрания. С тех пор папирус хранится в Государственном музее изобразительных искусств имени Пушкина в Москве, где он остается и по сей день.
Согласно палеографическому анализу и особенностям написания текста, который выполнен иератическим шрифтом, наиболее вероятно, что этот документ был создан на основе более ранних материалов, относящихся к 12-й династии. Его размеры составляют около 5,5 метров в длину и ширину от 3,8 до 7,6 сантиметров. Содержимое папируса разделено на 25 отдельных фрагментов.
Проблемы с решениями, предложенные советским востоковедом Василием Струве в 1930 году, стали основой для Московского папируса — известного математического памятника, который, наряду с математическим папирусом Райда, занимает важное место в истории математики. Московский папирус является более древним, а папирус Райда — более крупным из них.
## Упражнения из Московского папируса
Задачи в Московском папирусе не следуют строгому порядку, а решения содержат меньше деталей по сравнению с папирусом Райда. Однако, несмотря на это, Московский папирус известен своими геометрическими задачами. В задачах 10 и 14 вычисляются площадь поверхности и объем отрезка в виде куба соответственно. Остальные задачи являются более или менее распространенными.
## Проблемы с длиной судовых деталей
Задачи 2 и 3 посвящены вычислению длины частей судна. В первой из них определяется длина руля, а во второй — длина мачты корабля, которая является самой длинной на судне. Длина мачты составляет
1/3+1/5 от длины кедровой доски длиной 30локтей.
Все эти тексты посвящены так называемой теореме Пифагора, которая, вероятно, является самым древним и наиболее широко используемым открытием после арифметики и геометрии. Истоки математического мышления уходят своими корнями в понимание чисел, размеров и форм. Современные исследования когнитивных способностей животных показывают, что эти концепции являются неотъемлемой частью жизни не только человека, но и других живых существ. В доисторических обществах охотников-собирателей эти понятия были неотъемлемой частью повседневной жизни.
Со временем представление о числах эволюционировало. Это подтверждается тем, что в некоторых языках сохраняется различие между «один», «два» и «много», но не между числами, превышающими два.
Самым ранним известным математическим объектом являются кости Лебомбо, обнаруженные в горном массиве Лебомбо в Свазиленде и датируемые примерно 35 000 годом до нашей эры. Этот артефакт представляет собой 29 глубоких насечек на малоберцовой кости бабуина. Другие доисторические находки, обнаруженные в Африке и Франции в период между 35 000 и 20 000 годами до нашей эры, указывают на первые попытки количественной оценки времени.
Кость Исанго, обнаруженная у истоков реки Нил на северо-востоке Конго, датируется 20 000 годами до нашей эры. Она представляет собой три колонны выгравированных линий, которые проходят вдоль кости.
Существует две основные интерпретации этого древнего артефакта:
1. Возможно, кость Исанго содержит самую раннюю известную демонстрацию последовательности простых чисел.
2. Или же она может служить изображением полугодового лунного календаря.
В своей книге «Как развивалась математика: первые 50 000 лет» Питер Рудман утверждает, что концепция простых чисел могла возникнуть относительно недавно, примерно через 10 000 лет после появления концепции деления, которая датируется 10 000 годом до нашей эры. По его мнению, простые числа, вероятно, не были полностью осознаны примерно до 500 года до нашей эры.
Он также пишет, что «не было предпринято никаких попыток объяснить, почему соответствие чего-либо должно быть кратно 2, простым числам от 10 до 20 и некоторым числам, которые почти кратны 10».. Ученый Александр Маршак предполагает, что кость Исанго могла повлиять на дальнейшее развитие математики в Египте. Как и некоторые элементы кости Исанго, египетская арифметика также использовала умножение на 2. Однако эта гипотеза остается предметом споров.
В додинастический период истории Египта, который относится к пятому тысячелетию до нашей эры, были найдены наглядные геометрические узоры. Также утверждалось, что мегалитические памятники в Англии и Шотландии, датируемые третьим тысячелетием до нашей эры, включают в свой дизайн геометрические идеи, такие как круги, эллипсы и пифагорейские триады.
Несмотря на эти предположения, все они оспариваются. В настоящее время самое раннее бесспорное использование математики зафиксировано в вавилонских и египетских источниках династического периода. Это означает, что с момента достижения поведенческой и лингвистической эволюции человеку потребовалось по меньшей мере 45 000 лет, чтобы развить математику в том виде, в каком она существует сегодня.
История математики как науки началась в VI веке до нашей эры с пифагорейцев. Они ввели в обиход термин «математика», образованный от древнегреческого слова «урок», что означает предмет обучения.
Древнегреческие математики значительно продвинули методы, введя дедуктивные рассуждения, математическую валентность и доказательства. Они также расширили программу обучения математике.
Китайские математики внесли свой вклад в науку на ранних этапах, в том числе в разработку системы ценностей.
Сегодня мы используем цифры 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, которые пришли к нам из Индии. Они получили название арабских цифр, так как стали известны в Европе благодаря арабам. Правила представления этих цифр в десятичной системе счисления, вероятно, развивались в течение первого тысячелетия нашей эры. В Индии математика достигла своего расцвета и была передана на Запад благодаря усилиям арабских математиков. Эти учёные значительно развили и обогатили математику, которая стала известна в их культуре. Многие известные греческие и арабские математические тексты были переведены на латынь, что способствовало дальнейшему развитию математики в средневековой Европе.
С древних времён и в Средние века за эпохами расцвета математического творчества часто следовали периоды застоя. Однако в эпоху раннего итальянского Возрождения, в 16 веке, новые математические достижения стали появляться всё более быстрыми темпами, взаимодействуя с новыми научными открытиями. Этот процесс продолжается и по сей день.
Введение в историю математики в школе и вузе — это важный аспект подготовки будущих учителей, поскольку знание истории своего предмета помогает строить более качественный и эффективный учебный процесс. Мы будем исследовать различные подходы к преподаванию, их преимущества и недостатки, что в конечном итоге поможет будущим педагогам внедрить элементы истории на уроках математики.
Среди целей использования истории математики мы выделим следующие: формирование у учащихся научного мировоззрения, развитие познавательного интереса, углубление понимания изучаемого материала и подготовка к междисциплинарным связям. Методический аппарат книги предполагает использование различных форматов изучения исторического материала: от кратких экскурсий и обсуждений до углублённых тем, что позволяет интегрировать теорию с практическими примерами.
Мы надеемся, что каждая страница этой книги станет для читателя не только источником знаний, но и стимулом к размышлениям, стремлением узнать больше о той математической науке, что меняет мир и способствует его развитию. Данная книга адресована как студентам и преподавателям, так и всем, кто хочет осознать богатство и многообразие истории математики и открытий, которые продолжают формировать наше понимание чисел и форм.
Пусть путешествие по страницам этой книги вдохновит вас, откроет новые горизонты и позволит по-новому взглянуть на мир с точки зрения математики!
Упражнение №1: Тестовые задания по теме «Введение к книге „Математика: история возникновения, становления и современные пути развития“»
Каждый вариант включает контрольные вопросы для самопроверки, а также задания разной степени сложности для студентов с различным уровнем подготовки.
Вариант 1: Лёгкие тестовые задания (для слабых учащихся)
Контрольные вопросы:
Какое слово происходило от греческого слова «математика»?
а) Наука
б) Урок
в) Знание
г) Исследование
Кто из математиков в VI веке до нашей эры считается основателем науки математики?
а) Архимед
б) Пифагор
в) Евклид
г) Ньютон
Какую систему счисления использовали римляне?
а) Десятичную
б) Двоичную
в) Римскую
г) Шестнадцатеричную
Задания на соответствие:
Соедините математические объекты с их описаниями:
1) Кость Лебомбо
2) Индийская система
3) Теорема Пифагора
4) Математический папирус Рида
а) Древний текст о арифметике
б) Метод деления на 2
в) Один из древнейших математических артефактов
г) Основное правило геометрии
Вариант 2: Средние тестовые задания (для средних учащихся)
Контрольные вопросы:
Назовите три основные цели использования истории математики в образовательном процессе.
Какое преимущество имеет индийская позиционная десятичная система по сравнению с римской нумерацией?
а) Возможность представления отрицательных чисел
б) Сложение и вычитание чисел
в) Легкость в произведении чисел
г) Представление нуля как отдельного числа
В каком виде были зафиксированы самые ранние математические достижения?
а) Устные традиции
б) Письменные тексты
в) Визуальные примеры
г) Уроки в школах
Практическое задание:
Найдите в учебнике примеры именных теорем, используемых в школьной геометрии и составьте краткие описания их значимости.
Вариант 3: Трудные тестовые задания (для сильных учащихся)
Контрольные вопросы:
Объясните, как историко-генетический метод влияет на преподавание математики. Приведите примеры.
Какие артефакты и тексты о математике были обнаружены и каковы их значимость для науки?
а) Плимптон 322
б) Московский математический папирус
в) Математический папирус Рида
г) Кость Исанго
В какие периоды истории количество математических открытий взаимодействовало с новыми научными открытиями и как это отразилось на развитии математики?
Творческое задание:
Исследуйте влияние арабских математиков на развитие математики в Европе и подготовьте небольшой доклад, в котором расскажете о наилучших примерах перевода греческих текстов и их влиянии на европейскую математику.
Вывод
Эти задания могут использоваться для самопроверки, в групповой работе и в качестве подготовки к экзаменам. Преподаватели могут адаптировать задания в зависимости от уровня успеваемости студентов и выбрать наиболее подходящие, чтобы обеспечить их активное участие в процессе изучения математики и её истории.
Глава 1 Теоретико-методологические основы формирования историко-математических знаний у обучающихся
Математика — одна из ключевых дисциплин школьного образования, обладающая огромным потенциалом для развития и воспитания молодого поколения. Многие известные исследователи и методисты, такие как В. В. Бобынин, Ф. Клейн, Н. И. Лобачевский, М. М. Мордухай-Болтовской, Д. Пойа, А. Пуанкаре, И. И. Чистяков и Л. Эйлер, подчеркивали целесообразность использования историко-математических и историко-методологических знаний в процессе обучения.
В связи с этим, учитель должен уметь формировать у учащихся ценностное отношение к математическим знаниям как к инструменту активной деятельности, а также представление о математике как о постоянно развивающейся и важной составляющей культуры человечества. Теоретической и методологической основой нашего учебного пособия стали общепризнанные теории и концепции отечественных педагогов и психологов, такие как:
— Теория развивающего обучения, разработанная Л. В. Занковым, В. В. Давыдовым и Б. Д. Элькониным.
— Учебники по математике для начальной школы, созданные авторами.
— Работы педагогов, таких как В. В. Бобынин, Г. И. Глейзер, И. Я. Депман и современные методисты Ю. А. Дробышев, А. В. Тихоненко и В. Ф. Ефимов. Эти авторы исследовали вопросы применения исторического материала в математическом образовании и предлагали знакомить детей с историей науки для более глубокого понимания её основ.
Современная концепция развития образования, в основе которой лежит идея гуманитаризации, ставит перед школой задачу стимулировать учащихся к созидательной деятельности. Это отражено в задачах, которые ставятся перед учителями: формировать не только предметные знания и умения, но и общекультурные, социально значимые навыки, необходимые для будущей профессиональной и практической деятельности.
Он должен обучать детей способам мыслительной деятельности и организовывать учебный процесс так, чтобы у учащихся формировалась потребность к самообразованию.; Для более глубокого понимания сущности конкретных понятий и всей дисциплины в целом необходимо учитывать логику их развития и практические потребности. Это, в свою очередь, способствует совершенствованию как учебно-познавательной, так и профессиональной деятельности.
История математики и методология историко-научного поиска представляют собой важный источник, позволяющий раскрыть гуманитарный потенциал содержания образования. Интегральная сущность этого потенциала дает возможность рассматривать науку как неотъемлемую часть человеческой культуры.
Современные ученые, такие как Н. Я. Виленкин, Г. Д. Глейзер, Б. В. Гнеденко, И. Д. Депман, А. Н. Колмогоров, К. А. Рыбников, Л. П. Шибасов и А. П. Юшкевич, также признают важность данного подхода.
В последние десятилетия проблема усиления исторической составляющей школьного математического образования стала предметом диссертационных исследований В. А. Алексеевой, О. В. Витченко, И. А. Михайловой, С. В. Носыревой, О. В. Шабановой и других авторов.
В публикациях, посвященных вопросам обучения математике, всё чаще встречается термин «историзация школьного математического образования». Как отмечает И. А. Михайлова, этот термин отражает процесс более глубокого и всестороннего внедрения в образование принципа историзма. Он подразумевает введение системы историко-математических, историко-методологических и исторических знаний, что создает условия для развития способностей учащихся.
Всё это, в свою очередь, требует от студентов математических факультетов педагогических вузов формирования соответствующих знаний и умений.
Анализ государственных образовательных стандартов и учебных программ, которые изучаются на математических факультетах педагогических вузов, показал, что историко-математические знания формируются в процессе освоения следующих дисциплин:
* История математики;
* Общая методика обучения математике;
* Математические дисциплины;
* Курсы по выбору: «Основы физико-математического исследования» и «Введение в математику».
Необходимость и возможные пути улучшения историко-математической подготовки учителей математики были рассмотрены в работах и исследованиях многих учёных, таких как С. В. Белобородова, Н. Я. Виленкин, О. В. Витченко, Б. В. Гнеденко, Ю. А. Дробышев, О. Б. Епишева, А. Л. Жохов, О. Н. Журавлёва, А. Н. Колмогоров, А. Е. Малых, И. И. Мерлина, Т. С. Полякова, М. В. Потоцкий, Ю. В. Романов, К. А. Рыбников, А. Е. Томилова, Т. Т. Фискович, Л. П. Шибасов, 3. Ф. Шибасова, А. П. Юшкевич и другие. Математическое образование — это проверенное временем средство интеллектуального развития, которое может быть использовано в условиях массового обучения. Успешное изучение математики способствует более лёгкому и эффективному освоению других учебных предметов. Математика является самой точной наукой из всех основных.
Многие учёные, писатели и музыканты подчеркивают величайшее значение математики в жизни общества. Например, наш современник, знаменитый физик и математик Александр Данилович Александров (1917–1999), сделал очень яркий и точный вывод о роли математики в современном мире: «Значение математики сейчас непрерывно растёт. В этой науке постоянно рождаются новые идеи и методы, что значительно расширяет сферу её применения. Сейчас уже невозможно найти область человеческой деятельности, где бы математика не играла важной роли. Она стала незаменимым инструментом во всех науках о природе, технике и обществознании. Даже юристы и историки активно используют математические методы в своей работе».. Как было отмечено ранее, значение математики было признано очень давно и в различных областях знаний, что свидетельствует о её огромной важности для человечества.
Использование исторических элементов в обучении математике стало предметом обсуждения ещё в конце XIX и начале XX века. Этот вопрос активно обсуждался на Всероссийских Съездах преподавателей математики. Одним из ярких сторонников применения исторических знаний в процессе обучения был Виктор Викторович Бобынин (1849 — 1919 гг.).
Его первым и одним из самых значимых достижений стал доклад «Философское, научное и педагогическое значение истории математики». В этом докладе он приходит к выводам, что:
1. Преподавание каждой науки должно осуществляться в том же направлении, что и её развитие.
2. Для правильной и научной организации учебного процесса необходимо понимать исторические этапы развития науки, а также законы и практические условия, которые лежат в основе этого развития.; Теоретической основой методики преподавания математики является история математики. Она, как писал выдающийся учёный и математик Борис Владимирович Гнеденко (1912–1995), «должна предоставить искусству преподавания математики подробную программу, а также, совместно с философией математики, указать ему приёмы и методы для выполнения этой программы».
Борис Владимирович разделял эти взгляды и активно занимался вопросами преподавания математики. В частности, в диссертационном исследовании С. В. Белобородовой особое внимание уделяется профессиональной направленности историко-математической подготовки учителей математики в педагогических вузах. А. Е. Томилова рассмотрела вопросы отбора содержания курса истории математики для педагогических вузов. Ю. В. Романов изучил возможность историзации геометрической подготовки учителей как одного из путей повышения эффективности изучения геометрии.. Т. С. Полякова посвятила своё исследование истории отечественной методики преподавания математики, рассматривая её в контексте профессиональной подготовки студентов педагогических вузов.
Российские и зарубежные учёные накопили огромное количество историко-математических материалов, среди которых выделяются работы таких выдающихся мыслителей, как М. Кантор, Ж. Монтюкла, И. Г. Башмакова, Э. И. Березкина, К. Бойер, Н. Бурбаки, Б. А. Ван-дер-Варден, М. Е. Ващенко-Захарченко, И. Вилейтнер, А. И. Володарский, Г. А. Зверкина, Ф. Клейн, А. Н. Колмогоров, Э. Кольман, Дж. Кулидж, А. Е. Малых, Г. П. Матвиевская, Д. Д. Мордухай-Болтовской, О. Нейгебауэр, Б. А. Розенфельд, К. А. Рыбников, Р. А. Симонов, Дж. Стройк, Г. Цейтен, М. Шаль, А. П. Юшкевич и многие другие. Математика — это наука, которая не только развивает интеллект и познавательные способности, но и значительно расширяет кругозор учеников. Занятия математикой способствуют тренировке памяти и у взрослых людей, а также оказывают положительное влияние на формирование таких качеств личности, как внимательность, настойчивость, ответственность и аккуратность.
Учеными доказано, что раннее развитие математических способностей является одним из ключевых факторов, определяющих успешность обучения школьников практически по всем остальным предметам. Именно поэтому математику часто называют царицей наук.
Математика обладает уникальными знаками и символами, которые понятны всем остальным наукам. Практически все явления в природе и в обществе можно описать с помощью математических символов.
Математика создала логику, на которую в той или иной степени опираются все науки. Любой процесс в мире можно описать математически, даже такой, на первый взгляд, который кажется совершенно не связанным с математикой, как художественное творчество.
Без математики невозможны точные расчёты в химии, физике и астрономии. Её законы едины для всего мира. Криптография, экономика, логистика, биология, география — области применения математических знаний практически безграничны.
Математика учит человека логическому мышлению и установлению причинно-следственных связей, что помогает в освоении любой профессии.
История математики важна по нескольким причинам:
Изучение истории математики позволяет нам глубже понять, как формировались и развивались математические понятия и идеи, а также как развивалась сама наука и её основные направления.
Исторические экскурсы помогают оживить изложение систематического курса математики, делая его более увлекательным и интересным. Примеры из истории математики могут пробудить у обучающихся интерес к изучению предмета и углубить их понимание фактического материала.
Изучение истории математики способствует расширению умственного кругозора и повышению общей культуры учащихся. Это помогает нам осознать, что математика возникла и развивалась в тесной связи с практической деятельностью человека, а свойства, правила и теоремы, которые мы изучаем в школе, были получены в результате познания окружающего мира.
Учитель, который знает историю математики, может не только предвидеть трудности, с которыми могут столкнуться учащиеся при освоении школьной программы, но и использовать исторический опыт для их преодоления.
Методика обучения иностранным языкам представляет собой теоретическую и прикладную науку, занимающуюся научным обоснованием целей, содержания и методов обучения. Она разрабатывает эффективные приёмы и формы обучения, учитывая поставленные цели, содержание и конкретные условия, в которых осуществляется процесс.
Лингводидактика, являясь прикладной лингвистической дисциплиной, изучает обучение иностранным языкам и процесс их усвоения. В рамках своей работы она:
* Исследует общие закономерности, которые свойственны обучению языкам.
* Разрабатывает методы и средства обучения конкретному языку в зависимости от дидактических целей.
* Исследует влияние монолингвизма (одноязычия) и билингвизма (двуязычия) на процесс усвоения языка.
* Решает целый ряд смежных задач, связанных с обучением языкам.
Во второй половине 50-х годов некоторые молодые лингвисты начали использовать математические методы для изучения структуры языка. Это стало настоящим открытием для их коллег, которые были уверены, что гуманитарные науки, такие как лингвистика, не имеют ничего общего с математикой и другими точными науками.
Тем не менее, идея о тесной взаимосвязи между естественным языком и математикой не была в то время чем-то новым. Л. С. Выготский, автор книги «Мышление и речь», опубликованной в 1934 году, писал: «Первым, кто увидел в математике мышление, выходящее за пределы языка, по-видимому, был Декарт». И далее: «Наш обычный разговорный язык, с присущими ему колебаниями и несоответствиями грамматического и психологического, находится в состоянии подвижного равновесия между идеалами математической и фантастической гармонии и в непрерывном движении, которое мы называем эволюцией».
Учение о грамматических категориях, зародившееся в Древней Греции, уже представляло собой попытку описать ключевые аспекты строения языка с помощью абстрактных моделей, подобных тем, которые использовались древнегреческими математиками для описания пространственных форм. Однако привычность таких понятий, как падеж, род и так далее, которые, как писал Х. Штейнталь, стали «нашей второй натурой», мешает нам осознать, какой высокий уровень абстрактного мышления потребовался для их создания. Поэтому неудивительно, что первые попытки применить настоящие математические методы для описания языкового «идеала математической гармонии» были предприняты лишь в середине XX века.
Можно выделить две причины такого «запоздания». Во-первых, после значительного прогресса, достигнутого в античности, наука о языке снова начала активно развиваться только в XIX веке. Однако в течение всего этого столетия основное внимание лингвистов было сосредоточено на истории языка. И лишь в следующем веке, который стал для гуманитарных наук веком структурализма, лингвистика впервые после античного периода вновь обратилась к изучению языковых структур, но уже на качественно новом уровне.
Когда лингвисты осознали, что язык представляет собой, говоря словами Ф. де Соссюра, «систему чистых отношений», то есть систему знаков, физическая природа которых не имеет значения, а важны лишь связи между ними, стала очевидной параллель между языком и математическими конструкциями, которые тоже являются «системами чистых отношений». И уже в начале ХХ века тот же де Соссюр мечтал о том, чтобы исследовать язык с помощью математических методов.. В связи с этим можно выделить несколько терминов, которые отражают взаимосвязь математики с лингвистикой:
* лингвоматематика;
* лингвоалгебра;
* алгебраическая лингводидактика;
* геометрическая лингводидактика;
* лингвометодическая математика.
Эти термины позволяют рассмотреть различные аспекты взаимодействия математики с лингводидактикой и методикой преподавания как математики, так и иностранных языков.
Определения новых терминов
Лингвоматематика
Лингвоматематика — это междисциплинарная область, изучающая взаимосвязь между языковыми и математическими структурами через применение математических методов к языковым системам. В этом контексте лингвоматематика направлена на исследование закономерностей и моделей в языке аналогично математическим конструкциям, рассматривая их как системы отношений, что способствует оптимизации методов преподавания как математики, так и иностранных языков.
Лингвоалгебра
Лингвоалгебра представляет собой методологию, использующую алгебраические подходы для анализа языковых структур и взаимосвязей между языковыми единицами. Эта концепция позволяет интегрировать алгебраические методы в процесс обучения языкам, используя язык как объект исследования, где грамматические категории отображаются через алгебраические структуры, что усиливает понимание как математических концепций, так и языковой логики.
Алгебраическая лингводидактика
Алгебраическая лингводидактика — это направление методики преподавания, применяющее алгебраические методы и модели для обучения языков. Этот подход способствует интеграции логических и структурных элементов математики в языковое обучение, помогая учащимся осознать языковые структуры и взаимосвязи через алгебраические формы, что содействует более глубокому пониманию как языковых, так и математических концепций.
Геометрическая лингводидактика
Геометрическая лингводидактика — это методическое направление, которое использует геометрические модели для иллюстрации и преподавания языковых структур и категорий. Она применяется для визуализации лингвистических отношений, что позволяет учащимся видеть «формы» и «объемы» языковых конструкций, подобно тому, как в геометрии изучаются фигуры и их свойства. Этот подход способствует более рельефному пониманию языковых концепций и их взаимосвязей, а также создает базу для сравнения с геометрическими терминами, используемыми в математике.
Лингвометодическая математика
Лингвометодическая математика охватывает концепции и практические подходы, объединяющие методы математического обучения с методами преподавания языков. Этот термин подразумевает использование математических структур и логических выводов в языковом обучении, что позволяет ученикам развивать критическое мышление и аналитические навыки как в области языка, так и в математике. Лингвометодическая математика направлена на создание междисциплинарных уроков, где математические концепции служат инструментом для углубления понимания языковых явлений и наоборот.
Эти определения подчеркивают потенциальные синергии между языком и математикой, открывая новые горизонты для образования в условиях междисциплинарного подхода.
Термин «лингводидактика» был предложен Н. М. Шанским в 1969 году и с 1975 года признан Международной ассоциацией преподавателей русского языка и литературы (МАПРЯЛ) в качестве международного.
Обучение иностранному языку представляет собой процесс, в ходе которого учитель систематически и последовательно передает знания, умения и навыки в области иностранных языков. Этот процесс сопровождается активным и сознательным усвоением их учащимися, а также формированием и закреплением у детей качеств, которые учитель стремится в них воспитать.
Внедрение математических методов и «математического духа» в лингвистику способствовало её развитию в направлении большей точности и объективности. Однако на пути к дальнейшему прогрессу в этом направлении возникают серьезные препятствия. В настоящем учебном пособии автор размышляет о причинах сближения лингвистики и математики, о границах применения математических методов в лингвистике и о природе факторов, которые мешают взаимопониманию между математиками и лингвистами. Методика обучения математике — это педагогическая наука, которая изучает задачи, содержание и методы обучения этому предмету. Её цель — сделать процесс обучения более эффективным и качественным.
Методика обучения математике отвечает на вопрос, как правильно преподавать математику. Она охватывает все аспекты: от целей и содержания математического образования до методов, средств и форм обучения.
Основные задачи методики обучения математике:
Определение конкретных целей изучения математики на разных уровнях: по классам, темам и урокам.
Выбор содержания учебного предмета, соответствующего поставленным целям и способностям учащихся.
Разработка наиболее эффективных методов и организационных форм обучения, которые помогут достичь намеченных результатов.
Анализ необходимых средств обучения и составление рекомендаций по их использованию в практике учителя. Существует тесная связь между методикой обучения математике и методикой обучения иностранным языкам, а также лингводидактикой. Это особенно актуально, когда обучение математике осуществляется на иностранном языке или когда иностранные языки преподаются студентам, специализирующимся на математике.
— 1.1. Основной научный и понятийный аппарат математики как науки и её истории
История математики является неотъемлемой частью самой математики, как и другие её разделы. Она черпает своё содержание непосредственно из математики. Многие выдающиеся математики-методисты XVIII–XX веков считали, что математическое образование должно опираться на знания об истории математики.
Интерес к математике возрастает, когда формы и методы обучения становятся разнообразными, а учитель осознаёт, какую роль эта тема может сыграть в развитии способностей ученика.
Систематическое использование материалов по истории математики в образовательном процессе приносит значительную пользу. Факты из истории оживляют преподавание, повышают интерес учащихся к математике, точным наукам и технике, а также расширяют их кругозор. Это помогает им лучше понять взаимосвязи между различными разделами математики, что, в свою очередь, способствует более глубокому усвоению школьного курса.; Способствуют развитию трудолюбия у учащихся: подготовка и оформление докладов, математические вечера, стенгазеты и другие мероприятия. Умение преподнести материал в соответствии с требованиями Федерального государственного образовательного стандарта (ФГОС) является показателем высокого профессионализма каждого учителя математики.
Главная задача современного учителя математики — с помощью своего предмета оказывать своевременную поддержку в развитии личности каждого ученика. Способность эффективно выполнять эту функцию зависит от набора профессионально важных и значимых качеств, которые должны быть сформированы у будущего учителя.
Эти качества, согласно исследованиям Б. Ф. Ломова, Ю. П. Поваренкова, Е. И. Смирнова и В. Д. Шадрикова, составляют основу профессиональной культуры учителя. Они должны стать неотъемлемой частью подготовки студентов-математиков в педагогическом вузе, включая изучение истории математики. Именно на это нацелены нормативные документы.. В Государственном образовательном стандарте высшего профессионального образования (2005 г., специальность 032100.00 «Математика с дополнительной специальностью») в квалификационной характеристике выпускника сказано: «Выпускник, получивший квалификацию учителя математики, должен быть готов осуществлять обучение и воспитание обучающихся с учётом специфики преподаваемого предмета. Он также должен способствовать социализации и формированию общей культуры личности, а также осознанному выбору и последующему освоению профессиональных образовательных программ. Выпускник должен уметь использовать разнообразные приёмы, методы и средства обучения».
Научный аппарат математики действительно представляет собой множество инструментов и методов, используемых для исследования и решения различных задач в этой области. **Объект истории математики** — это процесс зарождения и развития математических знаний.
**Предмет истории математики** — это модели, которые отражают все важные аспекты исследуемого объекта. Эти модели включают в себя те стороны, свойства и отношения, которые были выявлены в ходе опыта и включены в практическую деятельность человека.
Предмет математики: Изучение количественных и качественных отношений, структур, изменений и пространства через абстрактные концепции, такие как числа, функции, структуры, формы и пространства.
Объект математики: Конкретные математические объекты, такие как числа, векторы, матрицы и функции, а также их свойства и взаимосвязи.
Методы, применяемые в математике
Аналитические методы: Использование алгебры и анализа для решения уравнений и задач.
Геометрические методы: Применение геометрических принципов для решения задач.
Комбинаторные методы: Исследование комбинаций и перестановок объектов.
Статистические и вероятностные методы: Подходы для анализа данных и оценки вероятностей событий.
Гипотезы математических исследований, цели и задачи
Гипотеза: Предположение о взаимосвязи математических объектов или о свойствах математической структуры, которые требуют доказательства. Например, гипотеза Римана о распределении простых чисел.
Цели исследований: Установление истинности гипотез, расширение математического аппарата и разработка новых методов исследования.
Задачи исследований: Доказательство новых теорем, решение открытых проблем, применение математики в других областях (физика, экономика и др.). В настоящее время накоплен богатый научно-методический опыт, посвященный различным аспектам изучения и применения истории математики на разных уровнях образования — как в школе, так и в вузе.
Например, в докторской диссертации Т. С. Поляковой убедительно доказывается, что содержание историко-методической подготовки учителей математики в педагогическом вузе необходимо расширить за счёт систематизации знаний по истории школьного математического образования.
Ряд кандидатских диссертаций посвящён разнообразным аспектам преподавания курса истории математики:
* H.A. Бурова исследует роль и значение этого курса как одного из ключевых факторов гуманизации и гуманитаризации математического образования.
* А. Е. Томилова рассматривает отбор содержания курса и методику его реализации.
* Ю. В. Романов изучает его влияние на геометрическую подготовку будущих учителей математики.
Методологические аспекты обучения истории математики были предметом исследований Т. А. Ивановой, Г. И. Саранцева, В. А. Тестова, М. В. Шабановой и других учёных.. В различных исследованиях были разработаны модели профессионально ориентированной историко-математической и историко-методической подготовки учителей математики в педагогических вузах. Эти модели были созданы такими учёными, как С. В. Белобородова, Н. А. Бурова, Ю. А. Дробышев, P.A. Майер, А. Е. Малых, С. Н. Марков, Т. С. Полякова, К. А. Рыбников, А. Е. Томилова и другими.
Кроме того, накоплен значительный опыт по формированию умений применять исторический материал в различных математических и методических курсах и спецкурсах. Этот опыт был получен благодаря усилиям таких авторов, как В. В. Афанасьев, И. Н. Власова, А. Л. Жохов, А. Е. Малых, Н. И. Мерлина и Л. П. Шибасов. Общий обзор научно-методических исследований и диссертаций в области истории математики, а также педагогического образования, имеет большое значение как для развития качества преподавания математики, так и для повышения уровня профессиональной подготовки будущих учителей. Ниже приведен анализ ключевых теорий, методов и их авторов, а также вклада их научных работ в данную область.
1. Психолого-педагогические теории культурно-исторической определенности науки и образования
Основные идеи: Эти теории основываются на предположениях, что обучение и воспитание не существуют в вакууме, а формируются под воздействием социальной и культурной среды. Главные идеи были выработаны такими учеными, как Л. С. Выготский и Г. В. Дорофеев.
Вклад авторов:
Л. С. Выготский: Развил понятие «зона ближайшего развития», подчеркивая, что обучение должно учитывать культурные контексты и развивать потенциальные способности учащихся.
Г. В. Дорофеев: Изучал влияние исторического контекста на формирование научных знаний, акцентируя внимание на взаимосвязи между традициями и индивидуальным опытом.
2. Теории профессиональной подготовки
Основные идеи: Исследования в этой области касаются формирований необходимых компетенций у будущих учителей математики, акцентируя внимание на концепциях профессионального обучения, как например, концепция профессионально-педагогического обучения.
Вклад авторов:
Н. Я. Виленкин и В. А. Гусев: Разработали методические рекомендации по внедрению инновационных подходов в обучение и развитие профессиональных навыков будущих учителей математики.
Г. И. Саранцев: Исследовал основные направления и методы подготовки учителей, особенно в области математического образования.
3. Теоретические положения психологии и методики подготовки учителей
Основные идеи: Фокусируется на методах обучения математике, психологических стратегиях и технологиях, включая инновационные подходы.
Вклад авторов:
Ю. М. Колягин: Подробно анализировал методологические аспекты, которые необходимо учитывать при обучении учителей, работая над принципами активного обучения.
В. М. Монахов: Изучал инновационные стратегии в обучении математике, акцентируя внимание на практическом опыте использования технологий.
4. Теоретические и содержательные основы обучения истории математики
Основные идеи: Сосредоточены на том, как исторический контекст может помочь в преподавании математики и как выпускники могут использовать исторические факты для углубления понимания математических концепций.
Вклад авторов:
И. К. Андронов и И. Г. Башмакова: Рассматривали содержание курсов истории математики и их значимость для педагогического образования, а также разработали методы, позволяющие интегрировать исторические аспекты в учебный процесс.
Б. В. Гнеденко: Классный математик, который подчеркивал значимость разработки и преподавания истории математики как стратегии гуманизации образования.
5. Теория деятельностного подхода
Основные идеи: Подход, основанный на активном участии учащихся в процессе обучения, что помогает развивать их способность к самостоятельной интеллектуальной деятельности.
Вклад авторов:
A. Н. Леонтьев: Сформулировал идеи деятельностного подхода к обучению, подчеркивая значение практической деятельности в учебном процессе.
Л. М. Фридман: Анализировал, как элементы деятельностного подхода можно интегрировать в преподавание математики, чтобы активизировать учебный процесс.
6. Методологические основы методики обучения математике
Основные идеи: Субстантивные теории касаются создания методик, способствующих эффективному обучению математике.
Вклад авторов:
G. И. Саранцев и Е. И. Смирнов: Работали над стратегиями и программами, которые ориентированы на обновление содержания математического образования и внедрение современных методов.
М. В. Шабанова: Исследовала связь между историей математики и методикой обучения, предлагая различные подходы к этой интеграции.
7. Комплексно-интегративный подход к построению педагогических концепций
Основные идеи: Данный подход направлен на синтезирование различных методик и теорий, позволяющих создать более целостную и эффективную систему педагогического образования.
Вклад авторов:
В. П. Беспалько: Разработал интегративные концепции, которые соединяют разнообразные методы преподавания и управления учебным процессом.
А. Л. Жохов: Исследовал структурирование учебных ситуаций, что может повысить качество образования в области математики.
Все вышеописанные теории, методы и исследования play crucial roles в фокусировке на значении истории математики в педагогическом обучении. Эти теории обуславливают гуманизацию образования, отлично подчеркивают значение педагогической практики и подчеркивают необходимость интеграции исторических знаний для формирования квалифицированных учителей математики, способных эффективно обучать новое поколение. Эти исследования будут служить основой для дальнейших разработок в области методики преподавания математики и депозитария исторического развивающего контекста.
Выдающиеся математики и их диссертации
Андрей Колмогоров — разработал новые вероятностные методы и обоснования.
Гипотеза исследования: Связи между вероятностью и математическим анализом.
Докторская диссертация: «Основные элементы теории вероятностей».
Григорий Перельман — предложил доказательство гипотезы Пуанкаре.
Гипотеза исследования: Структура трехмерных многообразий.
Доказательства: Методы геометрии Римана и топологии.
В области истории математики часто цитируют определение предмета математики и его периодизацию, предложенные А. Н. Колмогоровым. Он считал, что невозможно дать полное формальное определение предмета математики, и предложил свою версию на основе её истории.
**Принципы истории математики**
1. **Принцип историзма**: Обучение должно быть основано на понимании путей возникновения знаний.
2. **Историко-генетический метод**: Ученики в процессе обучения отражают общий исторический путь, который прошло человечество в освоении математических знаний.
**Методы истории математики**
1. **Воссоздание фактического содержания** истории развития математики, включая зарождение математических понятий, методов и теорий.
2. **Раскрытие многогранных связей** математики с практической деятельностью людей, с развитием других наук, а также с экономической и социальной структурой общества.
3. **Исследование закономерностей** развития науки, включая историческую обусловленность логической структуры современной математики, соотношение её частей, диалектику её развития и перспективы.
4. **Анализ влияния** развития математической науки на её преподавание в учебных заведениях.
В своей знаменитой статье «Математика» в Большой Советской энциклопедии, опубликованной в 1954 году, Колмогоров начинает с определения, данного Ф. Энгельсом в работе «Анти-Дюринге» (1877). Энгельс писал: «Чистая математика имеет своим предметом пространственные формы и количественные соотношения реального мира, а следовательно, она оперирует очень реальным материалом».
При этом он отмечает, что с развитием естествознания количество количественных соотношений и пространственных форм, изучаемых математикой, постоянно растёт, наполняя это определение всё более глубоким смыслом.. К этому определению неоднократно предлагались дополнения и уточнения, отражающие особенности современной математики. Например, Н. Бурбаки в своём определении утверждал, что математика — это совокупность абстрактных форм, математических структур.
Многие учёные, такие как В. И. Арнольд и Л. Д. Кудрявцев, считают, что модели являются основным предметом изучения математики. Согласно этому мнению, математика представляет собой область человеческих знаний, в которой исследуются математические модели — логические структуры, описывающие взаимосвязи между элементами.
В современной методологии науки принято различать объект и предмет математики. Ф. Энгельс определил объект математики как пространственные формы и количественные отношения, в то время как Н. Бурбаки, В. И. Арнольд и другие учёные сосредоточили внимание на предмете математики — моделях.
Следуя идеям классика истории математики К. А. Рыбникова, мы можем включить в состав математики следующие компоненты:
1) Факты, накопленные в процессе её развития.; 2) Гипотезы, которые подлежат дальнейшей проверке;
3) Теории и законы, отражающие результаты обобщения фактического материала;
4) Методология математики, представляющая собой общетеоретическую интерпретацию математических теорий и законов.
Все эти элементы тесно связаны между собой и находятся в постоянном развитии. История математики изучает, как это развитие происходило в конкретный исторический период и к каким результатам оно привело. Вот несколько видных математиков и их работы, которые внесли вклад в формирование математического аппарата, а также значения предмета и объекта математики, а также применяемые в ней методы.
Примеры учёных и их труды
Исаак Ньютон — «Математические начала натуральной философии» (Philosophiæ Naturalis Principia Mathematica, 1687)
Ньютон разработал основы математического анализа и методы, которые использовал для доказательства законов движения. Его работы стали основой для последующих исследований в физике и математике.
Готфрид Вильгельм Лейбниц — «Новая математическая логика» (Nova Methodus pro Maximis et Minimis, 1684)
Лейбниц ввёл дифференциальное и интегральное исчисление, разработав формулы, которые до сих пор широко используются в математическом анализе.
Георг Кантор — «Основания математической теории множеств» (Grundlagen einer allgemeinen Mannigfaltigkeitslehre, 1883)
Кантор сформулировал основы теории множеств, установил концепцию бесконечности и доказал существование различных уровней бесконечных множеств. Его работа оказала решающее влияние на современную математику.
Давид Гильберт — «Основы математики» (Die Grundlagen der Mathematik, 1920)
Гильберт предложил формализовать математику на основе аксиоматики и развил проблемы существования и построения математических объектов.
Предмет и объект математики
Как отметил К. А. Рыбников, «история математики — это наука об объективных законах развития математики». Цель истории математики как науки заключается в выявлении закономерностей, по которым развивается математика.
Объектом истории математики является процесс возникновения и развития математики. Предметом изучения служат модели этого процесса, которые включают в себя все важные аспекты — стороны, свойства и отношения, зафиксированные в опыте и применяемые в практической деятельности. Эти модели представляют собой модели развития математики.. В научной литературе по истории математики не существует единого названия для предмета своего изучения. Чтобы понять, из чего состоит предмет истории математики, исследователи ставят перед собой несколько задач:
1. **Реконструкция фактического содержания** истории развития математики. Это включает в себя изучение возникновения математических концепций, методов и теорий, а также анализ природы и особенностей развития математики. Кроме того, в рамках этого этапа исследуется развитие математики у разных народов в различные исторические периоды и вклад отдельных ученых в эту науку.
2. **Раскрытие многообразных связей** математики с другими науками и практическими потребностями людей. В частности, обращается внимание на влияние экономической и социальной структуры общества на содержание и характер развития математики.
3. **Исследование закономерностей развития** науки. Этот этап предполагает выявление исторической обусловленности логической структуры современной математики, соотношение ее частей, диалектику ее развития и перспективы.; 4) Осмысление влияния эволюции математической науки на ее преподавание в учебных заведениях.
История математики изучает зарождение математических концепций и теорий, анализирует причины их появления и исследует их дальнейшее развитие. Существует два основных подхода к изложению истории математики.
В первом подходе история математики представляется как непрерывный поток идей, переходящих от одного математика к другому и претерпевающих эволюцию. Например, Галилей оказал влияние на Кавальери, Кавальери — на Торричелли, Торричелли — на Паскаля, Паскаль — на Лейбница, а Лейбниц — на братьев Бернулли.
Особенно значительный след в истории математики оставил Эйлер, чьи последователи исчисляются тысячами. Спустя много лет после его смерти Лаплас сказал: «Почитайте Эйлера. Это наш общий учитель».
Эта книга охватывает период с XVI по XVIII века.. Этот подход к изучению истории математики, безусловно, важен и позволяет выделить ключевые вехи в её развитии. Однако он имеет и свои ограничения.
Этот подход не учитывает тесную взаимосвязь между математикой и обществом в целом. История математики — это неотъемлемая часть истории человечества. Преобладающие социальные и экономические условия во многом определяют направление математических исследований.
Например, почему в греческой математике большое внимание уделялось областям, а в итальянской математике XV — XVI веков — объёмам, вычислению центра тяжести и небесной механике? # Цели и задачи истории математики как науки
## Цели изучения истории математики:
* Формирование целостного представления о математике как о науке, находящейся в постоянном развитии.
* Углубление знаний о возникновении и эволюции математики.
* Понимание причин появления одних математических идей и отмирания других.
* Развитие навыков применения исторических знаний в процессе обучения математике.
## Задачи изучения истории математики:
Воссоздание исторического развития математики.
1. **Освещение возникновения** математических методов, понятий, идей, теорий и отдельных математических дисциплин.
2. **Выяснение характера и особенностей** развития математики у разных народов в определённые исторические периоды.
3. **Показ вклада** великих учёных прошлого, в том числе отечественных, в развитие математики.
4. **Демонстрация многогранных связей** математики с практическими потребностями и деятельностью людей, а также с развитием других наук.
5. **Освещение влияния** экономического, социального и идеологического состояния общества на характер развития математики и, наоборот, влияния математики на развитие общества.
6. **Показ формирования** исторических и логических связей между отдельными разделами математики.
7. **Раскрытие исторической обусловленности** логической структуры современной математики и диалектики её развития.
8. **Освещение соотношения** частей математики и перспектив её развития. Важно обратит внимание на то, как раскрывается взаимосвязь между развитием математической науки и её преподаванием в учебных заведениях.
Греческая математика была ориентирована на нужды сельскохозяйственного общества. А XV век — это эпоха великих географических открытий, когда Колумб открыл Америку в 1492 году, а Васко да Гама — морской путь в Индию в 1498 году. Корабли были необходимы для навигации, и их водоизмещение и остойчивость напрямую зависели от объёмов и положения центра тяжести. Чтобы ориентироваться в океане, необходимо рассчитать географические координаты. Или ещё один пример: почему на революцию пришли греки, а не египтяне или вавилоняне, хотя греки учились у них? Это связано с социально-политическим устройством жизни этих народов. В Египте правил фараон, чей авторитет был непререкаем. А Греция была демократическим государством, где решения обсуждались и доказывались их последовательность.
Таким образом, чтобы всесторонне понять процесс развития математики, нужно рассматривать его в тесной связи с развитием человеческого общества. Уже существующие математические структуры развиваются в некоторой степени независимо, но это саморазвитие происходит в условиях и на основе практической деятельности человека и определяется, иногда напрямую, иногда в конечном итоге, потребностями общества. Однако не все математические идеи возникли непосредственно из практических нужд.. Некоторые из них появились благодаря стремлению развивать математику как таковую. Английский математик Харди писал, что «настоящая» математика, созданная «настоящими» математиками — Ферма, Эйлером, Гауссом, Абелем и Риманом — практически не имеет практического применения. Однако со временем многие из этих идей нашли своё применение в решении практических задач.
Одним из ярких примеров такого формального понятия, о котором долгое время не было известно, является мнимое число. Теория комплексных чисел значительно упростила решение многих задач гидро- и аэромеханики.
С другой стороны, состояние науки в определённый период позволяет нам пересмотреть некоторые оценки прежних знаний. Например, стремительный рост информатики и вычислительной техники возродил интерес к приближённым методам, которые были популярны в прошлом. Электронные вычислительные машины сами по себе расширяют круг задач, которые можно решить с помощью математики.. Область применения математики постоянно растёт. Важно установить связи между историей математики и другими науками. Развитие математической науки непосредственно связано с её преподаванием в учебных заведениях. Множество авторов и преподавателей, как в России, так и за рубежом, внесли значительный вклад в методику преподавания математики, разработав теории и подходы, которые используются в образовательных учреждениях по сей день.
Ведущие авторы методик преподавания математики
В России:
А. Н. Колмогоров
Диссертация: Кандидатская диссертация «О некоторых вопросах теории функций и их применение к теории вероятностей».
Труды: «Методы математической статистики», «Основы математической обработки информации».
Вклад: Создание основ методики преподавания вероятности и статистики, важность точности в математическом языке.
А. Я. Хинчин
Диссертация: Докторская диссертация «Обобщенная теория вероятностей».
Труды: «Курс теории вероятностей», «Математическая статистика».
Вклад: Внедрение методов теории вероятностей в учебные планы, акцент на практическом применении математики.
И. В. Арнольд
Диссертация: Докторская диссертация «Качественная теория дифференциальных уравнений».
Труды: «Матhematics: Its Content, Methods and Meaning», «Уравнения математической физики».
Вклад: Применение методов геометрии к проблемам анализа, интеграция истории математики в педагогическую практику.
Н. Я. Виленкин
Диссертация: Докторская диссертация «Об одном классе функциональных уравнений».
Труды: «Иммунные системы и математический анализ».
Вклад: Разработка учебников, в которых теория и практика связаны через реальные жизненные приложения.
За границей:
Ричард Б. Гуд (США)
Труды: «Teaching Mathematics in College».
Вклад: Разработка методик активного обучения, акцент на решении практических задач.
Виктория Финк (Германия)
Труды: «Mathematics Education: A Critical Analysis».
Вклад: Исследование кросс-культурных подходов в преподавании математики.
Джон Дьюи (США)
Труды: «Experience and Education».
Вклад: Основоположник прогрессивного обучения, акцент на осмысленное развитие математических понятий.
Лейн Д. Конигсбург (США)
Труды: «Mathematics Teaching in the Middle School».
Вклад: Разработка методов интеграции технологий в преподавание математики.
Принципы и методы преподавания
Историко-генетический метод (разработан В. В. Бобыниным):
Принцип обучения через исследование исторического развития математических понятий.
Проблемно-ориентированное обучение (внедрено И. В. Арнольдом):
Стимулирование учащихся находить решения через анализ реальных проблем.
Деятельностный подход (развивает А. Н. Колмогоров):
Упор на активное участие студентов в процессе обучения через практические занятия.
Коллективное обучение (разработан Джоном Дьюи):
Совместная работа учащихся для развития критического мышления и кооперативных навыков.
Учебники и научные труды
А. Н. Колмогоров:
Учебник «Математика в школе». Внедрение новых методов в обучение математике через практическое применение теории вероятностей.
А. Я. Хинчин:
Книга «Курс теории вероятностей». Представляет подробно разработанные принципы преподавания теории вероятностей и статистики.
И. В. Арнольд:
«Создание задач по математике». Интеграция исторического контекста в изучение математических понятий.
Каждый из этих авторов и их работы сыграли важную роль в разработке и внедрении новых методов преподавания, которые сделали изучение математики более доступным и интересным, а также актуальным для практического применения в жизни студентов.
Связь между историей математики и философией вполне естественна. Во-первых, математика выделилась из натурфилософии. Во-вторых, методы теории познания используются в математике, в процессе её преподавания, а также в методологических и математических исследованиях. Диалектический метод позволяет установить взаимосвязи между различными компонентами методологической системы. В-третьих, во многих методических системах преподавания математики в школе и вузе подчёркивается важность мировоззренческой ориентации.
История науки, включая историю математики, является неотъемлемой частью всеобщей истории, истории общечеловеческой культуры. Без её изучения невозможно получить целостное представление о развитии человеческого общества. Поэтому мы рассматриваем историю математики в её последовательном развитии во времени, разделяя её на периоды, как это принято в общей истории.. При изучении истории математики мы всегда обращаем внимание на её связь с различными аспектами общества. Это касается и смены общественных формаций, и научно-технических революций, и значимых открытий, и событий в мировой культуре.
Тесная связь существует между математикой и физикой. Многие достижения в физике стали возможны благодаря математике, и, наоборот, решение физических задач часто приводило к созданию новых математических теорий. Например, создание дифференциального и интегрального исчислений Ньютона стало основой для развития механики.
Связь между историей математики и педагогикой более сложная. Она затрагивает, как развитие математической науки влияет на её преподавание.
Вывод
Математика с каждым годом расширяет свои горизонты, и работа таких великих учёных, как Ньютон, Лейбниц, Кантор и Гильберт, показала, насколько важен научный аппарат для её развития. Исследование гипотез и формулирование новых методов, используемых для доказательства теорем, делают математику одной из самых динамично развивающихся наук.
Многие математики внесли значительный вклад в историю образования, и реформы образования всегда были тесно связаны с математикой. В настоящее время история российского математического образования активно развивается.
Интересна связь между историей математики и информатикой. Она рассматривается с нескольких точек зрения.. Во-первых, использование компьютеров оказало значительное влияние на математику. Некоторые исследователи даже считают, что необходимо выделить отдельный период для изучения машинной математики.
Во-вторых, создание компьютерных учебников и образовательных систем по математике поставило перед методистами задачу их разработки.
В-третьих, сам курс истории математики является той областью, где создание и применение компьютерных учебников особенно актуальны.
Научный аппарат математики представляет собой совокупность инструментов, методов и правил, которые служат основой для исследований в этой области.
Проще говоря, это набор формул, условий и соотношений, позволяющих решать различные задачи. Например, для решения квадратного уравнения математический аппарат включает формулы для нахождения дискриминанта, условия, при которых дискриминант больше или равен нулю, а также формулы для вычисления первого и второго корня.
Кроме того, математический аппарат определяет комплекс подходов, применяемых для решения математических и статистических задач в различных областях научного знания.
Например, с помощью математического аппарата можно обосновать физические законы и правила или даже открыть новые законы.
Упражнение №2: Тестовое задание для закрепления материала по теме 1.1. Основной научный и понятийный аппарат математики как науки и её истории
Вариант 1: Тест для слабых учащихся
Контрольные вопросы для самопроверки знаний:
Какой объект изучает математика?
Что является предметом математики?
Назовите один из компонентов математики.
Какова основная цель изучения истории математики?
Выберите правильный ответ:
Объектом математики являются:
а) только числа
б) разнообразные математические объекты, такие как числа, функции, матрицы
в) только геометрические фигуры
Предметом математики можно считать:
а) факты и данные
б) количественные и качественные отношения, структуры и изменения
в) занятия по математике
Основная цель истории математики:
а) познакомить студентов с историей всех наук
б) изучить эволюцию математических понятий и идей
в) рассмотреть всё, что связано с математикой
Задания на соответствие:
Соедините термины с их определениями:
Объект математики
Предмет математики
Компоненты математики
а) Исследование взаимосвязей между элементами
б) Конкретные математические объекты
в) Факты, гипотезы и теории
Вариант 2: Тест для средних учащихся
Контрольные вопросы для самопроверки знаний:
Какие компоненты математики вы можете выделить?
В чем заключается предмет истории математики?
Назовите задачи истории математики.
Приведите примеры математических теорий, созданных «впрок».
Выберите правильные ответы:
Объектом истории математики является:
а) Процесс развития и возникновения математики
б) Инструменты, используемые математиками
в) Истории жизни выдающихся математиков
Задачи истории математики включают:
а) Исследование закономерностей развития математики
б) Анализ однообразных математических процедур
в) Искажение данных
Задания на соответствие:
Соедините примеры с соответствующими аспектами:
Исаак Ньютон
Готфрид Лейбниц
Георг Кантор
а) Основы теории множеств
б) Разработка основ математического анализа
в) Введение в дифференциальное и интегральное исчисление
Практическое задание:
Напишите короткое эссе (150—200 слов) о влиянии общественно-политических условий на развитие математики в одной из исторических эпох.
Вариант 3: Тест для сильных учащихся
Контрольные вопросы для самопроверки знаний:
Каковы основные подходы к изучению истории математики?
Назовите способы изложения истории математики.
Приведите примеры влияния развития математики на её преподавание.
Какие математические теории получили развитие благодаря потребностям науки и практики?
Выберите правильные ответы:
Основной научный аппарат математики включает:
а) Только законченные теории
б) Методы и инструменты для решения задач
в) Лишь вычисления
Классификация математических моделей подразумевает:
а) Соблюдение одного стандарта
б) Изучение применение различных моделей для описания реальных ситуаций
в) Устойчивую классификацию всех моделей
Задания на свободное заполнение:
Заполните пропуски в следующих утверждениях:
Как указал К. А. Рыбников, история математики — это наука об законах развития математики.
Труд _ стал основой для современных методов математического анализа.
Исследовательское задание:
Исследуйте, как социальные и экономические условия в разные исторические периоди повлияли на развитие определенной математической теории. Напишите короткий реферат (300—400 слов) на эту тему.
Эти тестовые задания помогут студентам углубить и закрепить понимание тематики урока, а также развить критическое мышление, анализ и исследовательские навыки, что важно для дальнейшего изучения математики и её истории.
1.2. Доисторические математические памятники
Хотя не все задачи, которые решались в доисторических математических источниках, были полностью сохранены, некоторые из них все же дошли до наших дней и позволяют нам оценить уровень развития математики в древности.
В Древнем Египте основными источниками, содержащими задачи, являются папирус Ахмеса, который включает 84 задачи, и московский папирус Голенищева, содержащий 25 задач. Все задачи из папируса Ахмеса, датированного примерно 1650 годом до нашей эры, носят прикладной характер и связаны с практикой строительства и размежеванием земельных наделов.
В Древнем Китае во II веке до нашей эры в сочинении «Математика в девяти книгах» было представлено 246 задач с ответами.
Одним из самых древних математических инструментов является кость Ишанго. Она представляет собой кость малоберцовой кости бабуина, к одному из концов которой прикреплён острый отщеп кварца. По всей длине кости сделаны три ряда насечек. По одним данным, возраст этого артефакта составляет от 9 до 6,5 тысяч лет, а по другим — более 20 тысяч лет. Вот несколько учёных, которые занимались изучением и расшифровкой доисторических математических памятников:
1. **Борис Александрович Тураев** (1868–1920) и **Василий Васильевич Струве** — русские академики. Они занимались исследованием и расшифровкой, например, московского папируса, который хранится в Музее изобразительных искусств имени Пушкина.
2. **Рind** — египтолог. В 1858 году он открыл «папирус Ахмеса», датированный 1650 годом до нашей эры. Этот ценный документ хранится в Лондоне в Британском музее и частично в Нью-Йорке.
3. **О. Нейгебауер** — немецкий математик. Его работы, опубликованные в 30-х годах XX века, стали основой для изучения вавилонской математики.
К другим доисторическим математическим памятникам относятся:
* Папирус Ахмеса (папирус Ринда) — это самый объёмный манускрипт, содержащий 84 математические задачи. Он был написан около 1650 года до нашей эры.
* Московский математический папирус включает в себя 25 задач и датируется примерно 1850 годом до нашей эры.
* Бамбуковые листки Цинхуа представляют собой самую раннюю в мире таблицу десятичного умножения, которая была создана в 305 году до нашей эры.
𝑉=13ℎ (𝑎2+𝑎𝑏+𝑏2).
Задачи Aha требуют нахождения неизвестной величины, называемой Aha, которая эквивалентна неизвестному X, если известны вся величина и ее часть. Папирус Райда также содержит четыре такие задачи. В московском папирусе также есть задачи Aha. Например, в задаче 19 задается количество, при сложении которого с двумя другими (то есть) и добавлением четырех, получается десять. То есть, используя современные математические обозначения, нас просят решить основное уравнение.
Проблемы Pefsu
Большинство задач на папирусе (десять из двадцати пяти) относятся к типу pefsu. Pefsu измеряет крепость пива, получаемого из зерна гекат (или хекат — единица объема у древних египтян, примерно соответствующая литрам).
Чем больше pefsu в пиве, тем оно слабее. Номера Pefsu указаны во многих списках заявок. Например, задача 8 переводится следующим образом:
(1) Пример расчета для буханок хлеба Pefsu.
(2) Если кто-то спросит вас: «У вас есть буханки хлеба пефсу?
(3) Давайте заменим их пивом пефсу,
(4) из сорта пива K»», и вы захотите узнать, сколько пива вам следует выпить,
(5) сначала посчитайте, сколько пшеницы нужно для приготовления буханок хлеба пефсу. Это даст вам количество, известное как хекат.
(6) Затем подумайте, сколько вы готовы заплатить за бутылку пива сорта «К».
(7) Эффект хеката можно сравнить с десертом, приготовленным из кувшина пива, сваренного из пшеницы из Верхнего Египта.
(8) После того как вы вычислите хекат, у вас получится результат.
(9) Повторите этот процесс один раз.
(10) И вот каков будет результат. Тогда вы можете сказать:
(11) «Смотрите! Количество пива, которое мы нашли, соответствует действительности». Для изучения и понимания доисторических математических памятников используются различные методы:
1. **Археологические материалы**. Они позволяют получить представление о знаниях древних людей в области арифметики и геометрии.
2. **Сравнительное языкознание**. Этот метод дает возможность определить, какие системы счисления и математические термины использовались в разные исторические периоды.
3. **Этнография**. На стыке с этнографией и фольклором изучается народная математика, которая может содержать информацию о дописьменной математике. Однако эти данные следует использовать с осторожностью, так как они могут отражать наслоения различных эпох.
Расшифровка доисторических математических памятников представляет значительные трудности, поскольку зачастую неизвестны ни язык древних народов, ни значения отдельных иероглифов.
# Бакинские задачи
Задачи 11 и 23 относятся к так называемому «бакинскому типу». Они посвящены производительности труда работников. Например, в задаче 11 говорится о том, сколько досок можно собрать к определённому времени. В задаче 23 речь идёт о производительности сапожника: «Когда сапожник шьёт только сандалии, он зарабатывает десять (10) долларов в день. Когда он только украшает (шьёт) сандалии, он украшает их пять (5) раз в день. Сколько всего он может приготовить и украсить в один и тот же день?»
## Геометрические задачи
Семь из 25 задач в папирусе являются геометрическими. Среди них: вычисление площади треугольника, площади полусферы (задача 10) и усечённой пирамиды.
## Две интересные геометрические задачи
### Задача 10
Десятая задача папируса требует вычисления площади полусферы, согласно Струве и Гиллингсу, или, возможно, площади полуцилиндра, как утверждает Пит. Ниже мы предполагаем, что речь идёт о полушарии.
В 10-й задаче речь идет о расчете размеров корзины: «У нас есть корзина, носик которой имеет длину. Какова его площадь? Возьмите его, так как корзина составляет половину сферы. Он дает единицу. Подсчитайте остальное, так оно и есть. Считай, что это его деньги. Давать. Найдите остальную часть этого числа после вычитания из него. Давать. Умножьте это на. Давать. Смотрите, вот это и есть тот самый район. Вы нашли это правильным.»
Решение можно выразить следующим уравнением:
Это говорит о том, что автор Московского папируса использовал явное число для приблизительного определения значения математической константы. Вот некоторые данные о том, кто, когда и как решал задачи, которые были представлены в доисторических математических памятниках:
**Древний Египет**
Папирус Ахмеса, известный также как папирус Ринда, является одним из самых объёмных манускриптов, содержащих 84 математические задачи. Он был написан около 1650 года до нашей эры.
**Древний Вавилон**
Более 500 глиняных табличек, на которых записаны математические задачи, датируются XX–VI веками до нашей эры. В этих документах можно найти решения квадратных и некоторых кубических уравнений, а также задачи с дробями.
**Древний Китай**
«Математика в девяти книгах» — сборник из 246 задач с ответами, датируемый II веком до нашей эры. В нём рассматриваются линейные и квадратные уравнения с числовыми коэффициентами, системы линейных уравнений, отрицательные числа и теорема Пифагора.
**Древняя Индия**
В религиозно-философских книгах Шульба-сутры, которые являются дополнением к Ведам, упоминаются различные математические операции: действия с дробями, извлечение корней, решение уравнений, суммирование арифметической и геометрической прогрессий, а также расчёт площади треугольника, параллелограмма и трапеции, объёма цилиндра, призмы и усечённой призмы.
Считается, что основателем математики является Имхотеп. Он жил примерно 5 тысяч лет назад, во времена правления фараона Джосера. Имхотеп создал подробные правила, которые были необходимы для подсчётов в земледелии, строительстве и астрономических вычислениях.
# Задача 14: Объем усеченной пирамиды с квадратным основанием
В 14-й задаче необходимо вычислить объем усеченной пирамиды, имеющей квадратное основание.
В задаче указаны параметры пирамиды: верхняя поверхность — квадрат со стороной, нижняя поверхность — квадрат со стороной и высота, как показано на рисунке. Объем был рассчитан в кубических локтях, что соответствует действительности.
Решение задачи можно описать следующим образом: «Вам говорят, что усеченная пирамида имеет высоту, длину у основания и на вершине. Возведя эти величины в квадрат, вы получите результат. Удвойте этот результат, и у вас будет. Затем уменьшите его до минимума, чтобы получить. Наконец, добавьте оба этих значения, и вы получите желаемый результат. Вы получите его дважды, и это будет правильный ответ». Решение задачи позволяет предположить, что египтяне умели вычислять формулу для определения объема усеченной пирамиды:
## Записи
1. **Количество буханок хлеба или кувшинов пива, которые можно произвести из одного геката (100 литров) пшеницы**. В качестве примера задачи можно привести следующий вопрос: «Из двух гекат (литров) пшеницы было приготовлено десять кувшинов пива. Сколько стоит пефсу пива?» Доисторические математические памятники были написаны на различных языках, в зависимости от страны, в которой они были созданы. Например, в Древнем Египте использовались иероглифическая и иератическая системы письма. В Греции же для обозначения чисел применялись арабский, греческий, еврейский и латинский языки.
Процесс перевода и исследования этих математических памятников имел свои особенности в разные периоды и в разных местах.
Впервые европейские учёные познакомились с античными открытиями в Испании. В XII веке там начали переводить основные труды великих греков и их исламских учеников с греческого и арабского языков на латынь. С XIV века главным местом научного обмена стала Византия. Особенно активно переводились и издавались «Начала» Евклида, которые постепенно обрастали комментариями местных геометров.
Первым известным математиком в средневековой Европе стал Леонардо Пизанский, известный под прозвищем Фибоначчи. Он был знаком с достижениями древних учёных благодаря арабским переводам и систематизировал значительную их часть в своей книге «Книга абака», которая была впервые опубликована в 1202 году, а затем переиздана в переработанном виде в 1228 году.
Поль Таннери — автор классических работ по истории античной науки. Его исследования в этой области, включая переводы сочинений греческих мыслителей, до сих пор остаются важными для историков науки.
Другими словами, пефсу — это количество продуктов питания (хлеба или пива), которое можно получить из единицы сырья (геката). Это означает, что можно выразить содержание хлеба в пшенице или пива в пшенице или другом сырье в виде пефсу.
2. **Если бы из 100 граммов пшеницы мы готовили кувшины с пивом, а из того же количества — кувшины с разбавленным пивом**, то в обоих случаях у нас было бы одинаковое количество.
3. **Подробное объяснение** представлено в разделе **Обсуждение**.
4. **На изготовление сандалий уходит целый день**. Кроме того, требуется ещё один день для украшения готовых сандалий и столько же — для их окончательной отделки.
Вот почему он может шить и украшать сандалии за считанные дни. Используя три метода, мы можем получить готовые и украшенные сандалии всего за один день. Вот некоторые особенности и отличительные черты доисторических математических текстов:
1. **Эмпирический подход.** Положения и приёмы были открыты методом проб и ошибок.
2. **Преобладание конкретных задач.** Результаты либо были представлены сразу, либо описывался краткий алгоритм их получения.
3. **Отсутствие доказательств.** При решении задач давались лишь предписания: «делай так-то и так-то», без каких-либо объяснений.
4. **Широкое использование таблиц.** Например, в математике древнего Вавилона для умножения использовался сложный набор таблиц.
5. **Формирование базовых представлений** о натуральных и дробных числах, геометрических фигурах и телах. Были разработаны методы решения простых прикладных задач.
Одним из самых древних математических артефактов является кость Ишанго. Этот инструмент был изготовлен из малоберцовой кости бабуина, к одному из концов которой был прикреплён острый отщеп кварца. По всей длине кости были нанесены три ряда насечек.
Согласно одним данным, возраст артефакта составляет от 9 до 6,5 тысяч лет, в то время как другие источники утверждают, что его возраст превышает 20 тысяч лет. Кость из Лембобо** — была обнаружена в 1970 году в горах Лембобо, на границе Южной Африки и Свазиленда. Её возраст составляет около 37 тысяч лет, хотя некоторые источники утверждают, что он может достигать 43 000–44 200 лет.
* **Кость Ишанго** — была найдена в 1950 году в Бельгийском Конго, на территории стоянки Ишанго, расположенной вблизи верховьев реки Нил. Возраст артефакта оценивается по-разному: от 9 до 6,5 тысяч лет назад или даже более 20 тысяч лет.
* **Папирус Ахмеса (папирус Ринда) ** — был открыт в 1858 году египтологом Риндом. Этот манускрипт содержит 84 математические задачи и датируется приблизительно 1650 годом до нашей эры.
* **Московский папирус** — был обнаружен в декабре 1888 года в Луксоре русским египтологом Владимиром Семёновичем Голенищевым. Этот свиток длиной 5,44 м и шириной 8 см включает 25 задач.
Упражнение №3 по теме «1.2. Доисторические математические памятники»
Раздел 1: Контрольные вопросы для самопроверки знаний
Что такое задачи Aha и как они соотносятся с современными математическими уравнениями?
Как определяется крепость пива в задачах типа pefsu?
Назовите три метода, используемых для исследования доисторических математических памятников.
Как вычисляется объем усеченной пирамиды с квадратным основанием согласно задачам древних? Опишите процесс решения задачи.
Почему важно учитывать социокультурный контекст при изучении доисторических математических памятников?
Раздел 2: Тестовые задания
Вариант А (для слабых учащихся)
Выберите правильный ответ:
Какой возраст имеют найденные артефакты, такие как кость Ишанго? a) 2 тысячи лет
b) 10 тысяч лет
c) 20—30 тысяч лет
d) Более 40 тысяч лет
Заполните пропуски:
Папирус Ахмеса содержит _ математических задач, написанных примерно в _ году до нашей эры.
Правда или ложь:
Задачи бакинского типа связаны с производительностью труда работников.
a) Правда
b) Ложь
Решите простое уравнение:
Если из 10 кувшинов пива в результате процесса остался 1 кувшин, сколько кувшинов пива было использовано? Ответ: _
Вариант Б (для средних учащихся)
Ответьте на вопрос:
Как задачи Aha могут быть переведены на современный математический язык? Приведите пример.
Решите задачу:
Если для подготовки 10 кувшинов пива требуется 2 геката пшеницы, сколько потребуется пшеницы для получения 25 кувшинов? Ответ: _ гекатов.
Сравните:
В каких аспектах задачи pefsu отличаются от задач Aha? Приведите примеры.
Задача по геометрии:
Вычислите объем усеченной пирамиды, если основания имеют стороны 4 и 2 метра, а высота составляет 3 метра. (Используйте формулу: V= (A1+A2+), где A1 и A2 — площади оснований).
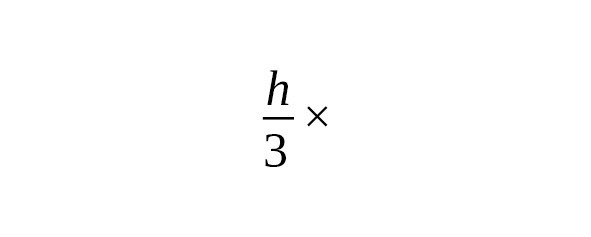
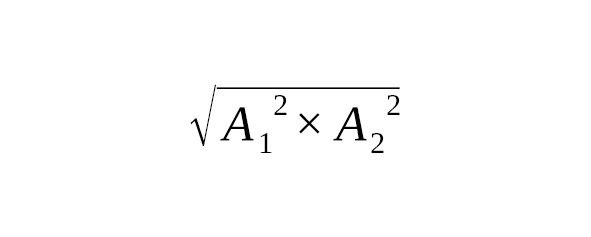
Обсудите:
Как социокультурные факторы могли влиять на развитие математических памятников в Древнем Египте и Вавилоне?
Решите кубическое уравнение по методам древних:
Найдите значение x в уравнении x3−27=0.
Переведите задачу в современный язык:
Задача 8 папируса, где «Сколько пива надо выпить для получения определенного количества пшеничного хлеба?» Как это можно записать в виде уравнения?
Выведите формулу:
Используя полученные данные о задачах Древнего Египта, выведите и объясните формулу для вычисления объема усеченной пирамиды, создавая свой собственный пример.
Дополнительные задания
Проект: Создайте модель одного из доисторических математических памятников с кратким описанием задач, которые были на нем представлены.
Рисунок: Изобразите схему, на которой будет показано, как вычисляется объем усеченной пирамиды, включая размеры и необходимые формулы.
Эти задания направлены на закрепление знаний о доисторических математических памятниках, их значимости и методах решения задач, применяемых в древних цивилизациях. Они помогут студентам лучше понять контекст, в котором развивалась математика, и её влияние на общественные и культурные структуры.
1.3. Происхождение алгебры и геометрии
Алгебра, геометрия и математика — три разных направления (дисциплины), каждое из которых обладает своими уникальными особенностями и предметом изучения.
Сходство между ними заключается в том, что все они относятся к математике — науке о количественных отношениях и пространственных формах, которые окружают нас в реальном мире.
Различия между ними проявляются в следующем:
* Алгебра концентрируется на символическом и абстрактном мышлении, операциях с числами и переменными, а также на решении уравнений и систем уравнений.
* Геометрия изучает формы, размеры, пространственные отношения и свойства фигур.
* Математика объединяет алгебру, геометрию и другие разделы, такие как арифметика, тригонометрия и высшая математика. Разделение между алгеброй, геометрией и математикой стало очевидным в IX веке благодаря труду персидского математика Аль-Хорезми. В своей книге «Китаб аль-джабр валь-мукабала» (Книга восстановления и уравновешивания) учёный систематизировал методы решения линейных и квадратных уравнений, заложив основу современной алгебры.
В 1637 году Рене Декарт в своей работе «Геометрия» сумел объединить алгебру и геометрию. Он восстановил алгебраическое понимание числа и предложил способ выражения геометрических утверждений на алгебраическом языке с помощью системы координат. Так появилась аналитическая геометрия — одно из самых значимых достижений в области математики.
До 1600 года геометрия являлась основой почти всей строгой математики. Даже в XVIII веке, когда алгебра и математический анализ уже были хорошо развиты, строгая математика рассматривалась как геометрия, а слово «геометр» было синонимом слова «математик».
Зарождение алгебры, геометрии и математики неразрывно связано с практическими потребностями человека в хозяйственной жизни.
Уже в III тысячелетии до нашей эры месопотамские государства Шумер, Аккад и Ассирия, а за ними Древний Египет и левантийское государство Эбла активно применяли арифметику, алгебру и геометрию для решения задач, связанных с налогообложением, торговлей, а также в астрономии — для учёта времени и составления календарей.
Понятие натурального числа возникло в процессе тщательного счёта и упорядочивания добытых на охоте зверей, изготовленных в мастерской горшков и собранного урожая. Понятие величины появилось в результате сравнения масс и объёмов различных сосудов и предметов. Формирование понятия геометрической фигуры происходило на основе изучения форм изделий, предметов, зданий и земельных участков.
Математика как самостоятельная наука зародилась в VI веке до нашей эры, когда пифагорейцы ввели в обиход термин «математика». Они же впервые попытались объединить геометрию и алгебру на основе арифметики.
Развитие алгебры происходило на базе уже достаточно развитой техники арифметических вычислений, которая была известна в Египте и Вавилонии. Начатки геометрии появились в результате необходимости измерять площади и объёмы, что было связано с развитием строительной техники, а несколько позднее — с астрономией.
Таким образом, возникновение алгебры, геометрии и математики стало результатом накопления и систематизации знаний, обусловленных как потребностями хозяйственной жизни человека, так и развитием науки в различных регионах.
Вот несколько книг, которые могут вам помочь в изучении истории математики, возникновения алгебры и геометрии, а также информации о первых формулах в разных странах:
«История математики» от К. В. Транчева
Эта книга предлагает читателям широкий обзор развития математики с древнейших времен до современности, включая вклад различных цивилизаций, таких как египтяне, шумеры, греки и арабы.
«Математика в древнем мире» (The Mathematics of Ancient Egypt) от И. Г. Бавиро — Книга исследует математические знания в Древнем Египте, включая информацию о геометрии, арифметике и различных формулами для расчета площадей и объемов.
«История математики» от И. Г. Хардии
Это издание рассматривает развитие алгебры и геометрии в разных культурах, таких как Древний Китай и Индия, охватывая как теорию, так и практическое применение.
«Математика в древнем Китае» от Дж. Чжана
Книга подробно описывает математические практики Древнего Китая, включая уникальные методы вычисления, которые использовались в этом регионе, а также их вклад в алгебру и геометрию.
«Алгебра и геометрия. От древних времен до ХХ века» от В. В. Федорова
Это исследование предоставляет обзор основных концепций алгебры и геометрии, их исторического развития и форм, применяемых в разных странах.
«Mathematics in the Time of the Pharaohs» от Richard J. Gillings
Это подробное исследование исследует вычисления и геометрические методы древних египтян и сравнивает их с аналогичными достижениями в других цивилизациях.
Эти книги дают возможность глубже понять, как развивалась математика в разных странах, какие формулы использовались и как они эволюционировали с течением времени. Если вас интересует конкретная тема или период, дайте знать, и я постараюсь предложить более целенаправленные рекомендации!
Наиболее подробную информацию о самых древних формулах алгебры и геометрии можно найти в книге «История математики» от К. В. Транчева и «Математика в древнем мире» от И. Г. Бавиро. Эти книги освещают важные этапы в развитии математики и представляют данные о многих культурах.
Примеры древних формул и их разработчиков:
Древний Египет:
Формула для площади прямоугольника: Площадь 𝑆=𝑎×𝑏 (где 𝑎 и 𝑏 — длины сторон).
Формула для площади треугольника: основаниевысота𝑆=12×основание×высота.
Обоснование: Египтяне использовали геометрическую интуицию и практический опыт для обоснования этих формул. Их применение можно было увидеть в строительстве и земельных измерениях.
Древний Вавилон:
Были известны квадратные уравнения. Один из методов решения квадратного уравнения 𝑎𝑥2+𝑏𝑥+𝑐=0 можно выразить через геометрические конструкции. Например, для уравнения 𝑥2=2 вавилоняне могли визуализировать его решение в виде квадрата.
Обоснование: Вавилоняне использовали численные методы и таблицы, что обеспечивало достаточно точные решения.
Древний Китай:
Положение Пифагора: 𝑎2+𝑏2=𝑐2 и его обобщенное использование. Например, в книге «Девять глав по математике» содержатся различные методы для вычисления площадей.
Обоснование: Китайские математики использовали как алгебраические, так и геометрические обоснования для своих выводов, включая доказательства через методы подмены и дополнения.
Доказательства и примеры:
Для доказательства теоремы Пифагора (которая известна с древнейших времен, но Причислена к греческим математикам), можно использовать следующие шаги:
Строим квадрат со стороной 𝑐 (гипотенуза) и на его основе строим два квадрата со сторонами 𝑎 и 𝑏.
Сравниваем площади: Площадь большого квадрата равна 𝑐2, а площадь двух небольших квадратов 𝑎2+𝑏2.
Выводим равенство: 𝑐2=𝑎2+𝑏2.
Эти доказательства, основанные на геометрических построениях, были доступны еще в античные времена.
В целом, книги, такие как «Математика в древнем мире», дают лучшее представление о таких древних формулах и концепциях, а также о том, как различные культуры достигали успехов в математике путем обоснования своих формул, используя простые геометрические построения и практическое применение.
Исторические записи о древних математиках и учёных не содержат сведений о полетах НЛО или контактах с пришельцами в том виде, в котором мы понимаем эти концепции сегодня. Материал по исследованию НЛО и пришельцев стал широко распространённым только в 20 веке. Однако, в древних культурах действительно встречались элементы мифологии и астрономии, которые можно интерпретировать как связи с космосом, но это не означает наличие уфологии в современном понимании.
Древние учёные и их интерес к астрономии
Мифология и астрономия: Многие древние культуры (например, шумеры, египтяне и мая) имели развитые астрономические знания. Они наблюдали за звёздами и планетами и создавали календари, основываясь на этих наблюдениях. Мифы, связанные с небом и звёздами, часто служили объяснением небесных явлений.
Трактаты по астрономии: Например, вавилонские астрономы использовали математические расчёты для предсказания солнечных и лунных затмений, используя простые тригонометрические и арифметические методы.
«Маги» и «колдуны»
Древние учёные и маги порой рассматривались как подобия современным учёным. Однако их методы и практики в большей степени основывались на наблюдениях и интуиции, чем на формализованной математике.
Математические формулы
Древние математические концепции использовались для:
Навигации и астрономических расчетов: Например, древние египтяне использовали геометрические формулы для определения высоты пирамид и расстояний.
Предсказания небесных явлений: Использование циклических периодов и заложенные в них числовые последовательности.
Современные параллели
По мере развития науки и философии, идеи о внеземных цивилизациях стали более популярными. Однако они появились только в XX веке вместе с такими направлениями, как уфология, но не имеют оснований в математических учениях древних учёных.
В заключение, хотя некоторые древние культуры действительно предполагали существование внеземных существ или божеств, это было скорее в рамках мифологических систем, чем в рамках научного исследования или математики, как мы её понимаем сегодня.
Пифагор и его математическая школа, известная как пифагорейцы, сделали значительный вклад в развитие математики и геометрии. Хотя большинство сведений о них сохранилось через труды других авторов, несколько ключевых концепций и формул можно выделить.
Основные формулы и теоремы пифагорейцев:
Теорема Пифагора:𝑎2+𝑏2=𝑐2. В этой формуле 𝑎 и 𝑏 — катеты прямоугольного треугольника, а 𝑐 — гипотенуза. Эта теорема утверждает, что сумма квадратов длины катетов равна квадрату длины гипотенузы.
Доказательство: одно из самых известных доказательств основано на построении квадратов на каждом из трёх сторон треугольника. Можно нарисовать квадрат со стороной 𝑐 на гипотенузе и два квадрата на катетах. При расчете площадей будет показано, что площадь квадрата на 𝑐 равна сумме площадей квадратов на 𝑎 и 𝑏.
Теорема о средних пропорциях: Если два числа 𝑎 и 𝑏 находятся в отношении, то существует еще одно число 𝑥, которое называется средним геометрическим и удовлетворяет:𝑎𝑏=𝑏𝑥Это приводит к уравнению 𝑏2=𝑎𝑥 и может быть использовано для нахождения пропорций в различных геометрических фигурах.
Пифагоровы тройки: Пифагорейцы изучали так называемые «пифагоровы тройки», как, например, (3, 4, 5) и (5, 12, 13). Эти тройки представляют собой целые числа, удовлетворяющие теореме Пифагора.
Описание работ и источников
«Элементы» Евклида — Один из наиболее известных кремнейгеометрии, в котором описываются различные теоремы, включая теорему Пифагора. Хотя сам Пифагор не оставил учебников, работы Евклида систематизировали и сохранили его достижения.
«Метафизика» Аристотеля — Здесь также можно найти ссылку на пифагорейскую философию и их представление о числах и отношении чисел к физическому миру.
Работы Платона — Платон был глубоким поклонником пифагорейских идей и неоднократно упоминал их в своих трудах. В частности, в диалоге «Тимей» он исследует связь между числами и природой.
Примеры доказательства:
1. Доказательство теоремы Пифагора с помощью квадрата
Построить квадрат на гипотенузе с площадью 𝑐2.
Построить два квадрата на катетах с площадями 𝑎2 и 𝑏2.
Если разрезать квадрат на гипотенузе и переставить его части, то они займут место двух меньших квадратов, что и доказывает, что 𝑎2+𝑏2=𝑐2.
2. Доказательство средних пропорций через подобие треугольников
Рассмотрим прямоугольный треугольник со сторонами 𝑎,𝑏,𝑐.
Произведем следующее: напрашивается вывод о том, что если один треугольник подобен другому, то отношения длин их соответствующих сторон равны, что и подтверждает среднюю пропорцию.
Таким образом, достижения пифагорейцев в области математики и геометрии положили начало многим аспектам, изучаемым и понятным в современном математическом образовании.
Различие между алгеброй, геометрией и математикой можно увидеть в работах различных учёных:
* **Аль-Хорезми**. В своём труде по алгебре он чётко отделил её от геометрии.
* **Декарт**. В работе «Геометрия» (1637) учёный открыл взаимосвязь алгебры и геометрии, введя понятия переменной величины и функции.
* **Дедекинд, Кантор и Гильберт**. Эти учёные стремились уточнить исходные понятия геометрии и других математических наук на логической основе.
Однако существует и точка зрения, согласно которой эти понятия не имеют чёткого разделения. Это формалистское или структуралистское понимание математики, которое оформилось к концу XIX века и акцентирует внимание на логических особенностях и специфических функциях математического знания.
Кроме того, стоит отметить, что развитие алгебры, геометрии и математики в Индии, Турции и Китае имело свои особенности.
В Индии средневековые математики достигли наибольших успехов в области теории чисел и численных методов. Индийцы существенно продвинулись в алгебре, разработав более богатую, хотя и несколько громоздкую, символику, чем у Диофанта.
Геометрия, напротив, не вызывала у индийцев такого же интереса, как у греков. Их доказательства теорем зачастую состояли из простого чертежа и слова «смотри». Формулы для вычисления площадей и объёмов, а также тригонометрические соотношения, вероятно, были унаследованы от греков.
В Древнем Китае уже были известны десятичная система счисления, специальная иероглифическая символика, приёмы работы с большими числами, а также различные вспомогательные счётные устройства, такие как узелки и счётная доска. Кроме того, в то время использовались циркуль, линейка и угольник.
В Турции в седьмом классе нет разделения на алгебру и геометрию — все дисциплины изучаются по одному учебнику. Задания по математике в этой стране кажутся очень лёгкими, особенно по алгебре, по сравнению с тем, что предлагают в России. Международный совет по науке (МСНС), основанный в 1931 году, представляет собой некоммерческую организацию, которая занимается планированием и координацией междисциплинарных исследований, направленных на решение значимых проблем, актуальных для науки и общества.
В последние годы география деятельности ICSU претерпела значительные изменения. Всё больше внимания уделяется поддержке научного потенциала развивающихся стран и интеграции их ученых в международные исследовательские проекты.
Создание трех региональных офисов ICSU, расположенных в Африке, Азии и Тихоокеанском регионе, а также в Латинской Америке и Карибском бассейне, представляет собой важное преобразование в структуре организации. Это изменение преследует две основные цели:
1. Расширение участия ученых и региональных организаций из развивающихся стран в программах и мероприятиях сообщества ICSU.
2. Более активное вовлечение МСНС в укрепление науки с учетом региональных приоритетов через научное сотрудничество.
Что касается Латинской Америки и Карибского бассейна, то это важный шаг в направлении преодоления барьеров между «островами конкуренции», которые существуют в каждой стране. В совокупности эти усилия могут существенно изменить повестку дня научных исследований в регионе.
Первым шагом на пути к созданию Регионального бюро стало формирование в 2006 году Регионального комитета по Латинской Америке и Карибскому бассейну, в который вошли известные ученые из региона.
По состоянию на апрель 2007 года Региональное отделение для Латинской Америки и Карибского бассейна было третьим стабильным отделением CIDA. Оно располагалось в Бразильской академии наук в Рио-де-Жанейро и финансировалось Министерством науки и технологий Бразилии, ICSU и Национальным советом по науке и технологиям (CONACYT) Мексики. С октября 2010 года этот офис будет находиться в Мексиканской академии наук при поддержке CONACYT. В рамках Стратегического плана ICSU на период с 2006 по 2011 годы Региональный комитет определил четыре приоритетных направления для дальнейшего развития:
1. **Преподавание математики**
2. **Биоразнообразие**
— Сохранение и использование биоразнообразия во всех странах Латинской Америки и Карибского бассейна.
— Полная интеграция научного сообщества малых стран региона в Международную программу по биоразнообразию (DIVERSITAS).
3. **Риски и стихийные бедствия**
— Предотвращение и смягчение рисков, особенно тех, что связаны с гидрометеорологическими явлениями. Особое внимание уделяется необходимым исследованиям в области социальных наук.
4. **Устойчивая энергетика**
— Оценка существующих энергетических мощностей в регионе LAC и анализ социальных последствий использования и освоения новых энергетических ресурсов.
Для реализации этих направлений были созданы четыре группы научного планирования, которые начали свою работу.
Группа научного планирования в области преподавания математики была создана для анализа текущего состояния данной сферы в регионе и разработки детальных целей и конкретных направлений исследований, которые будут осуществляться в ближайшие годы.
В состав группы вошли высококвалифицированные ученые из нескольких научных центров, которые провели огромную работу в крайне сжатые сроки.
Данный документ представляет собой заключительный отчет Группы научного планирования, который будет представлен научному сообществу в надежде, что он окажет значительное влияние на процесс преподавания математики в будущем. В последнее время во всем мире наблюдается растущее беспокойство по поводу качества математического и естественнонаучного образования. Анализируя последние данные, становится очевидно, что мы не достигаем удовлетворительного уровня в этой области. Это представляет собой серьезную проблему для стран Латинской Америки и Карибского бассейна (ЛАК).
Очевидно, что наши дети отстают от своих сверстников. Математика и естественные науки являются важнейшими инструментами для обучения на протяжении всей жизни и основой для прогресса нашей цивилизации. Мы должны срочно что-то изменить, особенно в странах, которые были очагом ярких цивилизаций, таких как майя и инки, внесших значительный вклад в науку и математику.
Дети в ALC не получают образования, необходимого им для полноценной жизни и продуктивной работы. Это подтверждается результатами международных оценок, таких как тенденции в международном изучении математики.
В разных странах мира регулярно проводятся исследования, такие как Международная программа по оценке достижений учащихся по математике и естественным наукам (TIMSS). Эти исследования предоставляют точные и актуальные данные об успеваемости школьников по математике и естественным наукам.
Чили стала единственной страной в нашем регионе, принявшей участие в TIMSS. Результаты оказались неудовлетворительными, особенно если сравнить их с результатами другой страны — Marruecos, чей ВВП на душу населения почти в девять раз меньше, чем в Чили.
Помимо TIMSS, существуют и другие международные оценки, такие как Программа международной оценки студентов (PISA) ОЭСР. PISA оценивает способности и знания учащихся, которые близки к завершению обязательного образования. Это не обычный школьный экзамен. Вместо того чтобы оценивать уровень знаний, PISA оценивает, насколько хорошо учащийся подготовлен к жизни после окончания 5-го класса начальной школы. PISA измеряет навыки грамотности и математики. Во многих странах низкий уровень владения математикой связан с различными недостатками в образовании.
Владение языком. ериод с 1955 по 1961 год
Первые преподаватели математики в Колумбии, за исключением иностранцев, которые были наняты на кафедры математики в различных колледжах и университетах, имели инженерное образование. В то же время преподаватели среднего и высшего образования проходили обучение в Педагогической школе для мальчиков Тунха.
В 1933 году эта школа была преобразована в Педагогический факультет, а в 1934 году — в Факультет педагогических наук. Первоначально они находились в Тунхе, а затем переехали в Боготу. В 1953 году они стали первыми двумя педагогическими университетами Колумбии после разделения на мужские и женские отделения в 1951 году.
В конце 1950-х годов в Колумбии было всего три программы по математике:
1. Программа Национального университета Боготы, которая впервые предложила степень бакалавра в 1951 году.
2. Программа Колумбийского педагогического университета в Тунхе, предлагавшая степень бакалавра математики. Позже этот университет был преобразован в Университет Национальной педагогики.
3. Программа Женского педагогического университета Боготы, также предлагавшая степень бакалавра. Позже этот университет также был преобразован в Национальный педагогический университет.
В 1959 году в Колумбию приехал Ютакеучи, что стало началом нового этапа в преподавании математики. Профессор Такеучи и другие, такие как Хорват, представили новые, ранее неизвестные предметы, такие как ряды Фурье и функциональный анализ.
История развития математики и ее преподавания в Колумбии началась с основания Колумбийского математического общества (SCM). Эта организация стала первым объединением специалистов и любителей математики в стране.
SCM было основано в 1955 году с целью содействия научно-исследовательскому прогрессу и улучшению качества математического образования в Колумбии. Кроме того, его миссия заключалась в представлении и объединении математического сообщества.
С момента своего появления общество проделало огромную работу, организуя мероприятия регионального и национального масштаба и публикуя журналы и материалы, отражающие его деятельность.
Его основными партнерами являются математики и преподаватели математики на университетском уровне. Согласно установленным правилам, к числу партнеров также относятся специализированные математические учреждения и студенты, успешно завершившие третий год обучения по специальности «Математика».
Чтобы реализовать свою миссию, Общество ставит перед собой следующие цели:
* Стимулировать исследования и улучшать качество преподавания математики.
* Выступать связующим звеном между математиками и учителями.
* Организовывать мероприятия и программы, способствующие развитию математики.
* Способствовать созданию и улучшению условий для тех, кто занимается развитием математики в различных областях, а также ее преподаванием и распространением.
Эти цели были сформулированы в 2009 году Колумбийским математическим обществом.
В 1956 году на национальном уровне был организован первый Колумбийский семинар по преподаванию математики в университетах. Его проведение было инициировано университетским фондом, который впоследствии стал ICFES (Колумбийский институт содействия высшему образованию). На этом семинаре присутствовала выдающаяся математик Лорен Шварц (Санчес, 2006).
1961—1998 годы стали периодом пионеров в развитии математического образования.
История математического образования как научной дисциплины в странах Америки относительно молода. В течение последних десятилетий произошло несколько значимых событий, которые оказали влияние на развитие математического образования во всем мире и, в частности, в Колумбии.
Одним из таких событий стал запуск советского спутника «Спутник» 4 октября 1957 года. Этот запуск заставил Соединенные Штаты Америки более серьёзно отнестись к преподаванию математики, чтобы не отставать от Советского Союза в гонке вооружений и космосе. В ответ на это в США был создан Математический проект Мэдисона, направленный на повышение качества математического образования.
Также в Канаде начался новый этап в изучении и преподавании математики с появлением проекта обучения математике в Шербруке.; Наконец, в те годы наиболее значимым событием стал Международный математический конгресс в Эдинбурге, который проходил в 1958 году. На этом конгрессе обсуждалась кардинальная реформа математического образования.
Ещё одним важным событием стал семинар в Роямаунте, который состоялся в 1959 году. На этом семинаре Дюдонне выступил с критикой классического математического образования, используя фразу «ниже Евклида». Он предложил новый подход к преподаванию математики, известный как Moderna Math. Этот подход основан на концепциях множества, взаимосвязи и функции, которые можно разделить на две большие категории: алгебраические структуры и топологические структуры (Баррантес и Руис, 1998), а также структуры порядка.
Вышеизложенные события послужили основой для учреждения Межамериканского комитета по математическому образованию (СИАЕМ), первая конференция которого прошла в Боготе с 4 по 9 декабря 1961 года под эгидой Международной комиссии по математическому образованию.
Основная цель этой конференции заключалась в изучении методов преподавания математики в средних школах и университетах, а также в принятии резолюций, направленных на проектирование будущего сотрудничества (Баррантес-и-Руис, 1998, стр. 9).
В этой первой конференции приняли участие представители 24 стран и 48 участников. На ней были рассмотрены различные аспекты, касающиеся подготовки учителей математики, работы учителей и улучшения качества преподавания.
В результате проведения первого CIAEM в 1962 году Министерство образования Колумбии предложило реформировать учебную программу по математике для бакалавриата. В первом классе было введено отдельное понятие целого.
Однако эта реформа не имела большого значения, так как фактически привела к разделению предмета, который соответствовал классической математике, на отдельные дисциплины: арифметику, алгебру, геометрию, тригонометрию, аналитическую геометрию и математический анализ. **Академические учреждения**
На университетском уровне математическое образование начинается в педагогических вузах, таких как Педагогический университет Тунджи и Национальный педагогический университет, а также на педагогических факультетах других университетов с общим образованием. Первоначально математическое образование включалось в курсы дидактики математики на бакалавриате по специальности «Математика», поскольку в пятидесятые и начале шестидесятых годов это понятие не было общеизвестным.
Вслед за педагогическими университетами в 1955 году в Университете Антиокии и в 1964 году в Атлантическом университете были введены степени бакалавра по математическому образованию — это стало первым подобным опытом в Карибском регионе.
Программы бакалавриата также были запущены в различных учебных заведениях, включая Промышленный университет Сантандера, Папский университет Хавериана, Университет дель Валле, Папский Боливарианский университет, Университет Кордовы, Университет Памплоны и Народный университет Сезара.
Цель программ заключалась в подготовке учителей для среднего образования, обладающих необходимой общей педагогической подготовкой. Однако специализированной подготовки по дидактике математики было недостаточно. Учебные планы включали лишь один или два курса общего характера по этому предмету, в то время как математический компонент иногда достигал 65% от общего числа дисциплин (Кубильос, 2006).
Учитывая эту тенденцию и нехватку учителей математики для высшего образования, вызванную ограниченным количеством программ по чистой математике в 60-х и 70-х годах, значительная часть выпускников была вынуждена поступать на преподавательскую работу в высшие учебные заведения.
В 1968 году спрос на преподавателей математики в технических специальностях стал настолько высоким, что бакалавры и инженеры были вынуждены сменить профессию, чтобы заполнить этот пробел (Restrepo, 1981).
Как уже упоминалось ранее, на начальном этапе своего становления в шестидесятые годы математическое образование рассматривалось как дидактический аспект математики. В то время другие дисциплины, такие как психология обучения, социология образования и философия образования, считались общими и не входили в структуру математического образования как интегративной науки.
Исследование… Несмотря на общие скромные достижения в математике в Латинской Америке, в этом регионе есть несколько ярких примеров того, как можно улучшить процесс преподавания и изучения математики, привлекая опытных математиков. Исследовательская группа ICSU-LAC по преподаванию математики собрала информацию из нескольких стран. Этот список, конечно, не является исчерпывающим, и, безусловно, существуют и другие положительные примеры, помимо тех, которые мы здесь представляем.
В следующем разделе мы будем рассматривать эти примеры без какого-либо определенного порядка.
## Аргентина
В этой стране прилагаются активные усилия для популяризации математики и подготовки специалистов, которые смогут преподавать этот предмет. Одним из наиболее значимых примеров являются так называемые международные семинары и дни решения задач, которые проводятся ежегодно в рамках Национальной математической олимпиады. Это ежегодное событие собирает более 300 преподавателей и группу экспертов со всего мира на одну неделю.
Аргентинские олимпиады по математике — одни из самых масштабных и престижных соревнований в Лос-Анджелесе. Они привлекают учащихся со всего мира, начиная с начальной школы и заканчивая старшей.
Университет Буэнос-Айреса (UBA) также вносит свой вклад в развитие математики, предлагая различные программы для широкой аудитории через свой базовый цикл по математике. Каждый год UBA организует увлекательные экскурсии по элементарной математике, собирая около 29 групп школьников.
В рамках этих экскурсий учащиеся имеют возможность прогуляться по выставке с гидом и насладиться заранее подготовленными математическими играми. Кроме того, проводятся лекции для разных аудиторий, включая учителей, студентов различных уровней и широкую публику.
Исторически сложилось так, что первые исследования в области математического образования были проведены в рамках SCM. Как отмечает Санчес (2001), первым исследовательским проектом по математике, получившим одобрение Colciencias, стал проект Виктора Альбиса, который был связан с историей математики в Колумбии и состоялся в 1974 году.
Однако, что касается математического образования, то первой исследовательской группой, созданной в 1981 году, стали Мэри Фальк из Университета Антонио Нариньо и Мириам Асеведо из Национального университета (Баскский, 2008). Позднее, в 1987 году, эта группа стала образовательной компанией Университета Анд.
Эта группа была известна публикацией серии текстов по математическому образованию, среди которых стоит отметить «Учитель, я не понимаю, почему убили математичку, если она была такой хорошей девочкой?» и другие. Она также приняла участие в нескольких работах на III CIBEM в Каракасе.
Алонсо Такахаши (1990) в своем исследовании охватывает историю развития математики как области знаний с колониальных времен до восьмидесятых годов, сравнивая состояние математики в Колумбии с другими странами, такими как Аргентина, Мексика, Бразилия и Венесуэла.
Согласно Ортису (2000), в период с 1991 по 1999 год COLLCIENCIAS финансировала 22 исследовательских проекта в области математического образования, которые были выполнены 15 исследовательскими группами. Из них 13 были университетскими, одна — из Министерства национального образования, а одна — совместной.
Работы охватывали разнообразные темы: совершенствование учебных процессов, разработка учебных программ, формирование математических концепций, культурное измерение математического образования, технологии преподавания, подготовка учителей, выявление трудностей в обучении, аргументативные формы, когнитивные стили, природа символических систем и сетевое обучение учителей.
Среди других выдающихся исследователей на национальном и международном уровне можно выделить:
* Карлоса Васко из Папского университета Хавериана, который внес значительный вклад в разработку учебных программ по математике в Колумбии. В 1993 году он представил обзор состояния математического образования в стране.
* Луис Карлос Арболеда, который специализируется на эпистемологии математики.
* Виктора Альбиса, изучающего историю математики и науки в целом.
* Клару Хелену Санчес, которая исследует историю математики и ее преподавания.
* Мириам Асеведо, занимающуюся дидактикой математики.
История событий в области математического образования в Колумбии началась относительно недавно. В 1961 году страна стала организатором первой Международной конференции по образованию в области математики (CIAM). На этом мероприятии была создана Межамериканская комиссия по математическому образованию, которая действует и по сей день.
В рамках первого CIAEM особое внимание уделялось преподаванию современных математических дисциплин и прикладных наук в этой области. Как отмечают Баррантес и Руис (1998), в ходе обсуждений были подняты вопросы подготовки учителей, роли практикующих учителей и совершенствования преподавания. По итогам конференции были сделаны выводы, подчеркивающие следующие аспекты:
Университеты играют ключевую роль в подготовке учителей математики для средних школ. Они осуществляют этот процесс под влиянием самых квалифицированных специалистов в области математики. Важно, чтобы педагогическая составляющая была представлена в надлежащих пропорциях. Куба занимает особое место в регионе Латинской Америки и Карибского бассейна. Здесь обучение преподавателей осуществляется на университетском уровне, а базовая подготовка педагогов в области математики отвечает высоким стандартам. Тем, кто желает посвятить себя преподаванию этого предмета, предлагаются специальные практики.
Сеть высших педагогических институтов, расположенных на базе университетов, играет ключевую роль в образовательной системе острова, особенно в сфере математики. На Кубе действует сильная учебная программа по математике и информатике для учителей.
Государственная политика, ориентированная на науку и технику, оказывает значительную поддержку не только математике, но и другим наукам в целом. В соответствии со стратегическим планом Кубы, точные науки не только способствуют техническому прогрессу, но и являются основой для укрепления образования на всех уровнях и стимулирования подготовки новых поколений кубинских ученых.
Для Кубы важно вовлечь все научное сообщество в процесс развития и совершенствования.
Процесс улучшения качества образования стал особенно заметен, особенно в области обучения математике, где активно используются различные подходы, включая неформальные информационные технологии.
Следует упорядочить контакты между преподавателями средних школ и университетами. Это позволит повысить качество обучения и обмена опытом. Кроме того, необходимо принять меры для улучшения экономического и социального положения учителей.
Действующие профессора, не имеющие ученой степени, должны иметь возможность получить ее. Также следует активизировать программы повышения квалификации учителей математики в средних школах.
Важно распространять мероприятия, проекты и публикации, направленные на улучшение и модернизацию преподавания математики.
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.
