
Бесплатный фрагмент - Математические задачи и головоломки
Для школьников младших и старших классов
Задачи
1. Нужно сосчитать!
Посмотрите внимательно на представленную геометрическую фигуру. Как Вы думаете, сколько треугольников в данной фигуре?
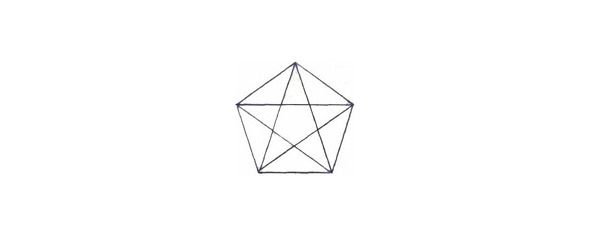
2. За три хода.
Разделите спички на 3 кучки — в одну 11, другую — 7 и в третью — 6 спичек. А сейчас нужно переложить спички из любой одной кучки в любую другую, так, чтобы спичек в каждой кучке было поровну, то есть, по 8 штук.
Но, нужно соблюсти условие: в кучку можно добавлять столько спичек, сколько в ней имеется. И сделать это нужно за 3 хода.
Примечание: Вместо спичек могут быть использованы другие предметы.
3..Дробим на части.
У нас есть число 45. Нужно раздробить его на четыре части так, что если к первой части прибавить 2, от второй отнять 2, третью умножить на 2, а четвертую разделить на 2, то все числа будут одинаковыми.
4. Попробуйте отвесить.
В пакете содержится 9 кг крупы. Необходимо при помощи чашечных весов с гирями в 50 и 200 граммов развесить всю крупу в два пакета: в один — 2 кг, в другой — 7 кг. Разрешается это сделать только 3-мя взвешиваниями.
5. Скоростное сложение.
Напишите одно под другим какие-нибудь 2 числа любой величины. Я припишу третье и мгновенно, слева направо напишу сумму всех трех чисел.
Например, вы написали:
72603294
51273081
Я припишу число: 48726918 и сразу назову вам сумму.
Сообразите! Какое число следует приписывать и как в этом случае быстро находить сумму?
6. Сколько их?
У мальчика столько же сестер, сколько и братьев, а у его сестры — сестер вдвое меньше, чем братьев.
Сколько в этой семье братьев и сколько сестер?
7. Лестница.
В доме 6 этажей. Подсчитайте, во сколько раз путь по лестнице на шестой этаж длиннее, чем путь по той же лестнице на третий этаж, если пролеты между этажами имеют по одинаковому числу ступенек?
8. Попробуйте угадать.
Половина — треть его. Попробуйте угадать, какое это число?
9. Сколько мне лет?
Когда моему отцу был 31 год, мне было 8 лет, а теперь отец старше меня вдвое. Сколько мне лет теперь?
10. От 1 до 19.
В девятнадцати кружках требуется расставить все целые числа от 1 до 19 так, чтобы сумма чисел в любых трех кружках, лежащих на одной прямой, равнялась 30.
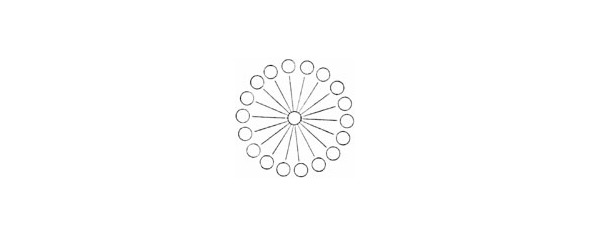
11. Головоломка
Какой знак надо поставить между написанными рядом цифрами 2 и 3, чтобы получилось число, большее двух, но меньшее трех?
12. Пять минут на размышления.
Представьте себе деревянный куб со сторонами 30 см, вся поверхность которого окрашена в один красный цвет.
1). Сколько потребуется разрезов, чтобы разделить куб на кубики со стороной 10 см?
2). Сколько получится таких кубиков?
3). Сколько кубиков будут иметь по 4 окрашенные грани?
4). Сколько кубиков будут иметь по 3 окрашенные грани?
5). Сколько кубиков будут иметь по 2 окрашенные грани?
6). Сколько кубиков будут иметь по 1 окрашенной грани?
7). Сколько кубиков будет не окрашенными?
13. Прогноз погоды (шутка).
Если в 12 часов ночи идет дождь, то можно ли ожидать, что через 72 часа будет солнечная погода?
14. Трехзначное число.
Если от задуманного мной трехзначного числа отнять 7, то оно разделится на 7, а если отнять от него 8, то оно разделится на 8, если отнять от него 9, то оно разделиться на 9. Какое число я задумал?
15. Сколько Вам лет?
— Не хотите сказать? Тогда скажите, сколько получится, если от числа, в 10 раз большего, чем число ваших лет, вычесть произведение какого-нибудь однозначного числа умноженного на 9. Благодарю вас, теперь мне известно, сколько вам лет.
Способ отгадывания: отделить от объявленного результата число единиц и сложить его с оставшимся числом. Например: от числа 170, которое в 10 раз больше число лет, отняли, скажем, 27. после этого объявили результат: 143. Определяем возраст: 14+3=17. Продумайте основу фокуса.
16. Угадать возраст.
Для разнообразия можно предложить умножить число лет на 2, прибавить 5, а сумму опять умножить на 5; попросить сказать результат. Последней цифрой результата, очевидно, будет 5. надо ее отбросить, а от оставшегося числа отнять 2. Разность и будет искомым возрастом. Пример: Пусть возраст 22 года. Производим требуемые действия: 22*2=44, 44+5=49, 49*5=245. Угадываем возраст: 24—2=22.
Необходимо доказать вариант угадывания возраста.
17. Сколько деталей?
В токарном цехе завода вытачиваются детали из свинцовых заготовок. Из одной заготовки — деталь. Стружки, получившиеся при выделке шести деталей, можно переплавить и приготовить еще одну заготовку.
Сколько деталей можно сделать, таким образом, из 36 свинцовых заготовок?
18. Спящий пассажир.
Когда пассажир проехал половину всего пути, то лег спать и спал до тех пор, пока не осталось ехать половину того пути, что он проехал спящим.
Какую часть пути пассажир проехал спящим?
19. Может ли быть такое число?
Может ли быть такое число, которое при делении на 3 дает в остатке 1, при делении на 4 — в остатке 2, при делении на 5 — в остатке 3 и при делении на 6 дает в остатке 4? Какое это число?
20. «Вечный» календарь.
Все «вечные» календари сводятся в основном к трем типам: табличные, механические и аналитические. Наибольший интерес для обыденной жизни представляют аналитические календари. Это, как правило, математическая формула, представляя в которую известные числа и производя несложные математические вычисления, можно определить день недели в любую дату, как в прошлом, так и в будущем. Из всего многообразия формул приведем одну (для нового стиля; кроме того, следует учесть, что годы 1700, 1800 и 1900 не високосные):
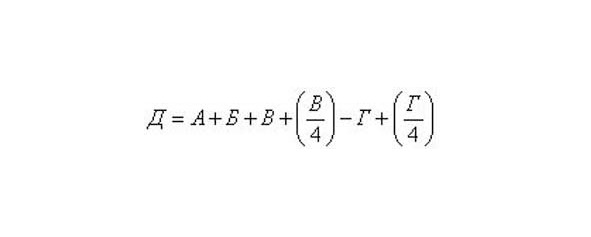
где А — календарное число месяца, Б — месячный коэффициент, В — номер года, Г — число столетий. Месячный коэффициент Б находится по таблице: январь — 6 (для високосных лет — 5), февраль — 2 (для високосных лет — 1), март — 2, апрель — 5, май — 7, июнь — 3, июль — 5, август — 1, сентябрь — 4, октябрь — 6, ноябрь — 2 и декабрь — 4.
В приведенной формуле символ () означает, что нужно взять только целую часть частного. По формуле вычисляем число Д. Если теперь разделить Д на 7, то остаток укажет день недели (1 — понедельник, 2 — вторник, 3 — среда и т.д.). Если Д делится на 7 без остатка, то это будет соответствовать воскресенью.
Вычислим день недели 22 июня 1941 г. А=22, Б=3, В=1941, (В/4) =485, Г=19, (Г/4) =4. После подстановки этих чисел в формулу получим Д = 2436. Это число на 7 делится без остатка. 22 июня 1941 года было, как известно, воскресенье.
21. Мальчики и яблоки.
Трое мальчиков имеют по некоторому количеству яблок. Первый из мальчиков дает другим столько яблок, сколько каждый из них имеет. Затем второй мальчик дает двум другим столько яблок, сколько каждый из них теперь имеет; и третий мальчик также дает каждому из двух других столько яблок, сколько имеется у каждого в этот момент. После этого у каждого из мальчиков оказывается по 8 яблок.
Сколько яблок было вначале у каждого мальчика?
22. Сколько у кого денег?
Двое крестьян поделили между собой 7 рублей, причем один получил на 3 рубля больше другого.
Сколько денег досталось каждому из них?
23. Они любят есть вместе.
Лошадь съедает стог сена за 2 дня, корова — за 3, овца — за 6. За сколько дней они съедят стог, если будут есть его, вместе?
24. Угадывание задуманного числа.
Задумайте число. Отнимите 1. Остаток удвойте и прибавьте первоначально задуманное число. Скажите результат. Я угадаю задуманное число.
25. Превратить 14 в пять.
Из спичек (счетных палочек) выложена цифра 14. Как превратить ее в цифру 5, переложив только одну спичку (счетную палочку)?

26. Сколько раз?
Сколько раз можно прочитать слово «ОРХИДЕЯ» в представленной фигуре?
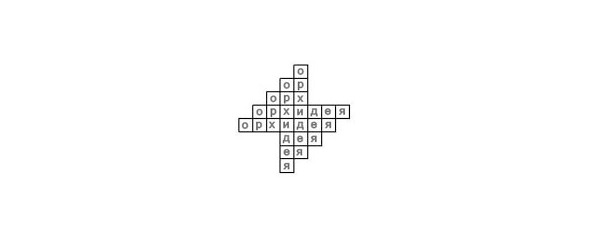
27. Исправить ошибку.
Берем 12 спичек (палочек) и выкладываем из них «равенство», как показано на рисунке.
Как видите, «равенство» 6–4 не может равняться 9.
Как переложить одну спичку так, чтобы получилось правильное равенство? Задача решается несколькими способами.
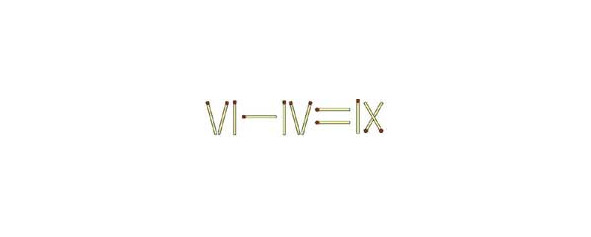
28. Хитроумная головоломка.
Из 6 спичек выложите дробь, как показано на рис. Не касаясь других спичек, нужно передвинуть только одну так, чтобы получилась арифметическая дробь равная 1. Спичку, изображающую горизонтальную черту дроби, двигать нельзя.
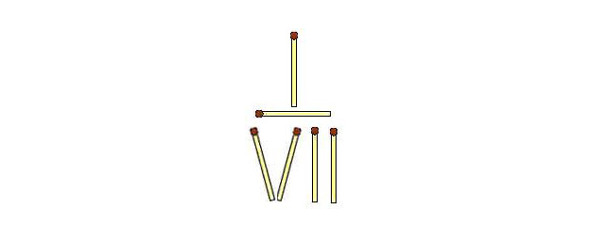
29. Жук.
На рисунке изображен «жук» из 10 спичек (счетных палочек). Необходимо изменить направление движения жука, переложив всего три спички (счетные палочки).

30. Сложить метр.
Каждая из имеющихся 13 спичек имеет длину 4,5 см. Как из них сложить метр?
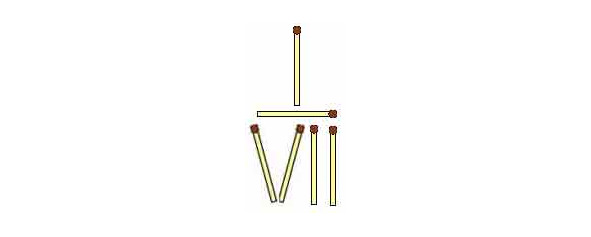
31. Превратить дробь.
На рисунке из семи спичек выложено число 1/7. Переложив всего одну спичку нужно превратить эту дробь в число 1/3. Попробуйте!
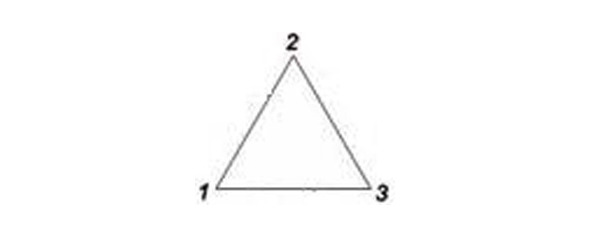
32. Волшебный числовой треугольник.
В вершинах треугольника помещены числа 1, 2 и 3. Разместите числа 4, 5, 6, 7, 8 и 9 по сторонам треугольника (по две цифры на каждой стороне) так, чтобы сумма всех чисел вдоль каждой стороны треугольника равнялась 17. Это нетрудно, так как известны числа в вершинах треугольника.
А сейчас попробуйте разместить числа 1, 2, 3, 4, 5, 6, 7, 8 и 9 вдоль сторон треугольника (по четыре цифры на стороне) так, чтобы сумма чисел на каждой стороне треугольника равнялась 20.
Числа в вершинах треугольника будут другие. В первом и втором случаях числа не повторяются и должны размещаться только по одному разу. Расположение чисел по сторонам треугольника может быть разнообразным.
33. Сколько стоит книга?
За книгу заплатили 1 рубль и еще половину стоимости книги. Сколько стоит книга?
34. Шутка.
Приготовьте 8 квадратов с числами 1, 2, 3, 4, 5, 6, 7, 8 и 9 и расположите их в два столбца, как показано на рисунке. Необходимо переместить всего два квадрата и добиться того, чтобы сумма чисел в обоих столбцах была одинаковой.
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.