Бесплатный фрагмент - Квантовая химия в примерах

1. Введение

Квантовая химия представляет собой фундаментальную область науки, объединяющую принципы квантовой механики с задачами изучения строения и свойств химических соединений. Её методы позволяют не только описывать уже известные вещества, но и предсказывать существование новых материалов с уникальными характеристиками, которые могут быть недостижимы в стандартных условиях.

Данная книга «Квантовая химия в примерах» призвана стать практическим руководством для тех, кто стремится глубже понять взаимосвязь между квантово-механическими моделями и реальными химическими структурами. В её основу положен оригинальный подход, сочетающий геометрическую интерпретацию волновых функций с анализом распределения потенциальных ям, занятых электронами и ядрами.

В первых главах читатель познакомится с базовыми понятиями, такими как модели атомов в виде кубических и гексаэдральных структур, правила заполнения электронных оболочек, а также принципы формирования химических связей через взаимодействие «треугольников» (вакантных потенциальных ям) и «крестиков» (областей, занятых фермионами). Далее будут рассмотрены конкретные примеры кристаллических решёток — от классических (медь, графит, алмаз) до экзотических соединений, стабильных только при экстремально высоких давлениях (например, динатриевый гелид Na2He, тригидрид серы H3S).

Отдельное внимание уделяется методологии предсказания химических реакций и материалов, в том числе с использованием алгоритмов эволюционного типа, таких как разработанный А. Р. Огановым. В книге также обсуждаются вопросы устойчивости структур, электропроводности, фазовых переходов и тепловых эффектов, что позволяет взглянуть на химические процессы через призму квантовой термодинамики.

Цель книги — не только изложить теоретические основы, но и дать читателю инструменты для самостоятельного моделирования и анализа химических систем. Представленные примеры, расчёты и графические иллюстрации помогут сформировать целостное представление о том, как квантовая механика определяет строение и поведение вещества на атомном уровне.

Мы надеемся, что этот материал будет полезен студентам, исследователям и всем, кто интересуется современной химией и её квантовыми основами.

Данное пособие является продолжением книги «Путешествие в квантовую механику».

Приятного чтения!

2. Общие положения о строении кристаллов и молекул

Во второй главе настоящей монографии мы рассмотрим химические соединения, состоящие из двух простых ионов, имеющих квантовые уровни с номером h=2. В Периодической таблице Менделеева исследуемые атомы расположены во втором периоде: Li, Be, B, C, N, O, F, Ne. На чертежах 2.1—2.4 изображены фрагменты молекулярных или кристаллических структур, включающие ядра и электроны.

Условные обозначения

Введём следующие обозначения:

Крестиками отмечены потенциальные ямы, занятые отрицательными фермионами (электронами (в дальнейшем — лептонами)).

Треугольниками обозначены пустые потенциальные ямы, участвующие в образовании химических связей.

В центре каждого иона находится положительно заряженное ядро.

Звёздочками выделены те области синусоидальной функции A``, в которых крестики и треугольники объединяются.

Типы химических связей

На иллюстрации 2.1 показаны две пары одиночных атомов: слева — разделённые, справа — соединённые в общую структуру.

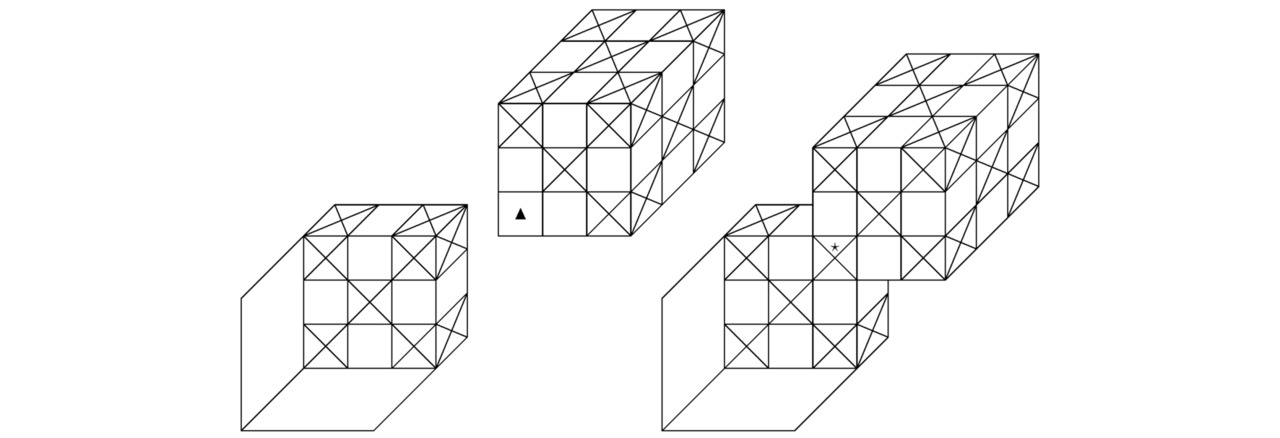
Треугольники внутри первого нуклида лежат на одной прямой, что позволяет им взаимодействовать с крестиками (потенциальными ямами с фермионами) другого нейтрального иона (см. изображение 2.2). Такое соединение является более прочным по сравнению с показанным на эскизе 2.1.

Наиболее стабильная химическая связь возникает при совмещении пары ионов вдоль двух параллельных плоскостей, перпендикулярных горизонтальному сечению синусоидальной функции A`` и удовлетворяющих условию A``=0, когда z=Rz/ (2*mz).

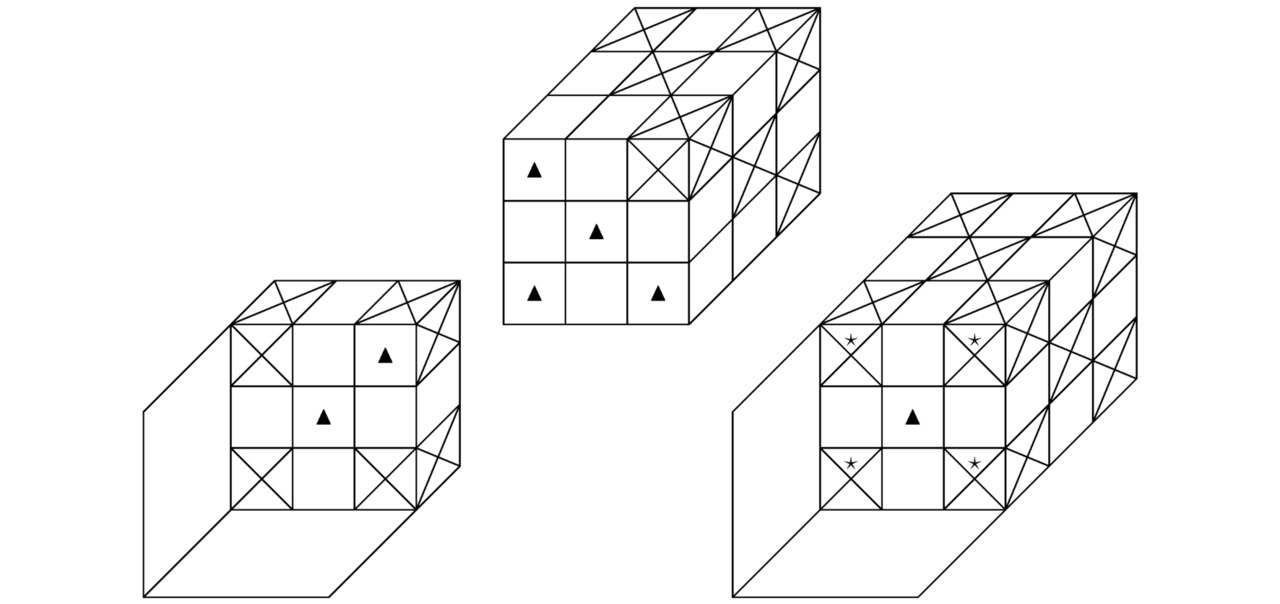
На картинке 2.3 треугольники локализованы в центрах граней взаимодействующих нуклидов. Такое расположение свободных потенциальных ям указывает на то, что синтезированный материал будет проявлять свойства дырочного полупроводника.

Ван-дер-Ваальсово взаимодействие

Силы Ван-дер-Ваальса, возникающие при поляризации молекул и образовании диполей, следует учитывать только в случае, когда все треугольники в квантовой системе заняты лептонами. Ярким примером является графен: двумерные слои графена притягиваются друг к другу, образуя трёхмерный графит. Вклад Ван-дер-Ваальсова взаимодействия становится особенно заметным, когда площадь поверхности соприкосновения монослоёв углерода C возрастает до некоторого максимума.

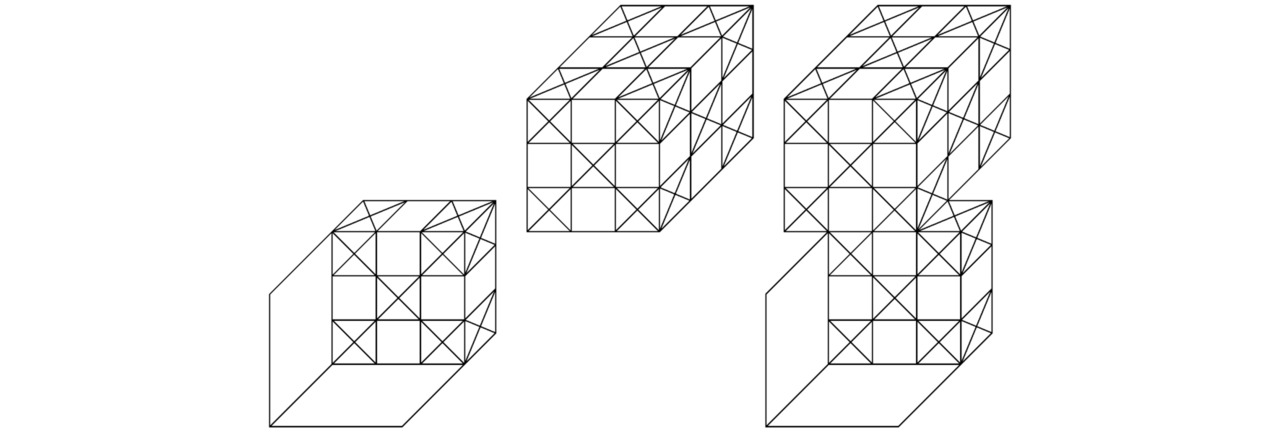
Ионы в узлах устойчивой химической структуры остаются неподвижными в пространстве потенциальных ям до тех пор, пока не изменятся полупериоды Rx/mx, Ry/my, Rz/mz, Rr/mr, Rθ/mθ, Rφ/mφ синусоидальных функций A`` или B``.

Условия реализации соединений

Если хотя бы один из треугольников на рисунках 2.1—2.3 остаётся незанятым отрицательно заряженным фермионом, синтез надлежащего химического соединения в природе невозможен. Исключения составляют потенциальные ямы, которые:

Соответствуют полностью или частично свободным орбиталям, относящимся к уровню h и более высоким уровням h+1,…, h+g (где (g∈N)) рассматриваемого химического элемента.

Могут вызвать дырочную проводимость в кристалле.

Например, для иона натрия Na+ в соединении Na2He орбиталь 3d10 остаётся пустой.

Представленный подход может быть применён для моделирования молекул, кристаллических решёток, других атомных соединений, а также для предсказания химических реакций.

3. «Запрещённая химия» А. Р. Оганова

Как известно, используя эволюционный алгоритм, предложенный А. Р. Огановым, можно спроектировать практически любую кристаллическую структуру, существующую при высоком давлении (Pb> 104 МПа). «Запрещённые» химические соединения, сконструированные с помощью специально созданной компьютерной программы «USPEX», как правило, бывают либо двумерными (слоистыми), либо трёхмерными. В девятом разделе данного пособия будут описаны основные свойства решёток Браве, рассмотренных в главах 3—6. Время t, необходимое для прогнозирования внутреннего строения анизотропных кристаллов, в большинстве случаев зависит как от числа ионов, участвующих в расчёте, так и от общего количества решений квантовых уравнений для этих частиц.

Принципы моделирования кристаллических решёток, аморфных тел и так далее

В любом устойчивом химическом соединении не должно быть пустых потенциальных ям, в которые могли бы попасть отрицательно заряженные фермионы. Исключение составляют незанятые электронами потенциальные ямы, соответствующие полностью или наполовину свободным подуровням в орбитальной диаграмме каждого нуклида, зафиксированного в узлах элементарной ячейки. Используя формулы (8.4) или (8.5) (см. [1]), можно определить минимальное число треугольников, локализованных в одиночном ионе. Также необходимо учитывать сумму потенциальных ям, отвечающих за дырочную проводимость, если таковая возникает в веществе.

Внутри любого однородного материала всегда наблюдается симметрия. При выполнении этого условия в изолированной квантовой системе устанавливается электростатическое равновесие между положительными ядрами и отрицательными фермионами.

Элементы молекул, кристаллических решёток и других химических структур должны располагаться в пространстве потенциальных ям наиболее компактно друг относительно друга. Если рассматриваемая совокупность атомов менее компактна, чем аналогичные соединения, то смоделированное вещество нельзя будет синтезировать в лаборатории.

Кристаллы характеризуются строгой пространственной периодичностью в расположении составляющих их частиц. Под периодичностью понимается повторяемость элементов решётки Браве в определённом направлении. Это требование не распространяется на квазикристаллы.

Если созданная химическая субстанция удовлетворяет изложенным выше правилам, то потенциальная энергия квантовой системы U0p принимает минимальное значение U0p=min. Таким образом, в реальных условиях катион водорода H+, например, будет стремиться к центру грани другого присоединяемого нуклида.

3.1 Динатриевый гелид

Рассмотрим металл Na2He, существующий при высоком давлении Pb≈113 ГПа. На рисунках 3.1—3.12, 4.1—4.18, 5.1—5.4 и 6.1—6.2 жирным шрифтом обозначены видимые ядра, а обычным — невидимые.

Сумма треугольников для нейтральных ионов гелия He0:

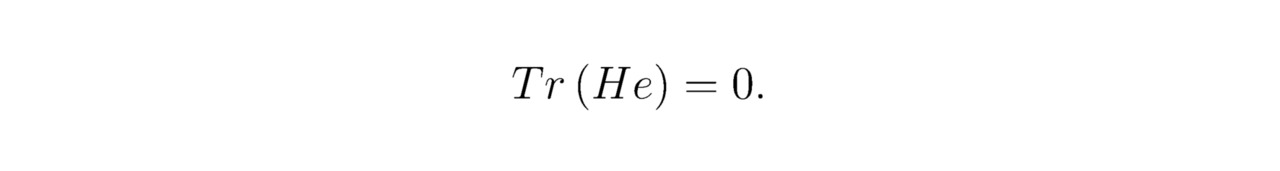
Для натрия Na величина Tr (Na) определяется выражением:

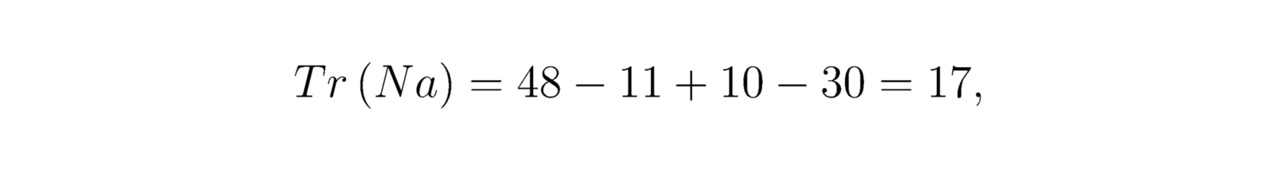
где:

48 — расчётное количество заполненных и незаполненных потенциальных ям на наружной оболочке гексаэдра (атома) уровня h=3 (см. таблицу 8.1, столбец 3 [1]);

11 — порядковый номер натрия Na;

10=30/3 — ядерный заряд неона Ne;

30 — трёхкратное количество электронов на скрытых оболочках (h=1 и h=2).

Основные компоненты элементарной ячейки Na2He показаны на чертежах 3.1 и 3.2.

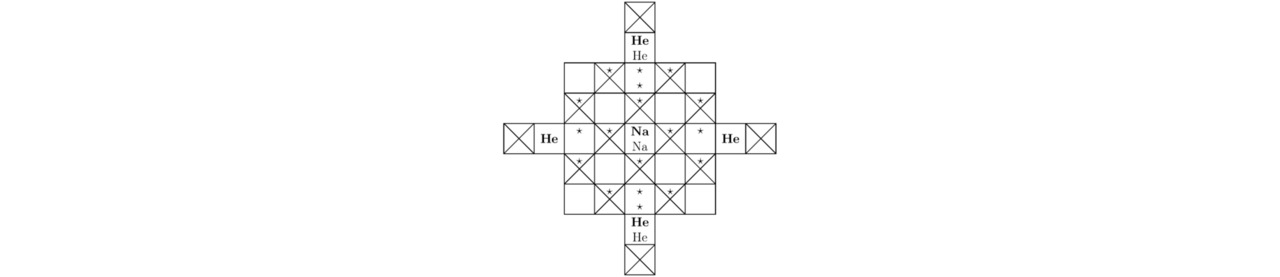
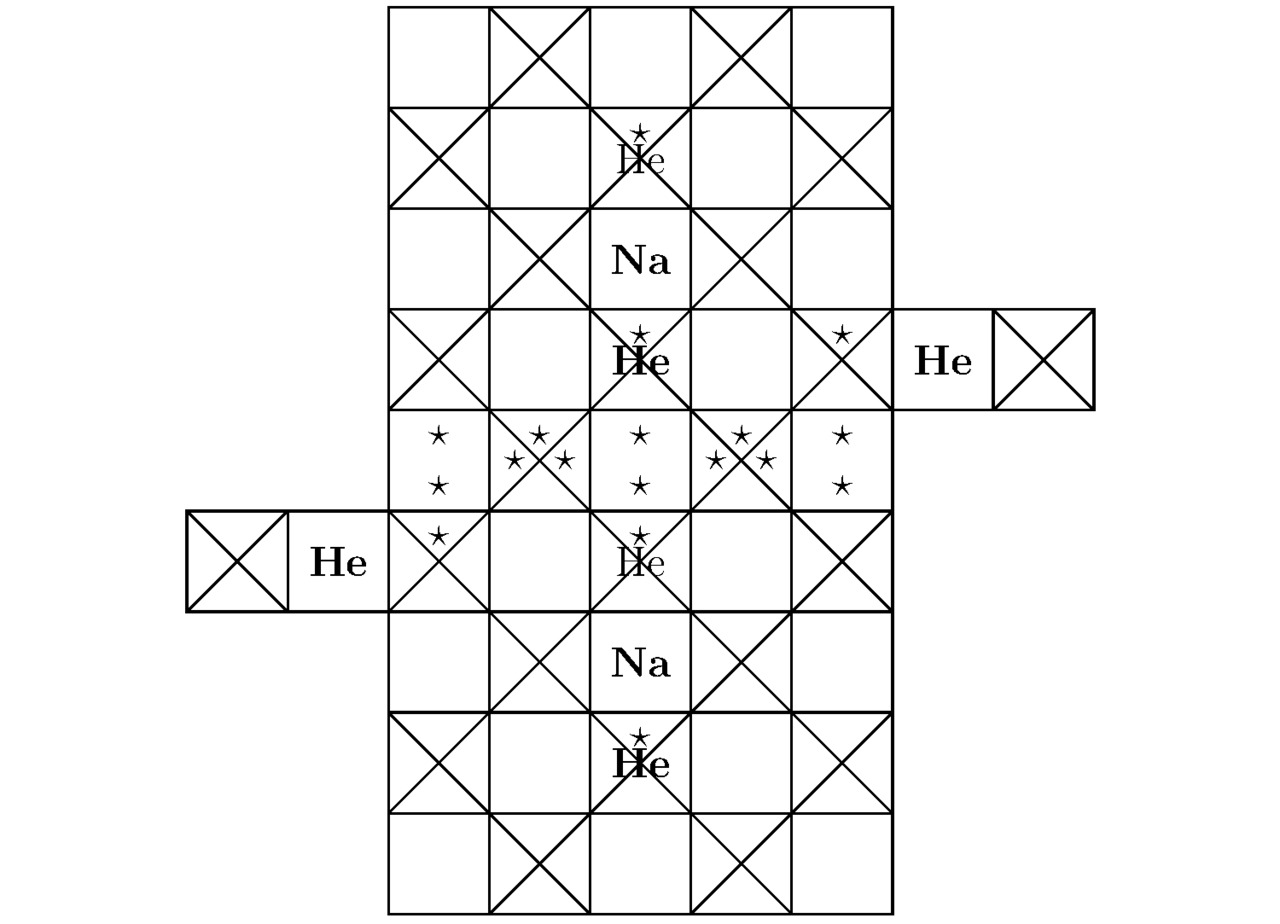
Минимальное количество крестиков для натрия Na:

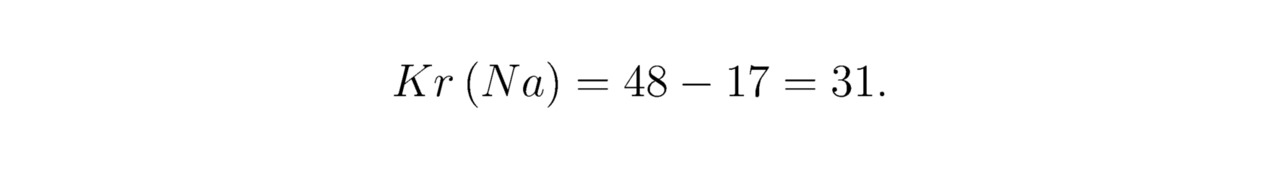
Для гелия He:

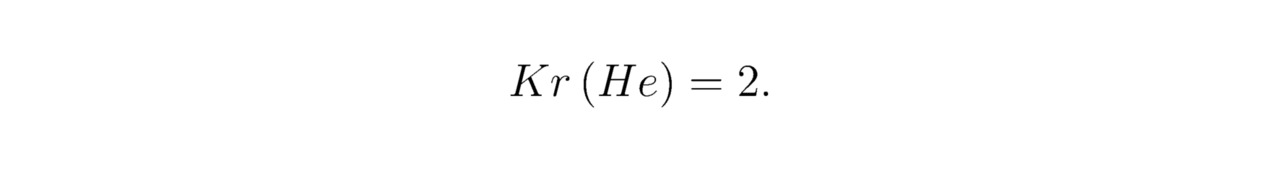
В кристаллической решётке Na2He подуровень 3d10 каждого нуклида натрия Na остаётся пустым. Таким образом, величина Tr (Na) без учёта свободных фермионов составит:

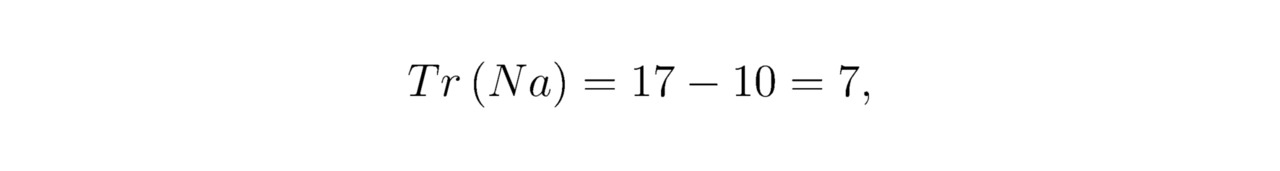
здесь 10 — полное число областей на орбитали 3d10, ограниченных линиями A``=0.

С учётом двух электронов, вытесненных на уровень h=4, получаем:

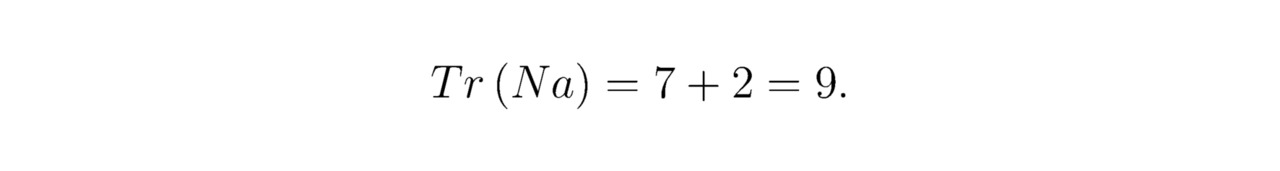
Если подуровень 3p6 внешней оболочки атома натрия окажется полностью свободным, то

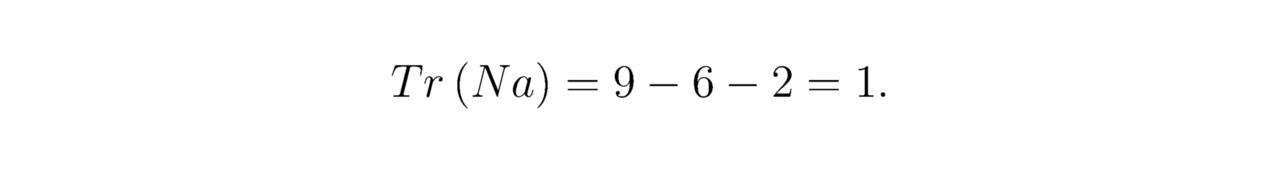
В процессе преобразования формы пространства потенциальных ям внутренняя энергия u твёрдого тела изменяется во времени t. Каждый нуклид стремится переместиться в сторону минимизации параметра U0p`-> min. При стабилизации полупериодов Rr/mr, Rθ/mθ и Rφ/mφ синусоидальной функции B`` система переходит из нестационарного состояния в стационарное или квазистационарное.

3.2 Дифторогелид кальция

Сумма треугольников для фтора F:

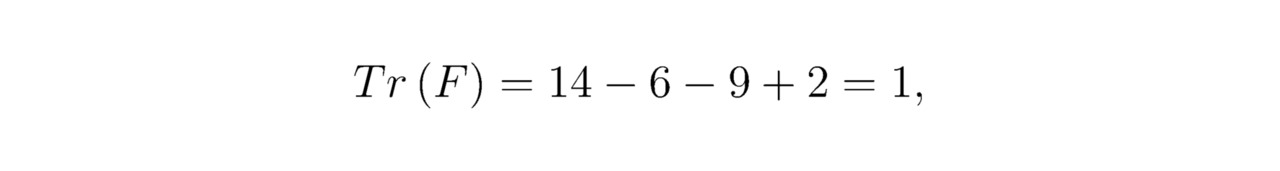
где:

14 — расчётное количество потенциальных ям на наружной оболочке атома уровня h=2;

6 — трёхкратное количество фермионов на уровне h=1;

9 — порядковый номер фтора;

2 = 6/3 — ядерный заряд гелия.

Сумма треугольников для кальция Ca:

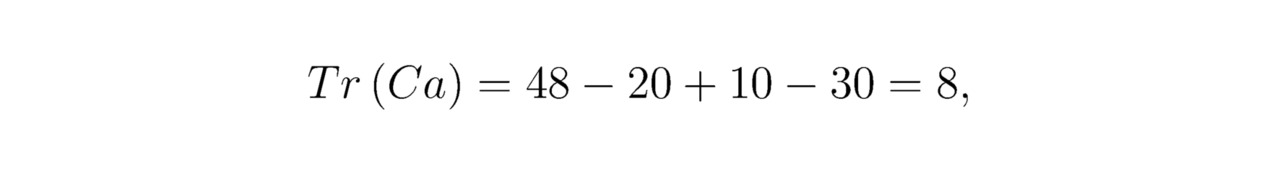
здесь:

48 — расчётное количество потенциальных ям на внешней оболочке иона уровня h=3;

20 — порядковый номер кальция;

10 = 30/3 — ядерный заряд неона;

30 — трёхкратное количество электронов на уровнях h=1 и h=2.

Число крестиков для фтора F:

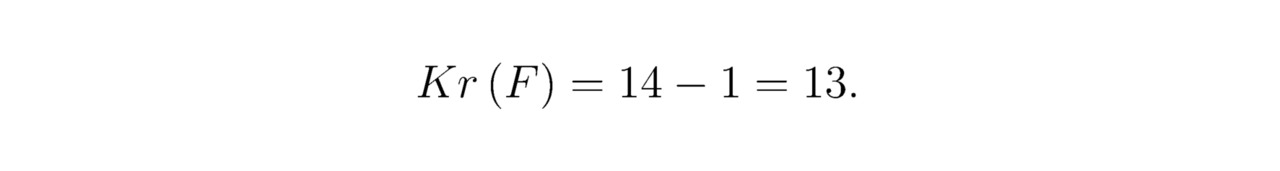
Для кальция Ca:

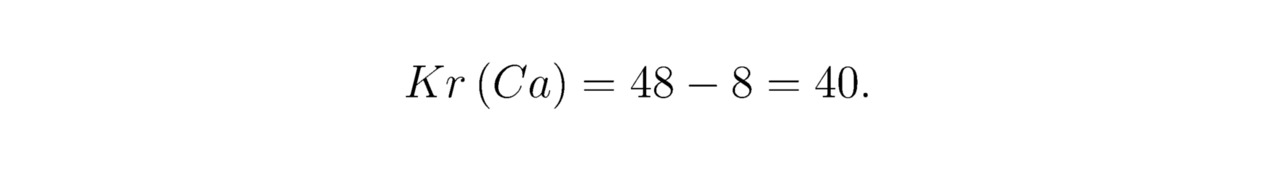
Сумма треугольников для гелия He вычислена в подразделе 3.1. Проекции элементарной ячейки CaF2He показаны на иллюстрациях 3.3 и 3.4.

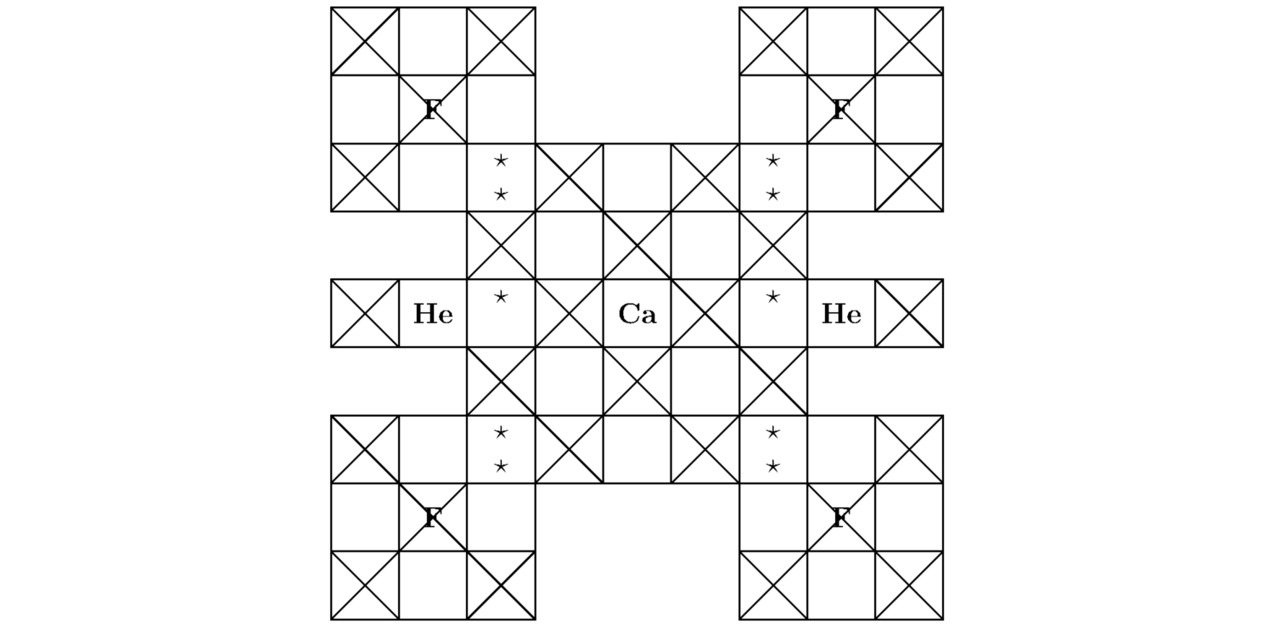
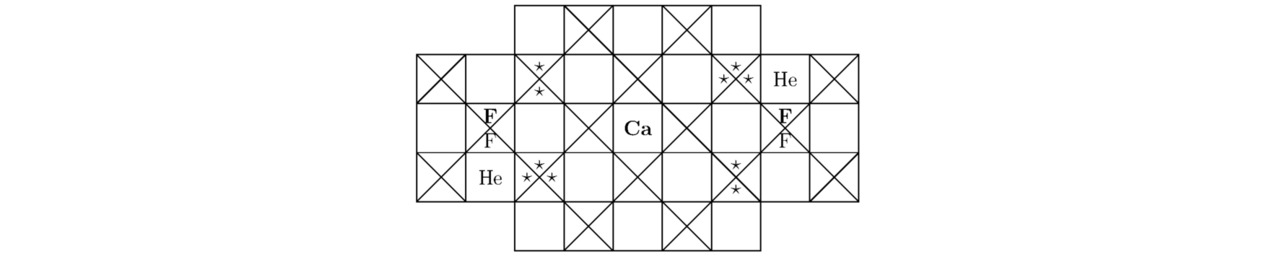
3.3 Дифторогелид магния

Моделируем кристалл MgF2He. Реагенты располагаются в пространстве потенциальных ям наиболее компактно, не нарушая законов симметрии. Определим число треугольников для магния Mg без учёта свободных фермионов:

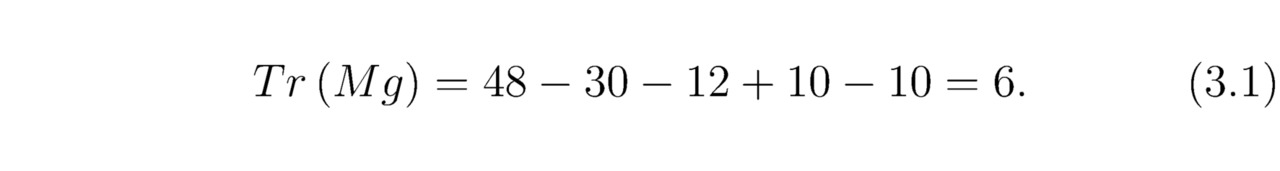
Подуровень 4s2 иона Mg2+ полностью заполнен электронами, поэтому:

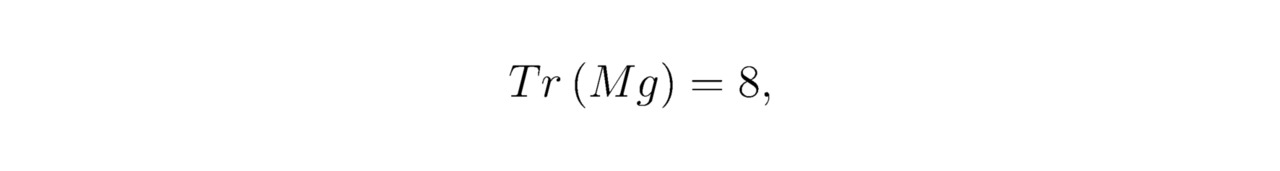
где:

48 — расчётное количество потенциальных ям на наружной оболочке уровня h=3;

30 — трёхкратное количество лептонов на уровнях h=1 и h=2;

12 — порядковый номер магния;

10 = 30/3 — ядерный заряд неона;

10 — максимальное количество вакантных ям на орбитали 3d10.

Число крестиков для катиона магния Mg2+:

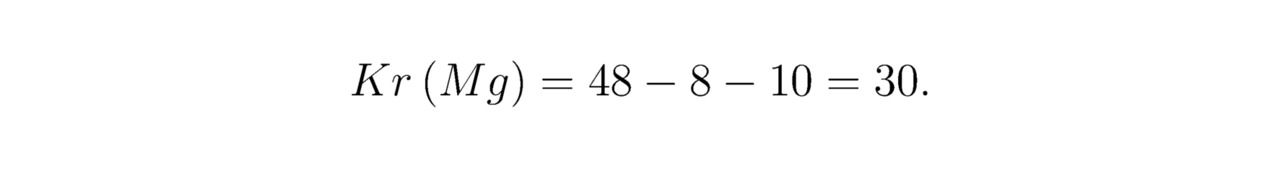
Параметры для гелия He и фтора F вычислены ранее. Основные компоненты кристаллической решётки MgF2He показаны на эскизах 3.5 и 3.6.

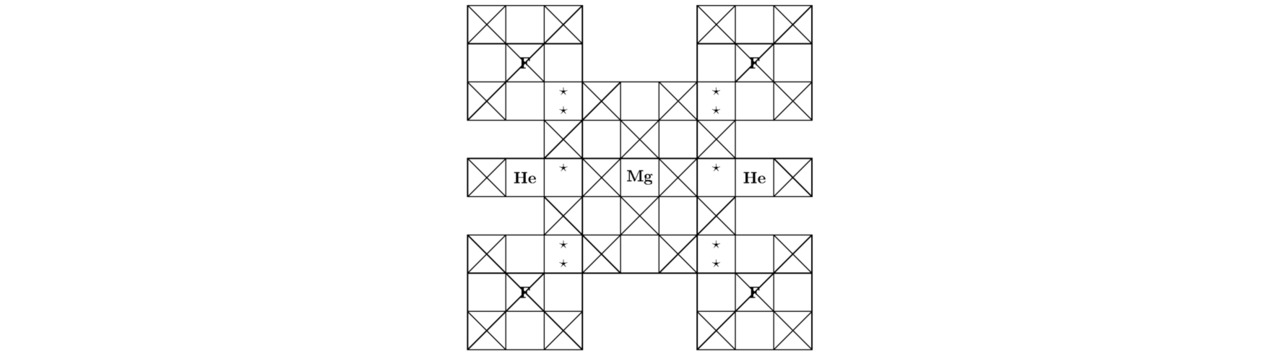
Моделируемый металл является проводником электрического тока, так как в процессе формирования элементарной ячейки произошло заполнение подуровня 4s2 атома магния двумя фермионами.

3.4 Тригидрид серы

Сумма треугольников для водорода H:

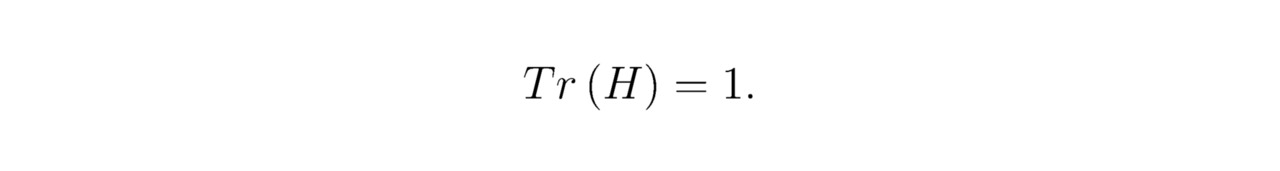
Для серы S:

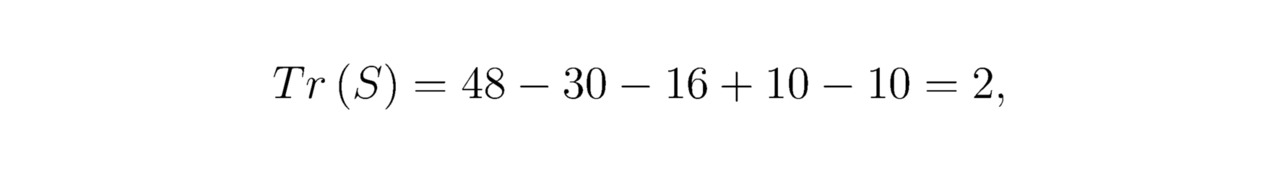
здесь:

48 — расчётное количество потенциальных ям на внешней оболочке уровня h=3;

30 — трёхкратное количество лептонов на уровнях h=1 и h=2;

16 — порядковый номер серы;

10 = 30/3 — ядерный заряд неона;

10 — максимальное количество вакантных ям на орбитали 3d10.

Число крестиков для водорода H:

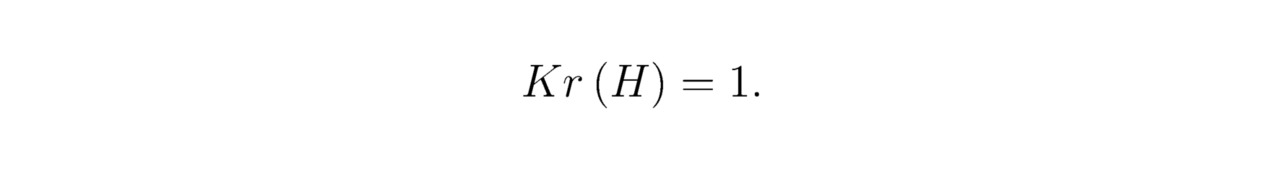
Для серы S:

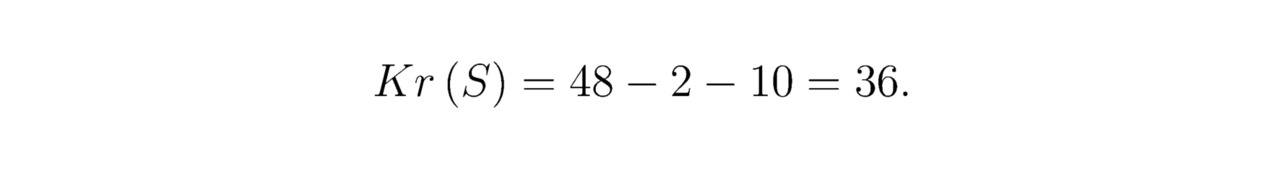
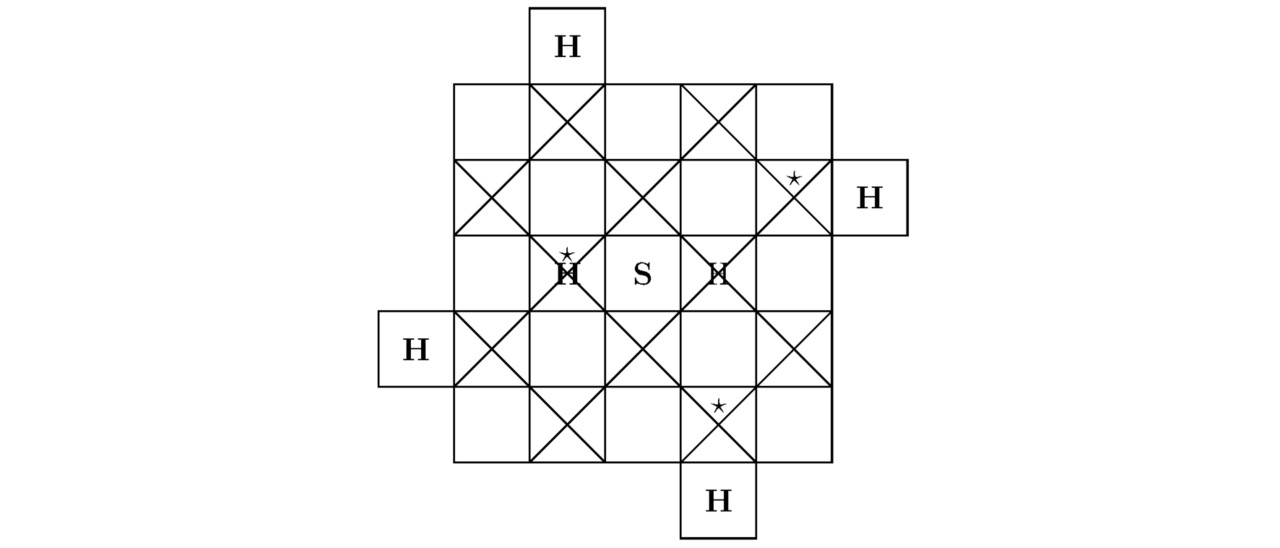
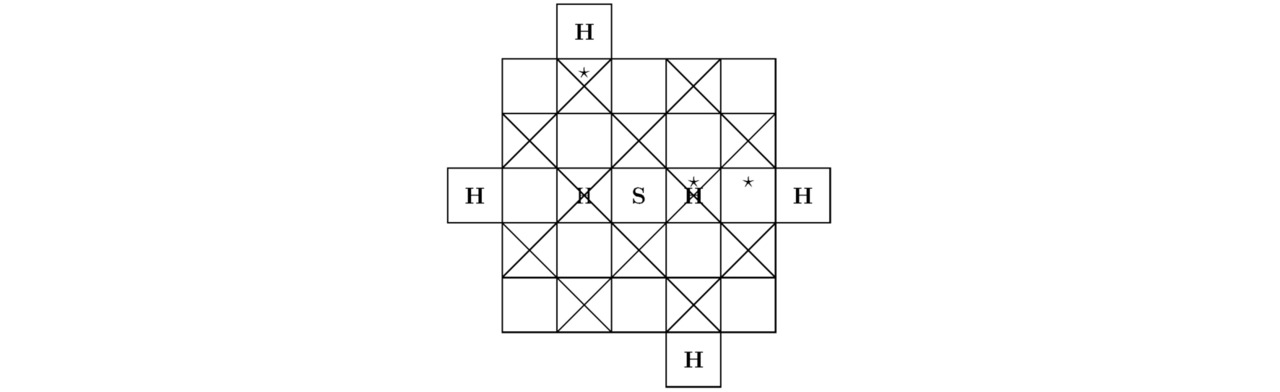
Тригидрид серы H3S является высокотемпературным сверхпроводником. Его возможно синтезировать из сульфида водорода H2S при давлении Pb≈152 ГПа и температуре T=197,5±6,5 K. В этих условиях электрическое сопротивление R`≈0 Ом, что приводит к сверхпроводимости. Проекции кристаллической решётки H3S показаны на чертежах 3.7 и 3.8.

3.5 Пентазолат натрия

Рассмотрим проблему хранения материалов, нестабильных при нормальных условиях (P =0,101325 МПа, T=273,15 K), таких как пентазол HN5 (структурная формула на эскизе 3.9).

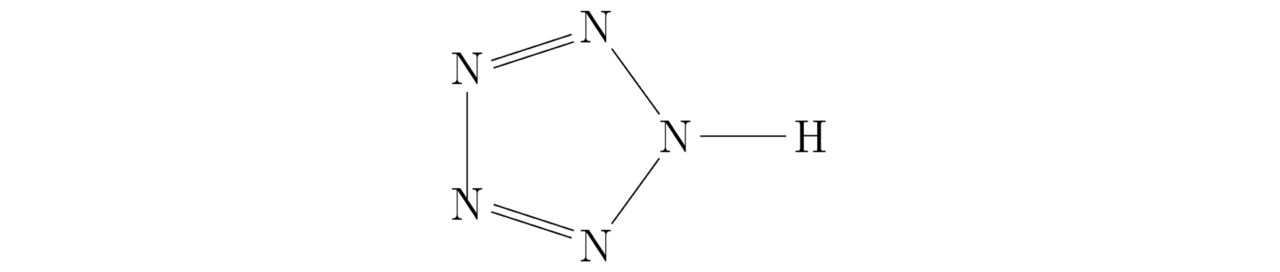
Сумма треугольников для отрицательно заряженной частицы азота N3-: