
КОРПУС НАУК
ФУНДАМЕНТАЛЬНЫЕ ЗНАНИЯ
— Корпус математики
— Корпус физики
— Корпус языка
— Корпус математики
Математика есть путь. Математика не должна пониматься как то, что является отвлечённым и сложным. Сейчас я хотел бы сказать о математике, которую выразил бы без единой формулы и цифры, и на языке. И очень не хотел бы, чтобы это считали «философией математики», хотел бы, чтобы это считали «математикой» как наукой, отраслью знания. Ведь мы все в плену заблуждений. Нам внушают, что математика — это цифры. Но кто сказал, что не может быть математики в словах и на словах? Именно такой математикой я хотел бы заняться.
Тема: «Вычисление наклона графики числа».
Под числом условимся понимать любое знаковое или семантическое выражение, которое имеет природу единичности и краткости, а следовательно может быть делённым или умноженным.
Любое число наклонено. Обычно считается в порядке вещей, что числа имеют ту или иную форму. Но на самом деле наклон числа, например, единицы или пяти — это наклон, от каждой части которого можно провести вектор, и фигура которая будет соединять отрезки вектора и будет называться графикой числа, которая отражает состояние вещества.
5
Рис.1
Получается, что взяв число «5» (см. рис.1), мы провели векторы (отрезки) от всех концов числа. И выяснили фигуру, которая обозначает число «5». Эта фигура называется «вещество числа 5».
То есть число «5» имеет вещественный аналог в жизни и практике жизнедеятельности людей.
Как мы видим из этого рисунка, оно имеет объём, потому что от нижней округлости числа идёт вверх как бы.
Кто придумал это число и другие числа именно в такой графике наклона? Судя по всему именно из природы изначально выводилось число, а не число было создано изначальным. И сейчас, через такой анализ мы восстанавливает картину числа.
То есть, всё же числовые и графические способы мы будем использовать в этой работе.
Число 5 на этом рисунке представляет собой также как плоский рисунок с одной линией пересечения, но также рисунок объёмный (при желании можно придать объём числу, если условиться что линия пересечения есть не пересечение, а форма объёмности фигуры.
И все такого рода фигуры в природе будут показателем фигуры, которая имеет в себе состояние «5».
Мы провели от числа 5 — пять векторов (отрезков), но один отрезок в две стороны, что и дало нам повод говорить об объёмности и сложности пятёрки.
Если в рамках изучения искусственного интеллекта использовать такое счисление в компьютере, то мы получим алгоритм мышления, который будет указывать на очень сложную структуру, но в мозге это должно быть именно такой формы число «5».
Получается, что математика не отдельная от природы вещь. Что изначально она была выведена из природы.
Но что может ещё значит графика (в данном случае числа «5»). Она может означать, что всё же первоначально мир мы видим как набор плоских цифр, а внутренне содержательно он больше и работает он сложнее нежели нам представляется.
Ведь если 5 ввести в функцию или уравнение, и сделать вычисление через окрестности отрезков чисел, то мы получим очень сложную структуру. Но это и будет примером мышления мозга. Дальше надо будет просто установить смысл. Один из смыслов числа «5» — это философия фигуры, которую мы получили — некая машинная направленность действия.
ФИЛОСОФСКАЯ КОНЦЕПЦИЯ МАТЕМАТИЧЕСКОЙ РЕАЛЬНОСТИ
Для многих остаётся непонятным почему те или иные вещи происходят с ними в жизни? Причинности предписывается воля богов или высшего Абсолюта, или факторы физического мира, которые провоцируют данное. Последнее в общем-то и правильно. Только оно действует не так, как полагают, здесь нет причины чёткой, поэтому вероятность заболевания — это всегда вероятность, и заболевания для одних, и не заболевание для других при прочих равных условиях.
Даже такие заболевания, как онкологии — это вероятностные заболевания. Но причина любого заболевания, любого события в жизни, любых процессов мира — это причина математическая. Весь мир — это мир, который живёт по математическим законам, тем, которые нам известны, и тем, которые нам не известны (ещё не открыты). Любой процесс — это математика. И потому решение той или иной задачи может быть смертью, если это конечное решение, или продолжением, если эта функция в геометрическом пространстве может контактировать.
Вся проблема в том, что мы вообще это всё не изучали, и потому причинность от нас скрыта. Небольшой успех имел в этом Лаплас, когда сказал, что надо знать состояние в одной точке Земли со всеми характеристиками, чтобы определить все объекты мира, но дело намного сложнее и большего усилия требует.
Математика в природе может быть приведена на примере. Например, что такое корень квадратный из двух в жизни? Это четыре в теории математики. А в социальных отношениях — это наше увеличение желаний вдвое под действием факторов, которые располагают к этому, то есть вписанности извлечения корня квадратного в математическое решение. Если вписанности нет, то извлекать нечего. Может быть попытка сложения, умножения, даже если это дробь или сложная конструкция чисел. Нужно же уравнение или что-то предполагающее решение. Потому, если мы хотим успеха в жизни, то нужно сочетание математических структур, потому что успех в математике, а значит и в жизни — это концепция, а концепция, как Гёделя (теорема о неполноте) или Пуанкаре (топологии) — это завершённое здание, к которому должен быть немалый путь и непонятно, как оно приходит, в жизни точно также.
Очень многие процессы могут быть непонятны. Заболевания могут возникать из-за совпадения чисел и состояний математики, которые не имеют решения, либо имеют его в плюс бесконечности, что возможно может являться смертью.
Математика очень сложная наука. Как и жизнь. Поэтому решить проблему существования можно с помощью своего ума, если суметь структуры математики вычислить. Но это невероятный успех, это бывает редко. И часто наши желания могут быть мнимыми числами, то есть корнем квадратным из минус единицы и не приводить к решениям, либо приводить при условии решения гипотезы Римана, где эти числа надо найти, а значит при сверх оригинальных и нетривиальных ходах.
Это и есть реальность. Математическая реальность. Но учитывая то, что огромное число концепций и идей в математике ещё не найдены, то при соблюдении даже всех условий правильной жизни, результата может не быть, либо по не понятному для нас, но математически верному иррациональному стечению обстоятельств получится большое достижение в жизни.
Мы заложники математического мира, а то, что мир математический объясняется из того, что математика — это единственный способ подтверждения физики, естественных наук и экспериментального изобретательства. Математика является также в теории не выявленной структурой, как практика одновременно. То есть она обширна и если познание бесконечно, то очень много ещё всего предстоит понять, и всё равно иррациональное останется, как непонятно число «пи» (3, 14…)
Мир — это очень сложное образование. Если мы говорим о политике, то далеко не политика и экономика решает, будем мы счастливы и реализуемся или нет, дело куда глубже, оно в структуре мира лежит и человеку не самая завидная роль отведена во всём этом. Но есть, правда, очень хорошая вещь, которая состоит в том, что человек может быть независимым сам в себе, и как бы структурировать то, что в нём есть, и тогда будет лучше любое решение, пускай и неочевидное, пускай и скрытое под структурами математики.
ФИЛОСОФИЯ И МАТЕМАТИКА Б. РИМАНА
На мой взгляд Риман поставил вопрос о реализации того, что сомнительно как первоначальное в природе. В уме мы представляем, что есть минус единица из корня квадратного, что это мнимое число, которое можно мысленно провести через координатную прямую, комплексное число, которое является реальным в мышлении. Но как можно представить, что мнимое число стало числом простым, которое на графике присутствует, в этом вся феноменология и пафос римановой математики.
Я не любитель греческой античной философии, но здесь концепция Парменида о существовании всего, что представимо в мыслях может быть состоятельной. Из новоевропейской философии более вразумительные примеры. Существование того, что в теории есть, и что потенциально может быть реализовано на практике — это контекст философии Э. Гуссерля Феноменология так и не стала практической наукой и строгой философией, но она предполагает наличие чего бы то ни было, что теоретически реально и практически может быть реально, но непонятен принцип.
Так и теория Римана — это не то, что практически может быть или не может, это обязательная практическая реальность мнимых числе, но непонятен принцип. Почему корень квадратный из минус единицы есть? Потому что на графике представима единица, представима минус единица и представимо увеличение на два, на порядок, на корень квадратный, но непонятно как. Хотя корень квадратный из минус единицы — это минус единица. Но надо вычислить это на графике (т.е. в природе), а принцип вычисления непонятен.
Но моя задача не в том, чтобы ставить вопрос и говорить только, что это непонятно, моя задача и давать ответы, потому что истинная философия не спрашивает, а отвечает по преимуществу.
«Все нетривиальные нули дзета-функции равны ½». Это очень серьёзное и значительное заявление Б. Римана! Нетривиальный ноль — это как раз решение мнимого числа, принцип, потому что ноль — сердцевина координатной прямой, а одна вторая — это простое число, которое делится на себя и на два. И здесь важно, что простое число есть ключевое число, потому что это тот минимум и одновременно основа жизни, которые существуют, то, что делится на себя, и на два в нашем двоичном мире, при двойственности сознания, природы и форм языка есть принципиальный момент.
Нетривиальный ноль — необычный ноль. Здесь есть очень интересный момент. Чтобы решить эту проблему, надо понимать, что концепции Пеано и Гёделя К., которые современная математика считает по форме принципиально нужными для решения гипотезы Римана, являются необходимыми, но смысл этих концепций по их форме в том, что должна быть введена переменная нового типа в решении.
Однажды это было сделано при создании дифференциальных уравнений. Это очень обогатило жизнь. Была создана просто новая переменная, например C. И всё, мир изменился, как создание электричества было также вводом дополнительной переменной.
Поэтому, когда мы берём ближайшее число от ноля до единицы, то здесь должна быть введена переменная. И это должно быть разложение числа: и ноля, и единицы. Но об этом ещё скажем.
Сейчас же подумаем над вопросом о существовании или не существовании. Гипотеза Римана признаёт существование и существование двух типов, хотя есть скептики, которые полагают, что может быть и опровергнута гипотеза Римана, не имеет она решения с их точки зрения. Очень сомнительно, потому что слишком очевидны и доказательны входные данные этой математики.
Так вот, если есть два уровня, которые обоснованы, то в нашей жизни надо также второй уровень вводить в практику, а не верить просто в него, и поэтому метафизика имеет право на существование. Квантовая механика во многом также зависит от решения римановой задачи и квантовые законы — это в общем-то метафизика, если понимать под метафизикой не миф (ложная трактовка), а очень сложную физику (трактовка позитивистская, моя).
Решение в разложении числа. Число может быть разложено (любое число) на десять чисел, с девятью до него, после него, или в разных пропорциях до и после. Потому что мы решили считать в древнем Египте и арабском мире в числовой сумме 10, хотя, заметьте, могло быть и может быть иначе. 1 и 0, это наши введённые данные. Но в рамках такой стратегии надо определить чему равно число. Сразу ясно, что равно только также единичной целочисленной из понятия 10 исходящей доктрине числа.
Если мы найдём значение числа или значения, то значит мы сможем внести минус единицу в корне квадратном и другие мнимые числа на график как подчисла, но подчисло — это число всё равно и есть расширение функции.
Это и будет философией второй переменной. Второй условно. Скорее дополнительной, потому что вторая переменная — это всё же дифференциальные счисления.
Риманова гипотеза может дать очень многое для решения проблемы кодирования-декодирования и искусственного интеллекта. Это очень интересная тема, потому что наше мышление работает не по системе линейных взаимодействий, а по алгоритму сложного действия.
Философски важно сказать, что математика ценна сама по себе, как ценен сам по себе человек, ему не надо доказывать важность его тела и структур тела, он просто есть, этим радует и чем-то занимается в жизни, так и математика с философией — это уникальные вещи сами по себе.
В гипотезе Римана есть один крайне необычный момент, о котором мы ещё подробно не сказали — это дзета-функция на графике. Дзета-функция описывается дугой на плоскости координат стремящейся к x и стремящейся к y, эта функция дана в двух точках, примерно единицы, а описывает сплошную большого масштаба и до плюс бесконечности. Это говорит о том, что в числах заключена геометрия. В малом заключено большое описание и развитие, если это малое точно, как точна вся математика.
Что такое математика? Это форма высшего мышления, которая имеет своей спецификой многомерное мышление фиксации на разного рода вещах. Я бы дал такое определение.
Биология, нейроморфология часто бывают интересны для нашей обычной жизни, а математика может быть и крайне элитарной, а потому не так популярной и в то же время крайне интересной, если мы покажем через философию ту жизнь и наш мир, которые в ней заключены.
Философия — это форма математического мышления, имеющего свободный выбор акцентуации на предметах мира. Это уже о философии конкретно. Гипотеза Римана — это математическое и философское учение о первоначале, раскрываемое через два аргумента реальности.
Философствование об образе жизни
Что есть образ жизни? Особенно для философа. Важно установить, что образ жизни есть презентация человеком самого себя для тех, кто видит его на длинной дистанции. У философа принципиально не может быть понятия «распорядок», он не имеет границ и граней, и когда И. Кант или А. Шопенгауэр имели распорядок дня якобы, то это была фикция, фэйк, это было внешнее, на самом деле они его нарушали и внутри себя, и внешне, просто существовала привычка говорить, что у них есть распорядок дня. Философ ценен для мира тем, что он может прожить жизнь полную наслаждения мыслить и при этом не делать ничего практически важного для мира, это обосновывает гуманизм и достижения демократии, цивилизации и прав человека в мире. Но обычно практика приходит, потому что философия слишком широка и обязательно касается каких-то практических вопросов и решает их.
Образ жизни — это образ мышления. Когда человек не может решить задачу образа мышления или чувствует отягощение от мыслей вообще, то мы должны говорить либо о временном затруднении, либо о действительной слабости его как мыслителя. Образ жизни и единственная этика для трёх категорий людей: философа, математика и гения — это генерирование в себе своего Я. Никакая не самоидентификация, а генерирование Я, то есть любовь к своим достоинствам и преимуществам, как умного и сверх умного человека. Это позволяет раскрепоститься.
Здесь нет биологии. Она есть на уровне внешних обобщений. А на уровне действительного мышления здесь другое — гуманитарная матрица личности, воля Ницше и свобода Спинозы, что имеет равноправное место с биологией и физиологией мышления. Равноправное потому, что мир — это разное описание, но никогда не материя, которая едина.
Философствование, вот интересное слово. Оно есть. Оно существует и характеризует собой всегда одну из черт универсального гения, поэтому уже только — это элитарная вещь. Для просто философа — это хлеб, которым он питается в сознании. Поэтому философствовать значит учиться жить, перефразируя Монтеня М.
Ведь что такое естественная наука? Это описание реальности через аксиоматику конкретной науки. Но аксиоматик может быть много. Поэтому философия как самая свободная из всех видов познавательной деятельности стратегия может выявить самые важные основания везде и во всём.
Образ жизни — это момент ощущения эйфории существования. Если нет эйфории, то нет никакого образа жизни, а есть лишь попытка жить. Настоящее существование либо в эйфории время от времени, либо в генерировании своего Я.
Я — это есть квадрат, иногда куб человека, иногда корень квадратный и мы должны умножать, увеличивать меру. Причём постоянно обнуляя и опять возводя в степень, это математическая игра с числом Я.
Когда русские философы дореволюционного времени говорили о смысле жизни, истине, путях и направлениях развития человека, истории, то они говорили о чём угодно, только не о мышлении. Мышление характеризуется тем, что оно реализовав себя в процессе обсервационного качества рефлексии о чём угодно, уже не видит проблемы в объективных вещах, оно уже в самом себе решение проблемы человека.
То, о чём я пишу — разминка или бег лёгкой трусцой в философии, потому что говорили об этом и другие, но ведь в истории всё дано сразу, только проявляется одно, другое, третье в разное время по разному, убывая или увеличиваясь, и вот сейчас время для меня опять проявить эту тему, и это моё открытие, никаких переоткрытий нет, есть моё открытие и открытие этого же другим.
Потому предмет философии — это парадокс. Философия работает только с парадоксами и их следствиями. Если нет парадокса, то это уже следствие какого-то парадокса или не дошедшая до парадокса мысль.
Истина в мышлении парадоксальна по отношению к истине смысла жизни, потому что это всё равно, что поцелуй экспромтом девушки, важнее теории семейной жизни и ухаживания этому предшествующего.
Итак, философия есть образ жизни философа и часто гения. Гений полиматического типа всегда философ. Почему? Потому что он в своих размышлениях имеет силу ума, которая реализует главную потребность — элитарность мыслей за даром.
Новая таблица умножения
Мною изобретена новая таблица умножения. Говорить об этом я могу в своей теории чисел исходя из того, что в природе нет ничего начинающегося и заканчивающегося, а всегда присутствует процесс. Поэтому любое число — это процесс, а не конечный результат.
Возьмём число 1 и разложим его. 1 — это 0 (то, что предшествует) и 2 (то, что последует). Поэтому 1 — это и 0, и 2, и одновременно 0, 2 и 1. Причём именно на одну единицу мы добавляем и прибавляем после числа, потому что единица — это мера минимального целого числового дискретного дифференцирования.
Также с каждым числом. Причём умножение будет строиться на основании умножения такого типа 2*2= 2 (1;3) *2 (1;3) = (1*1) * (3*3) =1*9=9. То есть умножение данного вида есть умножение подчисел, а значит самого подробного описания числа. Таким образом получается, что 2*2=9.
Какой философский смысл мы можем извлечь из данного решения? Очевидно, что 2*2=4 по сравнению с 2*2=9 стоит в отношении ½+1 (когда речь о 2 в 2*2=4), поэтому любое математическое утверждение — это примерно половина истины, если брать данный пример.
Когда мы говорим о человеке, то речь идёт о том, что любая деятельность организма — это то, что происходит и то, что стоит за данным, и подчисло деятельности по функции и значению намного больше. Поэтому глубинная анатомия и физиология человека и животных, а также физика и химия природы намного сложнее, глубже, интересней, чем то, с чем мы имеем дело на поверхности процесса.
Но будет ли правильным оба утверждения: и 2*2=4 и 2*2=9? Я полагаю, что это будет два правильных решения, но первое неполное, а второе полное и как это ни парадоксально, второе также для практики будет феноменально важным.
Если мы возьмём две коробки с печеньем и умножим их на другие две коробки с печеньем, то получим четыре коробки, но то, что предшествует каждой коробке — это набор коробки печеньем, то есть 1 и реализация печенья в потреблении магазинами и людьми, то есть 2, и потому полное решение будет именно 9, если перемножить все функции коробок.
Мною проделана работа по созданию всей таблицы умножения, введению в оборот всех чисел, которые получаются, когда мы умножаем все подчисла всех чисел.
Но есть ещё один очень интересный момент, который заключается в том, что 1-2-3-4-5-6-7-8-9- (1—0) — это десятичная созданная людьми система счисления, а может быть другая система счисления, где на 10 не заканчивается числовой целочисленный ряд.
Это может быть, например, 1-2-3-4-5-6-7-8-9-в-р-1в-2р-3в-4р-5в-6р-7в-8р-9в-вр-в1-р2-в3-р4-в5-р6-в7-р8-в9-рв….и так далее.
В этом направлении надо продолжать работать. Эту систему счисления я предложил как альтернативу, но может быть ещё система счисления, в которой ещё что-то другое, и это будет давать нам совершенно другой взгляд на мир и на вещи.
Получается, что число — это ещё и универсальный не инвариант, то есть не постоянное значение и только фиксируемая величина. Если предположить, что мы живём в мире не десятичного счисления, а цифро-буквенного перебора, как предложил я, то это повлияет и на изучение циклов Земли (астрономия), и на изучение мозга (искусственного интеллекта в частности), и на изучение самой математики, и что самое главное техники, технологий и изобретательства.
Философски значимо здесь то, что может быть иное в математической топологии, которую ввёл Пуанкаре и неоднозначность смыслов.
Математика создаёт что-то для того, чтобы больше познавать мир. Если мы говорим, что математика — это точная наука, то мы говорим правду, но только с той оговоркой, что это наука и потому точные вычисления расширяются, увеличиваются, их много и они постоянно должны аккумулироваться нашими усилиями.
Я убеждён на основании научных изысканий, что наш мозг работает по математическим и геометрическим стратегиям и потому вся математика в нём, и все принципы дифференцирования, к примеру, в геометрии, конечно, а не числе, в веществе гармонично отражены, поэтому любое математическое понятие может быть гуманитарным языком описано, как смысл.
МАТЕМАТИКА и ГЕОМЕТРИЯ прообразования
Задача 1 Обнаружение уплотнений, как они возможны?
Решим такую задачу: дано 2 физических объекта разной формы и два физических объекта одинаковой формы, это диск и треугольник и два квадрата. Нужно вычислить с точки зрения прообразовательной математики как эти объекты влияют друг на друга при нахождении на равном друг от друга расстоянии. Для решения задачи можно применять любые способы и методики вычисления, но пользуясь понятийным языком Прообраза.
Ответ и решение:
Квадраты. У квадратов по четыре угла. Каждый угол направлен своей энергетической силой во все возможные стороны. Всепричинность как понятие о прошлом, настоящем и будущем также в этих предметах прообразует их новые конфигурации в бытии фрагментации. Это неподвластная нам тема. Нам же подвластно решить взаимодействие квадратов на окружающую природу. А оно таково, что они излучают всеми своими четырьмя поверхностями энергию во всех возможных направлениях, одновременно считывая информацию с природы и с человека (ов), если они там находятся.
Квадрат по отношению к квадрату излучает комбинации поверхностей 1—1, 2—2, 3—3, 4—4. Сами поверхности не ровные, так как в природе нет ничего ровного и абсолютно точного и потому они могу излучать следующие комбинации: 0,5- 0,5 или 1,3—1,4, 2—0,1, 3—1,5, 4- (-3). Конфигурации и вариации самые разнообразные и полностью вычислить объём комбинаций даже в обычных квадратов средней лабораторной величины невероятно сложно, а точнее очень трудоёмкая работа.
Но выясняется интересная деталь, излучение стороны квадрата, которую мы берём за фиксированную величину есть излучение положительного вектора 4 на вектор -3. Как такое возможно? (это одна из вариаций, обозначенных мной) Получается, что отрицательное излучение, которое есть внутреннее излучение стороны квадрата неполная картина математического взаимодействия, а лишь раскрытие подробности излучений. То есть правильная формула должна выглядеть так: 4—4 (-3), а ещё более правильно (-3) -4-4- (-3), но это симметричная формула, а на самом деле здесь также бесчисленные вариации цифрового прообразования.
Но нам нужно выяснить: а что если детально просчитать максимально большое количество вариаций излучений? (только точнее не «энергии», а «потока измерения» (пизма). Получится результат, который позволит говорить о множественности структур мира как внешних так и внутренних, это будет фактологической стороной. И также практический момент-сторона — это перспектива нащупывания в пространстве стыков, уплотнений и наложений равнонаправленных и тождественных величин с целью «прогибать» математическое бытие и совершать движение в этом уплотнении с помощью теории вычисления и практики механистического применения оборудования (машин) для передвижения в бытии. Под бытием обозначим математические вогуности и прогибы. Внешний порядок дел благодаря внутренним вычислениям. В этом пионерство математического прообразования.
Но ещё в задаче у нас сказано о диске и треугольнике. Дело в том, что здесь ещё легче нащупать взаимодействия, так называемые стыки и уплотнения, потому что пизма здесь не симметричная, а стремится к разностям значений, а значит уплотнения будут на стыках очень очевидны.
Примерно это можно в цифровом виде изобразить так: 1, 2, 3, 4, 5, 6+∞ → 1, 2, 3, 4 (диск-треугольник) и в итоге стыки. Но значения также зависят от формы и местоположения, разворота и состояния покоя или движения предметов, их нахождения в помещении или на природе, всё это даёт пизмы и также образует стыки, на которых может прогибаться математическое бытие и осуществляться движение.
В обычных же условиях пизмы практически не ощущаются нами, но при конструктивных научных взаимодействиях они будут являть уплотнения и тем самым давать альтернативные источники движения и горючего, потому что пизмы не только дают способность двигаться, но при правильно обозначенных математических конфигурациях ещё это движение и осуществляют.
Но нужно разобраться ещё по крайней мере в двух вещах (Примечание)
Что такое Всепричинность в данных конфигурациях пизм?
Каков наиболее просто общий знаменатель взаимодействий пизм?
1.Всепричинность в данных вычислениях может использоваться, а может и не использоваться. Без неё можно обойтись, но в то же время если её использовать, то это может дать результаты для установления телепортации, потому что в теории и практике Прообраза время находится и предугадывается в одной точке существования и в то же время само движение пизм внутри тела может придать ему движение без изменения внешнего природного, с помощью также стыков внутри тела и возможно наложений пизм.
2. Общий знаменатель может быть найден, но это требует как раз вычислений огромного числа математиков. Сейчас же можно сказать, что математические тождества — это ориентир к нахождению физических уплотнений пизм, а также геометрические вариации уплотнений естественного характера и искусственным путём может дать результат в пизмах.
ПИЗМА — ПОТОК ИЗМЕРЕНИЯ
(Фукалов А.) Математика моего философского дискурса:
А — элемент, который подразумевает всяческую потенцию и начальность, А является сугубо начавшимся, А является всяческим отправным уже длящимся математическим периодом, константой и парадигмой (всё вместе элемент Потенции)
Б — элемент организованного «би», то есть дуализма, который обозначает организационные ряды любого уровня, Б является вторым фокусом любой математической операции — дуальностью. Он может быть представим как (1=2=4=8=Б) — пример дуализма, (2:2≠Б) — пример не дуального фокуса, при котором нет размножения дуальности.
PS: вообще любая математическая система стремится к обособленности, любой результат (финал ЧМ или математическое решение) — это выведение «одинокого числа», то есть крайне суженной результирующей функции в результате масштабных вычислений и коопераций уравнений.
В — элемент удвоения результата, самая логическая доминанта, когда требуется увеличение после дуальности на пропорционально двоичный экзистенциал, который описывает предыдущий и одновременно другой, потому что его константы увеличены вдвое силой нарастания потенциала и его утверждения в среде.
(15—5=10≠В), но 15—15, либо (15+15=30=В) — пример фокуса удвоения В.
Г — элемент информационного содержательного стояния, единица содержания, которая может включать любую геометрическую сообщность.
Г= +++++ {
— — - — {
*** {КЛАССИЧЕСКАЯ МАТРИЦА
:: {СОДЕРЖАНИЙ
= {
Данные четыре числа называются философским математическим квадратом, который образует законченный цикл любого действия в природе, которое так или иначе обозначает содержательные основания нашей жизни, в любых возможных сферах при физическом линейном мире и разноугловых восприятиях и анализах (боковом, верхнем и синтетическом)
Может возникнуть вопрос о смысле математики. И я сразу отвечаю, что описание, кардинальные узловые понятия и принцип как феноменальность математического таргетирования наиболее важные, чем вычисления вещи, часто вычисления вообще дело считающих, а не математиков фундаментального пошива.
Д — элемент тасования, от которого зависит субординация единиц информации и их зарядов в сочетании с числовыми носителями, чем больше Д, тем объёмнее математическая матрица содержаний. Пример:
+++++ +++++
— — - — * * * *
::: = = =
22 22
Д= (+ (5²) → (- (4) → (* (4) → (: (3) ← (22 (2²) =Д
Как видно Д выполняет функцию описания и завершения, а потом и генерального начала функции, целью которой является выяснения содержаний.
Что касается числа, то, с одной стороны, оно не нужно, потому что главное — это принцип математической концепции, а с другой стороны, раздел математики должен быть посвящён числу, которое было отчуждаемо, специальный раздел, и его можно назвать «Числовая математика», главным принципом которой служить может чисто числовое концептуальное интегрирование, а не вычисление, опять же.
20 40 55→↗ движение чисел, их увеличение в двоичном акте
30 50 45→↗↙ — это обозначение движения чисел, их увеличения и уменьшения в троичном акте
Результат — это фикция, главное принцип. Для практических нужд промышленности или экономики результат также не имеет значения, результат в старом смысле. В подлинном новом смысле результат — это выявление принципа с натуральными объёмами характеристик.
2+2=4 — это фикция (но кое-где нужная, для детей на начальном этапе постижения математики и арифметики, например)
2
+
2
=
3 элемента с двумя похожими характеристиками и одной связующей (+) характеристикой, которые геометрически «зависают», и стремятся к самозакольцованной структуре.
В 3D видении — это плавающие прямоугольные содержания, которые могут служить крепкой физической нормированной субстратной функцией и уплотнением.
Математический реализм
Мы должны установить, что число имеет вписанность, что число не является независимым аргументом, что число есть изначальность, которая имеет числовую прелюдию и числовые следствия (следствие).
Это означает, что любое число может иметь и должно иметь решение уже только потому, что оно является действительным числом.
Почему мы можем знать, что 0 есть -1 и +1 решение? Потому что элементарная таблица умножения, всеми признанная имеет такое же значение единичного состава, это следует из того, что 1*2=2 или 2*2=4, или 4*3=12. Что производят эти умножения? Они производят операцию данных чисел на двиочный код. Здесь только два действия: состав данных и операция.
Но это отчуждение числа. Потому что умножение не является базовой характеристикой мира. Базовой характеристикой является сложение и вычитание. И потому реальное число и реальное вычисление имеет операцию в уравнении или примере сложения данных каждого числа со следующим парным по порядку числом в уравнении или примере.
Реализмом мы это можем назвать потому, что показывает данное реальную окрестность решения, которую можно перенести на график координатной прямой и выявить фигуру. Это тем более важно, потому что позволяет найти в физике, генетике, морфологии и биологии, и других дисциплинах подвижную функцию, а не точечное статичное число.
Также из геометрических фигур можно уже геометрическим методом выводить данную вписанность и следствия вписанности.
Также может быть применена 3D-метрия к любому из видов перечисленных математических операций.
В мировоззренческом смысле это означает, что мы можем проводить решения только уже начатые и только которые закончатся следующим аналоговым продолжением.
Если мы говорим о причине Бога, то должны сказать, что на языке математики он выводится как раз из реальных вычислений, которые не сразу очевидны.
Математика — это наука, которая теперь может быть в практике естествознания себя проявить.
О третьей переменной в математике
Третья переменная — это следующая за первой переменной, которая есть описание процесса в формах внешней логики математика до 17 века, в том числе Евклидова геометрия, до Ньютона-Лейбница; следующая за второй переменной, которая есть в обобщённом смысле дифференциальная и интегральная математика, в которой дифференциал — это простые операции до бесконечного множества, а интеграл сравнивается с производной и первообразной, а также другие сложные структуры, то, что помогло Галуа создать алгебру и ввело всякие уравнения, функции, графики и обслуживающую математику современного типа; переменной же третьего типа является такая переменная в математике, которая произвольно создана, но до кратного размера величины в три операции, которые её характеризуют как на графике, так и в числовом выражении, которая должна быть объяснена средствами математики первых двух видов. Это произвольно говоря может быть 2 в степени 2, в степени 2 и в степени 2 (пример лёгкого решения), а может быть троичность другого сложного типа — произвольный эллипс, который имеет внутри себя треугольник и описывается тремя точками вне треугольника и эллипса со значениями 34, 56, 76, и нужно вычислить состояние фигуры. Такой пример может быть взят для того, чтобы понять природу геодезической линии окружности, но через влияние внешних факторов разных величин вне окружности.
Третью переменную в математическом дискурсе дискуссивного характера можно отнести к разделу математики — анализу. Теория анализа сложных систем, если более точно. Но в то же время есть третья переменная будет введена в топологию или в теорию вариационных уравнений, это также будет приемлемо, как и для любой другой теории. Обозначение же третьей переменной я предлагаю следующее — «T» (THREE).
Если мы допустим четвёртую переменную, то она должна вычисляться в размере четырёх членов данных, но она будет той же Т, потому что система тройственна: переменная-неизвестная-созданное (общий дискурс) и на практике: три созданных действия: переменные (в данном случае четыре), их создание в произвольном порядке и вычисление с помощью данных любой системы математики (третий цикл). Может быть пять, шесть, семь переменных, но три этапа разложения операций Т.
В жизни мы постоянно что-то создаём, потом это описываем. В математике долгое время было решение исходя из накопления данных, мы же должны вообразить проблему, создать её и имеющимися данными решить, что принципиально другой уровень математического творчества.
Мир состоит из трёх констант. Геометрия Евклидова типа описывала мир на самом деле также тремя константами, просто они были слабо проявленными в двух случаях и лишь в линейном определении от точки до точки, от принципа к принципу наиболее ярко описываемы.
Дифференциальные и интегральные исчисления оказались второй переменной, в сложных вариантах исчислений же третья переменная больше видна, нежели в Евклидовой геометрии вторая, которая, как сказано было, присутствовала, как и третья.
Вариационные исчисления возьмём. Возможны ли вычисления третьей переменной в уже имеющихся задачах, например, задачах с вариационными исчислениями? Такие вычисления возможны, но при условии что существует троичная трансформация операций, должно быть по крайней мере два очень не похожих (графическое и числовое или степенное и отрицательное, и т.д.) в вычислениях. Если это будет, то мы говорим что уравнение или задача (проблема, теорема) данного вида имеет решение Т, если же не существует такого разграничения, то мы говорим, что уравнение данного типа архаическое «А», подчёркивая традиционный характер решения, и оно не имеет решения Т, так как не входит в область определения троичной трансформации, при этом имея троичные системы в своём содержании, но слабо выражено, что характерно для всех примеров.
Конкретно вариационные исчисления, я полагаю, бывают разные и для одних есть решение Т — типа, а для других нет решение Т — типа.
Эксклюзивное содержание таких решений и преобразований заключается в том, что существующий мир трёхмерен, но трёхмерность как физическая величина совсем не является причиной уравнений Т-типа, потому что Т уравнения отражают функции подобий трёхмерности, то есть каждое наше действие, осмысливаемое в мозге имеет тезис-антитезис и синтез, но в Т решении это создание (синтез как бы вначале, как это не парадоксально), а потом тезис и антитезис или антитезис и тезис (что также парадоксально), но соответствует квантовой природе запутанности симметрического типа, потому не противоречиво и имеет доказательства.
Третья переменная в математике (дадим определение-вывод): это переменная Т типа, которая публикует Т размерности в окрестности непротиворечивости и доказывается обратными данными. (Фукалов А. В., 17)
Основные математические проблемы
1.Нахождение результата окрестности постоянного наклона во время перехода одной функции в другую функцию x типа.
2.Описание растяжимости как феномена математического процесса в числовой форме без натуральной геометрии.
3.Развитие идеи пространственной математической алгоритмизации до уровня объективных материальных числовых констант.
4.Нахождение угла препарирования при любом типе физических операций и действий.
5.Объяснение формального акта деятельности чего бы то ни было как системы, которая не утрачивает своей целостности через дискретные промежутки, то есть ответ на вопрос об общей не детерминированной нити аутентичного поведения процесса.
6.Описание формализованного трёхмерного наложения.
7.Вычисление теории вероятности поведения субъекта на основании данных единицы поведения, то есть нахождение константы единичности и определение её следствий до уровня ограничения до другого деления в конкретном объёме содержания.
8.Ответ на вопрос об алгоритме, который запутан сам в себе, то есть о том, чем является не структурированный алгоритм в условиях важности симметрии для ответа в топологии. Раскрытие не эстетической математической результирующей для решения определённого класса задач.
9.Обоснование полифункции через вписанность объёма любого типа.
10.Создание учения о не нулевом нуле и описание таблицы умножения на основе такого не нулевого решения.
11.Создание унифицированного определения любой функции, уравнения и решения через один обозначающий на письме знак, который раскрывается на множество подзнаков за счёт фильтрации геометрии знака, инклюзивная сенсорная математика в действии.
12.Решение задачи вычисления последовательности комбинирования решения без натурального решения, чтобы решить задачу исходя из начального аргумента манипуляции числом.
Определить средний вариант решения, исключающий полное решение и отсутствие решение, то есть создать любой произвольный решаемый объём функций.
13.Описать природу в формулах и геометрически зафиксировать данное.
+∞ в математике
+∞ в математике или -∞ является очень интересным математическим конструктом. Самое первое — это конструкт, который для самой точной науки математики является самым не точным. Бесконечность не является чем-то определимым. Но математика требует того, чтобы в ней всё было строго и нормировано и мы попытаемся эту брешь закрыть и сказать о формализованной плюс и минус бесконечности.
Правильно будет говорить о том, что «бесконечность» — это распределение функции (функция же это равенство одного решения с другим, часто в уравнении) до расстояния, в котором одно повторяющееся решение. Бесконечность надо определить как количество повторов, которые не имеют значения, имеют понимание, как не играющие роли одинаковые дискретности.
Поэтому +∞ является формой увеличения повторов при едином решении, а -∞ является формой уменьшения повторов при едином решении. Получается так, если бы было иначе и бесконечность имела бы значения самого разного рода, но которые не видны, то это могло бы опровергать материальное решение, которое мы видим, что опровергало бы a priori истину решения в видимом варианте.
Что такое уравнение?
Уравнение — это форма числового выражения решения, в котором есть неизвестные, но которое эти неизвестные сводит к равенству чаще всего. То есть уравнение — это что-то неизвестное, но предполагается, что оно должно быть решено и предполагается, что ответ уравняет неизвестные с предполагаемым числом и решением.
Потому нужно сказать, что решение уравнения вида x²+y²=c² есть уравнение, в котором могут быть подставлены величины, при c=3, например, а может быть и не подставлено ничего и тогда мы получим просто формальную запись уравнения. Что редко бывает в математике. Но должно быть, потому что уравнение без предполагаемых известных величин со значением есть уравнение, которое определяет другой уровень организации числа. Для мировоззрения это значит, как животный мир (чистое уравнение без числового подставления) и мир людей, одушевлённый мир (с уровнем значения отдельных переменных в виде числа).
Принцип первоначального объёма для произвольно выбранного в пространстве объёма любого вида
Принцип «гармошки» пространства
В этой работе я хотел бы рассказать о своих решениях проблемы пространственного объёма. Дело в том, что современная наука использует любые геометрические фигуры плоского пространства и стереометрические фигуры трёхмерного пространства как a priori являющимися фигурами данного пространства. Но истина состоит в том, что это всего лишь вольное предписание объекту его пространственной характеристики и метрики в том или ином координационном расположении. В то время как каждый объект пространства должен быть обоснован не как свободно выбранная фигура, а как математически вписывающаяся в данное пространство фигура, которая строго алгоритмизирована в данном конкретном пространстве.
Для начала надо сказать, что наше пространство — это пространство, в котором любой произвольный объём будет иметь две характеристики: многогранность трёхмерного Декартова пространства для объекта и однородность. Многогранность включает любые формы принятые в геометрии для отображения на Декартовой системе координат, а однородность в соответствии с доказанной гипотезой Пуанкаре — наличие строгой трёхмерной заполненности пространства геометрическими содержаниями насколько я эту гипотезу и её доказательство понимаю.
Если бы объёмы были разнородны в трёхмерном Декартовом пространстве, то они бы не поместились в Декартовы координаты и представляли бы собой разнородные дискретности, что не имело бы никакого положительного математического и физического решения. Это я назвал бы условно принципом «гармошки пространства», потому что он отражает заполненность и геометрическое движение данных координат и их производных по принципам, которые вписываются только в однородную геометрию нашего мира.
Единица Объёма
Любой объём должен быть алгоритмизирован, иначе это лишь произвольные вектора «условного» объёма.
Когда мы имеем некую фигуру в пространстве, которую называем объёмом, то мы должны установить, что у этой фигуры, в зависимости от того, какую часть её мы рассматриваем, есть касательная от которой надо провести прямые линии, которые опишут эту касательную перпендикулярно вверх, перпендикулярно вниз, экстраполируют длину касательной вперёд, с двумя отрезками, соединяющими экстраполированную прямую с касательной и двумя поперечными отрезками, которые создадут непрерывность вектора по отношению к данной фигуре. Это и будет алгоритмизированным объёмом данной касательной, который будет составлять 9/10 отрезков от касательной, сама же касательная 1/10 от объёма и будет называться единицей объёма.
Данный отрезок будет являться отрезком места и времени в искривлённом пространстве-времени Эйнштейна (или пространстве Минковского, если рассматривать только геометрическую составляющую вопроса), 9/10 отрезков начального объёма будут площадью через которую произошло искривление к данному объёму. И все Начальные Объёмы будут показывать изначальный векторный рисунок отрезков искривления.
a
c d (рис.1) b
Что объясняет это решение
Данное можно проводить с любой геометрической фигурой и объёмом и через него мы вычислим алгоритмическое обоснование места в пространстве данной вещи. Также оно покажет как бы степень «проваленности» в пространстве исходя из теории относительности об искривлении пространства и времени. И насколько я представляю в математике дифференциальные и интегральные исчисления, когда находится производная и первообразные, имеют целью описание движения, как писал Лейбниц с максимально увеличивающимся делением отрезков f (x) ^f (y), здесь же мы имеем дело с движением внутри пространства для вычисления первоначальной, которая даст понимание геометрического алгоритмизирования данного объёма в конкретном пространстве. И получается, что объект есть лишь 1/10 от настоящего пространственного объёма, в который он вписан. И всегда только 1/10, и 9/10 начальный объём, потому что десятеричность является решением законченного цикла деления на отрезки пространства в данном гипостазированном пространстве.
Крайне важным является понятие «касательной». У каждой фигуры, объёма и вещи есть касательная, которая отрезок, который и вписан другими девятью данными отрезками начального объёма. Если всю фигуру описывать целиком во всех отрезках, то, например, у куба 12 отрезков, значит будет (12*10) =120 изначальных отрезков, каждые 9/10 из которых от каждого отрезка будут первоначальными.
Особенным образом обстоит дело с шаром и сферой, и любым шарообразным или элипсойдным объёмом, потому что в силу того, что он состоит из огромного числа отрезков, которые в свою очередь можно также удлинять и сокращать за счёт соседних дискретных векторов, которые обозначены отрезками, является сверх фигурой, которая имеет в виде исключения от всех остальных фигур приближающиеся к бесконечности первоначальные и потому в физике космоса именно сферы и эллипсы являются планетами и так вписаны в гравитационное пространство, что они имеют суперискривления, которые дают им силу движения в эйнштейновском пространстве относительных систем отсчёта.
(рис.2) На этом рисунке я показал произвольно некоторое большое количество векторов (отрезков). Таким образом, следующие выводы:
1). Существуют объёмы в пространстве, которые должны быть описаны в алгоритмах, потому что у каждого местоположения должно быть обоснование.
2). Пространство однородно, но трёхмерно.
3). Создание прямых, как следствий касательных и их отрезки, которые имеют законченный цикл фигуры есть первоначальные Объёма.
4). Единица объёма — это касательная.
5). Сфера, эллипс, шар — стремящиеся к +∞ первоначальные Объёма.
6). Алгоритмизация всех касательных даст полную картину вписывания объёма в искривлённом пространстве-времени Эйнштейна.
PS: нужно сказать, что также отрезки имеют равные по длине стороны, и если производить движение во времени, то это позволит при таком алгоритмизировании также показать геометрию искривления уже не в статичном, а в развивающемся и детерминирующем пространстве. Но когда мы описали начальный объём, это значит что этот объём уже сам не может быть описан через алгоритмизацию, потому что в моей логике начального аргумента я доказываю, что если что-то описано как предельное решение, то оно не может быть само рассмотрено как то, что может быть решено через такое же решение, потому что тогда возникнет логика бесконечности решений, которая обессмысливает хоть какое-то понимание.
Тезисы
Язык математики — это физика (физика звука и цвета), потому что сама математика не есть математика в полном смысле, так как орудует физическими категориями сложения, вычитания, умножения, деления и так далее. Но физика до этого пользовалась лишь частично математическим, в то время как могла описать любой процесс на словах.
Геометрия — это то, что должно быть подлинным, аутентичным вычислением, она даёт готовую картинку. Ранее из числа выводили геометрию, теперь геометрия должна выводить геометрию из самой себя.
Физика и генетика, и другие естественные науки лишь частично описывают мир, в его малой части, в то время как дело физики исследовать сущности явлений (звуков, цветов, расстояния, числа и отношений, и т.д.), исследовать конкретное расстояния и движения, времени и угла, и т.д., до этого исследовалось лишь внешнее (результаты через уравнения), которое есть условное описание, но сущности в том нет.
Нынешняя же физика и математика тоже хороши и в том состоянии, в котором они есть, и потому надо продолжать исследования и в этих формах.
Что такое вычисление? Уравнение, интегрирование, вычисление производной? Это пересказ в числах того, что может быть объяснено на словах, а если не может быть объяснено, то в том нет сущности, а значит это отчуждённое, не истинностное вычисление или уравнение.
Математическое обоснование физических законов параллельного опосредованного смежного пространства.
ИСТОРИЯ МАТЕМАТИЧЕСКИХ ИДЕЙ С ПОЗИЦИЙ NOT PARALLELISM OF SPACE
Проблема 1. Классическая линейная каузальность параллелизма в представлении Евклида как историческая математическая фикция комбинаторных и постулативных табуляций.
Мы должны установить, что Евклидова геометрия имеет в своих каузальных основания воздействие и на современную математическую моделирующую геометрию. Евклидова геометрия не была изжита геометрией Лобачевского, но лишь подвергнута новой версии параллелизма. Тезис о том, что параллельные пересекаются или не пересекаются — это однородная сферическая данность пространственных систем Лобачевского на самом деле дополнивших, а не изменивших или опровергнувших математическую теорию Евклида.
Античных, арабских и средневековых математиков притом мы должны выделить, как действующих в инвариантных пифагорейских топиках модальностей и проектно-вычислительных трансформированиях. Даже философическая математика фундаментального порциального значения как математика Эвариста Галуа — это оснвоания, которые не изжили пифагореизм, а были версией математики линейных процессов инвариантов.
Если мы возьмём за утверждение истиностности гиперциклическую формулу:
A→∫←B=A (a+b+c+300.000x)
→∫←B (-a+ (-b) + (-c) + (300.000y) =
E (m∙c²) =A (E (+m∙c²) →∫←B (E (-m∙c²), то
Данная формула уже будет выражением нелинейной математической комплексной однозначности или числовой перефириии, не дополнительной качественной формацией, а процессом по меньшей мере опровержения, по большей мере — нового блокового подхода к инвариантам.
Дело в том, что я использовал здесь формулу не параллельности, использовав эйншетейновские преобразования в ней как предшествующее условие, но не коренное значимое тестирование математической идеи данного типа.
Классическая линейная казуальнсоть не изживает себя даже в плоскости гёделевской неполноты, потому что теория Курта Гёделя — это резервный вариант крайнего случая аналитической дискурсивности и он подвержен правилу исключения, которое состоит в общем контексте дифференцирований, интегрирований и вероятностных подходов любого математического уровня тестирования.
Если же обратиться к геометрии Эйлера, то может показаться, что данный прогностицизм форм также явление упорядоченное в логику линейности, но это, как и всё о выше сказанном с одной стороны так, а с другой стороны показывает одномоментную косность мышления, потому что иная вариация подхода — это не совершенно новое в координатах пространства и алгебры, а парадокс и праксис системы иной геометрии мышления. И потому Эйлер ближе к нелинейности, нежели Гёдель к нелинейный преобразованиям как следствия инерциальных вычислений его теории.
Пример парадокса и праксиса показал в своих вычислениях чётности, нечетности …., но современная нам математическая наука XX века именуется мной наукой подробизма или подробизации (интенциональный оказиях уплотнения информации вокруг кардинально стационарных базисных структур числа и линии).
На самом деле лишение математики XX века того, что называлось ancient philosophy (древняя философия) — это артефакт изъятия из математики структур числового фундаментального апробирвоания. «Древняя» математика стала пониматься как историзм, как историческая ликвидность, в то время как должна была пониматься как альтернативная парадигма мышления, как est, но никак не как исторически минувшее подразумеваемое «худшее», это неминуемо повлекло преобразование главной сущности математического в геометрическое, главная сущность — числовая проектность и интериоризированность стала отчуждённой спецификой мышления математика, что привело к фоновым подробизмам. Если бы число как phenomenon сохранило себя, то сейчас, исходя из дуалистических проностических интрпретаций можно было бы сказать, что мы увидели бы математический субстрат.
Сущность и основание мира таково, что субстрат получается из совокупности содержаний (числовых верификаций и флуктуаций), а не из форм числового поведения (легитимная геометрия к XX веку), но математики всего мира поверили именно в геометрию, а не число.
Теорема Ферма, как бренд геометрии стала самым ярким выражением и отправным фор-пост симптомом будущего геометризирвоанного подробизма. Но в геометрии нет тем не менее ничего плохого, дело в другом — геометрия могла бы быть другой, конституционально и конвенционально обозначенной community числа, и оппозиционной entre философии числа, а основываясь на некоей единой научной парадигме с единого стандарта математиками геометрия явилась консервированным и капитулирвоанным в своих основаниях явлением.
Положения Евклида и Лобачесвского в такой ситуации стали апофеозом мало структурно и пространственно определённой работы. Это была обеднённая геометрия, вдохновлявшая парадоксализмами, но как видим, парадоксальности не было, потому что стереометрические константы, которыми оперировал Лобачевский в антогонистической позиции Евклиду оказались лишь пунктуальностью единой лиги детерминирования обеднённой числом геометрии.
Исторические сведения говорят нам о том, что Евклид не так и отличался в постулатах от Лобачевского, что в его приложениях к своему учению в разных видах содержится Лобачевский, а Лобачевский во многих своих положениях подтверждает дефиниции Евклида. Здесь нет коренного позитивного перелома сциентистской направленности.
Математика начала XXI века выдвигает ряд проблем, особенно элитарные среди которых теории игр, вероятностей, числа «пи» и так называемые задачи «тысячелетия». Но данные математические проблемы есть конструкты для вычислений, простых компиляций и ревизии знаемого, но не нового.
В истории математики новое, например, показали элегантные подходы к числовым размерностям Роберта Гука (дифференцирование), Готфрида Лейбница (логарифмирвоание), Тьюринга (кибрнетические новации возникновения) и кодирвоание Нэша, а потом и Феймана. Матемтика же сводилась тем временем также к выравниванию единой геометрии слова. Многовариантность подходов и духа математики являлась неписанными правилами жизни неправильной. Даже язык Леви-Стросс в своём структурализме начал подводить под математический базис, чем занималась также Кристева и многие другие до сих пор полагают что такую сложную реальность как язык можно свети к современной геометризирвоанной математической корреляции актов коммуникации.
Чуть позже я хотел бы разобрать и те формулы, которые уже опубликовал выше. А сейчас сказать о том, что депозиты результата являлись следствием деятельности гениальных умов, таких как Рене Декарт в первую очередь, и уже упомянутый Эварист Галуа, хотя для древнего мира в совершенно альтернативно равноценной позиции расёты арифметики и астрономии в виде представлений Птолемея и Галилея, Ньютона и Гальтона.
Египетская математика, индийская математика и вообще восточная математическая традиция, к слову, была порывом к великому движению духа мысли в русле специфической крайне интересной фигуративной символической ветви математики, но, как мне кажется, была заглушена спонтанными политическими и историческими условиями, и есть альтернатива для развития её как ветви сейчас.
При этом я совсем не утверждаю что научный мир, математический мир должен быть плюральным, и это догма, я хочу сказать, что плюральность в науке и математике — дело немногих, и ею должны воспользоваться как философией немногие, и значение её для этих немногих и всего мира в роли патерналисткого генерирования, которое совсем не обозначает, что будет узнано, скорее это будет интеллектуальная афшора, и в этом нет ничего плохого, главное чтоб ещё одно значимое условие было выполнено — непротивление плюральной математике.
Je va parle не только от себя, но когда я говорю от себя, я говорю как представитель числового направления и борьбы с отчуждением числа. Надо понимать, что польза математики числа в том, что из него может родить всякая возможная геометрия, чего не может быть при выведении числовых материалов для геометрии. Число рождает «из», а геометрия «для», и в это существенно смысловое и агрегатное развитие методов математический транзакций и борьбы с тривиальными «конусами».
Высшая философия и Высшая техника
Я могу с уверенностью сказать о том, что изучение и понимание огромного массива научной литературы, философских концепций, истории, авангардных идей открытие, опыт жизни и феноменология событий, которые мне даны чуткостью и интеллектом открывают мне грандиозность и восторг жизни. И в общем-то уже здесь эта грандиозная жизнь является высшей материей пребывания. Но то, что после жизни не гарантирует нам называемое нами словом «продолжение» (continuing), потому что всё говорит о том, что грандиозное здесь, а там, за гранью функций организма — может ничего не быть, это ни доказать, ни опровергнуть, слишком сложная логика действует в мире. Но есть данность настоящего дня, и можно сделать максимально много для того, чтобы наши дни именно сейчас и сразу стали очень длинными, возможно в другой математической координате времени, и что самое главное — для того, чтобы иметь возможность философствовать (philosophyng). Освоение двух-трёх технологий позволит нам жить. Это нельзя назвать трансгуманизмом, потому что я говорю о том, что можно изобрести в таком виде, в котором уже не важно живы мы или мертвы, что восстановит из мёртвости, не надо спешить и что-то примитивным образом замораживать, как это делают трансгуманисты с мозгами, нужно всего-то создать принципиальных две-три вещи, чтобы активизировать бытие. И это только для одной цели — чтобы иметь счастье философствовать (successful). Потому что гарантий нет. И даже более того — иметь жизнь, которая постоянно под угрозой небытия — это самая красивая из возможных картин жизни, самая трагически пахнущая, но и самая красивая и возможно природа этого и хочет, чтобы мы опасно ходили и в итоге держались на плаву, ставя на карту вообще всю жизнь и всё бытие.
Я хочу сказать, что мой труд будет одновременно научным и философским, я не разделяю эти вещи. И даже хочу более того сказать, что пора уже развенчать миф о том, что математика является языком науки и только с помощью математики можно заниматься такими науками как физика, химия или астрономия. Это большое заблуждение. Чтобы что-то понять, чтобы что-то изобрести надо это объяснить на словах, это будет первое и самое главное, то есть надо быть ритором — вот первое условие учёного (и древние, и даже геометры и математики так и делали), скорость записи с помощью формул — это отчуждение понимания, это надо понимать хорошо — это второе. То есть отчуждение. И третье, когда речь заходит о непосредственной практике нужно (necessary) составлять, конструировать или экспериментально доказывать что-то с помощью подавляющего числа людей, которые к этой работе, скажем прямо «черновой» предназначены. Знатоки счёта, черчения и компьютерного и информационного программирования — это как плотники и столяры, электрики и строители, они делают непосредственно объекты, в то время как сейчас заставляют реальных философов и учёных этим заниматься, то есть вычислять интеграл, дифференциал, возводит в период, пользоваться понятием бесконечно малых, это огромная ошибка. Этого ничего знать не надо, это дело практиков. Вы думаете Циолковский, который придумал ракетный двигатель был способен его сконструировать, и ракету в целом, чтоб её запустить в космос? Нет. И древние греки не создали дифференциальных и интегральных уравнений только потому, что там почти не было «чернорабочих» в хорошем смысле этого слова. Потому создавать идею — это удел единиц. А её реализация — удел большинства. Хорошо ли мог Эдисон, создатель электродвигателя, как вы думаете, чинить розетки, делать проводку или создавать электростанции? Он создал принцип. А у нас так замалёвано всё это, что считается всерьёз, что без знания математики физик не физик, химик не химик. Впрочем в образовании и науке как социальном институте ещё много чего надо изменять в лучшую сторону.
Моя философия в том, чтобы принять меры к продолжению нашего бытия ради философии, это наука в стиле великих мыслителей. И сразу «с места в карьер». Телепортация и в итоге непрерывные переходы в другие пространственные географические места, Машина Времени, и в итоге непрерывное пребывание отдельных функций организма в разных временах ради постоянного долголетия, как бы вибрируя и не старея и состояние мира как фрагментационное, то есть не длящееся и не конечное, за счёт чего пребывание в сюжетах разных приятных миров и отсутствия психических сломов — вот то, что нам нужно. И на всё это есть готовые ответы и решения. Уже сейчас можно сказать о них, и уже ряд вещей мною написаны. Философски это означает то, что мы снимем психическую девиацию, пространственную девиацию и временную девиацию.
Сейчас это может коробить, вызывать сомнение, но только потому, что человек в том потоке времени, в котором он находится, проходит обычную эволюцию чувств, идёт переформатирование психики, чего можно избежать либо миллионами лет эволюции, либо философски-технически-научно и тогда быстро и без болезненных и долгих лет.
Философ — это человек, который открывает двери в новое (opening new horizons).
Я знаю людей, которые не хотят жить долго и даже вечно. Это их выбор. Я не настаиваю. Я говорю про себя и свою рефлексию, которая указывает мне на то, что я хочу, потому что в мире есть философия. И я уже знаю, что реально могу быть восстановлен, если что, потому что уже есть знание об этом.
Я думаю, даже хорошо, что мы так мало знаем о мире, что мы так мало можем, потому что через это открывается наше встраивание в бытие настоящего.
Я бы не хотел также, чтобы меня отождествляли с космистами, такими как Фёдоров, Циолковский и Вернадский, при всём уважении к ним и уже упомянутом ранее одном из них, потому что космизм — это направление в русской философии, которое плохо тем, что не конкретно. Это очень расплывчатые и отвлечённые, порой даже сказочные, а значит младенствующие размышления, как и их противоположность — трансгуманизм — который конкретен очень, пошло конкретен, то есть предлагает примитивную конкретику.
Наука и философия нуждаются также, как это может показаться, ни в каком ни среднем пути Конфуция или Лао-Цзы, философия и наука, о которых я говорю должны быть просто идентичными философией и наукой, философия и наука одна — настоящая и реальная.
Потому традиционализм или наоборот Постмодернизм — это философии, которые философии, но я говорю о научной философии, это философии точно, не как космизм и трансгуманизм, но не научные.
А философия и наука в одном — это самая высшая степень натуральности философии, потому что сам мир — это наука и материя науки, как писал Гегель: мир сам себя осознаёт и познаёт.
Итак, все эти размышления очень конкретны по отношению к рассматриваемым мной вопросам, потому уже сейчас через метод прообраза объясняют то, что открытия, перечисленные мной работают на принципе сюжетов. Нужно создавать сюжет идентичный тому который есть или был, с помощью синтеза физиологического материала и компьютерного точного моделирвоания и в итоге получить место или человека, котоыре мы хотим, потому что в природе нет параллельности, и при возникающем параллелизме объект перейдёт в место где параллелизм возникает, будучи неспособным быть сразу в двух местах. Все перечисленные сюжеты, и сам Гегель могут быть потому с нами. Но когда речь о телепортации надо уже создавать копию нас с вами, чтобы нас туда перенести, а когда человека восставить из условного «небытия» просто сделать функции его как он есть в доли секунды хотя бы, но всего, потому что начало и конец человека. И вообще человек — это средоточие ансамбля всех функций возможных в нём. И потому человечность и жизнь как счастье проявляются, когда есть целостное мышление или цельное занятие, потому что это идентичности человека соответствует.
Когда же Маркс пишет о том, что человек есть то, что делает из него общество и что в протесте против устаревшей формации рождается преодоление отчуждения, то он пишет всего лишь вариант социологического и политического единства, которое может и не реализовываться, если есть индивидуальная жизнь субъекта истории — человека целостного (human subject).
Перечисленное мной очень легко вычислить с помощью техники, для этого надо лишь скопировать все функции, сделать информационную карту человека или объекта и потом с добавлением реальных физиологических структур на свободном каркасе из чего-либо воспроизвести живую материю и компьютерных геометрический импульс. Если речь об умерших, то нужно смоделировать чувства, эмоции этого человека. То, что мы получим этого именно человека, а не того, который может по одной из физических теории о слоении времён придти из другого измерения исключено, потому что там воспроизводится целостность только той координаты, в которой человек есть. Если бы всего вот этого мы не делали, то теория слоения времён была бы для нас утешением, что чисто гносеологически мы вечны, потому что слоение во временах предполагает все возможные сюжеты жизни. Напомню, что это учение о том, что у нас бесконечное число вариантов действий, но выбираем мы что-то одно, а все остальные варианты реализуются в другом слое потенции, и не могут не реализовываться, потому что сама гносеология их наличия совокупна имманентно с их заполнением.
Итак, Высшая философия и Высшая техника реализуются в перечисленных мной вещах. Бояться нам теперь вообще нечего, потому что мы точно это всё реализуем во времени в связи с тем, что данное подпадает под один из фундаментальных законов — целостности экологии, который выведен мной и гласит о том, что всё есть природа, и катастрофы уничтожения природы, Вселенной, например, быть не может, потому что природа есть и просто есть и саму себя она не уничтожает и не рождает. This is my special agreement on science abilities with nature and future society.
ФИЛОСОФИЯ МИНИМУМА
Я сейчас буду говорить о философии минимума, но в общем-то и о науке минимума, потому что эти понятия для меня нераздельны. Минимум — это строительная основа всего нашего мира. Дело в том, что все возникшие некогда виды материи, органического вещества и структурные связи возникали из минимального объекта, минимального по своим характеристикам объёма и воздействия на себя и другие объекты.
Всё в природе рождается из минимума. Если что-то возникает, то оно возникает из минимальных по силе предпосылок. Я хочу сказать о том, что когда мужчина и женщина зачинают ребёнка, происходит минимальное перемешивание жидкостей, а до этого минимальные физиологические движения, а до этого просто мысль и неуловимая тяга, а до этого решение реализовать всё это в минимуме миниморуме — мысли.
Когда строится здание — это то, что предшествовало ему — помыслили о создании объекта. И создатель, помысливших, руководитель фирмы, сам не строит, строят другие, у него же была мысль, пускай и в контексте других мыслей, других людей.
Любое зерно даёт всход изначально являясь минимальной сущностью. Но мы получаем, как и в случае с зачатым человеком развёрнутое сложное органическое существо. Минимум приходит в голову к мыслителю, и потом рождается целая система, целое учение, которое из этого минимума лишь развёртывается.
Но мы привыкли всё мерить объёмом и массивностью. В этом проблема человеческой цивилизации (цивилизации в моём смысле как одной мощной современности) — если что-то создать грандиозное, то из объёма материалов, если что-то создать мощное, типа ракеты или завода по обогащению урана, то нужны мощные объекты, средства и время. Никому в голову не придёт мысль, что дом может расти, равно как и завод, как посеянный, как зерно, развиваясь, это сочтут абсурдом, но ведь дом — это часть биосферы, всего-навсего изменённые материалы и материи мира, но никак не инородные.
Потому вывод тут интересен до восторга: мы может с помощью мышления и кратких записей организовывать создание объектов, потому что так мы и делаем в обычной привычной жизни, но не принимать в этом участия массивным трудом и массивными стройками. Программа и так активирована, она разовьётся либо сама, либо через совпадение наших с ней усилий. Это всё равно что ответить на вопрос друга: «Да, через километр отсюда идут гулянья». И либо поверить в эти гулянья, либо идти и смотреть. Факт один — они идут, потому что заложены.
Никакой магии ведь нет, никакой метафизики, есть работа с материальными фактами. Нечто похожее, может даже об этом у физиков и речь, говорится в науке о также неких минимальных определяющих характеристиках в развитии чего-то, но физики так сложно пишут, не могут подобрать слов и потому получается кавардак с этой их концепцией. А дело проще, дело лучше. В жизни существует самый большой минимум — это мысль и предшествующее ей намерение в виде воодушевления (о силе которого ещё писал Лоренц К.), и все производные материальные факты от этого воодушевления и мысли. Но если построить мысль так, чтобы описать кратко создание объекта того или иного типа без участия сил и энергетических ресурсов, то по-идее материя должна развернуться, важно чтоб это было описано на грамотном стилистическом научном языке и по методу градации развития стройки или появления объекта. Всего, с чем мы хотим иметь дело.
Мы организуем процесс, в его узловых характеристиках и создастся объект, либо на основе имеющихся конфигураций в мире, либо (что сейчас невероятно представить) вырастет как бы сам.
Но тогда может возникнуть вопрос: а математика, все расчёты, физические вычисления, этого всего что не надо? И отвечая на этот вопрос, я постараюсь максимально быть философом. Дело просто. Математика и вычисления ради красоты и сведения к тому чего хотим этих вычисления существуют, но не ради выведения иного. Если мы проследим ход вычислений, то так и окажется. А в природе любой организм развивается из минимума без всяких вычислений и гипотез, алгоритмов и аксиом.
Когда во время Первой мировой войны были найдены люди с пробитыми черепными коробками и случайно установлена связь между полушариями головного мозга, их областями и поведением человека, то это, не удивляйтесь, была операция сведения знания, а не открытия. Чтобы понять как работает мозг нужно этим мозгом быть (здесь нам повезло, мы все мозги в каком-то смысле) и уже из этого выводить остальное.
Но о минимуме, о философском минимуме. Дело просто. Он существует, это огромная физическая «концентрация», ввожу этот термин, и она действует в природе постоянно в разных формах. И если человек вдруг задумает помириться с тем, кто на него обижен, нужен всего минимум этического усилия, а если захочет освоить науку, тоже минимум. Мир же отчуждает смысл этих понятий и говорит о каких-то объёмах и невозможности изобретения без максимума силы и объекта как средоточия материи. Вот в чём дело. Но это не истинностная, а конвенциональная убеждённость, просто так решили.
Но у меня нет никаких конвенций в повествовании и поэтому я хочу сказать о том, что очень даже актуально (для философа по крайней мере) — определять что научно, а что не научно, кто учёный, а кто нет? Учёным считает человек с дипломом определённого профиля, владеющий научной терминологией и ведущий исследования. Диплом профиля, вы понимаете, разносторонней личности не нужен, либо невозможен из-за её обширности (какой-то другой диплом есть, а интересов много), так что это уже грубейшая ошибка науки, второе — научная терминология и соответствующие ей знания — у гения точно может быть своё обозначение тех же вещей, а для свободного учёного свободно изучать, своим методом альтернатива и возможность найти больше. Ведь что такое терминология — это придуманные нами понятия, а я придумаю другие, по-другому, и чем они хуже? Может даже лучше. Ну и исследования, многие учёные без диплома больше любят дисциплину, чем учёные профиля, которые даже меньше ей уделяют внимания и желания. Потому любая вещь в природе может быть создана из минимума вне зависимости от того кто это, главное, чтоб он знал как это делать.
Другое дело, если данное будет массовым. Ну первое — оно будет массовым неизбежно. А второе — ничего страшного тут не будет, так как усложняя данную процедуру развитие объектов будет крайне постепенным и обусловленным социальными сложными контактами.
А почему же так устроено? Отчего в природе существует вот этот phenomenon — минимум. Размышляя над этим вопросом, я пришёл к установлению, что так происходит потому, что человек и природа, вообще органическая материя есть крайний случай универсализма. Это крайне универсальные моменты жизни. Здесь нет ничего удивительного, развитие жизни имеет универсализм. Но есть философы в истории, которые спорили об универсальном, отвергали его в пользу реального, например, не разбирая все эти споры, я скажу лишь, что универсализм не победим и не преодолим как сфера теории познания, потому что он всеобъемлет любую сторону жизни, а всё, что не универсально, обязательно несёт на себе негативистские очертания, нечто искажённое. Мера же универсализма незыблемо велика.
Теория Условно Стойкого Пространства
Безусловно значимым является то, что современный природный мир должен быть подвержен анализу. Эйнштейн, который позаимствовал E=mc2 у Пуанкаре, и Лейбница, который сейчас считается main stream современной физики может ещё быть подвержен ревизии и утилизации в своих теоретических основаниях, так как времени с создания его теории прошло очень немного, это конец 20 века, минимум и миниморум в историческом процессе. Я хочу сказать о том, что, если мы принимаем какую-то идею, то она принимается (в силу истинности) в продолжении огромного числа лет, а не сразу, то, что принимается практически сразу, не есть развёрнутый в истории продукт, а потому ложный феномен.
Я бы сказал, что Эйнштейн не прав, потому что он рассматривает пространство-время (это первая уже сразу ошибка, так как пространство — это следствие, а время — это многовариантная координата специфики) как искривлённое — то есть для него существует невидимое глазу искривление. Он был близок хоть к какой-то истинности, но на самом деле если бы пространство и время были искривлены, то мы ощущали бы в течение жизни смену видений мира, объектов мира, подобно тому, как ощущаем изменения в ландшафтах, в руслах рек, видим как изменяются наши близкие, старея или рождаясь и так далее, но относительно пространств и времени мы такого не наблюдаем. А по идее это должно быть, потому что нет ничего не развивающегося, не проявляющегося, не детерминирующего и не коррелирующего. И пространство должно меняться. По-сути, если бы Эйнштейн был прав (и Пуанкаре), то мы бы наблюдали смену зрительного восприятия геометрических форм природы. Но мы этого не наблюдаем.
Если же принять за истину постулат о том, что пространство есть не развивающаяся, или для нас развивающаяся крайне медленно, в силу его огромной протяжённости до абсолютности, то есть для нас как бы статичное, потому что его много и оно не фиксируется для нас в движении, то наше восприятие может быть частичным или целостным, или приближающимся к целостному. Я имею ввиду то, что пространство для нас условно недвижимо, и может по разному видеться, в зависимости от нашей способности его видеть, а эта способность заключается в той территориальной зоне, в которой мы обитаем.
И с навыками некоей географической зоны мы можем видеть его уже в другой зоне точно также. На примере, это будет то, что некоторые люди, которые долгое время живут в той или иной среде (близкой к воздушной, или подземной) иначе реагируют на геометрию мира. Но таких примеров мало, мы всё же живём в мире прямоугольного.
Мы живём в мире прямоугольного видения, потому что земная реальность — это векторное, прерывистое, линейное, дискретное, квантируемое объектами пространство. Оно линейно. Земля круглая, но мы живём воспринимая не сферически, а линейно, потому что живём на поверхности Земли.
То есть, верно сказать, что пространство-время не искривлены, а в отдельном космическом пространстве иные для восприятия, но по сути пространство и время одно, развивающееся, но имеющее близкую к абсолютной природу и потому для нас недвижимо фактически в силу своего масштаба.
Физики могут мне сказать, что я должен обосновать это формулами. На что я скажу, что математические расчёты и формулирование ответа на теорию — это «чёрная работа», которую должны выполнять счетоводы, и ничего плохого в том нет. А критерий истинности (забудьте про шарлатана от науки Поппера) знания в его аргументации лексическими средствами. Любая же математика может как подтвердить, так и запутать, и усомнить в истине. Вообще задача математики в том, чтобы выводить геометрию из отношений, а не вычислять (но это отдельный разговор, это мои математические теории).
Но всё же можно дать некую архаическую формулу тому, о чём я говорю: E=x*L, E=x*L2, E=y*xL, E=y*xL2, E=x*l, E=y*l, где E- энергия, хy- воспринимающий реальность, L,l — виды реальности в зависимости от воспринимающего реальность.
Конечно, это очень кратко. Очень условно. Но мы должны извлечь также отсюда философскую суть. А она заключается в том, что для человека важно понимать окружающую действительность исходя не из данных опыта, а исходя из данных всевозможных трансформаций опыта под действием смены положения наблюдения. Но и то смены, которая даст результат только через время, потому что человек должен навыкнуть иметь другой взгляд и другое видение, другую форму восприятия воспитывают, но по сути мы имеем дело с условно не движимой субстанцией.
Эйнштейн не был философом, следовательно a priori на 50 процентов, на половину как минимум он был не прав. Любой учёный не философ не прав фактом того, что он не философ на 50%, потому что философ — это человек, которого сущностное отличие забота о природе, знание о природе, он и есть часть этой природы.
Условно стойкое пространство, вот то, с чем мы должны иметь дело. Когда же мы говорим о скорости света, то мы должны сказать, что достижение скорости света (приближение к скорости света), безусловно является для материального объекта резанированием с пространством и потому не время замедляется, а объект начинает двигаться уже не линейно, а по нарастающей спирали, циклом, и другой тип движения является отображением изменения отношения к пространству материального объекта. Также как в моей физике объект, который стремится к силе Абсолютного Покоя (постоянно усиливаемая тишина и консервация тела), начинает резонировать многонапрвленным в разные плоскости одновременно взрывом, либо при минимальной изоляции движением циклического развития, что происходит с чёрными дырами.
Если нам интересен вопрос о состоянии природы, о том, есть ли многомерность пространства, то надо сказать, что есть не трёхмерность, не четырёхмерность, а мерность, стремящаяся к абсолютной, потому что геометрическое разнообразие велико, и при преодолении скорости света до скорости в два раза больше скорости света объект уже будет резуонировать своим навыком к среде по другому и в другой геометрии.
В этом нет ничего сложного, многомерность к абсолютности является всего-навсего составной частью всеобщей эклектики мира, которую наше сознание упорядочивает. Но о времени. Время, в отличие от пространства для нас изменяется в восприятии, кажется текущим быстрее или медленнее, и потому время — это категория, имманентная нам самим, для человека важно знать, что скорость протекания времени в нём не зависит от него, но повлиять на неё можно лишь научно, моделируя своё время, что дело будущего. То есть И. Кант по всем статьям не прав, время и пространство не в сознании, время в человеке как следствие, а пространство в природе как следствие, и они разделены, а сознание их конституирует в силу гармонии, заложенной в него.
Условно Стойкое Пространство, можно ли его ощутить в динамике движения? Приблизиться к скорости движения пространства. Я вообще не верю в ответ такого типа: «нет». Конечно же можно, но для этого надо либо смоделировать Пространство и тогда угадать с его функциональными характеристиками и по закону не тождества материального геометрического мира сочлениться с ним (но это не лучший путь в данном случае), либо провести некое прицепление к Условно Стойкому Пространству, в результате чего мы будем двигаться с его силой и сможем обозреть его сущностное величие. Но для этого прицепления к Нему, нужно набрать хотя бы минимальную форму объёма единицы объекта движимой этим Пространством, нужно принять объём, как атом, который есть единица этого Пространства, и таким объёмом будет в первую очередь гамма геометрий, которые могут отражать полноту мира, но выявить их дело длительное и в истории должное быть развитым.
Теория Математики. Формулы Бытия
Стационарные формулы
Математические модели — это тождества на уникальные бытийные формулы мироздания, которые воспроизводят априорную картину жизни в том или ином участке земли, и способствуют повторной математической операции с целью физического анализа природы и всего земного, живого, энергоёмкого.
Таким образом мы берём точку a — это будет некая топология малого размера, стационарная, для которой нам надо вычислить формулу (практическая математика)
Пускай этой топологией будет в — человек 1, с- человек 2 и z — речь. Представим, что в спрашивает с: «Отличная погода?», с отвечает в: «Так тепло будет и завтра!»
Мы взяли речь двух людей, произвольную речь, но особенность здесь как раз в произвольности, это некая вероятностная беседа, спонтанно возникающая у знакомых людей.
Теперь обозначим формулой их речь, потому что в теории Всепричинности важно каждое слово. (Теория Всепричинности — это теория, которая объясняет всё в мире наличием связанных и воздействующих друг на друга причин, которые скрыто или явно, но должны поддаваться логическому объяснению)
С=О_Р?; В=Т_t _в2_I_Z2!
где,
О-«отличная»,
_-«связка»
Р- «погода»
Т-«так»
t- «тепло»
в2-«будет»
z2- «завтра»
I — «и»
Но что такое связка? Более правильное оформление отношений речи можно выразить через понимание накопления информации, то есть суммирования, только суммирование даёт результат и реакцию. Смотрим:
С=О+Р?; В=Т+t +в2+I+Z2!
Также важно понять: а что будет вместо языкового «;»? Если мы всё это сводим в единую формулу бытия данной топологии вопроса и ответа, то я думаю, что более разумно это будет выглядеть так:
С=О+Р→ В=Т+t +в2+I+Z2!
то есть «→» — знак следствия, который стирает грань между вопросительным и утвердительным в топологии общения и настаивает на следствии речи вообще. Тогда»!» просто упраздняется.
С=О+Р→ В=Т+t +в2+I+Z2
Итак, мы дали математическое описание речи как факта, и теперь через основное уравнение мироздания, должны спроецировать из временной движимой точки бытия данное уравнение во вторую реальность (пока условимся на двух реальностях.
Основное уравнение бытия: α→∫←β
Следовательно подставляем значения по зеркальному методу:
→∫←
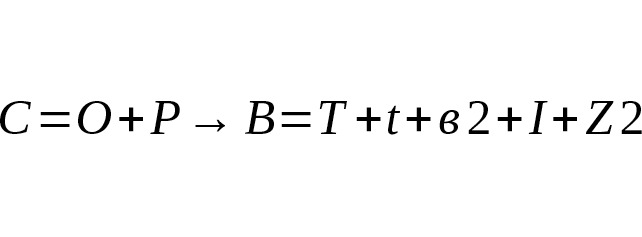
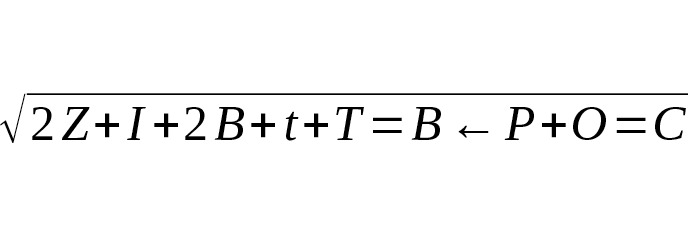
То есть формула зеркально отобразится, но в ином математическом измерении условно мы её обозначим под корень, как особенную и получится, что в и с, общающиеся не есть главные элементы бытия, но природа слов есть главная доминанта математического моделирования
Бытие во втором измерении будет насыщеннее в два раза, обратно противоположно законам природы во времени, но имеющее также жизнь в себе. А слова — это вообще самое главное в моделировании, так как они заключают чувство, разум, дух и результат человека как продуцирующего общение и бытие.
Но не обязательно измерений будет 2, возможна ещё такая формула, если бытие будет в трёх измерениях. На Земле всегда в одном, а там оно суммируется до многих значений:
→∫←
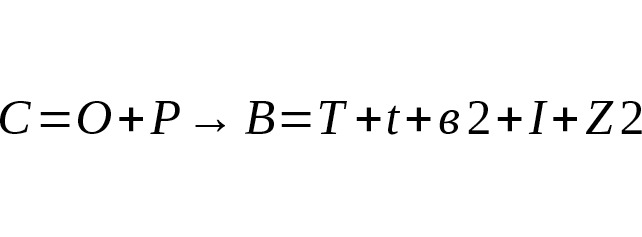
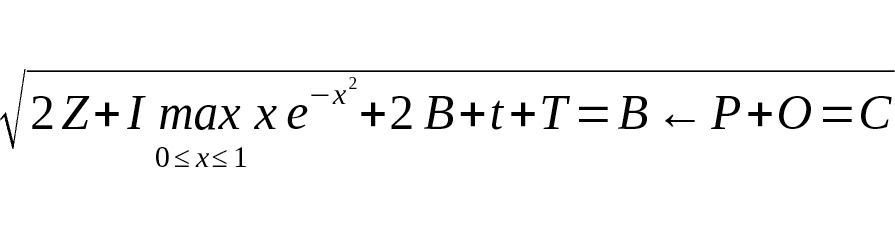
С помощью логарифма предела мы приходим к максимальному значению связки, немного абстрагируясь от остального. Но важен тот факт что самое мало значимое на вид несёт самую высокую информативную нагрузку.
Таким образом мы нашли наглядность. Но нам надо вычислить смысл. Если мы даём наименования и создаём, а точнее отображаем функцию, то в неё мы читаем закодированные смыслы будущего бытия. И в плане теологической проверки нам нужно уяснить положительные и отрицательные экзистенциалы, что даст нам повод морально оценить данную топологию и её бытийный и вечный смысл (смыслы).
Во-первых, надо сказать, что мы промоделировали две фразы, и это стационарное моделирование. Но может быть активное моделирование не стационарной топологической системы и тогда многое изменится. Пока же мы должны сказать ещё о том, что слово играет главную роль, но также системой топологического вида может быть и человек, но только в контексте мышления. Само по себе тело ничего не значит без процессов протекающих в нём и главным образом мышления. Но вернёмся к моральной нагрузке.
Стационарная формула приводит нас к геометрическому пониманию. Так, положительно до +∞ и отрицательное до -∞ записывается:
∞+=→∫← = +∞
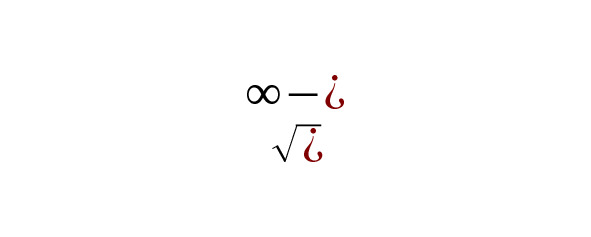
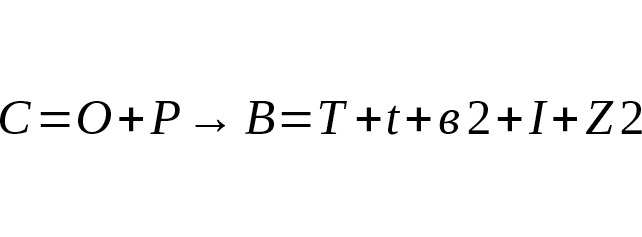
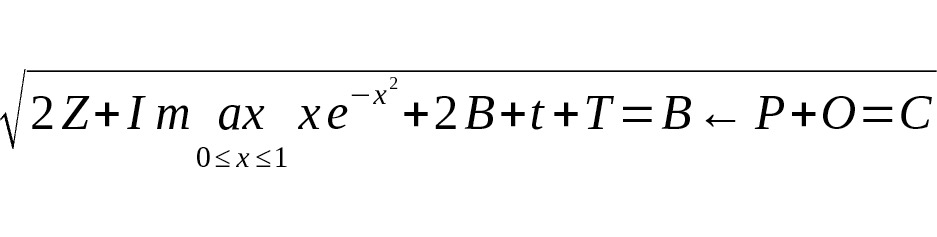
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.
