Бесплатный фрагмент - Комбинаторика и нейросети

Комбинаторика и нейросети

История комбинаторики восходит к древним цивилизациям. Вот основные этапы её развития:

Первые упоминания о комбинаторике встречаются в Индии, где учёные уже во II веке до н. э. исследовали различные соединения элементов. Считается, что индийцы использовали методы комбинаторики для анализа структур в поэзии.

В XII веке индийский математик Бхаскара работал над сочетаниями и перестановками, что свидетельствует о дальнейшем развитии этой науки.

В XVII веке комбинаторика начала формироваться как научная дисциплина. В 1654 году Блез Паскаль исследовал биномиальные коэффициенты, что стало важным шагом в комбинаторной теории. В этом же веке Пьер Ферма высказался о связи комбинаторики с теорией чисел.

Термин «комбинаторика» вошёл в научный обиход после публикации работы Готфрида Вильгельма Лейбница «Рассуждение о комбинаторном искусстве» в 1665 году, в которой обсуждались сочетания и перестановки. И действия над ними.

Яков Бернулли в 1713 году в своём труде «Ars conjectandi» («Искусство предугадывания») рассматривал размещения, что ещё больше углубило комбинаторные теории.

Современная символика сочетаний была разработана разными авторами и широко принята в учебных пособиях. Этот период стал расцветом комбинаторной математики.

Комбинаторика продолжила свое развитие, охватывая такие области, как теории графов, оптимизация, статистика и информатика. В последние десятилетия она стала неотъемлемой частью различных научных дисциплин [2,3].

Комбинаторика на сегодняшний день играет важную роль в математике и смежных областях, являясь основой для многих современных исследований и приложений [1,4].

Комбинаторика — раздел математики, в котором изучаются воп [росы о том, как определить сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

1.Основные правила комбинаторики

Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств — правило суммы и правило произведения.

Правило суммы

Если конечные множества не пересекаются, то число элементов X U {или} Y равно сумме числа элементов множества X и числа элементов множества Y.

То есть, если на первой полке стоит X книг, а на второй Y, то выбрать книгу из первой или второй полки, можно X+Y способами.

Пример 1.Допустим, что нам необходимо добраться из пункта А в пункт Б. При этом, это можно сделать различными способами (смотрите схему 1):

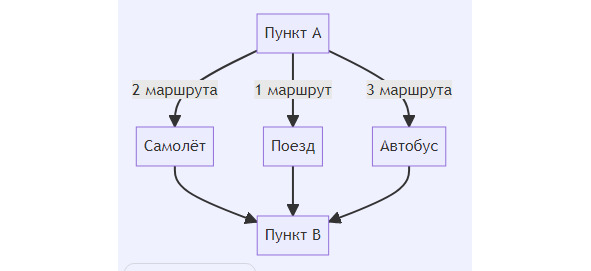
В этой схеме:

Существует 2 маршрута самолетом.

1 маршрут поездом.

3 маршрута автобусом.

Таким образом, общее количество маршрутов от пункта A до пункта B составляет:

2+1+3 = 6 (маршрутов или способов).

Правило произведения

Если элемент X можно выбрать k способами, а элемент Y — m способами, то пару (X,Y) можно выбрать k*m способами.

То есть, если на первой полке стоит 5 книг, а на второй 10, то выбрать одну книгу с первой полки и одну со второй можно 5*10 = 50 способами.

Пример 2.Смотрите схему 2.

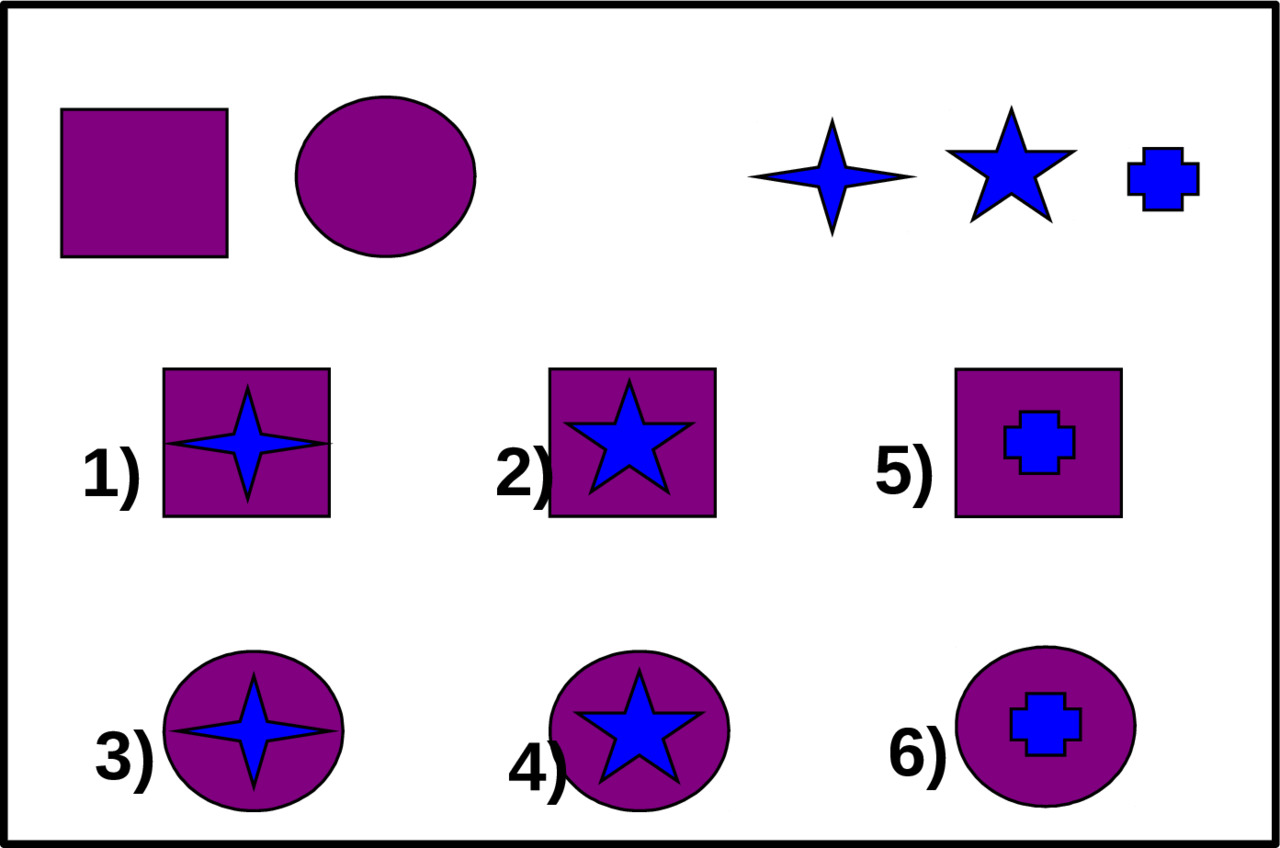
На данной схеме показано применения правила умножения для 5 объектов. Эти объекты можно выбрать 3*2 = 6 способами.

Очень часто для наглядного решения задачи применяются круги Эйлера [3,5,6].

Пример 3. Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским — 28, французским — 42. Английским и немецким одновременно владеют 8 человек, английским и французским — 10, немецким и французским — 5, всеми тремя языками — 3. Сколько туристов не владеют ни одним языком?

Решение

Выразим условие этой задачи графически. Обозначим одним кругом тех, кто знает английский, другим кругом — тех, кто знает французский, и третьим кругом — тех, кто знают немецкий.

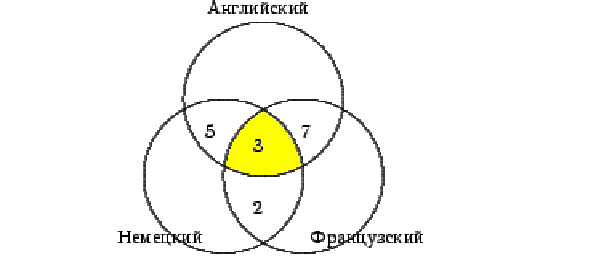
Английским и французским языком владеют 10 человек, а 3 из них владеют еще и немецким (см. схему 1). Следовательно, только английским и французским владеют 10 — 3 = 7 человек (см. схему 2).

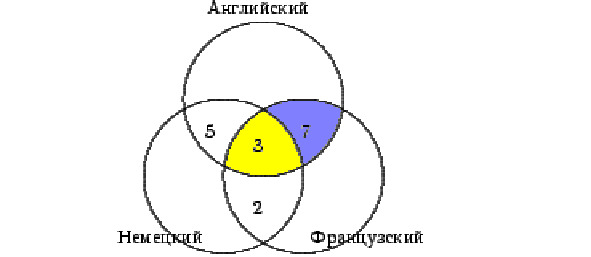
Аналогично получаем, что только английским и немецким владеют 8 — 3 = 5 человек, а немецким и французским 5 — 3 = 2 туриста. Вносим эти данные в соответствующие части схемы (см. схему 3).

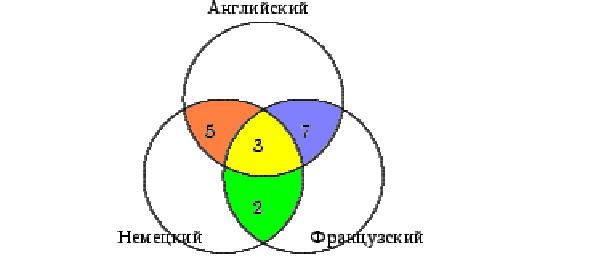
Определим теперь, сколько человек владеют только одним из перечисленных языков. Немецкий знают 30 человек, но 5+3+2=10 из них владеют и другими языками, следовательно, только немецкий знают 20 человек. Аналогично получаем, что одним английским владеют 13 человек, а одним французским — 30 человек.

Вносим эти данные в соответствующие части схемы (см. схема 4).

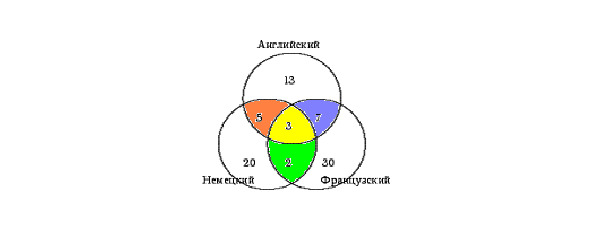
По условию задачи всего 100 туристов. 20+13+30+5+7+2+3 = 80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним из данных языков.

Ответ: 20 человек не владеют ни одним из данных языков.

2.Основные формулы комбинаторики

2.1. Размещения без повторений

Пример 4. Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны?

Это пример задачи на размещение без повторений. Размещаются здесь 10 цифр по 6. А варианты, при которых одинаковые цифры стоят в разном порядке считаются разными.

Если X-множество, состоящие из n элементов, m≤n, то размещением без повторений из n элементов множества X по m называется упорядоченное множество А, содержащее m элементов из m элементов.

Количество всех размещений из n элементов по m обозначают: