
Бесплатный фрагмент - Книга-тренажер: «Базовая подготовка к ЕГЭ по информатике в компьютерной форме»
Авторский курс
Введение
В данной книге приведена теоретическая часть для каждого задания и рассмотрены основные подходы к решению задач компьютерного ЕГЭ по информатике. Книгу можно использовать как справочник по теории на те или иные задания или как тренажер для нарешивания задач. Наилучшим психологическим подходом на экзамене считается такой: вы решаете все задания, которые легко вам даются, а более сложные пропускаете. После чего, воодушевленные своими успехами в решении задач, приступаете к решению задач, более сложных на ваш взгляд. Далее, если осталось время, то начинаете проверку заданий, которые решили. И напоследок при наличии времени начинаете прорешивать все задания вторым способом и сверяетесь с тем, что у вас получилось при решении первым способом. Если выявились расхождения в ответах, то ищите ошибку. Такая тактика позволит вам набрать максимальное число баллов на экзамене. В книге рассмотрено решение задачи на языке Python, т.к. на нем код получается более коротким в сравнении с другими языками, что поможет сэкономить время на экзамене и набрать более высокий балл. Если вы хотите решать задачи без языков программирования, то читайте книгу в любой последовательности по номерам: 1, 4, 7, 11, 10 — можно решать в любом порядке. Остальные задачи 2, 6, 12, 14, 16, 17, 22, 23, 8, 5, 19—21, 17, 5, 13, 3, 9, 18, 25, 24, 26, 27 лучше осваивать в указанном порядке. В конце каждой задачи есть раздел: «задачи для самостоятельного решения. Пробуйте самостоятельно написать код, стараясь не подглядывать на похожее решение, и также решать вторым аналитическим способом, в тех заданиях, где это возможно.
Каждый вариант экзаменационной работы включает в себя 27 заданий, различающихся уровнем сложности и необходимым для их выполнения программным обеспечением. В ответах на экзамене не нужно вводить отрицательные числа в качестве ответа и дробные числа. Если таковые числа у вас получились, то нужно прочитать еще раз условие задачи, возможно пересмотреть решение и ввести ответ, отличный от отрицательного и дробного числа, т.к. экзаменом такой формат ввода не предусмотрен.
Ответы на все задания представляют собой одно или несколько чисел, или последовательности символов (букв или цифр).
С 2021 г. ЕГЭ по информатике и ИКТ проводится в компьютерной форме, что позволило включить в КИМ задания на практическое программирование (составление и отладка программы в выбранной участником среде программирования), работу с электронными таблицами и информационный поиск.
Общее время выполнения работы — 235 мин.
В книге задания разбиты по темам на основании кодификатора и спецификации контрольных измерительных материалов для проведения в 2025 г. единого государственного экзамена по информатике и ИКТ, подготовленных Федеральным государственным бюджетным научным учреждением «Федеральный институт педагогических измерений». В книге рассмотрены все основные типы задач, которые встречались в тренировочных, репетиционных и диагностических работах, ЕГЭ по информатике основной и досрочной волны 2021–2025 годах.
Книга не отменяет занятия с репетитором, и другого обучения, а дополняет эту работу. Если захотите позаниматься со мной онлайн или у Вас остались вопросы, то пишите мне на мои контакты, что указаны в заключении книги. В 2024—2025 годах подготовил 6 выпускников по информатике к ЕГЭ, ОГЭ, результаты баллов на ЕГЭ, ОГЭ, было, стало: 15 — 74, 45−87, 35- 90, 56- 87, 29−76, 28- 85 баллов. Средний балл 83 балла
Глава 1. Моделирование и компьютерный эксперимент. Задача №1. Анализ информационных моделей
Граф — это способ графического представления информации. Объекты в нем — это вершины (узлы), а связи между объектами — ребра (дуги). То есть граф — это набор вершин и связывающих их ребер. Путь в графе — это конечная последовательность вершин, каждая из которых (кроме последней) соединена со следующим ребром. Граф может содержать циклы (первая вершина пути может совпадать с последней). Обычно в задачах используют взвешенный граф, т.е. граф, в котором с каждым ребром связано число (вес). Например, расстояние, стоимость и т. д. Граф обычно задается таблицей, в которой на пересечении строки и столбца с наименованиями вершин записано числовое значение (вес) ребра, соединяющего эти вершины.
Задачи на графы лучше всего решать вручную аналитически, хотя есть и программное решение, которое часто у моих учеников приводит к ошибкам ввиду ее неоднозначной сложности для учеников (поэтому здесь мы приводить ее не будем). Рекомендую программу «Ножницы», которая стандартно будет у вас открываться на экзамене в среде Windows. Вы можете скопировать картинку, нажать пуск/ найти/ввести слово «ножницы» и в открывшейся программе попытаться рисовать, решая данные задачи тем методом, что будет предложено ниже. Рассмотрим их.
Пример 1.1

На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населенных пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Е. В ответе запишите целое число — так, как оно указано в таблице. Решение: Из вершины B выходит 5 ребер, значит, в таблице соответствующий пункт должен иметь дороги в 5 других (строка должна содержать 5 заполненных клеток). Такой пункт в таблице один: П6. На графе из вершины Е выходит 4 ребра, значит, в таблице соответствующий пункт должен иметь дороги в 4 других (строка должна содержать 4 заполненные клетки). Такой пункт в таблице один: П4. Таким образом, нам нужно найти расстояние между П6 и П4. На пересечении П6 и П4 находится цифра 20. Ответ: 20.
Пример 1.2

На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах. Известно, что длина дороги ВД меньше дороги ВЕ. Определите длину дороги ГЖ.
Решение: для начала расставим количество путей, которые выходят из каждой вершины. Минимальное число путей — это 2.
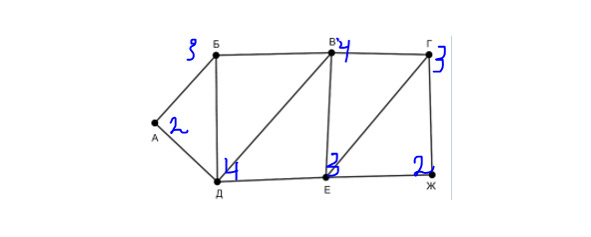
Им соответствует вершина А и Ж. Мы видим в таблице, что в П5 есть два пути. Поэтому предположим, что П5=А, тогда П4=Ж. Т. к. П5 пересекается в значении 10 с П6 и П6=3, то П6=Б. Аналогично получаем, что П7=Д. Далее П7 пересекается с П3, то П3=В. Т. к. П6 пересекается с П2, то П2=В, остается, что П3=Е. Осталась одна вершина — это П1=Г. Условие, что ВЕ> ВД, 23> 16. Это условие истинно, значит, наше предположение изначальное, что П5=А, а П4=Ж, а не наоборот — истинное. А если бы было ложное, тогда что? Тогда бы пришлось рисовать заново, предполагая, что П5=Ж, а П4=А. Смотрим по таблице пересечение П1 и П4 — это число 2. Ответ: 2.
Пример 1.3

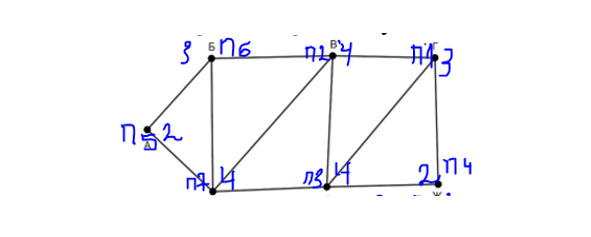
На рисунке слева схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе.
Определите номера пунктов, соответствующих пунктам З и Ж на графе. В качестве ответа запишите два числа в порядке возрастания без разделителей — найденные номера.
Решение:
Пункт К соединяется с вершинами Г (4 вершины) и В (4 вершины). П8 соединяется как раз с двумя вершинами П1 и П2, каждая из которых имеет по 4 дороги, значит, П8=К. Т. к. П8 соединяется с П1 и П2 имеет четыре вершины, то можно предположить, что П1=В, а П2=Г. П1 соединяется с П5, и т. к. П5 имеет 2 вершины, то П5=З. Ранее выяснили, что П2=Г и П2 пересекается с П3, которая имеет 2 вершины, значит, П3=Ж. Ответ: 35.
Задачи для самостоятельного решения
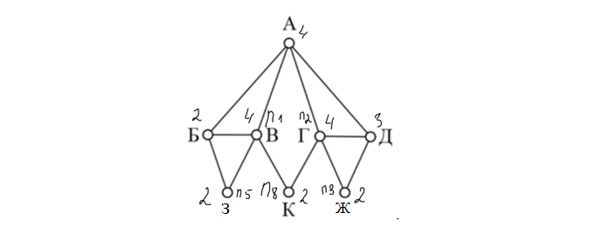
Задача 1.4. На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину кратчайшего пути из пункта А в пункт В, если передвигаться можно только по указанным дорогам. В ответе запишите целое число — длину пути в километрах.

Задача 1.5. На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами.

Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно без пробелов и знаков препинания, указанные на графе буквенные обозначения пунктов от П1 до П8: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.
Задача 1.6. На рисунке схема дорог N-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).
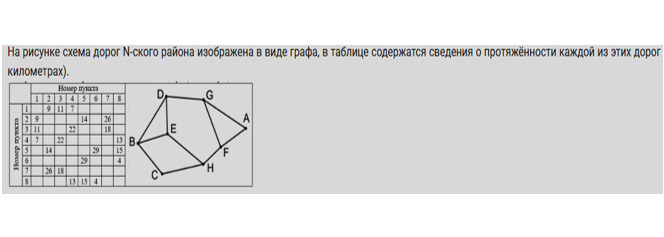
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта A в пункт G и из пункта D в пункт E.
Глава 2. Алгебра логики и базы данных. Задание №2. Алгебра логики
Алгебра логики или булева алгебра — так их называют. Как вы думаете, для чего вообще нужна алгебра логики, кроме как мучить детей? Представьте, что по проводу течет ток. Если ток есть в проводе, то обозначим это действие за 1, т.е. истина. Если же тока нет, то ноль, т.е. ложь. Сборка различных схем на компьютере осуществляется как раз схемами, которые представлены на рис.1.
Рисунок №1
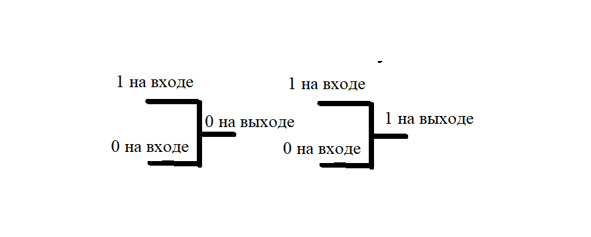
Причем можно усложнить схемы, сделать их большими и громоздкими. В компьютере, понятное дело, используются большие логические схемы взаимодействий. Учить это не хочется, но важно понять, как это работает. Для этого и придумали алгебру логики. Какая бы сложная схема ни получилась, ее всегда можно упростить до двух проводов, далее буду говорить до 2 переменных, на языке алгебры логики. Высказывание — повествовательное предложение, о котором можно сказать, истинно оно или ложно. В алгебре простым высказываниям ставятся в соответствии логические переменные (А, В, С и т.д.). Пример высказываний:
Рисунок №2

Логическая переменная — это простое высказывание. Логические переменные обозначаются прописными и строчными латинскими буквами (a-z, A-Z) и могут принимать всего два значения — 1, если высказывание истинно, или 0, если высказывание ложно.
Логическая формула (логическое выражение) — формула, содержащая лишь логические переменные и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА (1) или ЛОЖЬ (0).
Логическое умножение — конъюнкция. Принятые обозначения: /\, •, и, and. Этой операции соответствует знак умножения. Например, переменные А=0, B=0, то F=A*B=0*1=0. То же самое можно представить в виде примера А=«Немцы победили русских в Великой Отечественной войне»=0, ложь, т.к. русские выиграли, B=«Лимон кислый на вкус»=1, истина, т.к. это соответствует действительности. Тогда A*B=0*1=0, т.к. мы настаиваем, чтобы и А, и B выполнялось (через действие умножение), поэтому значением выражения будет ложь. Остальные значения таблицы истинности вы можете посмотреть на Рисунке №3. Логическая формула истинна только в одном случае и ложна в трех других.
Рисунок №3


Логическое сложение (дизъюнкция). Объединение двух (или нескольких) высказываний в одно с помощью союза ИЛИ. Обозначение: \/, +, или, or.
Рисунок №4
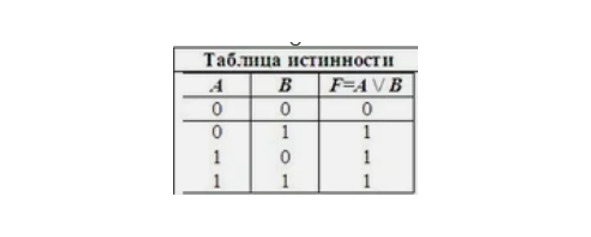
На рисунке №4 функция истинна в трех случаях и ложна только в одном, когда ложь. Дизъюнкции соответствует знак сложения.
Отрицание (инверсия), от лат. InVersion — переворачиваю — Рисунок №5:
Соответствует частице НЕ, словосочетаниям НЕВЕРНО, ЧТО или НЕ. Обозначение: не А, ¬А, not. В данной функции значения функции меняются наоборот. Если А=0, то F= Не А=1.
Рисунок №5

Логическая функция импликация. Обозначается cтрелкой ->. В языке программирования соответствует операции меньше либо равно <=. Как из лжи А=0 получить ложь B=0? Рассмотрим на примере A=2> 3 — ложь, то прибавим к обоим частям неравенства +2 и получим тоже ложь B = 4> 5. Если из лжи А=0 и B=0 можно получить ложь, значит, истина A -> B=1. A= -5> 3 — ложь, то обе части неравенства возведу в квадрат и получим уже истину B= 25> 9, тогда при A=0 и B=0 получаю, что А -> B=1. Из истины А=1 мы не можем получить B=0, поэтому A -> B=0. Если вы поняли смысл, как мы получили логические высказывания, то вам не потребуется зубрить таблицы истинности.
Рисунок №6

Вы еще не устали от логики)?
Последняя функция эквиваленция. Обозначается как на рисунке №7.
Функция истинна A <-> B=1 только в двух случаях: либо когда обе логических переменных А и B истинны, или когда А и B — ложны.
В каком же приоритете выполняются данные операции, спросите Вы? Да все очень просто: сначала отрицание, затем конъюнкция (умножение), потом дизъюнкция (сложение), далее импликация и эквиваленция.
Рисунок №7

Функция на рисунке №7 истинна A <-> B=1 только в двух случаях: либо когда обе логических переменных А и B истинны, или когда А и B — ложны.
В каком же приоритете выполняются данные операции, спросите Вы? Да все очень просто: сначала отрицание, затем конъюнкция (умножение), потом дизъюнкция (сложение), далее импликация и эквиваленция.
Рисунок №8

В ЕГЭ представлено две задачи на знания алгебры логики. Это задачи №2 и №15. Рассмотрим основные типы этих задач ниже.
В ЕГЭ представлено две задачи на знания алгебры логики. Это задачи №2 и №15. Рассмотрим основные типы этих задач ниже.
Пример 2.1

Логическая функция F задается выражением (x ⟶ y) ∧ (x ∨ ¬z) ∧ (x ≣ ¬w). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
Решение: Первый способ — это написание программы на языке программирования Python. Код представлен ниже.
print (’x’,’y’,’z’,’w’)
def f (x,y,z,w):
return (not x or y) and (x or not z) and (x == (not w)) # условие из задачи, преобразовали x ⟶ y= not x or y
for x in range (0,2): # изменение переменных от истины до лжи.
for y in range (0, 2):
for w in range (0, 2):
for z in range (0, 2):
if f (x,y,z,w) == 1: # условие истинности из задачи
print (x,y,z,w)
После запуска программы мы можем заметить строку, содержащую 0 0 0 1. Если сравнить эту строку со строками из таблицы (что в условии), то в данной таблице мы не найдем строку с тремя нулями, поэтому строку 0 0 0 1 можем смело исключить из решения. Рассмотрим оставшиеся три строки, которые необходимо сопоставить с таблицей, что в условии. Второй столбец с тремя единицами соответствует второму столбцу из таблицы, значит, второй столбец — Y. В первую ячейку третьего столбца однозначно можно поставить только ноль, и тогда образуется первая строка 1 1 1 0. Т.к. в последней строчке из рисунка №7 стоит такая же строка 1 1 1 0, что в условиях таблицы, то третий столбец — однозначно W. На рисунке №7 в первой и третьей ячейке третьей строки стоят нули, которые мы можем перенести в таблицу из условия на соответствующие места и однозначно определить, что Z — это первый столбец, а Z — третий.
x y z w
0 1 0 1
1 1 0 0
1 1 1 0
Второй способ решения этой же задачи состоит в том, что мы составляем таблицу истинности без помощи компьютера. Заполняем первую строку, если w=0, то x=1, а y=1, а z — или ноль, или один. Итого получим почти две одинаковые строчки, за исключением значения z. 1 1 0 0 и 1 1 1 0. Теперь предположим, что W=1, тогда x=0. Т.к. в условии есть столбец с тремя единицами, то необходимо в ручном решении тоже получить такой столбец, поэтому y=1, а z=0. Ответ: ZYWX.
Пример 2.2. Логическая функция F задается выражением (¬z) ∧ x ∨ x ∧ y. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.

Решение: расставим скобки, выражение (¬z) ∧ x ∨ x ∧ y является дизъюнкцией двух конъюнкций: ((¬z) ∧ x) ∨ (x ∧ y). В обеих конъюнкциях присутствует x. То есть при x = 0 все выражение равно нулю. Только в третьем столбце напротив нулей стоят значения функции F=0, поэтому третий столбец — это x. Также можно заметить, что выражение ((¬z) ∧ x) ∨ (x ∧ y) =1, если x =1 и выполняется хотя бы одно из условий: y = 1 или z = 0. Из четвертой строки следует, что Перем.1 = z, а Перем.2 = y. Ответ: zyx.
Пример 2.3. Дан фрагмент таблицы истинности для выражения F. Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значения x4 не совпадает с F.
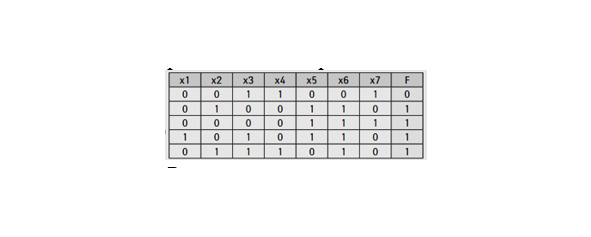
Решение: таблица истинности выражения с семью переменными (x1…x7) содержит 27=128 строк. В приведенном фрагменте таблицы x4 не совпадает с F в 4-х строках, а совпадает только в последней нижней строке. Во всех остальных может не совпадать. Тогда максимально возможное количество строк, где значения x4 и F не совпадают, будет 128—1=127. Ответ: 127.
Задачи для самостоятельного решения
Задача 2.4. Логическая функция F задаётся выражением: (x ∧ ¬ y) ∨ (y ≣ z) ∨ w. На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w. В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Задача 2.5. Для функции F известен фрагмент таблицы истинности, представленный ниже. Определите, какое максимальное количество единиц может быть в столбце F полной таблицы истинности, если известно, что при значении x4 = 1 значение функции равно 1.

Задача 2.6. Логическая функция F задаётся выражением:

((x ≡ y) → (¬z ∨ w)) ≡ ¬ ((w → x) ∨ (y → z)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Задача №3. Электронные таблицы
Теория по электронным таблицам к данной задаче приведена в главе №5, а сама задача — под номером 9. Здесь мы не будем повторяться, а лишь дополним, что эту задачу можно решать с помощью функции ВПР. Однако при использовании ВПР учащиеся часто допускают ошибки, поэтому мы разберём более простой способ решения — без ВПР. А уже после того как вы освоите этот способ, при желании сможете попробовать решить задачу с применением ВПР. В «трёх задачах» часто встречаются вопросы про выручку и прибыль. Не путайте эти понятия!
Выручка — это количество рублей (или других денежных единиц), которые магазин получил за продажу товаров. Проще говоря, это доход. Прибыль — это сумма, оставшаяся после вычета расходов на закупку товаров из выручки. То есть прибыль = доходы — расходы.
Пример: если магазин закупил оптом 1000 яблок по 2 рубля и продал их по 3 рубля, то выручка составит: 1000 × 3 = 3000 рублей, расходы: 1000 × 2 = 2000 рублей, прибыль: 3000 — 2000 = 1000 рублей.
Таким образом, чтобы найти прибыль, мы вычитаем расходы из выручки. А чтобы найти выручку, достаточно посчитать общую сумму продаж. Также помните: если в задаче спрашивают, на сколько увеличилось количество упаковок/кг, то речь идёт о разнице между поступившим и проданным количеством.
Обращайте внимание, в каких единицах нужно дать ответ: часто требуется перевод в секунды, минуты или килограммы — в зависимости от условия задачи.
Пример 3.1
Ссылка на файл к задаче https://clck.ru/3MqPin
Решение: заходим на лист «Товар» и с помощью функции поиска находим пастилу ванильную (артикул 25) и пастилу с клюквенным соком (артикул 26).
Далее переходим на лист «Магазин», включаем фильтр (через меню главное/фильтр), нажав на кнопку, и в выпадающем списке выбираем район Заводской. Мы видим, что ID магазинов в этом районе — M2 и M16.
Теперь переходим на лист «Движение товаров». Включаем фильтр аналогично предыдущему шагу. Далее выполняем следующие действия: в столбце «Дата» устанавливаем флажки напротив дат 14 и 20 августа 2023 года, в столбце «Артикул» выбираем значения 25 и 26, в столбце «Тип операции» выбираем значение «Продажа».
Теперь в ячейку H1 вписываем заголовок: итого. В ячейку H2 вводим формулу: =E3482*G3482, где E — количество, G — вес одной единицы товара.
Затем растягиваем формулу вниз за правый нижний угол ячейки до ячейки H5859. После этого выделяем диапазон ячеек от H3482 до H5859 и в строке состояния (внизу Excel) смотрим сумму. Получаем значение 467300 — это масса в граммах. Переводим в килограммы: 467300 / 1000 = 467,3 кг. Ответ: 467 (файл с готовым решением https://clck.ru/3MqPqG)
Пример 3.2

Файл к задаче https://clck.ru/3MqPm9
Решение: Заходим на лист «Артисты» и с помощью поиска находим исполнителя Guns N» Roses — его ID равен 88. Затем переходим на лист «Альбомы», находим столбец «ID исполнителя» и выбираем значение 88. Таким образом, находим все альбомы данного исполнителя — их ID: 90, 91, 92.
Далее переходим на лист «Треки». Включаем фильтр (в предыдущем задании описано, как это сделать), и в столбце «ID альбома» выбираем значения 90, 91, 92.
Теперь переходим к расчёту длительности треков. Напомним: в одной секунде — 1000 миллисекунд. Чтобы перевести миллисекунды в секунды, делим на 1000. Чтобы перевести секунды в минуты, делим результат на 60.
В ячейку I1 вводим формулу: = (СУММ (E1147:E1188) /1000) /60.
Результат вычисления: 205,9255 — это суммарная продолжительность всех треков альбомов исполнителя Guns N» Roses в минутах. Ответ: 205 (файл с готовым решением https://clck.ru/3MqR8m)
Задачи для самостоятельного решения
Задача 3.3

Файл к заданию: https://clck.ru/3Mrrko
Задача 3.4 Файл к заданию: https://clck.ru/3Mrryo


Задача 3.5

Файл к заданию: https://clck.ru/3MrsCy
Задача 3.5. Для групповых операций с файлами используются маски имен файлов. Маска представляет собой последовательность букв, цифр и прочих допустимых в именах файлов символов, в которых также могут встречаться следующие символы: символ»?» (вопросительный знак) означает ровно один произвольный символ. Символ «*» (звездочка) означает любую последовательность символов произвольной длины, в том числе «*» может задавать и пустую последовательность. Определите, какое из указанных имен файлов не удовлетворяет маске: bys??.*
1) byste. m 2) bys23.exe 3) bystem. dll 4) byszx.problem
Глава 3. Кодирование и линейные алгоритмы. Задача №4. Кодирование и декодирование информации
Кодирование информации — процесс преобразования сигнала из формы, удобной для непосредственного использования информации, в форму, удобную для передачи, хранения или автоматической переработки. Декодирование (операция, обратная кодированию) — перевод кодов в набор символов первичного алфавита. Кодирование может быть равномерное и неравномерное. При равномерном кодировании каждый символ исходного алфавита заменяется кодом одинаковой длины. На примере внизу мы видим, что все буквы имеют одинаковую длину — 2 бита, например, А=00, поэтому код равномерный.
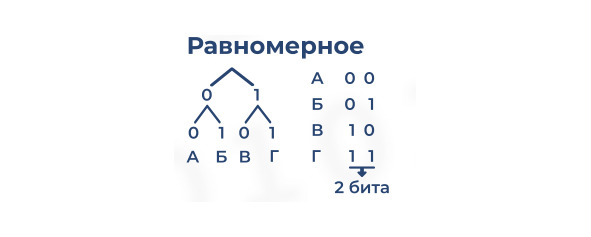
При неравномерном кодировании разные символы исходного алфавита могут заменяться кодами разной длины.
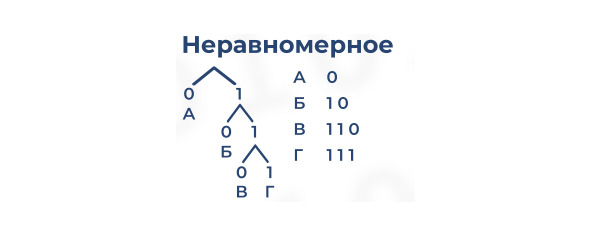
Сообщение однозначно декодируемо с начала, если выполняется условие Фано: никакое кодовое слово не является началом другого кодового слова. Сообщение однозначно декодируемо с конца, если выполняется обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова.
Пример 4.1. Для передачи сообщений, содержащих только буквы К, Л, М, Н, О, П, Р, решили использовать неравномерный двоичный код, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известны кодовые слова, использованные для некоторых букв: К — 11, Л — 000, П — 0010, Р — 1011. Какое кодовое слово надо назначить для буквы М, чтобы код удовлетворял указанному условию и при этом длина слова МОЛОКО после кодирования была наименьшей? Если таких кодов несколько, укажите код с наименьшим числовым значением.
Решение:
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.
