Бесплатный фрагмент - Как понять алгебру

ВВЕДЕНИЕ

Внутри вас есть голос, который всегда говорит: «Ты не можешь этого сделать. Оставь это на потом».

Это неправда, но вы верите этому голосу, потому что получаете пользу от принятия совета. Вы получаете хороший предлог, чтобы ускользнуть от вашей работы. Вы можете гулять с друзьями, смотреть телевизор или делать все, что захотите. Однако вы не можете испытывать подлинное удовольствие от своего развлечения, потому что есть часть вас, которая хочет гордиться своими достижениями. Этот голос говорит: «Продолжай пытаться! Ты можешь это сделать! Ты умница». Верьте тому, что говорит этот голос! Этот учебник покажет вам способ мышления, который поможет вам понять математику. Этот учебник предназначен для всех, кто хочет чувствовать себя комфортно, используя математическую формулу; кто хочет постичь красоту алгебраических выражений.

Испытывали ли вы когда-нибудь разочарование, глядя на свой учебник по математике? Забудьте это! Полюбите математику!

КАК РЕШАТЬ УРАВНЕНИЯ

Математика — восхитительная сфера деятельности. Имея только ручку и лист бумаги, можно придумывать все, что угодно. Можно бродить по бумаге с цифрами и символами, заботясь только об одном: равенство должно быть равенством, не более того. Представим, что вы первый великий математик. Люди знакомы только с арифметикой: как складывать, вычитать, умножать и делить. В школе изучают скучные вещи типа таких выражений:

2 +3 = 5 или 7 — 4 = 3

Вы первый, кто подозревает, что есть способ выразить общую идею уравнений, написанных выше.

Сначала вы пишете: a + b = c или c — a = b. Вы можете открыть общие правила, которые могут помочь людям решить любое уравнение. Чтобы проверить открытие, вы должны провести эксперименты с числами.

Напишем простое уравнение: 4 +8 = 12

Прибавим любое число к левой части уравнения.

4 +8 +3 = 12

Что мы получили?

15 = 12

Это неправильно! Как исправить уравнение? Попробуйте добавить к правой части уравнения такое же число, которое вы добавили к левой части уравнения.

4 +8 +3 = 12 +3. Что у вас получилось? 15 = 15

Вы открыли первое правило уравнений. Это правило гласит: «Если вы прибавите одно и то же число к левой и правой части уравнения, это уравнение все равно будет верным». Чтобы выразить это правило в общем виде, вы можете написать:

Если a + b = c, то a + b + n = C + n, где a, b, c, n равны любым числам.

Вы гений? Конечно! Давайте попробуем еще один эксперимент.

Что произойдет, если вычесть любое число из левой части уравнения?

5+2=7

5+2 — 5=7

Что мы получили? 2 = 7

Это неверно, но вы уже знаете, как исправить уравнение. Вы должны вычесть одно и то же число из левой и правой частей уравнения.

5 +2 — 5 = 7 — 5. Тогда 2 = 2.

Можете себя поздравить! Вы открыли второе правило уравнений. Это правило гласит: «Если вы вычтете одинаковые числа из левой и правой частей уравнения, это уравнение все равно будет верным».

Или вы можете написать:

если a + b = c, то a + b — n = c — n, где a, b, c, n равны любым числам.

Какие еще виды экспериментов вы можете провести? Вы можете умножить одну часть уравнения на некоторое число. Напишем уравнение:

5 — 1 = 4

Что будет, если левую часть уравнения умножить на 7?

(5 — 1) 7 = 4, тогда 28 = 4

Это неверно. Попробуйте умножить обе части уравнения на 7.

(5 -1) 7= 4 х 7. Тогда 28 = 28

Вы открыли еще одно правило для уравнений. Третье правило гласит:

«Если вы умножите левую и правую часть уравнения на одно и то же число, это уравнение все равно будет верным».

Если a — b = c, то (a — b) n = (c) n

Еще один эксперимент. Что произойдет, если разделить половину уравнения на любое число?

4 +6 = 10

(4 +6) /2 = 10, тогда 5 = 10.

Вы можете спросить себя: «Сколько раз я буду совершать одну и ту же ошибку?»

Но у вас есть знания, чтобы решить эту проблему.

Вы должны разделить обе части уравнения на одно и то же число.

(4 +6) / 2 = 10/ 2, тогда 5 = 5

Вы открыли четвертое правило уравнений. Это правило гласит:

«Если вы разделите левую и правую часть уравнения на одно и то же число, уравнение все равно будет верным».

Итак, вы можете написать:

Если a + b = c, то (a + b) /n = c/n

Где a, b, c — любые числа, но n не равно 0, потому что нельзя делить числа на 0.

Люди спросят вас: «Какую пользу вы можете извлечь из этих правил?»

Ваш ответ будет таким: «Вы можете использовать эти правила для решения любого уравнения».

Напишем уравнение, в котором одно число неизвестно.

Х — 3 = 11

Как мы можем решить это уравнение? Попробуйте применить первое правило:

Если вы прибавите одно и то же число к левой и правой части уравнения, это уравнение будет верным. Для нашего уравнения удобно добавить 3 к обеим частям уравнения.

Х — 3 +3 = 11 +3

Поскольку -3 +3 = 0

Тогда Х = 11 +3

Итак, Х=14

Давайте попробуем решить уравнение, где все числа представлены буквами.

Х — b = с

Примените первое правило, чтобы решить это уравнение

Х — b + b = с + b

Так как -b + b = 0, то

Х = с + b.

Чтобы решить уравнение X + b = c, мы можем применить второе правило.

Если X + b = c, то

Х + b — b = с — b тогда

Х = с — b.

Следующий пример: Х +7 = 15

Вычтите 7 из обеих частей уравнения:

Х +7 — 7 = 15 — 7 и Х = 8

Не читайте дальше, пока не выполните упражнения из практики 1.

Практика 1. Решение уравнений

Решите для Х:

1. X — 5 = 0

2. X +11 = 3

3. X — ab = 4

4. X — Y = Z

5. X — 2a = c

6. X +3ab = bc

7. X + k = 1 + k

8. X — ab = a — ab

9. X + c = c — b

10. X — 2a = a — ab

11. X + cb = 3cb — c

12. X — 5 + a = 2a — 5

13. X +3 — k = 6 — 3k

14. X — 1 — ab = ab — 1

15. X — a — b = a — b

16. X +2a — 3c = 3a — 2c

Вы можете найти ответы в приложении 1. Если ваш ответ неверен, попробуйте решить еще раз.

Если вы не можете найти правильный ответ, прочитайте решение в приложении 2.

Давайте решим уравнение

4Х — 5 = 15

Вы можете применить первое правило.

4Х — 5 +5 = 15 +5, тогда 4Х = 20.

Как найти Х? Вы можете применить четвертое правило.

Если вы разделите обе части уравнения на одинаковые числа, это уравнение все равно будет верным.

4Х/4=20/4, тогда Х=5.

Чтобы решить уравнение

аX — b = с

Примените первое правило.

аХ — b + b = с + b,

тогда

аX = с + b

Теперь применим четвертое правило.

Если aX = c + b, то aX/a = (c + b) /a

тогда X = (c + b) /a

Не читайте дальше, пока не выполните упражнения из практики 2.

Практика 2. Решение уравнений

Решите для Х:

1. 2X — 3 = 5

2. 3X — 5 = 4

3. 5X +6 = 36

4. 8X — 5 = 43

5. 7X — 2 = 19

6. 4X +8 = 20

7. 6X — a = 2a

8. 2X + b = 13b

9. 7X +3a = a + b

10. 4X — 2a = 4 +2a

11. 4X — 3a = a

12. 3X — 2b = 6 — 14b

13. 6X — 2a = 24b — 20a

14. aX — 3a = ab — 2a

15. 2aX + ab = 2a — ab

16. 3aX — c = 3ac — 7c

Ответы в приложении 1.

Решения в приложении 2.

Если у вас есть такое уравнение:

Х/а — 5 = 6

Тогда примените первое правило:

Х/а — 5 +5 = 6 +5

Х/а = 6 +5

Х/а = 11

Затем примените третье правило.

Х/а * а = 11 * а

Х = 11а

Давайте решим уравнение:

2X — 4b = 2bc

Примените первое правило:

2Х — 4b +4b = 2bc +4b,

тогда 2X = 2bc +4b

Разделите обе части уравнения на 2:

2Х/ 2 = (2bc +4b) / 2

Вы должны знать, как делить двучлен на одночлен.

Если вы забыли, вы можете найти правило самостоятельно.

Вы можете попробовать написать

(2bc+4b) /2 = 2bc/2 +4b/2

Давайте проверим. Предположим, что c = 2 и b = 3.

Чтобы разделить двучлен на 2, попробуйте разделить каждый одночлен на 2

2*3*2/2 +4*3/2 = 12

А теперь попробуйте сначала решить двучлен, а потом разделить на 2.

(2*3*2 +4*3) /2, тогда 24/2 = 12

Мы получили тот же ответ. Это означает, что

(а + b) /2 = а/2 + b/2.

Мы открыли правило: чтобы разделить двучлен на число, разделите каждый одночлен внутри двучлена на это число. Вернитесь к своему уравнению.

2Х = 2bс +4b. Тогда:

2Х/2=2bс/2+4b/2

Тогда: X = bc +2b

Вы можете вынести за скобки b и получить X = b (c +2)

Всякий раз, когда вы не знаете правило, вы можете поставить любые цифры вместо букв и проверить равенство. Откройте для себя правила самостоятельно.

Решим более сложное уравнение:

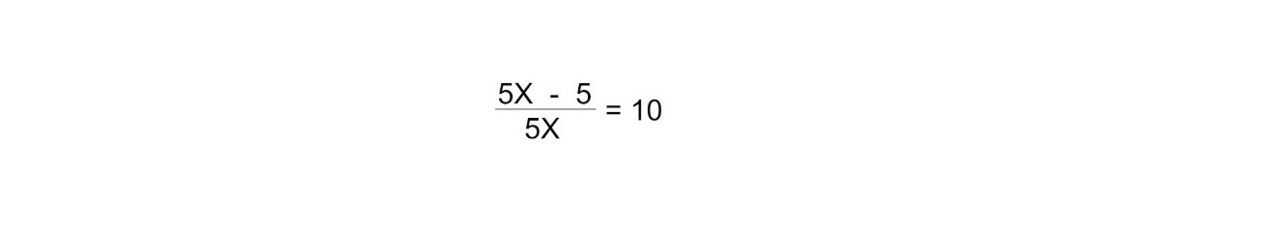
5X — 5 = 50X

Используйте 2-е правило, вычтите 5X с обеих сторон:

5X — 5 — 5X = 50X — 5X

— 5 = 45X

or 45X = — 5

Поделите обе части уравнения на 45.

45X/45 = -5/45

X = — 1/9

Следующие уравнение:

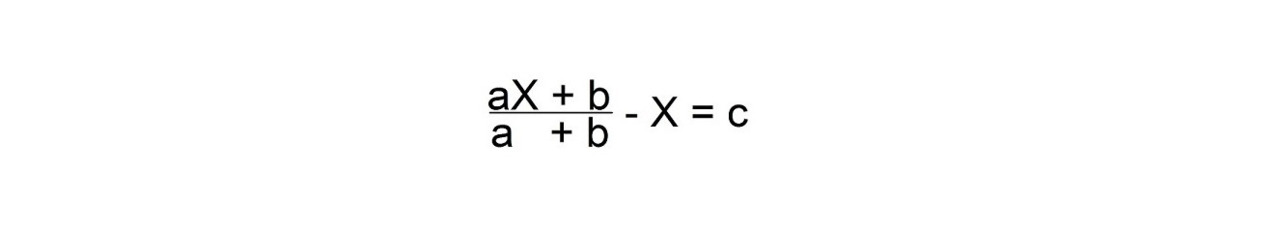
Для этого умножьте — Х на (а + в) и поделите его на (а + в). Мы можем это сделать, потому что

(а + в) / (а + в) = 1

Тогда мы получим:

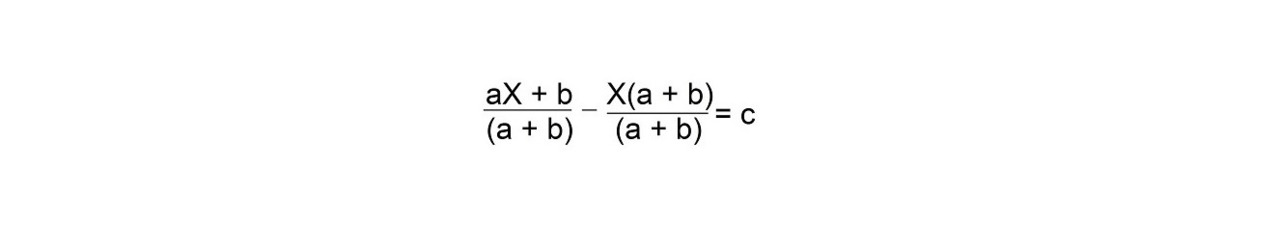
Или:

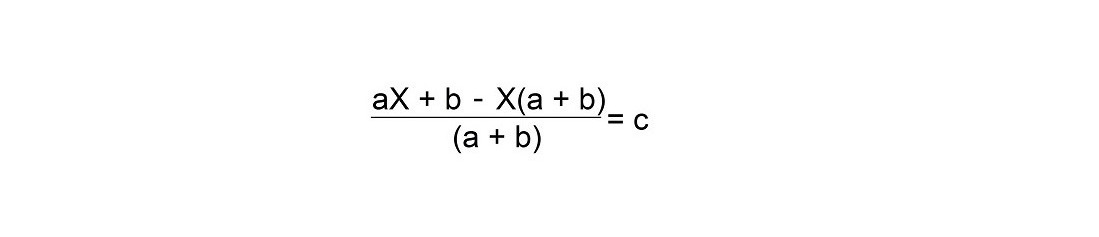
Умножаем -Х на а + b скобках и получаем:

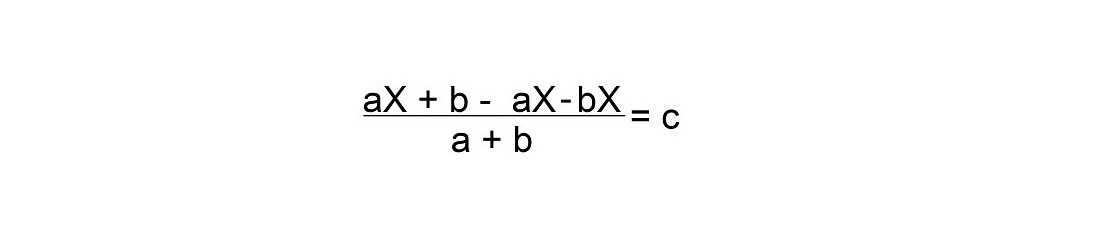
Умножьте обе части уравнения на (a + b)

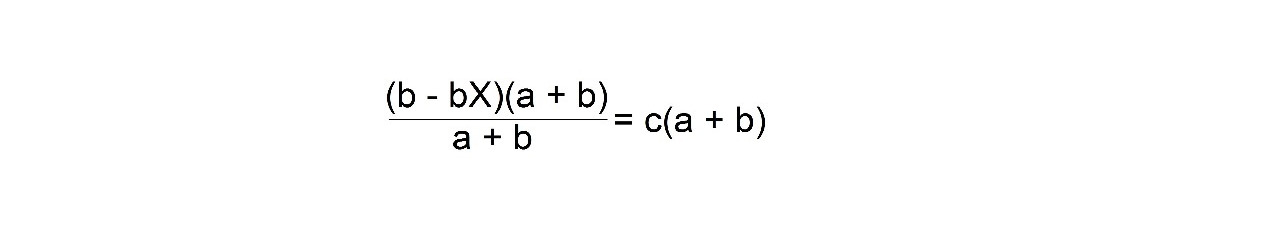
Тогда b — bX = c (a + b)

Примените 2-е правило, вычтите b из обеих частей уравнения:

b — bX — b =c (a + b) — b

Тогда -bX =c (a + b) -b Разделим обе части на b:

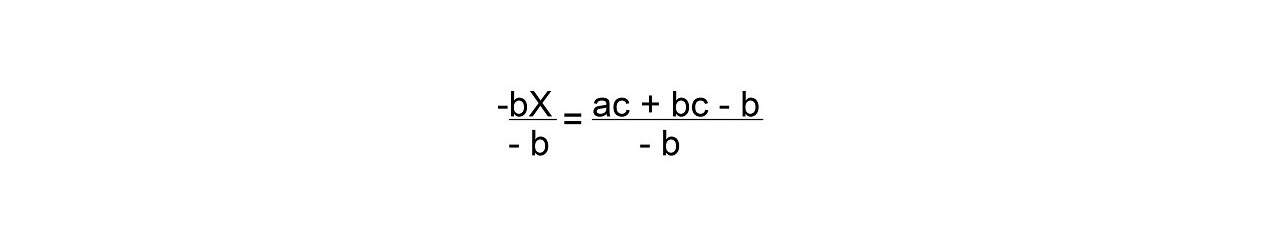
Чтобы сделать это алгебраическое выражение более красивым, умножьте числитель и знаменатель на (-1).

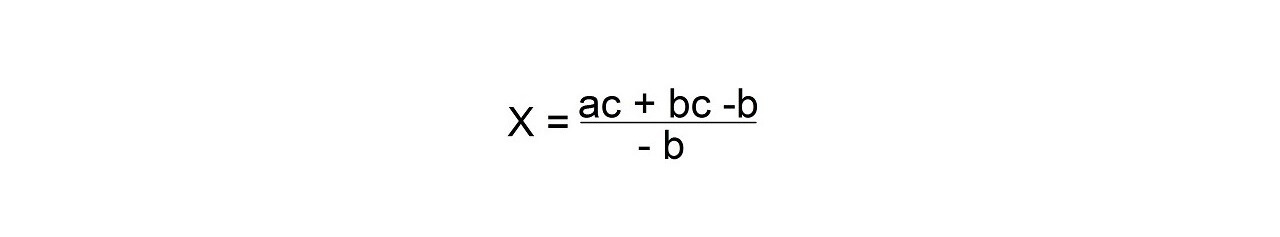
Вы можете сделать это, потому что (-1) / (-1) = 1. Если вы умножите любое число на 1, число не изменится.

Тогда

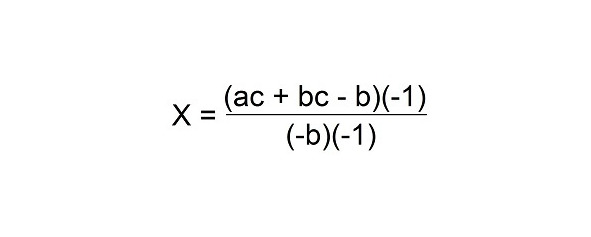
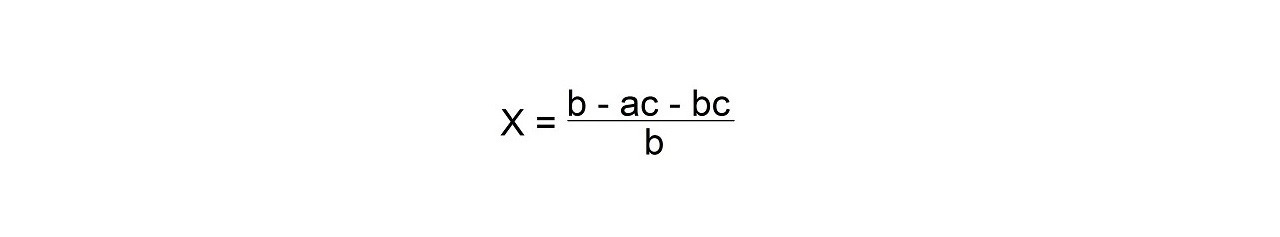
Следующее уравнение:

— 2Х = а — b

Вам не удобно иметь минус перед 2Х.

Вы можете преобразовать уравнение в более удобный вид.

Умножаем обе части уравнения на -1

(-2X) (-1) = (a — b) (-1), тогда вы получите

2Х = –- а + b или 2Х = b — а

Делим обе части уравнения на 2.

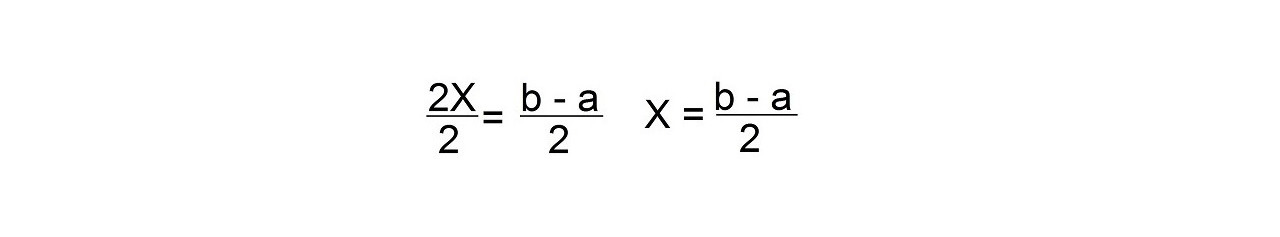
Есть и другой способ решить это уравнение:

— 2Х = а — b

Разделим обе части уравнения на -2

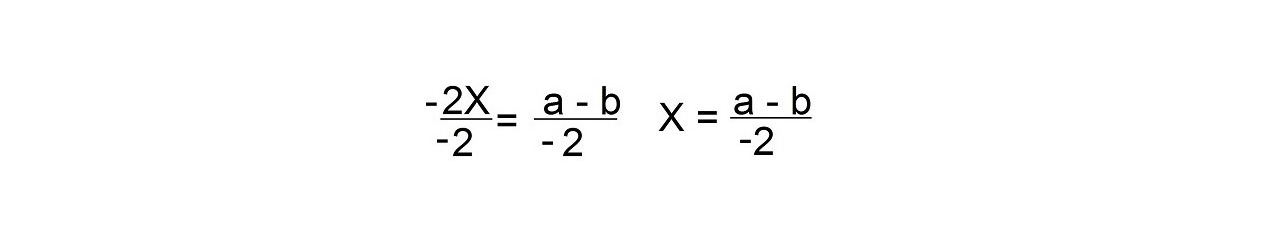
Чтобы ваш результат был более красивым, вы можете умножить числитель и знаменатель на — 1

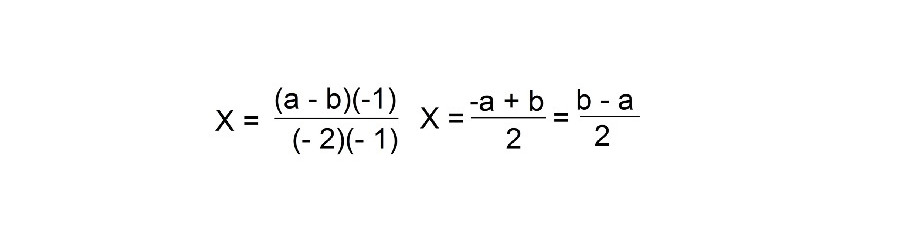
Следующее уравнение:

3а — 6Х = 6Х — 9а

Вы можете видеть, что в левой части уравнения у вас есть -6X

А с правой стороны у вас +6X. Вам удобнее иметь + перед X. Поэтому вы оставляете +6X в правой части и избавляетесь от -6X в левой части уравнения.

Прибавьте 6X к обеим частям уравнения:

3а — 6Х +6Х = 6Х — 9а +6Х, тогда получим 3а = 12Х — 9а

Прибавьте 9a к обеим частям уравнения:

3a +9a = 12X — 9a +9a тогда 12a = 12X

X = a

Не читайте дальше, пока не выполните упражнения из практики 3.

Практика 3. Решение уравнений

Решите для Х:

1. 1 — X = 5 — a

2. 1 — 2X = X — 4

3. a — 3X = b — X

4. 2a — 4X = 2X — 4a

5. 4b — 2X = 2X — 4b

6. ab + aX = 2aX + ac

7. ab + aX = 2aX — ac

Продолжим и обсудим уравнение: aX — bX = a — b

Вынесите за скобки множитель X, который является общим множителем для бинома aX — bX,

тогда вы получите X (a — b) = a — b

Разделите каждую часть уравнения на a — b

X (a — b) / (a — b) = (a — b) / (a — b)

X = 1

Не читайте дальше, пока не выполните упражнения из практики 4.

Практика 4. Решение уравнений

Решите для Х:

1. bX — 2b = aX — 2a

2. b — 2bX = a — 2aX

3. aX — bX = 1

4. aX — bX — cX = 2a — 2b — 2c

5. 3abX — 5a = 3acX +13a

6. aX — bX = ac — bc

7. 9a — 4X = 5a — 2X

8. X — aX = 2 — 2a

9. aX — bX = b — a

Продолжим и решим уравнение: aX — bX = 2b — 2a

Вынесите за скобки X в левой части уравнения.

Х (а — b) = 2b — 2а

Вынесите за скобки 2 в правой части уравнения.

X (a — b) = 2 (b — a)

Разделите обе части на (a — b).

Умножаем числитель на -1

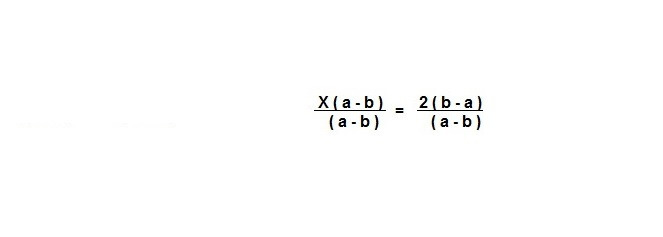
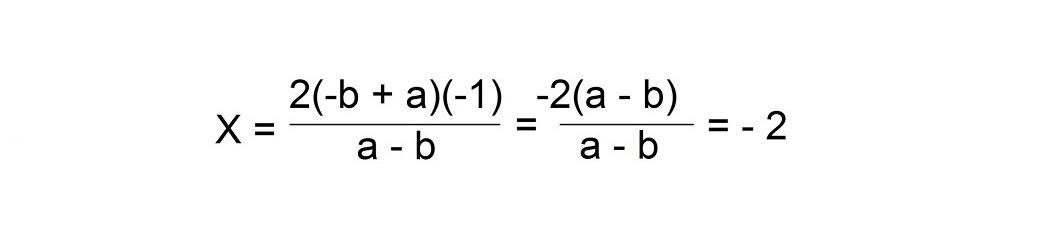
Или вы можете упростить это алгебраическое выражение, вынеся за скобки (-1) в знаменателе

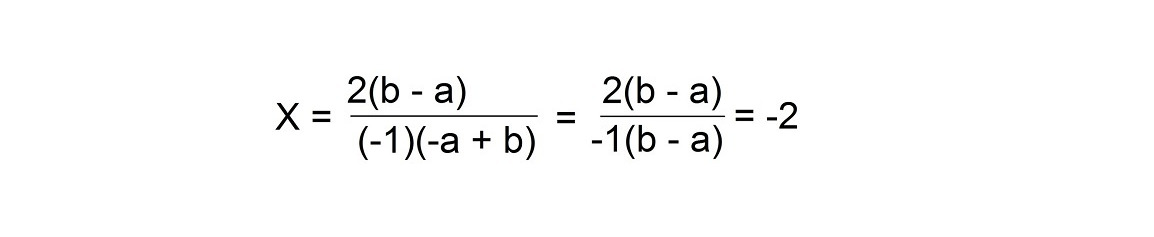
Практика 5. Решение уравнений

Решите для Х:

1. 5aX — 5bX = 10b — 10a

2. aX — bX — cX = c + b — a

3. 2X — 3aX = 6a — 4

4. 3aX — 9bX = 27b — 9a

5. 4bX — cX = 8c — 32b

6. abX — acX = ac — ab

7. X/2 — aX = 1 — 2a

8. aX/5 +2a = 5a — 4aX

Вы можете найти ответы в приложении 1 и решения в приложении 2.

СИСТЕМЫ УРАВНЕНИЙ

Посмотрите на уравнение X + Y = 3. X и Y неизвестны. Вы не можете найти ни X, ни Y из этого уравнения. Вам нужна дополнительная информация об «отношениях» между ними. Такая информация может быть включена в дополнительное уравнение. Например: X — Y = — 1. Теперь у вас есть система из 2-х уравнений:

1. X + Y = 3

X — Y = -1

Есть несколько способов ее решения. Первый способ: найти X в любом уравнении, например, первом.

Для этого вычтите Y из каждой части уравнения:

Х + У — У = 3 — У; Найти Х

Х = 3 — У

Затем подставьте (3 — Y) вместо X во втором уравнении (X — Y = -1).

Вы получите: 3 — Y — Y = -1 или 3 — 2Y = -1

Теперь решите это уравнение относительно Y. Прибавьте 2Y к обеим частям уравнения.

 3 — 2Y +2Y = -1 +2Y

 3 = -1 +2Y

Прибавьте 1 к обеим частям уравнения.

3 +1 = -1 +1 +2Y

4 = 2Y

Поменяем местами 4 и 2Y.

2Y = 4

Разделите обе части уравнения на 2.

2Y/2 = 4/2

Y = 2.

Теперь подставьте 2 вместо Y в любом исходном уравнении, чтобы найти X.

Одно из исходных уравнений: X + Y = 3.

Х +2 = 3;

Вычтите 2 из обеих частей уравнения.

Х+2 — 2=3 — 2;

Х = 1

Y = 2

Второй способ решения:

1. Х + У = 3

Х — У = -1

Вы можете просуммировать левые части обоих уравнений и просуммировать правые части обоих уравнений.

X + Y = 3 и X — Y = -1 Тогда

(Х + Y) + (Х — Y) = 3 + (-1)

Или вы можете написать это так:

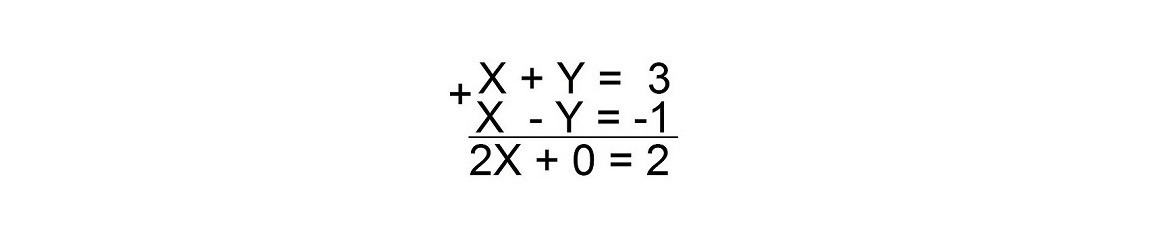
Если 2 Х = 2 то Х = 1

Поставьте 1 вместо X в любое уравнение.

1 + У = 3

Вычтите 1 из обеих частей уравнения.

1 + Y — 1 = 3 — 1

Y = 3 — 1

Y=2

Мы можем решать системные уравнения, используя их графики. Если мы построим каждое уравнение, мы получим две прямые линии. Точка пересечения линий будет иметь значения X и Y, соответствующие обоим уравнениям.

Чтобы нарисовать график для уравнения, мы должны привести его к общему виду:

Y = аХ + b

Начнем с первого уравнения: X + Y =3

Вычтите X из обеих частей уравнения

Х — Х + У = 3 — Х
Y = 3 — Х

Найдите две точки, чтобы нарисовать линию для первого уравнения. Присвойте любое значение X и вычислите значение Y.

Х = 3; Y (3) = 3 — 3 = 0

Х = 6; У (6) = 3 — 6 = — 3

Чтобы провести прямую линию достаточно двух точек.

Найдем две точки для второго уравнения.

Приведите уравнение к общему виду.

Х — У = -1

Вычтите X из обеих частей уравнения.

Х — Х — У = — 1 — Х — У = — 1 — Х

Умножьте обе части на -1

— Y (-1) = (-1) (-1) — X (-1)

У = Х +1

Найдите две точки, чтобы нарисовать линию для второго уравнения. Присвойте любое значение X и вычислите значение Y.

Х = 5; Y (5) = 5 +1 = 6

Х = -5; Y (-5) = — 5 +1 = -4

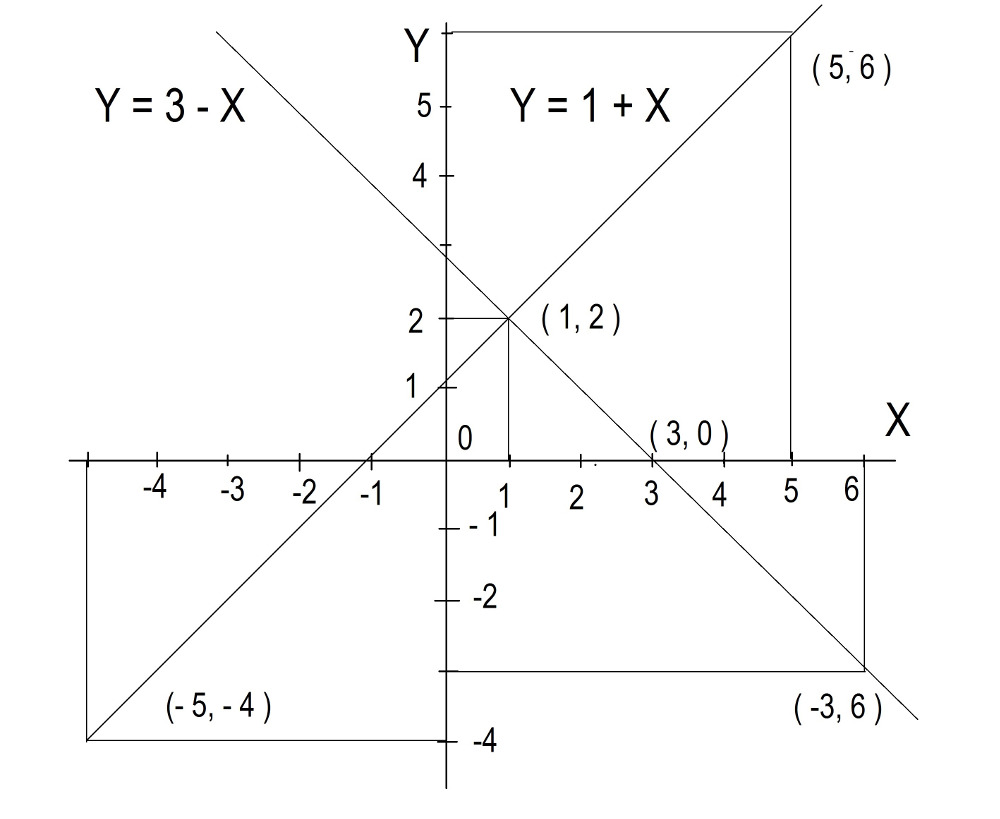
Теперь мы можем рисовать графики для обеих линий.

На графике 1 вы видите, что точка пересечения линий имеет X = 1

и Y =2.

Это те же самые значения, которые мы нашли ранее.

Следующая система уравнений:

2. 2Х + У = 5

Х + У = 2

В этом случае у нас есть + перед X и Y в обоих уравнениях.

Чтобы исключить один неизвестный член уравнения, вы можете вычесть второе уравнение из первого.

(2X + Y) — (X + Y) = 5 — 2=3 или:

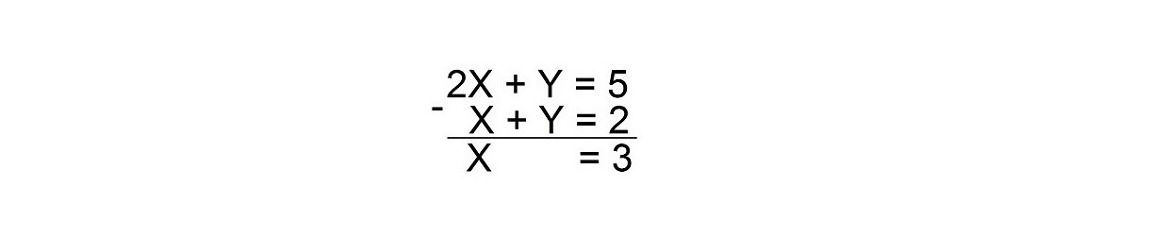
Подставьте 3 вместо X в любое исходное уравнение.

3 + У = 2

Вычтите 3 из обеих частей уравнения.

3 + Y — 3 = 2 — 3

Y = 2 — 3 = — 1

Y = -1

Ответы: Х = 3; Y = -1;

Решим эти уравнения с помощью графика.

Первое уравнение: 2X + Y = 5.

Приведите уравнение к общему виду: Y = aX + b

Вычтите 2X из обеих частей уравнения.

2X — 2X + Y = 5 — 2X
Y = 5 — 2X

Найдите две точки, чтобы начертить первую линию. Присвойте любое значение X и вычислите значение Y.

Х = 0; Y (0) =5—2*0; Y (0) = 5

Х = 4; Y (4) = 5 — 2 * 4 = 5 — 8 = — 3

Найдем две точки для второго уравнения.

Х + У = 2

Приведите уравнение к общему виду Y = aX + b.

Х — Х + У = 2 — Х;

Y = 2 — Х

Найдите две точки, чтобы начертить вторую линию. Присвойте любое значение X и вычислите значение Y.

Х = 4; У (4) = 2 — 4 = — 2

Х = — 4; Y (-4) = 2 — (-4) = 2 +4 = 6

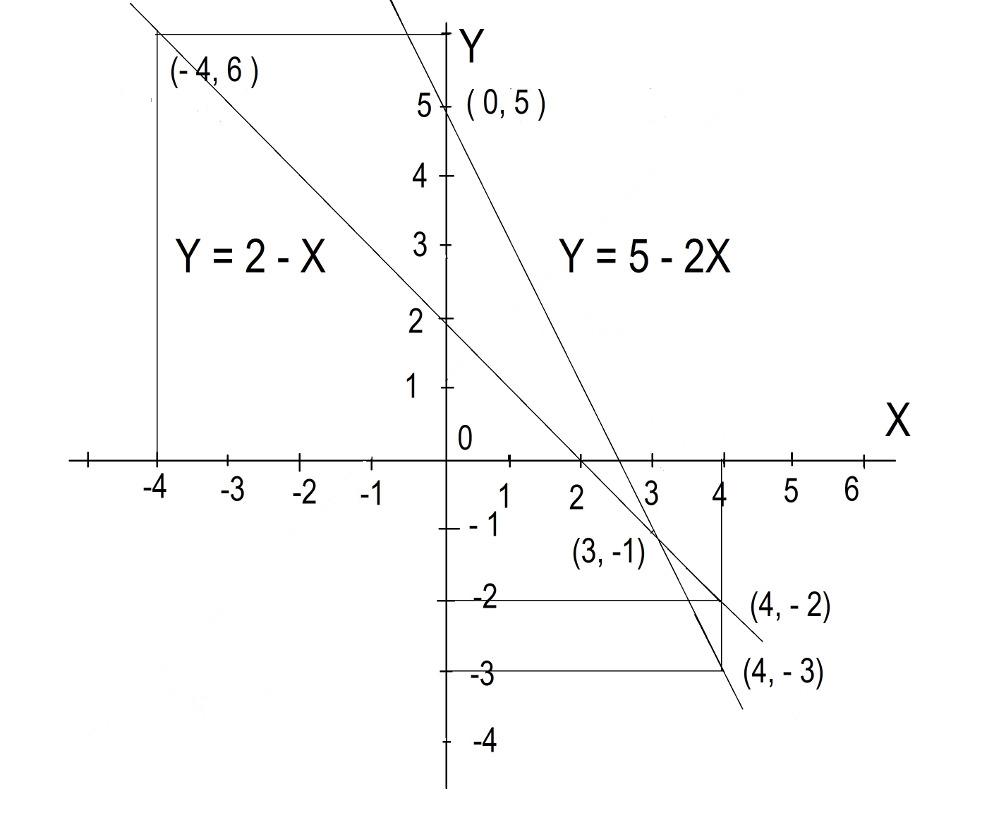
На графике 2 мы видим, что точкой пересечения является (3, -1). Тот же ответ, который мы нашли раньше: X = 3, Y = -1.

Следующая система уравнений:

3. Х — У = 3

3X — 2Y = 4

Чтобы исключить один неизвестный член уравнения, например X, вы должны получить одно и то же число перед X в первом и во втором уравнении. А для того чтобы исключить Y вы должны получить одно и то же число перед Y в первом и втором уравнении. В нашем случае перед Y у вас есть -1 в первом уравнении и -2 во втором уравнении.

Чтобы получить -2Y в первом уравнении, вы должны умножить обе части уравнения на два. Тогда вы получите:

2Х — 2У = 6

3Х — 2У = 4

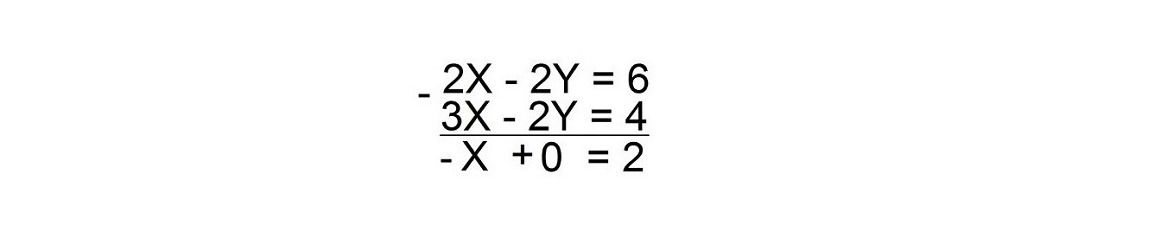
Умножьте обе части уравнения -X = 2 на -1

(-Х) (-1) = 2 (-1)

тогда Х = — 2

Поставьте -2 вместо X в любом исходном уравнении.

— 2 — У = 3

Прибавьте 2 к обеим частям уравнения

— 2 — У +2 = 3 +2

— У = 5

Умножьте обе части уравнения на — 1

— Y * (-1) = 5 * (-1)

У = — 5

Вы можете проверить свой результат. Поставьте -2 вместо X и -5 вместо Y в оба уравнениях:

Проверьте первое уравнение:

1. Х — У = 3

— 2 — (- 5) = 3

— 2 +5 = 3

3 = 3

Проверьте второе уравнение:

2. 3X — 2Y = 4

3* (- 2) — 2* (- 5) = 4

— 6 +10 = 4

4 = 4

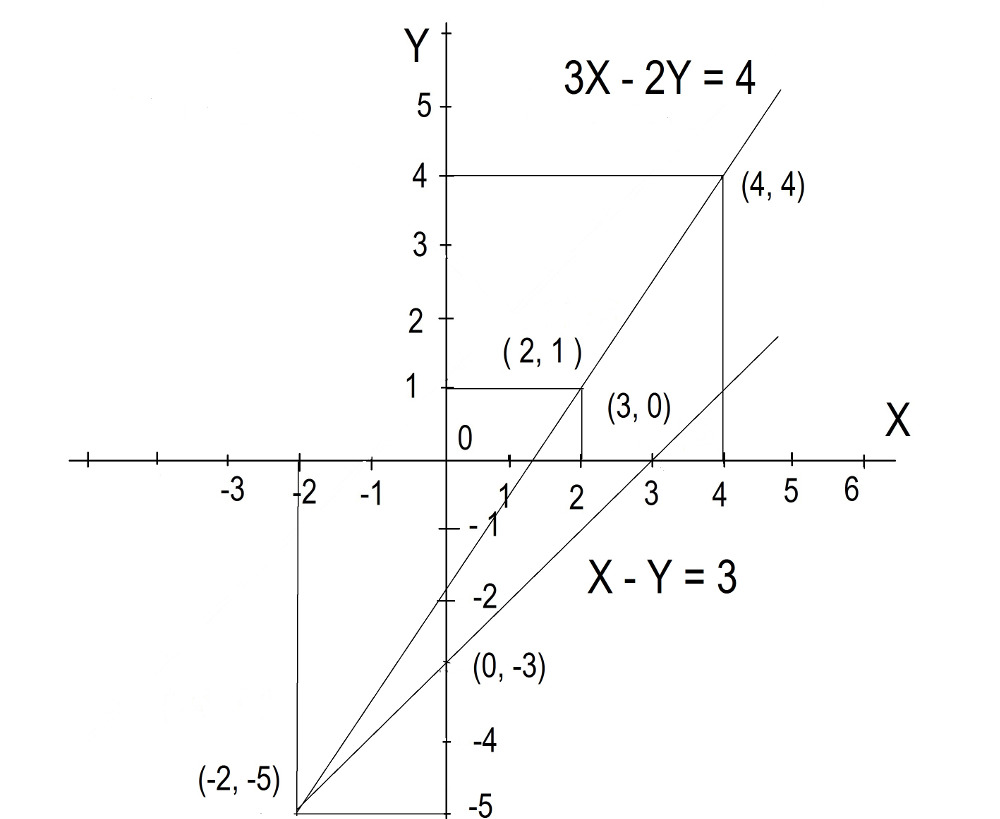
Давайте решим эти уравнения с помощью графиков.

Первое уравнение X — Y = 3

Приведите уравнение к общему виду: Y = aX + b

Вычтите Х из обеих частей уравнения:

Х — Х — У = 3 — Х

— Y = 3 — X умножить обе части на -1

У = Х — 3

Найдите две точки, чтобы начертить первую линию. Присвойте любое значение X и вычислите значение Y.

Х = 0; Y (0) = 0 — 3 = — 3

Х = 3; Y (3) = 3 — 3 = 0

Второе уравнение 3X — 2Y = 4

Приведите уравнение к общему виду. Вычтите 3X с обеих сторон.

3X — 3X — 2Y = 4 — 3X
-2Y = 4 — 3X

Разделите каждый член уравнения на -2

— 2Y/ (-2) = 4/ (-2) — 3X/ (-2)

Y = — 2 +3X/2

Поменяйте порядок членов в правой части уравнения

Y = 3X/2 — 2

Найдите две точки, чтобы начертить вторую линию. Присвойте любое значение X и вычислите значение Y.

Найдем чему равен Y при X = 4;

X = 4; Y (4) = 3*4/2 — 2 = 6 — 2 = 4

Найдем чему равен Y при X = 2;

X = 2; Y (2) = 3*2/2 — 2 = 3 — 2 = 1

Практика 6. Решение уравнений

1. X + Y = 1

X — Y = — 5

2. X + Y = 1

2X — 2Y = 6

3. X +2Y = 1

2X + Y = — 4

4. 2X + Y = 5

X +3Y = 0

5. 3X — Y = 5

4X +2Y = 10

6. 4X +2Y = 10

4X — 2Y = 6

7. X — Y = 1.5

7X +2Y=6

8. 3X + Y = 9

X — 3Y = 3

9. 5X — 2Y = -7

X +3Y= 2

10. 9X +3Y = 12

X — 2Y = — 1

КВАДРАТНЫЕ УРАВНЕНИЯ

Рассмотрим следующее уравнение:

6Х^2 +3Х — 3 = 0 
Х^2 здесь и далее означает Х в квадрате.

Выразите левую часть уравнения в виде произведения двух двучленов. Для этого разложите первый и последний члены уравнения на множители. Разложите 6X^2 на множители.

Вы можете выразить 6X^2 как 3X * 2X.

Затем вы можете выразить -3 как 1 (-3) или 3 (-1)

Тогда:

6Х^2 +3Х — 3= (2Х — 1) (3Х +3)

Вы можете проверить, равно ли выражение в левой части уравнения выражению в правой части.

6X^2 +3X — 3 = (2X — 1) (3X +3)?

Умножьте (2X — 1) на (3X +3), и вы получите

6X^2 +6X — 3X — 3 или 6X^2 +3X — 3

Два выражения равны. Теперь вы можете написать

(2Х — 1) (3Х +3) = 0

Если произведение двух двучленов равно 0, то каждый из них может быть равен 0.

(2Х — 1) = 0 и (3Х +3) = 0

Решите первое уравнение:

Прибавьте 1 к обеим частям уравнения

2X -1 +1 = 0 +1

2Х = 1

Разделите обе части уравнения на 2:

2X/2 = 1/2, тогда X = 0,5

Решите второе уравнение: (3X +3) = 0

Вычтите -3 из обеих частей уравнения.

3Х +3 — 3 = 0 — 3

3Х =- 3

Разделите обе части уравнения на 3:

3Х/3 = -3/3

и Х = — 1

Чтобы проверить свое решение, подставьте каждый результат в исходное уравнение.

Исходное уравнение: 6X^2 +3X — 3=0.

6 * (0,5) (0,5) +3 (0,5) — 3 = 0

1,5 +1,5 — 3 = 0

3 — 3 = 0

Это же уравнение можно решить другим способом.

Представьте 6X^2 как 6X * X

Тогда 6X * X +3X — 3 = 0

Разложите многочлен на множители:

(6Х — 3) (Х +1) = 0

Вы можете проверить:

(6Х — 3) (Х +1) = 6Х^2 +6Х — 3Х — 3=

= 6Х^2 +3Х — 3

Вы получили исходное уравнение. Давайте решим это.

(6Х — 3) = 0

Прибавьте 3 к обеим частям уравнения.

6Х — 3 +3 = 0 +3

6Х = 3

Разделите каждую часть уравнения на 6

6Х/6 = 3/6

Х = 0,5

так как (6X — 3) (X +1) = 0

(Х +1) = 0

Решите это уравнение, вычитая 1 из обеих частей уравнения

Х +1 — 1 = 0 -1

Х = -1

Вы получите те же результаты.

Мы можем решить это уравнение с помощью формулы:

X = [-b +/- sqrt (b^2 — 4ac)] / 2a

sqrt [] — здесь и далее означает квадратный корень.

6X^2 +3X — 3 = 0

a = 6 (a number in front of X)

b=3 (b number in front of Y)

c=-3 (a number without X or Y)

X = [-b +/- sqrt (b^2 — 4ac)] /2a

X= [-3 +/- sqrt (3^2 — 4*6* (-3))] /2*6

X= [-3 +/- sqrt (9 — (-72)] /12

X = [-3 +/- sqrt (9 +72)] /12

X = [-3 +/- sqrt (81)] /12

X = (-3 +/- 9) /12

X = (-3 -9) /12 = -12/12 = -1

X = (-3 +9) /12 = 6/12 = 0.5

Мы получили тот же результат: X = -1 и X = 0,5.

Практика 7. Решение квадратных уравнений

1. 3X^2—75=0

2.2X^2—9X +4 = 0

3.3X^2 -5X -2=0

4. 4X^2—13X +3 = 0

5.7X^2 — 29X +4 =0

6. 5X^2 — 28X +15=0

7. 18X^2 +12X -6=0

8. 3X^2 -12X +9=0

9. 24X^2 +55X-24=0

10. 12X^2 — 45X -12=0

11.8X^2 — 28X +12=0

12.12X^2 -48=0

13.2X^2 -11X +9=0

14.14X^2 -27X +9=0

15.5X^2 -37X +14=0

ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ

Десятичный логарифм

Значение логарифмов и как их понимать. Давайте посмотрим на этот пример.

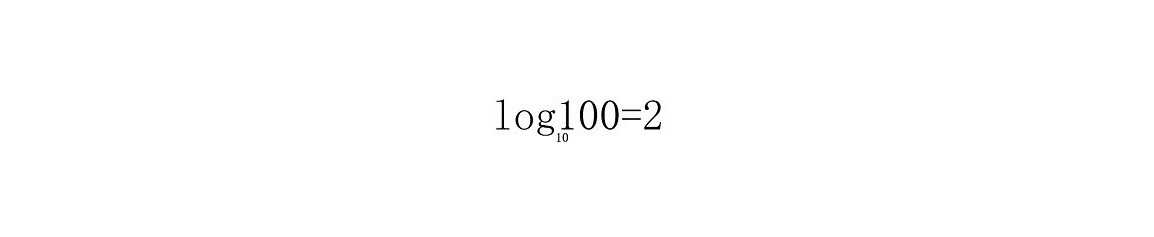
В нашем примере 100 — это аргумент логарифма. 10 — основание логарифма, а 2 — показатель степени логарифма. Логарифмы по основанию 10 известны как десятичные логарифмы.

Как вы можете получить 2, используя 100 и 10? Вы можете попробовать выполнить все возможные расчеты. Например, 100 — 10 = 90. Это не 2. 100+10 не 2. 100/10 не 2. Что осталось?

10 ^ 2 = 100

Это означает, что логарифм аргумента — это степень, в которую необходимо возвести основание, чтобы получить аргумент. Логарифм 100 равен 2, потому что, для того чтобы получить 100 при основании 10, мы должны возвести 10 в степень 2.

Основание алгоритма не может быть равна 1 или 0. Давайте разберемся, почему.

Представьте себе следующий пример. В какую степень нужно возвести 1, чтобы получилось 100?

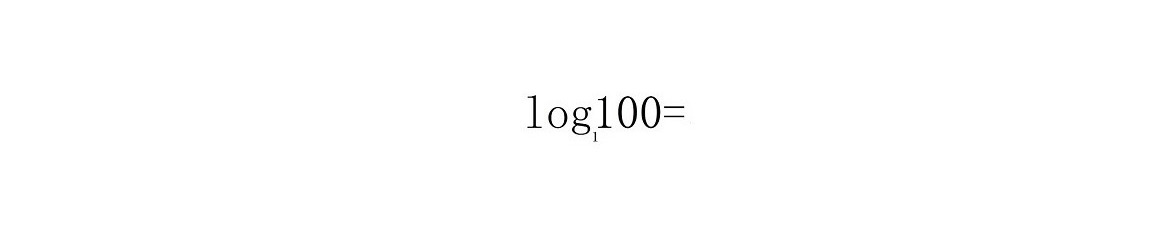
То же самое с нулем. 0 * 0 = 0

Логарифм может быть равен 0, потому что 10, возведенное в степень 0, = 1.

Поскольку любое число, возведенное в степень 0, равно 1, логарифм 1 по любому основанию равен 0. Это правило называется правилом нулевого показателя.

Давайте посмотрим на другом примере.

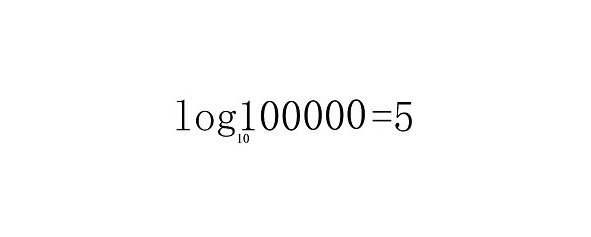
Вы можете представить 10000 как 100*100. Тогда

Вы уже знаете, что логарифм 100 равен 2, а логарифм 1000 равен 3. Тогда вы можете написать:

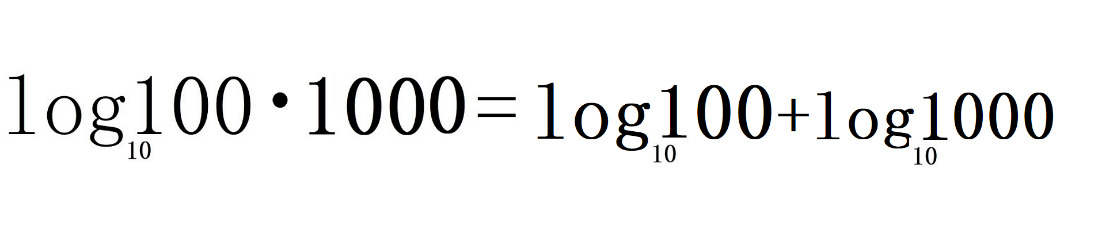
Или в общем виде:

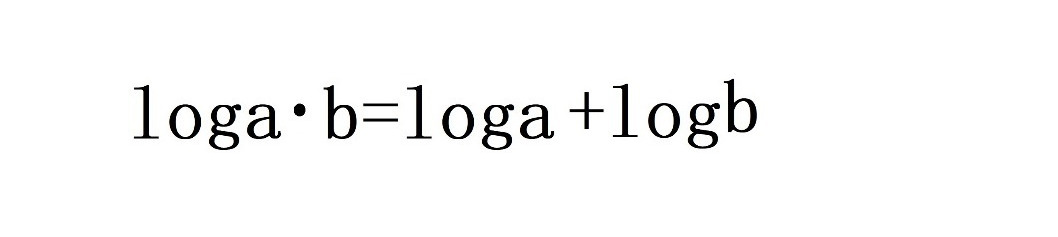
или

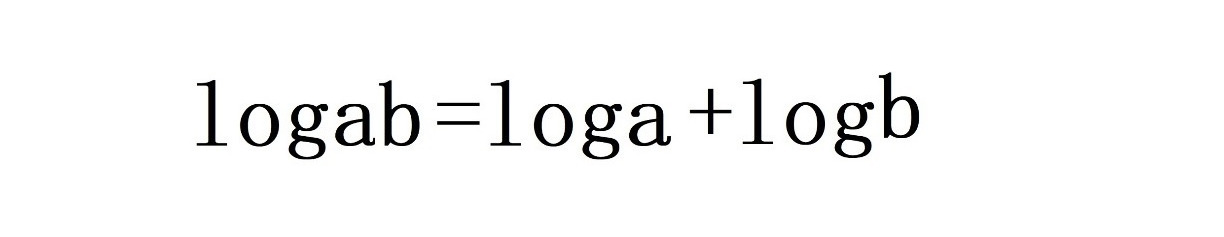
Вы открыли правило:

Логарифм произведения двух чисел равен сумме логарифма первого числа и логарифма второго числа.

Теперь посмотрите на этот пример

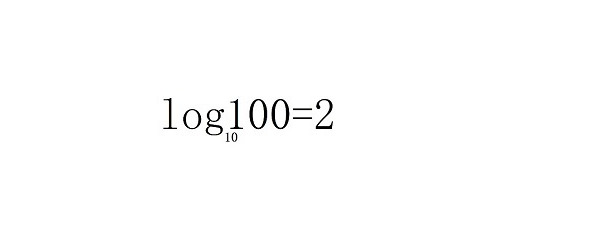
Тогда

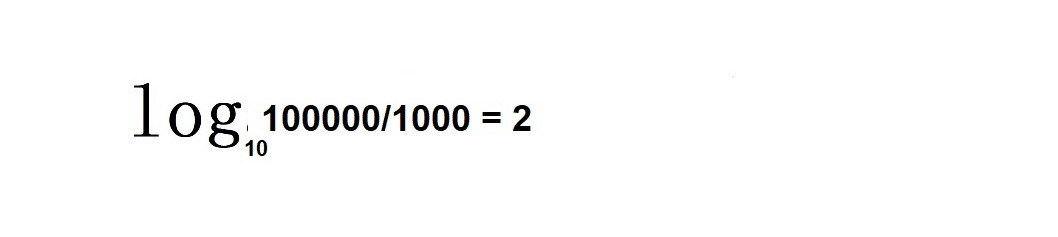
Вы знаете, что логарифм 100000 = 5, а логарифм 1000 = 3.

5 — 3 = 2 тогда

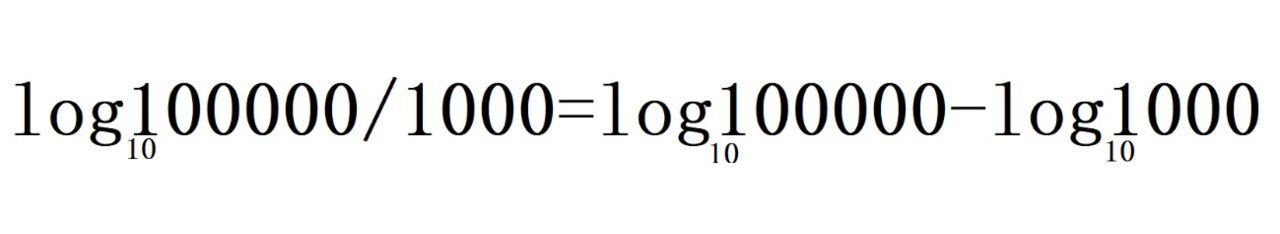
Или в общем виде:

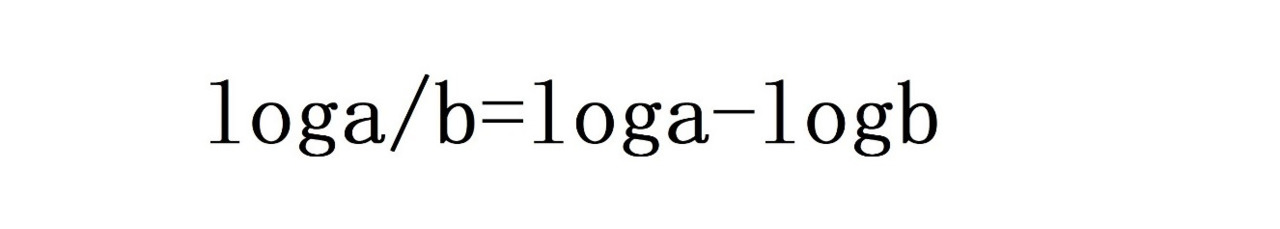
Вы открыли еще одно правило:

Логарифм частного двух чисел равен разности логарифма числителя и логарифма знаменателя.

Давайте посмотрим на этот пример

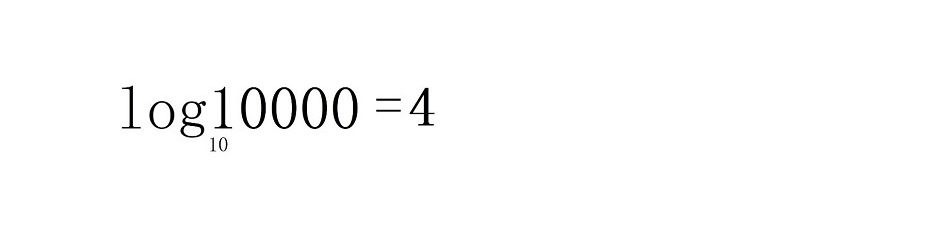
Мы можем написать: