
Бесплатный фрагмент - Как надо думать
Что вы узнаете
Под какой личиной скрывается психологическая инерция и как ее разоблачить.
Как накачивать умственные «мускулы» и увеличивать остроту мышления
Какие бывают логические задачи и головоломки и как с ними справляться
Для чего надо уметь воображать и как этому научиться
Борьба с психологической инерцией
Первое орудие труда человека — каменный топор — представлял собой кусок камня со сколотым краем, крест накрест привязанный к палке. Найденные впоследствии бронзовые топоры были также сделаны с крестообразными канавками. Оказалось, что древние ремесленники тысячелетиями продолжали повторять «привычную» форму топора.
Первые архитектурные колонны были сделаны из стволов деревьев. Появившиеся потом каменные колонны покрывались тончайшей резьбой, с ювелирной точностью повторяющей узор коры дерева.
Первым животным, которое человек использовал в качестве тягловой силы, был вол — могучее создание с низко опущенной шеей. Для него придумали соответствующую упряжь –ярмо, лежащее на холке. Когда были приручены лошади, на них одевали то же ярмо. При этом две трети «лошадиной силы» тратилось впустую, на сопротивление неудобной упряжи. Более трех тысяч лет понадобилось для изобретения упряжи с хомутом, она появилась только в средние века!
Что заставляло людей выполнять лишнюю работу, не позволяло в течение многих тысяч лет заметить свои ошибки? Косность, ограниченность?.. Вряд ли. Ведь в то же время жили гениальные скульпторы, философы, математики. Они создавали прекрасные произведения, выдвигали смелые идеи, изобретали невиданные механизмы.
Психологическая инерция — вот сила, которая держит человека в плену привычных понятий, не дает вырваться за пределы стандартных представлений, внушает боязнь нового, необычного. Психологическая инерция окружает нас давно усвоенными понятиями, мнением известных людей, иностранными названиями. Этот «спрут» всеми своими щупальцами заставляет людей оставаться на прежнем уровне, в рамках привычных суждений и идей.

Психологическая инерция — это «свойство человека мыслить по прямой аналогии».
Было замечено, что разные задачи рассчитаны на разное проявление инерции мышления:
инерция в понимании условия задачи
инерция в понимании вопроса
инерция в выборе способа решения
Тот, кто смотрел фильм «Мой любимый клоун», наверняка помнит эту сцену.
На рынке клоуны покупают дыню. Продавец просит 25 руб. Они спрашивают, нельзя ли меньше.

— Нет
— А 30 руб.
— Нет
— А все-таки, может отдашь за 30?
— Нет, не могу.
До продавца не сразу доходит…
Типичная инерция в понимании условия задачи: продавца целый день просят снизить цену, он настолько привык к этому, что даже не вслушивается в смысл обращения, по инерции отвечает отказом.
Грузовик в туннеле
Грузовик, который принимаем за материальную точку, весит 5 тонн и двигается со скоростью 60 километров в час. Он начинает въезжать в туннель длиной два километра. На сколько километров он въедет в туннель?
Туннель свободный, незакрытый, автомобильных пробок нет, бензина хватит и т. д.
Подсказка: вес и скорость не имеют значения.
Затруднения вызывает именно вопрос. Несмотря на все примечания и подсказки, народ пытается сложить тонны с километрами и куда-нибудь пристроить скорость.
А всего-то надо присмотреться к вопросу: грузовик въезжает в туннель, и что? Он там останется? Нет… он должен выехать с другой стороны.
В чем разница между «въезжать» и «выезжать»? До середины туннеля грузовик въезжает, а после этого он уже выезжает.
Третий вид психологической инерции — инерция в выборе способа решения — наглядно демонстрирует задача о лампочках и соответствующих им выключателях, которую мы рассматривали в первой книге этой серии «Зачем надо думать».
В комнате находятся три лампочки. Снаружи, за закрытой дверью — три выключателя. Каждой лампочке соответствует свой выключатель. Вы находитесь рядом с выключателями и можете включать — выключать любой из них несколько раз. В комнату с лампочками можно зайти только один раз. Как определить, какой выключатель управляет каждой лампочкой?
Несмотря на очевидную невозможность увидеть за один раз, как распределяются три лампочки и три выключателя, очень многие решатели пытаются «посмотреть» и «подсмотреть».
Вместо того, чтобы атаковать задачу «в лоб», надо немного отстраниться от нее и переформулировать вопрос. Требуется узнать, какой выключатель командует каждой из этих лампочек. Узнать, т. е. получить информацию.
Какими, в принципе, способами человек получает информацию?
Визуальный способ (на глаз)
Аудио способ (на слух)
На ощупь
По запаху
Остается выбрать подходящие для данного случая способы, и задача решена.
Вывод: чтобы предолеть психологическую инерцию, надо решать задачу «на расстоянии», мысленно представить себе всю ситуацию вокруг рассматриваемых объектов, в пространстве и во времени.
Существуют различные классификации и множество видов инерции мышления. Рассмотрим некоторые из них, наиболее часто встречающиеся.
Инерция привычки — привычного принципа действия, привычных свойств, привычного внешнего вида и т. п.
Например:
на необитаемом песчаном острове надо ощутимо сдвинуть с места гранитную скалу весом полторы тонны, длиной 5 метров и высотой 6 метров. Как это сделать?
Скала — это что-то огромное, неподвижное, сразу вспоминается «умный в гору не пойдет». Заменим термин «скала» чем-нибудь попроще: камень, штуковина.
Каждое свойство этой штуковины описывается определенным параметром, имеющим числовое значение. Что дано? Вес, высота, ширина. Чего не хватает? Толщины. Подсчитаем… Удельный вес гранита 2500 кг/куб. м, получается, что
толщина 2 см. Огромная гора исчезла, растаяла. Эту тонкую стенку достаточно пальцем ткнуть, и она упадет.
Задача для тренировки.
Как закрепить толстую свечку на вертикальной деревянной стенке, если для этого можно пользоваться только молотком, коробочкой с маленькими гвоздиками и спичками?
Подсказка: замените термин более общим определением.
Инерция несуществующего запрета — я уверен, что так нельзя, или все знают, что так нельзя.
Например:
Назовите как можно больше натуральных веществ цвета сирени.
Натуральные вещества — значит их никто не красил, они от природы такие. А какого цвета бывает сирень? Сиреневая и… белая. Вот и исчезло главное препятствие, белых веществ в природе видимо-невидимо: снег, молоко, заячья шерстка зимой и прочая, прочая…
Задача для тренировки.
Как бросить сырое яйцо на 3 метра, чтобы оно не разбилось?
Подсказка: представьте себе эту ситуацию в динамике, во времени и в пространстве.
Инерция лишней информации
Например:
Проводятся военно-спортивные соревнования для старшекласников. Участвуют две команды. Очередное задание получают два человека: по одному от каждой команды. Требуется, ориентируясь по карте местности, выйти к реке и перебраться на другой берег. На берегу выясняется, что в их распоряжении есть только маленький плот, который может выдержать не больше одного подростка. Как быть?
Если отбросить все подробности, то по условию задачи два человека подошли к берегу реки. Где они были раньше, откуда они подошли? Они шли вместе или каждый сам по себе? Сколько берегов у реки? Два, правый и левый. Значит, если два человека подошли каждый к своему берегу реки, они сумеют переправиться на противоположный берег по очереди, без особых затруднений.
Задачи для тренировки.
Представьте себе, что Вы владеете небольшим магазином-пекарней, который открыт с 7 часов утра до 7 часов вечера. За это время магазин обслуживает от 80 до 100 покупателей. В пекарне работают 6 человек, все они состоят в родственных отношениях с владельцем бизнеса. Сколько лет хозяину пекарни?
Петух вскочил на двускатную крышу сарая и снес яйцо прямо на ее ребре. Угол наклона одного ската гораздо больше, чем другого. В какую сторону покатится яйцо?
Подсказка: не отвлекайтесь на подробности, выделите главное действие или главное действующее лицо.
Инерция специальных терминов
Например:
Работник электрической компании умер в воскресенье. Выплатят ли ему компенсацию?
Термин» работник электрической компании» привлекает внимание и отвлекает от сути вопроса. Заменим термин более общим определением: человек.
Человек умер в воскресенье. Умер… о какой компенсации может идти речь?
Задачи для тренировки.
1. Есть ли в Китае 7 ноября?
Подсказка: внимательно читайте условия задачи — каждое слово может содержать в себе ловушку.
2. Получит ли прихожанин католической церкви разрешение на вступление в брак с двоюродной сестрой своей вдовы?
Инерция авторитетов
Например:
английский журнал «Electronic Components» разместил в одном из своих выпусков вопрос: круглое, с хвостом и все разбивает. Что это такое?
Хорошо, что мы сумеем обнаружить «щупальцы» психологической инерции в самых различных ситуациях, но этого недостаточно. Надо еще уметь преодолеть влияние психологической инерции, научиться бороться с ней.
Каждая ситуация, описываемая в задачах, возникла не на пустом месте и не в данный момент. Другими словами, надо рассматривать условия задачи в движении: как эти условия выглядели в недавнем прошлом, как они изменятся в ближайшем будущем, т. е. помнить о пространстве и времени.
Каждый объект обладает определенными свойствами и выполняет определенные функции, поэтому надо концентрировать внимание именно на требуемых функциях и свойствах, а не на объекте.
Термины уводят наше внимание в сторону, заменяйте их на более общие определения.
Внимательно читайте условия задачи — каждое слово может содержать в себе ловушку.
Не старайтесь изменить условия задачи — это типичное проявление психологической инерции, только зря потратите время.
Кроме того, существует универсальная методика преодоления психологической инерции — Развитие Творческого Воображения (РТВ), которую мы рассмотрим в последней главе этой книги.
А пока проверьте себя и своих друзей, насколько вы свободны от инерции мышления.
Задачи для тренировки
1. Сколько будет 2 в кубе? 6 в кубе? 11 в кубе? Угол в кубе?
2. Если пять первоклассников решают пять задач по арифметике за пять минут, то сколько надо одному первокласснику на одну задачу?
3. Есть месяцы длиной в 30 дней, есть — в 31 день. А в каком месяце имеется 28-е число?
4. Его хранят, чтобы он бездельничал, и выбрасывают, чтобы он начал приносить пользу. Что это?
5. Сторожевого пса привязали к крыльцу дачи 10-тиметровой веревкой. Тем не менее, он сумел пробежать 60 метров. Как?
6. Два приятеля участвовали в школьных соревнованиях по шахматам. Каждый из них набрал максимальное количество очков и стал чемпионом своего класса. Как им это удалось?
7. По размерам это больше, чем слон, но при этом не весит ни грамма. Что это?
8. Мальчик соскочил с лестницы высотой 12 м и даже не ушибся. Как ему это удалось?
9. Какой рукой удобнее размешать сахар в стакане с чаем?
10. На какой вопрос нельзя правдиво ответить «да»?
11. На какой вопрос нельзя правдиво ответить «нет»?
12. В электричках стоп-краны делают красного цвета. А в аэробусах? Цвета лазури? Синего? Желтого?
13. Кто при Екатерине Второй ходил вверх головой?
14. Какое слово из 11 букв все дети, взрослые и даже учителя пишут неправильно?
15. В начале 20-го века один фельдкурат (армейский священник) предсказывал любому желающему фамилию его будущей жены. Как ему это удавалось?
16. Парикмахер небольшого итальянского города всегда говорил, что он предпочитает подстричь и побрить двух туристов, чем одного местного жителя. Почему?
17. Два человека молча стоят на мосту и смотрят в разные стороны: один — на север, другой — на юг. Вдруг один из них спрашивает другого «почему ты улыбаешься?» Как он смог увидеть эту улыбку?
18. Какие два месяца подряд имеют по 31 дню?
19. Сестра моей сестры, но мне она не сестра. Как это?
20. Сколько кубометров земли содержится в яме размерами: глубина 2 м, ширина 4 м, длина 5м?
21. Сколько кусочков сахара можно положить в пустой мешок?
22. По статистике японские женщины употребляют больше риса, чем сингапурские. Почему?
23. Вес курицы составляет 2 кг и еще треть курицы. Каков вес курицы?
24. В подвале хранилось 60 бутылок десертного вина. В течение года выпили все вино, кроме 10 бутылок мадеры. Сколько вина осталось?
25. Из Нижнего Новгорода вниз по Волге вышел туристский теплоход «Лев Толстой». В то же время из Астрахани вверх по течению вышел сухогруз. «Лев Толстой» идет со скоростью 25 км/час, но делает остановки возле туристских объектов. Сухогруз движется без остановок со скоростью 12 км/час. Какое судно будет ближе к Астрахани в момент их встречи?
26. Горело 5 свечей, 2 свечи задули. Сколько свечей осталось?
27. Сколько зверей удалось спасти во время библейского потопа?
28. Сколько раз встречается цифра 9 в числах от 1 до 100?
29. Сколько раз встречается число 9 в числах от 1 до 100?
30. Хирург возвращается домой очень усталый и, несмотря на неурочный час — 6 часов вечера, ложится спать. Будильник в его мобильном телефоне звонит каждое утро в 7 часов. Сколько времени ему удастся проспать?
31. Пациент должен получить три таблетки с промежутком в полчаса между приемом. Сколько времени придется потратить на всю процедуру?
32. На столе стоят две лампы: керосиновая и газовая. Что вам надо зажечь прежде всего?
33. На одной руке 5 пальцев, на двух — 10. Сколько пальцев на 10 руках?
34. При раскопках на территории Италии нашли монету, на которой было выбито 25 г. до н. э. Может ли такое быть?
35. Отец с сыном купались в море. Отец утонул, а сына доставили в больницу. Врач в приемном покое узнал в нем своего сына. Как это может быть?
36. Папа Карло решил стать тренером футбольной команды, для чего ему надо вырезать деревянных футболистов. У него есть достаточно длинное полено, которое надо распилить на 11 частей. Сколько раз ему придется пилить?
37. Три палочки положили на стол, а получилось четыре. Каким образом?
38. Дирижабль плывет на восток в потоке воздуха. Куда при этом «смотрят» закрепленные на нем флаги?
39. Что становится больше, если его перевернуть вверх ногами?
40. Можно ли зажечь спичку под водой?
41. На поверхности пруда плавает одна кувшинка, которая постоянно делится и разрастается. Каждый день площадь, которую занимают кувшинки, увеличивается в два раза. Через месяц покрытой оказывается вся поверхность пруда. За сколько времени покроется кувшинками вся поверхность пруда, если изначально на поверхности будут плавать две кувшинки?
42. Если в 12 часов ночи идет дождь, то можно ли ожидать, что через 72 часа будет солнечная погода?
43. Самолет разбился на границе между Германией и Австрией. Где похоронят уцелевших пассажиров?
Развитие интеллектуальных способностей
Кроме головоломных задач с подвохами и ловушками, существует множество логических задач. Для их решения требуются те самые интеллектуальные способности, которые мы упоминали в книге «Зачем надо думать»: логичность, пытливость, глубина ума, гибкость и подвижность ума и т. д.
Можно выделить несколько типичных видов логических задач и рассмотреть методы решения каждого вида.
Интересная математика
Кто есть кто
Пересечения
Взвешивания
Переливания
Ось времени
Истина — ложь
Существуют определенные приемы решения логических задач:
метод рассуждений, с помощью которого решаются самые простые логические задачи. В ходе решения используются рассуждения, последовательно учитывающие все условия задачи, которые постепенно приводят к выводу и правильному ответу.
метод таблиц, применяемый при решении текстовых логических задач. Решение логических задач заключается в построении таблиц, которые позволяют наглядно представить условие задачи, контролировать процесс рассуждений и помогают сделать правильные логические выводы.
метод графов состоит в переборе возможных вариантов развития событий и окончательном выборе единственно верного решения.
метод блок-схем — метод, широко используемый в решении логических задач на переливание. Он заключается в том, что сначала в виде блоков выделяются операции, затем устанавливается последовательность выполнения этих операций.
метод кругов Эйлера используется для решения задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи. Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
Интересная математика
Математические задачи — самая обширная категория среди логических задач. Обычно сложность заключается не в математических вычислениях, а в трудности выбора способа вычисления. Иногда авторы математических задач специально запутывают условия, но чаще задачи основаны на невозможности закостенелого мышления среднестатистического человека изменить привычные шаблоны.
Решение математических задач поможет вам избавиться от этой закостенелости.
Маша и медведи
Маша принесла своим друзьям медведям торт. Известно, что старший медведь съедает торт за 2 дня, средний медведь — за 3 дня, младший медведь — за 6 дней. За сколько дней три медведя вместе съедят торт?
Решение
Используем метод рассуждений.
Так как старший медведь съедает торт за 2 дня, то за 1 день он съедает 1/2 торта.
Так как средний медведь съедает торт за 3 дня, то за 1 день он съедает 1/3 торта.
Так как младший медведь съедает торт за 6 дней, то за 1 день он съедает 1/6 торта.
Вместе все три медведя за 1 день съедят 1/2+1/3+1/6=1, то есть один торт.
Ответ. За 1 день.
Туристы
Группа туристов отправилась в поход. В первый день они прошли 1/3 пути, во второй — 1/3 остатка, в третий — 1/3 нового остатка. В результате им осталось пройти 32 км. Сколько километров был маршрут туристов?
Решение
Используем метод рассуждений, но решаем задачу с конца.
Так как осталось 32 км, а в третий день туристы прошли остаток, то 32 км будут составлять 2/3 последнего остатка. Тогда сам последний остаток будет равен
32 : 2/3 = 48 (км).
Эти 48 км будут составлять 2/3 длины маршрута, оставшегося пройти после первого дня. Тогда весь маршрут, который осталось пройти, будет равен
48 : 2/3 = 72 (км).
Эти 72 км составляют вновь 2/3, но уже всего маршрута туристов, а значит, весь маршрут будет равен 72 : 2/3 = 108 (км). Задача решена.
Ответ. 108 км
Можно решать такие задачи табличным методом, но заполнять таблицу надо также с конца.
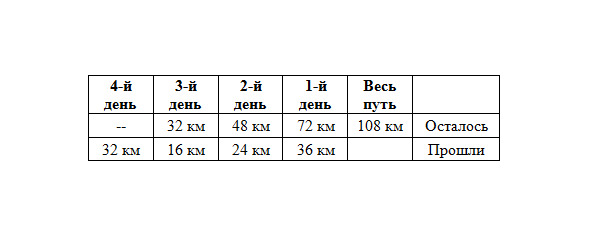
Обратите внимание: каждый день туристы проходят треть пути, в две трети остаются. Значит, остаток каждый день в 2 раза больше, чем пройденный путь.
Если остаток третьего дня 32 км, то пройденный путь 16 км.
Тогда остаток второго дня 48 км (32км+16км), а пройденный путь 24 км.
Соответственно, остаток первого дня 72 км, пройденный путь 36 км, а весь маршрут составлял 108 км.
Муха
Два поезда, находящиеся на расстоянии 200 км, движутся навстречу друг другу со скоростью 50 км/ч каждый. Муха берёт старт с одного из поездов и летит по направлению к другому со скоростью 75 км/ч. Долетев до другого поезда, муха разворачивается и летит назад к первому. Так она летает туда и обратно, пока два поезда не сталкиваются, и насекомое погибает.
Какое расстояние успела пролететь муха?
Решение
Используем метод рассуждений.
Есть два способа решить эту задачу, один — простой, другой — тяжёлый. Тяжёлый способ решения задачи: просчитать каждый отрезок пути. «Мы пойдем другим путем».
Поезда сближаются друг с другом со скоростью 100 км/час, значит, через 2 часа они столкнутся. За это время муха успеет налетать 150 км.
Ответ. 150 км
Задачи для тренировки.
1. Уравнять дыню
Арбуз и лимон весят столько, сколько дыня.
Два арбуза весят столько, сколько дыня и лимон вместе.
Сколько надо лимонов, чтобы уравнять в весе дыню?
2. Побег из тюрьмы
Опасный преступник по кличке Бешеный Джо ночью сбежал из тюрьмы. Охранники обнаружили это только спустя полчаса после побега и бросились в погоню вместе со сторожевым псом. Джо бежал со скоростью 3 мили в час, а его преследователи — 4 мили в час. Пес со скоростью 12 миль в час носился взад-вперед между охранниками и беглецом. Наконец, преступник был схвачен.
Сколько миль за это время успел набегать неутомимый пёс?
3. Гуси
Над озерами летели гуси. На каждом озере садилась половина гусей и еще полгуся, остальные летели дальше. Все сели на семи озерах. Сколько было гусей?
4. Вес семьи
Мама и две ее дочери весят — 140 кг. Мама весит на 10кг больше, чем старшая дочь, а вместе на 80 кг больше, чем младшая. Сколько весит младшая дочь?
5. Ступеньки
Лена живет на четвертом этаже. При этом, поднимаясь к себе, домой, она проходит по лестнице 60 ступенек. Юля живет в этом же подъезде на втором этаже. Сколько ступенек проходит Юля, поднимаясь к себе, домой на второй этаж?
6. Диофант
Мало что известно о жизни одного греческого математика из Александрии, которого называют родоначальником алгебры. Предполагается, что он жил в 3-м веке нашей эры. По рассказам, на его надгробии была высечена следующая эпитафия:
«Детство Диофанта 1/6 жизни заняло; 1/12 жизни Диофант бороду растил; ещё 1/7 жизни Диофанта прошла до того, как он женился. Через 5 лет после свадьбы у Диофанта родился сын, который прожил только половину лет, что прожил его отец. А через 4 года после смерти сына умер Диофант»
Сколько лет прожил Диофант?
7. Грибы
Грибник собрал 100 килограммов грибов. Влажность грибов была 99% (они на 99% состояли из воды). Решил их подсушить и через некоторое время грибы усохли до влажности 98%. Сколько стали весить грибы после сушки?
8. Коровы на лугу
Шесть коров съедают всю траву на лугу за 12 дней, а 5 коров — за 16 дней. Сколько коров съедят всю траву на лугу за 24 дня?
Подсказка: трава ежедневно прирастает на одну и ту же величину.
9. Ведро воды
Папе ведра воды хватает на две недели, а если вместе с сыном, то на 10 дней. Вопрос: на сколько дней хватит сыну ведра воды, если он будет пить один?
10. Яблоки
У двух девочек есть по несколько яблок. Если одна даст другой 2 яблока, то у нее их станет в 2 раза меньше. А если вторая девочка даст первой 2 яблока, то у них станет поровну.
Сколько яблок у девочек?
11. Зубчатые колеса
Сколько оборотов сделает каждое из колес находящихся в сцеплении до возвращения в исходное положение, если у одного 12 зубьев, а у другого 54?
12. Если бы…
Если бы четверть от 20 была равна 4, то чему бы была равна треть от 10?
13. Завещание
Завещание в пользу жены и ребенка, который должен родиться: если родиться мальчик, то он получает 2/3, а жена 1/3. Если родится девочка, то она получает 1/3, а мать 2/3.
На свет появились близнецы — девочка и мальчик. Как разделить наследство?
14. Близнецы
В одном удивительном классе вместе учатся четыре пары близнецов! Однажды на школьный праздник вместе с детьми этого класса пришли все мамы и папы. Вместе их получилось 85 человек.
Сколько учеников в классе?
15. 120
Чему равна одна треть от одной четвёртой от одной пятой от половины от 120?
16. Стоимость книги
За книгу заплатили тысячу рублей. Осталось заплатить столько, сколько бы осталось заплатить, если б за неё заплатили столько, сколько осталось заплатить. Сколько она стоит?
Кто есть кто
Задачи типа «Кто есть кто?» — это настоящие логические задачи. Смысл таких задач в том, что даны отношения между предметами, и следуя по цепочке этих отношений, вы приходите к правильному результату.
Задачи типа «Кто есть кто?» решаются разными методами — метод графов, методом таблиц, несложные задачи поддаются даже методу рассуждений.
Футбол
Четыре футбольных команды: итальянская команда «Милан», испанская — «Реал», российская — «Зенит», английская — «Челси» встретились в групповом этапе лиги чемпионов по футболу. Их тренировали тренеры из этих же четырех стран: итальянец Антонио, испанец Родриго, русский Николай, англичанин Марк.
Известно, что национальность у всех четырех тренеров не совпадала с национальностью команд. Требуется определить тренера каждой команды, если известно:
а) Зенит не тренируется у Марка и Антонио.
б) Милан обещал никогда не брать Марка главным тренером.
Решение
Используем метод графов.
Исходя из условий задачи, получаем следующий граф.
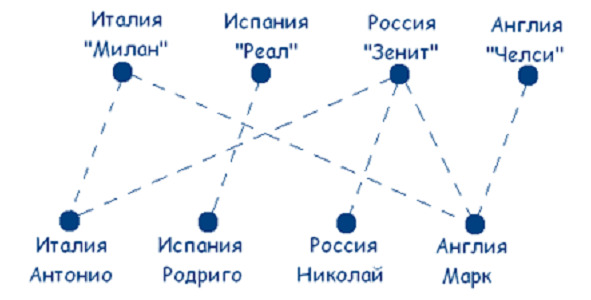
Сразу можем сделать вывод, что российская команда «Зенит» тренируется у испанца Родриго. Чертеж примет следующий вид:
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.
