Бесплатный фрагмент - Как измеряется информация?

Измерение информации — важная задача теории информации, поскольку позволяет количественно оценить объем передаваемых сообщений, количество информации, содержащейся в сообщении, и степень неопределенности ситуации.

Рассмотрим основные подходы измерения информации с подробными пояснениями и примерами.

1. Условная мера количества информации (бит)

Информация измеряется в битах (от англ. bit — binary digit). Один бит — это количество информации, необходимое для выбора одного из двух равновероятных исходов.

Формула Хартли:

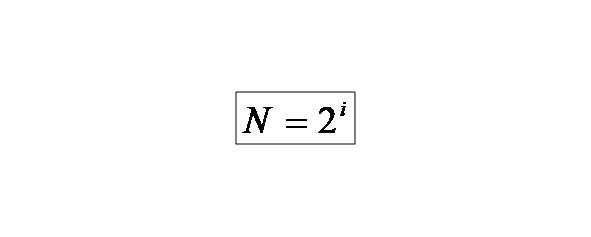
Где, N — количество равновероятных возможных событий; I — количество информации в сообщении о том, что произошло одно из N событий.

Предположим, вы подбрасываете монету. Есть два равновероятных события: выпадение орла или решки (N=2). Измерим количество информации:

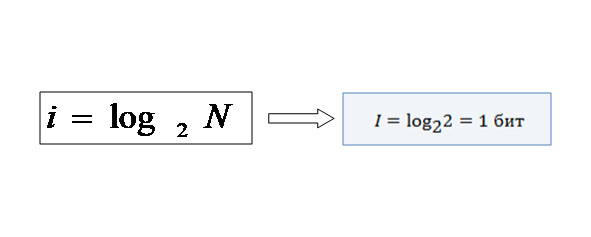
Это значит, что результат броска монеты несет ровно один бит информации.

Пример 1:

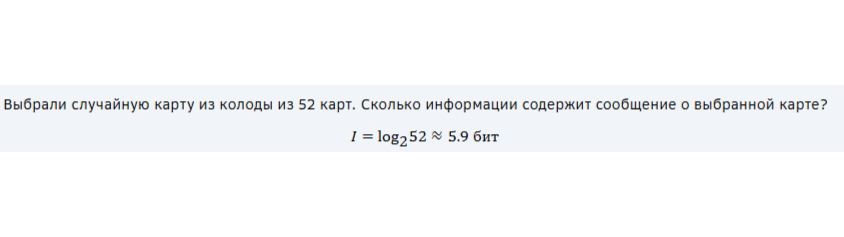
2. Информация по Шеннону (энтропия)

Шеннон предложил учитывать вероятность каждого события, чтобы точнее измерять информацию. В отличие от формулы Хартли, здесь учитывается случай, когда события не равновероятны

Энтропия показывает среднее количество информации, которое мы получаем при наблюдении события.

Пример 2:

Рассмотрим игральный кубик. Событие выпадения каждой грани имеет одинаковую вероятность 1/6. Тогда энтропия равна:

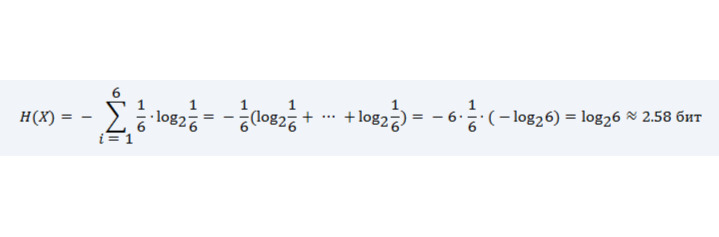
Таким образом, бросок кубика несет примерно 2.58 бита информации.

Пример.3. Рассмотрим другой пример, где вероятности граней неодинаковы:

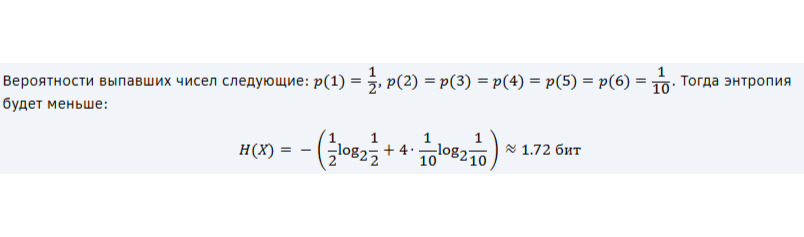
Здесь энтропия уменьшилась, потому что одно событие стало значительно вероятнее остальных.

3. Количество информации при передаче сообщения

При передаче сообщения важно понимать, сколько информации передается через канал связи. Для этого используют понятие информационной пропускной способности канала.

Пример 4:

4. Примеры практического применения:

a) Кодирование текста

Текстовые файлы кодируются различными способами. Например, ASCII-кодировка использует 8 бит на символ, UTF- 8 — переменное количество байтов (от 1 до 4 байт).

b) Компрессия данных

Алгоритмы сжатия данных (например, ZIP, RAR) используют принципы уменьшения избыточности, основываясь на понятиях энтропии и условной вероятности.

c) Передача цифровых сигналов

Для эффективной передачи данных по каналам связи используется теория информации, позволяющая минимизировать потери информации и повысить надежность передачи.

Заключение

Таким образом, измерение информации осуществляется разными методами в зависимости от контекста и цели анализа.

Основные понятия включают бит, энтропию Шеннона и пропускную способность каналов связи. Эти методы позволяют эффективно оценивать объемы информации, оптимизировать передачу данных и разрабатывать эффективные алгоритмы обработки информации.

Решение задач и примеров

Давай разберём три примера задач, связанных с кодированием текста, сжатием данных и передачей цифровых сигналов. Каждый пример сопровождается подробным пошаговым решением.

Задача №1: Кодирование текста

Определить объём памяти, который потребуется для хранения текста, состоящего из 100 символов, закодированных в формате Unicode UTF-8. Известно, что первые 128 символов ASCII занимают 1 байт, символы кириллицы — 2 байта.

Решение:

1. Определение структуры кодировки UTF — 8:

— Символы ASCII (кодировка первых 128 символов): 1 байт (8 бит).

— Кириллические символы (диапазон 128–255): 2 байта (16 бит).

2. Расчёт объёма памяти:

Предположим, что текст состоит из 50 латинских букв (ASCII) и 50 русских букв (кириллица).

— Латинские буквы (ASCII):

50 символов × 1 байт = 50 байт.

— Русские буквы (UTF-8):

50 символов × 2 байта = 100 байт.

Итого общий объём памяти:

Ответ:

Объём памяти, необходимый для хранения такого текста, составляет 150 байт.

Задача №2: Сжатие данных (алгоритм Хаффмана)

Используя алгоритм Хаффмана, построить оптимальное кодирование для следующего набора символов с заданными вероятностями: