Бесплатный фрагмент - Excel и задача о восьми ферзях

Глава 1. Постановка задачи

Ферзь — сильнейшая шахматная фигура, которая может ходить по вертикали, по горизонтали и по диагонали.

Одна из самых знаменитых шахматных задач — это расстановка восьми ферзей одного цвета на шахматной доске так, чтобы ни один из них не находился под боем другого.

Размер шахматной доски обычно составляет 64 клетки. Обычно для кодировки клеток строкам (горизонталям) доски присваивают номера от 1 до 8 включительно, а столбцам (вертикалям) добавляют буквы латинского алфавита. Поля чередуются по цветам, левое верхнее поле доски обычно носит кодировку a8 и окрашивается в белый цвет. Правое верхнее поле — это поле h8, оно обычно бывает черного цвета.

На рисунке 1.1 покажем, как обычно выглядит пустая шахматная доска с учетом общепринятой кодировки.

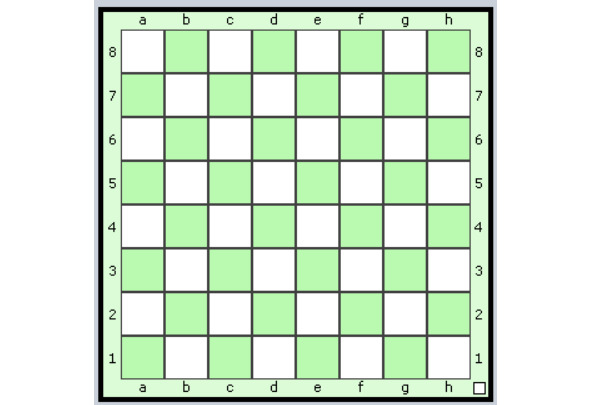
Пустая шахматная доска содержит 4 угловые клетки. Это клетки a1, a8, h1 и h8.

Любая клетка шахматной доски — это пересечение одной вертикали и одной горизонтали. Это значит, что если надо поставить ферзи таким образом, чтобы они не угрожали друг другу, тогда наличие ферзя на любой клетке доски предполагает, что в той же вертикали, которой принадлежит клетка с этим ферзем, других ферзей уже не может быть. Кроме того, и в этой же горизонтали, где расположен этот ферзь, тоже не может быть другого ферзя.

То же самое можно сказать и про диагонали шахматной доски. Если в каком-то поле доски находится ферзь, то в каждой диагонали доски, которой принадлежит эта клетка (это поле доски), не может быть другого ферзя. Каждая из четырех угловых клеток доски принадлежит только одной диагонали доски. Именно те диагонали доски, через которые проходят угловые клетки доски, являются самыми большими диагоналями шахматной доски. Всего таких больших диагоналей — ровно две.

Одна большая диагональ — белопольная, вторая — чернопольная. Белопольная диагональ идет из левого верхнего угла доски в правый нижний, а чернопольная диагональ — из левого нижнего угла в правый верхний.

Если же клетка доски не находится в самом углу этой доски, то эта клетка принадлежит сразу двум диагоналям доски. Одна из этих диагоналей будет параллельна самой большой белопольной диагонали, а вторая — самой большой чернопольной диагонали.

Итак, как было сказано ранее, если мы ставим ферзя на какое-то поле доски, то каждая из диагоналей, которой принадлежит эта клетка, не может содержать другого ферзя.

Решение задачи о восьми ферзях означает, что необходимо расположить на доске ровно 8 ферзей одного цвета с учетом всего того, что была здесь сказано. При этом на доске будет следующая ситуация:

1. В каждой вертикали доски должен находиться ровно один ферзь.

2. В каждой горизонтали доски должен находиться ровно один ферзь.

3. Поскольку всех диагоналей на доске намного больше, чем 8, то нельзя сказать, что в каждой диагонали доски (большой и маленькой) нужно разместить одного ферзя. Но при этом можно однозначно сказать, что в каждой диагонали шахматной доски должно находиться не больше одного ферзя.

Глава 2. Реализация в Эксель

2.1. Минимум автоматизации

При решении задачи о восьми ферзях в Эксель можно начать с того, что использовать Эксель просто как холст, как тетрадку, используя минимум из всех возможностей Эксель.

Вначале создадим нужный файл, который будет отвечать за решение этой задачи. Это должен быть не простой файл, а файл с поддержкой макросов. Это значит, что у этого файла будет расширение: «xlsm». Перед расширением можно задать имя: «Восемь_ферзей».

Далее можно изменить ширину столбцов. Рекомендуемая ширина — около 2,6 условных единиц. Это необходимо сделать для того, чтобы каждая клетка Эксель была больше похожа на квадрат, чем на простой прямоугольник. Ведь каждая ячейка Эксель будет символизировать клетку шахматной доски, а клетка доски — это именно квадрат.

Итак, начнем с составления первого варианта решения задачи.

Выделим квадрат размером 8 на 8 клеток Эксель. Этот квадрат будет символизировать шахматную доску (рисунок 2.1).

Мы добавили внешние границы квадрату, который символизирует шахматную доску. Ячейка A1 Эксель (левая верхняя ячейка рисунка) будет означать поле a8 шахматной доски (тоже левое верхнее поле).

Теперь можно начать составлять возможные позиции, при которых на доске будет находиться 8 ферзей, не угрожающих друг другу.

Начнем с того, что предположим, что в первой позиции в верхней строке ферзь будет в первом (левом) столбце. Допустим, что цифра 1 будет символизировать ферзя, а какой-то символ (например, буква «х» будет означать те клетки, в которых ферзя точно не может быть.

Покажем эту ситуацию на рисунке 2.2.

Далее продолжим заполнять наш квадрат единицами. Следующая строка — вторая строка сверху. Ячейки A2 и B2 Эксель не могут содержать единицу, так как там уже находятся символы «х». Это значит, что самый первый столбец, где можно предполагать наличие единицы в строке 2 Эксель, — это столбец C Эксель, ячейка C2. Поставим там единицу, а также добавим символы «х» везде, где это необходимо. Покажем ситуацию на рисунке 2.3.

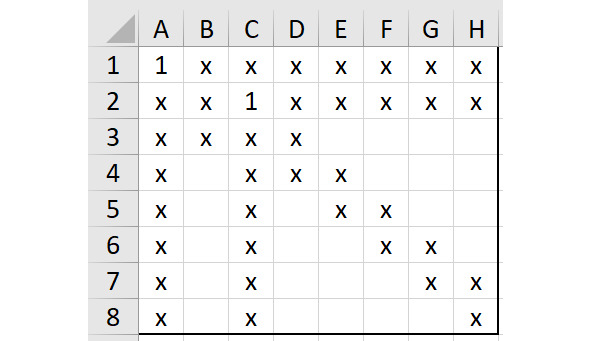
Затем заполняем строку 3. Здесь первые 4 ячейки уже заняты. Ближайшее свободное место, где можно разместить единицу, — это ячейка E3 Эксель. Поместим туда единицу, а также добавим символы «х» везде, где это будет необходимо. Покажем результат на рисунке 2.4.

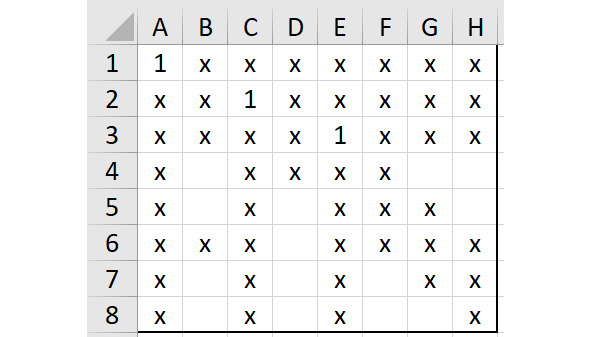
Затем надо заполнить строку 4 Эксель.

Но здесь можно просто применить логику. В строке 4 пока всего 3 свободные клетки. Но если мы поместим единицу в ячейку B4 или H4, то это будет значить, что для столбцов F и G не осталось ни одного варианта, которые позволили бы разместить в этих столбцах два ферзя, поскольку эти варианты не оставляют две свободные клетки в этих столбцах так, чтобы в этих клетках можно было разместить 2 ферзя, не угрожающих друг другу.

Но и в ячейке G4 тоже нельзя разместить единицу, поскольку в этом случае без вариантов останется столбец H. Напомню, что правильное решение задачи предполагает, что в каждом столбце должен быть ровно один ферзь (поскольку ферзей 8, и столбцов на доске тоже 8), поэтому ошибкой можно считать не только наличие двух и более ферзей в одном столбце, но и создание ситуации, при которой в каком-то столбце нет ферзя, но при этом нет возможности его там разместить, поскольку все ячейки одного столбца уже «простреливаются» другими ферзями.

Следовательно, можно прийти к выводу: в ситуации, изображенной на рисунке 2.3, в ячейке E3 размещать единицу нельзя, можно попробовать другие варианты. Начнем с варианта, когда единица будет в ячейке F3 (рисунок 2.5).

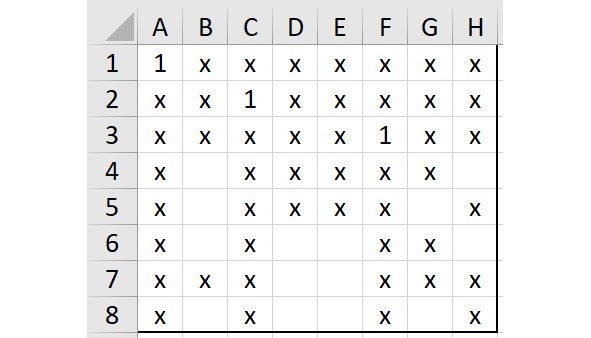
Попробуем поместить единицу в ячейку B4 (рисунок 2.6):

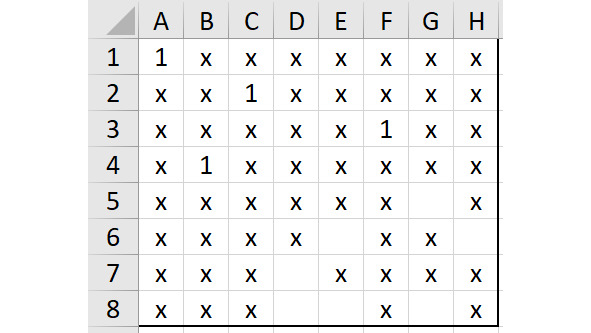
Здесь тоже можно рассуждать логически. В строке 5 Эксель есть только одно свободное место, но если туда поместить единицу, тогда в столбце H не останется вариантов для единицы. Это значит, что при ситуации на рисунке 2.5 в ячейку B4 нельзя поместить единицу. Попробуем найти другое место для единицы в строке 4 после той ситуации, что показана на рисунке 2.5. Между прочим, остается всего один вариант: нужно поместить единицу в ячейку H4. Покажем сложившуюся ситуацию на рисунке 2.7.

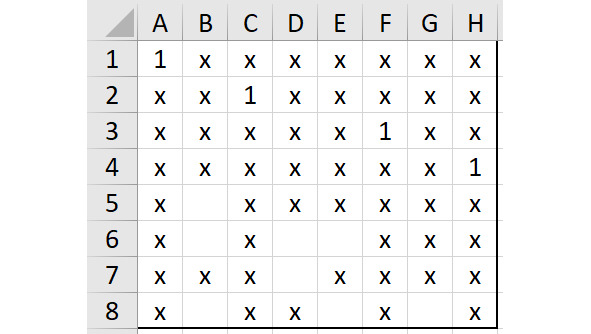
Если проанализировать эту ситуацию, то станет очевидным, что при такой расстановке единиц (ферзей) правильный ответ на задачу получить нельзя, потому что единственная свободная ячейка в столбце G закрывает все варианты для столбца E.

Если присваивать код каждой позиции, тогда этот код будет представлять собой 8-значное число. Первая цифра этого числа будет показывать, в каком столбце находится единица в первой (верхней) строке, вторая цифра — в каком столбце будет единица во второй сверху строке, и так далее.

Все возможные варианты нужно перебирать таким образом, чтобы каждый следующий вариант был чуть больше предыдущего, чтобы разница в числах, образованных кодами этих вариантов, была минимальной. В принципе, мы именно так и начали подбирать варианты: начали с того, что предположили, что первая единица будет в строке 1 и в столбце 1, а вторая — в строке 2 и столбце 3, следовательно, сам код начинался с сочетаний цифр 13…

Итак, только что мы перебрали несколько вариантов расстановки ферзей, и все они показали свою несостоятельность, ошибочность, отсутствие правильного решения. Хотя мы еще разобрали далеко не все возможные варианты, но если вспомнить о кодировке, которую мы присвоили всем возможным вариантам, то уже сейчас можно смело сказать: все варианты кода, которые начинаются с сочетаний цифр 135… и 136…, оказались ошибочными.

Теперь можно начать проверку варианта 137… Это значит, что в первой строке будет единица в столбце 1, во второй строке — в столбце 3, в третьей строке — в столбце 7.

Покажем этот вариант на рисунке 2.8, добавим на этом рисунке символы «х» везде, где это необходимо.

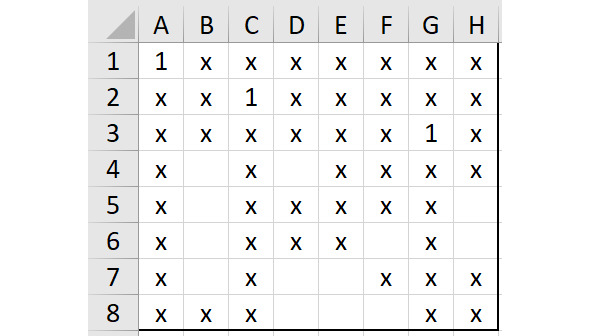
К сожалению, если чуть-чуть внимательней присмотреться к тому варианту, что показан на рисунке 2.8, можно его сразу же «забраковать»: ведь в строке 4 есть только две свободные клетки. Наличие единицы в ячейке B4 сделает отсутствие решений для столбцов D и E, поскольку там останутся только 4 пустые клетки, и они будут настолько близко друг к другу, что в них может расположиться только одна единица, и это значит что для второй единицы нет места. А если мы поставим единицу в ячейке D4, тогда похожая безвыходная ситуация будет создана для столбцов E и F, там останутся только 3 пустые клетки, в них нельзя разместить две единицы по всем ранее оговоренным правилам.

Это значит, что можно пробовать тестирование следующего кода, а именно. 138… (в первой строке единица в столбце 1, во второй строке — в столбце 3, в третьей строке — в столбце 8). Покажем эту ситуацию на рисунке 2.9, добавим к единицам нужные символы «х».

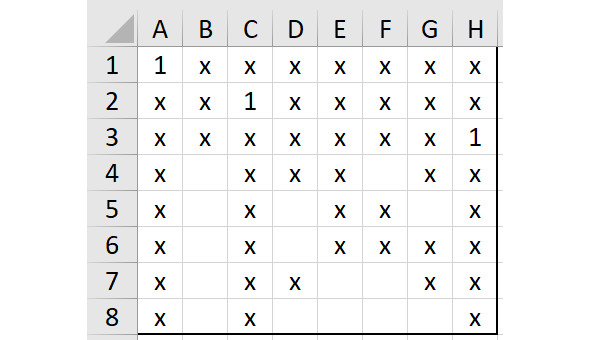
Строка 4. Тут две свободные клетки, но единица в ячейке B4 будет означать безвыходную ситуацию, потому что все свободные клетки в столбцах E и F не позволят разместить там два ферзя. Поэтому поставим единицу в ячейку F4. Останется единственное свободное поле в столбце G — оно будет в ячейке G8. Поставим там единицу и добавим символы «х» везде, где это необходимо. Покажем ситуацию на рисунке 2.10.

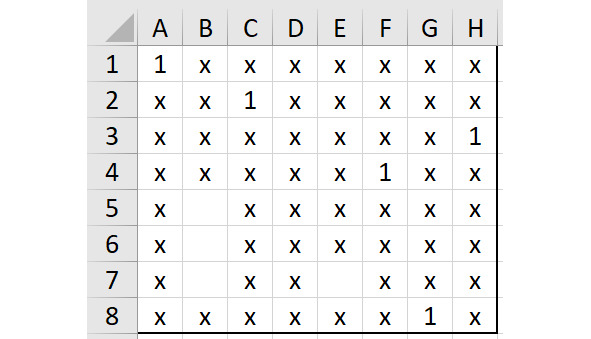
Но здесь тоже тупик, безысходность: нет свободных клеток для единицы в столбце D.

Снова надо искать следующие варианты.

Теоретически, следующий возможный код позиции будет начинаться с цифр 142… (варианты с 13… все закончились и показали свою несостоятельность).

Но тут возникает мысль: может быть, можно для начала хотя бы немного воспользоваться помощью компьютера и Эксель при поиске нужных вариантов.

Для начала сделаем следующее:

1. Добавим суммирование значений каждой строки и каждого столбца в том диапазоне, который символизирует шахматную доску. Здесь же можно с помощью условного формата особо выделать такие значения, которые превысят единицу (в каждой строке и в каждом столбце не может быть больше одной единицы).

2. Добавим подсчет количества символов «х» в каждом столбце того самого диапазона, который символизирует шахматную доску. Это можно сделать с помощью функции СЧЁТЕСЛИ. Вот, например, как будет выглядеть формула для ячейки A10, где будет осуществляться подсчет количества символов «х» в столбце 1 (в левом столбце, или в столбце A Эксель, в ячейках от A1 до A8). Покажем эту формулу на рисунке 2.11.

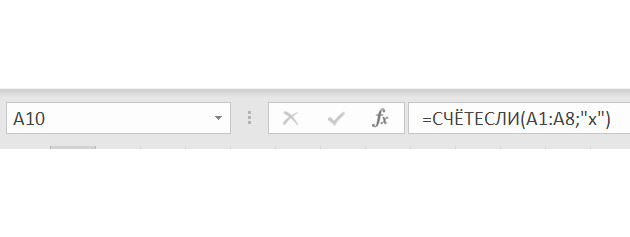
Здесь можно добавить условное форматирование, если особо выделить ячейки, сигнализирующее о наличии восьми символов «х» в одном столбце.

Теперь протестируем код 142… с учетом добавленных условных форматов (покажем ситуацию на рисунке 2.12).

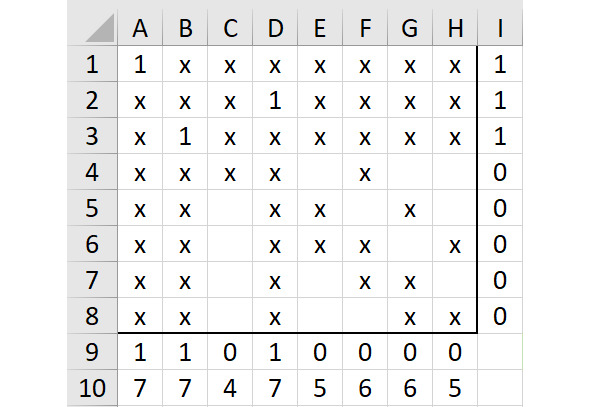
Сейчас надо заполнить строку 4. Вариант с единицей в ячейке E4 сразу исключаем, поскольку в этом случае без единиц останется весь столбец G.

Попробуем поместить единицу в ячейку G4 и добавим символы «х» везде, где это необходимо.

Можно также добавить условный формат тем суммам строк и столбцов внутри квадрата, символизирующего шахматную доску, если эта сумма будет равна нулю.

Покажем получившуюся ситуацию на рисунке 2.13.

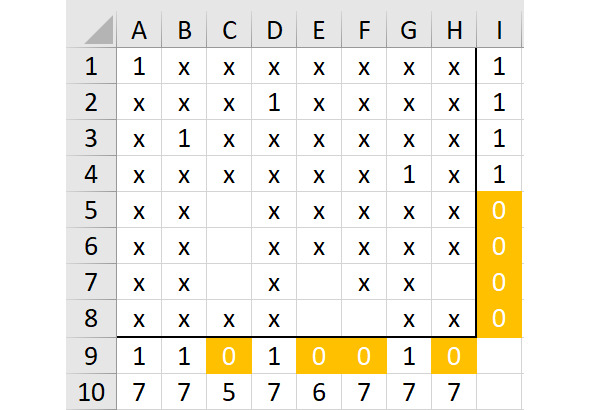
Этот вариант снова придется признать не правильным, потому что все пустые ячейки в столбцах E и F находятся слишком близко, в этих столбцах нельзя разместить две единицы.

Попробуем следующий вариант. После ситуации, показанной на рисунке 2.12, поместим единицу в ячейку H4. У полученной ситуации будет код: 1428…

Покажем ситуацию на рисунке 2.14.

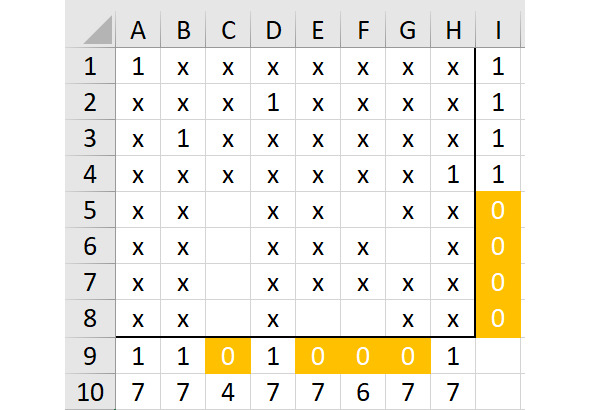
Здесь снова можно быстро увидеть, что единица в ячейке C5 не оставит вариантов для двух единиц в столбцах E и F. Правда, достаточно сказать только о том, что эта единица просто не оставит вариантов для единиц в столбце F. Поэтому строчку 5 начнем с единицы в ячейке F5. Хотя, если присмотреться к рисунку 2.14 чуть более внимательней, тогда станет очевидным: единица в ячейке F5 совсем не оставит вариантов для столбца G. А это значит, что картинка на рисунке 2.14 не имеет правильных решений.

Это значит, что правильный код не может начинаться с цифр 142…

Добавим контроль символов «х» в каждой строчке, добавим условное форматирование, чтобы особо выделить случаи, при которых в строке содержится 8 символов «х».

Затем найдем минимально возможную третью цифру кода, если точно известно, что при коде 142… правильных решений нет.

Покажем ситуацию на рисунке 2.15.

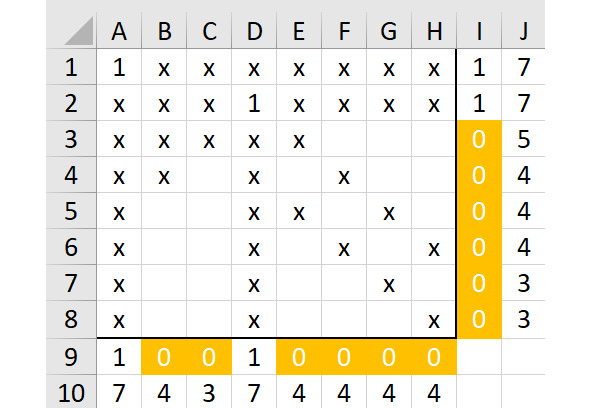
Здесь в ячейке B3 находится символ «х» не из-за того, что эта клетка «простреливается» стоящими рядом единицами, а просто потому, что мы этот вариант недавно уже исключили, он оказался непригодным.

Очевидно, что минимально возможный код в данной ситуации будет начинаться с цифр 146… Теперь добавим единицу в строку 3 и столбец 6, а также добавим символы «х» везде, где это необходимо (рисунок 2.16).

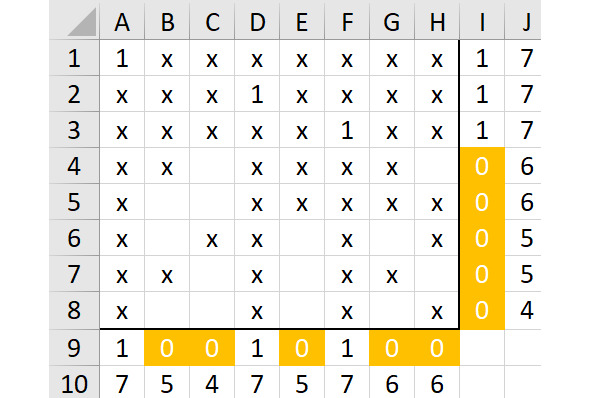
Затем нужно заполнить строку 4. Хотя в ней есть только две свободные клетки, можно быстро «отбраковать» ячейку C4, поскольку она не оставит вариантов для двух единиц в столбцах G и H. Это значит, что можно протестировать только ячейку H4. Покажем результат на рисунке 2.17.

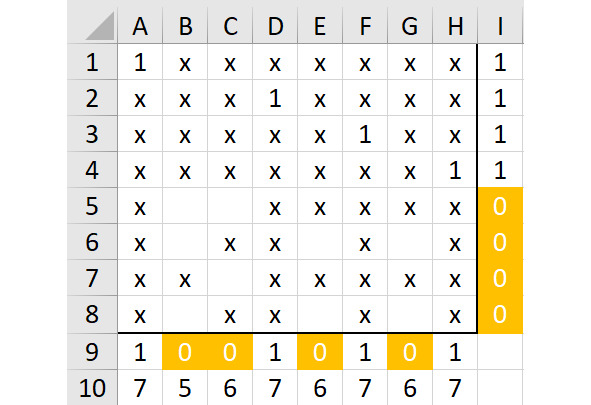
К сожалению, этот вариант тоже не приведет к решению задачи: свободные клетки в столбцах E и G не позволят там разместить две единицы по нашим правилам. А это значит, что все коды, которые начинаются с цифр 146…, являются неправильными.

Попробуем начать с кода 147… (рисунок 2.18).

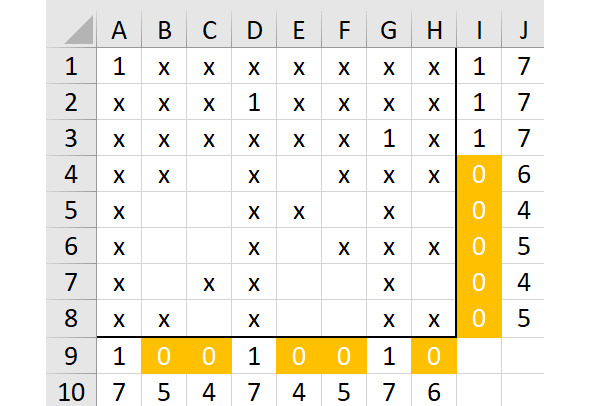
В строке 4 есть две свободные клетки. Попробуем начать заполнение с клетки C4 (рисунок 2.19).

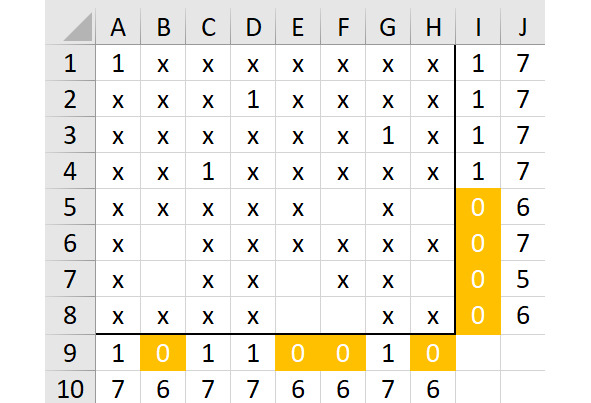
Далее лучше всего начать со строки 6, там только одна свободная клетка. Если говорить про строку 5, то единица в ячейке F5 не оставит вариантов для столбца H, но единица в поле H5 не оставит двух вариантов для столбцов E и F. Это значит, что снова «тупик», ищем другие варианты.

А следующий вариант такой. После ситуации на рисунке 2.18 надо поместить единицу в поле E4. Код полученной ситуации будет начинаться с цифр 1475…

Покажем это на рисунке 2.20.

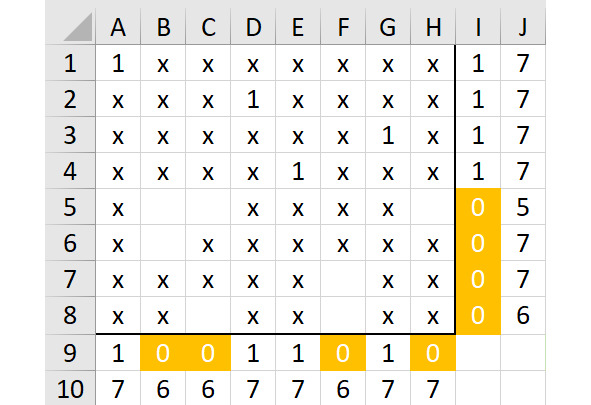
Давайте разберем чуть подробнее этот вариант. Единственная свободная ячейка в столбце H — это ячейка H5. Единица в H5 оставит единственное свободное поле в столбце F — это ячейка F8. Покажем это на рисунке 2.21, добавим на этом рисунке символы «х» везде, где это необходимо.

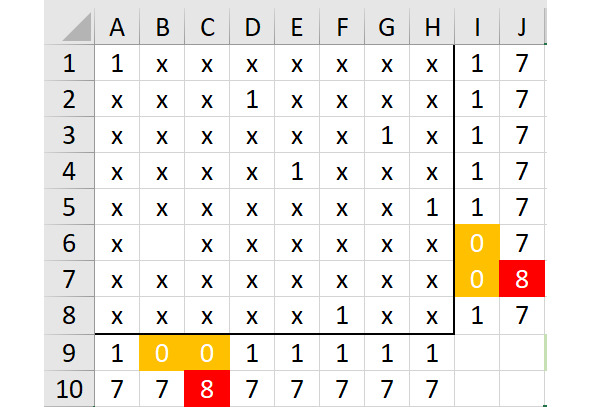
Вот здесь условный формат помог найти 2 ошибки: в строке 7 имеется 8 символов «х», то же самое и в столбце C. Это значит, что в этих линиях уже нет места для единиц, и снова вариант необходимо «забраковать».

Следующий вариант — это код 148…

Покажем его на рисунке 2.22.

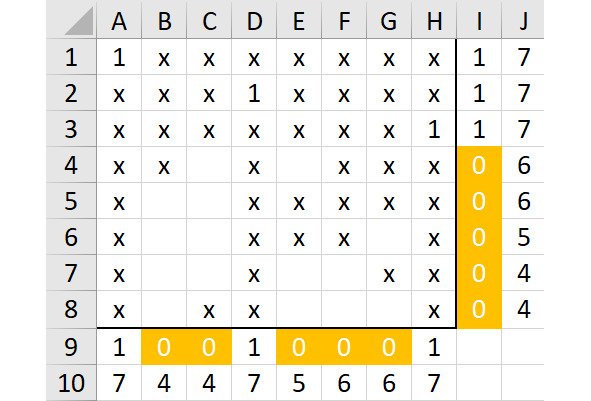
Но при этой ситуации, к сожалению, тоже нельзя получить правильного решения. Строка 4 — это всего две пустые ячейки. E4 «отметаем» стразу, потому что после этого в столбцах F и G останется слишком мало места, там нельзя разместить две единицы.

А если разместить единицу в ячейке C4, тогда похожая ситуация будет для столбцов E и F — в них тоже никак нельзя разместить две единицы.

Таким образом, все варианты, которые начинаются с кода 14…, показали свою ненадежность.

Теперь начнем с вариантов, которые начинаются с цифр 15…, и начнем с варианта 152… Покажем этот вариант на рисунке 2.23.

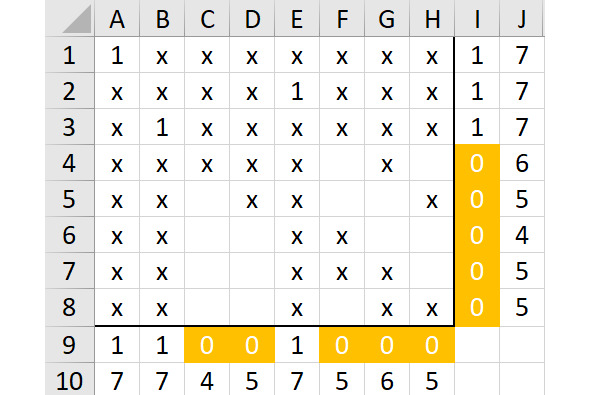
Затем поместим единицу в ячейку F4 и расставим символы «х» везде, где это необходимо, покажем результат на рисунке 2.24:

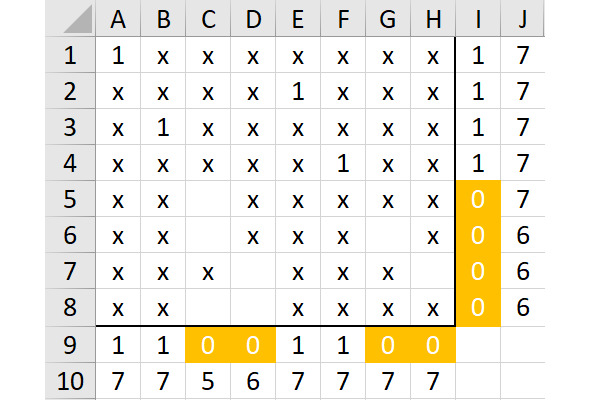
Этот вариант можно исключить уже на данном этапе, ведь очевидно, что в столбцах G и H две единицы размесить не получится.

Попробуем следующий вариант. Чисто теоретически, шифр (код) этого варианта должен начинаться с цифр 1528…

Покажем эту ситуацию, расставим символы «х» везде, где это необходимо) рисунок 2.25).

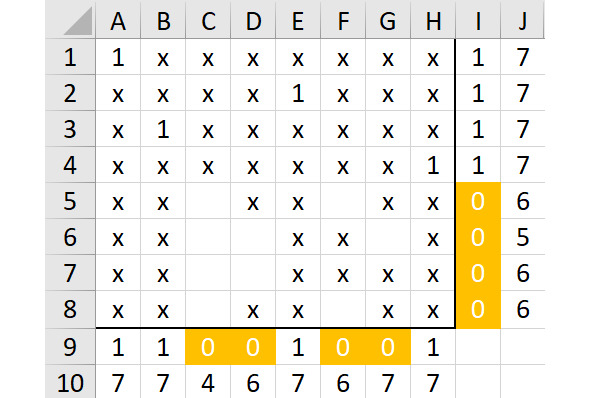
Но и здесь нельзя собрать нужную позицию. В строке 5 всего две свободные ячейки. Но единица в поле C5 не оставит вариантов для столбца F, а единица в ячейке F5 не оставит вариантов для столбца G.

Это означает, что надо искать другой вариант. по здравому размышлению, новый вариант должен начинаться с кодировки 157…

Покажем эту ситуацию на рисунке 2.26.

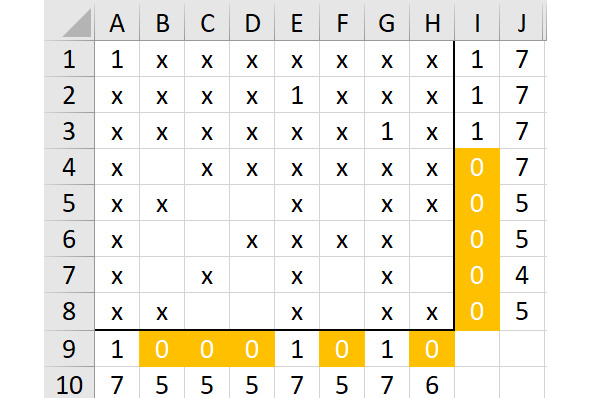
В данной ситуации в строке 4 есть только одна свободная клетка.

Поместим туда единицу.

Покажем ситуацию на рисунке 2.27.

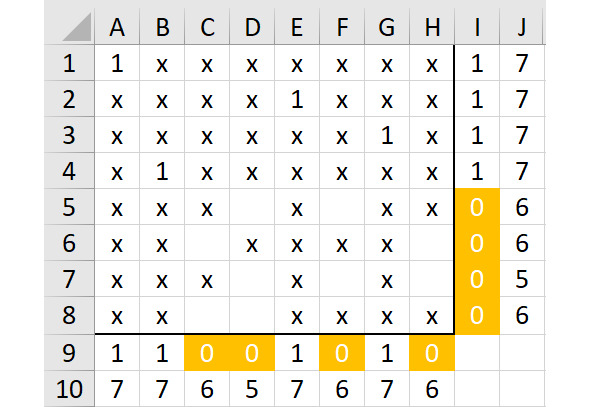
Далее нужно начать со столбца D, потому что единица в ячейке D5 или D7 не оставит ни одного варианта для единиц в столбце F. Это значит, что у нас остался один вариант для столбца D: это ячейка D8. После этого останется один вариант для столбца C, это ячейка C6.

Покажем полученный вариант на рисунке 2.28.

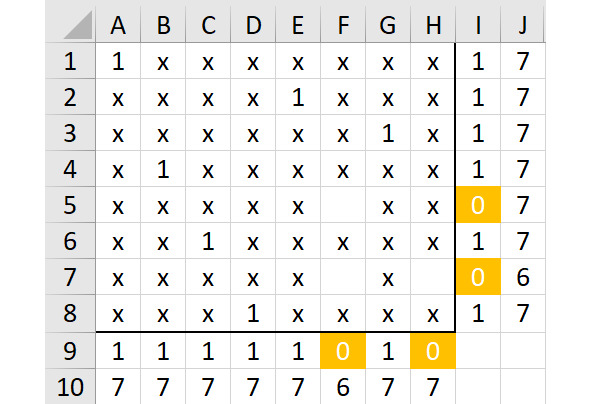
Но и здесь у нас «тупик»: три свободные ячейки во всем квадрате не позволят разместить две единицы по всем условиям задачи о восьми ферзях.

Итак, можно перейти к следующему варианту, код которого будет начинаться с цифр 158…

Покажем этот вариант на рисунке 2.29.

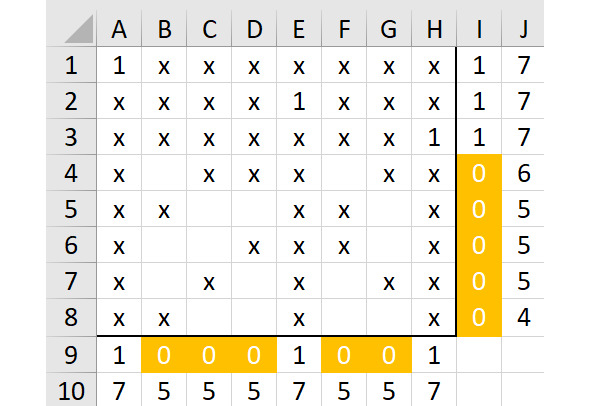
В строке 4 — всего две свободные ячейки.

Попробуем вариант, при котором единица будет в ячейке B4.

Покажем этот вариант на рисунке 2.30.

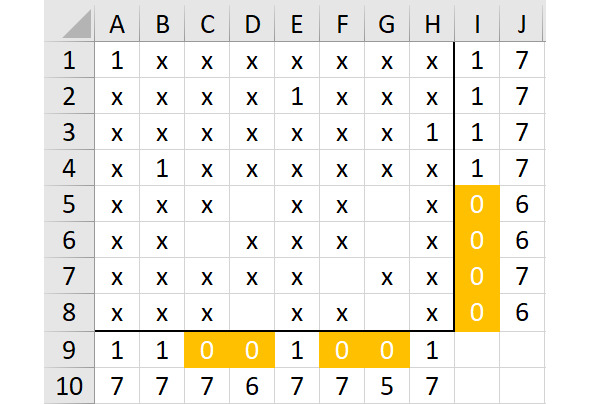
К сожалению, на этом рисунке тоже нет правильных вариантов. В строке 5 есть всего две свободные ячейки. Использование ячейки D5 будет означать, что без вариантов останется столбец C. Но единица в ячейке G5 оставит без вариантов весь столбец D.

Попробуем следующий вариант. Он будет начинаться с кодировки 1586…

Покажем этот вариант на рисунке 2.31.

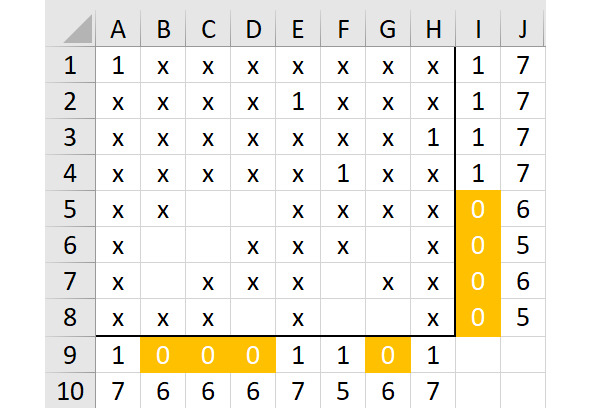
Далее попробуем поместить единицу в ячейку C5. Сразу же станет очевидным, что в столбце B останется место только в ячейке B7, а в столбце D — только в ячейке D8.

Покажем этот вариант на рисунке 2.32.

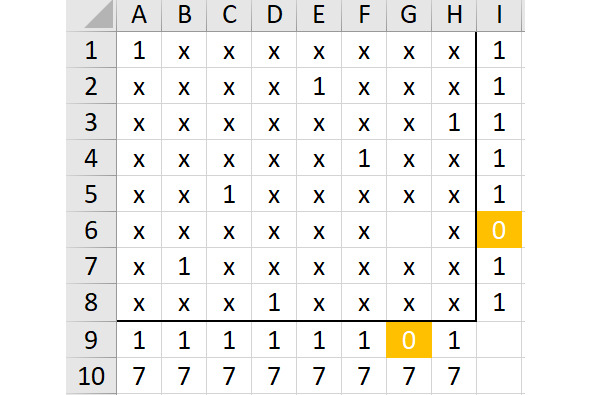
Итак, первый вариант найден, осталась одна свободная ячейка (G6), и эта ячейка не находится под «прострелом» других единиц.

Таким образом, код первого правильного варианта такой: 15863724.

Вот как будет этот вариант выглядеть на шахматной доске (рисунок 2.33):

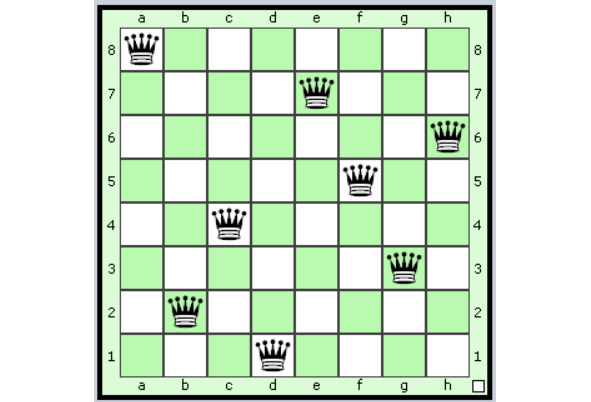
Этот вариант мы еще несколько раз покажем в данной книге (покажем, как он будет выглядеть в Эксель, а также покажем, как он будет выглядеть на доске с белыми ферзями).

Конечно же, можно и далее перебирать все возможные варианты вручную, но уже сейчас становится очевидным, что ручной перебор вариантов займет достаточно много времени. Поэтому лучше прекратить идею ручного поиска и составить такие макросы, которые значительно ускорят поиск необходимых вариаций. Просто сейчас мы показали краткий алгоритм того макроса, который будет искать эти самые варианты. Если закодировать каждый возможный вариант, то при переборе всех вариантов нужно исходить из того, что код каждого следующего варианта будет больше, чем код предыдущего.

Поиск вариантов будет более быстрым, если использовать возможности Эксель по максимуму.

2.2. Полная автоматизация (расчет кодов)

Для начала подготовим основной лист Эксель, в котором мы хотим осуществить перебор всех вариантов. Чтобы было удобней просчитывать количество единиц в каждой диагонали, которая имеется на шахматной доске, лучше всего продублировать каждую ячейку каждой диагонали. Если ячейки одной диагонали будут находиться в одном столбце Эксель, то суммирование диагонали станет более простым.

В принципе, не так сильно важно, как именно мы будем дублировать диагонали. В данной книге мы покажем только один из теоретически возможных вариантов.

На рисунке 2.34 покажем несколько дублеров диагоналей шахматной доски.