
Бесплатный фрагмент - Цифровые устройства
Учебник для колледжей
Введение
Предлагаемый учебник по предмету «Цифровые устройства» для колледжей, которые готовят специалистов связи, разработал преподаватель Алматинского колледжа связи Нсанов Мурат Алиевич (в настоящее время — преподаватель Алматинского Государственного колледжа транспорта и коммуникаций).
Первый вариант учебника был издан в Республике Казахстан в 1997 году для колледжей связи. Но ввиду бурного развития цифровой микроэлектроники, очень малого тиража и высокого спроса автор был вынужден существенно переработать и расширить учебник.
Данный второй вариант учебника прошел рецензирование со стороны преподавателей и специалистов, все необходимые этапы согласования и утверждения, был подготовлен к печати, включен в план издания, но во время финансового кризиса 2007—2010 гг. издание было приостановлено. В 2010 г. был переведен и издан в Республике Казахстан на казахском языке. Сейчас учебник готовится к переизданию, но только на казахском языке.
Предлагаемая разновидность второго варианта учебника переработана исключительно для использования в электронном виде, так как содержит множество цветного графического материала.
Учебник может быть полезен не только студентам и преподавателям учебных заведений, которые готовят специалистов связи, но и студентам других отраслей, где используются устройства цифровой микроэлектроники.
***
Информатизация общества — одна из важнейших задач, стоящих перед нашей страной. Решение этой задачи невозможно без интенсивного развития средств передачи и обработки информации.
Процессы передачи и обработки информации целесообразно вести при дискретном характере их представления, так как цифровые методы обеспечивают меньшую зависимость качества передачи от расстояния между пользователями, большую гибкость и простоту организации обмена информацией, значительно большую точность и помехоустойчивость, простоту управления и легкость автоматизации. Поэтому в настоящее время любая современная техника связи: радио- и телевизионная, телефонная, телеграфная, аппаратура многоканальной связи, а также контрольная, измерительная и диагностирующая аппаратура в основном состоит из микросхем самых разнообразных цифровых устройств. Это приводит к острой необходимости базовой подготовки техников связи в области цифровых устройств, которая требуется при изучении, эксплуатации, ремонте и наладке аппаратуры связи. Именно изучению принципов построения и функционирования цифровых устройств, применяемых в технике связи, и посвящен данный учебник.
Предмет содержит четыре раздела: первый раздел знакомит учащихся с основными понятиями и элементной базой цифровой техники, во втором разделе изучаются принципы построения и функционирования цифровых устройств, в третьем и четвертом — цифровые устройства соответственно комбинационного (шифраторы и дешифраторы, мультиплексоры и демультиплексоры, преобразователи кодов, сумматоры, субтракторы, компараторы, АЛУ, устройства и узлы контроля) и последовательностного (интегральные триггеры, регистры и регистровые файлы, счетчики, распределители, запоминающие устройства) типа.
Каждую тему обязательно следует сопровождать проведением практических занятий и (или) лабораторных работ (Сборник лабораторных работ тоже размещен в Интернете) для закрепления полученных знаний, а также для получения практических умений и навыков работы с цифровыми микросхемами. Эту же цель преследует и курсовое проектирование, предусмотренное в программе предмета и учебных планах. Хотя база примеров учебника дается в основном на микросхемах российской серии КР1533 с указанием функциональных аналогов американской фирмы «Texas Instruments» и некоторых других фирм, любой колледж сравнительно легко может адаптировать излагаемый материал для проведения практических занятий и лабораторных работ к имеющейся у него материально-технической базе.
Небольшая часть учебника, отмеченная знаками «***» и напечатанная более мелким шрифтом, содержит достаточно важные в современных условиях, но пока не включенные в программу предмета темы ко времени работы над книгой из-за недостатка времени по учебным планам. Они здесь даются для расширения и углубления знаний учащихся.
***
Специалисты любого направления деятельности сталкиваются с различными действующими в мире стандартами, что представляет определенные трудности при эксплуатации оборудования производства различных стран и фирм. Это в полной мере относится к условным графическим обозначениям элементов и устройств цифровой техники. Здесь действуют стандарты ISO (Международная организация по стандартизации), CEN (Европейский комитет по стандартизации), IEC (Международная электротехническая комиссия), CENELEC (Европейский комитет по электротехническим стандартам) и др., а также стандарты различных стран: ГОСТ (Российская Федерация, Республика Казахстан и некоторые другие страны), DIN (Германия), BS (Великобритания), AFNOR (Франция), JIS (Япония), KOR (Республика Корея), стандарты США — ANSI (Американский национальный институт стандартизации), EIA (Альянс отраслей электронной промышленности), IEEE (Институт инженеров по электротехнике и электронике) и т. д.
Поэтому в данной книге указаны стандарты изображения элементов и устройств цифровой микроэлектроники в соответствии со стандартами РФ, РК и др. (условно названы «восточные») а также в соответствии со стандартами США, Республики Корея, Германии и др. (условно названные «западные»).
С глубокой признательностью автор примет любые замечания, предложения и поправки специалистов, коллег-преподавателей и студентов, которые будут полезны при переработке данной книги в процессе дальнейшего развития цифровой техники.
Если появятся какие-либо вопросы к автору, то можно непосредственно связаться с ним по адресу электронной почты: murat.nsanov@gmail.com.
Как сказано в аннотации, автор рекомендует использовать формат fb2 и читалку CoolReader. При этом для наиболее удобного чтения желательно установить черный шрифт на белом фоне. На взгляд автора лучше использовать шрифт Times New Roman размером 18. Обязательно нужно отключить переносы: при настройке в позиции «Текст» — «Переносы» выбрать «Disable hyphenation».
Каждый читатель устанавливает в читалках наиболее удобные ему параметры книги, поэтому ни автор, ни издательство не может убрать пустые места и ликвидировать некоторые другие недостатки, зависящие от установленных параметров.
Раздел 1. Логические элементы
1.1. Общие сведения о цифровых сигналах и цифровых устройствах
В современных цифровых устройствах (ЦУ) мы имеем дело лишь с двумя видами сигналов: логического 0 и логической 1. Эти цифровые сигналы обычно представляются в потенциальной форме с положительной логикой сигналов, когда сигналу логического 0 соответствует положительное постоянное напряжение низкого уровня, а сигналу логической 1 — положительное постоянное напряжение более высокого уровня. Например, для микросхем серии КР1533 сигналу логического нуля соответствует напряжение не более +0,8 В, а сигналу логической 1 — напряжение не менее +2 В. В дальнейшем никогда не следует забывать о физическом смысле цифровых сигналов логического 0 и логической 1: это постоянное напряжение разной величины!
Любая информация в ЦУ может быть представлена совокупностью определенного количества сигналов логического 0 и логической 1 в двух формах:
— Последовательной, когда в одной цепи идет последовательное чередование сигналов через равные тактовые временные интервалы Т. Например так, как показано на рис. 1.1.
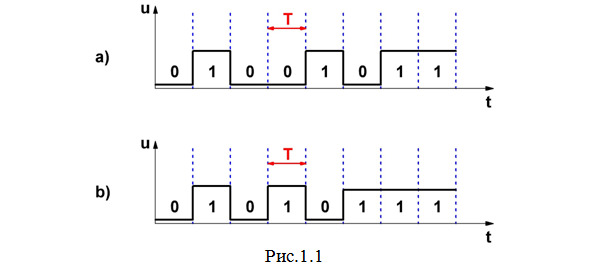
— Параллельной, когда в разных нескольких цепях одновременно действуют соответствующие сигналы, причем каждый сигнал в своей цепи.
Такая комбинация цифровых сигналов, несущая какую-либо информацию, называется кодовым словом или просто кодом. В англоязычной литературе она называется просто словом (word). Таким образом, изображенные на рис.1.1а и рис.1.1b совокупности сигналов представляют собой кодовые слова 01001011 и 01010111. Именно так выражаются буквы К и W английского алфавита в коде КОИ-8 (KOI-8). С помощью кодовых слов можно представить не только буквы, но и другие знаки, а также рисунки (в том числе схемы и диаграммы), звуковую информацию (речь, музыку), телевизионные изображения и т. д.
Устройства, предназначенные для передачи, приема и обработки цифровой информации (то есть информации, выраженной кодовыми словами), называются цифровыми устройствами.
По способу функционирования ЦУ могут быть двух видов:
— Комбинационные ЦУ, не обладающие памятью (т.е. не способные запоминать результаты выполненных операций). Здесь значения сигналов на выходах (выходное кодовое слово) определяются только совокупностью сигналов на входах (входным кодовым словом) в данный момент времени.
— Последовательностные ЦУ (устройства с памятью), способные запоминать результаты выполненных операций и хранить эту информацию на своих выходах в виде кодовых слов. У них значение выходного кодового слова определяется не только входным кодовым словом в данный момент времени, но и хранившимся на выходах кодовым словом в предыдущий момент времени.
1.2. Общие сведения о логических элементах
Любые узлы цифровой аппаратуры строятся с помощью устройств, которые называются логическими элементами (ЛЭ). В основном применяются лишь 5 ЛЭ, общие сведения о которых приведены в табл.1.1.
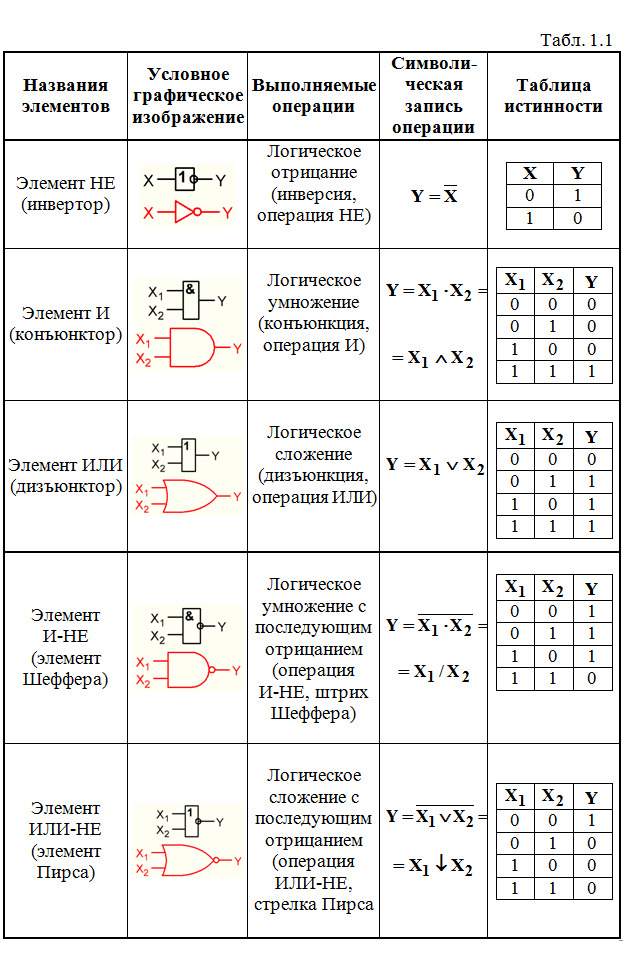
П р и м е ч а н и е. В колонке «Условное графическое изображение элемента» приведены два рисунка каждого элемента: вверху — в соответствии с «восточным» стандартом, внизу красным цветом — в соответствии с «западным» стандартом (см. Введение).
Входы элементов всегда изображаются слева. Сигналы, которые подаются на входы, называются логическими переменными или логическими аргументами и обозначаются обычно буквами «Х» с нумерацией: Х1, Х2, Х3 и т. д.
Выходы элементов всегда изображаются справа. Сигналы, которые формируются на выходах, называются логическими функциями и обозначаются обычно буквами «Y» или f (X).
В соответствии с «восточным» стандартом ЛЭ и любые другие устройства цифровой микроэлектроники поворачивать нельзя, по «западному» стандарту — можно.
ЛЭ выполняет указанную в табл.1.1 соответствующую операцию со входными сигналами, а результат выполненной операции формируется на его выходе.
Элементы НЕ всегда имеют только один вход.
Элементы И, ИЛИ, И-НЕ, ИЛИ-НЕ могут иметь не только два (как показано в табл.1.1), но и три, и четыре входа (иногда даже больше — до 8). Соответственно элементы при этом будут выполнять операции с двумя, тремя, четырьмя и более входными сигналами (смотрите тему 1.5).
Элементы ИЛИ в основном (но не всегда!) имеют лишь два входа. Если требуется выполнить логическое сложение трех и более сигналов, то используются несколько элементов ИЛИ с двумя входами.
С настоящего момента следует иметь в виду, что результат логического сложения сигналов 1 \/ 1 = 1 отличается от результата арифметического сложения тех же сигналов 1 + 1 = 2. Поэтому не следует путать эти две разновидности операции сложения.
Элементы, которые имеют два или более входа, в название элемента должны включать цифру, которая указывает на количество входов, например: элемент 2И (элемент И с двумя входами), элемент 3ИЛИ-НЕ (элемент ИЛИ-НЕ с тремя входами) и т. д.
Смысл названий элементов заключается в следующем:
— Элемент НЕ. На выходе элемента формируется НЕ такой сигнал, какой подается на вход.
— Элемент И. На выходе элемента формируется сигнал логической 1 только тогда, когда сигналы логической 1 поступают И на первый, И на второй, И на все остальные входы.
— Элемент ИЛИ. На выходе элемента формируется сигнал логической 1, когда сигнал 1 поступает ИЛИ на первый вход, ИЛИ на второй вход, ИЛИ на любой другой вход, ИЛИ на несколько входов одновременно.
— Элемент И-НЕ сначала выполняет логическое умножение (операцию И) входных сигналов, а затем полученный результат инвертирует (делает операцию НЕ). Структура элемента 2И-НЕ приведена на рис.1.2а.
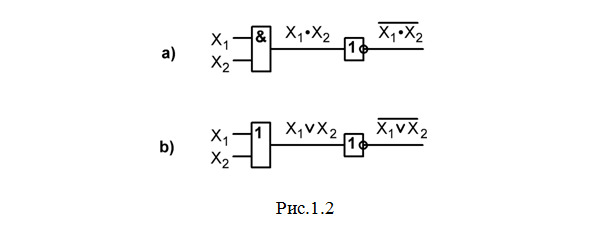
— Элемент ИЛИ-НЕ сначала выполняет логическое сложение (операцию ИЛИ) входных сигналов, а затем полученный результат инвертирует (делает операцию НЕ). Структура элемента 2ИЛИ-НЕ приведена на рис.1.2b.
Таблица, полностью описывающая работу логического элемента или любого другого ЦУ, называется таблицей истинности: здесь показываются все возможные комбинации сигналов, которые могут поступать на входы, и что при этом получается на выходах. Ни в коем случае не следует заучивать наизусть таблицы истинности логических элементов, нужно только понять смысл выполняемой элементом операции!
Приведенные в табл.1.1 таблицы истинности элементов И, ИЛИ, И-НЕ, ИЛИ-НЕ составлены для двухвходовых элементов. Рекомендуется учащимся попытаться самостоятельно составить таблицы истинности этих элементов, если они будут иметь три и более входа. При этом следует иметь в виду, что количество возможных комбинаций входных сигналов увеличится и будет составлять 2n, где n — количество входов.
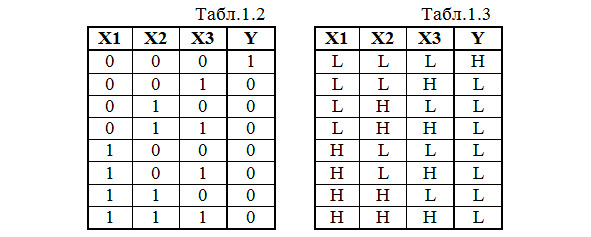
Пример 1. Составим таблицу истинности элемента 3ИЛИ-НЕ (табл.1.2):
В технической и справочной литературе таблицы истинности могут иметь несколько иной вид. Вместо сигналов логического 0 и логической 1 могут стоять знаки:
— логический 0: Н (низкий) или L (low — низкий) уровень напряжения;
— логическая 1: В (высокий) или Н (high — высокий) уровень напряжения.
Например, таблица истинности этого же элемента 3ИЛИ-НЕ может выглядеть следующим образом (табл.1.3).
Изучением внутреннего устройства элементов мы здесь заниматься не будем, т.к. это представляет практический интерес лишь для разработчиков этих элементов. Нам достаточно знать только следующее:
— что все элементы построены на прекрасно знакомых любому учащемуся компонентах (резисторах, транзисторах, диодах и т.д.) по интегральной технологии;
— какие транзисторы использованы для построения интересующего нас элемента и по какой схеме они включены (см. тему 1.4).
Если все-таки появится необходимость ознакомиться с внутренней структурой какого-либо элемента, то следует обратиться к соответствующей справочной или учебной литературе.
Цифровые устройства, построенные с помощью логических элементов, могут работать в двух режимах:
— статическом, когда сигналы на входах и выходах элементов удерживаются неизменными достаточно длительное время;
— динамическом, когда сигналы на входах и выходах элементов меняются (частота изменения достигает порядка ГГц в современных устройствах) в процессе работы.
Контроль работы ЦУ, работающих в статическом режиме, производится очень просто путем измерения уровней напряжения на входах и выходах элементов обычными электронными вольтметрами (можно и осциллографами). А вот контроль работы ЦУ, работающих в динамическом режиме, можно производить только с помощью осциллографов, сравнивая полученные осциллограммы с эталонными временными диаграммами.
В цифровой технике временной диаграммой является график зависимости значений сигнала на входе или на выходе элемента или устройства (напомним, что любое значение сигнала — это постоянное напряжение) от времени.
После окончания изучения данной темы учащиеся должны показать знание основных логических элементов: их название, условное графическое изображение, выполняемые операции и их символическую запись; уметь определять в статическом режиме значения сигналов на выходах логических элементов в схемах ЦУ при наличии определенных сигналов на входах; уметь чертить временные диаграммы, описывающие работу ЦУ в динамическом режиме.
Пример 2: Дана схема ЦУ, построенная на логических элементах (рис.1.3).
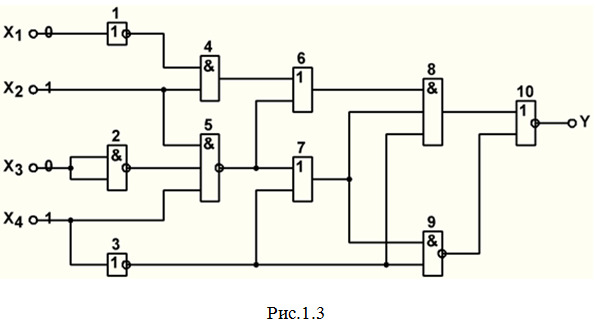
З а д а н и я:
1. Указать названия всех элементов, и какие операции они выполняют.
2. Исследовать работу схемы в статическом режиме: по заданным (рис.1.3) значениям сигналов на входах ЦУ определить значения сигналов на входах и выходах всех элементов.
3. Проанализировать работу схемы в динамическом режиме: построить временные диаграммы для всех элементов при заданных (рис.1.4) изменениях входных сигналов. Для некоторого упрощения уровень логического нуля примем равным точно 0.
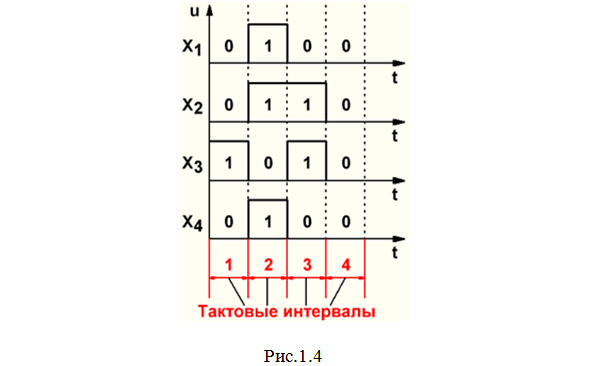
О т в е т ы
1. Названия элементов и выполняемые операции (номер каждого элемента стоит над его изображением в схеме):
1,3 — элементы НЕ, выполняют операцию логического отрицания (инвертирование).
4 — элемент 2И, выполняет операцию логического умножения.
8 — элемент 3И, выполняет операцию логического умножения.
6,7 — элементы 2ИЛИ, выполняют операцию логического сложения.
2,9 — элементы 2И-НЕ, выполняют операцию логического умножения с последующим инвертированием полученного результата.
5 — элемент 3И-НЕ, выполняет операцию логического умножения с последующим инвертированием полученного результата.
10 — элементы 2ИЛИ-НЕ, выполняет операцию логического сложения с последующим инвертированием полученного результата.
2. Исследование работы схемы в статическом режиме. Значения сигналов на выходах всех элементов показаны на рис.1.5.
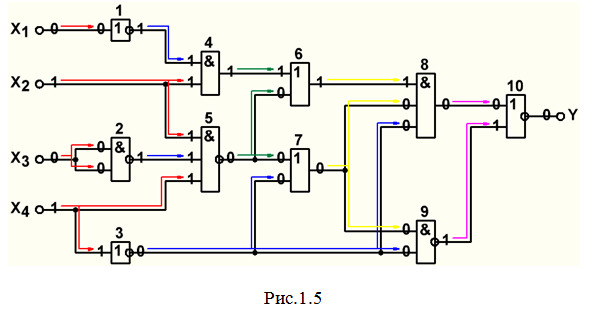
Рассмотрим более подробно происходящие процессы.
Со входов Х1, Х2, Х3, Х4 указанные в задании сигналы (рис.3) поступают на входы элементов (на какие элементы — указано красными стрелками на рис.1.5).
а) Сначала срабатывают элементы 1, 2 и 3, стоящие в 1-й колонке:
— Элемент 1 инвертирует поступающий на его вход сигнал 0 и на выходе формирует сигнал 1, который далее проходит на вход элемента 4 (прохождение сигнала указано синей стрелкой).
— Элемент 2 выполняет операцию И-НЕ: сначала умножает поступающие на его входы сигналы 0 и 0, а затем полученный результат инвертирует. В результате на выходе элемента формируется сигнал 1, который далее проходит (синяя стрелка) на вход элемента 5.
— Элемент 3 инвертирует поступающий на его вход сигнал 1 и на выходе формирует сигнал 0, который далее проходит (синие стрелки) на входы элементов 7, 8 и 9.
б) На следующем этапе срабатывают элементы 4 и 5, стоящие во 2-й колонке:
— Элемент 4 выполняет умножение поступающих на его входы сигналов 1 и 1. В результате на выходе элемента формируется сигнал 1, который далее проходит (зеленая стрелка) на вход элемента 6.
— Элемент 5 выполняет операцию И-НЕ: сначала умножает поступающие на его входы три сигнала 1, 1 и 1, а затем полученный результат инвертирует. В результате на выходе элемента формируется сигнал 0, который далее проходит (зеленые стрелки) на входы элементов 6 и 7.
в) Далее срабатывают элементы 6 и 7, стоящие в 3-й колонке:
— Элемент 6 выполняет логическое сложение поступающих на его входы сигналов 1 и 0. В результате на выходе элемента формируется сигнал 1, который далее проходит (желтая стрелка) на вход элемента 8.
— Элемент 7 выполняет логическое сложение поступающих на его входы сигналов 0 и 0. В результате на выходе элемента формируется сигнал 0, который далее проходит (желтые стрелки) на входы элементов 8 и 9.
г) Затем срабатывают элементы 8 и 9, стоящие в 4-й колонке:
— Элемент 8 выполняет умножение поступающих на его входы трех сигналов 1, 0 и 0. В результате на выходе элемента формируется сигнал 0, который далее проходит (розовая стрелка) на вход элемента 10.
— Элемент 9 выполняет операцию И-НЕ: сначала умножает поступающие на его входы сигналы 0 и 0, а затем полученный результат инвертирует. В результате на выходе элемента формируется сигнал 1, который далее проходит (розовая стрелка) на вход элемента 10.
д) В конце срабатывает элемент 10, который выполняет операцию ИЛИ-НЕ: сначала делает логическое сложение поступающих на его входы сигналов 0 и 1, а затем полученный результат инвертирует. В результате на выходе элемента формируется сигнал 0, который проходит на выход схемы Y.
3. Анализ работы схемы в динамическом режиме.
а) Сначала определим, как меняются сигналы на выходе элемента 1 (рис.1.6а). На вход этого элемента сигналы поступают со входа X1 (показано красным цветом на рис.1.6а), которые меняются следующим образом: в первом такте — 0, во втором — 1, в третьем — 0, в четвертом — 0. Элемент 1 — это элемент НЕ, который инвертирует данные поступающие сигналы и на своем выходе Y1 формирует последовательность 1011 (на рис.1.6а показано синим цветом).
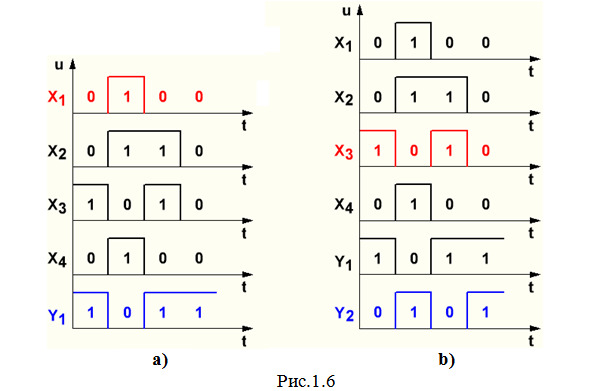
б) Теперь рассмотрим изменение сигналов на выходе элемента 2 (рис.1.6b). На оба входа этого элемента поступают сигналы со входа X3 (показано красным цветом на рис.1.6b), которые меняются так: в первом такте — 11, во втором — 00, в третьем — 11, в четвертом — 00. Элемент 2 — это элемент 2И-НЕ, который выполняет умножение данных поступающих сигналов с последующим инвертированием полученных результатов и на своем выходе Y2 формирует последовательность 0101 (на рис.1.6b показано синим цветом).
По полученным результатам можно сделать еще один важный вывод: элементы И-НЕ (а также элементы ИЛИ-НЕ) с объединенными входами выполняют функцию элемента НЕ, т.е. производят инвертирование поступающих сигналов.
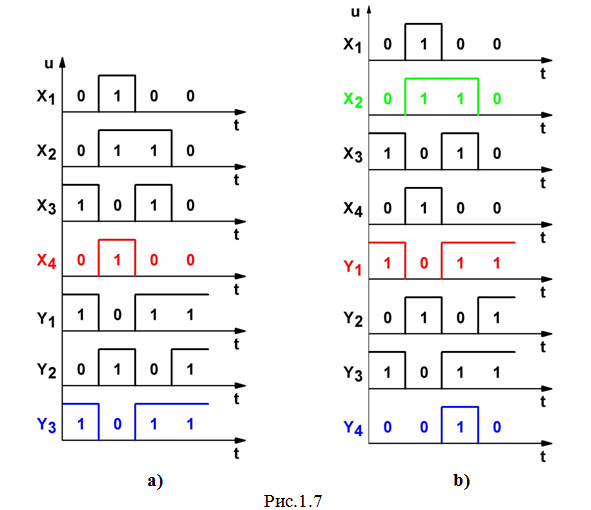
в) Далее проанализируем изменение сигналов на выходе элемента 3 (рис.1.7a). На вход этого элемента сигналы поступают со входа X4 (показано красным цветом на рис.1.7a), которые меняются следующим образом: в первом такте — 0, во втором — 1, в третьем — 0, в четвертом — 0. Элемент 3 — это элемент НЕ, который инвертирует данные поступающие сигналы и на своем выходе Y3 формирует последовательность 1011 (на рис.1.7a показано синим цветом).


1.3. Интегральные микросхемы (ИМС). Маркировка ИМС
Логические элементы выпускаются в виде интегральных микросхем (ИМС или просто ИС). ИМС называют схему, компоненты которой нераздельно связаны и электрически соединены между собой так, что все устройство рассматривается как единое целое. Функциональную сложность любой ИМС принято характеризовать степенью интеграции — количеством компонентов N в микросхеме. По степени интеграции различают:
— ИМС малой степени интеграции: менее 100;
— ИМС средней степени интеграции: N = 100 ÷ 1000;
— БИС (большие интегральные схемы): N = 1000 ÷ 10000;
— СБИС (сверхБИС): N = 10000 ÷ 106 (миллион);
— УБИС (ультраБИС): N = 106 ÷ 109 (миллиард);
— ГБИС (гигаБИС): более 109.
В данной книге рассматриваются в основном элементы цифровой техники и ЦУ, выпускаемые преимущественно в виде ИМС средней степени интеграции и БИС.
Внимание! Следует всегда иметь в виду, что элементы цифровой техники и различные цифровые устройства выпускаются как в виде отдельных микросхем средней степени интеграции и БИС, так и входят составными частями в микросхемы БИС, СБИС, УБИС и ГБИС многофункциональных ЦУ. Например: в АЛУ, интерфейсы, микропроцессоры и другие специализированные микросхемы отдельных отраслей техники, которые изучаются как в данном предмете, так и в соответствующих специальных курсах. Но в любом случае принцип их работы, структура и назначение выводов остаются одинаковыми!
Рассмотрим структуру маркировки ИМС российского производства (в других странах каждая фирма, выпускающая микросхемы, применяет свою систему условных обозначений; смотрите, например, Приложение 2 или [Л9, Л16]).
Например, ИМС имеет нанесенную на корпусе маркировку: КР1533ЛИ2. Структуру такой маркировки можно условно разделить на 4 части:
КР — одна или две буквы (их может и не быть). Здесь буква К при ее наличии показывает, что данная ИМС выпускается для широкого применения. Если есть другая буква, то она указывает материал и тип корпуса или его отсутствие. Наиболее часто в цифровой технике встречаются: М — керамический микрокорпус; Р — пластмассовый корпус типа 2.
1533 — три или четыре цифры номера серии, по которому можно судить о структуре ИМС (смотрите тему 1.4). Кроме этого, первая цифра номера серии показывает конструктивно-технологическое исполнение ИМС: 1,5,7 — полупроводниковые (7 — бескорпусные); 3 — прочие (пленочные, керамические и т.д.); 2,4,6,8 — гибридные, где отдельные компоненты изготовлены по разной технологии.
Цифровые ИМС в основном выполнены по полупроводниковой технологии, поэтому имеют первую цифру номера серии 1 или 5.
П р и м е ч а н и е. Вопросы, посвященные конструктивно-технологическому исполнению ИМС, типам и материалам их корпусов освещаются в предмете «Учебная электромонтажная практика». При желании этот же материал можно найти практически в любом справочнике по ИМС.
ЛИ — две буквы, указывающие функциональное назначение ИМС. Для микросхем, содержащих различные логические элементы, эти буквы приведены в теме 1.5. После окончания изучения предмета все учащиеся должны будут знать данную часть маркировки ИМС для основной группы ЦУ.
2 — одна-три цифры порядкового номера ИМС в данной серии по функциональному признаку.
В конце маркировки иногда добавляется еще одна буква разброса параметров (численные значения разброса конкретных параметров определяются по справочнику) у двух или более одинаковых микросхем данной серии.
1.4. Структура ИМС
Работающие в настоящее время ИМС цифровой техники по принципу построения могут иметь следующую структуру на кремниевой основе:
— ТТЛ (транзисторно-транзисторная логика). Здесь используются обычные биполярные транзисторы, включенные по наиболее распространенной схеме с общим эмиттером (ОЭ). Такую структуру имеют, например, ИМС серий 133, 155.
— ТТЛШ (ТТЛ с диодами Шоттки). Применение здесь диодов Шоттки, включенных между коллектором и базой транзисторов, не позволяет транзисторам входить в режим насыщения. Это приводит к ускорению переключения транзисторов и, следовательно, к повышению быстродействия ИМС. Микросхемы ТТЛШ-структуры условно делятся на две группы: а) маломощные (например, ИМС серий 533, 555, 1533); b) быстродействующие (например, ИМС серий 530, 531, 1531).
— ЭСЛ (эмиттерно-связанная логика). Здесь также используются обычные биполярные транзисторы, но они включены по другой схеме в отличие от ИМС структур ТТЛ и ТТЛШ. В микросхемах ЭСЛ-структуры используется принцип переключения токов в транзисторах, работающих на общую эмиттерную нагрузку (отсюда и название структуры). Другими словами, здесь базовым элементом является дифференциальный усилитель. Такую структуру имеют, например, ИМС серий 500, 1500, 1590.
— МОП (металл-окисел-полупроводник) или МДП (металл-диэлектрик-полупроводник). Это схемы на полевых транзисторах р или n-типов с обогащенным каналом, КМОП (комплементарные МОП) -схемы на дополняющих транзисторах. Например, ИМС серий 561, 564, 1554, 1561, 1564, 5514, 5564, 5584.
Кроме этого, существуют микросхемы на основе арсенида галлия GaAs, выполненные на полевых транзисторах с затвором Шоттки. Например, ИМС серии 6500.
1.5. ИМС логических элементов
П р и м е ч а н и е: Аналоги приведенных ниже микросхем производства в основном американской фирмы «Texas Instruments» приведены в Приложении 3.
У микросхем логических элементов третья часть маркировки начинается с буквы Л, а вторая буква показывает, какие конкретно логические элементы содержит данная ИМС:
ЛН — элементы НЕ. Например, микросхема КР1533ЛН1 (рис.1.10), содержащая 6 элементов НЕ.
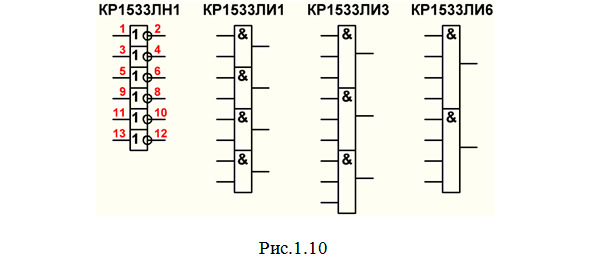
Красным цветом здесь показана нумерация выводов корпуса микросхемы (смотрите окончание данного параграфа), но далее мы это показывать не будем, чтобы не загромождать рисунки. При необходимости следует обратиться к Приложению 1 данной книги или к соответствующей справочной литературе.
ЛИ — элементы И. Например, микросхемы: КР1533ЛИ1 (рис.1.10), содержащая 4 элемента 2И; КР1533ЛИ3 (рис.1.10), содержащая 3 элемента 3И); КР1533ЛИ6 (рис.1.10), содержащая 2 элемента 4И.
ЛЛ — элементы ИЛИ. Например, микросхема КР1533ЛЛ1 (рис. 1.11), содержащая 4 элемента 2ИЛИ.
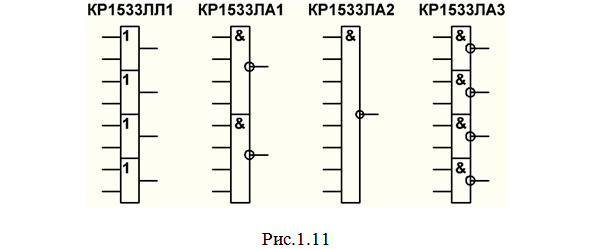
ЛА — элементы И-НЕ. Например, микросхемы: КР1533ЛА1 (рис.1.11), содержащая 2 элемента 4И-НЕ; КР1533ЛА2 (рис.1.11), содержащая 1 элемент 8И-НЕ; КР1533ЛА3 (рис.1.11), содержащая 4 элемента 2И-НЕ; КР1533ЛА4 (рис.1.12), содержащая 3 элемента 3И-НЕ.
ЛЕ — элементы ИЛИ-НЕ. Например, микросхемы: КР1533ЛЕ1 (рис.1.12), содержащая 4 элемента 2ИЛИ-НЕ; КР1533ЛЕ4 (рис.1.12), содержащая 3 элемента 3ИЛИ-НЕ; КР531ЛЕ7 (рис.1.12), содержащая 2 элемента 5ИЛИ-НЕ.
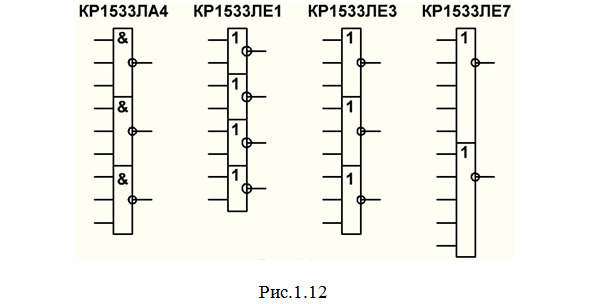
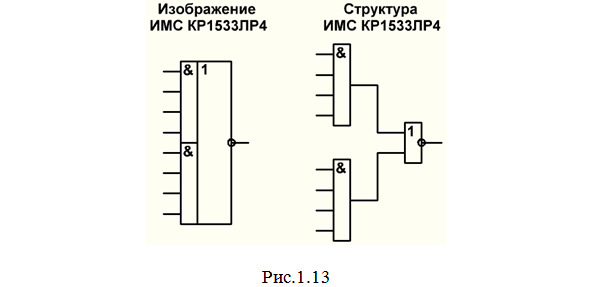
ЛР, ЛБ — комбинированные ИМС, содержащие разные логические элементы, причем обычно внутри микросхемы уже выполнены соединения между этими элементами. Например, микросхема КР1533ЛР4 (рис.1.13). Она содержит два элемента 4И и один элемент 2ИЛИ-НЕ, причем выходы элементов 4И внутри микросхемы уже соединены со входами элемента 2ИЛИ-НЕ.
ЛП — прочие. Содержат логические элементы, не включенные в табл.1.1. Например, микросхема КР1533ЛП5 (рис.1.14) содержит элементы, выполняющие логическую операцию «исключающее ИЛИ» (в случае двух аргументов ее еще называют «неравнозначностью» или «суммой по модулю 2»), смотрите табл.1.4.

У данного элемента есть одна интересная особенность (следите по табл. 1.4): при наличии постоянного сигнала 0 на одном входе сигнал с другого входа «проходит» на выход в прямом виде; а при наличии на одном входе постоянного сигнала 1 элемент инвертирует сигнал, поступающий на другой вход. Указанная особенность используется, в частности, в схеме исправления ошибок при передаче информации с помощью корректирующего кода Хэмминга (см. тему 3.24).
Рассмотренные микросхемы относятся к ИМС со средней степенью интеграции, которые имеют двухрядное расположение выводов (рис.1.15). БИС, СБИС и ГБИС обычно имеют 4-рядное расположение выводов (рис.1.16).


Нумерация этих выводов производится от «ключа» (рис.1.15 и 1.16) против часовой стрелки (рис.1.17а).

Не логические выводы часто снабжаются крестиками (рис.1.17б). К ним, в частности, относятся выводы для питания, которые обозначаются: положительный +UСС, отрицательный -GND (общий провод, от слова ground — заземление), но они на рисунках ИМС изображаются довольно редко.
1.6. Основные параметры, характеризующие работу ИМС
Познакомимся с основными параметрами ИМС, которые имеют значение при эксплуатации, ремонте и наладке цифровой аппаратуры.
UСС — напряжение питания. Для ИМС серии КР1533 и некоторых других оно составляет 5 В ± 10%.
UL (L — low — низкий) — напряжение низкого уровня (уровня логического 0) на входе UIL (I — input — вход) и на выходе UOL (O — output — выход). Для ИМС серии КР1533 нормой является: UIL — не более 0,8 В; UOL — не более 0,5 В.
UH (H — high — высокий) — напряжение высокого уровня (уровня логической 1) на входе UIH и на выходе UOH. Для ИМС серии КР1533 нормой является: UIH — не менее 2,0 В; UOH — не менее 2,7 В.
IL — ток низкого уровня на входе IIL и на выходе IOL. Для ИМС серии КР1533 нормой является IIL = -200 мкА; IOL = 8 мА.
IH — ток высокого уровня на входе IIH и на выходе IOH. Для ИМС серии КР1533 нормой является IIH = 20 мкА; IOH = -0,4 мА.
PB — потребляемая (рассеиваемая) мощность на один вентиль (логический элемент НЕ): PB = (PL + PH) /2, где PL и PH — потребляемая мощность при наличии на выходе элемента соответственно низкого уровня логического 0 и высокого уровня логической 1. В статическом режиме для ИМС серии КР1533 нормой является PB = 1,2 мВт.
Следует иметь в виду, что для микросхем на биполярных транзисторах величины PL и PH отличаются довольно существенно, причем меньшей величиной является PH. Микросхемы на полевых транзисторах потребляют настолько малую мощность, что для них разницу между PL и PH практически можно не учитывать.
В динамическом режиме потребляемая микросхемой мощность возрастает, увеличиваясь с ростом частоты.
tP — время задержки распространения сигнала. Данная величина представляет собой промежуток времени между изменением сигнала на входе и соответствующим изменением сигнала на выходе. tP является динамической характеристикой работы ИМС, по ней обычно судят о быстродействии микросхем. Очевидно, что при уменьшении tP быстродействие возрастает.
Различают время задержки распространения сигнала при включении tPHL (когда сигнал на выходе элемента меняется с 1 до 0) и при выключении tPLH (когда сигнал на выходе элемента меняется с 0 до 1). Эти величины для элемента НЕ показаны на рис.1.18.
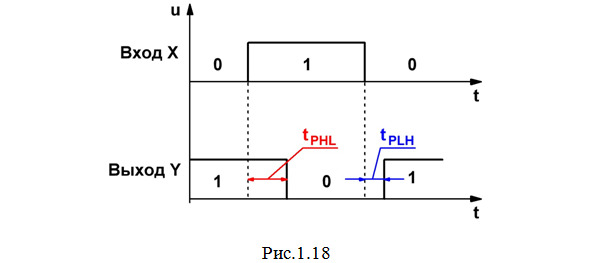
В качестве примера приведем значения tPHL и tPLH для микросхемы КР1533ЛН1: tPHL — не более 11 нс; tPLH — не более 8 нс.
КН — нагрузочная способность или коэффициент разветвления по выходу. Показывает, какое максимально допустимое количество элементов можно подключить к выходу каждого элемента данной микросхемы. Например, на рис.1.3 к выходу 3-го элемента присоединены три других элемента — 7-й, 8-й и 9-й. Допустимо ли это, вы можете сказать сами: обычные микросхемы ТТЛШ-структуры имеют КН = 10.
UП — помехоустойчивость, которая оценивается в статическом и динамическом режимах. Статическая помехоустойчивость определяется максимально допустимой величиной повышения (относительно уровня 0) или понижения (относительно уровня 1) напряжения на входах, которое еще не приводит к изменению сигнала на выходе. Для микросхем серии КР1533 нормой является UП = 0,4В. Динамическая помехоустойчивость зависит от формы и амплитуды сигнала помехи, а также от скорости переключения микросхемы (быстродействия) и ее статической помехоустойчивости.
N — надежность. Ее обычно характеризуют максимально допустимым количеством отказов за единицу времени. Для микросхем серии КР1533 нормой является N = 10—6 отказов в час.
1.7. Сравнительная характеристика ИМС различных структур
Основными параметрами, позволяющими производить сравнение по качеству микросхем различных структур и серий, являются статическая потребляемая мощность и среднее время задержки распространения сигнала в пересчете на один вентиль. Для наглядности типовые значения РВ и tP приведены на графике (рис.1.19).
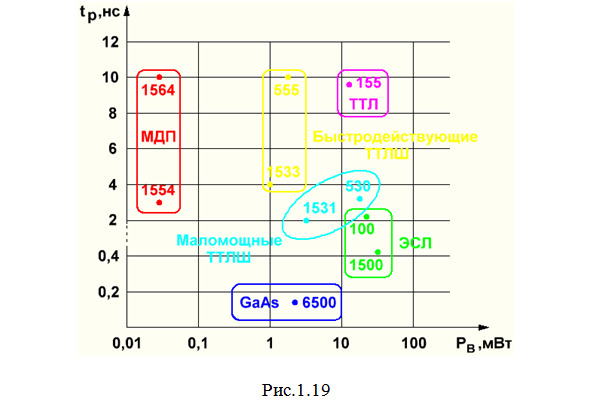
Из этого графика видно, что наихудшими параметрами характеризуются микросхемы ТТЛ-структуры. Поэтому в настоящее время интенсивно идет процесс их вытеснения микросхемами других структур. Однако следует иметь в виду, что в ныне функционирующей аппаратуре микросхемы ТТЛ-структуры (особенно ИМС серии 155) распространены очень широко и будут работать еще очень долго. Первым разработчиком ИМС по технологии ТТЛ является фирма «Texas Instruments», которая выпустила ИМС серии SN74 (аналог — серия 155).
Применение диодов Шоттки и усовершенствование технологии позволило уменьшить потребляемую мощность и увеличить быстродействие в микросхемах ТТЛШ-структуры по сравнению с ИМС структуры ТТЛ.
Наименьшую потребляемую мощность при сравнимом с ИМС других структур быстродействии имеют микросхемы МОП-структуры, построенные на полевых транзисторах. Но наряду с указанным очевидным преимуществом они имеют и недостатки: чувствительность к статическому электричеству, значительный разброс всех параметров, повышенное выходное сопротивление (до 1 кОм). Разработка первых микросхем МОП серии CD4000 (аналог — серия 561) была выполнена фирмой «RCA».
Наивысшее быстродействие достигается в микросхемах ЭСЛ-структуры, т.к. здесь транзисторы работают в ненасыщенном (линейном) режиме. Но большая потребляемая мощность и низкая помехоустойчивость не позволяют применять их достаточно широко. ИМС структуры ЭСЛ используются в тех случаях, когда предъявляются повышенные требования к быстродействию (например, в запоминающих устройствах). Первым разработчиком ИМС по технологии ЭСЛ была фирма «Motorola», которая выпустила серию МС10000 (аналог — серия 500).
Приведенный анализ подтверждает следующее: в настоящее время наибольшее распространение имеют ИМС структур ТТЛШ и МОП.
Сверхвысокое быстродействие при сравнимой с другими структурами потребляемой мощности достигается в микросхемах на основе арсенида галлия, но сравнительно высокая стоимость, недостаточно разработанная технология и некоторые другие недостатки пока не позволяют применять данные микросхемы в широких промышленных масштабах.
1.8. Элементы с открытым коллекторным выходом
Некоторые микросхемы структуры ТТЛ и ТТЛШ имеют открытые коллекторные выходы (ОК), у них нет резистора коллекторной нагрузки в выходном транзисторе. Для формирования выходного перепада напряжения (чтобы имелась возможность установки на выходе и уровня логического 0, и уровня логической 1) к выходу элемента с ОК требуется подключать нагрузочное сопротивление, поэтому такие микросхемы применяются для обслуживания устройств, которые и будут представлять собой для ИМС коллекторную нагрузку. К ним относятся индикаторы, сигнальные лампы, светодиоды, коаксиальные кабели и т. д. В условном изображении таких микросхем ставится знак, показанный на рис.1.20 внутри элементов 2И.
Примерами ИМС с ОК, содержащими логические элементы, являются: КР1533ЛН2, КР1533ЛИ2, КР1533ЛИ4, КР1533ЛА7, КР1533ЛА9, КР1533ЛА10, КР1533ЛП12, которые имеют структуру, аналогичную соответственно микросхемам КР1533ЛН1 (рис.1.10), КР1533ЛИ1 (рис.1.10), КР1533ЛИ3 (рис.1.10), КР1533ЛА1 (рис.1.11), КР1533ЛА3 (рис.1.11), КР1533ЛА4 (рис.1.12), КР1533ЛП5 (рис.1.14).
Выходы нескольких элементов с ОК можно присоединять к общей нагрузке RH (смотрите рис.1.20).

Такое соединение, позволяет реализовать логическую функцию И, поэтому называется «монтажным И» и изображается так, как показано в зеленом прямоугольнике на рис.1.20.
1.9. Буферные элементы
Некоторые элементы кроме логических операций выполняют еще и другие функции. Такие элементы обычно называют буферными. Применяются они в основном для двух целей:
1. Для подключения большого количества элементов, число которых превышает Кн обычных микросхем. У них повышенный коэффициент разветвления, достигающий, например, в микросхемах серии 1533 величины Кн = 30. В изображении таких ИМС ставится знак, показанный на рис.1.21 внутри элементов. К ним относятся КР1533ЛН8, КР1533ЛИ8, КР1533ЛИ10, КР1533ЛЛ4, КР1533ЛА21, КР1533ЛА22, КР1533ЛА24, КР1533ЛЕ10, которые имеют структуру, аналогичную соответственно микросхемам КР1533ЛН1 (рис.1.10), КР1533ЛИ1 (рис.1.10), КР1533ЛИ3 (рис.1.10), КР1533ЛЛ1 (рис.1.11), КР1533ЛА3 (рис.1.11), КР1533ЛА1 (рис.1.11), КР1533ЛА4 (рис.1.12), КР1533ЛЕ1 (рис.1.12).
Некоторые микросхемы с повышенной нагрузочной способностью могут иметь еще и открытые коллекторные выходы. Например, ИМС КР1533ЛН10, КР1533ЛА23, КР1533ЛЕ11, КР1533ЛП17, которые имеют структуру, аналогичную соответственно микросхемам КР1533ЛН1 (рис.1.10), КР1533ЛА3 (рис.1.11), КР1533ЛЕ1 (рис.1.12), КР1533ЛП16 (рис.1.21).

2. Разъединение между собой отдельных узлов цифровой аппаратуры для исключения их взаимного влияния в некоторых режимах работы. Такие элементы в отличие от других имеют три состояния: в одном состоянии на выходе устанавливается уровень логической 1; в другом состоянии — уровень логического 0; а в третьем (так называемое Z-состояние или высокоомное состояние или состояние с высоким импедансом) выходы элемента вообще размыкаются, отключая присоединенные к ним ЦУ. Если в последнем случае измерить сопротивление элемента со стороны выходов, то оно окажется практически бесконечно большим, поэтому данное состояние и называют высокоомным. Условное изображение подобных ИМС содержит знак, показанный на рис.1.22 внутри элементов.
Для примера можно привести микросхему КР1533ЛП8 (рис.1.22).
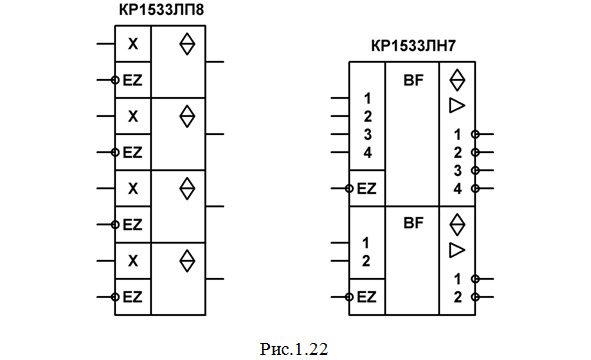
Она содержит 4 буферных повторителя, каждый из которых имеет управляющий состояниями вход EZ (E — enable — давать возможность, разрешать). При установке логического 0 на входе EZ элементу разрешается работать в качестве обычного повторителя, а если на этот вход подать сигнал 1, то элемент переходит в Z-состояние и его выход размыкается (состояние разомкнутого выхода принято обозначать: Z или Roff). Управляющий состояниями вход иногда называют разрешением по выходу и обозначают ЕО (Е — enable, O — output).
В некоторых случаях вход EZ делается общим для нескольких элементов. Например, в микросхеме КР1533ЛН7 (рис.1.22) содержится шесть буферных элементов НЕ с тремя состояниями выходов и повышенной нагрузочной способностью, разделенных на две группы по 4 и 2 элемента. Каждая группа элементов имеет свой управляющий состояниями вход EZ. Подача сигнала 1 на такой вход переводит в Z-состояние сразу все элементы соответствующей группы.
Подобные микросхемы, содержащие объединенные в группы элементы НЕ или повторители с тремя состояниями, которые имеют еще и повышенную нагрузочную способность, называют шинными формирователями или магистральными приемопередатчиками.
П р и м е ч а н и е. Часть линий, сгруппированных по функциональному назначению, называется шиной. Например, информационная шина, по всем линиям которой передается информация; шина управления, по линиям которой передаются сигналы управления; и т. д. Совокупность шин называется магистралью.
У таких ИМС в третьей части маркировки обычно ставят буквы АП, хотя иногда используется маркировка ЛП или ЛН (как, например, в только что рассмотренной микросхеме). Условное графическое изображение формирователей имеет, как правило, буквы BF (от английского buffer — буфер). Применяются они обычно в микропроцессорных системах и системах обработки данных с магистральной организацией обмена информацией.
Можно привести еще один пример шинного формирователя: КР1533АП4 (рис.1.23). Данная ИМС содержит два четырехразрядных магистральных передатчика, каждый из которых имеет по четыре буферных повторителя с тремя состояниями и повышенным коэффициентом разветвления.
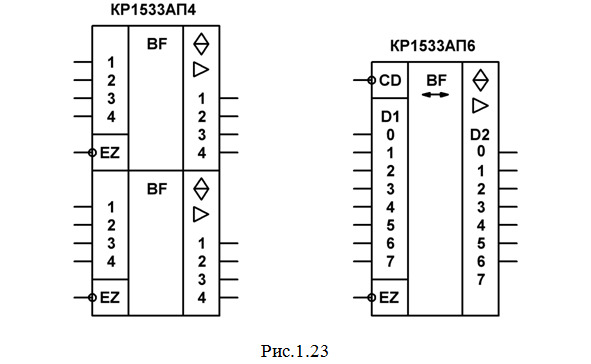
Некоторые формирователи могут передавать информацию в обоих направлениях. Например, восьмиразрядный двунаправленный приемопередатчик КР1533АП6 (рис.1.23) содержит 8 буферных повторителя с тремя состояниями и повышенной нагрузочной способностью, у которых изменение направления передачи информации производится с помощью сигнала на дополнительном входе CD: при CD = 1 передача информации производится от D1 к D2, при CD = 0 — наоборот.
***1.10. Мажоритарные элементы
Мажоритарный (от английского majority — большинство) элемент формирует на своем выходе такой сигнал, который действует на большинстве его входов.
В качестве примера можно рассмотреть микросхему КР1533ЛП3 (рис.1.24). Она содержит три мажоритарных элемента «два из трех» (т.е. на выходе формируется такой сигнал, который действует не менее чем на двух входах из трех), работа каждого из них описывается таблицей истинности (табл.1.5).
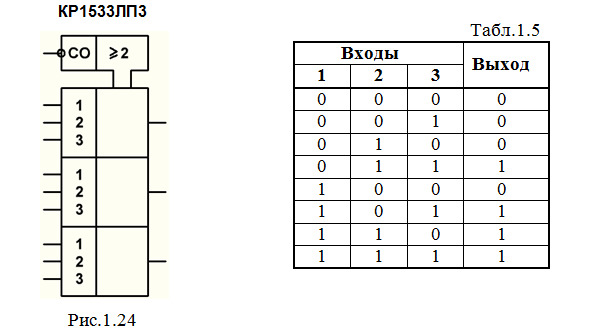
ИМС имеет общий для трех элементов управляющий вход СО, на котором для нормальной работы должен поддерживаться уровень логического 0. При СО = 1 значение выходного сигнала определяется только сигналом на входе 3.
1.11. Преобразователи уровней
При использовании в аппаратуре микросхем различной структуры возникает необходимость их согласования по таким важнейшим параметрам, как уровни сигналов и потребляемая мощность.
Эту задачу решают специальные ИМС, которые получили название: преобразователи уровней логических сигналов.
Микросхемы любых преобразователей в третьей группе маркировки имеют первую букву П, а вторая буква указывает на конкретный вид преобразователя. Для ИМС преобразователей уровней принято обозначение: ПУ.
Для примера рассмотрим микросхему К564ПУ9 (рис.1.25).
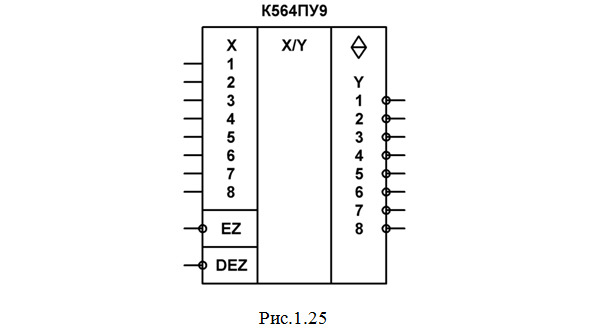
Она может выполнять одновременное преобразование 8 сигналов как от уровня ТТЛ (ТТЛШ) к МОП, так и от уровня МОП к ТТЛ (ТТЛШ). Входы ЕZ и DEZ предназначены для управления режимами работы:
— при подаче на вход DEZ сигнала 0 микросхема выполняет преобразование сигналов МОП уровня в ТТЛ (ТТЛШ) при любом сигнале на входе EZ;
— при одновременной установке сигналов 1 на входах EZ и DEZ микросхема выполняет преобразование сигналов ТТЛ (ТТЛШ) уровня в МОП;
— если же на входе EZ установить уровень логического 0, а на вход DEZ подать 1, то микросхема переходит в Z-состояние.
Следует учесть, что выходные сигналы инвертируются, т.к. на выходах стоит графический знак операции логического отрицания.
П р и м е ч а н и е. В настоящее время выпускаются микросхемы МОП-структуры, прямо совместимые со стандартными сериями ТТЛ (ТТЛШ). Например, микросхемы серий 1564, КР1564, КР1594 (аналоги — соответственно серии ММ54НС, ММ74НС и 74АСТ фирмы «National Semiconductor»).
Раздел 2. Основы синтеза и анализа работы цифровых устройств
Целью тем, изложенных в разделе 2, является овладение учащимися основам синтеза (разработки структуры и построения схем) ЦУ с помощью логических элементов и анализа (проверки правильности) их работы.
2.1. Формы записи логических функций
Предположим, задана таблица истинности (табл.2.1 на рис.2.1), описывающая работу ЦУ, которое имеет три входа Х1, Х2, Х3 и один выход Y1.
Цель: с помощью логических элементов построить схему, которая будет работать так, как указано в этой таблице.
Первым этапом работы является запись зависимости выходной логической функции (значений сигнала на выходе) Y1 от значений логических переменных Х1, Х2, Х3 (значений сигналов на входах) в базисе И, ИЛИ, НЕ (т.е. с использованием операций логического умножения, сложения и отрицания). Такая запись может выполняться в двух формах:
1. СДНФ (совершенная дизъюнктивная нормальная форма) представляет собой несколько многочленов (минтермов), объединенных операцией логического сложения (дизъюнкции), почему форма и названа дизъюнктивной. Она составляется для значений функции Y, равных 1, количество которых и определяет число многочленов. Каждый многочлен представляет собой логическое умножение всех переменных (в данном случае — трех переменных Х1, Х2, Х3), причем для нулевого значения любой переменной следует брать ее инверсию.
Запишем СДНФ для заданной в табл.2.1 логической функции Y1 на рис.2.1.
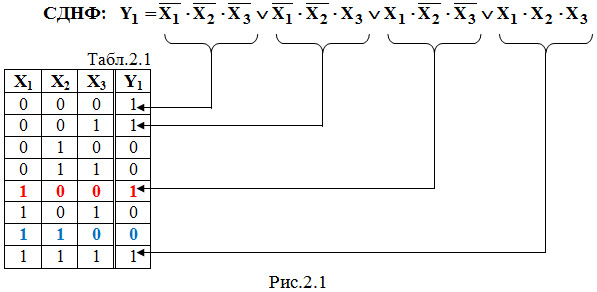
Приведем еще два примера составления СДНФ для логических функций Y2 и Y3, заданных в табл.2.2 на рис.2.2.

2. СКНФ (совершенная конъюнктивная нормальная форма) представляет собой несколько многочленов (минтермов), объединенных операцией логического умножения (конъюнкции), почему форма и названа конъюнктивной. Она составляется для значений функции Y, равных 0, количество которых и определяет число многочленов. Каждый многочлен представляет собой логическое сложение всех переменных (в данном случае — трех переменных Х1, Х2, Х3), причем для значения любой переменной X = 1 следует брать ее инверсию.
Запишем СКНФ для заданной в табл.2.1 логической функции Y1 (на рис.2.3).
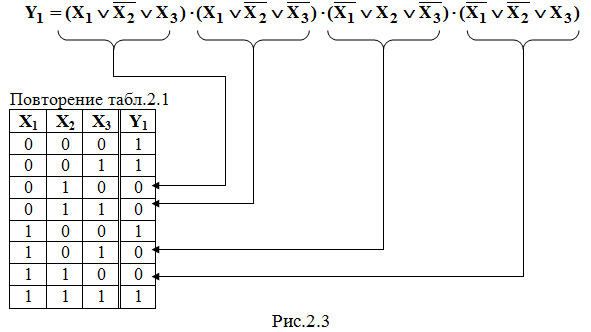
П р и м е ч а н и е:
Символом операции НЕ (инвертирования) обычно является черточка над буквой, как показано в табл.1.1. Именно такой символ мы применяли при записи СДНФ для функций Y1, Y2, Y3 и СКНФ для функции Y1. Но довольно часто, особенно на рисунках карт Вейча (Карно) и в изображениях микросхем, используется другой символ инвертирования — апостроф рядом с буквой: Y = X′. Как уже упоминалось во Введении, при выполнении лабораторных работ, а также в демонстрационных материалах применяется компьютерная программа исследования работы элементов и устройств цифровой микроэлектроники Electronics Workbench, где для изображения инверсных выводов как раз употребляется второй вариант символа инвертирования. Поэтому в дальнейшем для привыкания мы будем практиковать оба варианта символа инвертирования.
Приведем еще два примера записи СКНФ для функций Y2 и Y3, заданных в табл.2.2, где будем использовать два варианта записи символа инвертирования (рис.2.4):

В дальнейшем мы будем применять апостроф преимущественно в текстовом материале и формулах, а черточку над буквами — на рисунках.
2.2. Минимизация логических функций
методом Вейча
Любая совершенная нормальная форма (СДНФ или СКНФ) содержит очень большое количество логических операций, поэтому схемная реализация ЦУ непосредственно по СДНФ (или по СКНФ) потребует соответствующего числа логических элементов, которые должны будут выполнять данные операции. Поэтому невольно напрашивается вопрос: а нельзя ли логические выражения вида СДНФ или СКНФ упростить, чтобы количество операций (и, соответственно, количество элементов в схеме ЦУ) стало меньше? Оказывается, что в подавляющем большинстве случаев это сделать можно!
Процесс упрощения логических выражений любой совершенной нормальной формы записи получил название: минимизация от латинского minimum. Существует несколько способов ручной минимизации, но практически наиболее простым и наглядным является метод Вейча (несколько модифицированный метод Карно), который мы и будем здесь рассматривать. Его единственным недостатком является невозможность применения для минимизации логических выражений, содержащих более чем 5 переменных; но т.к. это случается довольно редко, то с указанным недостатком вполне можно мириться.
Сущность данного метода заключается в применении так называемых карт (диаграмм) Вейча, которые представляют собой прямоугольники, разделенные на клетки (карты Карно несколько отличаются от карт Вейча, но суть метода та же; — смотрите окончание данного параграфа). Количество клеток в карте определяется числом наборов переменных (числом комбинаций входных сигналов) N = 2n, где n — это количество переменных; причем каждой клетке строго соответствует свой набор переменных, определяемый по обычной координатной сетке.
Рассмотрим два наиболее часто встречающихся случая:
1. Для ЦУ с n = 3 входами максимальное число наборов переменных (смотрите таблицы 2.1 и 2.2 таких устройств) равно 2n = 23 = 8, следовательно и карта Вейча будет иметь 8 клеток (рис.2.5):

2. Для ЦУ, имеющего n = 4 входа, максимальное число наборов переменных равно 2n = 24 = 16, поэтому карта Вейча тоже будет иметь 16 клеток (рис.2.6).
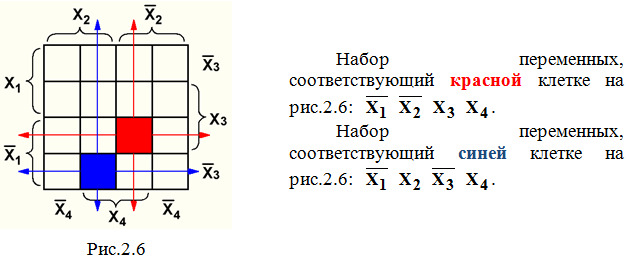
Главной особенностью любой карты Вейча является возможность объединения соседних клеток карты. Области объединения должны быть прямоугольными и содержать 2n (2,4,8,16) клеток. Допускается сворачивать карту в цилиндр с объединением соседних граней; примерами такого объединения являются: область 1 на рис.2.7 и область 3 на рис.2.8. Не допускается включать в объединение пустые клетки.
Рассмотрим примеры объединения клеток.
1. В карте Вейча с 8 клетками (рис.2.7).
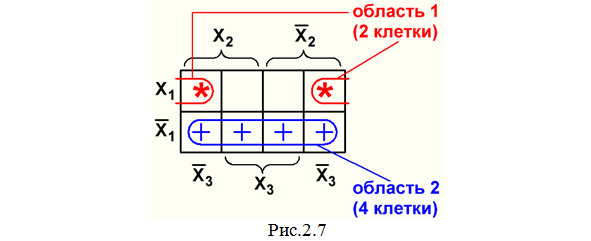
2. В карте Вейча с 16 клетками (рис.2.8).
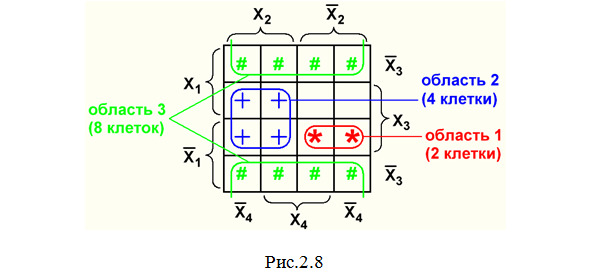
В каждой такой области объединения выполняется операция «склеивания», в результате которой остается только один многочлен только с теми переменными, которые входят во все объединенные клетки. А переменные типа X1 и X1′, X2 и X2′, X3 и X3′, X4 и X4′ «сокращаются». Это можно объяснить на следующем примере: возьмем два многочлена СДНФ (аналогичный результат получается и с многочленами СКНФ), соответствующих двум клеткам области 1 рис.2.7:
Х1·Х2·X3′ \/ X1·X2′·X3′;
одинаковые переменные вынесем за скобки:
X1·X3· (X2 \/ X2′);
легко проверить, что выражение в скобках при любых значениях X2 (0 или 1) дает 1, тогда:
X1·X3·1 = X1·X3.
Итак, в результате «склеивания» двух клеток области 1 рис.2.7 получается: X1·X3.

Приведем примеры (рис.2.10) «склеивания» клеток в карте Вейча на рис.2.4:
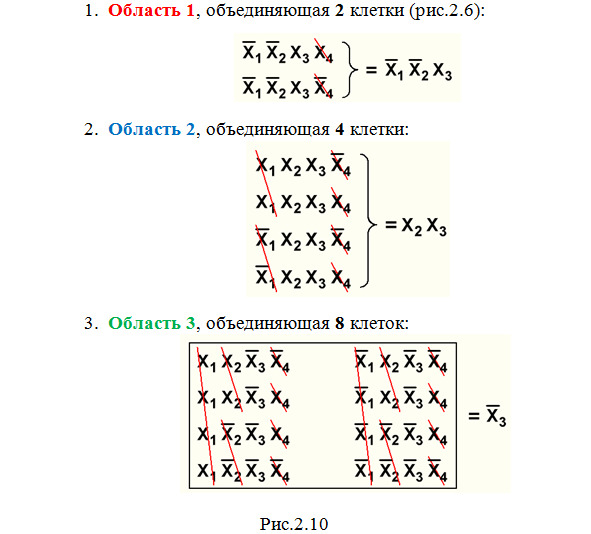
Очевидно, что при объединении всех клеток любой карты сокращаются все переменные, и результат «склеивания» дает 1.
Из сравнения полученных результатов можно сделать вывод: чем больше объединяется клеток, тем проще получается результат «склеивания», т.е. итоговое логическое выражение содержит меньше операций, и, соответственно, схема ЦУ будет иметь меньше логических элементов.
Теперь приведем порядок минимизации:
— Чертим карту Вейча с нужным количеством клеток.
— Клетки карты, соответствующие минтермам СДНФ (или СКНФ) обозначаем символом «1».
— Объединяем все клетки с «1». Количество клеток в каждом объединении должно быть максимальным, а самих областей объединения должно быть как можно меньше. П р и м е ч а н и е: любое количество клеток с «1» могут одновременно входить в две или больше области объединения.
— В каждой области производим операцию «склеивания», в результате чего получаем многочлены минимальной формы: МДНФ или МКНФ.
Приведем несколько примеров минимизации:
Пример 1. Минимизация СДНФ функции Y1 из темы 2.1 (рис.2.11):
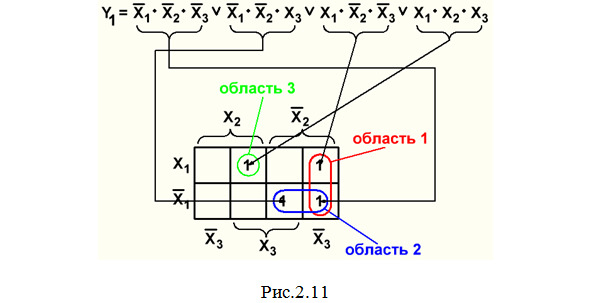
Покажем на рис.2.12 результаты"склеивания» двух клеток в областях 1 и 2 этой карты.
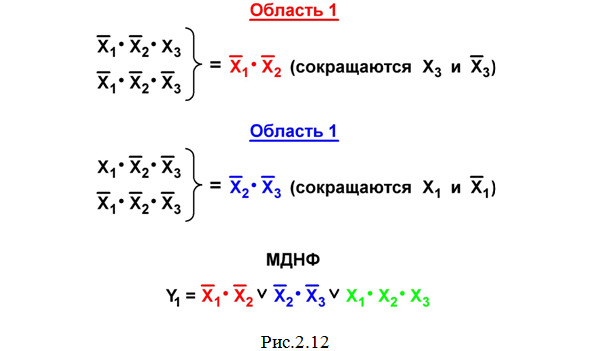
Область 3: Эта клетка остается одна — ни с какими другими клетками, содержащими «1», ее объединить нельзя. Поэтому соответствующий данной клетке многочлен Х1·Х2·Х3 не сокращается и входит в минимальную дизъюнктивную нормальную форму (МДНФ) без изменения.
В результате на этом же рис.2.12 записываем МДНФ (красным, синим и зеленым цветом показаны минтермы, которые получились в результате «склеивания» клеток в областях объединения соответствующего цвета на рис.2.11).
Пример 2. Минимизация СДНФ функции Y2 из темы 2.1 (рис.2.13):
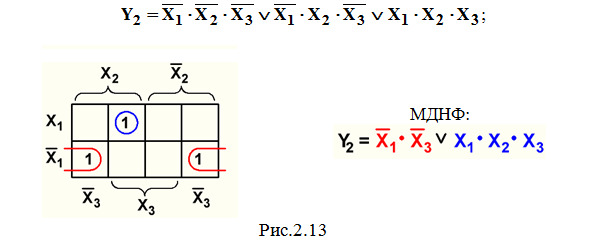
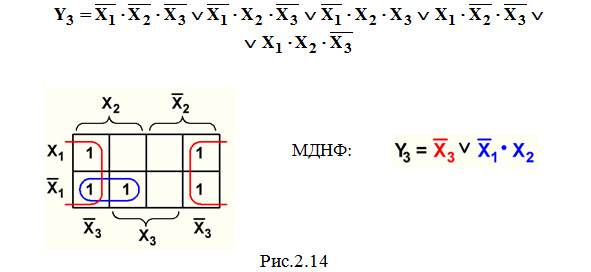
Пример 3. Минимизация СДНФ функции Y3 из темы 2.1 (рис.2.14):
Совершенно аналогично выполняется минимизация логических функций, записанных в СКНФ. Рассмотрим примеры:
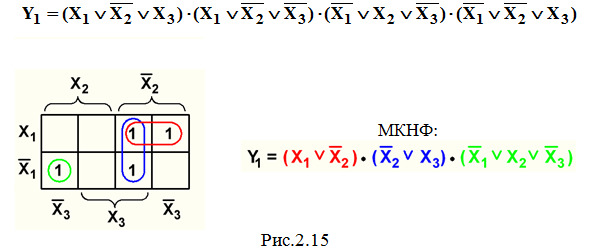
Пример 4. Минимизация СКНФ функции Y1 из темы 2.1 (рис.2.15):
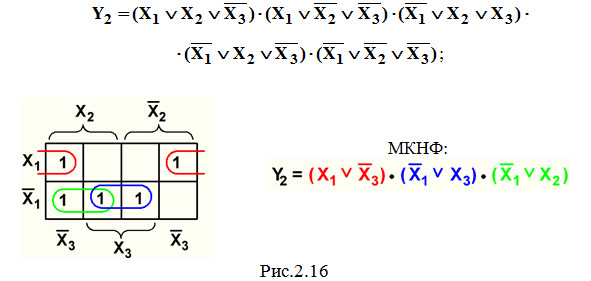
Пример 5. Минимизация СКНФ функции Y2 из темы 2.1 (рис.2.16).
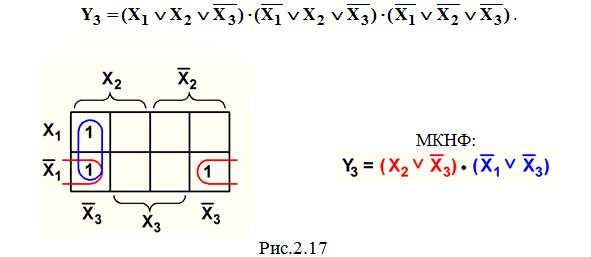
Пример 6. Минимизация СКНФ функции Y3 из темы 2.1 (рис.2.17).
***
Модификация карт Вейча, предложенная Карно, заключается в небольшом изменении координатной сетки (на рис. 2.18 показаны карты Карно для минимизации функций трех и четырех переменных дизъюнктивной формы).
Основным достоинством карт Карно по сравнению с картами Вейча является возможность их заполнения непосредственно по значениям сигналов в таблице истинности, не записывая СДНФ (или СКНФ). Но если координатная сетка карт Вейча одинаково применима для минимизации функций как дизъюнктивной, так и конъюнктивной форм, то в координатной сетке карт Карно для минимизации функций конъюнктивной формы прямые и инверсные значения переменных меняются местами по сравнению с координатной сеткой карт Карно для минимизации функций дизъюнктивной формы. На рис. 2.18 показано заполнение карт Карно, объединение клеток и результат минимизации функций Y1 (см. табл. 2.1) и Y4 в виде МДНФ.
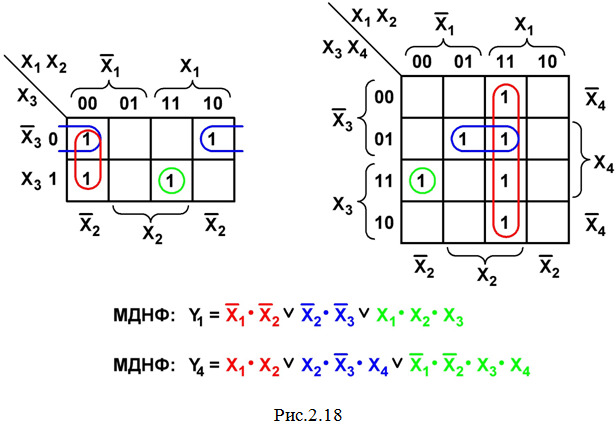
Сравнивая эти результаты с МДНФ примера 1 данной темы и примера из темы 2.8, мы легко убеждаемся, что они полностью совпадают с полученными при использовании карт Вейча.
2.3. Подбор микросхем, построение и анализ работы схем ЦУ в базисе И, ИЛИ, НЕ. Оценка качества схем
Построение схем производится таким образом, чтобы соблюдался порядок выполнения операций в логическом выражении согласно элементарным правилам как обычной алгебры, так и алгебры логики.
Достаточно очевидно, что при построении схем ЦУ по МДНФ порядок выполнения операций должен быть следующим:
— Логическое отрицание входных сигналов Х, то есть первыми в схеме должны стоять элементы НЕ.
— Логическое умножение (элементы И).
— Логическое сложение (элементы ИЛИ).
Пример 1. МДНФ (см. пример 1 из темы 2.2):
Y1 = X1′·X2′ \/ X2′·X3′ \/ X1·X2·X3.
Определяем количество операций (и, соответственно, требуемых логических элементов) для реализации этой МДНФ:
1. В данном логическом выражении стоят 4 знака операции логического отрицания. Но следует учесть, что инвертирование одного и того же сигнала X2 просто встречается два раза. Поэтому схема должна содержать 3 элемента НЕ для отрицания сигналов X1, X2 и X3.
2. Для выполнения первого умножения X1′·X2′ потребуется один элемент 2И, т.к. в этой операции участвуют два сигнала: X1′ и X2′.
3. Для выполнения второго умножения X2′·X3′ также потребуется один элемент 2И.
4. В третьем многочлене X1·X2·X3 требуется умножение трех сигналов, поэтому здесь нужно использовать один элемент 3И.
Таким образом, для выполнения операций умножения мы должны использовать 2 элемента 2И и один элемент 3И.
5. Логическое сложение трех многочленов X1′·X2′; X2′·X3′ и X1·X2·X3 требует применения одного элемента 3ИЛИ. Но нужно сразу учесть, что в серии КР1533 и во многих других нет микросхем, содержащих элементы 3ИЛИ. Поэтому для реализации нужного нам сложения придется использовать 2 элемента 2ИЛИ.
По записи МДНФ видно, что именно в такой последовательности нужно выполнять операции: сначала логическое отрицание НЕ, затем логическое умножение И, и в конце логическое сложение ИЛИ.
Подбираем микросхемы. В данном случае для построения схемы достаточно взять:
— Одну микросхему КР1533ЛН1 (см. рис.1.12), содержащую 6 элементов НЕ. Т. к. нам требуется только 3 элемента НЕ, то в данной микросхеме 3 элемента оказываются лишними и использоваться они не будут.
— Одну микросхему КР1533ЛИ1 (см. рис.1.12), содержащую 4 элемента 2И (здесь два элемента оказываются лишними), и одну микросхему КР1533ЛИ3 (см. рис.1.12), содержащую 3 элемента 3И (из нее 2 элемента использоваться не будут).
— Одну микросхему КР1533ЛЛ1 (см. рис.1.13), содержащую 4 элемента 2ИЛИ (два элемента этой микросхемы оказываются лишними).
Строим схему ЦУ в базисе И, ИЛИ, НЕ (термин «базис И, ИЛИ, НЕ» означает, что в данной схеме будут использоваться только элементы И, ИЛИ, НЕ), причем операции должны производиться в установленной нами последовательности: сначала НЕ, затем И, и в конце ИЛИ. Обращаем внимание, что при необходимости указывать направление передачи сигналов входы и выходы могут быть начерчены не кружочками (как в Разделе 1), а стрелками.
а) Чертим все три входа Х1, Х2 и Х3 (рис.2.19а).
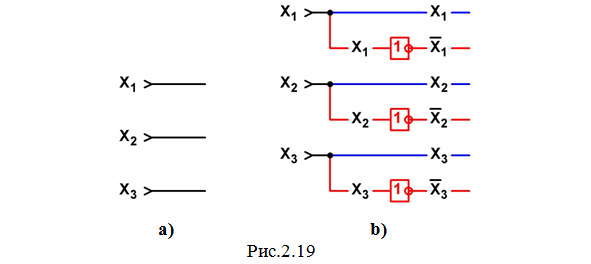
В дальнейшем на каждом следующем этапе все новые элементы, которые будут включаться в схему, показываются красным цветом.
b) Смотрим на МДНФ и видим, что операции НЕ должны выполняться в данном случае со всеми тремя переменными, т.к. в этом выражении имеются величины X1′, X2′ и X3′. Поэтому на всех трех входах ставим элементы НЕ (рис.2.19b.). Входы элементов подключаем ко входам схемы X1, X2 и X3, на выходах будут формироваться инверсные значения входных сигналов X1′, X2′ и X3′.
Сразу же нужно учесть еще один момент: снова смотрим на МДНФ и обнаруживаем, что наряду с инверсными значениями всех (еще раз повторяем: в данном случае всех) сигналов X1′, X2′ и X3′ нам потребуются и их прямые значения, поэтому выводим в схему и провода, показанные синим цветом.
c) Теперь переходим к выполнению операций логического умножения. Начнем с операции X1′·X2′ (смотрите МДНФ). Чертим элемент 2И; на один его вход подаем X1′, на другой — X2′; на выходе получаем результат умножения: X1′·X2′. К настоящему моменту мы будем иметь схему, изображенную на рис.2.20a.
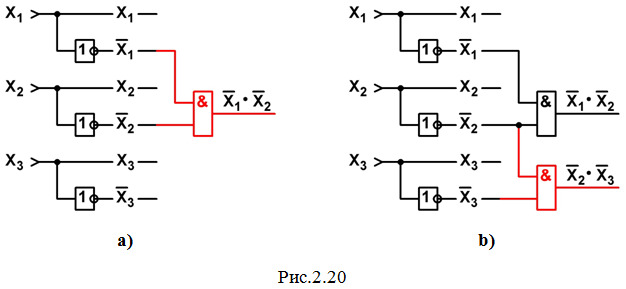
d) Реализуем следующую операцию умножения: X2′·X3′ (смотрите МДНФ). Чертим еще один элемент 2И; на один его вход подаем X2′, на другой — X3′; на выходе получаем результат: X2′·X3′. Теперь схема примет вид рис.2.20b.
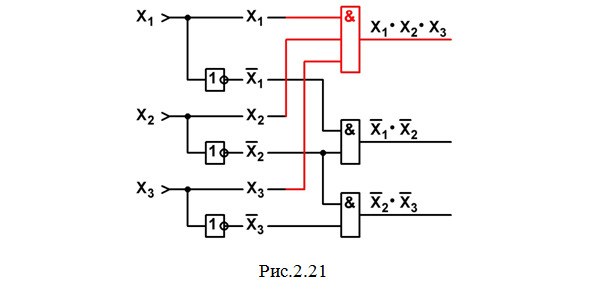
e) В последнем многочлене МДНФ X1·X2·X3 нужно выполнить операцию умножения с тремя сигналами, поэтому чертим элемент 3И. На один его вход подаем X1, на второй — X2 и на третий — X3; на выходе получим результат: X1·X2·X3. И схема теперь будет иметь вид рис.2.21.
f) Переходим к реализации операций логического сложения полученных многочленов: X1′·X2′, X2′·X3′ и X1·X2·X3 с помощью двух элементов 2ИЛИ. Как известно, при перемене мест слагаемых сумма не меняется; поэтому совершенно безразлично, в какой последовательности мы будем выполнять эти операции. Начнем с логического сложения многочленов X1′·X2′ и X1·X2·X3. Начертим элемент 2ИЛИ; на один его вход подадим X1′·X2′, на другой — X1·X2·X3; на выходе получим результат сложения: X1′·X2′ \/ X1·X2·X3. Теперь схема будет выглядеть так, как на рис.2.22.
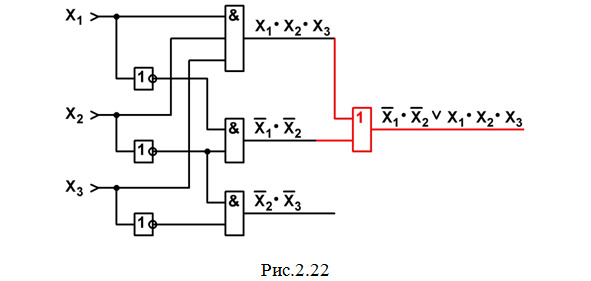
g) Остается лишь к величине (X1′·X2′ \/ X1·X2·X3) прибавить многочлен X2′·X3′. Чертим последний элемент — элемент 2ИЛИ; на один его вход подаем (X1′·X2′ \/ X1·X2·X3), на другой — X2′·X3′; на выходе этого элемента (так как он последний) получаем значение выходной функции Y1. И схема примет вид рис.2.23.
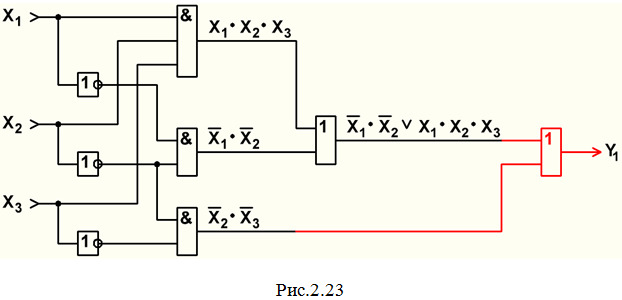
Теперь уберем вспомогательные надписи, укажем входы и выход, проставим позиционное обозначение всех элементов схемы с соответствующей нумерацией.
Микросхемы на чертежах обозначаются буквой D (от английского device — устройство) с соответствующим номером, например: D1, D2, D3 и т. д. Допускается в позиционное обозначение добавлять вторую букву: DА (A — analogy) — аналоговая микросхема, DD (D — digital) — цифровая микросхема; но это делается обычно тогда, когда в схеме присутствуют микросхемы обоих типов. А так как у нас в дальнейшем на чертежах будут только цифровые микросхемы, то мы вторую букву ставить не будем. Нумерацию микросхем и любых других элементов следует по возможности выполнять сверху вниз «колонками», начиная с левой стороны схемы.
На нашем чертеже в первой колонке стоят элементы НЕ из микросхемы КР1533ЛН1, которую поэтому следует обозначить D1. Но как обозначить отдельные элементы этой ИМС? Существует следующее правило: если микросхема содержит несколько элементов, то они обозначаются с двойной нумерацией через точку, причем первая цифра указывает номер микросхемы, а вторая — номер элемента в этой микросхеме. В данном случае первый элемент НЕ из микросхемы КР1533ЛН1 (напомним, что ее мы обозначили D1) нужно обозначить D1.1, второй элемент — D1.2, третий — D1.3.
Во второй колонке первым стоит элемент 3И из микросхемы КР1533ЛИ3, поэтому ее мы обозначим следующим по порядку номером D2. В указанной микросхеме используется один элемент 3И, который будет иметь обозначение D2.1.
В этой же второй колонке далее стоят два элемент 2И из микросхемы КР1533ЛИ1, их мы обозначим D3.1 и D3.2.
Последними в схеме стоят два элемента 2ИЛИ из микросхемы КР1533ЛЛ1, их нужно обозначить D4.1 и D4.2.
Кроме этого, у всех элементов схемы следует указать нумерацию их выводов в корпусе микросхем (смотрите предпоследний абзац темы 1.5 и Приложение 1).
В результате получаем окончательный вариант схемы (рис.2.24).
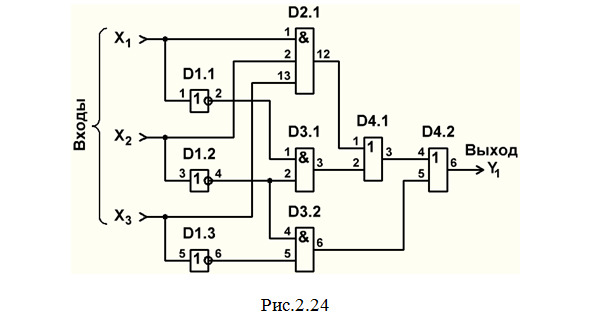
П р и м е ч а н и я :
— в дальнейшем для достижения учебных целей мы не будем ставить нумерацию выводов корпусов микросхем, чтобы не загромождать чертежи;
— будем оставлять вспомогательные надписи, которые помогут учащимся разбираться в построении схем.
— в реальных чертежах отдельных плат или ТЭЗов (типовых элементов замены) входы и выходы оформляются иначе, чем показано на рис.2.26. Подробнее об этом будет сказано при подготовке к курсовому проектированию, а сейчас пока подписывать входы и выходы будем именно так.
Любая реальная схема дополняется сведениями о всех используемых здесь микросхемах, любых других элементах и устройствах в виде специальной таблицы, которая имеет официальное название «Перечень элементов» (табл.2.3). По стандарту указанная таблица должна помещаться либо на поле чертежа, либо после него.
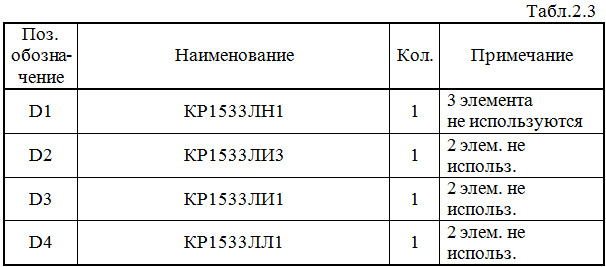
П р и м е ч а н и я к таблице:
1. Названия заголовков устанавливаются стандартом и их обязательно нужно сокращать именно так, как показано в табл.2.3.
2. Размеры таблицы также устанавливаются стандартом:
— ширина колонок по порядку слева направо: 20 (Позиционное обозначение), 110 (Наименование), 10 (Количество), 45 (Примечание) мм;
— высота строки заголовков — 15 мм;
— высота всех остальных строк — не менее 8 мм.
3. В колонке «Примечание» мы в дальнейшем будем указывать количество элементов из указанной микросхемы, которые в данной схеме использоваться не будут.
Выполним анализ работы ЦУ хотя бы в одном статическом режиме (рис.2.25). Для этого на входы подадим цифровые сигналы, например: Х1 = 1, Х2 = 0, Х3 = 0. По схеме, последовательно указывая значения сигналов на входах и выходах всех элементов (см. тему 1.2), определяем, что на выходе ЦУ формируется сигнал Y1 = 1. Сравниваем полученный результат с таблицей истинности данного ЦУ (соответствующая строка выделена красным цветом в табл.2.1) и делаем вывод: в данном случае (при заданных значениях входных сигналов) устройство сработало правильно.
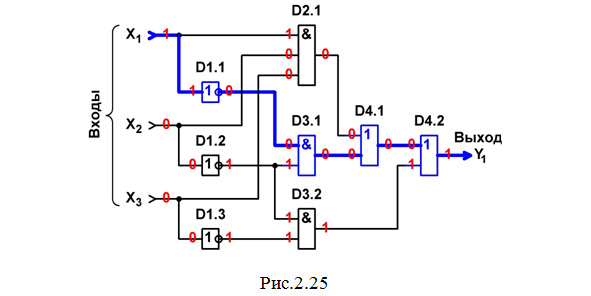
На основании вышеприведенного анализа нельзя сделать вывод о правильности построения данной схемы. Такой вывод будет корректным только в том случае, если выполнить анализ работы ЦУ для всех 8 статических режимов (то есть для всех комбинаций входных сигналов) согласно таблице истинности (см. табл.2.1).
При необходимости анализ работы ЦУ в динамическом режиме производится так, как описано в теме 1.2.
Оценка качества схем в основном производится по двум параметрам: аппаратурным затратам W и задержке T.
Аппаратурные затраты W обычно определяются количеством используемых корпусов микросхем (значение ряда других параметров — потребляемой мощности, надежности и др. — допустимо считать приблизительно пропорциональными W). В данном случае мы берем:
— 3 элемента НЕ из микросхемы КР1533ЛН1, которая содержит в целом 6 элементов; то есть используем 3/6 = 0,5 корпуса ИМС;
— 1 элемент 3И из микросхемы КР1533ЛИ3 (здесь всего — 3 элемента), т.е. используем 1/3 = 0,33 корпуса ИМС;
— 2 элемента 2И из микросхемы КР1533ЛИ1, содержащей в целом 4 элемента; т.е. используем 2/4 = 0,5 корпуса ИМС;
— 2 элемента 2ИЛИ из микросхемы КР1533ЛЛ1, которая содержит всего 4 элемента; т.е. используем 2/4 = 0,5 корпуса ИМС.
Итого величина аппаратурных затрат получается равной:
W = 0,5 + 0,33 + 0,5 + 0,5 = 1,83 корпуса.
П р и м е ч а н и е: лишние элементы частично занятых корпусов микросхем не учитываются, поскольку они могут быть использованы в других узлах.
Наряду с аппаратурными затратами очень важным критерием качества схем является задержка Т. В схемах, построенных с помощью микросхем средней степени интеграции, задержка достаточно объективно оценивается средним временем задержки распространения сигнала tP (см. §1.6) входящих в нее элементов по максимально длинному пути сигналов от входа к выходу. В рамках одной серии обычно полагают, что задержка любого логического элемента равна некоторой усредненной для данной серии величине τ, которая вместе с tP непосредственно элемента включает в себя и приближенную задержку на линиях связи между элементами. Для микросхем серии КР1533 значение τ можно принять равным 8 нс.
Рассмотрим все возможные пути прохождения сигналов по схеме (рис.2.14) от входов к выходу и определим соответствующую величину задержки:
— со входа Х1 через 3 элемента — D2.1, D4.1 и D4.2, поэтому
Т = 3τ = 3·8 = 24 нс;
— со входа Х1 через 4 элемента — D1.1, D3.1, D4.1 и D4.2 (этот путь на рис.2.24 выделен жирной синей линией);
Т = 4τ = 4·8 = 32 нс;
— со входа Х2 через 3 элемента — D2.1, D4.1 и D4.2;
Т = 3τ = 3·8 = 24 нс;
— со входа Х2 через 4 элемента — D1.2, D3.1, D4.1 и D4.2;
Т = 4τ = 4·8 = 32 нс;
— со входа Х3 через 3 элемента — D2.1, D4.1 и D4.2;
Т = 3τ = 3·8 = 24 нс;
— со входа Х3 через 3 элемента — D1.3, D3.2 и D4.2;
Т = 3τ = 3·8 = 24 нс.
Таким образом, для данной схемы максимальная задержка составляет Т = 4τ = 4·8 = 32 нс.
П р и м е ч а н и е. Строго говоря, полученное численное значение (в данном случае 32 нс) особого значения не имеет, так как задержка (да и аппаратурные затраты тоже) используются в основном для сравнительной оценки качества различных вариантов схем одного и того же ЦУ. Кроме этого, схема может строиться не на микросхемах логических элементов, а включаться целиком в состав какой-либо другой микросхемы, что приведет к существенному уменьшению задержки из-за сокращения линий связи между элементами внутри микросхемы, выполненной по интегральной технологии. Поэтому в большинстве случаев достаточно оперировать величиной Т = 4τ, не указывая его численное значение.
Приведем ряд других примеров, но уже без подробных пояснений.
Пример 2. МДНФ (см. пример 2 из §2.2):
Y2 = X1′·X3′ \/ X1·X2·X3.
Подсчитываем требуемое количество элементов: 2 элемента НЕ +1 элемент 2И и 1 элемент 3И +1 элемент 2ИЛИ.
Подбираем микросхемы: по одной микросхеме КР1533ЛН1, КР1533ЛИ1, КР1533ЛИ3 и КР1533ЛЛ1.
Строим схему ЦУ в базисе И, ИЛИ, НЕ (рис.2.26).
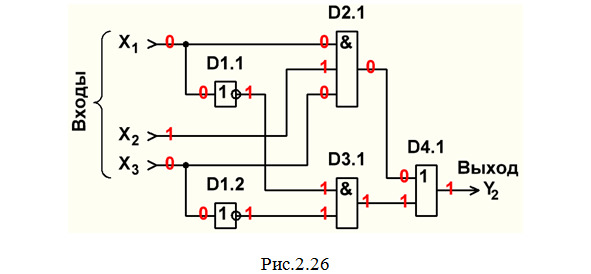
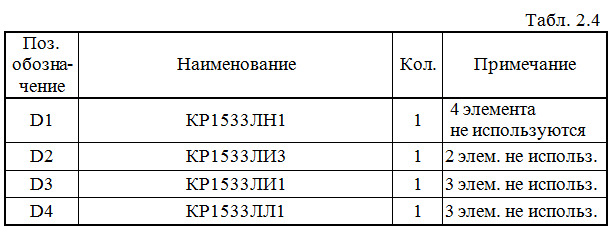
Составляем перечень элементов к этой схеме (табл.2.4).
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.26 и красную строку в табл.2.2).
Определим аппаратурные затраты и задержку:
W = 2/6 + 1/3 + 1/4 + 1/4 = 0,33 + 0,33 + 0,25 + 0,25 =
= 1,16 корпуса; T = 3τ.
Пример 3. МДНФ (см. пример 3 из темы 2.2):
Y3 = X3′ \/ X1′·X2
Подсчитываем требуемое количество элементов: 2 элемента НЕ +1 элемент 2И +1 элемент 2ИЛИ.
Подбираем микросхемы: по одной микросхеме КР1533ЛН1, КР1533ЛИ1 и КР1533ЛЛ1.
Строим схему ЦУ в базисе И, ИЛИ, НЕ (рис.2.27).
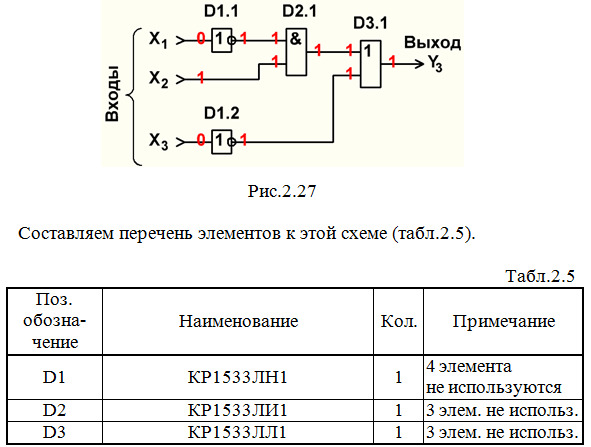
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.27 и красную строку в табл.2.2).
Определим аппаратурные затраты и задержку:
W = 2/6 + 1/4 + 1/4 = 0,33 + 0,25 + 0,25 = 0,83 корпуса;
T = 3τ.
Рассмотрим примеры построения схем по МКНФ. Здесь первыми опять будут выполняться операции НЕ. А порядок выполнения операций логического умножения и сложения изменится, так как по законам алгебры логики (и обычной алгебры тоже) сначала должны выполняться операции в скобках — ИЛИ, а уже затем — операции И.
Пример 4. МКНФ (см. пример 4 из темы 2.2):
Y1 = (X1 \/ X2′) · (X2′ \/ X3) · (X1′ \/ X2 \/ X3′).
Подсчитываем требуемое количество элементов: 3 элемента НЕ +4 элемента 2ИЛИ (в третьей скобке для выполнения логического сложения трех сигналов мы вынуждены использовать 2 элемента 2ИЛИ, так как нужного здесь в принципе элемента 3ИЛИ нет в микросхемах серии КР1533) +1 элемент 3И.
Подбираем микросхемы: по одной микросхеме КР1533ЛН1, КР1533ЛЛ1 и КР1533ЛИ3.
Строим схему ЦУ в базисе И, ИЛИ, НЕ (рис.2.28).
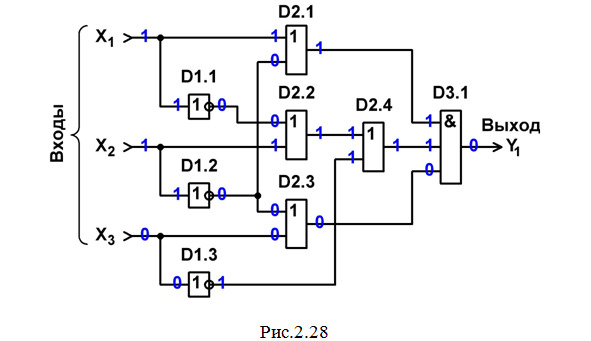
Составляем перечень элементов к этой схеме (табл.2.6).
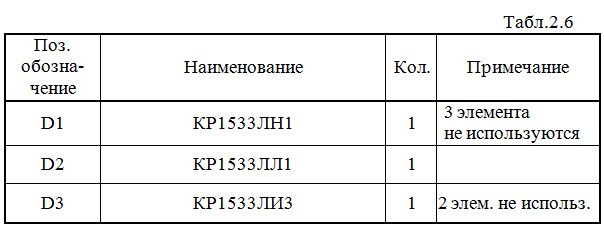
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.28 и соответствующую синюю строку в табл.2.1).
Определим аппаратурные затраты и задержку:
W = 3/6 + 1 + 1/3 = 0,5 + 1 + 0,33 = 1,83 корпуса; T = 4τ.
Пример 5. МКНФ (см. пример 5 из темы 2.2):
Y2 = (X1 \/ X3′) · (X1′ \/ X3) · (X1′ \/ X2).
Подсчитываем требуемое количество элементов: 2 элемента НЕ +3 элемента 2ИЛИ +1 элемент 3И.
Подбираем микросхемы: по одной микросхеме КР1533ЛН1, КР1533ЛЛ1 и КР1533ЛИ3.
Строим схему ЦУ в базисе И, ИЛИ, НЕ (рис.2.29).
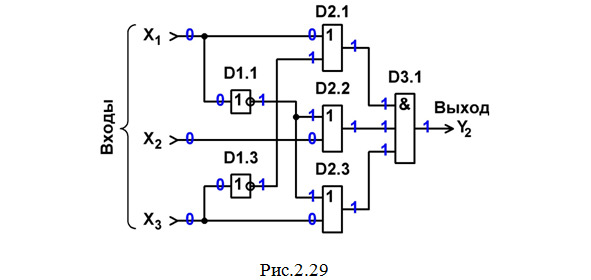
Составляем перечень элементов к этой схеме (табл.2.7).
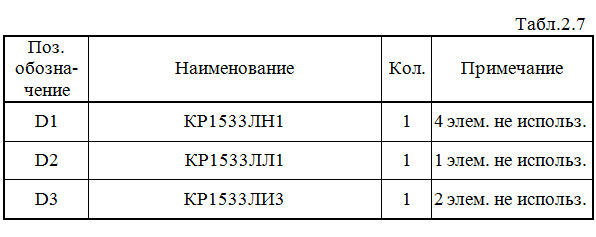
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.29 и синюю строку в табл.2.2).
Определим аппаратурные затраты и задержку:
W = 2/6 + 3/4 + 1/3 = 0,33 + 0,75 + 0,33 = 1,41 корпуса;
T = 3τ.
Пример 6. МКНФ (см. пример 6 из темы 2.2):
Y3 = (X2 \/ X3′) · (X1′ \/ X3′).
Подсчитываем требуемое количество элементов: 2 элемента НЕ +2 элемента 2ИЛИ +1 элемент 2И.
Подбираем микросхемы: по одной микросхеме КР1533ЛН1, КР1533ЛЛ1 и КР1533ЛИ1.
Строим схему ЦУ в базисе И, ИЛИ, НЕ (рис.2.30).
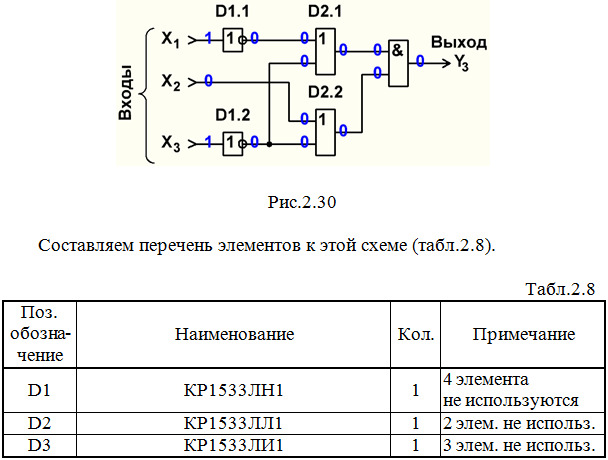
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.30 и синюю строку в табл.2.2).
Определим аппаратурные затраты и задержку:
W = 2/6 + 2/4 + 1/4 = 0,33 + 0,5 + 0,25 = 1,08 корпуса;
T = 3τ.
2.4. Переход к базису И-НЕ. Подбор микросхем, построение и анализ работы схем ЦУ в базисе И-НЕ
Значительно чаще для построения схем ЦУ используют не элементы И, ИЛИ, НЕ, а элементы И-НЕ (базис И-НЕ) или ИЛИ-НЕ (базис ИЛИ-НЕ). При этом в большинстве случаев улучшается качество схем, да и сами схемы по структуре получаются проще.
Переход к базису И-НЕ производится от МДНФ и его конечная цель заключается в следующем: следует так преобразовать МДНФ, чтобы в итоговом логическом выражении не было операций И, ИЛИ, НЕ, а были бы только операции И-НЕ.
Переход выполняется в следующем порядке (под буквами А, B, C, D и т. д. понимаются логические сигналы 0 или 1, а также любые логические операции и выражения, дающие в результате опять же сигналы 0 или 1):
1. Используется закон двойного отрицания (двойной инверсии):
A = A′′.
Справедливость этого закона проверить несложно, если вместо А подставить 0 или 1.
2. Применяется первая форма закона де Моргана:
(B \/ C \/ D \/ …)′ = B′·C′·D′·…
Правильность и этого закона тоже проверить несложно, если вместо В, С, D и т. д. подставить любую комбинацию сигналов 0 и 1.
3. Полученное логическое выражение рекомендуется записать с использованием символа «штрих Шеффера» (смотрите табл.1.1), например:
(X1·X2)′ = X1 / X2.

Пример 1. МДНФ (см. пример 1 из темы 2.2):
Y1 = X1′·X2′ \/ X2′·X3′ \/ X1·X2·X3.
Переходим к базису И-НЕ. Для этого сначала используем закон двойного отрицания:

Определяем требуемое количество элементов с учетом нужного количества входов у каждого элемента:
— для выполнения операций логического отрицания сигналов X1, X2 и X3 берем три элемента 2И-НЕ (смотрите П р и м е ч а н и е выше);
— чтобы выполнить операцию в первой скобке, следует использовать элемент 2И-НЕ, так как в данной операции участвуют два сигнала: X1′ и X2′;
— для реализации операции во второй скобке нужен элемент 2И-НЕ, потому что здесь в операции тоже участвуют два сигнала: X2′ и X3′;
— чтобы выполнить операцию в третьей скобке, придется взять элемент 3И-НЕ, так как в данной операции участвуют три сигнала: X1, X2 и X3;
— и последним мы должны поставить элемент 3И-НЕ, потому что на его входы будут поступать три сигнала, являющиеся результатами операций в трех скобках.
Всего в схеме ЦУ: 5 элементов 2И-НЕ (напомним, что из них — три элемента для выполнения логического отрицания!) +2 элемента 3И-НЕ.
Подбираем микросхемы. Элементы 2И-НЕ имеются в составе микросхемы КР1533ЛА3 (см. рис. 1.13), содержащей 4 элемента 2И-НЕ; так как нам требуется 5 таких элементов, то придется взять две микросхемы КР1533ЛА3, причем в одной из них три элемента использоваться не будут. Элементы 3И-НЕ входят в состав микросхемы КР1533ЛА4 (см. рис. 1.14), содержащей 3 элемента 3И-НЕ; нам нужны два элемента, поэтому достаточно использовать одну микросхему КР1533ЛА4, причем один элемент данной ИМС оказывается лишним.
Строим схему ЦУ в базисе И-НЕ (рис. 2.32).
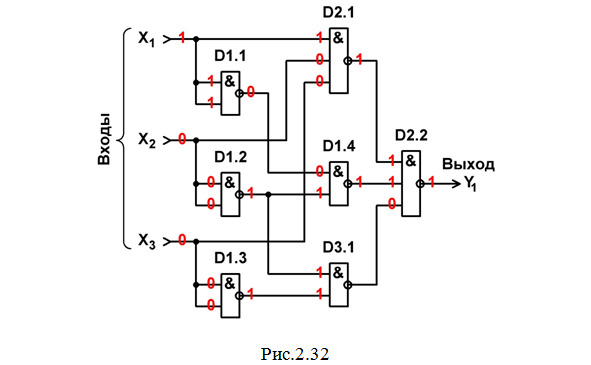
На этом же рис.2.32 выполнен анализ работы схемы ЦУ в статическом режиме для одной комбинации входных сигналов (см. красную строку в табл. 2.1).
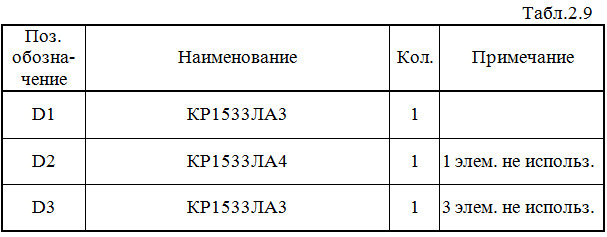
Составляем перечень элементов к этой схеме (табл.2.9).
Определим аппаратурные затраты и задержку:
W = 1 + 2/3 + 1/4 = 1 + 0,67 + 0,25 = 1,92 корпуса; T = 3τ.
Пример 2. МДНФ (см. пример 2 из темы 2.2):
Y2 = X1′·X3′ \/ X1·X2·X3.
Переходим к базису И-НЕ:
Y2 = [(X1′·X3′) \/ (X1·X2·X3)]′′ = [(X1′·X3′)′· (X1·X2·X3)′]′ =
= [(X1′/X3′) / (X1/X2/X3)].
Подсчитываем требуемое количество элементов: 4 элемента 2И-НЕ (из них — 2 элемента для выполнения логического отрицания) +1 элемент 3И-НЕ.
Подбираем ИМС: по одной ИМС КР1533ЛА3 и КР1533ЛА4.
Строим схему ЦУ в базисе И-НЕ (рис.2.33).
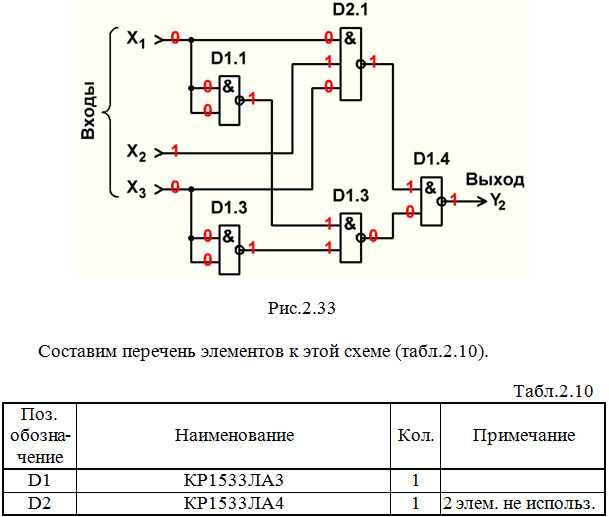
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.33 и красную строку в табл.2.2).
Определим аппаратурные затраты и задержку:
W = 1 + 1/3 = 1 + 1,33 = 1,33 корпуса; T = 3τ.
Пример 3. МДНФ (см. пример 3 из темы 2.2):
Y3 = X3′ \/ X1′·X2.
Переходим к базису И-НЕ:
Y3 = (X3′ \/ X1′·X2)′′ = [(X3′)′ \/ (X1′·X2)′]′ = (X3) / (X1′ / X2).
Обратим внимание, что в МДНФ переменная была с отрицанием, затем после применения закона де Моргана у нее появилось второе отрицание, что по закону двойной инверсии дает прямое значение X3. На будущее следует иметь в виду весьма простое правило: если в логическом выражении базиса И, ИЛИ, НЕ имеется минтерм, содержащий только одну переменную, то при переходе к базису И-НЕ эта переменная будет обязательно менять свое значение на противоположное: если она была без отрицания, то будет с отрицанием; если же она была с отрицанием, то будет без него.
Подсчитываем требуемое количество элементов: 3 элемента 2И-НЕ (из них — 1 элемент для логического отрицания).
Подбираем микросхему: одна микросхема КР1533ЛА3.
Строим схему ЦУ в базисе И-НЕ (рис.2.34):
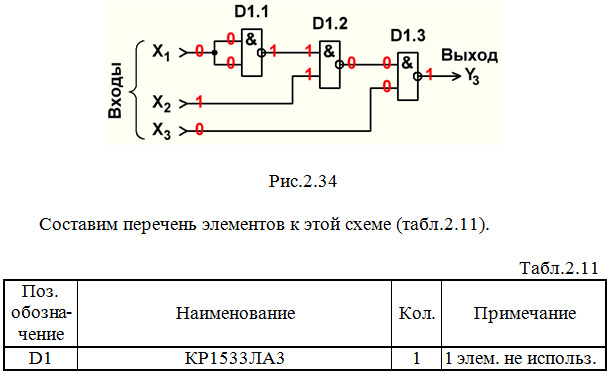
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.34 и красную строку в табл.2.2).
Определим аппаратурные затраты и задержку:
W = 3/4 = 0,75 корпуса; T = 3τ.
2.5. Переход к базису ИЛИ-НЕ. Подбор микросхем, построение и анализ работы схем ЦУ в базисе ИЛИ-НЕ
Аналогично описанному в предыдущем параграфе переходу к базису И-НЕ от МДНФ производится переход к базису ИЛИ-НЕ, только теперь уже от МКНФ:
1. Используется закон двойного отрицания (двойной инверсии):
A = A′′
2. Применяется вторая форма закона де Моргана:
(B·C·D·…)′ = B′ \/ C′ \/ D′ \/…
3. Полученное логическое выражение рекомендуется записать с использованием символа «стрелка Пирса» (смотрите табл.1.1), например:
(X1 \/ X2)′ = X1 ↓ X2.
П р и м е ч а н и е :
В итоговом логическом выражении должны содержаться только операции ИЛИ-НЕ. Но кроме них, как правило, остаются все-таки операции НЕ, которые в данном случае следует выполнять с помощью элементов 2ИЛИ-НЕ путем объединения входов этих элементов.
Пример 1. МКНФ (см. пример 4 из темы 2.2):
Y1 = (X1 \/ X2′) · (X2′ \/ X3) · (X1′ \/ X2 \/ X3′).
Переходим к базису ИЛИ-НЕ. Для этого сначала используем закон двойного отрицания:

Подсчитываем требуемое количество элементов: 5 элементов 2ИЛИ-НЕ (из них 3 элемента — для отрицания) +2 элемента 3ИЛИ-НЕ.
Подбираем микросхемы: две микросхемы КР1533ЛЕ1 и одна микросхема КР1533ЛЕ4.
Строим схему ЦУ в базисе ИЛИ-НЕ (рис.2.35).
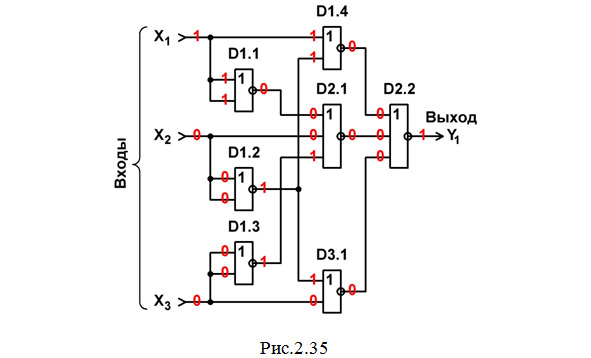
Составляем перечень элементов к этой схеме (табл.2.12).
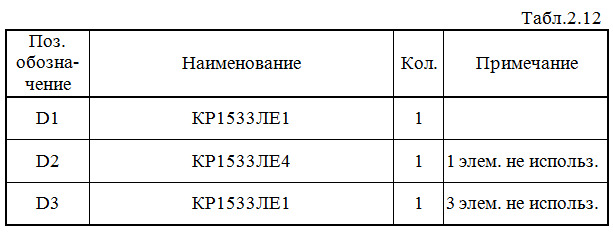
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.35 и синюю строку в табл.2.1).
Определим аппаратурные затраты и задержку:
W = 1 + 2/3 + 1/4 = 1 + 0,67 + 0,25 = 1,92 корпуса; T = 3τ.
Пример 2. МКНФ (см. пример 5 из темы 2.2):
Y2 = (X1 \/ X3′) · (X1′ \/ X3) · (X1′ \/ X2).
Переходим к базису ИЛИ-НЕ:
Y2 = [(X1 \/ X3′) · (X1′ \/ X3) · (X1′ \/ X2)]′′ =
= [(X1 \/ X3′) ′ \/ (X1′ \/ X3) ′ \/ (X1′ \/ X2)′]′ =
= (X1 ↓ X3′) ↓ (X1′ ↓ X3) ↓ (X1′ ↓ X2).
Подсчитываем требуемое количество элементов: 5 элементов 2ИЛИ-НЕ (из них 2 элемента — для отрицания) +1 элемента 3ИЛИ-НЕ.
Подбираем микросхемы: две микросхемы КР1533ЛЕ1 и одна микросхема КР1533ЛЕ4.
Строим схему ЦУ в базисе ИЛИ-НЕ (рис.2.36).
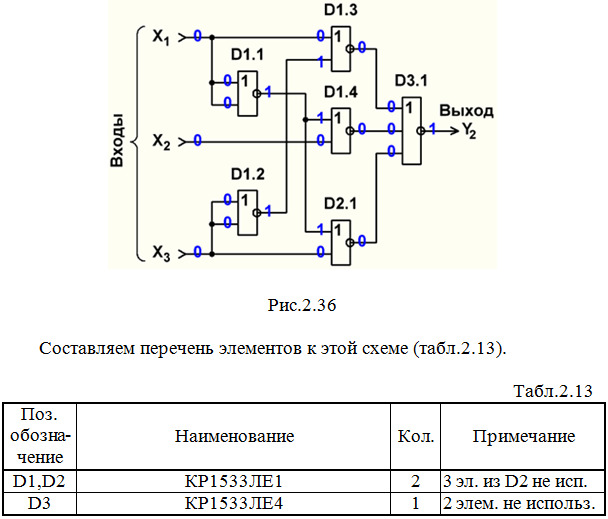
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.36 и синюю строку в табл.2.2).
Определим аппаратурные затраты и задержку:
W = 1 + 1/4 + 1/3 = 1 + 0,25 + 0,33 = 1,58 корпуса; Т = 3τ.
Пример 3. МКНФ (см. пример 6 из темы 2.2):
Y3 = (X2 \/ X3′) · (X1′ \/ X3′).
Переходим к базису ИЛИ-НЕ:
Y3 = [(X2 \/ X3′) · (X1′ \/ X3′)]′′ = [(X2 \/ X3′)′ \/ (X1′ \/ X3′)′]′ =
= [(X2 ↓ X3′) ↓ (X1′ ↓ X3′)].
Подсчитываем требуемое количество элементов: 5 элементов 2ИЛИ-НЕ (из них 2 элемента — для отрицания).
Подбираем микросхемы: две микросхемы КР1533ЛЕ1.
Строим схему ЦУ в базисе ИЛИ-НЕ (рис.2.37).
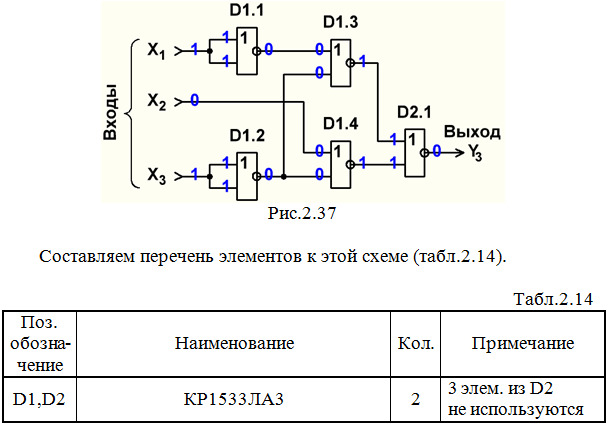
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.37 и синюю строку в табл.2.2).
Определим аппаратурные затраты и задержку:
W = 1 + 1/4 = 1 + 0,25 = 1,25 корпуса; T = 3τ.
2.6. Использование в схемах элементов разных базисов и комбинированных микросхем
Очень часто для достижения лучшего быстродействия или уменьшения аппаратурных затрат в схемах цифровых устройств используют элементы разных базисов. Приведем пример:
Пример 1. МКНФ (см. пример 4 из темы 2.2):
Y1 = (X1 \/ X2′) · (X2′ \/ X3) · (X1′ \/ X2 \/ X3′).
В данном логическом выражении базиса И, ИЛИ, НЕ преобразуем последний многочлен с использованием закона двойного отрицания и первого закона де Моргана:
(X1′ \/ X2 \/ X3′) = (X1′ \/ X2 \/ X3′)′′ = (X1′)′· (X2)′· (X3′)′ =
= X1 / X2′ / X3.
Теперь с учетом полученного результата исходное логическое выражение примет вид:
Y1 = (X1 \/ X2′) · (X2′ \/ X3) · (X1 / X2′ / X3).
Определим требуемое количество элементов: 1 элемент НЕ +2 элемента 2ИЛИ +1 элемент 3И-НЕ (для выполнения операции в третьей скобке) +1 элемент 3И.
Подбираем микросхемы: по одной микросхеме КР1533ЛН1, КР1533ЛЛ1, КР1533ЛА4 и КР1533ЛИ3.
Строим схему ЦУ (рис. 2.38):
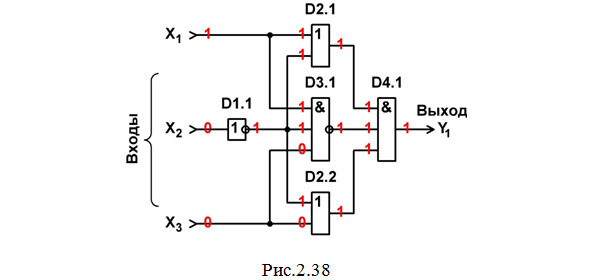
Составим перечень элементов к этой схеме (табл. 2.15).
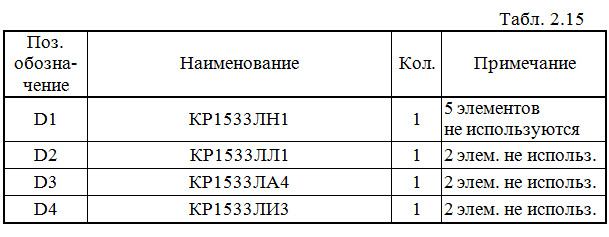
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.38 и красную строку в табл.2.1).
Определим аппаратурные затраты и задержку:
W = 1/6 + 2/4 + 1/3 + 1/3 = 0,17 + 0,5 + 0,33 + 0,33 =
= 1,33 корпуса; T = 3τ.
Полученные результаты сравним с этими же параметрами, характеризующими работу схемы рис. 2.27, построенной по исходной МКНФ:
W = 1,83 корпуса; T = 4τ.
Хорошо видно, что преобразование только лишь одного многочлена МКНФ и вытекающая из этого необходимость использования в схеме элементов разных базисов привело: во-первых, к уменьшению задержки (3τ вместо 4τ); и, во-вторых, к уменьшению аппаратурных затрат (1,33 корпуса вместо 1,83).
***
Иногда для достижения тех же целей увеличения быстродействия, уменьшения аппаратурных затрат, но в основном для уменьшения количества внешних соединений (то есть таких соединений, которые выполняются не внутри микросхемы, а снаружи путем монтажа) между микросхемами и элементами микросхем применяют комбинированные ИМС (смотрите, например, рис. 1.15 из параграфа 1.5). Приведем пример:
Пример 2. МДНФ (см. пример 1 из темы 2.2):
Y1 = X1′·X2′ \/ X2′·X3′ \/ X1·X2·X3.
Логическое отрицание, как и в указанном примере 1 из темы 2.2, будем делать с помощью тех же элементов НЕ из микросхемы КР1533ЛН1. А для выполнения остальных операций воспользуемся микросхемой КР1533ЛР13 (рис. 2.39).
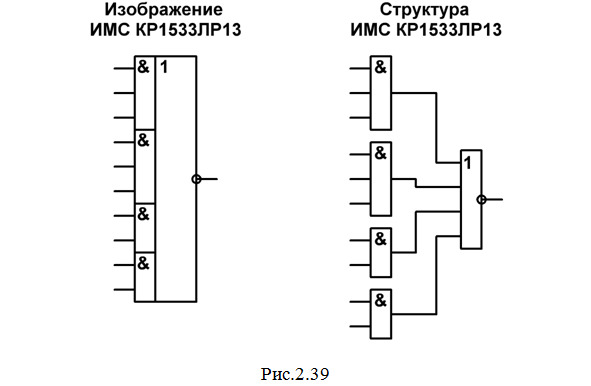
Но здесь нужно учесть, что в данной микросхеме на выходе стоит элемент ИЛИ-НЕ, поэтому выходной сигнал получится инвертированным. Чтобы получить на выходе все-таки прямое значение сигнала, выполним его повторное отрицание с помощью еще одного элемента НЕ из микросхемы КР1533ЛН1.
Строим схему ЦУ (рис. 2.40):
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.