Бесплатный фрагмент - Базовая оценка минерализации

Моей жене Татьяне и моим дочерям Эмилии и Оливии, без которых эта книга была бы завершена на год раньше.

Андрей Вяльцев

Моим учителям в школе, институте и жизни: Афанасьевой А. И., Большаковой Г. Н., Салову Л. А., Горштейну А. Е., Пертелю А. И., Калабину Н. В.

Георгий Кирьяков

ВВЕДЕНИЕ

Введение в «умной» книге обычно самая понятная и легко читаемая ее часть. Мы постарались немного изменить этот старинный красивый обычай и сделать весь текст максимально понятным и не очень снотворным. Очень надеемся, что это у нас получилось. Хотя, безусловно, в некоторых местах мозги напрягать придется, что может вызвать приступ неудержимой зевоты. Но тут уж увы — так со всеми книгами, чуть более сложными, чем «Буратино».

Начнем с того, о чем эта книга. Эта книга посвящена основам трехмерного моделирования месторождений твердых полезных ископаемых. Хочется сразу подчеркнуть: именно твердых, причем «традиционных» — руд черных, цветных и драгоценных металлов. Ни один из авторов книги не имеет никакого опыта в моделировании жидких или газообразных полезных ископаемых. Поэтому если вам надо моделировать что-то нефтегазовое или месторождение подземных вод — боимся, в этой книге вы не сможете найти очень много полезного.

По нашему мнению, в любом сложном вопросе главное — понимание его сути, а не бездумное заучивание формул и определений. Именно поэтому формул в книге не очень много, а те объяснения, которые приводятся, зачастую далеки от строгого научного освещения рассматриваемых вопросов, но зато данные объяснения построены таким образом, чтобы была понятна суть. По крайней мере, мы старались сделать их такими.

Что касается инструментов. В мире существует довольно большое количество специализированного программного обеспечения для моделирования и статистической обработки данных. Мы постарались излагать материал без «привязки» к какому-либо конкретному программному обеспечению, хотя более опытные читатели без труда смогут заметить скриншоты из наиболее распространенных прикладных программ для моделирования. Тем не менее все, что здесь изложено, может быть приложено к любому существующему программному обеспечению (мы так думаем!).

Теперь о том, для кого предназначена эта книга. Нам кажется, что книга будет полезна геологам, которые начинают заниматься моделированием месторождений. Или уже начали, но ушли не очень далеко от начала. Или ушли далеко, но некоторые начальные моменты все равно не очень поняли. Также нам кажется, что книга может быть полезна студентам геологических специальностей вузов. К сожалению, в настоящее время геологические вузы дают не очень большую базу по вопросам моделирования, а в том, что дают, нередко присутствуют пробелы на довольно важных местах. Данная книга предназначена (в том числе), чтобы эти пробелы максимально сократить.

В случае, если вы постараетесь читать материал не совсем «по диагонали» и попытаетесь делать задания, которые приведены в данной книге, нам кажется, что у вас есть неплохой шанс овладеть следующими навыками:

— проводить статистический анализ данных опробования полезных компонентов;

— выполнять декластеризацию и композитирование;

— определять уровни аномальных («ураганных») содержаний;

— подготавливать данные опробования к интерполяции;

— определять изменчивость содержаний в зависимости от направлений;

— правильно подбирать модели вариограмм (или хотя бы не совсем наобум);

— подбирать настроечные параметры для интерполяции содержаний;

— производить оценку содержаний методами ближайшего соседа, обратных расстояний, обычного кригинга и индикаторного кригинга;

— сопоставлять исходные данные опробования с оценкой в блочной модели;

— производить классификацию минерализации согласно кодексу JORC.

Книга создана на основе учебного курса, который можно найти на широко известном обучающем ресурсе Stepik. Если книга покажется интересной — милости просим и туда. Книга — штука неизменяемая, а в учебном курсе что-то может быть изложено по-другому — понятнее или глубже.

Примеры файлов и тренажеры, используемые по ходу книги, расположены на GitHub.

Да, чуть не забыли. Кратко об авторах. Авторы настоящей книги — геологи, более 10 лет занимающиеся моделированием месторождений непосредственно в добывающих организациях. Основная часть того, что мы намоделировали за свою профессиональную жизнь — это месторождения золота и цветных металлов. Те примеры, которые встречаются в книге, либо взяты непосредственно из нашей практики, либо созданы «по мотивам» реальных ситуаций.

Авторы выражают благодарность Некрасову Андрею за вычитку книги, устранение ошибок и внесение рациональных предложений по ее дополнению.

Если в ходе изучения изложенного материала у вас возникнет недопонимание прочитанного и/или горячее желание что-то переспросить или возразить — добро пожаловать в telegram-канал «Ресурсные геологи». Мы, скорее всего, где-то там присутствуем.

ГЛАВА 1. СОЗДАНИЕ И ОБРАБОТКА РУДНОЙ ВЫБОРКИ

Рудная выборка

Что это — «рудная выборка»?

Рудную выборку можно определить как часть данных опробования, которая характеризует «возможно рудную» часть геологического пространства, моделируемую зону минерализации. Рудная выборка — это единственный источник для оценки содержания полезных компонентов в вашей модели. Пробы, по каким-либо причинам не включенные в рудную выборку, в оценке содержаний не участвуют.

Создание рудной выборки — очень важный шаг в процессе моделирования. Рудная выборка — это основа вашей будущей модели. Ошибки, сделанные на этом этапе, скорее всего, приведут к ошибкам в модели и вполне могут создать проблемы при обработке данных.

Способ формирования рудной выборки зависит от выбранной методики моделирования. В данной главе будем считать, что моделирование выполняется способом, который является наиболее часто используемым, а именно — с помощью построения каркасов минерализации. Необходимо сделать замечание, что каркасное моделирование — отдельная большая тема и в книге не рассматривается.

В описанном случае рудная выборка — это те пробы, которые находятся внутри каркасов минерализации. При этом не все пробы, попавшие в каркасы, могут входить в рудную выборку.

Причин, по которым проба в пределах каркасов может быть исключена из рудной выборки, масса. В качестве примера можно привести:

— проблемы при проходке выработок, приведшие к низкому выходу материала проб (например, низкому выходу керна). Тут также возможны варианты: от попадания скважины в ослабленную зону разрывного нарушения до низкой квалификации персонала буровой;

— недоверие к данным опробования, полученным в предыдущие периоды. Чаще всего такая неприятность случается с «историческими» данными, полученными несколько десятилетий назад;

— несоответствие выбранного способа опробования геологическим особенностям месторождения — например, бурение слишком малым диаметром на месторождении с высокой локальной изменчивостью (например, на месторождениях с крупным видимым золотом);

— неудачная схема опробования, не соответствующая моделируемому объему. Например, зачастую на месторождениях, разведанных в 40-50-е годы прошлого века на Северо-Востоке России, опробование месторождений выполнялось бороздовым способом по подземным выработкам и только по наиболее «интересной» части — по визуально видимой жиле или зоне прожилкования. А зона околорудных изменений либо не опробовалась вовсе, либо опробовалась по сильно разреженной сети (или вообще 5-7-10 проб на весь объект). В итоге такой схемы опробования мы имеем огромную массу бороздовых проб, освещающих только богатую часть минерализации и редкие пробы, дающие отдаленное представление о качестве измененных пород за пределами визуально выделяемого оруденения (и которые показывают вполне себе промышленные содержания по нынешним временам). В принципе, и в более позднее советское время (60–70–80-е) бороздовые пробы на месторождениях, отрабатываемых подземным способом, были крайне популярны. Да, в позднее время бороздами старались осветить всю мощность зоны минерализации, но даже в этом случае опробовать то, что осталось «за стенкой» подземной выработки, физически невозможно. При интерполяции по такой выборке «в лоб» мы неизбежно получим существенное завышение содержаний. Поэтому при такой ситуации приходится как-то выкручиваться, в том числе и исключая пробы из рудной выборки. В ряде случаев приходится поступать как в той сценке: «здесь играть, здесь не играть, здесь я рыбу заворачивал» — т. е. использовать бороздовые пробы при оконтуривании, но не использовать при интерполяции (или использовать фрагментарно).

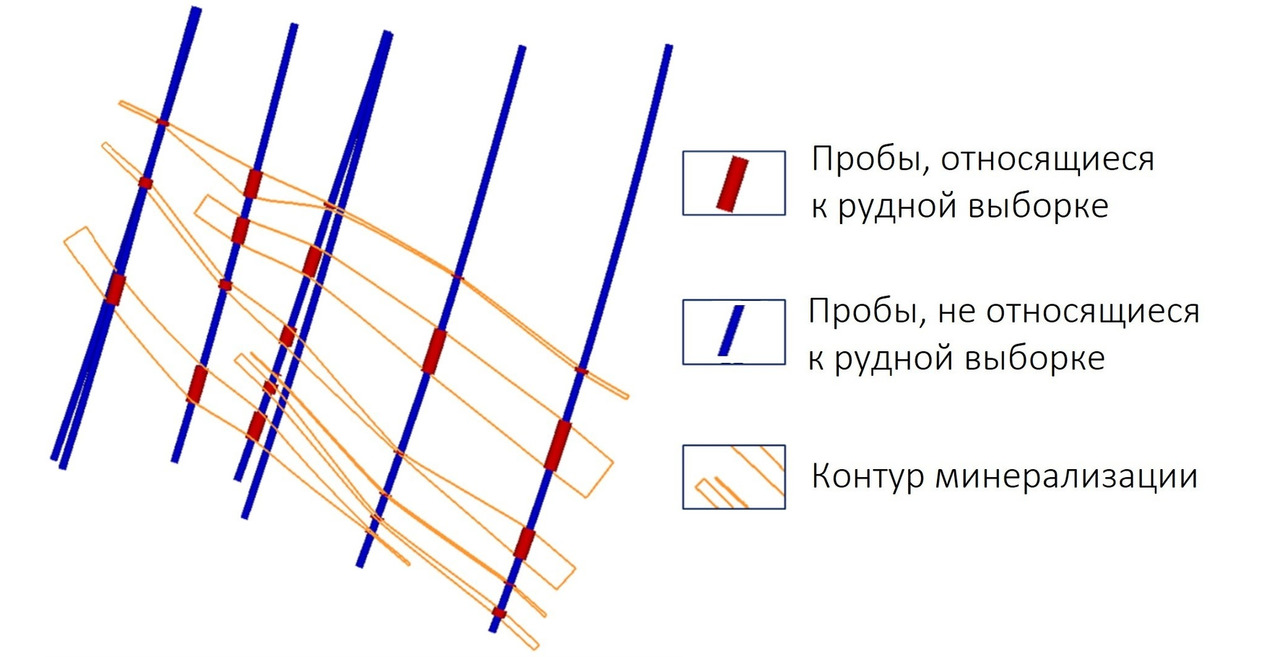
Оценку содержания в вашей будущей модели вы будете выполнять только по рудной выборке. Все пробы, которые остались за пределами каркасов минерализации, а также пробы, попавшие в каркасы, но исключенные из выборки, сколь бы «интересными» содержаниями они ни характеризовались, на качество вашей модели оказывать влияние не будут.

Этапы формирования рудной выборки

Рудная выборка — это важная часть ваших отчетных материалов. Практически это один из «китов» моделирования. Отсутствие рудной выборки в составе материалов моделирования — случай нередкий и очень печальный. По сути, отсутствие возможности понять, по каким данным выполнена оценка, кардинально снижает «ценность» модели (например, в этом случае невозможно достоверно сказать — использованы ли данные за тот или иной период разведки для построения модели или нет). Процесс моделирования должен быть «прозрачным» для любого, кто работает с моделью: у такого специалиста должна быть возможность понять, по каким данным выполнена оценка содержаний. Да, в общем, не исключен вариант, что этим специалистом будете вы сами через N месяцев. Неужели вы считаете, что будете помнить все аспекты моделирования? Или, может, вы настолько не любите себя, что не хотите облегчить жизнь себе из будущего?

Необходимо отметить следующий важный момент: пробы, исключенные из рудной выборки, в обязательном порядке также должны быть освещены в отчетных материалах с четким обоснованием причин исключения. Причина «что-то она мне не понравилась» вряд ли может считаться приемлемой.

К моменту формирования рудной выборки в вашем распоряжении уже есть каркасные модели минерализации. В каркасах может присутствовать поле зонального контроля, т. е. индивидуальный номер рудного тела или домена, а может и не присутствовать — опять же, зависит от выбранной методики моделирования. Методика построения каркасов в данной книге не рассматривается — как уже было сказано, это отдельная большая тема. Просто давайте будем считать, что каркасы минерализации вы уже построили, вы их проверили, и вы в них уверены.

«Стандартные» этапы формирования рудной выборки включают в себя:

— Выборка проб каркасами минерализации или кодирование проб каркасами (зависит от используемого программного обеспечения).

— Композитирование проб.

— Определение необходимости декластеризации и собственно декластеризация (если нужна).

— Определение необходимости урезки аномальных содержаний («ураганов»).

— Прочие трудно формализуемые манипуляции с рудной выборкой.

Каждый шаг должен сопровождаться анализом результатов этого шага. Крайне не рекомендуется «шагать вслепую», то есть выполнять следующий шаг, не оценив и не проанализировав результат сделанного. Такие действия рано или поздно приведут к тому же, к чему может привести прогулка с завязанными глазами — либо вляпаетесь во что-то нехорошее, либо вовсе куда-нибудь провалитесь.

Забегая немного вперед: все этапы моделирования, а не только создание рудной выборки, должны быть «прозрачными» — то есть стороннему наблюдателю должно быть «видно», что и как вы делали с вашими данными. Поэтому каждый шаг моделирования (в том числе и создание рудной выборки) должен сопровождаться прилагаемым результатом шага. То есть выбрали пробы каркасами — файл необработанной выборки сохранили в составе отчетных материалов. Композитировали — композитированная выборка отправляется в отчетные материалы. Урезали — аналогично. И то же самое с каждым этапом моделирования.

Выборка проб каркасами минерализации

Выборка/кодирование проб каркасами минерализации, в принципе, довольно простой шаг и в большинстве ПО выполняется с помощью нескольких «взмахов мышкой», тем не менее напомним о важных моментах в этой процедуре:

1. Если в каркасах минерализации присутствует номер рудного тела (рудной зоны, рудного домена), то выбор/кодирование проб каркасами должен выполняться с учетом этой особенности каркасов — т. е. в рудной выборке это поле также должно присутствовать.

2. При использовании номера рудного тела перечень номеров в рудной выборке должен совпадать с таковым в рудных каркасах. То есть количество и номера рудных тел в рудной выборке должны полностью соответствовать таковым в каркасах минерализации. Если внезапно в рудной выборке номеров рудных тел оказалось меньше, чем в каркасах, это, скорее всего, свидетельствует о проблемах с каркасами. Как бы вы ни были уверены в корректности последних, проверить их еще раз будет нелишним.

3. Крайне желателен визуальный анализ выбранных проб в сочетании с каркасами минерализации на предмет необоснованных изменений залегания тел или непонятных «подвесок» — вполне возможно, что в этих участках есть какая-то неприятность с каркасом.

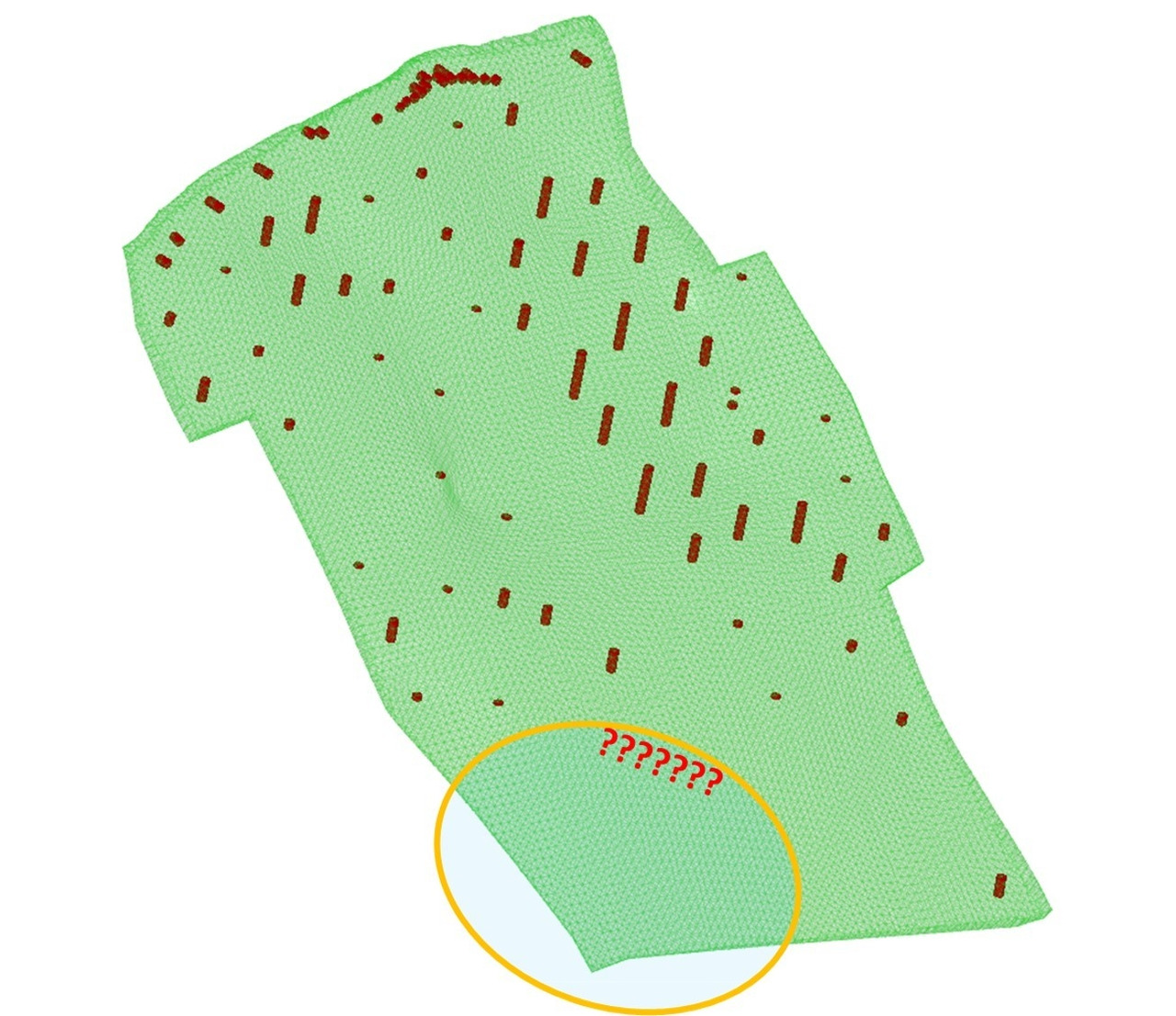
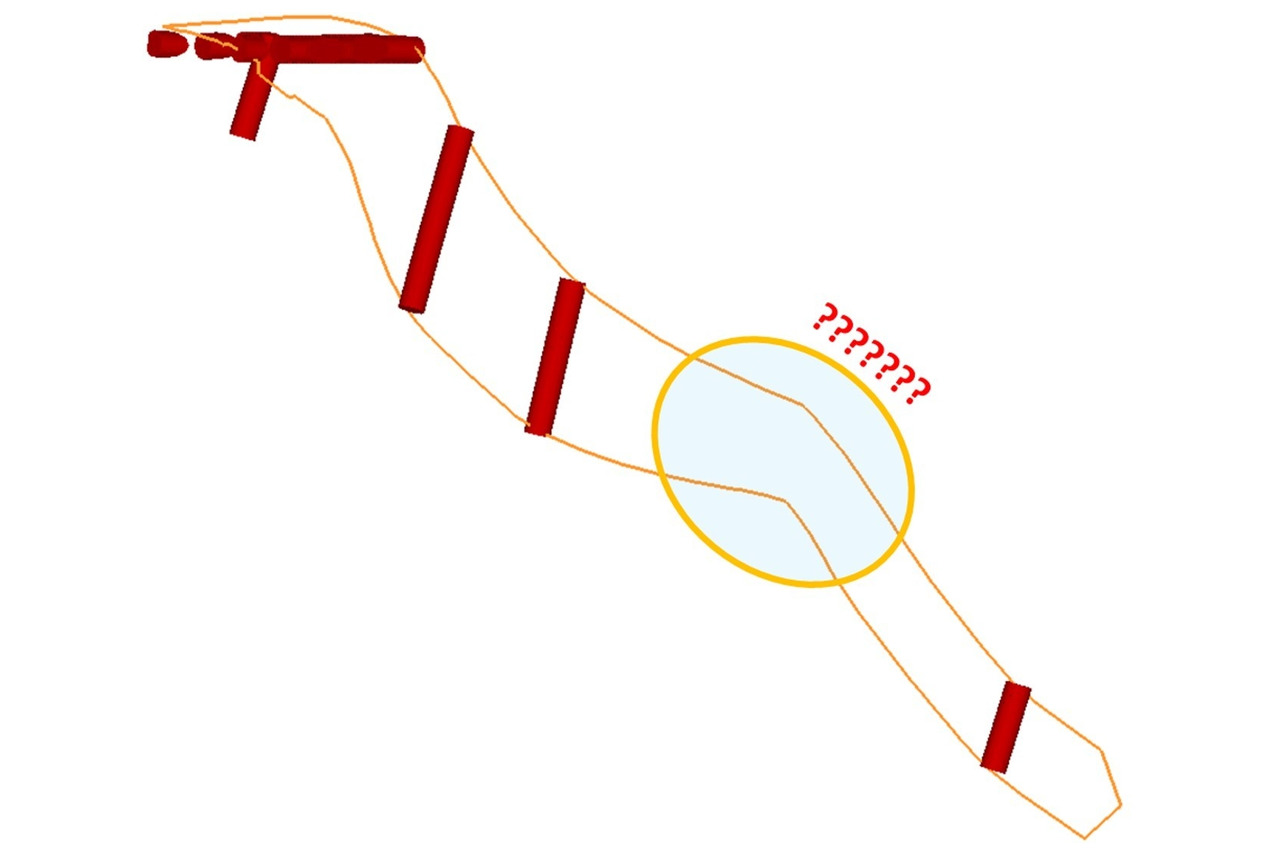
4. Также нелишним будет произвести анализ количества выработок, освещающих каждое рудное тело. Схема проверки примерно следующая:

— Составляется список номеров рудных тел. Если моделирование велось с использованием каркасов, лучше всего такой список составить именно на основе каркасов.

— Для каждого номера рудного тела выполняется подсчет количества выработок, освещающих данное тело. Если в результате подобной проверки обнаружатся рудные тела с нулевым количеством выработок, это однозначно ошибка (это может быть как ошибка в данных опробования, так и ошибка в каркасах — тут уж ищите причину сами). В случае наличия номеров, для которых количество выработок равно 1, необходимо напрячь память и вспомнить, присутствовали ли в ваших каркасах линзы, опирающиеся на единичные пересечения.

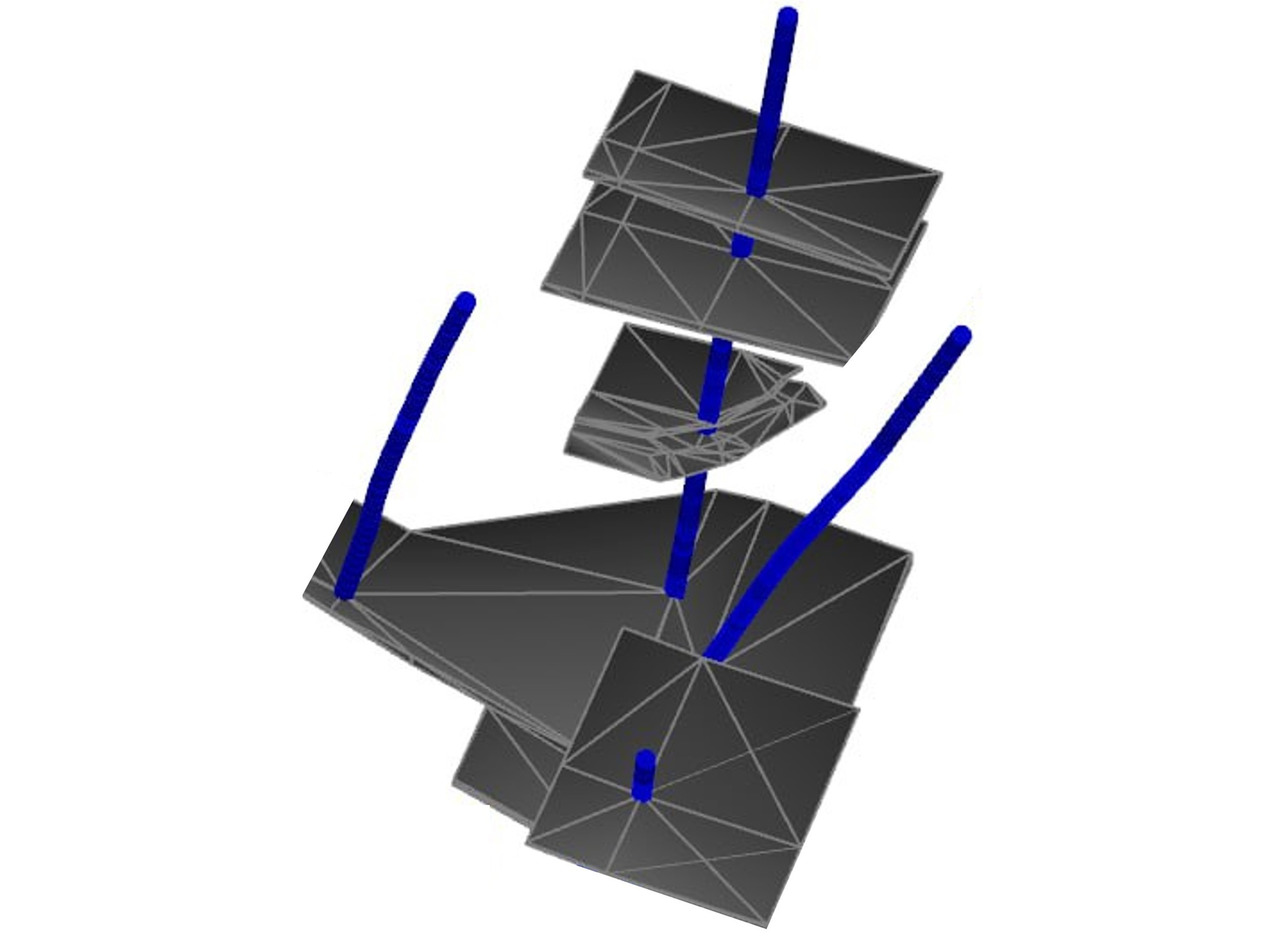
Если вы таких линз не строили, а тела с числом выработок равным единице присутствуют — очевидно, это тоже ошибка. Вообще, вопрос о целесообразности построения линз на единичных пересечениях — не самый однозначный. С одной стороны, этим мало кто занимается — возни много, толку мало: подобные линзы имеют низкую категорию достоверности и при технико-экономических расчетах обычно не используются. Кроме того, при нормальной степени разведанности месторождения на долю таких линз обычно приходится крайне незначительная часть ресурсов. И это при том, что оконтуривание таких линз должно выполняться по тем же принципам, что и оконтуривание «больших» тел — т. е. трудозатраты для их построения довольно значительны (а если считать трудозатраты «на единицу металла», значительно выше, чем для «больших» тел). Исходя из этого, кажется, что смысла в таких построениях почти нет. С другой стороны, подобная линза представляет собой цель для постановки доразведки: ну раз одна выработка что-то подсекла, давайте сгустим сеть — вдруг будет что-то интересное. И при редкой разведочной сети такое единичное пересечение может дать рудное тело неплохого размера, что, в свою очередь, может изменить перспективы того или иного локального участка (а если дело происходит на фланге рудной зоны — то может и не локального). В общем, решение о том, стоит ли возиться с подобными случаями, принимаете вы. Но мы бы рекомендовали при наличии времени постараться построить линзы хотя бы на наиболее «интересных» пересечениях, которые невозможно проследить.

5. Выбранные пересечения очень нелишне проанализировать на соответствие их используемым параметрам кондиций. В случае обнаружения пересечений, которые таким параметрам не удовлетворяют, будет полезным проанализировать причины попадания таких пересечений в контуры рудных тел (то есть это не обязательно ошибка).

6. Если вот совсем хочется помучиться, будет нелишним проанализировать рудную выборку на предмет «геометрического» соответствия каркасам: совпадают ли концы пересечений с узлами каркасов. По-хорошему должны совпадать полностью. Если вдруг обнаружилось, что это «не совсем так», стоит проанализировать причины такого несоответствия.

Краткое резюме

1. Рудная выборка — та часть данных опробования, которая характеризует моделируемую зону минерализации. Это единственный источник оценки содержаний в вашей модели.

2. Рудная выборка — это не просто исходные пробы, характеризующие минерализацию. Это пробы, которые подверглись всем тем трансформациям, которые вы посчитали необходимым произвести с исходными данными: выборка, композитирование, декластеризация, исключение отдельных групп проб, урезка ураганных содержаний и т. д.

3. Отчетные материалы должны отражать все манипуляции с пробами для получения рудной выборки. При этом в отчетных материалах должны присутствовать результаты всех сделанных вами шагов обработки:

— Вы выполнили выборку проб каркасами рудных тел — файл проб, выбранных каркасами, отправляется в состав отчетных материалов.

— Вы решили, что та или иная группа проб (или отдельные пробы) не должна участвовать в оценке содержаний — файл рудной выборки с исключенными пробами отправляется в состав отчетных материалов (то есть это уже второй файл рудной выборки в отчетных материалах).

— Вы композитировали пробы на среднюю длину (вычислили вес декластеризации) — аналогично: результат в отчетные материалы.

— Вы урезали аномально высокие содержания… ну, вы поняли.

4. Отчетные материалы, не содержащие рудную выборку, «стоят» очень немного. Отчетные материалы также в обязательном порядке должны содержать обоснование всех манипуляций:

— Выполнили композитирование — приводите гистограмму (гистограммы), из которых следует, что длина композитирования выбрана верно.

— Выполнили исключение проб — очень внятно и подробно пишем, почему эти пробы не достойны носить гордое звание членов рудной выборки.

— Урезали содержания — приводим все необходимые графики, расчеты и, естественно, уровни урезки (авторам встречались довольно забавные случаи, когда в отчете приведены графики, расчеты, скриншоты и т. д., но таблицу с уровнями урезки исполнитель предоставить забыл).

5. Кроме всего прочего, рудная выборка — неплохой инструмент проверки ваших построений.

Рудная выборка — это основа вашей будущей модели. В отношении нее в полную силу действует стандартное правило «мусор на входе — мусор на выходе». Попытаемся пояснить эту неложную истину реальными примерами из собственной практики работ.

# Пример из практики

Месторождение золота. Минерализация представлена серией тел субмеридионального простирания с размерами ~300—400×150—200 м и средней мощностью около 30 м. Месторождение имеет довольно длительную историю освоения: оно изучалось начиная с 60-х годов прошлого века. В результате этих работ на площади месторождения была создана разведочная сеть с шагом 50×50 м (в центральной части). В текущем веке изучение продолжилось, и разведочная сеть была сгущена до 50×25 м и 25×25 м.

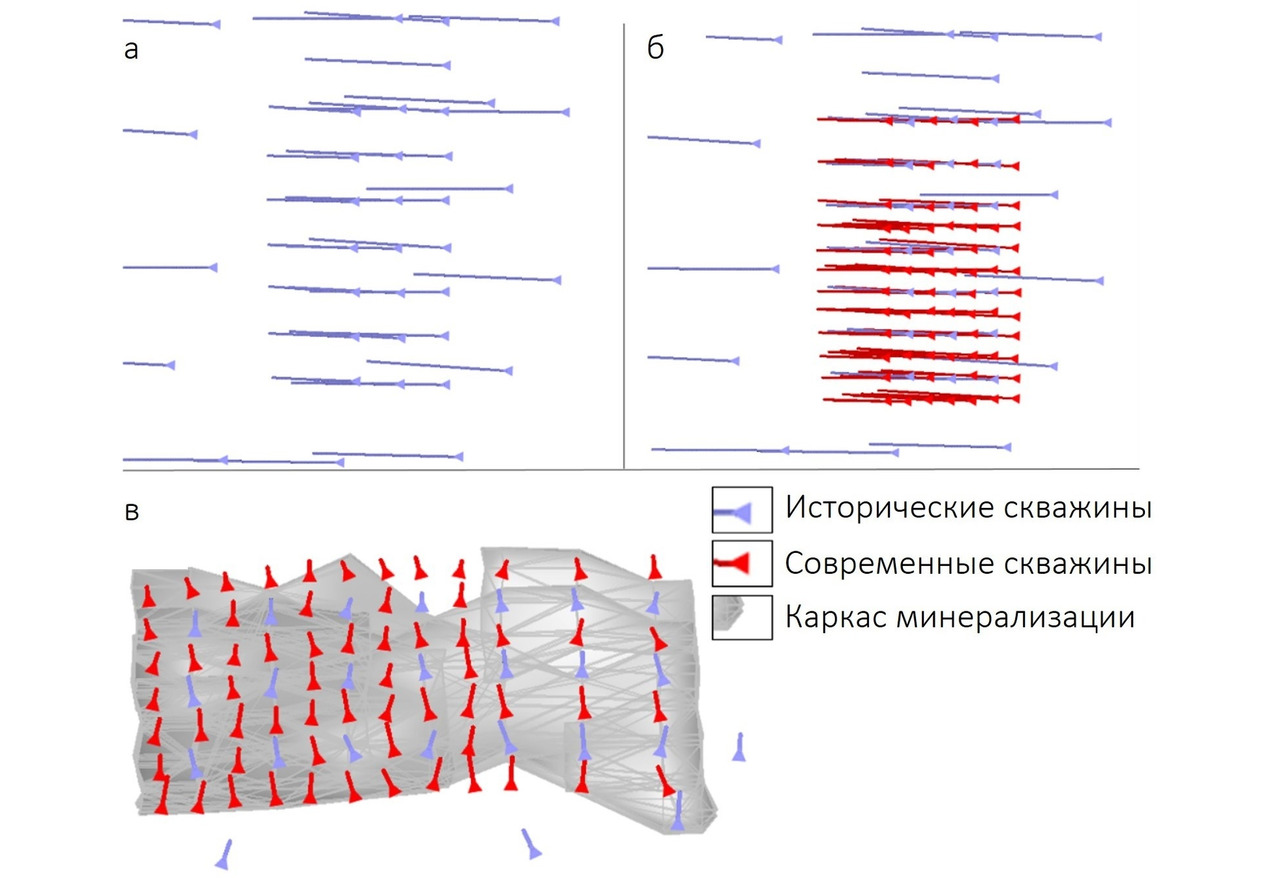
Далее на основании всей имеющейся информации по опробованию было выполнено моделирование зон минерализации и запланированы добычные работы. При этом на некоторых участках, запланированных к первоочередной отработке, к моменту начала добычи разведочная сеть не была сгущена до 25×25 м. Внезапно при добычных работах был получен довольно ощутимый «неотход» металла на фабрике. Разница между «содержаниями по модели» и «содержаниями по факту переработки» составила -18%.

Возникли закономерные стандартные вопросы «Почему не выполнили?». И вот только на этом этапе у геологов появилось желание выполнить анализ данных, т. е. сопоставить данные исторического и современного бурения. По результам переработки сделали вывод, что причина неотхода кроется в ошибочной оценке содержаний, тогда как оценка количества минерализации выполнена верно.

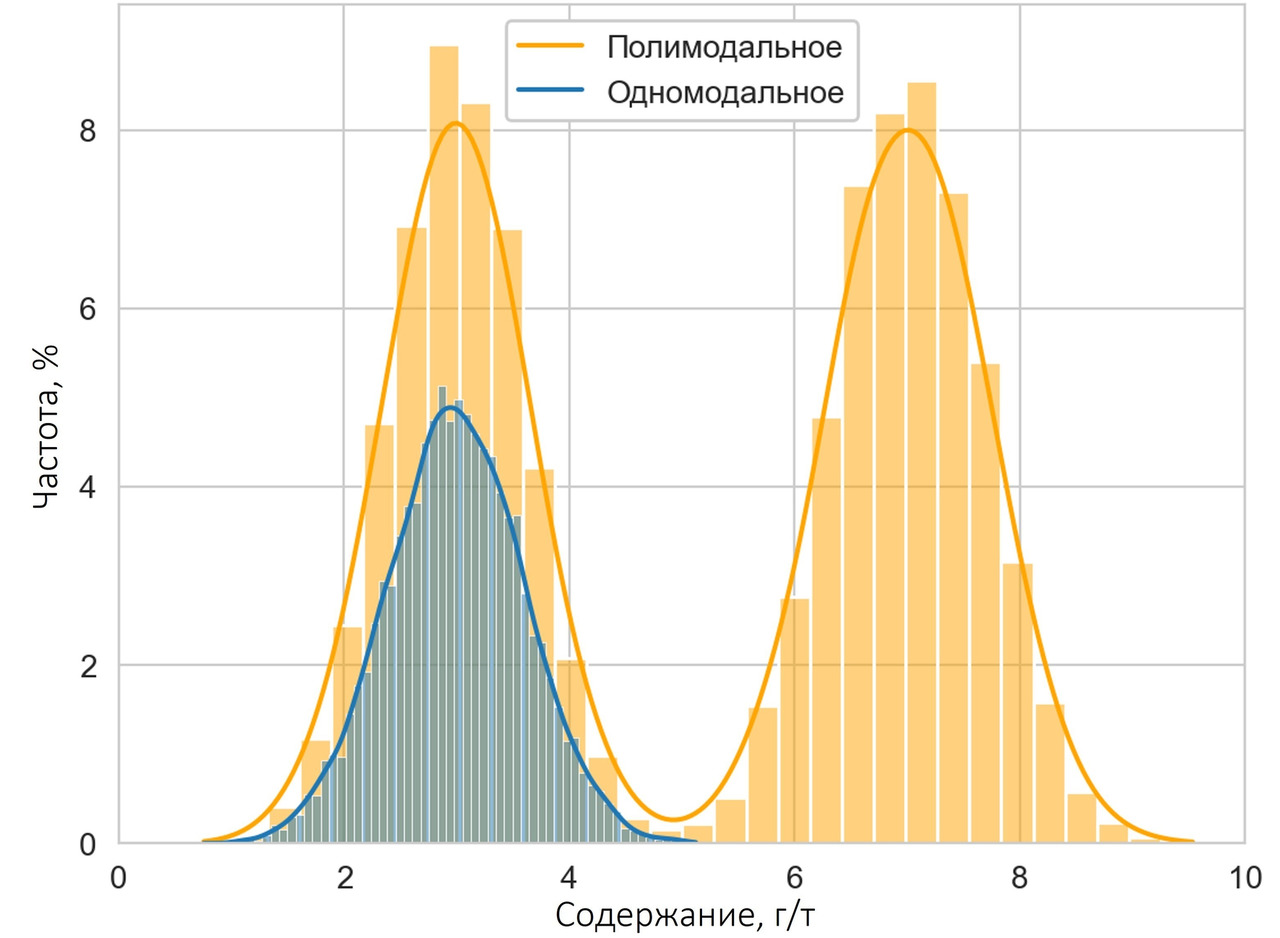
Предположение о том, что исторические данные завышают содержания, было изначально проверено с помощью гистограммы, построенной по полному набору данных. Подобная гистограмма, к некоторому удивлению, наличие полимодальности не обнаружила. Разбивка полного набора данных на группы «исторические»/«современные» особой ясности не внесла.

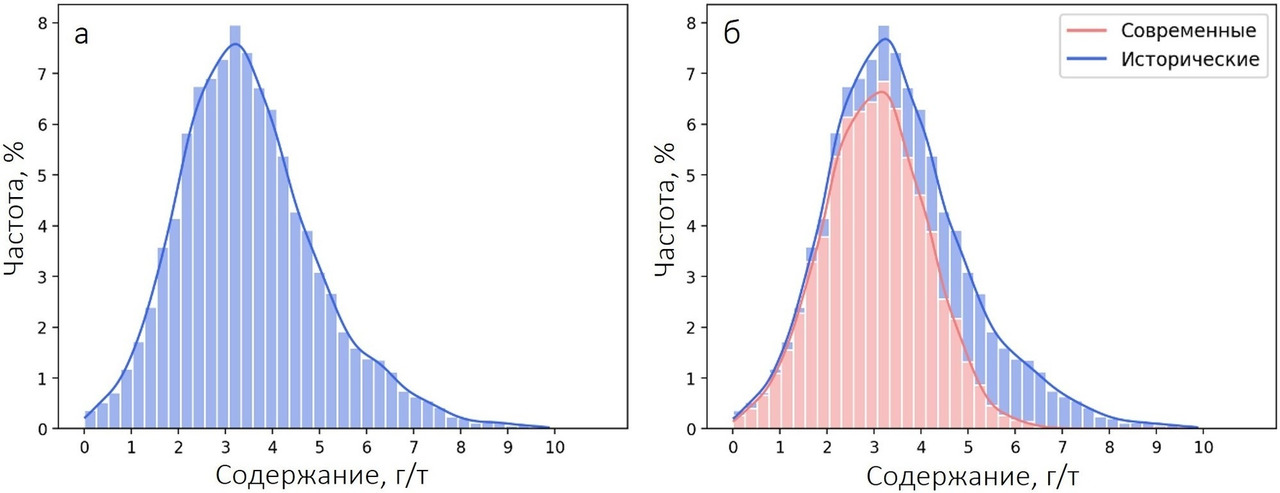
Однако геологов не покидало ощущение, что что-то здесь не так. А что именно? Давайте посмотрим на гистограмму с разбивкой. Невооруженным взглядом видно, что исторических данных намного меньше, чем современных. Кроме того, если присмотреться чуть внимательнее, можно заметить некоторый рост количества исторических данных в области повышенных содержаний.

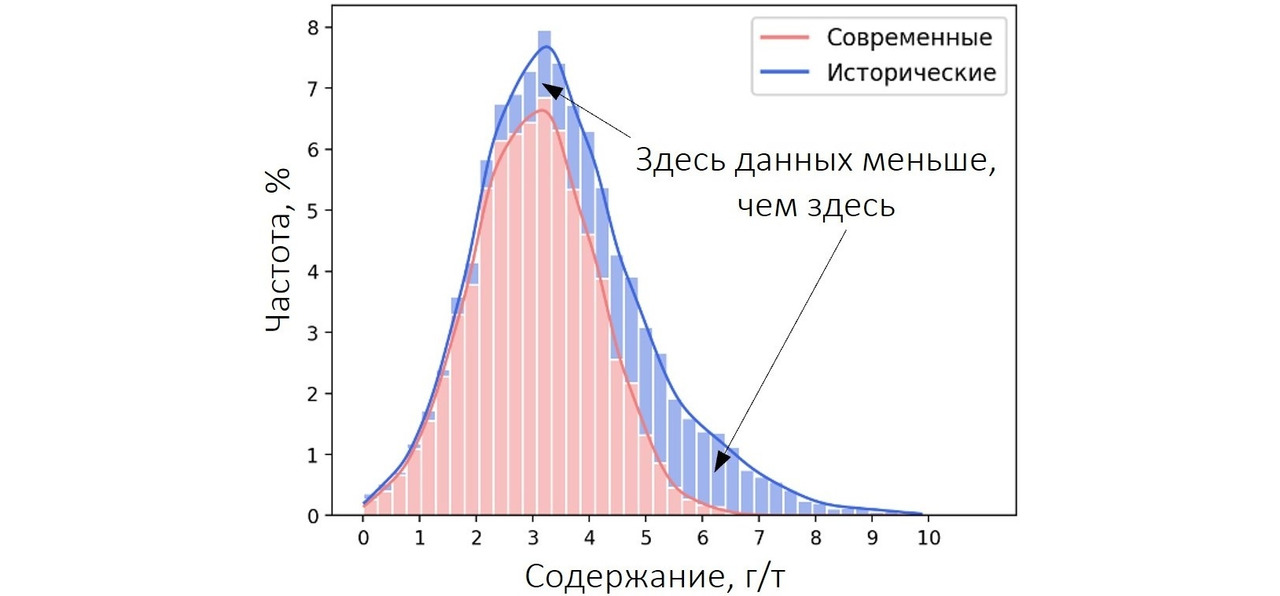
При этом доли соответствующих данных рассчитаны от общего количества наблюдений (исторические + современные). Почему это важно? А потому, что при одинаковом масштабе отображения разницу между (условно) 50 и 30 на глаз видно прекрасно, между 5 и 3 — уже хуже, между 0.5 и 0.3 — намного хуже, а разницу между 0.05 и 0.03 вы на глаз не увидите, хотя соотношение между перечисленными величинами сохраняется. То есть чем меньше сравниваемые величины, тем сложнее их различить визуально. Давайте теперь построим ту же гистограмму, но без какого-либо смешивания выборок. И доли проб будем считать от количества данных соответствующего периода: доли исторических данных — в процентах от количества исторических данных, доли современных — в процентах от современных данных.

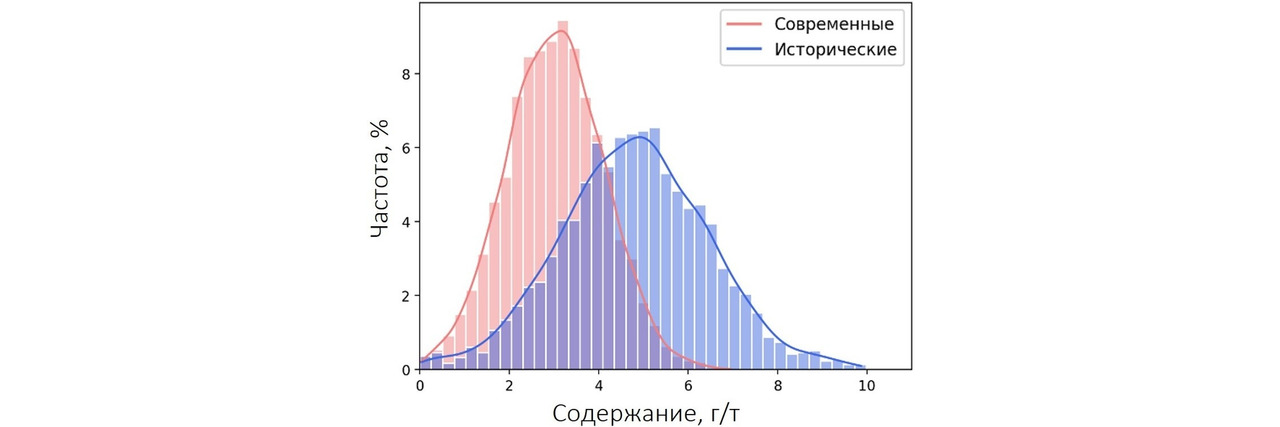
Что тут скажешь… Полимодальность, однако. Давайте дополнительно посмотрим квантиль-квантильную диаграмму.

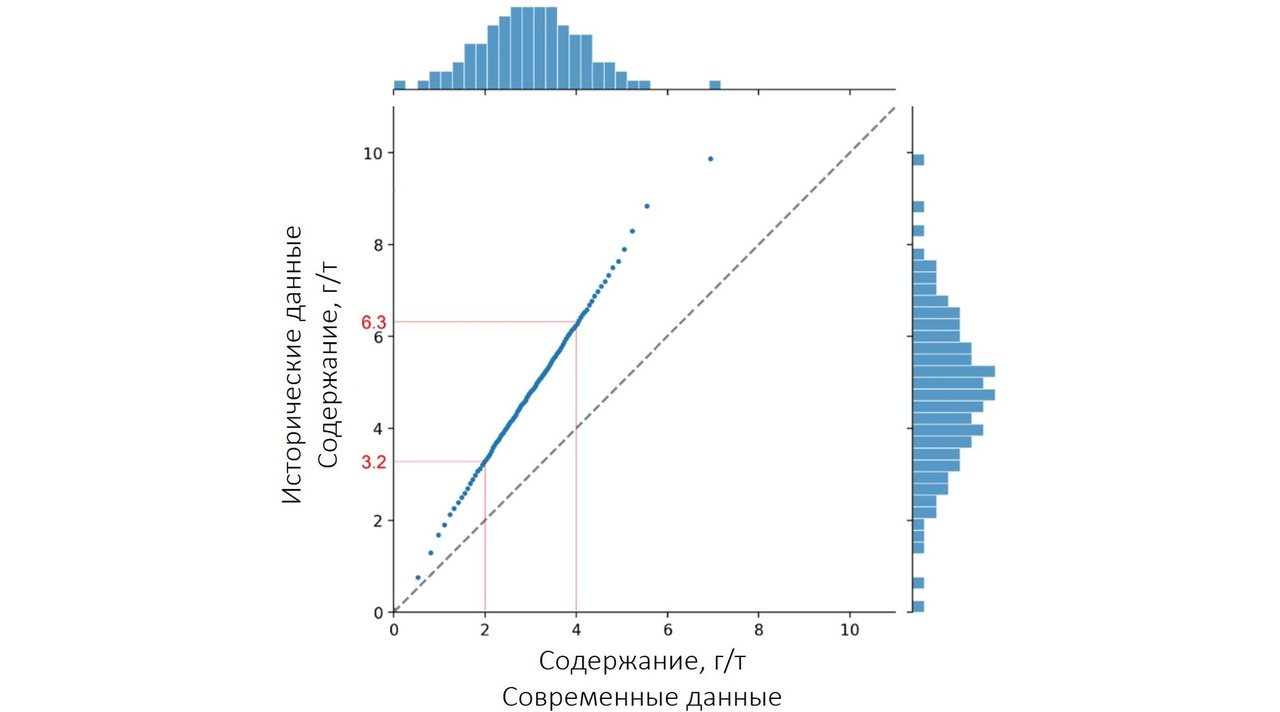
Вот тут вообще красота: систематическое завышение содержаний в исторических данных по всему диапазону содержаний. В результате тяжких раздумий было принято решение выполнить полное перемоделирование месторождения, исключив из рассмотрения исторические данные. Закономерный финал: количество минерализации осталось почти тем же, а вот содержания упали довольно ощутимо. Неприятно, но это лучше, чем недополучение металла в процессе переработки. Вывод из описанного душераздирающего примера очень прост: получив в руки перед началом моделирования исторические данные, не поленитесь выполнить сравнительный анализ данных, полученных в разное время и/или разными способами. Иначе на вас запросто «повесят» недополученный металл. А оно вам надо?

# Пример из практики

Пример, аналогичный предыдущему, только теперь на месторождении серебра.

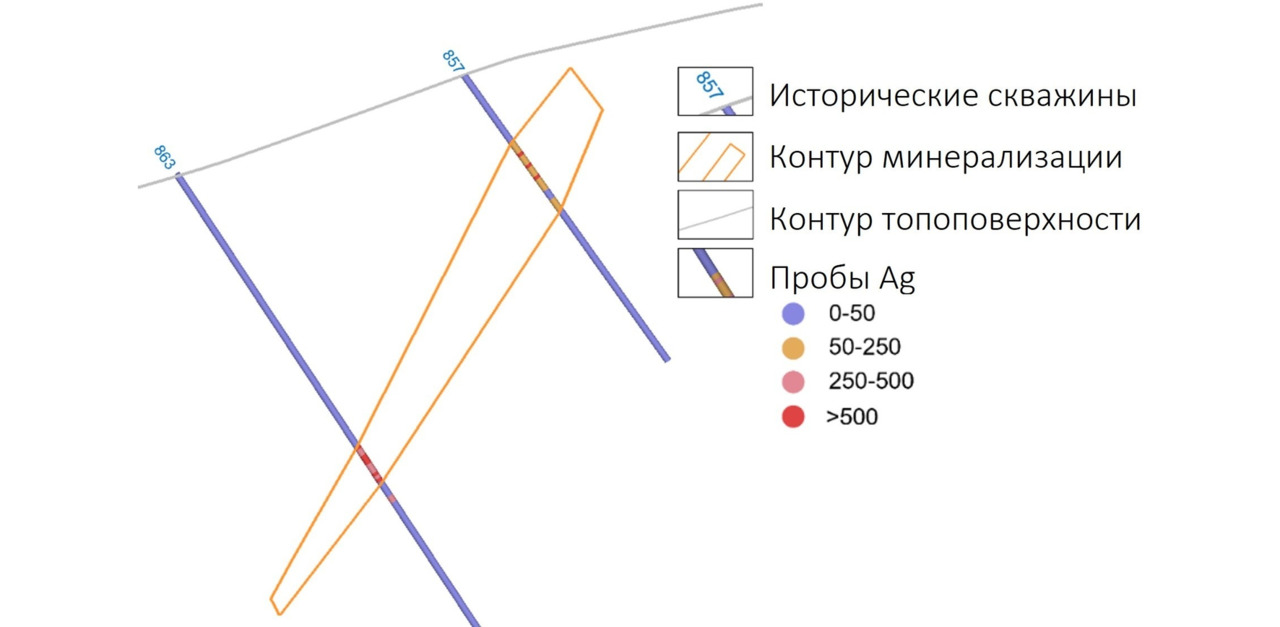
После построения модели по историческим данным были начаты работы по сгущению сети. Для нескольких скважин было выполнено заверочное бурение, заключавшееся в бурении новых скважин в непосредственной близости от заверяемых. Заверке подверглись 8 скважин. В результате выполненных работ по 5 скважинам было обнаружено несоответствие данных предыдущих периодов современным, выраженное в ощутимом смещении границ ранее построенных зон минерализации.

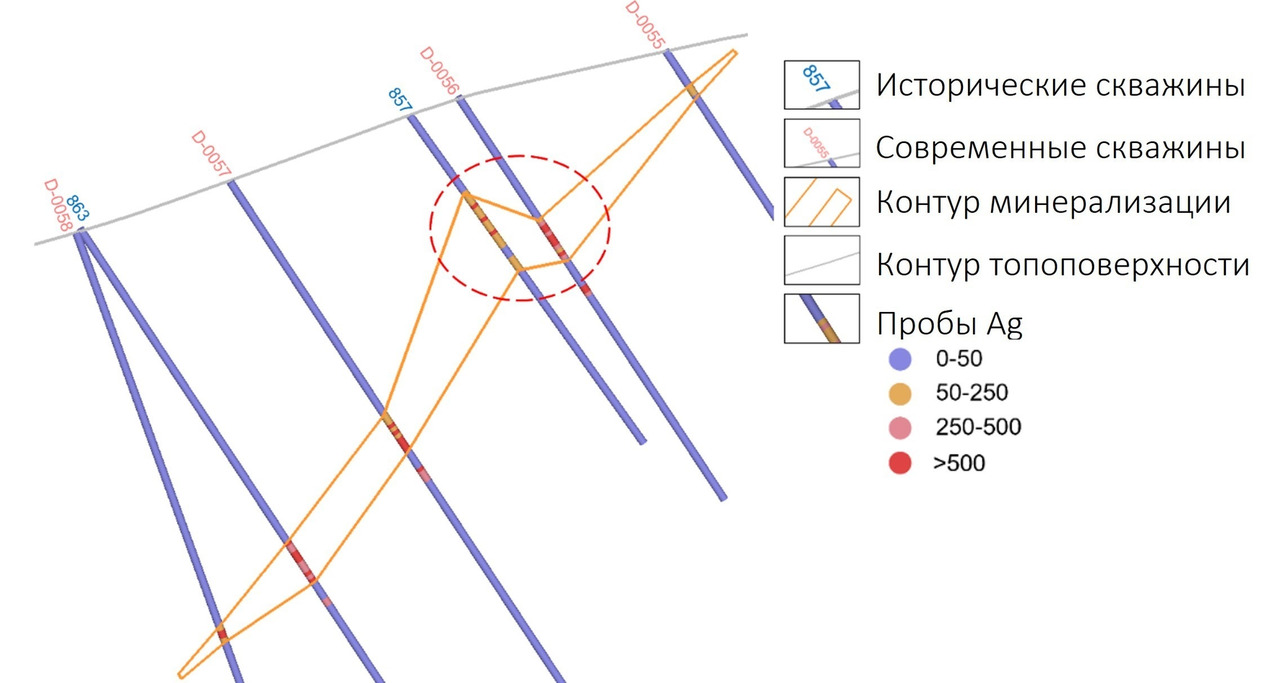
Геологи проигнорировали несоответствие между современными и историческими данными и отстроили контур минерализации с использованием всех данных. Но внезапно с началом выполнения сопровождающей эксплуатационной разведки минерализация в ожидаемых местах не была вскрыта.

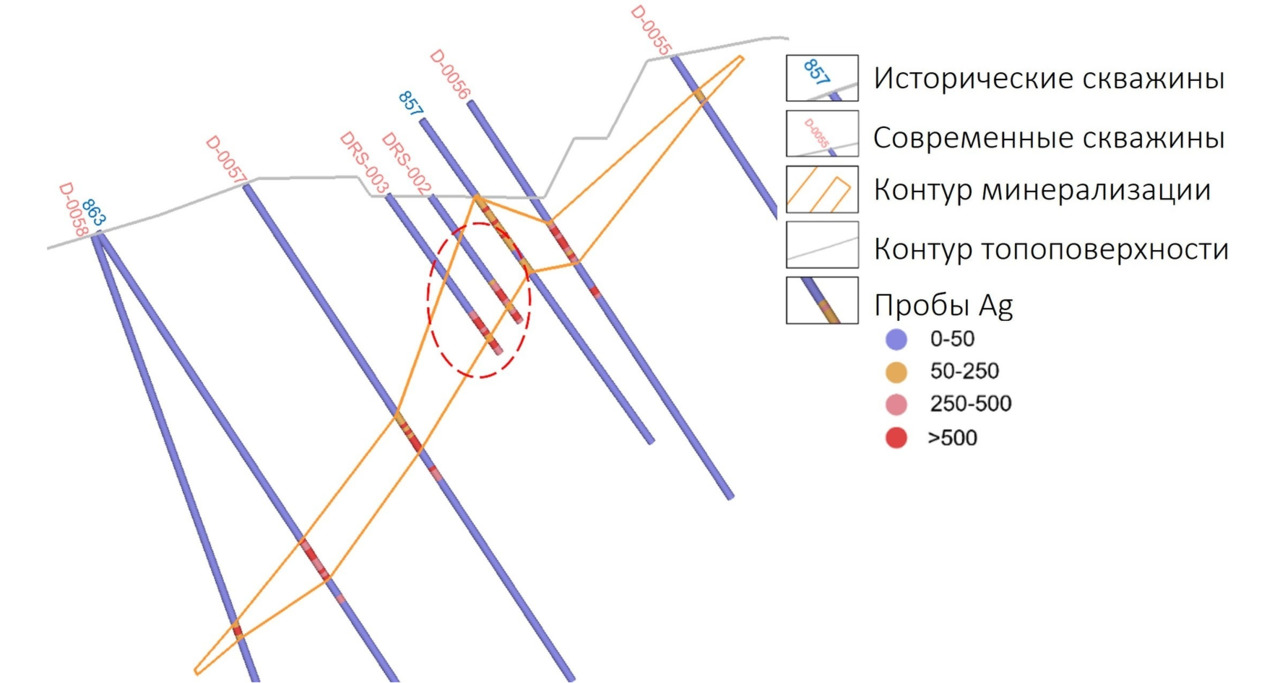
И только после того как выявленное и проигнорированное несоответствие в данных привело к проблемам при добыче, было принято решение выполнить анализ соответствия исторических и современных данных. Анализ показал, что по части скважин предыдущих периодов не совпадают не только пространственное положение минерализованных зон, но и содержания.

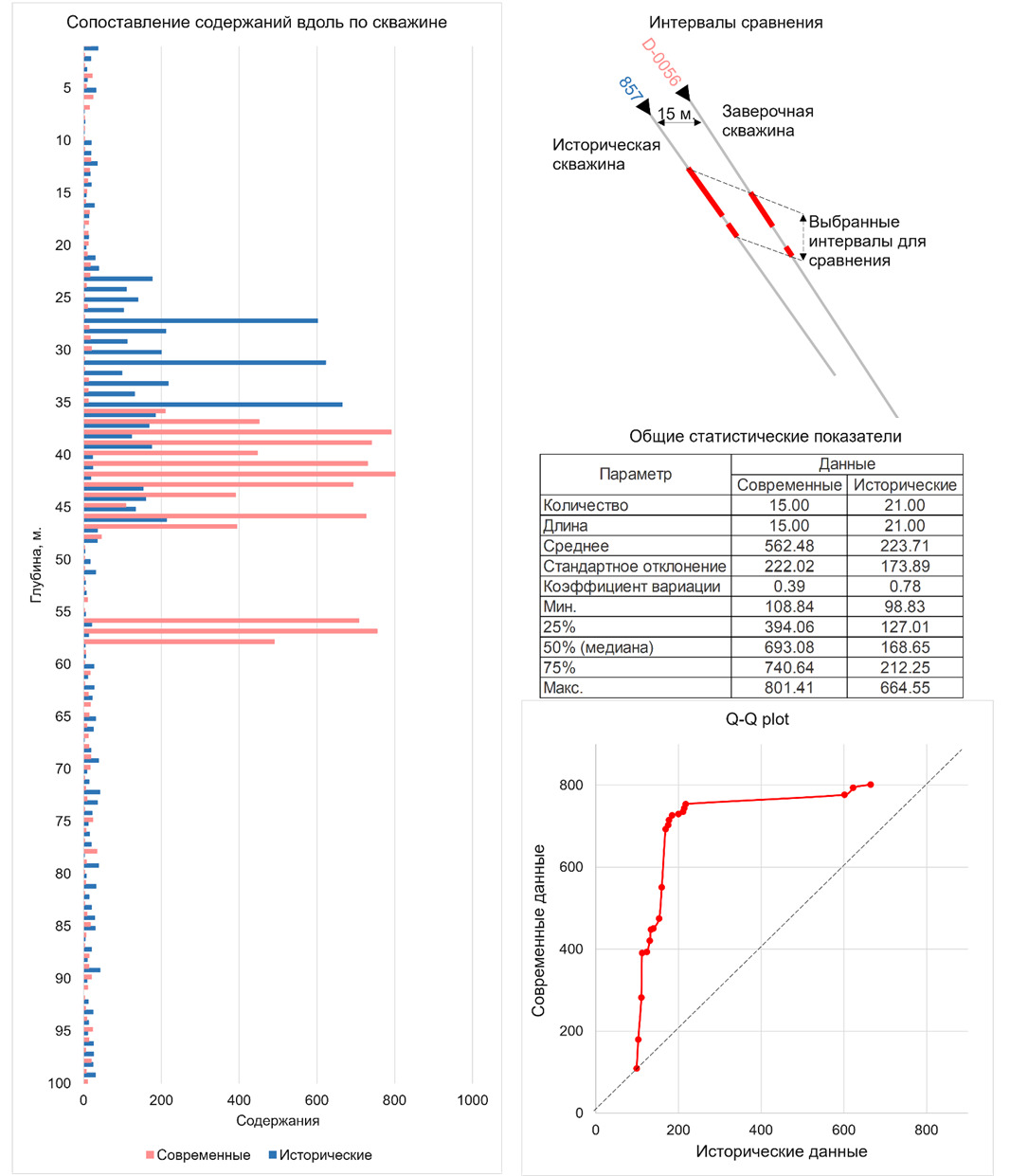
По результатам выполненного сопоставления было принято решение исключить из рудной выборки исторические скважины с неподтвержденными данными и провести перемоделирование в соответствующих участках. Там, где расхождений выявлено не было, исторические данные не исключались.

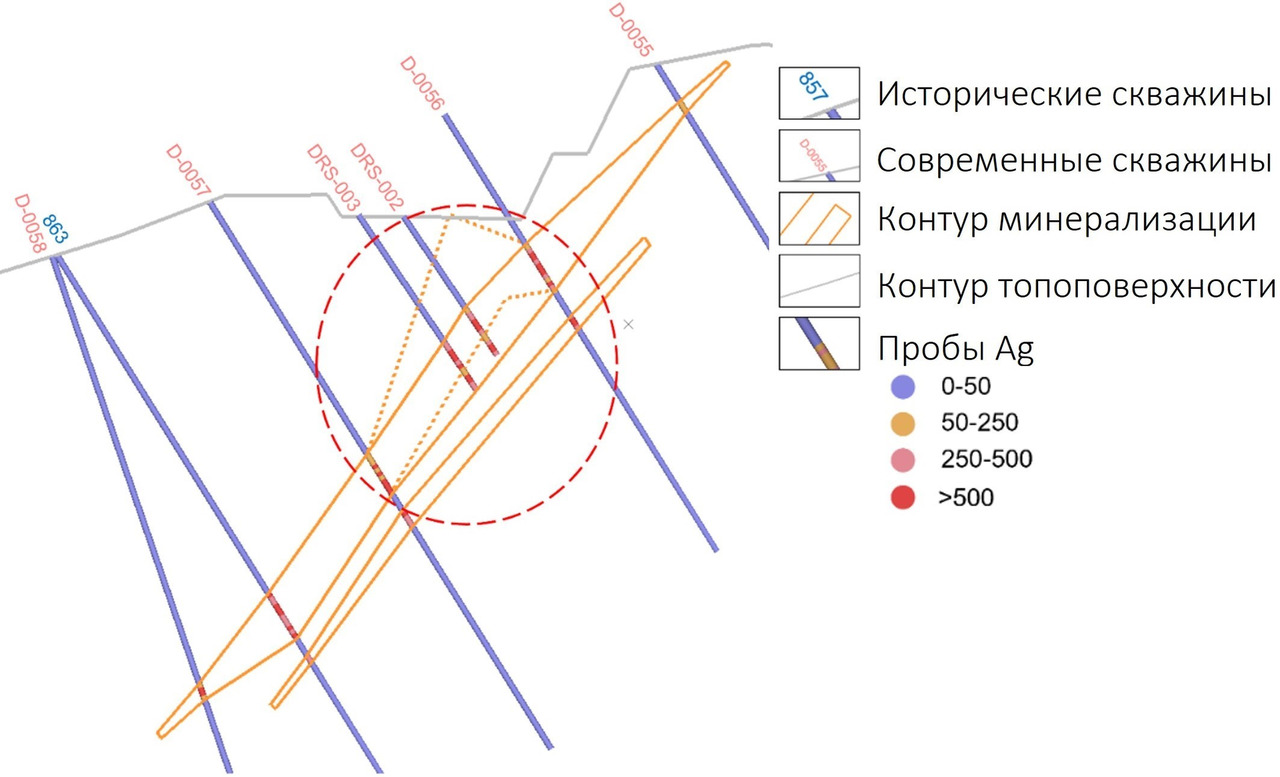
В данном случае все кончилось относительно благополучно, если не считать неверно рассчитанных календарных планов отработки, предполагаемого получения прибыли, времени, потраченного на поиск и устранение проблем, а также нервов всех вовлеченных в эту поучительную историю.

# Пример из практики

Месторождение золота, представленное кварцевыми жилами с крайне высоким содержанием. Жилы сопровождаются зонами дробления и прожилкования, а также метасоматической проработки. Мощность стержневых жил составляет первые метры, зон околожильных изменений — до 10–15 м.

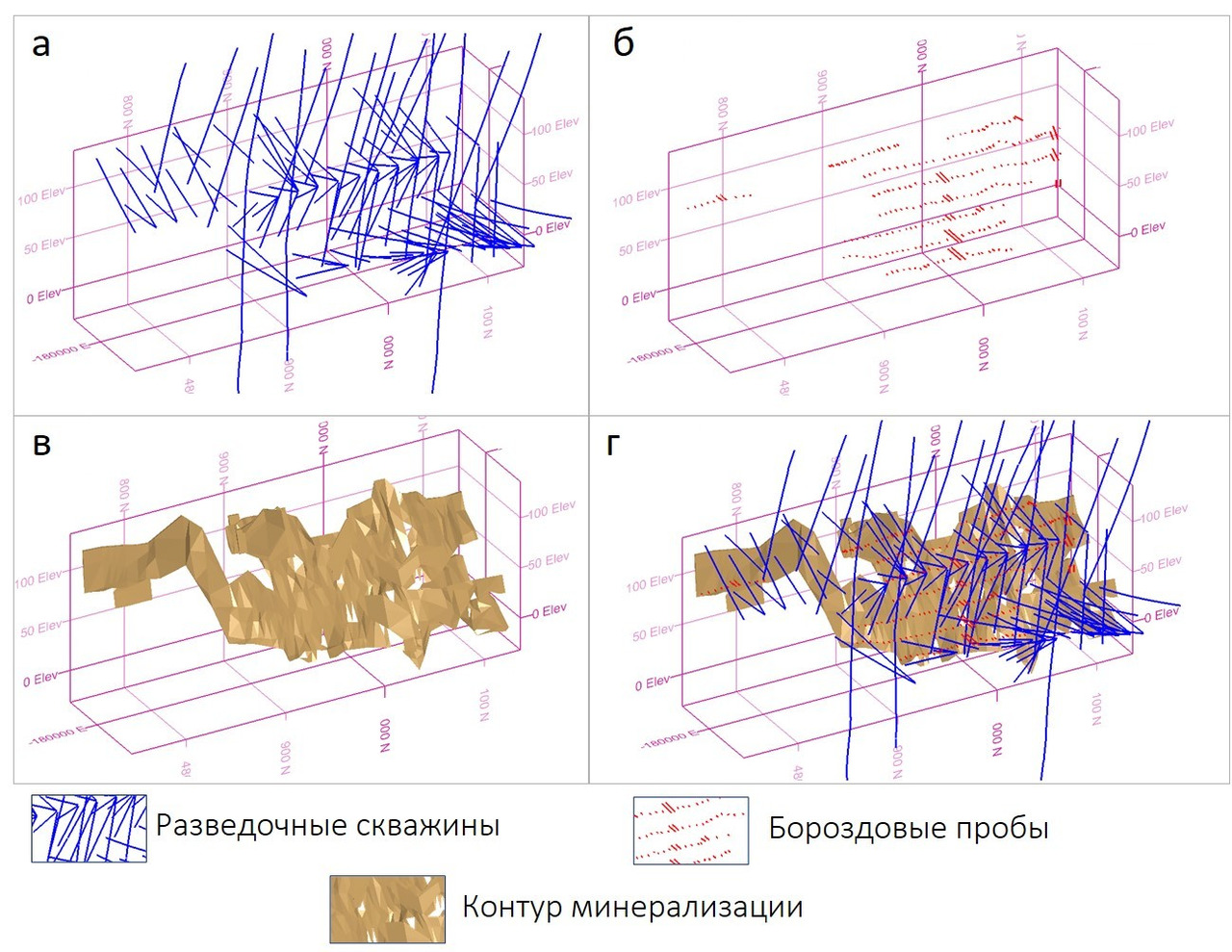
Месторождение отрабатывалось подземным способом с 50-60-х годов предыдущего века. В текущем столетии изучалось скважинами колонкового бурения по сети ~20—25×20—25 м (на флангах — реже). Историческое опробование представлено довольно объемным массивом бороздовых проб, отобранных по горизонтам подземных выработок с шагом ~2—3 м. Основная проблема исторического опробования заключается в том, что опробованию подвергались главным образом стержневые жилы с высокими содержаниями (20–30 г/т, зачастую выше), а зоны дробления и метасоматической проработки пристального внимания не удостаивались. Современные данные представлены результатами анализов кернового опробования, отобранного по всей минерализованной зоне (стержневая жила + зальбанды). Несложно догадаться, что в настоящее время промышленный интерес представляют не только стержневые жилы, но и зоны околорудных изменений.

Проблема в том, что современных данных, по сравнению с историческим опробованием, не так чтобы очень много: по минерализации, представленной на рисунке выше, более 60% массива опробования составляют бороздовые пробы, а керновые — соответственно, не более 40%. Причем приведенный пример — не самый «страшный» — бывают случаи, когда доля исторических данных составляет около 80% массива опробования.

Моделирование «в лоб» по всему массиву данных и последующая отработка всей массы минерализованных пород ожидаемо привело к факту «неотхода» металла на фабрике.

И вот здесь начинается самое интересное. Во-первых, не очень понятно, как сопоставлять исторические данные с современными. Просто сравнить полностью выборку современных данных и полностью выборку исторических данных — не вариант, учитывая схему опробования. Любые попытки подобного сопоставления дают совершенно ожидаемый результат завышения содержаний в данных предыдущих периодов.

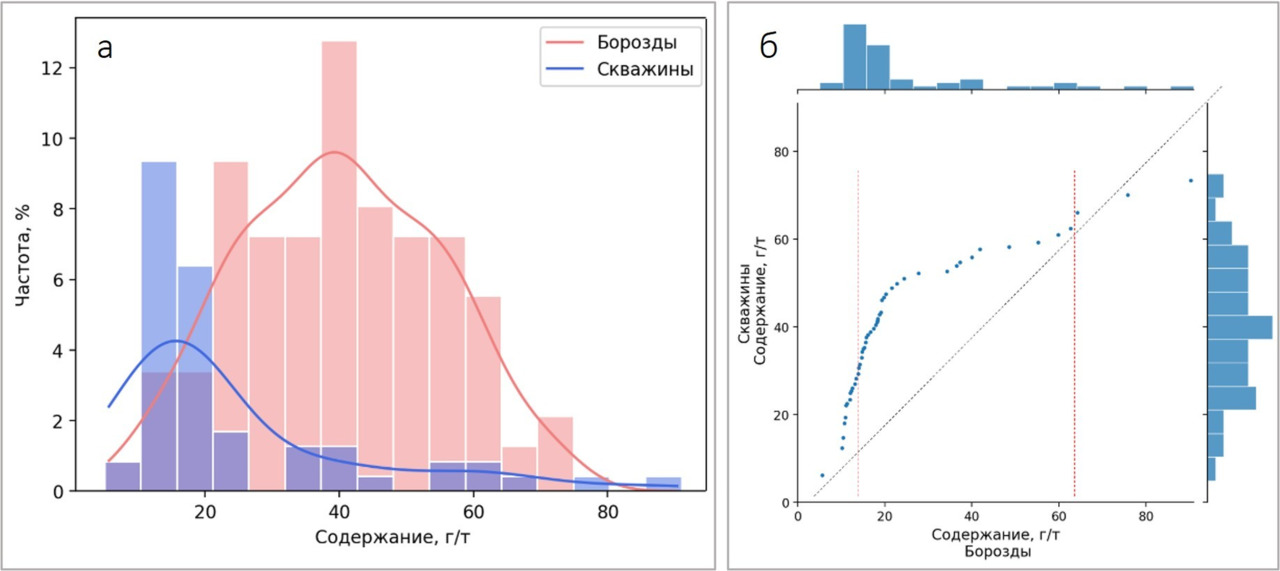
И в данном случае непонятно: то ли причина завышения — принципиальные различия в схеме опробования, то ли действительно имеет место завышение. Или обе причины. Выделить сопоставимые части не представляется возможным: как было сказано чуть выше, основная масса проб — это пробы из стержневых жил. Однако пробы из околожильных пород тоже присутствуют, беда в том, что непонятно, в каком соотношении: литологическая характеристика в исторических данных отсутствует. То есть понятно, что проб из околожильного пространства существенно меньше, но насколько? Опять же, есть опробование из зальбандов, сколько его — непонятно, но в любом случае историческими данными вся зона минерализации почти нигде не пересечена. И что делать? Просто выбросить исторические бороздовые пробы? Мы сразу лишаемся 60% данных опробования. Неприятно, однако.

Сопоставлять ближайшие пробы? Хорошо, если часты случаи, как на рисунке ниже.

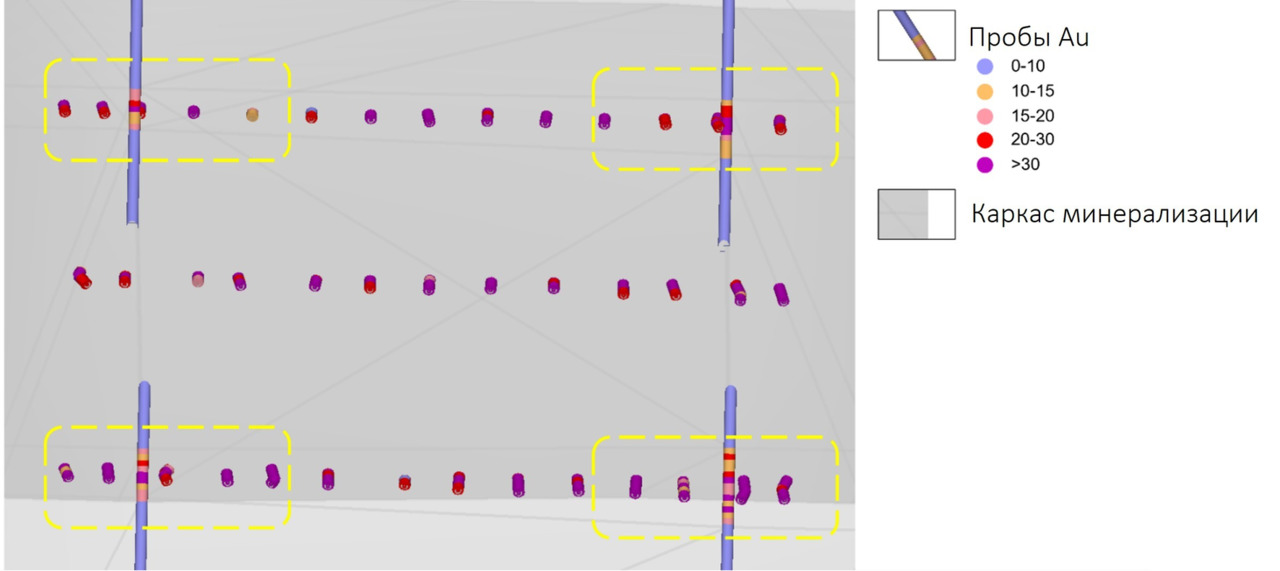
Но чаще всего так не получится: борозды отбирались по горизонтам выработок, а разведка скважинами запроектирована таким образом, чтобы освещать пространство между горизонтами. Соответственно, между ближайшими пробами может быть и 5, и 10 м, и мы возвращаемся в исходную точку.

Можно, конечно, сделать вид, что все прекрасно, никакого завышения нет, и пытаться моделировать по всей выборке. Результат такого моделирования приведен выше — неотход металла на фабрике. И причина понятна — бороздовые пробы «задавливают» массой: поисковый эллипсоид набирает максимум из исторических данных, а современные игнорируются.

В общем, что делать — непонятно. К сожалению, однозначного окончательного решения у этой проблемы нет. Варианты есть, но они все не идеальны:

— Введение понижающего коэффициента. Самый простой способ и, наверное, самый «лежащий на поверхности». Но в итоге мы получаем новую искусственную величину, которая ведет себя довольно непредсказуемо в разных частях одного и того же месторождения. Понижающий коэффициент может несколько сгладить очевидное неподтверждение содержаний (а при избыточном усердии даже привести к переотходу металла), но эффект от его применения скорее психологический (ну что-то же делать надо!). В общем, на наш взгляд, путь откровенно тупиковый. Вообще, любое введение искусственных понижающих/повышающих и прочих коэффициентов, не имеющих никакого обоснования, кроме «давайте подгоним», — это тупиковый путь.

— Постепенное разбуривание минерализации скважинами и создание плотной регулярной сети данных. Идеальный вариант, если бы не одно «но»: данные нужны «вотпрямщас», поскольку отработка уже идет.

— Попытка выделять внутри минерализации домены стержневых жил, опираясь только на содержания с последующей интерполяцией раздельно по жилам и околожильным породам. Тоже очень неплохой вариант. На бумаге. На практике также начинают «вылезать» проблемы с определением граничного содержания для стержневой жилы и т. д.

Описанная ситуация является почти типичной на месторождениях Северо-Востока России, изучение которых началось в «глубоко советское» время. Очень часто здесь массив исторических данных представляет собой эдакий «чемодан без ручки»: и использовать невозможно, и выбросить жалко. В каждом конкретном случае решение чаще всего принимается волевым порядком, сопровождается довольно ощутимыми рисками, а специалист, принявший это решение, впоследствии зачастую имеет полный набор бодрящих последствий.

Общий статистический анализ одной величины

Прежде чем переходить к обсуждению темы, заявленной в заголовке, дадим краткое пояснение. По мнению авторов, понимание смысла терминов и смысла формул намного важнее, чем механическое заучивание определений и формул без их смыслового наполнения. Поэтому в ряде случаев будут использованы методы объяснения, очень далекие от наукообразности и не выдерживающие никакой критики с точки зрения высокой статистики. Но зато, надеемся, позволяющие понять суть объясняемых терминов. Строгие академические определения желающие смогут найти в справочниках и учебниках по статистике.

Генеральная совокупность и выборка

Первое, что необходимо обсудить в рамках настоящей главы, это такие понятия, как выборка и генеральная совокупность.

Выборка — это любой набор данных, имеющихся в распоряжении исследователя. Это может быть набор данных опробования по отдельному горизонту, по отдельному рудному телу, группе тел, участку месторождения или всему месторождению целиком. Или просто случайно попавший в руки геолога отдельный журнал опробования. То есть выборка — это тот реальный набор данных, который есть в распоряжении геолога.

Генеральная совокупность — некая математическая абстракция, это выборка, которая содержит все возможные значения некоторой величины для данного объекта. То есть это «все возможные данные». Например, генеральной совокупностью можно считать данные о содержании какого-либо компонента в каждой точке рудного тела (генеральная совокупность содержаний по данному рудному телу), участку месторождения (генеральная совокупность содержаний по участку месторождения). Из подобного «определения» становится ясно, почему генеральная совокупность — это абстракция: просто потому, что в большинстве случаев она недостижима. Даже обладая бесконечным финансированием, невозможно получить содержания в каждой точке рудного тела/участка/месторождения.

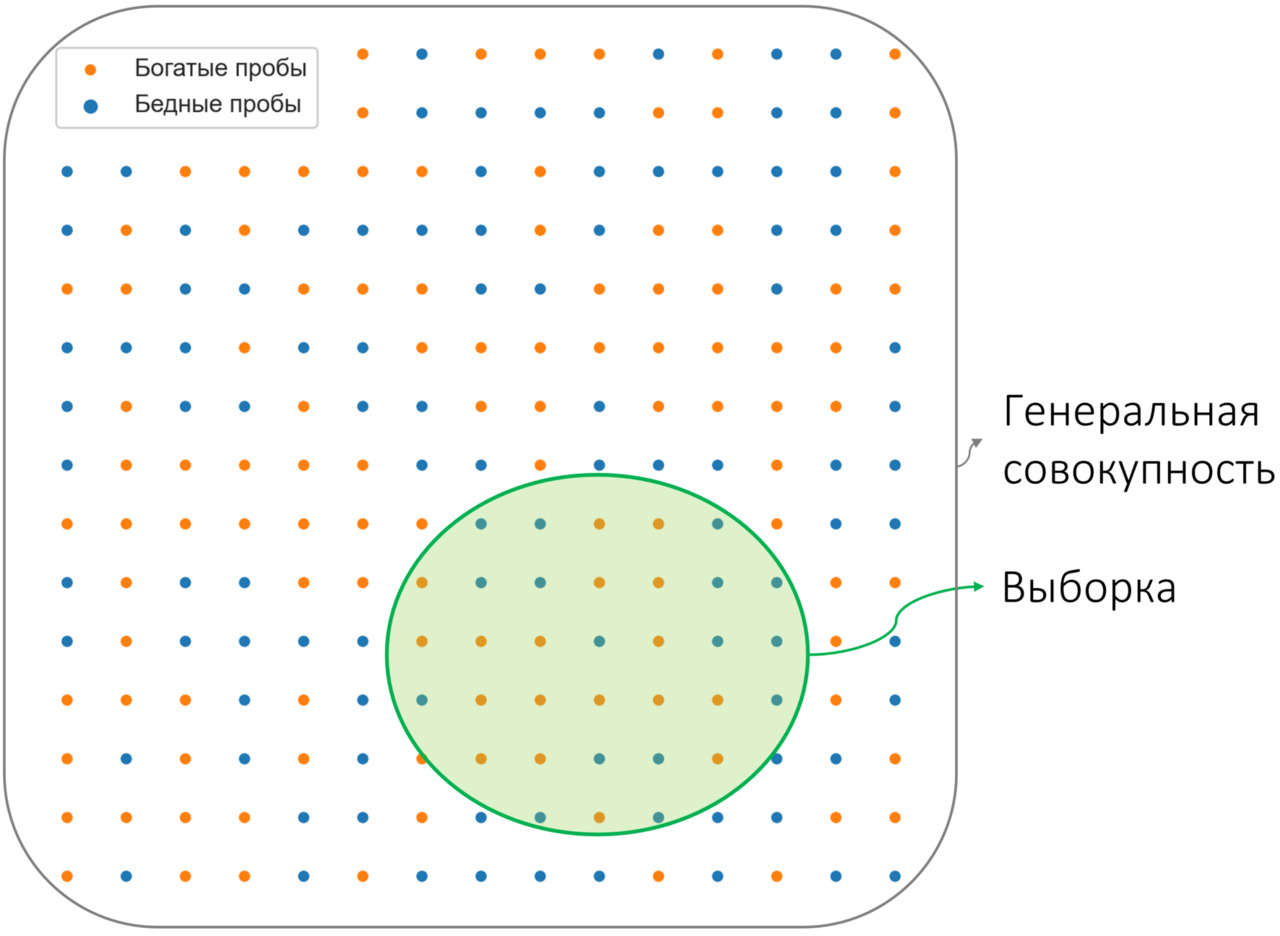
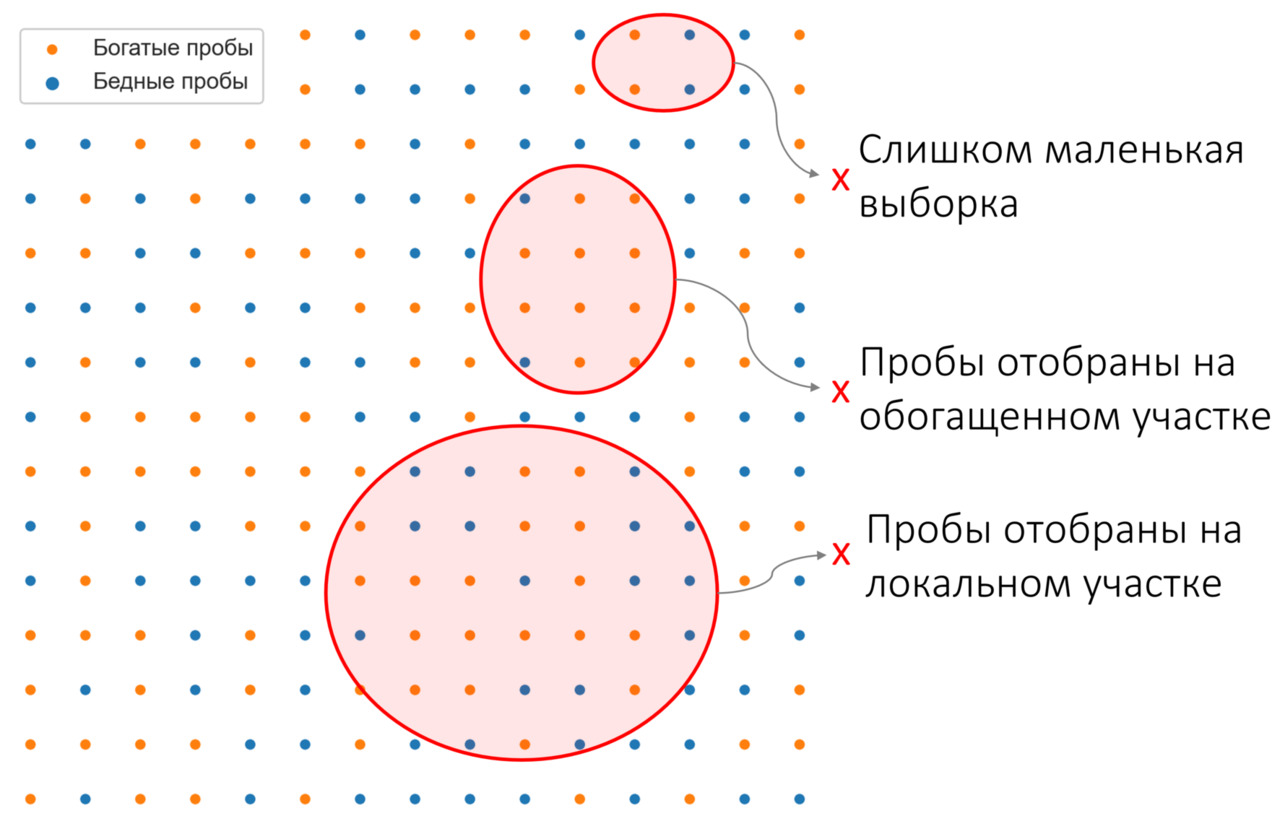
Выборка может характеризовать генеральную совокупность «хорошо» или «плохо», то есть быть представительной (репрезентативной) или непредставительной (нерепрезентативной). Представительностью принято называть характеристику, которая показывает то, насколько хорошо выборка, имеющаяся в распоряжении геолога, отражает реальные статистические характеристики изучаемого объекта. Представительность — бинарная характеристика: она либо есть, либо ее нет. Например, выборка бороздового опробования по одному горизонту крупного рудного тела, скорее всего, «плохо» характеризует генеральную совокупность содержаний данного тела. Выборка, отобранная из какого-то локального участка рудного тела, скорее всего, тоже будет непредставительной (даже если проб там «много»).

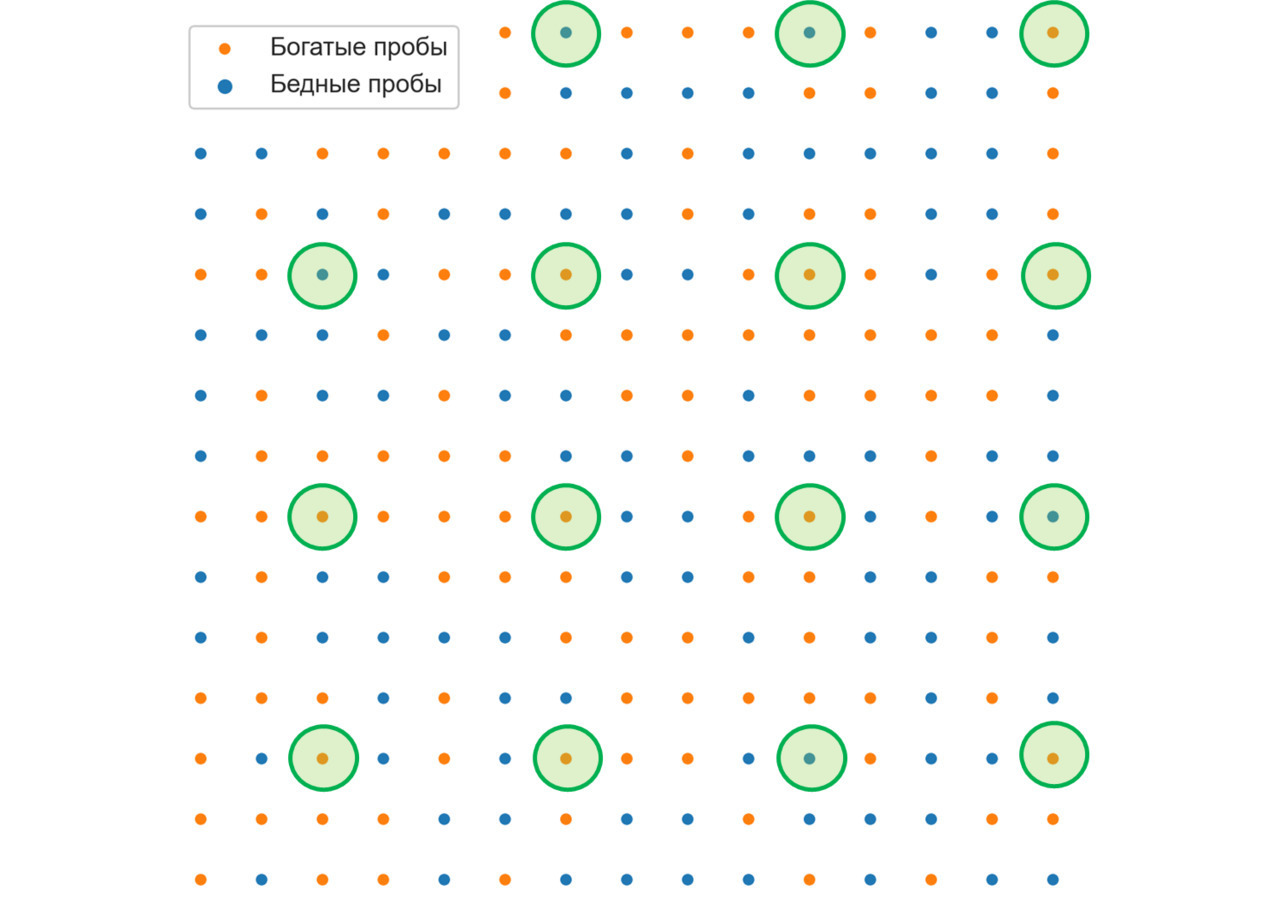
Напротив, данные опробования этого тела, отобранные по регулярной сети (вопрос о плотности сети, позволяющей получить представительную выборку, решается в каждом случае индивидуально), скорее всего, являются представительными для данного тела (но, скорее всего, непредставительными для всего месторождения). Поэтому при заявлении «эта выборка является представительной» неплохо бы уточнять, представительной для чего.

Гистограмма

В большинстве случае объем выборки таков, что ее невозможно всю «охватить взглядом». Однако желание понять, что из себя представляет тот массив данных, который есть в распоряжении, возникает сразу же после появления этого массива. И одним из наилучших способов получить это понимание является графический, поскольку подавляющее количество информации человек получает с помощью зрения. Просто просмотр числовых значений при большом объеме выборки мало что дает, поэтому хочется как-то «генерализовать» всю эту информацию. Для такой генерализации и визуального представления существует очень полезный вид диаграмм, называемый гистограммами. Гистограммы представляют собой столбчатый график, в котором по горизонтали отложены значения изучаемой величины, по вертикали — частота встречаемости значений, а все данные сгруппированы в то или иное количество классов содержаний равной величины и представлены, соответственно, столбцами. Равенство классов в данном случае означает равенство разброса содержаний (не количества наблюдений!) в каждом классе.

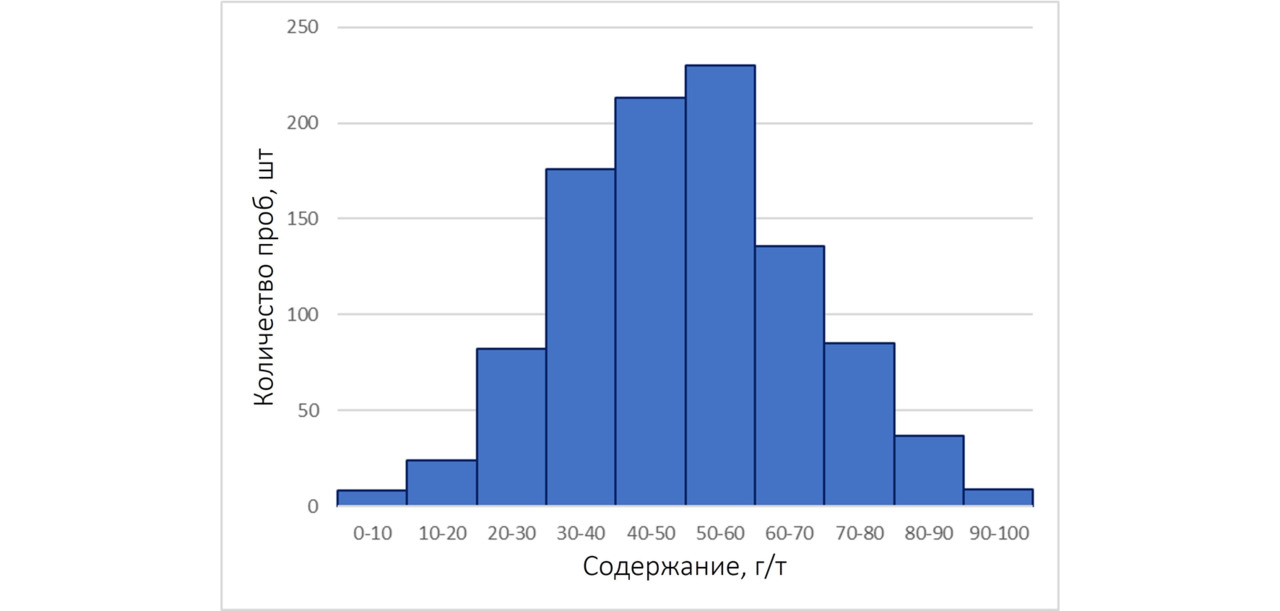
Методика построения гистограммы проста и незамысловата:

— Определяем размах изучаемой величины.

— Решаем, на какое количество классов содержаний будем разбивать наши данные. Количество классов содержаний — это количество столбцов на создаваемой гистограмме (точнее, максимальное количество столбцов). Например, мы определили, что размах содержаний составляет 100 г/т — от 0 г/т до 100 г/т. Далее мы захотели разбить весь диапазон на 10 классов содержаний (о выборе количества классов содержаний чуть дальше). В этом случае границы классов будут следующими: от 0 до 10 г/т, от 10 до 20 г/т, от 20 до 30 г/т… от 90 до 100 г/т.

— Для каждого класса содержаний подсчитываем количество проб, попавших в класс. При подсчете обычно в класс включают нижнюю границу — т. е. содержание 10 г/т войдет в класс от 10 до 20 г/т, а не в класс от 0 до 10 г/т. Хотя возможна и обратная схема. Но в любом случае — схема включения граничных содержаний должна быть едина, и каждая проба должна быть учтена только в одном классе.

— На оси абсцисс (горизонтальной, если забыли) отмечаем границы классов, на оси ординат (вертикальной) размечаем масштаб. И для каждого класса содержаний строим прямоугольник, такой, что вертикальные стороны совпадают с границами классов, а высота равна количеству проб в данном классе с учетом выбранного масштаба. В итоге должно получиться что-то, похожее на диаграмму, приведенную выше (с учетом особенностей используемого распределения).

Можно вместо натуральных величин частоты (т. е. «штук») использовать долю проб в данном классе от общего количества проб — количество проб не всегда информативно. Характер гистограммы от этого не изменится, поменяется только вертикальный масштаб.

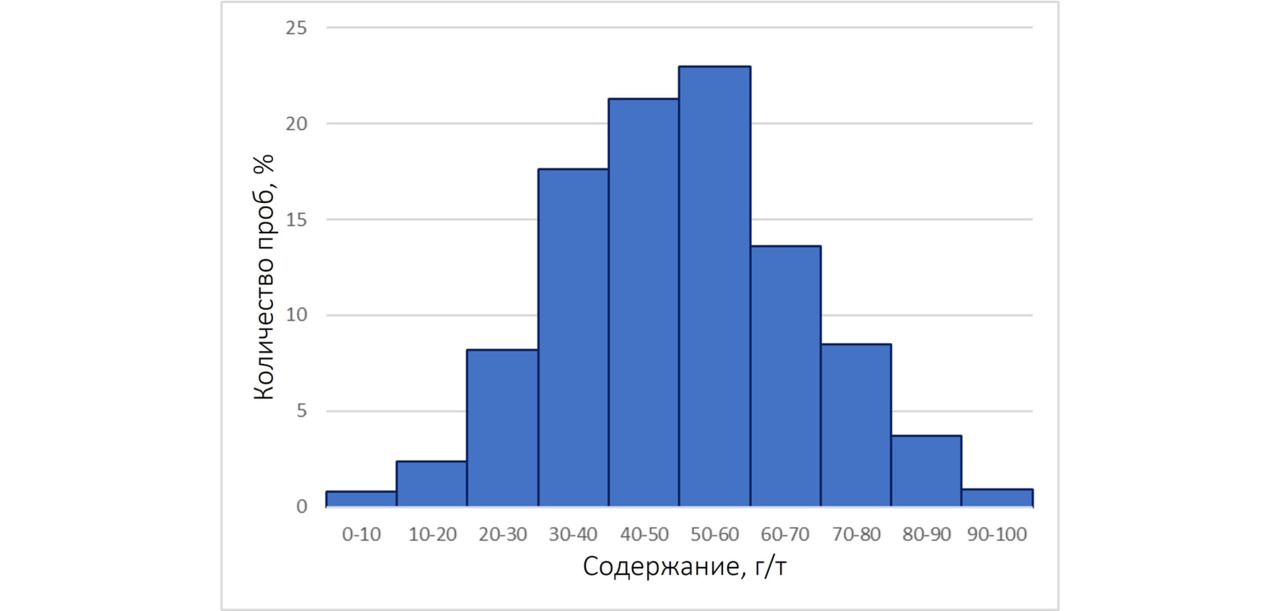
Если длина проб резко различна, то имеет смысл использовать взвешивание — в этом случае на длину пробы. Случается, что визуально видимую минерализацию опробуют более детально — секциями меньшего размера, тогда как слабо проявленные околорудные изменения — более длинными пробами. Гистограмма, построенная по количеству проб, в этом случае неправильно отражает характер распределения содержаний, и вместо количества проб в каждом классе в этом случае лучше подсчитывать суммарную длину проб. То есть в данном случае имеет смысл выполнять взвешивание на длину. Сравните две гистограммы ниже. Они построены по одним и тем же данным. Но гистограмма слева построена без взвешивания на длину, а справа — со взвешиванием. Очевидно, характер гистограмм несколько различен.

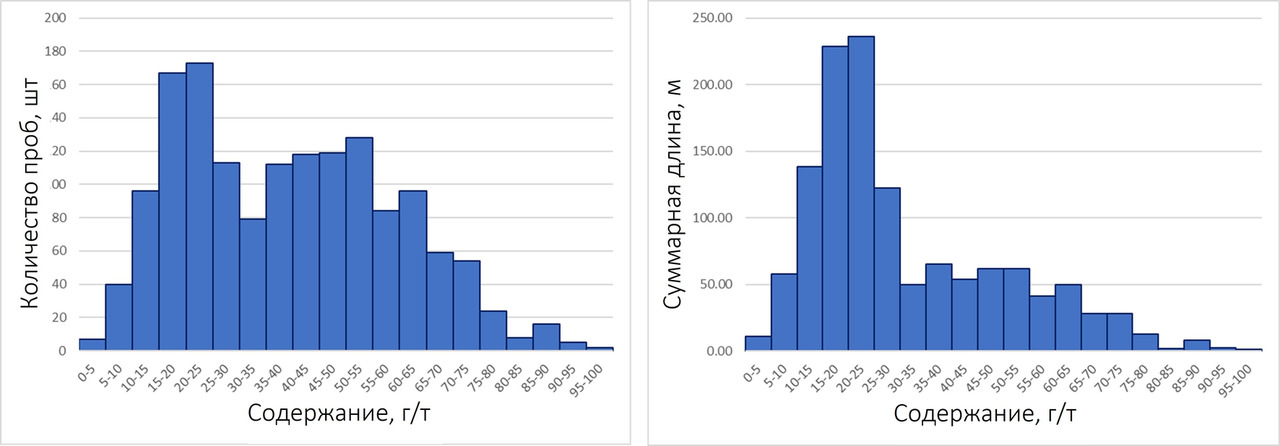
Взвешивание также имеет смысл выполнять при наличии участков, освещенных сетями разной плотности. В этом случае взвешивание должно выполняться на так называемый вес декластеризации (об этом чуть дальше).

Гистограмма — довольно удобный инструмент, который легко позволяет получить представление о характере распределения значений исследуемой величины по диапазону значений. По внешнему виду гистограммы можно судить о том, является ли выборка однородной или нет. Под однородностью понимается принадлежность всех значений изучаемой величины к одной и той же генеральной совокупности. Обычно однородные выборки одномодальные — т. е. на гистограммах таких выборок присутствует только один «горб». Наличие нескольких таких «горбов» может говорить о том, что в выборку попали значения, имеющие разную природу: например, пробы из стержневой жилы и зоны околорудных изменений или из минерализованных зон разных стадий рудообразования с разной продуктивностью. Или из первичных руд и из зоны окисления — причин может быть масса. Однако кроме естественных причин могут быть и причины технического характера.

Выше при объяснении механизма построения гистограммы было сказано, что диапазон значений разбивается на некоторое количество классов содержаний. Однако ничего не было сказано о том, как выбирается количество классов. Вопрос о количестве классов, на которые разбивать диапазон значений, не имеет однозначного ответа. «Классическим» вариантом разбивки на классы считается формула Стерджесса.

Количество классов ≈ 1 +3.22 * lg (N),

Здесь N — численность выборки, lg — десятичный логарифм.

Формула является эмпирической, т. е. ее единственное обоснование: «всегда так делали, и хорошо получалось».

Основной недостаток этой формулы — слишком малое количество классов, которое на больших выборках зачастую не позволяет увидеть важные особенности. Рост количества классов полностью объясняется особенностью поведения логарифма: сначала относительно быстрый рост, а затем замедление. На рисунке ниже можно увидеть зависимость между численностью выборки и количеством классов, определенных согласно этой формуле.

Выборку в 100 тыс. записей данное правило рекомендует разбить на 18 классов, в 200 тыс. — на 19, в 1 млн — только на 21. При построении гистограмм в соответствии с данной формулой можно увидеть только что-то очень явное, что чаще всего «и так понятно».

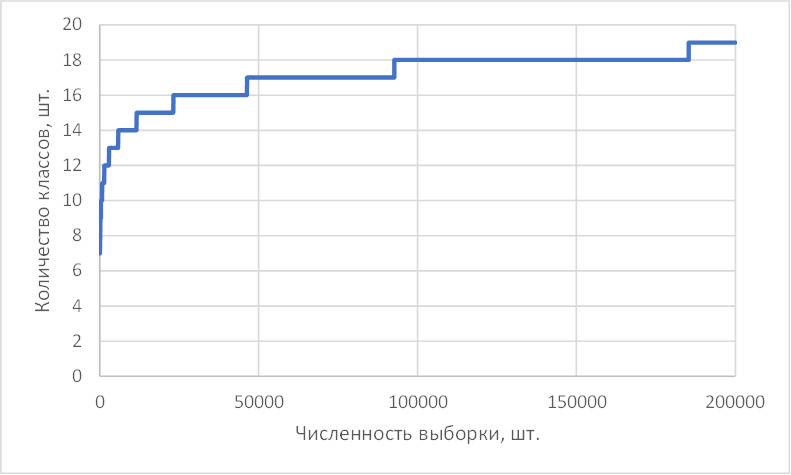
Эта особенность применяемого правила, скорее всего, объясняется тем, что во времена создания «классической» статистики обычная численность выборки составляла несколько сотен замеров. В настоящее же время объемы выборок принципиально возросли и применение этой формулы может быть не вполне оправдано.

Обычно количество классов подбирается таким образом, чтобы на гистограмме были видны важные особенности, но при этом гистограмма продолжала бы быть похожей на гистограмму, а не на творение художника-абстракциониста или на картинку с одинокими столбцами, разделенными «белым безмолвием». Обычно количество классов не превышает 50 (для выборок объема в несколько десятков тысяч значений). При избыточном количестве классов на небольших выборках очень несложно обнаружить неоднородность, обусловленную исключительно разбиением на классы. На рисунке ниже представлена гистограмма, построенная для выборки в 1000 записей, представляющих собой сгенерированное однородное (нормальное) распределение со средним 20 и стандартным отклонением 5. N для данного рисунка — количество классов разбиения.

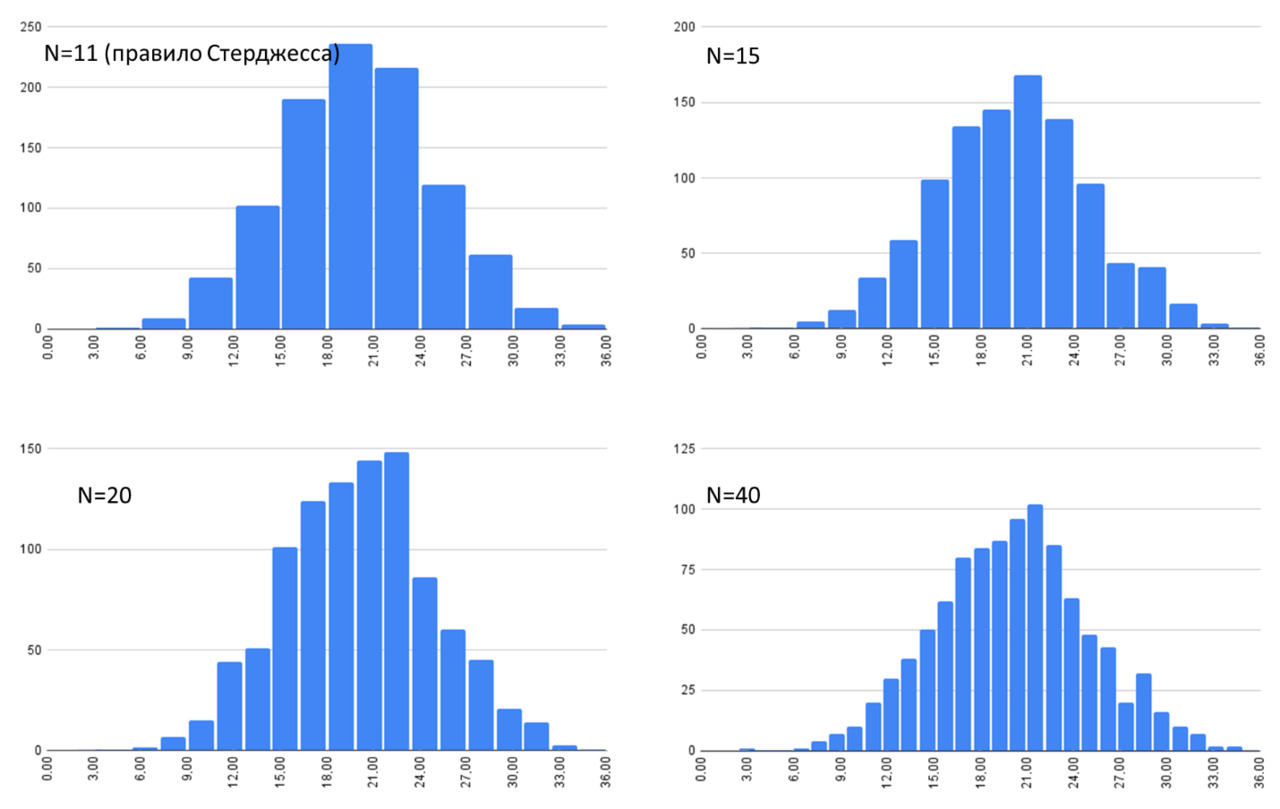
Можно видеть, что для выборки в 1000 значений при количестве классов, существенно превышающем правило Стерджесса, появляется ложная неоднородность (второй «горб») с границей в районе 28.

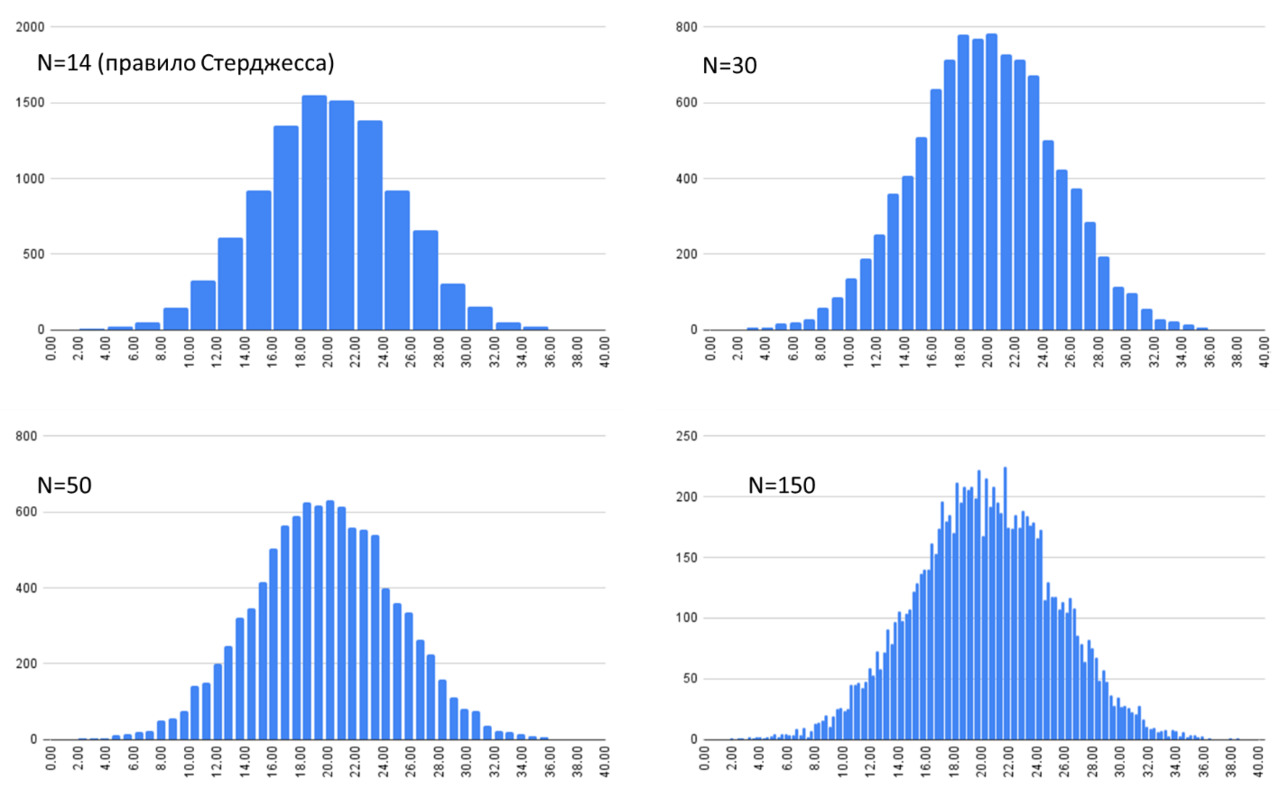
В то же время при достаточно большом количестве наблюдений получить искусственную неоднородность уже довольно сложно. На рисунке ниже показана аналогичная выборка, но с числом наблюдений 10000. То есть для выборки в 10000 наблюдений даже при десятикратном превышении правила Стерджесса явной неоднородности не отмечается. Нижняя граница численности выборки, после которой можно не очень опасаться искусственной неоднородности, вероятно, находится на уровне 4–5 тыс. наблюдений (в принципе, не очень большая редкость для геологии). При меньшем количестве классов, вероятно, не стоит кратно превышать те цифры, которые дает правило Стерджесса.

Среднее арифметическое

Генеральная совокупность в подавляющем большинстве случаев недостижима. Вы в своей работе будете всегда иметь дело с выборкой. У выборки, как и у генеральной совокупности, есть свои характеристики. В том случае, если выборка очень небольшая — например, 5-7-10 значений, вы можете видеть ее всю целиком, и никаких дополнительных характеристик выборки вам не нужно. Однако традиционно в геологии (и моделировании) вы будете иметь дело с выборками объемом в десятки, сотни и тысячи значений. Впрочем, и выборки в миллионы значений также не являются сугубо экзотичными. Поскольку физически невозможно держать эту выборку «в поле зрения», возникает необходимость каким-либо образом охарактеризовать ее относительно небольшим количеством величин, позволяющими получить представление о выборке без просмотра ее целиком.

Первое, что логично напрашивается — это минимальное и максимальное значения, а также размах. Если с минимумом и максимумом все понятно, то размах — это разница между максимумом и минимумом. То есть размах — это диапазон значений, полученных для данной выборки.

Следующая характеристика выборки — это выборочное среднее. Зачастую слово «выборочное» опускают и говорят просто о «среднем». Вообще говоря, существует довольно большое количество средних, однако чаще всего при упоминании «среднего» имеют в виду среднее арифметическое. Среднее (арифметическое) — это величина, которая рассчитывается по формуле, хорошо знакомой еще из школьного курса.

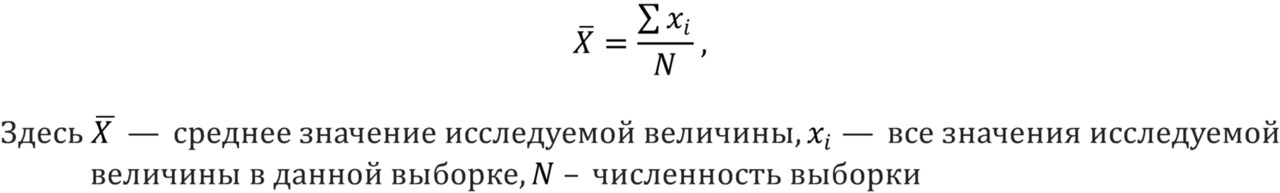
Например, среднее из 4, 10 и 19 равняется 11. То есть среднее — величина, промежуточная для реальных значений. Если рассматривать числа как точки на числовой прямой, то среднее — это точка «посередине» точек, соответствующих выборочным данным.

Среднее обладает некоторыми свойствами, также позволяющими лучше понять его смысл:

— если средней величиной заменить все значения выборки, то сумма значений выборки не изменится;

— если среднее значение вычесть из каждого значения выборки, то сумма этих разностей будет равна 0.

Необходимо отметить, что среднее (арифметическое) дает неплохое представление о выборке «симметричной», т. е. такой, в которой высоких и низких значений «примерно поровну». В том же случае, когда явно преобладают высокие или низкие значения, среднее дает смещенную оценку. Также на оценку среднего серьезное влияние оказывают значения, резко выделяющиеся из общей массы (причем неважно — в большую или меньшую сторону). В качестве примера можно рассмотреть коллектив небольшой организации, в которой 20 человек получают по 30 т. р., а генеральный директор — 2 млн. р. Очевидно, что среднее, равное для описанного случая, ~695 т. р., вряд ли корректно отражает ситуацию с уровнем доходов сотрудников организации — причем это справедливо как в отношении рядовых сотрудников, так и в отношении директора. Ну или можно рассмотреть известную шутку о том, что все посетители бара, куда заходит Билл Гейтс, мгновенно в среднем становятся миллионерами (правда, счастье длится ровно до того момента, пока этот уважаемый человек не покинет бар). Вопрос о методах выявления и компенсации аномальных значений в выборке — не самый простой и будет относительно подробно рассмотрен в главе, посвященной урезке ураганных содержаний.

Кроме фактора симметричности и наличия/отсутствия аномальных значений, на оценку среднего может повлиять и разница в других свойствах предметов (явлений), которые приводят к смещению оценки среднего. Одним из подобных факторов является свойство, которое принято называть весом.

Представим себе ситуацию смешивания двух объемов руды: одна смешиваемая руда характеризуется содержанием золота (почему бы и не золота?) 5 г/т, вторая — 10 г/т. Обычное среднее арифметическое, очевидно, в данном случае составит 7.5 г/т. То есть, если мы очень хорошо перемешаем рудный материал, то ожидаем увидеть в получившейся смеси эти самые 7.5 г/т. Но что будет, если масса «пятиграммовой» руды составит 10 т, а «десятиграммовой» — 1 т? Очевидно, что в результате смешивания мы получим 11 т руды. При этом из первой порции «придет» 50 г драгоценного металла, а из второй — 10 г. То есть в смеси всего будет содержаться 60 г. И среднее в этом случае составит 60/11 ≈ 5.45 г/т. Очевидно, цифра несколько отличается от ранее полученных 7.5 г/т (что, безусловно, обидно, зато позволило не впасть в ошибку при ожидании).

Учет подобных факторов при вычислении среднего называется взвешиванием, а среднее — средневзвешенным. Взвешивание используется при вычислении характеристик выборки довольно широко. Например, при композитировании данных опробования вдоль по скважинам (в этом случае используется взвешивание на длину проб). Или вычислении среднего по резко неравномерной сети (выполняется взвешивание на вес декластеризации). Вопросы способов вычисления весов рассматриваются в главах, посвященных декластеризации и композированию (впрочем, второе, по сути, является частным случаем первого).

Процентиль, медиана и мода

Кроме вычисления среднего с помощью указанных выше приемов, существуют другие способы краткой характеристики выборки, которые также дают представление о том, с чем имеет дело геолог. И следующие величины, которые мы рассмотрим, процентили или перцентили.

Процентиль — это характеристика выборки, представляющая собой значение, ниже которого находится заданная доля значений в данной выборке. То есть, если говорят, что для какой-то выборки 20% процентиль равен, предположим, 3.2, то это означает, что 20% значений этой выборки не превосходят значение 3.2.

В ряде руководств процентиль определяется как вероятность того, что наугад взятое значение, принадлежащее выборке, не превзойдет значения процентиль. В принципе, эти два определения описывают одну и ту же величину, только немного с разных позиций.

Существует довольно большое количество способов для расчета процентилей. Неплохой обзор способов их расчета приведен в англоязычной версии «Википедии» (причем, что печально, русская версия этой статьи отличается избыточной лаконичностью). Если вы испытываете неприязнь к «Википедии» как к источнику информации, в упомянутой статье содержатся ссылки на первоисточники — можно почитать непосредственно научные статьи.

Маловероятно, что вам потребуется вручную считать процентили, поскольку формулы для их расчета заложены практически во все ПО, имеющее отношение к обработке данных — от Google Sheets до статистических пакетов (естественно, и в пакетах для геологического моделирования эти возможности тоже есть). Просто необходимо помнить, что существуют разные методы их расчета, и процентили, рассчитанные в одном ПО, могут незначительно отличаться от тех же процентилей, рассчитанных в другом ПО. В подавляющем количестве случаев эти различия не оказывают какого-либо влияния на финальный результат обработки данных, поэтому пугаться несовпадения цифр не стоит.

Наиболее часто используемые процентили — это 25%, 50% и 75% процентили. Процентили 25 и 75 называются квартилями — первым и третьим, соответственно. Первый квартиль (т. е. 25 процентиль) отсекает четверть выборки «снизу», т. е. 25% наименьших значений. Третий квартиль (75 процентиль) отсекает четверть выборки «сверху» — т. е. 25% наибольших значений в данной выборке. Процентиль 50% называется медианой и делит выборку на две равные части по количеству наблюдений или весу. Также достаточно часто рассчитываются процентили с шагом 10%: 10%, 20%, 30% и т. д. Такие процентили называют децилями.

Медиана делит распределение пополам, квартили — на четверти, квинтили — на 5 частей, децили — на 10 частей, процентили — на 100 частей.

Разность между первым и третьим квартилями называется межквартильным размахом. Это довольно важная характеристика выборки. Она показывает размах значений половины членов выборки. На величине межквартильного размаха построены некоторые способы ограничения аномальных значений. Также межквартильный размах используется в построении диаграммы, называемой «ящик с усами» (собственно, квартили там являются границами ящика).

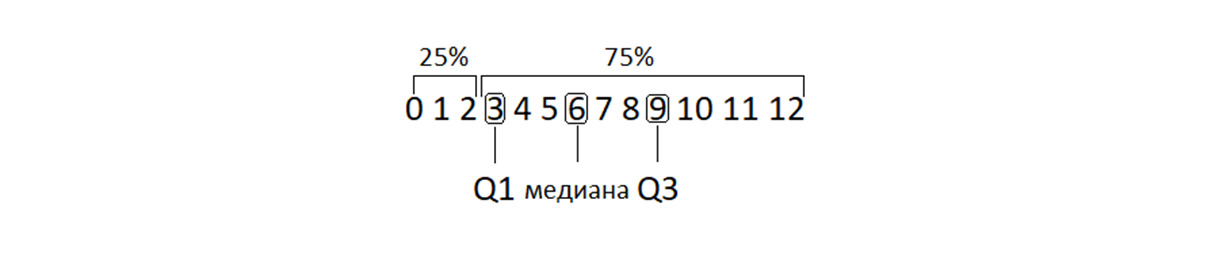
Здесь первый квартиль Q1 — число, отделяющее первую четверть выборки: 25% значений меньше, а 75% — больше него. Медиана — половина значений больше и половина меньше нее. Третий квартиль Q3 — это отсечка трех четвертей: 75% значений меньше и 25% значений больше него. Межквартильный размах — это расстояние между Q1 и Q3. Или, по-другому, межквартильный размах — это размах половины данных. Причем данных «из центра» распределения.

Медиана является одной из характеристик выборки. Положительное свойство медианы заключается в том, что на нее не оказывает влияние наличие в выборке аномальных значений. Например, в упомянутых примерах с избыточно меркантильным директором небольшого предприятия медиана будет равна тем самым 30 т. р., которые получают не менее 50% сотрудников описанной организации. И даже если директор начнет получать 4 млн р. (не изменив при этом зарплату остальному коллективу), медиана не сдвинется ни на копейку.

Для процентилей, как и для среднего, доступно взвешивание. В этом случае процентиль будет представлять собой величину, ниже которой находится часть выборки, содержащая заданную долю суммы весов. Если, например, речь идет о рудной выборке и взвешивании на длину пробы, то наглядно, например, первый квартиль можно представить себе как границу четверти суммарной длины проб с наименьшими содержаниями.

Еще одной характеристикой, позволяющей получить представление о выборке, является мода. Эта характеристика называется так совершенно заслуженно: мода — это наиболее часто встречаемое значение (т. е. наиболее «модное»). Мода так же, как и медиана, может служить характеристикой среднего, но чаще используется для характеристики выборки, представленной нечисловыми значениями (например, литологической характеристики). Выборка может содержать более одной моды. В этом случае говорят, что выборка полимодальная (мультимодальная).

Например в выборке 2, 2, 3, 4, 5, 6, 7, 7 модами будут значения 2 и 7. Значение 2 будет называться нижней модой, значение 7 верхней модой. Если два соседних значения встречаются одинаково часто, то мода считается как среднее арифметическое между ними. Например в выборке 2, 3, 3, 4, 4, 5, 6 модой будет значение 3.5 (три целых пять десятых) поскольку 3 и 4 находятся рядом и встречаются одинаково часто. На гистограмме значениям моды соответствует вершина графика (при одномодальном распределении) или несколько вершин графика (при полимодальном распределении).

Дисперсия

Кроме «точечных» характеристик исследуемой величины, также полезно знать и о степени отклонения значений исследуемой величины от среднего, а также «направлении» отклонения.

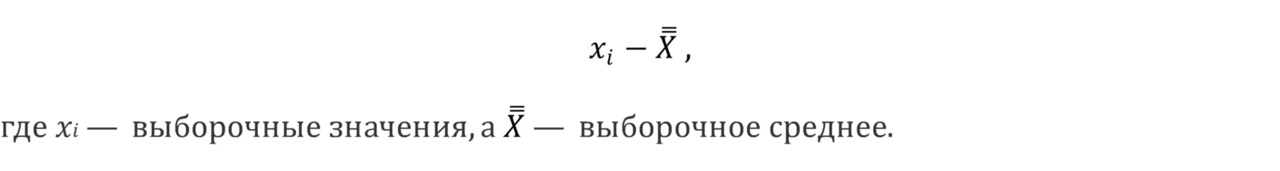
В результате этой операции будет получена новая величина, которая характеризует величину отклонения выборочного значения от среднего для каждого члена выборки. И значений этого отклонения — ровно столько же, сколько значений в выборке (отклонение рассчитано для каждого выборочного значения). Так же нам хочется понять, каково это отклонение в среднем, и хочется взять и усреднить полученные значения. Но в данном случае проблема заключается в том, что расчет среднего арифметического из значений отклонения даст 0. Просто по причине того, что среднее — это значение, «равноудаленное» от всех значений выборки. Выше было указано, что одно из свойств среднего — это то, что сумма отклонений всех выборочных значений от среднего равно 0. Из сложившегося неудобного положения можно найти два выхода:

— взять модуль (абсолютное значение) отклонений и усреднить их,

— возвести в четную степень полученные отклонения и усреднить их. Проще всего — возвести в квадрат.

Исторически сложилось так, что был выбран второй вариант — просто потому, что степенная функция является дифференцируемой во всей области определения, а модуль — нет. Для статистических расчетов, более сложных, чем обычно используются в геологии, необходимо, чтобы была возможность без лишних проблем интегрировать и дифференцировать функции. В этом отношении степенная функция значительно «удобнее», чем модуль. Поэтому мы имеем в качестве величины, характеризующей разброс данных, усредненную сумму квадратов отклонений.

Итого: чтобы не получить ноль при усреднении отклонений, требуется использовать квадрат величины отклонения. То есть выборочной дисперсией называется величина, рассчитанная по формуле:

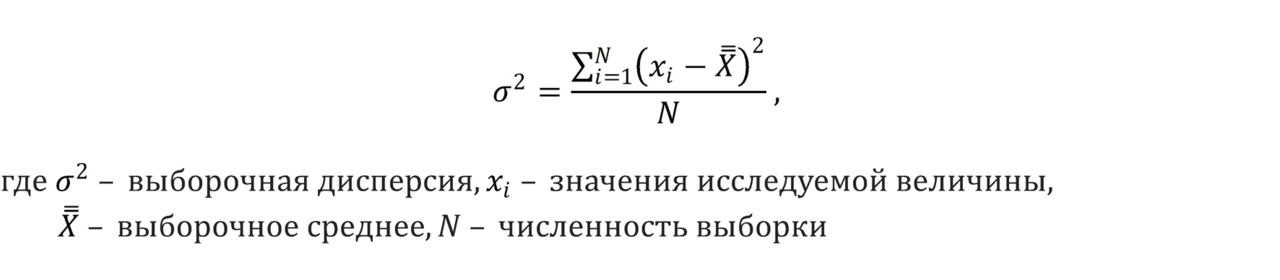
То есть выборочная дисперсия — среднее из квадратов отклонения случайной величины от ее среднего значения.

Считается (и доказывается в классических статистических работах), что выборочная дисперсия является смещенной оценкой дисперсии генеральной совокупности. Для оценки дисперсии генеральной совокупности используется чуть более сложная формула:

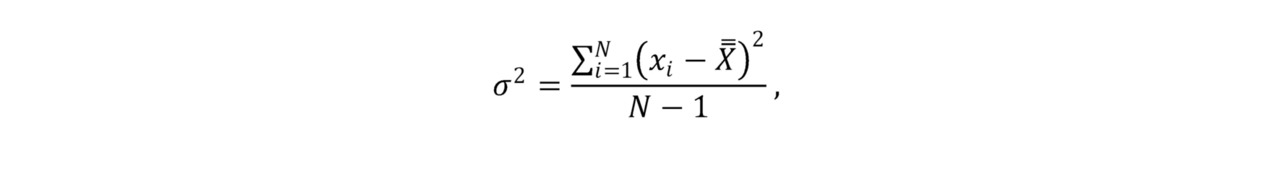
Выше мы с помощью несложных логических рассуждений вывели формулу дисперсии. Было бы нелишним понимать смысл этой формулы, но строгого запоминания этих формул не требуется, поскольку они заложены во всем ПО, работающем с данными (по крайней мере, авторам не встречалось ПО, где бы эти формулы не были заложены).

Выше приведены две формулы расчета дисперсии. Необходимо обратить внимание на то, что в задачах моделирования практически всегда мы имеем дело не с генеральными совокупностями, а со случайными выборками из генеральной совокупности. Поэтому мы не имеем точного значения дисперсии, а только ее оценку. В учебниках по математической статистике указано, что верхняя формула (где выполняется деление на численность выборки) дает смещенную оценку дисперсии, а нижняя (где деление выполняется на численность выборки минус 1) — несмещенную. Вторую формулу используют для оценки дисперсии генеральной совокупности.

Теперь о том, какую дисперсию считает ПО, которым мы имеем счастье пользоваться:

— Первым пунктом идет, естественно, великий и ужасный Excel. В Excel существует две формулы для расчета дисперсии (на самом деле, больше, но глобально — две, остальные — это вариации на тему «использовать логические значения / не использовать логические значения»): ДИСП. В и ДИСП. Г. Причем вторая, как сказано в ее кратком описании, рассчитывает дисперсию генеральной совокупности. Вот, казалось бы, «щасстье привалило». Однако нет: ручная проверка показывает, что результат работы функции ДИСП. Г совпадает с формулой смещенной оценки. В чем же проблема? А проблема очень простая: функция ДИСП. Г считает, что то, что она получила на вход, это и есть генеральная совокупность. А при генеральной совокупности — таки да, надо делить на численность генеральной совокупности. Но у нас-то не генеральная! Хорошо, если генеральная совокупность выглядит как «непьющие мужчины за 40 деревни Чуево-Кукуево» — там вообще считать нечего. Но в моделировании мы практически всегда имеем дело со случайной выборкой. Поэтому функцию ДИСП. Г мы забываем, как страшный сон.

Вывод: Excel для выборочной дисперсии (ДИСП. В) приводит ее несмещенную оценку.

— Google таблицы — аналогично: функция VAR рассчитывает несмещенную оценку, функция VARP совершенно аналогична ДИСП. Г Excel.

— Datamine. Дает смещенную оценку.

— Snowden Supervisor. Дает смещенную оценку.

— Micromine. Дает несмещенную оценку.

— Leapfrog. Дает несмещенную оценку.

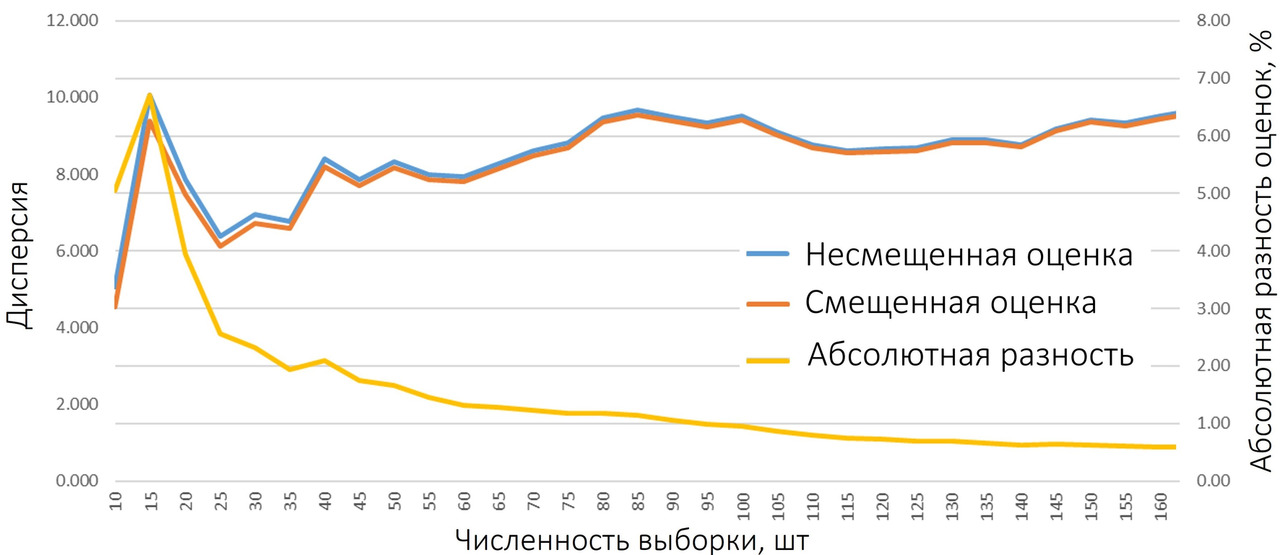
И вот вы прочитали предыдущие 6 пунктов и сидите в ужасе: «Чему верить?» А в общем, ничего страшного в описанной ситуации нет. Заметим, что при росте объема выборки (и соответственно, приближении ее к генеральной совокупности) разница между оценкой выборочной дисперсии и дисперсии генеральной совокупности уменьшается (ну просто потому, что разница между делением на 10 и 11 вполне ощутима, а на 10000 и 9999 — почти нет). Ниже представлен график разницы между смещенной и несмещенной оценкой для выборок различного объема, созданных с помощью генератора случайных чисел.

Выборка сгенерирована с помощью генератора случайных чисел (в генератор заложена дисперсия 10), поэтому абсолютные цифры могут несколько «гулять», но тенденция видна невооруженным глазом: при численности выборки более ~100 наблюдений разница между смещенной и несмещенной оценками падает ниже 1% от дисперсии (кстати, на втором листе файла Excel, ссылка на который была чуть выше, эти формулы заложены — можете поиграть с ними). Учитывая обычные объемы выборок для моделирования, можно не забивать себе голову вопросами «это смещенная или несмещенная оценка?».

Стандартное отклонение и коэффициент вариации

Глядя на формулу дисперсии, можно понять, что единицы измерения дисперсии — это квадраты тех единиц, в которых измеряется исследуемая величина. Во многих случаях это немного неудобно, поэтому имеет смысл взять квадратный корень из этой величины. Полученное значение принято называть среднеквадратичным отклонением или стандартным отклонением. Единицы измерения стандартного отклонения совпадают с единицами измерения исследуемой величины.

При работе с данными довольно часто мы имеем дело с разнопорядковыми величинами, часто еще и измеренными в разных единицах или несущих разный физический смысл. При этом время от времени возникает горячее желание сопоставить между собой разброс двух величин, имеющих разное среднее и зачастую измеренных в разных единицах. Для решения такой задачи требуется некая, видимо, безразмерная величина, которая должна показывать то, насколько разброс данных больше его среднего. То есть, например, отношение стандартного отклонения к среднему по выборке.

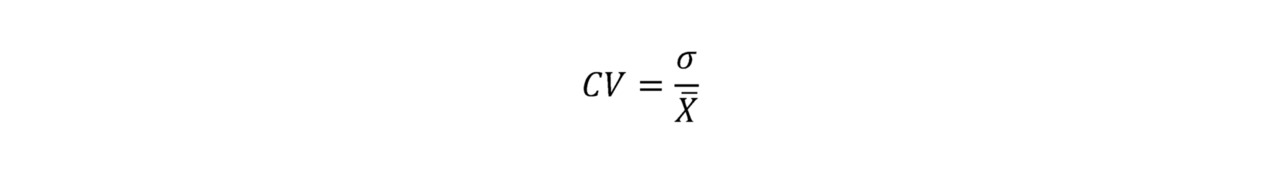
Эта величина называется коэффициентом вариации. Эта величина безразмерная (в том смысле, что не имеет «нормальных» единиц измерения — типа сантиметров, тонн или джоулей): и в числителе, и в знаменателе дроби присутствуют величины, измеряющиеся в одинаковых единицах. Коэффициент вариации может измеряться в долях единицы, а может в процентах (разница между «тем и этим» — 100). Коэффициент вариации характеризует степень изменчивости, «неустойчивости», «непостоянства» исследуемой величины. Он может быть использован для сравнения степени изменчивости различных величин — например, содержания металла и сквозного извлечения. Также он используется при проверке того, можно ли использовать кригинг для интерполяции. Считается, что коэффициент вариации больше 2 (или 200%) препятствует удачному использованию кригинга и требуются некоторые действия для его уменьшения — например, ограничение аномальных значений (урезка ураганов) или изучение вопроса об однородности выборки.

Общепринятого ранжирования величин по степени изменчивости на основе коэффициента вариации нет. В советское время предлагалось ранжировать выборки от весьма слабой изменчивости к весьма сильной по реперным значениям коэффициента вариации 0.2–0.4–0.8. По опыту работы с данными опробования золоторудных объектов можно сказать, что подавляющее большинство рудных выборок имеют коэффициент вариации содержаний не менее 0.8 (80%). Очень часто он превышает 2.

§ Задание 1.1

Для выборки значений содержаний проб:

0, 0.2, 0.6, 0.9, 0.9, 1.4, 1.6, 3

рассчитайте:

— Среднее.

— Мода.

— Медиана.

— Дисперсия (несмещенная).

— Стандартное отклонение.

— Коэффициент вариации.

Ответы округлите до двух знаков после запятой.

§ Задание 1.2

Скачайте выборку значений содержаний проб и рассчитайте:

— Среднее.

— Мода.

— Медиана.

— Дисперсия (несмещенная).

— Стандартное отклонение.

— Коэффициент вариации.

Ответы округлите до двух знаков после запятой.

Диаграмма накопленной частоты

Кроме гистограммы, классическим вариантом диаграммы, характеризующей выборку, считается также диаграмма накопленной частоты. Диаграмма накопленной частоты может быть построена как на сгруппированных данных, так и на не сгруппированных.

При построении диаграммы накопленных частот по сгруппированным данным выполняется разбиение всего диапазоны на классы (аналогично тому, как это делается для гистограммы), классы ранжируются по возрастанию, затем для каждого класса суммируется количество данных, попавших в этот класс с количеством данных, попавших во все классы, «ниже» данного. То есть частота данных в каждом классе накапливается от «низов» выборки до ее «верха». В качестве примера рассмотрим некоторую величину, распределенную следующим образом:

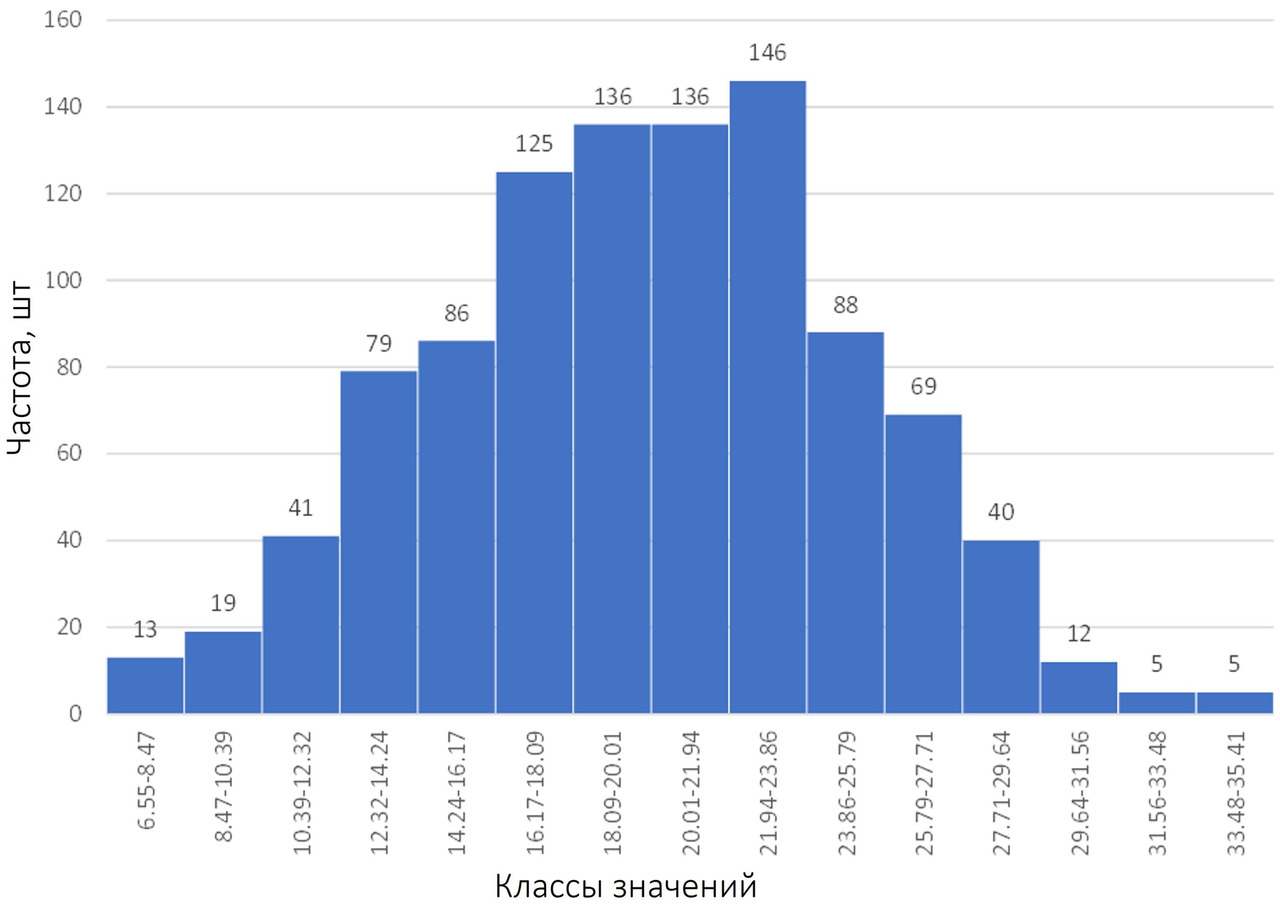
В табличном виде это распределение можно представить следующим образом:

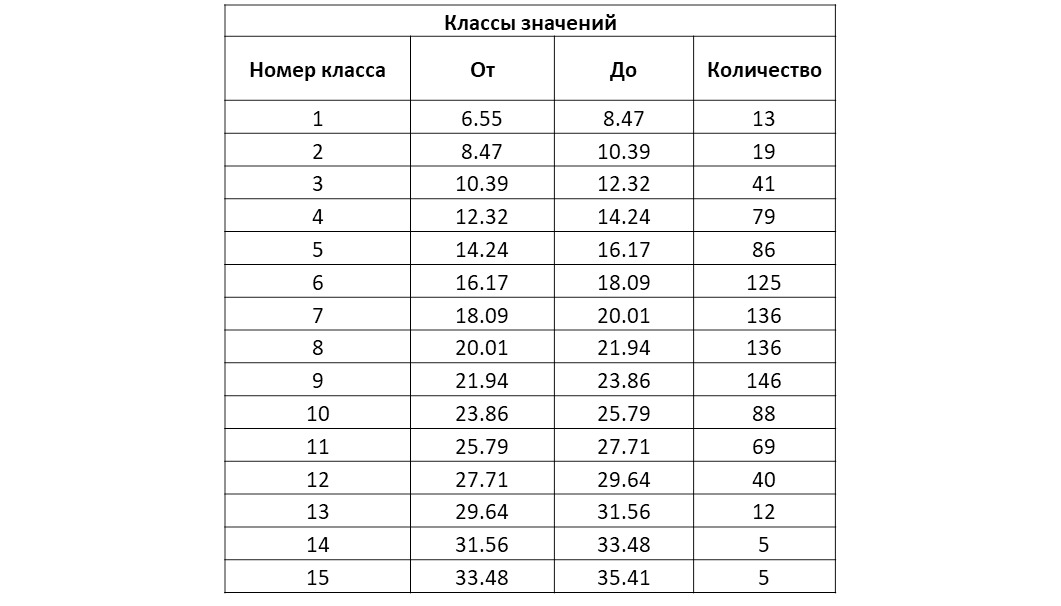
Выполним расчет накопленной частоты для приведенного примера:

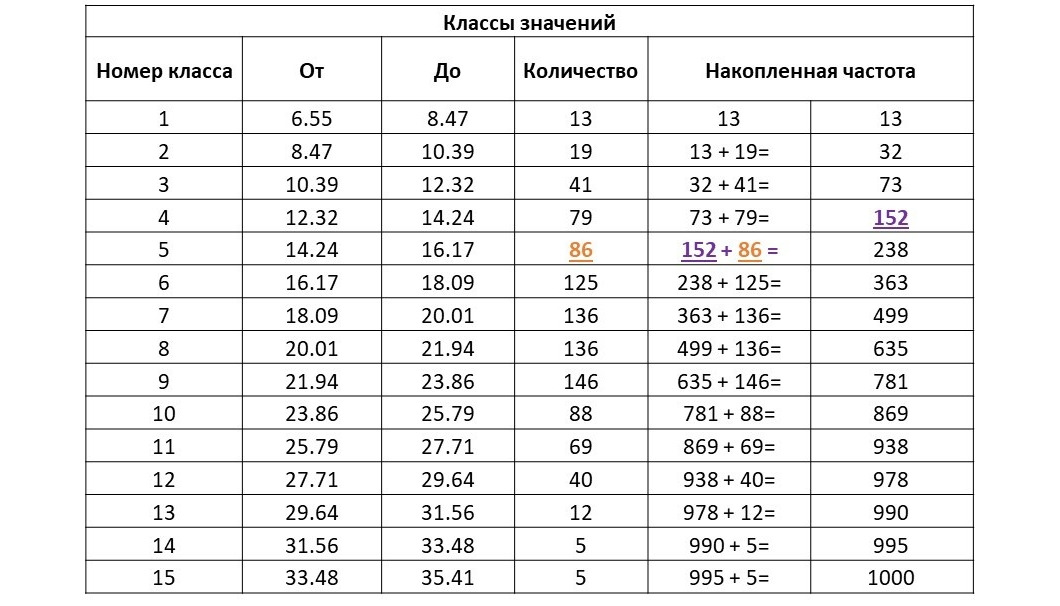
И теперь — построение графика:

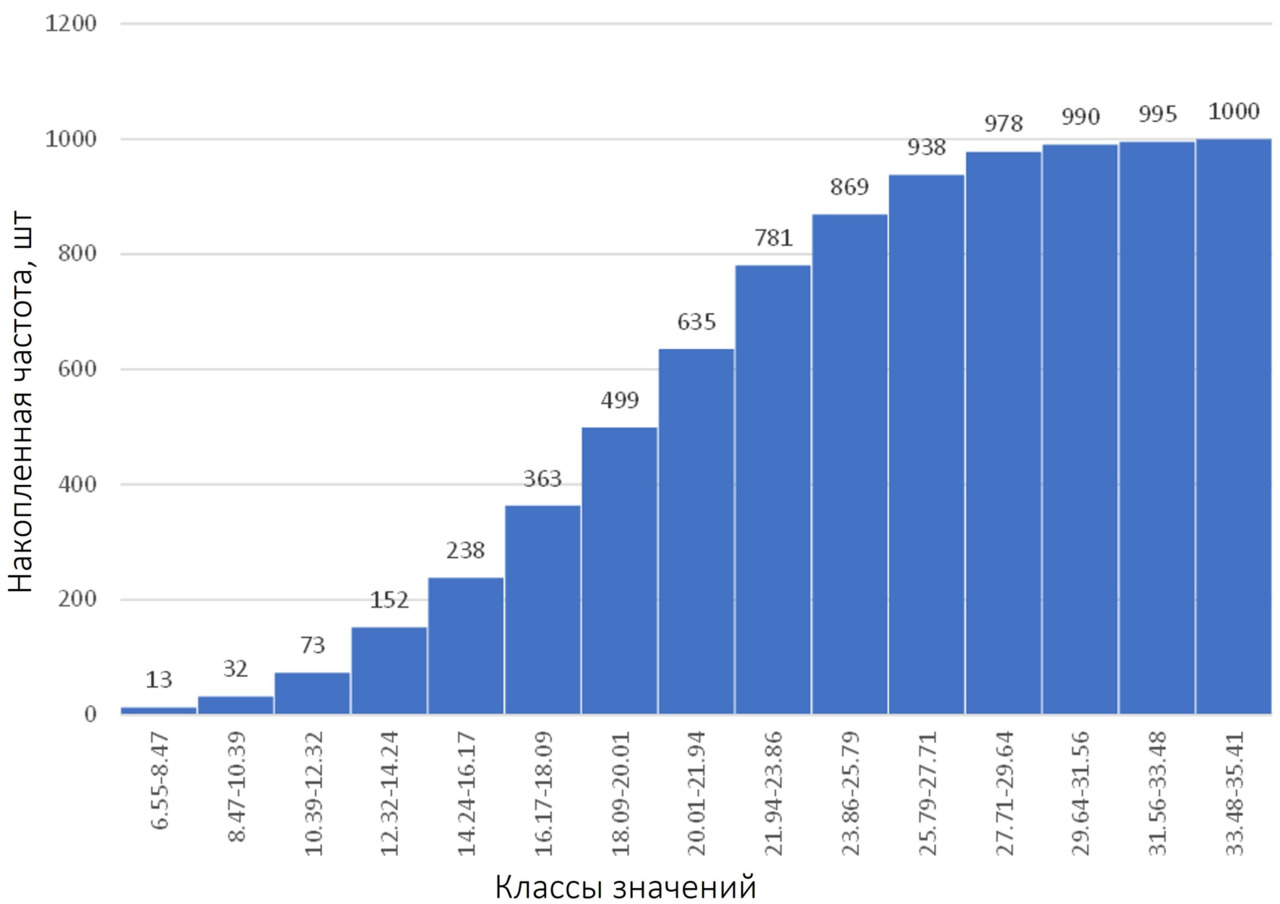
При построении диаграммы накопленных частот по не сгруппированным данным последовательность действий чуть другая:

— Данные ранжируются по возрастанию.

— Составляется ранжированный ряд уникальных значений.

— Для каждого уникального значения подсчитывается частота встречаемости.

— Для каждого уникального значения подсчитывается накопленная частота: частота встречаемости этого значения плюс частоты всех значений более низкой величины. То есть в данном случае в качестве классов значений (как в варианте со сгруппированными данными) выступают уникальные значения исследуемой величины.

График накопленных частот для того же распределения, что и выше по не сгруппированным данным, представлен на рисунке ниже.

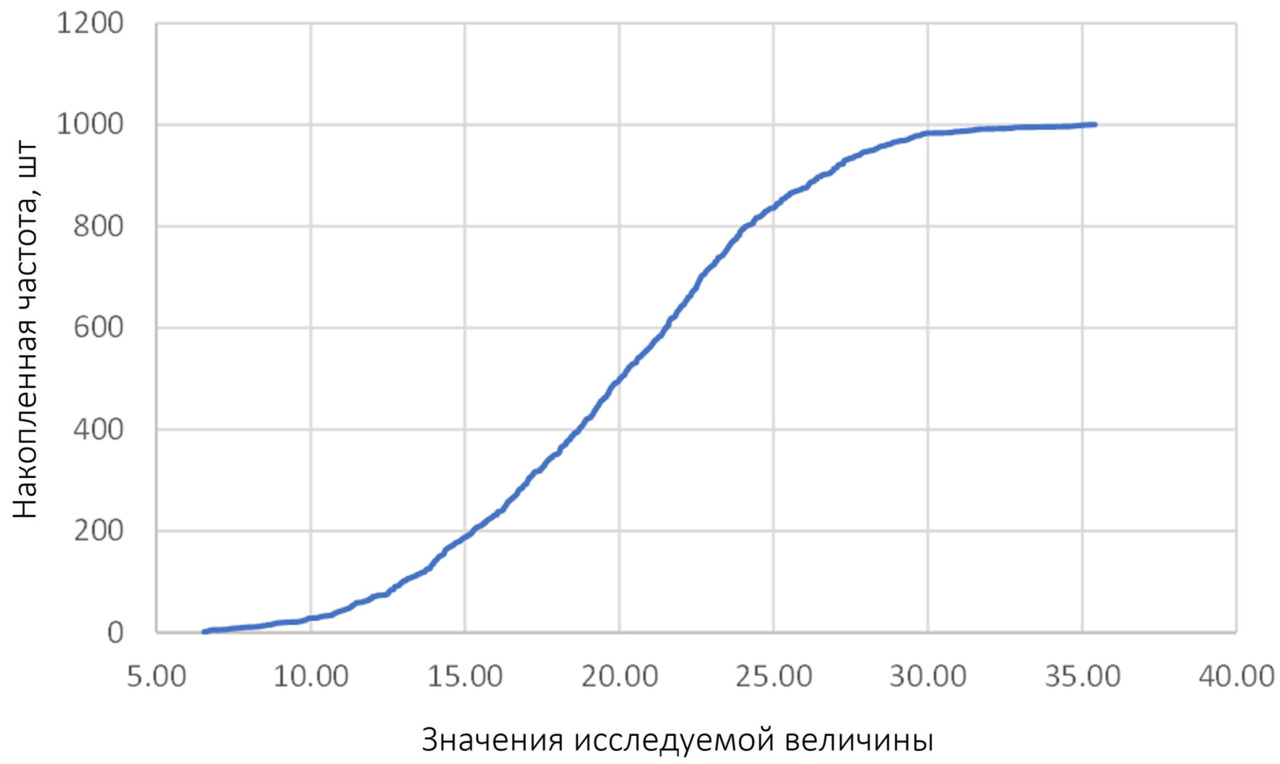
Коэффициент асимметрии

При построении гистограмм можно получить график как симметричный, в котором больших и малых значений «примерно поровну», так и асимметричный — с преобладанием высоких или низких значений. Для условий данных опробования цветных или драгоценных металлов асимметричный график встречается намного чаще симметричного. Логично, что нужна некая точная характеристика асимметрии, которая позволила бы избежать волюнтаризма в определении степени асимметричности выборки. Так давайте же сконструируем такую характеристику.

Итак, у нас есть набор выборочных значений, основная масса которых группируется «слева» или «справа». Логично задать себе вопрос: слева или справа от чего? Видимо, от среднего арифметического. То есть, если мы попытаемся рассчитать разность (Xi — Xсреднее), то среднее подобных разностей должно бы нам показать направление и величину отклонений выборочных данных от среднего. Возможно, должно, но не будет: сумма подобных разностей всегда будет нулевой — по механизму расчета среднего. Казалось бы, можно возвести в квадрат — как это делалось для расчета дисперсии. Но проблема в том, что знак разности (Xi — Xсреднее) нужен (мы ж хотим понимать — значение ушло «влево» или «вправо» от среднего), а при возведении в квадрат знак «потеряется». Логично тогда использовать нечетную степень — она позволит избежать обнуления суммы разностей, с одной стороны, и «не потеряет знак» разностей — с другой. Первая нечетная степень — 3. То есть логично рассчитать среднее арифметическое кубов разностей. Также хотелось бы, чтобы конструируемая величина допускала сравнение асимметрии распределений разнородных данных, возможно, даже измеренных в разных единицах. То есть эта величина должна быть безразмерной — как сконструированный ранее коэффициент вариации. И кажется вполне логичным, что наше среднее должно быть нормировано на стандартное отклонение — т. е. показывать, во сколько раз асимметрия выборки больше, чем характеристика ее размаха. Ну, а учитывая то, что:

— хочется получить безразмерную величину,

— стандартное отклонение имеет те же единицы измерения, что и выборочные данные,

— мы уже рассчитали среднее из кубов разностей,

становится понятным, что необходимо выполнить возведение в куб также и величины стандартного отклонения. Итоговая величина будет рассчитываться по формуле:

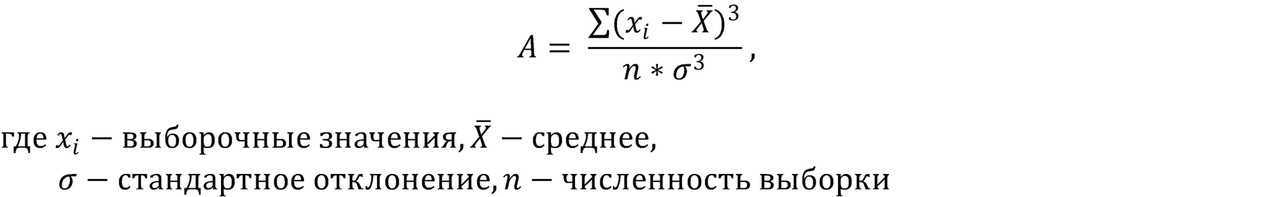
Полученная величина называется коэффициентом асимметрии или просто асимметрией. Коэффициент асимметрии показывает, куда и насколько сильно смещено среднее выборки относительно максимальной частоты распределения. В случае нулевого (или близкого к нулю) коэффициента асимметрии распределение симметрично и «высоких» значений примерно столько же, сколько «низких». В этом случае среднее и медиана выборки близки либо вообще равны.

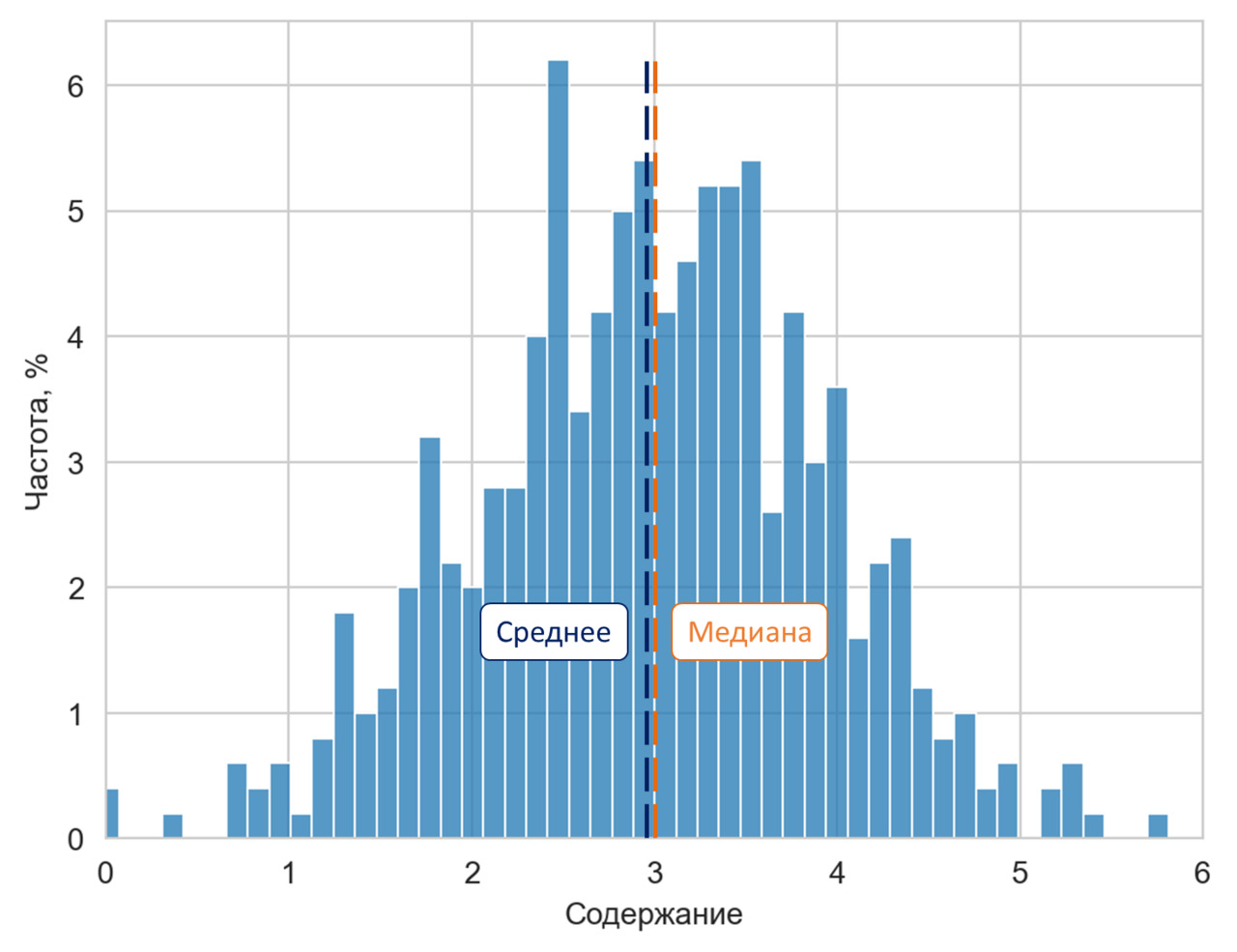
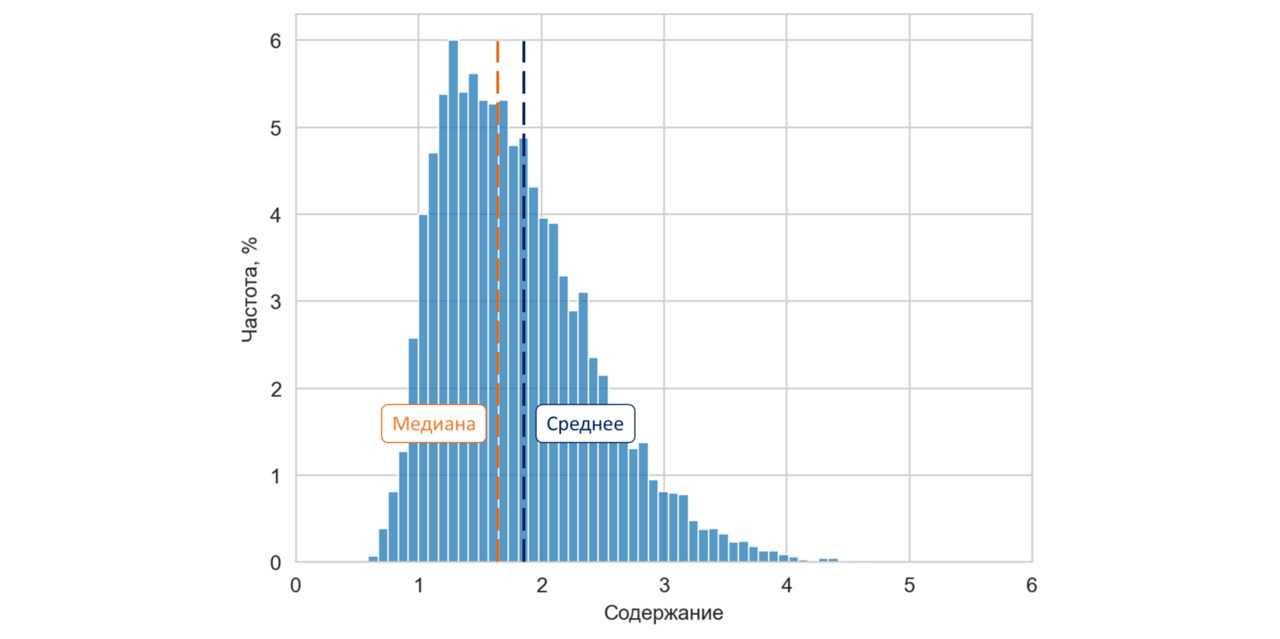
В случае отрицательного коэффициента асимметрии «высоких» значений больше, чем «низких». Среднее ниже медианы, то есть по оси значений смещено влево. В этом случае говорят, что распределение случайной величины имеет левую или отрицательную асимметрию.

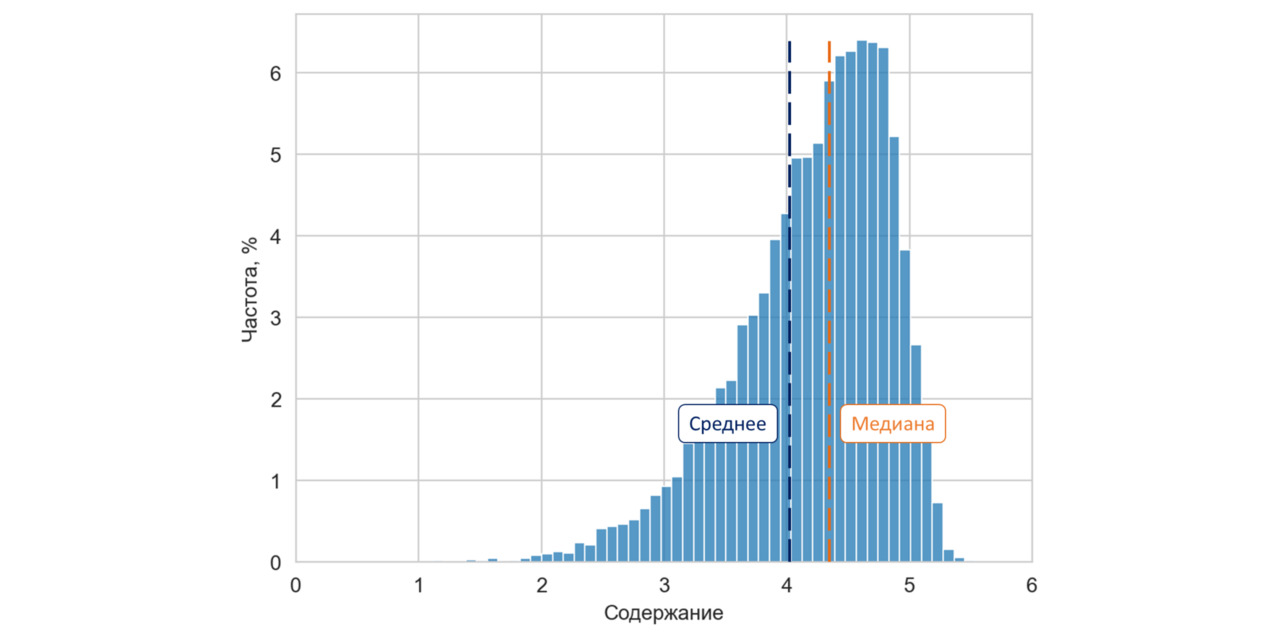
В случае положительного коэффициента асимметрии картина прямо противоположна: «низких» значений больше, чем высоких, среднее смещено относительно медианы вправо (помните пример с жадным директором предприятия? — добавьте к этому «нехорошему» человеку его зама, главбуха, еще парочку топ-менеджеров и получите правоасимметричное распределение зарплат).

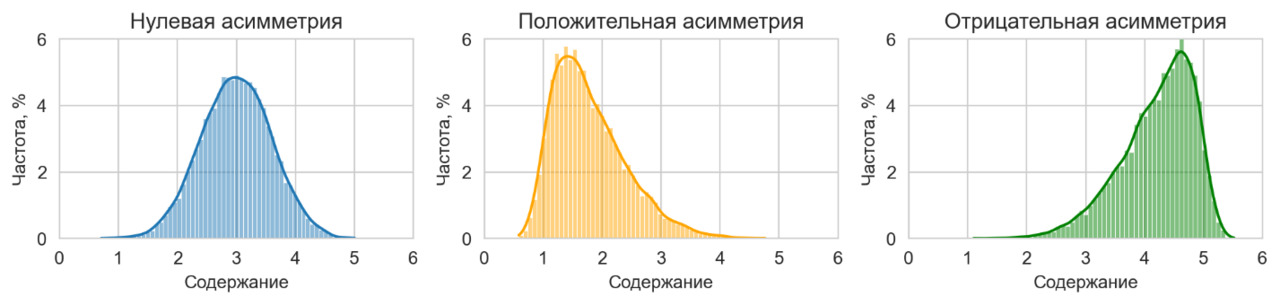
Отобразим графически все виды асимметрии по отдельности.

Диаграммы накопленной частоты будут выглядеть следующим образом.

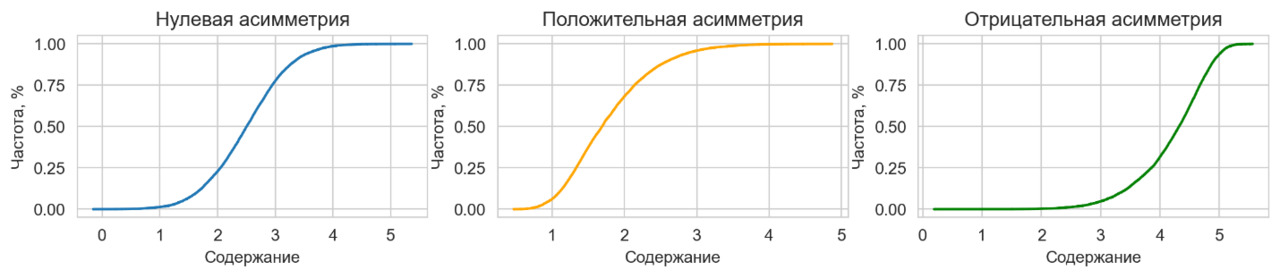
Сведем гистограммы на один график.

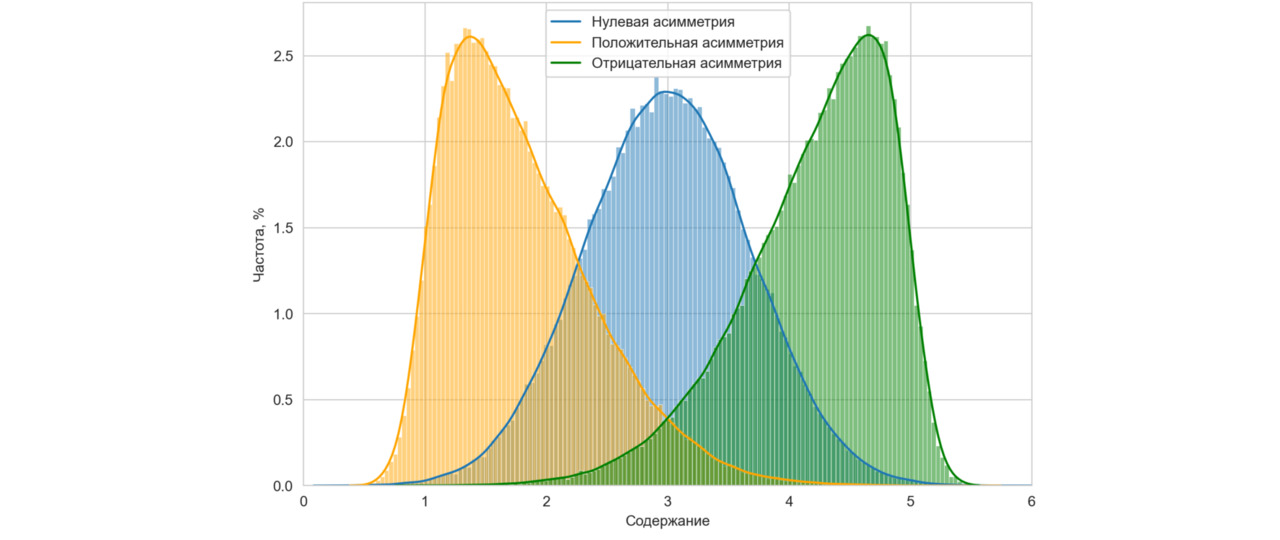
Кроме характеристики степени асимметрии, также существует характеристика того, насколько полученная гистограмма «острая» или «тупая».

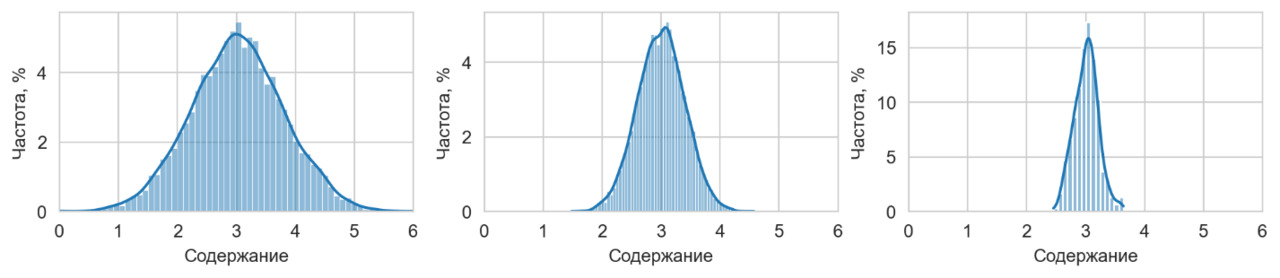
Характеристика, которая позволяет судить о степени «резкости» или «экстремальности», носит название коэффициента эксцесса. На практике коэффициент эксцесса используется значительно реже, поэтому в настоящей главе его смысл подробно не раскрывается.

Виды распределений

Нормальное распределение

В статистике существуют некоторые «стандартные» типы распределений, одним из которых является так называемое «нормальное» распределение. Этому распределению соответствуют распределения многих «бытовых» величин: рост и вес определенной группы людей, во многих случаях — распределение ошибок измерения и т. д. Поскольку это распределение является широко распространенным, его параметры хорошо изучены. Коэффициенты асимметрии и эксцесса нормального распределения равны нулю (точнее, неотличимы от нуля). Среднее арифметическое равно медиане.

Кроме того, для нормального закона существует так называемое «правило трех сигм», которое гласит, что:

— 68% значений находятся в пределах плюс-минус 1 стандартного отклонения от среднего значения;

— 95% значений находятся в пределах плюс-минус 2 стандартных отклонения от среднего значения;

— 99,7% значений находятся в пределах плюс-минус 3 стандартных отклонения от среднего значения.

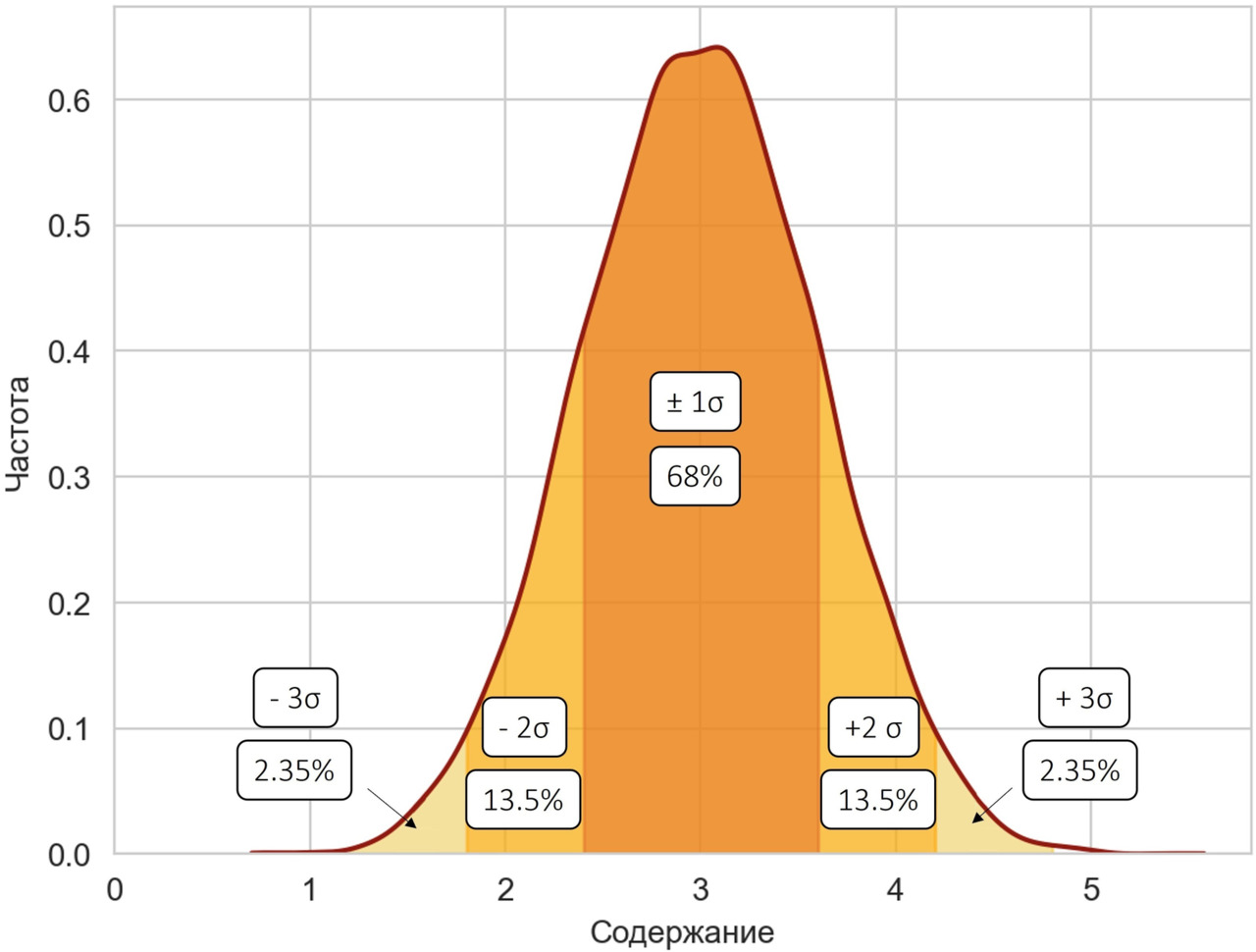
Это правило позволяет не только находить интервал, куда наверняка попадут практически все значения интересующей нас переменной, но и искать значения вне этого интервала. Эти значения называют выбросами. Появление выбросов не является «запрещенным» с точки зрения нормального распределения, но их наличие маловероятно, а потому подозрительно. Это правило было бы хорошим инструментом для поиска ураганных содержаний, если бы не одно «но»: для его применения требуется, чтобы распределение было, во-первых, однородным, а, во-вторых, не противоречило нормальному закону распределения. Что, к сожалению, чаще всего не так (причем зачастую не выполняется ни первое, ни второе требование).

Логнормальное распределение

Кроме нормального распределения, также достаточно распространенным является так называемое логарифмически нормальное, или короче — логнормальное распределение: такое, при котором нормальному распределению не противоречат логарифмы значений изучаемой величины. Логнормальное распределение имеет правостороннюю асимметрию — то есть его среднее смещено по оси абсцисс вправо от медианы, а коэффициент асимметрии положителен.

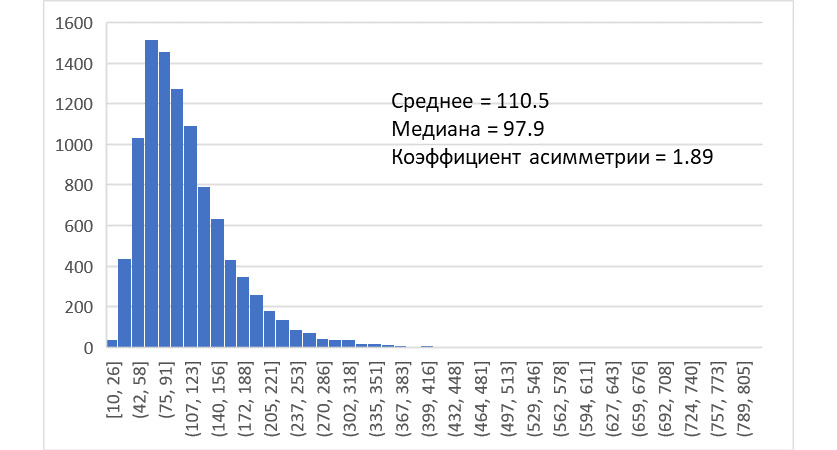
При работе с распределением со значительной правой асимметрией (например, логарифмически нормальным распределением) гистограммы, построенные обычным образом — т. е. в «натуральных» единицах, весьма «ненаглядны». Не в том смысле, что прямо вот «глаз не отвести», а в том, что смотрю — и ничего не вижу. Что неудивительно: большинство наблюдений сгруппировано «слева» и попадает всего в несколько классов значений. Соответственно, гистограмма распределения с большой правой асимметрией выглядит, например, как-то так.

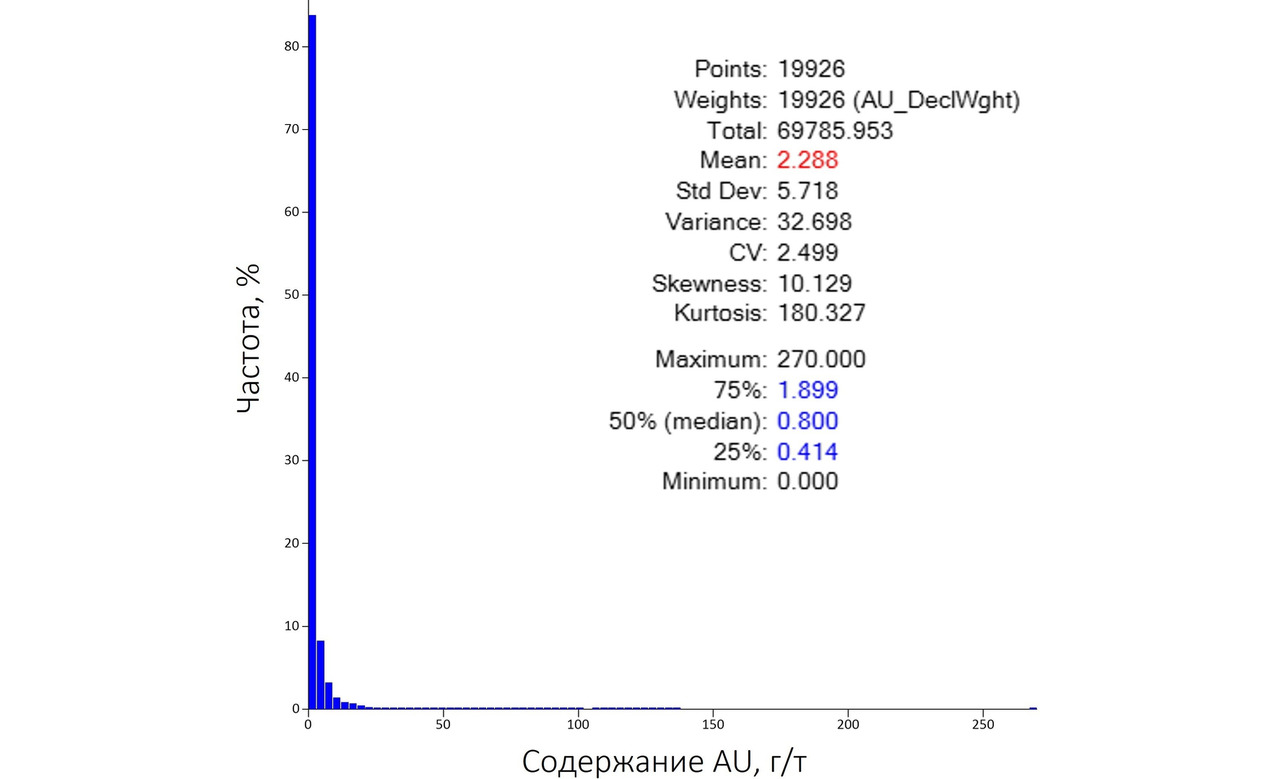
В общем, не очень читаемая гистограмма. В этом случае необходимо выполнить симметризацию распределения. Так исторически сложилось, что наиболее часто встречаемым способом симметризации является логарифмирование значений. В принципе, симметризацию можно выполнить, например, с помощью корня — квадратного, кубического и т. д. Но логарифмирование обычно дает наиболее качественную симметризацию.

Итак, логарифм. Логарифм — это показатель степени, в которую надо возвести основание, чтобы получить число, которое подвергается логарифмированию. С первого раза непонятно (со второго — тоже не очень). Зато понятно, что логарифм — это штука, у которой есть основание. Уже хорошо. То есть у вас есть некоторое число, которое вы решили подвергнуть логарифмированию. Для этого надо выбрать основание логарифмирования. Основание — тоже число. То есть для логарифмирования надо два числа: одно — которое подвергается логарифмированию, а второе — основание логарифма. А на выходе имеем показатель степени, в которое надо возвести основание, чтобы получить число, которое под знаком логарифма. Давайте это запишем:

log2 (8)

Здесь написано: «логарифм 8 по основанию 2». Возвращаемся к определению. Результатом логарифмирования будет показатель степени, в которое надо возвести основание, чтобы получить число, подвергаемое логарифмированию. В приведенном примере мы логарифмируем 8 по основанию 2. В какую степень надо возвести 2 (основание), чтобы получить 8? Очевидно, в 3-ю. То есть:

log2 (8) = 3

Также, исходя из сказанного, совершенно очевидно, что:

log3 (9) = 2

log5 (125) = 3

log10 (10000) = 4

Ну и напоминаем, что

log3 (1) = 0

log5 (1) = 0

log78 (1) = 0

Или в общем случае

loga (1) = 0, a ≠ 0, a ≠ 1

Опять же, чисто исторически сложилось, что в качестве основания логарифма чаще всего принимается два числа — число «e» и 10. Логарифм по основанию «e» называют натуральным, а по основанию 10 — десятичным. Обычно натуральный логарифм обозначают

ln (a),

а десятичный

lg (a)

Давайте кратко рассмотрим два наиболее часто встречающихся основания логарифма. С десяткой «все ясно» — это основание нашей системы счисления и совершенно логично равно количеству пальцев на руках (если бы наша цивилизация была цивилизацией токарей-математиков, основанием системы счисления могло бы быть и 8, и 6 — в зависимости от удачливости токарей). А что такое «e»? Это такое очень интересное число, которое является одной из фундаментальных математических констант (наряду, например, с числом π) и всплывает в большом количестве реальных проблем. Если есть несколько минут времени, можно посмотреть вот этот ролик про число «e». Что еще можно сказать про «e»? Ну, например, то, что оно иррациональное — то есть не может быть вычислено как частное двух целых чисел. В десятичной записи оно имеет бесконечное число знаков после запятой. Также число «e» является трансцендентным — то есть не является корнем ни одного многочлена с целыми коэффициентами. Впрочем, этот факт уже совсем не относится к делу.

Возвращаясь к логарифмированию. Различия в основаниях в подавляющем большинстве случаев никак не сказывается на результате, поскольку для логарифмов действует довольно простое правило замены основания:

loga (b) = logc (b) / logc (a),

то есть для перехода от десятичного логарифма к натуральному результат надо разделить на константу — на натуральный логарифм 10:

lg (a) = ln (a) / ln (10)

Ну или в обратную сторону — от натурального к десятичному:

ln (a) = lg (a) / lg (e)

Поэтому когда речь идет о логарифмировании какой-то выборки, то основание особой роли не играет: любые результаты логарифмирования отличаются друг от друга на постоянный множитель, что не оказывает никакого влияния на характер распределения.

У логарифма есть одно чрезвычайно полезное свойство (правда, в плане обработки выборок, кажется, не применимое):

log (a * b) = log (a) + log (b)

То есть с помощью логарифмирования умножение сводится к значительно более простой операции сложения. И эта особенность логарифмов, например, дала возможность создать аналоговую вычислительную машину, хорошо знакомую «бумерам» — логарифмическую линейку.

Ну и одно неприятное свойство логарифма: логарифм нуля не существует (а в выборках нули, увы, присутствуют).

Возвращаясь к нашим правоасимметричным выборкам. Представим, что в нашем распоряжении есть выборка с большой правой асимметрией (это не реальные данные, а сгенерированные для иллюстрации процедуры построения). Давайте построим по этой выборке сначала обычную гистограмму, потом — гистограмму в логарифмическом масштабе.

Для построения обычной гистограммы последовательно выполняем шаги:

— Определяем минимум, максимум и размах (Лист «Данные»).

— Задаем количество классов группировки и рассчитываем ширину класса (Лист «Данные»).

— Присваиваем каждому значению номер класса (Лист «Шаг 1 — обычный масштаб»).

— Для каждого класса рассчитываем количество данных, границы класса и его центр (Лист «Шаг 2 — обычный масштаб»).

— Строим гистограмму в «натуральном» масштабе (Лист «Шаг 3 — обычный масштаб»).

В итоге получается что-то вот такое:

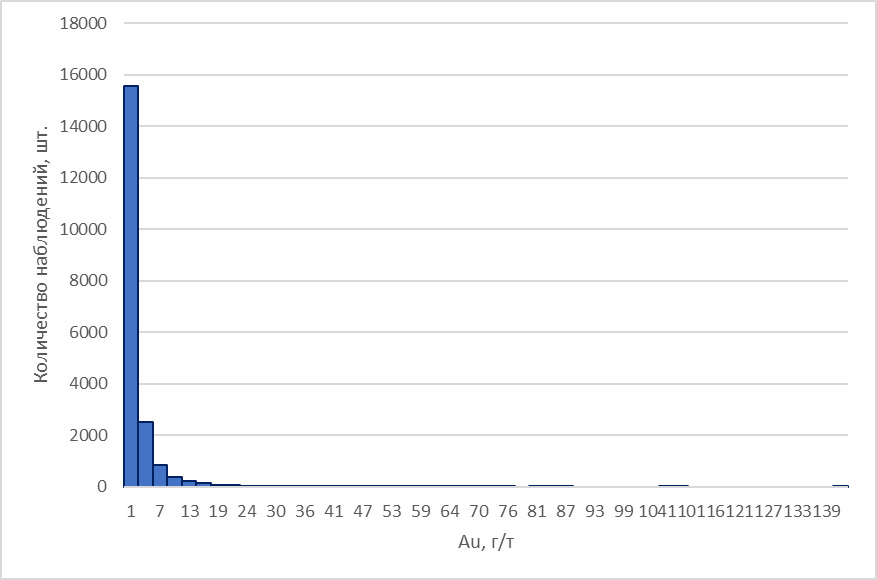
Как и предупреждали, наглядность полученного графика оставляет желать лучшего.

А теперь давайте построим гистограмму в логарифмическом масштабе. Последовательность действий точно такая же, кроме первого шага — данные необходимо логарифмировать:

— Логарифмируем данные. Пусть это будет натуральный логарифм — как сказано выше, основание логарифма не влияет на характер распределения (Лист «Лог. данные»).

— Определяем минимум, максимум и размах логарифмов (Лист «Лог. данные»).

— Задаем количество классов группировки и рассчитываем ширину класса по логарифмам (Лист «Лог. данные»).

— Присваиваем каждому значению номер класса (Лист «Шаг 1 — лог масштаб»).

— Для каждого класса рассчитываем количество данных, границы класса и его центр (Лист «Шаг 2 — лог масштаб»).

— Строим гистограмму в логарифмическом масштабе (Лист «Шаг 3 — лог масштаб»).

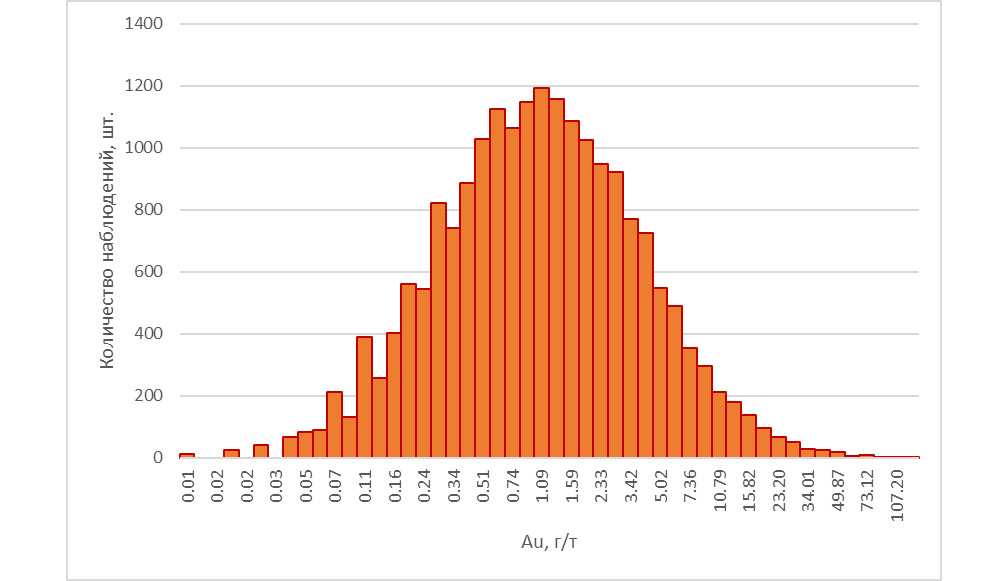
Красивее же, правда? Необходимо отметить, что в реальной работе вам не придется выполнять все эти нудные операции — практически любое ПО, которым вы будете пользоваться, обладает способностью к построению гистограмм — как в натуральном, так и в логарифмическом масштабе. И переход между натуральным и логарифмическим масштабом обычно выполняется с помощью одной «галочки» в настройках графика. Но понимать, что именно произошло и как строить такую гистограмму, необходимо.

Суммируя: при построении логарифмической гистограммы вы работаете не с исходными данными, а с их логарифмами.

Вероятностный график

Следующий довольно полезный график ­ — это нормальный вероятностный график, он же вероятностная кривая, он же Probability Plot. Слово «нормальный» в названии довольно часто опускается. Кроме того, для распределений с положительной асимметрией имеет смысл предварительно выполнить симметризацию распределения с помощью логарифмирования — в этом случае слово «нормальный» в названии графика вовсе неуместно.

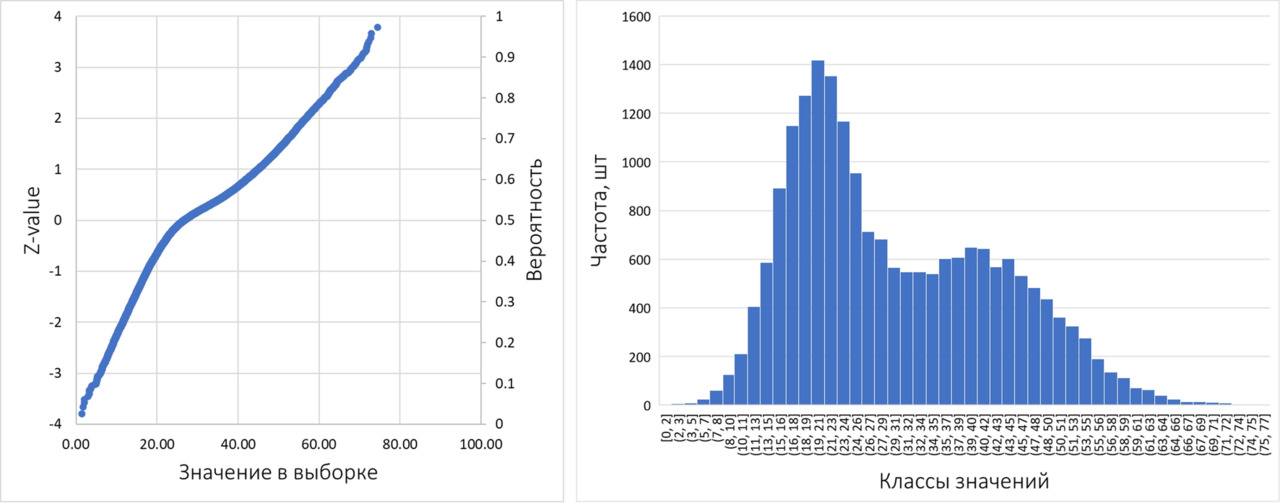
Вероятностный график позволяет визуально оценить однородность выборки, наличие выбросов (ураганных значений), близость исследуемого распределения нормальному (или в случае работы с логарифмами — логнормальному). По сути, вероятностный график — это квантиль-квантильная кривая, построенная по данным двух распределений: исследуемого и нормального. График обычно имеет вид некоторой ломаной кривой, либо серии точек.

По степени «прямоты» вероятностной кривой можно судить о близости рассматриваемого распределения нормальному закону, по наличии резких перегибов и относительно прямолинейных участков на графике — об однородности или неоднородности, а по наличию «срывов» и горизонтальных «ступенек» — о наличии выбросов.

В «докомпьютерную» эпоху для построения вероятностной кривой использовались специальные «вероятностные бланки». С появлением Excel потребность в подобных бланках отпала. Давайте рассмотрим алгоритм построения вероятностного графика на примере данного файла.

На листе «Выборки» с помощью генератора случайных чисел и формулы «НОРМ. ОБР» создаются две распределенные по нормальному закону выборки численностью по 10 000 значений каждая. На листе «Вероятностный график» выполняется объединение двух выборок и строится гистограмма. Для членов объединенной выборки рассчитывается их положение в упорядоченном ряду, для чего используется функция «РАНГ» (столбец «Ранг»).

По сути, результатом функции РАНГ является порядковый номер конкретного члена выборки в упорядоченном ряду. Будь наша выборка упорядочена, достаточно было бы пронумеровать члены итоговой выборки по порядку: «1-2-3…20000». Но выборка не упорядочена и нужна функция «РАНГ». Затем рассчитывается положение каждого члена исследуемой выборки как доля его порядкового номера от общей численности выборки (столбец «Положение члена выборки в долях численности распределения»).

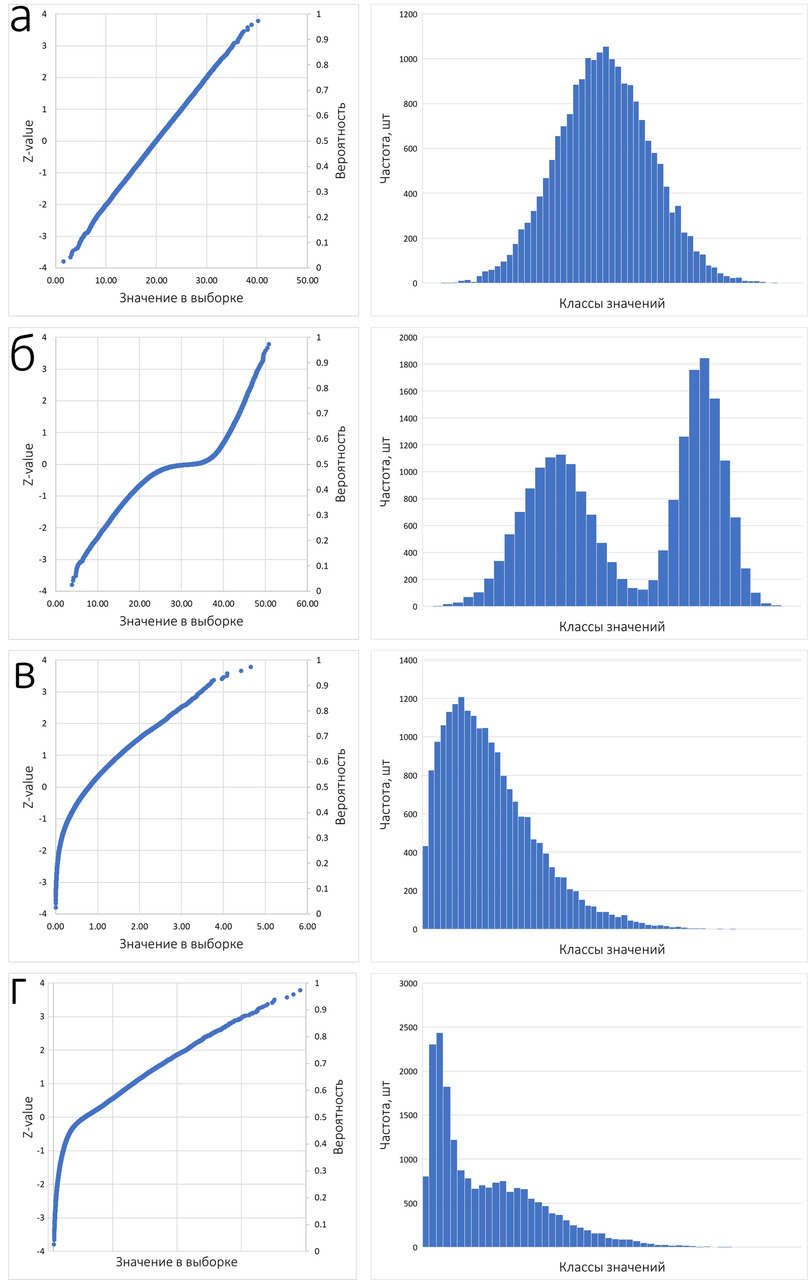
Завершающим шагом мы получаем член выборки из стандартного нормального распределения, который «должен стоять на том же месте». Для этого используется функция «НОРМ. СТ. ОБР» (столбец «Z-value»). Далее по двум рядам, т. е. членам исследуемой выборки и членам стандартной нормальной выборки, строится обычная диаграмма рассеяния. При наличии статистических пакетов или ПО для горно-геологического моделирования выполнять все подобные манипуляции не требуется и вероятностные кривые можно построить одним движением мышки. Обычно в специализированном ПО вместо Z-value на вертикальной оси откладывается значение вероятности нормального распределения. Для вывода этой оси в файле Excel выполнены дополнительные манипуляции, которые выразились в наличии второй вертикальной оси (справа). Обычно эта ось является единственной вертикальной осью на подобных графиках.

Диаграмма «ящик с усами»

Диаграмму «ящик с усами» («box and whisker plot») или диаграмму размаха можно рассматривать как сильно упрощенный вариант гистограммы, который позволяет визуально оценить размах основной массы значений рассматриваемой переменной. Диаграмма не имеет устоявшегося русскоязычного названия. То название, которое используется для обозначения этого типа диаграммы, по сути, является «калькой» с английского.

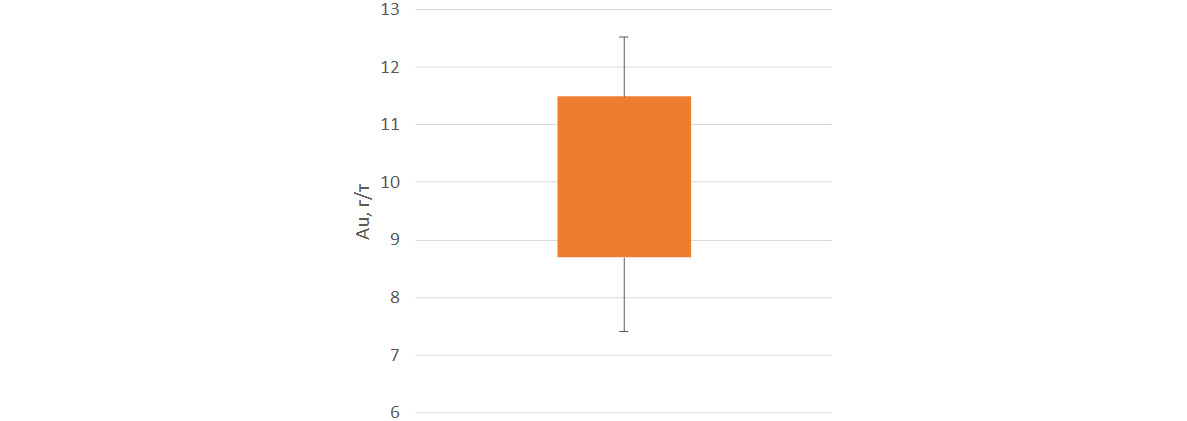
Как можно заметить, значения изучаемой величины отложены в данном случае по вертикальной оси. По горизонтальной оси пока не отложено ничего. Диаграмма может быть как «вертикальной» — как на рисунке выше, а может быть «горизонтальной». В этом случае оси меняются местами и значения изучаемой величины откладываются по горизонтальной оси.

Как-то так исторически сложилось, что авторам встречались преимущественно «вертикальные» варианты этой диаграммы, поэтому давайте дальше рассматривать именно его. «Горизонтальные» ящики с усами отличаются от «вертикальных» только номенклатурой осей.

Как следует из названия, у диаграммы есть два элемента — ящик и усы.

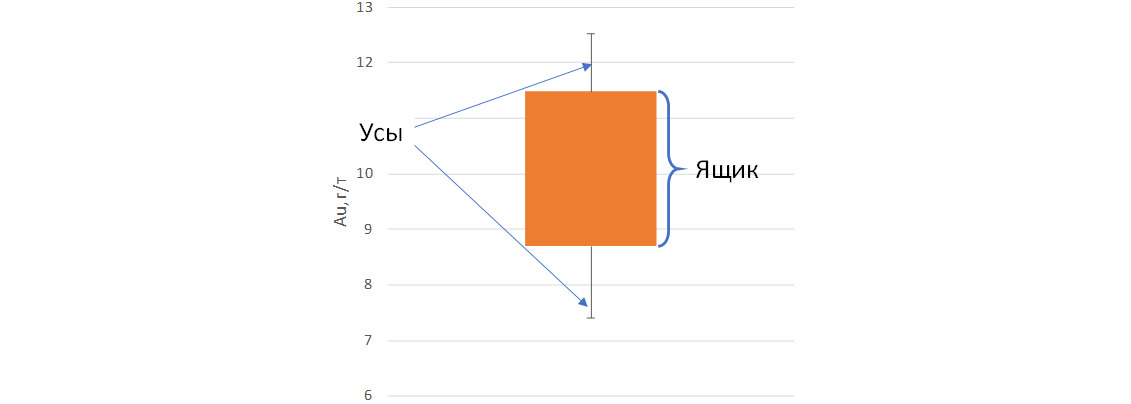
Для построения этого типа диаграммы нет каких-то строгих правил, однако обычно «дно» ящика — т. е. его нижняя граница — это первый квартиль (то есть граница 25% данных), а «верх» ящика — это обычно третий квартиль. То есть ниже нижней границы ящика находится 25% наблюдений, упорядоченных по возрастанию, также и выше верхней границы ящика находится 25% наблюдений, упорядоченных по возрастанию.

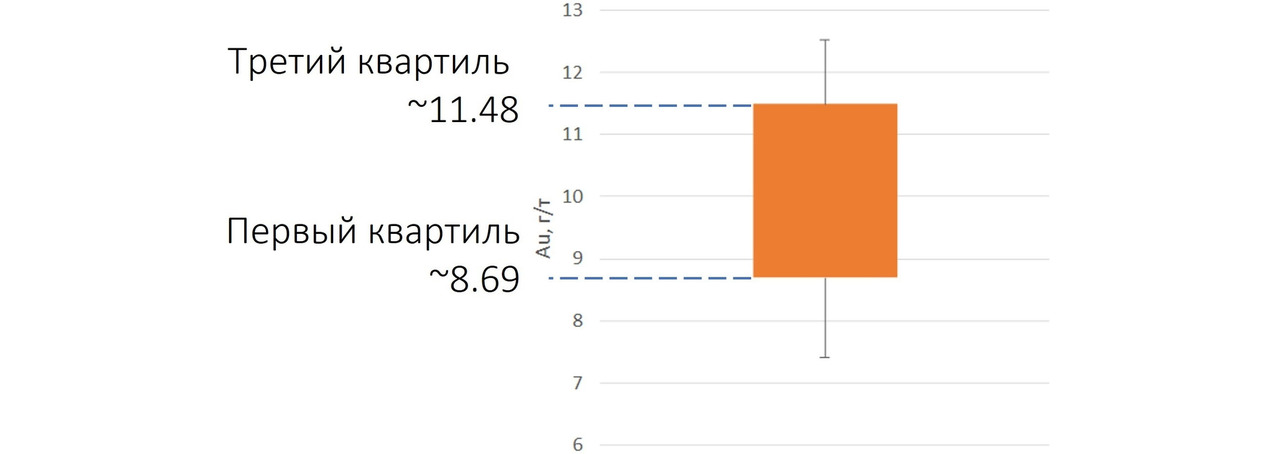
Выше 25%, ниже 25%, следовательно, в ящике находится 100 — 25 — 25 = 50% наблюдений.

С ящиком, кажется, разобрались. Теперь давайте разбираться с усами. Здесь уже вариаций намного больше. Усы могут строиться по минимуму/максимуму — как, например, это делает Excel (правда, он может также на этой диаграмме показывать выбросы — и тогда непонятно, как рассчитываются усы, а официальная справка ответа на этот вопрос не дает). Это могут быть границы первого и последнего децилей, т. е. они могут показывать границы, между которыми заключено 80% наблюдений. В ряде руководств «усы» строятся как полтора межквартильного размаха, который откладывается от границ ящика. Вместо межквартильного размаха может использоваться стандартное отклонение. В общем — широчайший простор для творчества. В любом случае обычно в пределах «усов» находится не менее 80% данных (вместе с теми 50% данных, которые находятся «внутри ящика»).

На диаграмму часто наносят медиану и среднее — и в этом случае можно судить о наличии асимметрии (о наличии асимметрии можно судить и по соотношению верхнего и нижнего усов). Также на эту диаграмму можно нанести точки, которые находятся выше/ниже усов, и в этом случае эти точки можно расценивать как выбросы.

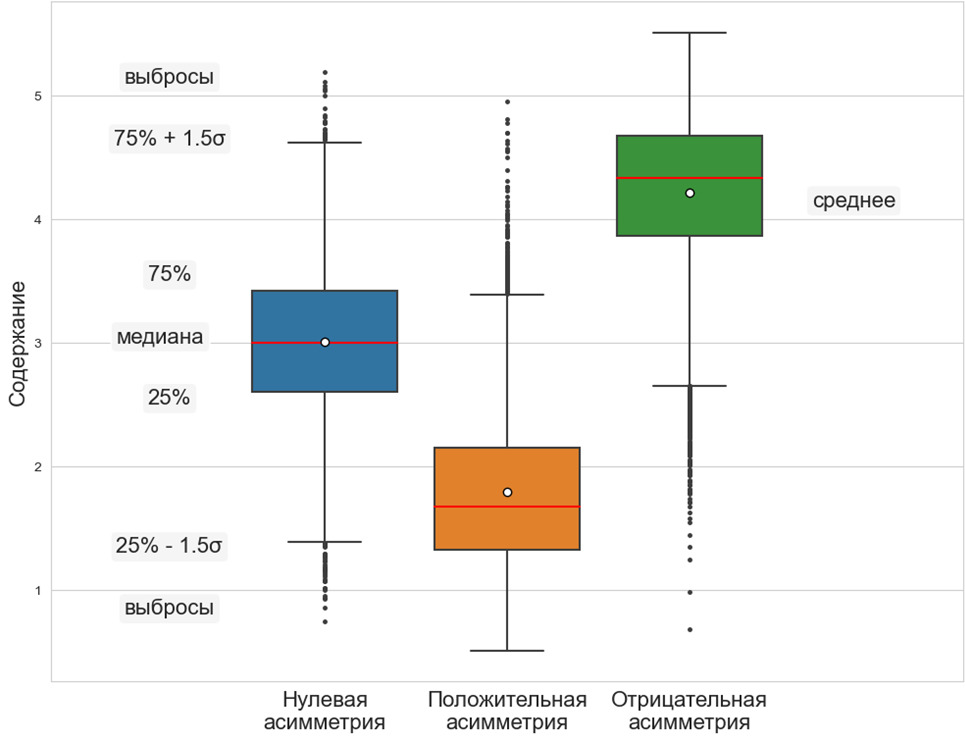
В общем, диаграмма довольно простая, но полезная. Наиболее часто этот тип диаграмм используют для простого визуального сравнения выборок по нескольким доменам на предмет наличия или отсутствия различий.

Давайте представим ситуацию, при которой в нашем распоряжении есть три геологически разнородных тела, несущих минерализацию. Разнородность может обнаруживаться в массе факторов: в минеральном составе интересующей нас минерализации, в принадлежности к разным стадиям рудообразования и т. д.

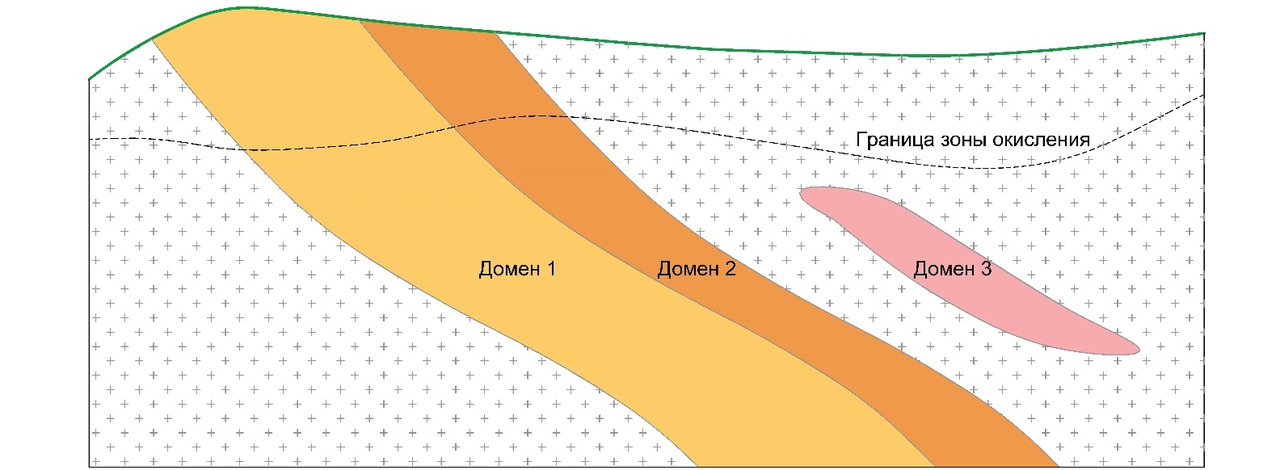
Нам интересно: те различия, которые мы фиксируем в геологических характеристиках, имеют ли какое-либо отражение в характеристиках количественных? Например, в содержании полезного компонента. Для этого данные опробования группируются по выделенным телам (доменам) и для каждой выборки строятся диаграммы «ящик с усами».

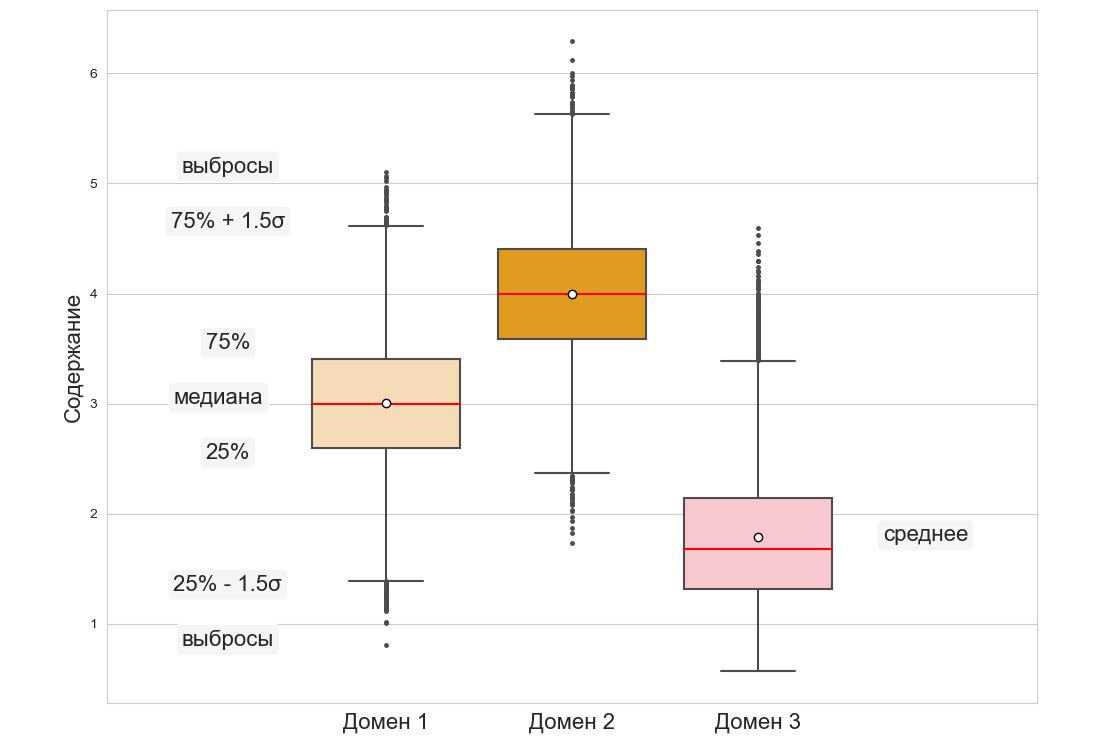
Увы, все три тела, выделенных по геологическим характеристикам, оказались различны и по содержаниям. Это различие имеет печальные для нас последствия: при моделировании придется учитывать найденную неоднородность и выполнять в три раза больше вычислений, чем если бы оказалось, что все три выборки схожи по параметрам распределения.

Можно заметить, что в ситуации, описанной выше, мы никак не использовали границу зоны окисления. Это неправильно: необходимо проанализировать вопрос о том, оказывают ли приповерхностные процессы существенное влияние на распределение полезного компонента. Для этого три ранее выделенных выборки необходимо разбить на еще более дробные части. Вот так:

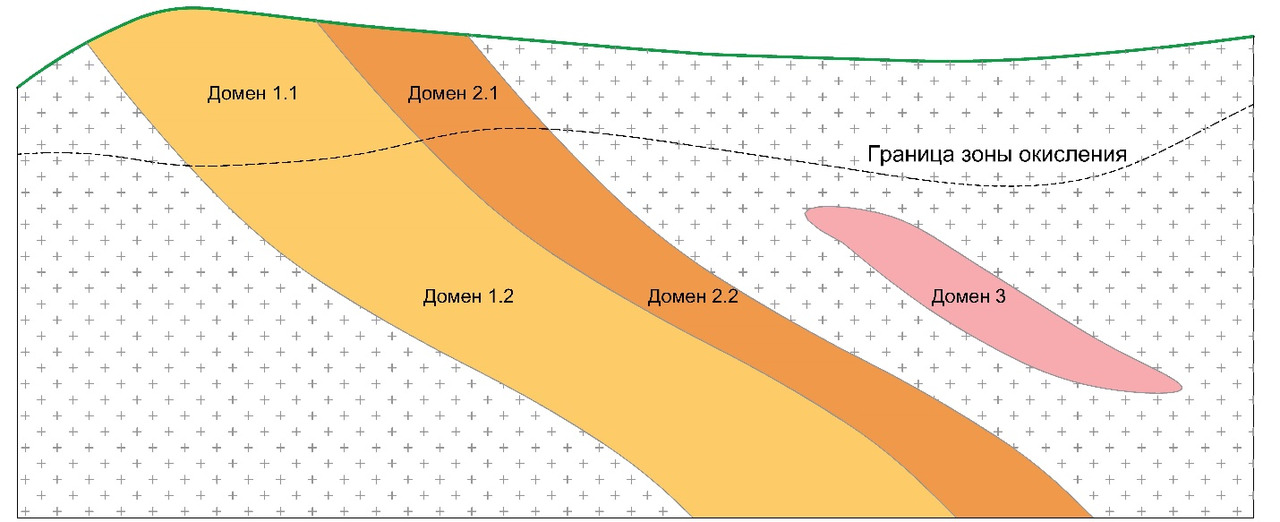
И выполнить ровно те же манипуляции, что для ранее выделенных трех частей нашего массива опробования. И вот здесь уже можно предположить, что первичная минерализация и минерализация, подвергшаяся приповерхностным изменениям, близки по характеристикам распределения: ящики с усами по доменам 1.1/1.2 и 2.1/2.2 похожи. Для того, чтобы убедиться в этом, необходимо использовать еще один тип диаграмм, который будет описан чуть позже. Здесь же хочется сказать, что, в общем, довольно простой тип диаграмм (у которого еще и название вызывает улыбку) позволяет довольно легко визуально сравнить большое количество выборок. Безусловно, это не строгий анализ, но для первичной разбраковки лучшего инструмента придумать сложно.

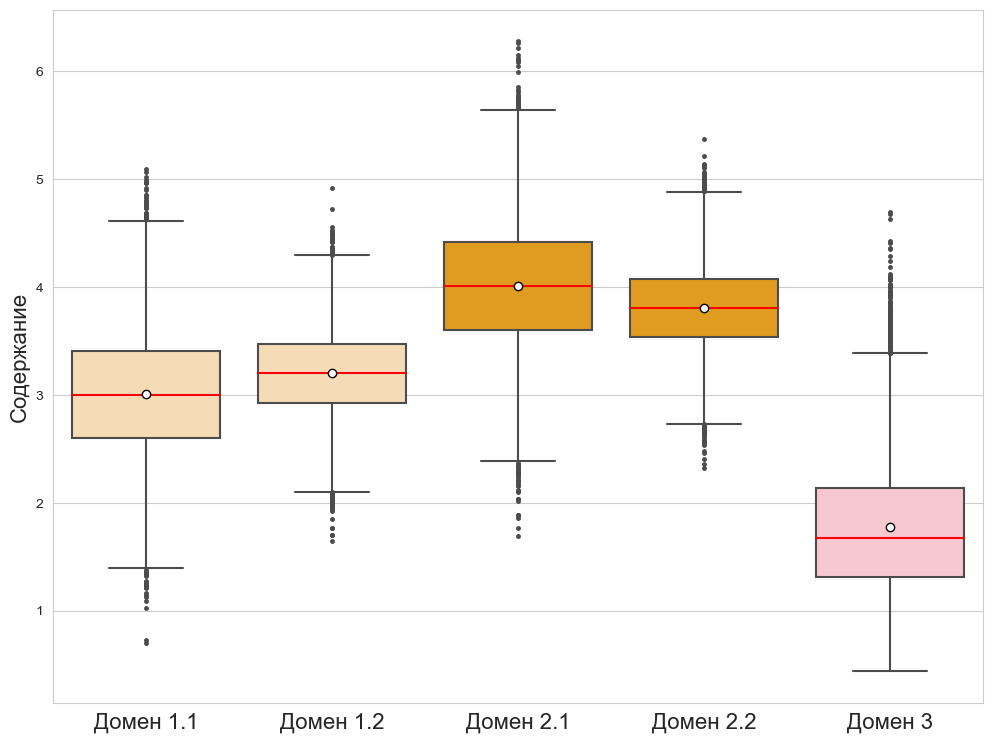
График квантиль-квантиль

На предыдущих страницах была смоделирована ситуация трех разнородных геологических тел, два из которых дополнительно испытали приповерхностные изменения. С помощью диаграммы «ящик с усами» мы выяснили, что тела 1, 2 и 3, скорее всего, друг от друга довольно сильно отличаются. Однако также мы выяснили, что выборки, отобранные из окисленной и неокисленной частей двух тел, кажется, не отличаются. Осталось провести более тщательное сравнение для того, чтобы принять решение о том, действительно ли «окисленная» и «неокисленная» выборки относятся к одной генеральной совокупности и при моделировании нет необходимости в разделении всего объема данных на 5 частей.

Принять подобное решение может помочь график, называемый квантиль-квантильной диаграммой. На сленге этот вид диаграммы часто называют «куку», а процесс построения — «кукованием», что объясняется «прямым» прочтением англоязычной версии названия диаграммы как «q-q plot».

Как было сказано, диаграмма строится по данным двух сравниваемых выборок. Для ее построения по каждой выборке рассчитываются процентили, и после расчетов данные наносятся на диаграмму в координатах «процентили по выборке 1» / «процентили по выборке 2». Получается что-то вроде вот такого:

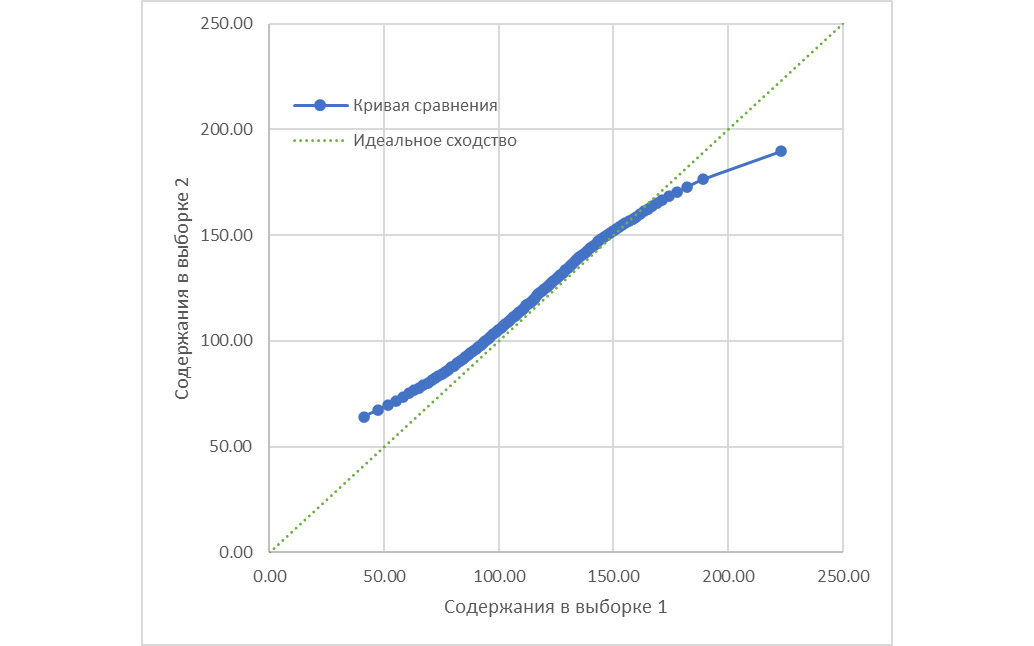
В некоторых случаях вдоль координатных осей графика строятся гистограммы (на самом деле, вопрос о том, строить или не строить здесь гистограммы, решается по принципу «а мое ПО это может?». Например, Python — может, и легко. А вот в Excel это сделать тяжело). Тонким зеленым пунктиром на графике нанесена линия «идеального сходства» — то есть та линия, вдоль которой выстроились бы точки, если бы две сравниваемые выборки были идентичны. Соответственно, о сходстве или различии выборок можно судить по степени соответствия реального графика и идеальной прямой.

Напомним внешний вид диаграммы «ящик с усами» для ситуации, описанной ранее.

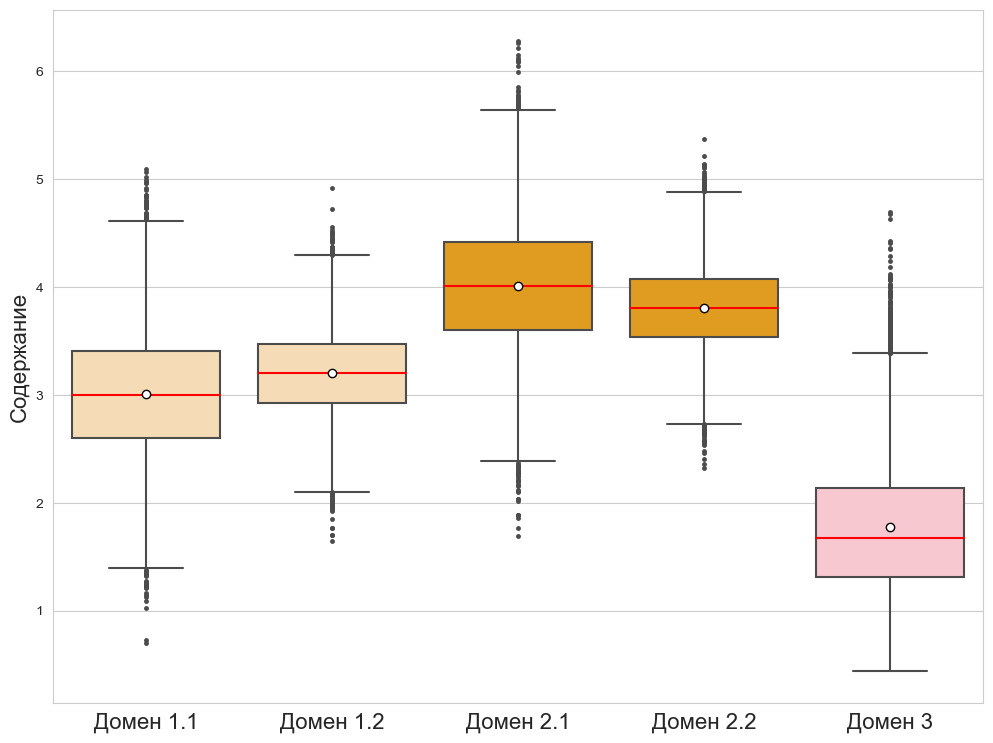
На основании этой диаграммы было высказано предположение, что выборки по доменам 1.1 и 1.2, возможно, схожи. Аналогичное предположение было сделано относительно доменов 2.1. и 2.2. Давайте посмотрим на квантиль-квантильные диаграммы этих двух пар доменов:

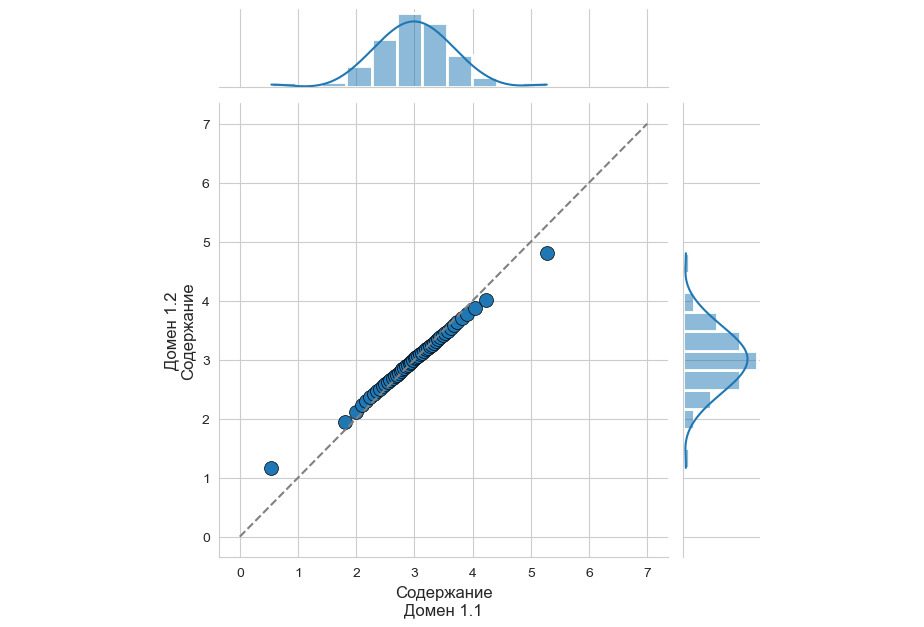
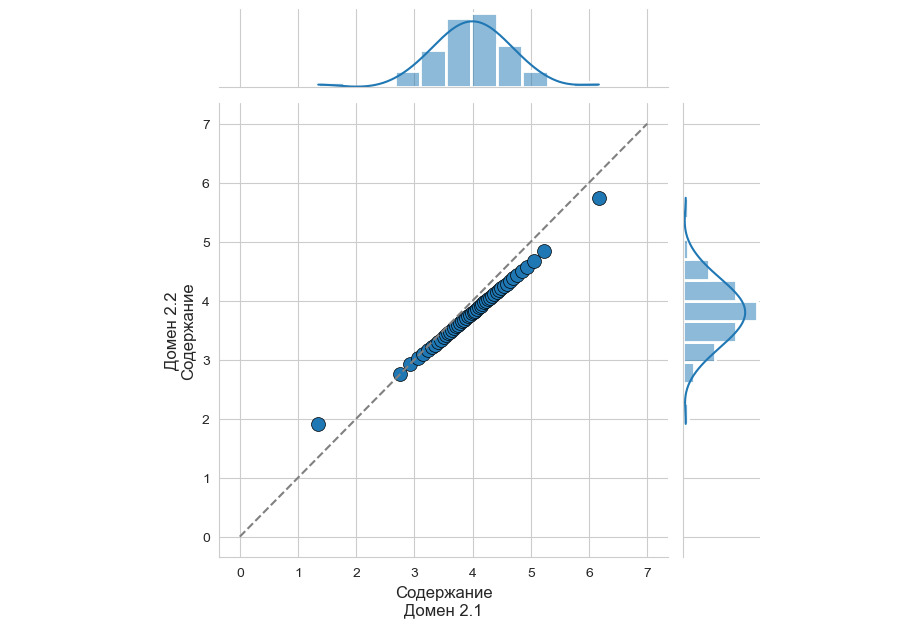
Судя по всему, рассматриваемые пары доменов достаточно схожи между собой, и никакого смысла в их разделении не просматривается. Давайте ради любопытства посмотрим квантиль-квантильные диаграммы по другой паре доменов. Например, 2.1 и 3:

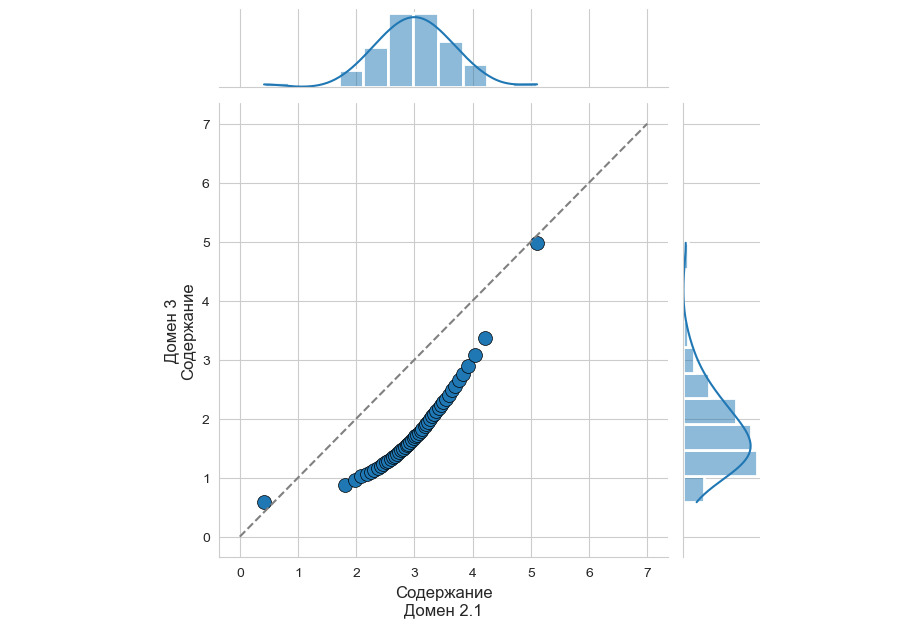
Видно, что различия между доменами 2.1 и 3 довольно существенные, и при моделировании данные домены смешивать крайне не рекомендуется.

Прочитав эту главу, человек, знакомый со статистикой, может сказать: «Позвольте, зачем это все, если есть такие замечательные вещи, как критерий Стьюдента, критерий Фишера?» И будет отчасти прав: в статистике для сравнения двух выборок действительно используются критерии. Однако есть одна неприятная особенность: эти критерии относятся к параметрическим — т. е. таким, применение которых основывается на предположении о законе распределения изучаемых выборок (причем, нормального закона). А ранее мы отмечали, что реальные выборки в геологии крайне редко подчиняются этому закону, да еще запросто могут быть неоднородными (причем, с негеометризуемой неоднородностью). Поэтому, увы, применение «классических» параметрических критериев сходства зачастую невозможно. Безусловно, существуют критерии непараматрические, но их применение ограничено уже используемым ПО: например, в популярных пакетах для геологического моделирования встроенный функционал для расчета U-критерия Манна — Уитни не встречено. С F-критерием Фишера ситуация лучше. Тем не менее частота использования этих критериев довольно низка, с пониманием их сути, вероятно, ситуация не лучше. А предложенные графики позволяют сделать, в принципе, обоснованный вывод о сходстве или различии двух выборок и, скорее всего, не сильно ошибиться.

Понимание производимых действий

При вычислении характеристик выборки (и вообще при работе с данными) необходимо помнить о смысле вычисляемых величин, чтобы не получить классическую «среднюю температуру по больнице», усреднив температуру пациентов инфекционного отделения с температурой экс-пациентов морга. То есть необходимо, чтобы природа данных была «примерно похожей». Например, если данные опробования представлены относительно большими пробами зоны рассеянной минерализации (например, 1–2 м) с заведомо более низкими содержаниями и пробами стержневых жил по 5—10 см с содержаниями, очевидно, значительно более высокими, то считать среднее по такой выборке, скорее всего, нет особого смысла (и взвешивание здесь не поможет) — просто потому, что такая выборка изначально геологически неоднородна. Безусловно, чисто механически эту величину получить можно, но будет ли она иметь смысл — вопрос дискуссионный. Данная проблема довольно часто встречается, например, при моделировании объектов с длительной историей освоения, когда в советское время опробованию подвергалось почти только визуально выделяемое оруденение (причем пробоотбор выполнялся бороздовым способом, да еще и не бороздами правильного сечения и почти только по штольневым горизонтам), а в современных условиях изучение этих же тел выполняется скважинами колонкового бурения по регулярной равномерной сети с примерно равной длиной секций опробования. В описанной ситуации расчет среднего по рудной выборке «в лоб» практически гарантированно приведет к получению смещенной оценки. К сожалению, абсолютно надежного рецепта устранения неоднородности выборки в таких случаях не существует, каждый объект необходимо рассматривать индивидуально.

Также при работе с данными опробования одно из основных требований к данным — равенство оснований. То есть примерное равенство объемов руды, которое подвергнуто опробованию. Рассматривать в рамках одной выборки данные рядового опробования скважин и валовых проб подземных выработок чисто механически возможно (математика многое стерпит), но вряд ли имеет смысл. Просто потому, что пробы меньшего основания (опробование скважин) заведомо показывают более высокие содержания с принципиально более высокой его вариативностью относительно проб с большим основанием (валовых проб).

При манипуляции с данными всегда необходимо понимать смысл этих манипуляций.

---

§ Задание 1.3

Скачайте и изучите тренажер графиков. Данные обновляются при нажатии клавиши «F9». Поэкспериментируйте с различными случайными входными данными и для себя ответьте на следующие вопросы:

— Как ведут себя среднее и медиана при нормальном распределении?

— Как ведут себя среднее и медиана при положительной асимметрии?

— Как ведут себя среднее и медиана при отрицательной асимметрии?

— Как ведут себя выбросы при нормальном распределении?

— Как ведут себя выбросы при положительной асимметрии?

— Как ведут себя выбросы при отрицательной асимметрии?

Декластеризация

Кластеризация