Аннотация. Изучение окружающего мира непосредственно сводит к необходимости ведения тех или иных прогнозов, которые сводятся уже к важности установления для них основных законов мироздания, которые можно наблюдать в ходе изучения тех или иных явлений. При этом часто использование физических законов, возможные для описания с использованием не только обычных уравнений, но и дифференциальных уравнений, первого и вторых порядков, в том числе и большого количества уравнений в частных производных, довольно часто используемых при этом исследовании и понимании.

Ключевые слова: дифференциальные уравнений в частных производных, обыкновенные дифференциальные уравнения, математическое моделирование, аналогия, закономерности.

Annotation. The study of the surrounding world directly reduces to the need to make certain forecasts, which are already reduced to the importance of establishing for them the basic laws of the universe, which can be observed during the study of certain phenomena. At the same time, there is often the use of physical laws that are possible to describe using not only ordinary equations, but also differential equations of the first and second orders, including a large number of partial differential equations, quite often used in this study and understanding.

Keywords: partial differential equations, ordinary differential equations, mathematical modeling, analogy, regularities.

Coming to the study of the laws of the world in physical science, certain laws were most often distinguished, the initial ones among which are the mechanical laws created by Newton and developed mathematically from his side, along with other scientists, among whom the figure of Leibniz stands out vividly. For an example of this statement, we can give the differential forms of the basic equations of motion (1), which in turn are reduced to certain values in the formulas of acceleration (2), force (3), work (4), power (5) and others.

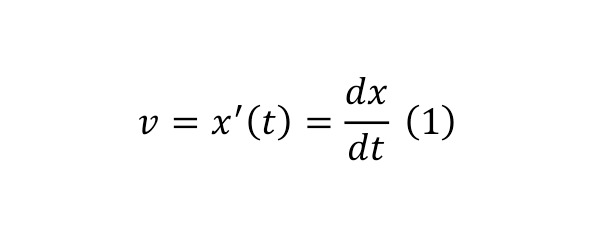
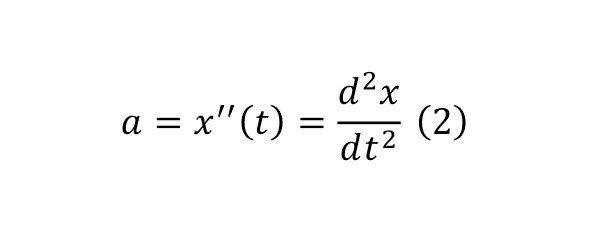
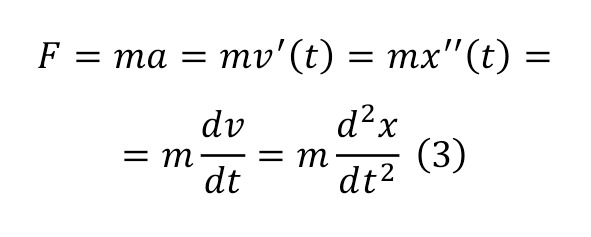
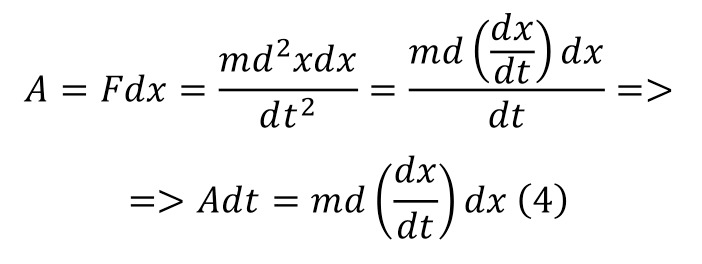
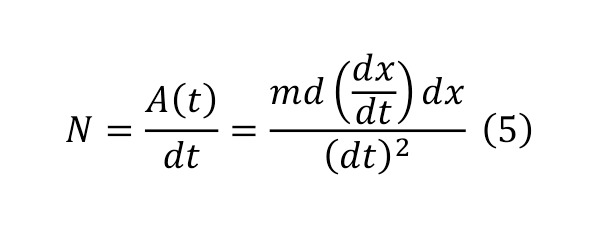
The present moments of understanding can most often be considered precisely in differential forms of meaning, for the reason that they can be numerically determined by introducing some transformations, namely, by converting (6) and taking a certain integral with the establishment of certain boundaries (7).

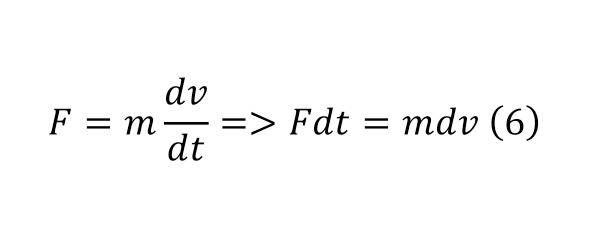
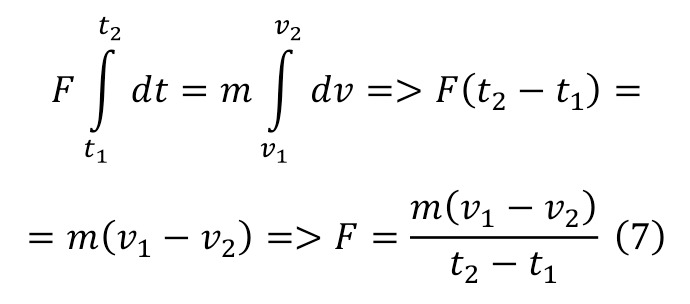
Such directions are developed not only in mechanical terms, but also in other branches of physics, electrostatics, electrodynamics, magnetostatics, magneto-dynamics and others can be a vivid example of this. To prove this, it is enough just to mention that the very concept of current strength is a derivative of the charge time, and voltage is a derivative of the work charge.

This statement can be given for a large number of very different understandings, but the important fact is that such an approach, unlike classical mathematical regulation, becomes the only one when it is necessary to describe the gravitational characteristics of space on the scale of the entire space. An example of this kind of phenomena, where the use of derivatives and, accordingly, differential equations becomes known quantum physics.

However, on the scale of phenomena where the classical mathematical apparatus can no longer perform its functions, it is not so much the usual classical derivatives that are reduced to ordinary differential equations that are important, unless, of course, the simplest cases are not taken into account, a vivid example of which is overcoming the potential well of a particle or describing its motion, or other similar trivial cases, only partial differential equations are more interesting.

Used literature

1. Pontryagin L. S. Ordinary differential equations. — M.: Nauka, 1974.

2. Tikhonov A. N., Samarsky A. A. Equations of mathematical physics. — M.: Nauka, 1972.

3. Tikhonov A. N., Vasilyeva A. B., Sveshnikov A. G. Differential equations. - 4th ed. — Fzimatlit, 2005.

4. Umnov A. E., Umnov E. A. Fundamentals of the theory of differential equations. — Ed. 2nd — 2007. — 240 p.

5. Charles Henry Edwards, David E. Penny. Differential Equations and the problem of eigenvalues: Modeling and calculation using Mathematica, Maple and MATLAB = Differential Equations and Boundary Value Problems: Computing and Modeling. — 3rd ed. - M.: "Williams", 2007.

6. Elsholts L. E. Differential Equations and Calculus of Variations. — M.: Science, 1969.

SOME OPERATIONS AND SPECIAL CASES OF MATHEMATICAL ANALYSIS IN THE EXPONENTIAL SET

Aliev Ibratjon Khatamovich

2nd year student of the Faculty of Mathematics and Computer Science of Fergana State University

Ferghana State University, Ferghana, Uzbekistan

Аннотация. Важность определения и преобразования ингенциальных чисел и настоящего множества с каждым днём становится всё более очевидном, особенно с входом данного понятия в математическую физику, но и как чисто математический объект они представляют не малый интерес, хотя при этом имеют и практическое применение. В настоящей работе, описаны методы проведения некоторых алгебраических операций с ними, в том числе с использованием формулы Эйлера и интеграллами.

Ключевые слова: ингенциальные числа, математический анализ, алгебраические операции, формула Эйлера, интегрирование, производные.

Annotation. The importance of defining and converting exponential numbers and a real set is becoming more and more obvious every day, especially with the entry of this concept into mathematical physics, but as a purely mathematical object they are of no small interest, although they also have practical applications. In this paper, methods of performing some algebraic operations with them are described, including using Euler’s formula and integrals.

Keywords: inertial numbers, mathematical analysis, algebraic operations, Euler formula, integration, derivatives.

The very process of logarithmization of an exponential number of a general form can be seen in (1).

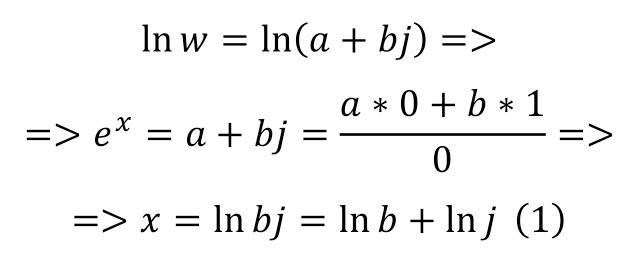
Thus, when logarithming, 2 parts of the expression itself are formed — the real one, as the natural logarithm of the coefficient of the ingential part and the logarithm of the ingential unit, which is defined in (2).

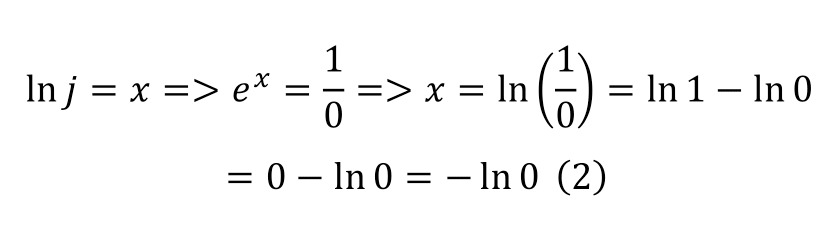
That is, in this case, the question arises to what degree it is necessary to raise the Euler number so that it gives an exponential unit. The answer is quite simple — it is a negative logarithm of zero (2) from this it follows that the logarithm of the exponential number is (3).

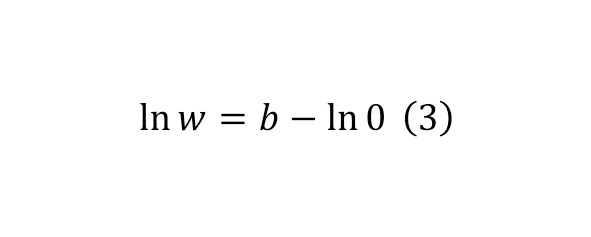
It is also interesting to solve the Euler equation with a tangential unit, and then with a general form of an exponential number, which was described further, taking the expressions as unknowns. And for this, we can initially proceed from Taylor expansions (4—6).

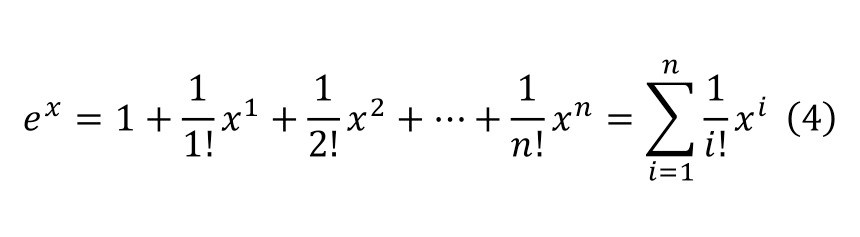
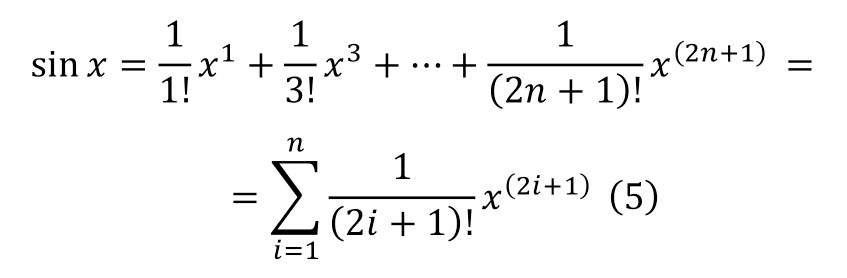
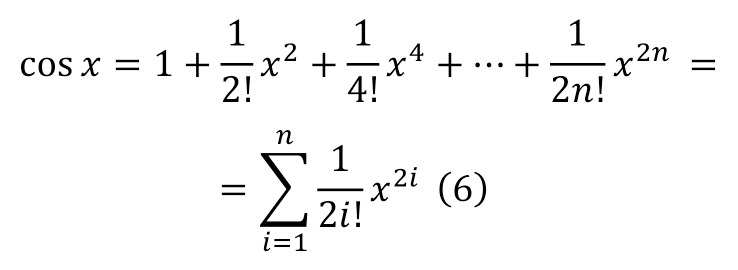
Which is easily proved, since when the unknown is zeroed, the sine in (5) is also zeroed, and the cosine in (6) is equal to one. And it already follows from this (7).

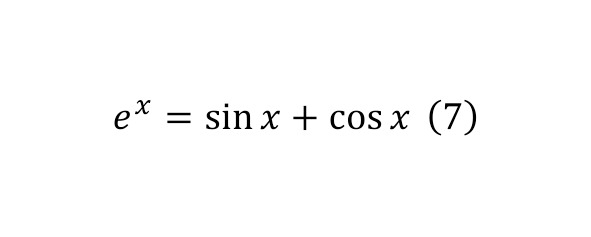
And the unknown in (7) can be all kinds of numbers, both complex, when substituting which the remarkable Euler equality follows, and exponential. And to begin with, let’s consider a special case with an exponential unit and perform the following transformations (8).

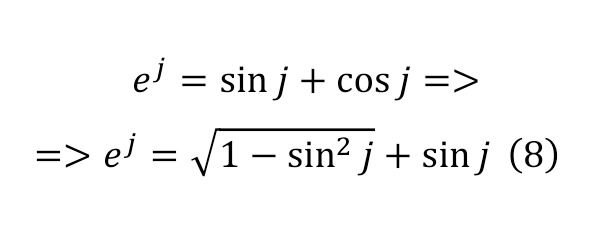
Based on this relation, we perform transformations in (9), leading to equation (10), while taking into account that this expression is identical, it is possible to differentiate both parts of the equation in (11) by performing the corresponding transformations.

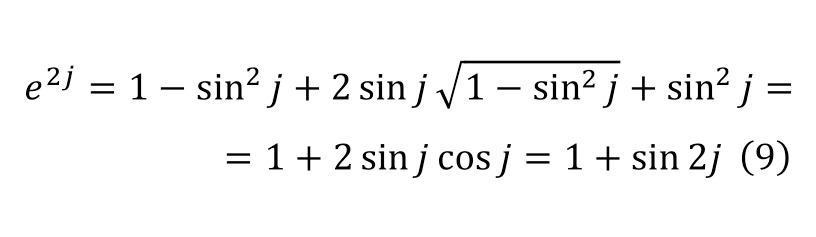
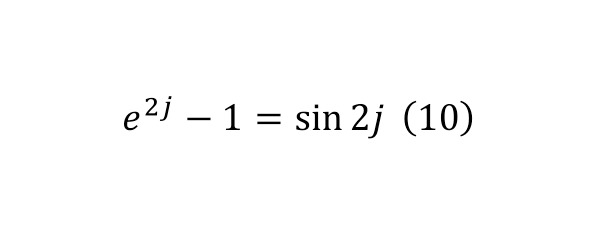
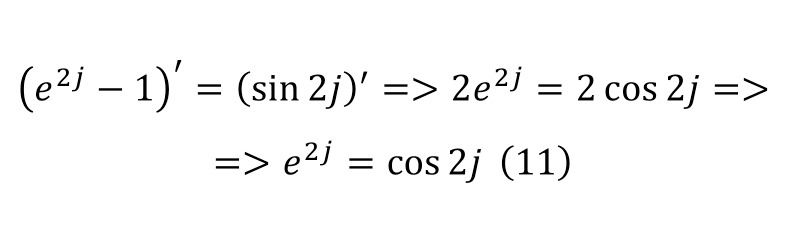
Since the final equality (11) can be represented as in (12), further carrying out additional differentiation, also introducing the condition that this is an identity, and in (13) the differentiation process for the right side of equality is described in detail. And for the left part there is no need for a detailed painting.

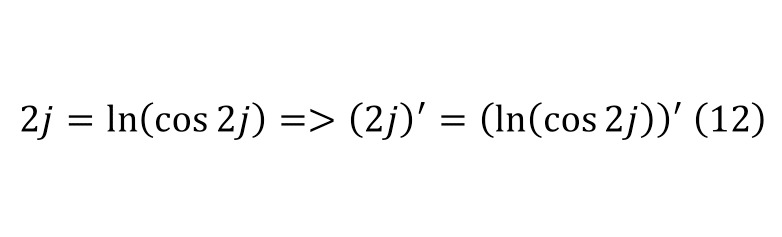
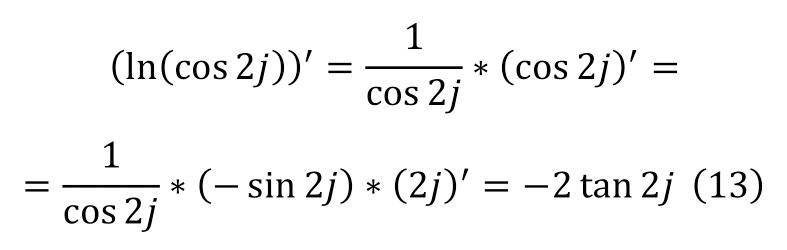
When the differentiation is made, it is enough to make elementary transformations, we get the trigonometric form of the special case (14).

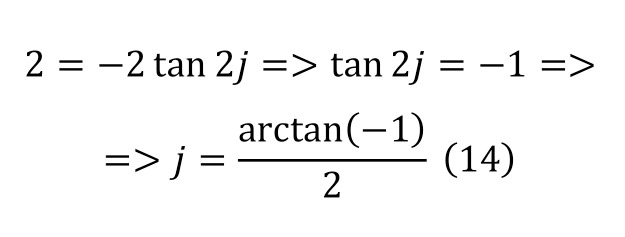
Now, when the general form for the doubly differentiated case is obtained, it is necessary to return to the primordial ones, because this is the identity, resulting in the following equalities (15—16).

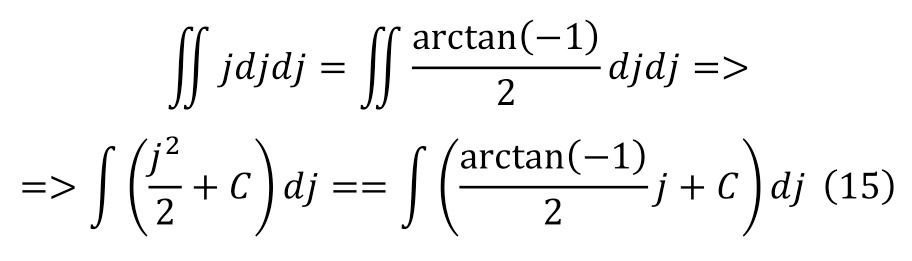
And indeed, this value is close to the most potential value, so this expression can be considered the second kind of writing of the exponential unit. Now, it is possible to proceed to the solution of the Euler equation for the general form of the intentional numbers, having carried out the first substitution and the usual replacement operations at stage (17) and (18) at the beginning.

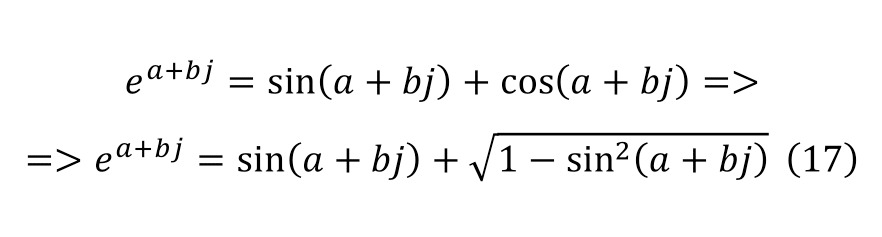
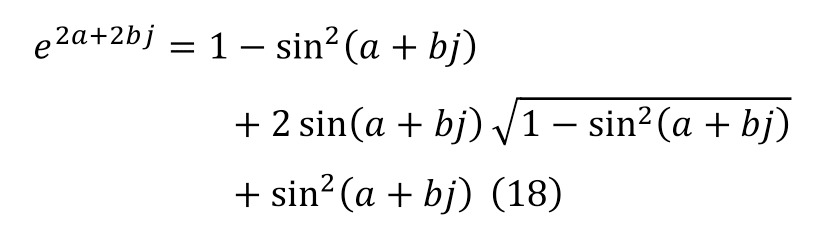
When the necessary transformations come to an end, and other actions no longer take place, it is also sufficient to differentiate both parts of equality as a valid identity (19).

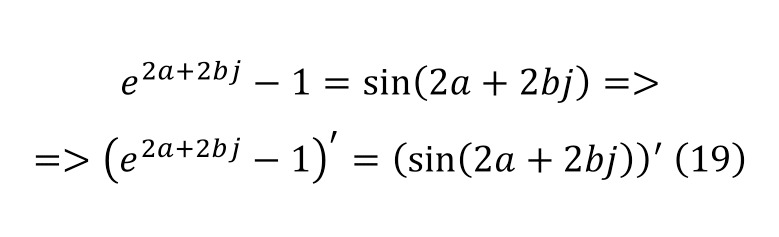
Differentiating the first part of the equality, we can come to the result in (20), and for the second part, the calculations will continue throughout (21).

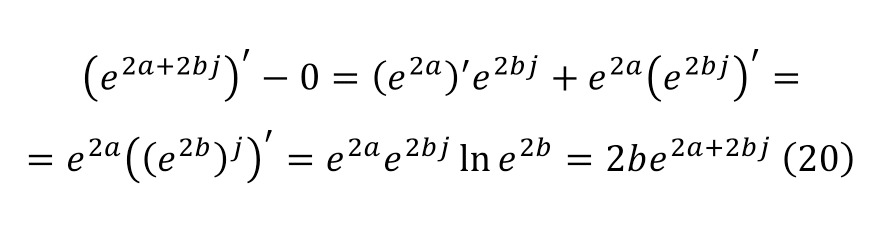
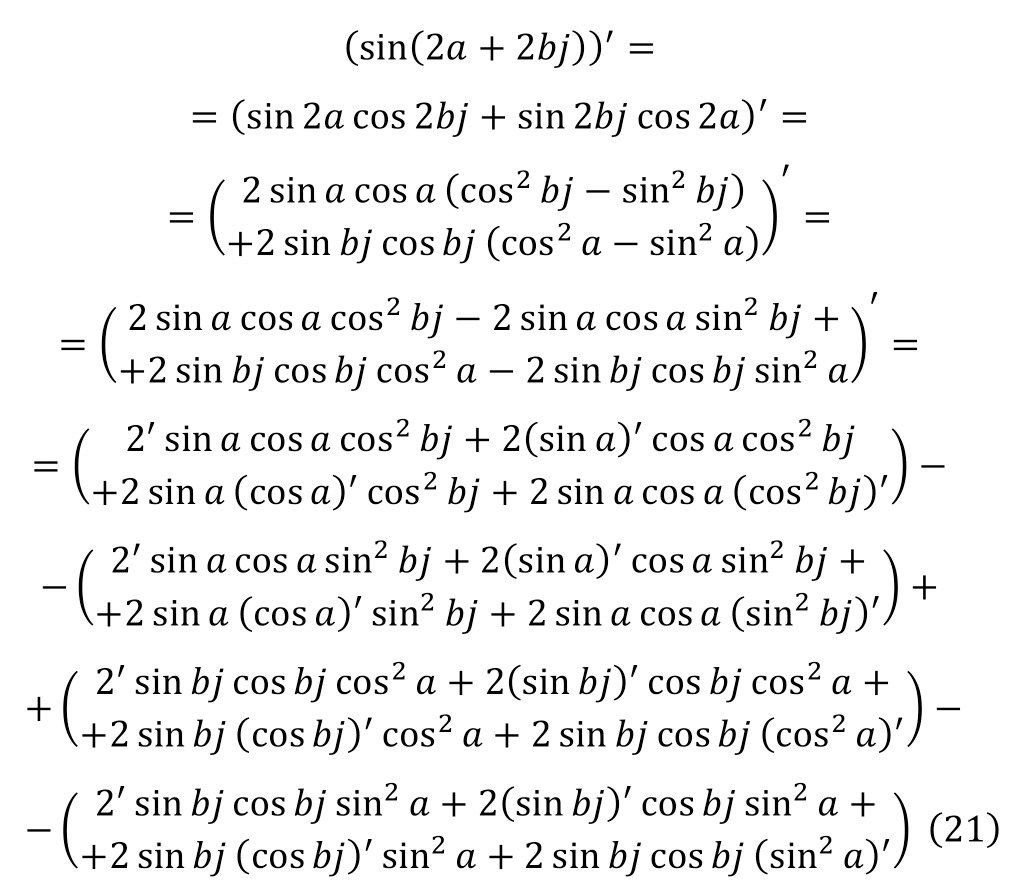
Then, applying (22—25), one can come to the form (26).

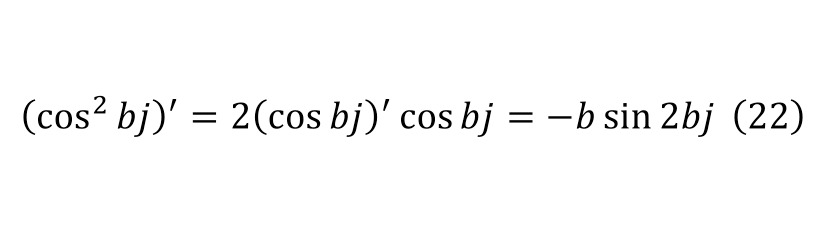
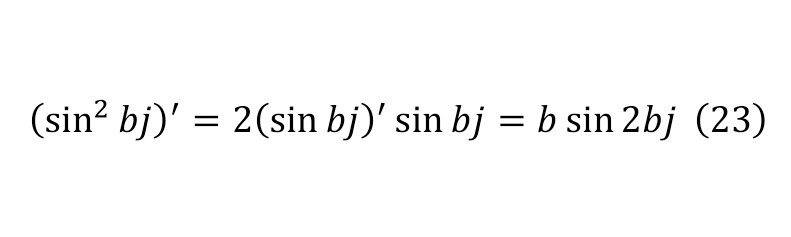
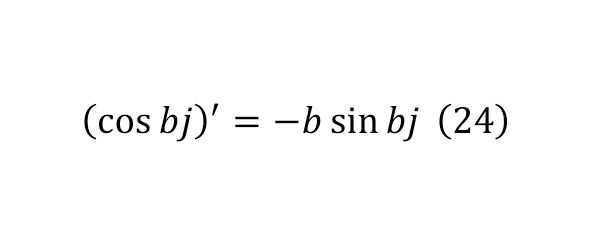
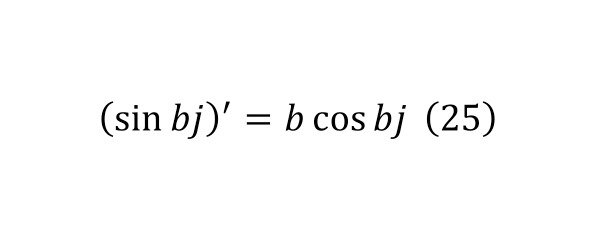
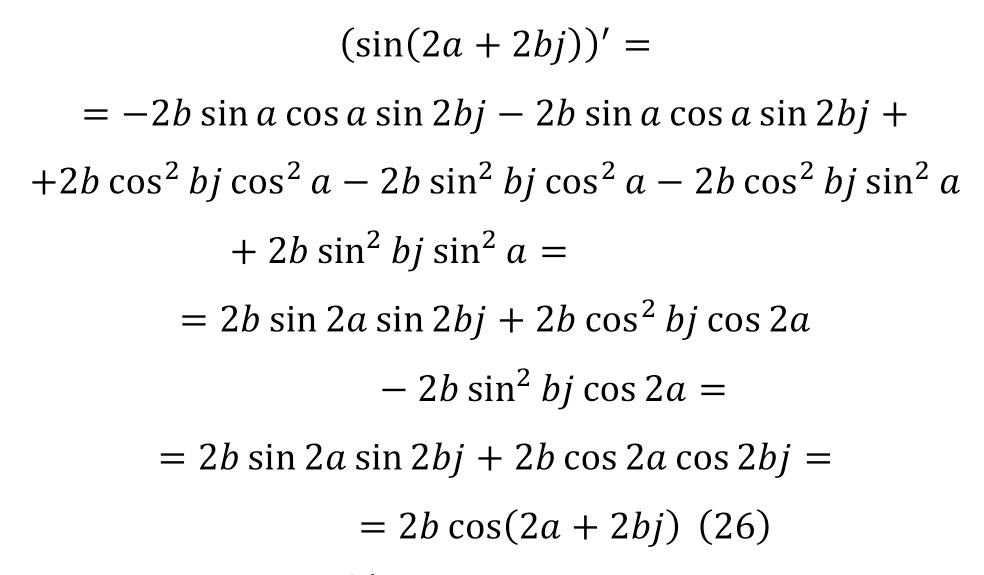
As a result, it is enough to equalize both results in (20) and (26), since these are two parts of the identity, and then get (27) with the necessary simplification, and already in (28) with additional simplification and differentiation as an identity.

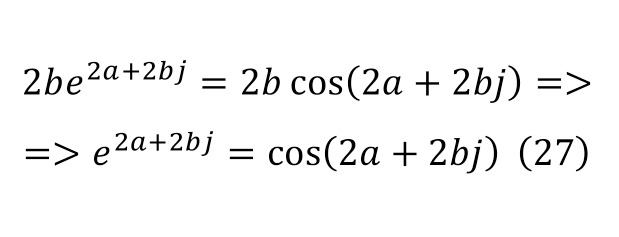
Бесплатный фрагмент закончился.

Купите книгу, чтобы продолжить чтение.