Бесплатный фрагмент - 400 математических графиков

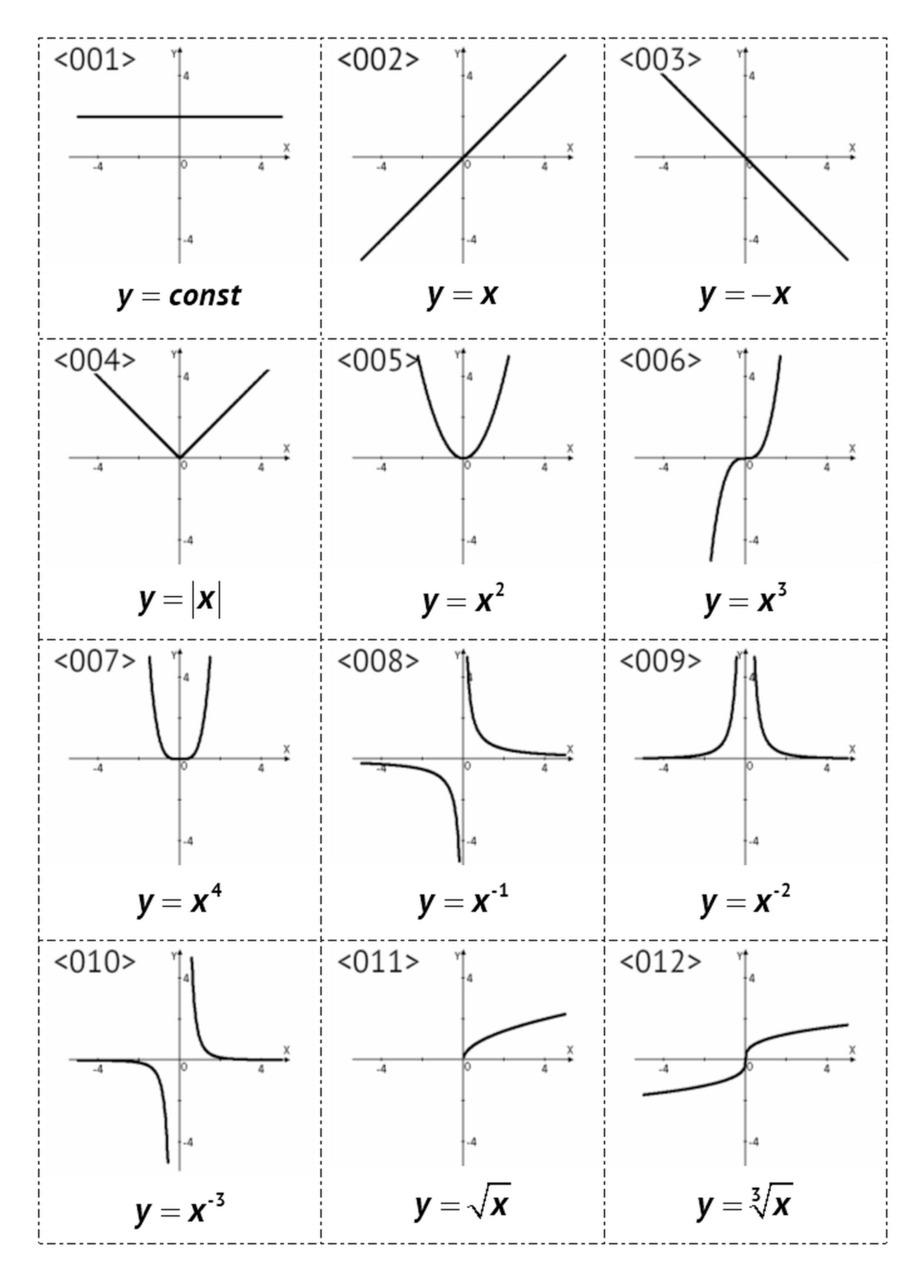
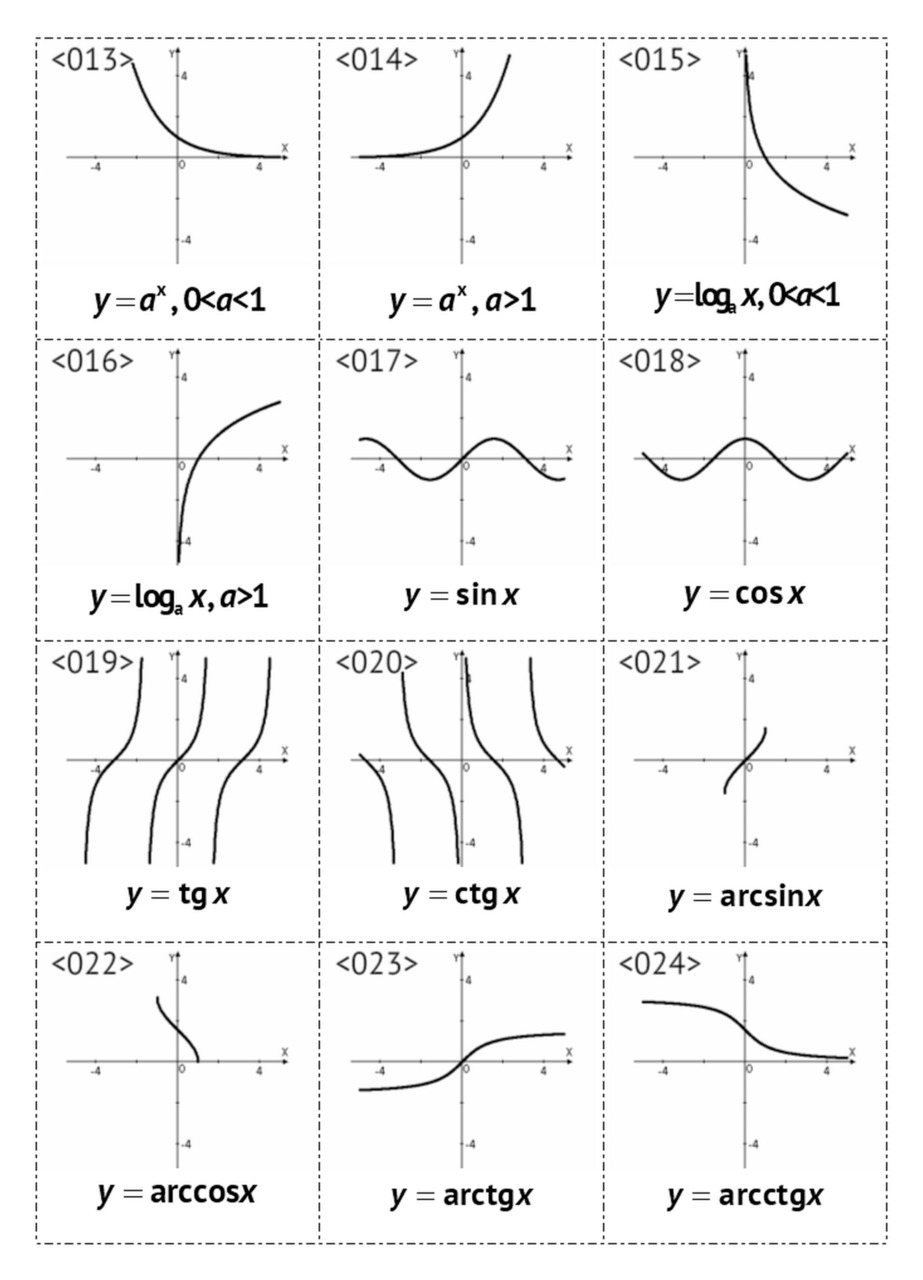
§1. Графики основных элементарных функций, <001> — <024>

В данном параграфе рассмотрены основные элементарные функции следующего вида:

— степенные y=xr,

— показательные y=ax,

— логарифмические logax,

— тригонометрические: sinx, cosx, tgx, ctgx,

— обратные тригонометрические: arcsinx, arccosx, arctgx, arcctgx.

Всего приведено 24 примера графиков.

Здесь и далее (до §8) используется

явный способ задания функций

в прямоугольной системе координат.

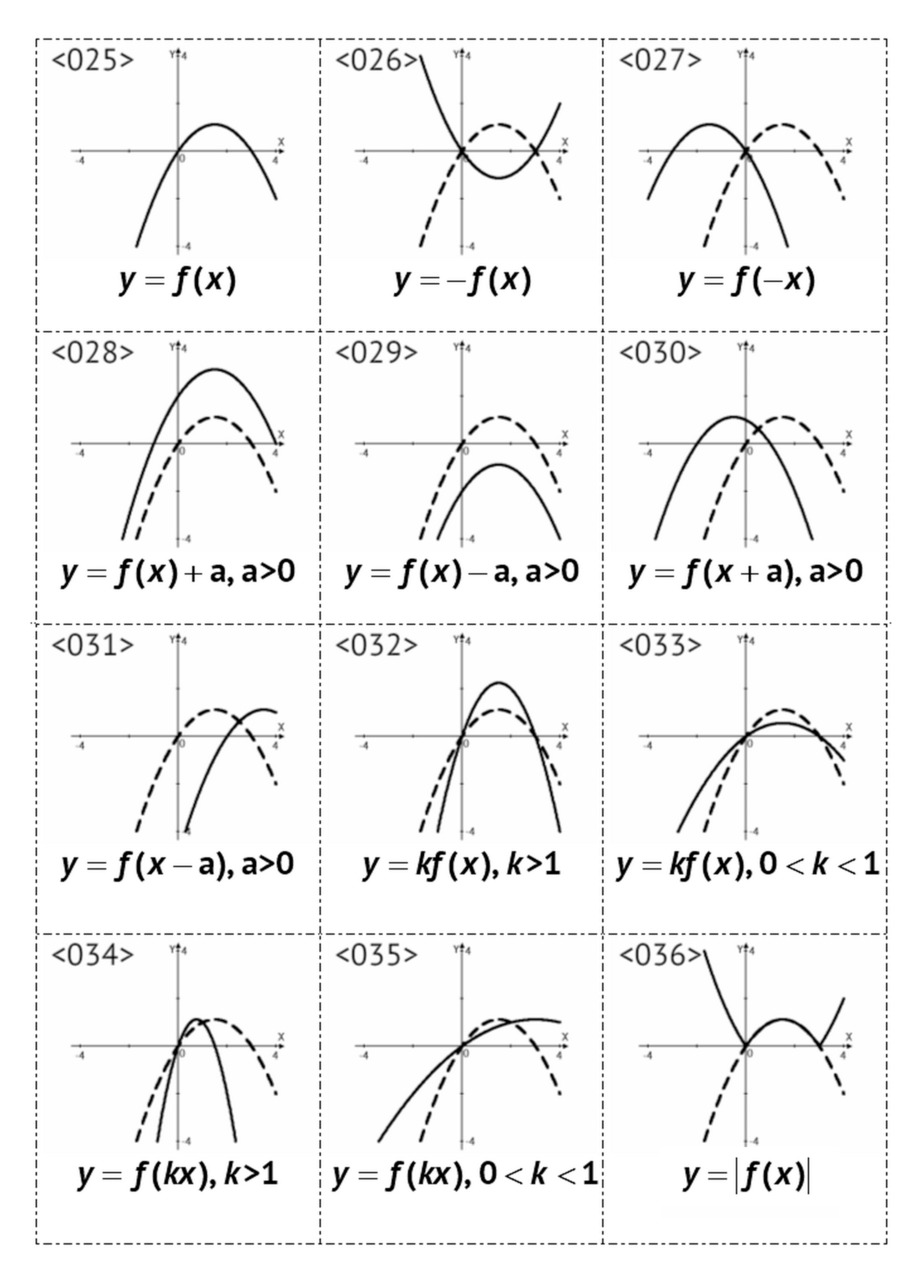
§2. Преобразования графиков, <025> — <048>

В данном параграфе рассмотрены преобразования графиков следующих типов:

— параллельный перенос: y=f (x+a), y=f (x) +a;

— растяжение и сжатие: y=f (kx), y=kf (x);

— симметричное отражение: y=f (-x), y=-f (x);

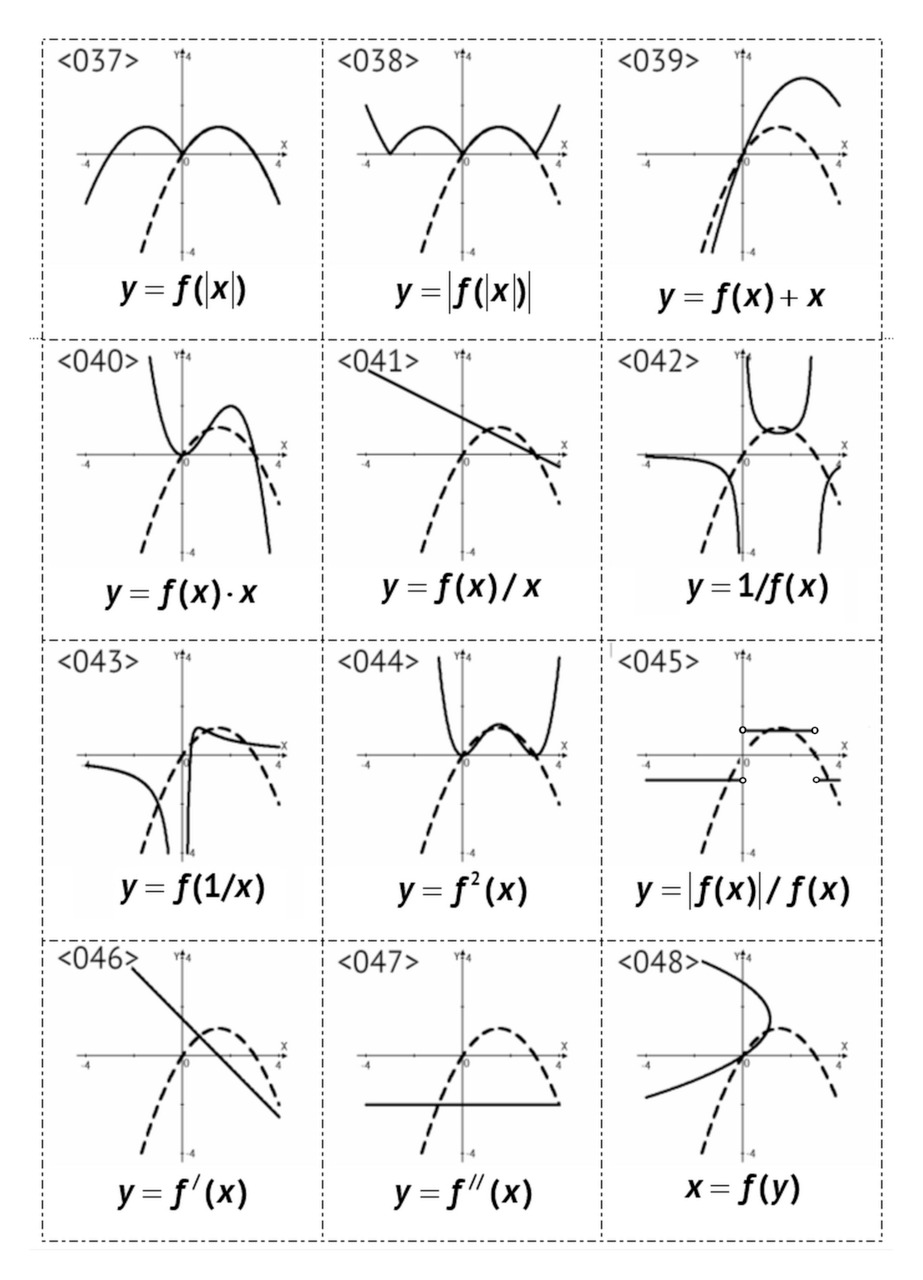
— инверсия: y=1/f (x), y=f (1/x);

— сложение y=f (x) +g (x);

— умножение y=f (x) g (x);

— деление y=f (x) /g (x);

— суперпозиция y=f (g (x)).

Всего приведено 24 примера преобразований.

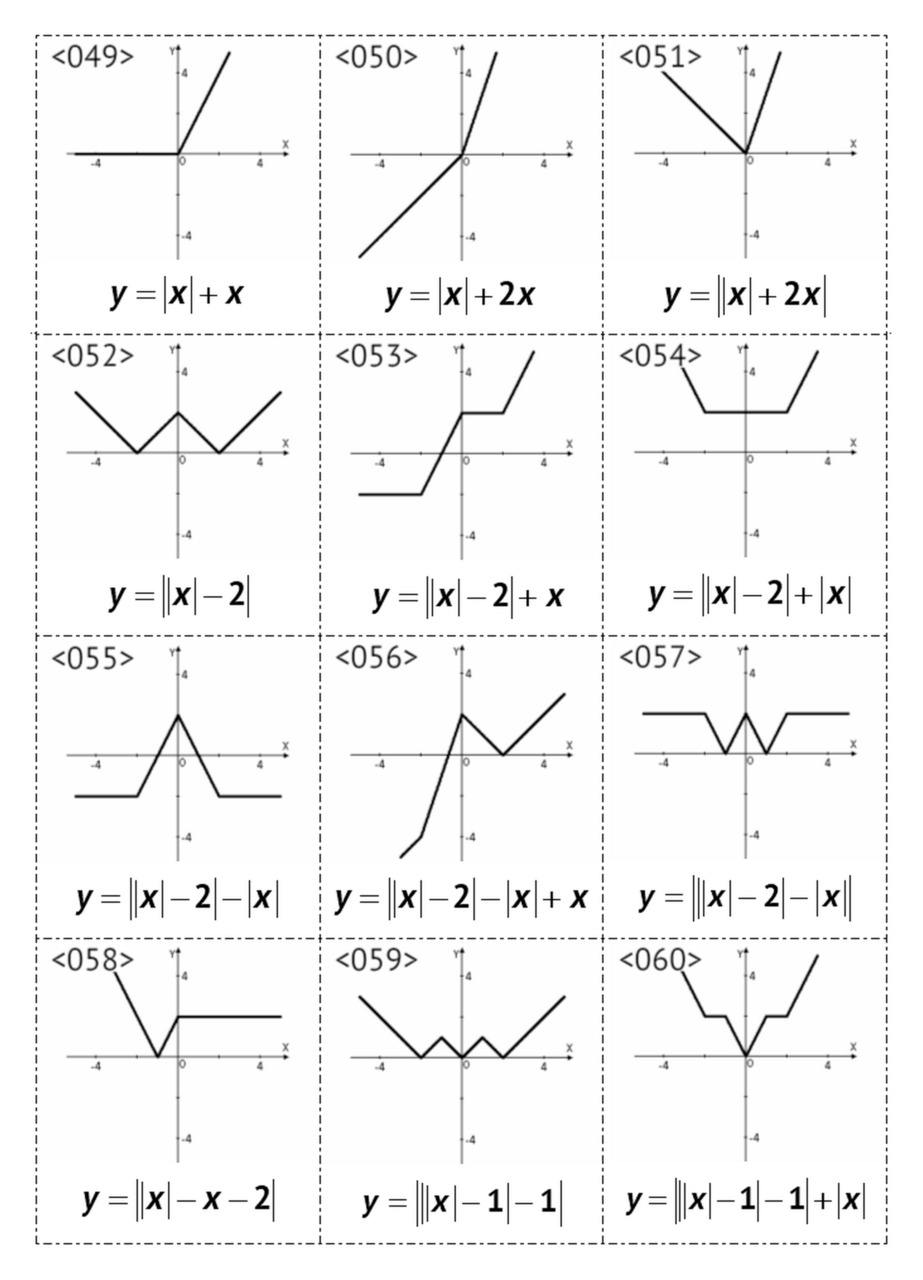
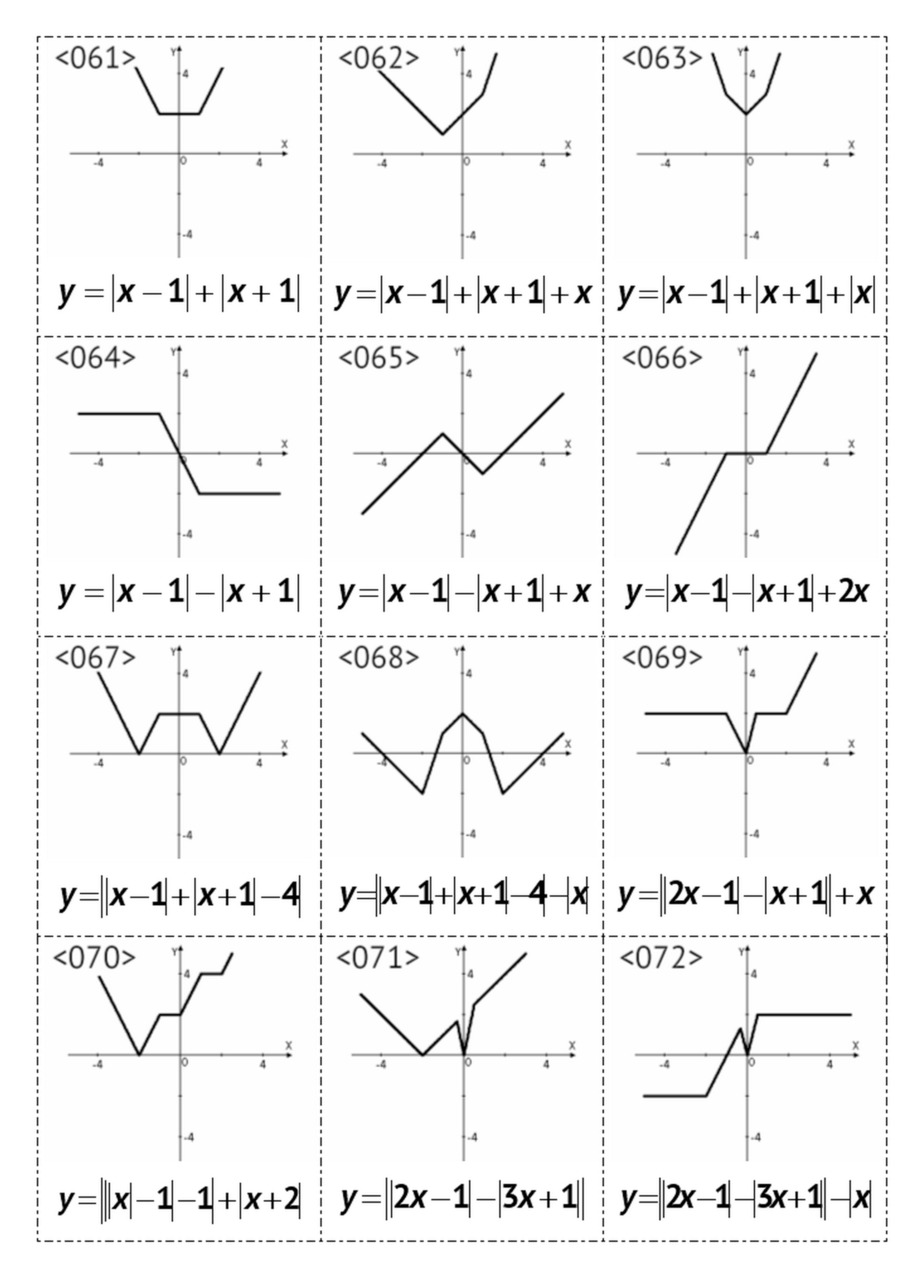
§3. Графики линейных функций, <049> — <072>

В данном параграфе рассмотрены линейные и кусочно-линейные графики функций, содержащих знак модуля.

Линейные функции и графики находят широкое применение для точного и приближенного моделирования явлений. Их применяют при решении задач:

— аппроксимации,

— интерполяции,

— экстраполяции,

— оптимизации.

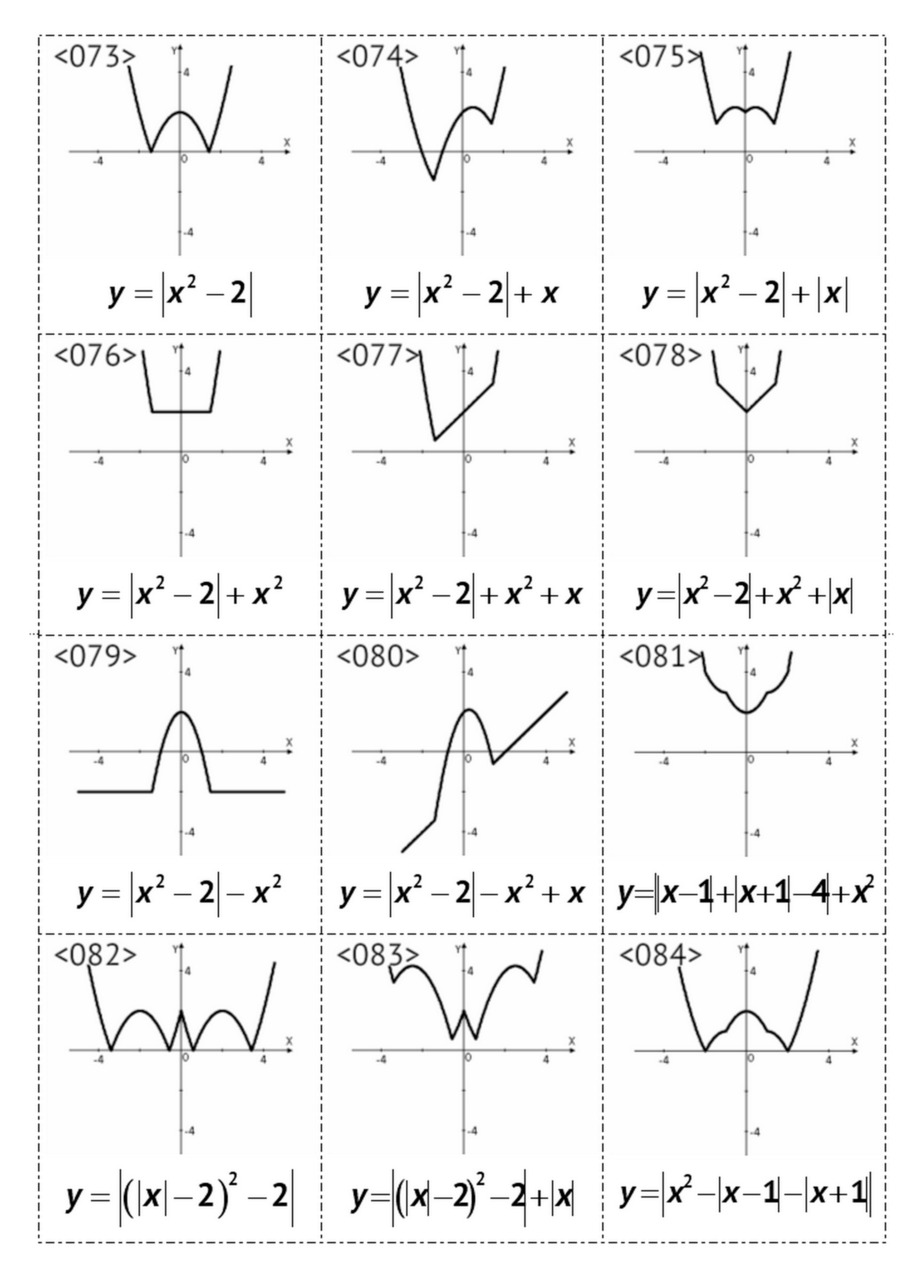
§4. Графики многочленов различных степеней, <073> — <096>

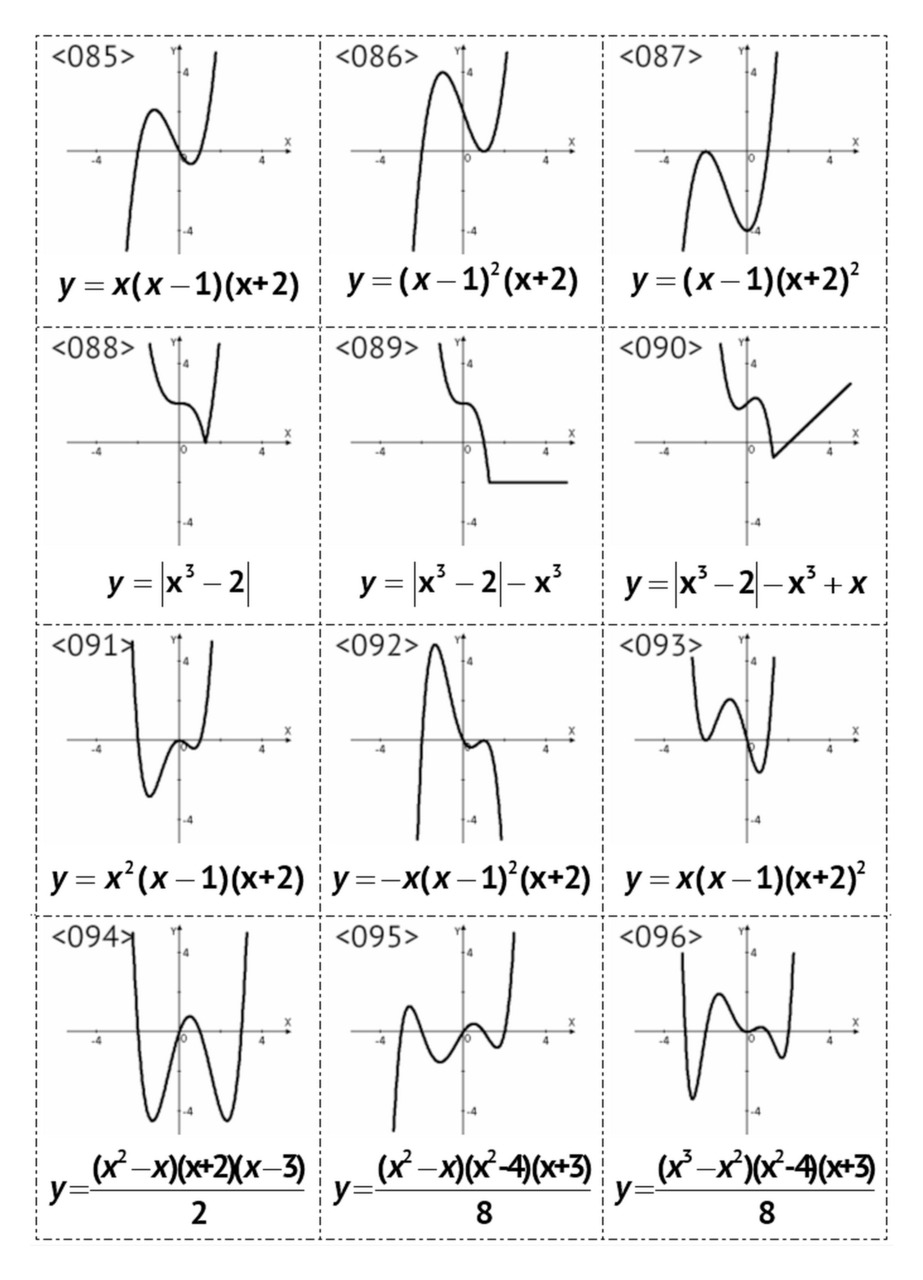
В данном параграфе рассмотрены графики многочленов 2-й, 3-й, 4-й, 5-й и 6-й степени.

В общем виде многочлен n-й степени от одной переменной может быть задан формулой

y=Pn (x) = a0xn+a1xn-1+a2xn-2+ … +an-1x+an.

Известно, что многочлен может иметь не более n действительных корней. Если многочлен имеет m действительных корней xi кратности mk, то он может быть представлен в виде разложения на множители:

y=Pn (x) =a0 (x-x1) m1 … (x-xm) mk (x2+px+q) l1 … (x2+rx+s) lr,

где квадратичные множители не имеют действительных корней. В такой форме можно увидеть точки пересечении графика с осью OX и примерный эскиз графика в окрестностях этих точек.

Например, многочлен 5- й степени на графике <095> имеет 5 различных (простых) корней. Многочлен 6- й степени на графике <096> имеет 4 простых корня и один корень кратности 2.

§5. Графики дробно-рациональных функций, <097> — <120>

В данном параграфе рассмотрены графики дробно-рациональных функций вида y= Pn (x) /Qm (x), где Pn (x) и Qm (x) — многочлены:

y=Pn (x) =a0xn+a1xn-1+a2xn-2+,.. +an-1x+an,

y= Qm (x) =b0xm+b1xm-1+b2xm-2+ … +bm-1x+bm.

Различают правильные дроби (когда n <m) и неправильные дроби (когда n больше или равно m). При некоторых условиях дроби могут быть преобразованы к более простому виду. Это позволяет в ряде случаев увидеть предполагаемый эскиз графика.

Например, фyнкция на графике <105> может быть записана в двух видах: y= (x3+1) /x2=x+1/ x2. Первая запись дает корни числителя и знаменателя. Вторая запись показывает, что функция получена путем сложении более простых фyнкций.