Бесплатный фрагмент - План семейного обучения

Проект обучения «Сохраним в детях любовь» (фрагмент из книги «Любовь сильнее страха»)

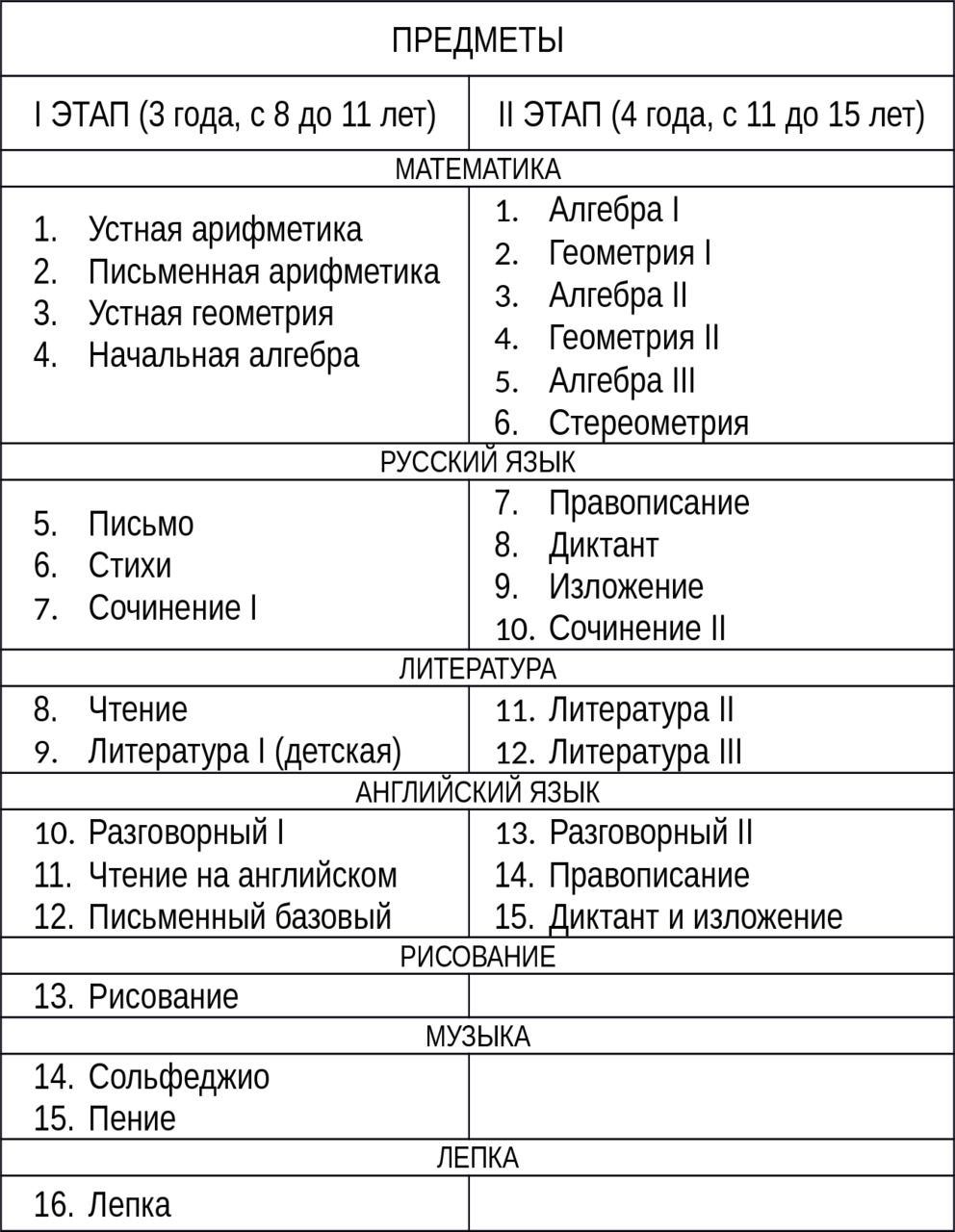
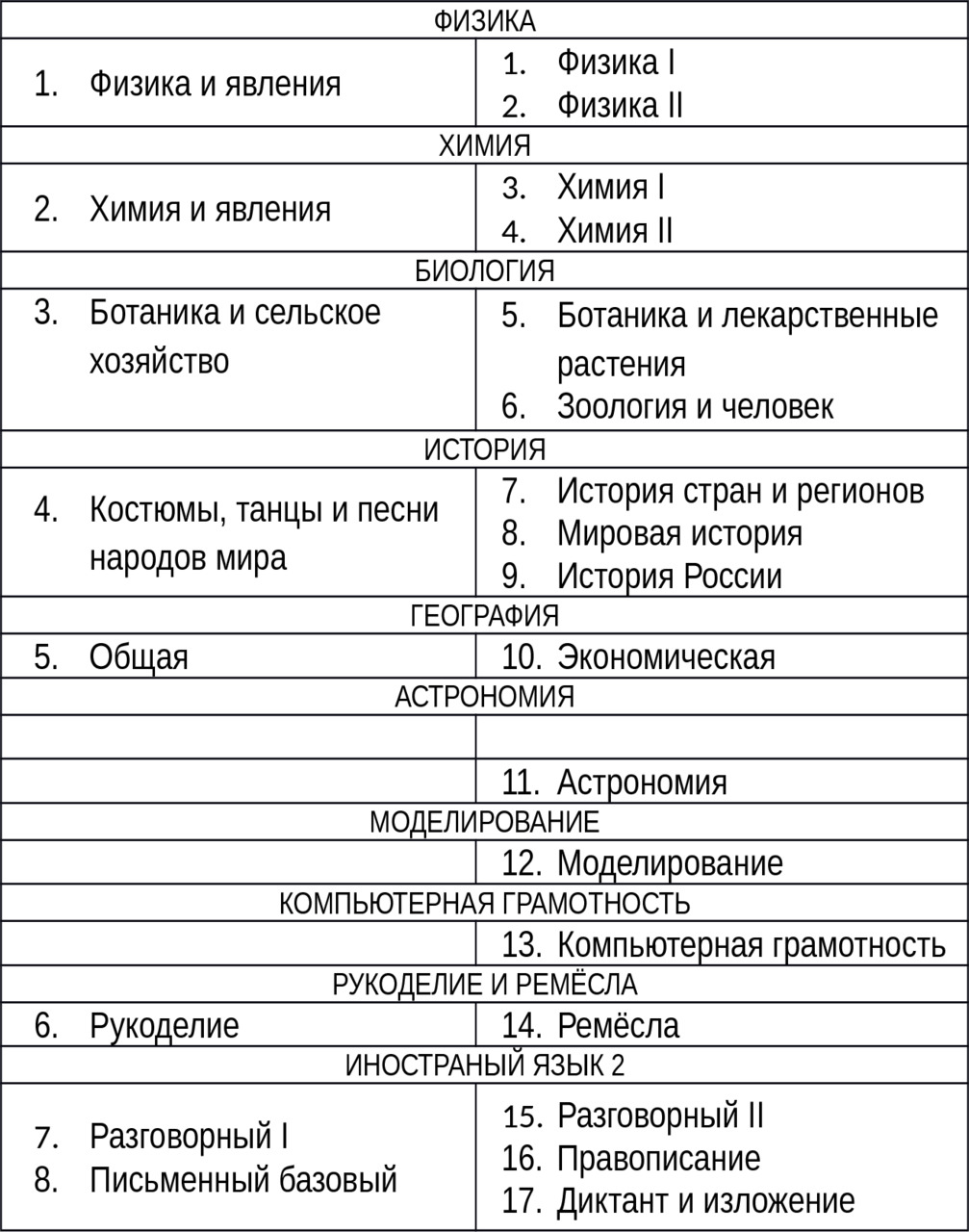
Проект обучения «Сохраним в детях любовь» включает все вышеуказанные принципы гармоничного школьного образования, включая: дать, а не взять, заинтересовать, а не запугать. Никаких оценок и осуждения, а также опросов и контрольных работ. Где ошибка — там совместное размышление и исправление. Программа основана на возрастных, психологических и физических особенностях для наилучшего освоения знаний и навыков. Позитив, любовь и доброта. По окончании школы — выпускной итоговый концерт, на котором ученики представят свои изобретения и достижения (совместные или личные), доставят радость себе и окружающим.

Существуют наборы с экспериментами по физике и химии для детей разного возраста, к ним приложено руководство, схемы, объяснения, формулы. Существуют информационные ресурсы по химии, физике, биологии и географии, другим предметам с опытами, картам, выкладками, где наглядно вместе с ребёнком можно сначала ознакомиться, а потом законспектировать и зарисовать полученные сведения.

Обучение детей — прекрасная возможность творчески восполнить собственные пробелы. Вы не сильны в решении задач? Есть задачники с подробными ответами. Главное — заинтересовать ребёнка, рассказать о связи теории с практикой на конкретных примерах, обучить базовым приёмам, обучаться совместно с ребёнком.

Подготовка по предметам

Единая методика подготовки по предметам является одним из основных элементов грамотного обучения детей. Чистота и порядок на рабочем месте, аккуратное оформление выполняемых работ делают обучение наглядным и понятным. Во время обучения нужно размещать перед глазами справочные материалы.

Для домашнего обучения нужно распечатать или изготовить самостоятельно памятку о правилах оформления задач по математике, физике и химии, оформлении сочинений и составлении таблиц.

Математика

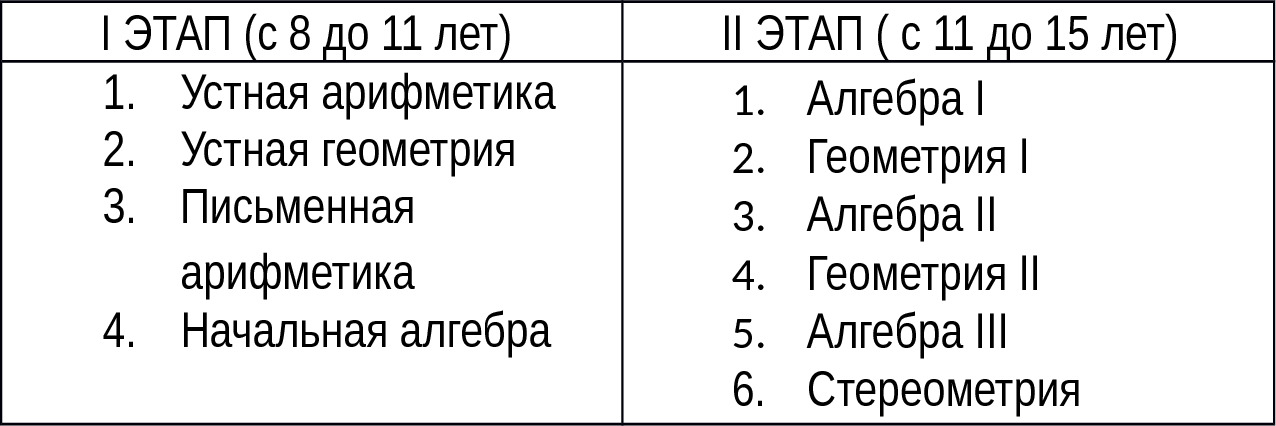
Основы математики ребёнок усваивает ещё с рождения. Ботинки малы, ботинки велики — сравнение по величине. Один носок, одна шапка — качественно разные предметы. Один носок белый, другой жёлтый — разное качество одинаковых предметов. Сначала еда, потом прогулка — понятие времени, идти быстрее — скорости, придётся идти долго — для ребёнка это понятие расстояния. Взять три конфеты, себе, маме и папе, — первый счёт. Подобрать ключ для замка, сложить новую фигуру из песка, из конструктора — начальная стереометрия. Более того, ребёнок прислушивается к словам взрослых в быту, в поездках, в магазине, играет со старшими детьми в более сложные игры, посредством этого осваивая и математику.

Рисование пальцами, карандашами, первые попытки письма на поздравительных открытках, изготовление аппликаций, поделок из бумаги, пластилина, природных материалов, бисероплетение и другие виды рукоделия — это не только тренировка мелкой моторики, развитие умственных способностей, но и основа для будущего изучения различных предметов, в том числе математики.

Как объяснить ребёнку применение математики на практике? Математика учит, как быстро сосчитать парами и тройками, сколько птиц сидит на дереве (пример), или считать десятками во время игры в прятки (пример). Математика помогает аккуратно разрезать торт на определённое количество кусков, когда торт один, а людей много (нарисовать пример). Математика позволяет просчитать путь кометы или расположение звезды (пример), построить дом, чтобы он был устойчивым и тёплым, (пример) или сделать автомобиль, чтобы он был удобным и хорошо ездил (пример). Откуда взять примеры? Подумать самим (детям ведь нужно понять суть, а не выкладки) или прочитать в книге, в интернете.

Математику легче изучать сначала устно, а потом письменно. В процессе устного изучения хорошо заодно потренировать руку в написании цифр и математических знаков. Для наглядности нужна таблица умножения, таблица квадратов двузначных чисел, сравнительная таблица графиков линейных функций и периодических, стандартные математические формулы. Таблица умножения есть на оборотной стороне тетрадей в клетку, а всё остальное можно изготовить вместе в процессе обучения ребёнка на твёрдой бумаге или купить. Если во время выполнения заданий эти материалы будут находиться перед глазами, то лучше усвоятся.

Устная арифметика

Нужна наглядная таблица умножения, две тетради и ручки для домашних заданий (домашнее задание будет в письменном виде для закрепления результата и формирования навыков письма, оформления работ в математике).

1 занятие. Первое и самое простое это для ребёнка, на самом деле, это таблица умножения. С неё лучше и начинать изучение арифметики. Дети её запоминают также хорошо, как и стихи. При изучении таблицы умножения попутно на пальцах (на счётах, на палочках) легко объяснить не только правила умножения, но и сложения.

Ребёнок сразу запоминает и все цифры, числа, ему наглядно видно, что от перемены мест слагаемых и множителей сумма не меняется. Кстати, наглядность и представление полной картины это один из основных принципов успеха в изучении любого предмета. Есть мыслительное пространство для сравнения и ассоциаций. Поэтому таблицу умножения изучают целиком, живо и весело. Дети это воспринимают как игру.

Например, дважды два — четыре, дважды три — шесть. Почему? Потому что две палочки плюс две палочки будет четыре. А две плюс две и ещё плюс две будет шесть. Нужно зарисовать оба этих примера в палочках на доске, а под каждым из них записать сумму, называя каждый знак вслух: 2+2=4 и 2+2+2=6.

Как часто нужно делать такие выкладки? Пару раз за занятие, ребёнку для начала нужно просто понять принцип образования таблицы умножения и запомнить её.

Прочитывать примеры для детей в таблице умножения лучше последовательно, так проще запомнить. На второй раз делать паузы для самостоятельного ответа детей. Всю ли таблицу умножения освоить сразу? Для ребёнка легче сначала запомнить одну половину, а потом другую.

Какое лучше дать домашнее задание ребёнку? На память записать первую часть таблицы умножения. Те ответы, которые он не помнит — оставить пропущенными. Для выполнения этого задания в конце первого занятия следует совместно с детьми потренироваться в записи цифр и вместе оформить начало домашнего задания в тетради (дата и наименование работы).

2 занятие. Устроить игру со второй частью таблицы умножения. Дополнительно можно показать сложение на более сложных примерах, например, пятью три и шестью два, показать пример рационального счёта: шестью два это по шесть два раза, а шесть это пять плюс один. Значит, шестью два это пять плюс один и ещё пять плюс один. Пять плюс пять будет десять (это же пять на два), а один плюс один будет два (это же один на два), а десять плюс два будет двенадцать. Всё это нужно нарисовать кружочками или палочками, снизу подкрепить математическими выкладками, а начинать с вопроса к детям — а как посчитать, сколько будет шестью два?

На втором занятии нужно собрать тетради для проверки, а в других тетрадях попросить детей записать на память вторую часть таблицы умножения (для этого опять совместно оформить тетрадь).

3 занятие. Совместно проработать ошибки из первого домашнего задания, закрепив в памяти первую часть таблицы умножения. Каждый неправильный или пропущенный пример стоит разобрать с точки зрения рационального счёта, как было указано выше.

Следует предложить детям по цепочке рассказать на память таблицу умножения (её первую часть), подсматривая в неё при необходимости. Также стоит ещё раз объяснить правила написания цифр.

В качестве домашнего задания предложить детям самостоятельно нарисовать и расписать по одному примеру в качестве рационального счёта из первых двух столбцов таблицы умножения.

4 занятие. Провести аналогично третьему, только со второй частью таблицы умножения, разобрать ошибки второй части домашнего задания. Усвоив принцип формирования таблицы умножения (детям важно почувствовать, что удобней просто запомнить значения, чем каждый раз складывать), им будет проще запомнить более громоздкую вторую часть. Кто-то справится с этим сразу, а кто-то постепенно.

Домашнее задание — разобрать ещё по одному примеру из первых двух столбцов. Причём, предложить сделать это иначе, даже при повторении примера, (например, семь это не только пять и два, но три и четыре). Так дети плавно перейдут к теме рационального счёта, сначала наглядно (на палочках), а потом в уме.

5 занятие. Устно разобрать ошибки после третьего урока и учиться рациональному счёту. Кстати, приучать детей считать на пальцах, по единичке, означает отучать их от заложенного природой объёмного зрения: ребёнку свойственного сразу видеть два, три или пять предметов, а девять разделять на две или три группы. Для этого можно использовать счётные палочки или скатать шарики из бумаги или фольги.

Сначала нужно каждому ребёнку дать по 10 палочек и попросить разделить их на две части. Каждый вариант записать в числовом виде на доске (2+8=10). Затем попросить разделить на три части, тоже записать. Затем пусть один ученик отдаст одну палочку (10—1=9), следующий две и так далее.

Для домашней работы нужно предложить детям представить любое число в виде суммы чисел и в виде разности: 5=1+4 и 5=6—1. Опять оформить вместе с учениками начало домашней работы. Кстати, во время исправления домашнего задания на уроке каждый ребёнок должен делать это самостоятельно во время разбора, а учителю следует только пометить ошибку и помочь оформить работу над ошибками. Так дети ещё и учатся письму.

6 занятие. Разобрать домашнее задание четвёртого урока по рациональному счёту, исправить ошибки. А затем совместно с детьми потренироваться в последовательном устном счёте, фиксируя примеры на доске: 1+1=2,1+2=3 и так далее до 21 (чтобы десять и круглые числа не были психологическим рубежом). Потом в обратную сторону: 21−1=20 и так далее, заканчивать нужно на минусе: 21−21=0, 21−22= –1 (чтобы и нулевое значение не было психологическим рубежом).

Более того, третьим этапом нужно дать ребёнку основу минусового счёта: 1−1=0, 1−2=−1 и так далее до −9, можно напомнить детям про уличный термометр зимой. А ещё нужно показать отрицательный счёт, начиная с другой цифры, например: 3−4=−1, 3−5=−2.

В качестве домашнего задания нужно определить каждому ребёнку разное число палочек и попросить их поровну разделить на двоих, потом на троих, потом на четверых, зарисовать результат. Это подготовит детей к вопросам о делении и дробях. Нужно заранее предупредить, если останутся лишние палочки, то пометить их отдельно.

7 занятие. После работы над ошибками пятого занятия нужно освоить счёт пятёрками и десятками до ста. Поможет игра «холодно — горячо», чтобы водящий считал одним из указанных способов по выбору, помогать ему при необходимости. Домашнее задание — расписать через запятую ход до заданного каждому числа по пять или по десять, например: число 25. Расписываем ход по пять шагов: 5, 10, 15, 20,25.

8 занятие. Посвящёно разбору домашнего задания шестого урока, когда на примере палочек дети увидели деление на целые части, деление с остатком. Нужно акцентировать на этом внимание и спросить у детей, что можно сделать с остатком (отдать одному, отдать ещё кому-то, поделить поровну — можно на примере фрукта). А затем показать, как записывать целое с дробной частью (половиной, третью, четвертью, до десятой части).

Домашнее задание — разделить целое число палочек на пятерых, на шестерых, на восьмерых, зарисовать результат, а остатки тоже разделить поровну (записав в виде дробей). Это подготовит детей к делению в уме.

9 занятие. После разбора домашних заданий счёта пятёрками и десятками нужно тренироваться в счёте на более крупных числах, используя при необходимости технику рационального сложения и вычитания. Например, 72+9, до 80 не хватает 8, остаётся ещё 1, значит всего 81, а потом другие варианты. Данное занятие лучше проводить исключительно в устном формате.

Для домашнего задания уже можно предложить детям придумать несколько вариантов счёта для персонально заданного примера, а потом разложить полученное число на составные части. Всё законспектировать. Примеры можно придумывать по ходу занятия.

10 занятие. После разбора домашнего задания по делению на палочках нужно показать ученикам, что деление это обратное действие умножению: 2х4=8, 8÷4=2. Дети уже это осознали на практике и легко запомнят примеры. Настало время делить в уме, используя, по-прежнему, таблицу умножения. Для домашнего задания будет полезно предложить детям преобразовать по одному столбцу таблицы умножения из умножения в деление: 5х7=35, а 35÷7=5 или 35÷5=7 (любой вариант, по выбору ученика).

11 занятие. После работы над ошибками домашнего задания девятого урока нужно освоить устное сложение и вычитание двузначных чисел: например, 22+48 или 25—17. Это предпоследнее занятие первой половины цикла, поэтому домашнее задание не требуется.

12 занятие. После разбора домашнего задания десятого урока остаётся время для деления в уме на более сложных примерах из второй половины таблицы умножения.

13 — 24 занятие. Вторая часть цикла посвящена устному решению задач по арифметике, включая задачи на сообразительность. Это позволит не только повторить материал, но и восполнить его для тех, кто пропустил занятия.

Так проходит первый цикл математики — устная арифметика. Дети осваивают основные математические операции, таблицу умножения, глубоко прорабатывают каждую тему. Кроме того, осваивают базовые навыки самостоятельной работы, её оформления, привыкают анализировать свои ошибки и исправлять их. Обучаются правильному написанию цифр и знаков. Устраняется основная проблема трудностей дальнейшего изучения ребёнком математики — пробелы в знаниях и понимании.

Устная геометрия

Для устной геометрии нужна плотная бумага (или альбом) и цветные карандаши, простой карандаш и линейка-треугольник с прямым углом, циркуль и транспортир, ножницы для рукоделия и скотч, одна тетрадь в клетку. Можно предложить детям сделать конструктор из бумаги. А для этого нужно научиться рисовать различные геометрические фигуры и изучить их свойства.

1 занятие. На первом занятии нужно предложить детям сделать заготовки для конструктора. Для этого нужно нарисовать различные геометрические фигуры на плотной бумаге и вырезать их. Но в конструкторе детали должны быть соразмерными. Поэтому все фигуры должны иметь какой-то общий параметр (диаметр, длину стороны или диагональ). Обозначим этот параметр для удобства и наглядности 4 сантиметра — на линейке от 0 до 4 или от 2 до 5, или от 4 в каждую сторону по 2 сантиметра.

Круг. Попробуем нарисовать круг простым карандашом от руки. Получился ли круг ровным? Равен ли его диаметр (расстояние между самыми удалёнными точками окружности) 4 см? Как нарисовать круг ровно? Для этого визуально находим центр нашего круга, ставим точку и проводим через неё линию. От центра точки в каждую сторону отмечаем на линии по 2 см, ставим ещё две точки. Потом с помощью транспортира от центра этой линии отмечаем ещё 2 точки на 90˚, соединяем их прямой линией через центр и опять откладываем по 2 см с каждой стороны.

Получилось 4 равных отрезка под прямым углом (прямым углом называется угол 90˚) или два равных отрезка, пересекающихся под прямым углом в точке, которая делит каждый отрезок пополам. Это будущий радиус и диаметр окружности. Теперь через 4 наружных конца отрезков нужно провести выгнутую кнаружи линию. Из четырёх секторов (показать, что такое сектор) получился более ровный круг.

Как нарисовать круг ещё ровнее? Также построить 4 перпендикулярных отрезка из одной точки по 2 см с помощью транспортира или линейки с прямым углом. А теперь в каждом из четырёх секторов провести ещё по три отрезка от центра длиной 2 см (радиус будущего круга). В итоге точек, через которые нужно провести окружность, стало больше. Круг стал ещё ровнее.

Можно нарисовать круг с заданным радиусом с помощью циркуля — пусть дети сами подумают, как это сделать. После этого нужно вырезать из бумаги три полученных круга (сначала вырезать часть бумаги с каждым рисунком, а потом из неё уже сам круг — так получится аккуратней).

Как нарисовать круг с помощью шаблона? Обвести. А что получится, если вырезать круг, сложить его пополам и разрезать по линии сгиба? Полукруг. А как нарисовать полукруг или четверть круга? (Пусть дети поразмыслят самостоятельно). В итоге получилось три круга, несколько полукругов и секторов.

Овал. Как нарисовать овал? Рисуем от руки. Получается не очень ровно. Теперь рисуем горизонтальный отрезок длиной 4 см, отмечаем середину, от неё вниз и вверх сторону откладываем перпендикулярно ещё по 1 отрезку длиной 1 см. Теперь аккуратно соединяем полученные точки. Вырезаем из бумаги оба овала.

Треугольник. У треугольника три угла. Как нарисовать остроугольный треугольник? Каждый его угол должен быть меньше прямого. Рисуем основание (нижнюю грань треугольника) длиной 4 см. Отмечаем с одной стороны угол, обращённый к линии, 70˚, а с другой 60˚.

В месте пересечений линии образует третья вершина треугольника, надо померить угол — он будет равен 50˚. Какая сумма получилась у углов? 180˚. Всегда ли так бывает? Это смогут выяснить дети на следующем курсе геометрии.

А что такое тупоугольный треугольник? Один угол у него больше прямого. Рисуем отрезок длиной привычной длины 4 см, от него откладываем кнаружи любой угол больше 90˚, проводим линию длиной, например, 3 см, соединяем вершины.

А что такое прямоугольный треугольник? Тот, у которого один угол 90˚. Рисуем отрезок длиной 4 см. К нему под прямым углом отрезок другой длины, соединяем вершины.

Как нарисовать равнобедренный остроугольный треугольник, чтобы боковые стороны были равны? Рисуем один отрезок длиной 4 см, под углом к нему меньше 90˚ второй отрезок длиной 4 см. Соединяем вершины. Аналогично рисуем равнобедренный тупоугольный и прямоугольный треугольник.

Как нарисовать равносторонний треугольник, у которого все стороны равны? Пробуем нарисовать треугольник с тремя сторонами ровно по 4 см. Угол между двумя сторонами оказывается мал или велик.

Попробуем нарисовать несколько разных углов от 0 до 90 с ходом в 10˚, каждый раз будем замерять третью сторону. (В итоге окажется, что нужный угол, как и оба других, будет равен 60˚, а сумма углов опять 180˚.)

А как построить равнобедренный треугольник, чтобы у него не боковые стороны были заданной величины, а третья сторона (основание)? Рисуем отрезок длиной 4 см, отмечаем на нём середину, от середины откладываем вверх перпендикулярную линию. Любая точка этой линии одинаково удалена от каждого конца отрезка — получается равнобедренный треугольник.

Сначала одним цветом рисуем равнобедренный прямоугольный треугольник — для этого линейку-треугольник размещаем вершиной с прямым углом на перпендикуляре так, чтобы обе соседние грани проходили через концы первого отрезка (основания). Теперь другим цветом отмечаем на перпендикуляре точку ниже, соединяем с концами отрезка.

Какой треугольник получился, какой угол в его вершине? Тупой, равнобедренный тупоугольный. А потом ещё одним цветом точку выше. Какой треугольник? Равнобедренный остроугольный. Теперь самостоятельно рисуем эти три треугольника. Вырезаем все треугольники из бумаги.

Квадрат. Берём вырезанную фигуру равнобедренного прямоугольного треугольника и обводим её карандашом. Затем зеркально отражаем треугольник относительно основания рисунка и опять обводим карандашом. Какая фигура получилась? Квадрат.

У квадрата 4 одинаковые стороны, а все углы прямые. Какой длины получилась диагональ квадрата? 4 см, как основание треугольника. А сторона? Меньше 3 см. Как построить квадрат для нашего конструктора со стороной 4 см с помощью нашего треугольника?

Основание треугольника как раз равно 4 см. Измерим транспортиром два других угла треугольника. Они оба равны 45˚. Значит, если два таких угла расположить рядом, получится прямой угол. Обводим треугольник, отражаем его через катет (боковую сторону), обводим второй раз, повторяем манипуляцию ещё два раза.

Получился квадрат с заданной стороной 4 см, для этого потребовалось четыре равнобедренных прямоугольных треугольника с гипотенузой 4 см. Значит, диагонали в квадрате пересекаются под прямым углом.

Как проще нарисовать квадрат с заданной стороной, используя карандаш и линейку с прямым углом? Рисуем отрезок 4 см, перпендикулярно к нему с каждой стороны ещё два отрезка по 4 см, соединяем свободные концы — квадрат готов. Вырезаем все полученные квадраты.

Прямоугольник. Берём прямоугольный треугольник с разными катетами, обводим, перемещаем, не переворачивая, к обратной стороне гипотенузы, ещё раз обводим — прямоугольник готов. У него равны не все (как у квадрата), а только противоположные стороны, все углы также прямые.

Как начертить прямоугольник с помощью квадрата? Обвести квадрат с трёх сторон, сместить в открытую сторону и дорисовать свободную часть. Также можно начертить прямоугольник с помощью отражённого квадрата от одной из его сторон.

Как проще начертить прямоугольник с помощью карандаша, линейки и прямого угла? Аналогично квадрату, только с разными соседними сторонами.

Теперь нужно вырезать все четыре прямоугольника. У первого прямоугольника нужно дорисовать вторую диагональ между противоположными углами и разрезать по этим линиям. Что получилось? Прямоугольник состоит из четырёх равнобедренных треугольников — двух остроугольных, а двух тупоугольных.

Ромб. Ромб это сжатый со стороны противоположных углов квадрат. Обводим равнобедренный остроугольный треугольник, отражаем зеркально от основания, ещё раз обводим — получился ромб. Также поступаем с равнобедренным тупоугольным треугольником — получается ромб. У ромба все стороны равны, противоположные углы равны. Если провести в ромбе диагонали, получится четыре одинаковых прямоугольных треугольника.

Как просто нарисовать ромб с заданной стороной? Построить равнобедренный треугольник с боковыми сторонами по 4 см, провести линию вниз через вершину перпендикулярно основанию (получится два одинаковых прямоугольных треугольника), отложить на ней второй раз расстояние от точки пересечения до вершины с помощью циркуля. Соединить полученную точку с боковыми вершинами ромба.

Параллелограмм. Ромб, квадрат и прямоугольник являются разновидностью параллелограмма. У параллелограмма 4 стороны, противоположные стороны параллельны. Как нарисовать обычный параллелограмм? По принципу прямоугольника. Обвести разносторонний тупоугольный треугольник, затем, не переворачивая фигуру, переместить её к противоположной стороне основания и обвести ещё раз. Стороны будут параллельны, почему? Дети сами смогут это доказать во время второго цикла геометрии.

Как проще построить параллелограмм? Построить прямоугольник. Продлить одну из его сторон, затем вместо боковых перпендикулярных к основаниям сторон проложить другие отрезки. Чтобы они были параллельны, их угол наклона к каждой стороне должен быть одинаковым (отмерить с помощью транспортира).

Трапеция. Расположим горизонтально прямоугольник и обведём его, затем произвольно отмерим на верхней стороне отрезок 4 см (не по центру), его конец слева соединим отрезком с левым нижним углом, а справа — с правым. Получилась трапеция, трапеция — это тоже четырёхугольник, только с двумя параллельными сторонами.

Как ещё можно нарисовать трапецию, например равнобокую? Обводим равнобедренный треугольник, расположив основанием вниз, затем отмеряем с помощью циркуля одинаковые отрезки от нижних углов на каждой стороне, соединяем прямой. Она будет параллельная основанию.

А ёще бывает прямоугольная трапеция. Обводим прямоугольник, продлеваем в одну сторону его нижнюю границу, а затем соединяем конец отрезка с ближайшим углом на верхней стороне.

Теперь вырезаем все оставшиеся фигуры. Домашнее задание — составить в альбоме композицию из деталей и раскрасить их соответствующим образом, при необходимости изготовить дополнительные детали другого размера. Например, из кругов разного размера сложить снеговика, из треугольников — ёлку, из овалов — облака.