Бесплатный фрагмент - Геометрия-7

Предисловие

Уважаемые дети и родители. Я продолжаю. Надеюсь предыдущий учебник «Геометрия. Начало» вам понравился. Если что-то было (или будет) непонятно, пишите мне по адресу evgeni123456@endex.ru, и я постараюсь ответить на все ваши вопросы.

Привожу для справок и повторения систему аксиом, которая принята в этом учебнике.

АКСИОМЫ ПЛАНИМЕТРИИ

Пусть задано множество (точек) и система его частей или, иначе говоря, подмножеств (прямых). Выполнены следующие утверждения.

Аксиомы принадлежности

А1. Существует хотя бы одна прямая и каждой прямой принадлежит хотя бы одна точка.

А2. Через две различные точки проходит одна и только одна прямая.

Аксиомы расстояния

А3. Любым двум точкам А и В соответствует неотрицательное действительное число |АВ|, которое называется расстоянием от точки А до точки B. Расстояние |АВ| равно 0 тогда и только тогда, когда точки А и B совпадают.

А4. |AB|=|BA|. То есть расстояние от А до В равно расстоянию от В до А.

А5. Треугольник со сторонами a, b и с существует тогда и только тогда, когда выполняются все три неравенства: a+b> c, a+c> b, b+c> a.

Аксиомы порядка

А6. Три точки принадлежат одной прямой тогда и только тогда, когда одна из них лежит между двумя другими.

А7. Любая точка прямой разбивает ее на два не пересекающихся луча. Любой луч содержит хотя бы одну точку.

А8. Любая прямая разбивает плоскость на две полуплоскости. Любая полуплоскость содержит хотя бы одну точку.

А9. Все точки отрезка, концы которого принадлежат полуплоскости, принадлежат этой полуплоскости. Все точки отрезка, концы которого принадлежат лучу, принадлежат этому лучу.

Аксиомы измерения

А10. Пусть задано неотрицательное число. На любом луче найдется одна и только одна точка, расстояние которой от начала луча равно этому числу. Отрезки равны тогда и только тогда, когда имеют равные длины.

А11. От любого луча в любую примыкающую к нему полуплоск ость можно отложить угол любой градусной меры от 0о до 180о. Такой угол только один. Стороны угла в 180о составляют прямую. Углы равны тогда и только тогда, когда имеют равные меры.

А12. Если луч ОМ проходит между сторонами ОА и ОВ какого-либо <AOB и разбивает его на два угла <AOM и <BOM, то сумма мер этих двух углов равна исходному углу.

Аксиома подвижности

А13. Задана полуплоскость (А, ВС) с примыкающим к ней лучом ВС, и другая полуплоскость (E, FG) с лучом FG. Существует одно и только одно перемещениие всей плоскости на себя, отображающее луч ВС на луч FG, а полуплоскость (A, BC) на полуплоскость (Е, FG).

Аксиома параллельных

А14. Пусть задана прямая (например, АВ). Через любую точку плоскости, не лежащую на данной прямой, проходит не более одной прямой, параллельной к данной прямой АВ.

Квант 1
Свойства равнобедренного треугольника

Фигура, свойства которой мы будем изучать дальше, — равнобедренный треугольник. Треугольником называется фигура, состоящая из трех не лежащих на одной прямой точек и трех попарно соединяющих их отрезков. Точки называются вершинами треугольника, а отрезки — сторонами. Треугольник обозначается специальным значком и тремя буквами: ∆ ABC.

Согласно аксиоме A5, сумма длин двух любых сторон треугольника строго больше длины его третьей стороны. Эта аксиома называется неравенством треугольника. Она показывает, каким не может быть треугольник. Например, не существует треугольника со сторонами 2, 2 и 5, т.к. 2+2 <5. Ее смысл также в том, что путь по прямой — самый короткий.

Длины сторон треугольника (Рис. 1) могут быть различными — такой треугольник будем называть разносторонним (1). Они могут быть все равные по длине, и треугольник будет называться равносторонним (2) или правильным. Но есть еще третий тип: у треугольника могут быть равны хотя бы две стороны, и он будет называться равнобедренным (3).

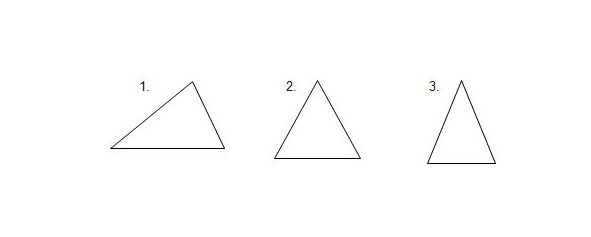
Первая большая задача, которую мы перед собой поставим — изучение свойств равнобедренного треугольника.

С математической точки зрения, равносторонний треугольник — тоже равнобедренный, потому что для того, чтобы треугольник был равнобедренным, нужно равенство хотя бы двух его сторон. Нужно четко понимать словосочетание «хотя бы». Продумайте следующую фразу: «Если на столе три конфеты, то хотя бы две конфеты на столе есть». Если это понятно — все в порядке.

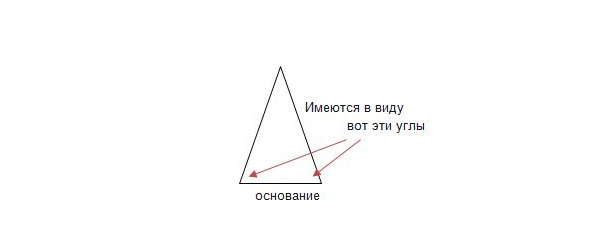
В равнобедренном треугольнике равные стороны называются боковыми. Третья сторона, которая может быть и не равной боковым, называется основанием. Такие названия связаны с тем, что древние греки изображали равнобедренные треугольники на чертежах, как правило, вершиной кверху, и тогда он был похож на человечка или на египетскую пирамиду.

Докажем теорему.

Т2.1. В равнобедренном треугольнике углы при основании равны (Рис.2).

Для доказательства (Рис.3) наложим треугольник на него самого изнаночной стороной.

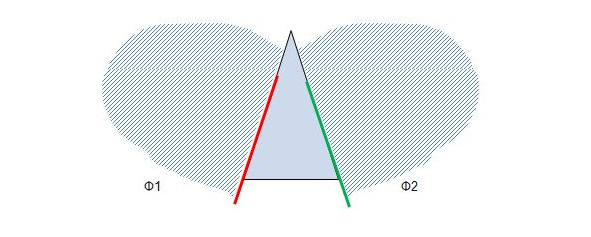
Мы совершим перемещение плоскости, такое, при котором флаг Ф1 с красным «держаком» перейдет во флаг Ф2 с зеленым «держаком». Уверен, у вас достаточно воображения, чтобы понять, что это означает просто переворачивание треугольника и наложение его на самого себя.

Тогда совпадут углы при вершине — ведь они равны (в перевернутом виде угол остается равным самому себе, следовательно, наложится сам на себя и совпадет).

Дальше совпадут боковые стороны, они равны, т.к. треугольник равнобедренный. То есть полностью треугольники совпадут. Наконец, углы при основании наложатся друг на друга и тоже совпадут. Значит они равны.

Теорема, о которой мы только что говорили, в обычных обозначениях записалась бы так. Дан равнобедренный ∆АВС, причем АВ=ВС. Утверждается, что <ВАС = <ВСА. После переворачивания получаем треугольник А1В1С1. Совмещаем В и В1, затем АВ и С1В1, ВС и В1A1… И треугольники совместятся. Это — хороший способ записи доказательства, но часто суть бывает легче усмотреть, используя не буквы, а стрелки. Если потребуется, вам будет легко записать то или иное доказательство так, как нужно на контрольной или на экзамене.

Верно и следующее утверждение.

Т2.2. Если у треугольника равны два угла, то он — равнобедренный. Доказательство такое же. Переворачиваем треугольник и накладываем сторону, к которой прилежат эти два угла саму на себя (она, естественно, совпадет сама с собой). То есть мы объявляем ее основанием. Другие две стороны пойдут по соответствующим сторонам (так как углы равны), и таким образом, получится совпадение.

Эта теорема — обратная к предыдущей (которая при этом называется прямой теоремой). Что такое «обратная теорема»? Если прямая теорема гласит: «Если А, то В» (если стороны равны, то равны и углы), то обратная будет: «Если В, то А» (у нас: если углы равны, то равны и стороны).

Еще небольшой экскурс в логику (в науку о правильном мышлении). Треугольник с разными углами НЕ может быть равнобедренным.

Почему?

Минута на размышление.

Потому что если бы он был равнобедренным, то углы при основании были бы равны, а у нас они НЕ равны. Такой тип доказательства, как мы знаем, называется «доказательством от противного» (хотя, в сущности, ничего противного в нем нет, совсем наоборот!)

Домашнее задание:

Решите следующие задачи на доказательство.

1) Дан треугольник, все стороны которого равны. Докажите, что равны все три его угла. 2) Дан треугольник, все три угла которого равны. Докажите, что равны все три его стороны. Такой треугольник называется равносторонним или правильным. 3) В треугольнике два угла разные. Докажите, что хотя бы две его стороны разные. 4) У треугольника все три стороны попарно разные. Докажите, что все три его угла попарно разные.

Квант 2
Медиана, биссектриса и высота равнобедренного треугольника

Итак, мы продолжаем изучение треугольников. Нам понадобятся следующие термины, мы их еще не определяли.

Медиана — отрезок, соединяющий вершину треугольника и середину противолежащей стороны (Рис.4).

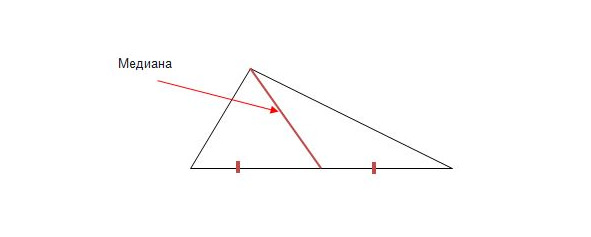
Черточки, которыми мы «маркируем» отрезки, означают, что отрезки равны. Биссектриса угла — луч, который делит угол пополам. Помните стишки? «Биссектриса — это такая крыса, которая бегает по углам и делит угол пополам». (Рис.5)

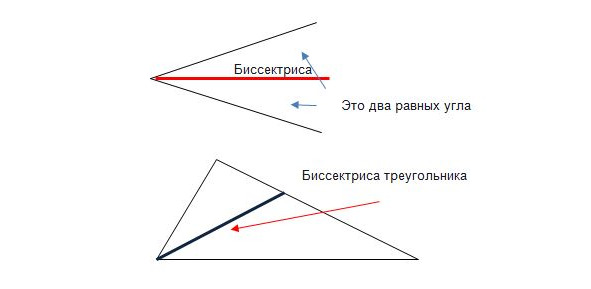
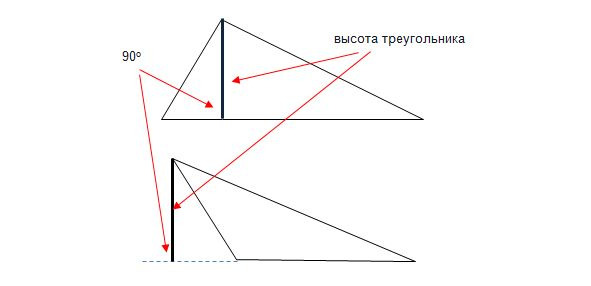
Биссектриса треугольника — часть биссектрисы угла треугольника, отрезок биссектрисы, соединяющий вершину и противолежащую сторону. Высота треугольника — отрезок перпендикуляра из вершины треугольника, соединяющий вершину и противолежащую сторону или ее продолжение. Рис.6

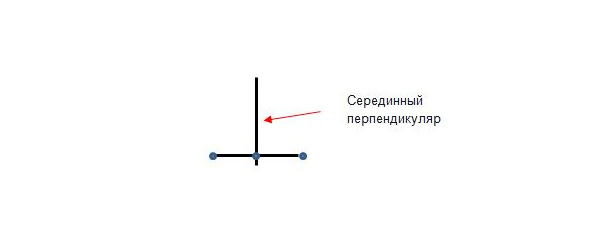
Серединный перпендикуляр — перпендикуляр, проведенный к середине отрезка и к прямой, которая этот отрезок содержит. Рис.7

Заметим, что при «перевороте» треугольника» (в предыдущем кванте) центральная точка основания наложится на себя, следовательно, углы биссектрисы при вершине наложатся друг на друга, то есть биссектриса и медиана совпадут. (Рис.8) Можно также увидеть, что два угла с вершиной в середине основания совпадут, то есть равны 180о/2=90о, значит совпадающие медиана и биссектриса совпадут также и с высотой треугольника из точки А (причем эта высота будет лежать на серединным перпендикуляре к основанию).